Economic Values and Resource Use

Abstract

Absolute decoupling of GDP growth from resource use implies that economic output can be increased without simultaneously increasing input. The essential meaning of this proposition is that the economic values that represent the GDP can be realized by increasing resource efficiency. Given that the GDP is first and foremost a measure of economic activity rather than welfare the possibility of absolute decoupling is theoretically limited. This paper demonstrates theoretically and empirically that economic values at the macroeconomic level are fundamentally determined by the use of production factors, primarily labor and physical capital. Technical innovations or efficiency gains increasing utility without raising the costs of production do not add to the GDP unless they stimulate investments in physical capital. Hence the neoclassical notion of productivity is only found to be relevant as a microeconomic concept. In practice, GDP growth is mostly explained by capital accumulation and a key question is whether or not capital accumulation can be decoupled from the use of materials and energy. This will determine the possibility of decoupling of GDP growth from resource use and environmental impact. Alternative measures of progress focusing on welfare rather than economic activity are more likely to achieve absolute decoupling.

From no source do so many errors, and so much difference of opinion in that science proceed, as from the vague ideas which are attached to the word value.

—David Ricardo

1. Introduction

Environmental researchers and commentators are increasingly concerned that growing levels of production and consumption push global ecosystems towards critical limits [1,2]. Vivid discussions about limits to economic growth have been ongoing at least since the early 1970s [3,4,5]. Yet, economic growth is a fundamental policy objective in nearly all modern societies. In 2015, world leaders adopted 17 Sustainable Development Goals suggested by the United Nations Development Programme (UNDP), including Goal 8: Decent work and economic growth [6]. In this context, sustainable economic growth means stimulating economic activity while not harming the environment. In a similar vein, the Organisation for Economic Co-operation and Development (OECD) among others has launched strategies for “green growth” [7].

There is an ongoing discussion about the possibility of decoupling of growth in economic output from resource use and environmental impacts [8,9,10]. In connection with the Sustainable Development Goals, the UNDP calls for improving global resource efficiency in consumption and production in order to decouple economic growth from environmental degradation. In most contexts, economic growth is explicitly or implicitly understood as an increasing gross domestic product (GDP). According to UNEP, decoupling is “indicated when economic output (GDP) is increasing relative to resource input” [9]. The essential meaning of this proposition is that the economic values that represent the GDP can be realized by increasing resource efficiency. A critical question is thus if and how the value of the GDP can be objectively determined.

Classical economics explain values by the use of production factors with special focus on labor inputs. Neoclassical economics, on the other hand, generally focus on prices as determined by the laws of supply and demand. Value theories in general are typically concerned with the nature of exchange values (prices) of various assets, goods and services but insufficient attention has been given to the laws determining the aggregated value of all the goods and services produced within an economic system. However, without a clear concept behind the processes of value formation at the macro level it is unproductive to try to resolve questions regarding the prospects for decoupling of GDP growth from resource consumption or environmental degradation.

Empirically, there is evidence of relative decoupling of growth from carbon emissions in some northern European and North American economies [11]. In regard to material resource use, UNEP finds that the total mass of material extraction grew by a factor of about eight during the 20th century while the GDP rose 23-fold. Annual extraction of construction materials grew by a factor of 34 [9]. None of these studies suggests absolute decoupling of growth from resource use. Bithas and Kalimeris [10] find that the potential for decoupling of economic growth from energy use is less promising on a per capita basis. The energy required to produce materials such as steel, aluminum, plastics and cement can be reduced through better technology and recycling, but ultimately there are fundamental thermodynamic as well as practical constraints on the potential to improve the energy intensity of material production [12].

The vision set out by policy makers is typically to reduce the resource intensity of the GDP so that the GDP can grow indefinitely in a finite material world [9]. However, there is an inherent conflict in this proposition since resource efficiency tends to reduce prices and thus primarily reduce the realization of economic values and the GDP. In practice, efficiency gains are often offset by secondary effects, also known as rebound effects [13,14]. A theoretical understanding of the mechanisms behind value formation is needed to address the conceptual links between GDP growth and resource use.

The aim of this paper is to demonstrate, theoretically and empirically, that GDP growth is well explained by inputs of labor and physical capital which is consistent with classical economic theory. This puts a theoretical restriction on the possibility to decouple GDP growth from resource use, since both labor and capital are critical economic resources. A further question beyond the scope of this paper is whether or not capital accumulation can be decoupled from the use of materials and energy, which is a crucial matter for sustainability.

It is clear that total economic values as defined by environmental economists, composed of both use values and non-use values, cannot be ultimately determined. The value of the GDP and its components, on the other hand, may be directly investigated by using empirical data. This study makes use of official national statistics from several countries, where numbers are presented in constant prices. The purpose of transforming economic data into constant prices is to separate volume changes from price changes resulting from monetary inflation or deflation. Although there are inherent problems associated with the application of constant prices (which are further discussed in Section 2) they do define the real value of goods and services in contrast to the nominal value which is sensitive to the monetary currency. It should be pointed out that values of goods and services expressed in constant prices are by no means fixed over time. Due to the evolution of production processes the real values of goods and services do change irrespective of changes in the value of money. Since increasing efficiency in the use of production factors tends to reduce the measured value of output, there is sometimes an inverse relationship between productivity and value formation which may seem contradictory but which is highly relevant to the analysis of productivity at the aggregate level.

Contemporary economics are usually influenced by neoclassical theory where total factor productivity (or multi-factor productivity) is seen as the most important component of economic growth. Total factor productivity refers to the productive capability of an economy in relation to all factor inputs and should not be confused with labor productivity, which only relates the amount of output in relation to inputs of labor. Unless specified, productivity in this paper is used synonymously with total factor productivity. Evidently, increasing productivity would be one way to achieve decoupling between resource use and economic output. The notion of productivity contradicts the foundations of classical economics and an important objective of this paper is to theoretically explain why the assumptions of neoclassical economics regarding productivity are not applicable at the macroeconomic level.

In the next section, the classical and neoclassical value theories are presented and discussed in a macroeconomic context and it is argued that the microeconomic foundations of neoclassical economics do not allow any meaningful interpretation of macroeconomic values such as the GDP. In Section 3, official macroeconomic data from the OECD and other sources will be used to empirically test the accuracy of the classical value theory at the aggregated level. In Section 4, the use of neoclassical production functions and the finding that productivity plays a major role in realizing GDP growth is critically evaluated in light of the empirical findings of Section 3. The results are discussed in Section 5 and linked to the possibilities of decoupling of GDP growth from resource use and environmental impacts. Section 6 concludes the study.

2. Value Theories

Value theories seek to explain the functioning of the economy—including price formation of goods and services in real markets—and do not primarily concern values in a logical or moral sense. The classical value theory or the labor theory of value sees economic values as something intrinsic to the goods and services produced in the economy. According to the neoclassical value theory, on the other hand, values are formed by interactions between agents in the market economy. The word value itself is more linked to the classical context, while neoclassical economists tend to focus on market prices. As long as real prices are concerned, as opposed to nominal prices, there is no difference between the two terms in practice.

The labor theory of value was first introduced by Adam Smith, who claimed that the natural price or exchange value of a commodity is related to its cost of production, which is in turn derived from the quantities of labor embodied in the products. In The Principles of Political Economy and Taxation (1817), David Ricardo developed the labor theory of value into a logically coherent and consistent system. Included in commodity values are not only the direct labor inputs, but also labor accumulated in fixed and circulating capital, i.e., tools, buildings and intermediate goods used as inputs in the process of production.

The neoclassical value theory started to develop after William Stanley Jevons, Carl Menger and Léon Walras simultaneously introduced the concept of marginal utility in the 1870s. Assuming that the marginal utility of consumers was reflected in market demand, and that the allocation of production factors on the supply side was determined by the marginal utility obtained by the employment of land, labor and capital, Alfred Marshall [15] set out to construct supply and demand curves intersecting at the point where an equilibrium price could be found (Marshallian scissors). Marshall’s combination of utilities and costs for the determination of prices is usually referred to as the neoclassical theory of value and is accepted by most economists and widely applied in e.g., general equilibrium models.

In 1848 John Stuart Mill [16] was able to maintain that:

Happily, there is nothing in the laws of Value which remains for the present or any future writer to clear up; the theory of the subject is complete: the only difficulty is […] to solve […] perplexities which occur in applying it.

History soon proved him wrong and, while in our time the neoclassical theory is clearly dominant, there are still heterodox schools of thought advocating the classical theory of value. Several aspects of the neoclassical theory, including the problem of aggregation, were discussed in “the two Cambridges debate” of the 1950s and 1960s (see e.g., [17,18]). Emerging from Cambridge in England is the neo-Ricardian school of thought which is essentially a modern interpretation of the classical value theory presented by Piero Sraffa in Production of Commodities by Means of Commodities [19]. Also, Marxist economics are largely centered around the labor theory of value and specifically on the determination of surplus value, i.e., the extent to which profits are appropriated from the value created by labor.

2.1. The Classical Theory

Labor-time is an absolute and objective quantity that can be compared through time and space. Embodied labor-time has the advantage of being intrinsic to the objects of production and simultaneously being an absolute property that can be externally measured. It is therefore possible to test the labor theory of value against empirical data, as will be demonstrated in Section 3.

According to the classical theory, labor is the source of all economic values, and all values are proportional to the human labor-time embodied in the products. The logic rests on the premise that all production costs can be derived from labor inputs. Labor-time is also what consumers in general offer in exchange for commodities–provided that they derive their incomes from wage labor. In this sense, the value of a unit of production as well as the value of any aggregated amount of production can always be measured against labor-time as a standard of value—disregarding for the moment the fact that wages differ between different sorts of labor.

However, labor is not the only factor of production, nor is it the only source of income. Consumers therefore do not necessarily have to offer labor-time in exchange for goods and services if they derive incomes from some other source. Moreover, the value of production includes all costs of production and not only labor wages. If labor is the ultimate source of all values, other sources of income as well as other costs of production have to be related to labor-time in one way or another.

In addition to labor, capital is the most important production factor and source of income. In productive capital, the classical economists included all sorts of food, clothing, buildings, tools, machinery and raw materials that were directed to assist in production. Common to all these forms of capital is that they are the results of previous production, and may therefore be regarded as accumulated labor. The capital value is then the sum of capital and labor costs of capital production, where the primary capital costs can be derived from secondary costs of labor and capital and so on in a recursive procedure until the full value is translated into labor units.

In a modern vocabulary, real capital corresponds closely to that part of capital that may be denoted as ”fixed capital”, including buildings, tools, machinery and other fixed structures. In addition to fixed capital, the classical economists identified “circulating capital”, which corresponds to the more modern concept of intermediate goods, that is, goods used as inputs in the production of other goods.

According to modern standards, value added in national accounts is defined as the sum of labor costs and capital costs (including rents, dividends, profits, et cetera), whereas intermediate goods and services are excluded from value added in any given sector of production. Within that framework, the GDP is the sum of all value added in the economy, that is the total contribution to value formation by labor and capital. The value of capital in national accounts is typically estimated by the perpetual inventory method (PIM) or similar methods, in which the value (cost) of capital investments in a given year is added to the existing capital stock, while correcting for asset lifetimes and depreciation. For instance, this is the official methodology applied by the OECD in producing the data further explored in the next section of this paper [20].

A key point to stress at this stage is that the data assembling in official national accounts apply methods that correspond closely to the principles of the labor theory of value, where the value added to the economy is represented by the costs of production in the form of remunerations to labor and capital, and where the value of capital is likewise represented by the costs of previous investments derived from capital and labor costs.

In general, the value of production factors other than labor and capital can be derived from the labor and capital employed in bringing them to market. This means, for example, that raw materials have no value in themselves in their natural state, and that their natural price is determined by the cost of extraction, refining, transportation and so on. This is obviously not always true in the short term when scarcity of certain resources may raise their price. However, according to this theory, the link between resource use and value formation goes through the use of physical capital and labor.

The classical economists were well aware that market prices do not always correspond with the labor embodied in all commodities, but they maintained that market prices are constantly gravitating towards the natural price determined by the labor value. If market demand is not equal to supply at any point in time, the market price is affected, although this in turn serves to adjust the level of production until demand meets supply and the market price moves towards the natural price. Market imperfections resulting in some goods or services being overvalued while others are undervalued are compatible with the theory of deviations leveling out as long as the aggregated value is regulated by total inputs of labor-time. Changing ratios of exchange between different goods and services do not necessarily result in a change in the GDP.

2.2. The Neoclassical Theory

In the neoclassical theory, the classical principle that economic values are determined by production costs is replaced by the laws of supply and demand. This suggests relations between market prices and consumer utility which are not apparent in the labor theory of value. The theory also assumes direct relationships between market prices and quantities of supply and demand. Within this framework it is logical that increased productivity or efficiency may raise the utility and value of supplied goods and services without increasing the cost of production. As will soon be demonstrated, however, these principles only make sense at the microeconomic level. In addition, under perfect competition and in the long run, market prices will gravitate toward the costs of production also in neoclassical economics. In the following, it is explained why utility, quantity and productivity cannot explain economic values at the macroeconomic level.

The first thing to observe is that the source of value—whether labor-time or utility—has to be reflected in market values in order to be measured and to influence the functioning of the real-world economy. In the neoclassical theory, this is achieved by assuming that the supply and demand curves express the preferences (utilities) of rational agents in the market place. However, as stated by the Sonnenschein-Mantel-Debreu theorem [21,22,23], aggregating individual preferences into curves of market demand yields arbitrary results. Strictly speaking, demand is not independent from supply if the populations of buyers and sellers consist of the same individuals, and this is more likely the higher the level of aggregation and fully apparent at the macroeconomic level.

It turns out that the derivation of prices from supply and demand at the microeconomic level has no implications for the aggregate value of all the goods and services produced within an economic system. One way of seeing this is through the lens of what is sometimes called Say’s law, in short stating that “supply creates its own demand”. What this actually means is that everything that is supplied to the economy in the form of production generates incomes which form the entire basis for effective demand. While demand may differ between different goods and services depending on how consumers prefer to distribute their incomes, aggregate demand is essentially a function of aggregate supply. The role of utility in the derivation of value is thus merely to influence the relative prices of goods and services in the market under the constraint of a given purchasing power. A general equilibrium can be found but the solution provides no information about the aggregated value of supply or demand.

Another thing to observe is that there cannot be any clear relation between value and quantity at the macroeconomic level, since quantity is not a well-defined concept in a complex economy. This further restricts the usefulness of supply and demand curves, but it also makes it difficult to evaluate any relationship between the monetary value of the GDP and the volume of produced goods and services. Constant prices derived from the application of deflators such as the consumer price index (CPI) is one way to establish such a relationship, but the purpose of these deflators is primarily to measure monetary inflation by monitoring prices in a fixed and reasonably representative market basket of goods and services.

From a neoclassical point of view, however, it is natural to insist that a fixed currency should somehow be gauged against the utility associated with its purchasing power. Hence attempts have been made to measure changes in “the cost of living” by adjusting for quality improvements of goods and services in the calculation of the CPI. However, in order to measure the cost of living and the utility experienced by consumers it is critically important to follow the development of new commodities as well as changes in consumption patterns which involves a number of practical difficulties. Despite improvements to the methodology, it is generally found that the CPI does not appropriately reflect changes in utility or the cost of living [24,25,26]. Changes in the relation between price and volume may be used to monitor changes in the value of money, but that involves treating the value of money as an unknown variable. Due to the changing composition of the market basket, the monetary value of macroeconomic output is not a sound representation of either the quantity or the quality of goods and services even at constant prices. However, with a constant value of money, it is possible to observe how values of goods and services change over time.

The inability to fix monetary values against the quantity and quality of economic aggregates is highly important also to the notion of productivity. Generally speaking, increasing productivity refers to the ability produce “more” (quantity or quality) with a given amount of input, and is hence closely related to the concept of decoupling of economic growth from resource use. Specifically, productivity is a measure of efficiency in the use of inputs per unit of output value. However, under perfect competition the factors of production are exactly remunerated according to their contribution to the value added in production, implying that value added is determined by the costs of production (i.e., the remuneration given to labor and capital). Costless improvements therefore do not create value under perfect competition unless accounting adjustments are made. According to the classical value theory, productivity is not a source of value. On the contrary, since value according to the classical economists is based on the costs of production, it is natural that increased productivity reducing the costs of production also reduces the value added in production; “Economy in the use of labor never fails to reduce the relative value of a commodity”, in the words of J.S. Mill.

For a single line of production there is no contradiction between productivity in terms of increasing resource efficiency and in terms of increasing revenue. If a firm can produce a given quantity of output with a reduced quantity of input factors it can increase its net income by means of decreasing its resource use, provided that its output can be sold at the same price as before. In the system as a whole, however, the reduction of input to one firm must be a reduction of output (and income) somewhere else in the economy. In a closed system, the net effect of the productivity gain will be exactly zero in terms of aggregate income. Productivity gains may increase output in terms of quantity but not in terms of value added. To stress this point clearly: For a single business, value added equals gross income minus expenditure. In a closed system, however, total income equals total expenditure and there can be no gain in value added if expenditures are cut. In terms of value, the notion of productivity is thus primarily relevant as a microeconomic concept.

Although utility, quantity, quality and productivity are all relevant concepts in a philosophical discussion about value, none of them appear to be able to satisfactorily connect to the aggregate value of production of a system. The subjective, relative and microeconomic approach of the neoclassical value theory does not facilitate the understanding of macroeconomic value formation. In addition, since utility cannot be measured by other means than through revealed preferences of market agents there is no way to falsify the hypothesis that utility regulates market values, and any proof of the hypothesis would be tautological. The economic measure of utility would be something like “the price that people are willing to pay” for any market good, but there is no reliable way to judge whether the price that people are actually paying is different from what they are willing to pay—notably not on the macro level. This may perhaps explain why the problem of what regulates the value of the GDP is still unsettled.

2.3. Other Value Theories

There are of course alternatives to the classical and neoclassical value theories. Other value systems have been proposed within the field of ecological economics. Some of these theories regard energy embodied in economic output (“eMergy”) as the primary input to all production of goods and services (e.g., [27,28,29]). However, although there have been more or less successful attempts to correlate the monetary value of output to energy embodied in production, these theories have been criticized on the grounds that output cannot be adequately measured in purely energetic terms [30]. There is a logical connection between energy use and the total metabolism of an economy, but a much weaker logical connection between energy use and exchange values. It seems unlikely that value in exchange as a form of human relations would be determined by energy content [31]. Empirical correlations between energy use and value of output might be explained by the strong relationship between capital and energy use [32]. Monetary prices must in some way be derived from human activities, leaving the classical and neoclassical value theories as the most interesting candidates for explaining the real value of societal production.

3. Empirical Testing of the Classical Theory

In recent years, there have been a number of attempts to empirically relate actual market prices of goods and services to prices of production derived from direct and indirect labor inputs in line with the classical theory (e.g., [33,34,35,36]). These studies typically explore input-output tables from official national accounts recording the input of labor and intermediate goods and services contained in the output for the various sectors of an economy. They generally find strong correlations between market prices and the sum of direct and indirect labor content with r² values of well over 0.9. However, none of these studies evaluate the relation between value and labor inputs at the macroeconomic level.

In this section, the labor theory of value will be examined in the light of empirical data at the macroeconomic level. In keeping with what was said earlier, the labor theory of value states that the value of production should be proportional to the amount of labor-time employed. The numerical relation is a monetary expression that depends on the value of money. If we assume that accurate deflators are in place to express the value of goods and services in constant prices, we may expect a linear correlation between labor-time (hours worked) and GDP. However, the labor-time accumulated in used-up capital should also be included [19]. Assuming that on an aggregated level the turnover time of real capital is reasonably constant (or slowly changing), the capital consumption is proportional to the standing stock of fixed capital. Since GDP measures the value added in aggregate production, circulating capital (intermediate products) is not included as capital but directly as goods and services.

In line with the labor theory of value, labor productivity is equivalent to the unit labor cost. The cost of labor depends on the labor embodied in labor itself, which is equal to the used-up capital per unit of labor time. This is the natural way to identify value and productivity in a production cost theory. To test this empirically, we first need to investigate the relation between GDP and worked hours in the aggregate economy, and next to investigate the relation between labor productivity and capital use.

In the short term, the magnitude of worked hours is likely to explain much of the variations in GDP including business cycles. This should be relevant on a time scale where the stock of fixed capital does not change very much, so that the use of capital is explained by variation in capacity utilization rather than variation in capacity as such. In the long term, the increase in labor productivity (i.e., the cost of labor) over time is likely to be more or less well explained by the stock of capital. With the arguments from the previous section regarding the notion of total factor productivity in mind, this is reasonable since increasing the volume of production only increases the value of production if associated with increased employment of production factors. Technical innovations or efficiency gains increasing the utility without raising the costs are not counted as increases in productivity since the prices of the products do not increase. Utility, once again, is not a source of value.

3.1. Macroeconomic Databases

The statistical database provided by the OECD (OECD.Stat) contains precisely the data needed to empirically test the labor theory of value as specified above. It gathers information from 35 national databases using a consistent methodology in order to allow comparisons between countries and over time. Specifically, information about GDP in constant prices, hours worked and stocks of fixed capital in constant prices (estimated by PIM) is available as well as labor productivity defined as GDP per worked hour. Methods used to produce the data can be found on the website [37]. The lengths of the data series differ between countries, and in this study the eleven countries with the longest records (minimum 15 years) have been selected in order to describe both the short- and the long-run principles of GDP growth. Together, these countries represent a relatively wide range of small- to medium-sized economies around the world.

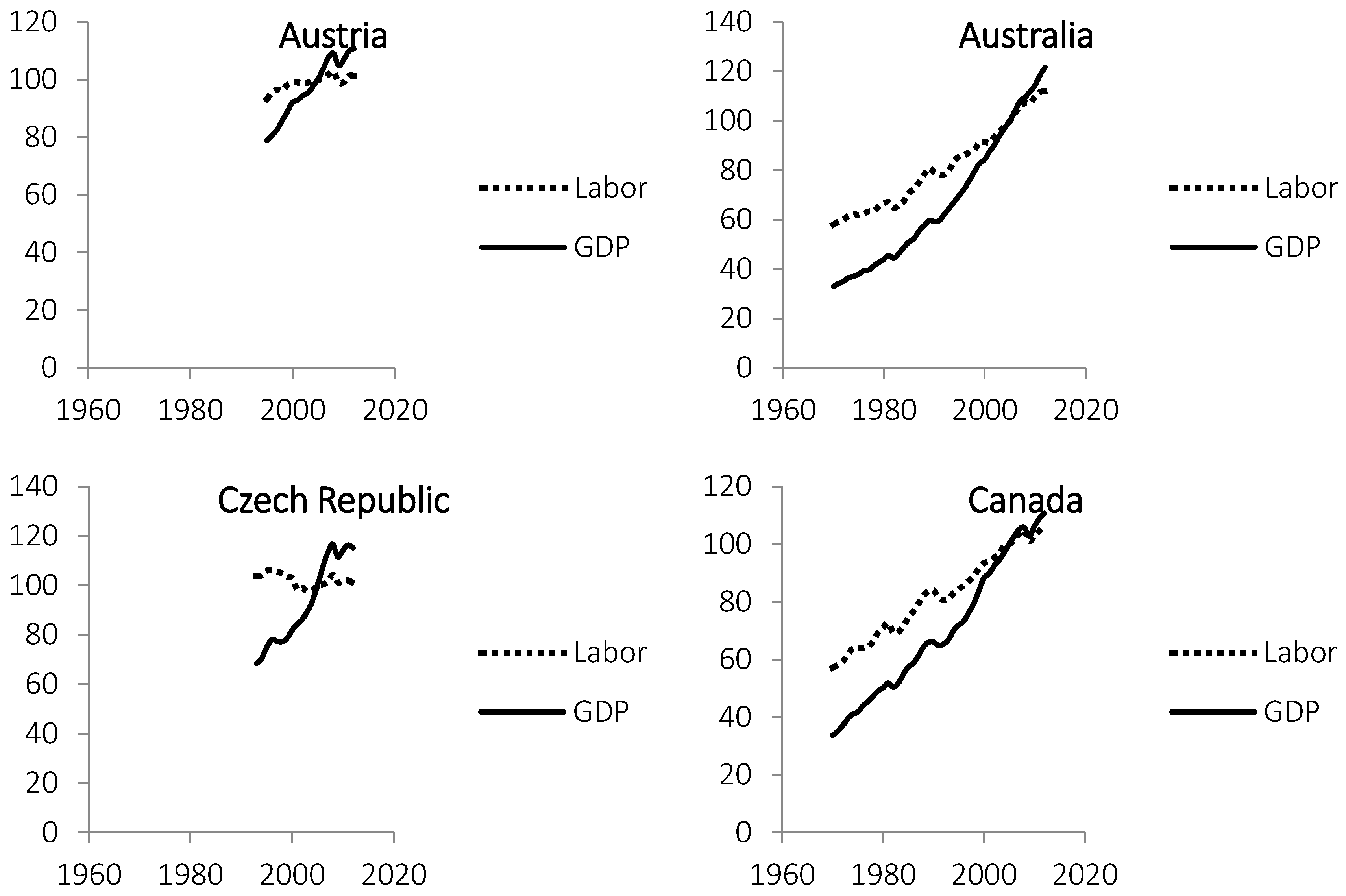
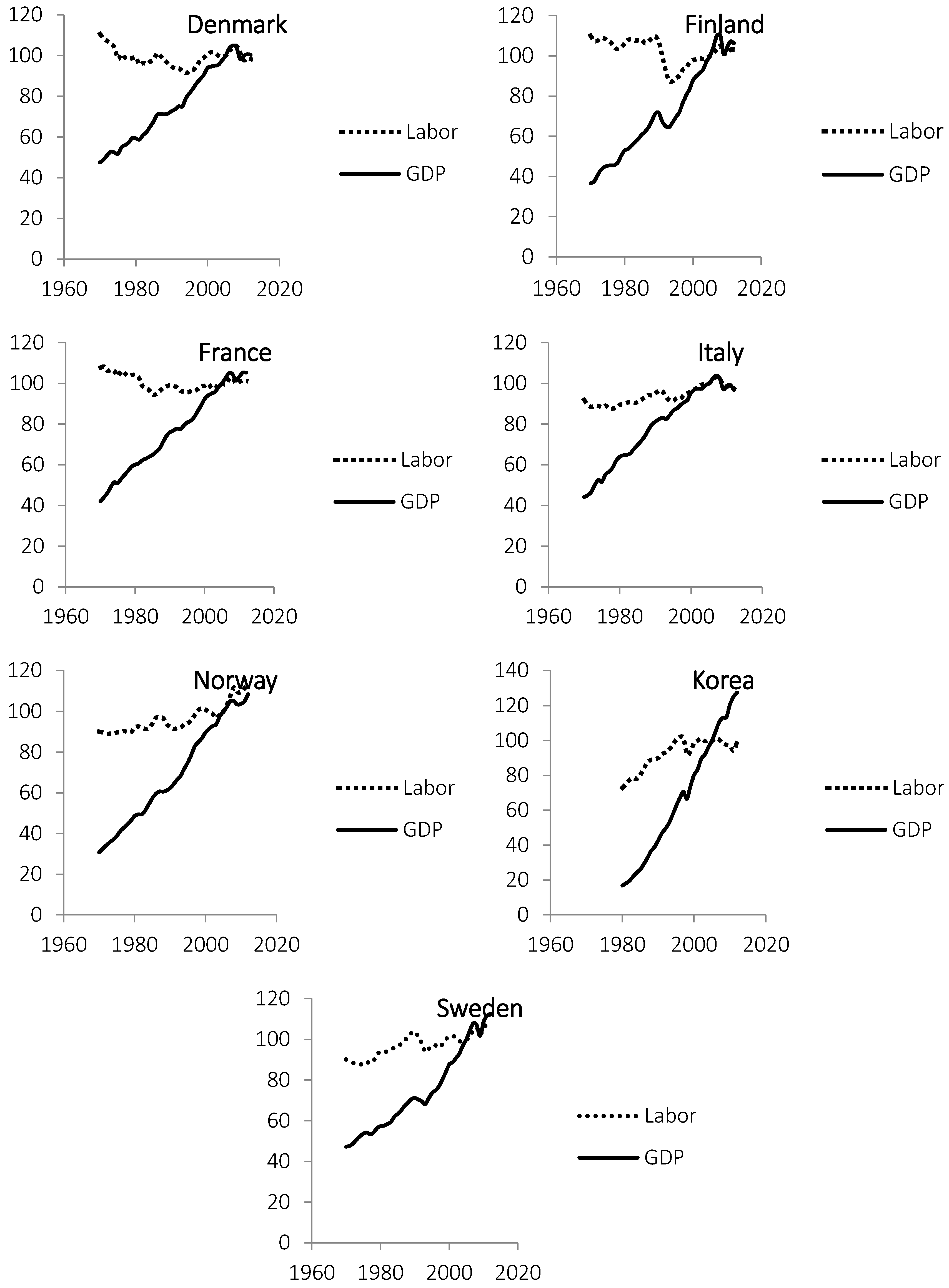
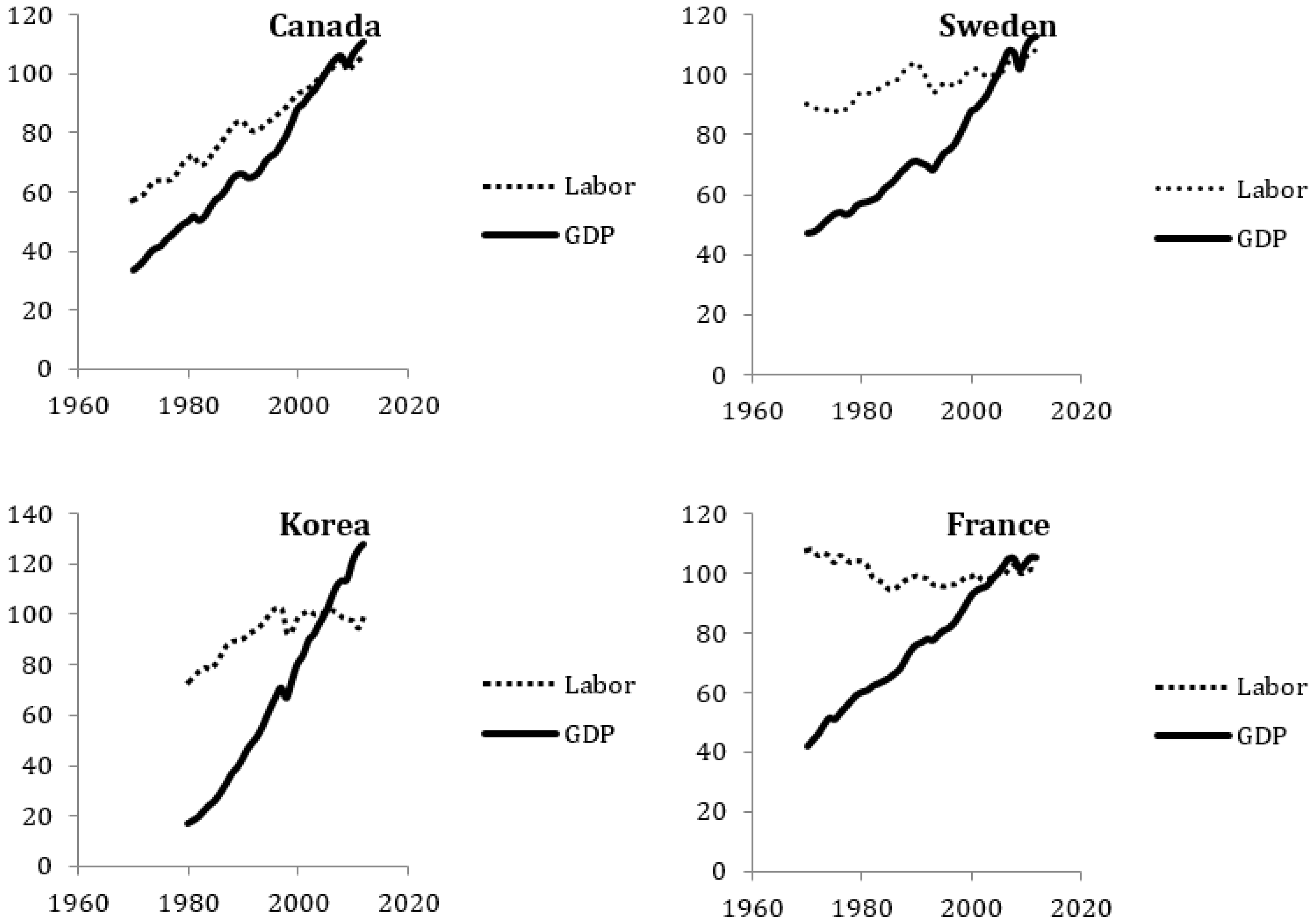
In Figure 1, time series for GDP and worked hours are shown for four illustrative cases. The data for all eleven countries are presented in Appendix. The data are normalized so that values in 2005 are set to 100. Long-term trends for the number of worked hours are either stable or increasing. In countries such as Canada, Korea and Australia, the increasing number of worked hours coincide with increasing population numbers. Short-term variations in worked hours correlate well with variations in GDP and can be explained by business cycles or known events such as the Swedish banking crisis in 1991 or the global economic downturn in 2008. In the long term, the GDP increases more than the number of worked hours in all countries, thereby implying increasing labor productivity.

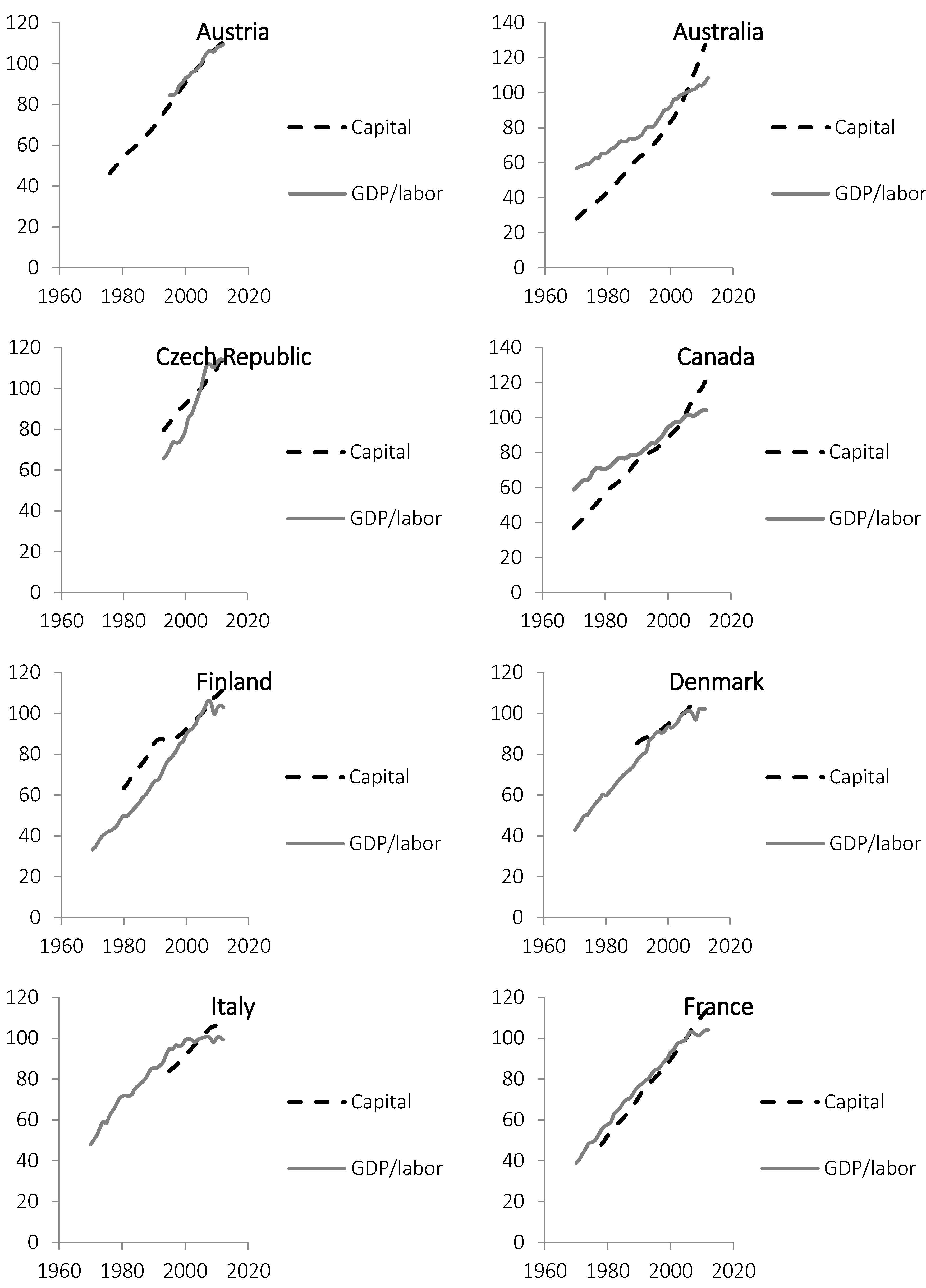
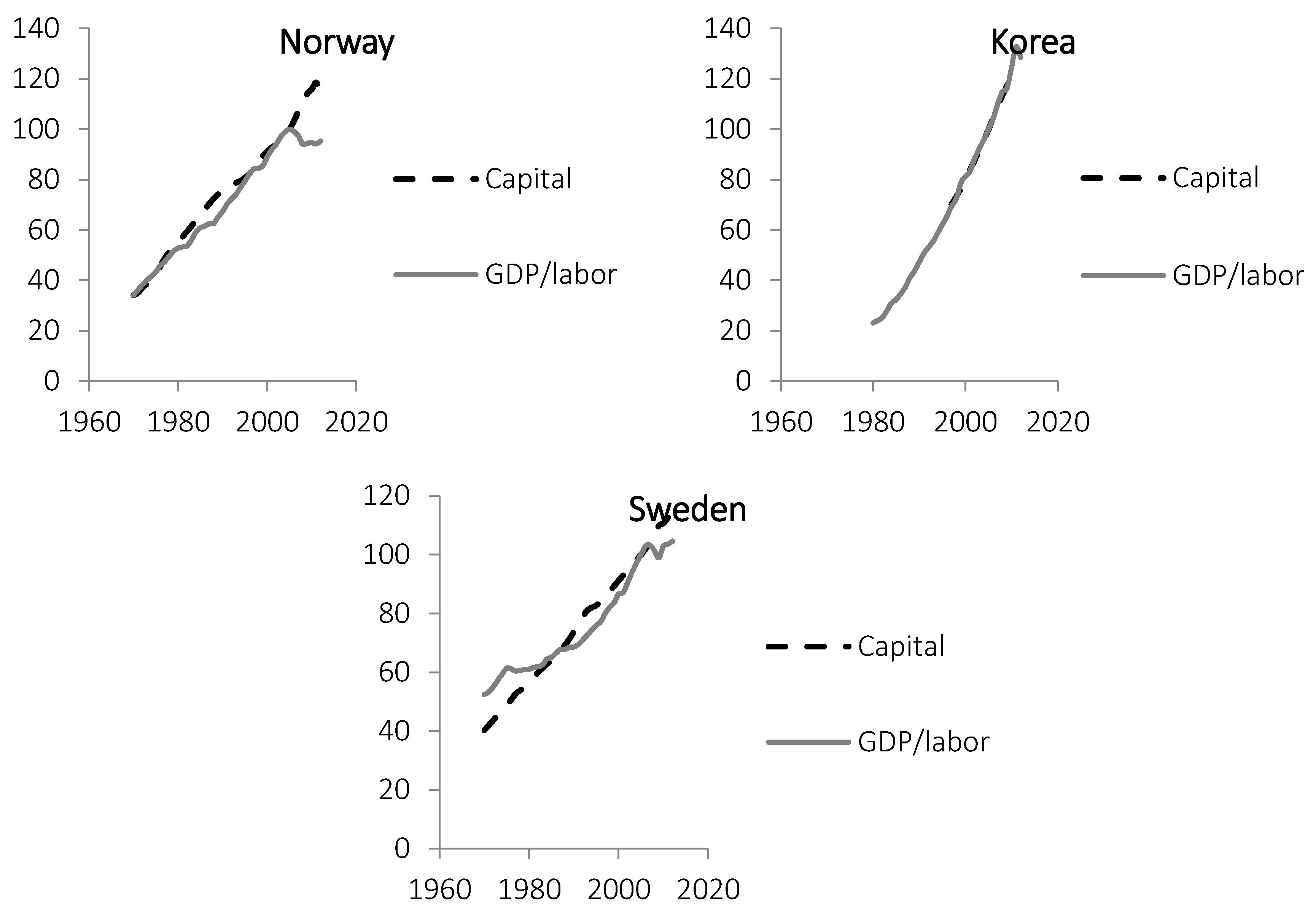
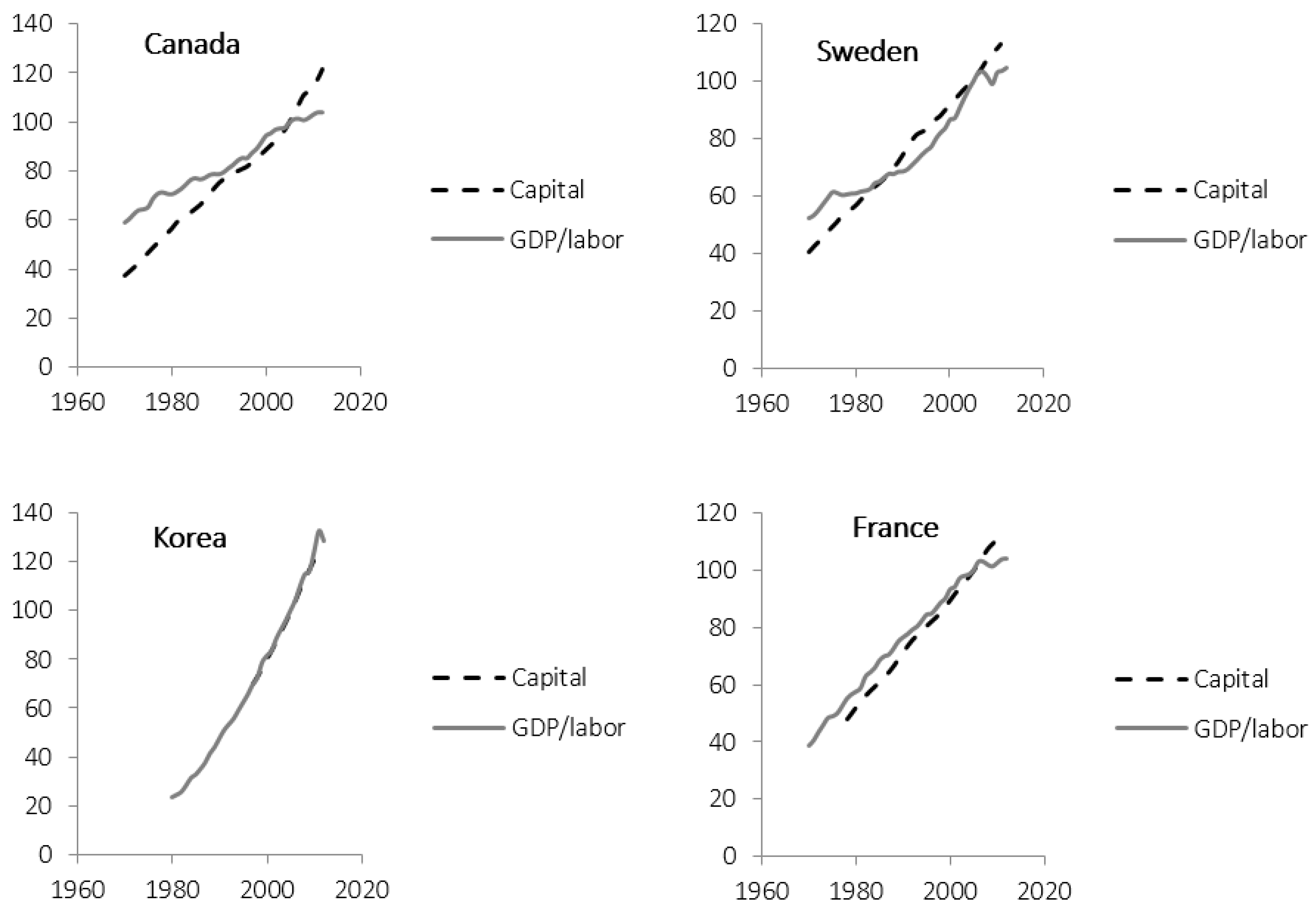
In Figure 2 and Appendix, time series for labor productivity (GDP per worked hour) and physical capital are shown for the same countries as in Figure 1. The data are normalized so that values in 2005 are set to 100. It appears that positive changes in the capital stock explain most of the long-term increases in labor productivity. The slopes of the two variables are similar for most countries with four visible exceptions: Australia, Canada, Czech Republic and Italy. After the downturn in GDP growth after 2008, the growth of capital stocks continued in all countries (see Appendix).

Statistic correlations between labor productivity and capital stocks are generally strong with r² values over 0.85 for all countries but Italy (

Table 1. Statistics for correlations between labor productivity and capital; number of years (n), correlation (r²) with and without intercept and slope without intercept.

	n	r2	r2 without Intercept	Slope without Intercept
Australia	42	0.97	−0.11	1.09
Austria	18	0.99	0.96	1.01
Canada	43	0.97	0.24	1.05
Czech Republic	20	0.95	0.77	0.95
Denmark	22	0.85	0.85	0.97
Finland	33	0.93	0.82	0.90
France	34	0.98	0.90	1.02
Italy	17	0.68	−8.98	1.02
Korea	15	0.99	0.99	1.01
Norway	43	0.94	0.93	0.92
Sweden	42	0.94	0.83	0.98

). This is not surprising since all variables are incrementally increasing with time. If labor productivity is plotted against capital stocks (not shown) the slope of the regression (with intercept set to 0) is very close to 1 in all countries, but r² values are low or very low for Australia, Canada, Czech Republic and Italy (Table 1, 4th column). If the intercept is forced to be 0, r² values lower than 0 are possible but rather meaningless as a statistical measure. The data series for the Czech Republic and Italy are relatively short with much noise from business cycles obscuring the long-term trends. In Australia and Canada, the long-term increase in the number of worked hours may render a different relation between the cost of labor and the cost of capital than in countries with a more constant level of worked hours, which could in turn influence the relation between labor productivity and capital. For the remaining seven countries, there appears to be a statistically strong 1:1 relationship between labor productivity and stocks of fixed capital. This strong relation holds for countries with long data series such as Norway and Sweden and for countries with data series starting at the beginning of the 1990s such as Austria, Denmark and Korea, thus covering both traditional industrial periods and modern periods where service and information sectors become increasingly important for economic investment.

3.2. Other Studies

More generally, without reference to the classical theory, empirical studies linking changes in GDP to changes in production factors are abundant. It is, for example, found that the difference in growth rates between the United States and Europe is primarily explained by larger population growth in the former, and that the difference between the two in per capita GDP is due to the fact that US citizens work more hours than European citizens [38]. It is also clear from the data presented by Abramovitz [39], Solow [40] and other formative studies in establishing the current practices of growth accounting that the use of labor and capital is highly correlated with economic output, although their results were typically interpreted differently (see Section 4).

One of the “stylized facts” about economic growth presented by Kaldor [41] is that the capital-output ratio in a given economy is roughly constant over time. The empirical evidence suggests that this holds over extended periods for many developed countries, but that the ratio is different between countries and may shift if structural changes occur in the economy [42,43,44]. In a recent policy paper from the OECD it was concluded that the capital-output ratio was relatively stable in most developed economies during the last 25 years, and that this stability in capital intensity is expected to continue over the next decades [45]. In the dataset used in this study, the capital-output ratios range between 2.2 and 3.7 with no general time trends in the data. This constant ratio is, of course, consistent with the finding of a 1:1 relationship between labor productivity and capital.

In summation, there is ample empirical support for the impact of labor and capital inputs on the value of output, and no indications of decoupling of macroeconomic growth from resource use in this sense. In the long run there is a near linear relationship between GDP growth and physical capital accumulation. Exploring the OECD database, the empirical evidence appears to be consistent with the principles of the labor theory of value. Thus the theory is not falsified by such data. Under the assumptions of neoclassical growth models, however, using the very same data yields completely different results, typically suggesting that total factor productivity explains most of the growth in GDP, and less importance is attributed to capital and labor.

4. On the Assumptions of the Neoclassical Growth Model

Growth models were first developed to conceptualize economic growth and the factors behind it, and to work out strategies to promote growth—both at the aggregate and industry levels. Pioneering work includes contributions by Cobb and Douglas [46], Harrod [47], Domar [48], Solow [49], Swan [50] and Cass [51], leading up to the modern growth accounting framework. Although the lack of consistency in the underlying assumptions of the models has been widely recognized, one of the most persistent justifications for their proliferation has been that empirically they “seem to work” [52]. But in what sense do they seem to work? They may offer a tight fit to empirical data, and they may seem to provide reasonable advice for promoting growth, emphasizing the role of innovation and technological change. In relation to the present inquiry about economic values and resource use at the macroeconomic level, however, there are two features of these models which are highly problematic, namely:

•

The assumption that models of physical production can be used for the modeling of economic values.

•

The modeling of macroeconomic production based on microeconomic principles.

The following two Subsections 4.1 and 4.2 are dedicated to these problems.

Measuring total factor productivity in principle does not require models since it is simply a ratio between the value of output per unit of input. If real output increases more than real inputs this reflects an increase in productivity. Such calculations were performed by Abramovitz [39], Kendrick [53] and Jorgenson and Griliches [54], but subsequently that methodology has largely been replaced by the use of production functions.

Productivity as measured in modern growth accounting is based on the neoclassical production function. In its aggregated form it is often credited to Solow [49] and Swan [50], and although different versions exist, the so-called Cobb-Douglas formulation is most useful for the purpose here:

Y = A K^α L^{1 − α}

(1)

In this model, Y represents real output, and K and L represent real inputs of capital and labor. The exponent α is usually taken to represent capital’s share of income and 1 − α is labor’s share of income. Equation (1) can be rearranged so that A becomes a ratio between output over input and hence an estimate of total factor productivity [40].

4.1. An Accounting Identity

If we consider a single production process using homogeneous production factors, there is a certain logic to the neoclassical production function and the way output is quantitatively related to inputs of capital and labor. However, once different kinds of production are aggregated to the macro level and physical quantities are replaced by economic data, various logical and practical problems are encountered.

By definition, value added in production is equal to

Y ≡ wL + rK

(2)

where w is the wage, r is the rate of profit and other symbols are the same as in Equation (1). Combining Equations (1) and (2), it is possible to evaluate the production function in value terms. Having K and L on both sides of the equation imposes strict conditions for the algebra to hold, but on the other hand, there is full flexibility for the value of A. It can be shown that if Equation (2) is differentiated and integrated, it can be readily transformed into Equation 1 with A as the constant of integration [55]. In growth accounting where the change in Y is evaluated as a function of changes in L and K, total factor productivity growth is merely a weighted average of the growth rates of w and r [49]. As demonstrated by Shaikh [56], Simon [57] and others, almost any value data will fit the Cobb-Douglas function well due to the accounting identity between values of inputs (Equation (1)) and outputs (Equation (2)) provided that α is not heavily fluctuating; hence, a tight fit offers little support for the underlying assumptions of the production function. If almost any data produces a tight fit it cannot provide much information about the nature of the real factor productivity [58]. Indeed, the finding that A typically explains 50%–90% of GDP growth should perhaps be alarming rather than convincing.

It is, of course, often articulated that A is merely a residual representing “any kind of shift in the production function” [40] and a measure of what we do not know. However, estimating total factor productivity using value data rather than physical data for output introduces a new dimension of uncertainty about the meaning of the concept. The physical logic of the production function disappears once total factor productivity is allowed to explain changes in economic value.

Aggregating different kinds of production and estimating total factor productivity at the macroeconomic level makes the application of value data even more problematic. The inappropriateness of adding up different kinds of real capital into a single quantity has been widely discussed [17,59], pointing out that there is no common property of heterogeneous capital other than the monetary value. Hence a physical interpretation of aggregate capital is not possible, and the same would be true of aggregate economic output. It is appropriate to emphasize that in official growth accounting the data are often disaggregated to the sector level which to some extent might work against some of the reservations made here. However, the substitution of economic data for physical quantities distorts the interpretation of total factor productivity just the same. The theoretical limitations of the aggregate production function are well summarized by Felipe and Fisher [60].

4.2. Decreasing Marginal Productivity

The logic behind the production function can be motivated in a microeconomic context, but the same logic disappears at the macro level. Since the sum of α and 1 − α is unity, the model assumes constant returns to scale—doubling capital and labor also doubles output. Conversely, since α < 1, both capital and labor exhibit diminishing returns individually and this is where neoclassical economics becomes the slave of mathematics.

Certainly, diminishing marginal returns is very much in harmony with neoclassical theory whereby, under normal circumstances, marginal costs and marginal rates of substitution are assumed to decrease with scale. The fundamental assumption is that the benefit or utility associated with the first unit of consumption or investment is larger than for the next unit. In line with this reasoning, the marginal benefit of GDP growth may be decreasing as well, but that is not the question here. For obvious reasons, value itself does not exhibit decreasing returns, and if labor is the measure of value, there can be no such thing as diminishing returns on labor. Hence, in terms of value, the neoclassical production function is incompatible with the classical labor theory of value.

In a given production process with homogeneous capital and labor there is reason to assume diminishing returns in quantitative terms. It is clear that a carpenter (laborer) is more productive with a hammer (capital) than without a hammer. However, adding a second hammer to the capital stock adds less to productivity than the first one, thus in terms of utility, it is apparently correct that the benefit per hammer exhibits diminishing returns. Yet the value of the products would increase in proportion to the cost of investment even if we invested in hammers only.

But why assume homogeneous capital and invest only in hammers? That is not a sound representation of reality. Regardless of theory, it is highly unusual to put more than one hammer in the hands of a carpenter. From this it is senseless to infer that capital in general must exhibit diminishing returns, since capital may assume many different forms (e.g., different tools for carpentry). This is even more apparent at the macro scale in a diversified economy. Precisely the fact that with time more and more useful machines, factories and infrastructures are accumulated in the economy is the most intuitive explanation for the increasing wealth of society. In the aggregate production function, neither capital nor labor are homogeneous factors and the case for diminishing returns in terms of quantity is thus very weak if not completely missing.

In terms of output value and at the macro scale, the assumption of diminishing returns is rarely motivated but still undisputed in most economic thinking. As indicated by the empirical data in Section 3 there is a near linear (1:1) relationship between capital and output, and it is only by assuming that capital exhibits diminishing returns that total factor productivity comes into play. In a stylized case based on several examples from the real world (including Sweden and France in the OECD data), GDP and capital grow at the same rate while labor remains constant. If capital’s share of input is 0.3, Equation (1) can be written as:

Y = constant · K^0.3

(3)

where the constant is the product of A and L^{1 − 0.3}. In this case, capital can only explain a fraction of GDP growth more or less by definition. This seems like an assumption rather than a result from the data.

The intention expressed by Solow [40] and others is indeed to separate the variations in output due to technology from those due to capital formation. Nevertheless, if the result of the separation is mathematically determined by capital’s share of output, it does not contain much information about the real contribution to GDP growth. Similarly in Figure 1, the variations in worked hours seem to perfectly explain most short-term variations in GDP. If the influence of L is moderated by an exponent, however, there is necessarily a part to be explained by the residual.

It should be emphasized that many of the problems associated with the neoclassical growth model are well known by researchers and discussions are ongoing. The point here is not to reject the idea of the production function or to discredit all aspects or uses of the model. However, the normal applications of the model and the occurrence of a residual can clearly not be taken as a confirmation of the underlying assumptions, which if they were correct at the aggregate level would undermine the labor theory of value. Reported contributions of technical change in growth accounting should not be confused with real estimates of resource efficiency in any quantitative sense.

5. Discussion

Understanding the theoretical foundations of economic value formation is crucial to addressing the long-term possibilities for decoupling of GDP growth from resource use and environmental degradation. Given the strong policy focus of GDP growth, the pure economic mechanisms of this complex question deserves further attention. If the labor theory of value is valid for the macro economy, this will put a theoretical restriction on the possibility of decoupling of economic growth from resource use. Empirical macroeconomic data reveal a strong relation between labor, capital and output which appear to be compatible with the labor theory of value, thus showing no indication of decoupling between these parameters. In particular, the very strong correlation between long-term growth and physical capital accumulation is notable.

In addition, the classical theory is logical in a macroeconomic context while the neoclassical value theory is not, as demonstrated in Section 2. Consequently, the notion of productivity, decoupling the value of input from the value of output, is only relevant as a microeconomic concept. Nevertheless, neoclassical production functions are used by national statistical offices worldwide to calculate total factor productivity in different economic sectors and for the total economy. Few reservations have been made against applying microeconomic assumptions at the macro scale. And since many studies using these models find that total factor productivity growth is a major component of output growth, a common conclusion is that growth is not primarily achieved by increasing resource use (see e.g., [61] for a review). A closer look at the data as suggested in Section 3, on the other hand, is sufficient to demonstrate the lack of decoupling.

Given that labor is a limited resource, the growth in output value hinges on the possibility of preserving past labor in the form of capital. A key question is whether or not capital accumulation can be decoupled from the use of materials and energy. This will determine the possibility of decoupling of GDP growth from the use of natural resources and other environmental impacts. As long as capital is made of materials, and given the strong relationship between capital and energy use [32], absolute decoupling between GDP growth and environmental impacts remains problematic by definition. The unsustainable role of capital accumulation in capitalist economies has been vividly discussed in the context of eco-Marxism (see e.g., [62]). Accumulating immaterial capital provides a theoretical possibility to decouple economic growth from the use of physical resources although no part of the historical growth remains unexplained by physical capital and labor.

Regarding capital as accumulated labor, it could reasonably also include so-called human capital inasmuch as time invested in research and education is preserved by society and its individuals and used as input in production. This is in fact an increasingly common assumption in neoclassical growth models (e.g., [45,63]). However, it is also possible to regard the impact of human capital as merely increasing the relative productivity of labor, much in the same way that technical change enhances the relative productivity of capital. In principle, education and research and development (R and D) could either be treated as consumption or as investments. Changes in the national accounting standards are underway in several countries in line with the SNA2008 recommendations stating that R and D should be recognized as part of capital formation.

From a sustainability point of view, the significance of natural capital such as forests, agricultural land and natural resources for the production of economic output is of special interest. Considered as a factor of production, such capital is absolutely crucial, although in the role of realizing the economic values constituting the GDP the function is less evident. There is no denying that the erosion of natural capital threatens the long-term sustainability of economic systems, but as mentioned earlier, the economic value of raw materials and energy can be derived from the labor and capital employed in bringing them to market. Natural capital in the form of land was not regarded as a source of value by the classical economists, although landlords were often able to obtain rent from the tenants and so claim part of the value created in production on their lands. The rationale of the classical standpoint can of course be challenged in this respect. In practice, however, the value of land is insignificant in relation to the value of total national capital in the developed nations as demonstrated by the extensive dataset compiled by Piketty [38].

In relation to decoupling, the term “green growth” [7] should also be mentioned. An essential component of this concept is that environmental investments may be an important driver of economic growth. To be sure, investments in renewable energy and fossil-free transport systems could reduce emissions of greenhouse gases if they replace fossil-based alternatives. Since they add more capital to the economy it would promote economic growth according to classical theory. On the other hand, the environmental benefit also depends on the dismantling of harmful activities and fossil-based capital which would counteract the process of growth. The net effect on growth as well as greenhouse emissions is a matter of balance. The more general relation between economic growth and resource use is of course a much wider topic.

It is clearly relevant to study the possibility for decoupling of production from resource use in real terms. This can be done by examining produced volumes of specific goods and services and how resource efficiency may be improved (e.g., [12,64]). However, by definition, such studies avoid the question of what happens when prices and economic values are reduced as a consequence of improved resource efficiency. A key point here is that the GDP is sensitive to such cost reductions, and that the design of environmental policies needs to account for precisely this problem. Clarifying the purpose of the GDP as such may contribute to solving this problem.

After all, the GDP is first and foremost a measure of economic activity which is fully in line with the classical value theory. But for the pioneers of the concept, it was not obvious if the GDP should attempt to measure national economic welfare or economic activity. Eventually, however, the aim became a measure of economic activity, justifying the inclusion of military spending and financial speculative activities into the GDP which by some accounts would be held as dis-utilities, as well as the exclusion of unpaid work and home gardening. Measuring all economic activities provides a tool to monitor the overall functioning of the economy with important implications for employment, investment opportunities, fiscal position and monetary policy.

From the different perspectives taken by the classical and neoclassical value theories, it is evident that there is an inherent conflict between measuring consumer utility and the measurement of economic activity. The attempts to incorporate quality adjustments in the definition of constant prices [24,65] indicate that the former perspective is gaining ground (see Section 2). Despite several modifications since the 1940s, though, the GDP does not attempt to measure welfare or wellbeing [66].

An indicator focusing on welfare rather than economic activity is more likely to achieve absolute decoupling of growth from resource use and environmental degradation. This means that formulations attached to the Sustainable Development Goals of the UNDP with targets such as ”at least 7 per cent GDP growth per annum in the least developed countries” may need to be reconsidered. In order to maximize benefits in society, using a gauge that is essentially measuring costs is probably ineffective. New measures of progress and national wellbeing accounts replacing or supplementing the GDP [67,68] are better placed to define economic development compatible with necessary reductions of resource use and environmental degradation. Furthermore, such measures are also more likely to achieve absolute decoupling from resource use and environmental degradation.

6. Conclusions

According to the classical theory of value suggested by Adam Smith and developed by David Ricardo, economic values are formed by the use of production factors, i.e., labor and capital. In this paper, it is demonstrated that this theory is consistent at the macroeconomic level and cannot be falsified by empirical data. It is also shown that the neoclassical theory of value is not consistent at the macro level and not possible to falsify by empirical data. If the classical theory is valid at the macro level, this puts a theoretical restriction on the possibility of decoupling of growth from resource use.

It has also been demonstrated that the neoclassical notion of productivity is only relevant as a microeconomic concept. In a closed system, total income equals total expenditure and there can be no gain in value from decreasing expenditures. Production functions attributing GDP growth to total factor productivity are based on microeconomic principles that should not be applied at the macroeconomic level, hence the finding that GDP growth not being primarily achieved by increasing resource use rests on dubious premises. That no such decoupling between economic output and the use of capital and labor occurs is clear from the official national statistics presented in this paper.

Further research is needed to explore the possibilities of decoupling of capital accumulation from physical resource use and environmental impacts, ultimately depending on the material intensity of capital. Although immaterial capital may also contribute, physical capital has historically been the most important form of value preservation, and a strong relationship between capital and energy use remains likely. Environmental impacts clearly depend on material resource use and the strong link between value formation and physical capital formation, in addition to the strong policy focus on GDP growth, provide the conditions for absolute decoupling.

Economic growth is usually defined in terms of GDP growth, following the classical theory of value that GDP measures the costs of production. However, higher costs or more economic activity do not by definition result in more utility or welfare. Alternative measures of progress focusing on welfare rather than economic activity are more likely to achieve absolute decoupling between human development and the consumption of environmental resources.