Sustainability-Oriented Financial Resource Allocation in a Project Portfolio through Multi-Criteria Decision-Making
Abstract
:1. Introduction
2. Sustainability in Project Portfolio Management: Latest Literature Review
3. Materials and Methods
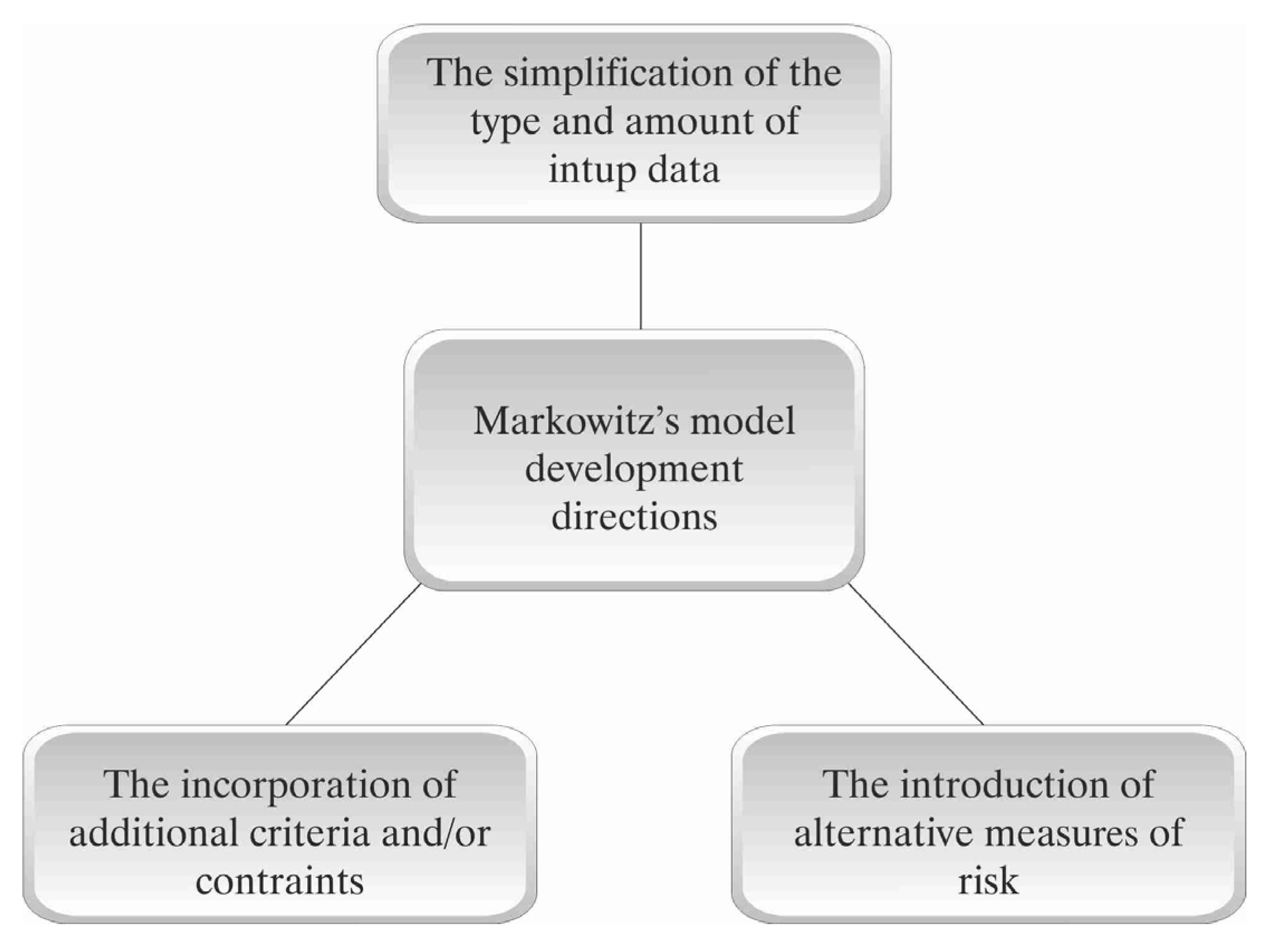
3.1. The Application of Multi-Criteria Decision-Making Methods in Developing Modern Portfolio Theory
- Multi-Objective Decision-Making (MODM) methods: An optimization problem is solved with an objective function while evaluating certain constraints. These methods are directly applied to solve a portfolio optimization problem.
- Multiple-Attribute Decision-Making (MADM) methods: Decision-making is intended for discrete comparison of alternatives. In scholarly works, methods falling within this group are usually used to rate assets to be included in a portfolio.
- No-Preference Methods (without the presence of a decision-maker)
- Posteriori Methods
- Priori Methods
- Interactive Methods
3.2. Development of a Sustainability-Oriented Model of Financial Resource Allocation in a Project Portfolio
3.2.1. Markowitz’s Mean-Variance Model
- = average return on a security i;
- = selling price of a security;
- = buying price of a security; and
- = number of periods analyzed.
- = average return on a project i;
- G = gain from investment;
- I = cost of investment; and
- = number of scenarios analyzed.
- = return on a financial instrument for period t;
- = average projected return on a financial instrument; and
- = probability of return for period t.
- = variance of the return of a project i;
- n = number of scenarios;
- = return on project i in scenario j; and
- = average return on project i
3.2.2. A Composite Sustainability Index of a Project
- CSIP = a composite sustainability index of a project;
- = the weight of sustainability indicator i; and
- = the normalized value of sustainability indicator i;
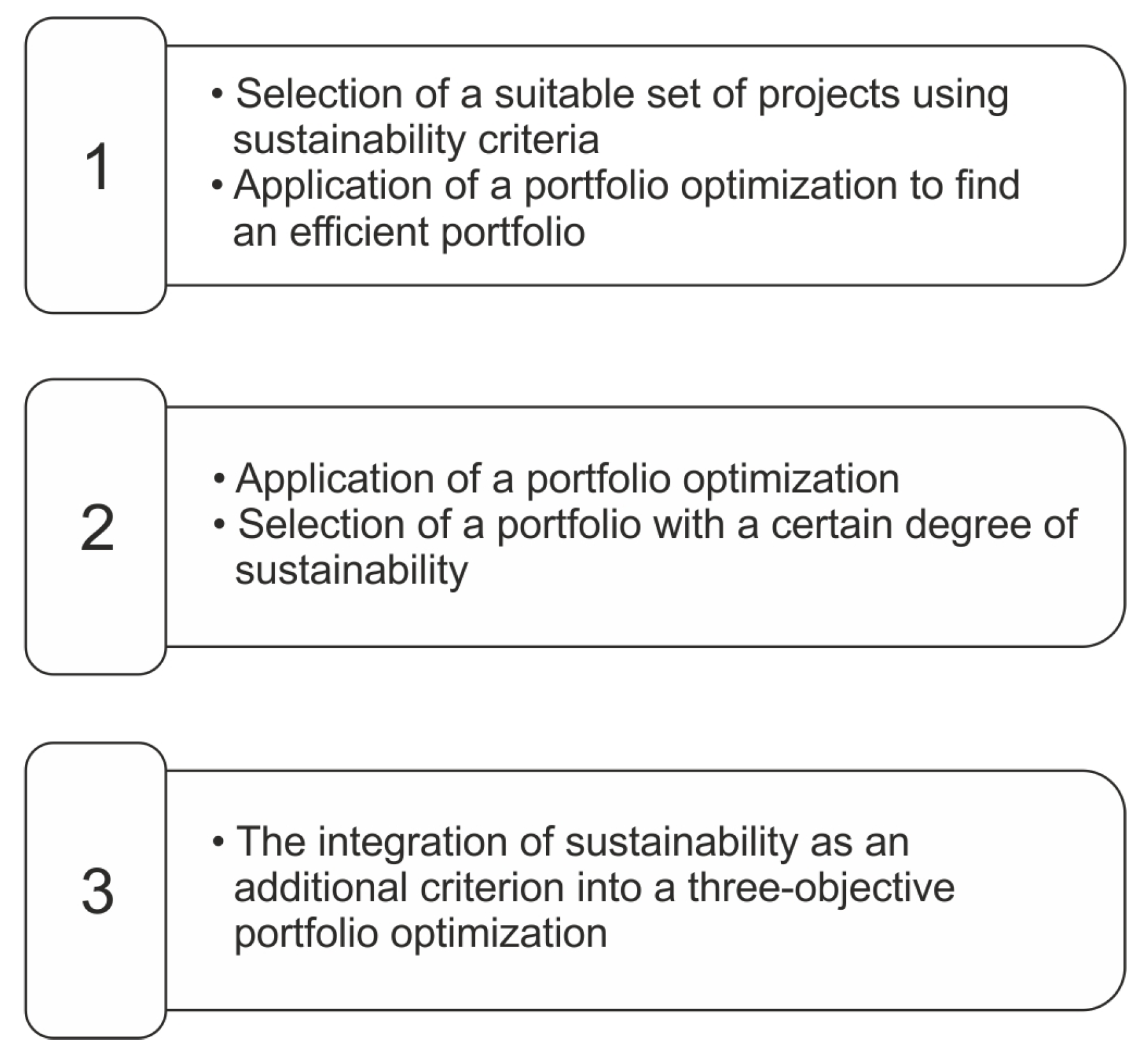
3.2.3. A Sustainability-Oriented Model of Financial Resource Allocation in a Project Portfolio
- There is a set of projects competing only for financial resources.
- The available financial resources are lower than the total amount of funds needed for all the projects.
- The maximum value of funds to be assigned to a project is defined.
- A funding decision is taken only once in a given period of time.
- All the projects are scheduled to start at the same time.
- The interdependence of projects is not assessed.
- Projects are not broken down into a set of activities or tasks.
- Model:
- Objective 1:
- Objective 2:
- Objective 3:
4. Results and Discussion
- extend the model to a planning-horizon version where resources are allocated over multiple funding periods;
- assess the interdependence of projects;
- incorporate scheduling; and
- use semi-variance or semi-deviation instead of variance.
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BSC | balanced scorecard |
| DEA | data envelopment analysis |
| EA | evolutionary algorithms |
| MH | metaheuristics |
| MCDM | multiple-criteria decision-making |
| MADM | Multiple-Attribute Decision-Making |
| MODM | Multi-Objective Decision-Making |
| SRI | socially responsible investment |
References
- Turner, J.R.; Müller, R. On the nature of the project as a temporary organization. Int. J. Proj. Manag. 2003, 21, 1–8. [Google Scholar] [CrossRef]
- Økland, A. Gap Analysis for Incorporating Sustainability in Project Management. Procedia Comput. Sci. 2015, 64, 103–109. [Google Scholar] [CrossRef]
- Martens, M.L.; Carvalho, M.M. The Challenge of Introducing Sustainability into Project Management Function: Multiple-Case Studies. J. Clean. Prod. 2015. [Google Scholar] [CrossRef]
- Hope, A.J.; Moehler, R. Balancing projects with society and the environment: A project, programme and portfolio approach. Procedia Soc. Behav. Sci. 2014, 119, 358–367. [Google Scholar] [CrossRef]
- Singh, R.K.; Murty, H.R.; Gupta, S.K.; Dikshit, A.K. An overview of sustainability assessment methodologies. Ecol. Indic. 2012, 15, 281–299. [Google Scholar] [CrossRef]
- Thomson, C.S.; El-Haram, M.A.; Emmanuel, R. Mapping sustainability assessment with the project life cycle. Proc. Inst. Civ. Eng.-Eng. Sustain. 2011, 164, 143–157. [Google Scholar] [CrossRef]
- Ebbesen, J.B.; Hope, A.J. Re-imagining the Iron Triangle: Embedding Sustainability into Project Constrains. PM World J. 2013, 2, 1–13. [Google Scholar]
- Brook, J.W.; Pagnanelli, F. Integrating sustainability into innovation project portfolio management—A strategic perspective. J. Eng. Technol. Manag. 2014, 46, 46–62. [Google Scholar] [CrossRef]
- Fernández-Sánchez, G.; Rodríguez-López, F. A methodology to identify sustainability indicators in construction project management—Application to infrastructure projects in Spain. Ecol. Indic. 2010, 10, 1193–1201. [Google Scholar] [CrossRef]
- Martens, M.L.; de Carvalho, M.M. An exploratory study of sustainability evaluation in Project management. Prod.: Manag. Dev. 2013, 11, 111–117. [Google Scholar] [CrossRef]
- Tufinio, S.P.; Mooi, H.; Ravestijn, W.; Bakker, H.; Boorsma, M. Sustainability in project management: Where are we? Int. J. Eng. 2013, 11, 91–100. [Google Scholar]
- Silvius, G.; Schipper, R. Sustainability in Project Management Competencies: Analyzing the Competence Gap of Project Managers. J. Hum. Resour. Sustain. Stud. 2014, 2, 40–58. [Google Scholar] [CrossRef]
- Silvius, A.J.G.; Schipper, R.; Nedeski, S. Sustainability in Project Management: Reality Bites. PM World J. 2013, 2, 1–14. [Google Scholar]
- Brones, F.; de Carvalho, M.M.; de Senzi Zancul, E. Ecodesign in project management: A missing link for the integration of sustainability in product development? J. Clean. Prod. 2014, 80, 106–118. [Google Scholar] [CrossRef]
- Marcelino-Sádaba, S.; González-Jaen, L.F.; Pérez-Ezcurdia, A. Using project management as a way to sustainability. From a comprehensive review to a framework definition. J. Clean. Prod. 2015, 99, 1–16. [Google Scholar] [CrossRef]
- Silvius, A.G.; Schipper, R. A Conceptual Model for Exploring the Relationship Between Sustainability and Project Success. Procedia Comput. Sci. 2015, 64, 334–342. [Google Scholar] [CrossRef]
- Eid, M. Integrating Sustainable Development into Project Management Processes. Available online: http://www.pmi.org/~/media/PDF/Surveys/pp_eid.ashx (accessed on 21 March 2015).
- Silvius, G.; Schipper, R. A maturity model for integrating sustainability in projects and project management. In Proceedings of the 24th World Congress of the International Project Management Association, Istanbul, Turkey, 1–3 November 2010.
- Sánchez, M.A. Integrating sustainability issues into project management. J. Clean. Prod. 2015, 96, 319–330. [Google Scholar] [CrossRef]
- Labuschagne, C.; Brent, A.C. Sustainable project life cycles in the manufacturing sector. Int. J. Proj. Manag. 2005, 23, 159–168. [Google Scholar] [CrossRef]
- Gareis, R.; Heumann, M.; Martinuzzi, A. Relating sustainable development and project management. In Proceedings of the IRNOP IX, Berlin, Germany, 11–13 October 2009.
- Vandaele, N.; Decouttere, C. Sustainable R&D portfolio assessment. Decis. Support Syst. 2013, 54, 1521–1532. [Google Scholar]
- Khalili-Damghani, K.; Tavana, M. A comprehensive framework for sustainable project portfolio selection based on structural equation modelling. Proj. Manag. J. 2014, 45, 83–97. [Google Scholar] [CrossRef]
- Eskerod, P.; Huemann, M. Sustainable development and project stakeholder management: What standards say. Int. J. Manag. Proj. Bus. 2013, 6, 36–50. [Google Scholar] [CrossRef]
- Shipper, R.; Rorije, H.; Silvius, G. Creating sustainability change: A new paradigm in project management. In Proceedings of the 24th World Congress of the International Project Management Association, IPMA, Istambul, Turkey, 1–3 November 2010.
- Yao, H.; Shen, L.; Tan, Y.; Hao, J. Simulating the impacts of policy scenarios on the sustainability performance of infrastructure projects. Autom. Constr. 2011, 20, 1060–1069. [Google Scholar] [CrossRef]
- Dobrovolskienė, N.; Tamošiūnienė, R. An Index to Measure Sustainability of a Business Project in the Construction Industry: Lithuanian Case. Sustainability 2016, 8, 14. [Google Scholar] [CrossRef]
- Salehi, K. A hybrid fuzzy MCDM approach for project selection problem. Decis. Sci. Lett. 2015, 4, 109–116. [Google Scholar] [CrossRef]
- Mohagheghi, V.; Mousavi, S.M.; Vahdani, B. A New Optimization Model for Project Portfolio Selection Under Interval-Valued Fuzzy Environment. Arabian J. Sci. Eng. 2015, 40, 3351–3361. [Google Scholar] [CrossRef]
- Zaraket, F.A.; Olleik, M.; Yassine, A.A. Skill-based framework for optimal software project selection and resource allocation. Eur. J. Oper. Res. 2014, 234, 308–318. [Google Scholar] [CrossRef]
- Yoshimura, M.; Fujimi, Y.; Izui, K.; Nishiwaki, S. Decision-making support system for human resource allocation in product development projects. Int. J. Prod. Res. 2006, 44, 831–848. [Google Scholar] [CrossRef]
- Gutjahr, W.J.; Katzensteiner, S.; Reiter, P.; Stummer, C.; Denk, M. Multi-objective decision analysis for competence-oriented project portfolio selection. Eur. J. Oper. Res. 2010, 205, 670–679. [Google Scholar] [CrossRef]
- Siew, R.Y.; Balatbat, M.C.; Carmichael, D.G. Measuring project sustainability maturity level-a fuzzy-based approach. Int. J. Sustain. Dev. 2016, 19, 76–100. [Google Scholar] [CrossRef]
- Pimentel, B.S.; Gonzalez, E.S.; Barbosa, G.N. Decision-support models for sustainable mining networks: Fundamentals and challenges. J. Clean. Prod. 2016, 112, 2145–2157. [Google Scholar] [CrossRef]
- Siew, R.Y.; Balatbat, M.C.; Carmichael, D.G. A proposed framework for assessing the sustainability of infrastructure. Int. J. Constr. Manag. 2016. [Google Scholar] [CrossRef]
- Siew, R.Y.J. Integrating Sustainability into Construction Project Portfolio Management. KSCE J. Civ. Eng. 2016, 20, 101–108. [Google Scholar] [CrossRef]
- Higham, A.P.; Fortune, C.; Boothman, J.C. Sustainability and investment appraisal for housing regeneration projects. Structural Survey 2016. [Google Scholar] [CrossRef]
- Markowitz, H.M. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar] [CrossRef]
- Huang, C.C.; Chu, P.Y.; Chiang, Y.H. A fuzzy AHP application in government-sponsored R&D project selection. Omega 2008, 36, 1038–1052. [Google Scholar]
- Mangram, E.M. A Simplified Perspective of the Markowitz Portfolio Theory. Glob. J. Bus. Res. 2013, 7, 59–70. [Google Scholar]
- Anagnostopoulos, K.P.; Mamanis, G. A portfolio optimization model with three objectives and discrete variables. Comput. Oper. Res. 2010, 37, 1285–1297. [Google Scholar] [CrossRef]
- Qi, Y.; Steuer, R.E.; Wimmer, M. An analytical derivation of the efficient surface in portfolio selection with three criteria. Ann. Oper. Res. 2015. [Google Scholar] [CrossRef]
- Ghosh, A.; Mahanti, A. Investment Portfolio Management: A Review from 2009 to 2014. In Proceedings of the 10th Global Business and Social Science Research Conference, Beijing, China, 23–24 June 2014.
- Hadi, A.S.; El Naggar, A.A.; Bary, M.N.A. New Model and Method for Portfolios Selection. Appl. Math. Sci. 2016, 10, 263–288. [Google Scholar]
- Anagnostopoulos, K.P.; Mamanis, G. The mean–variance cardinality constrained portfolio optimization problem: An experimental evaluation of five multiobjective evolutionary algorithms. Expert Syst. Appl. 2011, 38, 14208–14217. [Google Scholar] [CrossRef]
- Stasytytė, V. Investicijų Portfelio Sprendimų Paramos Sistema. Ph.D. Thesis, Vilnius Gediminas Technical University (VGTU), Vilnius, Lithuania, 2011. [Google Scholar]
- Steuer, R.E.; Wimmer, M.; Hirschberger, M. Overviewing the transition of Markowitz bi-criterion portfolio selection to tri-criterion portfolio selection. J. Bus. Econ. 2013, 83, 61–85. [Google Scholar] [CrossRef]
- Steur, R.E.; Qi, Y.; Hirschberger, M. Portfolio Selection in the Presence of Multiple Criteria, Handbook of Financial Engineering; Springer: New York, NY, USA, 2008; pp. 3–24. [Google Scholar]
- Jana, P.; Roy, T.K.; Mazumder, S.K. Multi-objective possibilistic model for portfolio selection with transaction cost. J. Comput. Appl. Math. 2009, 228, 188–196. [Google Scholar] [CrossRef]
- Aboulaich, R.; Ellaia, R.; El Moumen, S. The mean-variance-CVaR model for portfolio optimization modeling using a multi-objective approach based on a hybrid method. Math. Model. Nat. Phenom. 2010, 5, 103–108. [Google Scholar] [CrossRef]
- Trenado, M.; Romero, M.; Cuadrado, M.L.; Romero, C. Corporate social responsibility in portfolio selection: A “goal games” against nature approach. Comput. Ind. Eng. 2014, 75, 260–265. [Google Scholar] [CrossRef]
- Utz, S.; Wimmer, M.; Steuer, R.E. Tri-criterion modeling for constructing more-sustainable mutual funds. Eur. J. Oper. Res. 2015, 246, 331–338. [Google Scholar] [CrossRef]
- Aouni, B.; Colapinto, C.; La Torre, D. Financial portfolio management through the goal programming model: Current state-of-the-art. Eur. J. Oper. Res. 2014, 234, 536–545. [Google Scholar] [CrossRef]
- Gasser, S.M.; Kremser, T.R.; Rammerstorfer, M.; Weinmayer, K. Markowitz Revisited Social Portfolio Engineering. In Proceedings of the 27th Australasian Finance and Banking Conference 2014, Sydney, Australia, 16–18 December 2014.
- Lo, A.W.; Petrov, C.; Wierzbicki, M. It’s 11pm–Do you know where your liquidity is? The mean-variance-liquidity frontier. J. Invest. Manag. 2003, 1, 55–93. [Google Scholar]
- Fang, Y.; Lai, K.K.; Wang, S.Y. Portfolio rebalancing model with transaction costs based on fuzzy decision theory. Eur. J. Oper. Res. 2006, 175, 879–893. [Google Scholar] [CrossRef]
- Junkus, J.; Berry, T.D. Socially responsible investing: A review of the critical issues. Manag. Financ. 2015, 41, 1176–1201. [Google Scholar] [CrossRef]
- Ballestero, E.; Bravo, M.; Pérez-Gladish, B.; Arenas-Parra, M.; Plà-Santamaria, D. Socially responsible investment: A multicriteria approach to portfolio selection combining ethical and financial objectives. Eur. J. Oper. Res. 2012, 216, 487–494. [Google Scholar] [CrossRef]
- Dorfleitner, G.; Leidl, M.; Reeder, J. Theory of social returns in portfolio choice with application to microfinance. J. Asset Manag. 2012, 13, 384–400. [Google Scholar] [CrossRef]
- Bilbao-Terol, A.; Arenas-Parra, M.; Cañal-Fernández, V. A fuzzy multi-objective approach for sustainable investments. Expert Syst. Appl. 2012, 39, 10904–10915. [Google Scholar] [CrossRef]
- Bilbao-Terol, A.; Arenas-Parra, M.; Cañal-Fernández, V. Selection of socially responsible portfolios using goal programming and fuzzy technology. Inf. Sci. 2012, 189, 110–125. [Google Scholar] [CrossRef]
- Bilbao-Terol, A.; Arenas-Parra, M.; Cañal-Fernández, V.; Bilbao-Terol, C. Selection of socially responsible portfolios using hedonic prices. J. Bus. Ethics 2013, 115, 515–529. [Google Scholar] [CrossRef]
- Bilbao-Terol, A.; Arenas-Parra, M.; Canal-Fernandez, V.; Bilbao-Terol, C. Multi-criteria decision making for choosing socially responsible investment within a behavioral portfolio theory framework: A new way of investing into a crisis environment. Ann. Oper. Res. 2015. [Google Scholar] [CrossRef]
- Calvo, C.; Ivorra, C.; Liern, V. Fuzzy portfolio selection with non-financial goals: Exploring the efficient frontier. Ann. Oper. Res. 2014. [Google Scholar] [CrossRef]
- Cabello, J.M.; Ruiz, F.; Pérez-Gladish, B.; Méndez-Rodríguez, P. Synthetic indicators of mutual funds’ environmental responsibility: An application of the Reference Point Method. Eur. J. Oper. Res. 2014, 236, 313–325. [Google Scholar] [CrossRef]
- Utz, S.; Wimmer, M.; Hirschberger, M.; Steuer, R.E. Tri-criterion inverse portfolio optimization with application to socially responsible mutual funds. Eur. J. Oper. Res. 2014, 234, 491–498. [Google Scholar] [CrossRef]
- Peylo, B.T. A synthesis of modern portfolio theory and sustainable investment. J. Investig. 2012, 21, 33–46. [Google Scholar]
- Peylo, B.T.; Schaltegger, S. An equation with many variables: Unhiding the relationship between sustainability and investment performance. J. Sustain. Financ. Invest. 2014, 4, 110–126. [Google Scholar] [CrossRef]
- Oikonomou, I.; Platanakis, E.; Sutcliffe, C. Creating More Stable and Diversified Socially Responsible Investment Portfolios; Discussion Paper; ICMA Centre: Reading, UK, 2015. [Google Scholar]
- Andrianov, A.A. Approaches and Software for Multi-Objective Optimization of Nuclear Power Structures. Sustainability 2012, 4, 721–739. [Google Scholar] [CrossRef]
- Bernoider, E.; Stix, V. A Method Using Weight Restrictions in Data Envelopment Analysis for Ranking and Validity Issues in Decision Making. Comput. Oper. Res. 2007, 34, 2637–2647. [Google Scholar] [CrossRef]
- Liou, J.J.; Tzeng, G.H. Comments on “Multiple criteria decision making (MCDM) methods in economics: An overview”. Technol. Econ. Dev. Econ. 2012, 18, 672–695. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; MD Nor, K.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res.-Ekon. Istraž. 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Kildienė, S. State of art surveys of overviews on MCDM/MADM methods. Technol. Econ. Dev. Econ. 2014, 20, 165–179. [Google Scholar] [CrossRef]
- Zopounidis, C.; Galariotis, E.; Doumpos, M.; Sarri, S.; Andriosopoulos, K. Multiple criteria decision aiding for finance: An updated bibliographic survey. Eur. J. Oper. Res. 2015, 247, 339–348. [Google Scholar] [CrossRef]
- Steuer, R.E.; Na, P. Multiple criteria decision making combined with finance: A categorized bibliographic study. Eur. J. Oper. Res. 2003, 150, 496–515. [Google Scholar] [CrossRef]
- Mansini, R.; Ogryczak, W.; Speranza, M.G. Twenty years of linear programming based portfolio optimization. Eur. J. Oper. Res. 2014, 234, 518–535. [Google Scholar] [CrossRef]
- Lieberman, E.R. Soviet multi-objective mathematical programming methods: An overview. Manag. Sci. 1991, 37, 1147–1165. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Diwekar, U. Introduction to Applied Optimization; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Ioppolo, G.; Cucurachi, S.; Salomone, R.; Saija, G.; Shi, L. Sustainable Local Development and Environmental Governance: A Strategic Planning Experience. Sustainability 2016, 8, 180. [Google Scholar] [CrossRef]
- Filatovas, E. Daugiakriterinių Optimizavimo Uždavinių Sprendimas Interaktyviuoju Būdu. Ph.D. Thesis, Vilnius University (VU), Vilnius, Lithuania, 2012. [Google Scholar]
- Haugen, R.A. Modern Investment Theory, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Saborido, R.; Ruiz, A.B.; Bermúdez, J.D.; Vercher, E.; Luque, M. Evolutionary multi-objective optimization algorithms for fuzzy portfolio selection. Appl. Soft Comput. 2016, 39, 48–63. [Google Scholar] [CrossRef]
- Boasson, V.; Boasson, E.; Zhou, Z. Portfolio optimization in a mean-semivariance framework. Invest. Manag. Financ. Innov. 2011, 8, 58–68. [Google Scholar]
- Zhang, W.G.; Mei, Q.; Lu, Q.; Xiao, W.L. Evaluating methods of investment project and optimizing models of portfolio selection in fuzzy uncertainty. Comput. Ind. Eng. 2011, 61, 721–728. [Google Scholar] [CrossRef]
- Qin, Z.; Kar, S.; Zheng, H. Uncertain portfolio adjusting model using semiabsolute deviation. Soft Comput. 2016, 20, 717–725. [Google Scholar] [CrossRef]
- Jafarizadeh, B.; Khorshid-Doust, R.R. A method of project selection based on capital asset pricing theories in a framework of mean–semideviation behavior. Int. J. Proj. Manag. 2008, 26, 612–619. [Google Scholar] [CrossRef]
- Estrada, J. Mean-semivariance optimization: A heuristic approach. J. Appl. Financ. (Former. Financ. Pract. Educ.) 2008. [Google Scholar] [CrossRef]
- Mashayekhi, Z.; Omrani, H. An integrated multi-objective Markowitz–DEA cross-efficiency model with fuzzy returns for portfolio selection problem. Appl. Soft Comput. 2016, 38, 1–9. [Google Scholar]
- Costa, H.R.; de O Barros, M.; Travassos, G.H. A risk based economical approach for evaluating software project portfolios. ACM SIGSOFT Softw. Eng. Notes 2005, 30, 1–5. [Google Scholar] [CrossRef]
- Chen, C.T.; Cheng, H.L. A comprehensive model for selecting information system project under fuzzy environment. Int. J. Proj. Manag. 2009, 27, 389–399. [Google Scholar] [CrossRef]
- Tiryaki, F.; Ahlatcioglu, B. Fuzzy portfolio selection using fuzzy analytic hierarchy process. Inf. Sci. 2009, 179, 53–69. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012. [Google Scholar]
- S Original by Berwin A; Turlach R Port by Andreas Weingessel. Quadprog: Functions to Solve Quadratic Programming Problems. Available online: http://CRAN.R-project.org/package=quadprog (accessed on 23 December 2015).
- lpSolve: Interface to Lp_solve v. 5.5 to Solve Linear/Integer Programs. R Package Version 5.6.7., 2013. Available online: http://CRAN.R-project.org/package=lpSolve (accessed on 23 December 2015).
- Pérez-Gladish, B.; Rodríguez, P.M.; M’zali, B.; Lang, P. Mutual funds efficiency measurement under financial and social responsibility criteria. J. Multi-Criteria Decis. Anal. 2013, 20, 109–125. [Google Scholar] [CrossRef]
| Year | Reference | Article Type | Aim of the Article | Methods Used | Field of Application | Was Sustainability Considered in the Context of Project Portfolio Selection and/or Resource Allocation in a Project Portfolio? |
|---|---|---|---|---|---|---|
| 2015 | Økland [2] | Literature review | To undertake a review of sustainability in project management | Literature review of 205 papers | Not specified | No |
| 2015 | Martens, and Carvalho [3] | Literature review, case studies | To investigate how companies are introducing sustainability into project management | Literature review, multiple-case study approach | Not specified | No |
| 2015 | Marcelin-Sádaba et al. [15] | Literature review, conceptual | To present the latest developments concerning sustainability in project management and to propose a new conceptual framework to contribute towards sustainable management of a project | Literature review of 110 papers | Industrial and civil engineering projects | No |
| 2015 | Silvius and Schipper [16] | Literature review, conceptual | To develop a conceptual model for exploring the relationship between sustainability and project success | Literature review | Not specified | No |
| 2015 | Sánchez [19] | Conceptual | To present a theoretical framework to evaluate projects that takes into account profits and economic, environmental and social impacts | Literature review, BSC (balanced scorecard), DEA, case study | Not specified | No |
| 2016 | Dobrovolskienė and Tamošiūnienė [27] | Empirical | To develop a composite sustainability index of a project | Literature review, survey, MCDM | Construction projects | Partly |
| 2016 | Siew et al. [33] | Conceptual | To present a fuzzy-based approach to measure maturity levels. | Literature review, fuzzy-based approach | Not specified | No |
| 2016 | Pimentel et al. [34] | Literature review | To provide a review of the literature and case studies of Operations Research and Management Sciences in the area of sustainability | Literature review | Mining industry projects | No |
| 2016 | Siew et al. [35] | Conceptual | To propose a framework for assessing the sustainability of infrastructure projects | Literature review, MCDM | Infrastructure projects | No |
| 2016 | Siew [36] | Conceptual | To propose a way to measure sustainability across project portfolio | Literature review | Construction projects | Partly |
| 2016 | Higham et al. [37] | Structural survey | To assess the use, in practice, of appraisals frameworks regarding sustainability evaluation in social housing sector projects | Literature review, a survey | Housing regeneration projects | No |
| Project Code | Return | Risk | Sustainability Index |
|---|---|---|---|
| P1 | 0.4519 | 0.0526 | 0.6700 |
| P2 | 0.5435 | 0.0880 | 0.5700 |
| P3 | 0.5848 | 0.0942 | 0.6600 |
| P4 | 0.4413 | 0.0433 | 0.3300 |
| P5 | 0.3932 | 0.0633 | 0.7400 |
| P6 | 0.3640 | 0.0680 | 0.4500 |
| P7 | 0.4907 | 0.0342 | 0.3300 |
| P8 | 0.3912 | 0.0383 | 0.3900 |
| P9 | 0.5420 | 0.0582 | 0.6500 |
| P10 | 0.3718 | 0.0467 | 0.6400 |
| P11 | 0.4821 | 0.0562 | 0.6700 |
| P12 | 0.3511 | 0.1344 | 0.5700 |
| P13 | 0.5833 | 0.0785 | 0.5600 |
| P14 | 0.4614 | 0.0452 | 0.3700 |
| P15 | 0.4555 | 0.1889 | 0.7200 |
| P16 | 0.3910 | 0.0347 | 0.4500 |
| P17 | 0.5304 | 0.0266 | 0.5500 |
| P18 | 0.5909 | 0.0411 | 0.5900 |
| P19 | 0.5416 | 0.0531 | 0.6100 |
| P20 | 0.4707 | 0.1128 | 0.6500 |
| α | Return of Portfolio | ||
|---|---|---|---|
| α | Pearson Correlation | 1 | −0.743 ** |
| Sig. (2-tailed) | - | 0.000 | |
| N | 111 | 111 | |
| Return of portfolio | Pearson Correlation | −0.743 ** | 1 |
| Sig. (2-tailed) | 0.000 | - | |
| N | 111 | 111 | |
| Project Code | Financial Portfolio | Balanced Portfolio | Sustainable Portfolio |
|---|---|---|---|
| α = 0; = 0.5 | α = 0.5; = 0.5 | α = 1; = 0.5 | |
| P1 | 0.1244 | 0.2000 | |
| P2 | 0.0505 | ||
| P3 | 0.0673 | 0.1024 | 0.2000 |
| P4 | |||
| P5 | 0.1872 | 0.2000 | |
| P6 | |||
| P7 | 0.1090 | ||
| P8 | |||
| P9 | 0.1133 | 0.1759 | |
| P10 | |||
| P11 | 0.0266 | 0.1571 | 0.2000 |
| P12 | |||
| P13 | 0.0957 | ||
| P14 | |||
| P15 | 0.0242 | 0.2000 | |
| P16 | |||
| P17 | 0.2000 | ||
| P18 | 0.2000 | 0.1415 | |
| P19 | 0.1354 | 0.0685 | |
| P20 | 0.0021 | 0.0188 | |
| Return of portfolio | 0.5490 | 0.5014 | 0.4735 |
| Risk of portfolio | 0.0180 | 0.0231 | 0.0467 |
| Sustainability of portfolio | 0.5663 | 0.6640 | 0.6920 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobrovolskienė, N.; Tamošiūnienė, R. Sustainability-Oriented Financial Resource Allocation in a Project Portfolio through Multi-Criteria Decision-Making. Sustainability 2016, 8, 485. https://doi.org/10.3390/su8050485
Dobrovolskienė N, Tamošiūnienė R. Sustainability-Oriented Financial Resource Allocation in a Project Portfolio through Multi-Criteria Decision-Making. Sustainability. 2016; 8(5):485. https://doi.org/10.3390/su8050485
Chicago/Turabian StyleDobrovolskienė, Nomeda, and Rima Tamošiūnienė. 2016. "Sustainability-Oriented Financial Resource Allocation in a Project Portfolio through Multi-Criteria Decision-Making" Sustainability 8, no. 5: 485. https://doi.org/10.3390/su8050485
APA StyleDobrovolskienė, N., & Tamošiūnienė, R. (2016). Sustainability-Oriented Financial Resource Allocation in a Project Portfolio through Multi-Criteria Decision-Making. Sustainability, 8(5), 485. https://doi.org/10.3390/su8050485






