Abstract
By adopting an energy-input based directional distance function, we calculated the shadow price of four types of energy (i.e., coal, oil, gas and electricity) among 30 areas in China from 1998 to 2012. Moreover, a macro-energy efficiency index in China was estimated and divided into intra-provincial technical efficiency, allocation efficiency of energy input structure and inter-provincial energy allocation efficiency. It shows that total energy efficiency has decreased in recent years, where intra-provincial energy technical efficiency drops markedly and extensive mode of energy consumption rises. However, energy structure and allocation improves slowly. Meanwhile, lacking an integrated energy market leads to the loss of energy efficiency. Further improvement of market allocation and structure adjustment play a pivotal role in the increase of energy efficiency.
1. Introduction
Since the reform and opening up, extensive economic growth mode with high input and high energy consumption has made contributions to the boom of the Chinese economy with the side effect of energy and environmental problems. With the development of urbanization and industrialization, the contradiction of energy supply and demand would be evident in the long term due to the growth of energy consumption. For example, the energy consumption reached 42.6 trillion Ton of standard Coal Equivalent (Tce) in China in 2014. Saving energy and reducing consumption is necessary for sustainable development, owing to the non-renewability and scarcity of fossil fuels such as coal and gas. Therefore, in China’s 12th Five-Year Plan, there are some main targets proposed. The first target is to reduce the energy consumption in GDP by 16% compared with that in 2010 by the control of energy consumption intensity and total energy. The second one is to optimize energy structure by lowering the reliance on fossil fuels. The third target is to promote marketization of energy price by reforming energy pricing mechanism. To realize these aims, we need to answer these three questions: (1) Is the energy pricing reasonable in China? (2) Which level is the total macro-energy efficiency at in China? (3) Is the promotion of energy marketization and optimization of energy structure effective in China?
Compared with advanced level in the world, total energy efficiency in China is not high enough for low energy using efficiency. By evaluating total factor energy efficiency of different economies, China is found as the economy with the lowest value in 17 APEC countries or areas [1]. Even though total factor energy efficiency has greatly increased in China in recent years, and narrowed the gap with that of developed countries, China still has large quantities of energy consumption, leading to potentiality of energy-saving and emission-reduction [2]. Increasing numbers of scholars focus on energy inefficiency and technique inefficiency for the reason of low energy efficiency in China [3]. Firstly, as for the energy resources in China, the proportion of coal is too large while the production of clean energy is not enough, resulting in unreasonable energy input structure. This part of loss of the energy efficiency can be remedied by upgrading energy structure, aiming at restricting carbon emission intensity [4,5]. The other reason is energy market distortions resulted from government intervention. During the economic transformation, lag of energy marketization causes energy price distortion, which further restrains the improvement of energy efficiency in China [6,7]. Therefore, some measures, such as energy marketization, reduction of government intervention and optimization of energy allocation by market, contribute to the realization of energy saving and emission reduction.
In this paper, a macro-energy efficiency index in China (H) is established for quantized analyses of the impact of factors, such as energy structure and allocation on energy efficiency. The index is then decomposed into intra-provincial technical efficiency (ATE), allocation efficiency of energy input structure efficiency (AAE) and inter-provincial energy allocation efficiency (RE). The first index is the efficiency loss caused by technical inefficiency, while the other two are allocation inefficiency caused by market distortions. The result of the research would offer theoretical support for the assessment of energy structure adjustment and promotion of the market reform of energy prices.
The rest of the paper is organized as follows: Section 2 reviews the total factor energy efficiency and shadow price. Section 3 introduces energy-input based directional distance function (DDF) and estimation of energy shadow price and constructs macro-energy efficiency indices as well as corresponding deposition model. Section 4 is about data processing and analysis. Section 5 is an empirical analysis of a case. The last section is the conclusion.
2. Literature Review
To evaluate the energy efficiency in China accurately, we are required to select the indices of energy efficiency reasonably, which can mainly be divided into single factor energy efficiency and total factor energy efficiency. With the feature of easy comparison and simple calculation, single factor energy efficiency is introduced mainly for analyzing the relationship of single energy input and output. Early research mostly applied this method to evaluate energy efficiency. For example, energy consumption of the Chinese industrial sector in the 1990s was decomposed by an improved Laspeyres Index [8]. The research found that technical effect is the leading factor of the changes in industrial energy consumption. This method is criticized by many researchers because in the single factor energy efficiency, the contribution of labor and capital to output is neglected, and then the substitution effect among different production factors is not taken into account.
Therefore, Hu and Wang [9] proposed the concept of total factor energy efficiency originally, which brought production factors such as labor and capital into efficiency analysis. By considering the substitution effect between energy and other production factors, real production process could be well simulated. Thus, this method became the main evaluation method for energy efficiency. By window analysis of DEA method, total factor energy efficiency of 23 developing countries from 1980 to 2005 were tested before analyzing the relation between total factor energy efficiency and incomes based on Tobit model [4]. Meanwhile, a parametric meta-frontier approach based on the Shephard energy distance was introduced, dividing 30 provinces in China into three technical frontiers for analyzing efficiency differences due to technology gap among areas [10].
Some researches [11,12,13] discussed multiple inputs and outputs based on the model of multiple input and single output. That means they combined undesirable outputs such as pollutant during production process into output system, which better simulated the byproducts in actual production process such as carbon dioxide, sulfur dioxide and other industrial wastes. For example, Fujii et al. [11] employed a DDF that can handle multiple inputs and outputs to compute the change of TFP. Then it was found that environmentally sensitive productivity (ESPs) of China’s iron and steel industry had continuously improved, even in the period when the conventional economic productivity (CEP) declined in the 1990s. Moreover, Li et al. [12] brought byproducts (carbon dioxide and sulfur dioxide) into the production process, establishing an environmental total factor energy efficiency index. According to SBM model, energy efficiency is commonly lower than that regardless of bad output, which means energy efficiency in China is probable to be over-estimated. Moreover, Li et al. [13] introduced a meta-frontier framework with the improved DDF to measure the meta-frontier energy efficiency with carbon dioxide emissions. The research indicated that the main reason for low energy efficiency in China is managerial failure in the east and west areas, and technological differences in middle part.
Recently, more and more scholars [14,15,16,17] pay attention to the impact of the energy input structure and shadow price of total factor energy efficiency, resulting in incapability of estimating energy allocation efficiency, which was first analyzed by Ouyang and Sun [14] as well as Sheng [15,16]. As we know, underestimation of energy price leads to excessive energy consumption during production process. For example, Ouyang et al. [14] pointed out that factor prices of capital, labor and energy are distorted in China due to government regulations. Moreover, energy prices is relatively low compared with capital price, while is relatively high compared to labor price. Meanwhile, energy type would affect the energy allocation significantly [16,17]. Kumar et al. [16] estimated the Morishima elasticity of substitution between different fossil fuels and renewable resources, and found that the types of energy would make different contributions to total factor energy efficiency. All these factors would have further influence on total factor energy efficiency.
Energy shadow price reflects the marginal cost of production or marginal output, which is the price when production process gets best allocation. The estimation of shadow price can offer theoretical support for policy decision. In recent years, shadow price is widely used in the area of estimation of pollutant price [18,19,20,21]. For example, Kaneko et al. [18] used a non-parametric DDF approach to calculate the shadow prices of sulfur dioxide, and then estimated the regional pollution abatement cost under the financial allocation strategy in China. Moreover, Ishinabe et al. [19] evaluated the shadow price of greenhouse gas (GHG) emissions for 1024 international companies. Meanwhile, Molinos-Senante et al. [19] analyzed the carbon dioxide emission efficiency and shadow prices of sewage plant based on a parametric quadratic DDF and got the conclusion that shadow price mechanism of carbon dioxide contributes to emission reduction better than command-and-control regulation.
Among these studies, the methods to estimate the shadow price differ from one another, depending on the respective needs. For example, Sheng et al. [15] estimated energy shadow prices by non-parametric approach. With DEA to evaluate energy DDF, the result showed that both national and regional energy shadow prices are higher than market price. Further research (Sheng et al [16]) found that the situation of total factor energy inefficiency in China has improved during the 15 years. The similar method has been adopted by Kaneko et al. [18] and Li et al. [13]. Although the non-parametric DEA has the advantage of envelope characteristics, it shows the limitation of excluding statistical noise. Based on the stochastic frontier analysis (SFA), Ouyang et al. [14] analyzed the factor allocative efficiency of China’s industrial sector, and estimated the energy savings potential from the perspective of allocative inefficiency. Comparing with DEA, SFA has the limitation of envelopment, but it is convenient to do parametric test. Another method to estimate shadow price is parametric linear programming (PLP). It combines the envelope feature of DEA with parameters nature of SFA, which is widely used to estimate DDF [17,19]. For instance, Kumar et al. [17] applied quadratic function to approximate the distance function, and estimated the Morishima elasticity of substitution between different fossil fuels and renewable resources.
In this paper, we are extending the work of Ouyang and Sun [14], Sheng et al. [16] and Kumar et al. [17] to include energy structure. Firstly, an energy-input DDF is established to evaluate total factor energy efficiency. Next ,we break down the shadow price into four sources of energy. Similar to Kumar et al. [17], by adopting PLP, we set up a macro-energy index in China and divide energy inefficiency into three parts, energy technical inefficiency in each area, energy efficiency loss in each area due to irrational input structure and allocation inefficiency due to energy misallocation nationwide.
3. Methodology
3.1. Energy Efficiency and Directional Distance Function
Firstly, we assume that in each province there are J types of energy input, , N types of other input, , and M kinds of output, . Therefore, energy technology is represented by production possibility set T.
where T, as a set containing all possible input–output vectors, is constructed for describing technical efficiency of production. According to production theory, T is assumed as a closed finite set. Besides, both inputs and outputs should have the property of strong disposability. That means, if and , then .
Aiming at remanding the neglect of definition and measurement of energy efficiency, Zhou et al. [22] defined the energy-input based Shephard Distance Function.
According to production theory, the energy-input based Shephard Distance Function has two features. One is . The other is that is a homogeneous linear function of energy input. Meanwhile, energy-input based directional distance function reflects the maximal cuttable ratio of energy input when technique and other factor inputs (i.e., labor, capital, etc.) remain [23]. Therefore, , as the energy input when the maximal energy efficiency occurs in the area, is the optimal energy input theoretically.
Assuming that is direction vector and , the energy-input based directional distance function is
Corresponding to the homogeneity of the energy-input based Shephard Distance Function, the feature of the energy-input based directional distance function is
Let , the relation between directional distance function and the energy-input based Shephard Distance Function could be calculated.
Directional input distance function should satisfy the following constraints as well.
3.2. Energy Shadow price Evaluation
Shadow price of energy reflects both the scarcity and marginal use value of energy. Moreover, the scarcity of energy is pivotal for working out reasonable energy price, regulating the supply–demand relation of energy market and promoting enterprises to raise the energy using efficiency. As a result, decomposition of energy efficiency is analyzed by shadow price in this paper.
Dual relation between maximized profit function and energy-input based directional distance function should be considered for calculating the shadow price of energy input. We assume that price of J types of energy inputs are , price of M types of other input factors are , price of N types of outputs are . Then the profit function is
The profit function means that producer would earn the maximal profit when the output is given and all the factors except energy remain. Because be equivalent to , profit function could be converted as
It is feasible to reduce energy input along the direction g. Thus profit, function could be converted as
The surplus receipt is the value of conserved energy. After transposition,
Therefore, the defined directional distance function is
Envelope theorem is applied in Equation (12). Then the shadow price model is
Therefore, if the price of the jth output is , the shadow price of the ith type of energy could be calculated.
3.3. Parametric Forms of Directional Input Distance Function
Translog function is commonly introduced for parameterizing Shephard Distance Function but not directional distance function because the form of translog function cannot be limited to satisfy the transfer properties. Moreover, quadratic function is the second-order approximate of an unknown distance function, which could perfectly satisfy the properties of directional distance function [24]. Therefore, energy efficiency is estimated by quadratic directional distance function.
where .
Parameter linear program was used for the estimation of quadratic directional distance function in this paper according to Yuan [24] and Wang et al. [25].
S. t.
- (1)
- Energy-input based directional distance function
- (2)
- Monotonicity in inputs
- (3)
- Monotonicity in outputs
- (4)
- Homogeneous linear restriction
- (5)
- Symmetry of quadratic form
Therefore, shadow price of the i-th type of energy is
Energy efficiency of the corresponded area is
3.4. Establishment and Decomposition of Overall Energy Efficiency
Referring to the research of Li and Ng [26], a national index was constructed and called national energy efficiency. To build the index, the first step is to construct a virtual area, where the input and output of the area equals to national average. That is to say, and are national input, while is national output. When T is convex, national energy efficiency equals to the energy efficiency of the virtual area. Therefore, the national energy efficiency is: .
According to Li and Ng [26], the first factor equals to the sum of the minimal energy shadow input of all areas, , divided by the shadow price of total real energy input, . The factor equals to the weighted average of technical efficiency index of each area as well.
where is the shadow prices of minimal energy shadow input in China.
The second factor equals to the minimal real energy shadow input of each area, , divided by the sum of the minimal energy shadow input of all areas. Therefore, misallocation of available energy due to the price, which is called allocation efficiency of energy input structure, would lead to efficiency loss of energy structure.
where .
The third factor is the efficiency loss due to energy misallocation among areas. For example, when area A is under the condition of increasing returns to scale, while area B is under the condition of decreasing returns to scale, energy flows from area A to B would lead to the raise of total output. By eliminating the effect of the first two factors from total energy efficiency, the impact of misallocation is
where RE is inter-provincial energy allocation efficiency index. Based on the definitions above, national energy efficiency could be decomposed as
4. Data
After dropping the data of Hong Kong, Macau, Taiwan and Tibet, data of 30 areas from 1998 to 2012 are selected to make an input–output panel for empirical study. All data come from China Statistical Yearbook [27] and China Energy Statistical Yearbook [28].
The variables include the inputs (labor, capital stock and energy consumption), and an output (gross regional product). In previous studies, labor force was widely used as the index of labor input. However, human capital is a better index on measuring the contribution of labor during production [29]. Thus, the index in this paper is the number of the employees weighted by average education attainment of different areas at the end of the year. As for the capital stock, we introduce the permanent inventory method to estimate the capital input. According to the research [30], investment of fixed capital is selected as the investment index of the year. By constructing the price index of investment in the fixed assets from 1952 to 2010, the real investment prices of areas are calculated. The model for capital stock accounting is
where is the stock of capital in period , is depreciation rate, and is the amount of investment in period .
Data of merely energy consumption of each area come from China Energy Statistical Yearbook [28]. After categorizing the data into four main types, including coal, oil, gas and electricity (i.e., hydropower and nuclear power) based on energy balance sheet of each area, the measurement unit is converted to 1000 Tce by heat quantity. Specifically, data of Hainan in 2002 and data of Ningxia from 2000 to 2002 are estimated based on other data of the area. Gross regional product of each area is selected as the output in this paper. To eliminate the effect of price factor, we use gross regional product deflator. All nominal variables are deflated to real variables by using a price index for the year 2000.
In Figure 1 we will show the total energy consumption in China from 1998 to 2012, while sort out the descriptive analysis of total input and output in Table 1.
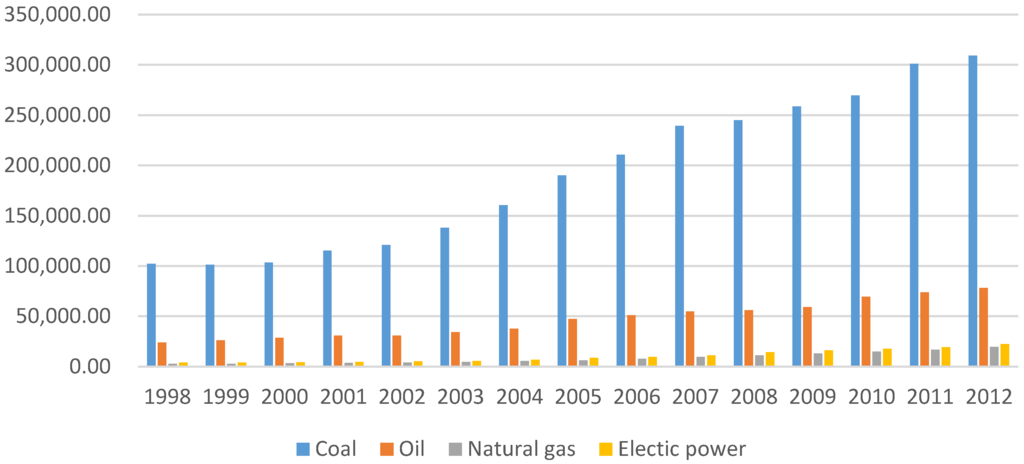
Figure 1.
Total energy consumption in China.

Table 1.
Descriptive analysis of total input and output.
5. Results and Discussions
5.1. Estimated Results ANALYSIS
In Table 2, we standardize the process of input and output data of 30 areas in China from 1998 to 2012, then estimate the parameters of the directional distance function by linear programming model.

Table 2.
Parameter estimation of quadratic directional distance function.
5.2. Results Analysis of Shadow Prices
Shadow prices of factors reflect the marginal output of energy; in other words, the scarcity of energy. When energy shadow price is higher than market price, firms would choose more energy input for higher profit during production. Therefore, shadow price is the key to work out reasonable energy price, regulate the supply–demand relation of energy market and promote enterprises to raise the energy using efficiency.
On the perspective of national condition, shadow price of coal, gas and electricity kept stable from 1998 to 2012. The shadow prices of the three types of energy decreased slightly annually before 2007, while had a modest rise since then. As shown in Figure 2, the shadow price of coal fluctuated dramatically, though the price maintained at a level of 0.400. Meanwhile, shadow prices of gas and electricity fluctuated around 0.150 and 0.100, respectively.
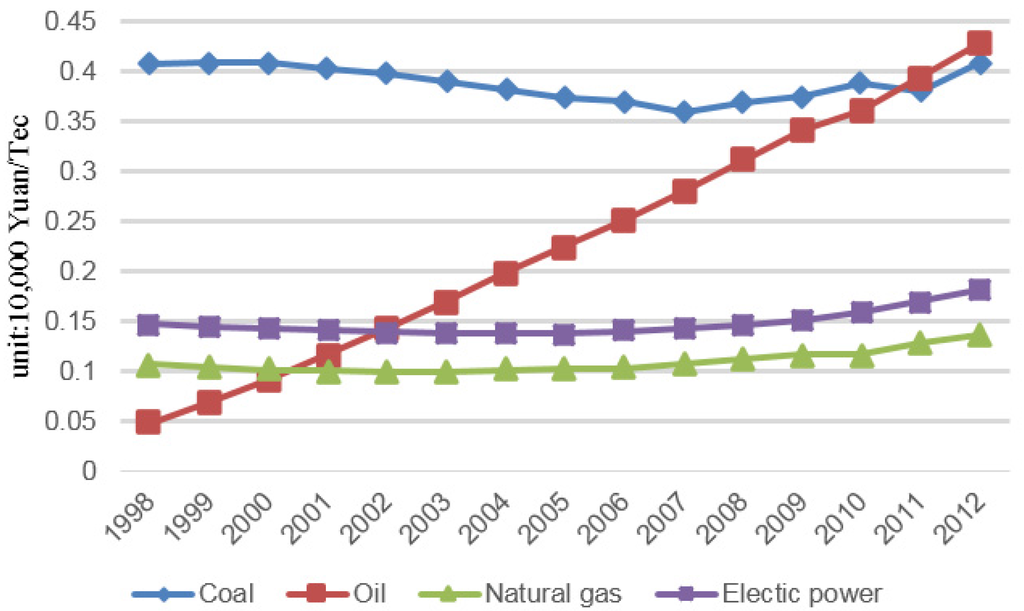
Figure 2.
Variation trend of shadow price of energy in China.
Remarkably, the shadow price of oil increase sharply, from 0.047 to 0.428 during the 15 years. It means that the marginal output soared rapidly. Over the same period, the price of crude oils soared from $20 per barrel in 1998 to $90 per barrel. Aiming at the increase on price of oil products in China, we refer to the explanation of Zheng et al. [31] and conclude the reasons as followed. For one thing, the cost of oil processing would raise due to higher emission standard (Chinese emission standard at Phase II to Phase VI) and higher requirement for oil quality. Moreover, improving the oil quality would increase the marginal output and also the shadow price of oil. Furthermore, as the oil price kept climbing, not only have small vehicles with low emissions become popular with consumers, but they have also been supported by national policy like tax allowance (half purchase tax for household car lower than 1.6 L). On such occasion, unit oil output would grow, and accordingly the shadow price of oil would increase.
As is shown in Table 3, shadow price of the four types of energy differs from each other. On the perspective of coal, areas with high shadow prices of coal (over 5000 Yuan/Tce) are Sichuan (0.822), Beijing (0.564), Xinjiang (0.516), Chongqing (0.509) and Guangdong (0.504). For example, shadow price of coal in Sichuan rose from 5330 Yuan/Tce to 18,020 Yuan/Tce, similar to Hunan, Beijing and Guangdong. That means the marginal output of coal increases significantly. In contrast, areas with low shadow price of coal (less than 3000 Yuan/Tce) are Hebei (0.184), Shanxi (0.192), Neimenggu (0.229), Shandong (0.261) and Jiangsu (0.293). Out of these areas, shadow price of Hebei is the lowest, whose value reached 560 Yuan/Tce, far lower than national average (3880 Yuan/Tce). Besides, shadow prices of coal in Heilongjiang, Hebei and Neimenggu had the greatest reduction, which means the marginal output of coal declined sharply in recent years.

Table 3.
Shadow price of each area (Unit: 10,000 Yuan/Tce).
As for oil, the areas with high shadow price of oil (over 3000 Yuan/Tce) include Hunan (0.351), Henan (0.309), Guangxi (0.309), Yunnan (0.307) and Hebei (0.305). Namely, shadow price of Hunan rose from 880 Yuan/Tce to 8450 Yuan/Tce, similar to that of Hubei, Henan, Jiangsu, Shanxi, Neimenggu, Sichuan and Chongqing, which means that the marginal output increased remarkably. On the contrary, areas with low oil shadow prices (less than 1500 Yuan/Tce) are Guangdong (0.054), Shanghai (0.097), Beijing (0.142) and Jiangsu (0.150). Specifically, the shadow price of Guangdong, at only 540 Yuan/Tce, is the lowest, far lower than the national average (2280 Yuan/Tce). Areas with growth rates that are far from the national average include Guangdong, Shandong, Jiangsu, Zhejiang, Liaoning.
On perspective of gas, areas with high shadow price of gas (over 1500 Yuan/Tce) are Hebei (0.183), Jiangsu (0.168), Henan (0.156), Shandong (0.153) and Hunan (0.150). Specifically, shadow price in Heibei is always higher than national average, increasing significantly in recent years, which is similar to Shanxi, Neimenggu, Zhejiang, Shandong and Henan. On the contrary, areas with low gas shadow prices (less than 800 Yuan/Tce) include Xinjiang (0.045), Hainan (0.056), Sichuan (0.066), Qinghai (0.067), Beijing (0.079) and Heilongjiang (0.078). For example, shadow price of Xinjiang decreased from a low value recently.
When it comes to electricity (i.e., nuclear power and hydropower), areas with high shadow price of electricity (over 2000 Yuan/Tce) include Shanghai (0.227) and Beijing (0.218). Besides, other areas such as Tianjin (0.198), Neimenggu (0.186), Hainan (0.180) and Xinjiang (0.191) have high electricity output. In contrast, areas with low shadow price of electricity (less than 1.000 Yuan/Tce) include Sichuan (0.060), Henan (0.061), Hunan (0.064), Anhui (0.089), Hubei (0.094) and Guangxi (0.092).
Based on previous studies, we categorize energy into four types, finding that shadow prices of the same type of energy differ in different areas, which also shows marginal output of energy in different areas varies. For example, when shadow price of coal reached 18,020 Yuan/Tce in Sichuan, shadow price of coal in Hebei is only 550 Yuan/Tce. In a perfectly competitive market, price of the same type of energy should be the same. This situation indicates the existence of trade barrier, which means energy factor is not complete circulation in different regions.
Besides, in areas with rich energy resources, energy marginal output is low in most areas. For example, in Shanxi and Neimenggu, the major coal producing provinces, coal shadow prices are lower than national average. This result is similar to the conclusion that the richer energy resource is, the lower energy price is [32], due to the lack of an integrated energy market. This factor has seriously hindered the scale economy of regional industries and has resulted in the loss of total factor energy efficiency.
Meanwhile, in Guangdong, Shanghai and Beijing, areas with large amount of oil importation, processing and consumption, marginal output of oil is lower than national average. Obviously, there are not rich resources in these areas. However, since most state-owned large petrochemical project located in these areas due to policy support, oil efficiency is too low to save resources. Therefore, compared with the lack of energy resources, misallocation of factor market resulting from administrative interference leads to the inefficiency of energy more seriously [33].
5.3. Results Analysis of Energy Efficiency
According to the average data value of the past years, areas with high energy efficiency are Qinghai (0.972), Ningxia (0.970), Guangxi (0.942), Gansu (0.952), Sichuan (0.952) and Hainan (0.951). Energy efficiencies of all these areas are higher than 0.950. On the contrary, areas with low energy efficiency are Liaoning (0.724), Yunnan (0.783), Jiangsu (0.806), Neimenggu (0.814) and Guizhou (0.845). Energy efficiencies of all these areas are lower than 0.850. All the Energy efficiency of each province and national energy efficiency decomposition is disposed in Table 4 and Figure 3.

Table 4.
Energy efficiency of each province and national energy efficiency decomposition.
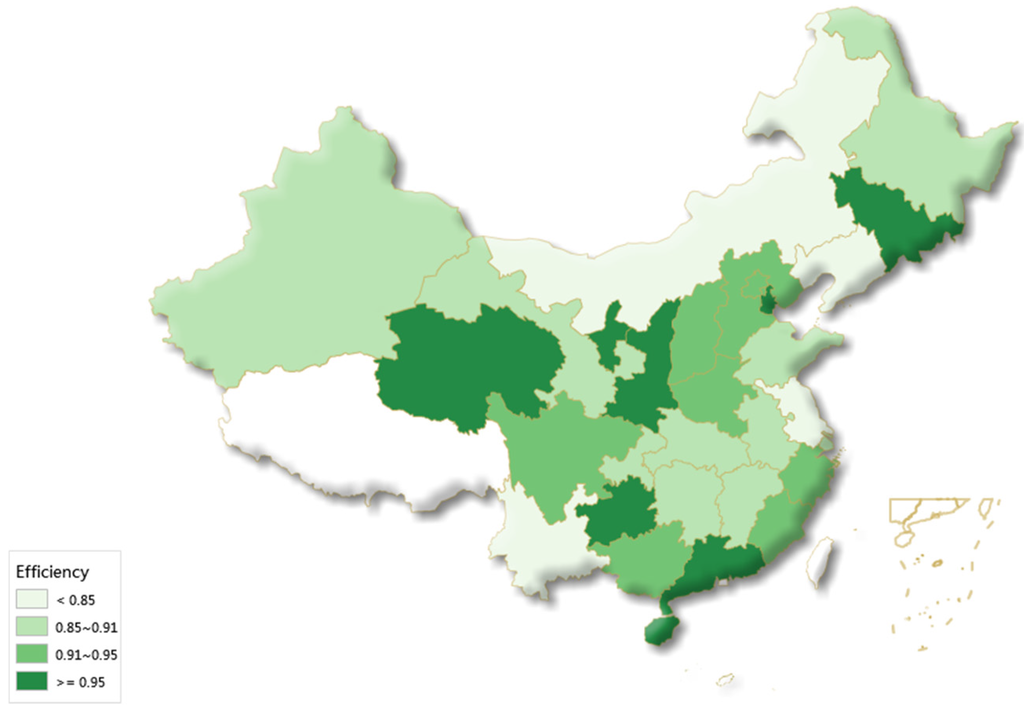
Figure 3.
Total factor energy efficiency in China.
The sorted result is consistent with results from other research [12,34]. Besides, total factor energy efficiency of Jiangsu, Guizhou, Shandong and Beijing shows an increasing tendency in fluctuation, reaching an advanced level of the country, especially Jiangsu, whose value increased from 0.413 to 1.000 during the 15 years. In contrast, there is a significant decline of energy efficiency in Liaoning, Yunnan, Xinjiang and Zhejiang. For example, total factor energy efficiency of Xinjiang is far lower than the national average due to the decreased fluctuation from 1998.
Based on the condition of the three regions, efficiency of the east area have fluctuated greatly with the decline in recent years. The efficiency drops from 0.937 in 2008 to 0.811 in 2012, illustrating the rise of extensive development mode. In the middle area, the result of significant decline is similar to the result of Li et al [12]. Li believes that the reason for the sharp decline is the drop of management efficiency in the middle area. On the contrary, energy efficiency performs well, even though the support policy is not as good as in the east area and energy endowment is not as good as that in the middle area. According to Lin et al [23], the result is due to the contribution of western development policy on energy efficiency.
Figure 4 shows the variation trend of national efficiency and its decomposition. As we see, macro-energy efficiency index (H) presents an invert U [35,36], which steadily rises from 1998 to 2003. After reaching the peak in 2002 and 2003, the energy efficiency keeps declining, even lower than 0.800 (i.e., 2007: 0.761) in recent years. These results imply that extensive mode of energy consumption rises in recent decades and the total energy utilization is not in an optimistic condition.
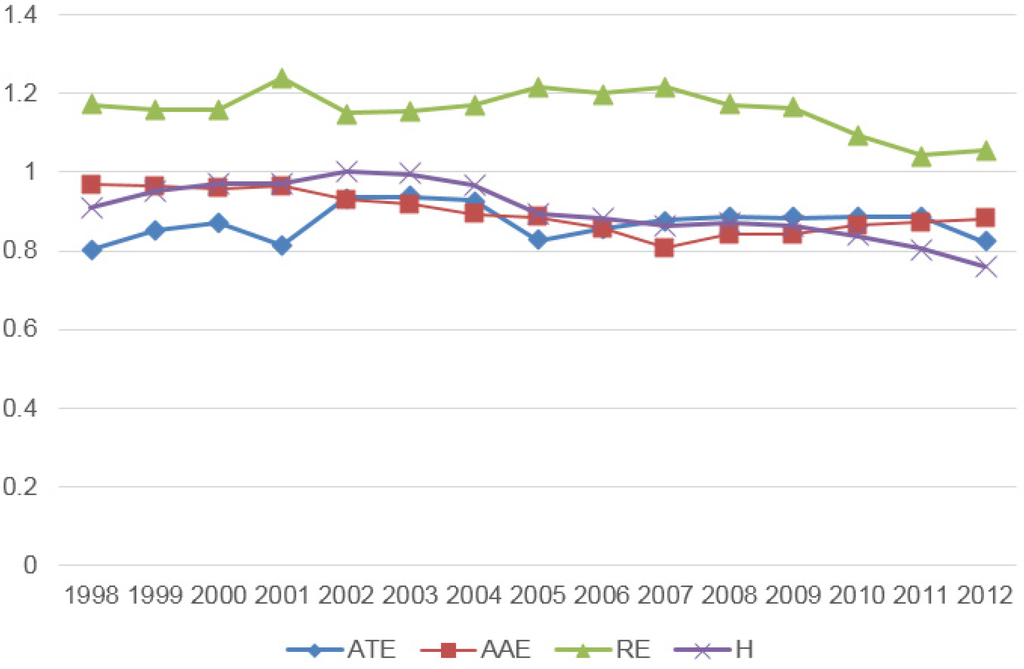
Figure 4.
Variation trend of national energy efficiency and its decomposition.
By decomposing macro-energy efficiency index (H) into intra-provincial technical efficiency (ATE), allocation efficiency of energy input structure (AAE) and inter-provincial energy allocation efficiency (RE), we found that ATE has similar trends to macro-energy efficiency nationwide, which presents an invert U as well. Moreover, the value of ATE decreases sharply recently, which is consistent with the result that technical inefficiency tends to increase [3]. AAE drops from 96.8% to 80.9% in the ten years since 1998 and presents a V. Not until 2008 did the value start to rise again and go back to 0.879. This fluctuation indicates that the improvement of energy structure could raise the energy efficiency effectively. Therefore, it is crucial for the government to adjust the policy of energy structure, which has already achieved some results. As for RE, its value is 1.171 in 1998, which means that energy allocation efficiency could increase by 0.170 if energy could flow freely among areas. Since 1998, energy allocation efficiency among areas increased in fluctuation, so that RE decreased from 1.171 to 1.054 during the 15 years accordingly. These results imply that marketization could break the inter-provincial energy barrier. During the past decades, liberalization in energy markets has developed remarkably.
6. Conclusions
In this paper, an energy-input based directional distance function was established for measuring total factor energy efficiency and shadow price of four types of energy (i.e., coal, oil, gas and electricity) among 30 areas in China from 1998 to 2012. Moreover, a macro-energy efficiency index in China was estimated and divided into intra-provincial technical efficiency, allocation efficiency of energy input structure and inter-provincial energy allocation efficiency. The main conclusions are as follows:
- By extending the work of prior research, we break down the shadow price into four sources of energy, and find that the shadow prices of different kinds of energy are quite different, and the same kind of energy also has different shadow prices in different regions. The situation indicates the existence of energy trade barriers among regions and the different contribution of the several types of energy to economy.
- Among the kinds of energy mentioned, the shadow price of oil has climbed dramatically, which means the efficiency of oil consumption has greatly improved. The increasingly rigid vehicle emissions standards and increasing tax allowance on smaller vehicles, may lead to the increase of marginal oil output.
- In areas with rich energy resources, energy marginal output is low in most areas due to the lack of an integrated energy market, resulting in the reduction of total factor energy efficiency. Besides, misallocation of factor market owing to administrative interference remarkably brings about the inefficiency of energy.
- Both the structure of energy input and inter-provincial allocation of energy impact on energy efficiency. Increasing values of the two indices in recent years imply the effect of China’s adjusted energy policy. Inter-provincial energy barrier will be broken for the marketization of energy factor and better negotiability of energy among areas. Specifically, it is of great necessity to realize marketing disposition of energy, energy structure adjustment and energy efficiency improvement for achieving reduction goal of carbon emission.
Thus, we call for a reform on energy factor market, in order to reduce the impact of administrative interference and make the market allocation effective. Besides, we suggest a need for greater environment regulation and greater emission standards to improve the total factor energy efficiency.
There are some limitations in this paper. First of all, the energy categories are roughly defined, which can be better classified in future research. Besides, we do not discuss carbon dioxide or other byproducts and, thus, may neglect the influence of bad outputs. Furthermore, the lack of a comparison between market prices and shadow prices needs to be extended in the future.
Acknowledgments
The authors are grateful for the financial support provided by GDUPS(2015), the National Science Foundation of China (71473105), National Social Science Foundation of China (14ZDB44), New Century Excellent Talents in University (NCET-110856), and Guangdong Project of Key Research Institute of Humanities and Social Sciences at Universities-IRESD (2012JDXM0009).
Author Contributions
Peihao Lai contributed to the data acquisition, methodological design and drafting of the article; Minzhe Du provided the statistical analysis and data interpretation; Bing Wang made substantial contributions to the concept and design of the article, helped to revise the manuscript and approved its final publication; and Ziyue Chen assisted in the literature review and conclusions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Appendix A1. Efficiency Decompositon Framework
According to Figure A1, a typical province could only reach point a instead of the production frontier of the province. Similarly, a country, as a whole, could only reach Point B instead of Point D in Figure A2. To reach the national optimal Point D, it is vital to improve the technical efficiency of the province, which means that achieves the optimal value and Point A is replaced by Point B. Then, improving provincial allocation efficiency is of great importance as well, which means achieves the optimal value and Point B moves to Point C. Finally, interprovincial efficiency is to increase, which means reaches the optimal value and Point C moves to Point D.
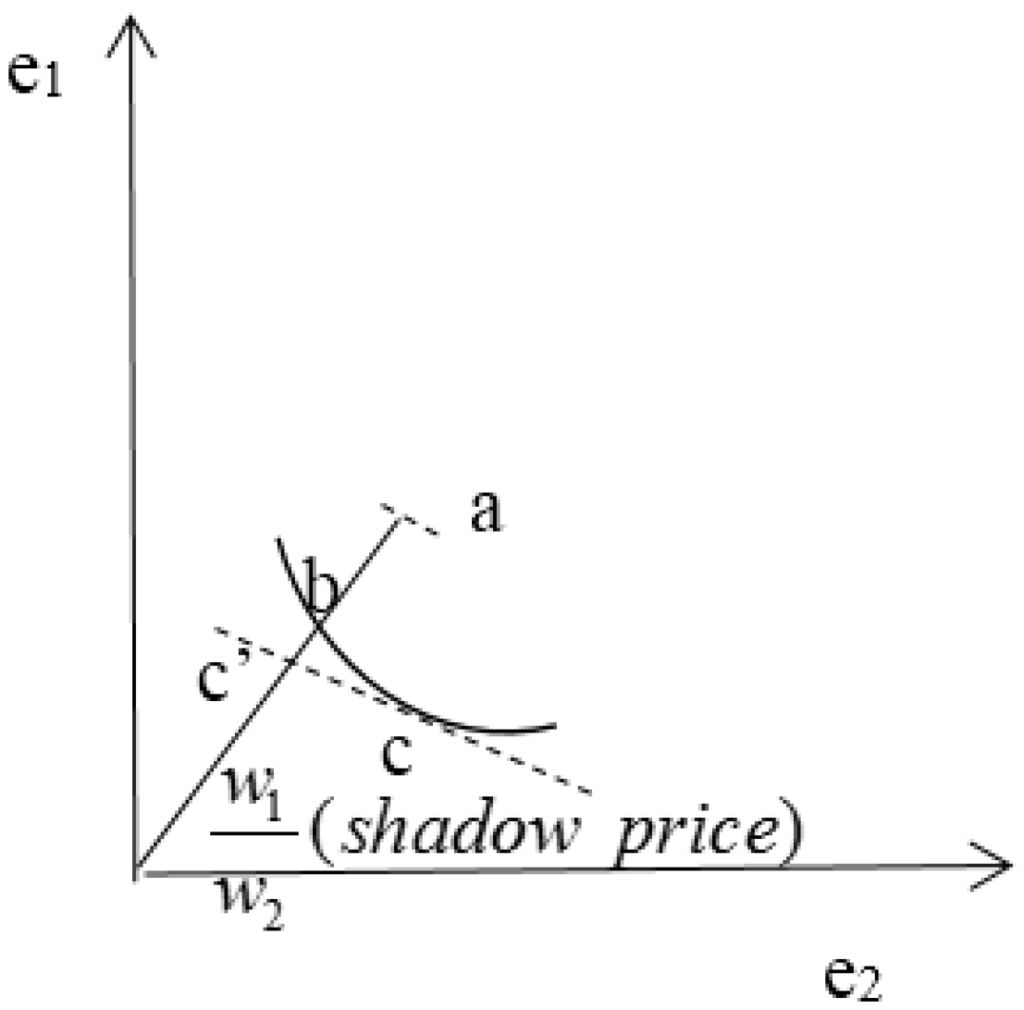
Figure A1.
Production frontier of a province.
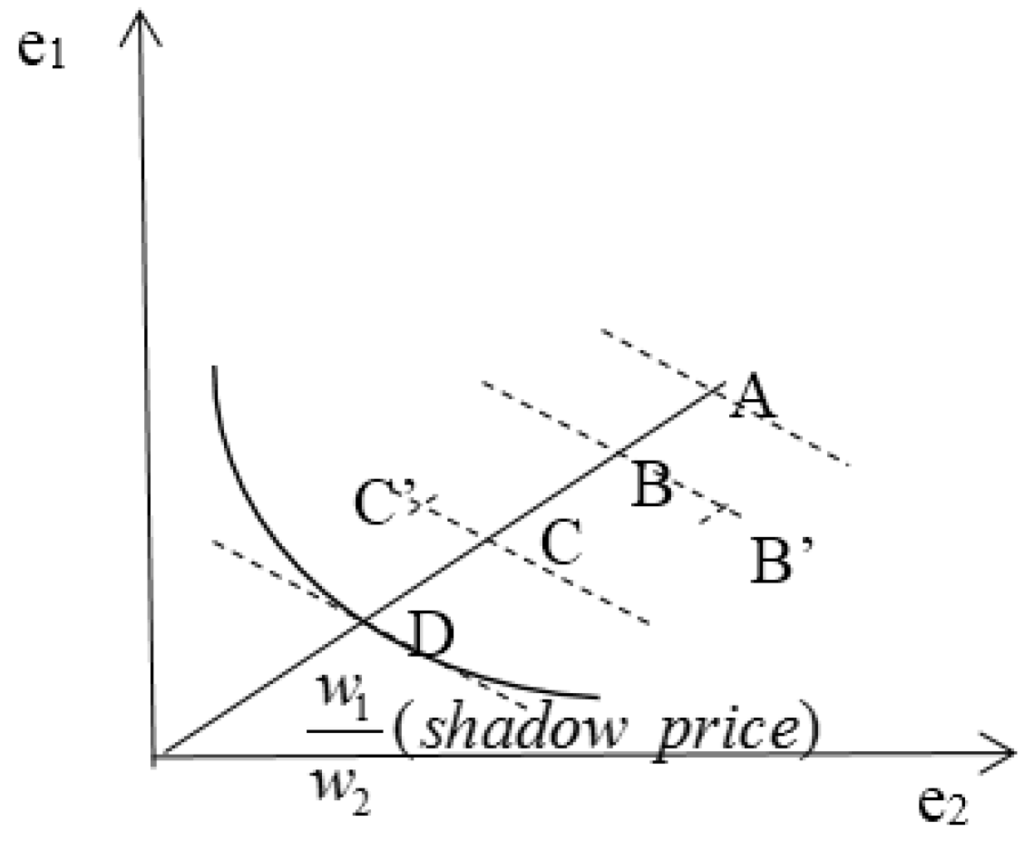
Figure A2.
Production frontier of a country.
Appendix A2. Depreciation Rate of Different Areas
We introduced the value of depreciation rate according to Wu’s research [37], where the value of depreciation rate differs from areas as is in Table A1.

Table A1.
Depreciation rate of different areas.
| Province | Beijing | Tianjin | Hebei | Shanxi | Neimenggu | liaoning | Jilin | Heilongjiang | Shanghai | Jiangsu |
| Depreciation rate (%) | 3.4 | 3.7 | 4.3 | 4 | 4.3 | 5.8 | 5.1 | 6 | 3.4 | 4.2 |
| Province | Zhejiang | Anhui | Fujian | Jiangxi | Shandong | Henan | Hubei | Hunan | Guangdong | Guangxi |
| Depreciation rate (%) | 4 | 5 | 4.5 | 3.7 | 5 | 4.1 | 4.5 | 4.5 | 6.9 | 3.3 |
| Province | Hainan | Chongqing | Sichuan | Guizhou | Yunnan | Shaanxi | Gansu | Qinghai | Ningxia | Xinjiang |
| Depreciation rate (%) | 2.2 | 4.6 | 4.6 | 2.8 | 2.7 | 3.3 | 2.7 | 2.4 | 2.8 | 2.6 |
Appendix A3. The Shadow Price of Each Energy from 1998 to 2012 are as Follow

Table A2.
The shadow price of coal.
| 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.437 | 0.442 | 0.451 | 0.442 | 0.463 | 0.461 | 0.486 | 0.511 | 0.541 | 0.569 | 0.628 | 0.678 | 0.721 | 0.763 | 0.876 |
| Tianjin | 0.405 | 0.406 | 0.412 | 0.408 | 0.396 | 0.395 | 0.384 | 0.378 | 0.381 | 0.384 | 0.386 | 0.382 | 0.403 | 0.400 | 0.421 |
| Hebei | 0.326 | 0.316 | 0.307 | 0.290 | 0.265 | 0.233 | 0.204 | 0.173 | 0.135 | 0.111 | 0.094 | 0.080 | 0.103 | 0.056 | 0.070 |
| Shanxi | 0.321 | 0.324 | 0.313 | 0.209 | 0.250 | 0.226 | 0.196 | 0.182 | 0.161 | 0.000 | 0.147 | 0.149 | 0.166 | 0.126 | 0.108 |
| Neimenggu | 0.358 | 0.351 | 0.344 | 0.336 | 0.322 | 0.305 | 0.271 | 0.239 | 0.220 | 0.208 | 0.158 | 0.153 | 0.136 | 0.034 | 0.000 |
| Liaoning | 0.380 | 0.418 | 0.407 | 0.398 | 0.361 | 0.338 | 0.296 | 0.330 | 0.311 | 0.276 | 0.269 | 0.247 | 0.317 | 0.351 | 0.432 |
| Jilin | 0.391 | 0.384 | 0.382 | 0.375 | 0.369 | 0.363 | 0.351 | 0.343 | 0.332 | 0.346 | 0.331 | 0.329 | 0.325 | 0.291 | 0.312 |
| Heilongjiang | 0.426 | 0.430 | 0.426 | 0.424 | 0.416 | 0.402 | 0.379 | 0.379 | 0.382 | 0.374 | 0.344 | 0.374 | 0.362 | 0.335 | 0.306 |
| Shanghai | 0.383 | 0.376 | 0.384 | 0.379 | 0.384 | 0.386 | 0.410 | 0.432 | 0.471 | 0.481 | 0.478 | 0.496 | 0.505 | 0.507 | 0.559 |
| Jiangsu | 0.361 | 0.351 | 0.352 | 0.346 | 0.337 | 0.330 | 0.298 | 0.246 | 0.231 | 0.241 | 0.265 | 0.271 | 0.276 | 0.219 | 0.277 |
| Zhejiang | 0.408 | 0.404 | 0.401 | 0.396 | 0.403 | 0.405 | 0.390 | 0.390 | 0.375 | 0.355 | 0.363 | 0.380 | 0.440 | 0.465 | 0.491 |
| Anhui | 0.386 | 0.380 | 0.373 | 0.363 | 0.356 | 0.343 | 0.335 | 0.324 | 0.314 | 0.297 | 0.283 | 0.264 | 0.249 | 0.238 | 0.239 |
| Fujian | 0.422 | 0.416 | 0.413 | 0.414 | 0.402 | 0.388 | 0.381 | 0.378 | 0.371 | 0.354 | 0.360 | 0.349 | 0.432 | 0.394 | 0.436 |
| Jiangxi | 0.413 | 0.412 | 0.409 | 0.411 | 0.407 | 0.392 | 0.381 | 0.385 | 0.373 | 0.355 | 0.359 | 0.349 | 0.361 | 0.334 | 0.352 |
| Shandong | 0.381 | 0.370 | 0.388 | 0.354 | 0.322 | 0.302 | 0.270 | 0.246 | 0.201 | 0.179 | 0.162 | 0.172 | 0.181 | 0.183 | 0.200 |
| Henan | 0.392 | 0.393 | 0.388 | 0.383 | 0.369 | 0.354 | 0.325 | 0.277 | 0.252 | 0.222 | 0.229 | 0.237 | 0.268 | 0.258 | 0.423 |
| Hubei | 0.411 | 0.409 | 0.411 | 0.403 | 0.399 | 0.393 | 0.388 | 0.415 | 0.415 | 0.400 | 0.480 | 0.472 | 0.373 | 0.338 | 0.398 |
| Hunan | 0.418 | 0.430 | 0.436 | 0.420 | 0.426 | 0.405 | 0.401 | 0.376 | 0.377 | 0.370 | 0.431 | 0.458 | 0.557 | 0.561 | 0.716 |
| Guangdong | 0.450 | 0.443 | 0.438 | 0.440 | 0.445 | 0.449 | 0.449 | 0.469 | 0.488 | 0.527 | 0.563 | 0.732 | 0.560 | 0.514 | 0.615 |
| Guangxi | 0.449 | 0.448 | 0.451 | 0.453 | 0.461 | 0.461 | 0.449 | 0.432 | 0.442 | 0.441 | 0.465 | 0.455 | 0.476 | 0.516 | 0.555 |
| Hainan | 0.428 | 0.413 | 0.424 | 0.425 | 0.435 | 0.446 | 0.456 | 0.448 | 0.460 | 0.451 | 0.465 | 0.459 | 0.473 | 0.526 | 0.523 |
| Chongqing | 0.459 | 0.465 | 0.480 | 0.446 | 0.447 | 0.458 | 0.465 | 0.509 | 0.526 | 0.536 | 0.548 | 0.545 | 0.578 | 0.557 | 0.615 |
| Sichuan | 0.533 | 0.565 | 0.572 | 0.594 | 0.603 | 0.594 | 0.612 | 0.658 | 0.711 | 0.745 | 0.741 | 0.798 | 1.099 | 1.802 | 1.707 |
| Guizhou | 0.391 | 0.392 | 0.394 | 0.408 | 0.400 | 0.371 | 0.347 | 0.321 | 0.299 | 0.287 | 0.296 | 0.274 | 0.265 | 0.245 | 0.221 |
| Yunnan | 0.428 | 0.431 | 0.437 | 0.434 | 0.431 | 0.423 | 0.436 | 0.421 | 0.392 | 0.393 | 0.399 | 0.378 | 0.397 | 0.432 | 0.484 |
| Shaanxi | 0.408 | 0.414 | 0.427 | 0.435 | 0.439 | 0.430 | 0.453 | 0.390 | 0.405 | 0.429 | 0.448 | 0.426 | 0.435 | 0.431 | 0.421 |
| Gansu | 0.426 | 0.425 | 0.425 | 0.417 | 0.414 | 0.416 | 0.416 | 0.421 | 0.424 | 0.420 | 0.415 | 0.434 | 0.395 | 0.377 | 0.391 |
| Qinghai | 0.419 | 0.421 | 0.423 | 0.420 | 0.432 | 0.441 | 0.453 | 0.464 | 0.465 | 0.461 | 0.466 | 0.474 | 0.502 | 0.551 | 0.590 |
| Ningxia | 0.402 | 0.402 | 0.400 | 0.397 | 0.395 | 0.392 | 0.393 | 0.374 | 0.373 | 0.382 | 0.358 | 0.356 | 0.345 | 0.314 | 0.324 |
| Xinjiang | 0.445 | 0.448 | 0.447 | 0.516 | 0.467 | 0.481 | 0.506 | 0.523 | 0.544 | 0.555 | 0.541 | 0.509 | 0.567 | 0.591 | 0.596 |
| eastern | 0.398 | 0.396 | 0.398 | 0.390 | 0.383 | 0.376 | 0.366 | 0.364 | 0.360 | 0.357 | 0.367 | 0.386 | 0.401 | 0.398 | 0.446 |
| central | 0.396 | 0.393 | 0.391 | 0.374 | 0.375 | 0.365 | 0.351 | 0.344 | 0.336 | 0.306 | 0.330 | 0.329 | 0.322 | 0.306 | 0.333 |
| western | 0.429 | 0.433 | 0.436 | 0.441 | 0.437 | 0.434 | 0.436 | 0.432 | 0.436 | 0.442 | 0.440 | 0.436 | 0.472 | 0.532 | 0.537 |
| Total | 0.408 | 0.408 | 0.409 | 0.402 | 0.398 | 0.389 | 0.381 | 0.374 | 0.369 | 0.359 | 0.369 | 0.375 | 0.389 | 0.380 | 0.408 |

Table A3.
The shadow price of oil.
| 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.005 | 0.022 | 0.042 | 0.061 | 0.078 | 0.106 | 0.122 | 0.142 | 0.157 | 0.175 | 0.187 | 0.211 | 0.240 | 0.283 | 0.303 |
| Tianjin | 0.014 | 0.035 | 0.051 | 0.079 | 0.106 | 0.131 | 0.160 | 0.189 | 0.222 | 0.253 | 0.281 | 0.313 | 0.318 | 0.337 | 0.371 |
| Hebei | 0.091 | 0.113 | 0.137 | 0.164 | 0.194 | 0.226 | 0.261 | 0.309 | 0.345 | 0.376 | 0.405 | 0.448 | 0.475 | 0.505 | 0.532 |
| Shanxi | 0.075 | 0.096 | 0.123 | 0.188 | 0.195 | 0.229 | 0.263 | 0.292 | 0.325 | 0.403 | 0.377 | 0.406 | 0.431 | 0.476 | 0.515 |
| Neimenggu | 0.054 | 0.080 | 0.105 | 0.133 | 0.163 | 0.190 | 0.223 | 0.254 | 0.280 | 0.303 | 0.339 | 0.360 | 0.387 | 0.442 | 0.481 |
| Liaoning | 0.042 | 0.042 | 0.061 | 0.093 | 0.125 | 0.154 | 0.210 | 0.193 | 0.214 | 0.246 | 0.260 | 0.288 | 0.253 | 0.239 | 0.209 |
| Jilin | 0.035 | 0.061 | 0.087 | 0.114 | 0.141 | 0.169 | 0.202 | 0.224 | 0.251 | 0.282 | 0.323 | 0.353 | 0.376 | 0.416 | 0.473 |
| Heilongjiang | 0.015 | 0.033 | 0.051 | 0.076 | 0.101 | 0.129 | 0.161 | 0.183 | 0.216 | 0.231 | 0.281 | 0.304 | 0.326 | 0.345 | 0.364 |
| Shanghai | 0.000 | 0.019 | 0.034 | 0.051 | 0.066 | 0.082 | 0.090 | 0.102 | 0.101 | 0.113 | 0.135 | 0.149 | 0.160 | 0.172 | 0.184 |
| Jiangsu | 0.069 | 0.088 | 0.100 | 0.120 | 0.139 | 0.154 | 0.173 | 0.184 | 0.185 | 0.189 | 0.188 | 0.194 | 0.174 | 0.171 | 0.128 |
| Zhejiang | 0.039 | 0.057 | 0.076 | 0.097 | 0.122 | 0.141 | 0.164 | 0.184 | 0.201 | 0.222 | 0.247 | 0.263 | 0.239 | 0.243 | 0.273 |
| Anhui | 0.089 | 0.114 | 0.141 | 0.169 | 0.197 | 0.227 | 0.256 | 0.286 | 0.316 | 0.347 | 0.380 | 0.413 | 0.441 | 0.467 | 0.486 |
| Fujian | 0.030 | 0.053 | 0.077 | 0.103 | 0.127 | 0.153 | 0.177 | 0.213 | 0.245 | 0.271 | 0.313 | 0.334 | 0.323 | 0.336 | 0.383 |
| Jiangxi | 0.057 | 0.081 | 0.106 | 0.129 | 0.158 | 0.186 | 0.225 | 0.252 | 0.288 | 0.327 | 0.365 | 0.409 | 0.441 | 0.468 | 0.523 |
| Shandong | 0.084 | 0.105 | 0.115 | 0.143 | 0.173 | 0.186 | 0.202 | 0.211 | 0.223 | 0.238 | 0.259 | 0.251 | 0.221 | 0.218 | 0.190 |
| Henan | 0.108 | 0.133 | 0.164 | 0.188 | 0.217 | 0.245 | 0.277 | 0.305 | 0.332 | 0.360 | 0.394 | 0.437 | 0.469 | 0.489 | 0.526 |
| Hubei | 0.078 | 0.101 | 0.127 | 0.155 | 0.180 | 0.207 | 0.240 | 0.267 | 0.303 | 0.321 | 0.366 | 0.401 | 0.421 | 0.450 | 0.516 |
| Hunan | 0.089 | 0.106 | 0.128 | 0.161 | 0.184 | 0.219 | 0.258 | 0.296 | 0.331 | 0.364 | 0.452 | 0.509 | 0.624 | 0.693 | 0.845 |
| Guangdong | 0.000 | 0.013 | 0.035 | 0.049 | 0.062 | 0.077 | 0.085 | 0.082 | 0.081 | 0.060 | 0.067 | 0.000 | 0.068 | 0.068 | 0.071 |
| Guangxi | 0.066 | 0.092 | 0.120 | 0.147 | 0.175 | 0.211 | 0.247 | 0.273 | 0.318 | 0.360 | 0.417 | 0.459 | 0.508 | 0.596 | 0.650 |
| Hainan | 0.012 | 0.044 | 0.065 | 0.090 | 0.114 | 0.138 | 0.165 | 0.202 | 0.234 | 0.268 | 0.304 | 0.347 | 0.386 | 0.415 | 0.468 |
| Chongqing | 0.033 | 0.054 | 0.076 | 0.106 | 0.133 | 0.156 | 0.182 | 0.223 | 0.256 | 0.291 | 0.342 | 0.389 | 0.428 | 0.454 | 0.504 |
| Sichuan | 0.059 | 0.076 | 0.102 | 0.123 | 0.148 | 0.181 | 0.209 | 0.229 | 0.241 | 0.270 | 0.316 | 0.329 | 0.294 | 0.554 | 0.570 |
| Guizhou | 0.069 | 0.091 | 0.120 | 0.153 | 0.184 | 0.221 | 0.258 | 0.281 | 0.319 | 0.351 | 0.381 | 0.423 | 0.459 | 0.503 | 0.551 |
| Yunnan | 0.060 | 0.084 | 0.111 | 0.137 | 0.168 | 0.203 | 0.237 | 0.291 | 0.322 | 0.364 | 0.413 | 0.460 | 0.500 | 0.578 | 0.681 |
| Shaanxi | 0.049 | 0.070 | 0.087 | 0.109 | 0.134 | 0.159 | 0.174 | 0.231 | 0.250 | 0.271 | 0.284 | 0.322 | 0.344 | 0.373 | 0.410 |
| Gansu | 0.046 | 0.072 | 0.095 | 0.126 | 0.158 | 0.180 | 0.220 | 0.250 | 0.287 | 0.326 | 0.370 | 0.420 | 0.450 | 0.491 | 0.546 |
| Qinghai | 0.022 | 0.047 | 0.073 | 0.099 | 0.123 | 0.150 | 0.183 | 0.215 | 0.254 | 0.298 | 0.337 | 0.386 | 0.452 | 0.513 | 0.579 |
| Ningxia | 0.025 | 0.050 | 0.076 | 0.103 | 0.131 | 0.160 | 0.191 | 0.232 | 0.270 | 0.315 | 0.344 | 0.389 | 0.431 | 0.487 | 0.533 |
| Xinjiang | 0.000 | 0.024 | 0.047 | 0.026 | 0.091 | 0.112 | 0.128 | 0.147 | 0.172 | 0.202 | 0.247 | 0.304 | 0.318 | 0.344 | 0.393 |
| eastern | 0.035 | 0.054 | 0.072 | 0.095 | 0.119 | 0.141 | 0.164 | 0.183 | 0.201 | 0.219 | 0.241 | 0.254 | 0.260 | 0.272 | 0.283 |
| middle | 0.059 | 0.083 | 0.108 | 0.139 | 0.163 | 0.191 | 0.223 | 0.251 | 0.283 | 0.317 | 0.349 | 0.384 | 0.411 | 0.441 | 0.484 |
| western | 0.044 | 0.067 | 0.092 | 0.115 | 0.146 | 0.175 | 0.205 | 0.239 | 0.270 | 0.305 | 0.345 | 0.385 | 0.416 | 0.485 | 0.536 |
| Total | 0.048 | 0.069 | 0.091 | 0.117 | 0.143 | 0.170 | 0.198 | 0.225 | 0.251 | 0.280 | 0.311 | 0.341 | 0.361 | 0.393 | 0.428 |

Table A4.
The shadow price of natural gas.
| 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.112 | 0.107 | 0.106 | 0.100 | 0.094 | 0.096 | 0.088 | 0.084 | 0.077 | 0.073 | 0.059 | 0.053 | 0.051 | 0.053 | 0.036 |
| Tianjin | 0.100 | 0.096 | 0.089 | 0.089 | 0.088 | 0.084 | 0.084 | 0.084 | 0.085 | 0.085 | 0.084 | 0.088 | 0.078 | 0.079 | 0.087 |
| Hebei | 0.124 | 0.126 | 0.126 | 0.129 | 0.134 | 0.141 | 0.153 | 0.174 | 0.188 | 0.200 | 0.212 | 0.235 | 0.250 | 0.272 | 0.291 |
| Shanxi | 0.122 | 0.119 | 0.119 | 0.141 | 0.128 | 0.131 | 0.135 | 0.136 | 0.139 | 0.178 | 0.136 | 0.135 | 0.132 | 0.145 | 0.152 |
| Neimenggu | 0.113 | 0.111 | 0.109 | 0.108 | 0.108 | 0.109 | 0.112 | 0.117 | 0.119 | 0.121 | 0.132 | 0.135 | 0.144 | 0.176 | 0.195 |
| Liaoning | 0.117 | 0.099 | 0.092 | 0.098 | 0.104 | 0.107 | 0.132 | 0.104 | 0.108 | 0.121 | 0.128 | 0.142 | 0.118 | 0.110 | 0.091 |
| Jilin | 0.103 | 0.102 | 0.101 | 0.099 | 0.097 | 0.095 | 0.096 | 0.090 | 0.089 | 0.092 | 0.103 | 0.106 | 0.108 | 0.120 | 0.136 |
| Heilongjiang | 0.089 | 0.085 | 0.079 | 0.079 | 0.077 | 0.076 | 0.078 | 0.072 | 0.075 | 0.067 | 0.082 | 0.078 | 0.077 | 0.077 | 0.078 |
| Shanghai | 0.109 | 0.109 | 0.105 | 0.103 | 0.098 | 0.095 | 0.087 | 0.085 | 0.072 | 0.073 | 0.076 | 0.075 | 0.073 | 0.069 | 0.064 |
| Jiangsu | 0.117 | 0.120 | 0.116 | 0.121 | 0.125 | 0.131 | 0.140 | 0.146 | 0.152 | 0.168 | 0.185 | 0.214 | 0.232 | 0.262 | 0.287 |
| Zhejiang | 0.115 | 0.113 | 0.109 | 0.110 | 0.116 | 0.121 | 0.129 | 0.136 | 0.143 | 0.153 | 0.168 | 0.177 | 0.167 | 0.176 | 0.207 |
| Anhui | 0.110 | 0.108 | 0.107 | 0.107 | 0.106 | 0.106 | 0.106 | 0.106 | 0.107 | 0.109 | 0.112 | 0.116 | 0.120 | 0.124 | 0.122 |
| Fujian | 0.109 | 0.108 | 0.106 | 0.106 | 0.103 | 0.102 | 0.100 | 0.107 | 0.112 | 0.116 | 0.130 | 0.132 | 0.112 | 0.112 | 0.132 |
| Jiangxi | 0.105 | 0.102 | 0.100 | 0.096 | 0.094 | 0.091 | 0.097 | 0.094 | 0.096 | 0.100 | 0.102 | 0.108 | 0.106 | 0.106 | 0.113 |
| Shandong | 0.110 | 0.112 | 0.107 | 0.114 | 0.125 | 0.126 | 0.132 | 0.137 | 0.146 | 0.162 | 0.186 | 0.196 | 0.193 | 0.220 | 0.230 |
| Henan | 0.113 | 0.111 | 0.110 | 0.111 | 0.114 | 0.117 | 0.124 | 0.131 | 0.141 | 0.155 | 0.172 | 0.198 | 0.223 | 0.245 | 0.280 |
| Hubei | 0.112 | 0.110 | 0.111 | 0.111 | 0.109 | 0.108 | 0.111 | 0.110 | 0.117 | 0.113 | 0.121 | 0.129 | 0.140 | 0.154 | 0.181 |
| Hunan | 0.115 | 0.109 | 0.106 | 0.109 | 0.104 | 0.108 | 0.114 | 0.120 | 0.124 | 0.128 | 0.160 | 0.177 | 0.222 | 0.249 | 0.308 |
| Guangdong | 0.087 | 0.085 | 0.089 | 0.088 | 0.090 | 0.094 | 0.093 | 0.087 | 0.093 | 0.092 | 0.111 | 0.089 | 0.154 | 0.182 | 0.259 |
| Guangxi | 0.110 | 0.108 | 0.106 | 0.103 | 0.100 | 0.102 | 0.102 | 0.096 | 0.101 | 0.106 | 0.116 | 0.123 | 0.134 | 0.162 | 0.179 |
| Hainan | 0.093 | 0.095 | 0.090 | 0.085 | 0.078 | 0.071 | 0.063 | 0.061 | 0.054 | 0.049 | 0.041 | 0.037 | 0.027 | 0.005 | 0.000 |
| Chongqing | 0.098 | 0.094 | 0.091 | 0.088 | 0.087 | 0.082 | 0.078 | 0.083 | 0.080 | 0.077 | 0.083 | 0.087 | 0.083 | 0.079 | 0.075 |
| Sichuan | 0.086 | 0.081 | 0.079 | 0.074 | 0.071 | 0.073 | 0.072 | 0.064 | 0.051 | 0.052 | 0.062 | 0.054 | 0.000 | 0.080 | 0.094 |
| Guizhou | 0.111 | 0.107 | 0.106 | 0.105 | 0.103 | 0.104 | 0.105 | 0.102 | 0.104 | 0.102 | 0.096 | 0.099 | 0.098 | 0.101 | 0.107 |
| Yunnan | 0.110 | 0.108 | 0.106 | 0.102 | 0.102 | 0.103 | 0.102 | 0.113 | 0.111 | 0.113 | 0.117 | 0.122 | 0.121 | 0.137 | 0.162 |
| Shaanxi | 0.106 | 0.101 | 0.095 | 0.090 | 0.086 | 0.081 | 0.070 | 0.087 | 0.079 | 0.071 | 0.060 | 0.067 | 0.064 | 0.068 | 0.076 |
| Gansu | 0.099 | 0.099 | 0.094 | 0.094 | 0.093 | 0.084 | 0.087 | 0.084 | 0.083 | 0.080 | 0.080 | 0.078 | 0.074 | 0.072 | 0.070 |
| Qinghai | 0.100 | 0.097 | 0.094 | 0.089 | 0.083 | 0.077 | 0.073 | 0.066 | 0.063 | 0.061 | 0.054 | 0.049 | 0.048 | 0.036 | 0.025 |
| Ningxia | 0.101 | 0.098 | 0.094 | 0.091 | 0.087 | 0.083 | 0.079 | 0.081 | 0.078 | 0.078 | 0.071 | 0.068 | 0.064 | 0.068 | 0.060 |
| Xinjiang | 0.089 | 0.087 | 0.084 | 0.047 | 0.072 | 0.065 | 0.053 | 0.041 | 0.032 | 0.026 | 0.029 | 0.038 | 0.015 | 0.001 | 0.000 |
| eastern | 0.109 | 0.106 | 0.103 | 0.104 | 0.105 | 0.106 | 0.109 | 0.110 | 0.112 | 0.117 | 0.125 | 0.131 | 0.132 | 0.140 | 0.153 |
| middle | 0.106 | 0.104 | 0.102 | 0.104 | 0.100 | 0.099 | 0.101 | 0.100 | 0.102 | 0.108 | 0.108 | 0.113 | 0.117 | 0.122 | 0.133 |
| western | 0.102 | 0.099 | 0.096 | 0.090 | 0.090 | 0.088 | 0.085 | 0.085 | 0.082 | 0.081 | 0.082 | 0.084 | 0.077 | 0.089 | 0.095 |
| Total | 0.106 | 0.104 | 0.101 | 0.100 | 0.100 | 0.099 | 0.101 | 0.101 | 0.103 | 0.107 | 0.112 | 0.116 | 0.117 | 0.127 | 0.136 |

Table A5.
The shadow price of electric power.
| 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.195 | 0.197 | 0.198 | 0.201 | 0.200 | 0.201 | 0.199 | 0.203 | 0.209 | 0.216 | 0.226 | 0.238 | 0.250 | 0.258 | 0.285 |
| Tianjin | 0.194 | 0.192 | 0.193 | 0.192 | 0.190 | 0.190 | 0.190 | 0.190 | 0.191 | 0.192 | 0.195 | 0.201 | 0.208 | 0.218 | 0.234 |
| Hebei | 0.124 | 0.125 | 0.123 | 0.122 | 0.122 | 0.123 | 0.124 | 0.121 | 0.123 | 0.131 | 0.137 | 0.143 | 0.150 | 0.165 | 0.181 |
| Shanxi | 0.167 | 0.165 | 0.163 | 0.164 | 0.161 | 0.159 | 0.159 | 0.159 | 0.158 | 0.164 | 0.157 | 0.159 | 0.167 | 0.172 | 0.178 |
| Neimenggu | 0.175 | 0.173 | 0.171 | 0.169 | 0.167 | 0.170 | 0.171 | 0.173 | 0.178 | 0.186 | 0.192 | 0.204 | 0.212 | 0.219 | 0.231 |
| Liaoning | 0.165 | 0.158 | 0.156 | 0.155 | 0.160 | 0.162 | 0.163 | 0.159 | 0.164 | 0.171 | 0.181 | 0.189 | 0.196 | 0.216 | 0.238 |
| Jilin | 0.174 | 0.172 | 0.169 | 0.167 | 0.165 | 0.162 | 0.161 | 0.160 | 0.161 | 0.160 | 0.168 | 0.174 | 0.184 | 0.190 | 0.199 |
| Heilongjiang | 0.167 | 0.165 | 0.166 | 0.165 | 0.163 | 0.163 | 0.161 | 0.160 | 0.158 | 0.161 | 0.164 | 0.163 | 0.166 | 0.173 | 0.181 |
| Shanghai | 0.199 | 0.201 | 0.201 | 0.204 | 0.205 | 0.206 | 0.206 | 0.214 | 0.219 | 0.228 | 0.236 | 0.246 | 0.263 | 0.280 | 0.299 |
| Jiangsu | 0.107 | 0.108 | 0.109 | 0.110 | 0.112 | 0.116 | 0.125 | 0.143 | 0.162 | 0.180 | 0.204 | 0.228 | 0.261 | 0.308 | 0.363 |
| Zhejiang | 0.144 | 0.144 | 0.141 | 0.140 | 0.138 | 0.139 | 0.143 | 0.145 | 0.157 | 0.165 | 0.171 | 0.178 | 0.196 | 0.218 | 0.242 |
| Anhui | 0.107 | 0.103 | 0.099 | 0.096 | 0.093 | 0.089 | 0.086 | 0.083 | 0.080 | 0.080 | 0.079 | 0.080 | 0.084 | 0.090 | 0.094 |
| Fujian | 0.164 | 0.163 | 0.161 | 0.159 | 0.158 | 0.158 | 0.157 | 0.154 | 0.154 | 0.157 | 0.159 | 0.168 | 0.181 | 0.191 | 0.199 |
| Jiangxi | 0.141 | 0.138 | 0.137 | 0.135 | 0.129 | 0.127 | 0.123 | 0.118 | 0.116 | 0.114 | 0.112 | 0.111 | 0.109 | 0.115 | 0.115 |
| Shandong | 0.079 | 0.077 | 0.073 | 0.076 | 0.079 | 0.084 | 0.092 | 0.097 | 0.111 | 0.120 | 0.132 | 0.148 | 0.168 | 0.190 | 0.220 |
| Henan | 0.070 | 0.061 | 0.048 | 0.047 | 0.046 | 0.045 | 0.046 | 0.053 | 0.059 | 0.065 | 0.066 | 0.065 | 0.068 | 0.083 | 0.089 |
| Hubei | 0.107 | 0.104 | 0.100 | 0.097 | 0.094 | 0.091 | 0.087 | 0.082 | 0.078 | 0.083 | 0.073 | 0.078 | 0.101 | 0.116 | 0.118 |
| Hunan | 0.097 | 0.094 | 0.091 | 0.088 | 0.082 | 0.080 | 0.073 | 0.071 | 0.068 | 0.067 | 0.049 | 0.044 | 0.022 | 0.029 | 0.012 |
| Guangdong | 0.124 | 0.126 | 0.122 | 0.121 | 0.122 | 0.119 | 0.119 | 0.116 | 0.127 | 0.151 | 0.163 | 0.201 | 0.204 | 0.243 | 0.289 |
| Guangxi | 0.123 | 0.119 | 0.113 | 0.109 | 0.103 | 0.098 | 0.094 | 0.093 | 0.085 | 0.082 | 0.073 | 0.073 | 0.071 | 0.065 | 0.078 |
| Hainan | 0.195 | 0.191 | 0.189 | 0.187 | 0.186 | 0.185 | 0.184 | 0.180 | 0.178 | 0.175 | 0.173 | 0.169 | 0.167 | 0.173 | 0.169 |
| Chongqing | 0.158 | 0.157 | 0.156 | 0.156 | 0.157 | 0.157 | 0.157 | 0.153 | 0.154 | 0.155 | 0.156 | 0.158 | 0.164 | 0.174 | 0.183 |
| Sichuan | 0.076 | 0.069 | 0.064 | 0.060 | 0.059 | 0.058 | 0.056 | 0.054 | 0.058 | 0.059 | 0.058 | 0.071 | 0.093 | 0.015 | 0.054 |
| Guizhou | 0.147 | 0.145 | 0.139 | 0.127 | 0.122 | 0.119 | 0.116 | 0.125 | 0.123 | 0.124 | 0.121 | 0.120 | 0.122 | 0.121 | 0.121 |
| Yunnan | 0.137 | 0.134 | 0.128 | 0.124 | 0.120 | 0.116 | 0.110 | 0.101 | 0.101 | 0.095 | 0.087 | 0.084 | 0.078 | 0.066 | 0.053 |
| Shaanxi | 0.152 | 0.150 | 0.147 | 0.146 | 0.142 | 0.141 | 0.143 | 0.139 | 0.141 | 0.144 | 0.150 | 0.153 | 0.161 | 0.170 | 0.183 |
| Gansu | 0.153 | 0.150 | 0.148 | 0.145 | 0.142 | 0.141 | 0.136 | 0.138 | 0.135 | 0.132 | 0.127 | 0.119 | 0.123 | 0.123 | 0.122 |
| Qinghai | 0.194 | 0.191 | 0.188 | 0.187 | 0.186 | 0.184 | 0.182 | 0.180 | 0.177 | 0.172 | 0.169 | 0.166 | 0.159 | 0.157 | 0.156 |
| Ningxia | 0.194 | 0.191 | 0.189 | 0.188 | 0.186 | 0.183 | 0.181 | 0.177 | 0.174 | 0.170 | 0.170 | 0.167 | 0.166 | 0.166 | 0.164 |
| Xinjiang | 0.191 | 0.190 | 0.189 | 0.184 | 0.189 | 0.188 | 0.191 | 0.187 | 0.189 | 0.190 | 0.190 | 0.190 | 0.192 | 0.198 | 0.204 |
| eastern | 0.154 | 0.153 | 0.151 | 0.152 | 0.152 | 0.153 | 0.155 | 0.157 | 0.163 | 0.171 | 0.180 | 0.192 | 0.204 | 0.224 | 0.247 |
| middle | 0.141 | 0.137 | 0.134 | 0.132 | 0.130 | 0.128 | 0.126 | 0.124 | 0.123 | 0.125 | 0.124 | 0.125 | 0.131 | 0.139 | 0.143 |
| western | 0.155 | 0.152 | 0.149 | 0.145 | 0.143 | 0.141 | 0.140 | 0.138 | 0.138 | 0.137 | 0.136 | 0.137 | 0.140 | 0.134 | 0.141 |
| Total | 0.147 | 0.145 | 0.142 | 0.140 | 0.139 | 0.138 | 0.137 | 0.137 | 0.139 | 0.143 | 0.146 | 0.151 | 0.159 | 0.169 | 0.181 |
References
- Hu, J.L.; Kao, C.H. Efficient energy-saving targets for APEC economies. Energy Policy 2007, 35, 373–382. [Google Scholar] [CrossRef]
- Zhang, X.P.; Cheng, X.M.; Yuan, J.H.; Gao, X.S. Total-factor energy efficiency in developing countries. Energy Policy 2011, 39, 644–650. [Google Scholar] [CrossRef]
- Sheng, P.F. The explanation for the low energy efficiency of China: Allocation inefficiency or technology inefficiency. Ind. Econ. Res. 2015, 1, 9–20. [Google Scholar]
- Wang, F.; Feng, G.F. Contribution of improving energy mix to carbon intensity target in China: Potential assessment. China Ind. Econ. 2011, 4, 127–137. [Google Scholar]
- Shi, D. Regional Differences in China’s Energy Efficiency and Conservation Potentials. China Ind. Econ. 2006, 10, 49–58. [Google Scholar]
- Fan, Y.; Liao, H.; Wei, Y.M. Can market oriented economic reforms contribute to energy efficiency improvement? Evidence from China. Energy Policy 2007, 35, 2287–2295. [Google Scholar] [CrossRef]
- Hang, L.; Tu, M. The impacts of energy prices on energy intensity: Evidence from China. Energy Policy 2007, 35, 2978–2988. [Google Scholar] [CrossRef]
- Zhang, Z.X. Why did the energy intensity fall in China’s industrial sector in the 1990s? The relative importance of structural change and intensity change. Energy Econ. 2003, 25, 625–638. [Google Scholar] [CrossRef]
- Hu, J.L.; Wang, S.C. Total-factor energy efficiency of regions in China. Energy Policy 2006, 34, 3206–3217. [Google Scholar] [CrossRef]
- Lin, B.Q.; Du, K. Technology gap and China’s regional energy efficiency: A parametric metafrontier approach. Energy Econ. 2013, 40, 529–536. [Google Scholar] [CrossRef]
- Fujii, H.; Kaneko, S.; Managi, S. Changes in environmentally sensitive productivity and technological modernization in China’s iron and steel industry in the 1990s. Environ. Dev. Econ. 2010, 15, 485–504. [Google Scholar] [CrossRef]
- Li, L.B.; Hu, J.L. Ecological total-factor energy efficiency of regions in China. Energy Policy 2012, 46, 216–224. [Google Scholar] [CrossRef]
- Li, K.; Lin, B. Metafroniter energy efficiency with CO2 emissions and its convergence analysis for China. Energy Econ. 2015, 48, 230–241. [Google Scholar] [CrossRef]
- Ouyang, X.L.; Sun, C. Energy savings potential in China’s industrial sector: From the perspectives of factor price distortion and allocative inefficiency. Energy Econ. 2015, 48, 117–126. [Google Scholar] [CrossRef]
- Sheng, P.F.; Yang, J. The Heterogeneity and convergence of energy’s shadow price in China—The estimation of nonparametric input distance function. Ind. Econ. Res. 2014, 1, 70–80. [Google Scholar]
- Sheng, P.F.; Yang, J.; Shackman, J.D. Energy’s Shadow Price and Energy Efficiency in China: A Non-Parametric Input Distance Function Analysis. Energies 2015, 8, 1975–1989. [Google Scholar] [CrossRef]
- Kumar, S.; Fujii, H.; Managi, S. Substitute or complement? Assessing renewable and nonrenewable energy in OECD countries. Appl. Econ. 2015, 47, 1438–1459. [Google Scholar] [CrossRef]
- Kaneko, S.; Fujii, H.; Sawazu, N.; Fujikura, R. Financial allocation strategy for the regional pollution abatement cost of reducing sulfur dioxide emissions in the thermal power sector in China. Energy Policy 2010, 38, 2131–2141. [Google Scholar] [CrossRef]
- Ishinabe, N.; Fujii, H.; Managi, S. The true cost of greenhouse gas emissions: Analysis of 1000 global companies. PLoS ONE 2013, 8, e78703. [Google Scholar] [CrossRef] [PubMed]
- Yagi, M.; Fujii, H.; Hoang, V.; Hoeng, V.; Managi, S. Environmental efficiency of energy, materials, and emissions. J. Environ. Manag. 2015, 161, 206–218. [Google Scholar] [CrossRef] [PubMed]
- Molinos-Senante, M.; Hanley, N.; Sala-Garrido, R. Measuring the CO2 shadow price for wastewater treatment: A directional distance function approach. Appl. Energy 2015, 144, 241–249. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Zhou, D.Q. Measuring economy-wide energy efficiency performance: A parametric frontier approach. Appl. Energy 2012, 90, 196–200. [Google Scholar] [CrossRef]
- Lin, B.Q.; Du, K.R. The energy effect of factor market distortion in China. Econ. Res. J. 2013, 9, 125–136. [Google Scholar]
- Yuan, P.; Cheng, S. Estimating shadow pricing of industrial pollutions in China. Stat. Res. 2011, 28, 66–73. [Google Scholar]
- Wang, B.; Huang, R.J. Regional green development efficiency and green total productivity growth in China: From 2000 to 2010—Base on parametric metafrontier analysis. Ind. Econ. Rev. 2014, 5, 16–35. [Google Scholar]
- Li, S.; Ng, Y.C. Measuring the productive efficiency of a group of firms. Int. Adv. Econ. Res. 1995, 1, 377–390. [Google Scholar] [CrossRef]
- National Bureau of Statistics. China Statistical Yearbook; China Statistics Press: Beijing, China, 1998–2012.
- Department of Energy Statistics, National Bureau of Statistics. China Energy Statistical Yearbook; China Statistics Press: Beijing, China, 1998–2012.
- Wang, B.; Liu, G.T. Energy conservation and emission reduction and China’s green economic growth—Based on a total factor productivity perspective. China Ind. Econ. 2015, 5, 57–69. [Google Scholar]
- Zhang, J.; Wu, G.Y.; Zhang, J.P. The Estimation of China’s provincial capital stock: 1952–2000. Econ. Res. J. 2004, 10, 35–44. [Google Scholar]
- Zheng, K.; Yao, G. The Main Reason for Surge of Domestic Oil price—A VARA Approach. South China J. Econ. 2006, 5, 83–94. [Google Scholar]
- Wang, J.; Zhong, W.Z. The Research of Regional Energy Intensity Difference in China—From the Factor Endowment Perspectcive. Ind. Econ. Res. 2009, 6, 44–51. [Google Scholar]
- Shi, B.; Shen, K.R. The Government Intervention, the Economic Agglomeration and the Energy Efficiency. Manag. World 2008, 10, 6–18. [Google Scholar]
- Wang, W.G.; Fan, D. Influential factor and convergence of total factor energy efficiency in China based on the malmquist-luenber index. Resour. Sci. 2012, 34, 1816–1824. [Google Scholar]
- Tang, L.; Yang, Z.L. Energy efficiency and industrial economic transition. J. Quant. Tech. Econ. 2009, 10, 34–48. [Google Scholar]
- Wang, K.L.; Yang, L.; Yang, B.C.; Cheng, Y.H. Energy economic efficiency, the energy environmental performance and regional economic growth. J. Manag. 2013, 26, 86–99. [Google Scholar]
- Wu, Y.R. The role of productivity in China’s growth: New estimates. China Econ. Q. 2008, 2, 827–842. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).