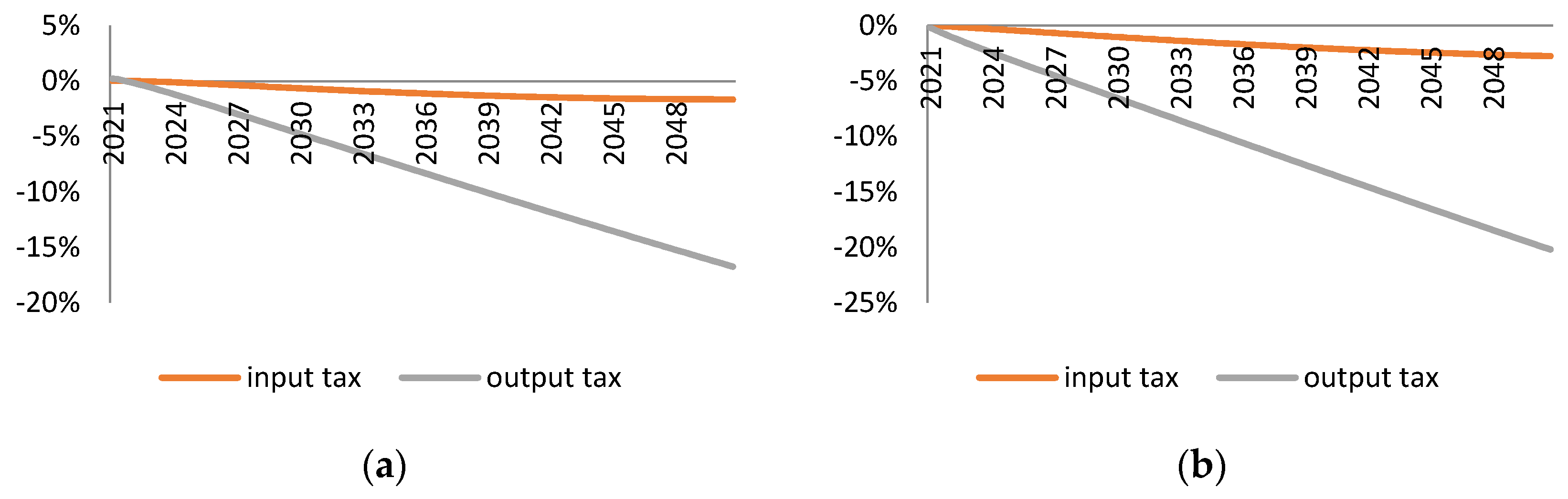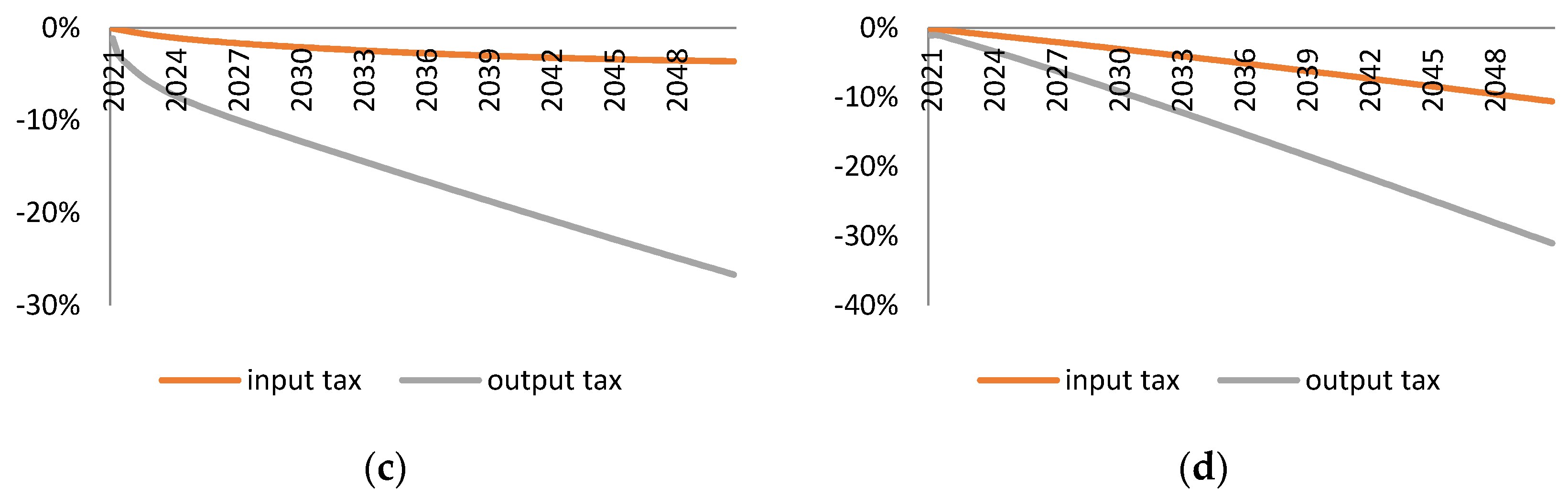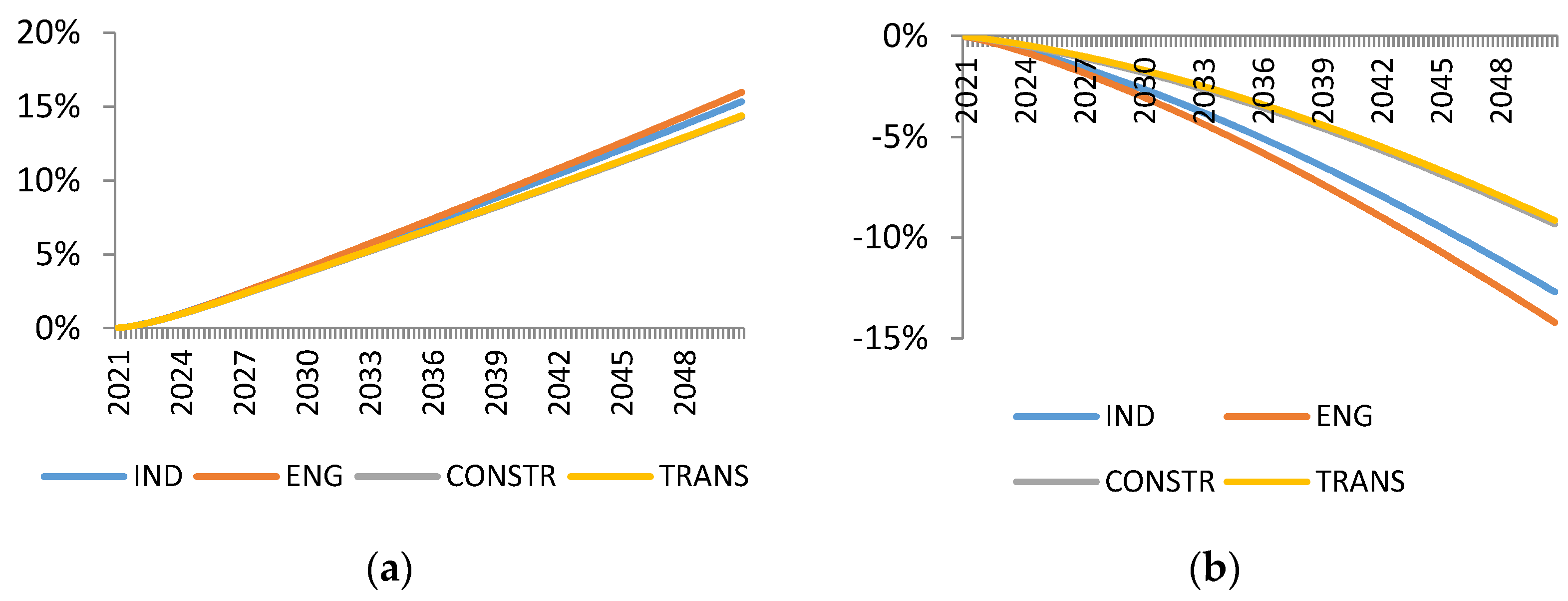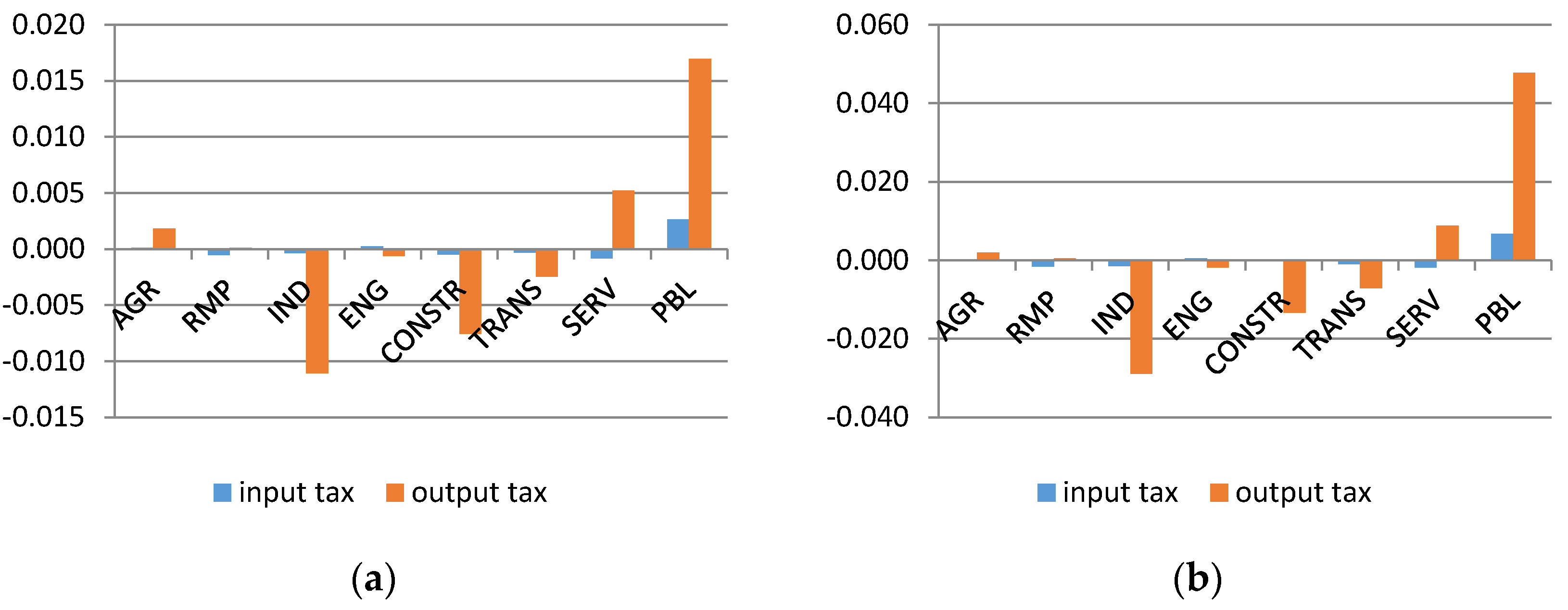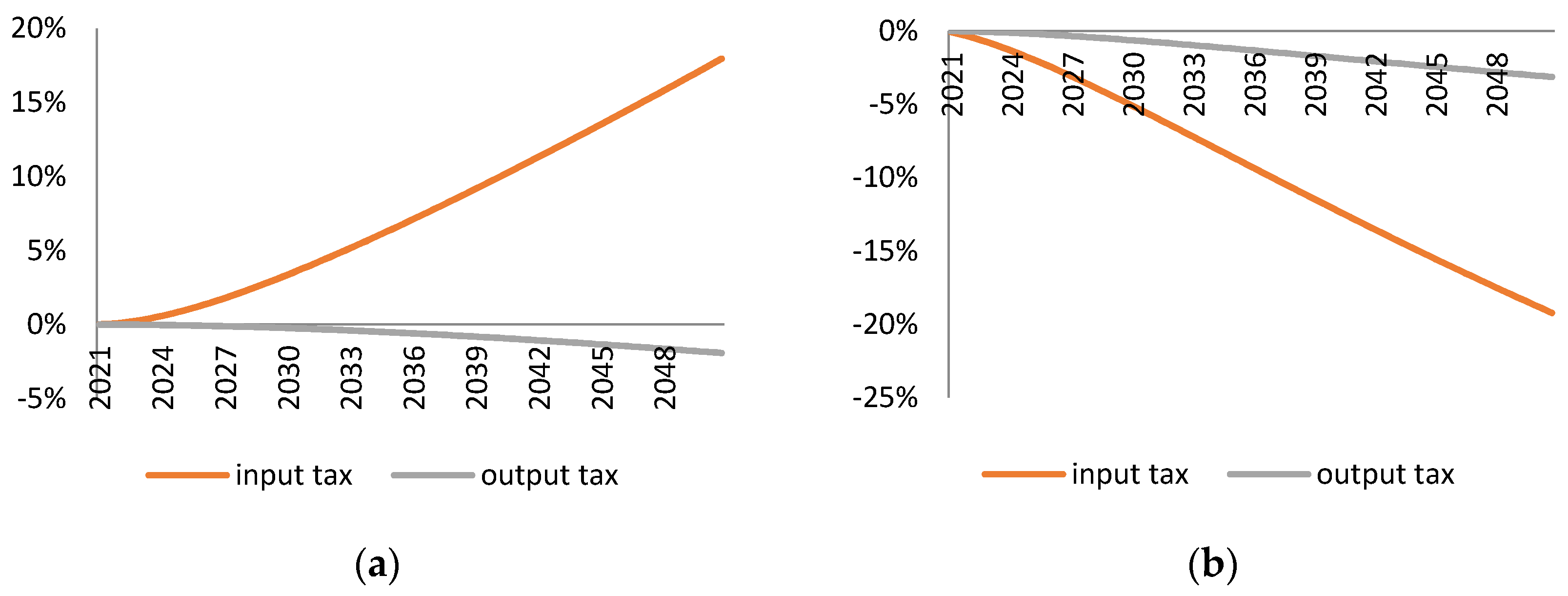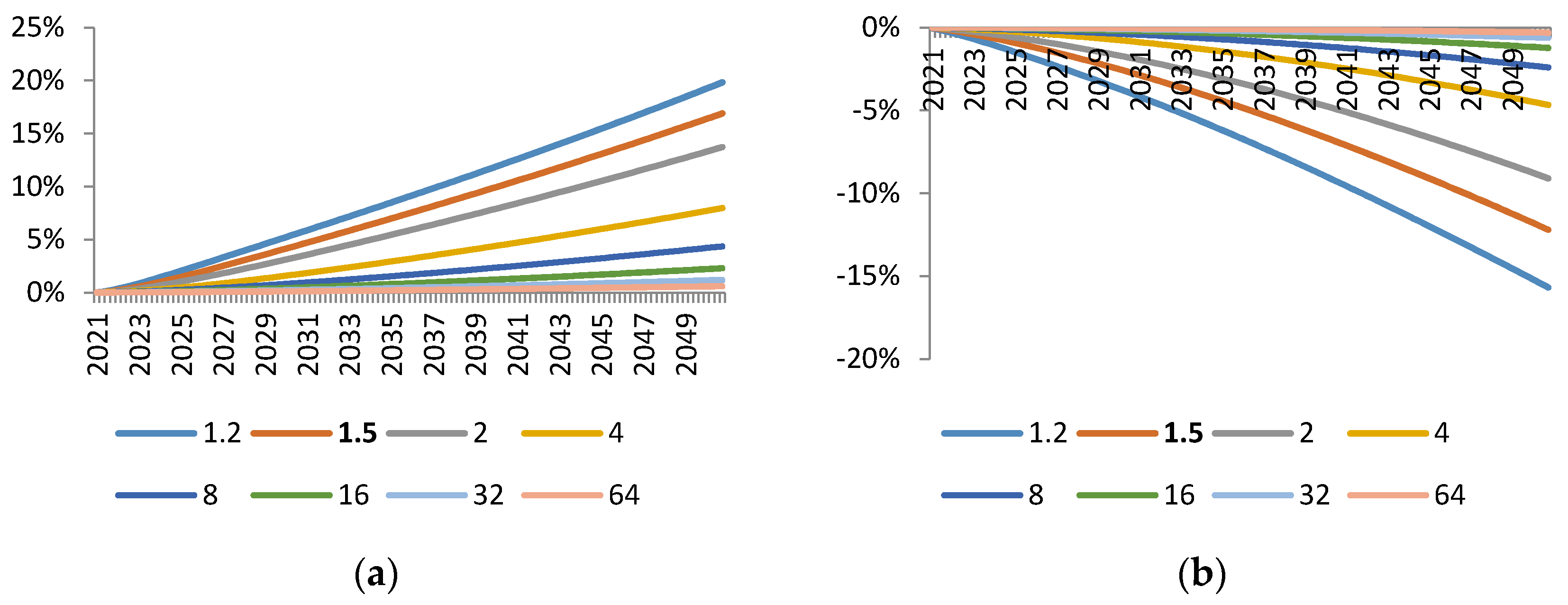1. Introduction
The need to limit the use of natural resources is becoming one of the most pressing issues for policy-makers. On the one hand, exhaustive use of resources, which are available only in limited supply, can potentially limit the production possibilities and welfare of future generations. On the other hand, use of resources such as fossil fuels increases air pollution and releases carbon to the atmosphere causing the greenhouse effect. The importance of the problem has been recognized by, among others, policy-makers in the European Union [
1], United States [
2], and China in its 12th five-year plan for years 2011–2015 [
3].
There are several policy options for resolving the problem of excessive resource use. If one thinks that today’s production puts a burden on future generations, a tax on today’s output constitutes a solution. If one thinks that the current market prices of resources do not reflect their true social costs (e.g., due to atmospheric pollution), then a tax on inputs [
4] constitutes a solution. Other options include performance standards, which require firms to limit the use of resources per unit of output and incentivize firms to adopt more efficient technologies, or R&D and deployment subsidies, which support development and adoption of cleaner technologies. In this paper we limit our attention to the first two policy options: a tax on input and a tax on output.
An input tax is a popular policy instrument for achieving fiscal and environmental goals. The most common example of this tax is the petroleum tax. In our study we examine the consequences of replacing this tax with a hypothetical tax on outputs of the most resource- and pollution-intensive industries, such as the cement, natural fertilizers, or electronic equipment industry. Using the classification of material and resource taxes proposed in [
4], the input tax falls into the category of taxation of materials when they enter into production, and the output tax as a tax levied on resource-intensive final products.
We use a multi-sector dynamic stochastic general equilibrium (DSGE) model of the EU27 area to simulate the impact of these taxes levied on industry, energy, construction, and transport sectors. We allow for endogenous investment in resource-efficiency improvement and account for labour market adjustments. We find that input and output taxation create contrasting incentives and have an opposite effect on resource efficiency, which implies different dynamics of material use and macroeconomic outcomes. Simulating tax rates which lead to an equal drop in material use, we find that the material input tax results in GDP and employment that is 15%–20% higher compared to the scenario with the output tax. Simulating tax rates that equate the tax revenue, we find that the output tax results in a much smaller drop in material use. Additionally, we find that using the tax revenue to reduce labour taxation is much more efficient in the case of input tax. Thus, the input tax implies smaller macroeconomic costs and better resource efficiency outcomes than the output tax in all variants of the simulations considered. This leads us to the conclusion that a material input tax is a more efficient instrument to achieve resource decoupling.
In the paper we highlight and discuss one reason for the different effects of input and output tax: a material tax provides an incentive for firms to substitute materials with material-saving technologies. Thus, a given reduction in material use is associated with a smaller reduction in production. Indeed, as we demonstrate in the sensitivity analysis, larger substitutability between materials and material-saving technologies is associated with lower GDP loss upon introduction of a material tax.
The ability of technology to substitute for the use of resources and energy has been documented in a range of empirical studies. For example, in [
5] it is shown that an energy-related patent, on average, leads to long-run energy savings worth $14.5 million (median present value of long run energy-savings from nine industries in which savings were observed: automotive, chemicals, copper, electrometallurgical, iron foundries, plastic film and sheet, pulp and paper, and steel pipes and tubes). Sue Wing [
6] uses industrial data on factor use and patent data to decompose changes in the US energy intensity by industries into changes in industrial composition, factor substitution, technological change induced by changes in energy prices, and the disembodied technological change. He finds that induced technological change leads to energy savings, although its contribution is small relative to the other factors in the decomposition. Fæhn
et al. [
7] finds that a 10% increase in the energy price leads to technology adoption that results in a 1% lower energy demand by new firms.
The paper contributes to the literature on the effectiveness of various policies aimed at the reduction of resource and material use. There are numerous theoretical studies which examine the optimal policy mix for reduction in the use of fossil fuels. Popp [
8] and Fischer
et al. [
9] find that a combination of carbon tax with R&D subsidies promoting efficient technologies brings more benefit than any of the single policies. Gerlach and van der Zwaan [
10] highlight the role of efficiency standards, which, as they argue, promote lower fuel consumption, as well as adoption and development of more efficient technologies. More recently, the literature was extended by studies which analyse policies promoting material efficiency. Soderholm and Tilton [
11] argue that policies should correct the externalities directly but should not set any targets for material efficiencies, as it is not clear what material efficiency target is socially optimal. In response to this argument, Allwood
et al. [
12] replied that although material efficiency may not be optimal from the economic perspective, it is going to face less political and social resistance than e.g., a carbon tax. Skelton and Allwood [
13] examined the impact of carbon prices on efficiency in the use of steel. They find that substitution possibilities between material and labour matters for the policy effects. We extend the analysis of [
13] by allowing for general equilibrium effects (e.g., adjustment of wages to changes in unemployment).
In contrast to the above papers, our paper does not suggest what the optimal policy mix is, but rather highlights what effects determine the success of the input tax when compared to the output tax. We extend the literature by analysing the impact of taxes not only on costs of policies in terms of GDP, but also in terms of employment.
In addition, the paper verifies whether the macroeconomic performance of both taxes changes under the alternative uses of tax revenue—reducing taxation on labour instead of transferring it to household. The importance of tax recycling has been evidenced by the literature on the double dividend hypothesis, which states that the cost of climate policies can be reduced if the revenue from taxes and fees on emissions is used to decrease other distortionary taxes. The authors in [
14] and [
15] demonstrated that models need to take into account the presence of non-environmental distortionary taxes in order to accurately assess the macroeconomic performance of environmental taxes. There are also studies which find support for the hypothesis by comparing the effects of various tax recycling at a national level (e.g., [
16,
17]).
In the next section we present our macroeconomic DSGE model which allows for endogenous adoption of material-saving technologies. We discuss the calibration of the model for the EU27 area, using an Input Output matrix and literature findings. We lay out a simulation strategy for taxation introduced from 2021. Although all model variables are simulated, we focus on taxation impacts on GDP, national accounts, labour market, resource use, and public finances until 2050. In the third section, we present our results. Firstly, we compare the impact of input and output taxes which lead to the same total reduction in resource use in 2050. Secondly, we compare the impact of input and output taxes which raise the same revenue in 2050. Next, we check how sensitive the results are to the alternative uses of tax revenue. Lastly, we conduct a sensitivity analysis and examine how our results change when we vary the parameter determining the substitutability between materials and material-saving technologies. In the final section we discuss our findings.
2. Materials and Methods
In this section we describe the model and the simulation setup. Regarding the model description, we specify the production structure of firms, which is crucial for the modelling of a firm’s response to input and output taxation, and is the focus of the paper. A detailed description of the remaining agents of the model and the solution method can be found in [
18], and a summary of variables and parameters which are discussed in this section can be found in
Table A1 in
Appendix A.
2.1. Model Description
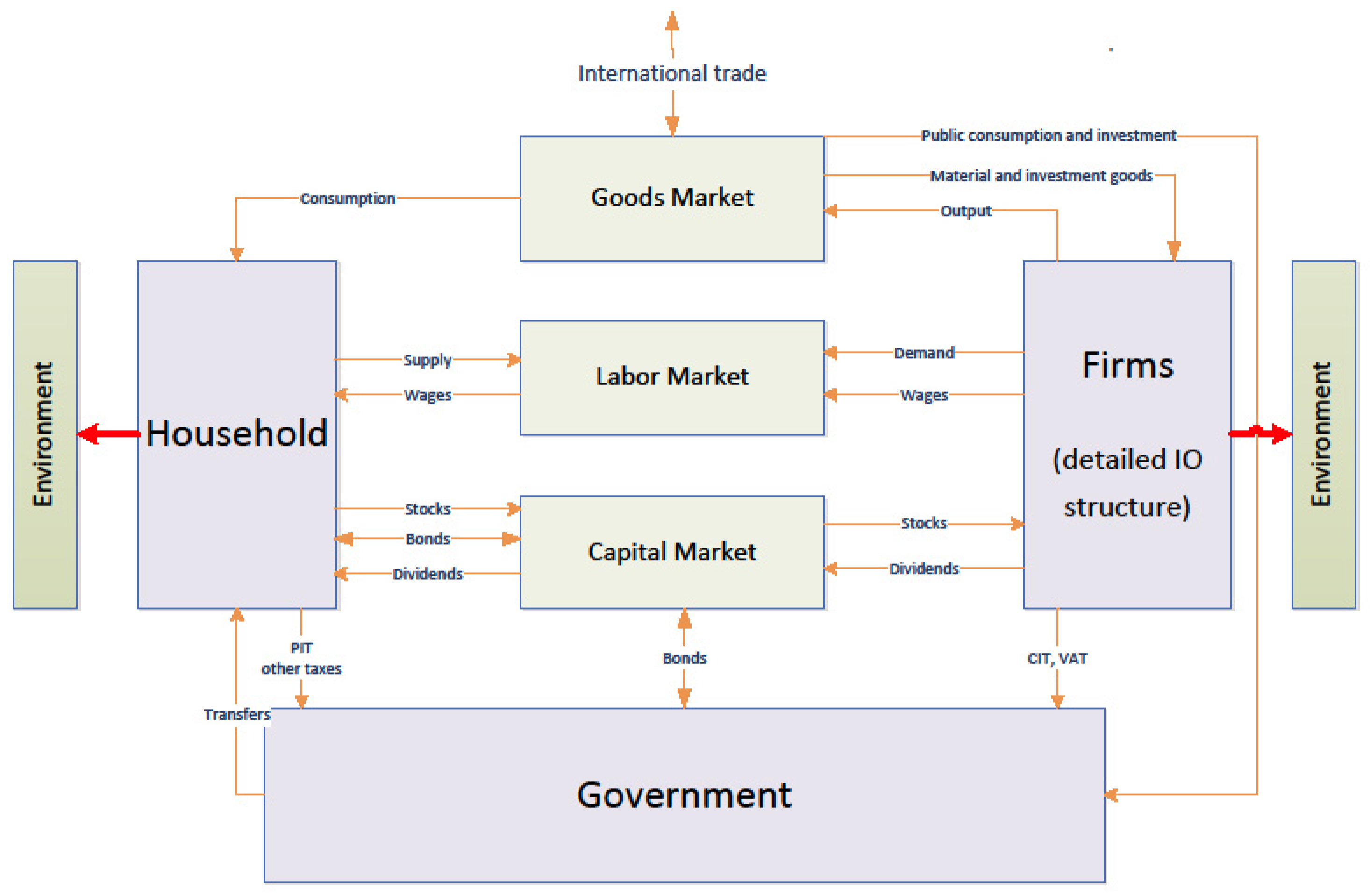
We use a multi-sector, large-scale dynamic stochastic general equilibrium (DSGE) model which we calibrate and estimate for the EU27 area (we calibrate our model to Eurostat Input Output tables and Eurostat only provides them for the EU27 area, which consists of all the current member states except for Croatia). The main economic agents in the model are: households, representative firms in each of the eight sectors and government. The basic scheme of the model is shown in
Figure 1.
The model is disaggregated into the following sectors: Agriculture (AGR), Raw Material Production (RMP), Industry (IND), Energy (ENG), Construction (CONSTR), Transport (TRANS), Market Services (SERV) and Public Services (PBL).
Table 1 summarizes the sector structure of the model.
In each sector
a representative firm maximises the expected, discounted profits:
where
is the stochastic discount factor mirroring the preferences of the household and
are the profits of the firm. The firm operates a multi-stage production technology using CES functions. In the first stage, capital
is combined with energy intermediate material
in order to produce composite good
:
where
is a parameter determining the share of energy in the composite good and
denotes the firm’s short-term elasticity of substitution between capital and energy. In the second stage the composite good
is combined with labour
in order to produce another composite good:
where parameter
sets the shares of the production factors, and
sets the firm’s short-term elasticity of substitution. In the final stage of production, the second composite good is combined with material good
:
where
is the share parameter of the production factors and
sets the firm’s short-term elasticity of substitution between materials and other factors of production.
Aggregate intermediate material is produced using goods from all sectors of the model in a two-step procedure. Since we are mainly interested in assessing effects of policies on the Materials Production sector (A02 and B in Eurostat CPA) we proceed with the following approach. We assume that material good is composed of a material good of the Raw Material Production sector
and a bundle of goods from remaining sectors
with a CES function, which also accommodates endogenous material efficiency. Then, the bundle of remaining material goods is produced using Leontief function. This can be summarized in the following equations:
As usual,
and
set the share and short-term elasticity in the CES composite, whereas parameters
set the share of material good of sector
in the production function of sector
. The variable
sets the material efficiency of sector
and, in the steady state, it is normalised to unity. Each intermediate material use variable
is a composite of home and foreign produced goods, which are additionally denoted by subscripts
H and
F:
Endogeneity of technology choices means that firms are allowed to change the characteristics of technology parameters of production function under market incentives. For instance, an increase in energy prices incentivizes the firm to invest in the more costly, energy-saving technology. Effectively, this gives firms the possibility to substitute inputs with capital. Importantly, these substitution possibilities are limited in the short-run: we assume that the efficiency of technology is the weighted average between past and today’s technology choices. In particular, we let
be determined by:
where
is the stock of capital,
is the level of investment and
is the firm’s choice of technology at time
. More efficient technology involves higher cost of capital goods. Specifically, the cost of capital goods is given by:
Parameter sets the degree of rigidity with respect to changes in technology and implicitly sets the medium- and long-term elasticity of substitution between materials and remaining inputs. Note that if , firms always choose .
The profit of the firm is given by the revenue from sales of good less the cost of labour, investment, intermediate materials, vacancy posting, and taxes. Goods produced by the sector firms are aggregated by final goods firms, which produce consumption, public, investment, and export goods. The final goods production structure is given by the Input-Output matrix.
The consumer maximises utility from consumption subject to her income which is composed of labour income less taxes, dividends from firms, and transfers from the government. The government collects labour, VAT, and environmental taxes and spends it on the purchase of the public good and on transfers to the household. The labour market is modelled according to the search and matching framework, similar to [
19,
20]. The unemployment rate is determined endogenously and depends on the number of vacancies generated by firms, and the intensity of job search by job seekers. The decisions of firms on the opening of vacancies depends on the current and future states of the economy. The key macroeconomic assumption of the DSGE model is that the economy is on the balanced growth path at the beginning of the time horizon and that it will continue on this path if no policies are introduced.
The sector structure of the model is calibrated using the NACE Rev. 2 Input-Output matrices for the year 2010 available from Eurostat. The flows are determined by the share parameters
which appear in equations determining the production structure. The elasticity parameters are set as follows:
—short-run elasticity between capital and energy in the production function of a firm. According to numerous studies, the elasticity of substitution between these factors is very low [
21,
22]. We set this parameter at 0.1.
—short-run elasticity between capital-energy composite and labour in the production function of a firm. The standard practice of DSGE models is to use the Cobb–Douglas specification, e.g. [
23], which implies a value of 1. We set this parameter to a value of 0.95,
i.e., lower than unity. This is motivated by the recent study in [
24], which shows that sector-specific elasticity estimates are significantly below unity.
—short-run elasticity between capital-energy-labour composite and materials in the production function of a firm. We set this elasticity at 0.3 following the CGE model in [
25].
—short-run elasticity between RMP material and other materials in the production function of a firm. A study in [
26] shows that the elasticity of substitution between fuels and other raw materials goods is low. We also set a small value of 0.1, although the RMP sector includes other materials apart from fuels.
—short-run elasticity between home and foreign goods in the production function of a firm. The literature regarding this elasticity shows that it can take a wide range of plausible values. For example, in a study [
27] it is estimated that for the G7 countries this elasticity is in the range between 0.1 and 2. Heathcote and Perri [
28] demonstrated that low values of this parameter result in a model that better reproduces business cycle properties of data. We set this value at 0.4.
2.2. Simulation Setup
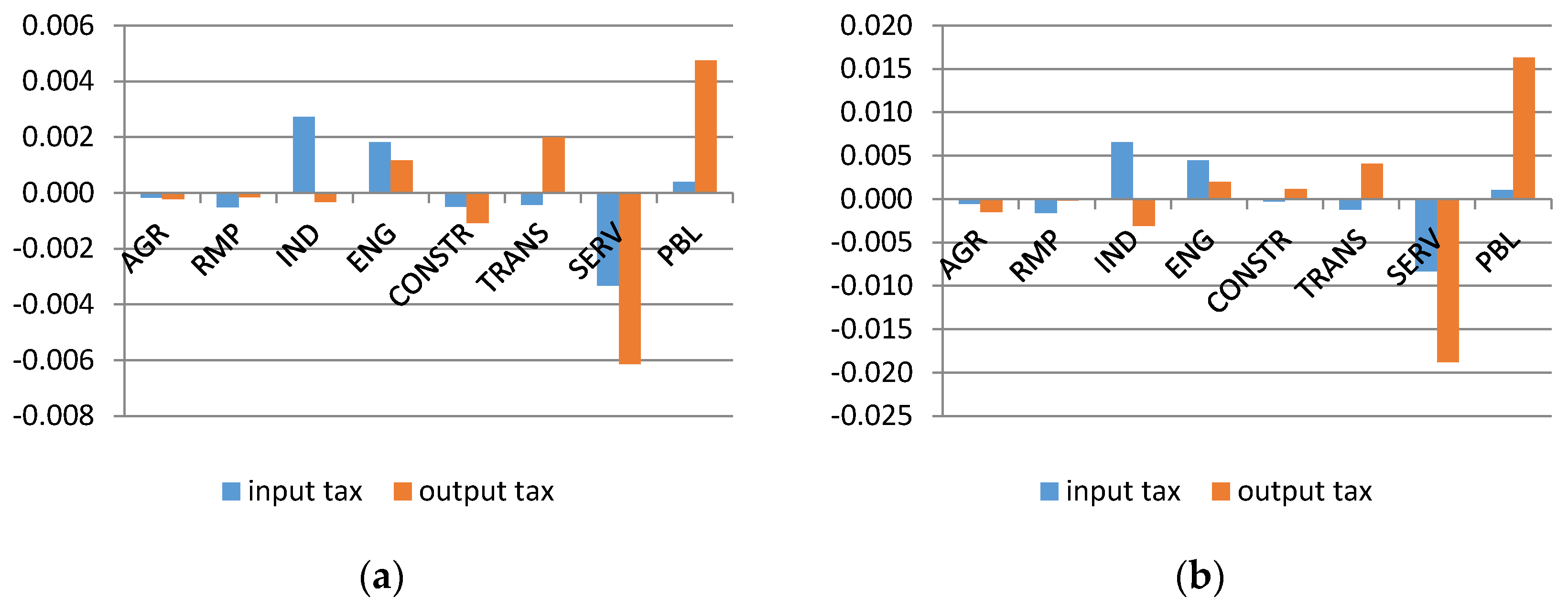
We use the model described in the previous subsection to compare the two tax schemes in their ability to reduce material use and their economic impact, measured among others in output, employment or sector shifts in the economy. We define the input tax as an excise-type tax on the purchase of the intermediate materials of the Raw Material Production sector by the Industry, Energy, Construction, and Transport sectors. We define the output tax as an excise (non-deductible) tax which is levied on the value added generated by these four sectors.
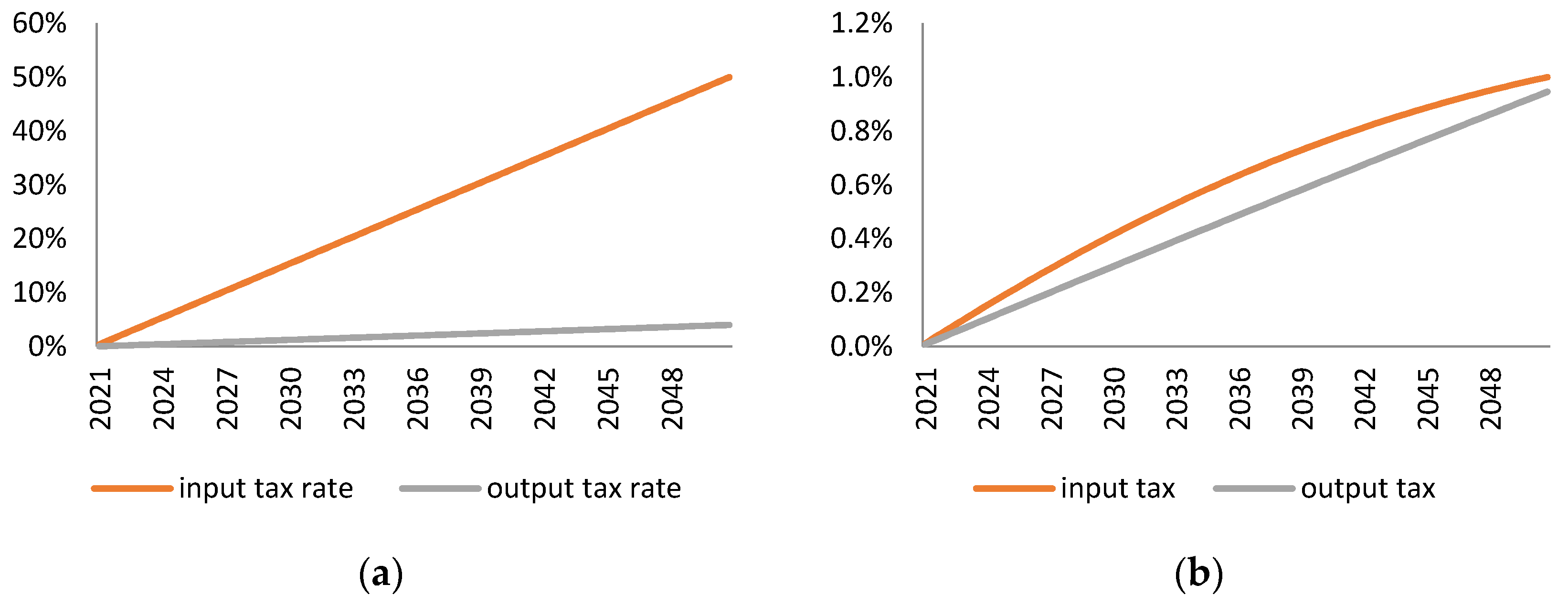
In order to assess the taxes along a possibly wide range of dimensions, we perform several simulation experiments. In the basic experiment we consider two simulations which differ in the basis for the comparison of the two taxes. In the first simulation we follow a material reduction approach. For each type of tax we simulate such a (roughly linear) path of tax rates that the resulting decrease of the RMP sector output gradually (linearly) reaches 20% in 2050 (from 0% in 2021). The start date is set in order to make the study relevant for the current debate on EU environmental policies. On the other hand, given that the target in our simulations is ambitious, we let the policies be introduced gradually until 2050. In the second simulation we follow a fiscal approach. For each type of tax we simulate such a linear path of tax rates that the revenue in 2050 reaches approximately 1% of GDP. For both of these simulations we assume that the revenues are used as a lump sum transfer to the household. Such fiscal closure allows us to analyse only the price incentives that the tax has for the behaviour of firms.
In the third simulation experiment we modify the fiscal closure. We follow the first simulation setup (material reduction approach) but we assume that 20% of the tax revenue is spent on lowering labour taxation. The main aim of this simulation is to compensate for the fact that the two taxes differ significantly in the total revenue they generate (higher in the case of the output tax). The offsetting effect of lower labour tax reduction will, therefore, be stronger in the case of the output tax.
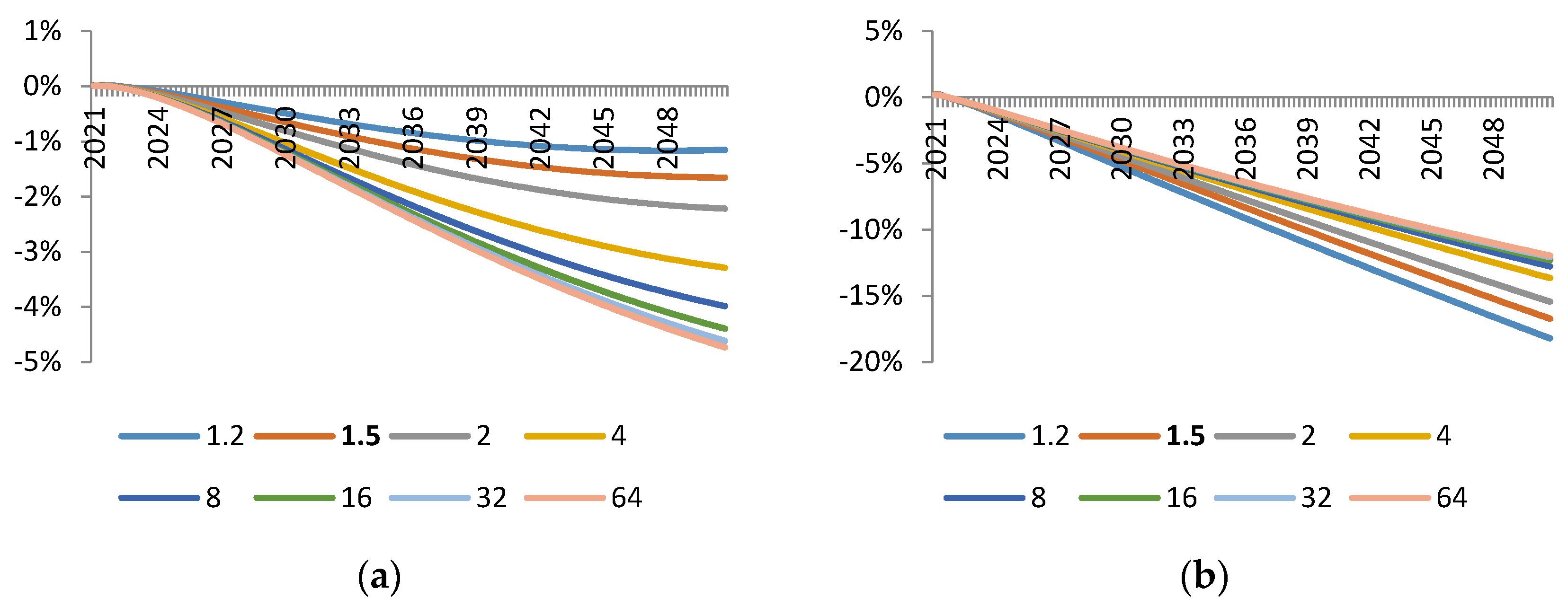
Lastly, we check the robustness of our results. Due to the fact that the results depend, to a large extent, on the endogenous material efficiency mechanism, we perform a sensitivity analysis with respect to the elasticity parameter which governs this mechanism. Again, we follow the material reduction approach as in the first simulation exercise. All simulations are performed using the Kalman filter [
18]. Results are expressed as deviations from the steady state of the model, which we interpret as the baseline growth scenario for the EU27.
4. Conclusions
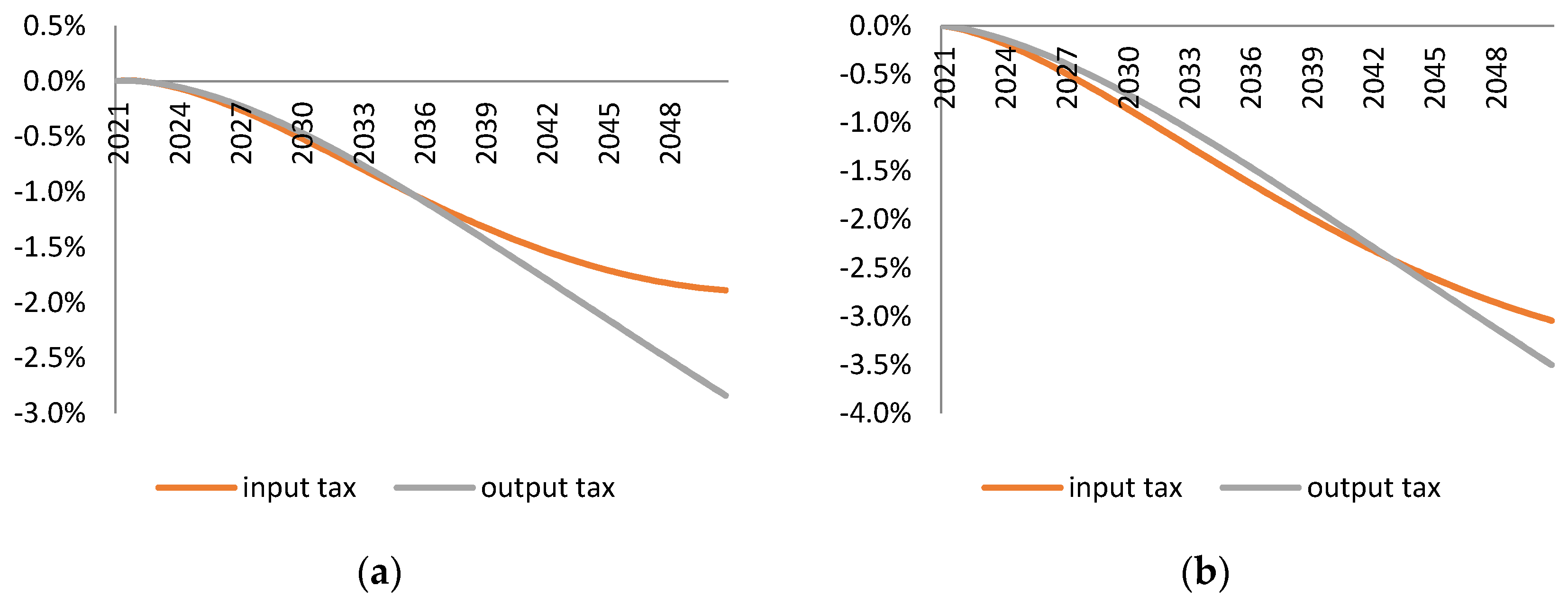
Our simulation results clearly indicate that the reduction of material use through the taxation of material input brings smaller economic costs than the same reduction achieved through the taxation of output in material-intensive sectors. In 2050, the input tax levied on the EU27 from 2021 results in a decline in GDP and employment which is lower by 16 and 17 percentage points respectively in comparison to the effects of the output tax levied in the same period. Furthermore, the input tax achieves the same material reduction target with smaller and less rapid changes in the sector structure of economy. Smaller structural change implies less need for re-skilling of the workforce and, therefore, could potentially entail lower social costs of environmental policy.
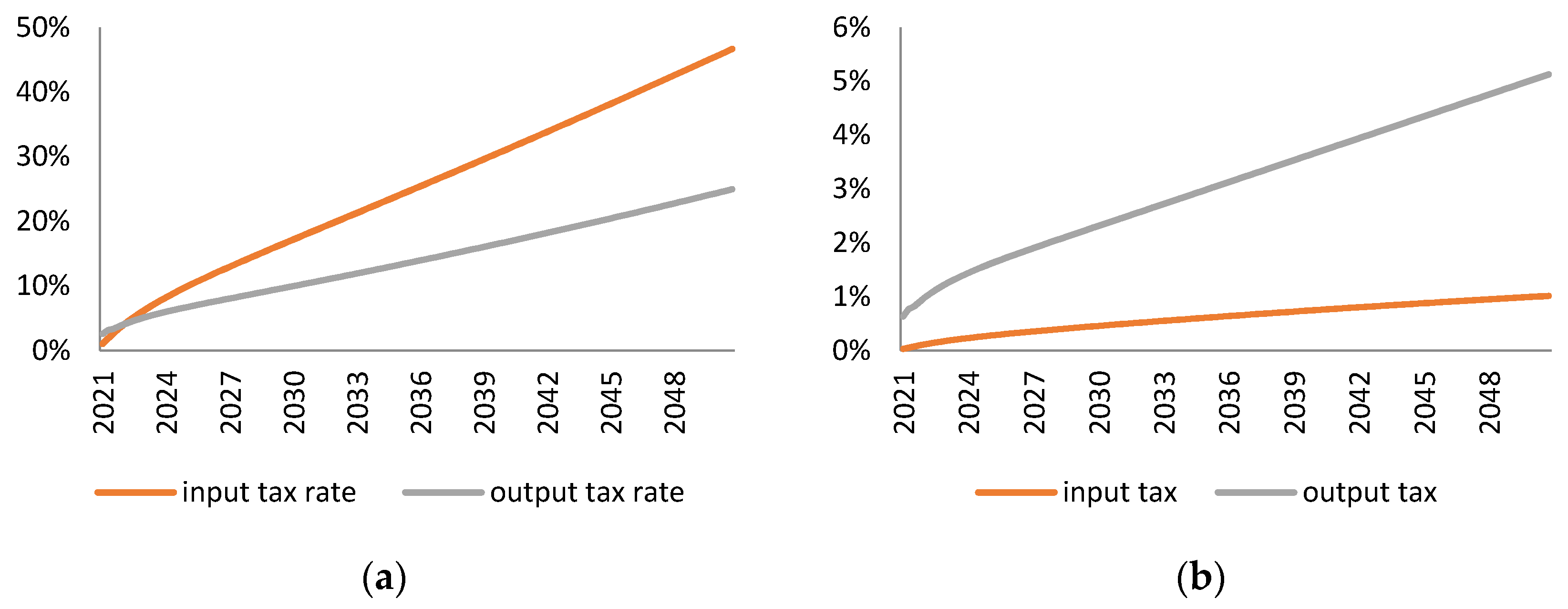
We find that a significant part of the difference between the macroeconomic effects of input and output tax could be traced down to the difference in technological adjustments induced by these taxes. Input tax incentivises firms in material-intensive sectors to invest in material-saving technologies. Since firms substitute materials with technology, they do not need a large cut in production in order to meet the material use reduction target. Indeed, the sensitivity analysis in
Section 3.4 shows that when firms do not have an option to invest in material-saving technology, the economic costs of input tax are much larger.
In contrast, the output tax creates no incentives for firms in material intensive industries to substitute materials with technology. A reduction in demand for firms’ products is a direct effect of the output tax. Firms respond to it with a reduction in the use of all factors of production. Since material-saving technology could be viewed as one of the factors, firms will also look for cuts in this domain. Indeed,
Figure 13 suggest that the output tax leads to a reduction in material-efficiency. The sensitivity analysis in
Section 3.4 indicates that when the firm does not have a possibility to economise on the quality of technology, the reduction in material efficiency is smaller.
In addition to the material reduction approach, we have considered two alternative simulation setups. First, instead of targeting a given reduction in material use, we set a fiscal goal: we identified and simulated the output and input tax rate paths which result in the same budget revenue in 2050. We also found that in this fiscal approach, the input tax involves smaller economic costs (in terms of GDP and employment) than the output tax.
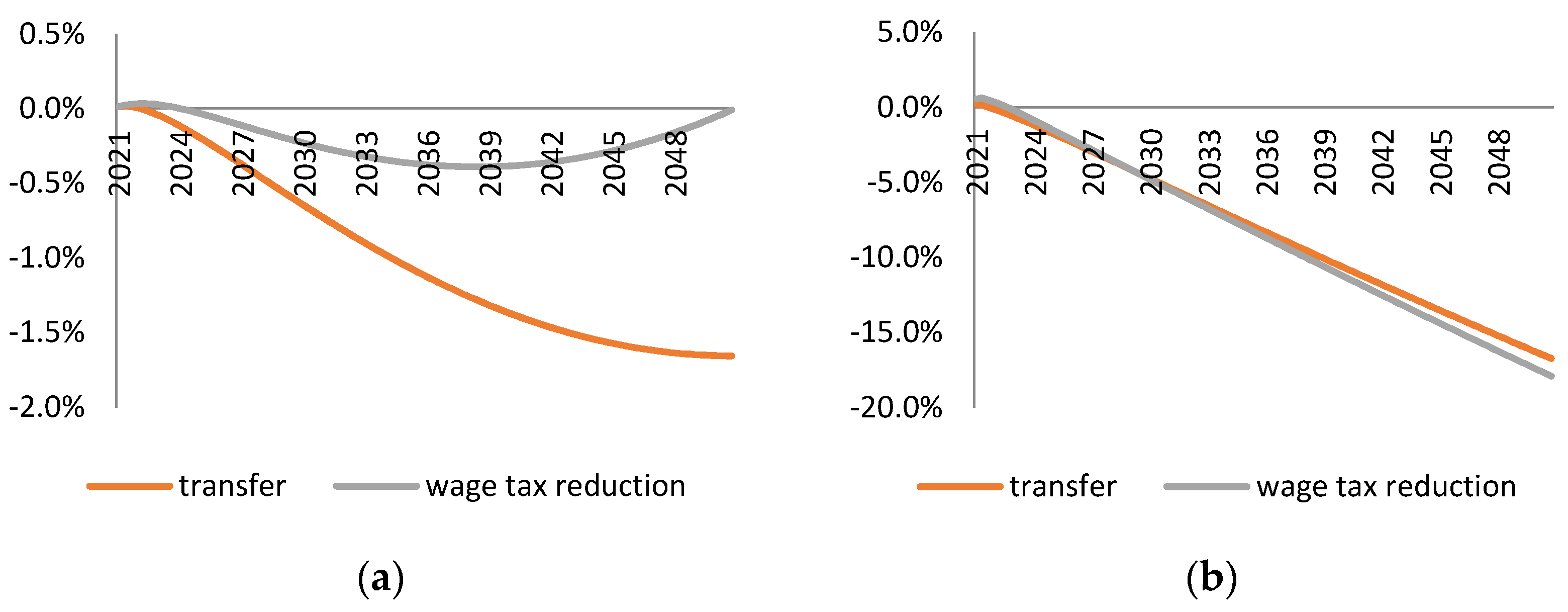
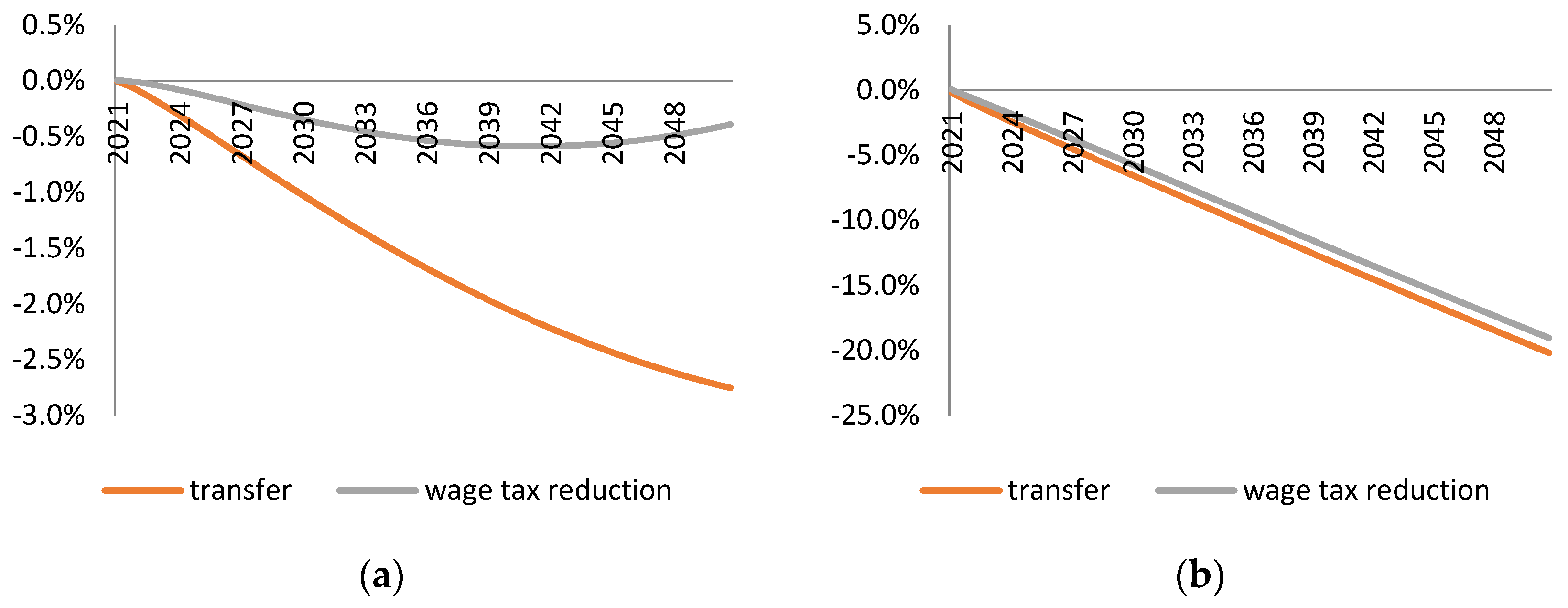
We also considered a scenario in which the tax revenue is partially used to reduce labour taxation. According to the double dividend hypothesis, this shall reduce the negative economic effects of environmental taxes. Indeed, the hypothesis is supported in the case of the input tax. If the tax revenue is used on reduction of the labour tax rate, the input tax has a negligible effect on GDP and employment in the long-run. In contrast, similar recycling of the output tax revenue barely affects the trajectory of GDP and employment loss implied by the output tax with a lump-sum transfer fiscal closure. The reason for this is that the labour tax reduction leads to more production and higher resource use. Thus, the output tax rate has to be even higher to meet the material reduction target which, in turn, introduces even more distortion in the economy.
All in all, we find that the input tax is a better tool to achieve resource decoupling than the output tax. However, output tax is superior in one regard—guaranteeing budgetary revenue. Since the input tax leads to much higher resource efficiency than the output tax, it cuts down its own base to a higher extent than the output tax. Thus, if policy-makers would treat these environmental taxes not only as an instrument to achieve resource decoupling, but also as an additional source of budgetary revenue, they would find the output tax more attractive than suggested by its poorer macroeconomic and resource-efficiency characteristics.