GIS-Based Integration of Subjective and Objective Weighting Methods for Regional Landslides Susceptibility Mapping
Abstract
:1. Introduction
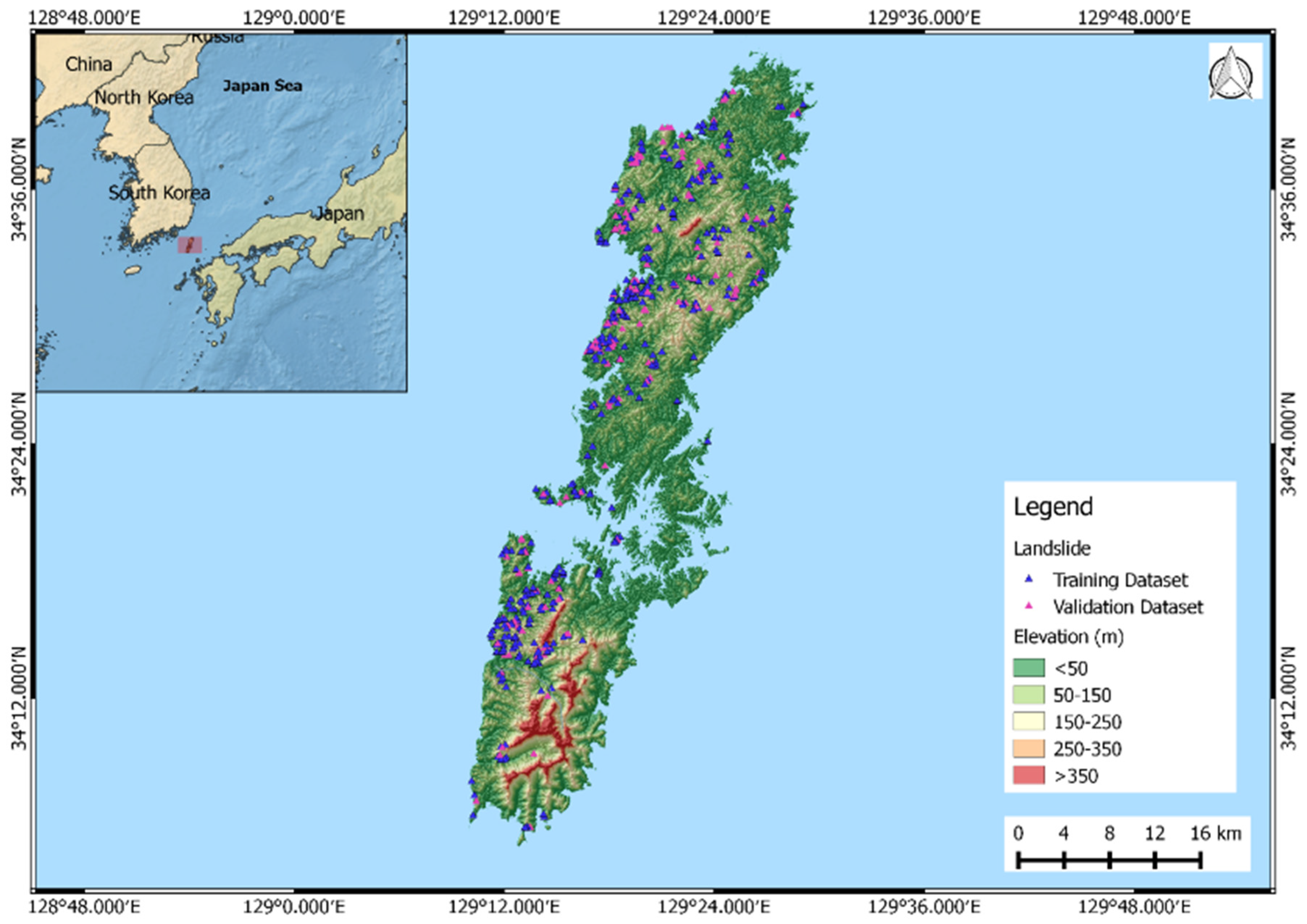
2. Study Area and Datasets
2.1. Historical Landslide Inventory
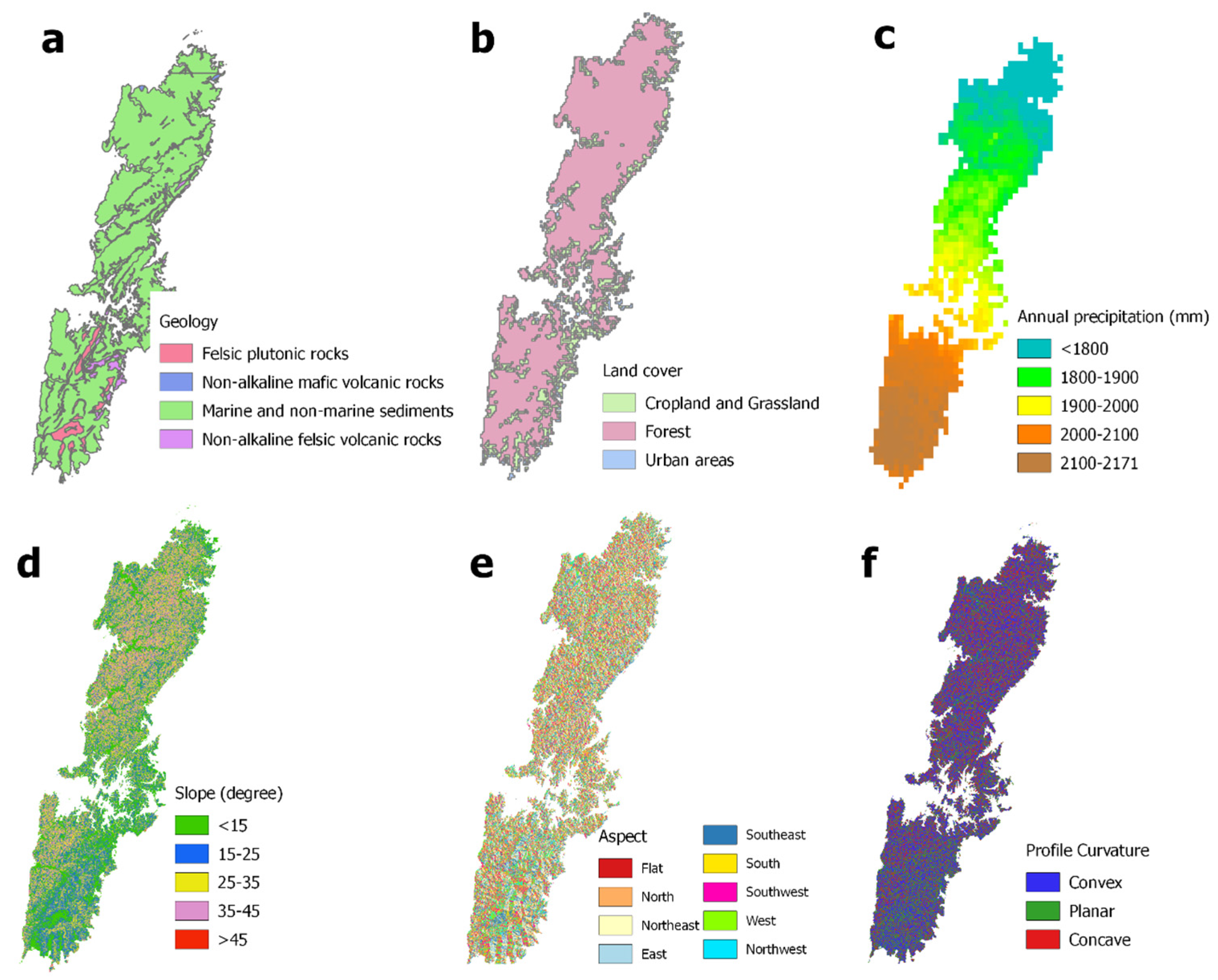
2.2. Landslide Predictive Factor
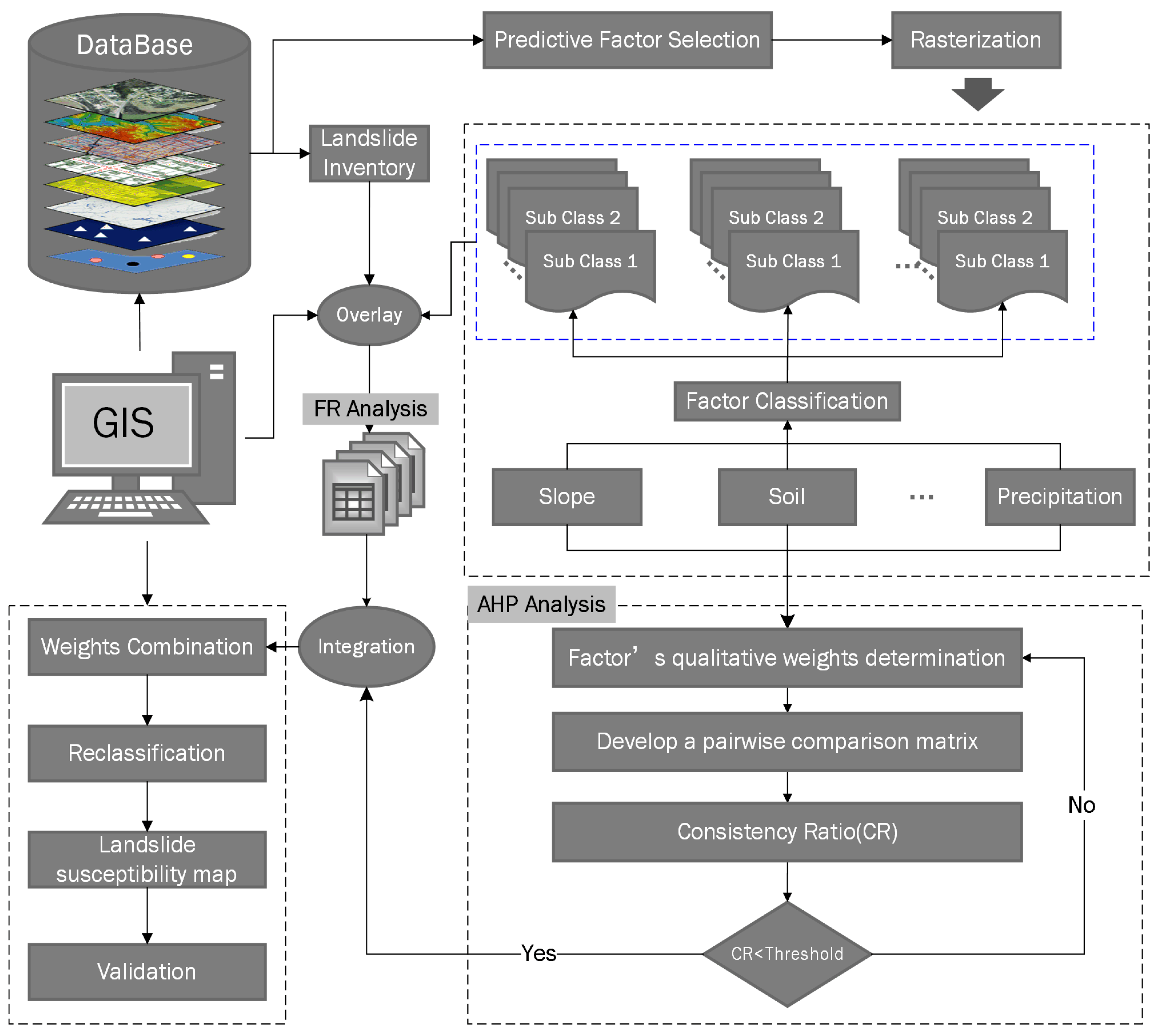
3. Methodology
3.1. Objectively Weighting of Subclasses Using FR
- (1)
- Classification of the landslide-predictive factors.
- (2)
- FR calculation for each class of landslide predictive factors. The landslide inventory is overlaid with each predictive factor map, and frequency ratio values of each class get calculated using Equation (2). This step was implemented on every landslide-predictive factor repeatedly.
- (3)
- Finally, the LSI was created by summing the FR values (Equation (3)) in the conventional FR method.
3.2. Subjectively Weighting of Factors Using AHP
- (1)
- Dividing the problem into a hierarchy tree analysis. Generally, for LSM, two-stage hierarchies should be developed. The first one is at the factor hierarchy, which is used to rate the factor’s contribution in landslide occurrence (WF). The other is the subclasses hierarchy, which is used to rate the relative contribution of subclasses within each factor in landslide contribution. In order to distinguish the subclasses’ weights here from that derived from the FR method, we name it subjectively determined subclasses’ weights (SSCW).
- (2)
- Creating a pairwise comparison matrix of the factors (or subclasses). In the comparison matrix, each factor (or subclass) was weighted subjectively against every other by assigning a series of discrete values between 1 and 9 (Table 2) based on the relative contribution of factors (or subclasses) to landslide occurrence. The matrix element value “1” means the two factors (subclasses) contribute equally to the landslides occurrence, and ”9” indicates that one factor was significantly more important than the other ones. The reciprocals values (between 1/2 and 1/9) indicate the inverse comparison results.
- (3)
- Checking the overall consistency of the pair-wise evaluations to reduce the bias in the decision-making process. The overall consistency was quantified using the eigenvalues of the matrix, which is an indicator of the inconsistencies in a set of pairwise ratings. It was suggested by [37] that for a consistent reciprocal matrix, the largest eigenvalue λmax is equal to the number of comparisons n. An index of consistency, known as the CR (Consistency Ratio), was thus employed to indicate the probability that the matrix judgments were randomly generated (Equation (4)).
- (4)
- Combining the subjectively determined weights using Equation (6) to produce the LSI.where is the weight of factor i (Table 4), is the subjectively determined weight of jth subclass within factor i using the AHP (see Table 1), n is the number of factors. The checking result of the consistency ratio of shown in Table 5.
3.3. Weighting Linear Combination Using the Integrated FR-AHP Method
4. Results and Discussion
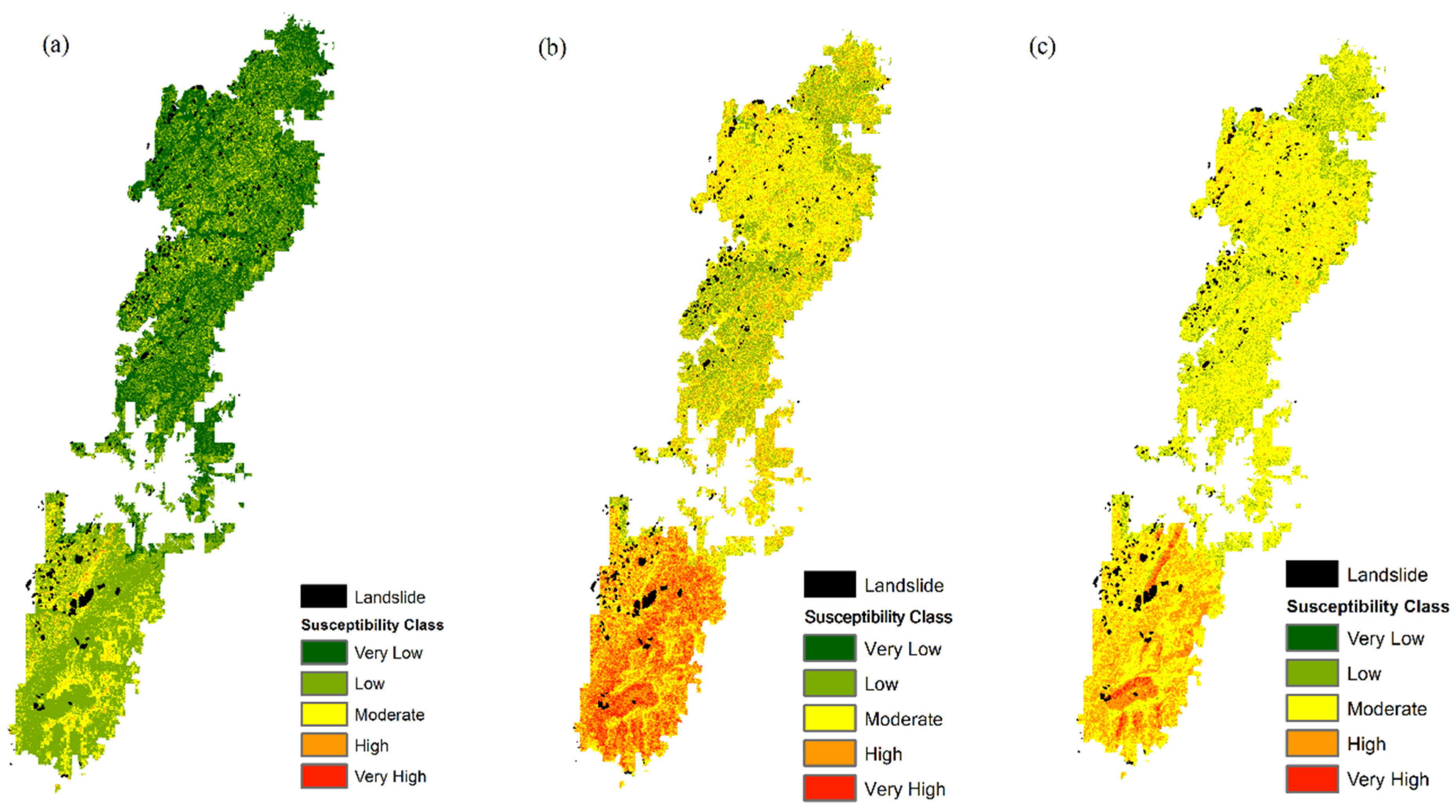
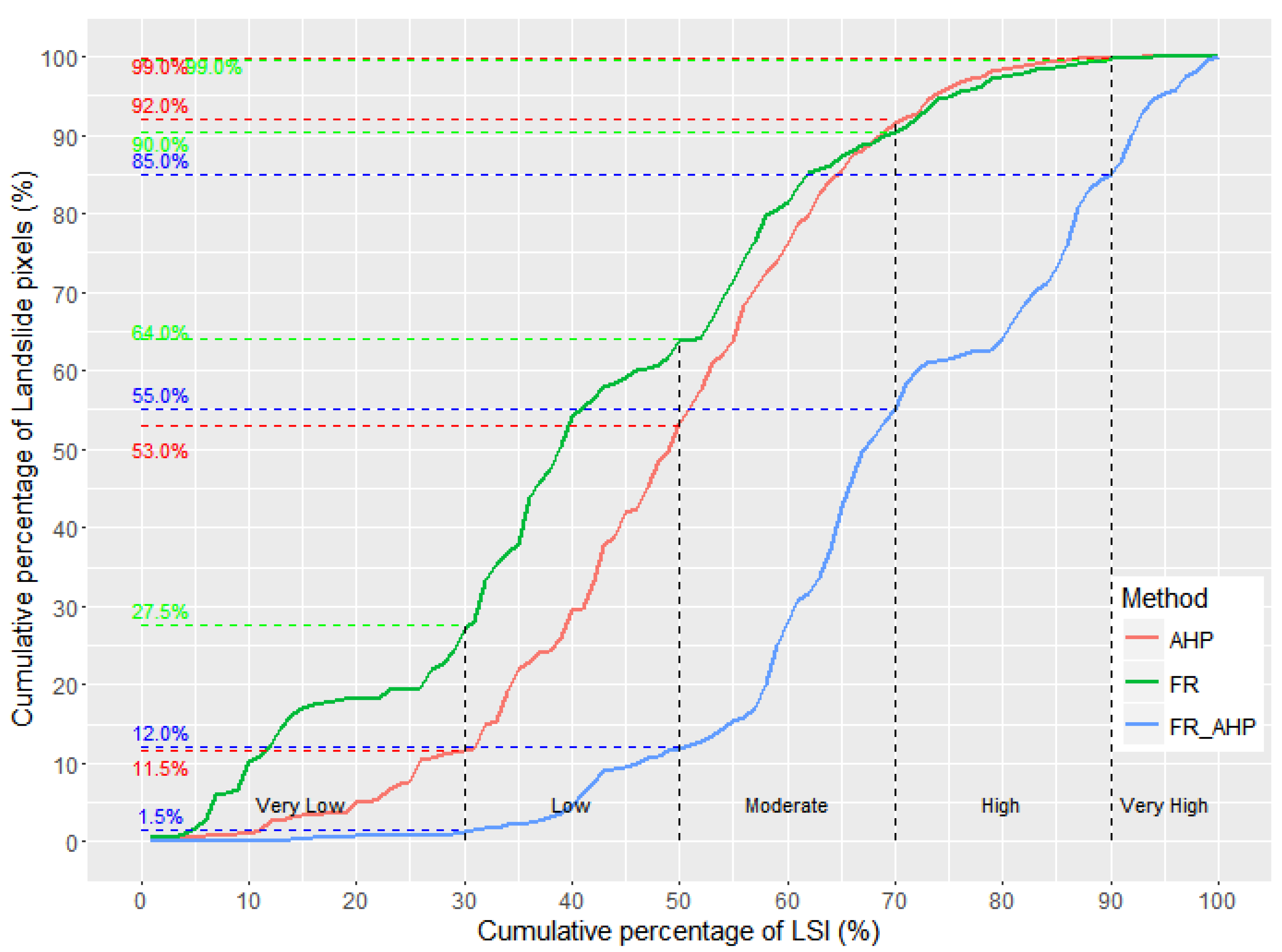
4.1. Landslide Susceptibility Maps and Validation
4.2. Discussions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bathrellos, G.D.; Gaki-Papanastassiou, K.; Skilodimou, H.D.; Papanastassiou, D.; Chousianitis, K.G. Potential suitability for urban planning and industry development using natural hazard maps and geological-geomorphological parameters. Environ. Earth Sci. 2011, 66, 537–548. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- The International Disaster Database. Available online: http://www.emdat.be/ (accessed on 2 February 2016).
- Wang, H.; Liu, G.; Xu, W.; Wang, G. GIS-based landslide hazard assessment: an overview. Prog. Phys. Geogr. 2005, 29, 548–567. [Google Scholar]
- Carrara, A.; Guzzetti, F.; Cardinali, M.; Reichenbach, P. Use of GIS Technology in the Prediction and Monitoring of Landslide Hazard. Nat. Hazards 2000, 20, 117–135. [Google Scholar] [CrossRef]
- Carrara, A.; Cardinali, M.; Detti, R.; Guzzetti, F.; Pasqui, V.; Reichenbach, P. GIS techniques and statistical models in evaluating landslide hazard. Earth Surf. Process. Landf. 1991, 16, 427–445. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Wang, W.D.; Guo, J.; Fang, L.G.; Chang, X.S. A subjective and objective integrated weighting method for landslides susceptibility mapping based on GIS. Environ. Earth Sci. 2012, 65, 1705–1714. [Google Scholar] [CrossRef]
- Kayastha, P.; Dhital, M.R.; De Smedt, F. Application of the analytical hierarchy process (AHP) for landslide susceptibility mapping: A case study from the Tinau watershed, west Nepal. Comput. Geosci. 2013, 52, 398–408. [Google Scholar] [CrossRef]
- Kil, S.-H.; Lee, D.; Kim, J.-H.; Li, M.-H.; Newman, G. Utilizing the Analytic Hierarchy Process to Establish Weighted Values for Evaluating the Stability of Slope Revegetation based on Hydroseeding Applications in South Korea. Sustainability 2016, 8, 58. [Google Scholar] [CrossRef]
- Rozos, D.; Bathrellos, G.D.; Skillodimou, H.D. Comparison of the implementation of rock engineering system and analytic hierarchy process methods, upon landslide susceptibility mapping, using GIS: A case study from the Eastern Achaia County of Peloponnesus, Greece. Environ. Earth Sci. 2010, 63, 49–63. [Google Scholar] [CrossRef]
- Chalkias, C.; Ferentinou, M.; Polykretis, C. GIS Supported Landslide Susceptibility Modeling at Regional Scale: An Expert-Based Fuzzy Weighting Method. ISPRS Int. J. Geo-Inf. 2014, 3, 523–539. [Google Scholar] [CrossRef]
- Chousianitis, K.; Del Gaudio, V.; Sabatakakis, N.; Kavoura, K.; Drakatos, G.; Bathrellos, G.D.; Skilodimou, H.D. Assessment of Earthquake-Induced Landslide Hazard in Greece: From Arias Intensity to Spatial Distribution of Slope Resistance Demand. Bull. Seismol. Soc. Am. 2016, 106, 174–188. [Google Scholar] [CrossRef]
- Hong, H.; Chen, W.; Xu, C.; Youssef, A.M.; Pradhan, B.; Tien Bui, D. Rainfall-induced landslide susceptibility assessment at the Chongren area (China) using frequency ratio, certainty factor, and index of entropy. Geocarto Int. 2016. [Google Scholar] [CrossRef]
- Chalkias, C.; Ferentinou, M.; Polykretis, C. GIS-Based Landslide Susceptibility Mapping on the Peloponnese Peninsula, Greece. Geosciences 2014, 4, 176–190. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, D.; Huang, Y.; Wang, Z.; Zhang, L.; Guo, Q.; Chen, W.; Chen, W.; Sang, M. Landslide Susceptibility Mapping Based on Selected Optimal Combination of Landslide Predisposing Factors in a Large Catchment. Sustainability 2015, 7, 16653–16669. [Google Scholar] [CrossRef]
- Skilodimou, H.D.; Kalivas, D.P.; Bathrellos, G.D. GIS-based landslide susceptibility mapping models applied to natural and urban planning in Trikala, Central Greece. Estud. Geol. 2009, 65, 49–65. [Google Scholar]
- Zhou, S.; Fang, L. Support vector machine modeling of earthquake-induced landslides susceptibility in central part of Sichuan province, China. Geoenviron. Disasters 2015, 2, 2. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Tien Bui, D. Spatial prediction of landslide hazard at the Yihuang area (China) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Li, Y.; Chen, G.; Tang, C.; Zhou, G.; Zheng, L. Rainfall and earthquake-induced landslide susceptibility assessment using GIS and Artificial Neural Network. Nat. Hazards Earth Syst. Sci. 2012, 12, 2719–2729. [Google Scholar] [CrossRef]
- Süzen, M.L.; Doyuran, V. A comparison of the GIS based landslide susceptibility assessment methods: Multivariate versus bivariate. Environ. Geol. 2004, 45, 665–679. [Google Scholar] [CrossRef]
- Galli, M.; Ardizzone, F.; Cardinali, M.; Guzzetti, F.; Reichenbach, P. Comparing landslide inventory maps. Geomorphology 2008, 94, 268–289. [Google Scholar] [CrossRef]
- Yalcin, A. GIS-based landslide susceptibility mapping using analytical hierarchy process and bivariate statistics in Ardesen (Turkey): Comparisons of results and confirmations. Catena 2008, 72, 1–12. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar]
- Bathrellos, G.D.; Karymbalis, E.; Skilodimou, H.D.; Gaki-Papanastassiou, K.; Baltas, E.A. Urban flood hazard assessment in the basin of Athens Metropolitan city, Greece. Environ. Earth Sci. 2016, 75, 319. [Google Scholar] [CrossRef]
- Ishida, H.; Hattori, T.; Takeda, Y. Comparison of species composition and richness between primary and secondary lucidophyllous forests in two altitudinal zones of Tsushima Island, Japan. For. Ecol. Manag. 2005, 213, 273–287. [Google Scholar] [CrossRef]
- Chough, S.K.; Jeong, K.S.; Honza, E. Zoned facies of mass-flow deposits in the Ulleung (Tsushima) Basin, East Sea (Sea of Japan). Mar. Geol. 1985, 65, 113–125. [Google Scholar] [CrossRef]
- National Research Institute for Earth Science and Disaster Prevention. Available online: http://www.bosai.go.jp/e/ (accessed on 20 March 2016).
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. Turn. AK, Schuster, RL Landslides Investig. mitigation, Spec. Rep. 1996, 247, 36–75. [Google Scholar]
- Hong, H.; Pradhan, B.; Jebur, M.N.; Bui, D.T.; Xu, C.; Akgun, A. Spatial prediction of landslide hazard at the Luxi area (China) using support vector machines. Environ. Earth Sci. 2015, 75, 40. [Google Scholar] [CrossRef]
- Wu, W.; Sidle, R.C. A distributed slope stability model for steep forested basins. Water Resour. Res. 1995, 31, 2097–2110. [Google Scholar] [CrossRef]
- Geospatial Information Authority of Japan. Available online: http://www.gsi.go.jp/ (accessed on 20 March 2016).
- Geological Survey of Japan. Available online: https://www.gsj.jp (accessed on 20 March 2016).
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Lee, S.; Talib, J.A. Probabilistic landslide susceptibility and factor effect analysis. Environ. Geol. 2005, 47, 982–990. [Google Scholar] [CrossRef]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists; Pergamon Press: Oxford, UK, 1994. [Google Scholar]
- Saaty, T.; Vargas, L. Models, Methods, Concepts & Applications of the Analytic Hierarchy Process; Springer US: New York, NY, USA, 2001. [Google Scholar]
- Malczewski, J. GIS and Multicriteria Decision Analysis; Wiley: New Jersey, NJ, USA, 1999; Volume 31. [Google Scholar]
- Bathrellos, G.D.; Gaki-Papanastassiou, K.; Skilodimou, H.D.; Skianis, G.A.; Chousianitis, K.G. Assessment of rural community and agricultural development using geomorphological–geological factors and GIS in the Trikala prefecture (Central Greece). Stoch. Environ. Res. Risk Assess. 2012, 27, 573–588. [Google Scholar] [CrossRef]
| Class | Frequency Ratio | Analytical Hierarchy Process | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % of | % of | FR (SCW) | (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | SSCW *2 | |||
| Elevation (m) | ||||||||||||||
| (1): < 50 | 1,722,254 | 31.66 | 11,360 | 24.11 | 0.76 | 1 | 0.0532 | |||||||
| (2): 50–150 | 2,317,957 | 42.61 | 23,416 | 49.69 | 1.17 | 2 | 1 | 0.0671 | ||||||
| (3): 150–250 | 967,849 | 17.79 | 9864 | 20.93 | 1.18 | 3 | 3 | 1 | 0.1297 | |||||
| (4): 250–350 | 278,907 | 5.13 | 2286 | 4.85 | 0.95 | 4 | 5 | 3 | 1 | 0.2837 | ||||
| (5): > 350 | 152,899 | 2.81 | 199 | 0.42 | 0.15 | 6 | 6 | 5 | 2 | 1 | 0.4663 | |||
| Slope (degree) | ||||||||||||||
| (1): < 15 | 1,029,316 | 18.92 | 8626 | 18.30 | 0.97 | 1 | 0.0357 | |||||||
| (2): 15–25 | 1,202,425 | 22.10 | 16,572 | 35.17 | 1.59 | 4 | 1 | 0.0799 | ||||||
| (3): 25–35 | 1,675,457 | 30.80 | 14,381 | 30.52 | 0.99 | 5 | 3 | 1 | 0.1296 | |||||
| (4): 35–45 | 1,266,394 | 23.28 | 6608 | 14.02 | 0.60 | 6 | 4 | 4 | 1 | 0.2746 | ||||
| (5): > 45 | 266,274 | 4.89 | 938 | 1.99 | 0.41 | 7 | 5 | 5 | 3 | 1 | 0.4804 | |||
| Aspect | ||||||||||||||
| (1): North | 599,013 | 11.07 | 3699 | 7.85 | 0.71 | 1 | 0.0392 | |||||||
| (2): Northeast | 717,111 | 13.25 | 4120 | 8.74 | 0.66 | 2 | 1 | 0.0622 | ||||||
| (3): East | 743,843 | 13.74 | 8192 | 17.39 | 1.26 | 3 | 2 | 1 | 0.1009 | |||||
| (4): Southeast | 638,667 | 11.80 | 10,655 | 22.61 | 1.92 | 4 | 3 | 2 | 1 | 0.1811 | ||||
| (5): South | 634,758 | 11.73 | 7004 | 14.86 | 1.27 | 5 | 4 | 3 | 2 | 1 | 0.2416 | |||
| (6): Southwest | 731,476 | 13.52 | 3476 | 7.38 | 0.55 | 4 | 3 | 3 | 1 | 1 | 1 | 0.1975 | ||
| (7): West | 729,024 | 13.47 | 4827 | 10.24 | 0.76 | 3 | 2 | 1 | 1/3 | 1/2 | 1/2 | 1 | 0.1061 | |
| (8): Northwest | 618,338 | 11.42 | 5147 | 10.92 | 0.96 | 2 | 1 | 1/2 | 1/2 | 1/3 | 1/2 | 1/2 | 1 | 0.0713 |
| TRI | ||||||||||||||
| (1): < 10 | 1,099,635 | 20.21 | 13,029 | 27.65 | 1.37 | 1 | 0.0546 | |||||||
| (2): 10–20 | 2,574,369 | 47.32 | 25,705 | 54.55 | 1.15 | 4 | 1 | 0.1520 | ||||||
| (3): 20–30 | 1,572,883 | 28.91 | 7774 | 16.50 | 0.57 | 5 | 2 | 1 | 0.2274 | |||||
| (4): > 30 | 192,911 | 3.55 | 617 | 1.31 | 0.37 | 6 | 4 | 4 | 1 | 0.5660 | ||||
| Lithology | ||||||||||||||
| (1): Felsic plutonic rocks | 190,448 | 3.66 | 4646 | 9.86 | 2.69 | 1 | 0.5594 | |||||||
| (2): Non-alkaline mafic volcanic rocks | 26,801 | 0.52 | 334 | 0.71 | 1.38 | 1/3 | 1 | 0.2568 | ||||||
| (3): Marine and non-marine sediments | 4,780,990 | 91.92 | 41,522 | 88.11 | 0.96 | 1/5 | 1/3 | 1 | 0.1214 | |||||
| (4): Non-alkaline felsic volcanic rocks | 203,076 | 3.90 | 623 | 1.32 | 0.34 | 1/6 | 1/4 | 1/3 | 1 | 0.0623 | ||||
| Land cover | ||||||||||||||
| (1): Cropland and Grassland | 946,235 | 18.01 | 4690 | 9.95 | 0.55 | 1 | 0.5278 | |||||||
| (2): Forest | 4,110,603 | 78.23 | 42,000 | 89.12 | 1.14 | 1/3 | 1 | 0.1396 | ||||||
| (3): Urban areas | 197,462 | 3.76 | 435 | 0.92 | 0.25 | 1/2 | 3 | 1 | 0.3325 | |||||
| MAP (mm) | ||||||||||||||
| (1): < 1800 | 691,693 | 13.28 | 2058 | 4.72 | 0.36 | 1 | 0.0557 | |||||||
| (2): 1800–1900 | 1,206,360 | 23.15 | 9565 | 21.93 | 0.95 | 2 | 1 | 0.0708 | ||||||
| (3): 1900–2000 | 1,230,154 | 23.61 | 7306 | 16.75 | 0.71 | 3 | 3 | 1 | 0.1369 | |||||
| (4): 2000–2100 | 526,374 | 10.10 | 2341 | 5.37 | 0.53 | 4 | 4 | 3 | 1 | 0.2383 | ||||
| (5): 2100–2171 | 1,555,556 | 29.86 | 22,353 | 51.24 | 1.72 | 5 | 6 | 4 | 4 | 1 | 0.4984 | |||
- *1 is the number of landslides in jth subclass of the factor i, is the area of the corresponding subclass, the total number of landslides and is the total area under investigation.
- *2 SSCW: Subjectively determined subclasses’ weights using AHP; MAP: mean annual precipitation; SCW: subclasses’ weight; TRI: terrain roughness index.
| Scale | Definition | Explanation |
|---|---|---|
| 1 | Equally | Two factors contribute equally to the landslide |
| 3 | Moderately | Experience and judgment slightly to moderately favor one activity over another |
| 5 | Strongly | Experience and judgment strongly or essentially favor one activity over another |
| 7 | Very Strongly | An activity is strongly favored over another and its dominance is showed in practice |
| 9 | Extremely | The evidence of favoring one factor over another is of the highest degree possible of an affirmation |
| 2, 4, 6 and 8 | Intermediate values | Used to represent compromises between the references in weight 1, 3, 5, 7, and 9 |
| Reciprocals | Opposites | Used for inverse comparison |
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
| Factor | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Factor Weight (FW) |
|---|---|---|---|---|---|---|---|---|
| 1–Slope | 1 | 5 | 5 | 7 | 7 | 8 | 8 | 0.4536 |
| 2–MAP | 1/5 | 1 | 4 | 4 | 5 | 6 | 7 | 0.2298 |
| 3–Land cover | 1/5 | 1/4 | 1 | 2 | 3 | 4 | 4 | 0.1135 |
| 4–Elevation | 1/7 | 1/4 | 1/2 | 1 | 2 | 4 | 5 | 0.0837 |
| 5–Aspect | 1/7 | 1/5 | 1/3 | 1/2 | 1 | 3 | 4 | 0.0602 |
| 6–Lithology | 1/8 | 1/6 | 1/4 | 1/4 | 1/3 | 1 | 3 | 0.0351 |
| 7–TRI | 1/8 | 1/7 | 1/4 | 1/5 | 1/4 | 1/3 | 1 | 0.0241 |
| Causative Factors | N | λmax | CI | RI | CR |
|---|---|---|---|---|---|
| All | 7 | 7.6897 | 0.0845 | 1.32 | 0.06402 |
| Elevation | 5 | 5.1967 | 0.0439 | 1.12 | 0.03920 |
| Slope | 5 | 5.4416 | 0.0986 | 1.12 | 0.08803 |
| Aspect | 8 | 8.1887 | 0.0191 | 1.41 | 0.01354 |
| TRI | 4 | 4.1980 | 0.0742 | 0.90 | 0.08244 |
| Lithology | 4 | 4.1470 | 0.0551 | 0.90 | 0.06122 |
| Land cover | 3 | 3.0536 | 0.0516 | 0.58 | 0.08897 |
| MAP | 5 | 5.1967 | 0.0439 | 1.12 | 0.03920 |
| Method | Class | VL | L | M | H | VH |
|---|---|---|---|---|---|---|
| FR | %A | 36.77 | 46.97 | 14.24 | 0.91 | 1.02 |
| %LA | 27.50 | 36.50 | 26.00 | 9.00 | 1.00 | |
| RLD | 0.75 | 0.78 | 1.83 | 9.89 | 0.98 | |
| AHP | %A | 6.23 | 27.79 | 45.84 | 18.13 | 2.01 |
| %LA | 11.5 | 41.5 | 39.00 | 7.00 | 1.00 | |
| RLD | 1.85 | 1.49 | 0.85 | 0.39 | 0.50 | |
| FR-AHP | %A | 3.00 | 12.74 | 68.38 | 14.04 | 1.83 |
| %LA | 1.50 | 10.50 | 43.00 | 30.00 | 15.00 | |
| RLD | 0.50 | 0.82 | 0.63 | 2.14 | 8.20 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Chen, G.; Fang, L.; Nie, Y. GIS-Based Integration of Subjective and Objective Weighting Methods for Regional Landslides Susceptibility Mapping. Sustainability 2016, 8, 334. https://doi.org/10.3390/su8040334
Zhou S, Chen G, Fang L, Nie Y. GIS-Based Integration of Subjective and Objective Weighting Methods for Regional Landslides Susceptibility Mapping. Sustainability. 2016; 8(4):334. https://doi.org/10.3390/su8040334
Chicago/Turabian StyleZhou, Suhua, Guangqi Chen, Ligang Fang, and Yunwen Nie. 2016. "GIS-Based Integration of Subjective and Objective Weighting Methods for Regional Landslides Susceptibility Mapping" Sustainability 8, no. 4: 334. https://doi.org/10.3390/su8040334
APA StyleZhou, S., Chen, G., Fang, L., & Nie, Y. (2016). GIS-Based Integration of Subjective and Objective Weighting Methods for Regional Landslides Susceptibility Mapping. Sustainability, 8(4), 334. https://doi.org/10.3390/su8040334





