New Hybrid Multiple Attribute Decision-Making Model for Improving Competence Sets: Enhancing a Company’s Core Competitiveness
Abstract
:1. Introduction
2. Review on Related Attributes in Competence Sets of Employee Capabilities
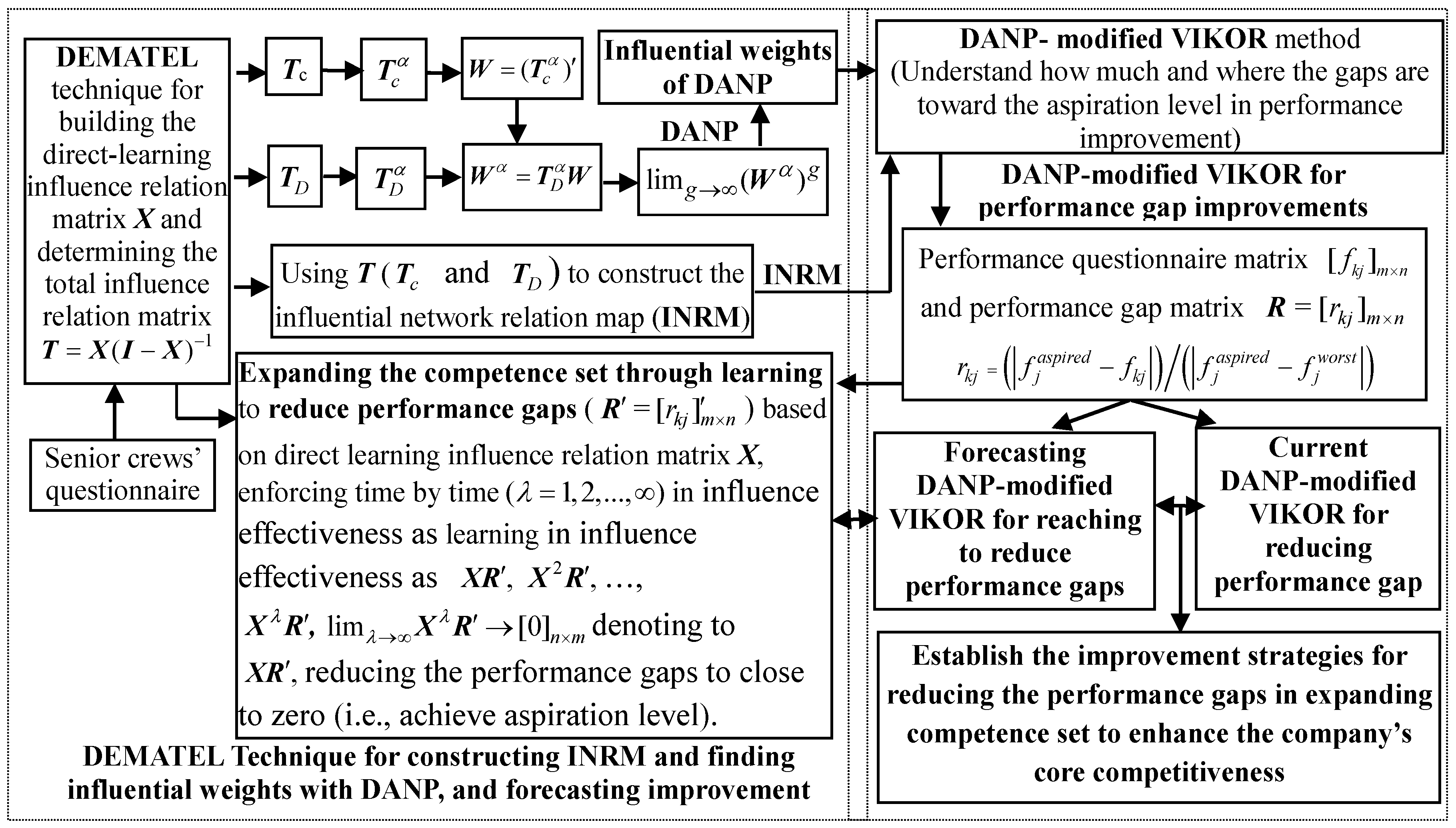
3. Hybrid MADM Model for Performance Gap Improvement
3.1. DEMATEL Technique for Constructing the INRM
3.2. DEMATEL Technique for Determining the DANP Influence Weights

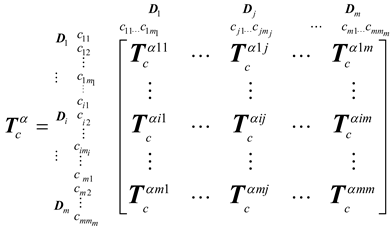
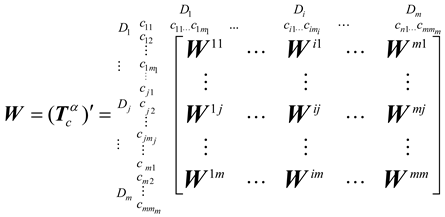

3.3. Modified VIKOR Method for Ranking and Improving Competence Sets
3.4. Performance Gap Improvement for Establishing Improvement Strategies
4. Empirical Case for Enhancing a Company’s Core Competitiveness
4.1. Problem Description
4.2. Results and Analysis
Performance of Competence Sets Determined Using the DANP-Modified VIKOR Method
4.3. Discussion and Implications
5. Conclusions and Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Competence set | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.000 | 0.098 | 0.094 | 0.058 | 0.083 | 0.077 | 0.041 | 0.060 | 0.073 | 0.081 | 0.067 | 0.083 | 0.074 | |
| 0.083 | 0.000 | 0.083 | 0.065 | 0.079 | 0.071 | 0.041 | 0.067 | 0.061 | 0.077 | 0.050 | 0.092 | 0.067 | |
| 0.090 | 0.092 | 0.000 | 0.058 | 0.090 | 0.077 | 0.043 | 0.075 | 0.069 | 0.079 | 0.083 | 0.098 | 0.081 | |
| 0.056 | 0.073 | 0.063 | 0.000 | 0.069 | 0.065 | 0.050 | 0.058 | 0.067 | 0.060 | 0.054 | 0.081 | 0.054 | |
| 0.083 | 0.077 | 0.092 | 0.069 | 0.000 | 0.088 | 0.052 | 0.070 | 0.077 | 0.086 | 0.075 | 0.090 | 0.069 | |
| 0.063 | 0.060 | 0.073 | 0.065 | 0.086 | 0.000 | 0.045 | 0.069 | 0.065 | 0.073 | 0.061 | 0.075 | 0.050 | |
| 0.038 | 0.047 | 0.038 | 0.038 | 0.044 | 0.040 | 0.000 | 0.043 | 0.038 | 0.033 | 0.045 | 0.058 | 0.033 | |
| 0.063 | 0.067 | 0.071 | 0.061 | 0.076 | 0.073 | 0.038 | 0.000 | 0.049 | 0.066 | 0.052 | 0.065 | 0.054 | |
| 0.067 | 0.063 | 0.067 | 0.071 | 0.067 | 0.056 | 0.046 | 0.054 | 0.000 | 0.075 | 0.069 | 0.077 | 0.056 | |
| 0.077 | 0.083 | 0.090 | 0.063 | 0.077 | 0.067 | 0.036 | 0.058 | 0.077 | 0.029 | 0.081 | 0.081 | 0.060 | |
| 0.075 | 0.048 | 0.090 | 0.054 | 0.067 | 0.067 | 0.043 | 0.056 | 0.079 | 0.081 | 0.000 | 0.090 | 0.060 | |
| 0.083 | 0.094 | 0.094 | 0.086 | 0.100 | 0.088 | 0.058 | 0.074 | 0.085 | 0.075 | 0.086 | 0.000 | 0.077 | |
| 0.071 | 0.054 | 0.070 | 0.056 | 0.060 | 0.052 | 0.046 | 0.043 | 0.056 | 0.056 | 0.069 | 0.083 | 0.000 |
| Competence set | Participants | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.100 | 0.100 | 0.400 | 0.300 | 0.500 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.500 | 0.400 | 0.500 | 0.200 | |
| 0.000 | 0.800 | 0.700 | 0.200 | 0.500 | 0.300 | 0.300 | 0.300 | 0.500 | 0.400 | 0.500 | 0.400 | 0.600 | 0.300 | |
| 0.200 | 0.200 | 0.300 | 0.200 | 0.500 | 0.300 | 0.200 | 0.200 | 0.500 | 0.500 | 0.200 | 0.300 | 0.700 | 0.100 | |
| 0.300 | 0.300 | 0.700 | 0.800 | 0.500 | 0.500 | 0.600 | 0.500 | 0.700 | 0.900 | 0.700 | 0.500 | 0.500 | 0.300 | |
| 0.400 | 0.400 | 0.400 | 0.500 | 0.400 | 0.300 | 0.600 | 0.300 | 0.700 | 0.700 | 0.300 | 0.500 | 0.800 | 0.300 | |
| 0.500 | 0.500 | 0.500 | 0.800 | 0.500 | 0.500 | 0.500 | 0.300 | 0.400 | 0.400 | 0.700 | 0.500 | 0.900 | 0.300 | |
| 1.000 | 1.000 | 0.400 | 0.500 | 0.800 | 0.300 | 0.800 | 0.500 | 0.700 | 1.000 | 0.900 | 0.500 | 0.600 | 0.300 | |
| 0.800 | 0.800 | 0.500 | 0.800 | 0.700 | 0.600 | 0.500 | 0.300 | 0.700 | 0.500 | 1.000 | 0.500 | 0.400 | 0.800 | |
| 0.900 | 0.900 | 0.400 | 0.500 | 0.500 | 0.500 | 0.500 | 0.400 | 0.700 | 0.600 | 0.700 | 0.500 | 0.500 | 0.500 | |
| 0.000 | 0.900 | 0.400 | 0.500 | 0.500 | 0.400 | 0.500 | 0.300 | 0.700 | 0.500 | 0.500 | 0.500 | 0.300 | 0.300 | |
| 0.000 | 0.000 | 0.300 | 0.300 | 0.500 | 0.300 | 0.500 | 0.200 | 0.500 | 0.500 | 0.500 | 0.500 | 0.800 | 0.500 | |
| 0.700 | 0.700 | 0.300 | 0.200 | 0.500 | 0.300 | 0.300 | 0.400 | 0.700 | 0.600 | 0.600 | 0.500 | 0.700 | 0.200 | |
| 0.600 | 0.600 | 0.400 | 0.500 | 0.500 | 0.400 | 0.400 | 0.400 | 0.300 | 0.400 | 0.600 | 0.500 | 0.700 | 0.700 | |
| (average gap) | 0.418 | 0.548 | 0.441 | 0.469 | 0.530 | 0.383 | 0.461 | 0.339 | 0.600 | 0.596 | 0.589 | 0.468 | 0.617 | 0.363 |
| Competence set | Participants () | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.3651 | 0.3651 | 0.3917 | 0.4071 | 0.4605 | 0.3418 | 0.3991 | 0.2934 | 0.5178 | 0.4955 | 0.5034 | 0.4159 | 0.5622 | 0.3272 | |
| 0.3656 | 0.3656 | 0.3452 | 0.3998 | 0.4358 | 0.3247 | 0.3781 | 0.2807 | 0.5105 | 0.4984 | 0.4825 | 0.3931 | 0.5155 | 0.2992 | |
| 0.3832 | 0.3832 | 0.4161 | 0.4389 | 0.4864 | 0.3598 | 0.4311 | 0.3172 | 0.5640 | 0.5399 | 0.5629 | 0.4493 | 0.5762 | 0.3620 | |
| 0.3241 | 0.3241 | 0.3144 | 0.3248 | 0.3947 | 0.2802 | 0.3306 | 0.2435 | 0.4459 | 0.4206 | 0.4312 | 0.3495 | 0.4720 | 0.2735 | |
| 0.3731 | 0.3731 | 0.4051 | 0.4228 | 0.4936 | 0.3617 | 0.4020 | 0.3095 | 0.5468 | 0.5275 | 0.5549 | 0.4296 | 0.5606 | 0.3357 | |
| 0.3160 | 0.3160 | 0.3375 | 0.3455 | 0.4112 | 0.2945 | 0.3546 | 0.2631 | 0.4907 | 0.4738 | 0.4444 | 0.3656 | 0.4652 | 0.2868 | |
| 0.1894 | 0.1894 | 0.2177 | 0.2243 | 0.2517 | 0.1912 | 0.2124 | 0.1607 | 0.2953 | 0.2767 | 0.2811 | 0.2314 | 0.3098 | 0.1826 | |
| 0.2657 | 0.2657 | 0.3209 | 0.3238 | 0.3713 | 0.2691 | 0.3269 | 0.2448 | 0.4330 | 0.4307 | 0.3947 | 0.3403 | 0.4704 | 0.2353 | |
| 0.2729 | 0.2729 | 0.3371 | 0.3490 | 0.4019 | 0.2851 | 0.3445 | 0.2535 | 0.4586 | 0.4524 | 0.4346 | 0.3576 | 0.4777 | 0.2658 | |
| 0.3533 | 0.3533 | 0.3827 | 0.3881 | 0.4542 | 0.3314 | 0.3831 | 0.2882 | 0.5204 | 0.5083 | 0.4960 | 0.4055 | 0.5602 | 0.3145 | |
| 0.3599 | 0.3599 | 0.3489 | 0.3747 | 0.4224 | 0.3139 | 0.3544 | 0.2763 | 0.4953 | 0.4759 | 0.4648 | 0.3747 | 0.4872 | 0.2763 | |
| 0.3768 | 0.3768 | 0.4522 | 0.4842 | 0.5222 | 0.3892 | 0.4647 | 0.3270 | 0.5880 | 0.5826 | 0.5715 | 0.4635 | 0.6180 | 0.3749 | |
| 0.2768 | 0.2768 | 0.3067 | 0.3132 | 0.3744 | 0.2661 | 0.3208 | 0.2352 | 0.4470 | 0.4329 | 0.4060 | 0.3315 | 0.4426 | 0.2319 | |
| (average gap) | 0.3253 | 0.4385 | 0.3519 | 0.3690 | 0.4217 | 0.3085 | 0.3617 | 0.2687 | 0.4856 | 0.4701 | 0.4640 | 0.3777 | 0.5013 | 0.2901 |
| Competence set | Participants () | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0092 | 0.0092 | 0.0099 | 0.0104 | 0.0119 | 0.0087 | 0.0102 | 0.0076 | 0.0137 | 0.0133 | 0.0131 | 0.0107 | 0.0141 | 0.0082 | |
| 0.0087 | 0.0087 | 0.0094 | 0.0099 | 0.0113 | 0.0082 | 0.0097 | 0.0072 | 0.0130 | 0.0126 | 0.0124 | 0.0101 | 0.0134 | 0.0077 | |
| 0.0096 | 0.0096 | 0.0104 | 0.0109 | 0.0125 | 0.0091 | 0.0107 | 0.0079 | 0.0143 | 0.0139 | 0.0137 | 0.0111 | 0.0148 | 0.0086 | |
| 0.0078 | 0.0078 | 0.0084 | 0.0088 | 0.0101 | 0.0074 | 0.0086 | 0.0064 | 0.0116 | 0.0112 | 0.0111 | 0.0090 | 0.0120 | 0.0069 | |
| 0.0095 | 0.0095 | 0.0103 | 0.0108 | 0.0123 | 0.0090 | 0.0106 | 0.0078 | 0.0142 | 0.0137 | 0.0135 | 0.0110 | 0.0146 | 0.0085 | |
| 0.0081 | 0.0081 | 0.0088 | 0.0093 | 0.0106 | 0.0077 | 0.0091 | 0.0067 | 0.0121 | 0.0118 | 0.0116 | 0.0094 | 0.0125 | 0.0073 | |
| 0.0052 | 0.0052 | 0.0057 | 0.0059 | 0.0068 | 0.0050 | 0.0058 | 0.0043 | 0.0078 | 0.0075 | 0.0075 | 0.0061 | 0.0080 | 0.0047 | |
| 0.0077 | 0.0077 | 0.0083 | 0.0087 | 0.0099 | 0.0073 | 0.0085 | 0.0063 | 0.0114 | 0.0111 | 0.0109 | 0.0089 | 0.0118 | 0.0068 | |
| 0.0080 | 0.0080 | 0.0086 | 0.0090 | 0.0103 | 0.0076 | 0.0089 | 0.0066 | 0.0119 | 0.0115 | 0.0114 | 0.0092 | 0.0123 | 0.0071 | |
| 0.0091 | 0.0091 | 0.0099 | 0.0104 | 0.0118 | 0.0086 | 0.0101 | 0.0075 | 0.0136 | 0.0132 | 0.0130 | 0.0106 | 0.0140 | 0.0081 | |
| 0.0084 | 0.0084 | 0.0091 | 0.0096 | 0.0109 | 0.0080 | 0.0094 | 0.0070 | 0.0126 | 0.0122 | 0.0120 | 0.0098 | 0.0130 | 0.0075 | |
| 0.0101 | 0.0101 | 0.0110 | 0.0115 | 0.0131 | 0.0096 | 0.0113 | 0.0084 | 0.0151 | 0.0146 | 0.0144 | 0.0117 | 0.0156 | 0.0090 | |
| 0.0075 | 0.0075 | 0.0081 | 0.0085 | 0.0097 | 0.0071 | 0.0083 | 0.0062 | 0.0112 | 0.0108 | 0.0107 | 0.0087 | 0.0115 | 0.0067 | |
| (average gap) | 0.0084 | 0.0113 | 0.0091 | 0.0095 | 0.0109 | 0.0079 | 0.0093 | 0.0069 | 0.0125 | 0.0121 | 0.0119 | 0.0097 | 0.0129 | 0.0075 |
| Competence set | Participants () | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1944 | 0.2619 | 0.2107 | 0.2211 | 0.2523 | 0.1846 | 0.2166 | 0.1608 | 0.2903 | 0.2814 | 0.2777 | 0.2258 | 0.2997 | 0.1737 | |
| 0.1839 | 0.2478 | 0.1993 | 0.2092 | 0.2386 | 0.1746 | 0.2049 | 0.1521 | 0.2746 | 0.2662 | 0.2627 | 0.2136 | 0.2835 | 0.1643 | |
| 0.2034 | 0.2741 | 0.2205 | 0.2314 | 0.2640 | 0.1932 | 0.2267 | 0.1683 | 0.3038 | 0.2945 | 0.2906 | 0.2363 | 0.3136 | 0.1818 | |
| 0.1644 | 0.2215 | 0.1782 | 0.1870 | 0.2133 | 0.1561 | 0.1832 | 0.1360 | 0.2455 | 0.2380 | 0.2349 | 0.1910 | 0.2534 | 0.1469 | |
| 0.2011 | 0.2709 | 0.2179 | 0.2287 | 0.2609 | 0.1909 | 0.2241 | 0.1663 | 0.3003 | 0.2910 | 0.2872 | 0.2336 | 0.3100 | 0.1797 | |
| 0.1724 | 0.2323 | 0.1869 | 0.1962 | 0.2238 | 0.1638 | 0.1922 | 0.1426 | 0.2575 | 0.2496 | 0.2463 | 0.2003 | 0.2658 | 0.1541 | |
| 0.1106 | 0.1490 | 0.1199 | 0.1258 | 0.1435 | 0.1050 | 0.1232 | 0.0915 | 0.1651 | 0.1601 | 0.1580 | 0.1285 | 0.1705 | 0.0988 | |
| 0.1623 | 0.2187 | 0.1760 | 0.1846 | 0.2107 | 0.1542 | 0.1809 | 0.1343 | 0.2424 | 0.2350 | 0.2319 | 0.1886 | 0.2502 | 0.1451 | |
| 0.1686 | 0.2272 | 0.1828 | 0.1918 | 0.2188 | 0.1601 | 0.1879 | 0.1394 | 0.2518 | 0.2441 | 0.2409 | 0.1959 | 0.2599 | 0.1507 | |
| 0.1931 | 0.2601 | 0.2093 | 0.2196 | 0.2506 | 0.1833 | 0.2152 | 0.1597 | 0.2883 | 0.2795 | 0.2758 | 0.2243 | 0.2976 | 0.1725 | |
| 0.1785 | 0.2405 | 0.1935 | 0.2030 | 0.2316 | 0.1695 | 0.1989 | 0.1476 | 0.2666 | 0.2584 | 0.2550 | 0.2074 | 0.2752 | 0.1595 | |
| 0.2143 | 0.2888 | 0.2323 | 0.2438 | 0.2781 | 0.2035 | 0.2388 | 0.1772 | 0.3200 | 0.3102 | 0.3062 | 0.2490 | 0.3304 | 0.1915 | |
| 0.1584 | 0.2134 | 0.1717 | 0.1802 | 0.2056 | 0.1504 | 0.1765 | 0.131 | 0.2365 | 0.2293 | 0.2263 | 0.184 | 0.2442 | 0.1415 | |
| (average gap) | 0.1774 | 0.2390 | 0.1922 | 0.2017 | 0.2302 | 0.1684 | 0.1976 | 0.1467 | 0.2648 | 0.2567 | 0.2534 | 0.2060 | 0.2734 | 0.1585 |
| Competence set | Participants () | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| (average gap) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
References
- Rodriguez, D.; Patel, R.; Bright, A.; Gregory, D.; Gowing, M.K. Developing competency models to promote integrated human resource. Hum. Resour. Manag. 2002, 41, 309–324. [Google Scholar] [CrossRef]
- Vakola, M.; Soderquist, K.E.; Prastacos, G.P. Competency management in support of organisational change. Int. J. Manpow. 2007, 28, 260–275. [Google Scholar]
- Rychen, D.S.; Salganik, L.H. Defining and Selecting Key Competencies; Hogrefe & Huber: Kirkland, WA, USA, 2001. [Google Scholar]
- Organizations for Economic Co-operation and Development, OECD. OECD Employment Outlook. 2012. Available online: http://www.keepeek.com/Digital-Asset-Management/oecd/education/better-skills-better-jobs-better-lives_9789264177338-en (accessed on 12 December 2012).
- Organizations for Economic Co-operation and Development, OECD. Available online: http://www.upf.edu/materials/bib/docs/3334/employ/employ12.pdf (accessed on 2 February 2013).
- Organizations for Economic Co-operation and Development, OECD. Better Skills Better Jobs Better Lives. Available online: http://www.keepeek.com/Digital-Asset-Management/oecd/education/better-skills-better-jobs-better-lives_9789264177338-en (accessed on 11 February 2013).
- O*net online. Available online: http://www.onetonline.org/ (accessed on 28 December 2014).
- Careeronestop. Available online: http://www.careeronestop.org/ (accessed on 26 November 2014).
- McClelland, D.C. Identifying competencies with behavioral-event interviews. Psychol. Sci. 1998, 9, 331–339. [Google Scholar] [CrossRef]
- Ennis, M.R. Competency Models: A Review of the Literature and the Role of the Employment and Training Administration (ETA); Office of Policy Development and Research, Employment and Training Administration, US Department of Labor: Washington, DC, USA, 2008; pp. 1–25. Available online: http://www.careeronestop.org/competencymodel/info_documents/opdrliteraturereview.pdf (accessed on 16 February 2016).
- Rothwell, W.J.; Wellins, R. Mapping your future: Putting new competencies to work for you. Training Dev. 2004, 58, 94–102. [Google Scholar]
- Industrial Development Bureau of the Ministry of Economic Affairs. 2013. Available online: http://www.moeaidb.gov.tw/external/ctlr?PRO=index&lang=1 (accessed on 4 December 2015).
- Shippmann, J.S.; Ash, R.D.; Battista, M.; Carr, L.; Eyde, L.D.; Beryl, H.; Kehoe, J.; Pearlman, K.; Prien, E.P.; Sanchez, J.I. The practice of competency modeling. Pers. Psychol. 2000, 53, 703–740. [Google Scholar] [CrossRef]
- Yu, P.L.; Zhang, D. Competence set analysis for effective decision making. Contr. Theor. Adv. Technol. 1989, 5, 523–547. [Google Scholar]
- Yu, P.L.; Zhang, D. A foundation for competence set analysis. Math. Soc. Sci. 1990, 20, 251–299. [Google Scholar] [CrossRef]
- Rothwell, W.J. The Workplace Learner: How to Align Training Initiatives with Individual Learning Competencies; American Management Association: New York, NY, USA, 2002. [Google Scholar]
- Hu, Y.C.; Chen, R.S.; Tzeng, G.H. Generating learning sequences for decision makers through data mining and competence set expansion. IEEE Trans. Syst. Man Cybern. Syst. 2002, 32, 679–686. [Google Scholar]
- Hu, Y.C.; Tzeng, G.H.; Chiu, Y.J. Acquisition of compound skills and learning costs for expanding competence sets. Comput. Math. Appl. 2003, 46, 831–848. [Google Scholar] [CrossRef]
- Huang, J.J.; Tzeng, G.H.; Ong, C.S. Optimal fuzzy multi-criteria expansion of competence sets using multi-objectives evolutionary algorithms. Expert Syst. Appl. 2006, 30, 739–745. [Google Scholar] [CrossRef]
- Yu, P.L.; Chianglin, C.Y. Decision traps and competence dynamics in changeable spaces. Int. J. Inf. Technol. Decis. Mak. 2006, 5, 5–18. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- McClelland, D.C. Testing for competence rather than for intelligence. Am. Psychol. 1973, 28, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Fulmer, R.M.; Conger, J.A. Identifying talent. Executive Excell. 2004, 21, 11. Available online: http://www.americascareers.com/CompetencyModel/Info_Documents/OPDRLiteratureReview.pdf (accessed on 16 February 2016). [Google Scholar]
- Gangani, N.; McLean, G.N.; Braden, R.A. A competency-based human resource development strategy. Perform. Improv. Q. 2006, 19, 127–139. [Google Scholar] [CrossRef]
- Boyatzis, R.E. The Competent Manager: A Model for Effective Performance; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Sandberg, J. Understanding human competence at work: An interpretative approach. Acad. Manag. J. 2000, 43, 9–25. [Google Scholar] [CrossRef]
- Byhanand, W.C.; Moyer, R.P. Using Competencies to Build a Successful Organization; Development Dimensions International, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Dubois, D.D.; Rothwell, W.J. The Competency Toolkit; Human Resource Development: Amherst, MA, USA, 2000; Volume 1. [Google Scholar]
- Fogg, C.D. Implementing Your Strategic Plan: How to Turn “Intent” into Effective Action for Sustainable Change; American Management Association: New York, NY, USA, 1999. [Google Scholar]
- Spencer, L.M.; Spencer, S.M. Competence at Work: Models for Superior Performance; John Wiley & Sons Inc.: New York, NY, USA, 1993. [Google Scholar]
- Employment and Training Administration (ETA). Available online: http://www.doleta.gov/ (accessed on 2 February 2015).
- Personnel Decisions Research Institutes, Inc. (PDRI); Aguirre International. Technical Assistance Guide for Developing and Using Competency Models—One Solution for a Demand-Driven Workforce System; Employment and Training Administration: Washington, DC, USA, 2005. [Google Scholar]
- Alavi, M.; Leidner, D.E. Review: Knowledge management and knowledge management systems: Conceptual foundations and research issues. MIS Q. 2001, 25, 107–136. [Google Scholar] [CrossRef]
- Li, J.M.; Chiang, C.I.; Yu, P.L. Optimal multiple stage expansion of competence set. Eur. J. Oper. Res. 2000, 120, 511–524. [Google Scholar] [CrossRef]
- Yu, P.L.; Zhang, D. Marginal analysis for competence set expansion. J. Optim. Theory Appl. 1993, 76, 87–109. [Google Scholar] [CrossRef]
- Li, H.L.; Yu, P.L. Optimal competence set expansion using deduction graphs. J. Optim. Theory Appl. 1994, 80, 75–91. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: Verlag, New York, NY, USA, 1981. [Google Scholar]
- Tzeng, G.H.; Teng, M.H.; Chen, J.J.; Opricovic, S. Multicriteria selection for a restaurant location in Taipei. Int. J. Hosp. Manag. 2002, 21, 171–187. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Tsaur, S.H.; Laiw, Y.D.; Opricovic, S. Multicriteria analysis of environmental quality in Taipei: Public preferences and improvement strategies. J. Environ. Manag. 2002, 65, 109–120. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Multicriteria planning of post-earthquake sustainable reconstruction. Comput-Aided Civ. Infrastruct. Eng. 2002, 17, 211–220. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Fuzzy multicriteria model for post-earthquake land-use planning. Nat. Hazard. Rev. 2003, 4, 59–64. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Extended VIKOR method in comparison with outranking methods. Eur. J. Oper. Res. 2007, 178, 514–529. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Lin, C.W.; Opricovic, S. Multi-criteria analysis of alternative-fuel buses for public transportation. Energy Policy 2005, 33, 1373–1383. [Google Scholar] [CrossRef]
- Lu, M.T.; Lin, S.W.; Tzeng, G.H. Improving RFID adoption in Taiwan’s healthcare industry based on a DEMATEL technique with a hybrid MCDM model. Decis. Support Syst. 2013, 56, 259–269. [Google Scholar] [CrossRef]
- Ferreira, F.A.F.; Santos, S.P.; Marques, C.S.E.; Ferreira, J. Assessing credit risk of mortgage lending using MACBETH: A methodological framework. Manag. Decis. 2014, 52, 182–206. [Google Scholar] [CrossRef]
- Yu, P.L.; Chen, Y.C. Dynamic multiple criteria decision making in changeable spaces: From habitual domains to innovation dynamics. Ann. Oper. Res. 2010, 197, 201–220. [Google Scholar] [CrossRef]
- Larbani, M.; Yu, P.L. Decision making and optimization in changeable spaces, a new paradigm. J. Optimiz. Theory Appl. 2012, 155, 727–761. [Google Scholar] [CrossRef]
- Huang, J.J.; Tzeng, G.H. New thinking of multi-objective programming with changeable space—In search of excellence. Technol. Econ. Dev. Econ. 2014, 20, 242–261. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Huang, K.W.; Lin, C.W.; Yuan, B.J.C. New idea of multi-objective programming with changeable spaces for improving the unmanned factory planning. In Management of Engineering & Technology (PICMET), 2014 Portland International; IEEE: Kanazawa, Japan, 2014; pp. 564–570. [Google Scholar]
- Shen, K.Y.; Yan, M.R.; Tzeng, G.H. Combining VIKOR-DANP model for glamor stock selection and stock performance improvement. Knowl. Based Syst. 2014, 58, 86–97. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Huxang, J.J. Multiple Attribute Decision Making—Methods and Applications; CRC Press: New York, NY, USA, 2011; p. 349. [Google Scholar]
- Tzeng, G.H.; Huang, J.J. Fuzzy Multiple Objective Decision Making; CRC Press: Boca Raton, FL, USA, 2014; p. 308. [Google Scholar]
- Liou, J.H.; Tzeng, G.H. Comments on “Multiple criteria decision making (MCDM) methods in economics: An overview”. Technol. Econ. Dev. Econ. 2012, 18, 672–695. [Google Scholar] [CrossRef]
- Liou, J.H. New concepts and trends of MCDM for tomorrow—in honor of Professor Gwo-Hshiung Tzeng on the occasion of his 70th birthday. Technol. Econ. Dev. Econ. 2013, 19, 367–375. [Google Scholar] [CrossRef]
- Zhou, Q.; Huang, W.; Zhang, Y. Identifying critical success factors in emergency management using a fuzzy DEMATEL method. Safety Sci. 2011, 49, 243–252. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Chiang, C.H.; Li, C.W. Evaluating intertwined effects in e-learning programs: A novel hybrid MCDM model based on factor analysis and DEMATEL. Expert Syst. Appl. 2007, 32, 1028–1044. [Google Scholar] [CrossRef]
- Lu, M.T.; Tzeng, G.H.; Cheng, H.; Hsu, C.C. Exploring mobile banking services for user behavior in intention adoption: Using new hybrid MADM model. Serv. Bus. 2015, 9, 541–565. [Google Scholar] [CrossRef]
- Hung, Y.H.; Chou, S.C.T.; Tzeng, G.H. Knowledge management adoption and assessment for SMEs by a novel MCDM approach. Decis. Support Syst. 2011, 51, 270–291. [Google Scholar] [CrossRef]
- Ou Yang, Y.P.; Shieh, H.M.; Tzeng, G.H. A VIKOR technique based on DEMATEL and ANP for information security risk control assessment. Inform. Sci. 2013, 232, 482–500. [Google Scholar] [CrossRef]
- Wang, Y.L.; Tzeng, G.H. Brand marketing for creating brand value based on a MCDM model combining DEMATEL with ANP and VIKOR methods. Expert Syst. Appl. 2012, 39, 5600–5615. [Google Scholar] [CrossRef]
- Opricovic, S. Multi-criteria Optimization in Civil Engineering; Faculty of Civil Engineering: Belgrade, Serbia, 1998. (In Serbian) [Google Scholar]
- Simon, H.A. A behavioral model of rational choice. Q. J. Econ. 1955, 69, 99–118. [Google Scholar] [CrossRef]
- Yu, P.L. Behavior bases and habitual domains of human decision/behavior—an integration of psychology, optimization theory and common wisdom. Int. J. Syst. Meas. Decis. 1981, 1, 39–62. [Google Scholar]
- Leontief, W.W. Quantitative input and output relations in the economic systems of the United States. Rev. Econ. Stat. 1936, 18, 105–125. [Google Scholar] [CrossRef]
- Leontief, W.W. Input-output economics. Sci. Am. 1951, 185, 15–21. [Google Scholar] [CrossRef]
- Simon, H.A. Theories of bounded rationality (Chap. 8). In Decision and Organization; McGuire, C.B., Radner, R., Eds.; North-Holland: Amsterdam, The Netherlands, 1972; pp. 161–176. [Google Scholar]
- Yu, P.L. Behavior bases and habitual domains of human decision/behavior—concepts and applications. In Multiple Criteria Decision-Making, Theory and Applications; Fandel, G., Gal, T., Eds.; Springer: New York, NY, USA, 1980; pp. 511–539. [Google Scholar]
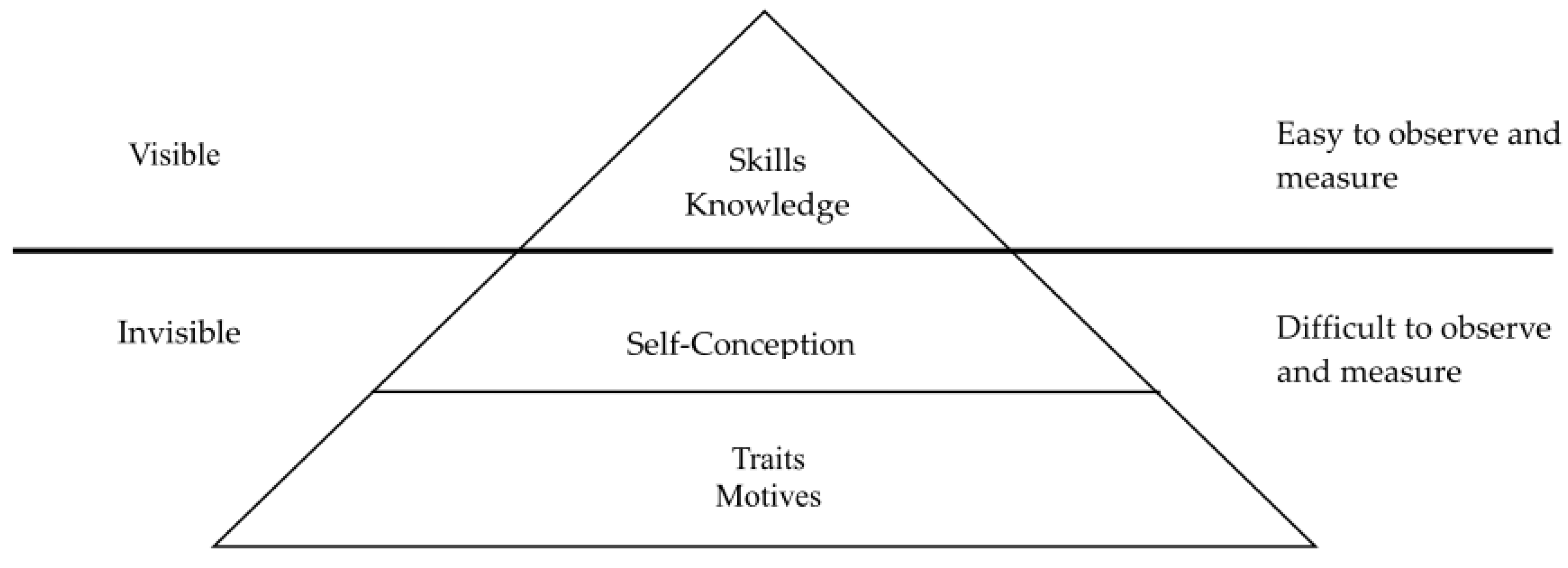

| Components | Definitions |
|---|---|
| Motivation competency | To train a person’s perceptions for career development, increased professionalism, and self-improvement through an understanding of workplace ethics. |
| Behavior competency | To establish self-position, understand the effectiveness of teamwork, and communicate efficiently with team members to achieve synergy. To solve problems by tolerating and overcoming differences of opinion among team members. |
| Knowledge/skills competency | To recognize environments and trends, to improve learning, and to actively innovate. To interactively strengthen knowledge and skills, to discover problems and opportunities in the workplace, and to effectively resolve problems by applying knowledge and skills. To be well prepared in a knowledge-based economy. |
| Competence for Knowledge | Definitions | |
|---|---|---|
| C1 | Administration and Management | Knowledge of business and management principles involved in strategic planning, resource allocation, human resources modeling, leadership technique, production methods, and coordination of people and resources. |
| C2 | Computers and Electronics | Knowledge of circuit boards, processors, chips, electronic equipment, and computer hardware and software, including applications and programming. |
| C3 | Customer and Personal Service | Knowledge of principles and processes for providing customer and personal services. This includes customer needs assessment, meeting quality standards for services, and evaluation of customer satisfaction. |
| C4 | Economics and Accounting | Knowledge of economic and accounting principles and practices, the financial markets, banking and the analysis and reporting of financial data. |
| C5 | Education and Training | Knowledge of principles and methods for curriculum and training design, teaching and instruction for individuals and groups, and the measurement of training effects. |
| C6 | English Language | Knowledge of the structure and content of the English language including the meaning and spelling of words, rules of composition, and grammar. |
| C7 | Fine Arts | Knowledge of the theory and techniques required to compose, produce, and perform works of music, dance, visual arts, drama, and sculpture. |
| C8 | Communications and Media | Knowledge of media production, communication, and dissemination techniques and methods. This includes alternative ways to inform and entertain via written, oral, and visual media |
| C9 | Foreign Language | Knowledge of the structure and content of a foreign (non-English) language including the meaning and spelling of words, rules of composition and grammar, and pronunciation. |
| C10 | Law and Government | Knowledge of laws, legal codes, court procedures, precedents, government regulations, executive orders, agency rules, and the democratic political process. |
| C11 | Personnel and Human Resources | Knowledge of principles and procedures for personnel recruitment, selection, training, compensation and benefits, labor relations and negotiation, and personnel information systems. |
| C12 | Psychology | Knowledge of human behavior and performance; individual differences in ability, personality, and interests; learning and motivation; psychological research methods; and the assessment and treatment of behavioral and affective disorders. |
| C13 | Sales and Marketing | Knowledge of principles and methods for showing, promoting, and selling products or services. This includes marketing strategy and tactics, product demonstration, sales techniques, and sales control systems. |
| Competence | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.000 | 0.098 | 0.094 | 0.058 | 0.083 | 0.077 | 0.041 | 0.060 | 0.073 | 0.081 | 0.067 | 0.083 | 0.074 | |
| 0.083 | 0.000 | 0.083 | 0.065 | 0.079 | 0.071 | 0.041 | 0.067 | 0.061 | 0.077 | 0.050 | 0.092 | 0.067 | |
| 0.090 | 0.092 | 0.000 | 0.058 | 0.090 | 0.077 | 0.043 | 0.075 | 0.069 | 0.079 | 0.083 | 0.098 | 0.081 | |
| 0.056 | 0.073 | 0.063 | 0.000 | 0.069 | 0.065 | 0.050 | 0.058 | 0.067 | 0.060 | 0.054 | 0.081 | 0.054 | |
| 0.083 | 0.077 | 0.092 | 0.069 | 0.000 | 0.088 | 0.052 | 0.070 | 0.077 | 0.086 | 0.075 | 0.090 | 0.069 | |
| 0.063 | 0.060 | 0.073 | 0.065 | 0.086 | 0.000 | 0.045 | 0.069 | 0.065 | 0.073 | 0.061 | 0.075 | 0.050 | |
| 0.038 | 0.047 | 0.038 | 0.038 | 0.044 | 0.040 | 0.000 | 0.043 | 0.038 | 0.033 | 0.045 | 0.058 | 0.033 | |
| 0.063 | 0.067 | 0.071 | 0.061 | 0.076 | 0.073 | 0.038 | 0.000 | 0.049 | 0.066 | 0.052 | 0.065 | 0.054 | |
| 0.067 | 0.063 | 0.067 | 0.071 | 0.067 | 0.056 | 0.046 | 0.054 | 0.000 | 0.075 | 0.069 | 0.077 | 0.056 | |
| 0.077 | 0.083 | 0.090 | 0.063 | 0.077 | 0.067 | 0.036 | 0.058 | 0.077 | 0.029 | 0.081 | 0.081 | 0.060 | |
| 0.075 | 0.048 | 0.090 | 0.054 | 0.067 | 0.067 | 0.043 | 0.056 | 0.079 | 0.081 | 0.000 | 0.090 | 0.060 | |
| 0.083 | 0.094 | 0.094 | 0.086 | 0.100 | 0.088 | 0.058 | 0.074 | 0.085 | 0.075 | 0.086 | 0.000 | 0.077 | |
| 0.071 | 0.054 | 0.070 | 0.056 | 0.060 | 0.052 | 0.046 | 0.043 | 0.056 | 0.056 | 0.069 | 0.083 | 0.000 |
| Competence | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.344 | 0.436 | 0.457 | 0.357 | 0.438 | 0.404 | 0.259 | 0.353 | 0.391 | 0.428 | 0.383 | 0.464 | 0.370 | |
| 0.401 | 0.327 | 0.427 | 0.345 | 0.415 | 0.380 | 0.247 | 0.342 | 0.362 | 0.404 | 0.350 | 0.449 | 0.347 | |
| 0.442 | 0.446 | 0.389 | 0.371 | 0.460 | 0.419 | 0.271 | 0.379 | 0.402 | 0.442 | 0.412 | 0.493 | 0.390 | |
| 0.343 | 0.360 | 0.372 | 0.255 | 0.369 | 0.341 | 0.234 | 0.305 | 0.335 | 0.354 | 0.322 | 0.400 | 0.305 | |
| 0.431 | 0.429 | 0.467 | 0.376 | 0.373 | 0.423 | 0.276 | 0.370 | 0.405 | 0.443 | 0.401 | 0.481 | 0.375 | |
| 0.362 | 0.363 | 0.396 | 0.327 | 0.398 | 0.293 | 0.237 | 0.326 | 0.346 | 0.379 | 0.340 | 0.411 | 0.313 | |
| 0.230 | 0.240 | 0.246 | 0.207 | 0.246 | 0.227 | 0.125 | 0.208 | 0.219 | 0.231 | 0.224 | 0.273 | 0.202 | |
| 0.344 | 0.350 | 0.374 | 0.308 | 0.371 | 0.344 | 0.219 | 0.246 | 0.315 | 0.355 | 0.315 | 0.382 | 0.301 | |
| 0.359 | 0.358 | 0.383 | 0.327 | 0.374 | 0.340 | 0.234 | 0.306 | 0.279 | 0.374 | 0.341 | 0.405 | 0.313 | |
| 0.413 | 0.421 | 0.451 | 0.358 | 0.430 | 0.392 | 0.253 | 0.349 | 0.393 | 0.376 | 0.394 | 0.459 | 0.356 | |
| 0.385 | 0.363 | 0.423 | 0.328 | 0.394 | 0.367 | 0.242 | 0.324 | 0.370 | 0.399 | 0.294 | 0.436 | 0.333 | |
| 0.456 | 0.467 | 0.495 | 0.411 | 0.489 | 0.447 | 0.297 | 0.395 | 0.435 | 0.458 | 0.432 | 0.426 | 0.403 | |
| 0.345 | 0.332 | 0.367 | 0.298 | 0.350 | 0.319 | 0.223 | 0.281 | 0.316 | 0.340 | 0.325 | 0.391 | 0.245 |
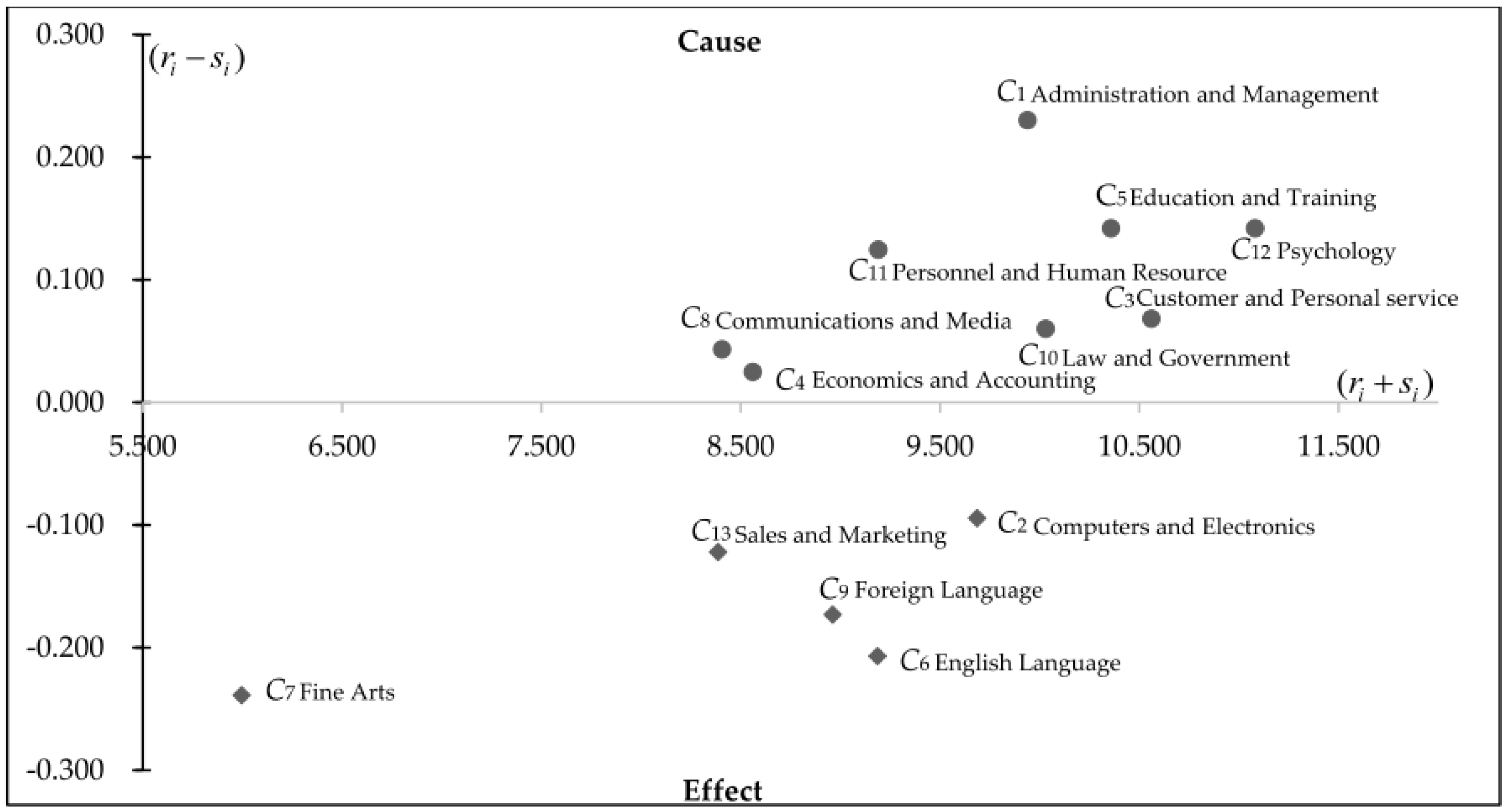
| Ranking | Competence set | Cause/Effect | |||||
|---|---|---|---|---|---|---|---|
| 1 | Administration and Management | 5.085 | 4.855 | 9.939 | 0.230 | cause | |
| 2 | Psychology | 5.612 | 5.470 | 11.081 | 0.142 | cause | |
| 3 | Education and Training | 5.250 | 5.108 | 10.358 | 0.142 | cause | |
| 4 | Personnel and Human Resources | 4.658 | 4.533 | 9.191 | 0.125 | cause | |
| 5 | Customer and Personal Services | 5.315 | 5.247 | 10.562 | 0.068 | cause | |
| 6 | Law and Government | 5.045 | 4.985 | 10.030 | 0.060 | cause | |
| 7 | Communications and Media | 4.225 | 4.182 | 8.408 | 0.043 | cause | |
| 8 | Economics and Accounting | 4.292 | 4.267 | 8.560 | 0.025 | cause | |
| 1 | Computers and Electronics | 4.797 | 4.891 | 9.688 | −0.095 | effect | |
| 2 | Sales and Marketing | 4.132 | 4.254 | 8.387 | −0.122 | effect | |
| 3 | Foreign Languages | 4.395 | 4.568 | 8.962 | −0.173 | effect | |
| 4 | English Language | 4.490 | 4.698 | 9.188 | −0.207 | effect | |
| 5 | Fine Arts | 2.879 | 3.118 | 5.997 | −0.239 | effect |
| Competence | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Influential weights |  | 0.0804 | 0.0804 | 0.0806 | 0.0796 | 0.0795 | 0.0794 | 0.0728 | 0.0729 | 0.0729 | 0.0727 | 0.0726 | 0.0727 |
| Competence set | DANP weights | Participants | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0836 | 0.100 | 0.100 | 0.400 | 0.300 | 0.500 | 0.300 | 0.300 | 0.300 | 0.700 | 0.700 | 0.500 | 0.400 | 0.500 | 0.200 | |
| 0.0804 | 0.000 | 0.800 | 0.700 | 0.200 | 0.500 | 0.300 | 0.300 | 0.300 | 0.500 | 0.400 | 0.500 | 0.400 | 0.600 | 0.300 | |
| 0.0804 | 0.200 | 0.200 | 0.300 | 0.200 | 0.500 | 0.300 | 0.200 | 0.200 | 0.500 | 0.500 | 0.200 | 0.300 | 0.700 | 0.100 | |
| 0.0806 | 0.300 | 0.300 | 0.700 | 0.800 | 0.500 | 0.500 | 0.600 | 0.500 | 0.700 | 0.900 | 0.700 | 0.500 | 0.500 | 0.300 | |
| 0.0796 | 0.400 | 0.400 | 0.400 | 0.500 | 0.400 | 0.300 | 0.600 | 0.300 | 0.700 | 0.700 | 0.300 | 0.500 | 0.800 | 0.300 | |
| 0.0795 | 0.500 | 0.500 | 0.500 | 0.800 | 0.500 | 0.500 | 0.500 | 0.300 | 0.400 | 0.400 | 0.700 | 0.500 | 0.900 | 0.300 | |
| 0.0794 | 1.000 | 1.000 | 0.400 | 0.500 | 0.800 | 0.300 | 0.800 | 0.500 | 0.700 | 1.000 | 0.900 | 0.500 | 0.600 | 0.300 | |
| 0.0728 | 0.800 | 0.800 | 0.500 | 0.800 | 0.700 | 0.600 | 0.500 | 0.300 | 0.700 | 0.500 | 1.000 | 0.500 | 0.400 | 0.800 | |
| 0.0729 | 0.900 | 0.900 | 0.400 | 0.500 | 0.500 | 0.500 | 0.500 | 0.400 | 0.700 | 0.600 | 0.700 | 0.500 | 0.500 | 0.500 | |
| 0.0729 | 0.000 | 0.900 | 0.400 | 0.500 | 0.500 | 0.400 | 0.500 | 0.300 | 0.700 | 0.500 | 0.500 | 0.500 | 0.300 | 0.300 | |
| 0.0727 | 0.000 | 0.000 | 0.300 | 0.300 | 0.500 | 0.300 | 0.500 | 0.200 | 0.500 | 0.500 | 0.500 | 0.500 | 0.800 | 0.500 | |
| 0.0726 | 0.700 | 0.700 | 0.300 | 0.200 | 0.500 | 0.300 | 0.300 | 0.400 | 0.700 | 0.600 | 0.600 | 0.500 | 0.700 | 0.200 | |
| 0.0727 | 0.600 | 0.600 | 0.400 | 0.500 | 0.500 | 0.400 | 0.400 | 0.400 | 0.300 | 0.400 | 0.600 | 0.500 | 0.700 | 0.700 | |
| (average gaps/regrets) | 0.418 | 0.548 | 0.441 | 0.469 | 0.530 | 0.383 | 0.461 | 0.339 | 0.600 | 0.596 | 0.589 | 0.468 | 0.617 | 0.363 | |
| (maximal gap/regret) | 1.000 | 1.000 | 0.700 | 0.800 | 0.800 | 0.600 | 0.800 | 0.500 | 0.700 | 1.000 | 1.000 | 0.500 | 0.900 | 0.800 | |
| (synthesizing index) | 0.709 | 0.774 | 0.570 | 0.634 | 0.665 | 0.491 | 0.631 | 0.419 | 0.650 | 0.798 | 0.795 | 0.484 | 0.758 | 0.581 | |
| Ranks | 10 | 12 | 4 | 7 | 9 | 3 | 6 | 1 | 8 | 14 | 13 | 2 | 11 | 5 | |
| Competence set | Participants () | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0630 | 0.0848 | 0.0683 | 0.0716 | 0.0817 | 0.0598 | 0.0702 | 0.0521 | 0.0940 | 0.0911 | 0.0900 | 0.0731 | 0.0971 | 0.0563 | |
| 0.0596 | 0.0802 | 0.0646 | 0.0677 | 0.0773 | 0.0566 | 0.0664 | 0.0493 | 0.0889 | 0.0862 | 0.0851 | 0.0692 | 0.0918 | 0.0532 | |
| 0.0659 | 0.0888 | 0.0714 | 0.0750 | 0.0855 | 0.0626 | 0.0734 | 0.0545 | 0.0984 | 0.0954 | 0.0941 | 0.0765 | 0.1016 | 0.0589 | |
| 0.0532 | 0.0717 | 0.0577 | 0.0606 | 0.0691 | 0.0506 | 0.0593 | 0.0440 | 0.0795 | 0.0771 | 0.0761 | 0.0619 | 0.0821 | 0.0476 | |
| 0.0651 | 0.0878 | 0.0706 | 0.0741 | 0.0845 | 0.0618 | 0.0726 | 0.0539 | 0.0973 | 0.0943 | 0.0930 | 0.0757 | 0.1004 | 0.0582 | |
| 0.0559 | 0.0753 | 0.0605 | 0.0635 | 0.0725 | 0.0530 | 0.0622 | 0.0462 | 0.0834 | 0.0808 | 0.0798 | 0.0649 | 0.0861 | 0.0499 | |
| 0.0358 | 0.0483 | 0.0388 | 0.0407 | 0.0465 | 0.0340 | 0.0399 | 0.0296 | 0.0535 | 0.0518 | 0.0512 | 0.0416 | 0.0552 | 0.0320 | |
| 0.0526 | 0.0708 | 0.0570 | 0.0598 | 0.0682 | 0.0499 | 0.0586 | 0.0435 | 0.0785 | 0.0761 | 0.0751 | 0.0611 | 0.0811 | 0.0470 | |
| 0.0546 | 0.0736 | 0.0592 | 0.0621 | 0.0709 | 0.0519 | 0.0609 | 0.0452 | 0.0816 | 0.0791 | 0.0780 | 0.0634 | 0.0842 | 0.0488 | |
| 0.0625 | 0.0843 | 0.0678 | 0.0711 | 0.0812 | 0.0594 | 0.0697 | 0.0517 | 0.0934 | 0.0905 | 0.0893 | 0.0726 | 0.0964 | 0.0559 | |
| 0.0578 | 0.0779 | 0.0627 | 0.0658 | 0.0750 | 0.0549 | 0.0644 | 0.0478 | 0.0863 | 0.0837 | 0.0826 | 0.0672 | 0.0891 | 0.0517 | |
| 0.0694 | 0.0935 | 0.0752 | 0.0790 | 0.0901 | 0.0659 | 0.0774 | 0.0574 | 0.1037 | 0.1005 | 0.0992 | 0.0806 | 0.1070 | 0.0620 | |
| 0.0513 | 0.0691 | 0.0556 | 0.0584 | 0.0666 | 0.0487 | 0.0572 | 0.0424 | 0.0766 | 0.0743 | 0.0733 | 0.0596 | 0.0791 | 0.0458 | |
| 0.057 | 0.077 | 0.062 | 0.065 | 0.075 | 0.055 | 0.064 | 0.048 | 0.086 | 0.083 | 0.082 | 0.067 | 0.089 | 0.051 | |
| 0.069 | 0.094 | 0.075 | 0.079 | 0.090 | 0.066 | 0.077 | 0.057 | 0.104 | 0.101 | 0.099 | 0.081 | 0.107 | 0.062 | |
| 0.063 | 0.085 | 0.069 | 0.072 | 0.082 | 0.060 | 0.071 | 0.052 | 0.095 | 0.092 | 0.091 | 0.074 | 0.098 | 0.057 | |
| Rank | 4 | 10 | 5 | 7 | 9 | 3 | 6 | 1 | 13 | 12 | 11 | 8 | 14 | 2 |
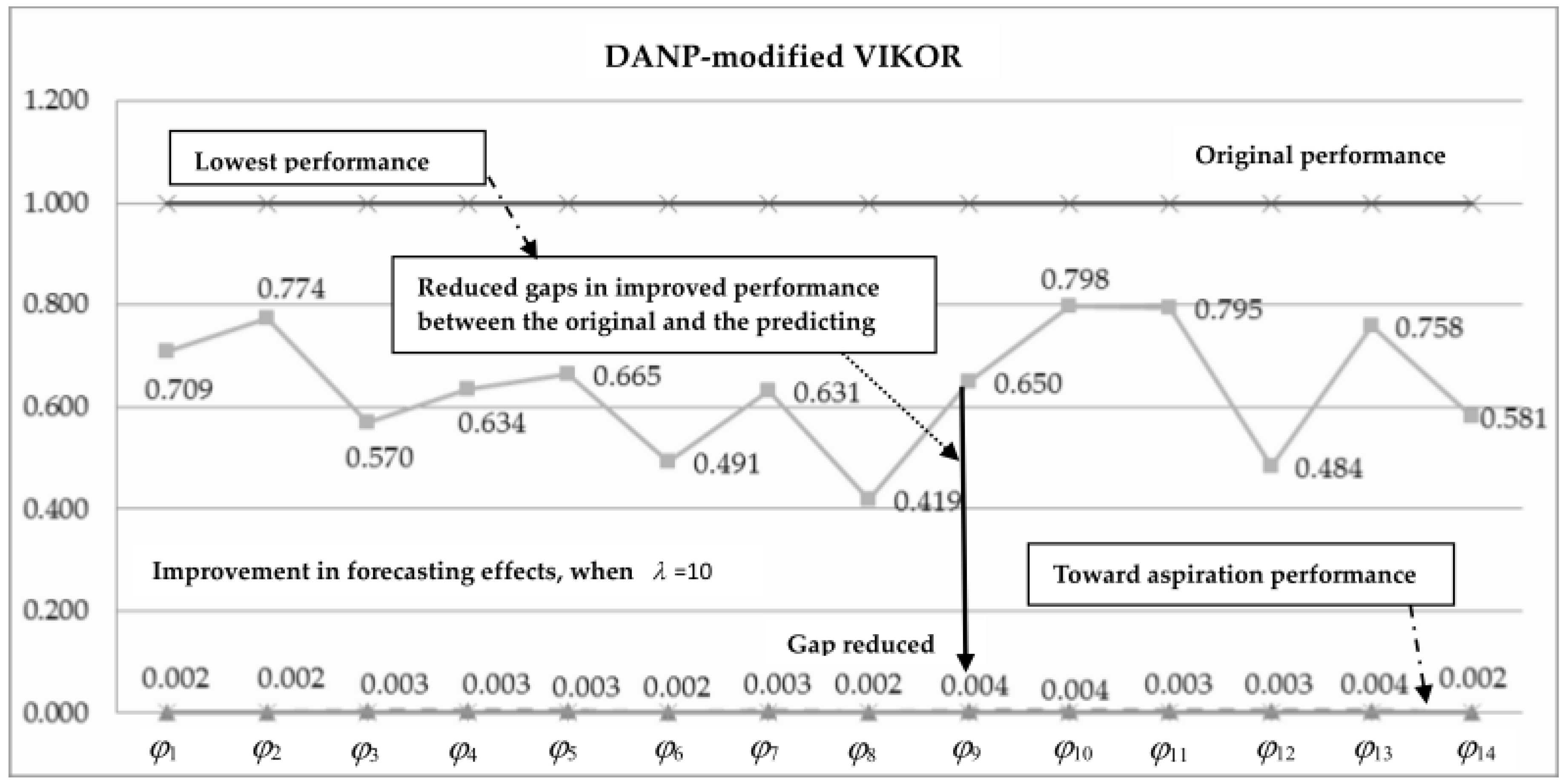
| Uk_current (synthesizing index) | 0.709 | 0.774 | 0.570 | 0.634 | 0.665 | 0.491 | 0.631 | 0.419 | 0.650 | 0.798 | 0.795 | 0.484 | 0.758 | 0.581 |
| Uk'_forecast (synthesizing index) | 0.063 | 0.085 | 0.069 | 0.072 | 0.082 | 0.060 | 0.071 | 0.052 | 0.095 | 0.092 | 0.091 | 0.074 | 0.098 | 0.057 |
| Rank for current performance | 10 | 12 | 4 | 7 | 9 | 3 | 6 | 1 | 8 | 14 | 13 | 2 | 11 | 5 |
| Rank for improvement-forecasting | 4 | 10 | 5 | 7 | 9 | 3 | 6 | 1 | 13 | 12 | 11 | 8 | 14 | 2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.-W.; Huang, J.-H.; Tzeng, G.-H. New Hybrid Multiple Attribute Decision-Making Model for Improving Competence Sets: Enhancing a Company’s Core Competitiveness. Sustainability 2016, 8, 175. https://doi.org/10.3390/su8020175
Huang K-W, Huang J-H, Tzeng G-H. New Hybrid Multiple Attribute Decision-Making Model for Improving Competence Sets: Enhancing a Company’s Core Competitiveness. Sustainability. 2016; 8(2):175. https://doi.org/10.3390/su8020175
Chicago/Turabian StyleHuang, Kuan-Wei, Jen-Hung Huang, and Gwo-Hshiung Tzeng. 2016. "New Hybrid Multiple Attribute Decision-Making Model for Improving Competence Sets: Enhancing a Company’s Core Competitiveness" Sustainability 8, no. 2: 175. https://doi.org/10.3390/su8020175
APA StyleHuang, K.-W., Huang, J.-H., & Tzeng, G.-H. (2016). New Hybrid Multiple Attribute Decision-Making Model for Improving Competence Sets: Enhancing a Company’s Core Competitiveness. Sustainability, 8(2), 175. https://doi.org/10.3390/su8020175






