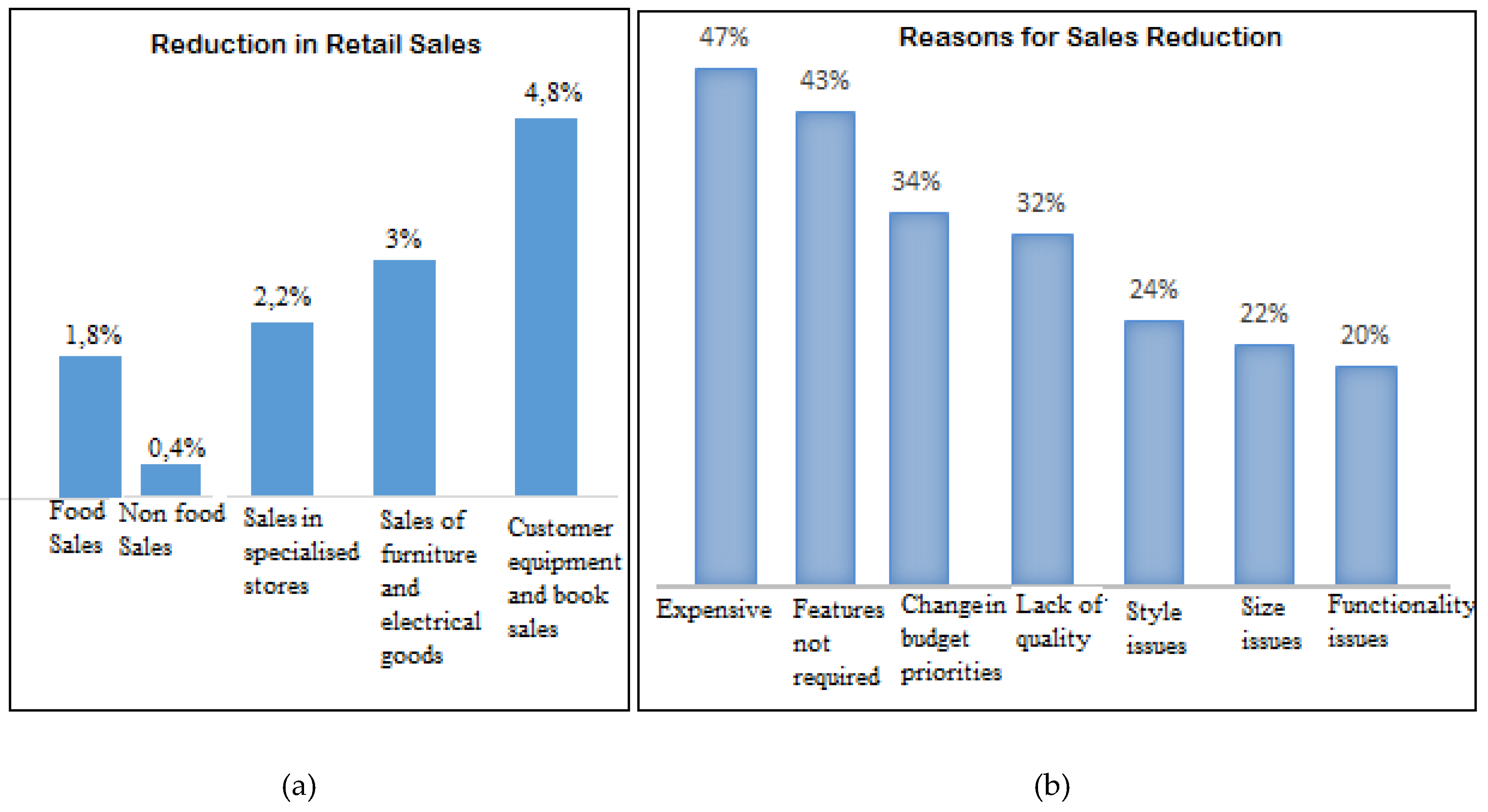
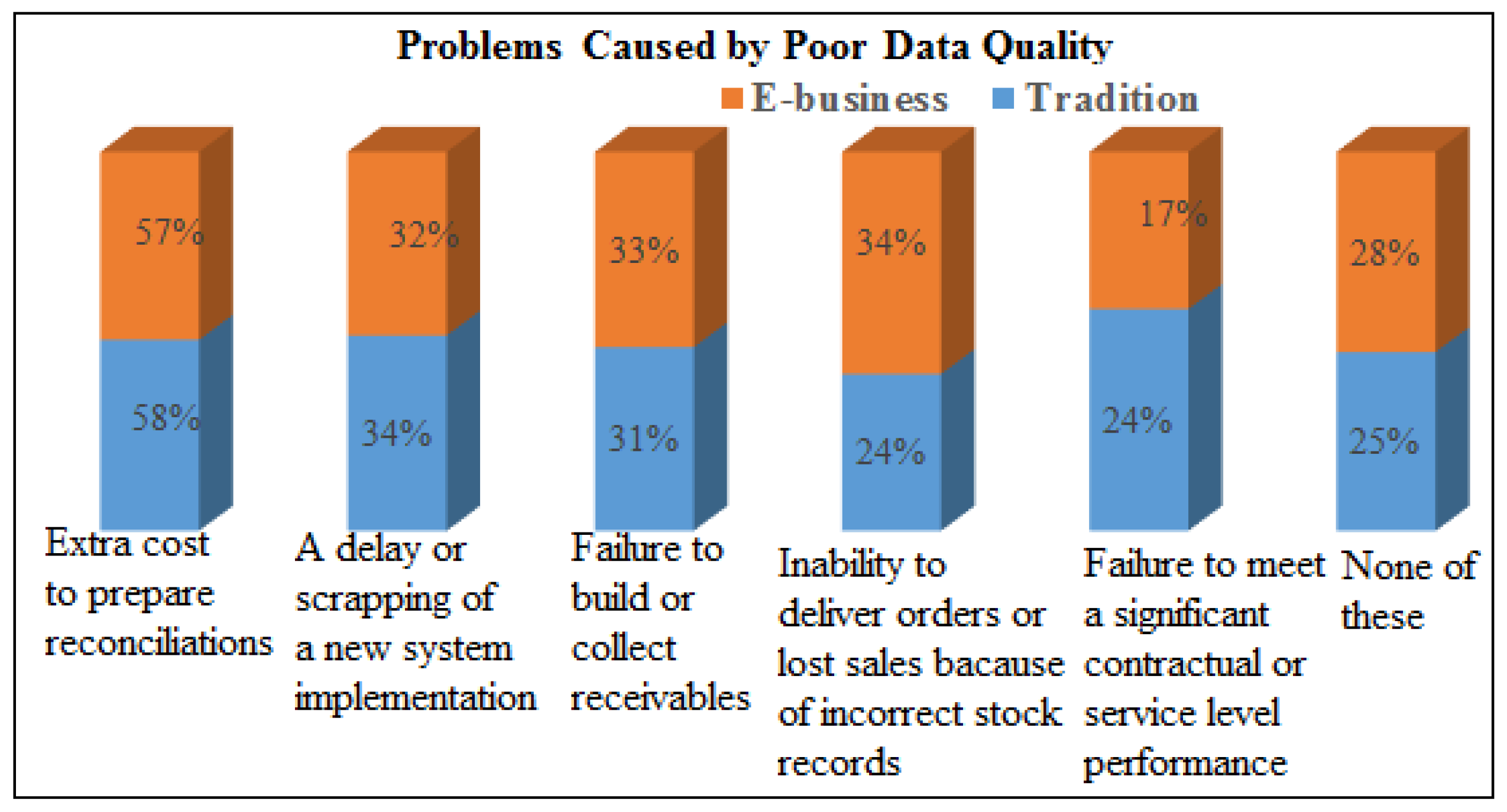
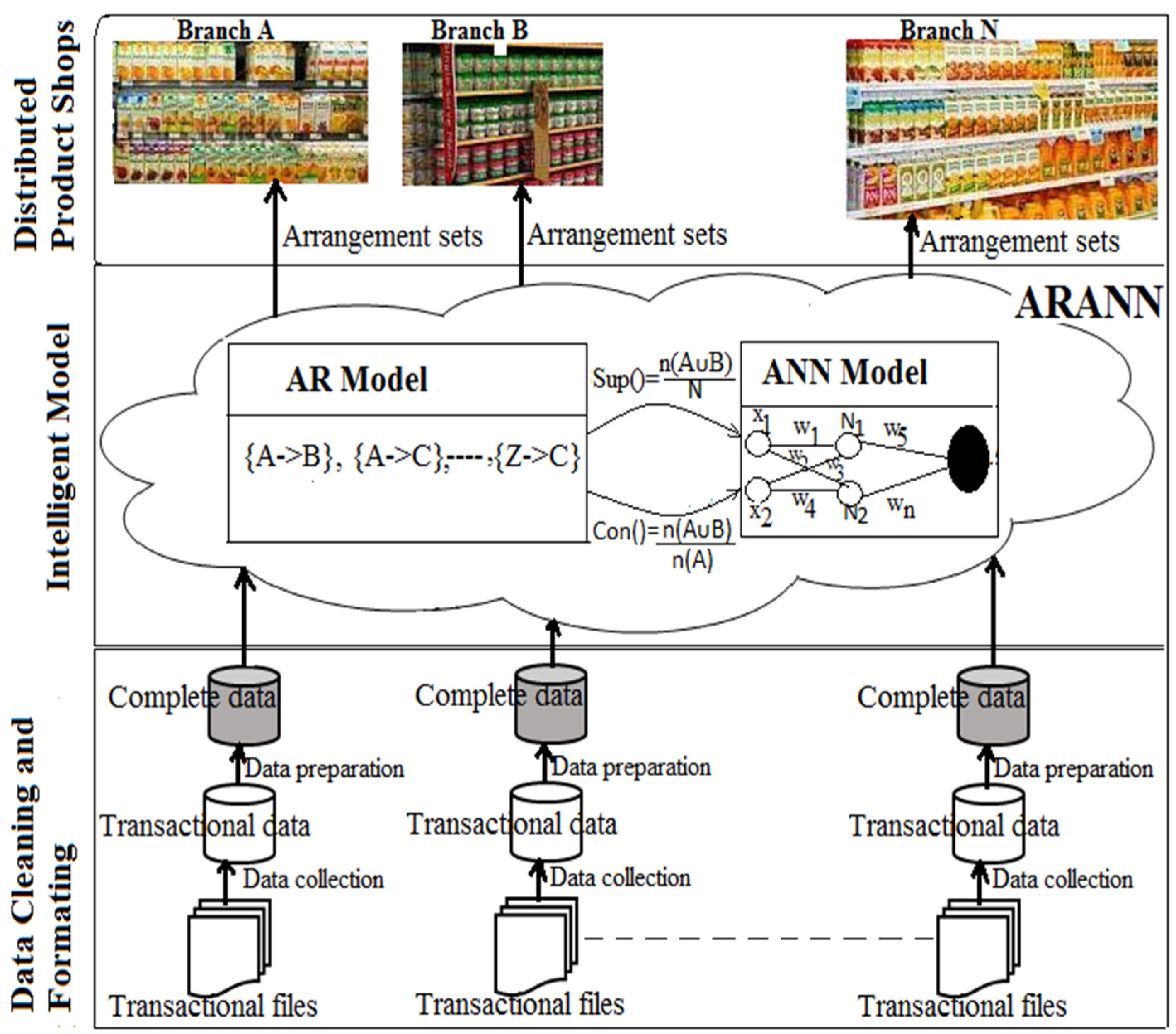
3.1. Proposed System Model for Distributed Retail Enterprises
This section explores the proposed system model for BI analytics in distributed retail enterprises. The proposed model has three layers, namely data cleaning and formatting, intelligent model and distributed product shops, as shown in
Figure 3. The data cleaning and formatting layer is found at the bottom of the proposed model. In this proposed model, data is collected from transactional systems branch per branch. The data is cleaned and formatted to the appropriate file type accepted by the proposed model. Processed data is input into the ARANN model branch per branch at the middle layer of the analytical model. The ARANN model cooperatively works between AR and ANN. Processed data from the bottom layer is passed into the AR model and it outputs confidence and support values. These values are passed into the ANN model as inputs in order to get the degree of belief (DoB). The DoB of sets generated is compared to the ARANN activations set. The accepted sets generated are applied on the top layer of the proposed model. This proposed model is deployed to each branch and patterns are generated independently. The choice is left for every retail enterprise branch to adopt the best results, depending on the market competitiveness and profit levels.
Figure 3.
Proposed intelligent analytics-based framework.
Figure 3.
Proposed intelligent analytics-based framework.
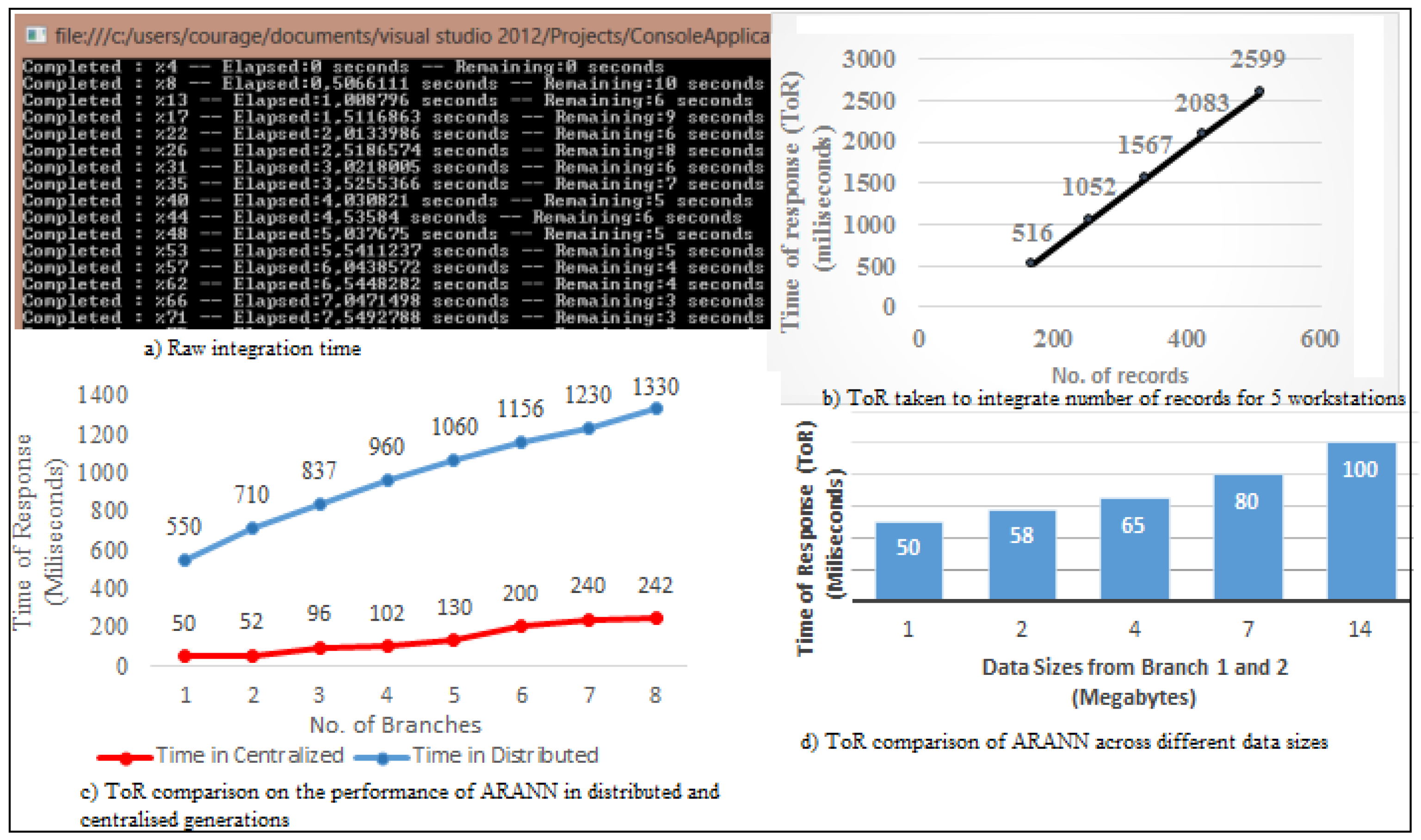
The proposed intelligent analytics-based framework has the following benefits: reduction in risk of passing misleading results to all branches, no one point of failure, consumption of fewer resources, faster construction of distributed systems and no need for data integration.
This proposed analytics-based model can be implemented using the pseudo-code presented in
Table 1.
Table 1 shows how ARANN generates product arrangement sets that can be used by retail enterprise managers to arrange products on shop shelves so as to attract customers to purchase more products than planned. The pseudo-code is further presented mathematically, as shown in Equations (5)–(14).
Table 1.
Pseudo-code for ARANN model.
Table 1.
Pseudo-code for ARANN model.
| | Pseudo-code |
|---|
| Steps | Input: Transactional data in database (D) = {t1, t2, t3, .., tn} |
| Support () |
| Confidence () |
| Weights (W) = {w1, w2, w3, .., wn} |
| |
| Output: Products pattern |
| | Step 1: D = {t1, t2, t3, .., tn} //Transactions in the database |
| Step 2: Ck = Candidate item set of size k |
| Step 3: Fk = frequent item set of size k |
| { |
|
for (k =1; Fk != Ø; k++) // Fk is not equal to empty set. |
| { |
| Scan the entire D to generate candidate sets Ck |
| { |
| Compare candidate support count from Ck with the minimum support count to generate Fk |
| } |
| } |
| Step 4: Generate Support () & Confidence () |
| { |
| Step 5: Input Support () & Confidence () into Neuron 1 (N1) and Neuron 2 (N2) as inputs |
| Step 6: Generate N1 by summing of the inputs with the corresponding weights and apply the output into sigmoid function |
| Step 7: Generate N2 by summing of the inputs with the corresponding weights and apply the output into sigmoid function |
| Step 8: Generate the summation of N1 & N2 after the sigmoid function and apply the output into sigmoid function to obtain Degree of Belief (DoB) |
| Step 9: Display products pattern where
DoB ≥ ARANN activation |
| } |
| } |
Mathematical description for the ARANN Model
The sup and con values feed the N1 as the inputs and are multiplied with the corresponding weights.
The output of N
1 after the sigmoid function
The sup and con values feed the N
2 as the inputs and are multiplied with the corresponding weights:
The output of N
2 after the sigmoid function
where
N1 and
N2 are Neuron 1 and 2 respectively;
W1,
W2, W3, W4,
W5 and
W6 are the corresponding weights;
O1 is Neuron 1 output after sigmoid function;
O2 is Neuron 2 output after sigmoid function,
F is input to final Neuron and
ARANN activation is the threshold value set.
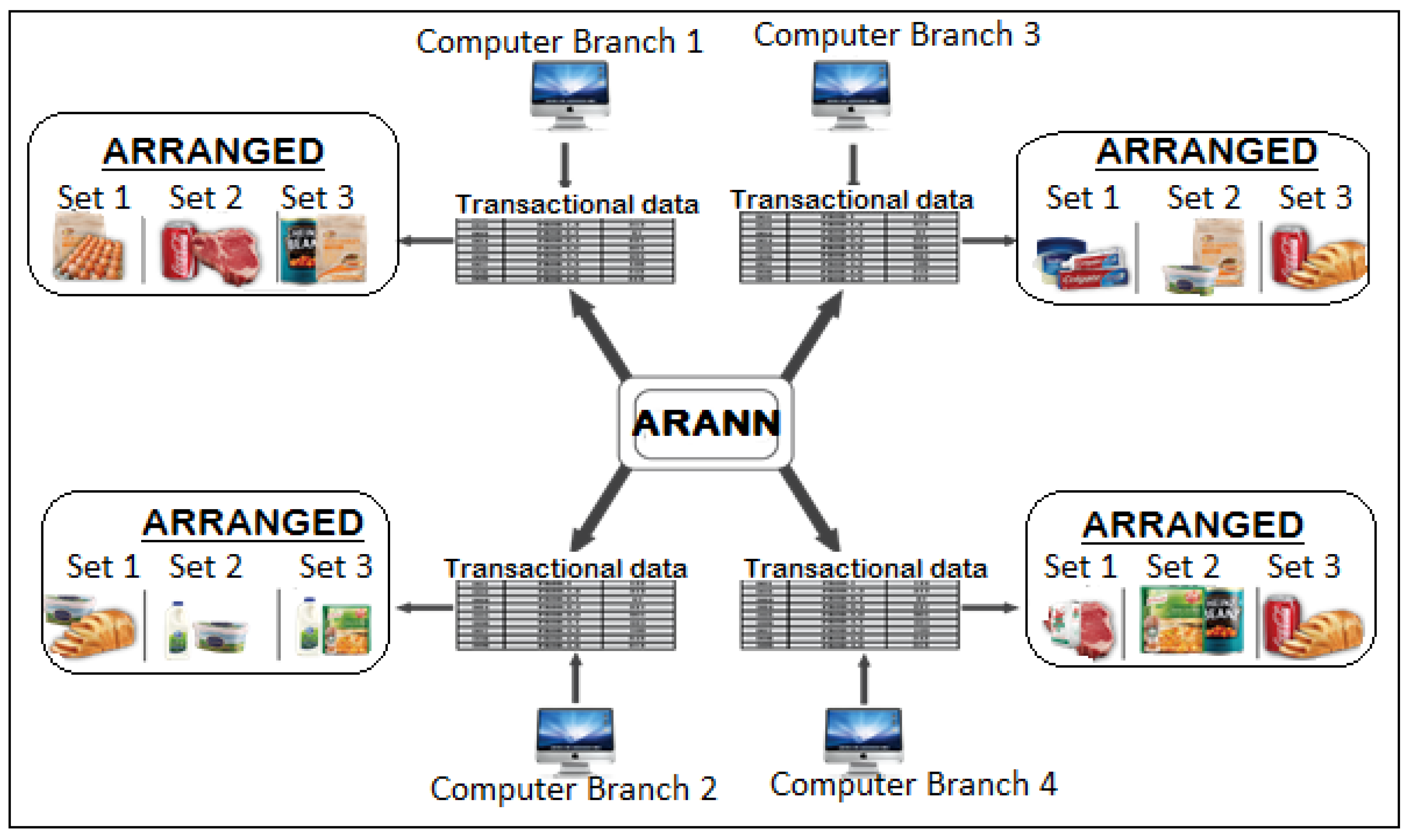
3.3. Scenario—Arrangement of Products on Shelves for Distributed Retail Branches
Figure 4 shows a scenario of how the analytical model displays placement results in distributed branches. Transactional data from each retail branch is loaded into the ARANN model to determine the arrangement sets.
Figure 4.
Intelligent Analytics-based Model for Four Branches.
Figure 4.
Intelligent Analytics-based Model for Four Branches.
Table 3.
Market basket transactional data for branch 3 of a retail enterprise.
Table 3.
Market basket transactional data for branch 3 of a retail enterprise.
| Market-basket Transaction Data—Branch 3 |
|---|
| TID | ITEMS |
| T300 | Colgate, Vaseline, Geisha, Margarine, Bread |
| T301 | Margarine, Bread, Coke, Colgate, Vaseline |
| T302 | Coke, Colgate, Chocolate, Bread, Sweets, Margarine |
| T303 | Geisha, Colgate, Chocolate, Towel, Vaseline, Sweets |
| T304 | Colgate, Vaseline, Sweets, Chocolate, Bread, Margarine, Coke |
Even weights were applied to each corresponding input to avoid bias on products. This was obtained by dividing the count of a_union_b over a number of records within the data set, where
a, and
b are different products. The following ARANN activation was used:
>= 0.75 strongly connected products (strongly accepted)
>= 0.65 moderately connected products (accepted)
< 0.65 weakly connected products (rejected)
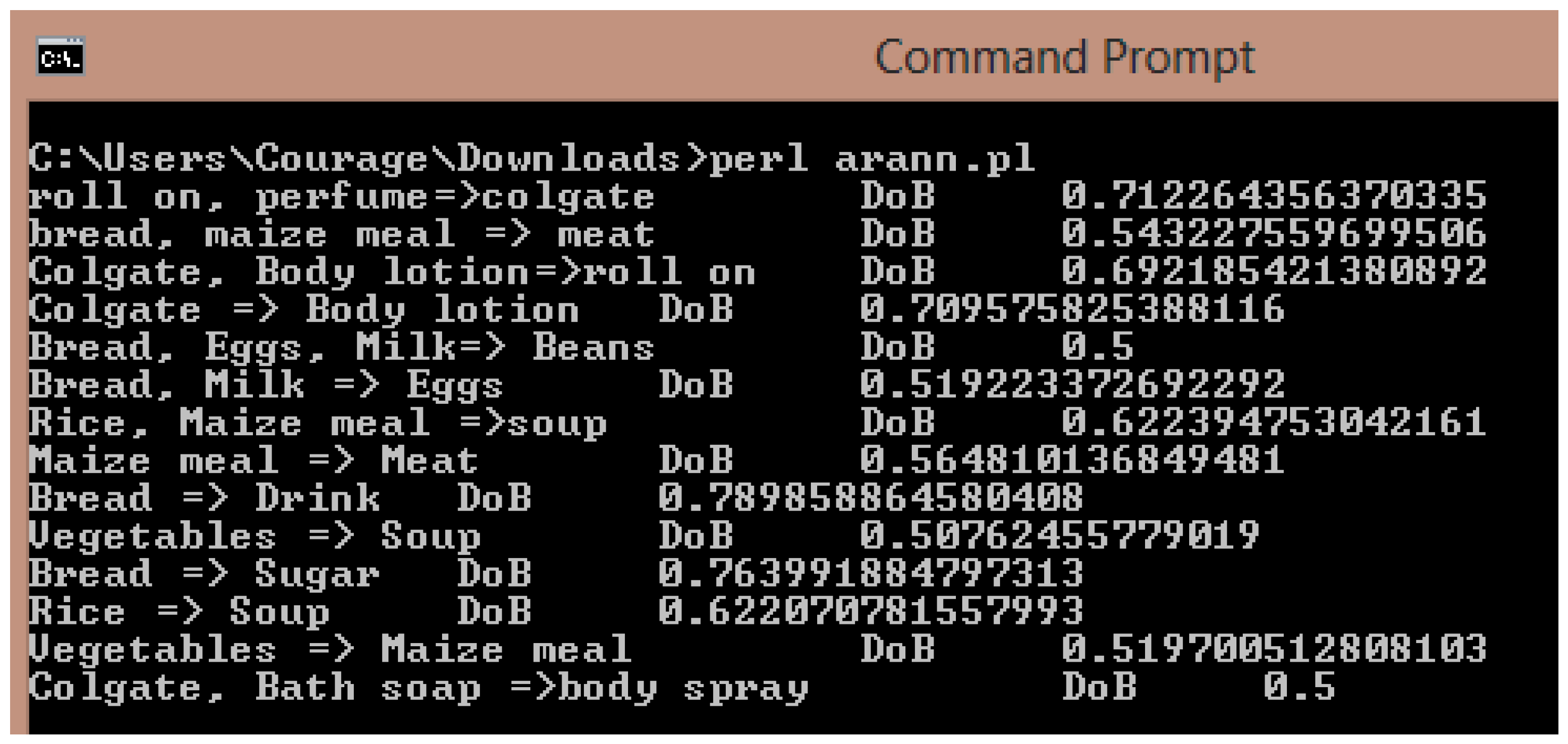
{Colgate, Vaseline} => {Bread}
Support = Confidence =
N1 = Supw1 + Conw3 N2 = Conw4 + Supw2
= (0.6 × 0.6) + (0.75 × 0.6) = (0.75 × 0.6) + (0.6×0.6)
= 0.81 = 0.81
O1 = O2 =
F = w5O1 + w6O2
= (0.6 × 0.69) + (0.6 × 0.69) = 0.83
DoB =
Product pattern => 0.70 >= 0.65
Therefore it is moderately connected and is accepted.
{Coke} => {Bread}
Support = Confidence =
N1 = (0.6 × 0.6) + (1.0 × 0.6) N2 = (1.0 × 0.6) + (0.6 × 0.6)
= 0.96 = 0.96
01 = O2 =
F = w5O1 + w6O2
= (0.6 × 0.72) + (0.6 × 0.72) = 0.86
DoB =
Product pattern => 0.70 >= 0.65
Therefore it is moderately connected and is accepted.
Table 4.
Market basket transactional data for branch 4 of a retail enterprise.
Table 4.
Market basket transactional data for branch 4 of a retail enterprise.
| Market-basket Transaction Data—Branch 4 |
|---|
| TID | ITEMS |
| T400 | Maize meal, Beef, Fish, Cooking oil, Soups, Bread, Coke |
| T401 | Cooking oil, Beans, Beef, Soups, Maize meal |
| T402 | Rice, Fish, Soups, Cooking oil, Bread |
| T403 | Fruits, Coke, Bread, Milk, Chocolate, Soups |
| T404 | Bread, Beef, Fruit, Coke, Sweets, Maize meal |
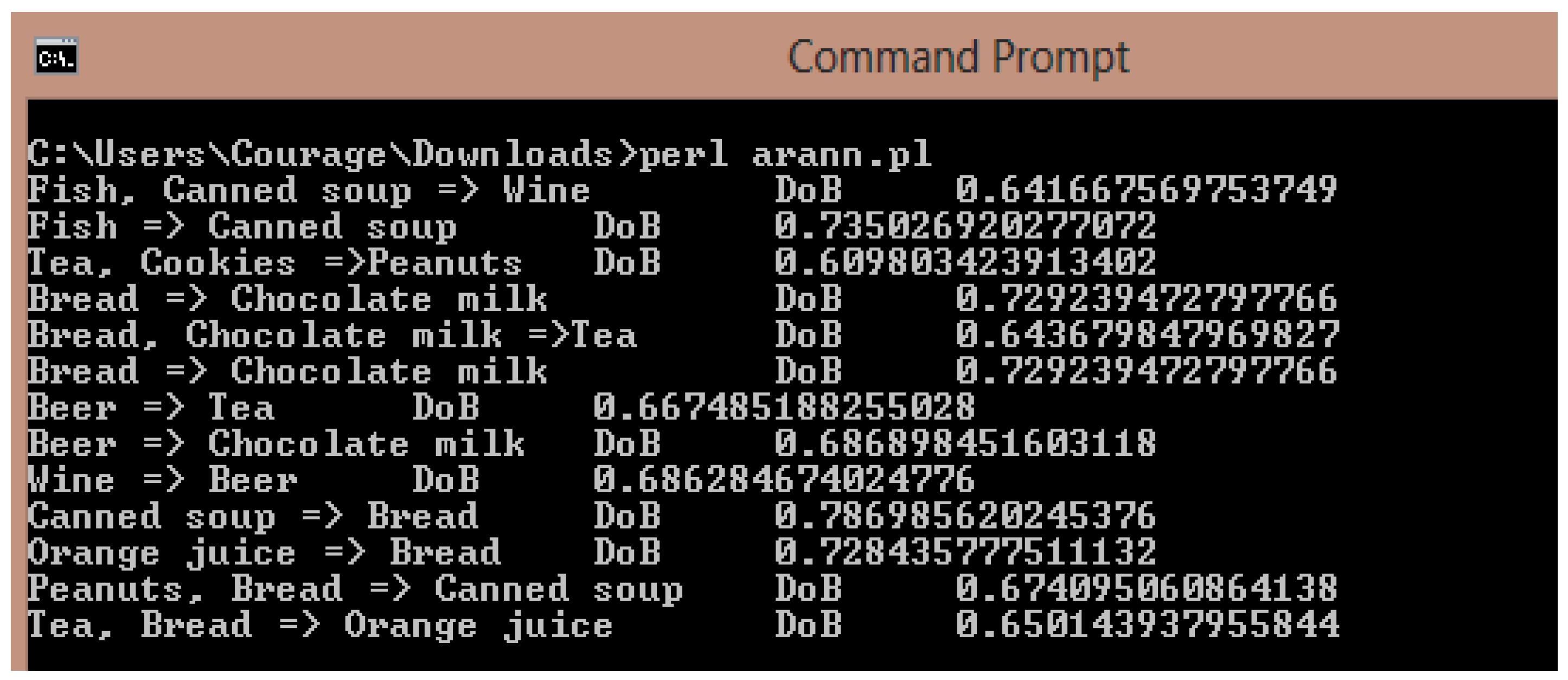
{Maize meal} => {Beef}
Support = Confidence =
N1 = (0.6 × 0.6) + (1.0 × 0.6) N2 = (1.0 × 0.6) + (0.6 × 0.6)
= 0.96 = 0.96
01 = O2 =
F = w5O1 + w6O2
= (0.6 × 0.72) + (0.6 × 0.72) = 0.86
DoB =
Product pattern => 0.70 >= 0.65
Therefore it is moderately connected and is accepted.
{Chocolate} => {Towel}
Support = Confidence =
N1 = (0.20 × 0.20) + (0.33 × 0.20) N2 = (0.33 × 0.20) + (0.20 × 0.20)
= 0.11 = 0.11
O1 = O2 =
F = (0.2 × 0.53) + (0.2 × 0.53) = 0.212
DoB =
Product pattern => 0.55 < 0.65
Therefore it is weakly connected and is rejected.