Research on Energy-Saving Production Scheduling Based on a Clustering Algorithm for a Forging Enterprise

Abstract

Energy efficiency is a buzzword of the 21st century. With the ever growing need for energy efficient and low-carbon production, it is a big challenge for high energy-consumption enterprises to reduce their energy consumption. To this aim, a forging enterprise, DVR (the abbreviation of a forging enterprise), is researched. Firstly, an investigation into the production processes of DVR is given as well as an analysis of forging production. Then, the energy-saving forging scheduling is decomposed into two sub-problems. One is for cutting and machining scheduling, which is similar to traditional machining scheduling. The other one is for forging and heat treatment scheduling. Thirdly, former forging production scheduling is presented and solved based on an improved genetic algorithm. Fourthly, the latter is discussed in detail, followed by proposed dynamic clustering and stacking combination optimization. The proposed stacking optimization requires making the gross weight of forgings as close to the maximum batch capacity as possible. The above research can help reduce the heating times, and increase furnace utilization with high energy efficiency and low carbon emissions.

1. Introduction

Energy efficiency is a buzzword of the 21st century. As a result of climate change, regulation of carbon dioxide emissions has been imposed globally, which has put much pressure on the manufacturing industry to reduce energy (particularly electric energy) [1]. With the need for energy efficient and low-carbon production, it is a big challenge for high energy-consumption enterprises to reduce energy use. Therefore, effective energy and utility management is a key factor to enhancing the competitive advantage of organizations, and promoting green and sustainable practices [2].

A number of researches have been carried out on sustainable manufacturing, among which green manufacturing is a major focus. Green manufacturing is a modern manufacturing mode with significant consideration given to environmental impacts and resource efficiency while assuring product functionality, quality and cost. Ahmed proposed a new green manufacturing system model that can capture various planning activities to migrate from a less green into a greener and more eco-efficient manufacturing mode through the use of green control metrics and tools in different manufacturing stages [3]. A comprehensive study and analysis by Vijayaraghavan [4] and Chuang [5] are reported with a view of enabling technologies and key success factors for green manufacturing systems. Considering the ecological, social and economic indicators, Corinne proposed an evaluation system of green manufacturing and measurement methods to quantify the index [6]. Barbara overviewed the development of green products and pointed to the need to strengthen green manufacturing, including product life cycle oriented assessment, manufacturing processes and supply chain decisions [7]. A green supply chain (GSC) performance measurement framework was delineated by using an intra-organizational collaborative decision-making (CDM) approach [8]. In China, Professor Liu Fei and his research team proposed green manufacturing and conducted a lengthy in-depth study on the implementation processes, key technologies and use promotion of green manufacturing [9]. Green manufacturing methodologies and theoretical frameworks have made some great achievements [10]. However, current researches have focused on manufacturing processes’ specification, management models and auxiliary tools with little guidance given on the energy-saving design of products.

Meanwhile, reducing and mitigating carbon emissions has become an increasingly important research topic for both industry and government. There is little awareness of the issue in developing countries such as Russia and China. Many valuable efforts are undertaken to reduce carbon footprints. However, these initiatives have largely focused on energy-efficient equipment and facilities development, energy sources with less pollution, and energy-saving programs’ implementation [11]. A comprehensive analysis of the energy consumption and CO₂ emissions in Taiwan is presented as well as the government policies and regulatory infrastructure for shifting to a low-carbon society, centering on feasible solutions with renewable energy, energy efficiency, and nuclear power [12]. As for low carbon manufacturing or energy-efficient production, a decision making framework for implementing Environmentally Benign Manufacturing (EBM) based on the Genetic Simulated Annealing Algorithm and low-carbon production based on an IPO (Input-Process-Output) model to improve environmental performance was provided. Another new mathematical programming model of flow shop scheduling problems, considering peak power load, energy consumption, and associated carbon footprint in addition to cycle time, was proposed as well as demonstrated by a simple case study of a flow shop with two machines to produce a variety of parts [13]. An energy-efficient model for flexible flow shop scheduling (FFS) based on an energy-efficient mechanism was proposed to solve multi-objective optimization with an improved, genetic-simulated annealing algorithm to make a significant trade-off between the makespan and the total energy consumption to implement feasible scheduling [14]. Holistic metrics to evaluate the energy efficiency in manufacturing companies, considering the different organization levels of production, such as machine or equipment level, production line level, and factory level, were presented [15]. Traditional production scheduling always considers performance indicators, such as processing time, cost, and quality, as optimization objectives in manufacturing systems, and little consideration is given to environment or energy related objectives. Besides, our literature review also suggests that few researches have considered scheduling for forging enterprises.

The job scheduling for forging can mainly be classified into two types: one is for cutting, forging and machining scheduling, which are similar to traditional machining scheduling, and the other one is for heat treatment scheduling, characterized by forging and heat treatment. Few researches on the latter have been carried out, and have mainly focused on the steel industry. The presented work here seeks to optimize forging scheduling with high energy efficiency and low carbon emissions. In Section 2, the production process and characteristics of DVR enterprise (a famous forging enterprise in China) are investigated and analyzed. Then, the above mentioned two types of forging scheduling problems are discussed in detail in Section 3 and Section 4, respectively. Finally, the conclusions are summarized.

2. Production Investigation and Analysis of DVR Enterprise

The DVR enterprise is mainly composed of a forging workshop, a machining workshop, a heat treatment workshop, a comprehensive workshop and an equipment maintenance workshop as well as a separate quality assurance department. The forging workshop is equipped with eight free forging hammers, including three 5-ton electro-hydraulic hammers, one 3-ton electro-hydraulic hammer, two 1-ton air hammer and two 750-kg air hammers. The machining workshop is equipped with a plurality of machine tools for turning, milling, drilling and planning in order to perform deep forging processing. The heat treatment workshop is configured with eight Ф2000 × 2000 electric furnaces with an annual output of 20,000 tons of forgings.

The DVR enterprise is divided into workshops corresponding to the machining process. Functions of each workshop are listed in Table 1.

Table 1. Functions of departments in DVR.

Department	Component	Functions
Production department	Forging workshop	Forging production, post-forging heat treatment, mold manufacturing and management…
Production department	Machining workshop	Rough machining, secondary machining, mold modification, forgings correction…
Production department	Heat treatment workshop	Normalizing, Quenching, tempering hardness test…
Production department	Comprehensive workshop	Cutting, product packaging, transferring of semi-finished products, outsourcing, raw materials and finished products management.
Service department	equipment maintenance workshop	Equipment management & maintenance
Service department	Process department	Prepare process plan
Service department	Quality assurance department	Inspection and document preparation

Table 1. Functions of departments in DVR.

Department	Component	Functions
Production department	Forging workshop	Forging production, post-forging heat treatment, mold manufacturing and management…
Production department	Machining workshop	Rough machining, secondary machining, mold modification, forgings correction…
Production department	Heat treatment workshop	Normalizing, Quenching, tempering hardness test…
Production department	Comprehensive workshop	Cutting, product packaging, transferring of semi-finished products, outsourcing, raw materials and finished products management.
Service department	equipment maintenance workshop	Equipment management & maintenance
Service department	Process department	Prepare process plan
Service department	Quality assurance department	Inspection and document preparation

The DVR enterprise generally produces two kinds of products: forgings by rotary hammer and rotational die. The forging process is illustrated by a typical production process as shown in Figure 1.

The forging production is normally composed of cutting, forging, machining and heat treatment.

(1)

Cutting. Cutting is the start of production and carried out by the sawing machine. Since steel products are widely used in the enterprise, cutting can be primarily used for assessing cost which is normally expressed by material utilization.

(2)

Forging. It is a critical procedure for production and also the focus of workshop management. The whole production process is mainly organized according to lead time and quality of forgings. The most important step in forgings’ production is the charging, which means forgings shall be reasonably arranged in a heating furnace and heated up to the initial temperature.

(3)

Machining. The machining of forgings is similar to common machining. To ensure individual production and small lot production, universal machine tools are arranged in workshops. Since the machining is not the critical business for a foundry works, the machining is normally outsourced.

(4)

Heat treatment. It is usually the final but a critical procedure in production. The heat treatment could comprise normalizing, annealing, solution treatment, quenching and tempering, and the commonly used treatment is thermal refining (quenching + tempering). The key point of heat treatment is similar to forging (how to arrange the heating furnace). However, the principles behind the arrangement vary greatly.

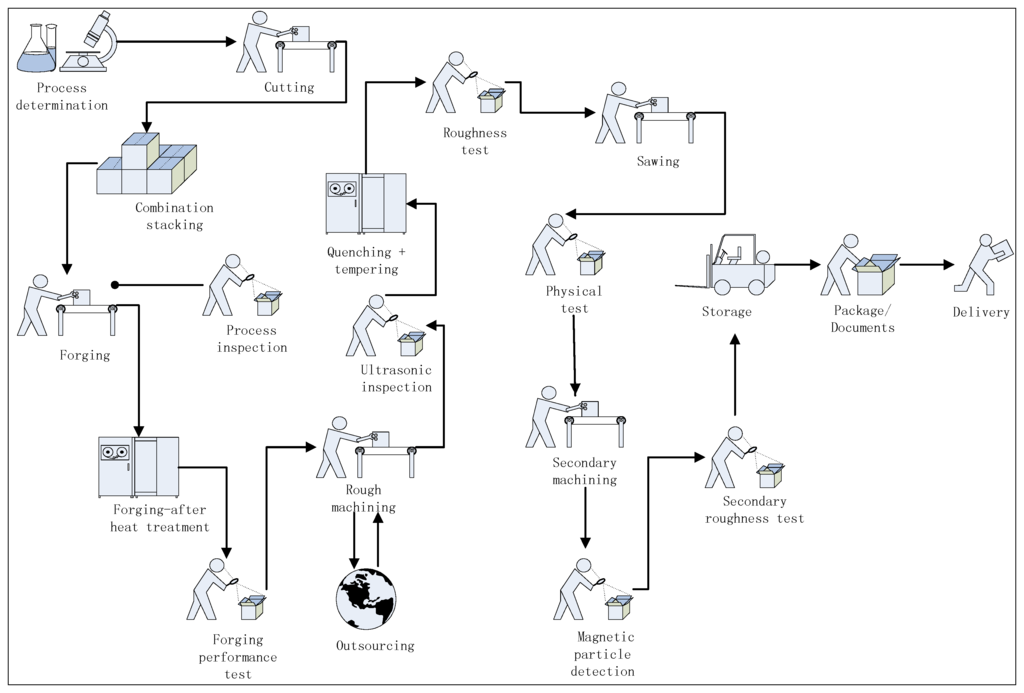
Figure 1. Typical forging production process.

Figure 1. Typical forging production process.

3. Forging Production Scheduling Based on Improved Genetic Algorithm

As with the previous procedure for forging, cutting provides raw material for subsequent production. Overall production is directly affected by the duration of cutting. Cutting and sawing are performed simultaneously, so sawing shall be taken into consideration for cutting scheduling. Currently, job scheduling in DVR is made manually by staff based on experience, resulting in inaccurate production forecasts and low capacity utilization. Moreover, it may take a long time to draw up a schedule. So, it is of great significance to improve production efficiency and machine utilization.

3.1. Scheduling Problem Description

Cutting and sawing are two different procedures, and sawing can be classified as post-forging, post-machining and post-heat treatment sawing. However, both procedures are carried out by sawing machine simultaneously (no order of priority) in the comprehensive workshop. So, job scheduling studied in this paper is simplified by considering cutting and sawing as one machining process (hereinafter both referred to as “cutting”).

Scheduling studied here can be described as follows: There are m sawing machines in a workshop to cut for n types of steel. Each sawing machine can only be used to cut one type of steel at a time. It is assumed that production is constant without interruption. Due to capability limitation of the sawing machine, each type of steel can only be cut on one or several machines within delivery. Thus, the problem stems from the parallel machine job-shop scheduling for a single machining process with particular processing constraints.

Let M_j denote the aggregate of sawing machines available for cutting of workpiece j, and t_ij and d_j denote the processing time and delivery time of workpiece j on sawing machine i from M_j, respectively. So, the following matrix T regarding process time and delivery time can be formed as follows:

$$\text{T}=\left[\begin{array}{ccccc}{\mathrm{t}}_{11}& {\mathrm{t}}_{12}& \dots & t_{1n}& d_1\\ t_{21}& t_{22}& \dots & t_{2n}& d2\\ ⋮& ⋮& & & ⋮\\ t_{m1}& t_{m2}& \cdots & t_{mn}& d_m\end{array}\right]$$

(1)

Once a workpiece is allocated onto a machine for processing, machining cannot halt until completion. A machine can only process one workpiece at a time. Let W_j ($W_j={\displaystyle \sum _{i=1}^m{t}_{ij}}$, m denotes the number of processes/machines) and T_j ($T_j=\max \{W_j-d_j,0\}$) denote completion time and delay of workpiece j, respectively, and μ_j denotes delay penalty coefficient of workpiece j. N = {1, 2, …, n} and M = {1, 2, …, m} denotes the aggregate of steels and aggregate of sawing machines, respectively.

According to the above analysis, the total completion time $H_1={\displaystyle \sum _{j=1}^n{W}_j}$, and the total delay penalty is as follows:

$$H_2={\displaystyle \sum _{j=1}^n{\mu }_j}{T}_j={\displaystyle \sum _{j=1}^n{\mu }_j}\max \{W_j-d_j,0\}$$

(2)

Thus, the scheduling problem can be expressed as follows:

$$f_1=\min {\mathrm{H}}_1$$

(3)

The objective of minimum total completion.

$$f_2=\min {\mathrm{H}}_2$$

(4)

The objective of minimum total delay penalty.

$$s.t.{\displaystyle \sum _{j=1}^m{S}_{ij}=1,i\in N}$$

(5)

$$S_{ij}=\left\{\begin{array}{l}1,\text{if workpiece j is allocated onto machine i for processing}\\ 0,\text{otherwise}\end{array}\right\}i\in N,j\in M$$

(6)

$$t_{ij}\ge 0, if and only if \text{machine} i \text{cannot process workpiece} j,t_{ij}=0$$

(7)

Equations (5) and (6) provide that a machine processes only one workpiece at a time without interruption. Equation (7) provides that each workpiece can only be processed by the machine from M_j.

The scheduling objective here is to allocate n workpieces to m machines under process constraints with the minimum objective function value f_min:

$$f_{min}={\lambda }_1{f}_1+{\lambda }_2{f}_2$$

(8)

For convenient optimization, the multi-objective linear weight method is used to convert the dual-objective problem into single-objective. Assume that ${\lambda }_1=1$ and ${\lambda }_2/{\lambda }_1=\alpha$. Here, $\alpha$ reflects the proportion of constraints of completion time and delivery time in production scheduling. Because the delivery should be strictly followed in enterprise, α should be assigned with a big value, indicating that the delivery time plays an important role in the production cycle. Then, Equation (8) can be converted to:

$$f_{min}=f_1+\alpha f_2$$

(9)

3.2. Coding

Real-number coding is used to code workpieces and machines. Workpiece $x_i(i\in N)$ is coded as $\text{X}= \left[1,\mathrm{2...},n\right]$ and machine $M_j(j\in N)$ as $M_j= \left[01,02,\mathrm{...},m\right]$. Due to the process constraints, a combined code is proposed for individual gene expression as $Z=\left[x_1{y}_1,x_2{y}_1,\mathrm{...},x_i{y}_j,\mathrm{...}\right]$, the length of which is equal to the number n of workpieces to be processed.

Take the chromosome Z = [101,201,301,402,502,603] as an example. It indicates that workpieces 1, 2 and 3 are allocated onto machine 01, workpieces 4 and 5 on machine 02, and workpiece 6 on machine 03.

3.3. Population Initialization

Randomly generate population, the initial size of which is γ, with workpiece gene as (x₁, x₂, …, x_n) (x_i, i ∈ N). For each x_i, randomly select a machine from M_j as the machine for processing it and code this machine as y_i to generate the initial machine gene (y₁, y₂, …, y_n). Then, Z = [x₁y₁, x₂y₂, ..., x_ny_n] is generated. This combination method for initialization provides for population diversity and process constraints between sawing machines and workpieces.

3.4. Genetic Operator

(1)

Selection

Evolutionary algorithms attempt to better select solutions corresponding to their objective values. The selection operator chooses better chromosomes to survive [16]. Individuals are selected by stochastic universal sampling and optimal individual reservation strategy.

(2)

Crossover

a.

Extended order crossover operator is adopted as follows:

b.

Provided two parent individuals for crossover are A and B. Randomly generate k numbers from steels set N = {1, 2, …, n} to form Γ = (Γ₁, Γ₂, …, Γ_k). Amplify Γ_i 100 times to form Ψ = (Ψ₁, Ψ₂, …,Ψ_k) and then select a gene cluster from A to form Z (Z₁, Z₂, …, Z_x) within the interval [Ψ₁,Ψ₁ + 100].

c.

For each gene Z_i, select a gene from B within the interval [Ψ₁,Ψ₁ + 100]. for exchange.

d.

As the above, exchange all Z_i so as to generate two filial generations.

For example, two parent individuals, A and B, are shown in Figure 2. The crossover is as follows:

a.

Randomly generate four numbers 2, 3, 4 and 5 from the aggregate of steels and amplify those numbers 100 times to form Ψ = (200, 300, 400, 500). Then, select genes from parent A within intervals [200,300], [300,400], [400,500] and [500,600], respectively, to form a gene cluster Z = (202, 301, 403, 502) (see the hatched section in Figure 2).

b.

For each gene Z_i in the cluster (take the gene Z_i = {202} as an example), select a gene {203} from B within the interval [200,300] and exchange them.

c.

Follow the above method to replace the gene cluster Z = (202, 301, 403, 502) to Z’ = (203, 302, 404, 501) so as to generate two filial generations A’ and B’.

(3)

Mutation

The heuristic insert mutation is adopted to better ensure population diversity and individual qualities after mutation as well as satisfy the process constraints. The procedures are as follows: randomly select a gene for mutation and then insert each machine number from the M_j (but excluding the gene for mutation) to replace the original to generate a plurality of individuals. Select the best one as filial generation.

Figure 2. Crossover illustration.

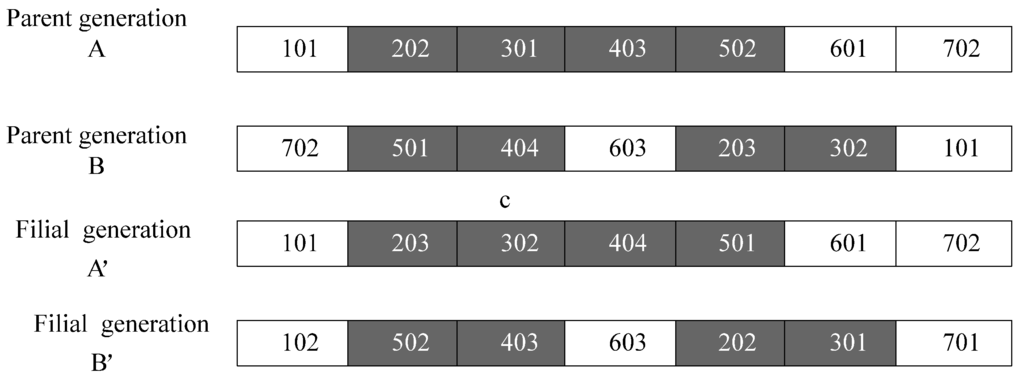
Figure 2. Crossover illustration.

Take the gene cluster A as an example to demonstrate mutation. The aggregate of sawing machines applicable to the gene Z_i = {202} is M_j = {1, 2, 3}. So, the gene clusters after variation are A1 and A2 (see Figure 3).

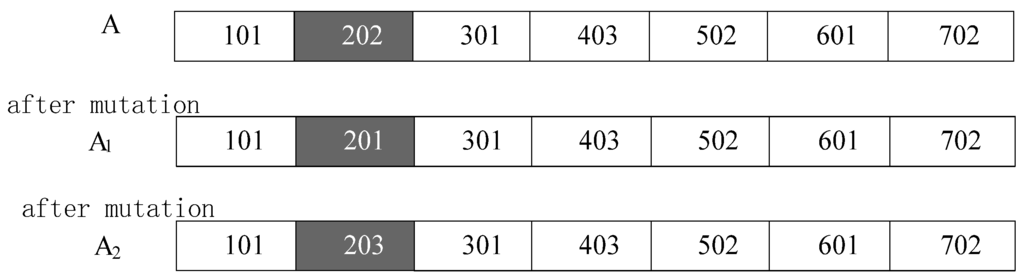
Figure 3. Mutation illustration.

Figure 3. Mutation illustration.

3.5. Case Study

Currently, in the comprehensive workshop there are 15 sawing machines which are classified into five types according to the type of steel ingot to be processed. Meanwhile, the specifications of workpieces to be machined are not fixed. So, according to the production characteristics of DVR, workpieces can be classified into 10 types by size, as shown in Table 2.

Table 2. Steel Classification for Cutting/Sawing.

No.	Size	No.	Size
1	12” ingot and 14” ingot	6	Φ200 less, □200 less
2	17” ingot	7	Φ200~Φ300, □200–□300
3	22” ingot	8	Φ300~Φ500, □300–□500
4	24” ingot	9	Φ500~Φ650, □500–□650
5	26” and bigger ingots	10	Φ650~Φ800, □650–□800

Note: the size refers to the dimension of raw material or section bar. For example, 12” represents the 12 inches ingot; Φ200 represents the round steel, dimension of which is Φ200; and □200 represents the square steel, the cross section of which is 200 × 200.

Table 2. Steel Classification for Cutting/Sawing.

No.	Size	No.	Size
1	12” ingot and 14” ingot	6	Φ200 less, □200 less
2	17” ingot	7	Φ200~Φ300, □200–□300
3	22” ingot	8	Φ300~Φ500, □300–□500
4	24” ingot	9	Φ500~Φ650, □500–□650
5	26” and bigger ingots	10	Φ650~Φ800, □650–□800

Note: the size refers to the dimension of raw material or section bar. For example, 12” represents the 12 inches ingot; Φ200 represents the round steel, dimension of which is Φ200; and □200 represents the square steel, the cross section of which is 200 × 200.

The number of workpieces to be processed is not fixed, but is normally within 15–20. In this paper, it is assumed for algorithm simulation that five machines are used to process 15 types of workpieces.

The number of workpiece types each machine can process and the time required for processing are given in Table 3, wherein machine numbers are listed transversally (columns 2–5) and product numbers are listed vertically. If the value in a cross cell is not zero, it means the corresponding machine can process this product and the value indicates the production time. Otherwise, it means the corresponding machine cannot process this product. The delivery time of each product is listed in the last column.

Table 3. Production time and delivery time of each workpiece.

No.	1	2	3	4	5	Delivery Time
1	8.5	8.2	8.5	0	0	15.5
2	5	0	0	0	0	12.5
3	7.4	7.2	0	0	0	10
4	0	0	0	3.4	3.6	12
5	6	5.7	0	0	0	4
6	10.7	10.2	10.3	0	0	18.5
7	0	0	0	4.2	4.5	20
8	0	0	5.5	5.6	5.9	8
9	0	0	4.5	4.8	4.9	14.5
10	5.2	5.2	0	0	0	17
11	0	0	5.7	5.4	5.6	5.5
12	0	9.7	9.4	0	0	13.6
13	4.5	4.8	4.7	0	0	17
14	5.6	5.9	0	0	0	7.5
15	0	0	0	3.3	3.7	20.5

Table 3. Production time and delivery time of each workpiece.

No.	1	2	3	4	5	Delivery Time
1	8.5	8.2	8.5	0	0	15.5
2	5	0	0	0	0	12.5
3	7.4	7.2	0	0	0	10
4	0	0	0	3.4	3.6	12
5	6	5.7	0	0	0	4
6	10.7	10.2	10.3	0	0	18.5
7	0	0	0	4.2	4.5	20
8	0	0	5.5	5.6	5.9	8
9	0	0	4.5	4.8	4.9	14.5
10	5.2	5.2	0	0	0	17
11	0	0	5.7	5.4	5.6	5.5
12	0	9.7	9.4	0	0	13.6
13	4.5	4.8	4.7	0	0	17
14	5.6	5.9	0	0	0	7.5
15	0	0	0	3.3	3.7	20.5

The set of machines available to each workpiece and corresponding production time can be easily found in this table. The size of the initial population is 50, the crossover probability is 0.75, the mutation probability is 0.25 and the end condition is 30th generation. To ensure the delivery time, the penalty coefficient α is set as 0.7.

After GA optimization, the optimal individual is: [502,1104,1401,302,405,1203,904,705,603,201,102,805,1001,1303,1504].

The arrangement of workpieces for machining is as shown in Table 4.

Table 4. Production schedule after GA optimization.

No. (Machine)	No. (Workpiece)	No. (Machine)	No. (Workpiece)
1	14, 2, 10, 13	4	11, 9, 15
2	5, 3, 1	5	4, 7, 8
3	12, 6

Table 4. Production schedule after GA optimization.

No. (Machine)	No. (Workpiece)	No. (Machine)	No. (Workpiece)
1	14, 2, 10, 13	4	11, 9, 15
2	5, 3, 1	5	4, 7, 8
3	12, 6

According to Table 3 and Table 4, the machining time of each sawing machine is shown in Figure 4. It can be seen from Figure 4 that as for optimal individuals, most workpieces are processed on machines within shortest production time. It indicates each machine runs at maximum capacity. Meanwhile, since the sizes of machines 1, 2 and 3 are bigger, their total work hours are longer than sawing machines 4 and 5 with smaller size. The result is consistent with actual job-shop production. The working hours of sawing machines 1, 2 and 3 are almost the same, indicating the production has been balanced. It shows that the proposed scheduling based on improved GA can satisfy the scheduling objectives and fit actual production in DVR. From the generalized view of energy saving and sustainability, the minimum production time means less machine operation time and, furthermore, less power consumption.

Figure 4. Production time diagram for sawing machine.

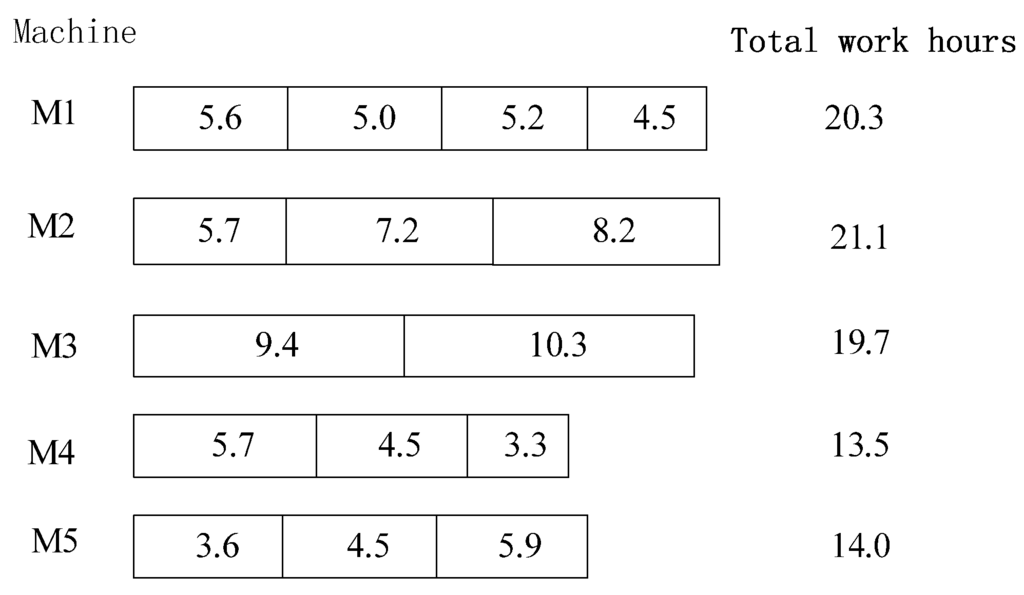
Figure 4. Production time diagram for sawing machine.

4. Stacking Combination Optimization for Free Forging

4.1. Stacking Problems Description

The purpose of stacking combinations is to cluster workpieces by certain rules and stack them into one furnace. The constraints for stacking are analyzed as follows:

(1)

The height of piled up material shall not exceed maximum height of furnace. Workpieces shall be stacked within effective heating area.

(2)

Workpieces stacked in one furnace should be easily distinguished by weights and specifications. Workpieces with similar specifications shall not be stacked into one furnace. If they have to be stacked into a furnace, label them with marks.

(3)

Workpieces with the same material and production batch number shall be stacked into one furnace as far as possible.

(4)

Workpieces with different kinds of material can be stacked into one furnace if heating process permits. However, stacking workpieces with the same specification but different kinds of materials shall be strictly prohibited.

(5)

Ingot shall be placed around 200 mm away from bottom and wall and at least 200 mm away from other ingots.

(6)

Mixing cold ingot with hot ingot is strictly prohibited. Unless otherwise specified, use minimum values for stacking temperature, heating temperature and heating rate (which means to follow the heating regulations for cold ingot).

The following definitions are presented before describing the stacking combination:

(1)

Maximum stacking coefficient η

The maximum stacking coefficient refers to the ratio between total material weights in the furnace and theoretical upper limit (10T), indicated by η = Σ/Ω.

(2)

Deviation coefficient ε

The difference between total material weights of a furnace and the corresponding upper limit of heating curve is called as the deviation coefficient for one single stacking plan ε = Σ−Ω’ (here, Σ denotes total material weights of a furnace and Ω’ denotes theoretical maximum weight set by heating curve corresponding to Σ).

(3)

Deviation ratio ζ

The deviation ratio ζ = ∣Ω’−Σ∣/Σ, which refers to the ratio between deviation coefficient and actual stacking. It can reflect whether the stacking is reasonable. The purpose of stacking combination optimization is to minimize ζ or control ζ within a reasonable range.

The stacking combination can be classified as a large-scale combination optimization problem which can be solved in two steps:

• Classify the material to be forged according to process and specifications. The material classified into a same type can be combined together for heating. A dynamic clustering method is proposed in this paper to realize automatic material classification based on stacking rules.
• For materials which can be combined, optimize the piling up according to the heating process curve, which is fundamental to increasing yield, saving energy for low-carbon production and increasing profit.

4.2. Dynamic Clustering for Forgings

Before dynamic clustering for forgings, an information model of forgings shall be created first, which can be expressed as W= {w₁, w₂, …,w_n}, representing all forgings to be classified (in W, indicating the number of forgings to be classified). w_i = (w_i1, …, w_ik, …, w_im) (i = 1, 2, …, n) represents the parameters set used to describe the forgings for classification (wherein m represents the number of characters’ parameters).

(1)

Normalization

As to characteristic parameters of forgings, since dimensions of parameters are different from each other, the influence of dimensions on clustering shall be eliminated before dynamic clustering in order to normalize data and thus facilitate analysis and comparison. This process is called normalization. The following equations are used for normalization:

a.

For indexes where the smaller, the better,

$$w_{ik}^{\prime }=\frac{w_{k\max }-w_{ik}}{w_{k\max }-w_{k\min }}$$

(10)

b.

For indexes where the bigger, the better,

$$w_{ik}^{\prime }=\frac{w_{ik}-w_{k\min }}{w_{k\max }-w_{k\min }}$$

(11)

where $i=1,2,\mathrm{..},n, k=1,2,\mathrm{..},m$ and x_kmax, x_kmin represent maximum and minimum of $\left\{w_{1k},w_{2k},\mathrm{...},w_{nk}\right\}$, respectively.

The index which is the smaller the better is to classify forgings with small differences of features into one type, and vice versa. For convenience, the index w_ik′ after normalization is still denoted by w_ik.

(2)

Determination of similarity coefficient

The second step is to determine the similarity degree among forgings which is called the similarity coefficient. Let r_ij ∈ [0,1] be used to represent the similarity coefficient between elements w_i and w_j. If r_ij = 0, w_i is entirely different from w_j without similarity. If r_ij = 1, they are completely similar to or same with each other. When i = j, r_ij is identically equal to 1. The normalized w_ik is used to determine r_ij.

r_ij can be determined by Euclidean distance dot product, max-min and geometrical average minimum. The Euclidean distance method not only can compare the differences in overall respect, but can indicate the area with great differences, and has a high accuracy and maneuverability. The most important is the index below used to calculate the similarity of forgings that can be considered with the same weight. So, the Euclidean distance here is adopted.

$$r_{ij}=1-\frac{1}{C}\sqrt{\frac{1}{n}{\displaystyle \sum _{k=1}^m{(x_{ik}-x_{jk})}^2}}$$

(12)

where $\sqrt{\frac{1}{n}{\displaystyle \sum _{k=1}^m{(x_{ik}-x_{jk})}^2}}=D_{ij}$ is called as Euclidean distance, and C is a constant. To enable $r_{ij}$ to fall within the interval [0,1], normally C ≧ max (D_ij).

According to the above computation, for a set X with capacity n, an n × n matrix can be obtained.

$$R={(r_{ij})}_{n\times n}=\left[\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1n}\\ r_{21}& r_{22}& \cdots & r_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ r_{n2}& r_{n2}& \cdots & r_{nn}\end{array}\right]$$

(13)

According to Equations (12) and (13), the matrix R also meets:

a.

Reflexivity. That is $\forall i,r_{ii}=1$.

b.

Symmetry. That is $\forall i,\forall j,r_{ij}=r_{ji}\in [0,1]$.

c.

For clustering, the abovementioned matrix R has to be transformed to an equivalent matrix in order to enable transitivity within the matrix [17].

Provided X is a set comprising n objects to be classified and R is the fuzzy similar matrix of X, it can be proven that there must exist a natural number p ≤ n − 1, which satisfies $R*=R^P=\mathrm{R}°\mathrm{R}°\mathrm{...}\mathrm{R}°$, and R* is called the transitive closure of R. In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R⁺ on set X such that R⁺ contains R and R⁺ is minimal. $R^{+}=\underset{i=\{1,2,\mathrm{3...}\}}{{\displaystyle \mathrm{U}}}{\mathrm{R}}^{\mathrm{i}}$ where ${\mathrm{R}}^{\mathrm{i}}$ is the i-th power of R, defined inductively by ${\mathrm{R}}^1=\mathrm{R}$ and for i > 0, ${\mathrm{R}}^{\mathrm{i}+1}=\mathrm{R}°{\mathrm{R}}^{\mathrm{i}}$ ($°$ denotes composition of relations) [18]. R* can be constructed by square self-synthesis method [19]. The square self-synthesis method is logical operation. The elements of ${\mathrm{R}}^2$ can be calculated as follows:

$${r_{ij}}^{(2)}=\underset{k=1}{\overset{m}{\vee }}(r_{ik}\wedge r_{kj})(\vee :logical addition operation; \wedge : logical multiplication operation)$$

(14)

(3)

Determination of λ

The final step is to decide λ within the interval [0,1] according to clustering granular. If r_ij ≥ λ, then r_ij is replaced with 1, and otherwise, replaced with 0. Since R is a symmetrical matrix, corresponding Boolean matrix R_λ can be obtained. In R_λ, if r_ij (λ) (i ≠ j) is equal to 1, then w_i and w_j can be clustered into one type. Therefore, various classifications can be obtained with different λ.

4.3. Stacking Optimization

4.3.1. Problem Analysis of Stacking Optimization

Once forgings are classified based on dynamic clustering, forgings with the same type have to be stacked in a defined sequence. Stacking optimization shall be considered together with heating curves for forgings. The heating time for each batch is determined by the heating curve shown in Table 5.

Table 5. Heating curves for typical steel ingots.

Material	Weight or Ingot Size
	2400kg or More Octagon Ingot	2400–1200kg 22” Ingot
20, 35, 45, Q235 (A3), A105, Q345 16Mn, 16MnD, 30Mn

Note: the heating process includes three stages. Stage ① is heat preservation, stage ② is heat up and stage ③ is heat equalizing.

Table 5. Heating curves for typical steel ingots.

Material	Weight or Ingot Size
	2400kg or More Octagon Ingot	2400–1200kg 22” Ingot
20, 35, 45, Q235 (A3), A105, Q345 16Mn, 16MnD, 30Mn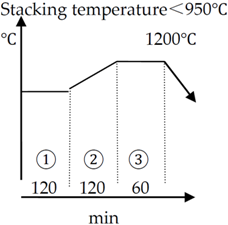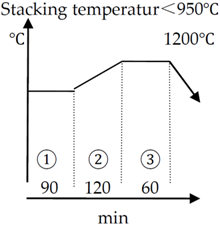

Note: the heating process includes three stages. Stage ① is heat preservation, stage ② is heat up and stage ③ is heat equalizing.

As seen from heating curves, the heating curve of different material and weight of steel varies. The weight can greatly affect the heating time. According to heating curves in Table 5, the curves are sectioned according to gross weight of steel. Based on the study on annealing and hot rolling in the steel industry, once the gross weight of steel for heating is increased by 5 tons, the heating curve shall be changed and the corresponding heating time has to be extended by half an hour. Because either the weight or the size of steel varies in practice, the gross weight of steel in one production plan would vary within a certain range. For example, if the gross weight is equal to or smaller than 3 tons, the heating time is 19 hours. If the gross weight is bigger than 3 tons but smaller than or equal to 4 tons, the heating time changes to 19.5 hours. According to the above mentioned process specification, it can be obviously seen that the heating time and the consumed resource are the same for steel to be heated with gross weight within 3–4 tons. Therefore, in order to optimize the stacking, the stacked weight each time shall be scheduled close to 4 tons (not 4.1 tons) in one production plan. In order to increase production efficiency and reduce energy consumption for low-carbon production, the stacked weight of steel each time scheduled in one plan shall be as close to the upper limit as possible, not the lower limit of boundary in the heating curve.

Meanwhile, stacking is also limited by the heating area in the furnace. So, the heating area can be used to convert the furnace capacity into forgings weight. During staking, the furnace capacity shall be maximized. That is, to make the gross weight of forgings as close to the maximum capacity as possible.

4.3.2. Mathematic Model for Stacking Optimization

Stacking optimization of forgings has not been broadly studied. Because stacking for forgings is very similar to the charging of the steel industry, stacking optimization can be considered a discrete combination optimization problem.

Provided the forgings for stacking are $\alpha =[{\alpha }_1,{\alpha }_{2,\mathrm{...},}{\alpha }_n]$ (n refers to the number of forgings and $\alpha$ refers to the aggregate of forgings to be stacked in one furnace after clustering, illustrated in 4.4) and the weight set $\omega =[{\omega }_1,{\omega }_2,\mathrm{...},{\omega }_n]$ (ω_i refers to the unit weight of forgings α_i). The number of forgings α_i is θ_j ($\theta =[{\theta }_1,{\theta }_2,\mathrm{...},{\theta }_n]$ is a number set). So, the total stacked gross weight of forgings is:

$$\Pi =[{\omega }_1,{\omega }_2,\mathrm{...},{\omega }_n]\times \left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ \begin{array}{l}{\theta }_3\\ \mathrm{...}\end{array}\\ {\theta }_n\end{array}\right]$$

(15)

(1)

Selection of heating furnace

The first step for stacking optimization is to select the heating furnace. Because the number of furnaces is limited and the heating can generate a lot of waste heat, the capacity of the heating furnace shall be considered when drawing up a process. Usually, the number of selected heating furnaces k can be obtained by using the following equation according to practical experience.

$$k=\text{Int}(\Pi /(7000{\lambda }^{\prime }))$$

(16)

Where $\Pi$ is the total weight of forgings to be stacked in a plan and ${\lambda }^{\prime }$ is the coefficient of difficulty. For forging with complicated shapes, assign a value >1 for ${\lambda }^{\prime }$, otherwise assign a value <1.

(2)

Objective function

The object of stacking optimization is to make the gross weight of each stacking as close to the upper limit of the theoretical heating curve as possible. Therefore, the following mathematical optimization model can be proposed:

$$f=\frac{1}{N}{\displaystyle \sum _{i=1}^N({\overline{x}}_i-x_i)}$$

(17)

where f refers to the average difference between gross weight of each stacking and the theoretical value set by corresponding heating curve and is also called the average deviation coefficient; N refers to the number of stackings to be optimized; x_i refers to the gross weight of forgings in each stacking; and ${\overline{x}}_i$ refers to theoretical weight set by heating curve corresponding to x_i.

The objective is to minimize the average deviation coefficient and ensure the stacked gross weight of each schedule is as close to the upper limit of the boundary in the heating curve with the shortest total heating time and highest production efficiency.

(3)

Constraints

The number of forgings a furnace can heat is limited. Since either the shape or size of forging varies greatly, it is very difficult to work out a reasonable stacking capacity of a furnace. To simplify the computation, the capacity constraint can be converted into the limitation on weight of forgings based on practical experiences. Since the stacking shall be considered comprehensively in the forging process and in the utilization of waste heat, usually the gross weight of forgings for each stacking is less than 4 tons. Therefore, constraint for selection can be expressed as: $x_i\le 8000\text{ \& }{\overline{x}}_i=\{5,6,7,8\}$.

This can increase the computation speed and fits for practical production of DVR.

(4)

Optimization

Step 1: Input unit weight matrix of forgings $\omega =[{\omega }_1,{\omega }_2,\mathrm{...},{\omega }_n]$ and a number set $\theta =[{\theta }_1,{\theta }_2,\mathrm{...},{\theta }_n]$.

Step 2: For each element θ_i, randomly assign a value within interval from 0 to θ_i and record as τ_i.

Form a new matrix $\tau =[{\tau }_1,{\tau }_2,\mathrm{...},{\tau }_n]$ (n refers to the total number of forgings and τ_i indicates the number of workpieces actual scheduled).

Step 3: calculate the weight of forgings scheduled for each stacking.

$$x_i=[{\omega }_1,{\omega }_2,\mathrm{...},{\omega }_n]\times \left[\begin{array}{c}{\tau }_1\\ {\tau }_2\\ {\tau }_3\\ {\tau }_4\end{array}\right]$$

(18)

Compare x_i with the theoretical weight set using the heating curve to obtain the absolute difference, namely the average deviation coefficient f. Then, update $\theta =[{\theta }_1-{\tau }_1,{\theta }_2-{\tau }_2,\mathrm{...},{\theta }_n-{\tau }_n]$.

Step 4: set end condition for iteration. In case of satisfying the condition, complete the iteration, otherwise return to Step 2. T_{n × k} matrix can be obtained.

$$T=\left[\begin{array}{cccc}{t}_{11}& t_{12}& \cdots & t_{1k}\\ t_{21}& t_{22}& \cdots & t_{2k}\\ ⋮& ⋮& ⋮& ⋮\\ t_{n1}& t_{n2}& \cdots & t_{nk}\end{array}\right]$$

(19)

where t_ij (i = 1, 2, …, n, j = 1, 2, …, k) refers to the number of workpieces i piled up in furnace j, n is the total number of forgings, k is the number of heating furnaces, and Matrix T refers to the stacking combination matrix.

4.4. Case Study

According to stacking rules analyzed in Section 4.2, feature parameters are investigated as shown in Table 6. “↑” is used to indicate the bigger the better and “↓” indicates the smaller the better.

Table 6. Parameters for forgings.

No.	Forging Tonnage (T)↑	Initial Temperature (°C)↓	Weight (kg)↑	Number of Heat (Times)↓	Stacking Temperature (°C)↓
1	5	1100	300	1	1200
2	3	1200	500	1	900
3	3	1100	400	1	1200
4	5	1100	500	2	1200
5	5	1100	400	2	900
6	5	1200	500	2	1200
7	5	1200	300	2	900
8	5	1200	500	1	1200
max	5	1200	500	2	1200
min	3	1100	300	1	900

Table 6. Parameters for forgings.

No.	Forging Tonnage (T)↑	Initial Temperature (°C)↓	Weight (kg)↑	Number of Heat (Times)↓	Stacking Temperature (°C)↓
1	5	1100	300	1	1200
2	3	1200	500	1	900
3	3	1100	400	1	1200
4	5	1100	500	2	1200
5	5	1100	400	2	900
6	5	1200	500	2	1200
7	5	1200	300	2	900
8	5	1200	500	1	1200
max	5	1200	500	2	1200
min	3	1100	300	1	900

(1)

After being normalized, we can get

$${(w_{ik})}_{8\times 5}=\left|\begin{array}{ccccc}1& 1& 0& 1& 0\\ 0& 0& 1& 1& 1\\ 0& 1& 0.5& 1& 0\\ 1& 1& 1& 0& 0\\ 1& 1& 0.5& 0& 1\\ 1& 0& 1& 0& 0\\ \begin{array}{l}1\\ 1\end{array}& \begin{array}{l}0\\ 0\end{array}& \begin{array}{l}0\\ 1\end{array}& \begin{array}{l}0\\ 1\end{array}& \begin{array}{l}1\\ 0\end{array}\end{array}\right|$$

(20)

(2)

Obtain similar matrix

Calculate the Euclidean distance.

$${\mathrm{D}}_{11}=\sqrt{\frac{1}{n}{\displaystyle \sum _{k=1}^m{(w_{ik}-w_{jk})}^2}}=0$$

(21)

$${\mathrm{D}}_{12}=\sqrt{\frac{1}{n}{\displaystyle \sum _{k=1}^m{(w_{ik}-w_{jk})}^2}}=\sqrt{\frac{1}{8}{\displaystyle \sum _{k=1}^5{(w_{1k}-w_{2k})}^2}}=\sqrt{\frac{1}{8}(1^2+1^2+{(-1)}^2+0^2+{(-1)}^2)}=0.707$$

(22)

Calculate in the same way to obtain similar matrix:

$$D={(D_{ij})}_{8\times 8}=\left|\begin{array}{cccccccc}0& 0.707& 0.395& 0.500& 0.530& 0.612& 0.612& 0.5\\ 0.707& 0& 0.530& 0.707& 0.637& 0.612& 0.612& 0.5\\ 0.395& 0.530& 0& 0.530& 0.612& 0.637& 0.612& 0.530\\ 0.500& 0.707& 0.530& 0& 0.395& 0.354& 0.612& 0.5\\ 0.530& 0.637& 0.612& 0.395& 0& 0.530& 0.395& 0.637\\ 0.612& 0.612& 0.637& 0.354& 0.530& 0& 0.5& 0.637\\ 0.612& 0.612& 0.612& 0.612& 0.395& 0.5& 0& 0.612\\ 0.5& 0.5& 0.530& 0.5& 0.637& 0.637& 0.612& 0\end{array}\right|$$

(23)

Assign C = 1 and then

$$R={(r_{ij})}_{8\times 8}=\left|\begin{array}{cccccccc}1& 0.293& 0.605& 0.500& 0.470& 0.388& 0.388& 0.5\\ 0.293& 1& 0.470& 0.293& 0.363& 0.388& 0.388& 0.5\\ 0.605& 0.470& 1& 0.470& 0.388& 0.363& 0.388& 0.470\\ 0.500& 0.293& 0.470& 1& 0.650& 0.646& 0.388& 0.5\\ 0.470& 0.363& 0.388& 0.650& 1& 0.470& 0.605& 0.363\\ 0.388& 0.388& 0.363& 0.646& 0.470& 1& 0.5& 0.363\\ 0.388& 0.388& 0.388& 0.388& 0.605& 0.5& 1& 0.388\\ 0.5& 0.5& 0.470& 0.5& 0.363& 0.363& 0.388& 1\end{array}\right|$$

(24)

(3)

Forgings classification (clustering)

$$R^8=R^4=\left|\begin{array}{cccccccc}1& 0.500& 0.605& 0.500& 0.500& 0.500& 0.500& 0.500\\ 0.500& 1& 0.500& 0.500& 0.500& 0.500& 0.500& 0.500\\ 0.605& 0.500& 1& 0.500& 0.500& 0.500& 0.500& 0.500\\ 0.500& 0.500& 0.500& 1& 0.650& 0.646& 0.605& 0.500\\ 0.500& 0.500& 0.500& 0.650& 1& 0.646& 0.605& 0.500\\ 0.500& 0.500& 0.500& 0.646& 0.646& 1& 0.605& 0.500\\ 0.500& 0.500& 0.500& 0.605& 0.605& 0.605& 1& 0.500\\ 0.500& 0.500& 0.500& 0.5& 0.500& 0.500& 0.500& 1\end{array}\right|$$

(25)

Forgings are classified into different clusters according to different λ.

If λ > 0.650,

$$R={(r_{ij})}_{8\times 8}=\left|\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ & 1& 0& 0& 0& 0& 0& 0\\ & & 1& 0& 0& 0& 0& 0\\ & & & 1& 0& 0& 0& 0\\ & & & & 1& 0& 0& 0\\ & & & & & 1& 0& 0\\ & & & & & & 1& 0\\ & & & & & & & 1\end{array}\right|$$

(26)

Just as seen from R, forgings are classified into eight clusters.

If 0.646 < λ ≤ 0.650, forgings are classified into seven clusters: (04, 05), 01, 02, 03,06,07,08.

If 0.605 < λ ≤ 0.646, forgings are classified into six clusters: (04, 05, 06), 01, 02, 03, 07, 08.

If 0.5 < λ ≤ 0.605, forgings are classified into four clusters: (01, 03), 02, (04, 05, 06, 07), 08.

If λ ≤ 0.5, all forgings can be put into the same class.

(4)

Stacking optimization

In most of the literature on heating scheduling for the steel industry, more sophisticated optimization algorithms were adopted. In the presented work, clustering of forgings enables a batch of forgings to be more regularly optimally stacked. Therefore, calculations are greatly reduced in order more easily and quickly find solutions to stacking optimization.

Select 0.5 < λ ≤ 0.605 for stacking optimization and forgings are classified into four clusters: (01, 03), 02, (04, 05, 06, 07), 08. With consideration of the stacking constraints mentioned in Section 4.1, the stacking tasks are combined by the workshop director according to his practical experience as (01, 03, 04, 05, 06, 07), shown in Table 7. So, the $\alpha =[{\alpha }_1,{\alpha }_{2,\mathrm{...},}{\alpha }_n]$ in Section 4.3.2 is $\alpha =[{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6]$. The ${\alpha }_1$ denotes the No. 01 forging task, ${\alpha }_2$ as No. 03, ${\alpha }_3$ as No. 04, ${\alpha }_4$ as No. 05, ${\alpha }_5$ as No. 06 and ${\alpha }_6$ as No. 07.

Table 7. Stacking after clustering.

No.	Unit Ingot Weight (kg)	Quantity
1	310	25
3	518	10
4	415	15
5	520	5
6	309	20
7	516	26

Table 7. Stacking after clustering.

No.	Unit Ingot Weight (kg)	Quantity
1	310	25
3	518	10
4	415	15
5	520	5
6	309	20
7	516	26

Then, ω = [310,518,415,520,309,516] and θ = [25,10,15,5,20,26], so the total weight of forgings Π = 41351.

Let coefficient of difficulty ${\lambda }^{\prime }$ = 1.

$$k=Int(\Pi /(7000{\lambda }^{\prime }))=Int(41351/7000)=6$$

(27)

To reduce the number of iterations and increase the computation efficiency, set deviation coefficient <10% as the end condition. Thus, the stacking combination matrix can be obtained.

$$T=\left[\begin{array}{cccccc}25& 0& 0& 0& 0& 0\\ 0& 10& 6& 0& 0& 0\\ 0& 0& 9& 5& 5& 0\\ 0& 0& 0& 0& 15& 2\\ 0& 0& 0& 0& 0& 11\\ 0& 0& 0& 0& 0& 13\end{array}\right]$$

(28)

According to matrix T, we can obtain the forging No. and quantities piled up in each furnace, as shown in Table 8.

Table 8. Stacking plan after optimization.

Furnace No.	Forging No.	Quantity	Gross Weight (T)	Deviation from Theoretical Value (T)	Average Difference f (%)
1	1	25	7.75	0.25	3.23
2	03, 04	10, 6	7.67	0.33	4.3
3	04, 05, 06	9, 5, 5	7.8	0.2	2.56
4	06, 07	15, 2	5.667	0.333	4.26
5	7	11	5.632	0.368	6.53
6	7	13	6.708	0.282	4.2

Table 8. Stacking plan after optimization.

Furnace No.	Forging No.	Quantity	Gross Weight (T)	Deviation from Theoretical Value (T)	Average Difference f (%)
1	1	25	7.75	0.25	3.23
2	03, 04	10, 6	7.67	0.33	4.3
3	04, 05, 06	9, 5, 5	7.8	0.2	2.56
4	06, 07	15, 2	5.667	0.333	4.26
5	7	11	5.632	0.368	6.53
6	7	13	6.708	0.282	4.2

Take #3 furnace as an example: 04, 05 and 06 workpieces are arranged for heating #3 furnace, the number of which is 9, 5 and 5, respectively. The deviation from the theoretical value is 0.2 and the deviation coefficient is 2.56%.

5. Conclusions

(1)

The presented work focuses on two types of scheduling for a forging enterprise. One is for cutting and machining scheduling, which is similar to traditional machining scheduling, and the other is for forging and heat treatment scheduling, characterized by stacking and heat treatment.

(2)

Dynamic clustering is proposed for forging combination before stacking optimization. The forgings to be optimized are clustered according to certain rules, which can greatly reduce the computations required in stacking optimization in order to more easily obtain a solution.

(3)

In reality, the production manager judges different forgings based on empirical criteria. This empirical standard is generally difficult to portray. In the fuzzy clustering analysis, λ (0 < λ < 1) is utilized to indicate the empirical criteria. The clustering results vary with λ, resulting in various heating plans with different production efficiency, energy consumption and carbon emissions.

(4)

The proposed stacking optimization involves ensuring the gross weight of forgings is as close to the maximum batch capacity as possible.

The proposed schedule for the forging enterprise here comprehensively considers forging clustering (combination) and stacking optimization, which can reduce the heating times, and increase the furnace utilization with high efficiency and low carbon emissions.