Wave Climate Resource Analysis Based on a Revised Gamma Spectrum for Wave Energy Conversion Technology
Abstract
:1. Introduction
2. Omnidirectional Wave Spectral Models
3. Methodology for Estimating the Available Wave Energy Resource
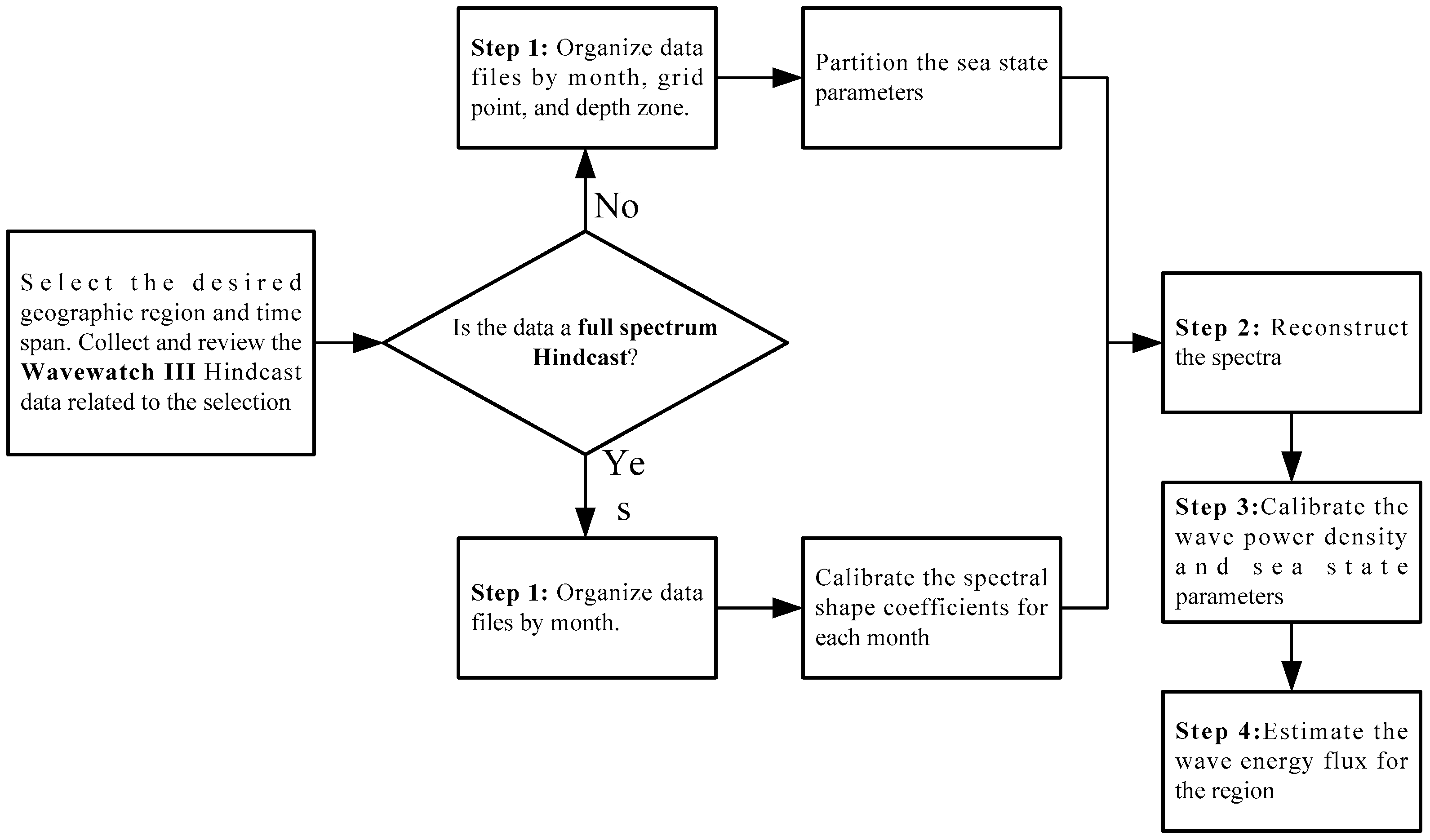
3.1. Preprocess WaveWatch III Multi-Partition Hindcast of Sea State Parameters
3.1.1. Calculating Nondirectional Spectrum from Directional Spectrum
3.1.2. Calculating the Spectral Moments from the Nondirectional Spectrum
3.1.3. Organizing the Directional Data
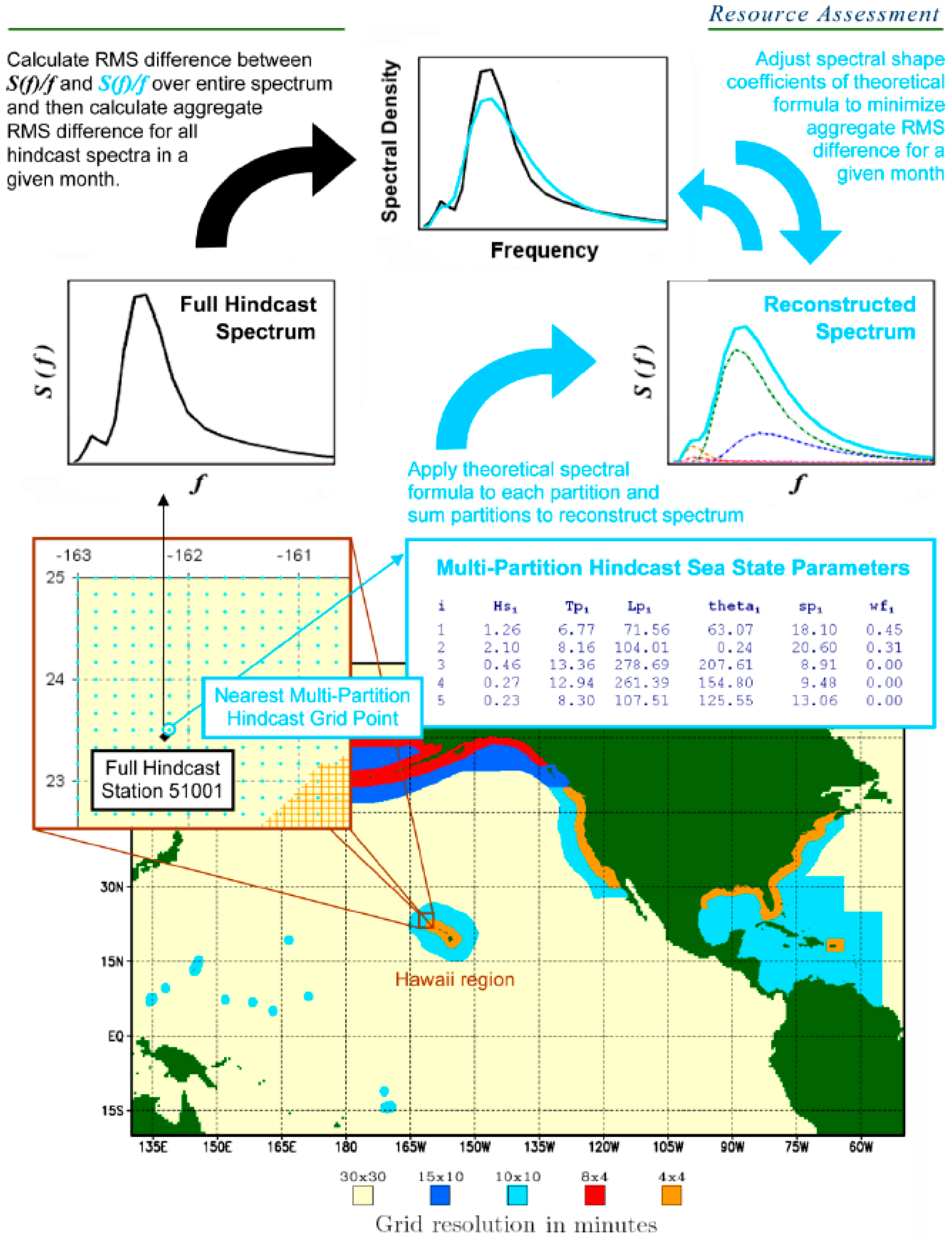
3.2. Calibrate the Spectral Shape Coefficients
3.2.1. Theoretical Gamma Spectral Formulation
3.2.2. Calibrating n and γ for Use in the Gamma Spectra
3.3. Reconstructing the Overall Spectra
3.4. Calculate Overall Sea State Parameters and Wave Power Density
3.5. Estimating the Total Wave Energy along a Depth Contour
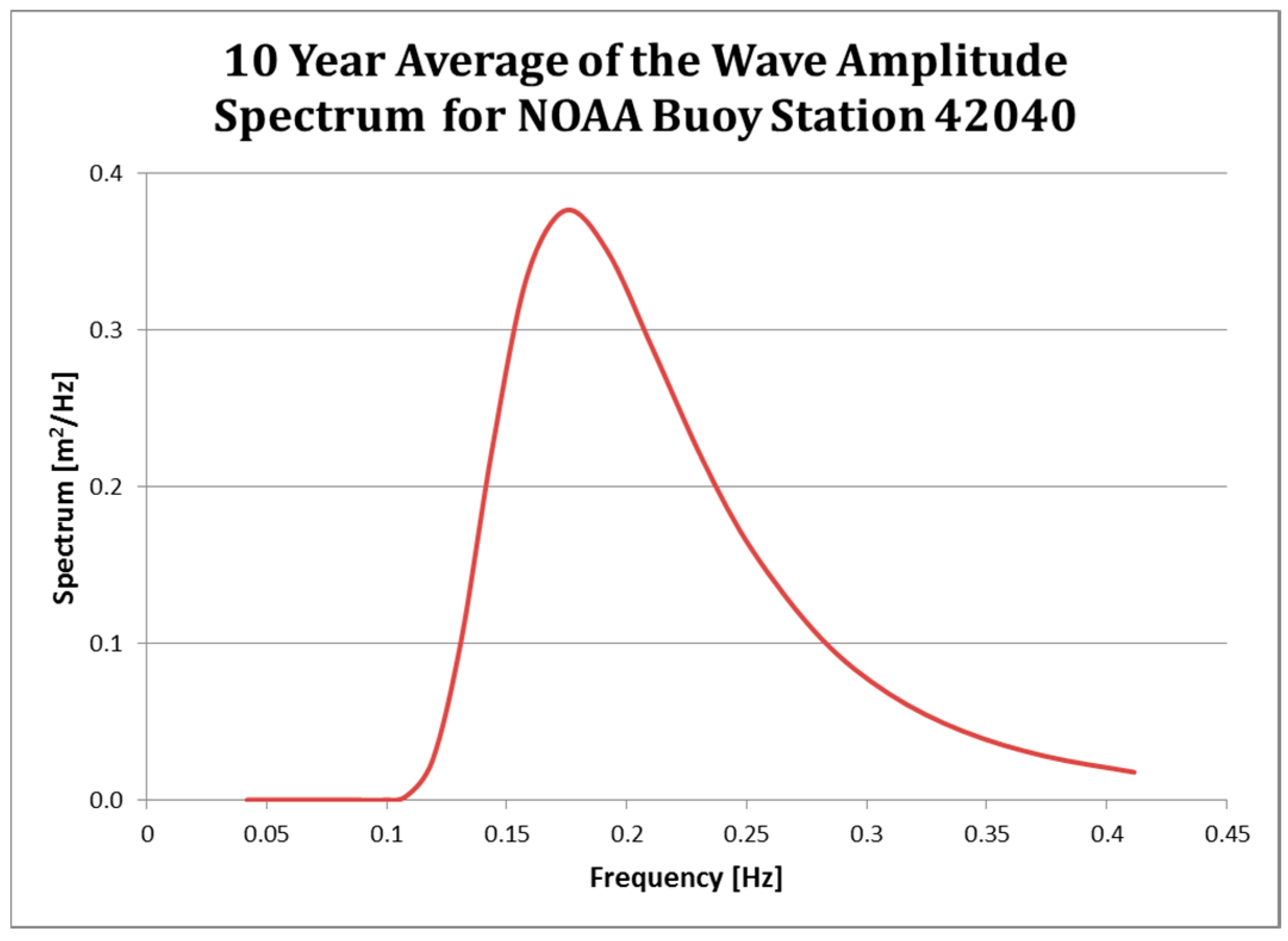
4. Calculated Results for a Localized Geographic Location
5. Conclusions
Author Contributions
Conflicts of Interest
Appendix A

References
- Pastor, J.; Liu, Y.-C. Power absorption modeling and optimization of a point absorbing wave energy converter using numerical method. J. Energy Resour. Technol. 2014, 136, 021207. [Google Scholar] [CrossRef]
- Pastor, J.; Liu, Y.-C. Frequency and time domain modeling and power output for a heaving point absorber wave energy converter. Int. J. Energy Environ. Eng. 2014, 5, 1–13. [Google Scholar] [CrossRef]
- Water Power Technologies Office. Available online: http://www1.eere.energy.gov/water/hydrokinetic/default.aspx (accessed on 1 November 2016).
- Smith, G.; Taylor, J. Preliminary Wave Energy Device Performance Protocol. Available online: http://www.waveandtidalknowledgenetwork.com/ItemDetails.aspx?id=401 (accessed on 1 November 2016).
- Smith, G.H.; Venugopal, V.; Fasham, J. Wave spectral bandwidth as a measure of available wave power. In Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering, Hamburg, Germany, 1–9 June 2006.
- Fusco, F.; Nolan, G.; Ringwood, J.V. Variability reduction through optimal combination of wind/wave resources—An Irish case study. Energy 2010, 35, 314–325. [Google Scholar] [CrossRef]
- Folley, M.; Whittaker, T.J.T. Analysis of the nearshore wave energy resource. Renew. Energy 2009, 34, 1709–1715. [Google Scholar] [CrossRef]
- Carballo, R.; Iglesias, G. A methodology to determine the power performance of wave energy converters at a particular coastal location. Energy Convers. Manag. 2012, 61, 8–18. [Google Scholar] [CrossRef]
- Duclos, G.; Babarit, A.; Clement, A.H. Optimizing of power take off of a wave energy converter with regard to the wave climate. ASME J. Offshore Mech. Arct. Eng. 2006, 128, 56–64. [Google Scholar] [CrossRef]
- Sarmento, A.J.N.A.; Pontes, M.T.; Melo, A.B. The influence of the wave climate on the design annual production of electricity by OWC wave power plants. AASME J. Offshore Mech. Arct. Eng. 2003, 125, 139–144. [Google Scholar] [CrossRef]
- Electric Power Research Institute. Mapping and Assessment of the United States Ocean Wave Energy Resource; EPRI Technical Report 1024637; Electric Power Research Institute: Palo Alto, CA, USA, 2011. [Google Scholar]
- Bretschneider, C.L. Wave Variability and Wave Spectra for Wind Generated Gravity Waves; Technical Memo No. 118; Beach Erosion Board, US Army Corps of Engineering: Washington, DC, USA, 1959. [Google Scholar]
- Pierson, W.J.; Moskowitz, L. Proposed spectral form for fully developed wind seas based on the similarity theory of S.A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of Wind-Wave Growth and Swell Decay during the Joint North Sea Wave Project (JONSWAP); Deutches Hydrographisches Institut: Hamburg, Germany, 1973. [Google Scholar]
- Ochi, M.K.; Hubble, E.N. Six-parameter wave spectra. In Proceedings of the 15th Coastal Engineering Conference, Honolulu, HI, USA, 1–17 July 1976; pp. 301–328.
- Boukhanovsky, A.V.; Soares, C.G. Modelling of multipeaked directional wave spectra. Appl. Ocean Res. 2009, 31, 132–141. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Cavalier, G.; Pastor, J.; Viera, R.J.; Guillory, C.; Judice, K.; Guiberteau, K.L.; Kozman, T.A. Design and construction of a wave generation system to model ocean conditions in the Gulf of Mexico. Int. J. Energy Technol. 2012, 4, 1–7. [Google Scholar]
- Guiberteau, K.L.; Liu, Y.-C.; Lee, J.; Kozman, T.A. Investigation of developing wave energy technology in the Gulf of Mexico. Distrib. Gener. Altern. Energy J. 2012, 27, 36–52. [Google Scholar] [CrossRef]
- MMAB Operational Wave Models. Available online: http://polar.ncep.noaa.gov/waves/#ww3products (accessed on 1 November 2016).
- Wavewatch III® Model. Available online: http://polar.ncep.noaa.gov/waves/wavewatch/wavewatch.shtml (accessed on 1 November 2016).
- Hsu, S.A.; Meindl, E.A.; Gilhousen, D.B. Determining the power-law wind-profile exponent under near-neutral stability conditions at sea. J. Appl. Meteorol. 1994, 33, 757–765. [Google Scholar] [CrossRef]
- ABP Marine Environmental Research. Atlas of UK Marine Renewable Energy Resources; Report R1106, Prepared for the UK Department of Trade and Industry; ABP Marine Environmental Research: Southampton, UK, 2004. [Google Scholar]
- Hagerman, G. Southern New England wave energy resource potential. In Proceedings of the Building Energy 2001, Boston, MA, USA, 23 March 2001.
- US Army Corps of Engineering. Direct Methods for Calculating Wavelength; Coastal Engineering Technical Note, CETN-1-17; US Army Corps of Engineering: Washington, DC, USA, 1985. [Google Scholar]
- Chen, H.-S.; Thompson, E.F. Interactive and Pade’s Solutions for the Water-Wave Dispersion Relation; Miscellaneous Paper CERC-85-4; US Army Engineer Waterways Experiment Station: Vicksburg, MI, USA, 1985. [Google Scholar]
- National Data Buoy Center, National Oceanic and Atmospheric Administration. Available online: http://www.ndbc.noaa.gov/station_page.php?station=42040 (accessed on 18 November 2013).
- Fenton, J.D.; McKee, W.D. On calculating the lengths of water waves. Coast. Eng. 1990, 14, 499–513. [Google Scholar] [CrossRef]
- Korde, U.A. A power take-off mechanism for maximizing the performance of an oscillating water column wave energy device. Appl. Ocean Res. 1991, 13, 75–81. [Google Scholar] [CrossRef]
- Wang, L.; Engstrom, J.; Leijon, M.; Isberg, J. Coordinated control of wave energy converters subject to motion constraints. Energies 2016, 9, 475. [Google Scholar] [CrossRef]
- Salter, S.H. Power conversion systems for ducks. In Proceedings of the International Conference on Future Energy Concepts, London, UK, 30 January–1 February 1979; pp. 100–108.
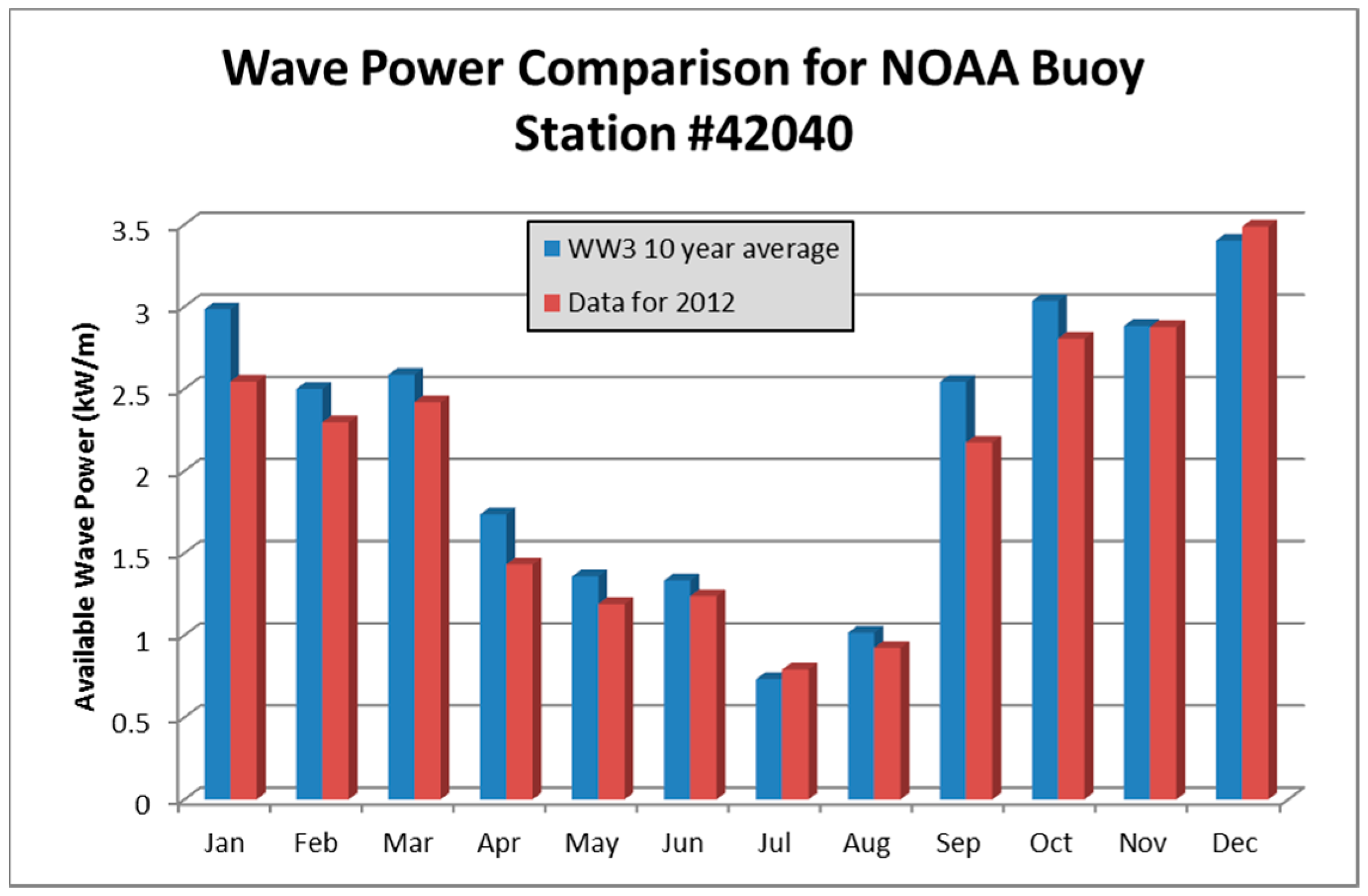
| Month | Predicted Power (kW/m) | NOAA Data [24] (kW/m) | Error | EPRI Data [11] (kW/m) | Error |
|---|---|---|---|---|---|
| January | 2983.57 | 2543.21 | 14.8% | 2523.16 | 15.4% |
| February | 2499.12 | 2295.20 | 8.2% | 2291.24 | 8.3% |
| March | 2585.30 | 2416.69 | 6.5% | 2412.19 | 6.7% |
| April | 1735.20 | 1429.99 | 17.6% | 1395.99 | 19.5% |
| May | 1357.28 | 1189.04 | 12.4% | 1119.24 | 17.5% |
| June | 1333.04 | 1237.11 | 7.2% | 1231.69 | 7.6% |
| July | 733.10 | 791.11 | 7.3% | 799.12 | 8.3% |
| August | 1014.97 | 922.53 | 9.1% | 909.54 | 10.4% |
| September | 2542.29 | 2172.37 | 14.6% | 2121.45 | 16.6% |
| October | 3034.14 | 2805.23 | 7.5% | 2794.99 | 7.9% |
| November | 2882.43 | 2875.59 | 0.2% | 2865.41 | 0.6% |
| December | 3401.58 | 3487.74 | 2.5% | 3499.52 | 2.8% |
| Average | 2175.17 | 2013.82 | 9.0% | 1996.96 | 10.1% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastor, J.; Liu, Y. Wave Climate Resource Analysis Based on a Revised Gamma Spectrum for Wave Energy Conversion Technology. Sustainability 2016, 8, 1321. https://doi.org/10.3390/su8121321
Pastor J, Liu Y. Wave Climate Resource Analysis Based on a Revised Gamma Spectrum for Wave Energy Conversion Technology. Sustainability. 2016; 8(12):1321. https://doi.org/10.3390/su8121321
Chicago/Turabian StylePastor, Jeremiah, and Yucheng Liu. 2016. "Wave Climate Resource Analysis Based on a Revised Gamma Spectrum for Wave Energy Conversion Technology" Sustainability 8, no. 12: 1321. https://doi.org/10.3390/su8121321
APA StylePastor, J., & Liu, Y. (2016). Wave Climate Resource Analysis Based on a Revised Gamma Spectrum for Wave Energy Conversion Technology. Sustainability, 8(12), 1321. https://doi.org/10.3390/su8121321







