The Optimization of Distributed Photovoltaic Comprehensive Efficiency Based on the Construction of Regional Integrated Energy Management System in China
Abstract
:1. Introduction
2. Analysis of Efficiency of Distributed Photovoltaic in China
2.1. The Trend Analysis of Distributed Photovoltaic
2.2. The Efficiency Analysis of Distributed Photovoltaic
3. The Introduction of Comprehensive Efficiency of Photovoltaic Generation and Analysis of Its Influencing Factors from the Perspective of SD
3.1. The Introduction of Distributed Photovoltaic Comprehensive Efficiency
3.2. The Applicability Analysis of Distributed Photovoltaic Comprehensive Efficiency from the Perspective of SD
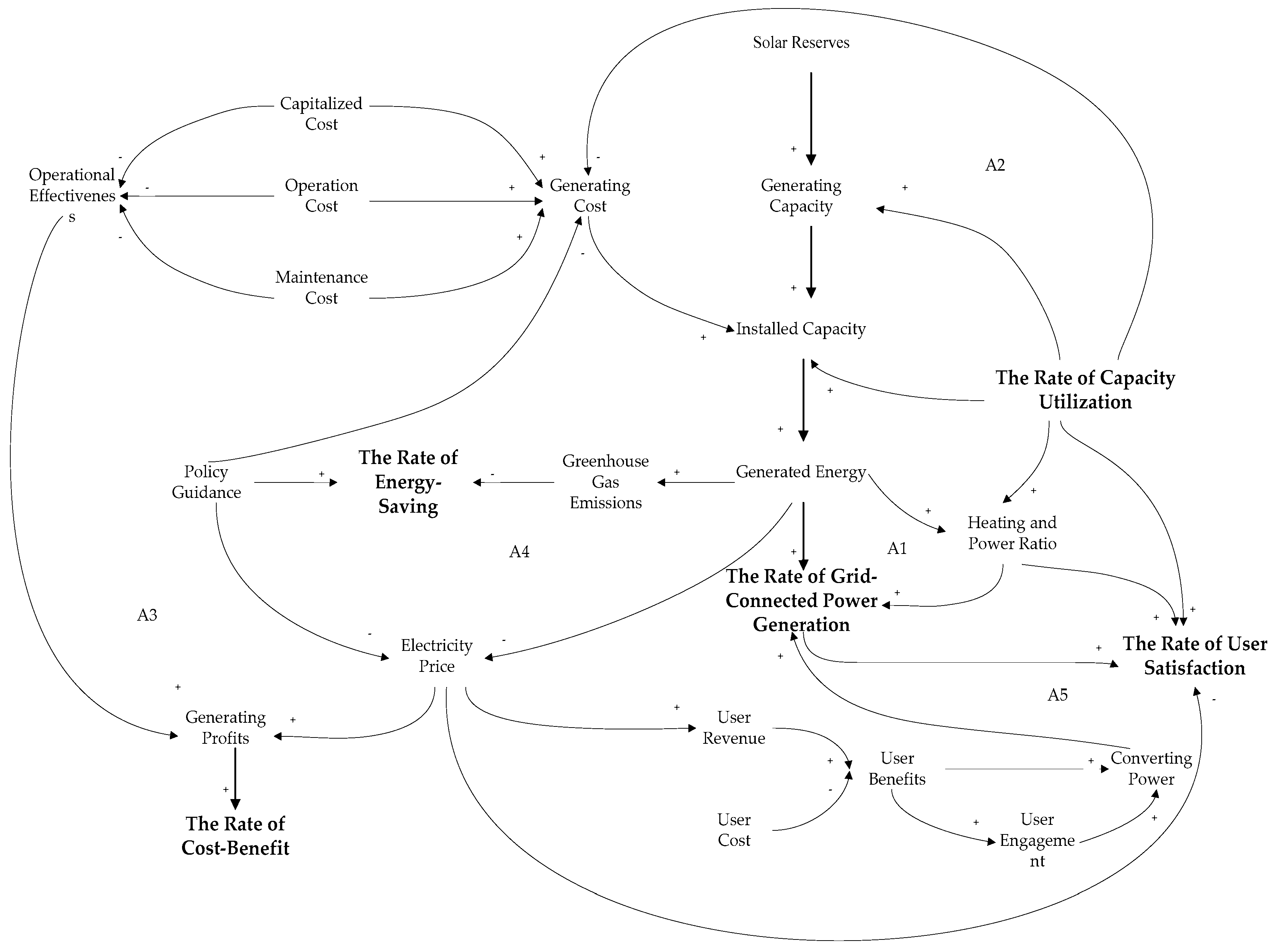
3.3. The Analysis of Distributed Photovoltaic Comprehensive Efficiency Based on SD
3.3.1. Cause-and-Effect Diagram
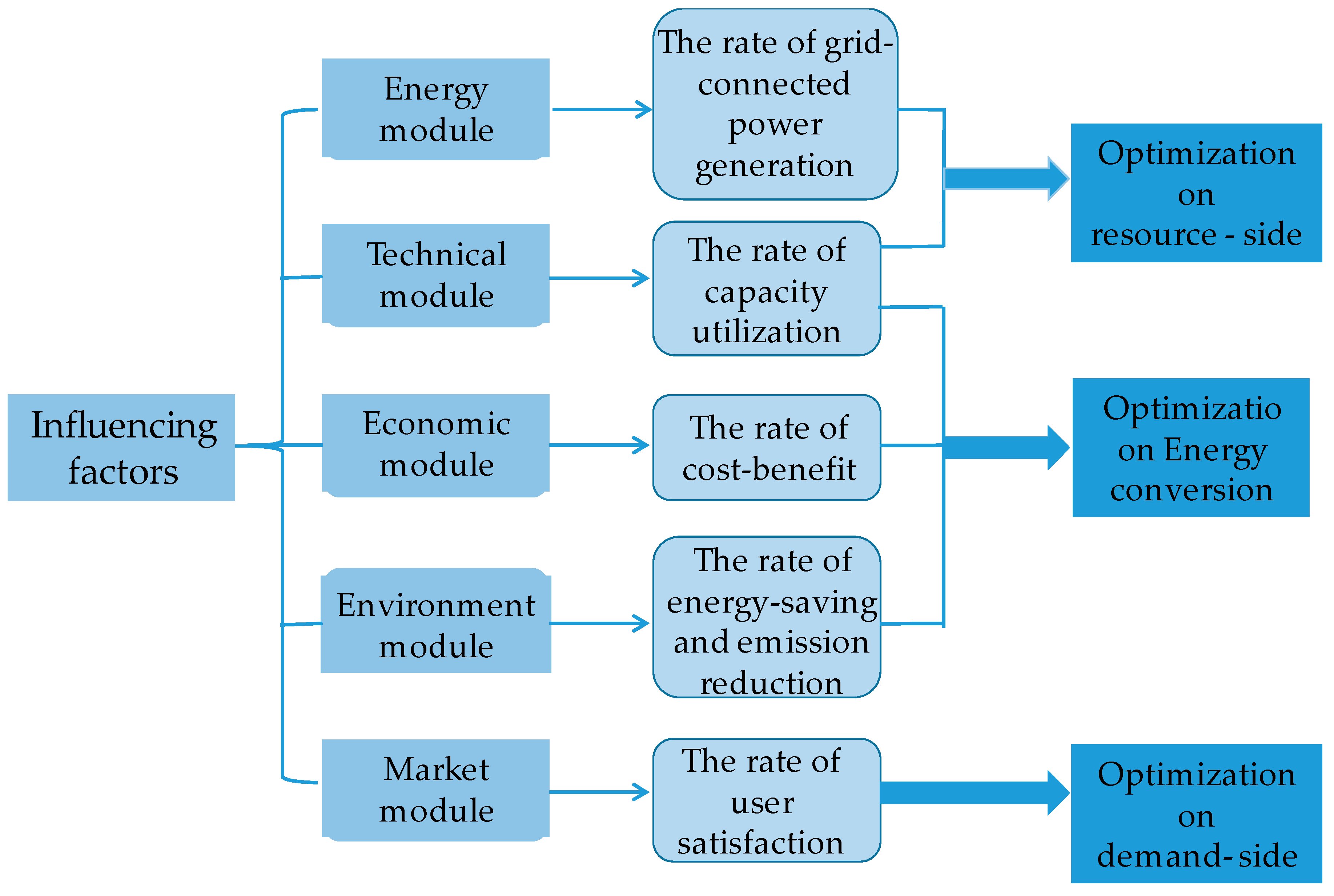
3.3.2. The Analysis of Sub-Modules
4. The Optimal Path of Comprehensive Efficiency of Distributed Photovoltaic Based on Regional Integrated Energy Management System
4.1. The Path Selection for Comprehensive Efficiency of Distributed Photovoltaic
4.1.1. The Selection of Optimal Direction Based on SD
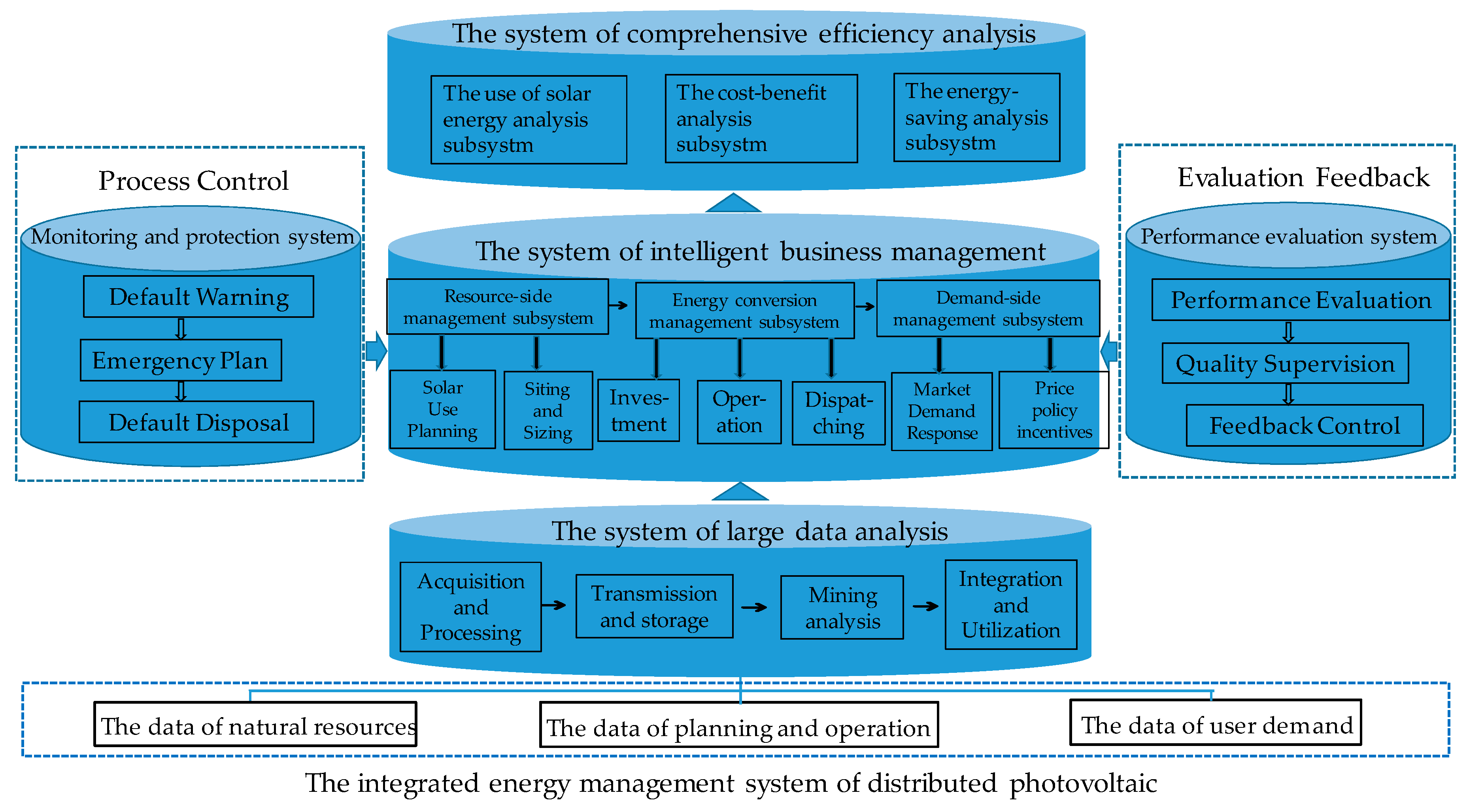
4.1.2. Optimal Content Based on Regional Integrated Energy Management System
4.2. The Implementation Methods of Optimization Path of Distributed Photovoltaic Comprehensive Efficiency
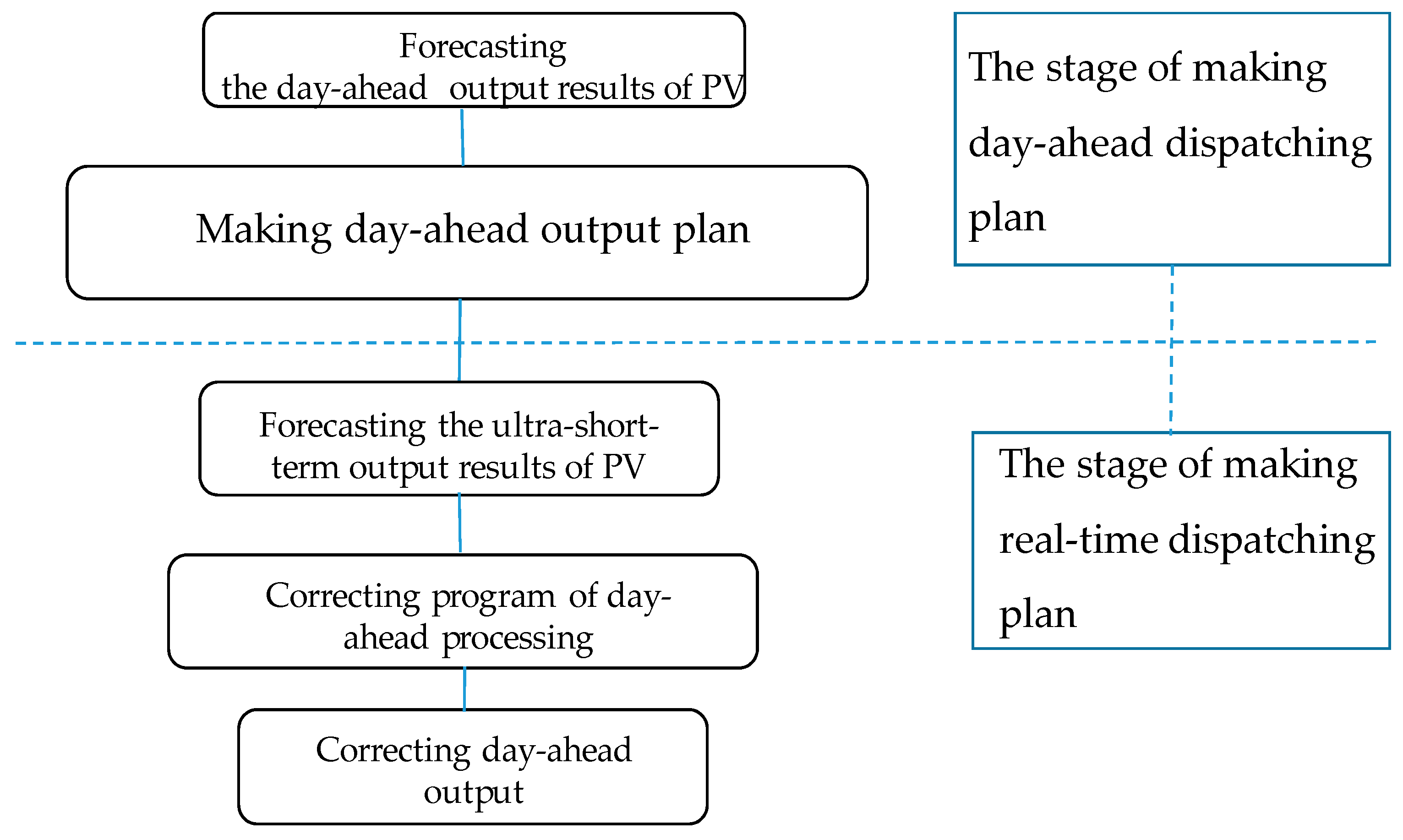
4.2.1. Introduction to the Methods
- (a)
- The Branch Power Constraintwhere represents the branch power; i and j represent the first and last branch node, respectively; and represents the upper limit of branch power.
- (b)
- The Node Voltage Constraintwhere represents voltage amplitude of the node i, and and represent the upper and lower limit of the voltage node respectively.
- (c)
- Distributed Photovoltaic Capacity Constraintwhere represents the active output of the i-node, and represents the maximum capacity of i-node which can access to distributed photovoltaic, measured in MW.
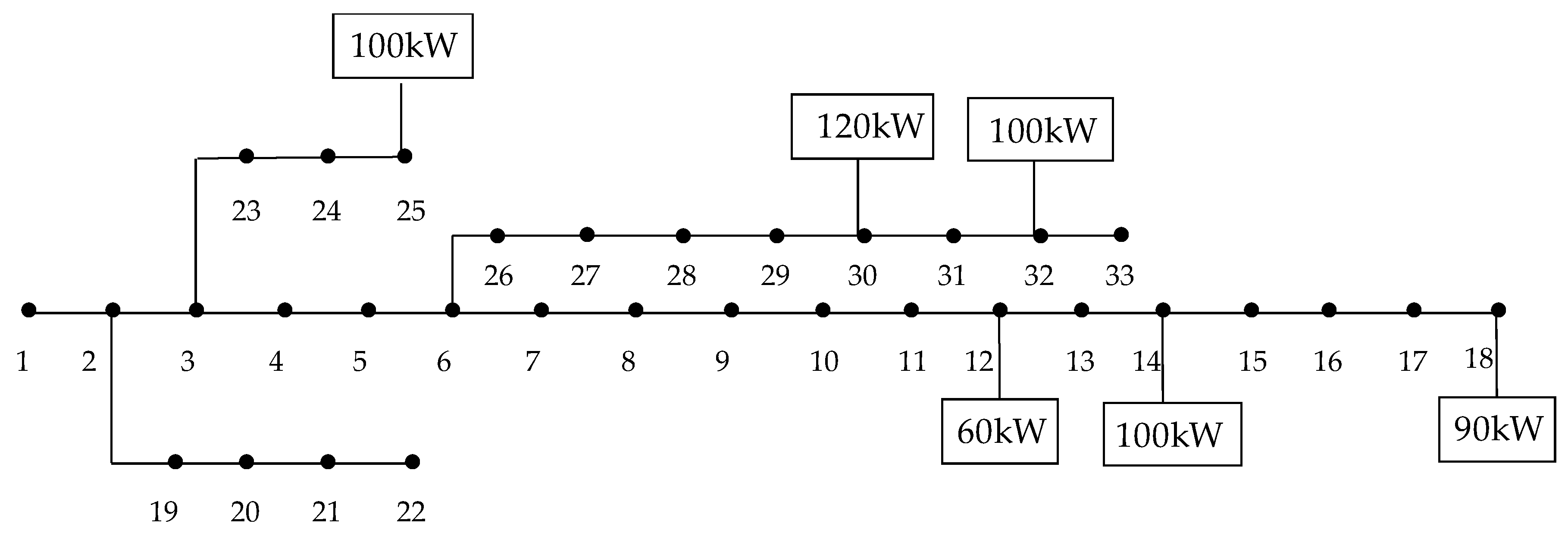
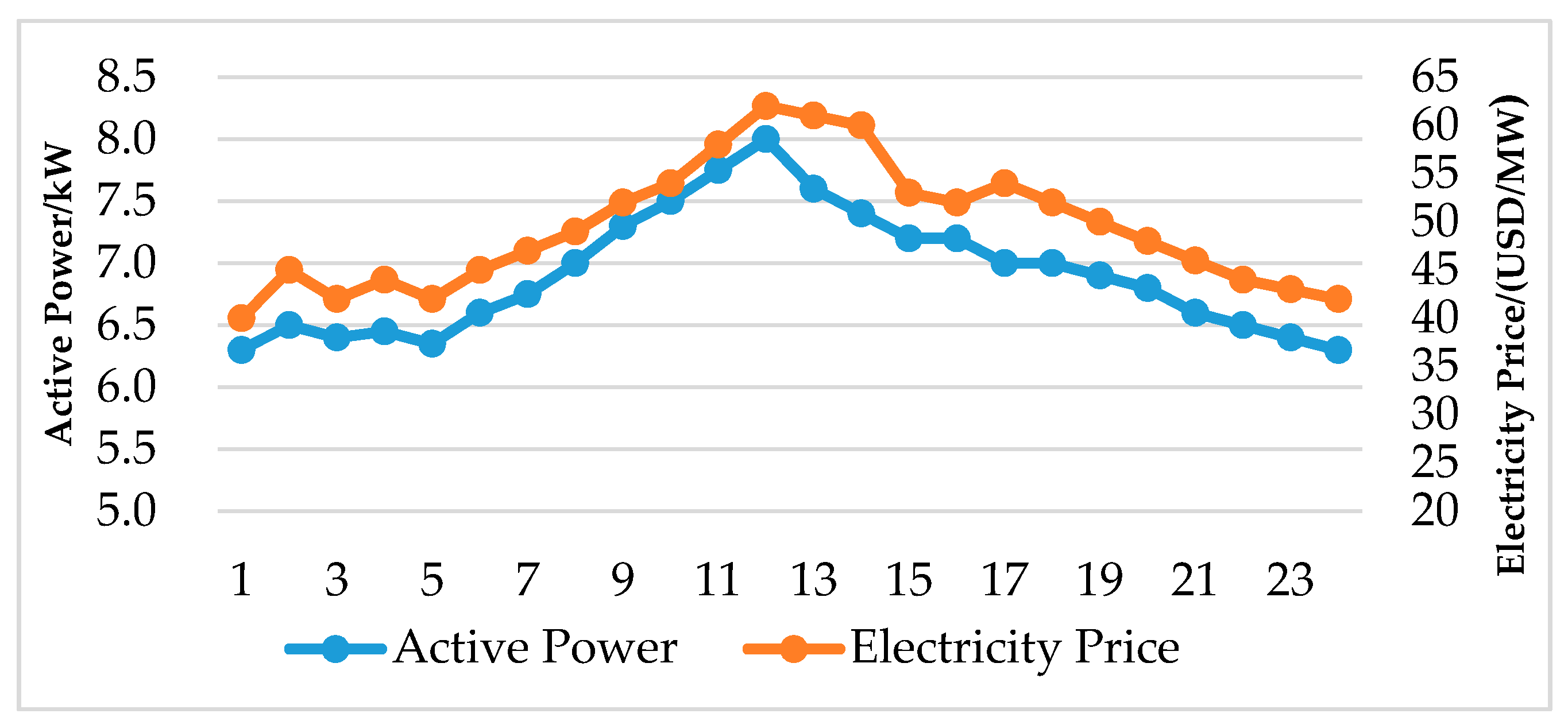
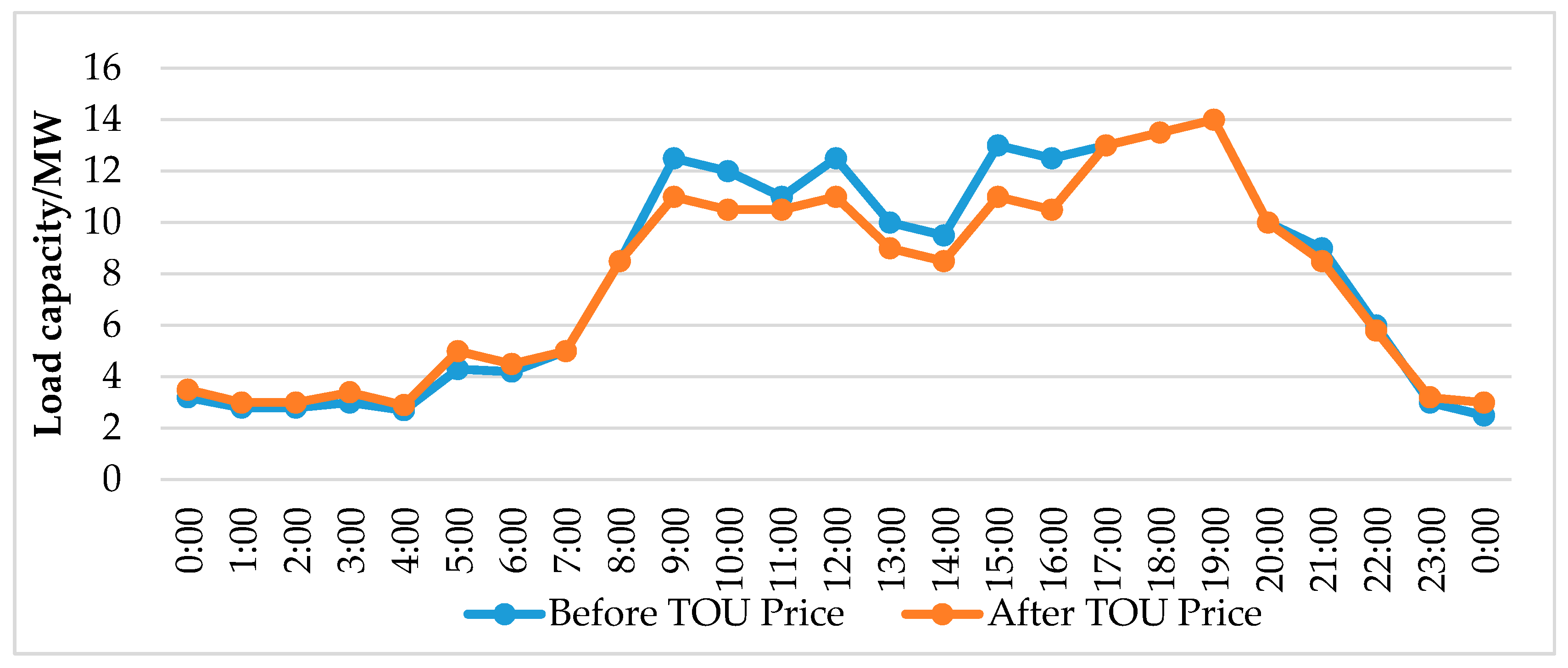
4.2.2. The Example Simulation
4.3. The Realization Guarantee of Optimal Path Based on the Regional Integrated Energy Management System
5. The Policy Recommendations for the Optimization of Comprehensive Efficiency of Distributed Photovoltaic
5.1. The Policy Suggestions of Industrial Incentives
5.2. The Policy Suggestions of Price Subsidy
5.2.1. Price Mechanism
5.2.2. Subsidy Mechanism
5.3. The Policy Suggestions of Operation Supervision
6. Conclusions
- (1)
- This paper proposed the concept of comprehensive efficiency of distributed photovoltaic after analyzing the current situation of distributed photovoltaic efficiency. According to the research and analysis using the theory of system dynamics, the comprehensive promotion of distributed photovoltaic relates to energy, technology, economy, environment and market, and depends on the factors of the rate of grid-connected power generation, the rate of capacity utilization, the rate of cost–benefit, the rate of energy-saving and emission reduction and the rate of users’ satisfaction. Analyzing the comprehensive efficiency of distributed photovoltaic on the basis of five factors makes sense of understanding the whole direction of optimization.
- (2)
- After analyzing the influencing factors of comprehensive efficiency, this paper clarified the direction of optimization from resource side, energy conversion and demand side, and established the core part of the regional integrated energy management system; that is, the system of intelligent business management. Then, the author proposed optimized path of the comprehensive efficiency of distributed photovoltaic from three various perspectives.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yin, Y.H.; Mizokami, S.; Alikawa, K. Compact development and energy consumption: Scenario analysis of urban structures based on behavior simulation. Appl. Energy 2015, 159, 449–457. [Google Scholar] [CrossRef]
- Liu, Y.S.; Yan, B.; Zhou, Y. Urbanization, economic growth, and carbon dioxide emissions in China: A panel cointegration and causality analysis. J. Geogr. Sci. 2016, 26, 131–152. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, J.M. Distributed Energy—A Perfect Match of Energy-Saving and Low-Carbon Technology; Wuhan University Press: Wuhan, China, 2012. (In Chinese) [Google Scholar]
- Wu, Q.; Ren, H.; Gao, W.; Ren, J. Multi-objective optimization of a distributed energy network integrated with heating interchange. Energy 2016, 109, 353–364. [Google Scholar] [CrossRef]
- Bashiri, M. Optimal scheduling of distributed energy resources in a distribution system based on imperialist competitive algorithm considering reliability worth. Neural Comput. Appl. 2014, 25, 967–974. [Google Scholar] [CrossRef]
- Mehleria, E.D.; Sarimveisa, H.; Markatosa, N.C. Optimal design and operation of distributed energy systems: Application to Greek residential sector. Renew. Energy 2013, 51, 331–342. [Google Scholar] [CrossRef]
- He, Y.X.; Xu, Y.; Xia, T.; Zhang, J.X. Business Impact and Policy on the Major Players in the Market of the Development of Distributed Energy in China. Math. Probl. Eng. 2016, 2016, 1–12. [Google Scholar] [CrossRef]
- Zeng, M.; Ouyang, S.J.; Shi, H.; Ge, Y.J.; Qian, Q.Q. Overall review of distributed energy development in China: Status quo, barriers and solutions. Renew. Sustain. Energy Rev. 2015, 50, 1226–1238. [Google Scholar]
- Knoop, K.; Lechtenböhmer, S. The potential for energy efficiency in the EU Member States—A comparison of studies. Renew. Sustain. Energy Rev. 2016, in press. [Google Scholar] [CrossRef]
- Granić, G. CO2 tax or fee as a single economic instrument for climate protection policy promoting Renewable Energy Sources and enhancing Energy Efficiency. Nafta Sci. J. 2014, 65, 107–113. [Google Scholar]
- Thollander, P.; Palm, J. Industrial Energy Management Decision Making for Improved Energy Efficiency-Strategic System Perspectives and Situated Action in Combination. Energies 2015, 8, 5694–5703. [Google Scholar] [CrossRef]
- Asghar, F.; Talha, M.; Kim, S.H. Development of Energy Management System for Micro-Grid with Photovoltaic and Battery system. J. Korean Inst. Intell. Syst. 2015, 25, 299–305. [Google Scholar] [CrossRef]
- Han, D.; Yan, Z.; Song, Y.; Sun, Q.; Zhang, Y. Dynamic assessment method for smart grid based on system dynamic. Autom. Electr. Power Syst. 2012, 36, 16–21. [Google Scholar]
- Tan, J.; Wang, B.; Li, Y. Application of System Dynamics on Comprehensive Benefits Valuation of Demand Response. Autom. Electr. Power Syst. 2014, 38, 128–134. [Google Scholar]
- Gangolells, M.; Casals, M.; Forcada, N.; Macarulla, M.; Giretti, A. Energy performance assessment of an intelligent energy management system. Renew. Sustain. Energy Rev. 2016, 55, 662–667. [Google Scholar] [CrossRef]
- Pazouki, S.; Haghifam, M.R. Optimal planning and scheduling of energy hub in presence of wind, storage and demand response under uncertainty. J. Electr. Power Energy Syst. 2016, 80, 219–239. [Google Scholar] [CrossRef]
- Cai, Y.P.; Huang, G.H.; Tan, Q.; Yang, Z.F. Planning of community-scale renewable energy management systems in a mixed stochastic and fuzzy environment. Renew. Energy 2009, 34, 1833–1847. [Google Scholar] [CrossRef]
- Du Plessis, G.E.; Liebenberg, L.; Mathews, E.H.; Du Plessis, J.N. A versatile energy management system for large integrated cooling systems. Energy Convers. Manag. 2013, 66, 312–325. [Google Scholar] [CrossRef]
- Tan, W.S.; Hassan, M.Y.; Majid, M.S.; Rahman, H.A. Optimal distributed renewable generation planning: A review of different approaches. Renew. Sustain. Energy Rev. 2013, 18, 626–645. [Google Scholar] [CrossRef]
- Soroudi, A.; Ehsan, M. A distribution network expansion planning model considering distributed generation options and techo-economical issues. Energy 2010, 35, 3364–3374. [Google Scholar] [CrossRef]
- Flores Robert, J.; Shaffer Brendan, P.; Brouwer, J. Dynamic distributed generation dispatch strategy for lowering the cost of building energy. Appl. Energy 2014, 123, 196–208. [Google Scholar] [CrossRef]
- Raoofat, M.; Malekpour, A.R. Optimal allocation of distributed generations and remote controllable switches to improve the network performance considering operation strategy of distributed generations. Electr. Power Compon. Syst. 2011, 39, 1809–1827. [Google Scholar] [CrossRef]
- Ratnam, E.L.; Weller, S.R.; Kellett, C.M. Central versus localized optimization-based approaches to power management in distribution networks with residential battery storage. J. Electr. Power Energy Syst. 2016, 80, 396–406. [Google Scholar] [CrossRef]
- Di Somma, M.; Yan, B.; Bianco, N. Operation optimization of a distributed energy system considering energy costs and energy efficiency. Energy Convers. Manag. 2015, 103, 739–751. [Google Scholar] [CrossRef]
- Mallikarjun, S.; Lewis, H.F. Energy technology allocation for distributed energy resources: A strategic technology-policy framework. Energy 2014, 72, 783–799. [Google Scholar] [CrossRef]
- Allan, G.; Eromenko, I.; Gilmartin, M. The economics of distributed energy generation: A literature review. Renew. Sustain. Energy Rev. 2015, 42, 543–556. [Google Scholar] [CrossRef]
- Zhi, Q.; Sun, H.H.; Li, Y.X.; Xu, Y.R.; Su, J. China’s solar photovoltaic policy: An analysis based on policy instruments. Appl. Energy 2014, 129, 308–319. [Google Scholar] [CrossRef]
- Ruggiero, S.; Varho, V.; Rikkonen, P. Transition to distributed energy generation in Finland: Prospects and barriers. Energy Policy 2015, 86, 433–443. [Google Scholar] [CrossRef]
- Hoppmann, J.; Huenteler, J.; Girod, B. Compulsive policymaking-The evolution of the German feed-in tariff system for solar photovoltaic power. Res. Policy 2014, 43, 1422–1441. [Google Scholar] [CrossRef]
- Shao, H.; Zhang, J.; Zhang, W. Economy and policy analysis of distributed photovoltaic. Electr. Power Constr. 2014, 35, 51–57. [Google Scholar]
- Panda, A.; Pathak, M.K.; Srivastava, S.P. Enhanced power quality based single phase photovoltaic distributed generation system. Int. J. Electron. 2016, 103, 1262–1278. [Google Scholar] [CrossRef]



| Policy Classification | Department | Name of Document | Year | Content |
|---|---|---|---|---|
| Integrated Planning | State Council | The Plan of Strategic Action for Energy Development (2014–2020) | 2014 | Regarding distributed energy as one of nine key areas of innovation—“Clarify the strategic direction and emphasis of energy technology innovation” |
| Priority Support | NDRC | The 13th Five-year plan for national economic and social development of the People’s Republic of China: the energy sector | 2016 | Accelerate the development of distributed photovoltaic industry in the eastern and southern regions of China |
| NEA | Opinions on the implementation of photovoltaic generation to alleviate poverty | 2014 | Expand distributed photovoltaic market by implementing distributed photovoltaic and agricultural photovoltaic poverty alleviation projects | |
| Electricity Price Subsidies | NDRC | Notice about perfection on the benchmark price policies of onshore wind and photovoltaic generation | 2015 | Encourage all local governments to determine the owners and grid purchase price of relevant new energy projects by market-oriented approach such as bidding |
| NDRC | Notice about promoting the healthy development of distributed photovoltaic industry by means of price lever | 2013 | Implement subsidy policies for overall photovoltaic generation, self-use of electricity will be free from various funds and surcharges | |
| Operational Regulation | NEA | Interim Measures for operational regulation of photovoltaic generation | 2013 | Take charge of operating, trading and information disclosing for grid-connected photovoltaic power plant projects |
| SGCC | Notice about work on distributed photovoltaic and network service | 2012 | According to the working principle “support, welcome, service”, optimize and simplify the process of synchronize and improve service levels |
| The Name of the Demonstration Zone | Cumulative Installed Capacity in 2015 (MW) | Self-Use Rate |
|---|---|---|
| Haidian District, Beijing Zhongguancun Haidian Park | 178 | 90% |
| Beijing Shunyi Development Zone | 200 | 70% |
| Shanghai Songjiang Industrial Zone | 50 | 90% |
| Tianjin Wuqing Development Area | 100 | 80% |
| Hebei Gaobeidian Development Zone | 150 | 80% |
| Hebei Baoding Yingli New Technology Development Zone | 60 | 100% |
| Jiangsu Wuxi High-Tech Industrial Development Zone | 50 | 100% |
| Jiangsu Nantong High-Tech Industrial Development Zone | 150 | 90% |
| Shaoxing waterfront beach industrial agglomeration area, Zhejiang | 150 | 70% |
| Hangzhou Tonglu Economic Development zone, Zhejiang | 50 | 70% |
| High-Tech Industrial Development Zone, Hefei, Anhui | 100 | 80% |
| High-Tech Industrial Development Zone, Xinyu, Jiangxi | 72 | 90% |
| High-Tech Industrial Development Zone, Taian, Shandong | 50 | 90% |
| High-Tech Industrial Development Zone, Zibo, Shangdong | 50 | 90% |
| San Shui Industrial Park, Foshan, Guangdong | 130 | 85% |
| Pearl Industrial Park, Conghua, Guangdong | 83 | 80% |
| Shenzhen Qianhai modern service industrial Cooperation Zone of Shenzhen and Hong Kong | 50 | 90% |
| Ningbo Hangzhou Bay Area | 150 | 80% |
| Self-Elasticity Coefficient E(i) | Cross-Elasticity Coefficient E(i,j) | ||
|---|---|---|---|
| −0.40 | Peak-Flat | Peak-Valley | Flat-Valley |
| 0.04 | 0.06 | 0.04 | |
| Time Period | Period Division | Price Fluctuation |
|---|---|---|
| Peak | 17:30–(Next day) 00:00 | Up 30% |
| Flat | 06:30–17:30 | No change |
| Valley | 00:00–06:30 | Down 30% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Long, Y.; Tan, Z.; Zhang, X.; Li, L. The Optimization of Distributed Photovoltaic Comprehensive Efficiency Based on the Construction of Regional Integrated Energy Management System in China. Sustainability 2016, 8, 1201. https://doi.org/10.3390/su8111201
Song X, Long Y, Tan Z, Zhang X, Li L. The Optimization of Distributed Photovoltaic Comprehensive Efficiency Based on the Construction of Regional Integrated Energy Management System in China. Sustainability. 2016; 8(11):1201. https://doi.org/10.3390/su8111201
Chicago/Turabian StyleSong, Xiaohua, Yun Long, Zhongfu Tan, Xubei Zhang, and Leming Li. 2016. "The Optimization of Distributed Photovoltaic Comprehensive Efficiency Based on the Construction of Regional Integrated Energy Management System in China" Sustainability 8, no. 11: 1201. https://doi.org/10.3390/su8111201
APA StyleSong, X., Long, Y., Tan, Z., Zhang, X., & Li, L. (2016). The Optimization of Distributed Photovoltaic Comprehensive Efficiency Based on the Construction of Regional Integrated Energy Management System in China. Sustainability, 8(11), 1201. https://doi.org/10.3390/su8111201






