Wind Energy Potential Assessment and Forecasting Research Based on the Data Pre-Processing Technique and Swarm Intelligent Optimization Algorithms
Abstract
:1. Introduction
2. Wind Energy Potential Assessment Methodologies and Results
2.1. Related Methodologies
2.1.1. Related Single Methodologies
Parameter Optimization Algorithms
Assessment Approach
2.1.2. Proposed Wind Energy Potential Assessment Model
| Algorithm 1: CS-Weibull | |
Input:
| |
Output:
| |
| Parameters: | |
| Num Cuckoos = 50; | number of initial population |
| Min Number Of Eggs = 2; | minimum number of eggs for each cuckoo |
| Max Number Of Eggs = 4; | maximum number of eggs for each cuckoo |
| Max Iter = 200; | maximum iterations of the Cuckoo Algorithm |
| Knn Cluster Num = 1; | number of clusters that we want to make |
| Motion Coeff = 20; | Lambda variable in COA paper, default = 2 |
| accuracy = 1.0 × 10−10; | How much accuracy in answer is needed |
| Max Num Of Cuckoos = 20; | maximum number of cuckoos that can live at the same time |
| Radius Coeff = 0.05; | Control parameter of egg laying |
| Cuckoo Pop Variance = 1 × 10−10; | Population variance that cuts the optimization |
| 1: /* Initialize population of n host nests xi (i = 1, 2, ..., n) randomly*/ | |
| 2: FOR EACH i: 1 ≤ i ≤ n DO | |
| 3: Evaluate the corresponding fitness function Fi | |
| 4: END FOR | |
| 5: WHILE (g < GenMax) DO | |
| 6: /* Get new nests by Lévy flights */ | |
| 7: FOR EACH i: 1 ≤ i ≤ n DO | |
| 8: xL = xi + α⊕Levy(λ); | |
| 9: END FOR | |
| 10: FOR EACH i: 1 ≤ i ≤ n DO | |
| 11: Compute FL | |
| 12: IF (FL < Fi) THEN | |
| 13: xi←xL; | |
| 14: END IF | |
| 15: END FOR | |
| 16: Compute FL | |
| 17: /*Update best nest xp of the d generation*/ | |
| 18: IF (Fp < Fb) THEN | |
| 19: xb←xp; | |
| 20: END IF | |
| 21: END WHILE | |
| 22: RETURN xb | |
| Algorithm 2: AC-Weibull |
Input:
|
Output:
|
| Parameters: Maximum iterations:50 The number of ant:30 Parameters of the important degree of information elements:1 Parameters of the important degree of the Heuristic factor:5 Parameters of the important degree of the heuristic factor:0.1 Pheromone increasing intensity coefficient:100 |
| NC_max—Maximum iterations:50 |
| m—The number of ant:30 |
| Alpha—Parameters of the important degree of information elements:1 |
| Beta—Parameters of the important degree of the Heuristic factor:5 |
| Rho—Parameters of the important degree of the heuristic factor:0.1 |
| Q—Pheromone increasing intensity coefficient:100 |
| 1: /*Initialize popsize candidates with the values between 0 and 1*/ |
| 2: FOR EACH i: 1 ≤ i ≤ n DO |
| 3: |
| 4: END FOR |
| 5: |
| 6: iter = 1; Evaluate the corresponding fitness function Fi |
| 7: /* Find the best value of repeatedly until the maximum iterations are reached. */ |
| 8: WHILE .() DO |
| 9: /* Find the best fitness value for each candidates */ |
| 10: FOR EACH DO |
| 11: Build neural network by using with the value |
| 12: Calculate by neural network |
| 13: /* Choose the best fitness value of the ith candidate in history */ |
| 14: IF (pBesti > fitness()) THEN |
| 15: pBesti = fitness() |
| 16: END IF |
| 17: END FOR |
| 18: /* Choose the candidate with the best fitness value of all the candidates */ |
| 19: FOR EACH DO |
| 20: IF (gBest > pBesti) THEN |
| 21: gBest = pBesti = |
| 22: = |
| 23: END IF |
| 24: END FOR |
| 25: /*Update the values of all the candidates by using ACO’s evolution equations.*/ |
| 26: FOR EACH DO |
| 27: |
| 28: |
| 29: END FOR |
| 30: |
| 31: iter = iter + 1 |
| 32: END WHILE |
2.2. Wind Energy Potential Assessment Case Study
2.2.1. Assessment Results in a Single Year
2.2.2. Seasonal and Whole Five-Year Assessment Results
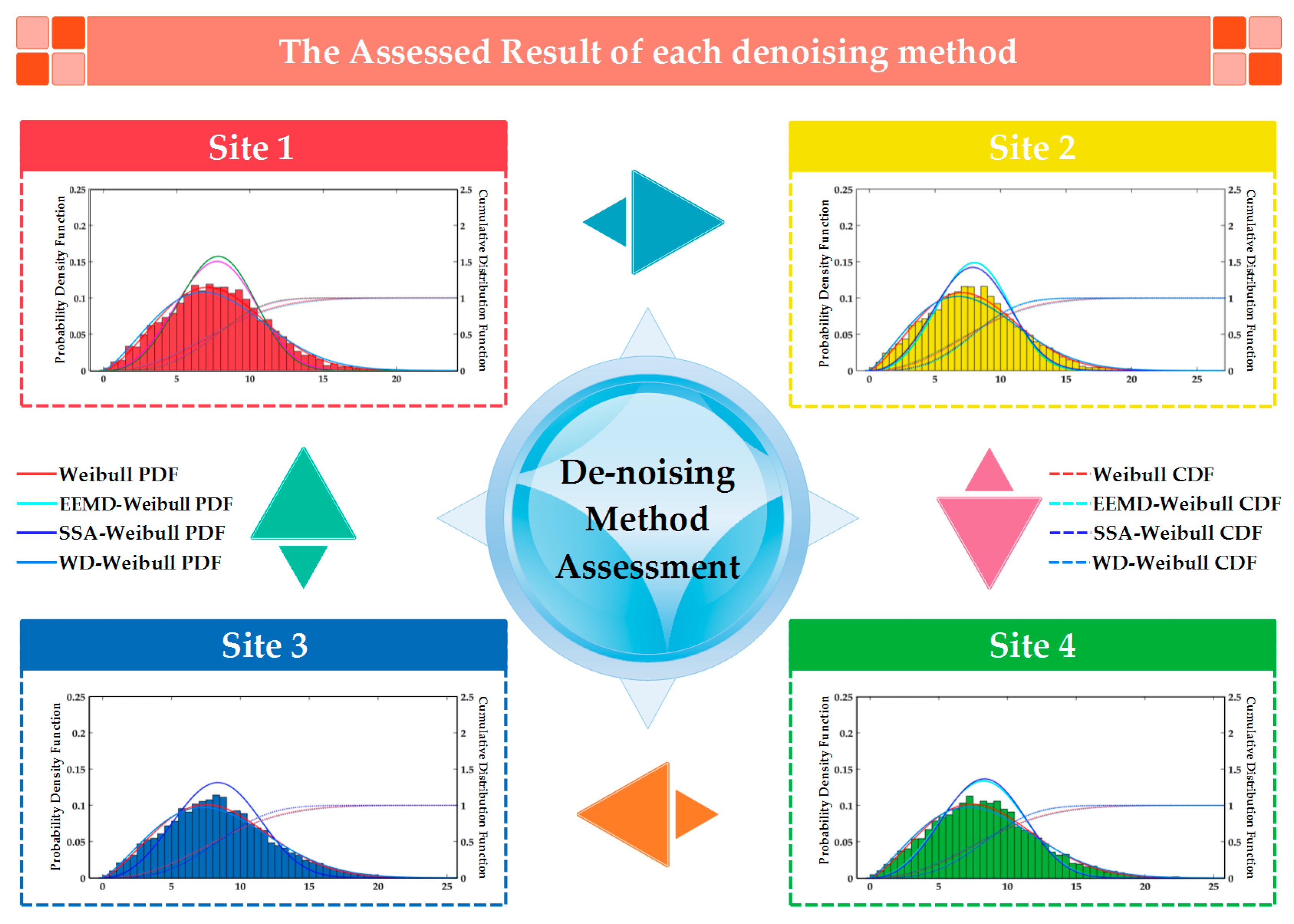
3. Connection between Energy Assessment and Forecasting
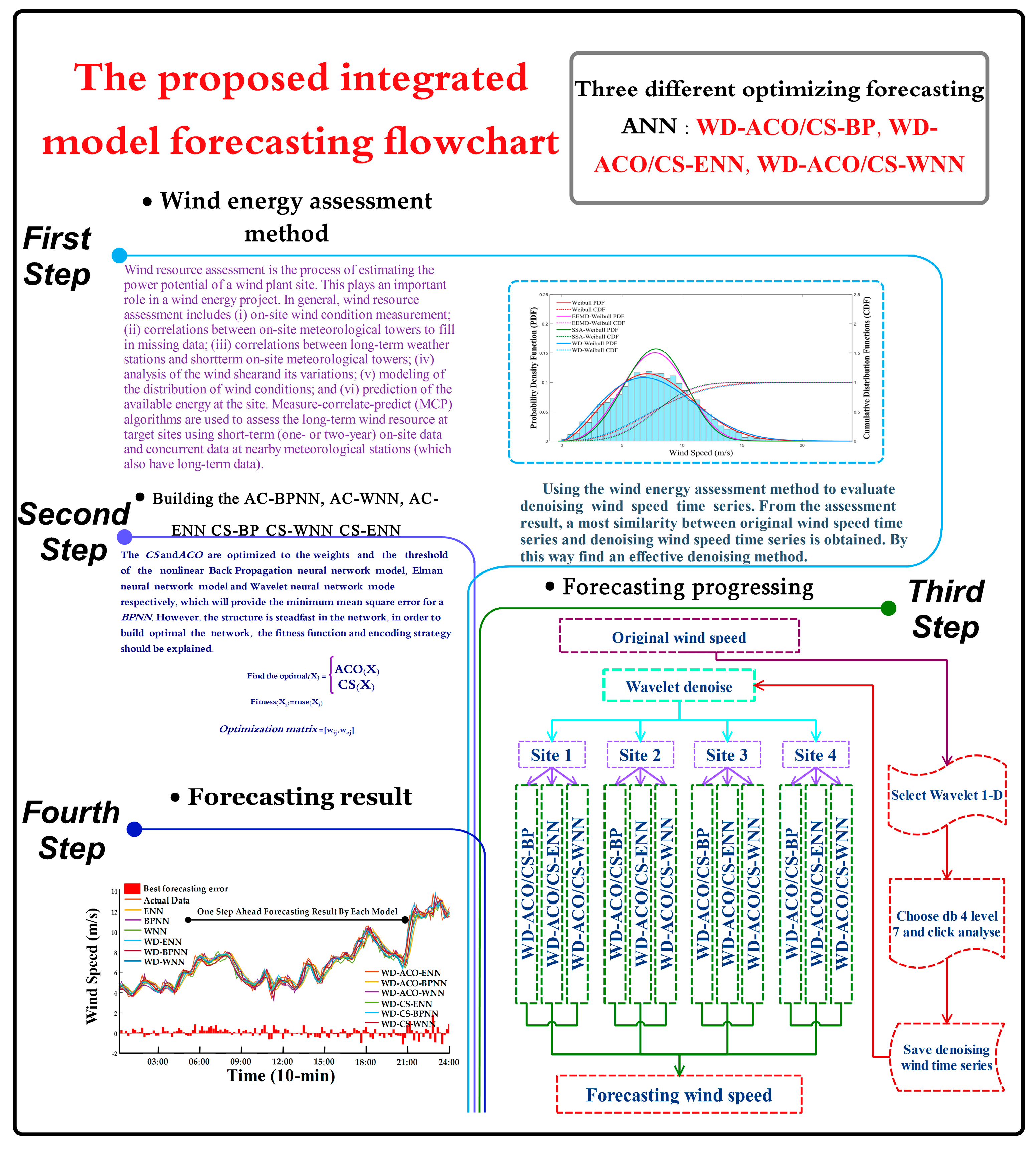
4. Proposed Integrated Forecasting Framework and Forecasting Results
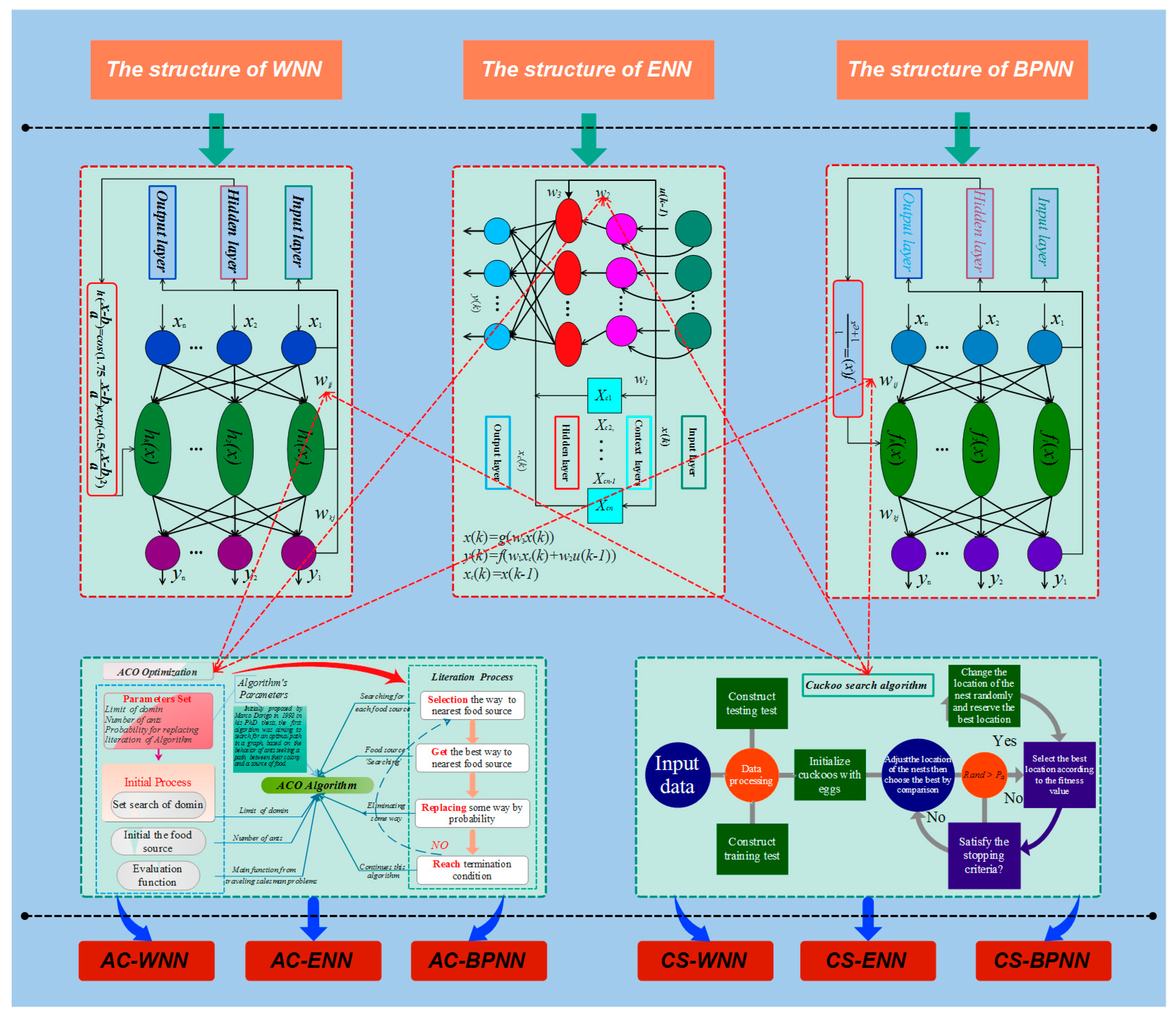
4.1. Basic Neural Network Forecasting Models
4.1.1. Back Propagation Neural Network
4.1.2. Wavelet Neural Network
4.1.3. Elman Neural Network
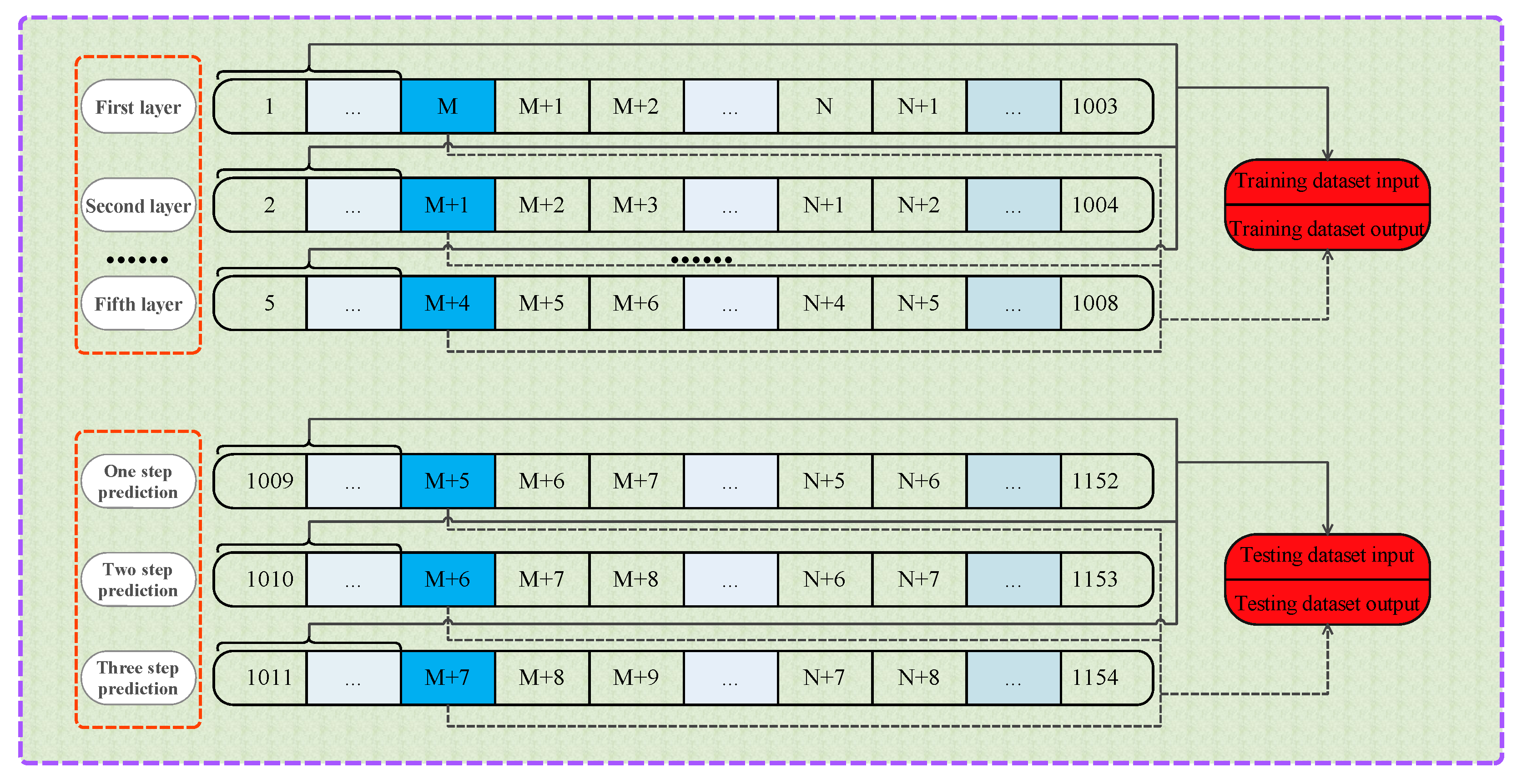
4.2. Structure of the Proposed Integrated Forecasting Framework
| Algorithm 3: Three Neural Networks Optimized by the CS Algorithm | |
Input:
| |
Output:
| |
| Parameters: | |
| Num Cuckoos = 50 | number of initial population |
| Min Number Of Eggs = 2; | minimum number of eggs for each cuckoo |
| Max Number Of Eggs = 4; | maximum number of eggs for each cuckoo |
| Max Iter = 200; | maximum iterations of the Cuckoo Algorithm |
| Knn Cluster Num = 1; | number of clusters that we want to make |
| Motion Coeff = 20; | Lambda variable in COA paper, default = 2 |
| accuracy = 0 × 10−10; | How much accuracy in answer is needed |
| Max Num Of Cuckoos = 20; | maximum number of cuckoos that can live at the same time |
| Radius Coeff = 0.05; | Control parameter of egg laying |
| Cuckoo Pop Variance = 1 × 10−10; | population variance that cuts the optimization |
1: /* Initialize population of n host nests xi (i = 1, 2, ..., n) randomly*/ | |
| 2: FOR EACH i: 1 ≤ i ≤ n DO | |
| 3: Evaluate the corresponding fitness function Fi | |
| 4: END FOR | |
| 5: WHILE (g< GenMax) DO | |
| 6: /* Get new nests by Lévy flights */ | |
| 7: FOR EACH i: 1 ≤ i ≤ n DO | |
| 8: xL=xi+α⊕Levy(λ); | |
| 9: END FOR | |
| 10: FOR EACH i: 1 ≤ i ≤ n DO | |
| 11: Compute FL | |
| 12: IF (FL < Fi) THEN | |
| 13: xi←xL; | |
| 14: END IF | |
| 15: END FOR | |
| 16: Compute FL | |
| 17: /*Update best nest xp of the d generation*/ | |
| 18: IF (Fp < Fb) THEN | |
| 19: xb←xp; | |
| 20: END IF | |
| 21: END WHILE | |
| 22: RETURN xb | |
| Algorithm 4: Three Neural Networks Optimized by the AC Optimization Algorithm |
Input:
|
Output:
|
| Parameters: Maximum iterations:50 The number of ant:30 Parameters of the important degree of information elements:1 Parameters of the important degree of the Heuristic factor:5 Parameters of the important degree of the heuristic factor:0.1 Pheromone increasing intensity coefficient:100 NC_max—Maximum iterations:50 m—The number of ant:30 Alpha—Parameters of the important degree of information elements:1 Beta—Parameters of the important degree of the Heuristic factor:5 Rho—Parameters of the important degree of the heuristic factor:0.1 Q—Pheromone increasing intensity coefficient:100 |
| 1: /*Initialize popsize candidates with the values between 0 and 1*/ |
| 2: FOR EACH i DO |
| 3: |
| 4: END FOR |
| 5: |
| 6: iter = 1; Evaluate the corresponding fitness function Fi |
| 7: /* Find the best value of repeatedly until the maximum iterations are reached. */ |
| 8: WHILE .() DO |
| 9: /* Find the best fitness value for each candidates */ |
| 10: FOR EACH DO |
| 11: Build neural network by using with the value |
| 12: Calculate by neural network |
| 13: /*Choose the best fitness value of the ith candidate in history */ |
| 14: IF (pBesti > fitness()) THEN |
| 15: pBesti = fitness() |
| 16: END IF |
| 17: END FOR |
| 18: /* Choose the candidate with the best fitness value of all the candidates */ |
| 19: FOR EACH DO |
| 20: IF (gBest > pBesti) THEN |
| 21: gBest = pBesti = |
| 22: = |
| 23: END IF |
| 24: END FOR |
| 25: /*Update the values of all the candidates by using ACO’s evolution equations.*/ |
| 26: FOR EACH DO |
| 27: |
| 28: |
| 29: END FOR |
| 30: |
| 31: iter = iter + 1 |
| 32: END WHILE |
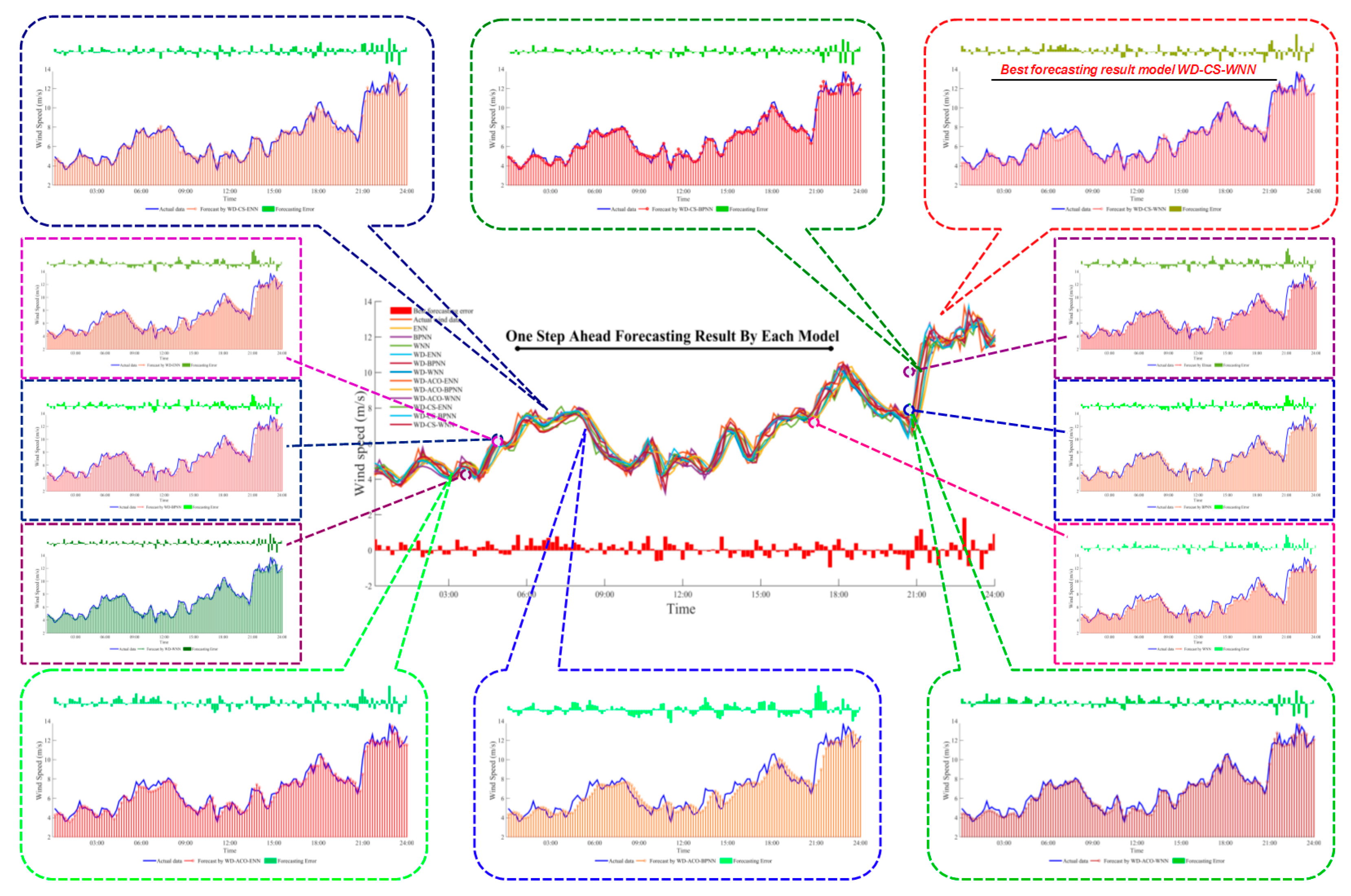
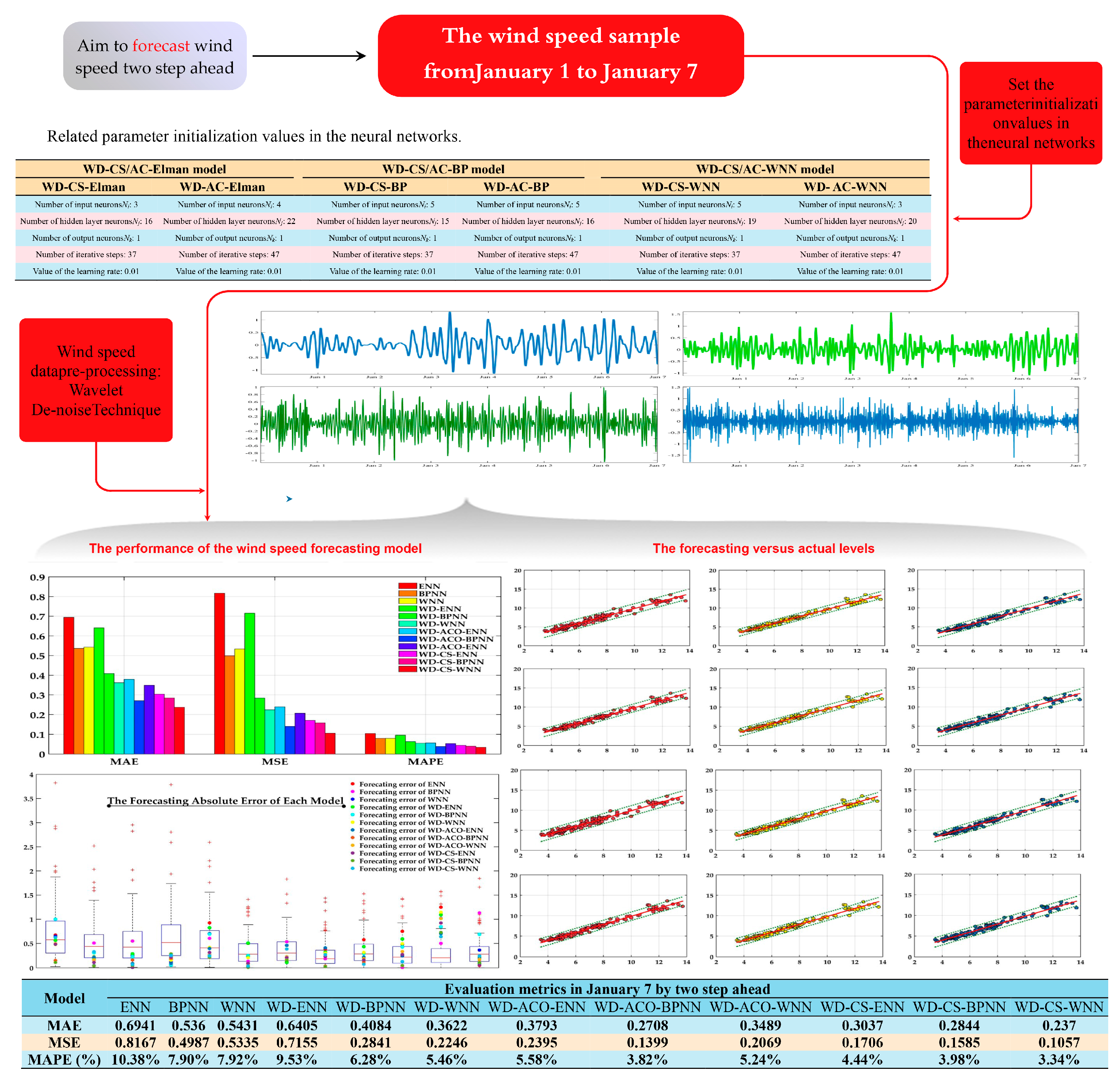
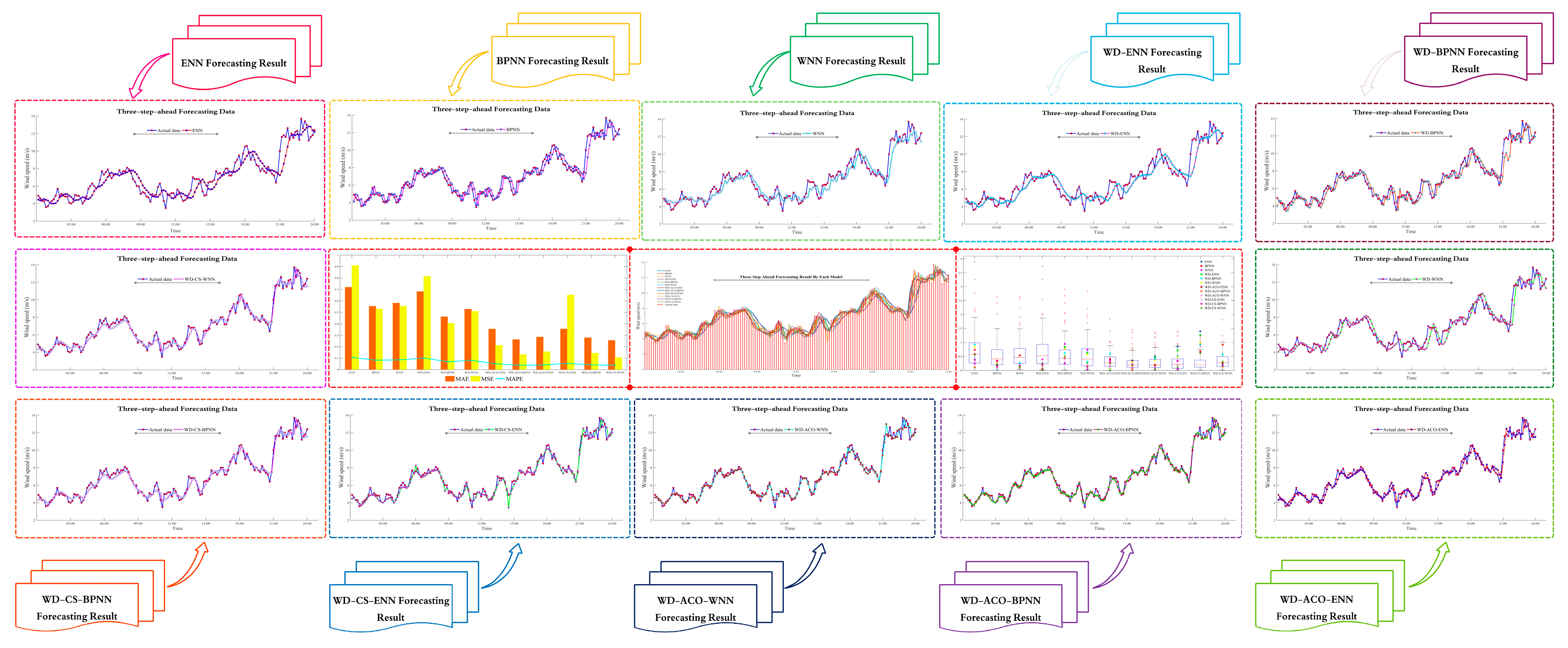
4.3. Wind Speed Forecasting Case Study
5. Conclusions
Acknowledgement
Author Contributions
Conflicts of Interest
Appendix A
| [125, 40] | [122.5, 40] | ||||||||||
| Parameter | MM | MLE | LSE | Bayesian Prior | Bayesian Posterior | MM | MLE | LSE | Bayesian Prior | Bayesian Posterior | |
| 2009 | k | 8.7667 | 8.7684 | 8.7686 | 8.775 | 8.7602 | 8.9165 | 8.9194 | 8.917 | 8.928 | 8.916 |
| c | 2.482 | 2.482 | 2.4575 | 2.4523 | 2.5002 | 2.3113 | 2.3113 | 2.3021 | 2.2635 | 2.3293 | |
| MAE | 0.0115 | 0.0092 | 0.0206 | 0.008 | 0.0145 | 0.0128 | 0.0157 | 0.0153 | 0.0177 | 0.0133 | |
| SSE | 0.1992 | 0.1649 | 0.2123 | 0.1696 | 0.1976 | 0.3635 | 0.0363 | 0.0309 | 0.0322 | 0.0224 | |
| RMSE | 0.0121 | 0.0122 | 0.0216 | 0.011 | 0.0164 | 0.018 | 0.0161 | 0.0139 | 0.014 | 0.0127 | |
| R2 | 0.9439 | 0.9441 | 0.9419 | 0.942 | 0.9447 | 0.9511 | 0.9514 | 0.9503 | 0.9466 | 0.9527 | |
| 2010 | k | 8.5254 | 8.5267 | 8.525 | 8.5162 | 8.5189 | 8.906 | 8.9078 | 8.9062 | 8.9055 | 8.8965 |
| c | 2.5432 | 2.5432 | 2.5484 | 2.5332 | 2.5607 | 2.4737 | 2.4737 | 2.4714 | 2.3815 | 2.4949 | |
| MAE | 0.0101 | 0.0086 | 0.0145 | 0.0109 | 0.0111 | 0.0123 | 0.0097 | 0.0078 | 0.0094 | 0.0106 | |
| SSE | 0.1472 | 0.134 | 0.1083 | 0.1505 | 0.1851 | 0.1979 | 0.166 | 0.1644 | 0.1116 | 0.1758 | |
| RMSE | 0.0116 | 0.0209 | 0.0193 | 0.0229 | 0.021 | 0.0119 | 0.0109 | 0.0111 | 0.0092 | 0.011 | |
| R2 | 0.8905 | 0.8908 | 0.8907 | 0.8885 | 0.8902 | 0.9056 | 0.9058 | 0.9054 | 0.8923 | 0.9068 | |
| 2011 | k | 8.6657 | 8.6678 | 8.6657 | 8.6688 | 8.6579 | 8.8481 | 8.85 | 8.8499 | 8.8562 | 8.8493 |
| c | 2.4147 | 2.4147 | 2.4153 | 2.3754 | 2.437 | 2.4617 | 2.4617 | 2.4396 | 2.4272 | 2.4713 | |
| MAE | 0.0156 | 0.0136 | 0.0122 | 0.0138 | 0.013 | 0.0114 | 0.0118 | 0.0114 | 0.0107 | 0.0111 | |
| SSE | 0.2727 | 0.2412 | 0.2745 | 0.2872 | 0.3014 | 0.2065 | 0.1801 | 0.1646 | 0.1663 | 0.1287 | |
| RMSE | 0.015 | 0.012 | 0.0134 | 0.0131 | 0.0137 | 0.0125 | 0.011 | 0.012 | 0.0092 | 0.0084 | |
| R2 | 0.9386 | 0.9389 | 0.9386 | 0.935 | 0.9393 | 0.9615 | 0.9617 | 0.9604 | 0.96 | 0.9621 | |
| 2012 | k | 8.6999 | 8.7006 | 8.707 | 8.7159 | 8.6974 | 8.7481 | 8.7507 | 8.7494 | 8.7627 | 8.7487 |
| c | 2.6504 | 2.6504 | 2.5806 | 2.5914 | 2.6551 | 2.3396 | 2.3396 | 2.3128 | 2.2814 | 2.3555 | |
| MAE | 0.0171 | 0.0153 | 0.013 | 0.0145 | 0.014 | 0.0128 | 0.0114 | 0.0116 | 0.0139 | 0.0129 | |
| SSE | 0.3563 | 0.3237 | 0.279 | 0.3263 | 0.304 | 0.1998 | 0.2063 | 0.1957 | 0.205 | 0.1392 | |
| RMSE | 0.0189 | 0.0178 | 0.0176 | 0.0146 | 0.0118 | 0.014 | 0.0127 | 0.0118 | 0.0108 | 0.0123 | |
| R2 | 0.9522 | 0.9522 | 0.9451 | 0.9467 | 0.9525 | 0.9464 | 0.9466 | 0.9427 | 0.9386 | 0.9486 | |
| 2013 | k | 9.1137 | 9.1155 | 9.1173 | 9.1303 | 9.1136 | 9.3264 | 9.3291 | 9.328 | 9.3426 | 9.3066 |
| c | 2.4728 | 2.4728 | 2.4282 | 2.4069 | 2.4829 | 2.3573 | 2.3573 | 2.3302 | 2.3099 | 2.3895 | |
| MAE | 0.015 | 0.0196 | 0.0156 | 0.0172 | 0.019 | 0.0122 | 0.0163 | 0.0151 | 0.0112 | 0.0154 | |
| SSE | 0.3543 | 0.342 | 0.4021 | 0.3286 | 0.3146 | 0.3301 | 0.221 | 0.2597 | 0.2208 | 0.1968 | |
| RMSE | 0.0196 | 0.0123 | 0.016 | 0.0154 | 0.0196 | 0.0157 | 0.0156 | 0.014 | 0.0124 | 0.0141 | |
| R2 | 0.9603 | 0.9604 | 0.9549 | 0.9527 | 0.9614 | 0.9534 | 0.9535 | 0.9494 | 0.9469 | 0.9563 | |
| Frist season | k | 8.8812 | 8.8827 | 8.8828 | 8.8854 | 8.8741 | 8.7847 | 8.786 | 8.7892 | 8.7987 | 8.7844 |
| c | 2.5116 | 2.5116 | 2.4928 | 2.4921 | 2.5293 | 2.5463 | 2.5463 | 2.4959 | 2.4757 | 2.5485 | |
| MAE | 0.0149 | 0.0117 | 0.0138 | 0.0132 | 0.0106 | 0.0127 | 0.0108 | 0.0121 | 0.0104 | 0.0109 | |
| SSE | 0.3556 | 0.3537 | 0.2258 | 0.3241 | 0.2447 | 0.296 | 0.2494 | 0.2022 | 0.1519 | 0.1361 | |
| RMSE | 0.0164 | 0.0105 | 0.0112 | 0.0126 | 0.0143 | 0.0118 | 0.0118 | 0.0132 | 0.0108 | 0.0095 | |
| R2 | 0.9431 | 0.9433 | 0.9421 | 0.9424 | 0.9432 | 0.9624 | 0.9625 | 0.9573 | 0.9552 | 0.9626 | |
| Second season | k | 8.4894 | 8.4913 | 8.4912 | 8.499 | 8.4896 | 9.1952 | 9.1979 | 9.1971 | 9.2135 | 9.1931 |
| c | 2.4451 | 2.4451 | 2.4199 | 2.3963 | 2.4474 | 2.3463 | 2.3463 | 2.3114 | 2.2909 | 2.3632 | |
| MAE | 0.0138 | 0.0163 | 0.0159 | 0.0143 | 0.0142 | 0.0148 | 0.015 | 0.0108 | 0.0108 | 0.0152 | |
| SSE | 0.4155 | 0.3622 | 0.2766 | 0.4315 | 0.2447 | 0.2865 | 0.2507 | 0.2978 | 0.1967 | 0.162 | |
| RMSE | 0.0162 | 0.0141 | 0.0102 | 0.0134 | 0.0144 | 0.0151 | 0.0123 | 0.0142 | 0.0121 | 0.0102 | |
| R2 | 0.9688 | 0.9689 | 0.9674 | 0.966 | 0.969 | 0.9416 | 0.9417 | 0.9361 | 0.9333 | 0.9439 | |
| Third season | k | 8.3375 | 8.3396 | 8.3387 | 8.3478 | 8.3338 | 10.0181 | 10.0205 | 10.19 | 10.0272 | 10.0131 |
| c | 2.404 | 2.404 | 2.3842 | 2.3635 | 2.4117 | 2.4104 | 2.4104 | 2.3981 | 2.37 | 2.4253 | |
| MAE | 0.0185 | 0.0163 | 0.0154 | 0.0203 | 0.0147 | 0.0174 | 0.015 | 0.0145 | 0.0162 | 0.0139 | |
| SSE | 0.5327 | 0.4134 | 0.2902 | 0.3252 | 0.3152 | 0.3496 | 0.336 | 0.2731 | 0.1733 | 0.1516 | |
| RMSE | 0.0211 | 0.0123 | 0.0098 | 0.0125 | 0.0165 | 0.0161 | 0.019 | 0.0174 | 0.0139 | 0.0138 | |
| R2 | 0.9654 | 0.9655 | 0.9638 | 0.9623 | 0.9658 | 0.968 | 0.9682 | 0.967 | 0.9646 | 0.9689 | |
| Fourth season | k | 8.3236 | 8.3255 | 8.3257 | 8.3346 | 8.3236 | 9.8607 | 9.8634 | 9.8613 | 9.8691 | 9.8567 |
| c | 2.4474 | 2.4474 | 2.4174 | 2.3868 | 2.4502 | 2.3862 | 2.3862 | 2.3791 | 2.3379 | 2.4014 | |
| MAE | 0.0204 | 0.0206 | 0.0214 | 0.0202 | 0.0153 | 0.0231 | 0.0148 | 0.0126 | 0.0164 | 0.0201 | |
| SSE | 0.5769 | 0.3247 | 0.3222 | 0.7405 | 0.3709 | 0.4212 | 0.277 | 0.323 | 0.2356 | 0.1386 | |
| RMSE | 0.0229 | 0.0193 | 0.0148 | 0.0177 | 0.0169 | 0.0226 | 0.0136 | 0.016 | 0.0149 | 0.0143 | |
| R2 | 0.9623 | 0.9624 | 0.9594 | 0.9563 | 0.9625 | 0.9515 | 0.9517 | 0.9509 | 0.947 | 0.9525 | |
| [125, 42.5] | [120, 40] | ||||||||||
| Parameter | MM | MLE | LSE | Bayesian Prior | Bayesian Posterior | MM | MLE | LSE | Bayesian Prior | Bayesian Posterior | |
| 2009 | k | 9.3913 | 9.3939 | 9.3917 | 9.3997 | 9.3705 | 9.116 | 9.1188 | 9.1168 | 9.1292 | 9.1008 |
| c | 2.3695 | 2.3695 | 2.3637 | 2.3129 | 2.4019 | 2.3332 | 2.3332 | 2.3168 | 2.2747 | 2.3632 | |
| MAE | 0.0091 | 0.009 | 0.0085 | 0.0083 | 0.0111 | 0.0129 | 0.0118 | 0.0102 | 0.0106 | 0.0144 | |
| SSE | 0.153 | 0.1415 | 0.1098 | 0.1377 | 0.2181 | 0.2284 | 0.0192 | 0.0148 | 0.0158 | 0.0273 | |
| RMSE | 0.0105 | 0.01 | 0.0088 | 0.0114 | 0.0115 | 0.0143 | 0.0121 | 0.0113 | 0.0121 | 0.0164 | |
| R2 | 0.9483 | 0.9485 | 0.9476 | 0.9414 | 0.9496 | 0.9515 | 0.9517 | 0.9491 | 0.9425 | 0.9546 | |
| 2010 | k | 9.3789 | 9.3816 | 9.3804 | 9.3937 | 9.3694 | 9.2611 | 9.2637 | 9.2621 | 9.2731 | 9.2589 |
| c | 2.3631 | 2.3631 | 2.3398 | 2.3223 | 2.3857 | 2.3693 | 2.3693 | 2.3525 | 2.3225 | 2.3851 | |
| MAE | 0.0106 | 0.0098 | 0.0174 | 0.0197 | 0.0122 | 0.0135 | 0.0134 | 0.0132 | 0.0106 | 0.0123 | |
| SSE | 0.2211 | 0.0192 | 0.0219 | 0.0352 | 0.0228 | 0.2617 | 0.0203 | 0.0228 | 0.0207 | 0.026 | |
| RMSE | 0.0116 | 0.0103 | 0.0166 | 0.0166 | 0.012 | 0.0155 | 0.0128 | 0.0134 | 0.0112 | 0.013 | |
| R2 | 0.9563 | 0.9565 | 0.9532 | 0.9513 | 0.9586 | 0.9521 | 0.9523 | 0.95 | 0.9465 | 0.9538 | |
| 2011 | k | 9.4401 | 9.4418 | 9.441 | 9.4427 | 9.4286 | 9.3573 | 9.3596 | 9.3576 | 9.3635 | 9.3551 |
| c | 2.4878 | 2.4878 | 2.4768 | 2.4519 | 2.5089 | 2.4081 | 2.4081 | 2.4034 | 2.3843 | 2.4221 | |
| MAE | 0.0084 | 0.0081 | 0.0084 | 0.0088 | 0.0072 | 0.0122 | 0.0103 | 0.0099 | 0.0094 | 0.0114 | |
| SSE | 0.135 | 0.1316 | 0.116 | 0.1334 | 0.1318 | 0.1997 | 0.1684 | 0.1908 | 0.164 | 0.1707 | |
| RMSE | 0.0091 | 0.0085 | 0.0092 | 0.0099 | 0.0085 | 0.0128 | 0.0127 | 0.0126 | 0.0124 | 0.0106 | |
| R2 | 0.9435 | 0.9437 | 0.9427 | 0.9406 | 0.9439 | 0.9523 | 0.9525 | 0.9522 | 0.9516 | 0.9527 | |
| 2012 | k | 9.474 | 9.477 | 9.4752 | 9.491 | 9.4718 | 9.5578 | 9.5602 | 9.5604 | 9.5754 | 9.5567 |
| c | 2.3138 | 2.3138 | 2.2888 | 2.2702 | 2.3311 | 2.4041 | 2.4041 | 2.3672 | 2.3377 | 2.4165 | |
| MAE | 0.0115 | 0.0114 | 0.0097 | 0.0078 | 0.0097 | 0.0113 | 0.0123 | 0.0114 | 0.0124 | 0.0115 | |
| SSE | 0.1659 | 0.1368 | 0.1236 | 0.1678 | 0.1288 | 0.1955 | 0.1764 | 0.1677 | 0.1943 | 0.2051 | |
| RMSE | 0.0117 | 0.0113 | 0.0089 | 0.0089 | 0.011 | 0.0153 | 0.0128 | 0.0136 | 0.0128 | 0.0139 | |
| R2 | 0.9501 | 0.9502 | 0.9465 | 0.9443 | 0.9523 | 0.9451 | 0.9452 | 0.9392 | 0.9346 | 0.9469 | |
| 2013 | k | 9.9172 | 9.92 | 9.9183 | 9.9305 | 9.8908 | 9.8139 | 9.8168 | 9.815 | 9.8281 | 9.8021 |
| c | 2.3632 | 2.3632 | 2.3463 | 2.3296 | 2.3979 | 2.3461 | 2.3461 | 2.3276 | 2.3049 | 2.3697 | |
| MAE | 0.0088 | 0.0126 | 0.0101 | 0.0108 | 0.011 | 0.0128 | 0.0133 | 0.012 | 0.0156 | 0.0143 | |
| SSE | 0.1737 | 0.1448 | 0.1612 | 0.1798 | 0.1817 | 0.2652 | 0.1911 | 0.2227 | 0.1907 | 0.284 | |
| RMSE | 0.0129 | 0.0097 | 0.0145 | 0.0152 | 0.0107 | 0.0154 | 0.0113 | 0.0163 | 0.0139 | 0.0135 | |
| R2 | 0.9099 | 0.9101 | 0.9075 | 0.9056 | 0.9126 | 0.9352 | 0.9354 | 0.9328 | 0.9304 | 0.9371 | |
| Frist season | k | 8.8483 | 8.8504 | 8.8494 | 8.8555 | 8.8373 | 8.5098 | 8.511 | 8.512 | 8.5129 | 8.5088 |
| c | 2.4295 | 2.4295 | 2.415 | 2.3759 | 2.4538 | 2.5505 | 2.5505 | 2.5258 | 2.5243 | 2.5537 | |
| MAE | 0.0108 | 0.0098 | 0.0076 | 0.0092 | 0.0909 | 0.0115 | 0.0104 | 0.0095 | 0.0111 | 0.0086 | |
| SSE | 0.233 | 0.2075 | 0.1337 | 0.1205 | 0.2132 | 0.256 | 0.1912 | 0.1854 | 0.2061 | 0.2218 | |
| RMSE | 0.0126 | 0.119 | 0.009 | 0.0086 | 0.1062 | 0.0134 | 0.0126 | 0.0116 | 0.0125 | 0.0107 | |
| R2 | 0.938 | 0.9382 | 0.9362 | 0.931 | 0.9397 | 0.9598 | 0.9599 | 0.9589 | 0.9589 | 0.9598 | |
| Second season | k | 9.6043 | 9.6064 | 9.6055 | 9.6124 | 9.6005 | 8.512 | 8.5142 | 8.5111 | 8.5123 | 8.506 |
| c | 2.4357 | 2.4357 | 2.4202 | 2.3852 | 2.4497 | 2.3962 | 2.3962 | 2.4099 | 2.3319 | 2.4178 | |
| MAE | 0.0097 | 0.0114 | 0.0092 | 0.0106 | 0.1252 | 0.0142 | 0.0086 | 0.0118 | 0.0111 | 0.0108 | |
| SSE | 0.2289 | 0.2304 | 0.1575 | 0.1511 | 0.2289 | 0.2775 | 0.194 | 0.2431 | 0.2149 | 0.2718 | |
| RMSE | 0.0131 | 0.126 | 0.0094 | 0.0091 | 0.1431 | 0.0138 | 0.0108 | 0.0154 | 0.0114 | 0.0112 | |
| R2 | 0.96 | 0.9602 | 0.9584 | 0.9544 | 0.9612 | 0.941 | 0.9412 | 0.9414 | 0.9367 | 0.941 | |
| Third season | k | 10.6024 | 10.6045 | 10.6047 | 10.6118 | 10.5606 | 9.1138 | 9.1158 | 9.1144 | 9.1175 | 9.097 |
| c | 2.4809 | 2.4809 | 2.4578 | 2.4353 | 2.5237 | 2.4523 | 2.4523 | 2.4452 | 2.4137 | 2.4805 | |
| MAE | 0.0152 | 0.0158 | 0.0111 | 0.0099 | 0.1236 | 0.0133 | 0.0103 | 0.0122 | 0.0159 | 0.0168 | |
| SSE | 0.2674 | 0.2676 | 0.1401 | 0.1755 | 0.2621 | 0.3613 | 0.2327 | 0.2206 | 0.2689 | 0.2856 | |
| RMSE | 0.0125 | 0.1726 | 0.0141 | 0.0141 | 0.1475 | 0.0152 | 0.0134 | 0.0187 | 0.0159 | 0.0137 | |
| R2 | 0.9241 | 0.9242 | 0.9208 | 0.9177 | 0.9268 | 0.9434 | 0.9436 | 0.9427 | 0.9392 | 0.9443 | |
| Fourth season | k | 10.4945 | 10.4971 | 10.4953 | 10.5032 | 10.4674 | 8.9929 | 8.9946 | 8.9945 | 8.9987 | 8.9824 |
| c | 2.4081 | 2.4081 | 2.3979 | 2.3609 | 2.4402 | 2.4898 | 2.4898 | 2.4709 | 2.4613 | 2.5114 | |
| MAE | 0.0223 | 0.0155 | 0.0122 | 0.0137 | 0.1556 | 0.018 | 0.016 | 0.0121 | 0.0187 | 0.0114 | |
| SSE | 0.2982 | 0.2365 | 0.1894 | 0.1714 | 0.3003 | 0.3541 | 0.2217 | 0.2847 | 0.3054 | 0.3246 | |
| RMSE | 0.0163 | 0.1347 | 0.017 | 0.0142 | 0.1822 | 0.0214 | 0.0175 | 0.0206 | 0.0178 | 0.0137 | |
| R2 | 0.9404 | 0.9406 | 0.9393 | 0.9349 | 0.9417 | 0.9403 | 0.9405 | 0.9385 | 0.9379 | 0.9412 | |
References
- Liu, F.J.; Chang, T.P. Validity analysis of maximum entropy distribution based on different moment constraints for wind energy assessment. Energy 2011, 36, 1820–1826. [Google Scholar] [CrossRef]
- Al-Yahyai, S.; Charabi, Y.; Al-Badi, A.; Gastli, A. Nested ensemble NWP approach for wind energy assessment. Renew. Energy 2012, 37, 150–160. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Chi, D. Wind energy potential assessment for the site of Inner Mongolia in China. Renew. Sust. Energ. Rev. 2013, 21, 215–228. [Google Scholar] [CrossRef]
- Jung, S.; Kwon, S.-D. Weighted error functions in artificial neural networks for improved wind energy potential estimation. Appl. Energ. 2013, 111, 778–790. [Google Scholar] [CrossRef]
- Boudia, S.M.; Benmansour, A.; Ghellai, N.; Benmedjahed, M.; Hellal, M.A.T. Temporal assessment of wind energy resource at four locations in Algerian Sahara. Energy Convers. Manag. 2013, 76, 654–664. [Google Scholar] [CrossRef]
- Quan, P.; Leephakpreeda, T. Assessment of wind energy potential for selecting wind turbines: An application to Thailand. Sustain. Energy Technol. Assess. 2015, 11, 17–26. [Google Scholar] [CrossRef]
- Siyal, S.H.; Mörtberg, U.; Mentis, D.; Welsch, M.; Babelon, I.; Howells, M. Wind energy assessment considering geographic and environmental restrictions in Sweden: A GIS-based approach. Energy 2015, 83, 447–461. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Wang, H. Short-term wind speed forecasting based on spectral clustering and optimised echo state networks. Renew. Energy 2015, 78, 599–608. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Short-term wind speed prediction using empirical wavelet transform and Gaussian process regression. Energy 2015, 93, 1456–1466. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E.P. Linear and non-linear autoregressive models for short-term wind speed Forecasting. Energy Convers. Manag. 2016, 112, 115–124. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S.; Zhou, Q.; Jiang, H. Medium-term wind speeds forecasting utilizing hybrid models for three different sites in Xinjiang, China. Renew. Energy 2015, 76, 91–101. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Wei, X. A hybrid wind speed forecasting model based on phase space reconstruction theory and Markov model: A case study of wind farms in northwest China. Energy 2015, 91, 556–572. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Ma, K.; Zhang, Y. A self-adaptive hybrid approach for wind speed forecasting. Renew. Energy 2015, 78, 374–385. [Google Scholar] [CrossRef]
- Shukur, O.B.; Lee, M.H. Daily wind speed forecasting through hybrid KF-ANN model based on ARIMA. Renew. Energy 2015, 76, 637–647. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Fei, S.W. A hybrid model of EMD and multiple-kernel RVR algorithm for wind speed prediction. Electr. Power Energy Syst. 2016, 78, 910–915. [Google Scholar] [CrossRef]
- Tuba, M.; Subotic, M.; Stanarevic, N. Modified cuckoo search algorithm for unconstrained optimization problems. In Proceedings of the European Computing Conference, Paris, France, 28–30 April 2011; pp. 263–268.
- Cheng, Y. The basic principle and applications of ACA. Pioneer. Sci. Technol. Mon. 2011, 4, 117–121. [Google Scholar]
- Wang, X.; Ni, J.; Wan, W. Research on the ant colony optimization algorithm with multi-population hierarchy evolution. In Advances in Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; pp. 222–230. [Google Scholar]
- Alavi, K.O.; Mostafaeipour, A.; Goudarzi, N.; Jalilvand, M. Assessing different parameters estimation methods of Weibull distribution to compute wind power density. Energy Convers. Manag. 2016, 108, 322–335. [Google Scholar]
- Guo, Z.; Wu, J.; Lu, H.; Wang, J. A case study on a hybrid wind speed forecasting method using BP neural network. Knowl.-Based Syst. 2011, 24, 1048–1056. [Google Scholar] [CrossRef]
- Xun, L.; Xie, H. Wavelet neural networks based on Genetic algorithm. Comput. Digit. Eng. 2007, 35, 5–7. [Google Scholar]
- Lin, F.J.; Kung, Y.S.; Chen, S.Y.; Liu, Y.H. Recurrent wavelet-based Elman neural network control for multi-axis motion control stage using linear ultrasonic motors. IET Electri. Power Appl. 2010, 4, 314–332. [Google Scholar] [CrossRef]
- Mabrouk, A.B.; Abdallah, N.B.; Dhifaoui, Z. Wavelet decomposition and autoregressive model for time series prediction. Appl. Math. Comput. 2008, 199, 334–340. [Google Scholar] [CrossRef]
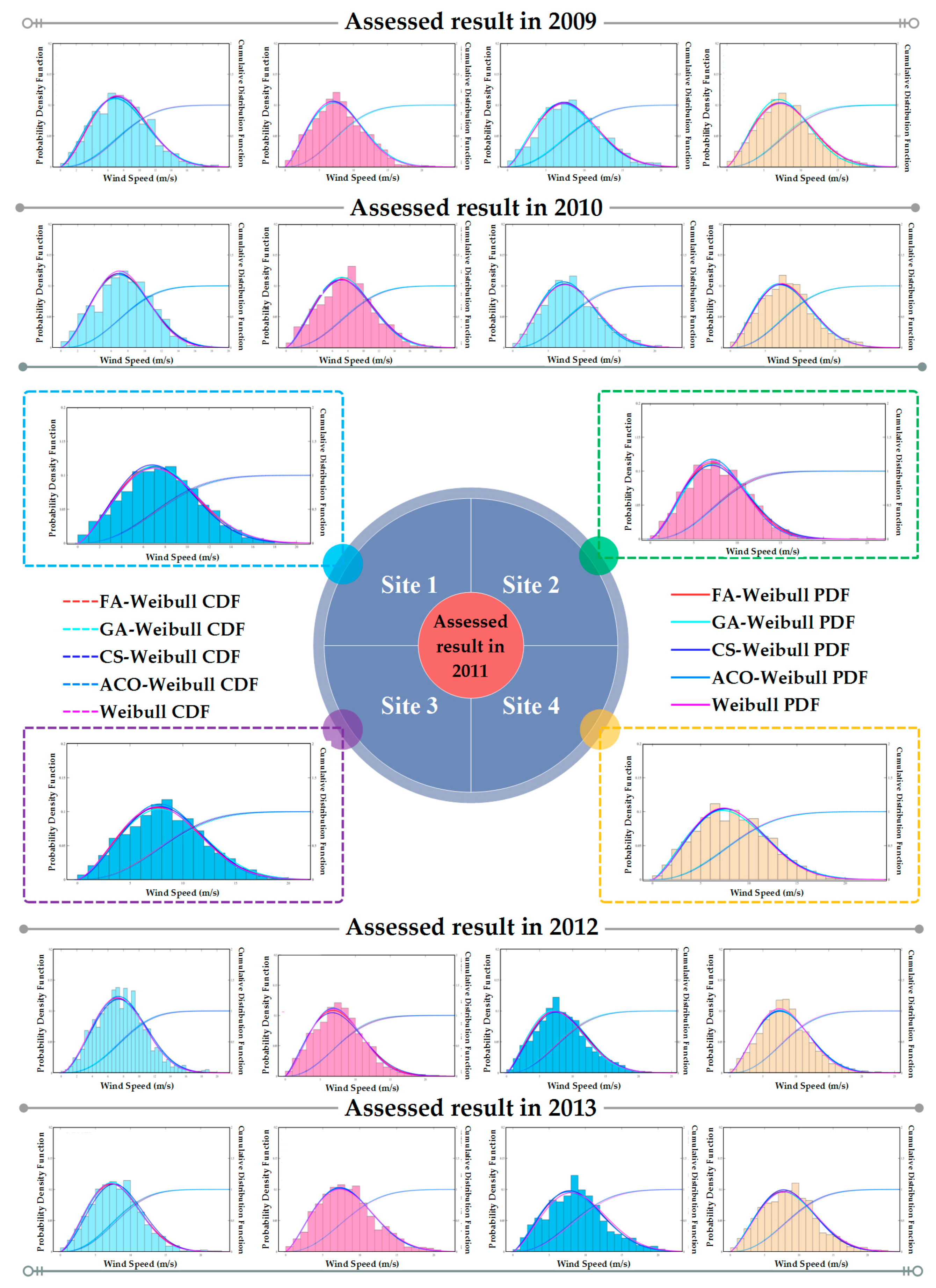

| Year | Location | Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| k | c | k | c | k | c | k | c | k | c | ||
| 2009 | [125, 40] | 8.7640 | 2.4639 | 8.8335 | 2.4720 | 8.6774 | 2.3610 | 8.7977 | 2.5163 | 8.6647 | 2.3911 |
| [122.5, 40] | 8.9071 | 2.2820 | 8.9486 | 2.3102 | 8.9575 | 2.3271 | 8.9068 | 2.2727 | 9.0692 | 2.2952 | |
| [125, 42.5] | 9.3749 | 2.3343 | 9.3496 | 2.3395 | 9.4958 | 2.3334 | 9.2328 | 2.3137 | 9.5514 | 2.2632 | |
| [120, 40] | 9.1034 | 2.2975 | 9.0616 | 2.2924 | 9.0640 | 2.2824 | 9.0777 | 2.2848 | 9.0771 | 2.2464 | |
| 2010 | [125, 40] | 8.5128 | 2.5368 | 8.4264 | 2.5082 | 8.5374 | 2.4931 | 8.4146 | 2.6055 | 8.4698 | 2.5977 |
| [122.5, 40] | 8.8703 | 2.4150 | 8.8024 | 2.3689 | 8.9940 | 2.4491 | 8.8427 | 2.3433 | 8.8317 | 2.3450 | |
| [125, 42.5] | 9.3758 | 2.3384 | 9.4127 | 2.4018 | 9.4375 | 2.2186 | 9.1811 | 2.3137 | 9.2791 | 2.3050 | |
| [120, 40] | 9.2529 | 2.3407 | 9.3029 | 2.3145 | 9.2146 | 2.2642 | 9.2177 | 2.3221 | 9.2638 | 2.2973 | |
| 2011 | [125, 40] | 8.6536 | 2.3900 | 8.5027 | 2.4063 | 8.7914 | 2.4158 | 8.7627 | 2.3635 | 8.4863 | 2.4199 |
| [122.5, 40] | 8.8432 | 2.4407 | 8.9470 | 2.3791 | 8.6923 | 2.5384 | 8.7069 | 2.4521 | 8.7714 | 2.4255 | |
| [125, 42.5] | 9.4285 | 2.4654 | 9.4127 | 2.4018 | 9.4375 | 2.2186 | 9.1811 | 2.3137 | 9.2791 | 2.3050 | |
| [120, 40] | 9.3535 | 2.3933 | 9.3490 | 2.4015 | 9.4402 | 2.4068 | 9.2729 | 2.3980 | 9.4762 | 2.3849 | |
| 2012 | [125, 40] | 8.7022 | 2.6191 | 8.8743 | 2.6429 | 8.7155 | 2.7055 | 8.6536 | 2.6316 | 8.5899 | 2.6867 |
| [122.5, 40] | 8.7489 | 2.3077 | 8.8006 | 2.2135 | 8.6432 | 2.3733 | 8.6839 | 2.3543 | 8.7321 | 2.3135 | |
| [125, 42.5] | 9.4797 | 2.2912 | 9.6149 | 2.2855 | 9.6716 | 2.3484 | 9.3894 | 2.2559 | 9.3296 | 2.2571 | |
| [120, 40] | 9.5509 | 2.3681 | 9.5599 | 2.3318 | 9.6412 | 2.3350 | 9.4275 | 2.3973 | 9.5487 | 2.3346 | |
| 2013 | [125, 40] | 9.1047 | 2.4338 | 9.3672 | 2.5225 | 8.9671 | 2.4108 | 9.0099 | 2.4329 | 9.0650 | 2.4348 |
| [122.5, 40] | 9.3218 | 2.3288 | 9.2955 | 2.3155 | 9.2901 | 2.3395 | 9.3866 | 2.2920 | 9.3724 | 2.4228 | |
| [125, 42.5] | 9.9150 | 2.3428 | 9.6149 | 2.2855 | 9.6716 | 2.3484 | 9.3894 | 2.2559 | 9.3296 | 2.2571 | |
| [120, 40] | 9.8089 | 2.3211 | 9.7684 | 2.3783 | 9.8906 | 2.3387 | 9.9891 | 2.3479 | 9.4410 | 2.2976 | |
| Year | Metric | Location [125, 40] | Location [122.5, 40] | ||||||||
| Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | ||
| 2009 | MAE | 0.01 | 0.008 | 0.0166 | 0.0079 | 0.0114 | 0.0127 | 0.0122 | 0.0124 | 0.014 | 0.0117 |
| SSE | 0.1752 | 0.1615 | 0.1697 | 0.1688 | 0.1665 | 0.2856 | 0.0283 | 0.0278 | 0.0274 | 0.02 | |
| RMSE | 0.011 | 0.0096 | 0.0167 | 0.0095 | 0.0133 | 0.014 | 0.0131 | 0.013 | 0.0129 | 0.011 | |
| R2 | 0.9594 | 0.9689 | 0.9677 | 0.9689 | 0.969 | 0.9638 | 0.9677 | 0.9679 | 0.9675 | 0.9693 | |
| 2010 | MAE | 0.0089 | 0.0086 | 0.014 | 0.0098 | 0.0095 | 0.01 | 0.0096 | 0.007 | 0.008 | 0.0094 |
| SSE | 0.1366 | 0.1163 | 0.0977 | 0.1315 | 0.1751 | 0.1744 | 0.162 | 0.1434 | 0.1081 | 0.1546 | |
| RMSE | 0.0097 | 0.017 | 0.015 | 0.0219 | 0.021 | 0.0109 | 0.01 | 0.0094 | 0.0082 | 0.0098 | |
| R2 | 0.9812 | 0.9836 | 0.9837 | 0.9852 | 0.9824 | 0.9723 | 0.9735 | 0.975 | 0.9758 | 0.9738 | |
| 2011 | MAE | 0.0098 | 0.0081 | 0.0075 | 0.0074 | 0.0071 | 0.0155 | 0.0145 | 0.0152 | 0.0154 | 0.0156 |
| SSE | 0.1684 | 0.0137 | 0.0102 | 0.0098 | 0.0102 | 0.4313 | 0.3707 | 0.4039 | 0.3945 | 0.3968 | |
| RMSE | 0.0107 | 0.0107 | 0.0093 | 0.0091 | 0.0093 | 0.0172 | 0.0153 | 0.0152 | 0.0168 | 0.0172 | |
| R2 | 0.9732 | 0.9864 | 0.9871 | 0.9865 | 0.9878 | 0.9612 | 0.974 | 0.9726 | 0.9732 | 0.9726 | |
| 2012 | MAE | 0.0112 | 0.0102 | 0.0101 | 0.0088 | 0.0098 | 0.0127 | 0.0122 | 0.0117 | 0.011 | 0.0107 |
| SSE | 0.2196 | 0.2012 | 0.1727 | 0.1568 | 0.1957 | 0.2939 | 0.2633 | 0.2509 | 0.2767 | 0.2603 | |
| RMSE | 0.0122 | 0.0107 | 0.0116 | 0.0109 | 0.0106 | 0.0142 | 0.0141 | 0.0098 | 0.0145 | 0.0089 | |
| R2 | 0.9611 | 0.9679 | 0.9689 | 0.9675 | 0.9677 | 0.9621 | 0.9719 | 0.973 | 0.9702 | 0.973 | |
| 2013 | MAE | 0.012 | 0.0115 | 0.0109 | 0.0107 | 0.0106 | 0.0098 | 0.0091 | 0.0091 | 0.0096 | 0.0096 |
| SSE | 0.2509 | 0.2404 | 0.2406 | 0.2477 | 0.2408 | 0.1691 | 0.1472 | 0.1584 | 0.1353 | 0.1193 | |
| RMSE | 0.0131 | 0.0114 | 0.0114 | 0.0109 | 0.0108 | 0.0108 | 0.0092 | 0.0095 | 0.0088 | 0.0083 | |
| R2 | 0.9588 | 0.9679 | 0.9672 | 0.9688 | 0.9685 | 0.9598 | 0.9629 | 0.9625 | 0.963 | 0.9638 | |
| Year | Metric | Location [125, 42.5] | Location [120, 40] | ||||||||
| Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | ||
| 2009 | MAE | 0.0086 | 0.0077 | 0.0078 | 0.0079 | 0.0095 | 0.0104 | 0.0104 | 0.0081 | 0.0084 | 0.012 |
| SSE | 0.1285 | 0.1181 | 0.1043 | 0.1352 | 0.1801 | 0.189 | 0.0186 | 0.0139 | 0.0128 | 0.024 | |
| RMSE | 0.0094 | 0.0089 | 0.0084 | 0.0096 | 0.011 | 0.0114 | 0.0113 | 0.0098 | 0.0094 | 0.0128 | |
| R2 | 0.9667 | 0.977 | 0.9772 | 0.9772 | 0.9753 | 0.9603 | 0.9671 | 0.9678 | 0.968 | 0.9671 | |
| 2010 | MAE | 0.0104 | 0.0082 | 0.017 | 0.0156 | 0.0111 | 0.0111 | 0.011 | 0.0112 | 0.0099 | 0.0109 |
| SSE | 0.1891 | 0.0179 | 0.0179 | 0.0292 | 0.018 | 0.2185 | 0.0198 | 0.0226 | 0.0171 | 0.0205 | |
| RMSE | 0.0114 | 0.0085 | 0.0154 | 0.0138 | 0.0109 | 0.0122 | 0.0104 | 0.0111 | 0.0097 | 0.0106 | |
| R2 | 0.96 | 0.9689 | 0.9675 | 0.9681 | 0.9682 | 0.9629 | 0.9779 | 0.9783 | 0.9783 | 0.9779 | |
| 2011 | MAE | 0.0087 | 0.008 | 0.0081 | 0.0081 | 0.0087 | 0.0106 | 0.0086 | 0.0103 | 0.0114 | 0.0114 |
| SSE | 0.1311 | 0.115 | 0.1146 | 0.1145 | 0.1159 | 0.1968 | 0.1631 | 0.1637 | 0.1681 | 0.1598 | |
| RMSE | 0.0095 | 0.0089 | 0.013 | 0.0112 | 0.0089 | 0.0116 | 0.0085 | 0.011 | 0.0111 | 0.0108 | |
| R2 | 0.972 | 0.9791 | 0.9777 | 0.9768 | 0.9777 | 0.9709 | 0.9792 | 0.9791 | 0.9787 | 0.979 | |
| 2012 | MAE | 0.0117 | 0.01 | 0.012 | 0.0075 | 0.0089 | 0.0118 | 0.01 | 0.0104 | 0.0105 | 0.0108 |
| SSE | 0.2454 | 0.2202 | 0.2079 | 0.2074 | 0.2106 | 0.2459 | 0.202 | 0.2143 | 0.241 | 0.2395 | |
| RMSE | 0.0129 | 0.01 | 0.0118 | 0.0085 | 0.0098 | 0.013 | 0.0117 | 0.0121 | 0.0129 | 0.0126 | |
| R2 | 0.9555 | 0.9677 | 0.9678 | 0.9688 | 0.9688 | 0.9527 | 0.9616 | 0.9612 | 0.9597 | 0.9606 | |
| 2013 | MAE | 0.008 | 0.0079 | 0.007 | 0.0071 | 0.0071 | 0.0094 | 0.009 | 0.009 | 0.009 | 0.009 |
| SSE | 0.1141 | 0.1094 | 0.1007 | 0.1101 | 0.1075 | 0.1605 | 0.1573 | 0.1496 | 0.1487 | 0.165 | |
| RMSE | 0.0088 | 0.0082 | 0.0081 | 0.0082 | 0.0082 | 0.0105 | 0.0101 | 0.0101 | 0.0101 | 0.0102 | |
| R2 | 0.9695 | 0.9724 | 0.9708 | 0.9719 | 0.9711 | 0.9683 | 0.9757 | 0.9758 | 0.977 | 0.9765 | |
| Year | Location | Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| k | c | k | c | k | c | k | c | k | c | ||
| First season | [125, 40] | 8.8783 | 2.4995 | 8.7346 | 2.4672 | 8.8899 | 2.4843 | 8.9504 | 2.5312 | 9.0739 | 2.5050 |
| [122.5, 40] | 8.4810 | 2.4155 | 8.5773 | 2.4602 | 8.5504 | 2.4739 | 8.4547 | 2.3004 | 8.4565 | 2.4358 | |
| [125, 42.5] | 8.3325 | 2.3793 | 8.2784 | 2.3348 | 8.4630 | 2.3661 | 8.3952 | 2.4016 | 8.3189 | 2.4561 | |
| [120, 40] | 8.3127 | 2.4108 | 8.1171 | 2.3689 | 8.1427 | 2.3983 | 8.3542 | 2.4110 | 8.3612 | 2.5259 | |
| Second season | [125, 40] | 8.8763 | 2.4987 | 8.9835 | 2.5008 | 9.0052 | 2.5024 | 8.8521 | 2.5184 | 8.8892 | 2.5043 |
| [122.5, 40] | 8.4767 | 2.4164 | 8.4805 | 2.3422 | 8.5348 | 2.4547 | 8.4797 | 2.4253 | 8.4911 | 2.3732 | |
| [125, 42.5] | 8.3273 | 2.3814 | 8.4297 | 2.4016 | 8.4137 | 2.3879 | 8.3766 | 2.3781 | 8.2740 | 2.3765 | |
| [120, 40] | 8.3089 | 2.4112 | 8.4085 | 2.4653 | 8.2526 | 2.4110 | 8.2994 | 2.3859 | 8.2654 | 2.3733 | |
| Third season | [125, 40] | 8.8758 | 2.4979 | 8.7143 | 2.4186 | 8.8830 | 2.5541 | 8.8317 | 2.5629 | 8.9194 | 2.5700 |
| [122.5, 40] | 8.4756 | 2.4155 | 8.4651 | 2.4173 | 8.4580 | 2.4278 | 8.3614 | 2.3911 | 8.3312 | 2.4068 | |
| [125, 42.5] | 8.3253 | 2.3807 | 8.4535 | 2.4995 | 8.1392 | 2.3061 | 8.4979 | 2.4102 | 8.1919 | 2.2587 | |
| [120, 40] | 8.3071 | 2.4105 | 8.3858 | 2.3251 | 8.3593 | 2.3892 | 8.2110 | 2.3520 | 8.2030 | 2.3716 | |
| Fourth season | [125, 40] | 8.5040 | 2.5343 | 8.5563 | 2.5138 | 8.4628 | 2.5109 | 8.4846 | 2.4697 | 8.5909 | 2.6049 |
| [122.5, 40] | 8.4873 | 2.3548 | 8.6227 | 2.3595 | 8.3183 | 2.3839 | 8.6632 | 2.3741 | 8.4646 | 2.3547 | |
| [125, 42.5] | 9.1023 | 2.4282 | 8.9945 | 2.3896 | 9.2803 | 2.4511 | 9.0967 | 2.5114 | 8.9921 | 2.4545 | |
| [120, 40] | 8.9880 | 2.4722 | 9.0008 | 2.4356 | 8.9397 | 2.4269 | 9.0066 | 2.5159 | 9.0729 | 2.4519 | |
| Whole five year | [125, 40] | 8.7459 | 2.4777 | 8.7803 | 2.5185 | 8.6852 | 2.4593 | 8.7637 | 2.4517 | 8.7309 | 2.5006 |
| [122.5, 40] | 8.9356 | 2.3463 | 8.9927 | 2.3533 | 8.9114 | 2.3423 | 8.9625 | 2.3901 | 8.9716 | 2.3568 | |
| [125, 42.5] | 9.5135 | 2.3473 | 9.5286 | 2.3890 | 9.5193 | 2.3575 | 9.5760 | 2.3962 | 9.4849 | 2.3152 | |
| [120, 40] | 9.4131 | 2.3379 | 9.4744 | 2.3499 | 9.3931 | 2.2968 | 9.5049 | 2.3542 | 9.3308 | 2.3495 | |
| Year | Metric | Location [125, 40] | Location [122.5, 40] | ||||||||
| Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | ||
| First season | MAE | 0.01 | 0.0096 | 0.0071 | 0.0088 | 0.0093 | 0.0171 | 0.0162 | 0.0165 | 0.0164 | 0.0167 |
| SSE | 0.2175 | 0.02 | 0.0192 | 0.0207 | 0.0205 | 0.641 | 0.6625 | 0.6353 | 0.6556 | 0.6049 | |
| RMSE | 0.0109 | 0.01 | 0.0087 | 0.0073 | 0.0106 | 0.0187 | 0.0151 | 0.0176 | 0.017 | 0.0174 | |
| R2 | 0.9734 | 0.9785 | 0.9781 | 0.9793 | 0.979 | 0.9572 | 0.9635 | 0.9612 | 0.9627 | 0.963 | |
| Second season | MAE | 0.01 | 0.0091 | 0.0095 | 0.0091 | 0.0097 | 0.0172 | 0.0127 | 0.0109 | 0.0102 | 0.0167 |
| SSE | 0.2177 | 0.1976 | 0.2981 | 0.14 | 0.1428 | 0.6421 | 0.5993 | 0.35 | 0.4908 | 0.613 | |
| RMSE | 0.0109 | 0.0085 | 0.0104 | 0.0072 | 0.0072 | 0.0188 | 0.0167 | 0.0127 | 0.0151 | 0.0147 | |
| R2 | 0.9733 | 0.9792 | 0.9789 | 0.9792 | 0.979 | 0.9572 | 0.9609 | 0.9613 | 0.9605 | 0.958 | |
| Third season | MAE | 0.01 | 0.0897 | 0.0666 | 0.0651 | 0.0585 | 0.0172 | 0.016 | 0.0128 | 0.0149 | 0.0159 |
| SSE | 0.2176 | 0.2109 | 0.1801 | 0.1298 | 0.1574 | 0.6423 | 0.0626 | 0.0454 | 0.0481 | 0.058 | |
| RMSE | 0.0109 | 0.0102 | 0.0094 | 0.008 | 0.0088 | 0.0188 | 0.0169 | 0.0144 | 0.0148 | 0.0163 | |
| R2 | 0.9733 | 0.9737 | 0.9734 | 0.9739 | 0.9738 | 0.9571 | 0.9619 | 0.9627 | 0.9636 | 0.9634 | |
| Fourth season | MAE | 0.0122 | 0.0114 | 0.0108 | 0.0115 | 0.0104 | 0.0105 | 0.0097 | 0.0095 | 0.0095 | 0.01 |
| SSE | 0.3312 | 0.273 | 0.2068 | 0.2739 | 0.236 | 0.2397 | 0.1982 | 0.1979 | 0.1291 | 0.1055 | |
| RMSE | 0.0135 | 0.0104 | 0.009 | 0.0104 | 0.0115 | 0.0115 | 0.0105 | 0.0105 | 0.0085 | 0.0077 | |
| R2 | 0.9691 | 0.9693 | 0.9697 | 0.9693 | 0.9703 | 0.977 | 0.9813 | 0.9825 | 0.9832 | 0.9826 | |
| Whole five year | MAE | 0.0131 | 0.0114 | 0.0129 | 0.0115 | 0.0106 | 0.015 | 0.0141 | 0.013 | 0.0116 | 0.0198 |
| SSE | 1.4982 | 1.4616 | 1.3454 | 1.2164 | 1.1307 | 1.9688 | 1.7822 | 1.5466 | 1.6229 | 1.7183 | |
| RMSE | 0.0143 | 0.014 | 0.0134 | 0.0127 | 0.0123 | 0.0164 | 0.0153 | 0.0118 | 0.0134 | 0.0183 | |
| R2 | 0.9645 | 0.9785 | 0.9786 | 0.9784 | 0.9786 | 0.9568 | 0.9688 | 0.9693 | 0.9694 | 0.9681 | |
| Year | Metric | Location [125, 42.5] | Location [120, 40] | ||||||||
| Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | Weibull | FA-Weibull | GA-Weibull | CS-Weibull | AC-Weibull | ||
| First season | MAE | 0.0126 | 0.0126 | 0.0122 | 0.011 | 0.0087 | 0.0151 | 0.0133 | 0.0114 | 0.0118 | 0.0072 |
| SSE | 0.3507 | 0.0288 | 0.0323 | 0.0234 | 0.0186 | 0.4995 | 0.4634 | 0.3285 | 0.3661 | 0.2851 | |
| RMSE | 0.0139 | 0.0109 | 0.0116 | 0.0098 | 0.0088 | 0.0165 | 0.0159 | 0.0134 | 0.0142 | 0.0125 | |
| R2 | 0.9644 | 0.9688 | 0.9679 | 0.9684 | 0.969 | 0.9589 | 0.9652 | 0.9658 | 0.9631 | 0.966 | |
| Second season | MAE | 0.0127 | 0.0114 | 0.0118 | 0.0096 | 0.0125 | 0.0151 | 0.0138 | 0.0147 | 0.0131 | 0.0149 |
| SSE | 0.3517 | 0.0308 | 0.0367 | 0.0319 | 0.0333 | 0.5005 | 0.4468 | 0.4697 | 0.3217 | 0.4802 | |
| RMSE | 0.0139 | 0.0115 | 0.0126 | 0.0117 | 0.012 | 0.0166 | 0.0127 | 0.0155 | 0.0107 | 0.0147 | |
| R2 | 0.9645 | 0.967 | 0.9664 | 0.9665 | 0.9665 | 0.9589 | 0.9631 | 0.9613 | 0.9631 | 0.9624 | |
| Third season | MAE | 0.0127 | 0.0113 | 0.0141 | 0.0098 | 0.0135 | 0.0151 | 0.0115 | 0.008 | 0.0139 | 0.0109 |
| SSE | 0.3521 | 0.3095 | 0.3336 | 0.2939 | 0.3497 | 0.5009 | 0.4929 | 0.4391 | 0.4979 | 0.4929 | |
| RMSE | 0.0139 | 0.0108 | 0.0128 | 0.0088 | 0.013 | 0.0166 | 0.0162 | 0.0113 | 0.0165 | 0.0169 | |
| R2 | 0.9644 | 0.9669 | 0.9666 | 0.9673 | 0.966 | 0.9588 | 0.9618 | 0.9631 | 0.9596 | 0.9617 | |
| Fourth season | MAE | 0.0091 | 0.0089 | 0.0074 | 0.0075 | 0.0881 | 0.0096 | 0.0084 | 0.0084 | 0.0087 | 0.0085 |
| SSE | 0.1803 | 0.1769 | 0.1031 | 0.1033 | 0.1717 | 0.202 | 0.1568 | 0.157 | 0.1701 | 0.1853 | |
| RMSE | 0.0099 | 0.0962 | 0.0081 | 0.0081 | 0.0946 | 0.0105 | 0.0099 | 0.0099 | 0.0101 | 0.0101 | |
| R2 | 0.9712 | 0.976 | 0.9786 | 0.9784 | 0.9762 | 0.9712 | 0.9796 | 0.9791 | 0.9779 | 0.9785 | |
| Whole five year | MAE | 0.0116 | 0.0112 | 0.0101 | 0.0118 | 0.0143 | 0.012 | 0.0103 | 0.013 | 0.0104 | 0.0124 |
| SSE | 1.1793 | 1.6723 | 1.3886 | 1.7188 | 1.6658 | 1.2646 | 0.9585 | 1.3108 | 0.9469 | 1.2449 | |
| RMSE | 0.0127 | 0.0126 | 0.0115 | 0.0128 | 0.0159 | 0.0132 | 0.0119 | 0.0139 | 0.0118 | 0.0136 | |
| R2 | 0.9608 | 0.9692 | 0.9692 | 0.9693 | 0.9687 | 0.9602 | 0.9688 | 0.9687 | 0.969 | 0.9687 | |
| Metric | Location [125, 40] | Location [122.5, 40] | ||||
| EEMD-Weibull | SSA-Weibull | WD-Weibull | EEMD-Weibull | SSA-Weibull | WD-Weibull | |
| k | 8.6156 | 8.6133 | 8.7345 | 8.8592 | 8.8369 | 8.9252 |
| c | 3.3543 | 3.5266 | 2.2940 | 3.4234 | 3.2418 | 2.1892 |
| MAE | 0.0044 | 0.0048 | 0.0043 | 0.0053 | 0.0046 | 0.0045 |
| SSE | 0.2787 | 0.3299 | 0.3142 | 0.4161 | 0.3233 | 0.3133 |
| RMSE | 0.0062 | 0.0067 | 0.0061 | 0.0075 | 0.0067 | 0.0063 |
| R2 | 0.9861 | 0.9870 | 0.9897 | 0.9767 | 0.9826 | 0.9857 |
| Metric | Location [125, 42.5] | Location [120, 40] | ||||
| EEMD-Weibull | SSA-Weibull | WD-Weibull | EEMD-Weibull | SSA-Weibull | WD-Weibull | |
| k | 9.4236 | 9.4138 | 9.5075 | 9.2853 | 9.3002 | 9.4049 |
| c | 3.1842 | 3.1809 | 2.2305 | 3.1982 | 3.2783 | 2.2173 |
| MAE | 0.0042 | 0.0041 | 0.0041 | 0.0043 | 0.0044 | 0.0045 |
| SSE | 0.2500 | 0.2423 | 0.2454 | 0.2559 | 0.2762 | 0.2463 |
| RMSE | 0.0059 | 0.0058 | 0.0059 | 0.0059 | 0.0061 | 0.0009 |
| R2 | 0.9879 | 0.9876 | 0.9899 | 0.9884 | 0.9885 | 0.9898 |
| WD-CS/AC-ENN Model | WD-CS/AC-BPNN Model | WD-CS/AC-WNN Model | |||
|---|---|---|---|---|---|
| WD-CS-ENN | WD-AC-ENN | WD-CS-BPNN | WD-AC-BPNN | WD-CS-WNN | WD-AC-WNN |
| Number of input neurons Ni: 3 | Number of input neurons Ni: 4 | Number of input neurons Ni: 5 | Number of input neurons Ni: 5 | Number of input neurons Ni: 5 | Number of input neurons Ni: 3 |
| Number of hidden layer neurons Nj: 16 | Number of hidden layer neurons Nj: 22 | Number of hidden layer neurons Nj: 15 | Number of hidden layer neurons Nj: 16 | Number of hidden layer neurons Nj: 19 | Number of hidden layer neurons Nj: 20 |
| Number of output neurons Nk: 1 | Number of output neurons Nk: 1 | Number of output neurons Nk: 1 | Number of output neurons Nk: 1 | Number of output neurons Nk: 1 | Number of output neurons Nk: 1 |
| Maximum of iterative steps:1000 | Maximum of iterative steps: 1000 | Maximum of iterative steps: 1000 | Maximum of iterative steps: 1000 | Maximum of iterative steps: 1000 | Maximum of iterative steps: 1000 |
| Value of the learning rate: 0.01 | Value of the learning rate: 0.01 | Value of the learning rate: 0.01 | Value of the learning rate: 0.01 | Value of the learning rate: 0.01 | Value of the learning rate: 0.01 |
| Horizon | Criterion | Single Model | Model Optimized by the WD | Model Optimized by the WD and CS | Model Optimized by the WD and AC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ENN | BPNN | WNN | WD-ENN | WD-BPNN | WD-WNN | WD-CS-ENN | WD-CS-BPNN | WD-CS-WNN | WD-AC-ENN | WD-AC-BPNN | WD-AC-WNN | ||
| One-step-ahead | MAE | 0.6387 | 0.5164 | 0.5424 | 0.5579 | 0.4067 | 0.2769 | 0.2842 | 0.2681 | 0.2168 | 0.3612 | 0.2845 | 0.3131 |
| MSE | 0.6951 | 0.4561 | 0.5503 | 0.5554 | 0.2913 | 0.1484 | 0.1545 | 0.1376 | 0.0851 | 0.2203 | 0.1636 | 0.1755 | |
| MAPE | 0.0961 | 0.0770 | 0.0788 | 0.0832 | 0.0619 | 0.0593 | 0.0402 | 0.0379 | 0.0383 | 0.0534 | 0.0361 | 0.0371 | |
| Two-steps-ahead | MAE | 0.6941 | 0.5360 | 0.5431 | 0.6405 | 0.4084 | 0.3622 | 0.3037 | 0.2844 | 0.2370 | 0.3793 | 0.3408 | 0.3489 |
| MSE | 0.8167 | 0.4987 | 0.5335 | 0.7155 | 0.4541 | 0.4546 | 0.506 | 0.4585 | 0.4557 | 0.4895 | 0.4399 | 0.4469 | |
| MAPE | 0.1038 | 0.0790 | 0.0792 | 0.0953 | 0.0698 | 0.0646 | 0.0744 | 0.0698 | 0.0634 | 0.0728 | 0.0682 | 0.0684 | |
| Three-steps-ahead | MAE | 0.7199 | 0.5535 | 0.5814 | 0.6815 | 0.4620 | 0.5285 | 0.3556 | 0.3192 | 0.3153 | 0.3553 | 0.2624 | 0.2850 |
| MSE | 0.9084 | 0.7310 | 0.7546 | 0.8149 | 0.7046 | 0.6995 | 0.6527 | 0.6042 | 0.6059 | 0.2117 | 0.1310 | 0.1569 | |
| MAPE | 0.1065 | 0.0818 | 0.0850 | 0.1007 | 0.0786 | 0.0755 | 0.0845 | 0.0792 | 0.0781 | 0.0838 | 0.0677 | 0.0704 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, C.; Wu, J. Wind Energy Potential Assessment and Forecasting Research Based on the Data Pre-Processing Technique and Swarm Intelligent Optimization Algorithms. Sustainability 2016, 8, 1191. https://doi.org/10.3390/su8111191
Wang Z, Wang C, Wu J. Wind Energy Potential Assessment and Forecasting Research Based on the Data Pre-Processing Technique and Swarm Intelligent Optimization Algorithms. Sustainability. 2016; 8(11):1191. https://doi.org/10.3390/su8111191
Chicago/Turabian StyleWang, Zhilong, Chen Wang, and Jie Wu. 2016. "Wind Energy Potential Assessment and Forecasting Research Based on the Data Pre-Processing Technique and Swarm Intelligent Optimization Algorithms" Sustainability 8, no. 11: 1191. https://doi.org/10.3390/su8111191
APA StyleWang, Z., Wang, C., & Wu, J. (2016). Wind Energy Potential Assessment and Forecasting Research Based on the Data Pre-Processing Technique and Swarm Intelligent Optimization Algorithms. Sustainability, 8(11), 1191. https://doi.org/10.3390/su8111191






