International Comparison of Total Factor Ecology Efficiency: Focused on G20 from 1999–2013

Abstract

Little attention has been paid to international ecological efficiency, especially taking ecological footprint (EF), labor, and capital into account as multi-inputs to produce GDP in the total-factor framework. This study evaluates the total-factor ecological efficiency (TFEcE) of G20 during the period of 1999–2013 by employing slack-based measure (SBM) with EF as the index of comprehensive ecological inputs. Findings show that the average level of TFEcE of G20 from 1999 to 2013 is at a low level of about 0.54, which means there is a large space for the improvement of TFEcE. Furthermore, TFEcE of G20 is very imbalanced and there is a big gap between developed countries and developing countries in the G20. For the developing countries and developed countries in the G20, the analysis of factors that affect national TFEcE shows different statistical significance in the truncated regression model.

1. Introduction

Efficient ecology consumption is a top priority in the ecological field in terms of both resource conservation and control of climate change. Over the last few decades, the world has witnessed large ecological degradation problems, including increasing greenhouse gas emission, high energy consumption, deforestation, land erosion, and groundwater exhaustion. Thus, it is necessary to take both economic and ecological factors into account in policy-making. In general, accepting declining economic growth as a consequence of decreased ecological consumption is not practicable. Improving ecological efficiency, not only maximizing economic objectives but also minimizing ecological concerns, is important for every economy.

Ecological efficiency is concerned with creating more value with less impact [1]. In empirical studies, ecological efficiency has always been measured in the presence of the ratio of macroeconomic variables (especially GDP (gross domestic product)) to ecological inputs. Despite the wide-ranging literature that has investigated the relationship between GDP and ecological inputs, most of the studies have focused on utilizing CO₂ emissions or energy consumption as an indicator of ecological inputs which just represents a portion of them. Thus, to have a better understanding of ecological efficiency, this study will utilize the ecological footprint (EF) as a comprehensive indicator of ecological inputs.

Ecology input alone cannot produce any output. Ecology must be put together with other inputs, such as labor and capital, to produce GDP. Consistent with the view that single-factor energy efficiency index has some disadvantages in empirical studies [2], likewise, single-factor ecological efficiency index (ecological inputs to GDP ratio) in the previous literature would also lead to misleading conclusions. Therefore, a multi-input model considering other inputs in a total-factor framework should be applied to correctly assess the ecological efficiency.

Different from the papers such as Hu and Wang [3] who only took energy into account as ecological inputs in a total-factor framework, and different from the existing papers using EF to evaluate single-factor ecology efficiency, this paper considers EF, labor, and capital as multi-inputs to assess the ecological efficiency in a total-factor framework, and we have named this index total-factor ecological efficiency (TFEcE).

The purpose of this study is to evaluate the TFEcE of the G20 during the period of 1999–2013 by employing slacks-based measure (SBM). To our knowledge, little attention has been paid to international ecological efficiency, especially taking ecological footprint (EF), labor, and capital into account as multi-inputs to produce GDP in the total-factor framework. This paper is organized as follows. Section 2 reviews the previous studies. Section 3 gives the methodology and describes the data we use for our analysis. Section 4 presents the empirical results and discussions. Finally, Section 5 concludes this paper.

2. Literature Overview

Different from the previous research which studies the EF and total-factor framework separately, this paper combines the concept of EF with the framework of total-factor. Our study is particularly related to two strands of literature.

The first strand focuses on ecological efficiency. Ecological-efficiency is concerned with creating more value with less impact [1]. The concept of ecological efficiency was originated from environmental efficiency [4], then in 1989 Schaltegger and Sturm (1989) [5] first described it as a “business like to sustainable development”. Later, ecological efficiency was popularized by the establishment of the World Business Council for Sustainable Development (WBCSD) [6].

Although ecological efficiency assessment is a complicated and multidisciplinary task [7], it is widely measured as the ratio between the added value of a product or service and the ecological impacts of the product or service. In empirical study, GDP is often used as the numerator, and consumption of energy [3], emissions of CO₂ [8], domestic extraction [9] or material flow [10] is usually placed in the denominator as indicators of ecological pressure.

The most comprehensive measure of humanity’s overall impact may be EF, which was first proposed by Rees [11] and elaborated by Wackernagel and Rees [12]. Since then, EF is widely applied to assess sustainability. Moffatt [13] suggested that by combining EF with more methods, further detailed work of relevance to policy makers would become available. Kratena [14] described the concept of ecosystem pricing in an input-output system based on the concept of the EF. Chen et al. [15] stated that the ratio of GDP to EF can be considered as a measure of the resource efficiency. Fu et al. [16] calculated the resource productivity (RP) by using the EF as an indicator of the natural resource input and GDP as the output in the equation of RP = GDP/EF. By using the data of EF, Miao et al. [17] measured ecological carrying capacity, ecological deficit, and surplus in Anhui province in China.

The second strand of research related to this paper is concerned with total-factor framework, especially with total-factor energy efficiency. Hu and Wang [3] argued that energy alone cannot produce any output and energy needs to be put together with labor and capital in order to produce outputs. Therefore, a multiple model should be applied to correctly evaluate the energy efficiency. Under the total-factor framework, Hu and Wang [3] first proposed the total-factor energy efficiency (TFEE) index and employed it to analyze energy efficiencies of 29 administrative regions in China. By incorporating water as an input as well as using conventional inputs such as capital stock and labor employment, Hu et al. [18] calculated the total-factor water efficiency and found that there was a U-shape relation between the total-factor water efficiency and per capita real income among areas in China. Furthermore, Hu and Kao [19] studied energy-saving target ratios for 17 APEC economies and discovered an increasing trend except for Canada and New Zealand. Honma and Hu [20] employed the data envelopment analysis (DEA) to calculate the regional TFEE in Japan, and 14 inputs (3 production factors, 11 energy sources) are included in this model. Zhang et al. [21] used a total-factor framework to investigate energy efficiency in 23 developing countries during the period of 1980–2005, and found that China experienced the most rapid rise in TFEE. Chang and Hu [22] introduced the total-factor energy productivity index (TFEPI) based on the concept of TFEE and the Luenberger productivity index to evaluate the energy productivity change of regions in China. Li and Hu [23] computed the ecological total-factor energy efficiency (ETFEE) of 30 provinces in China for the period 2005–2009 through the SBM with undesirable outputs. Zhang et al. [24] proposed a metafrontier slack-based efficiency measure approach to assess ETFEE and empirically analyzed regional ETFEE of China during 2001–2010.

The first strand of literature related to ecological efficiency only regarded ecological input as a single input to produce GDP, while neglecting other key inputs such as capital and labor; the second strand of literature related to the total-factor energy efficiency only considered energy as ecological input, while ignoring other ecological inputs such as water, forest, and land. Therefore, this paper attempts to use EF as the index of comprehensive ecological inputs, as well as taking labor and capital into account, to assess the ecological efficiency of G20 in a total-factor framework.

3. Methodology and Data Source

In this section, we first calculate EF which is the aggregate area of land and water in six ecological categories, then consider EF as the comprehensive measurement of ecological inputs and introduce it into the SBM model which takes capital and labor into account, to assess the TFEcE of G20 in a total-factor framework.

3.1. Ecological Footprint

EF is a simple assessment method for sustainable development from the perspective of the aggregate area of productive lands and water required to produce all the resources consumed and to assimilate all the wastes produced [25]. EF transfers the consumption of different ecological resources into various productive lands, and the lands can be divided into six types: arable land, pasture land, forest land, fisheries land, fossil energy land, and built-up land.

The calculation method of EF from 1999–2013 for G20 is mainly based on the compound approach proposed by Wackernagel et al. [26]. The computational formula for EF is as follows:

$$\mathrm{EF}={\displaystyle \sum }\frac{P_i}{Y_{Pi}}\times Y{F}_i\times EQ{F}_i$$

(1)

In the above Equation (1), EF represents the total ecological footprint; i is the type of resource consumed by a certain amount of population; P_i is the quantity of the ith resource consumed; Y_Pi is the average productivity for producing ith type of resource; YF_i is the yield factor of ith land type, which describes the extent to which a biologically productive area in a given country is more (or less) productive than the global average of the same bioproductive area; EQF_i is the equivalence factor of ith land type, which represents the world average productivity of given productive land relative to the global average productivity of all productive lands.

The consumption of biological resources (including arable land, pasture land, forest land, and fisheries land) cannot be calculated directly, so the trade adjustment is conducted. The steps are as follows. First, calculate the biological resources manufacturing footprint based on national statistics of biological production. Second, calculate the biological resources net export trade footprint based on national trade data of biological resources. Third, deduct net export trade footprint from manufacturing footprint.

3.2. Slacks-Based Measure (SBM) Model

Data Envelopment Analysis (DEA) is a non-parametric statistical method based on linear programming technique to assess the efficiencies of decision-making units (DMU) that refer to a set of firms or a set of countries in empirical studies. Built upon the basic DEA models of Charnes et al. [27] and Banker et al. [28], Tone [29] proposed the SBM to measure efficiency based on input excesses and output shortfalls. Being a non-radial approach, SBM overcomes the conventional radial DEA method’s overestimating-limitation which is caused by neglecting slack variables [30]. Furthermore, SBM directly accounts for input and output slacks in efficiency measurements, with the advantage of capturing the whole aspect of inefficiency [24].

Assume that there are i = 1, …, N countries, and each country is a DMU using input vector $\mathit{x}\in {\mathrm{R}}_{+}^m$ to produce output vector $\mathit{y}\in {\mathrm{R}}_{+}^{\mathrm{n}}$. In this paper, the output vector is national GDP. The input vector contains EF, capital stock, and labor employment. The fractional programming problem of SBM model is expressed as follows:

Minimize

$$\mathsf{\rho }=\frac{1-\left(1/m\right){{\displaystyle \sum }}_{i=1}^m{s}_i^{-}/x_{io}}{1+\left(1/n\right){{\displaystyle \sum }}_{r=1}^n{s}_r^{+}/y_{ro}}$$

(2)

Subject to

$$\begin{array}{l}{x}_o=X\lambda +S^{-},\\ {\mathrm{y}}_o=Y\lambda -S^{+},\lambda \ge 0,\\ s^{-}\ge 0,s^{+}\ge 0.\end{array}$$

(3)

where each country has m inputs and n outputs; ${\mathrm{s}}_i^{-}$, ${\mathrm{s}}_r^{+}$, x_o, and y_o represent the input slack, the output slack, the inputs, and the outputs for the oth country respectively; S⁻, S⁺, X, and Y are the corresponding matrices of the input slack, the output slack, the inputs, and the outputs; $\lambda$ is a nonnegative multiplier vector. $\mathsf{\rho }$ is the overall efficiency score for the oth country. If $\mathsf{\rho }=1$ (which indicates that all the slack variables are 0), the oth country is SBM-efficient.

3.3. Total-Factor Ecology Efficiency (TFEcE)

TFEE in Hu and Wang [3], Li and Hu [23] is defined as:

$$\mathrm{TFEE}\left(o,t\right)=\frac{Targetenergyinput\left(o,t\right)}{Actualenergyinput\left(o,t\right)}$$

(4)

where TFEE(o,t) is the total-factor energy efficiency for region o at time t. In Hu and Wang [3], Li and Hu [23], the target energy input for each region is defined as:

$$\mathrm{Target}\mathrm{energy}\mathrm{input}\left(o,t\right)=\mathrm{Actual}\mathrm{energy}\mathrm{input}\left(o,t\right)-\mathrm{Total}\mathrm{energy}\mathrm{input}\mathrm{slack}\left(o,t\right)$$

(5)

Total energy input slacks, which can be obtained from SBM in Hu and Wang [3] and Li and Hu [23], represent the gap between the target level and actual level. Total energy input slack can be regarded as the inefficient portion of actual energy consumption.

Following the TFEE proposed by Hu and Wang [3] and Li and Hu [23], this paper uses EF instead of energy as the ecological inputs to build the index of TFEcE for country o at time t.

According to Formula (3), the input slacks are the total amount that can be reduced without decreasing the output levels. With respect to ecological inputs, the above slacks are called the “ecology input slacks” and the amount of slacks in ecological input is regarded as the inefficiency portion of actual ecological consumption. Based on the slacks of ecology input obtained from Formula (3), considering labor, capital, and EF simultaneously, we can work out the ecology-saving target ratio (ESTR). The formula is as below:

$$\mathrm{ESTR}\left(o,t\right)=\frac{\mathrm{Ecology}\mathrm{input}\mathrm{slack}\left(o,t\right)}{Actualecologyinput\left(o,t\right)}$$

(6)

where ESTR represents each country’s inefficient level of ecology consumption. ESTR ($o,t$) refers to the ESTR in the oth country and the tth year. TFEcE in this paper has the following relation with ESTR:

$$\mathrm{TFEcE}\left(o,t\right)=1-\mathrm{ESTR}\left(o,t\right)$$

(7)

where TFEcE (o, t) refers to the TFEcE in the oth country and the tth year. A zero ESTR value implies a country on the frontier with the best TFEcE up to one among the observed countries, while a country with the value of ESTR larger than zero indicates that ecology should and could be saved at the same output level. Therefore, TFEcE lies always between zero and unity and a higher TFEcE implies higher ecological efficiency in a total-factor framework.

3.4. Data and Material

The G20 member countries are chosen as the research object because they have worldwide representatives including both developed and less-developed countries. Furthermore, the GDP of G20 accounts for about 90% of the world GDP and their population accounts for about two-thirds of the world population. G20 consists of the following economies: Argentina, Australia, Brazil, Canada, France, Germany, India, Indonesia, Italy, Japan, Republic of Korea, Mexico, Russian Federation, Saudi Arabia, South Africa, Turkey, UK, USA, and China. The EU is excluded due to the incompleteness of data. The data used in this paper comes from that of 19 countries in the G20 from 1999–2013.

EF refers to various types of resources meeting the daily consumption of a certain human population. In this paper, arable products include cereals, pulses, oil crops, eggs, and vegetables. Forest products include fruit and wood. Pasture products include cattle, mutton, pig, and milk. Fisheries products include fish. Fossil energy land is related to oil, natural gas, and coal. In addition, the consumption of hydro-electricity is converted into that of built-up land.

The above data of the agricultural products (including arable products and pasture products), forest products, and fisheries products are mainly from the FAO STAT, provided by Food and Agriculture Organization of the United Nations. The consumption quantities of oil, natural gas, coal, and hydro-electric can be obtained from BP’s statistical review of world energy. We adopt the value of the equivalence factors proposed by Wackernagel and Rees [12].

In SBM model, EF, capital stock and labor are employed as inputs, and GDP as output. EF is calculated by the above method. Capital stock from 1993 to 2013 with 2005 prices is calculated using the Perpetual Inventory Method as the following equation shows:

$$K_t=I_t+K_{t-1}\left(1-\delta \right)$$

(8)

where I_t is the capital formation in the year t, which can be obtained from Penn World Table 7.1. δ is depreciation rate and is set to be 6% according to the relevant literature [31]. K_t is the capital stock in the year t. Initial capital stock is estimated by the equation proposed by Nehru and Dhareshwar [32]:

$$N{K}_i=I_i/\left(\delta +g\right)$$

(9)

where NK_i is the initial capital stock of the research period, I_i is the initial capital formation. g is the average capital growth rate during the research period. δ is depreciation rate.

Data on labor and GDP are collected from the World Development Indicators of the World Bank, and GDP is transformed into constant 2005 U.S. dollars by GDP deflators.

4. Empirical Analysis

4.1. Evaluation of EF in G20 from 1999 to 2013

As shown in Figure 1, the total EF of G20 maintains a stable growth trend from 1999 to 2013, increasing from 9.62 billion ha in 1999 to 12.03 billion ha in 2013, and achieving a growth of about 25%.

The six different land types of EF are also shown in Figure 1. Fossil energy land contributed most to the total EF among the six components, accounting for 33.77%, and followed by forest and pasture land, whose contributions were 25.38% and 23.42% respectively. Arable land ranked fourth with the percentage of 16.9%. The contributions of fisheries and built-up land to total EF were relatively small, and the average proportions were 0.03% and 0.52%, respectively.

Over the study period, the proportions of six land types have changed considerably. The EF of fisheries land was the fastest growing component during 1999–2013, and it increased by 67.75% from 2.6 million ha in 1993 to 4.4 million ha in 2013. The EF of forest land obtained the lowest growth rate of only 2%. The growth rates of pasture, arable, fossil energy, and built-up land were 29.62%, 33.69%, 40.97%, and 53.57% respectively.

The national level of EF is shown in

Table 1. EF by countries from 1999 to 2013 (10 million ha).

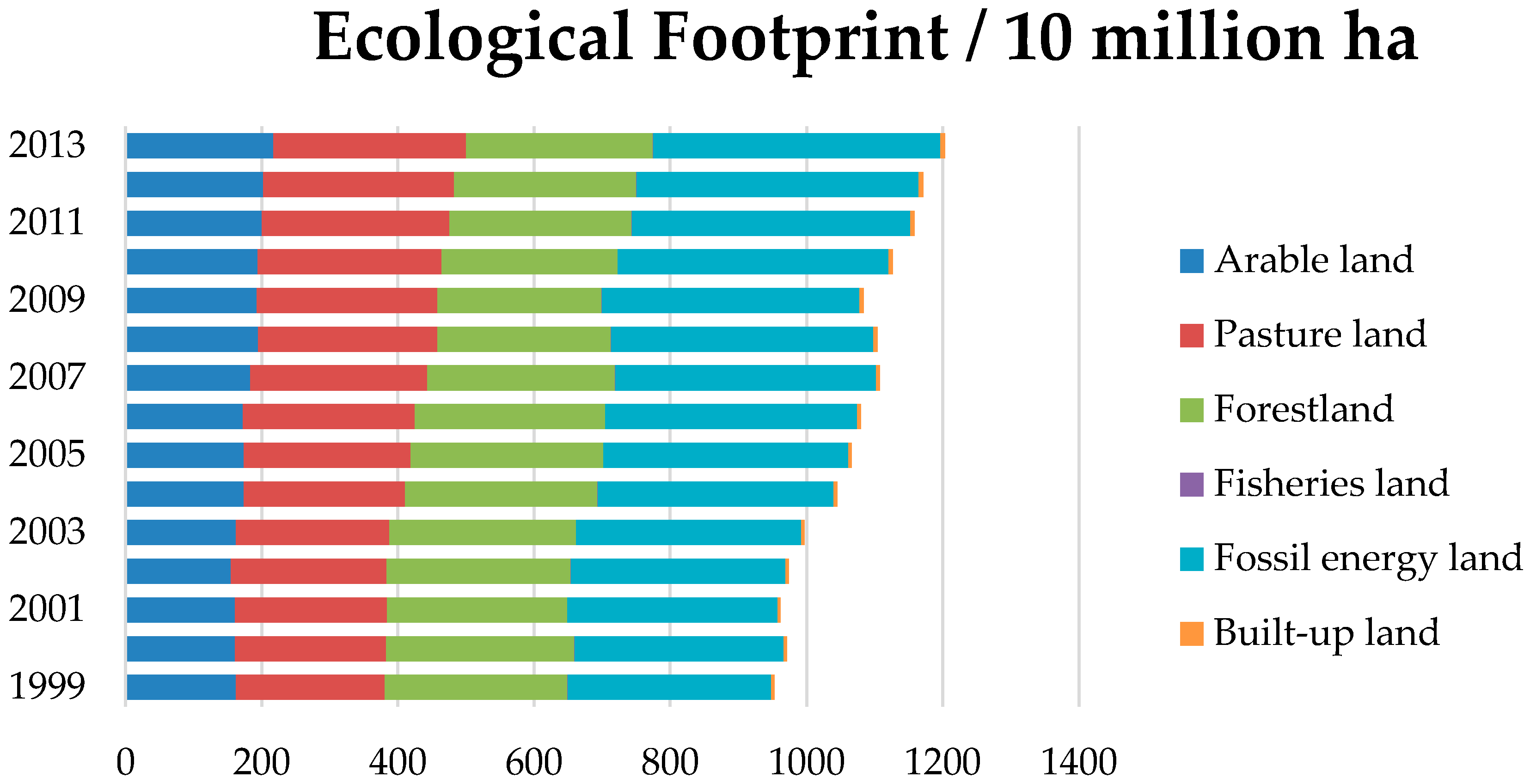
Country	1999	2001	2003	2005	2007	2009	2011	2013
Argentina	14.300	12.697	13.011	14.628	15.451	15.806	15.668	17.982
Australia	18.171	19.589	20.588	20.148	19.967	19.079	19.038	18.047
Brazil	56.337	56.131	63.123	62.603	65.376	64.610	70.363	72.958
Canada	52.264	50.286	50.966	55.581	47.944	38.424	44.034	45.613
France	32.510	32.970	31.140	31.796	31.779	30.973	30.466	29.471
Germany	39.436	39.998	41.125	42.017	44.893	40.650	42.199	43.103
India	105.680	109.126	113.883	121.451	131.497	137.890	148.858	153.258
Indonesia	28.795	26.894	29.429	28.806	29.879	31.059	34.722	35.370
Italy	22.529	21.891	22.016	22.485	21.955	20.385	20.495	18.806
Japan	36.860	35.777	36.273	36.309	35.873	32.181	33.826	35.254
Republic of Korea	12.980	13.604	14.287	14.384	15.003	15.064	16.264	16.908
Mexico	22.168	23.402	23.925	24.882	26.087	25.356	26.274	26.512
Russian	66.106	75.103	74.506	74.765	80.060	75.070	81.699	80.829
Saudi Arabia	7.237	7.731	8.707	9.747	10.553	11.609	13.195	14.351
South Africa	11.473	11.599	12.446	13.077	13.141	13.682	13.398	13.321
Turkey	14.643	14.168	15.593	16.530	18.293	18.366	21.336	23.095
UK	22.343	22.470	22.628	22.537	22.338	21.039	20.612	20.949
USA	244.785	240.907	245.511	255.476	252.503	226.666	234.256	239.207
China	153.842	156.807	167.147	209.142	234.635	254.332	281.315	298.441

. Due to the limited space, only data in some specific years are listed. According to the results in Table 1, the EF of G20 countries displays two evolving trends during the research period. Firstly, the EF of seven countries (Australia, Canada, France, Italy, Japan, UK, and USA) declined over time, with the biggest fall taking place in Italy. Secondly, the remaining 12 countries presented an upward trend in EF, with China increasing the most.

China and USA were the two countries with the highest EF. China’s EF, with the total growth of 94% from 1999 to 2013, exceeded that of the USA in 2008 and the gap of EF between China and USA extended to 59.25 10 million ha in 2013. India’s EF ranked the third and increased by nearly half from 105.68 10 million ha in 1999 to 153.26 10 million ha in 2013. Compared with these three countries, the EF of the remaining countries were at lower levels. Among all the countries, the EF of Saudi Arabia was the smallest, but its growth rate was the highest, which was 98.31%, from 7.24 10 million ha in 1993 to 14.35 10 million ha in 2013.

4.2. Analysis of the G20’s TFEcE

According to the Formulas (6) and (7) in Section 3, we calculate the TFEcE of G20, and the results are shown in

Table 2. Total-factor ecology efficiency (TFEcE) by countries (1999–2013).

Country	1999	2001	2003	2005	2007	2009	2011	2013
Argentina	0.267	0.290	0.270	0.182	0.167	0.150	0.191	0.154
Australia	0.384	0.373	0.356	0.379	0.389	0.378	0.376	0.408
Brazil	0.333	0.334	0.288	0.323	0.312	0.208	0.283	0.260
Canada	0.220	0.269	0.354	0.208	0.225	0.408	0.307	0.251
France	0.930	0.933	0.672	0.657	0.642	0.630	0.647	0.648
Germany	0.758	0.743	0.688	0.652	0.615	0.641	0.620	0.598
India	0.245	0.250	0.299	0.392	0.264	0.265	0.177	0.203
Indonesia	0.356	0.414	0.417	0.507	0.363	0.365	0.357	0.359
Italy	1.000	1.000	0.811	0.770	0.766	0.770	0.741	0.830
Japan	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
Republic of Korea	0.702	0.675	0.711	0.693	0.669	0.668	0.594	0.593
Mexico	0.557	0.569	0.574	0.425	0.508	0.580	0.568	0.614
Russian	0.467	0.629	0.436	0.394	0.230	0.121	0.238	0.239
Saudi Arabia	0.648	0.673	0.568	0.568	0.593	0.640	0.545	0.514
South Africa	0.462	0.582	0.574	0.533	0.404	0.203	0.204	0.208
Turkey	0.649	0.585	0.612	0.552	0.275	0.248	0.254	0.242
UK	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
USA	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
China	0.238	0.253	0.238	0.271	0.281	0.330	0.268	0.285
Developed countries	0.764	0.767	0.716	0.692	0.690	0.714	0.683	0.684
Developing countries	0.397	0.434	0.412	0.398	0.312	0.274	0.282	0.285

. In general, the average TFEcE of G20 from 1999 to 2013 is at a low level of about 0.54, which urgently needs to be improved. The actual ecological inputs could be reduced by almost 46%, with output unchanged, through ecological efficiency improvement. This indicates that the improvement of ecological efficiency is an effective way to maintain economic growth, and meanwhile, to relieve ecological pressure.

According to the human development index of United Nations Development Program (UNDP) and the classification of countries proposed by the World Bank, the developed countries mentioned in this study include Australia, Canada, France, Germany, Italy, Japan, Republic of Korea, Saudi Arabia, USA, and UK, and the rest belong to the developing countries.

As Table 2 presents, TFEcE of the G20 is very imbalanced. There is a big gap between developed countries and developing countries. For the average value, TFEcE of developed countries reached 0.714, double what it is in developing countries, 0.352. For the median value, TFEcE of developed countries reached 0.705, which is 1.97 times that of developing countries, 0.358. For the degree of divergence, the standard deviation of TFEcE in developed countries is 0.031, just a half of that in developing countries, 0.062. According to the gap between developed countries and developing countries in the G20 in terms of their TFEcE, it showed an upward trend with fluctuation, rising from 0.367 in 1999 to 0.399 in 2013. In 2009, the gap reached a maximum, which is 0.439.

In order to further confirm the gap between developed countries and developing countries, Mann-Whitney U rank test is applied to carry out a significance test. We can see from

Table 3. Significance test of TFEcE between developed and developing countries.

Countries	Mann-Whitney U	Wilcoxon W	Z-Value	p-Value
Developed vs. Developing	0.000	120.000	−4.666	<0.001

Notes: Mann-Whitney U test is a nonparametric test of the null hypothesis that the distribution of the two populations which the two independent samples come from has no significant difference.

, there exists a significant difference between the TFEcE of developed countries and that of developing countries.

In terms of specific countries, three countries—USA, UK, and Japan—found the optimal efficiency during the research period, and they are all developed countries. These three countries are followed by Italy, France, Republic of Korea, and Germany at 0.84, 0.71, 0.67, and 0.66, respectively. The TFEcE of Saudi Arabia, Mexico, and Turkey are around the average level of all the countries. South Africa, Indonesia, and Australia gain almost the same TFEcE, fluctuating around 0.39. The country with the lowest TFEcE score is Argentina, and the average score is 0.21 during 1999–2013.

It is worth noting that among those developed countries, TFEcEs of Canada and Australia, respectively 0.386 and 0.275, are relatively lower than other developed countries. TFEcE assessment involves input variables (EF, labor, and capital), as well as an output variable (GDP). The main reason of the lower TFEcEs of the two countries is that their EF inputs are relatively high. Statistics data can be used to illustrate. Compared with France, labor, capital, and GDP values of Australia were 37.5%, 41.7%, and 32.5%, respectively, while the EF value that Australian occupied is just 60.1% of that of France. Compared with France, labor, capital, and GDP values of Canada were respectively 62.2%, 52.3%, and 52.9%, but the EF value that Canada occupied is 153.7% of that of France. EF consists of six different ecological land types. Different resource endowments of Australia and Canada lead to different occupation of ecological land types. The pasture land footprint in Australia (which accounts for 40.5% of the country’s total EF) and the forestland footprint in Canada (which accounts for 57.7% of the country’s total EF) are relatively higher, and which lead to the higher total EF and also the lower TFEcEs of them.

Russia, Brazil, and China, the three most populous developing countries, have relatively low TFEcE scores. Though China’s TFEcE is small, its growth rate is the highest at 19.7% from 0.238 in 1999 to 0.285 in 2013. The TFEcE of China in 1993 was only 0.238, which was lower than that of Argentina, while in 2013 the TFEcE of China was 1.85 times as high as that of Argentina. China’s TFEcE ranked 18th in 1999 and 12th in 2013, which may benefit from the relevant effective measures taken by Chinese government, including the “National Program on Climate Change” first proposed by developing countries in 2006 and the “Energy Conservation Binding Targets” established in 2009.

4.3. Comparison of G20 Countries’ TFEcE and TFEE

The essential difference between TFEE proposed by Hu and Wang [3] and TFEcE in this paper is whether to incorporate the comprehensive ecological impacts. TFEcE takes not only the energy inputs, but also the water, forest, and arable inputs into account, which evaluates ecology efficiency more comprehensively. Table 2 and

Table 4. TFEE, difference between TFEcE and TFEE by countries (1999–2013).

Country	Total-Factor Energy Efficiency					Difference between TFEcE and TFEE
	1999	2001	2005	2009	2013	1999	2001	2005	2009	2013
Argentina	0.558	0.563	0.409	0.312	0.295	0.291	0.273	0.228	0.162	0.141
Australia	0.604	0.604	0.588	0.521	0.524	0.219	0.231	0.210	0.143	0.116
Brazil	0.527	0.571	0.477	0.560	0.445	0.194	0.237	0.154	0.352	0.186
Canada	0.483	0.565	0.459	0.443	0.430	0.263	0.296	0.251	0.034	0.179
France	1.000	1.000	1.000	1.000	1.000	0.070	0.067	0.343	0.370	0.352
Germany	0.720	0.709	0.896	0.880	0.799	−0.038	−0.034	0.244	0.238	0.200
India	0.383	0.320	0.476	0.458	0.454	0.138	0.070	0.084	0.193	0.250
Indonesia	0.481	0.419	0.432	0.512	0.450	0.125	0.005	−0.075	0.148	0.091
Italy	1.000	1.000	0.914	0.905	0.938	0.000	0.000	0.144	0.135	0.108
Japan	0.784	0.754	0.908	0.872	0.741	−0.216	−0.246	−0.092	−0.128	−0.259
Republic of Korea	0.633	0.691	0.660	0.637	0.461	−0.069	0.016	−0.033	−0.030	−0.133
Mexico	0.674	0.664	0.739	0.660	0.555	0.117	0.095	0.314	0.080	−0.059
Russian	0.509	0.510	0.418	0.386	0.327	0.042	−0.119	0.025	0.265	0.088
Saudi Arabia	0.360	0.367	0.266	0.272	0.229	−0.288	−0.306	−0.301	−0.367	−0.285
South Africa	0.450	0.501	0.481	0.186	0.186	−0.013	−0.080	−0.052	−0.017	−0.023
Turkey	0.533	0.644	0.770	0.577	0.437	−0.116	0.059	0.218	0.330	0.195
UK	1.000	1.000	1.000	1.000	1.000	0.000	0.000	0.000	0.000	0.000
USA	1.000	1.000	1.000	1.000	1.000	0.000	0.000	0.000	0.000	0.000
China	0.328	0.391	0.269	0.284	0.318	0.090	0.139	−0.002	−0.046	0.033

respectively show the TFEcE and TFEE of G20, and Table 4 also presents the difference between TFEcE and TFEE of G20.

Without considering other ecological impacts, TFEE may overestimate the country’s performance. As Table 4 shows, during 1999–2013, the average of TFEE of G20 is 0.617, while the average of TFEcE is 0.543. The Mann-Whitney U rank test proves that the difference between TFEE and TFEcE presents a statistical significance with a p-value less than 0.001 as

Table 5. Significance test between TFEcE and TFEE in G20.

Indicators	Mann-Whitney U	Wilcoxon W	Z-Value	p-Value
TFEcE vs. TFEE	66,386.000	146,186.000	−4.071	<0.001

shows. The comparative result means that consideration of EF as comprehensive ecological inputs has a significant influence on the country’s ecology efficiency.

At the national level, Table 4 shows the gap between TFEE and TFEcE of G20. The countries can be divided into three groups. The first group includes UK and USA. There is no difference between TFEE and TFEcE for these two countries, because they always stand on the efficient frontier and rank first for both TFEE and TFEcE for each year. The second group includes Japan, Republic of Korea, Saudi Arabia, and South Africa. The TFEE of these countries are lower than their TFEcE. In this group, Saudi Arabia presents the biggest difference between TFEE and TFEcE, which are 0.35 and 0.6 respectively. The main reason may be that Saudi Arabia is an “oil kingdom”, one of the countries that has the largest oil reserves and production. The process of production, exploration, and exploitation of petroleum need to consume much energy, and the relative low price of oil also induces more energy consumption. These factors lead to low TFEE score in Saudi Arabia. However, Saudi Arabia’s TFEcE is higher than its TFEE, which indicates that Saudi Arabia has made efforts to improve efficiency of other ecological inputs. The efforts on other ecological impacts made by these countries in the second group would be ignored if we only considered the energy input as the whole ecological inputs. The rest of the countries belong to the third group, whose TFEE is higher than their TFEcE. These countries have paid more attention to energy consumption, with less attention to biological EF (including arable lands, pasture lands, forest lands, and fisheries lands). Taking China as an example, the average of TFEE is 0.31, while the TFEcE score is 0.28. This indicates that China has achieved much more progress in energy saving, with less progress in other ecological inputs reduction. For the countries in the last group, they should vigorously promote energy savings and other biological EF reduction at the same time.

4.4. Factors of National TFEcE

TFEcE of all the G20 countries every year lies always between zero and unity, thus it is a limited dependent variable. In order to distinguish the influential factors of national TFEcE, we follow the method of Li and Hu [23] and employ the truncated regression model based on the truncated characteristics of TFEcE data. Truncated regression models arise in many applications of statistics, cases where observation values in the outcome variable are below or above certain thresholds are systematically excluded from the sample.

Three factors are investigated in this paper. R&D represents the ratio of research and development expenditure to GDP. Tra is on behalf of the foreign dependence degree, which is the ratio of total exports and imports to GDP. Ind refers to the ratio of the secondary industry to GDP. All the data are obtained from the World Bank (World Development Indicators). Due to data limitations, the reduced sample data set from 2003–2013 is employed in this section. Saudi Arabia is excluded due to data missing in this section.

The truncated regression model is set as:

$${\mathrm{TFEcE}}_{o,t}={\beta }_0+{\beta }_{1}R\&D_{o,t}+{\beta }_{2}Tr{a}_{o,t}+{\beta }_{3}In{d}_{o,t}+{\epsilon }_{o,t}$$

(10)

where TFEcE_o,t refers to the TFEcE in the oth country and the tth year; β₀ is the constant term; β₁, β₂, and β₃, are the parameters of the independent variables, respectively; and ε_o,t is the error term.

From the above descriptive statistics analysis and significance test in Section 4.2, we can find that there is significance difference in TFEcE between developed countries and developing countries, while an analysis on all the G20 countries of Formula (10) may cover it up. Therefore,

Table 6. Factors of national TFEcE scores in G20.

Variables	All the Countries		Developed Countries		Developing Countries
	Coefficient	Significant Test	Coefficient	Significant Test	Coefficient	Significant Test
		p-Value		p-Value		p-Value
Independent Variable
R&D	0.2507	0.000	0.5328	0.019	−0.0950	0.001
Tra	−0.0010	0.594	−0.0085	0.138	0.0045	0.000
Ind	−0.0214	0.000	−0.0738	0.024	−0.0003	0.894
Constant term	0.8487	0.000	2.3007	0.002	0.1934	0.013

respectively analyzes the factors that influence TFEcE of the whole G20 countries, G20 developed countries and G20 developing countries. Overall, the result of all the G20 countries is basically consistent with that of G20 developed countries, while different from the one of G20 developing countries. Such results show the necessity of dividing G20 into developing countries and developed countries when analyzing the factors that influence TFEcE.

First, to all the G20 countries, the coefficient of R&D is significantly positive which indicates that R&D has a significantly positive impact on TFEcE. It can be seen from Table 6 that R&D shows different statistical significance in the truncated regression model. The higher R&D contributes to the higher TFEcE in developed countries, while it is opposite in developing countries. For the developed countries, the increase of R&D can boost technical progress, which may enhance the ecological resources usage efficiency and introduce much more ecologically-friendly technology to replace the traditional technology. For the developing countries, the improvement of labor efficiency and capital efficiency would be superior to that of ecological efficiency, because ecological resources are at a relatively low price or even free in developing countries. So, the R&D is more likely to be distributed to boost the technical progress related to labor or capital efficiency, rather than the improvement of the ecological efficiency. Therefore, we could not find that R&D promotes the increase of TFEcE in developing countries.

Second, to all the G20 countries, the coefficient of Ind is significantly negative which indicates that the ratio of the secondary industry to GDP has a significantly negative impact on TFEcE. It can be seen from Table 6 that the relationship between Ind and national TFEcE is different in developing countries and developed countries. Although Ind has led to a decrease in TFEcF in developed countries on average, it has not significantly done so to the developing countries. For developing countries, the ratio of the secondary industry to GDP not only stands for the industry structure but also represents the level of industrial development. Although the countries with a high ratio of secondary industry to GDP may develop a certain energy-intensive industry, the economic level of which are still above-average among the developing countries, which means compared with other developing countries with lower Ind, they tend to pay more attention to ecological problems. Due to the above-mentioned reasons, the relationship between Ind and national TFEcE is not significant in the developing countries.

Third, to all the G20 countries, the coefficient of Tra is not significant which indicates that there is not a significant relation between foreign dependence degree and TFEcE. It can be seen from Table 6 that Tra is beneficial to the higher national TFEcE in the developing countries, which is consistent with the internationalization effect. Based on imports and exports, the enterprises in developing countries could be affected by the strict ecological regulations of developed countries, and so their ecological protection awareness and technology level have improved. For the developed countries, we do not find internationalization effect is significantly beneficial to TFEcE. Developed countries are always the exporting countries of green technology and eco-friendly concepts in international trade. Thus, from the perspective of TFEcE, international trade may be not significantly beneficial to developed countries.

5. Conclusions

This paper studies the ecological efficiency of G20 using the index of TFEcE which is constructed on the viewpoint of total-factor framework by taking the ratio of target ecology input from an SBM model to the actual ecology input. The TFEcE index not only considers EF as the comprehensive ecological inputs, but also takes capital and labor into account as multi-inputs to produce GDP. The main conclusions are as follows:

For the G20 countries, the total EF of G20 maintains a stable growth trend from 1999 to 2013, increases from 962.459 10 million ha in 1999 to 1203.475 10 million ha in 2013, and achieves a growth of about 25%. Fossil energy land contributes most to the total EF among the six components, accounting for 33.77%. The contribution of forest and pasture land are 25.38% and 23.42%, respectively.

In general, the average level of TFEcE of G20 from 1999 to 2013 is at a low level of about 0.54, which means there is a large space for improvement in the TFEcE of G20 countries. This indicates that the improvement of ecological efficiency is an effective way to maintain economic growth, and meanwhile, to relieve ecology pressures. Furthermore, TFEcE of G20 is very imbalanced. There is a big gap between developed countries and developing countries. The average level of developed countries is 0.727, of which the USA, UK, and Japan always have optimal efficiency from 1999 to 2013, while the average value of developing countries is only 0.376, among which Argentina is at the lowest level of 0.21.

Without considering other ecological impacts, TFEE in Hu and Wang [3] may overestimate the countries’ performance. We find that there are significant differences between TFEE and TFEcE. Some countries—such as Japan, Republic of Korea, and Saudi Arabia—obtain higher score in TFEcE than that in TFEE due to a good performance in biological footprint. Some countries such as China, gain lower score in TFEcE than that in TFEE due to too much biological footprint consumption.

For the developing countries and developed countries, the analysis of factors that affect national TFEcE shows different statistical significance in the truncated regression model. The higher ratio of R&D expenditure to GDP contributes to a higher TFEcE in the developed countries, while a lower TFEcE in developing countries. Although the ratio of the secondary industry to GDP have negative effects on the developed countries’ TFEcE, it has not significantly done so to the developing countries. The higher foreign dependence degree is beneficial to the higher national TFEcE in the developing countries.

Our study presents several policy implications.

First, as global warming, deforestation, land erosion, and loss of biodiversity have become global issues nowadays, governments should not only focus on the consumption and utilization of energy efficiency, but analyze the use efficiency of ecological resources from the view of ecological footprint. TFEcE indicator that integrates labor, capital, and ecological inputs could provide more comprehensive evaluation criteria for the policy-making of sustainable development.

Second, although there exists significant difference between developed countries and developing countries, not all the developed countries have a high TFEcE. Australia and Canada, as developed countries, have higher total EF values because of a larger pasture and forest land footprint. For these two countries, we recommend they pay more attention to improving the use efficiency of pasture and forest land footprint to cut down the occupation of the total EF and thus increasing their TFEcE.

Third, developed countries and developing countries should take different measures to promote TFEcE. Since developing countries have to realize ecological protection when pursuing economic growth, they face more severe challenges. We suggest that developing countries, on the one hand, guide R&D expenditure and its distribution to improve ecological efficiency, thus promoting domestic green technology innovation, on the other hand, developing countries should actively obtain internationalization effects, promoting TFEcE by acquiring green spillovers through international trade.