A Study of the Time–Space Evolution Characteristics of Urban–Rural Integration Development in a Mountainous Area Based on ESDA-GIS: The Case of the Qinling-Daba Mountains in China
Abstract
:1. Introduction
2. Study Area and Data Processing
2.1. Overview of Study Area
2.1.1. Natural Resource and Environmental Basis
2.1.2. Overview of Social and Economic Development
2.2. Data Sources and Pre-Processing
3. Research Methods
3.1. Multi-Index Comprehensive Evaluation Method
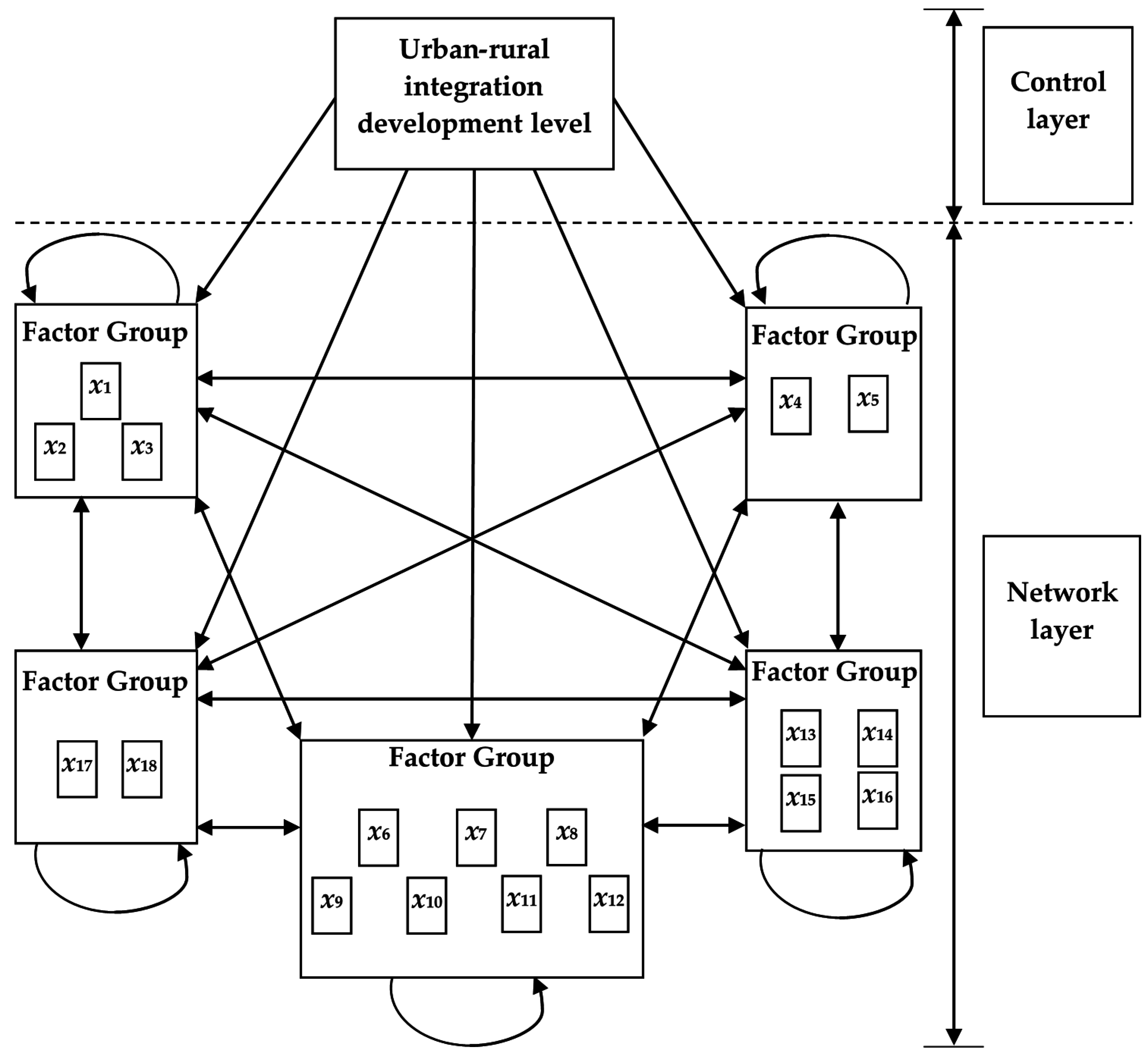
3.2. Network Analysis Method
3.3. Exploratory Spatial Data Analysis
4. Calculation of the Urban–Rural Integration Development Level of the Qinling-Daba Mountains
4.1. Evaluation Object
4.2. Establishment of Index System
4.3. Influence Factor Weight
5. Time–Space Analysis of Urban–Rural Integration Development Level
5.1. Historical Evolution of the Urban–Rural Integration Development Level of the Qingling-Daba Mountains
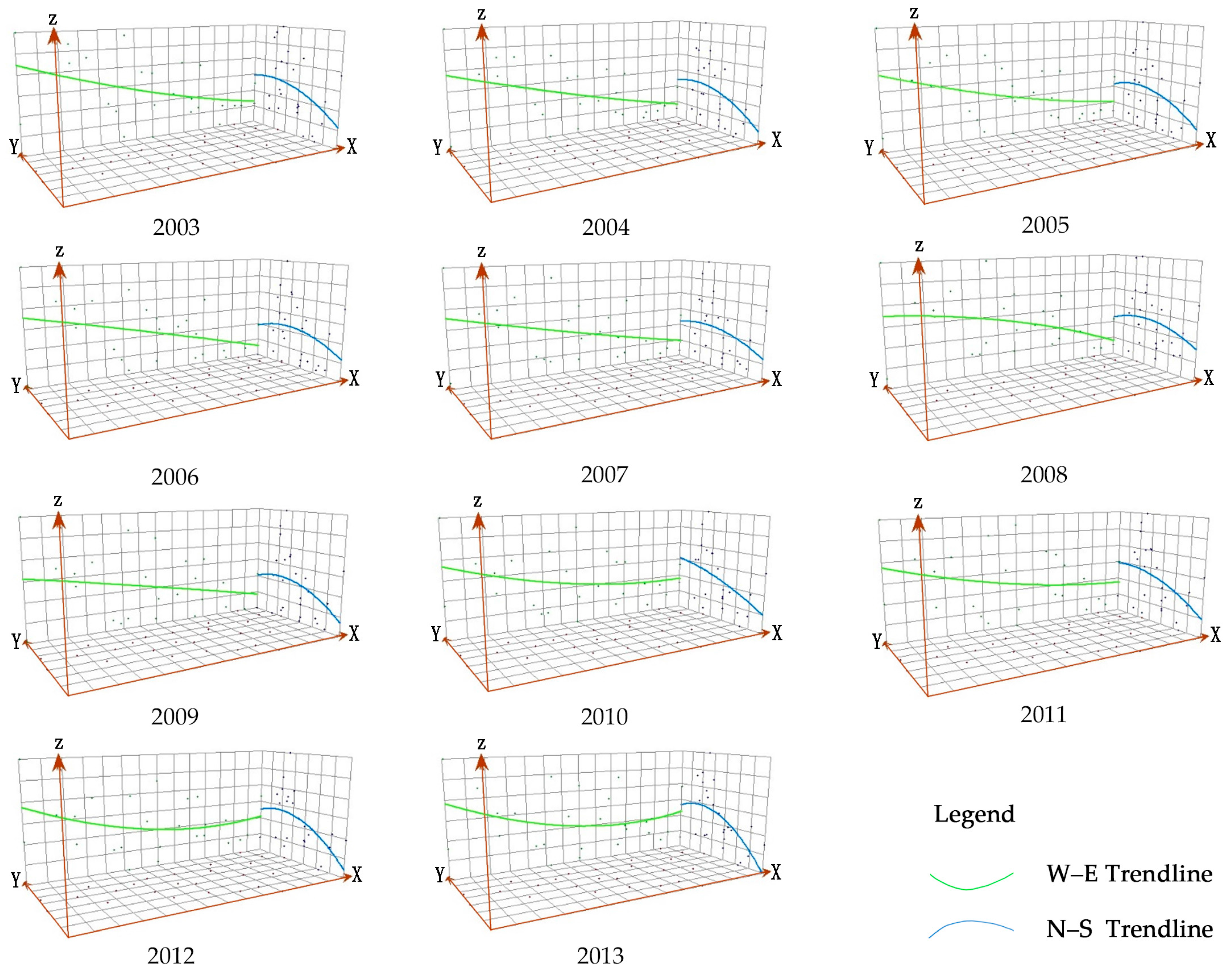
5.2. Exploratory Spatial Data Analysis of the Urban–rural Integration Development Level in the Qinling-Daba Mountains
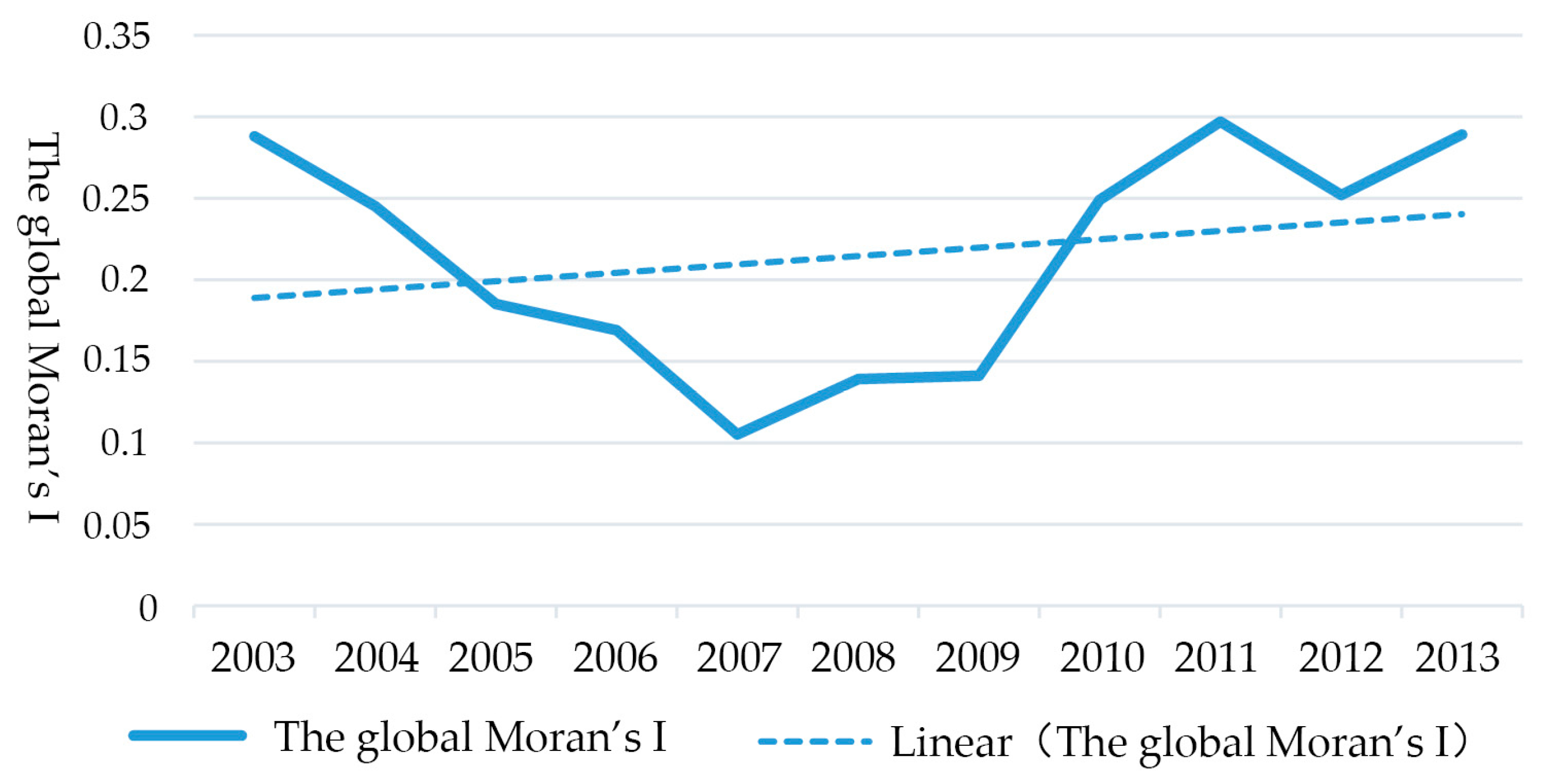
5.2.1. Global Spatial Autocorrelation Analysis
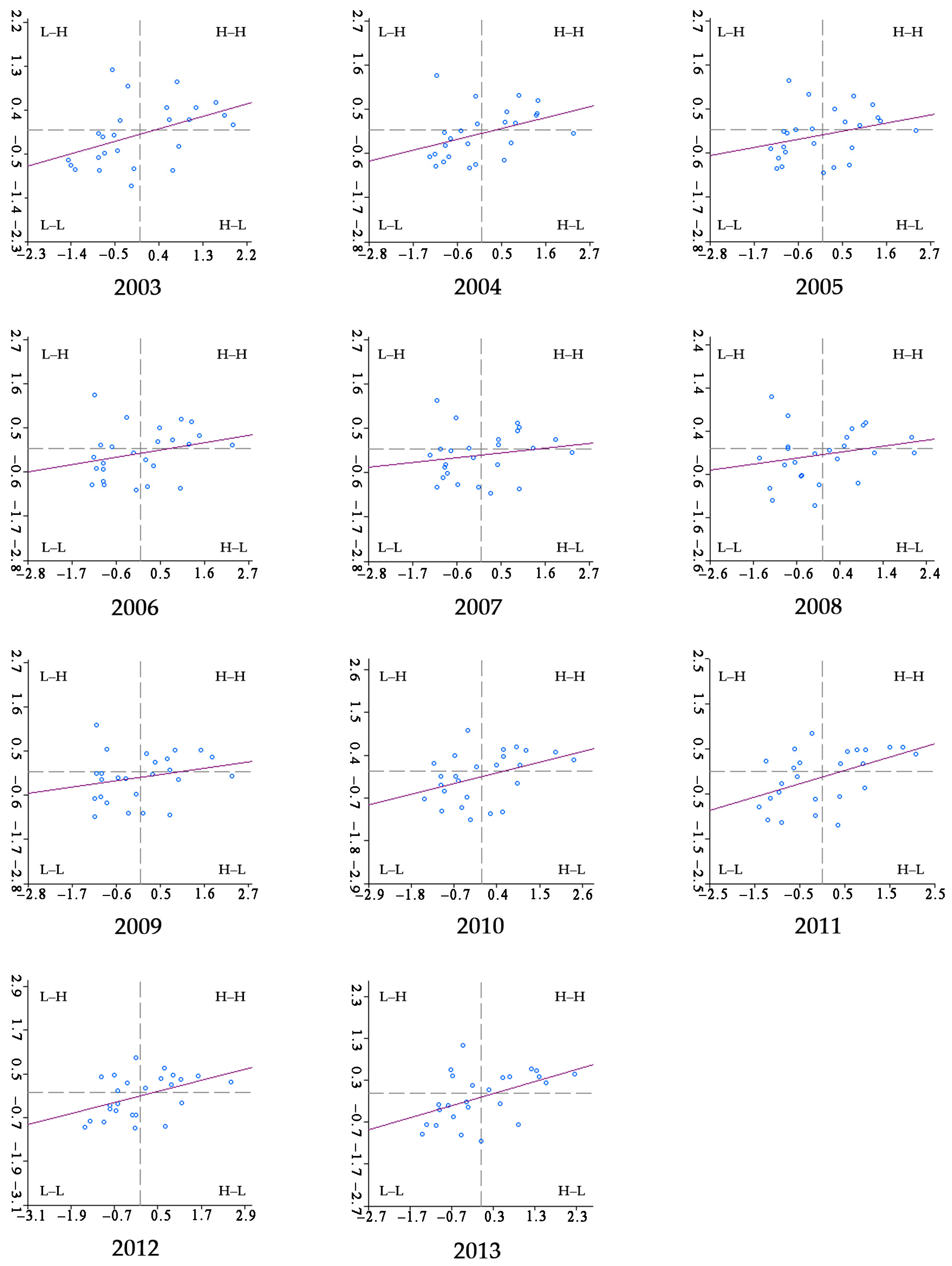
5.2.2. Local Spatial Autocorrelation Analysis
6. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, Y.S.; Long, H.L.; Chen, Y.F.; Wang, J.Y.; Li, Y.R.; Li, Y.H.; Yang, Y.Y.; Zhou, Y. Progress of research on urban-rural transformation and rural development in China in the past decade and future prospects. J. Geogr. Sci. 2016, 26, 1117–1132. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X. New urbanization: A new vision of China’s urban-rural development and planning. Front. Arch. Res. 2015, 1, 166–168. [Google Scholar] [CrossRef]
- Su, C.W.; Liu, T.Y.; Chang, H.L.; Jiang, X.Z. Is urbanization narrowing the urban-rural income gap? A cross-regional study of China. Habitat Int. 2015, 48, 79–86. [Google Scholar] [CrossRef]
- Liu, Y.S.; Lu, S.S.; Chen, Y.F. Spatio-temporal change of urban-rural equalized development patterns in China and its driving factors. J. Rural Stud. 2013, 32, 320–330. [Google Scholar] [CrossRef]
- Zhan, J.Y.; Lu, Q.; Deng, X.Z. Construction of urban-rural interaction evaluation model and its application in Shandong Province. Geogr. Res. 2003, 22, 495–502. (In Chinese) [Google Scholar]
- Torre, A.; Wallet, F. Towards New Paths for Regional and Territorial Development in Rural Areas. Eur. Plan. Stud. 2015, 23, 175–181. [Google Scholar] [CrossRef]
- Amato, F.; Maimone, B.; Martellozzo, F.; Nolè, G.; Murgante, B. The Effects of Urban Policies on the Development of Urban Areas. Sustainability 2016, 8, 297. [Google Scholar] [CrossRef] [Green Version]
- Horlings, L.G.; Kanemasu, Y. Sustainable development and policies in rural regions; insights from the Shetland Islands. Land Use Policy 2015, 49, 310–321. [Google Scholar] [CrossRef]
- Yue, W.Z.; Zhang, Y.T.; Ye, X.Y.; Cheng, Y.Q.; Leipnik, M.R. Dynamics of Multi-Scale Intra-Provincial Regional Inequality in Zhejiang, China. Sustainability 2014, 6, 5763–5784. [Google Scholar] [CrossRef]
- Liu, Y.L.; Luo, T.; Liu, Z.Q.; Kong, X.S.; Li, J.W.; Tan, R.H. A comparative analysis of urban and rural construction land use change and driving forces: Implications for urban-rural coordination development in Wuhan, Central China. Habitat Int. 2015, 47, 113–125. [Google Scholar] [CrossRef]
- Tong, G.; Wang, T. The Estimated and Assessed Study on Urban–Rural Integration Course in Northeast China; Springer: Berlin/Heidelberg, German, 2015; pp. 637–644. [Google Scholar]
- Xuan, G.F.; Xu, J.G.; Zhao, J. An Analysis of Urban Social Space Based on ESDA—A Case Study of the Central Urban District in Shanghai. Sci. Geogr. Sin. 2010, 30, 22–29. [Google Scholar]
- Chen, D.; Wang, Y.; Ren, F.; Du, Q. Spatio-Temporal Differentiation of Urban-rural Equalized Development at the County Level in Chengdu. Sustainability 2016, 8, 422. [Google Scholar] [CrossRef]
- Qi, Y.J.; Yu, Y.; Dong, W. Coordination Analysis on Urbanization Level and Land Use Efficiency of Xinjiang Based on ESDA. Environ. Eng. Manag. J. 2013, 12, 1819–1823. [Google Scholar]
- Martellozzo, F.; Clarke, K.C. Measuring urban sprawl, coalescence, and dispersal: A case study of Pordenone, Italy. Environ. Plan. B Plan. Des. 2011, 38, 1085–1104. [Google Scholar] [CrossRef]
- Hayashi, T. Measuring rural-urban disparity with the Genuine Progress Indicator: A case study in Japan. Ecol. Econ. 2015, 120, 260–271. [Google Scholar] [CrossRef]
- Yu, A.T.W.; Wu, Y.Z.; Zheng, B.B.; Zhang, X.L.; Shen, L.Y. Identifying risk factors of urban-rural conflict in urbanization: A case of China. Habitat Int. 2014, 44, 177–185. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, H.X.; Dang, X.H. A Study on Regional Coordinative Development of Urban-rural and Evaluation. Stat. Dec. 2015, 31, 102–105. (In Chinese) [Google Scholar]
- Li, Y.Y.; Chen, Y.; Sun, L. The Coordinative Development of Urban and Rural and its Evaluation Methods. J. Agrotech. Econ. 2004, 23, 24–30. (In Chinese) [Google Scholar]
- Zhao, C.Y. A Study on Coordinative Development of Urban-Rural Areas and Its Impact Factors in China. Ph.D. Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2008. [Google Scholar]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process. J. Syst. Sci. Syst. Eng. 2012, 95, 129–157. [Google Scholar]
- Wang, L.F. The Theory and Algorithm of Analytic Network Process. Syst. Eng. Theory Pract. 2001, 21, 44–50. (In Chinese) [Google Scholar]
- Golcuk, I.; Baykasoglu, A. An analysis of DEMATEL approaches for criteria interaction handling within ANP. Expert Syst. Appl. 2016, 46, 346–366. [Google Scholar] [CrossRef]
- Vinodh, S.; Balagi, T.; Patil, A. A hybrid MCDM approach for agile concept selection using fuzzy DEMATEL, fuzzy ANP and fuzzy TOPSIS. Int. J. Adv. Manuf. Technol. 2016, 83, 1979–1987. [Google Scholar] [CrossRef]
- Chatterjee, K.; Bandyopadhyay, A.; Ghosh, A.; Kar, S. Assessment of environmental factors causing wetland degradation, using Fuzzy Analytic Network Process: A case study on Keoladeo National Park, India. Ecol. Model. 2015, 316, 1–13. [Google Scholar] [CrossRef]
- Kim, D.; Lee, H.; Lim, U. Exploring the Spatial Distribution of Occupations Vulnerable to Climate Change in Korea. Sustainability 2016, 8, 34. [Google Scholar] [CrossRef]
- Wang, L.; Li, T.; Cao, X.S. Spatial Difference of Urban and Rural Harmonious Development with ESDA-GIS Framework in Guangdong Province. Econ. Geogr. 2012, 32, 44–50. (In Chinese) [Google Scholar]
- Yang, L.X.; Yang, G.S.; Yao, S.M.; Yuan, S.F. A Study on the Spatial Heterogeneity of Grain Yield Per Hectare and Driving Factors Based on ESDA-GWR. Econ. Geogr. 2012, 32, 120–126. (In Chinese) [Google Scholar]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An Introduction to Spatial Data Analysis. In Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications; Fischer, M.M., Getis, A., Eds.; Springer: Berlin/Heidelberg, German, 2010; pp. 73–89. [Google Scholar]
- Sridharan, S.; Tunstall, H.; Lawder, R.; Mitchell, R. An exploratory spatial data analysis approach to understanding the relationship between deprivation and mortality in Scotland. Soc. Sci. Med. 2007, 65, 1942–1952. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.Y.; Chen, Z.N. Reserach on the Regional Economic Disparity in Guangdong Province Based on GIS Spatial Analysis. Econ. Geogr. 2007, 27, 558–561. (In Chinese) [Google Scholar]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Wang, Y.F.; Liu, Y.S.; Li, Y.H.; Li, T.T. The spatio-temporal patterns of urban-rural development transformation in China since 1990. Habitat Int. 2016, 53, 178–187. [Google Scholar] [CrossRef]
- Zeng, L.; Lei, J.; Lu, Q. Construction of evaluating indicator system of urban-rural int eraction and the comparative analysis of regional urban-rural correlative-degree in China. Geogr. Res. 2002, 21, 763–771. (In Chinese) [Google Scholar]
- GU, Y.K.; Xu, Y.J. Study on the Evaluating Index of the Urban-rural Integration. Zhejiang Soc. Sci. 2004, 20, 95–99. (In Chinese) [Google Scholar]
- Zhang, S.M.; Liu, H.; Ren, J. A Quantitative Analysis and Study of Regional Urban- Rural Interaction in Shandong Province. J. Shandong Norm. Univ. Nat. Sci. 2004, 19, 65–68. (In Chinese) [Google Scholar]
- Wan, S.W. The Construction and Appliation of the Urban-rural Integration Evaluating Index System—Taking Henan Province as an Example. Econ. Surv. 2008, 25, 60–63. (In Chinese) [Google Scholar]
- Xie, H.L.; Kung, C.C.; Zhao, Y.L. Spatial disparities of regional forest land change based on ESDA and GIS at the county level in Beijing-Tianjin-Hebei area. Front. Earth Sci. 2012, 6, 445–452. [Google Scholar] [CrossRef]
- Lincaru, C.; Atanasiu, D.; Ciucă, V.; Pirciog, S. Peri-urban Areas and Land Use Structure in Romania at LAU2 Level: An Exploratory Spatial Data Analysis. Procedia Environ. Sci. 2016, 32, 124–137. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, J.X. Economic Space Evolution of Yangtze River Delta City Group Based on Country Scale. Econ. Geogr. 2010, 30, 1112–1117. (In Chinese) [Google Scholar]
- Tang, Y.; Mason, R.J.; Wang, Y. Governments’ functions in the process of integrated consolidation and allocation of rural-urban construction land in China. J. Rural Stud. 2015, 42, 43–51. [Google Scholar] [CrossRef]
- Gao, Z. Development Path of Urban-rural Integration. Asian Agric. Res. 2012, 4, 53–59. [Google Scholar]
- Li, Y.; Hu, Z. Approaching Integrated Urban-rural Development in China: The Changing Institutional Roles. Sustainability 2014, 7, 7031–7048. [Google Scholar] [CrossRef]

| Factor Group | Factors | Factor Number | Factor Weight |
|---|---|---|---|
| Population subsystem | Urbanization rate | x1 | 0.077 |
| Occupied population proportion of non-agricultural industries | x2 | 0.074 | |
| Non-agricultural industries proportion in country working population | x3 | 0.065 | |
| Space subsystem | Urban density | x4 | 0.102 |
| Penetration rate of telephone | x5 | 0.042 | |
| Economic subsystem | Per capita GDP | x6 | 0.081 |
| Economic density | x7 | 0.063 | |
| Proportion of non-agricultural industries output value | x8 | 0.061 | |
| Agricultural mechanization level | x9 | 0.016 | |
| Fixed-asset investment per capita | x10 | 0.066 | |
| Total retailing of social consuming goods per capita | x11 | 0.030 | |
| Urban and rural residents per capita income ratio | x12 | 0.011 | |
| Social subsystem | Teacher/pupil ratio in common elementary and middle schools | x13 | 0.084 |
| Number of health agency beds per 10,000 people | x14 | 0.061 | |
| Number of health workers per 10,000 people | x15 | 0.066 | |
| Number of social welfare adopting unit beds per 10,000 people | x16 | 0.019 | |
| Environment subsystem | Green coverage ratio in built-up areas | x17 | 0.051 |
| Per capita public green areas in built-up areas | x18 | 0.030 |
| County | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nanzheng | 0.498 | 0.437 | 0.422 | 0.419 | 0.422 | 0.424 | 0.431 | 0.373 | 0.354 | 0.374 | 0.414 |
| Chenggu | 0.517 | 0.503 | 0.527 | 0.510 | 0.528 | 0.504 | 0.505 | 0.482 | 0.522 | 0.544 | 0.482 |
| Yang | 0.331 | 0.315 | 0.316 | 0.326 | 0.293 | 0.280 | 0.300 | 0.314 | 0.341 | 0.333 | 0.365 |
| Xixiang | 0.295 | 0.271 | 0.279 | 0.282 | 0.279 | 0.278 | 0.283 | 0.277 | 0.300 | 0.339 | 0.368 |
| Mian | 0.466 | 0.448 | 0.448 | 0.518 | 0.479 | 0.475 | 0.496 | 0.481 | 0.523 | 0.492 | 0.572 |
| Ningqiang | 0.290 | 0.198 | 0.258 | 0.232 | 0.236 | 0.237 | 0.269 | 0.349 | 0.386 | 0.403 | 0.391 |
| Lueyang | 0.618 | 0.613 | 0.630 | 0.638 | 0.645 | 0.607 | 0.661 | 0.637 | 0.654 | 0.699 | 0.665 |
| Zhenba | 0.188 | 0.177 | 0.229 | 0.237 | 0.267 | 0.315 | 0.298 | 0.278 | 0.272 | 0.243 | 0.291 |
| Liuba | 0.571 | 0.505 | 0.504 | 0.488 | 0.486 | 0.446 | 0.473 | 0.445 | 0.476 | 0.481 | 0.488 |
| Foping | 0.593 | 0.499 | 0.519 | 0.542 | 0.595 | 0.601 | 0.604 | 0.506 | 0.586 | 0.542 | 0.594 |
| Hanyin | 0.304 | 0.293 | 0.333 | 0.383 | 0.345 | 0.348 | 0.354 | 0.324 | 0.307 | 0.321 | 0.334 |
| Shiquan | 0.444 | 0.405 | 0.465 | 0.461 | 0.423 | 0.432 | 0.439 | 0.426 | 0.458 | 0.432 | 0.455 |
| Ningshan | 0.437 | 0.410 | 0.394 | 0.424 | 0.479 | 0.480 | 0.572 | 0.587 | 0.620 | 0.595 | 0.558 |
| Ziyang | 0.169 | 0.192 | 0.207 | 0.257 | 0.259 | 0.271 | 0.282 | 0.230 | 0.248 | 0.259 | 0.302 |
| Langao | 0.341 | 0.298 | 0.360 | 0.386 | 0.363 | 0.359 | 0.361 | 0.357 | 0.394 | 0.400 | 0.435 |
| Pingli | 0.253 | 0.241 | 0.254 | 0.248 | 0.247 | 0.278 | 0.270 | 0.275 | 0.347 | 0.345 | 0.332 |
| Zhenping | 0.453 | 0.402 | 0.435 | 0.485 | 0.484 | 0.461 | 0.482 | 0.443 | 0.456 | 0.390 | 0.386 |
| Xunyang | 0.268 | 0.224 | 0.244 | 0.257 | 0.262 | 0.296 | 0.331 | 0.315 | 0.339 | 0.345 | 0.400 |
| Baihe | 0.177 | 0.196 | 0.225 | 0.260 | 0.299 | 0.312 | 0.384 | 0.346 | 0.395 | 0.401 | 0.404 |
| Luonan | 0.255 | 0.218 | 0.238 | 0.223 | 0.236 | 0.238 | 0.264 | 0.332 | 0.306 | 0.301 | 0.326 |
| Danfeng | 0.252 | 0.236 | 0.248 | 0.257 | 0.254 | 0.233 | 0.265 | 0.286 | 0.278 | 0.322 | 0.355 |
| Shangnan | 0.349 | 0.315 | 0.389 | 0.354 | 0.398 | 0.349 | 0.403 | 0.409 | 0.452 | 0.494 | 0.528 |
| Shanyang | 0.263 | 0.222 | 0.243 | 0.229 | 0.214 | 0.204 | 0.285 | 0.256 | 0.267 | 0.295 | 0.361 |
| Zhenan | 0.470 | 0.425 | 0.442 | 0.405 | 0.420 | 0.408 | 0.482 | 0.490 | 0.516 | 0.513 | 0.505 |
| Zhashui | 0.310 | 0.322 | 0.328 | 0.347 | 0.332 | 0.386 | 0.414 | 0.445 | 0.502 | 0.517 | 0.579 |
| Year | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Global Moran’s I | 0.288 | 0.245 | 0.185 | 0.169 | 0.105 | 0.139 | 0.141 | 0.249 | 0.297 | 0.252 | 0.289 |
| p-value | 0.020 | 0.024 | 0.037 | 0.038 | 0.045 | 0.042 | 0.041 | 0.022 | 0.001 | 0.021 | 0.018 |
| Z-value | 2.350 | 2.262 | 2.112 | 2.106 | 1.987 | 2.013 | 2.057 | 2.268 | 2.476 | 2.285 | 2.462 |
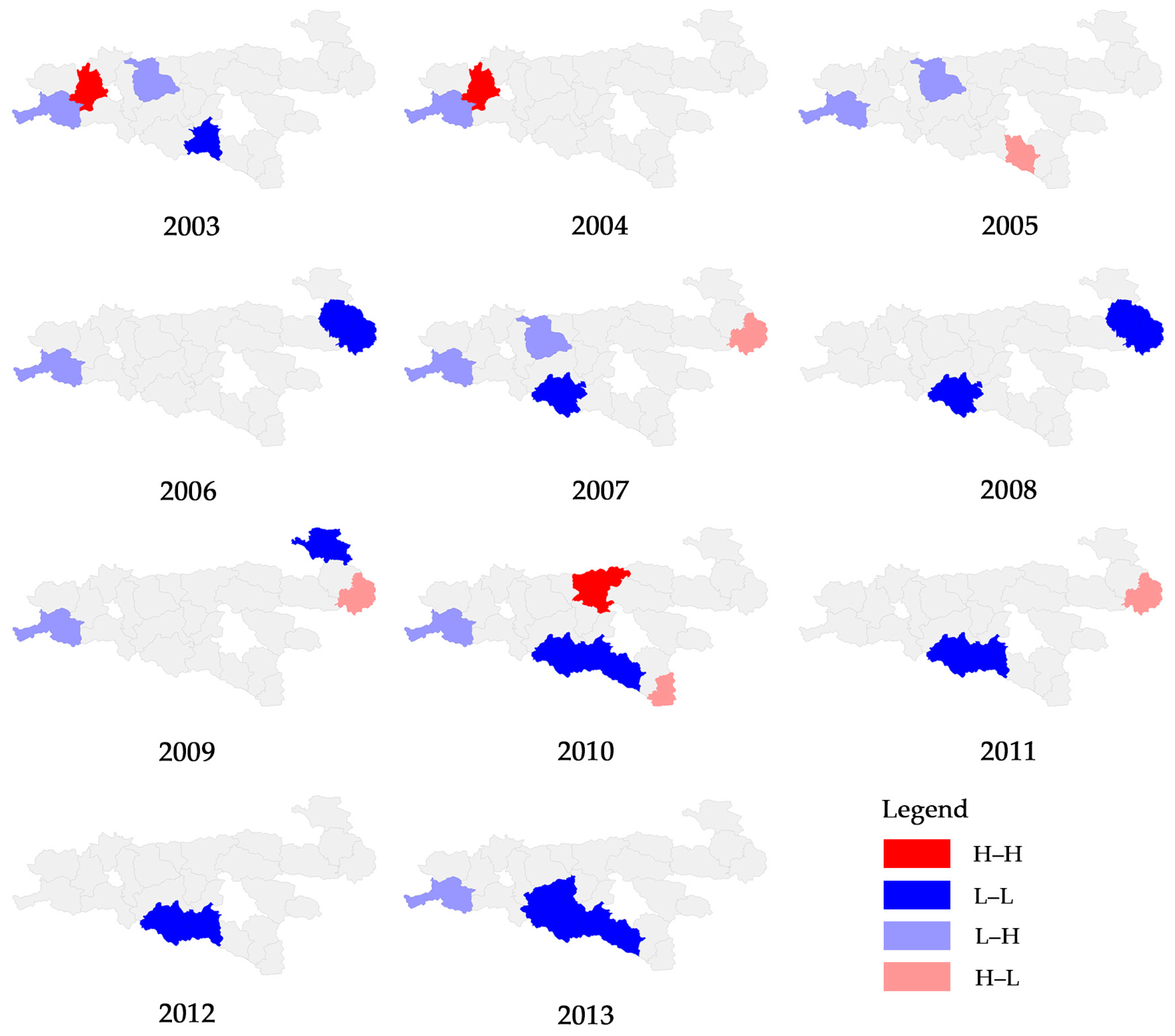
| Year | Counties in H–H Quadrant | Counties in L–L Quadrant |
|---|---|---|
| 2003 | Lueyang, Foping, Liuba, Chenggu, Nanzheng, Mian, Shiquan, Ningshan | Ziyang, Baihe, Zhenba, Danfeng, Pingli, Luonan, Shanyang, Xunyang, Xixiang, Hanyin, Langao, Shangnan |
| 2004 | Liuba, Chenggu, Foping, Mian, Nanzheng, Ningshan, Shiquan | Zhenba, Ziyang, Baihe, Luonan, Shanyang, Xunyang, Danfeng, Pingli, Xixiang, Hanyin, Langao, Shangnan |
| 2005 | Chenggu, Foping, Liuba, Shiquan, Mian, Nanzheng, Ningshan | Ziyang, Baihe, Zhenba, Luonan, Shanyang, Xunyang, Danfeng, Pingli, Xixiang, Hanyin |
| 2006 | Lueyang, Foping, Mian, Chenggu, Liuba, Shiquan, Ningshan, Nanzheng | Luonan, Shanyang, Zhenba, Ziyang, Xunyang, Danfeng, Baihe, Zhashui, Shangnan |
| 2007 | Foping, Chenggu, Liuba, Ningshan, Mian, Shiquan, Nanzheng | Shanyang, Luonan, Pingli, Danfeng, Ziyang, Xunyang, Zhenba, Xixiang, Baihe, Hanyin, Langao |
| 2008 | Foping, Ningshan, Mian, Liuba, Shiquan, Nanzheng | Shanyang, Danfeng, Luonan, Ziyang, Xixiang, Xunyang, Baihe, Zhenba, Hanyin, Shangnan, Langao |
| 2009 | Foping, Ningshan, Mian, Zhenan, Liuba, Shiquan, Zhashui | Luonan, Danfeng, Pingli, Ziyang, Xixiang, Shanyang, Zhenba, Xunyang, Hanyin, Langao, Baihe |
| 2010 | Lueyang, Ningshan, Foping, Zhenan, Mian, Zhashui, Liuba, Shiquan | Ziyang, Pingli, Xixiang, Zhenba, Danfeng, Xunyang, Hanyin, Luonan, Baihe, Langao |
| 2011 | Lueyang, Ningshan, Foping, Mian, Zhenan, Zhashui, Liuba, Shiquan | Ziyang, Zhenba, Danfeng, Xixiang, Luonan, Hanyin, Pingli, Langao, Baihe |
| 2012 | Lueyang, Ningshan, Foping, Zhashui, Zhenan, Mian, Liuba, Shiquan | Zhenba, Ziyang, Luonan, Hanyin, Danfeng, Xixiang, Pingli, Zhenping, Langao, Baihe |
| 2013 | Lueyang, Foping, Zhashui, Mian, Ningshan, Zhenan, Liuba, Shiquan | Zhenba, Ziyang, Luonan, Pingli, Hanyin, Danfeng, Xixiang, Zhenping, Xunyang, Baihe, Langao |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Cui, P. A Study of the Time–Space Evolution Characteristics of Urban–Rural Integration Development in a Mountainous Area Based on ESDA-GIS: The Case of the Qinling-Daba Mountains in China. Sustainability 2016, 8, 1085. https://doi.org/10.3390/su8111085
Wu X, Cui P. A Study of the Time–Space Evolution Characteristics of Urban–Rural Integration Development in a Mountainous Area Based on ESDA-GIS: The Case of the Qinling-Daba Mountains in China. Sustainability. 2016; 8(11):1085. https://doi.org/10.3390/su8111085
Chicago/Turabian StyleWu, Xin, and Peng Cui. 2016. "A Study of the Time–Space Evolution Characteristics of Urban–Rural Integration Development in a Mountainous Area Based on ESDA-GIS: The Case of the Qinling-Daba Mountains in China" Sustainability 8, no. 11: 1085. https://doi.org/10.3390/su8111085
APA StyleWu, X., & Cui, P. (2016). A Study of the Time–Space Evolution Characteristics of Urban–Rural Integration Development in a Mountainous Area Based on ESDA-GIS: The Case of the Qinling-Daba Mountains in China. Sustainability, 8(11), 1085. https://doi.org/10.3390/su8111085





