Trend Prediction and Decomposed Driving Factors of Carbon Emissions in Jiangsu Province during 2015–2020
Abstract
:1. Introduction
2. Methodology and Data
2.1. Data Source
2.2. GM (1, 1) Model
2.3. Polynomial Regression Analysis
- (1)
- Determine the number of polynomials by observing the changing trend of the actual data.
- (2)
- Transform the general polynomial into a linear function , where .
- (3)
- Estimate the parameters by using the ordinary least-square method.
- (4)
- Calculate the predicted values with the estimated multivariate linear function.
2.4. LMDI Decomposition Model
3. Results
3.1. Forecasting Results
3.2. LMDI Decomposition Results
4. Discussion
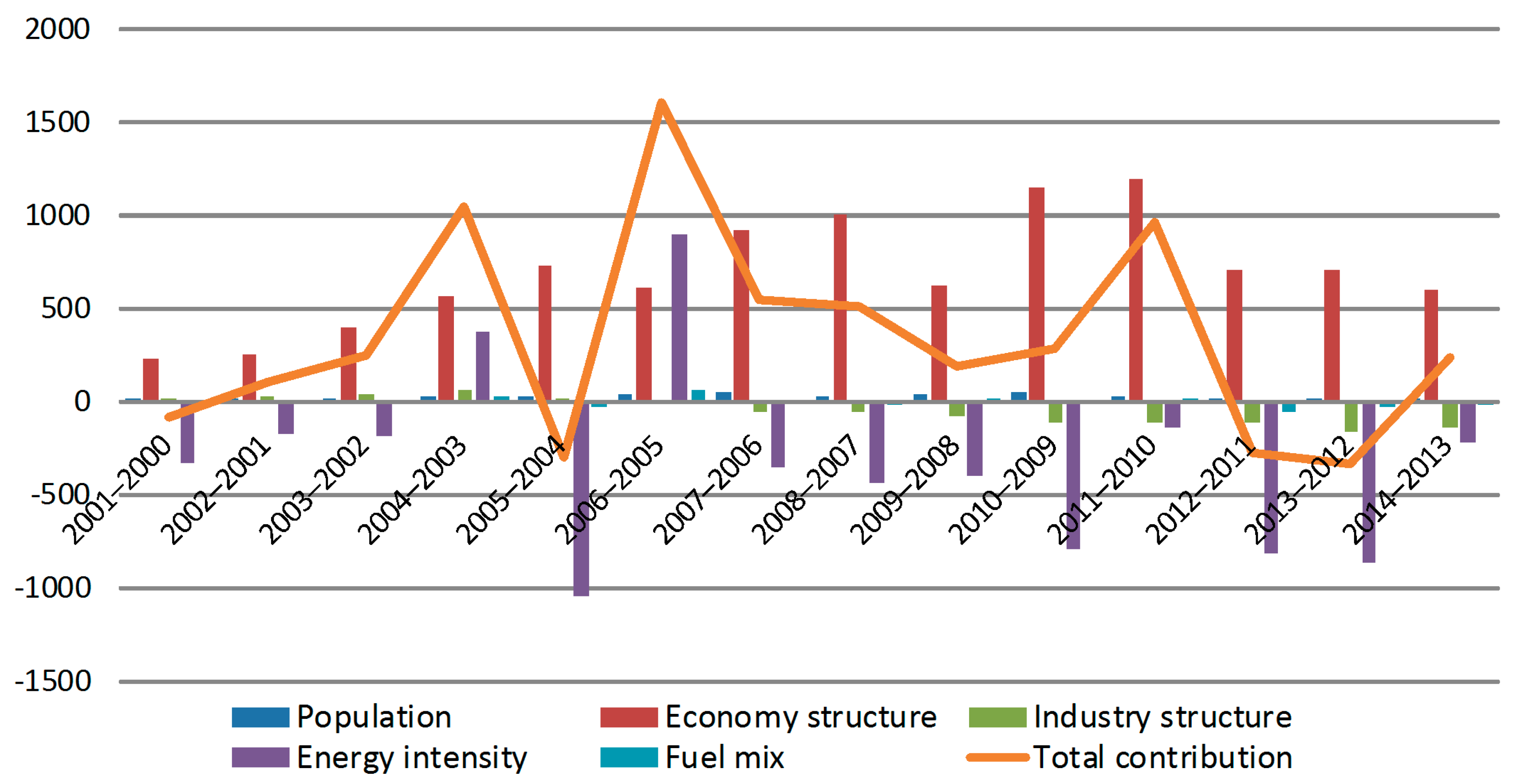
4.1. Economic Factors Analysis
4.2. Energy Intensity Factor Analysis
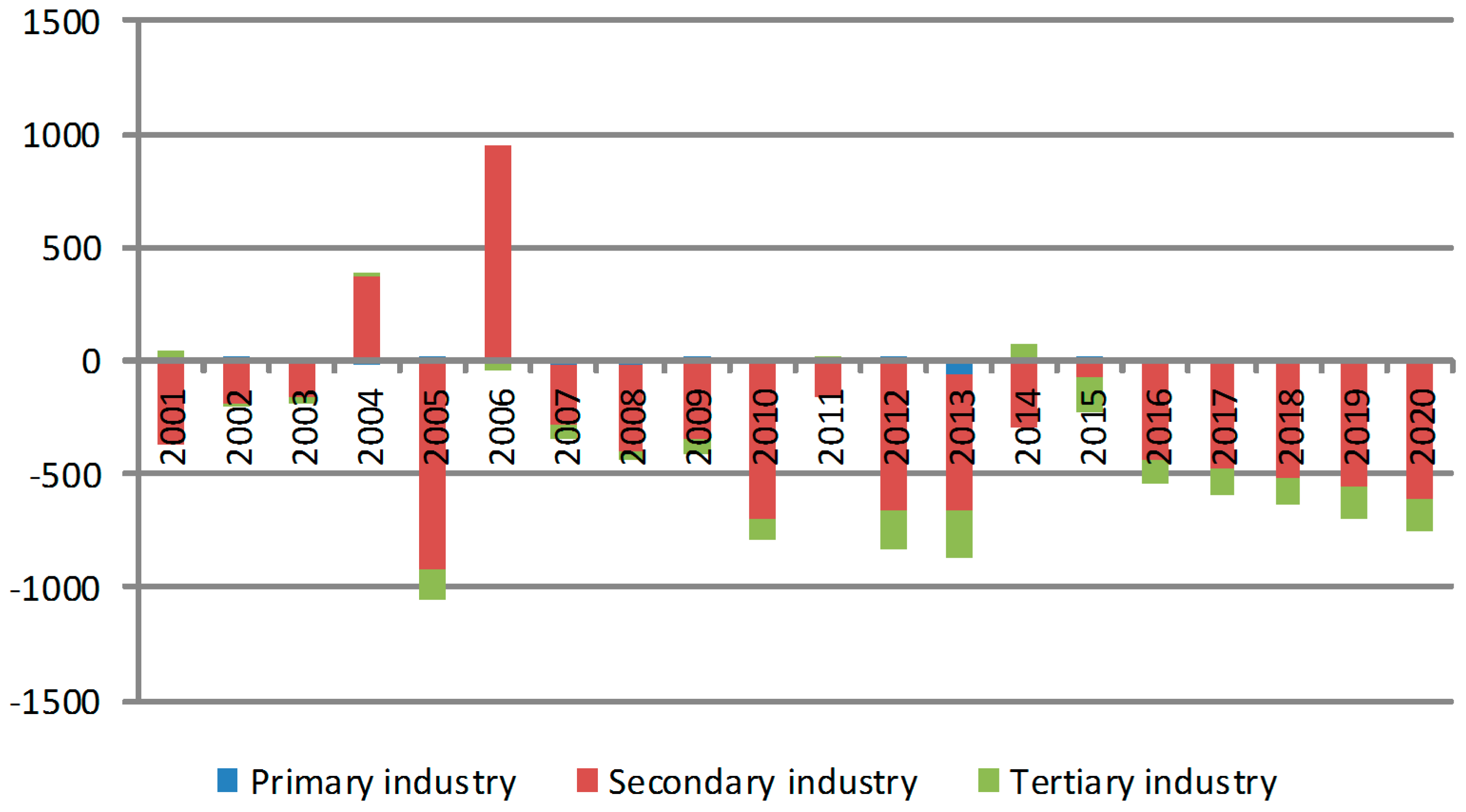
4.3. Industrial Structure Factor Analysis
- (1)
- Covering a period of 2000–2005, the effect on carbon emission amount from the industrial structure fluctuates and the absolute value is small. Therefore, the change of the industrial structure has a limited restricting effect on carbon emissions.
- (2)
- During the period of 2006–2014, the absolute value of contributions from the industrial structure on emission reduction has increased, which obviously shows trend of carbon emission reduction.
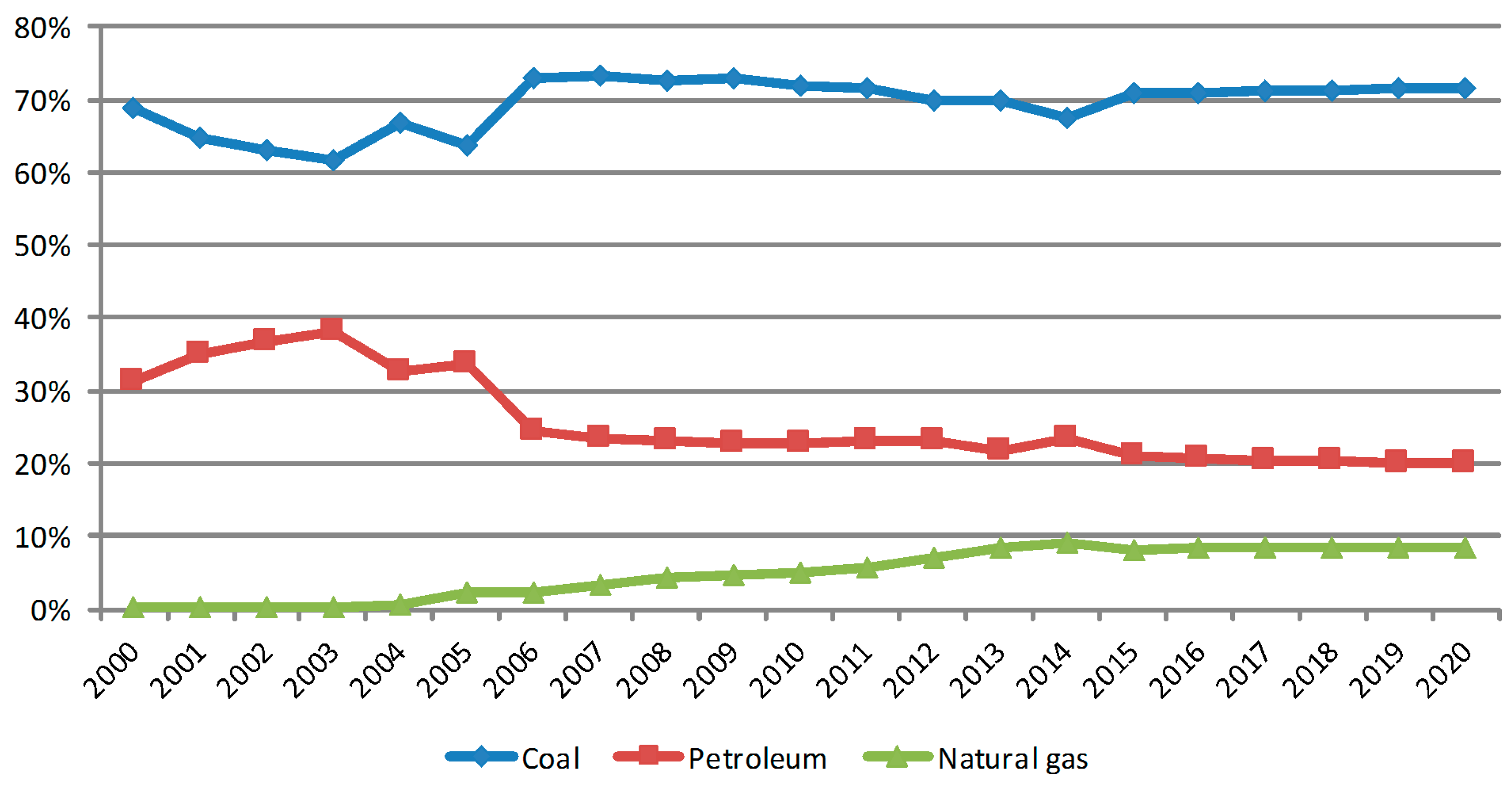
4.4. Energy Structure Factor Analysis
4.5. Demographic Factors Analysis
5. Conclusions and Suggestions
5.1. Conclusions
- (1)
- During the period of 2015–2020, the carbon emission of Jiangsu Province will increase at a constant pace.
- (2)
- (3)
- Changes in the level of population size and structure, as well as industrial and energy-consumption structures, will also affect carbon emissions.
- (4)
- It is very likely that Jiangsu province will achieve a decrease of 40%–50% in CO2 emissions per unit of GDP in 2020 as compared to the 2005 target. According to the prediction results, the population will increase to 83.4 million in 2020 from 75.88 million in 2005; total GDP of the three industries (primary, secondary, tertiary) will be 17,274.7 billion yuan ($2.6044 trillion, USD); and carbon emissions will reach 130.4 million tons per year. Under such circumstances, the CO2 emissions per unit of GDP of the primary, secondary, and tertiary industry in 2020 will decrease by 55.11%, 42.96%, and 75.2%, respectively, as compared to 2005.
5.2. Suggestions
- (1)
- The economic growth speed of Jiangsu will not undergo a significant decrease in the short term. Thus, it can be seen that with respect to Jiangsu, it is not enough to only rely on the control of economic growth for emission reduction; what is more important is to cooperate with other emission reduction related affairs.
- (2)
- As energy intensity is the key factor for reducing carbon emissions, it is necessary for enterprises to improve energy utilization efficiency. In terms of the energy consumption structure of Jiangsu, enterprises should be encouraged to control the rate of raw coal consumption and total energy consumption, and promote the usage of natural gas or other clean energies. Furthermore, as the largest negative contribution of the energy intensity factor comes from the secondary industry, it is suggested that the adjustments and upgrades of the industrial structure should be adhered to and new environmental protection technologies should be used to transform existing industrial enterprises.
- (3)
- As the transformation process of development centers changes to the tertiary industry, focus should be paid to the carbon emission of the tertiary industry, for there is a great need for energy in some parts of the tertiary industry, such as the catering and transportation industries. Therefore, the adjustment of the industrial structure should not only be focused on reducing the proportion off secondary industries, but the characteristics of the tertiary industry should also be considered.
- (4)
- It is essential for each city to revise original policies to meet long-term emission reduction targets, and pay attention to the industry that can achieve low- or zero-emissions in all stages of their life cycles.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kais, S.; Sami, H. An econometric study of the impact of economic growth and energy use on carbon emissions: Panel data evidence from fifty eight countries. Renew. Sustain. Energy Rev. 2016, 59, 1101–1110. [Google Scholar] [CrossRef]
- Kuznets, P.; Simon, P. Economic growth and income inequality. Am. Econ. Rev. 1955, 45, 1–28. [Google Scholar]
- Lau, L.S.; Choong, C.K.; Eng, Y.K. Carbon dioxide emission, institutional quality, and economic growth: Empirical evidence in Malaysia. Renew. Energy 2014, 68, 276–281. [Google Scholar] [CrossRef]
- Gallego-Álvarez, I.; Segura, L.; Martínez-Ferrero, J. Carbon emission reduction: The impact on the financial and operational performance of international companies. J. Clean. Prod. 2014, 103, 149–159. [Google Scholar] [CrossRef]
- Burke, P.J.; Shahiduzzaman, M.; Stern, D.I. Carbon dioxide emissions in the short run: The rate and sources of economic growth matter. Glob. Environ. Chang. 2015, 33, 109–121. [Google Scholar] [CrossRef]
- Tan, X.; Dong, L.; Chen, D.; Gu, B.; Zeng, Y. China’s regional CO2, emissions reduction potential: A study of Chongqing city. Appl. Energy 2016, 162, 1345–1354. [Google Scholar] [CrossRef]
- Ertugrul, H.M.; Cetin, M.; Seker, F.; Seker, F.; Dogan, E. The impact of trade openness on global carbon dioxide emissions: Evidence from the top ten emitters among developing countries. Ecol. Indic. 2016, 67, 543–555. [Google Scholar] [CrossRef]
- Leong, C.C.; Blakey, S.; Wilson, C.W. Genetic Algorithm optimised Chemical Reactors network: A novel technique for alternative fuels emission prediction. Swarm Evol. Comput. 2015, 27, 180–187. [Google Scholar] [CrossRef]
- Gardezi, S.S.S.; Shafiq, N.; Zawawi, N.A.W.A.; Khamidi, M.F.; Farhan, S.A. A multivariable regression tool for embodied carbon footprint prediction in housing habitat. Habitat Int. 2016, 53, 292–300. [Google Scholar] [CrossRef]
- Pao, H.T.; Fu, H.C.; Tseng, C.L. Forecasting of CO2, emissions, energy consumption and economic growth in China using an improved grey model. Energy 2012, 40, 400–409. [Google Scholar] [CrossRef]
- Deng, J.L. Control problems of Grey system. Syst. Contr. Lett. 1982, 1, 288–294. [Google Scholar]
- Wang, J.; Jiang, H.; Zhou, Q.; Wu, J.; Qin, S. China’s natural gas production and consumption analysis based on the multicycle Hubbert model and rolling Grey model. Renew. Sustain. Energy Rev. 2016, 53, 1149–1167. [Google Scholar] [CrossRef]
- Chen, L.; Lin, W.; Li, J.; Tian, B.; Pan, H. Prediction of lithium-ion battery capacity with metabolic grey model. Energy 2016, 106, 662–672. [Google Scholar] [CrossRef]
- Hamzacebi, C.; Karakurt, I. Forecasting the Energy-related CO2 Emissions of Turkey Using a Grey Prediction Model. Energy Sources Part A Recover. Util. Environ. Eff. 2015, 37, 1023–1031. [Google Scholar] [CrossRef]
- Wang, X.; Cai, Y.; Xu, Y.; Zhao, H.; Chen, J. Optimal strategies for carbon reduction at dual levels in China based on a hybrid nonlinear grey-prediction and quota-allocation model. J. Clean. Prod. 2014, 83, 185–193. [Google Scholar] [CrossRef]
- Ang, B.W.; Zhang, F.Q. A survey of index decomposition analysis in energy and environmental studies. Energy 2000, 25, 1149–1176. [Google Scholar] [CrossRef]
- Ang, B.W. Decomposition analysis for policy making in energy: Which is the preferred method? Energy Policy 2004, 32, 1131–1139. [Google Scholar] [CrossRef]
- Wang, Q.W.; Wang, Y.Z.; Zhou, P.; Wei, H.Y. Whole process decomposition of energy-related SO2 in Jiangsu Province, China. Appl. Energy 2016. Available online: http://www.sciencedirect.com/science/article/pii/S0306261916306705 (accessed on 19 May 2016). [Google Scholar]
- Ma, P.; Wang, L.S.; Guo, N. Modeling of hydronic radiant cooling of a thermally homeostatic building using a parametric cooling tower. Appl. Energy 2014, 127, 172–181. [Google Scholar] [CrossRef]
- Wang, Q.W.; Hang, Y.; Zhou, P.; Wang, Y.Z. Decoupling and attribution analysis of industrial carbon emissions in Taiwan. Energy 2016, 113, 728–738. [Google Scholar] [CrossRef]
- Wang, Q.W.; Chiu, Y.H.; Chiu, C.R. Driving factors behind carbon dioxide emissions in China: A modified production-theoretical decomposition analysis. Energy Econ. 2015, 51, 252–260. [Google Scholar] [CrossRef]
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2001; China Statistic Press: Beijing, China, 2001. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2002; China Statistic Press: Beijing, China, 2002. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2003; China Statistic Press: Beijing, China, 2003. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2004; China Statistic Press: Beijing, China, 2004. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2005; China Statistic Press: Beijing, China, 2005. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2006; China Statistic Press: Beijing, China, 2006. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2007; China Statistic Press: Beijing, China, 2007. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2008; China Statistic Press: Beijing, China, 2008. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2009; China Statistic Press: Beijing, China, 2009. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2010; China Statistic Press: Beijing, China, 2010. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2011; China Statistic Press: Beijing, China, 2011. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2012; China Statistic Press: Beijing, China, 2012. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2013; China Statistic Press: Beijing, China, 2013. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2014; China Statistic Press: Beijing, China, 2014. (In Chinese)
- Jiangsu Statistical Bureau. Jiangsu Statistical Year Book 2015; China Statistic Press: Beijing, China, 2015. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2001; China Statistic Press: Beijing, China, 2001. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2002; China Statistic Press: Beijing, China, 2002. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2003; China Statistic Press: Beijing, China, 2003. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2004; China Statistic Press: Beijing, China, 2004. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2005; China Statistic Press: Beijing, China, 2005. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2006; China Statistic Press: Beijing, China, 2006. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2007; China Statistic Press: Beijing, China, 2007. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2008; China Statistic Press: Beijing, China, 2008. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2009; China Statistic Press: Beijing, China, 2009. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2010; China Statistic Press: Beijing, China, 2010. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2011; China Statistic Press: Beijing, China, 2011. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2012; China Statistic Press: Beijing, China, 2012. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2013; China Statistic Press: Beijing, China, 2013. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2014; China Statistic Press: Beijing, China, 2014. (In Chinese)
- State Statistical Bureau. China Energy Statistical Yearbook 2015; China Statistic Press: Beijing, China, 2015. (In Chinese)

| Original Fuels | Factors | Aggregated Fuels | Factors |
|---|---|---|---|
| Raw Coal | 0.7559 | Coal | 0.7889 |
| Cleaned Coal | 0.7559 | ||
| Coke | 0.8550 | ||
| Gasoline | 0.5538 | Oil | 0.56715 |
| Diesel | 0.5921 | ||
| Fuel Oil | 0.6185 | ||
| Liquefied Petroleum Gas | 0.5042 | ||
| Natural Gas | 0.4483 | Natural Gas | 0.4483 |
| Variables | Definitions | Unit |
|---|---|---|
| R | Population | 1.0 × 104 persons |
| G | GDP | 1.0 × 108 yuan |
| Gi | GDP of industrial sectors | 1.0 × 108 yuan |
| Ei | Gross energy consumption of industrial sectors | 1.0 × 104 tce |
| Eij | Consumption of fuel j in industrial sector i | 1.0 × 104 tce |
| Cij | CO2 emissions arising from fuel j in industrial sector i | 1.0 × 104 tons |
| r | Population size | 1.0 × 104 persons |
| w | GDP per capita | yuan/person |
| si | Share of GDP of industrial sector i | Percentage point |
| ei | Energy intensity in industrial sector i | tce/1.0 × 104 yuan |
| nij | Fuel mix (share of consumption of fuel j in gross Energy consumption in industrial sector i) | Percentage point |
| kij | CO2 emission coefficient: CO2 emission per unit of Fuel j in industrial sector i | 1.0 × 104 tons |
| Additive Decomposition | |
|---|---|
| Change Scheme | LMDI Formulae |
| Prediction Terms | C Value | P Value |
|---|---|---|
| Population | 0.1536 | 1.0000 |
| Primary Industry GDP | 0.1351 | 1.0000 |
| Secondary Industry GDP | 0.1511 | 1.0000 |
| Tertiary Industry GDP | 0.0795 | 1.0000 |
| Primary Industry Coal Consumption | 0.3891 | 1.0000 |
| Primary Industry Oil Consumption | 0.4019 | 0.9333 |
| Primary Industry Natural Gas Consumption | model is not suitable for prediction | |
| Secondary Industry Coal Consumption | 0.4185 | 1.0000 |
| Secondary Industry Oil Consumption | 0.3208 | 0.8889 |
| Secondary Industry Natural Gas Consumption | 1.4430 | 0.3333 |
| Tertiary Industry Coal Consumption | 0.6940 | 0.7333 |
| Tertiary Industry Oil Consumption | 0.2309 | 1.0000 |
| Tertiary Industry Natural Gas Consumption | 1.4464 | 0.3333 |
| Prediction Terms | Prediction Model | Adjusted R2 |
|---|---|---|
| Secondary Industry Natural Gas Consumption | Y = −0.202X3 + 8.639X2 − 32.021X + 27.044 | R2 = 0.9906 |
| Tertiary Industry Natural Gas Consumption | Y = −0.22X3 + 1.387X2 − 9.005X + 11.305 | R2 = 0.9054 |
| Prediction Terms | Unit | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|
| Population | /10,000 persons | 8079.24 | 8130.83 | 8182.75 | 8234.99 | 8287.58 | 8340.50 |
| Primary Industry GDP | 1.0 × 108 RMB | 4301.58 | 4773.69 | 5297.61 | 5879.04 | 6524.27 | 7240.33 |
| Secondary Industry GDP | 1.0 × 108 RMB | 39,486.8 | 44,824.1 | 50,882.8 | 57,760.5 | 65,567.9 | 74,430.5 |
| Tertiary Industry GDP | 1.0 × 108 RMB | 39,193.4 | 46,392.8 | 54,914.8 | 65,502.2 | 76,492.5 | 91,076.2 |
| Primary Industry Coal Consumption | 1.0 × 104 tce | 35.10 | 34.09 | 33.11 | 32.16 | 31.23 | 30.33 |
| Primary Industry Oil Consumption | 1.0 × 104 tce | 358.61 | 383.63 | 410.41 | 439.05 | 469.69 | 502.47 |
| Primary Industry Natural Gas Consumption | 1.0 × 104 tce | 0 | 0 | 0 | 0 | 0 | 0 |
| Secondary Industry Coal Consumption | 1.0 × 104 tce | 8865.8 | 9563.3 | 10,315.5 | 11,127.0 | 12,002.3 | 12,946.5 |
| Secondary Industry Oil Consumption | 1.0 × 104 tce | 371.87 | 348.84 | 327.23 | 306.96 | 287.95 | 270.11 |
| Secondary Industry Natural Gas Consumption | 1.0 × 104 tce | 896.88 | 984.51 | 1068.77 | 1148.44 | 1222.29 | 1289.13 |
| Tertiary Industry Coal Consumption | 1.0 × 104 tce | 21.32 | 20.36 | 19.45 | 18.58 | 17.75 | 16.96 |
| Tertiary Industry Oil Consumption | 1.0 × 104 tce | 1908.72 | 2068.22 | 2241.04 | 2428.31 | 2631.23 | 2851.11 |
| Tertiary Industry Natural Gas Consumption | 1.0 × 104 tce | 132.05 | 150.82 | 170.12 | 189.81 | 209.76 | 229.85 |
| Year | Population | Economy Structure | Industry Structure | Energy Intensity | Fuel Mix | Total Contribution |
|---|---|---|---|---|---|---|
| 2001–2000 | 10.11 | 228.10 | 0.52 | −326.77 | −4.00 | −92.04 |
| 2002–2001 | 15.17 | 258.33 | 23.93 | −181.72 | −6.65 | 109.06 |
| 2003–2002 | 17.99 | 390.85 | 43.72 | −190.45 | −12.64 | 249.46 |
| 2004–2003 | 27.73 | 567.95 | 56.64 | 370.05 | 21.67 | 1044.04 |
| 2005–2004 | 30.68 | 732.04 | 11.69 | −1045.57 | −29.47 | −300.64 |
| 2006–2005 | 36.84 | 613.55 | −8.00 | 896.50 | 60.10 | 1598.97 |
| 2007–2006 | 47.14 | 917.56 | −59.39 | −353.43 | −6.93 | 544.95 |
| 2008–2007 | 29.92 | 997.84 | −58.91 | −437.24 | −18.05 | 513.55 |
| 2009–2008 | 38.33 | 625.59 | −79.54 | −404.40 | 8.46 | 188.43 |
| 2010–2009 | 49.02 | 1149.17 | −121.51 | −789.77 | −3.12 | 283.79 |
| 2011–2010 | 26.68 | 1188.22 | −112.33 | −142.57 | 4.15 | 964.15 |
| 2012–2011 | 20.11 | 700.65 | −116.01 | −824.69 | −53.40 | −273.35 |
| 2013–2012 | 17.75 | 704.92 | −162.01 | −865.38 | −37.55 | −342.27 |
| 2014–2013 | 18.58 | 595.54 | −136.42 | −225.31 | −16.22 | 236.16 |
| Total | 386.04 | 9670.29 | −717.64 | −4520.76 | −93.65 | 4724.28 |
| Year | Population | Economy Structure | Industry Structure | Energy Intensity | Fuel Mix | Total Contribution |
|---|---|---|---|---|---|---|
| 2016–2015 | 59.69 | 1306.05 | −131.46 | −545.84 | −16.54 | 671.90 |
| 2017–2016 | 64.26 | 1410.97 | −146.14 | −591.58 | −10.11 | 727.40 |
| 2018–2017 | 69.15 | 1524.03 | −162.27 | −641.26 | −2.87 | 786.79 |
| 2019–2018 | 74.41 | 1645.81 | −179.97 | −695.01 | 5.12 | 850.36 |
| 2020–2019 | 80.05 | 1776.93 | −199.38 | −752.97 | 13.79 | 918.43 |
| Total | 347.57 | 7663.80 | −819.23 | −3226.66 | −10.61 | 3954.87 |
| Year | Primary Industry | Secondary Industry | Tertiary Industry | Total Effects |
|---|---|---|---|---|
| 2016–2015 | −9.86 | −149.47 | 27.87 | −131.46 |
| 2017–2016 | −10.57 | −165.12 | 29.55 | −146.14 |
| 2018–2017 | −11.33 | −182.24 | 31.30 | −162.27 |
| 2019–2018 | −12.15 | −200.95 | 33.13 | −179.97 |
| 2020–2019 | −13.05 | −221.37 | 35.04 | −199.38 |
| Average | −11.39 | −183.83 | 31.38 | −163.85 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, D.; Ma, T.; Li, Z.; Tang, J.; Bethel, B.J. Trend Prediction and Decomposed Driving Factors of Carbon Emissions in Jiangsu Province during 2015–2020. Sustainability 2016, 8, 1018. https://doi.org/10.3390/su8101018
Tang D, Ma T, Li Z, Tang J, Bethel BJ. Trend Prediction and Decomposed Driving Factors of Carbon Emissions in Jiangsu Province during 2015–2020. Sustainability. 2016; 8(10):1018. https://doi.org/10.3390/su8101018
Chicago/Turabian StyleTang, Decai, Tingyu Ma, Zhijiang Li, Jiexin Tang, and Brandon J. Bethel. 2016. "Trend Prediction and Decomposed Driving Factors of Carbon Emissions in Jiangsu Province during 2015–2020" Sustainability 8, no. 10: 1018. https://doi.org/10.3390/su8101018
APA StyleTang, D., Ma, T., Li, Z., Tang, J., & Bethel, B. J. (2016). Trend Prediction and Decomposed Driving Factors of Carbon Emissions in Jiangsu Province during 2015–2020. Sustainability, 8(10), 1018. https://doi.org/10.3390/su8101018






