Abstract
Exposure to hazardous concentrations of volatile organic compounds indoors in small workshops could affect the health of workers, resulting in respirative diseases, severe intoxication or even cancer. Controlling the concentration of volatile organic compounds is required to prevent harmful conditions for workers in indoor environments. In this document, PI and fuzzy PI controllers were used to reduce hazardous indoor air benzene concentrations in small workplaces. The workshop is represented by means of a well-mixed room model. From the knowledge obtained from the model, PI and fuzzy PI controllers were designed and their performances were compared. Both controllers were able to maintain the benzene concentration within secure levels for the workers. The fuzzy PI controller performed more efficiently than the PI controller. Both approaches could be expanded to control multiple extractor fans in order to reduce the air pollution in a shorter time. The results from the comparative analysis showed that implementing a fuzzy logic PI controller is promising for assuring indoor air quality in this kind of hazardous work environment.
1. Introduction
Volatile organic compounds (VOCs) are a large group of carbon-based chemicals that easily evaporate at room temperature [1]. Diverse industries commonly use paints, solvents, varnishes and fuels that generate VOCs, such as benzene. Indoor environments with poor ventilation can accumulate hazardous concentrations of VOCs, impacting human health. Severe human exposure to benzene may cause narcosis: headache, dizziness, drowsiness, confusion, tremors and loss of consciousness [2]. In the long term, benzene may impact the health of the operator, producing damage to the reproductive, immune, nervous, endocrine, cardiovascular and respiratory systems, as well as cancer [3,4,5,6]. Detection of VOCs is of paramount importance for human safety and industrial hygiene in hazardous environments [7].
Extracting or ventilation systems are commonly used to avoid large accumulation of VOCs in the indoors of occupational spaces in factories and laboratories. Extracting systems are generally operated continuously in open loop mode and at a constant rate. These system are unable to extract toxic gases opportunely if the concentration of VOCs suddenly increases. Efficient control systems for hazardous processes would require measuring the variations of VOC concentrations in real time and then make a decision to operate the extraction device. Diverse well-mixed room (WMR) and near-field-far-field (NF-FF) mathematical models have been used to describe the dynamics of VOCs in occupational spaces. The WMR approach is a simple model assuming that compounds are homogeneously distributed throughout the room [8]. The near-field-far-field (NF-FF) mathematical model is composed of two zones, and it is based on the idea that the closer a person is to a source of generation, the greater is the exposure, and vice versa. The NF zone is located at the center of the contaminated zone, and the FF zone is composed of the remaining space of the room [9,10,11]. From a control point of view, either in the WMR or in the NF-FF models, it is important to detect sudden toxic spills to opportunely activate the nearest extractor(s) to the hazardous zone at maximum power. The VOCs extracted from indoors can be biofiltered before they are released to the environment [12]
The complexity, nonlinear behavior and uncertainties used in hazardous chemical processes require the use of efficient control strategies. Nowadays, proportional-integral (PI) and proportional integral-derivative (PID) controllers are widely used to control industrial processes [13]. These controllers have great acceptability due to their simplicity and ease of implementation. The PID approach has the following advantages:
- Minimum rise time, which is the time required for the system response to rise from 10% to 90% (over damped), 5% to 95% and 0% to 100% (under damped) of the final steady-state value of the desired response.
- Minimum overshoot and the maximum overshoot is the highest peak value of the response curve measured from the desired response of the system.
- Minimum settling time, which is the time required for the response to reach and stay within 2% of its final value.
Diverse PI and PID controllers have been used to control indoor occupational exposure of VOC concentrations. A system to control greenhouse air temperature and CO2 concentrations by means of simultaneous ventilation and enrichment was reported in [14]. A dual-mode demand control ventilation strategy to be used in buildings in which the number of occupants varies frequently was developed in [15]. A qualitative study of different faults that can appear in air handling units due to incorrect control of outdoor air is given in [16].
A different kind of controller is based on fuzzy logic, which was developed by Lofti Zadeh [17]. Fuzzy logic is well suited to processes with poor known dynamics and uncertainties. Fuzzy logic can help to compensate for the lack of information, adding the knowledge and experience from personnel related to the process using IF-THEN rules. Few fuzzy logic approaches have been used to control indoor occupational exposure of VOC concentrations. Five fuzzy controllers were developed to regulate the satisfaction requirements of occupants in indoor spaces [18]. A new indoor air quality control based on fuzzy logic was developed to control natural ventilated indoor environments where no other ventilation approaches exist or can be installed due to space limitation or economic reasons [19]. An integral automated regulation system to control the indoor environment based on the bioclimatic concept was reported in [20]. Therefore, the aim of this manuscript is to design, simulate and compare the performance of a classic PI controller and a fuzzy logic PI controller based on a WMR model to control hazardous benzene spilling. The results of the simulations show that the experimental implementation is promising.
2. Process Description
The case study was a washing process using petroleum distillate solvents to remove oil, grease and dirt from small metal parts [21]. This is a brief description of the process. A liquid solvent is kept in a small tank that is used as a reservoir. The solvent was pumped up from the reservoir tank into a waste-high basin through a scrub brush appliance. The metal parts are flushed with the solvent and, at the same time, scrubbed with a brush. Later, the solvent is drained and returned to the reservoir tank. Benzene is present in the cleaning solvent (less than 0.1%, w/w), either as a constituent in the fresh solvent or in materials, such as gasoline washed from the parts into the device. The washer basin is 2.58 ft long and 1.71 ft wide, and the tank holds 9.4 gallons of a solvent containing aliphatic and aromatic hydrocarbons [21]. The solvent density was 0.78 g/mL. The solvent was spiked with benzene to attain 135 ppm benzene w/w at reference time t = 0. After 221 min of use of the washer, the benzene content decreased to 84 ppm w/w. After an additional 266 min of use, the benzene content decreased to 32 ppm w/w. The washer was located in a room with dimensions of 80 ft × 58 ft × 25 ft (volume = 3290 m3) and had no open windows, open doors, nor mechanical air supply inlets nearby. The supply/exhaust air rate for the room was not determined. A fixed position sampling device was located 2.04 ft above the front edge of the basin while cleaning was performed.
3. Well-Mixed Room Model
The aim of this paper is to propose an automatic controller to guarantee secure benzene concentrations indoors by manipulating the supply exhaust air rate in the room. The selected case study is the solvent part washer process addressed in [22]. The room is modeled as a near-field-far-field model, in which the room is separated into two well-defined zones: the NF model is where the spill originates, considered as half of a sphere, while the FF zone is the remainder of the room. The NF was conceptualized as a rectangular box of air situated over the wash basin. Figure 1a shows the representation of the NF-FF model. The parameter Q is very important in this model, since it is related to the ventilation rate, allowing the removal of the contaminants in the room. According to [22], the contribution of the general room benzene concentration is negligible and can be ignored. Then, the NF-FF model can be simplified to a well-mixed room model (Figure 1), since the contribution of the FF model is less than 6%.
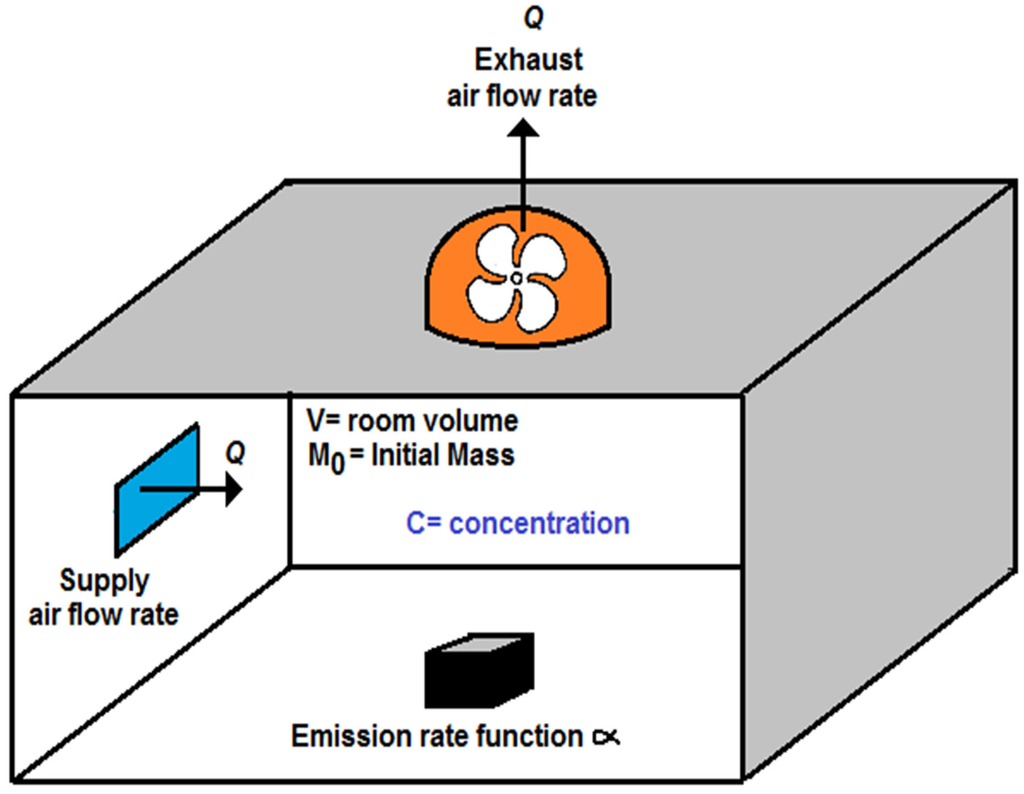
Figure 1.
Representation of a well-mixed room.
Then, the well-mixed room model model can be simplified to:
where C(t) is the benzene concentration (mg/m3), α (min−1) is the loss emission rate constant, M0 (mg) is the initial chemical mass in the source, V (m3) is the room volume and Q is the supply/exhaust air flow rate (m3/min). To avoid a dangerous benzene concentration indoors, an adequate fan extracting system must be installed. Then, it can be understood that the ventilation rate Q (m3/min) is a critical parameter to extract dangerous compounds. In general, Q is often considered as a constant i.e., a fan extracting gases at a fixed rate; however, when an abrupt spill happens, a fixed extractor will not operate properly to exhaust the undesirable compounds; it will be necessary to vary the speed of the extractors, and this takes more sense if control systems are used. Then, to describe the dynamics of Q, we use the fan law [25], which is represent as:
where Q(t) is the exhaust air flow rate, Qold is the exhaust air flow rate at the previous moment and ϑnew and ϑold are the actual speed and previous speed of the fans (motors) in rpm, respectively. Using the fan law, it is possible to manipulate the exhaust air flow rate in the room, and that is what we do with the controller.
Model assumptions:
- The use of Equation (2) in Equation (1) is an adequate approximation to control the well-mixed room assuming that the time variation of Q(t) is slower compared to C(t).
4. Proportional-Integral Control System
Proportional-integral-derivative (PID) controllers are widely used in industrial control systems because of the reduced number of parameters to be tuned. They provide control signals that are proportional to the error between the reference signal and the actual output (proportional action), to the integral of the error (integral action) and to the derivative of the error (derivative action) [13]. The corresponding equation is given as:
Where u(t) is the actuating signal, e(t) is the error signal, Kp is the proportional gain constant, Ki is the integral gain constant and Kd is the derivative gain constant. The PID control offers the simplest and yet most efficient solution to many real-world control problems by means of its three-term functionality covering treatment to both transient and steady-state responses. The PID is the most common form of feedback control used at the industrial level; however, most of the control loops are actually proportional-integral (PI) [26].
The PI controller is a standard solution for most industrial applications. The main reason is its relatively simple structure, which can be easily understood and implemented in practice, and that many sophisticated control strategies, such as model predictive control, are based on it. An application with large speed capabilities requires different PI gains than an application that operates at a fixed speed. In addition, industrial equipment that is operating over a wide range of speeds requires different gains at the lower and higher end of the speed range in order to avoid overshoots and oscillations. Generally, tuning the proportional and integral constants for a large speed control process is expensive and time consuming. The task is further complicated when incorrect PI constants are sometimes selected due the lack of understanding of the process [27]. The control action law of a PI controller is defined by the following equation:
The objective of the proposed proportional-integral controller shown in Figure 2 is to maintain the concentration of benzene vapors C(t) in ppm of the process given in [21], within the acceptable levels suggested by ATSDR (Agency for Toxic Substances and Disease Registry) [28]. From Equation (1), the value of C(t) can be estimated as the information of several benzene sensors inside the small workshop. The PI controller uses the feedback error e(t) to generate a duty cycle that controls the extractor fans’ speed, reducing C(t).
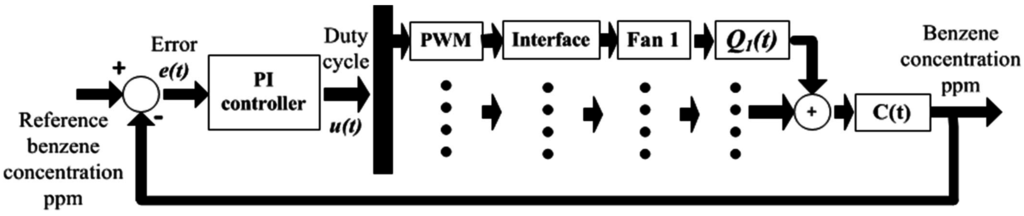
Figure 2.
Proposed PI control system.
As an extracting system, a DC fan/motor is proposed with three inlet duct connections [29], and the estimated number of fans depends on the workshop volume. The removed benzene concentrations from the ducts could be treated by air biofiltration, which involves the degradation of volatile organic compounds using microorganisms [12,30]. The conventional PI controller gains (Kp and Ki) are tuned at rated conditions based on Ziegler–Nichols tuning rules and had fixed values during the different operating conditions [31]. The PI gains are specified in Table 1.

Table 1.
Proportional-integral controller gains.
| Parameter | Gain |
|---|---|
| Kp | 3.7265 × 10−3 |
| Ki | 1.0062 |
The PI controller sets its output range between zero and one; this range characterizes the duty cycle required by a pulse width modulator (PWM) that controls the DC motor connected to the fan. For instance, if the controller output is one, the fan will rotate at full speed (rpm), since a 100% duty cycle is provided by the PWM to the DC motor. The new values of Q(t) were calculated using Equation (2). Notice from Figure 1 that if multiple fan extractors are used, the fuzzy controller output signal would be the same for each extractor.
5. Fuzzy Proportional-Integral Control System
5.1. Fuzzy Logic Controller
According to [32], fuzzy control provides a formal methodology to represent, manipulate and implement human’s heuristic knowledge about how to control a system. Figure 3 depicts the block diagram of a fuzzy logic controller, in which a closed-loop control system is embedded. The process outputs are denoted by y(t); its inputs are denoted by u(t); and the reference input to the fuzzy controller is denoted by r(t).
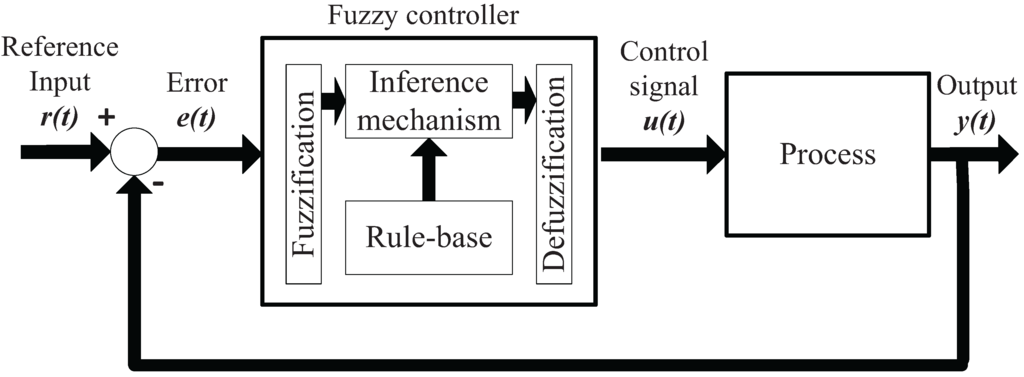
Figure 3.
Scheme of a fuzzy logic controller.
The fuzzy controller has four main components: The rule-base, which holds the knowledge, in the form of a set of rules, describing the best way to control a system. The membership functions are used to quantify knowledge. The inference mechanism evaluates which control rules are relevant at the current time and then decides what input of the plant should be enabled. The fuzzification interface modifies the inputs, so that they can be interpreted and compared to the rules in the rule-base. The defuzzification interface transforms the conclusions reached by the inference mechanism into the inputs of the plant.
5.2. Fuzzy PI Control Design
In a fuzzy controller, the designer must collect information about the way an artificial decision should act in the closed-loop system. Sometimes, this information comes from a human expert performing the control task, while at other times, the designer can aid with the understanding of the plant dynamics and propose a set of rules about how to control the system. These rules basically state that, ‘If the plant output and reference input are behaving in a certain manner, then the plant input should be modified to achieve the control operational goals’. A fuzzy controller can be combined with classical control to obtain PD, PI and PID fuzzy controllers. The fuzzy PID control generates incremental control output from the error, the change in error and the acceleration error. Fuzzy PI-type control is known to be more practical than fuzzy PD controllers, which have difficulties in removing the steady-state error [33]. Equation (4) can be derivated to obtain the PI control law as [34]:
then:
where is the change of the control signal, e(t) is the feedback error and and is the change of error. If Equation (6) is applied to the control systems presented in Figure 2 and Figure 3, then a two-term fuzzy control, namely the PI fuzzy logic controller (PI FLC), can be obtained (see Figure 4). The concentration error (CE) and the concentration error change (CEC) use the gains Ki and Kp from Table 1.
The fuzzification stage for the PI FLC uses e(t) and as the control inputs. The three input triangular membership functions [35] used in input scaling are low, medium and high. The membership functions for the two inputs are similarly selected as shown in Figure 5 and Figure 6.
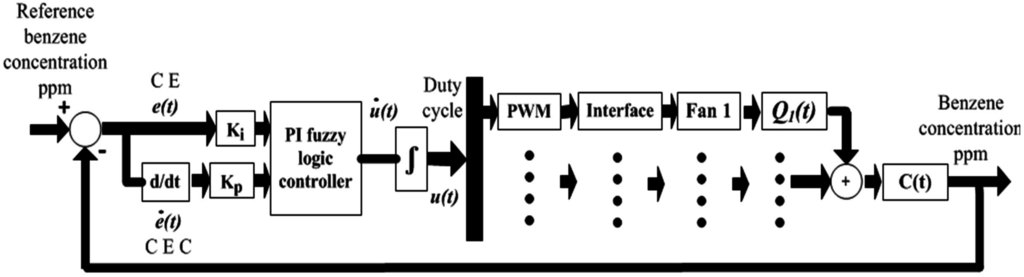
Figure 4.
Proposed fuzzy PI control system.
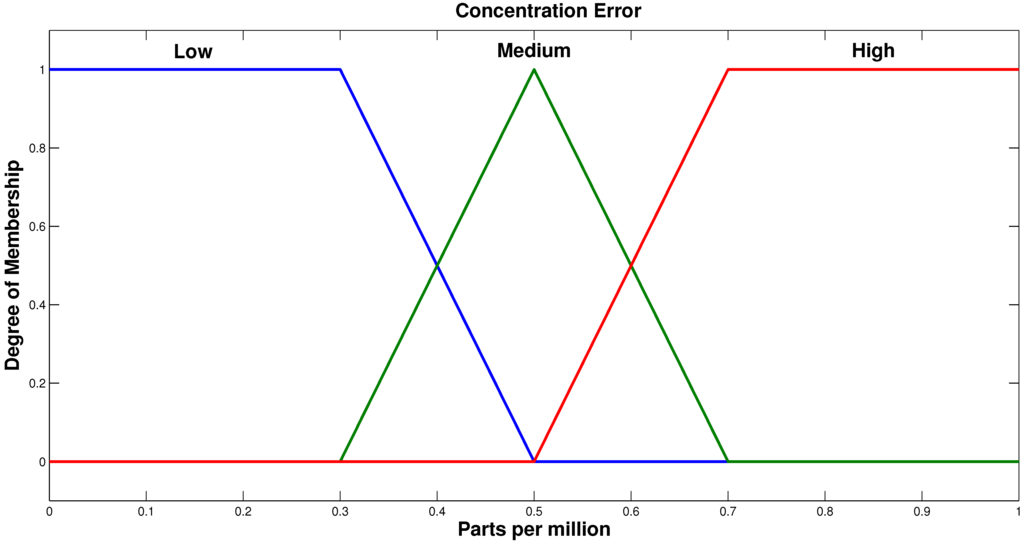
Figure 5.
Fuzzy set for the input variable concentration error.
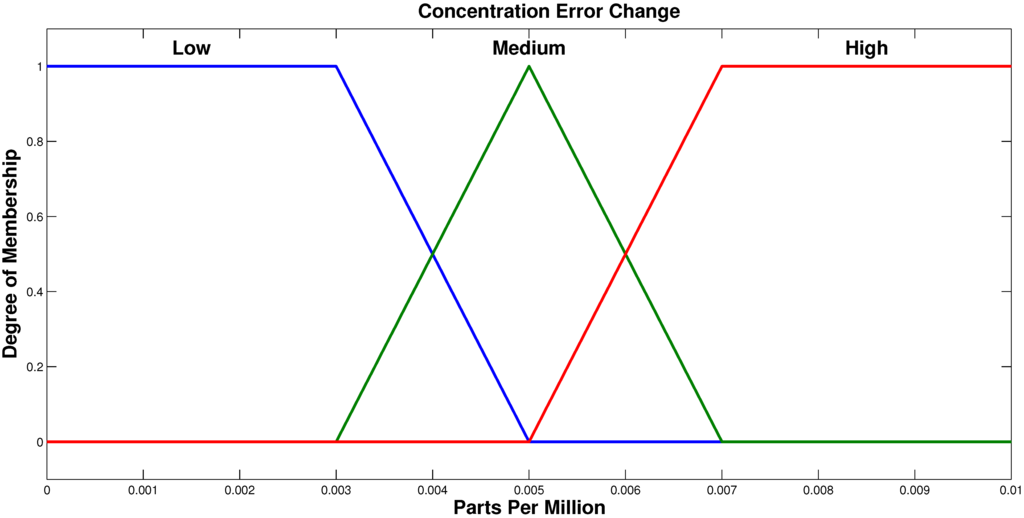
Figure 6.
Fuzzy set for the input variable concentration error change.
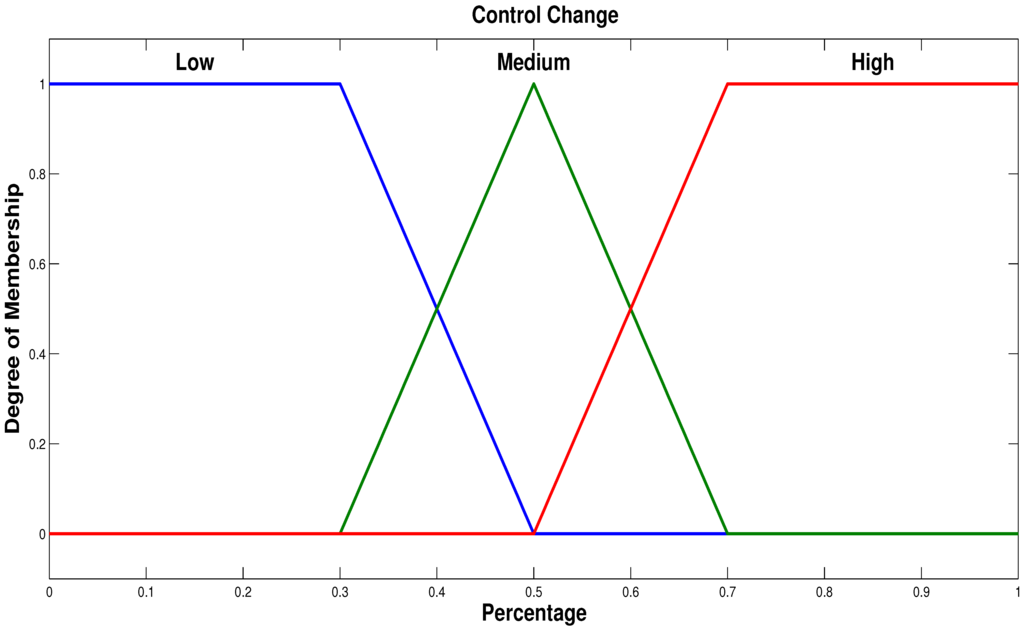
Figure 7.
Fuzzy set for the output variable control change.
As reported in [19], the PI FLC output range can be set between zero and one. The output triangular membership functions for are presented in Figure 7. The number of output membership functions are low, medium and high.
Based on the input and output membership functions, nine fuzzy control rules are possible for the Mamdani PI FLC. Table 2 shows the set of IF-THEN rules used in the rule-based system.

Table 2.
Rule-based system for the fuzzy controller.
| Number | Fuzzy Rules |
|---|---|
| 1 | If concentration error is low and concentration error change is low, then control change is low |
| 2 | If concentration error is low and concentration error change is medium, then control change is medium |
| 3 | If concentration error is low and concentration error change is high, then control change is high |
| 4 | If concentration error is medium and concentration error change is low, then control change is medium |
| 5 | If concentration error is medium and concentration error change is medium, then control change is medium |
| 6 | If concentration error is medium and concentration error change is high, then control change is high |
| 7 | If concentration error is high and concentration error change is low, then control change is high |
| 8 | If concentration error is high and concentration error change is medium, then control change is high |
| 9 | If concentration error is high and concentration error change is high, then control change is high |
The Zadeh logical “and” used in the rule-based system for the fuzzy controller is defined as:
where µA, µB are the membership functions of the Fuzzy Sets A and B, respectively. The resulting fuzzy control rule-base is presented in Table 3.

Table 3.
Fuzzy control rule-base. CE, concentration error; CEC, concentration error change.
| CEC | Low | Medium | High | |
|---|---|---|---|---|
| CE | ||||
| Low | Low | Medium | High | |
| Medium | Medium | Medium | High | |
| High | High | High | High | |
To convert the fuzzy sets into real numbers, the centroid defuzzifier is used. The output change of the PI FLC is given as:
where hi is the value of the output member for the i-th rule and µi is the output membership value for the i-th rule [17,33]. The resulting signal from Equation (9) has to be integrated to obtain the final duty cycle required in the PWM.
6. Simulation Results
The PI and fuzzy logic PI controllers of Figure 2 and Figure 4 were implemented in the software MATLABTM. The simulation required three extractor fans, and the initial condition for the benzene concentration is C(0) = 5 ppm with a simulation time of 10 min. Figure 8 shows the simulated duty cycle performed for both controllers.

Table 4.
Parameters used in the well-mixed room model.
| Parameter | Value |
|---|---|
| C(0) | 5 ppm |
| Q(0) | 169 m3min−1 |
| α | 0.0021 min−1 |
| M0 | 3750 mg |
| V | 0.26 m3 |
| ϑ(0) | 1000 rpm |
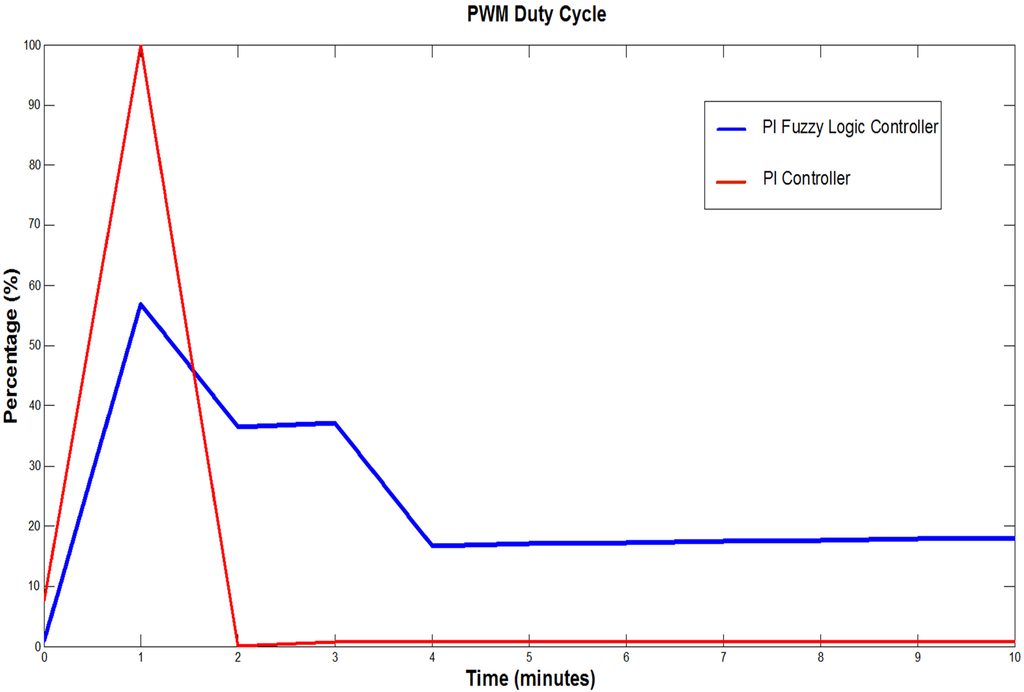
Figure 8.
Duty cycle response for the proposed control systems.
In order to have a good perspective of the duty cycle signal, Figure 8 is represented as a percentage scale from 0–100. To extract the accumulation of benzene, the controllers had the following behavior: In the first stage the PI controller reached a value of 100% of the PWM; meanwhile, the PI FLC produced a maximum value of 56.887% for its duty cycle. In the next period of time (minutes), it can be observed that the duty cycle for the PI FLC decreased to 18.058%. At the same time, it is observed that the duty cycle for the PI controller decreased from a value of 100% to 0.804%. Therefore, the PI controller will stress the performance of the extractor fans due to peak behavior of its duty cycle, while the PI FLC controller has a maximum duty cycle behavior with 56.887% of the extractor fan speed. Figure 9 presents the decrease in benzene concentration once the controllers are enabled. It is worth remarking that the response was similar for both controllers taking C(t) to 0.0080 ppm and below the acceptable level of 1 ppm, and the response behavior for Q(t) shown in Figure 10 had a maximum value of 300 m3/min. This was achieved in 1 min. The PI fuzzy logic controller response signals from the duty cycle and benzene concentrations have more effective behavior than the results presented in [36] in which a fuzzy controller was used for the same purpose.
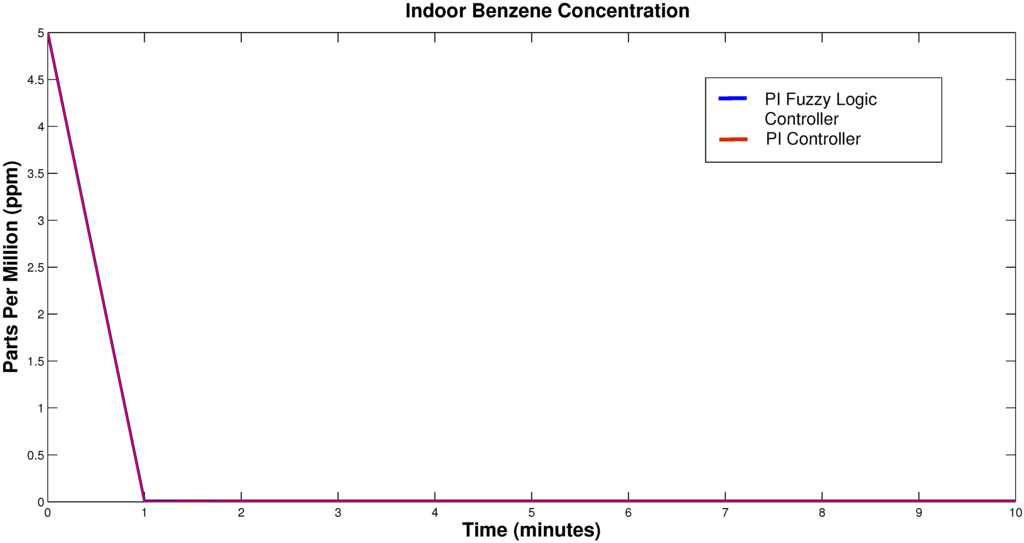
Figure 9.
Performance of the benzene concentration C(t).
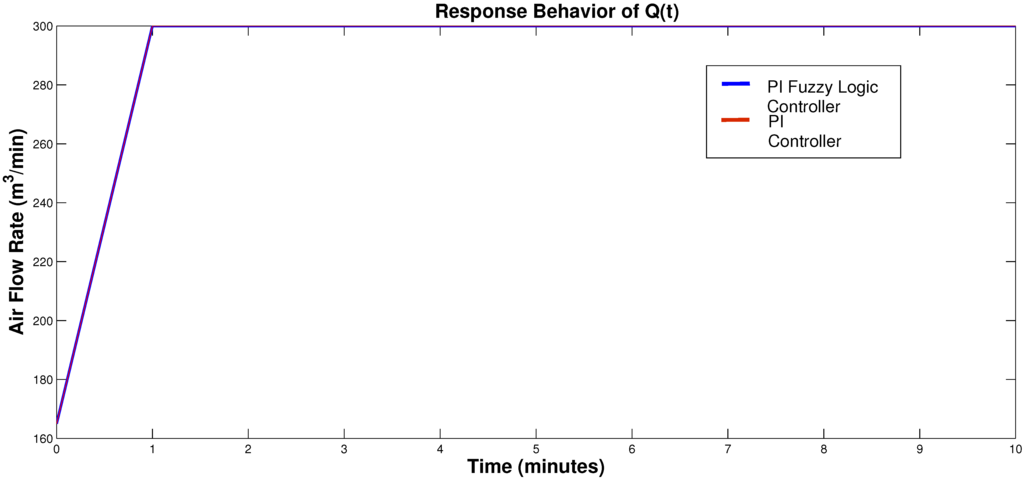
Figure 10.
Performance of the supply/exhaust air flow rate Q(t).
7. Conclusions
In this paper, a PI and fuzzy PI control systems were designed to reduce the air pollution from benzene concentrations of a washing process in a small workshop. The simulation results showed the effectiveness of both control systems taking the benzene concentration C(t) to 0.0080 ppm in one minute. The designed PI controller had the expected behavior for a controller tuned with the Ziegler–Nichols method. The proposed PI FLC provided proper actions taken by inferences from the fuzzy rule-based system of the controller. Each control system could be expandable to control multiple extractor fans for reducing the air pollution in a short time. However, it could be observed in the last section that the duty cycle from PI FLC presented a more efficient signal response for PWM than the PI controller. This means a better performance for extractor fans, because they reduced the air pollution using slightly more than half of the speed as the full-speed performance given by the PI controller. It can be concluded from the comparative analysis of both control systems that implementing a PI fuzzy logic controller for this kind of processes is promising for ensuring indoor air quality in this kind of work environment.
Acknowledgments
The authors would like to thank the Sonora University (UNISON) and the Centro de Investigación y Asistencia en Tecnología y Diseño del Estado de Jalisco A.C. (CIATEJ) for the support in this research.
Author Contributions
Nun Pitalúa-Díaz and Enrique J. Herrera-López developed the research ideas and global design. Guillermo Valencia-Palomo and Alvaro González-Angeles contributed in the analysis of the results. Ricardo A. Rodríguez-Carvajal and Nohe R. Cazarez-Castro helped out in the revision of the document.
Conflicts of Interest
The authors declare no conflict of interest.
References
- MDH. Minnesota Department of Health Fact Sheet. Available online: http://www.health.state.mn.us/divs/eh/indoorair/voc/ (accessed on 6 January 2015).
- WHO (World Health Organization). Preventing disease through healthy environments exposure to benzene; a major public health concern. Available online: http://www.who.int/ipcs/features/benzene.pdf (accessed on 6 January 2015).
- Bahadar, H.; Mostafalou, S.; Abdollahi, M. Current understandings and perspectives on non-cancer health effects of benzene: A global concern. Toxicol. Appl. Pharmacol. 2014, 276, 83–94. [Google Scholar] [CrossRef] [PubMed]
- IARC, International Agency for Research on Cancer (IARC)–Summaries & Evaluations. Available online: http://www.inchem.org/documents/iarc/suppl7/benzene.html (accessed on 6 January 2015).
- Ireland, B.; Collins, J.J.; Buckley, C.F.; Riordan, S.G. Cancer mortality among workers with benzene exposure. Epidemiology 1997, 8, 318–320. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.T. Advances in understanding benzene health effects and susceptibility. Annu. Rev. Publ. Health 2010, 31, 133–148. [Google Scholar] [CrossRef] [PubMed]
- Manes, G.; Collodi, G.; Fusco, R.; Gelpi, L.; Manes, A.; di Palma, D. Real-Time monitoring of volatile organic compounds in hazardous sites. In Environmental Monitoring; Ekundayo, E., Ed.; InTech: Rijeka, Croatia, 2010; pp. 219–244. [Google Scholar]
- Sakhvidi, M.J.; Barkhordari, A.; Salehi, M.; Behdad, S.; Fallahzadeh, H. Application of mathematical models in combination with Monte Carlo simulation for prediction of isoflurane concentration in an operation room theater. Ind. Health 2013, 51, 545–551. [Google Scholar] [CrossRef]
- Delgado-Saborit, J.M.; Aquilina, N.J.; Meddings, C.; Baker, S.; Harrison, R.M. Estimating benzene exposure at a solvent parts washer. Environ. Health Persp. 2009, 117, 1571–1579. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kang, D.; Choi, D.; Yeo, M.; Kim, K. VOC emission from building materials in residential buildings with radiant floor heating systems. Air Qual. Res. 2012, 12, 1398–1408. [Google Scholar] [CrossRef]
- Persoons, R.; Maitre, A.; Bicout, D.J. Modelling the time profiles of organic solvent concentrations for occupational exposure assessment purposes. Ann. Occup. Hyg. 2011, 55, 421–435. [Google Scholar] [CrossRef] [PubMed]
- Eun-Hee, L.; Hee-Wook, R.; Kyung-Suk, C. Removal of benzene and toluene in polyurethane biofilter immobilized with Rhodococcus sp. EH831 under transient loading. Bioresour. Technol. 2009, 100, 5656–5663. [Google Scholar]
- Kanojiya, R.G.; Meshram, P.M. Optimal tuning of PI controller for speed control of DC motor drive using particle swarm optimization. In Proceedings of the International Conference on Advances in Power Conversion and Energy Technologies (APCET), Mylavaram, India, 2–4 August 2012; pp. 1–6.
- Linker, R.; Gutman, P.O.; Seginer, I. Robust controllers for simultaneous control of temperature and CO2 concentration in greenhouses. Control Eng. Pract. 1999, 7, 851–862. [Google Scholar] [CrossRef]
- Chao, C.Y.H.; Hu, J.S. Development of a dual-mode demand control ventilation strategy for indoor air quality control and energy saving. Build. Environ. 2004, 39, 385–397. [Google Scholar] [CrossRef]
- Ginestet, S.; Marchio, D.; Morisot, O. Evaluation of faults impacts on energy consumption and indoor air quality on an air handling unit. Energ. Build. 2008, 40, 51–57. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kolokotsa, D. Comparison of the performance of fuzzy controllers for the management of the indoor environmental. Build. Environ. 2003, 38, 1439–1450. [Google Scholar] [CrossRef]
- Jaradat, M.; Al-Nimr, M. Fuzzy logic controller deployed for indoor air quality control in naturally ventilated environments. J. Electr. Eng. 2009, 600, 12–17. [Google Scholar]
- Košir, M.; Krainer, A.; Kristl, Ž. Integral control system of indoor environment in continuously occupied spaces. Automat. Constr. 2012, 21, 199–209. [Google Scholar] [CrossRef]
- Brinkman, D.W.B. Volatile solvent evaporation from an operating parts washer. Safety-Kleen Corp.: Elk Grove, IL, USA, 1990. [Google Scholar]
- Nicas, M.; Plisko, M.J.; Spencer, J.W. Estimating benzene exposure at a solvent parts washer. J. Occup. Environ. Hyg. 2006, 3, 284–291. [Google Scholar] [CrossRef] [PubMed]
- Keil, C.B.; Nicas, M. Predicting room vapor concentrations due to spills of organic solvents. Am. Ind. Hyg. Assoc. J. 2003, 64, 445–454. [Google Scholar] [CrossRef]
- Nicas, M. Using mathematical models to estimate exposure to workplace air contaminants. Chem. Health Safety 2003, 64, 10–21. [Google Scholar] [CrossRef]
- Stamper, E.; Koral, R. Handbook of Air Conditioning, Heating, and Ventilating; Industrial Press Inc.: New York, NY, USA, 1979. [Google Scholar]
- Heong, A.K.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar] [CrossRef]
- Singh, S.; Pandey, A.K.; Dipraj, Y. Design of Pi controller to minimize the speed error of D.C. servo motor. IJSTR 2012, 1, 95–98. [Google Scholar]
- Agency for Toxic Substances and Disease Registry (ATSDR). Toxicological Profile for Benzene; U.S. Department of Health and Human Services, Public Health Service: Atlanta, GA, USA, 2007. [Google Scholar]
- Nuaire. ES-OPUSDC Extract fans, Catalogue. Available online: http://www.nuaire.info/catalogue/ESOPUSDC.pdf (accessed on 12 January 2015).
- Rahul, K.M.; Chandrajit, B. Biodegradation of waste gas containing benzene by using corn-cob based biofilter. RJCS 2012, 2, 60–65. [Google Scholar]
- Kumar, R.; Daya, M.L. A novel self-tuning fuzzy based PID controller for speed control of induction motor drive. In Proceedings of the International Conference on Control Communication and Computing (ICCC), Thiruvananthapuram, India, 13–15 December 2013; pp. 62–67.
- Passino, K.M.; Yurkovich, S. Fuzzy Control; Addison-Wesley: Menlo Park, CA, USA, 1998. [Google Scholar]
- Gopala-Rao, K.A.; Amarendra-Reddy, B.; Durga-Bhavani, P. Fuzzy Pi and integrating type fuzzy PID controllers of linear, nonlinear and time-delay systems. IJCA 2010, 1, 41–47. [Google Scholar]
- Dongrui, W.; Woei, W.T.P. Interval type-2 fuzzy PI controllers: Why they are more robust. In Proceedings of the IEEE International Conference on Granular Computing, San Jose, CA, USA, 14–16 August 2010; pp. 803–807.
- Zhao, H.; Guo, S.P. Selecting green supplier of thermal power equipment by using a hybrid MCDM method for sustainability. Sustainability 2014, 6, 217–235. [Google Scholar] [CrossRef]
- Pitalúa-Díaz, N.; Herrera-López, E.J.; Velázquez-Contreras, L.E.; Álvarez-Chávez, C.R.; Munguia-Vega, N. Controlling indoor benzene concentrations using a fuzzy system. In Proceedings of the 15th IFAC Symposium on Control, Optimization and automation in Mining, Mineral & Metal Processing, San Diego, CA, USA, 25–28 August 2013; pp. 449–454.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).