Low Carbon Footprint Routes for Bird Watching
Abstract
:1. Introduction
2. Experimental Materials and Methods
2.1. Research Materials
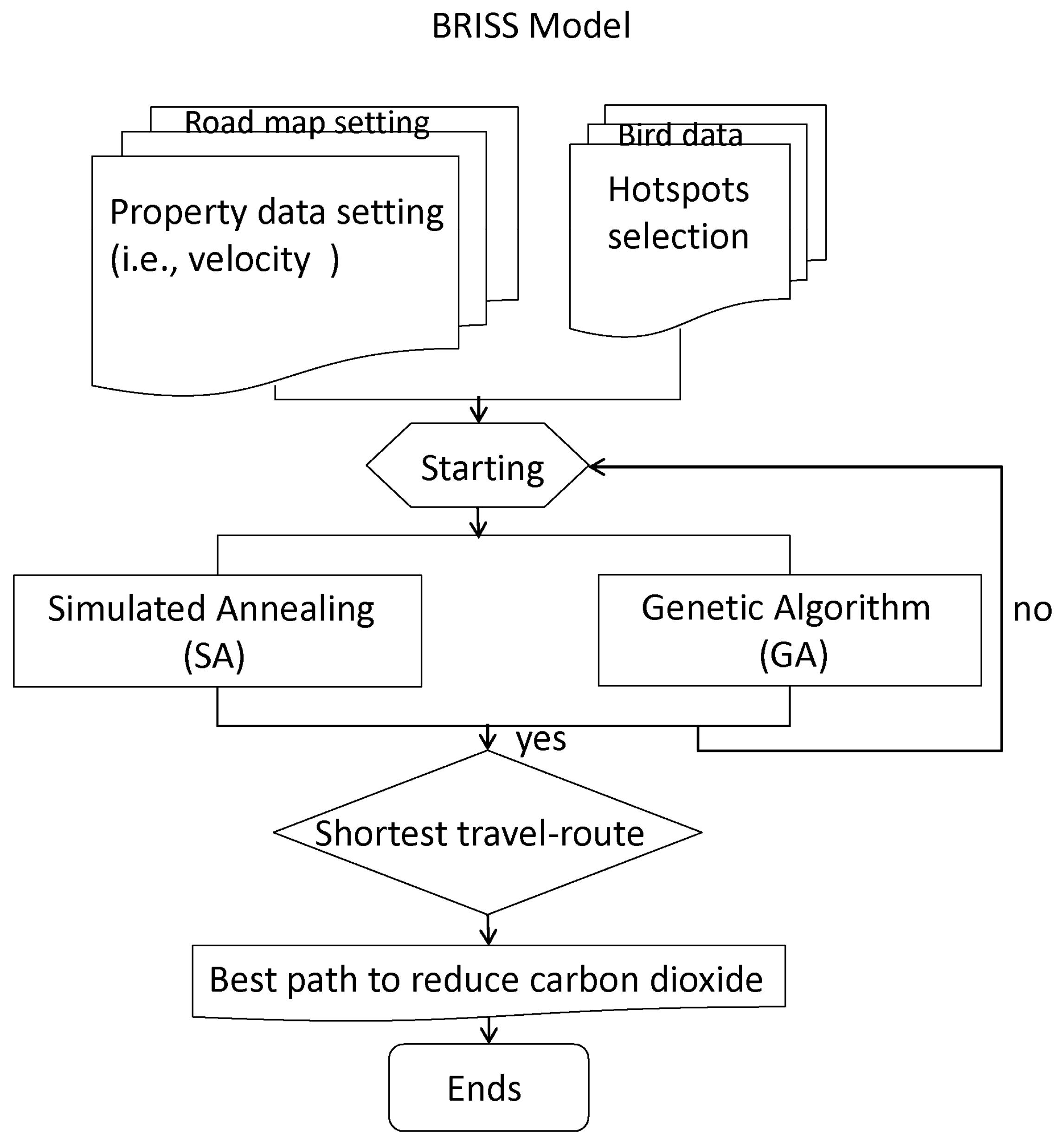
2.2. Research Methods
2.2.1. Diversity Calculation
2.2.2. SA Calculation
- : Current solution
- : New solution
- : Current energy state which is determined by function
- : Next energy state which is determined by function
- : Temperature
- Procedure Simulated Annealing;
- {General form of a SA optimization}
- ; {Starting value}
- Initialize heuristic parameters; repeat
- perturb
- If accept , then
- Until “time to adapt parameters”;
- Adapt parameters until “terminating criterion”;
- End.
2.2.3. GA Calculation
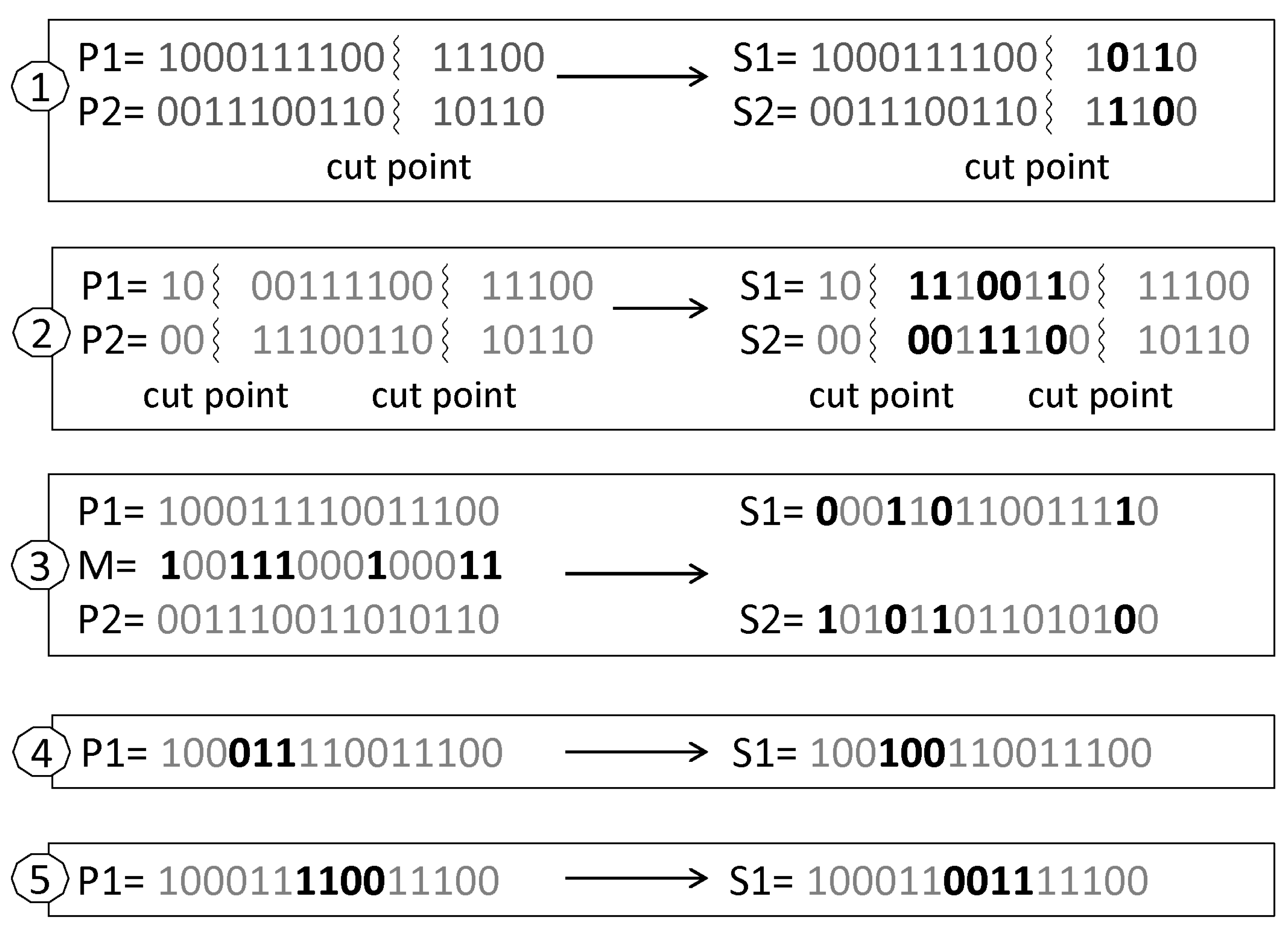
Initialize population; Sum + = fitness of all individuals; End for For all members of population Evaluate population; Probability = sum of probabilities plus (fitness / sum) Sum of probabilities + = probability End for While termination criteria not satisfied Select parents for reproduction; Loop until new population is satisfied for this solution Try this twice Number = random between 0 and 1 for all members of population If number > probability but less than next probability then This has been selected End for End Perform recombination and mutation; Create offspring End loop
3. Results and Discussion
3.1. Results
| Common Name | Scientific Name | Individual Number | Ratio |
|---|---|---|---|
| Grey Heron | Ardea cinerea | 1686 | 15% |
| Tufted Duck | Aythya fuligula | 1652 | 14% |
| Little Egret | Egretta garzetta | 1169 | 10% |
| Black-crowned Night-heron | Nycticorax nycticorax | 1082 | 9% |
| Chinese Bulbul | Pycnonotus sinensis | 1002 | 9% |
| Great Egret | Ardea alba | 888 | 8% |
| Eurasian Tree Sparrow | Passer montanus | 493 | 4% |
| Pacific Swallow | Hirundo tahitica | 375 | 3% |
| Red Turtle Dove | Streptopelia tranquebarica | 241 | 2% |
| Barn Swallow | Hirundo rustica | 225 | 2% |
| 8813 | 76% |
| December 2008 | January 2009 | February 2009 | |||
|---|---|---|---|---|---|
| No. 0 | 2.522 | No. 7 | 2.351 | No. 14 | 2.575 |
| No. 1 | 2.152 | No. 8 | 2.267 | No. 15 | 2.528 |
| No. 2 | 2.128 | No. 9 | 2.259 | No. 16 | 2.516 |
| No. 3 | 2.127 | No. 10 | 2.205 | No. 17 | 2.360 |
| No. 4 | 2.062 | No. 11 | 2.134 | No. 18 | 2.357 |
| No. 5 | 2.057 | No. 12 | 2.123 | No. 19 | 2.320 |
| No. 6 | 2.022 | No. 13 | 2.038 | No. 20 | 2.312 |
| No. 21 | 2.282 | ||||
| No. 22 | 2.281 | ||||
| No. 23 | 2.219 | ||||
| No. 24 | 2.145 | ||||
| No. 25 | 2.046 | ||||
| No. 26 | 2.042 | ||||
| No. 27 | 2.007 | ||||
| Simulated Annealing Algorithm (SA) | Genetic Algorithm (GA) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S. | E. | Travel Dist. (km) | Travel Time | Carbon Emissions (kg) | S. | E. | Travel Dist. (km) | Travel Time | Carbon Emissions (kg) |
| 0 | 1 | 10.91 | 14m49s | 0.88 | 0 | 1 | 10.91 | 14m49s | 0.88 |
| 1 | 3 | 7.98 | 9m23s | 0.65 | 1 | 3 | 7.98 | 9m23s | 0.65 |
| 3 | 2 | 6.62 | 9m12s | 0.54 | 3 | 2 | 6.62 | 9m12s | 0.54 |
| 2 | 5 | 15.38 | 22m7s | 1.25 | 2 | 5 | 15.38 | 22m7s | 1.25 |
| 5 | 4 | 10.33 | 11m44s | 0.84 | 5 | 4 | 10.33 | 11m44s | 0.84 |
| 4 | 6 | 8.49 | 11m4s | 0.69 | 4 | 6 | 8.49 | 11m4s | 0.69 |
| Totals | 59.71 | 1h18m19s | 4.84 | Totals | 59.71 | 1h18m19s | 4.84 | ||
| Simulated Annealing Algorithm (SA) | Genetic Algorithm (GA) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S. | E. | Travel Dist. (km) | Travel Time | Carbon Emissions (kg) | S. | E. | Travel Dist. (km) | Carbon Emissions (kg) | |
| 7 | 8 | 12.67 | 16m40s | 1.03 | 7 | 8 | 13.63 | 16m12s | 1.10 |
| 8 | 9 | 12.34 | 15m15s | 1.00 | 8 | 9 | 15.00 | 20m0s | 1.22 |
| 9 | 10 | 12.08 | 17m14s | 0.98 | 9 | 10 | 11.60 | 16m40s | 0.94 |
| 10 | 11 | 3.85 | 5m1s | 0.31 | 10 | 11 | 2.90 | 3m49s | 0.23 |
| 11 | 12 | 15.86 | 21m36s | 1.28 | 11 | 12 | 16.48 | 22m23s | 1.33 |
| 12 | 13 | 20.19 | 27m11s | 1.64 | 12 | 13 | 20.17 | 27m10s | 1.63 |
| Totals | 76.99 | 1h42m57s | 6.24 | Totals | 79.78 | 1h46m14s | 6.46 | ||
| Simulated Annealing Algorithm (SA) | Genetic Algorithm (GA) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S. | E. | Travel Dist. (km) | Travel Time | Carbon Emissions (kg) | S. | E. | Travel Dist. (km) | Travel Time | Carbon Emissions (kg) |
| 14 | 15 | 2.12 | 2m32s | 0.17 | 14 | 15 | 2.12 | 2m32s | 0.17 |
| 15 | 16 | 13.04 | 17m47s | 1.06 | 15 | 16 | 13.04 | 17m47s | 1.06 |
| 16 | 17 | 3.69 | 4m46s | 0.30 | 16 | 17 | 3.69 | 4m46s | 0.30 |
| 17 | 18 | 1.33 | 1m54s | 0.11 | 17 | 18 | 1.56 | 2m13s | 0.13 |
| 18 | 19 | 2.00 | 2m29s | 0.16 | 18 | 19 | 2.27 | 2m51s | 0.18 |
| 19 | 20 | 4.17 | 6m5s | 0.34 | 19 | 20 | 4.41 | 6m24s | 0.36 |
| 20 | 21 | 7.24 | 10m19s | 0.59 | 20 | 21 | 7.34 | 10m30s | 0.59 |
| 21 | 22 | 8.13 | 11m42s | 0.66 | 21 | 22 | 8.13 | 11m42s | 0.66 |
| 22 | 23 | 6.12 | 7m51s | 0.50 | 22 | 23 | 6.12 | 7m51s | 0.50 |
| 23 | 24 | 2.13 | 3m7s | 0.17 | 23 | 24 | 2.25 | 3m14s | 0.18 |
| 24 | 25 | 5.11 | 6m36s | 0.41 | 24 | 25 | 5.11 | 6m36s | 0.41 |
| 25 | 26 | 13.42 | 18m35s | 1.09 | 25 | 26 | 12.77 | 17m46s | 1.03 |
| 26 | 27 | 20.17 | 27m10s | 1.63 | 26 | 27 | 20.05 | 26m58s | 1.62 |
| Totals | 88.67 | 2h0m17s | 7.18 | Totals | 88.86 | 2h1m10s | 7.20 | ||
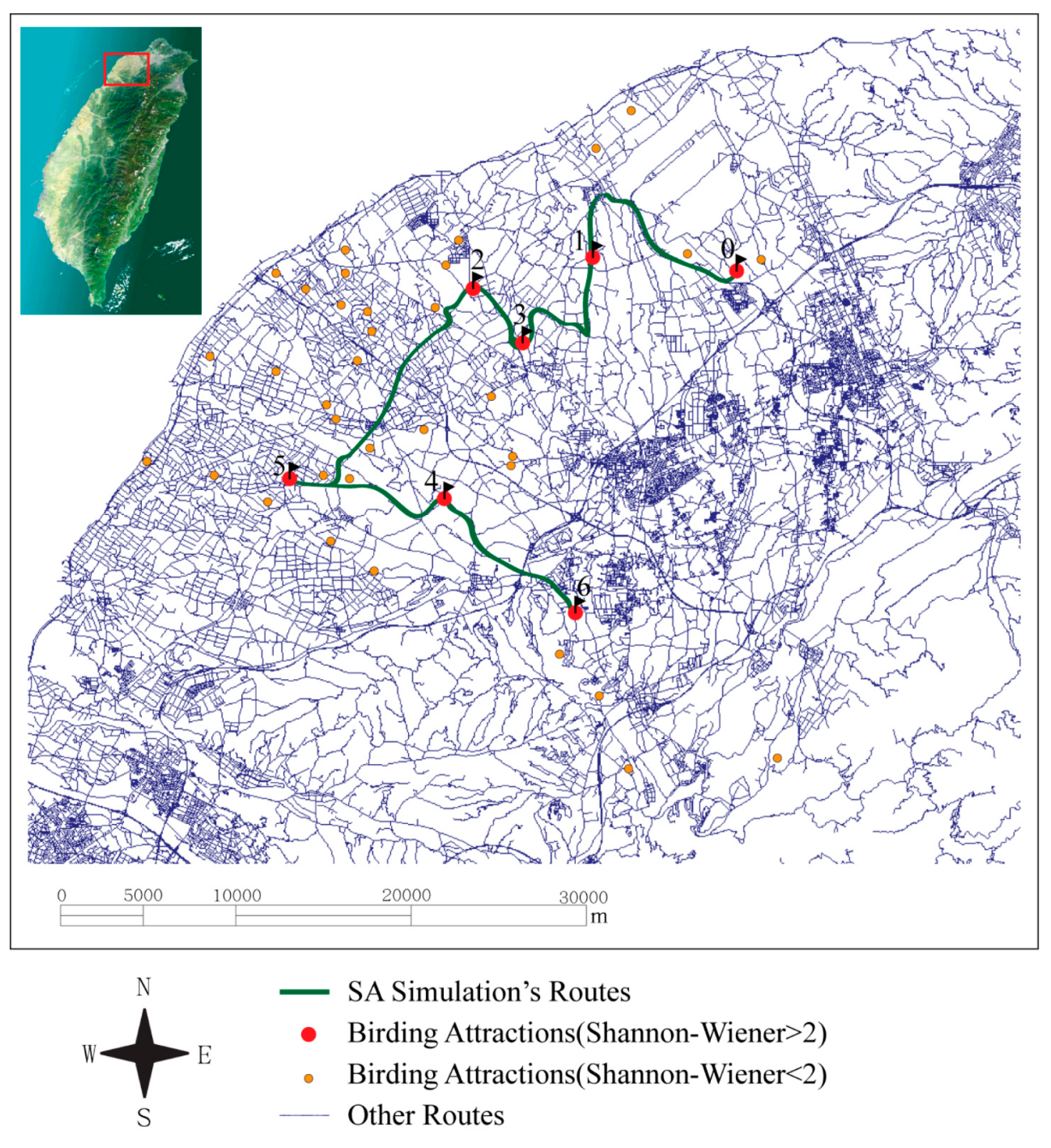
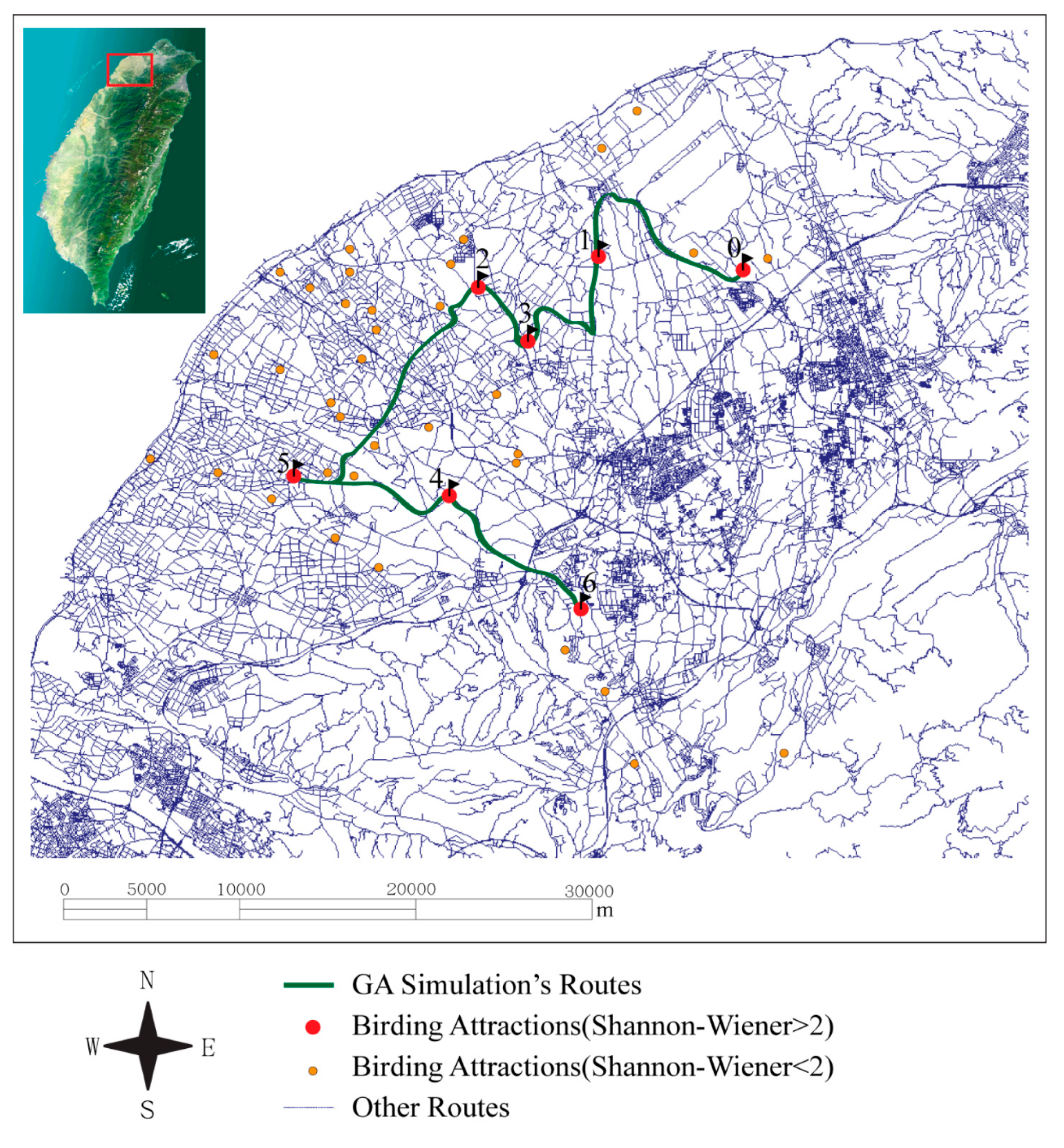
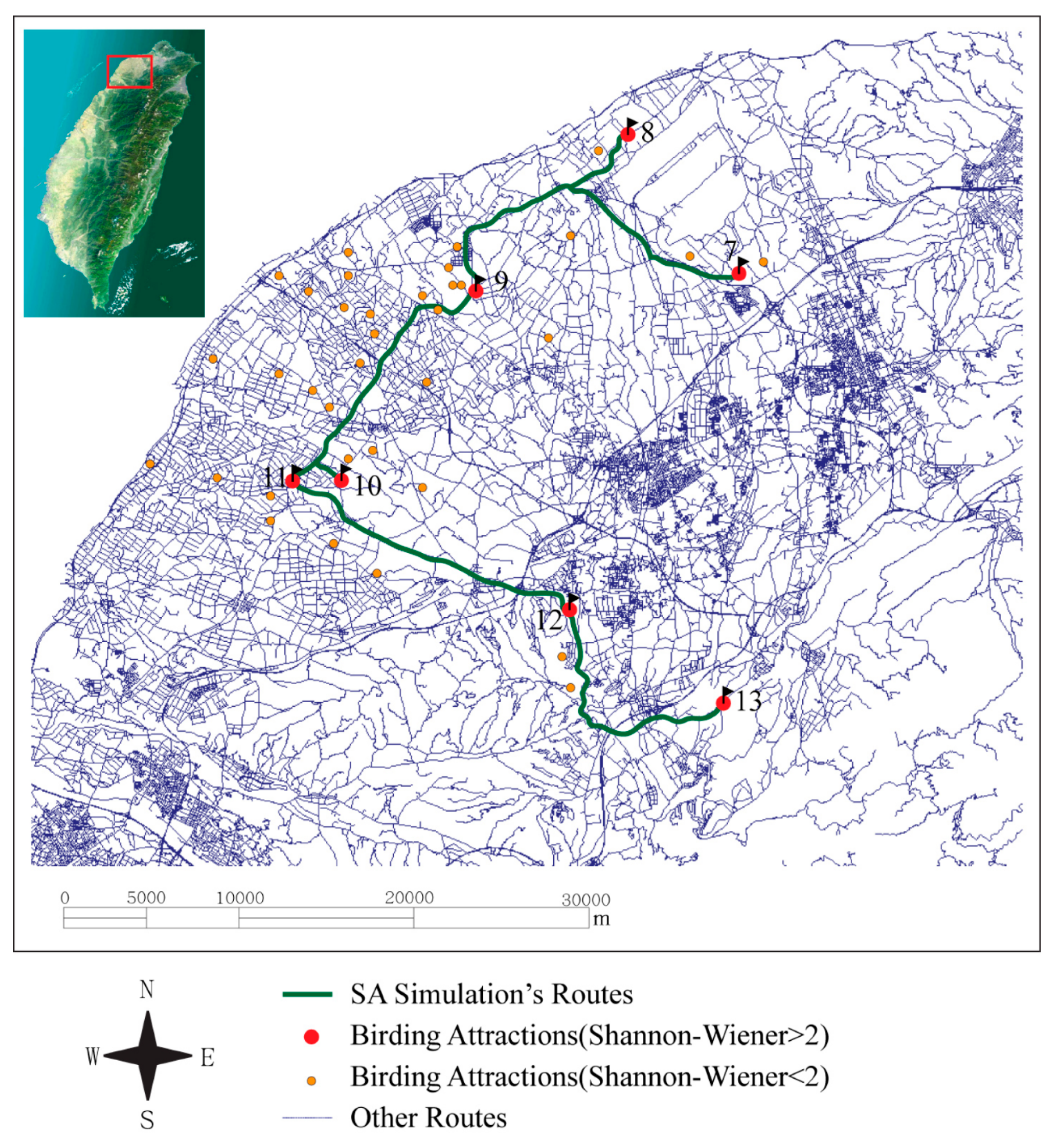
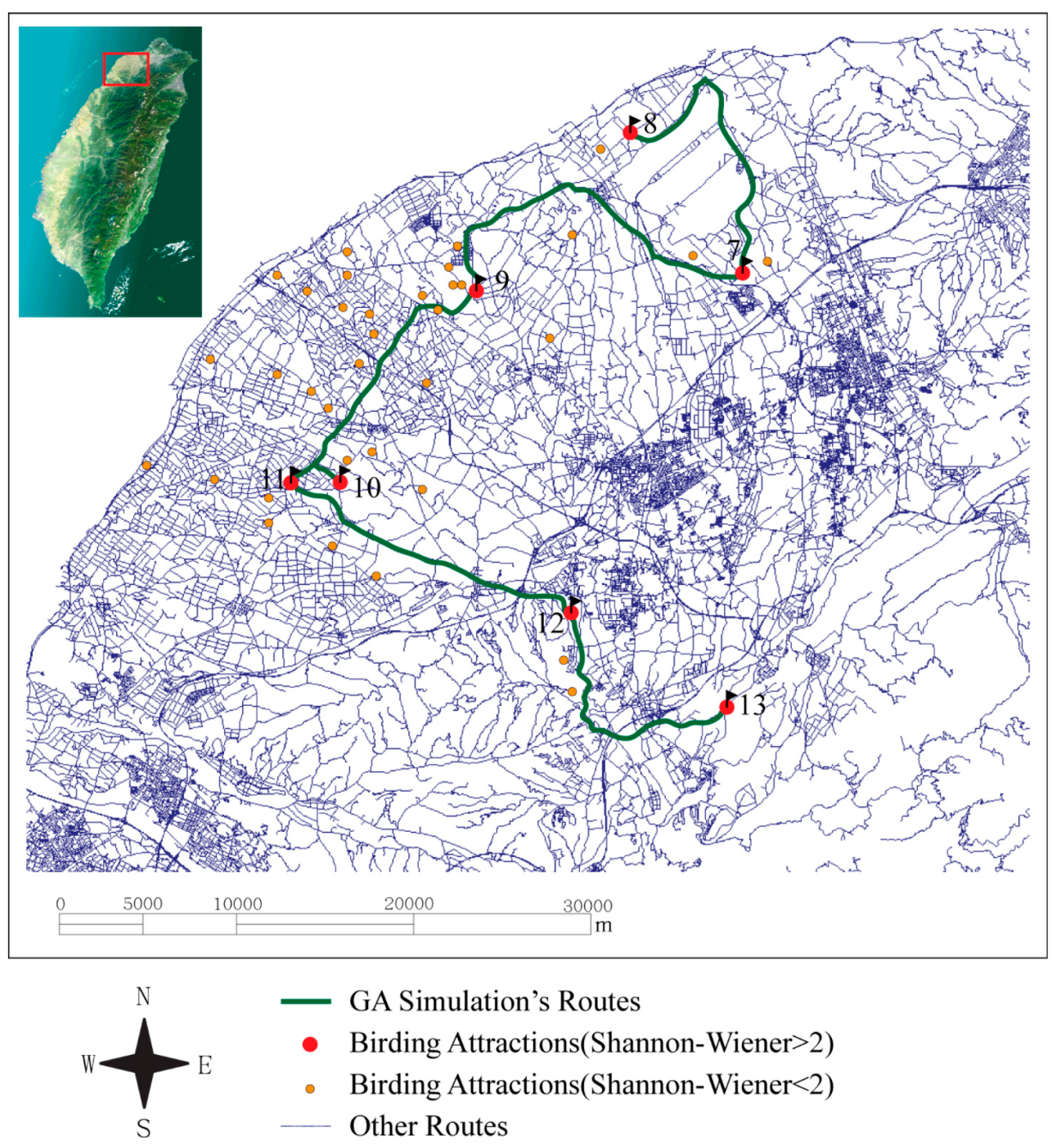
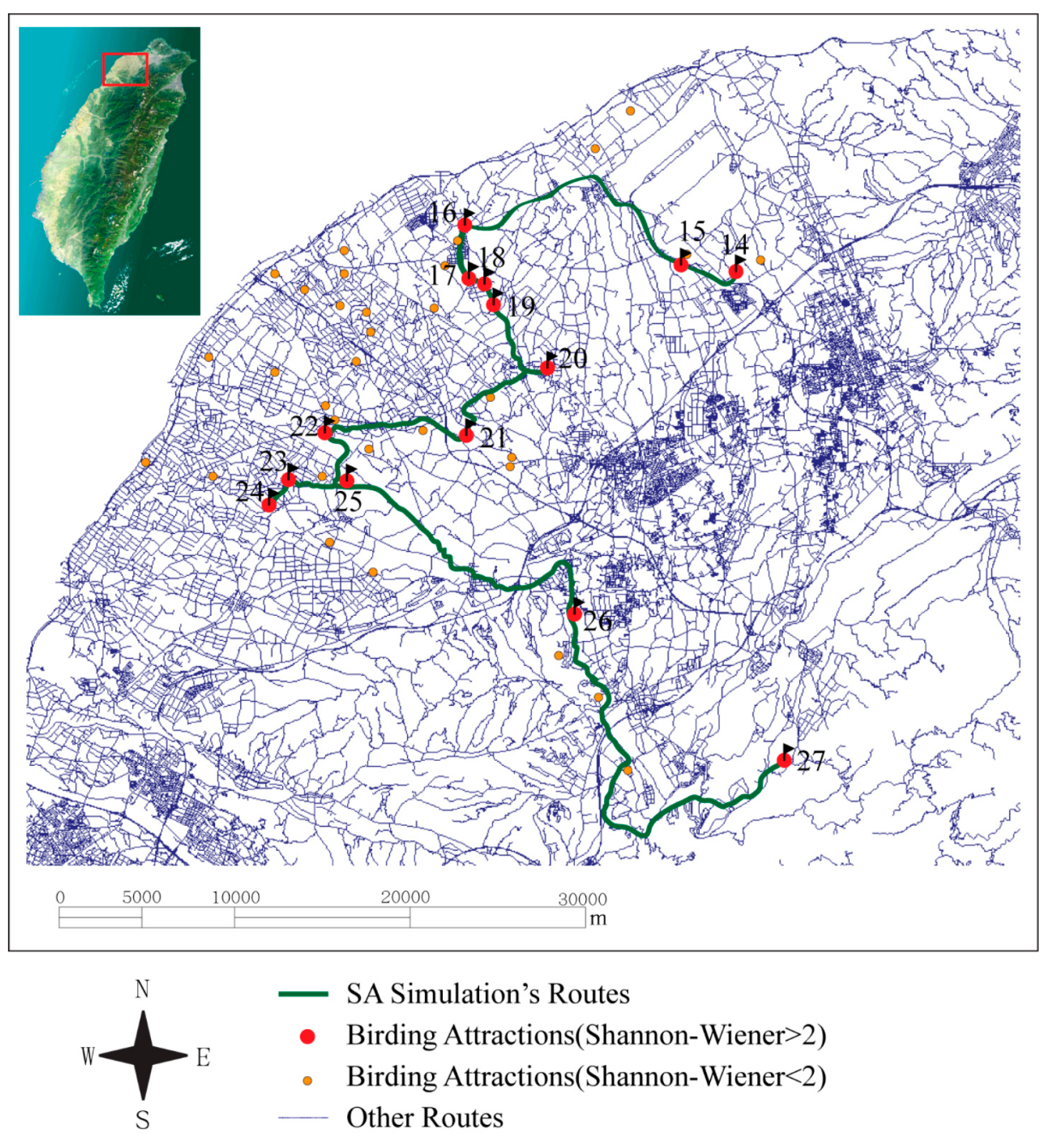
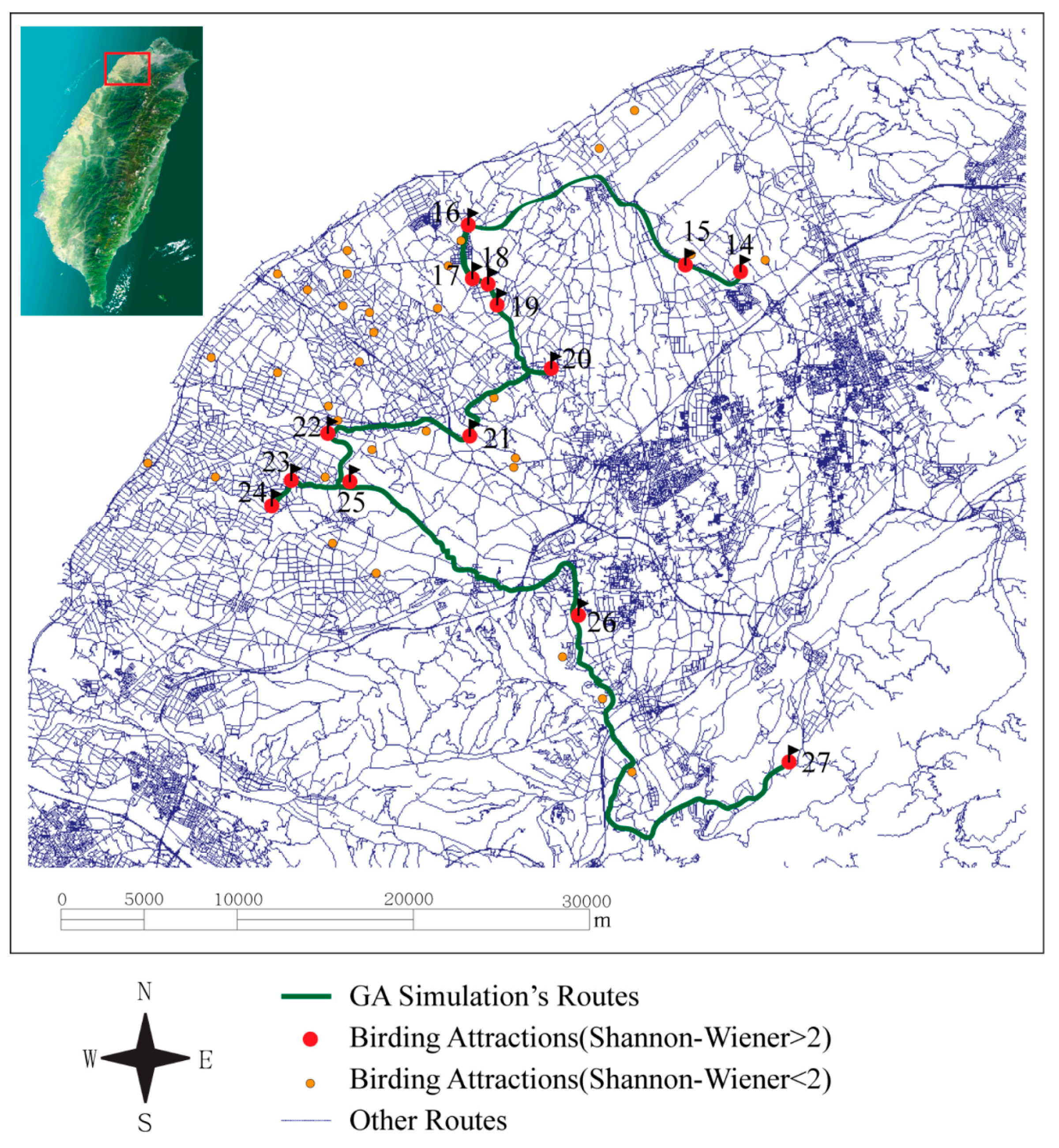
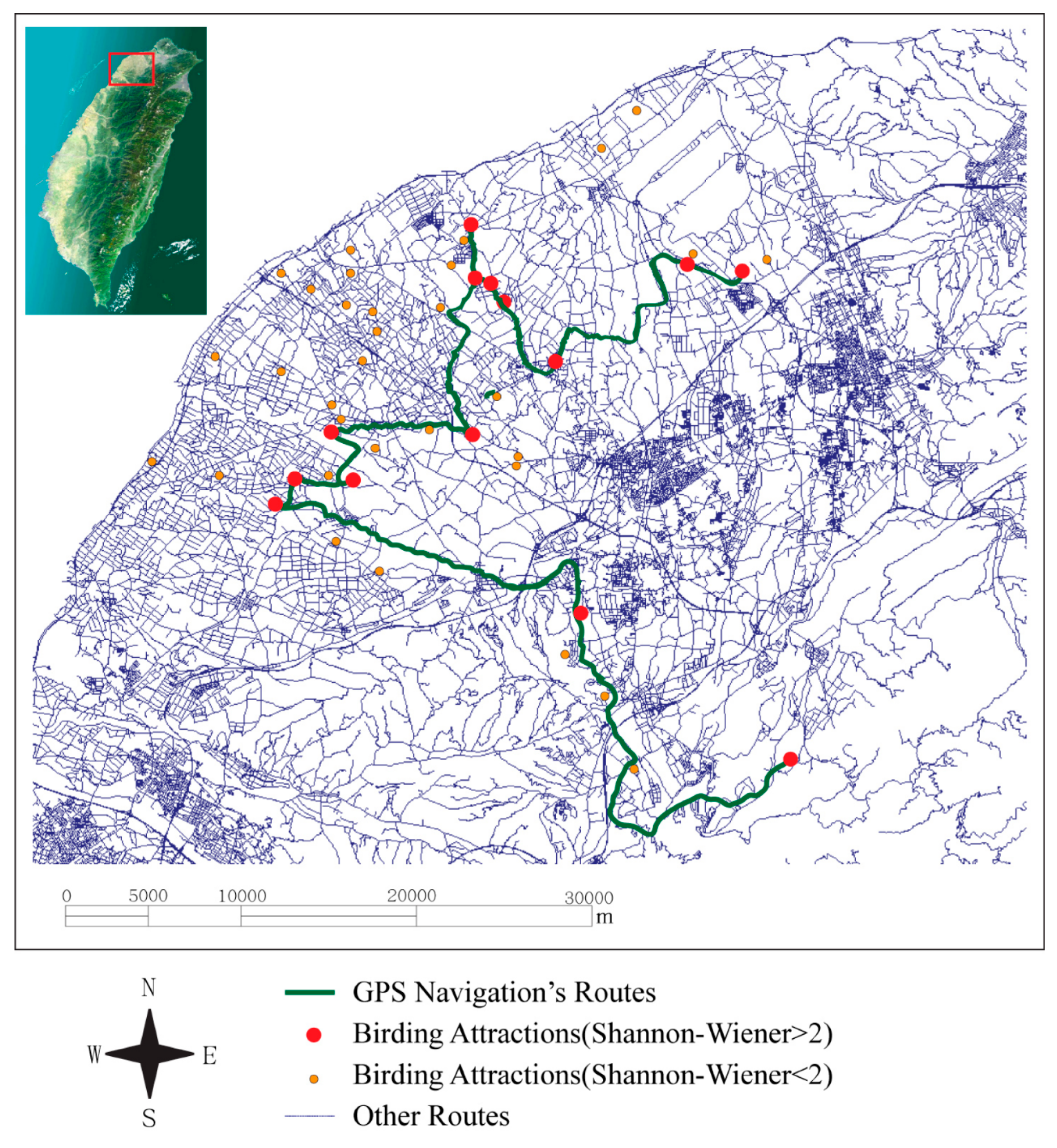
3.2. Discussion
3.2.1. Behaviors of Birds and Bird Watchers
3.2.2. Model Formation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gössling, S. Carbon neutral destinations: A conceptual analysis. J. Sustain. Tour. 2009, 17, 17–37. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The pollution-routing problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Pradenas, L.; Oportus, B.; Parada, V. Mitigation of greenhouse gas emissions in vehicle routing problems with backhauling. Expert Syst. Appl. 2013, 40, 2985–2991. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Dickinson, J.E.; Robbins, D. Representations of tourism transport problems in a rural destination. Tour. Manag. 2008, 29, 1110–1121. [Google Scholar] [CrossRef]
- Lawton, L.J.; Weaver, D.B. Normative and innovative sustainable resource management at birding festivals. Tour. Manag. 2010, 31, 527–536. [Google Scholar] [CrossRef]
- Lee, T.H.; Jan, F.-H.; Yang, C.-C. Conceptualizing and measuring environmentally responsible behaviors from the perspective of community-based tourists. Tour. Manag. 2012, 36, 454–468. [Google Scholar] [CrossRef]
- Horng, J.-S.; Hu, M.-L.; Teng, C.-C.; Lin, L. Energy saving and carbon reduction management indicators for natural attractions: A case study in Taiwan. J. Sustain. Tour. 2012, 20, 1125–1149. [Google Scholar] [CrossRef]
- Chen, S.-M.; Chien, C.-Y. Solving the traveling salesman problem based on the genetic simulated annealing ant colony system with particle swarm optimization techniques. Expert Syst. Appl. 2011, 38, 14439–14450. [Google Scholar] [CrossRef]
- Majumdar, J.; Bhunia, A.K. Genetic algorithm for asymmetric traveling salesman problem with imprecise travel times. J. Comput. Appl. Math. 2011, 235, 3063–3078. [Google Scholar] [CrossRef]
- Rodríguez, B.; Molina, J.; Pérez, F.; Caballero, R. Interactive design of personalised tourism routes. Tour. Manag. 2012, 33, 926–940. [Google Scholar] [CrossRef]
- Henderson, D.; Vaughan, D.E.; Jacobson, S.H.; Wakefield, R.R.; Sewell, E.C. Solving the shortest route cut and fill problem using simulated annealing. Eur. J. Oper. Res. 2003, 145, 72–84. [Google Scholar] [CrossRef]
- Hong, W.-C. Traffic flow forecasting by seasonal SVR with chaotic simulated annealing algorithm. Neurocomputing 2011, 74, 2096–2107. [Google Scholar] [CrossRef]
- Suzuki, Y. A decision support system of vehicle routing and refueling for motor carriers with time-sensitive demands. Decis. Support Syst. 2012, 54, 758–767. [Google Scholar] [CrossRef]
- Kuo, Y. Using Simulated Annealing to minimize fuel consumption for the time-dependent vehicle routing problem. Comput. Ind. Eng. 2010, 59, 157–165. [Google Scholar] [CrossRef]
- Curtin, K.M.; Voicu, G.; Rice, M.T.; Stefanidis, A. A Comparative Analysis of Traveling Salesman Solutions from Geographic Information Systems. Trans GIS 2014, 18, 286–301. [Google Scholar] [CrossRef]
- Curtin, K.M. Network analysis in geographic information science: Review, assessment, and projections. Cartogr. Geogr. Inf. Sci. 2007, 34, 103–111. [Google Scholar] [CrossRef]
- Curtin, K. Network data structures. Encycl. Geogr. Inf. Sci. 2008, 314–317. [Google Scholar]
- Fraser, A. Simulation of genetic systems by automatic digital computers. I. Introduction. Aust. J. Biol. Sci. 1957, 10, 484–491. [Google Scholar]
- Hurley, S.; Moutinho, L.; Witt, S.F. Genetic algorithms for tourism marketing. Ann. Tour. Res. 1998, 25, 498–514. [Google Scholar] [CrossRef]
- Yücenur, G.N.; Demirel, N.Ç. A new geometric shape-based genetic clustering algorithm for the multi-depot vehicle routing problem. Expert Syst. Appl. 2011, 38, 11859–11865. [Google Scholar]
- Hong, W.-C.; Dong, Y.; Zheng, F.; Wei, S.-Y. Hybrid evolutionary algorithms in a SVR traffic flow forecasting model. Appl. Math. Comput. 2011, 217, 6733–6747. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculation by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Ware, J.M.; Taylor, G.E.; Anand, S.; Thomas, N. Automated Production of Schematic Maps for Mobile Applications. Trans. GIS 2006, 10, 25–42. [Google Scholar] [CrossRef]
- Yu, V.F.; Lin, S.-W.; Lee, W.; Ting, C.-J. A simulated annealing heuristic for the capacitated location routing problem. Comput. Ind. Eng. 2010, 58, 288–299. [Google Scholar] [CrossRef]
- Delmelle, E.M.; Li, S.; Murray, A.T. Identifying bus stop redundancy: A gis-based spatial optimization approach. Comput. Environ. Urban Syst. 2012, 36, 445–455. [Google Scholar] [CrossRef]
- Fan, W.; Machemehl, R.B. Using a simulated annealing algorithm to solve the transit route network design problem. J. Transp. Eng. 2006, 132, 122–132. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Fang, W.-T.; Chu, H.-J.; Cheng, B.-Y. Modeling waterbird diversity in irrigation ponds of Taoyuan, Taiwan using an artificial neural network approach. Paddy Water Environ. 2009, 7, 209–216. [Google Scholar] [CrossRef]
- Tramer, E.J. Bird species diversity: Components of Shannon’s formula. Ecology 1969, 50, 927–929. [Google Scholar] [CrossRef]
- Baker, B.M.; Ayechew, M.A. A genetic algorithm for the vehicle routing problem. Comput. Oper. Res. 2010, 30, 787–800. [Google Scholar] [CrossRef]
- Kuan, S.N.; Ong, H.L.; Ng, K.M. Solving the feeder bus network design problem by genetic algorithms and ant colony optimization. Adv. Eng. Softw. 2006, 37, 351–359. [Google Scholar] [CrossRef]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic Algorithms; Springer-Verlag: London, UK, 1999. [Google Scholar]
- Xu, T.; Wei, H.; Hu, G. Study on continuous network design problem using simulated annealing and genetic algorithm. Expert Syst. Appl. 2009, 36, 1322–1328. [Google Scholar] [CrossRef]
- Xu, T.; Wei, H.; Wang, Z.-D. Study on continuous network design problem using simulated annealing and genetic algorithm. Expert Syst. Appl. 2009, 36, 2735–2741. [Google Scholar] [CrossRef]
- Deng, A.-M.; Mao, C.; Zhou, Y.-T. Optimizing research of an improved simulated annealing algorithm to soft time windows vehicle routing problem with pick-up and delivery. Syst. Eng. Theory Pract. 2009, 29, 186–192. [Google Scholar] [CrossRef]
- Janssens, G.K.; Caris, A.; Ramaekers, K. Time Petri nets as an evaluation tool for handling travel time uncertainty in vehicle routing solutions. Expert Syst. Appl. 2009, 36, 5987–5991. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Gazanfari, M.; Alinaghian, M.; Salamatbakhsh, A.; Norouzi, N. A new mathematical model for a competitive vehicle routing problem with time windows solved by simulated annealing. J. Manuf. Syst. 2011, 30, 83–92. [Google Scholar] [CrossRef]
- Baños, R.; Ortega, J.; Gil, C.; Fernández, A.; de Toro, F. A Simulated Annealing-based parallel multi-objective approach to vehicle routing problems with time windows. Expert Syst. Appl. 2013, 40, 1696–1707. [Google Scholar] [CrossRef]
- Zhao, F.; Zeng, X. Optimization of user and operator cost for large-scale transit network. J. Transp. Eng. 2007, 133, 240–251. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Wu, Y. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong. Eur. J. Oper. Res. 2011, 209, 141–155. [Google Scholar] [CrossRef]
- Nazif, H.; Lee, L. Optimised crossover Genetic Algorithm for capacitated vehicle routing problem. Appl. Math. Model. 2012, 36, 2110–2117. [Google Scholar] [CrossRef]
- Liu, L.; Mu, H.; Luo, H.; Li, X. A simulated annealing for multi-criteria network path problems. Comput. Oper. Res. 2012, 39, 3119–3135. [Google Scholar] [CrossRef]
- Zhang, F.; Cao, X.; Yang, D. Intelligent scheduling of public traffic vehicles based on a hybrid genetic algorithm. Tsinghua Sci. Technol. 2008, 13, 625–631. [Google Scholar] [CrossRef]
- Marinakis, Y.; Marinaki, M. A hybrid genetic—Particle Swarm Optimization Algorithm for the vehicle routing problem. Expert Syst. Appl. 2010, 37, 1446–1455. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, B. Fuzzy vehicle routing model with credibility measure and its hybrid intelligent algorithm. Appl. Math. Comput. 2006, 176, 673–683. [Google Scholar] [CrossRef]
- Ghoseiri, K.; Ghannadpour, S.F. Multi-objective vehicle routing problem with time windows using goal programming and genetic algorithm. Appl. Soft Comput. 2010, 10, 1096–1107. [Google Scholar] [CrossRef]
- Ursani, Z.; Essam, D.; Cornforth, D.; Stocker, R. Localized genetic algorithm for vehicle routing problem with time windows. Appl. Soft Comput. 2011, 11, 5375–5390. [Google Scholar] [CrossRef]
- Zarandi, M.H.F.; Hemmati, A.; Davari, S. The multi-depot capacitated location-routing problem with fuzzy travel times. Expert Syst. Appl. 2011, 38, 10075–10084. [Google Scholar] [CrossRef]
- Osman, I.H. Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem. Ann. Oper. Res. 1993, 41, 421–451. [Google Scholar] [CrossRef]
- Lin, C.K.Y.; Kwok, R.C.W. Multi-objective metaheuristics for a location-routing problem with multiple use of vehicles on real data and simulated data. Eur. J. Oper. Res. 2006, 175, 1833–1849. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Tavakkoli-Moghaddam, R. A hybrid simulated annealing algorithm for location and routing scheduling problems with cross-docking in the supply chain. J. Manuf. Syst. 2013, 32, 335–347. [Google Scholar] [CrossRef]
- Salimifard, K.; Shahbandarzadeh, H.; Raeesi, R. Green transportation and the role of operation research. Int. Conf. Traffic Transp. Eng. (ICTTE 2012) 2012, 26, 74–79. [Google Scholar]
- Shukla, N.; Choudhary, A.K.; Prakash, P.K.S.; Fernandes, K.J.; Tiwari, M.K. Algorithm portfolios for logistics optimization considering stochastic demands and mobility allowance. Algorithm Portf. Logist. Optim. Considering stoch. Demands mobil. Allow. 2013, 141, 146–166. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, W.-T.; Huang, C.-W.; Chou, J.-Y.; Cheng, B.-Y.; Shih, S.-S. Low Carbon Footprint Routes for Bird Watching. Sustainability 2015, 7, 3290-3310. https://doi.org/10.3390/su7033290
Fang W-T, Huang C-W, Chou J-Y, Cheng B-Y, Shih S-S. Low Carbon Footprint Routes for Bird Watching. Sustainability. 2015; 7(3):3290-3310. https://doi.org/10.3390/su7033290
Chicago/Turabian StyleFang, Wei-Ta, Chin-Wei Huang, Jui-Yu Chou, Bai-You Cheng, and Shang-Shu Shih. 2015. "Low Carbon Footprint Routes for Bird Watching" Sustainability 7, no. 3: 3290-3310. https://doi.org/10.3390/su7033290
APA StyleFang, W.-T., Huang, C.-W., Chou, J.-Y., Cheng, B.-Y., & Shih, S.-S. (2015). Low Carbon Footprint Routes for Bird Watching. Sustainability, 7(3), 3290-3310. https://doi.org/10.3390/su7033290








