Profit Distribution in Guaranteed Savings Contracts: Determination Based on the Collar Option Model
Abstract
:1. Introduction
2. Background
2.1. An ESCO’s Business Structure in a Guaranteed Savings Contract
| Term | Definition |
|---|---|
| Energy savings | Energy reductions from the installation of the energy reduction system |
| Target savings | The maximum energy savings that the ESCO calculates through an energy usage diagnosis or other methods to guarantee a level of performance |
| Performance guarantee | The act of guaranteeing an energy reduction value from installing the energy reduction system. The ESCO provides this guarantee to the energy user |
| Guaranteed savings | The amount of guaranteed energy reductions that the ESCO provides to the user, which must be more than 80% of the target reduction value |
| Performance guarantee period | The period to recover the entire project investment amount through the guaranteed energy savings |
| Profit distribution | The distribution of profits resulting from surpassing the target reduction value between the energy user and the ESCO |
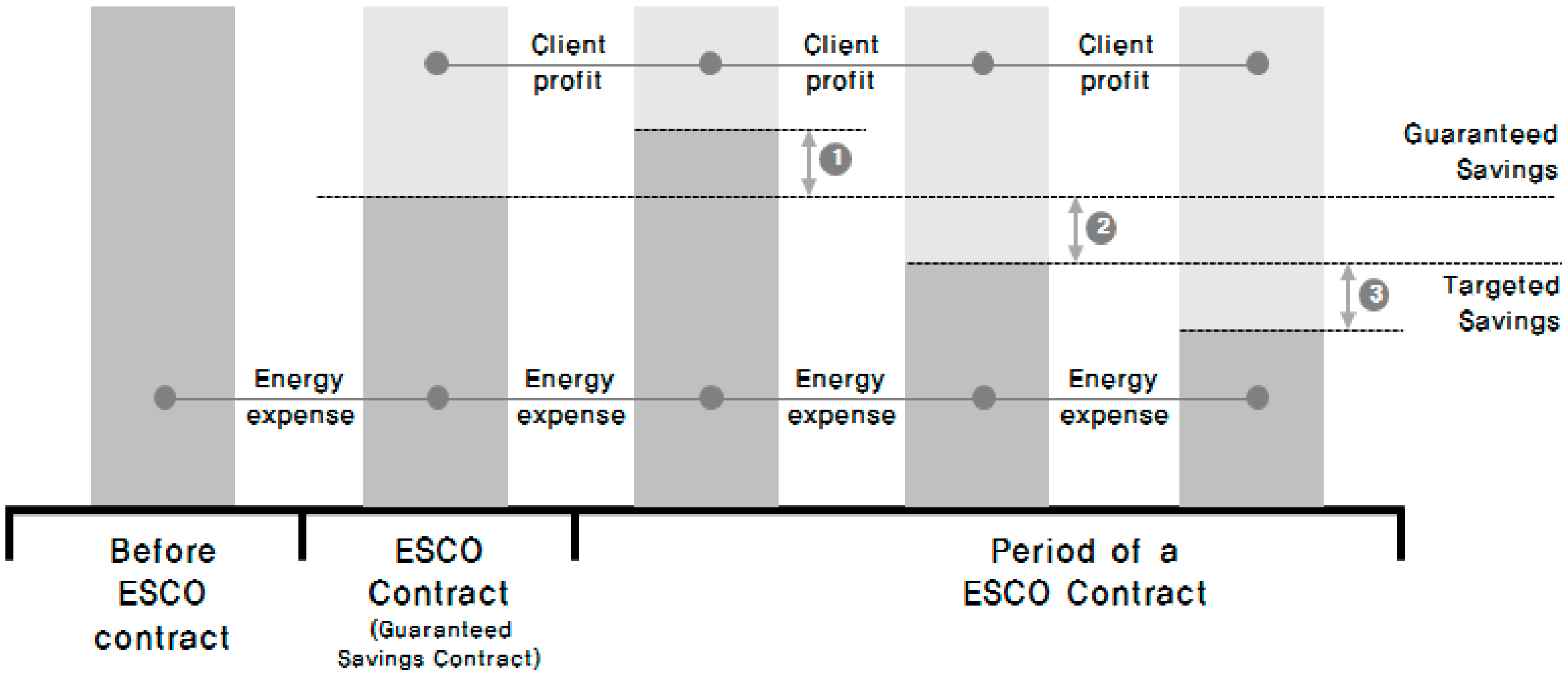
2.2. Literature Review
2.3. Real Options
| Financial Options | Real Options |
|---|---|
| Stock price | Present value of expected incomes |
| Exercise price | Costs of irreversible follow-on investment |
| Time to maturity | Time until the investment opportunity disappears |
| Volatility of stock return | Variability of project value |
| Risk-free rate of return | Risk-free rate of return |
| Methods | Advantages | Disadvantages |
|---|---|---|
| BSOPM | Simple to calculate the option value. | Only applicable to European options; Only works with normal distributions; Require advanced financial knowledge; Required assumptions limit the use of the model (price, volatility, duration); Able to deal with only one factor of uncertainty. |
| BOPM | Effective when dealing with one factor of uncertainty; Provides project managers with an appropriate evolution of the underlying asset; Estimates the value of several option futures. | Requires advanced financial knowledge; Able to deal with only one factor of uncertainty. |
| RADT | Allows mapping complex problems; Able to deal with multiple uncertainties; Enables decision makers to develop insights into ROs; Useful in the case of a possible drastic change in systems. | Does not provide the true value of the project; If the number of branches is high, it becomes too complicated and unclear. |
| MCS | Demonstrates graphically the analysis results; Able to deal with multiple uncertainties; Not required to understand financial theory; Helpful for problems with path-dependency; User-friendly multiple document interface. | Lacks transparency; Hard methodology to implement with American options. |
| HROs | Able to deal with multiple uncertainties; Combining the best of decision analysis and options analysis; Independent handling of technical and financial parts. | Hard methodology to implement (it requires highly sophisticated mathematical modeling skills). |
3. Research Methodology
3.1. Profit Distribution Framework Using the Collar Option Model


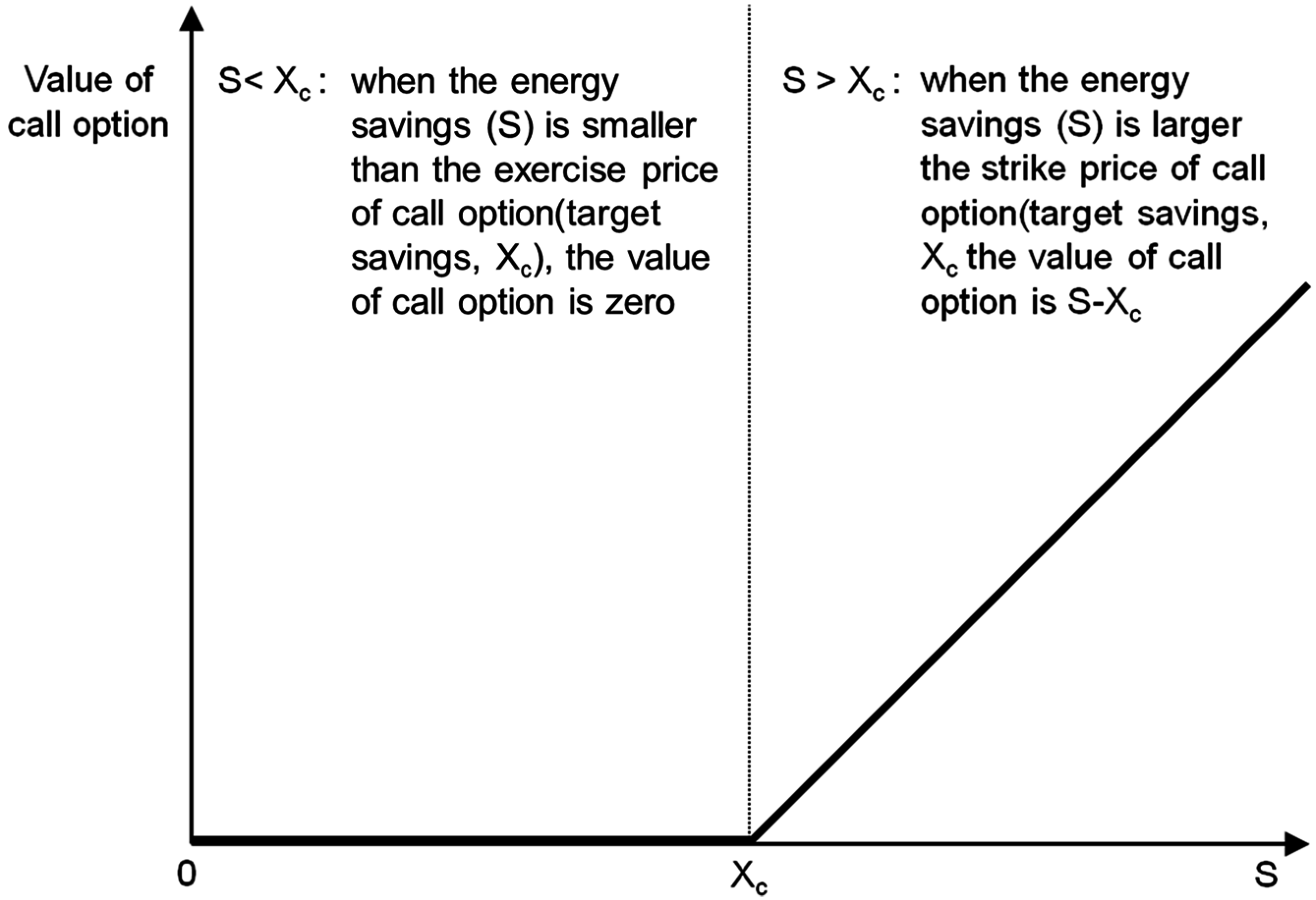
3.2. Binomial Lattice Model to Calculate the Option Value
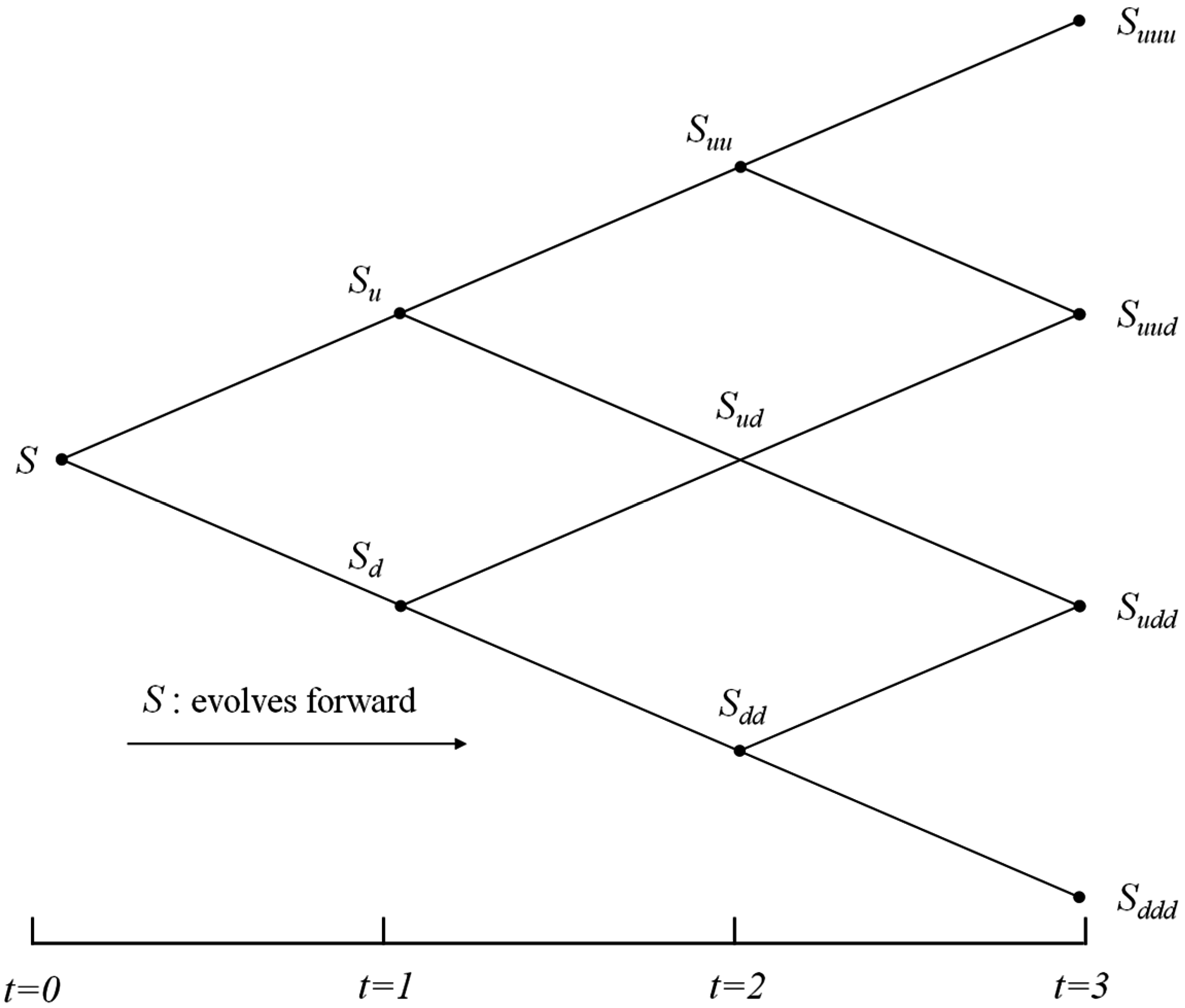
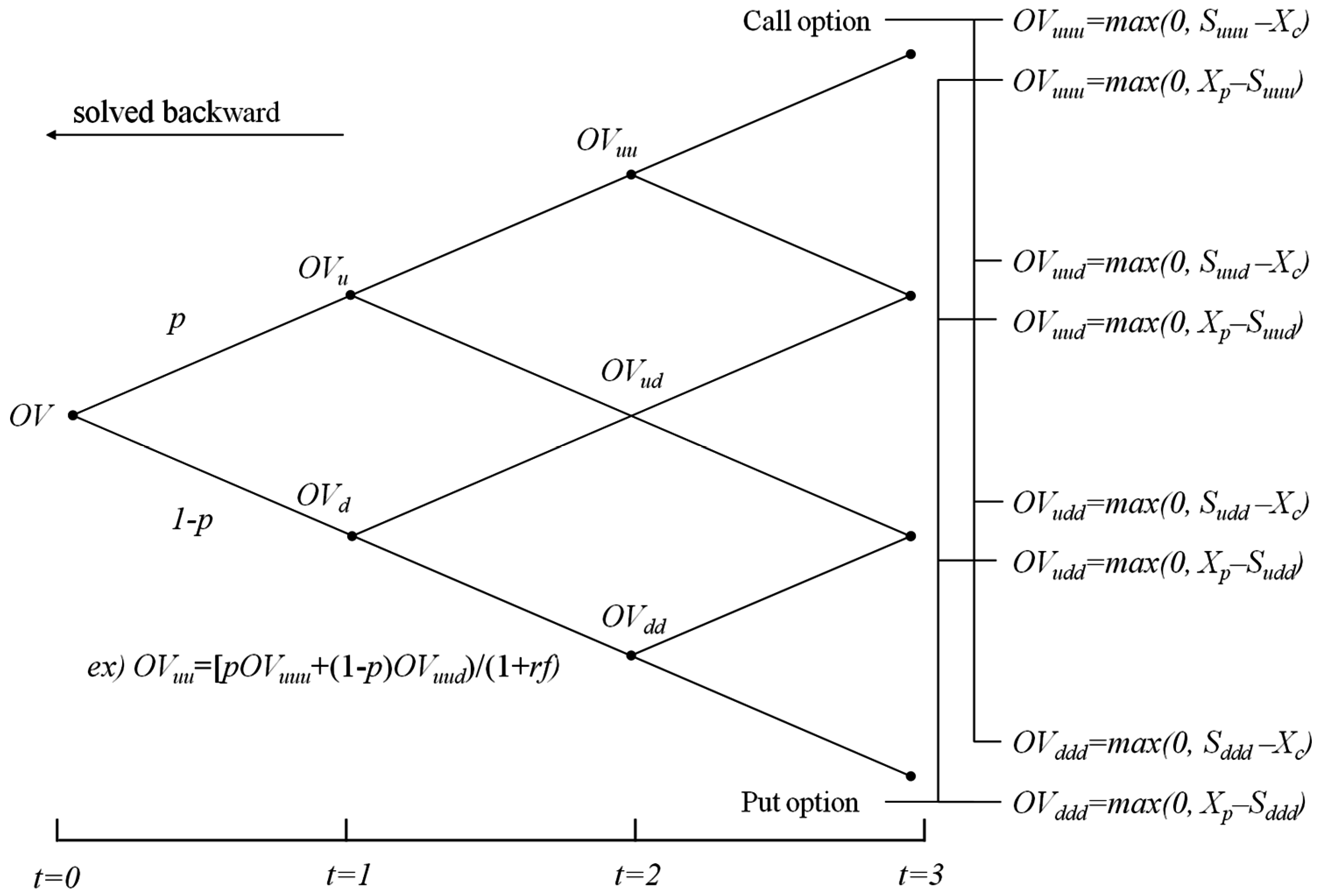
4. Applications
4.1. Data Collection
| Category | Details | |
|---|---|---|
| Year Built | 1994 (20 years since completion) | |
| Site area | 97,140.28 m2 | |
| Principal use | Office space | |
| Building size | 1 floor underground, 7 floors aboveground | |
| Building area | 17,512.66 m2 | |
| Total floor area | 30,147.63 m2 | |
| Equipment | Absorption chiller-heater, steam boiler | |
| Total project cost | Heat insulation | 317,570 USD |
| Windows | 298,010 USD | |
| Total | 615,580 USD | |
| Category | Estimated Value |
|---|---|
| Target savings | 88,200 USD/year |
| Guaranteed savings | 70,560 USD/year |
| Expected savings | 77,616 USD/year |
| Performance guarantee period | 9 years |
| Year | Interest Rate | Inflation Rate | Real Discount Rate | Average Discount Rate |
|---|---|---|---|---|
| 2004 | 3.75 | 3.6 | 0.14 | 0.96 |
| 2005 | 3.57 | 2.8 | 0.74 | |
| 2006 | 4.36 | 2.2 | 2.11 | |
| 2007 | 5.01 | 2.5 | 2.45 | |
| 2008 | 5.67 | 4.7 | 0.93 | |
| 2009 | 3.23 | 2.8 | 0.42 | |
| 2010 | 3.18 | 3.0 | 0.17 | |
| 2011 | 3.69 | 3.6 | 0.09 | |
| 2012 | 3.43 | 2.2 | 1.20 | |
| 2013 | 2.70 | 1.3 | 1.38 |
| Time | Investment Cost | Guaranteed Savings (Constant) | Guaranteed Savings (Discounted) | Guaranteed Savings (Discounted) Accumulated Sum |
|---|---|---|---|---|
| 0 | 615,580 | |||
| 1 | 70,560 | 69,889 | 69,889 | |
| 2 | 70,560 | 69,225 | 139,114 | |
| 3 | 70,560 | 68,566 | 207,680 | |
| 4 | 70,560 | 67,914 | 275,594 | |
| 5 | 70,560 | 67,269 | 342,863 | |
| 6 | 70,560 | 66,629 | 409,492 | |
| 7 | 70,560 | 65,995 | 475,487 | |
| 8 | 70,560 | 65,368 | 540,855 | |
| 9 | 70,560 | 64,746 | 605,601 | |
| 10 | 70,560 | 64,131 | 669,731 |
4.2. Results
| Year | Gas | Electricity | Energy Cost (USD) | Change Rate | Volatility | ||
|---|---|---|---|---|---|---|---|
| Used Amount (Nm3) | Unit Price (USD/Nm3) | Used Amount (KWh) | Unit Price (USD/KWh) | ||||
| 2004 | 58,717 | 0.925 | 2,575,682 | 0.127 | 381,425 | 10.00 | |
| 2005 | 74,759 | 0.925 | 2,743,321 | 0.127 | 417,554 | 9.05 | |
| 2006 | 47,324 | 0.925 | 2,442,482 | 0.127 | 353,970 | −16.52 | |
| 2007 | 48,783 | 0.925 | 2,649,536 | 0.127 | 381,615 | 7.52 | |
| 2008 | 42,286 | 0.925 | 2,526,969 | 0.127 | 360,039 | −5.82 | |
| 2009 | 65,515 | 0.925 | 2,637,817 | 0.127 | 395,604 | 9.42 | |
| 2010 | 51,018 | 0.925 | 2,520,640 | 0.127 | 367,313 | −7.42 | |
| 2011 | 82,245 | 0.925 | 2,661,946 | 0.127 | 414,144 | 12.00 | |
| 2012 | 69,083 | 0.925 | 2,629,320 | 0.127 | 397,825 | −4.02 | |
| 2013 | 50,736 | 0.925 | 2,544,804 | 0.127 | 370,121 | −7.22 | |
| Variables | Estimated Value |
|---|---|
| Underlying asset (S) | 668,158 USD |
| Put option exercise price (Xp) | 607,416 USD |
| Call option exercise price (Xc) | 759,270 USD |
| Volatility(σ) | 10.0% |
| Risk-free rate (rf) | 2.00% |
| Time interval | 1 year |
| Rise Rates (u) | 1.105 |
| Fall Rates (d) | 0.905 |
| Risk-neutral probability (p) | 0.576 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 668,158 | 738,429 | 816,090 | 901,919 | 996,775 | 1,101,606 | 1,217,463 | 1,345,505 | 1,487,013 | 1,643,403 |
| 604,574 | 668,158 | 738,429 | 816,090 | 901,919 | 996,775 | 1,101,606 | 1,217,463 | 1,345,505 | |
| 547,041 | 604,574 | 668,158 | 738,429 | 816,090 | 901,919 | 996,775 | 1,101,606 | ||
| 494,984 | 547,041 | 604,574 | 668,158 | 738,429 | 816,090 | 901,919 | |||
| 447,880 | 494,984 | 547,041 | 604,574 | 668,158 | 738,429 | ||||
| 405,258 | 447,880 | 494,984 | 547,041 | 604,574 | |||||
| 366,693 | 405,258 | 447,880 | 494,984 | ||||||
| 331,797 | 366,693 | 405,258 | |||||||
| 300,223 | 331,797 | ||||||||
| 271,653 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 15,601 | 7752 | 2968 | 701 | 35 | 0 | 0 | 0 | 0 | 0 |
| 26,993 | 14,614 | 6186 | 1638 | 85 | 0 | 0 | 0 | 0 | |
| 45,073 | 26,745 | 12,654 | 3823 | 204 | 0 | 0 | 0 | ||
| 72,083 | 47,139 | 25,240 | 8916 | 491 | 0 | 0 | |||
| 109,348 | 79,094 | 48,592 | 20,775 | 1182 | 0 | ||||
| 155,580 | 124,237 | 88,651 | 48,357 | 2842 | |||||
| 205,472 | 178,411 | 147,538 | 112,433 | ||||||
| 251,901 | 228,741 | 202,158 | |||||||
| 295,224 | 275,619 | ||||||||
| 335,764 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 94,651 | 131,390 | 179,186 | 239,637 | 313,746 | 401,651 | 502,707 | 616,249 | 742,924 | 884,133 |
| 49,234 | 72,693 | 105,559 | 150,319 | 209,192 | 283,386 | 372,254 | 473,321 | 586,235 | |
| 19,704 | 31,498 | 49,766 | 77,475 | 118,322 | 176,092 | 252,589 | 342,336 | ||
| 4619 | 8182 | 14,492 | 25,669 | 45,467 | 80,535 | 142,649 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | ||||||
| 0 | 0 | 0 | |||||||
| 0 | 0 | ||||||||
| 0 |
| Category | Estimated Value |
|---|---|
| Value of guarantee | 15,601 USD |
| Value of right to profit | 94,651 USD |
| ESCO Profit distribution ratio | 16.5% |
| Xc (USD) | Volatility (%) | Xp (USD) | |||||
|---|---|---|---|---|---|---|---|
| 560,000 | 580,000 | 600,000 | 620,000 | 640,000 | 668,158 | ||
| 668,158 | 5% | 0.17% | 0.34% | 0.77% | 1.21% | 1.92% | 4.21% |
| 10% | 7.07% | 8.58% | 10.10% | 13.34% | 17.10% | 22.39% | |
| 15% | 16.64% | 19.07% | 23.15% | 27.24% | 31.32% | 37.07% | |
| 680,000 | 5% | 0.19% | 0.37% | 0.84% | 1.31% | 2.07% | 4.56% |
| 10% | 7.42% | 9.01% | 10.60% | 14.01% | 17.95% | 23.51% | |
| 15% | 17.19% | 19.71% | 23.93% | 28.15% | 32.37% | 38.31% | |
| 710,000 | 5% | 0.24% | 0.46% | 1.05% | 1.64% | 2.59% | 5.69% |
| 10% | 8.49% | 10.32% | 12.14% | 16.04% | 20.5% | 26.91% | |
| 15% | 18.78% | 21.54% | 26.15% | 30.76% | 35.37% | 41.86% | |
| 740,000 | 5% | 0.30% | 0.58% | 1.33% | 2.07% | 3.27% | 7.19% |
| 10% | 9.90% | 12.02% | 14.14% | 18.68% | 23.94% | 31.35% | |
| 15% | 20.70% | 23.74% | 28.82% | 33.90% | 38.98% | 46.13% | |
| 770,000 | 5% | 0.40% | 0.79% | 1.80% | 2.81% | 4.43% | 9.74% |
| 10% | 11.05% | 13.42% | 15.79% | 20.87% | 26.74% | 35.01% | |
| 15% | 23.06% | 26.44% | 32.09% | 37.75% | 43.41% | 51.38% | |
| 800,000 | 5% | 0.54% | 1.05% | 2.39% | 3.73% | 5.89% | 12.95% |
| 10% | 12.51% | 15.20% | 17.88% | 23.63% | 30.28% | 39.64% | |
| 15% | 24.88% | 28.53% | 34.63% | 40.74% | 46.85% | 55.44% | |
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pachauri, R.; Reisinger, A. IPCC Fourth Assessment Report; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- Pachauri, R.; Meyer, L. IPCC Fifth Assessment Report; IPCC: Copenhagen, Denmark, 2014. [Google Scholar]
- International Energy Agency (IEA). Energy Technology Perspectives 2010; IEA: Paris, France, 2010. [Google Scholar]
- Li, X.; Yang, F.; Zhu, Y.; Gao, Y. An assessment framework for analyzing the embodied carbon impacts of residential buildings in China. Energy Build. 2014, 85, 400–409. [Google Scholar] [CrossRef]
- Zabaneh, G. Zero net house: Preliminary assessment of suitability for Alberta. Renew. Sustain. Energy Rev. 2011, 15, 3237–3242. [Google Scholar] [CrossRef]
- Ionescu, C.; Baracu, T.; Vlad, G.; Necula, H.; Badea, A. The historical evolution of the energy efficient buildings. Renew. Sustain. Energy Rev. 2015, 49, 243–253. [Google Scholar] [CrossRef]
- Pfeiffer, A.; Koschenz, M.; Wokaun, A. Energy and building technology for the 2000 W society-potential of residential buildings in Switzerland. Energy Build. 2005, 37, 1158–1174. [Google Scholar] [CrossRef]
- Cellura, M.; Guarino, F.; Longo, S.; Mistretta, M. Different energy balances for the redesign of nearly net zero energy buildings: An Italian case study. Renew. Sustain. Energy Rev. 2015, 45, 100–112. [Google Scholar] [CrossRef]
- Ministry of Land Infrastructure and Transport (MOLIT). Available online: http://www.molit.go.kr/USR/NEWS/m_71/dtl.jsp?id=95072458 (accessed on 2 July 2015).
- DeCanio, S.J. The Efficiency Paradox: Bureaucratic and Organizational Barriers to Profitable Energy-Saving Investments. Energy Policy 1998, 26, 441–454. [Google Scholar] [CrossRef]
- Jaffe, A.B.; Stavins, R.N. The Energy-Efficiency Gap-What Does it Mean. Energy Policy 1994, 22, 804–810. [Google Scholar] [CrossRef]
- Goldman, C.A.; Hopper, N.C.; Osborn, J.G. Review of US ESCO industry market trends: An empirical analysis of project data. Energy Policy 2005, 33, 387–405. [Google Scholar] [CrossRef]
- Xu, P.; Chan, E.H.; Qian, Q.K. Success factors of energy performance contracting (EPC) for sustainable building energy efficiency retrofit (BEER) of hotel buildings in China. Energy Policy 2011, 39, 7389–7398. [Google Scholar] [CrossRef]
- Larsen, P.; Goldman, C.; Satchwell, A. Evolution of the U.S. energy service company industry: Market size and project performance from 1990–2008. Energy Policy 2012, 50, 802–820. [Google Scholar] [CrossRef]
- Painuly, J.; Park, H.; Lee, M.; Noh, J. Promoting energy efficiency financing and ESCOs in developing countries: Mechanisms and barriers. J. Clean. Prod. 2003, 11, 659–665. [Google Scholar] [CrossRef]
- Patari, S.; Sinkkonen, K. Energy Service Companies and Energy Performance Contracting: Is there a need to renew the business model? Insights from a Delphi study. J. Clean. Prod. 2014, 66, 264–271. [Google Scholar] [CrossRef]
- De T’Serclaes, P. Financing Energy Efficient Homes: Existing Policy Responses to Financial Barriers; International Energy Agency: Paris, France, 2007. [Google Scholar]
- Golove, W.H.; Eto, J.H. Market Barriers to Energy Efficiency: A Critical Reappraisal of the Rationale for Public Policies to Promote Energy Efficiency; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1996.
- Brown, M.A. Market failure and barriers as a basis for clean energy policies. Energy Policy 2001, 29, 1197–1207. [Google Scholar] [CrossRef]
- Du, P.; Zheng, L.Q.; Xie, B.C.; Mahalingam, A. Barriers to the adoption of energy-saving technologies in the building sector: A survey study of Jing-jin-tang, China. Energy Policy 2014, 75, 206–216. [Google Scholar] [CrossRef]
- Zhang, X.; Platten, A.; Shen, L. Green property development practice in China: Costs and barriers. Build. Environ. 2011, 46, 2153–2160. [Google Scholar] [CrossRef]
- Shi, Q.; Zuo, J.; Huang, R.; Huang, J.; Pullen, S. Identifying the critical factors for green construction—An empirical study in China. Habitat Int. 2013, 40, 1–8. [Google Scholar] [CrossRef]
- Steinberger, J.; Niel, J.; Bourg, D. Profiting from megawatts: Reducing absolute consumption and emissions through a performance-based energy economy. Energy Policy 2009, 37, 361–370. [Google Scholar] [CrossRef]
- Vine, E. An International Survey of the Energy Service Company (ESCO) Industry. Energy Policy 2005, 33, 691–704. [Google Scholar] [CrossRef]
- Gan, D. Energy Service Companies to Improve Energy Efficiency in China: Barriers and Removal Measures. Procedia Earth Planet. Sci. 2009, 1, 1695–1704. [Google Scholar]
- Jensen, J.O.; Nielsen, S.B.; Harsen, J.R. Greening Public Buildings: ESCO-Contracting in Danish Municipalities. Energies 2013, 6, 2407–2427. [Google Scholar] [CrossRef]
- Li, J.; Colombier, M. Managing carbon emissions in China through building energy efficiency. J. Environ. Manag. 2009, 90, 2436–2447. [Google Scholar] [CrossRef] [PubMed]
- Myers, S. Finance theory and financial strategy. Interfaces 1984, 14, 126–137. [Google Scholar] [CrossRef]
- Trigeorgis, L.; Mason, S. Valuing managerial flexibility. Midl. Corp. Financ. J. 1987, 5, 14–21. [Google Scholar]
- Copeland, T.; Antikarov, V. Real Options: A Practitioner’s Guide; Texere: New York, NY, USA, 2003. [Google Scholar]
- Martins, J.; Marques, R.C.; Cruz, C.O. Real Options in Infrastructure: Revisiting the Literature. J. Infrastruct. Syst. 2015. [Google Scholar] [CrossRef]
- Cui, Q.; Johnson, P.; Quick, A.; Hastak, M. Valuing the Warranty Ceiling Clause on New Mexico Highway 44 Using a Binomial Lattice Model. J. Constr. Eng. Manag. 2008, 134, 10–17. [Google Scholar] [CrossRef]
- Kim, B.; Lim, H.; Kim, H.; Hong, T. Determining the Value of Governmental Subsidies for the Installation of Clean Energy Systems Using Real Options. J. Constr. Eng. Manag. 2012, 138, 422–430. [Google Scholar] [CrossRef]
- Park, T.; Kim, B.; Kim, H. Real Option Approach to Sharing Privatization Risk in Underground Infrastructures. J. Constr. Eng. Manag. 2013, 139, 685–693. [Google Scholar] [CrossRef]
- Lee, H.W.; Choi, K.; Gambatese, J.A. Real Options Valuation of Phased Investments in Commercial Energy Retrofits under Building Performance Risks. J. Constr. Eng. Manag. 2014. [Google Scholar] [CrossRef]
- Kashani, H.; Ashuri, B.; Shahandashti, S.M.; Lu, J. Investment Valuation Model for Renewable Energy Systems in Buildings. J. Constr. Eng. Manag. 2015. [Google Scholar] [CrossRef]
- Mirzadeh, I.; Birgisson, B. Evaluation of Highway Projects under Government Support Mechanisms Based on an Option-Pricing Framework. J. Constr. Eng. Manag. 2015. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Polit. Econ. 1973, 81, 637–659. [Google Scholar] [CrossRef]
- Hull, J.C. Options, Futures, and Other Derivatives; Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Shan, L.; Garvin, M.J.; Kumar, R. Collar Options to Manage Revenue Risks in Real Toll Public-Private Partnership Transportation Projects. Constr. Manag. Econ. 2010, 28, 1057–1069. [Google Scholar] [CrossRef]
- Bettis, J.C.; Bizjak, J.M.; Lemmon, M.L. Managerial Ownership, Incentive Contracting, and the Use of Zero-Cost Collars and Equity Swaps by Corporate Insiders. J. Financ. Quant. Anal. 2001, 36, 345–370. [Google Scholar] [CrossRef]
- Cox, J.; Ross, S.; Rubinstein, M. Option pricing: A simplified approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Ho, P.S.; Liu, L.Y. How to Evaluate and Invest in Emerging A/E/C Technologies under Uncertainty. J. Constr. Eng. Manag. 2003, 129, 16–24. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Tae, S.; Shin, S. Profit Distribution in Guaranteed Savings Contracts: Determination Based on the Collar Option Model. Sustainability 2015, 7, 16273-16289. https://doi.org/10.3390/su71215816
Lee S, Tae S, Shin S. Profit Distribution in Guaranteed Savings Contracts: Determination Based on the Collar Option Model. Sustainability. 2015; 7(12):16273-16289. https://doi.org/10.3390/su71215816
Chicago/Turabian StyleLee, Sanghyo, Sungho Tae, and Sungwoo Shin. 2015. "Profit Distribution in Guaranteed Savings Contracts: Determination Based on the Collar Option Model" Sustainability 7, no. 12: 16273-16289. https://doi.org/10.3390/su71215816
APA StyleLee, S., Tae, S., & Shin, S. (2015). Profit Distribution in Guaranteed Savings Contracts: Determination Based on the Collar Option Model. Sustainability, 7(12), 16273-16289. https://doi.org/10.3390/su71215816





