Estimating the Impact of Urbanization on Air Quality in China Using Spatial Regression Models
Abstract
:1. Introduction
2. Data
2.1. AQI Record
| AQI Categories (Index Values) | SO2 (μg/m3, 24-h) | NO2 (μg/m3, 24-h) | CO (μg/m3, 24-h) | O3 (μg/m3, 1-h) | PM2.5 (μg/m3, 24-h) | PM10 (μg/m3, 24-h) |
|---|---|---|---|---|---|---|
| Good (Up to 50) | 0–50 | 0–40 | 0–2 | 0–160 | 0–35 | 0–50 |
| Moderate (51–100) | 51–150 | 41–80 | 3–4 | 161–200 | 35–75 | 51–150 |
| Unhealthy for Sensitive Groups (101–150) | 151–475 | 81–180 | 5–14 | 201–300 | 75–115 | 151–250 |
| Unhealthy (151–200) | 476–800 | 181–280 | 15–24 | 301–400 | 115–150 | 251–350 |
| Very Unhealthy (201–300) | 801–1600 | 281–565 | 25–36 | 401–800 | 150–250 | 351–420 |
| Hazardous (301–500) | 1601–2620 | 566–940 | 37–60 | 801–1200 | 250–500 | 421–600 |
2.2. Urbanization Index
| The Subsystem of Urbanization | Index | Acronym Index |
|---|---|---|
| Demographic urbanization | The proportion of urban population (%) | UR |
| Total population (104 people) | TP | |
| Non-agricultural population (104 people) | NP | |
| Economic urbanization | Proportion of the added value of secondary industry to GDP (%) | SI |
| GDP (104 Yuan) | GDP | |
| GDP per capita (Yuan) | PGDP | |
| Spatial urbanization | Urban development land (sq km) | UL |
| Population density (people/sq km) | PD | |
| Urban development land per capita (m2/people) | PUL | |
| Social urbanization | Private car ownership | PC |
| Private cars per unit of urban development land | PPC | |
| Total retail sales of consumer goods (108 Yuan) | TG |
2.3. Variable Selection and Data Pre-Processing
| Variables | Minimum | Maximum | Mean | Standard Error | Standard Deviation |
|---|---|---|---|---|---|
| AQI | 41.15 | 175.70 | 84.53 | 1.47 | 25.06 |
| UR | 10.46 | 100.00 | 38.52 | 1.20 | 20.36 |
| TP | 20.00 | 2970.00 | 440.82 | 17.71 | 301.06 |
| UL | 13.00 | 2915.56 | 133.65 | 13.30 | 226.16 |
| SI | 17.48 | 79.36 | 50.78 | 0.59 | 9.99 |
| PD | 14.57 | 8248.04 | 901.04 | 50.15 | 852.51 |
| PGDP | 8404.47 | 466,996.14 | 51,233.46 | 2834.88 | 48,192.94 |
| PPC | 310.00 | 15,426.00 | 3595.79 | 139.27 | 2367.57 |
| AQI | UR | TP | UL | SI | PD | PGDP | PPC | ||
|---|---|---|---|---|---|---|---|---|---|
| AQI | Spearman’s correlation | 1.00 | 0.199 ** | 0.367 ** | 0.254 ** | 0.171 ** | 0.459 ** | 0.207 ** | 0.134 * |
| sig.(2-tailed) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | ||
| UR | Spearman’s correlation | 0.199 ** | 1.00 | −0.09 | 0.437 ** | 0.08 | 0.08 | 0.611 ** | −0.326 ** |
| sig.(2-tailed) | 0.00 | 0.15 | 0.00 | 0.18 | 0.16 | 0.00 | 0.00 | ||
| TP | Spearman’s correlation | 0.367 ** | −0.09 | 1.00 | 0.483 ** | −0.177 ** | 0.351 ** | −0.06 | 0.194 ** |
| sig.(2-tailed) | 0.00 | 0.15 | 0.00 | 0.00 | 0.00 | 0.35 | 0.00 | ||
| UL | Spearman’s correlation | 0.254 ** | 0.437 ** | 0.483 ** | 1.00 | −0.155 ** | 0.244 ** | 0.456 ** | −0.151 * |
| sig.(2-tailed) | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.01 | ||
| SI | Spearman’s correlation | 0.171 ** | 0.08 | −0.177 ** | −0.155 ** | 1.00 | 0.149 * | 0.149 * | −0.03 |
| sig.(2-tailed) | 0.00 | 0.18 | 0.00 | 0.01 | 0.01 | 0.01 | 0.57 | ||
| PD | Spearman’s correlation | 0.459 ** | 0.08 | 0.351 ** | 0.244 ** | 0.149 * | 1.00 | 0.09 | 0.09 |
| sig.(2-tailed) | 0.00 | 0.16 | 0.00 | 0.00 | 0.01 | 0.13 | 0.11 | ||
| PGDP | Spearman’s correlation | 0.207 ** | 0.611 ** | −0.06 | 0.456 ** | 0.149 * | 0.09 | 1.00 | −0.06 |
| sig.(2-tailed) | 0.00 | 0.00 | 0.35 | 0.00 | 0.01 | 0.13 | 0.29 | ||
| PPC | Spearman’s correlation | 0.134 * | −0.326 ** | 0.194 ** | −0.151 * | −0.03 | 0.09 | −0.06 | 1.00 |
| sig.(2-tailed) | 0.02 | 0.00 | 0.00 | 0.01 | 0.57 | 0.11 | 0.29 | ||
3. Methodology
3.1. Measures of Spatial Dependence and Heterogeneity
3.2. Spatial Regression Models
3.2.1. Spatial Lag Model (SAR) and Spatial Error Model (SEM)
3.2.2. Geographically Weighted Regression (GWR)
4. Results and Interpretations
4.1. Spatial Pattern of AQI
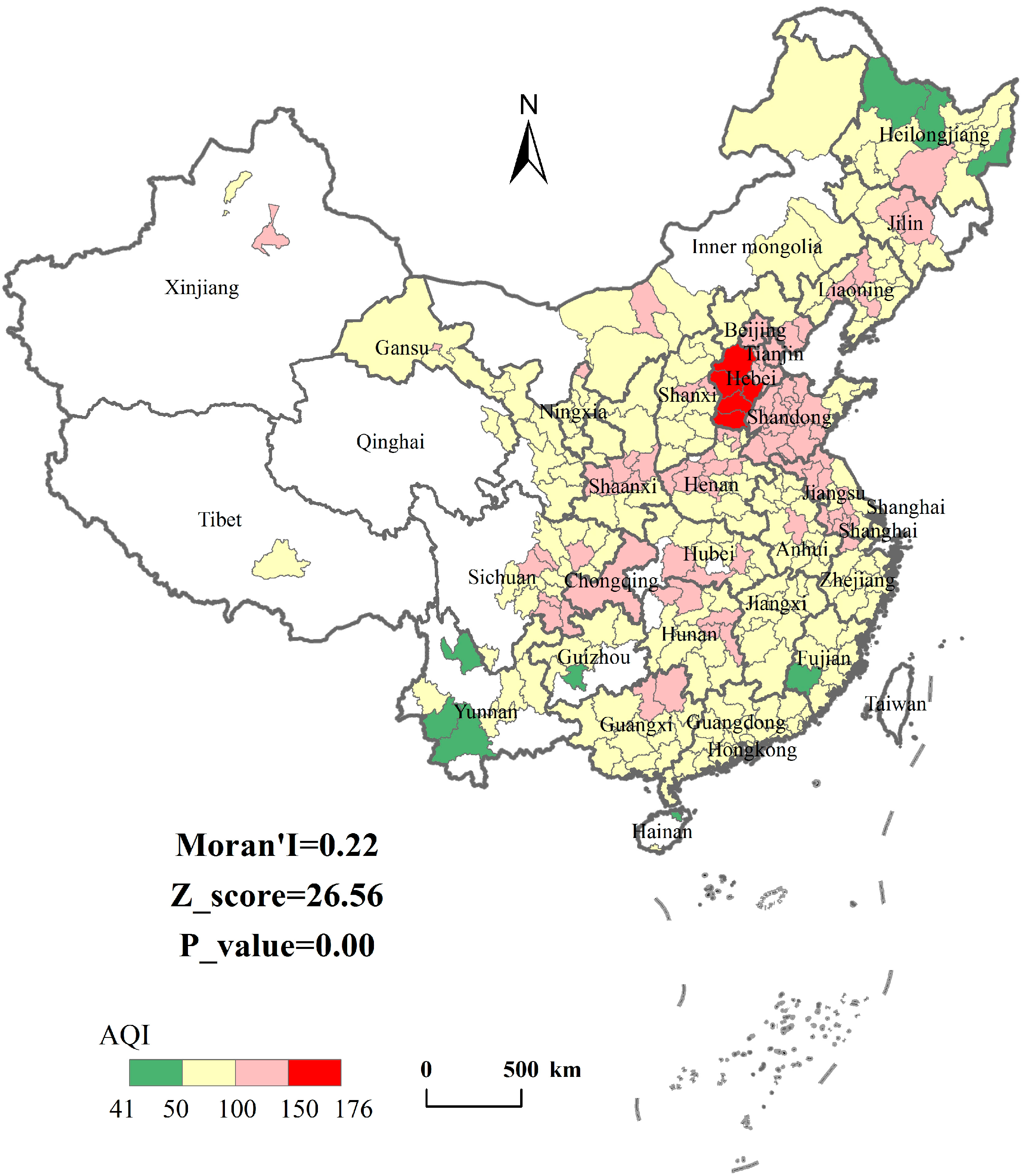
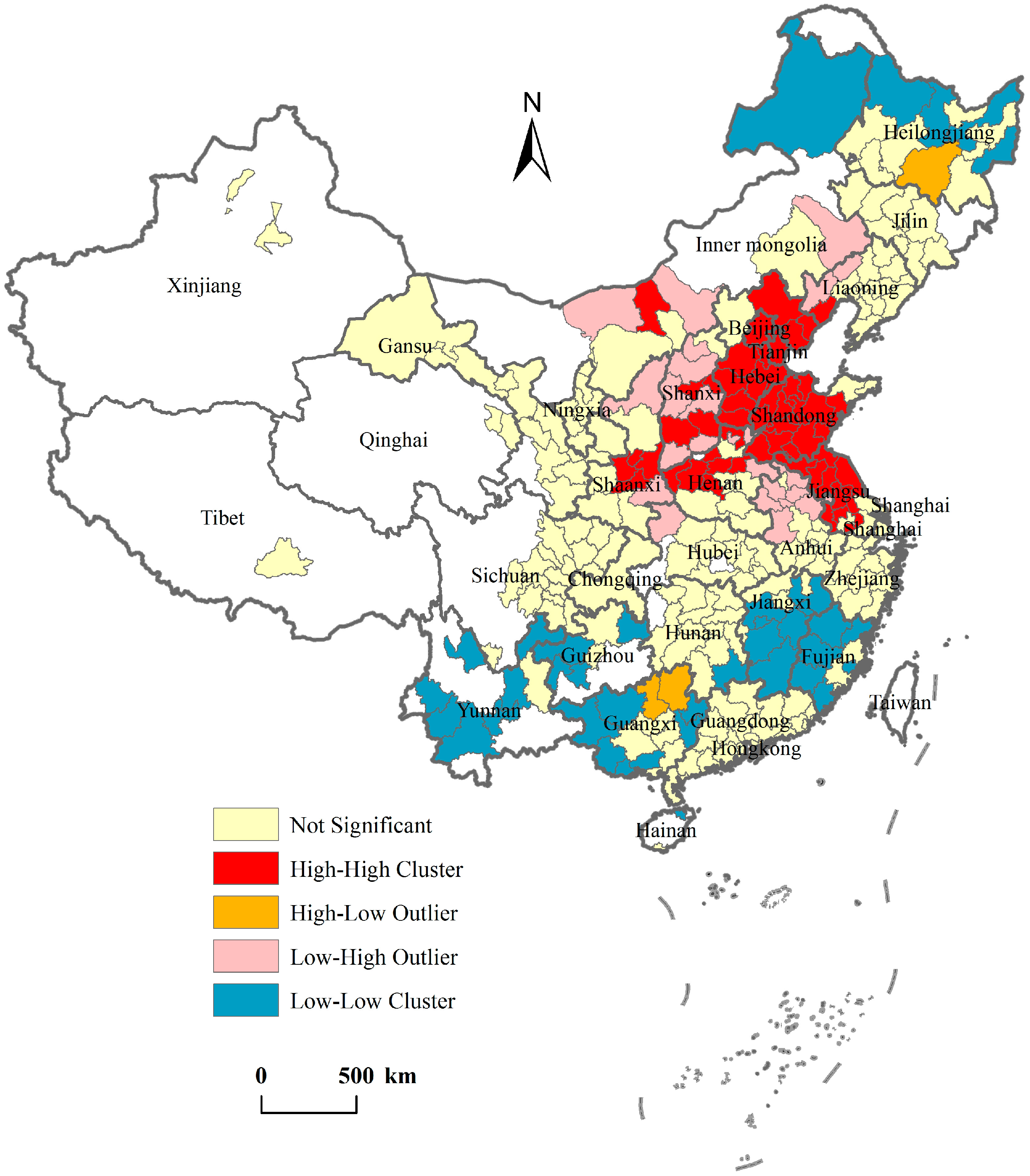
4.2. Estimation Results and Model Comparisons
| Model | Coefficient | t-Statistic | Probability |
|---|---|---|---|
| constant | 0.002 | 0.048 | 0.961 |
| UR | 0.171 ** | 2.447 | 0.015 |
| TP | 0.254 *** | 3.246 | 0.001 |
| UL | 0.074 | 0.532 | 0.595 |
| SI | 0.163 *** | 3.073 | 0.002 |
| PD | 0.302 *** | 5.602 | 0.000 |
| PGDP | 0.045 | 0.584 | 0.559 |
| PPC | 0.129 ** | 2.291 | 0.023 |
| R2 | 0.338 | ||
| Adjusted R2 | 0.321 | ||
| F-statistic | 20.484 | ||
| P(F-statistic) | 0.000 | ||
| AIC | 715.992 | ||
| Spatial Dependence | MI/DF | Value | Probability |
| Moran’s I (error) | 0.056 | 7.016 *** | 0.000 |
| LM (lag) | 1.000 | 42.059 *** | 0.000 |
| Robust LM (lag) | 1.000 | 14.105 *** | 0.001 |
| LM (error) | 1.000 | 28.963 *** | 0.000 |
| Robust LM (error) | 1.000 | 1.009 | 0.315 |
| Variables | Min. | Lower Quartile | Median | Mean | Global (OLS) | SAR (ML) | Upper Quartile | Max. |
|---|---|---|---|---|---|---|---|---|
| UR | −0.006 | 0.128 | 0.253 | 0.225 | 0.1708 ** | 0.171 ** | 0.336 | 0.381 |
| TP | 0.040 | 0.166 | 0.233 | 0.267 | 0.254 *** | 0.246 *** | 0.311 | 0.774 |
| UL | −0.110 | −0.069 | −0.035 | 0.000 | 0.074 | 0.066 | 0.062 | 0.932 |
| SI | 0.067 | 0.112 | 0.133 | 0.132 | 0.163 *** | 0.110 ** | 0.148 | 0.219 |
| PD | 0.186 | 0.239 | 0.259 | 0.273 | 0.302 *** | 0.272 *** | 0.296 | 0.497 |
| PGDP | −0.212 | 0.019 | 0.075 | 0.087 | 0.045 | 0.037 | 0.143 | 0.257 |
| PPC | −0.201 | 0.054 | 0.175 | 0.149 | 0.129 ** | 0.118 ** | 0.253 | 0.321 |
| Intercept | −0.269 | −0.075 | 0.091 | 0.053 | 0.002 | −0.037 | 0.192 | 0.238 |
| W_AQI | n.a. | n.a. | 0.603 *** | |||||
| No. of observations | 289 | 289 | 289 | |||||
| Bandwidth | 857196 | n.a. | n.a. | |||||
| R2 | 0.495 | 0.338 | 0.380 | |||||
| Adjusted R2 | 0.431 | 0.321 | n.a. | |||||
| AIC | 679.866 | 715.992 | 700.132 |

4.3. Spatial Distribution of GWR Estimation
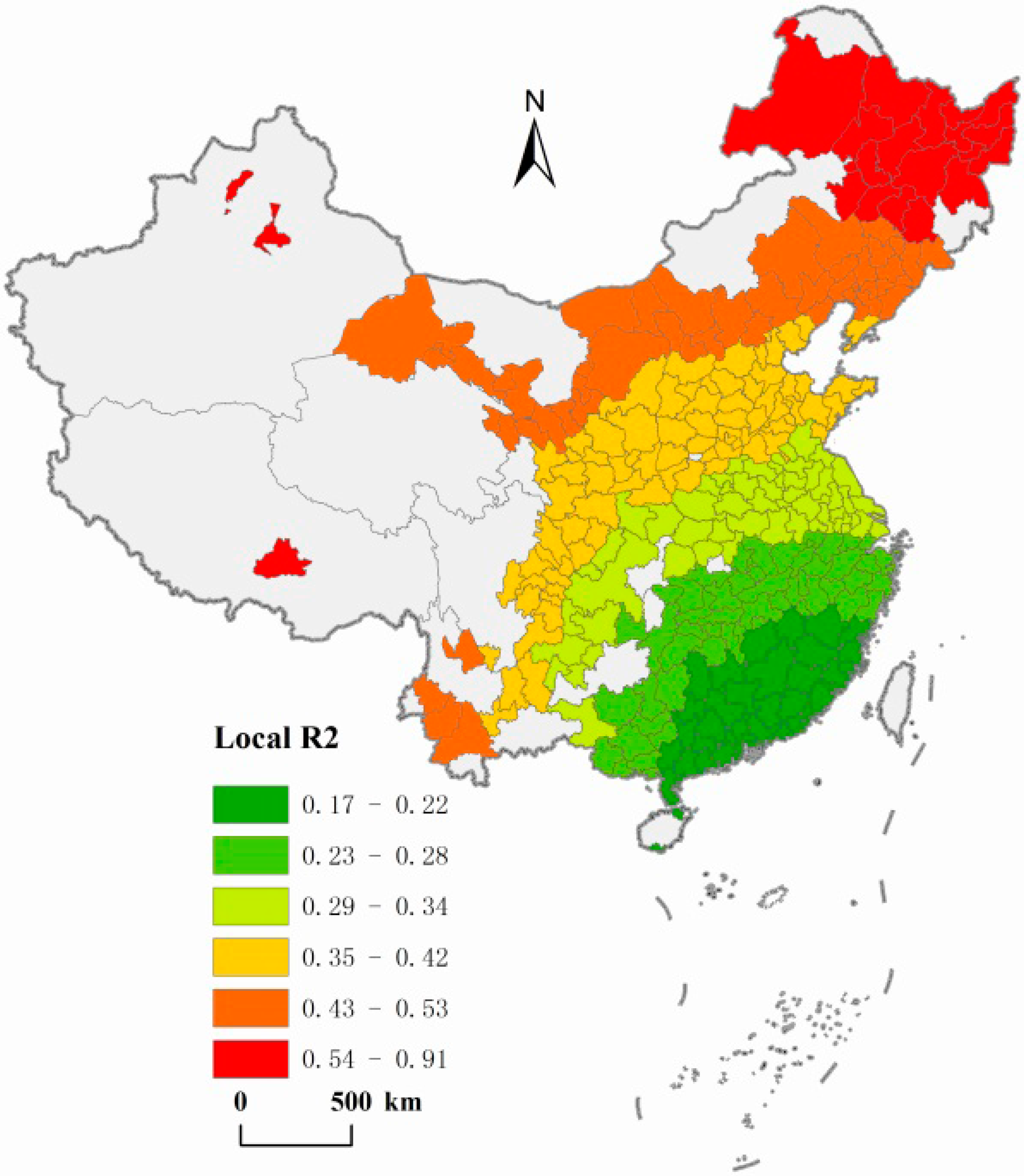
5. Conclusions and Policy Implications
5.1. Conclusions
5.2. Policy Implications
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chan, C.K.; Yao, X. Air pollution in mega cities in china. Atmos. Environ. 2008, 42, 1–42. [Google Scholar] [CrossRef]
- Kan, H.; Chen, B.; Hong, C. Health impact of outdoor air pollution in china: Current knowledge and future research needs. Environ. Health Perspect. 2009. [Google Scholar] [CrossRef] [PubMed]
- Matus, K.; Nam, K.-M.; Selin, N.E.; Lamsal, L.N.; Reilly, J.M.; Paltsev, S. Health damages from air pollution in China. Glob. Environ. Chang. 2012, 22, 55–66. [Google Scholar] [CrossRef]
- Wong, E. Air Pollution Linked to 1.2 Million Premature Deaths in China. 2013. Available online: http://ming3d.com/sustainable/wp-content/uploads/2013/04/Air-Pollution-linked-to-Premature-Deaths.pdf (accessed on 18 November 2015).
- Rohde, R.A.; Muller, R.A. Air pollution in China: Mapping of concentrations and sources. PLoS ONE 2015. [Google Scholar] [CrossRef] [PubMed]
- Crane, K.; Mao, Z. Costs of Selected Policies to Address Air Pollution in China; RAND Corporation: Santa Monica, CA, USA, 2015. [Google Scholar]
- Zhang, D.; Liu, J.; Li, B. Tackling air pollution in China—What do we learn from the great smog of 1950s in London. Sustainability 2014, 6, 5322–5338. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, C.; Pei, T.; Haynie, S.; Fan, J. Quantitative estimation of urbanization dynamics using time series of DMSP/OLS nighttime light data: A comparative case study from China’s cities. Remote Sens. Environ. 2012, 124, 99–107. [Google Scholar] [CrossRef]
- Beirle, S.; Boersma, K.F.; Platt, U.; Lawrence, M.G.; Wagner, T. Megacity emissions and lifetimes of nitrogen oxides probed from space. Science 2011, 333, 1737–1739. [Google Scholar] [CrossRef] [PubMed]
- Hopke, P.K.; Cohen, D.D.; Begum, B.A.; Biswas, S.K.; Ni, B.; Pandit, G.G.; Santoso, M.; Chung, Y.-S.; Davy, P.; Markwitz, A. Urban air quality in the Asian region. Sci. Total Environ. 2008, 404, 103–112. [Google Scholar] [CrossRef] [PubMed]
- NBSC. China Statistical Yearbook 2014; China Statistics Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.G.; Bai, X.M.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.L.; Wang, J. A theoretical analysis of interactive coercing effects between urbanization and eco-environment. Chin. Geogr. Sci. 2013, 23, 147–162. [Google Scholar] [CrossRef]
- Zhou, N.; Fridley, D.; Khanna, N.Z.; Ke, J.; McNeil, M.; Levine, M. China’s energy and emissions outlook to 2050: Perspectives from bottom-up energy end-use model. Energy Policy 2013, 53, 51–62. [Google Scholar] [CrossRef]
- Liu, L.; He, P.; Zhang, B.; Bi, J. Red and green: Public perception and air quality information in urban China. Environ. Sci. Policy Sustain. Dev. 2012, 54, 44–49. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, S.; Castro, R.; Pan, X. PM2.5 monitoring and mitigation in the cities of China. Environ. Sci. Technol. 2012, 46, 3627–3628. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Liu, W.; Lu, D. Challenges and the way forward in China’s new-type urbanization. Land Use Policy 2015, in press. [Google Scholar] [CrossRef]
- Bai, X.; Shi, P.; Liu, Y. Society: Realizing China’s urban dream. Nature 2014, 509, 158–160. [Google Scholar] [CrossRef] [PubMed]
- Molina, M.J.; Molina, L.T. Megacities and atmospheric pollution. J. Air Waste Manag. Assoc. 2004, 54, 644–680. [Google Scholar] [CrossRef] [PubMed]
- Tai, A.P.; Mickley, L.J.; Jacob, D.J. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States: Implications for the sensitivity of PM2.5 to climate change. Atmos. Environ. 2010, 44, 3976–3984. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, X.; Gong, D.; Quan, W.; Zhao, X.; Ma, Z.; Kim, S.-J. Evolution of surface O3 and PM2.5 concentrations and their relationships with meteorological conditions over the last decade in Beijing. Atmos. Environ. 2015, 108, 67–75. [Google Scholar] [CrossRef]
- Asimakopoulos, D.; Flocas, H.; Maggos, T.; Vasilakos, C. The role of meteorology on different sized aerosol fractions (PM10, PM2.5, PM2.5–10). Sci. Total Environ. 2012, 419, 124–135. [Google Scholar] [CrossRef] [PubMed]
- Gebhart, K.A.; Kreidenweis, S.M.; Malm, W.C. Back-trajectory analyses of fine particulate matter measured at big bend national park in the historical database and the 1996 scoping study. Sci. Total Environ. 2001, 276, 185–204. [Google Scholar] [CrossRef]
- Han, L.; Zhou, W.; Li, W.; Meshesha, D.T.; Li, L.; Zheng, M. Meteorological and urban landscape factors on severe air pollution in Beijing. J. Air Waste Manag. Assoc. 2015, 65, 782–787. [Google Scholar] [CrossRef] [PubMed]
- Leibensperger, E.M.; Mickley, L.J.; Jacob, D.J. Sensitivity of us air quality to mid-latitude cyclone frequency and implications of 1980–2006 climate change. Atmos. Chem. Phys. 2008, 8, 7075–7086. [Google Scholar] [CrossRef]
- Ramsey, N.R.; Klein, P.M.; Moore, B. The impact of meteorological parameters on urban air quality. Atmos. Environ. 2014, 86, 58–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, A.; Mao, H.; Nie, W.; Zhou, D.; Liu, L.; Huang, X.; Fu, C. Impact of synoptic weather patterns and inter-decadal climate variability on air quality in the north China plain during 1980–2013. Atmos. Environ. 2015, in press. [Google Scholar] [CrossRef]
- Hirota, K. Comparative studies on vehicle related policies for air pollution reduction in ten Asian countries. Sustainability 2010, 2, 145–162. [Google Scholar] [CrossRef]
- Schmale, J.; von Schneidemesser, E.; Dörrie, A. An integrated assessment method for sustainable transport system planning in a middle sized German city. Sustainability 2015, 7, 1329–1354. [Google Scholar] [CrossRef]
- Hao, J.; Wang, L. Improving urban air quality in China: Beijing case study. J. Air Waste Manag. Assoc. 2005, 55, 1298–1305. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, M.Z. Review of solutions to global warming, air pollution, and energy security. Energy Environ. Sci. 2009, 2, 148–173. [Google Scholar] [CrossRef]
- De Leeuw, F.A.; Moussiopoulos, N.; Sahm, P.; Bartonova, A. Urban air quality in larger conurbations in the European Union. Environ. Model. Softw. 2001, 16, 399–414. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, S.; Wang, H.; Ren, Y.; Du, K.; Xu, W.; Zheng, H.; Jiang, B. Quantifying the impacts of socio-economic factors on air quality in Chinese cities from 2000 to 2009. Environ. Pollut. 2012, 167, 148–154. [Google Scholar] [CrossRef] [PubMed]
- Ryu, Y.-H.; Baik, J.-J.; Lee, S.-H. Effects of anthropogenic heat on ozone air quality in a megacity. Atmos. Environ. 2013, 80, 20–30. [Google Scholar] [CrossRef]
- Han, L.; Zhou, W.; Li, W.; Li, L. Impact of urbanization level on urban air quality: A case of fine particles (PM2.5) in Chinese cities. Environ. Pollut. 2014, 194, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Cho, H.-S.; Choi, M.J. Effects of compact urban development on air pollution: Empirical evidence from Korea. Sustainability 2014, 6, 5968–5982. [Google Scholar] [CrossRef]
- Stone, B., Jr. Urban sprawl and air quality in large us cities. J. Environ. Manag. 2008, 86, 688–698. [Google Scholar] [CrossRef] [PubMed]
- Xia, T.-Y.; Wang, J.; Song, K.; Da, L. Variations in air quality during rapid urbanization in Shanghai, China. Landsc. Ecol. Eng. 2011, 10, 181–190. [Google Scholar] [CrossRef]
- Beelen, R.; Hoek, G.; Vienneau, D.; Eeftens, M.; Dimakopoulou, K.; Pedeli, X.; Tsai, M.-Y.; Künzli, N.; Schikowski, T.; Marcon, A. Development of no 2 and no x land use regression models for estimating air pollution exposure in 36 study areas in Europe–the escape project. Atmos. Environ. 2013, 72, 10–23. [Google Scholar] [CrossRef]
- Borrego, C.; Martins, H.; Tchepel, O.; Salmim, L.; Monteiro, A.; Miranda, A.I. How urban structure can affect city sustainability from an air quality perspective. Environ. Model. Softw. 2006, 21, 461–467. [Google Scholar] [CrossRef]
- Nowak, D.J.; Hirabayashi, S.; Bodine, A.; Greenfield, E. Tree and forest effects on air quality and human health in the United States. Environ. Pollut. 2014, 193, 119–129. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Liu, X. Temporal and spatial differences and imbalance of China’s urbanization development during 1950–2006. J. Geogr. Sci. 2009, 19, 719–732. [Google Scholar] [CrossRef]
- The Daily Urban Air Quality. Available online: http://datacenter.mep.gov.cn/ (accessed on 18 November 2015).
- World Health Organization. Air Quality Guidelines: Global Update 2005. 2006. Available online: http://www.euro.who.int/__data/assets/pdf_file/0005/78638/E90038.pdf (accessed on 18 November 2015).
- Fang, M.; Chan, C.K.; Yao, X. Managing air quality in a rapidly developing nation: China. Atmos. Environ. 2009, 43, 79–86. [Google Scholar] [CrossRef]
- NBSC. China City Statistical Yearbook 2014; China Statistics Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- NBSC. China’s Regional Economic Statistical Yearbook 2014; China Statistics Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Biao, Q.; Chuanglin, F. The dynamic coupling model and its application of urbanization and eco-environment in Hexi corridor. J. Geogr. Sci. 2005, 15, 491–499. [Google Scholar] [CrossRef]
- Li, Y.F.; Li, Y.; Zhou, Y.; Shi, Y.L.; Zhu, X.D. Investigation of a coupling model of coordination between urbanization and the environment. J. Environ. Manag. 2012, 98, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Xue, B.; Geng, Y.; Müller, K.; Lu, C.; Ren, W. Understanding the causality between carbon dioxide emission, fossil energy consumption and economic growth in developed countries: An empirical study. Sustainability 2014, 6, 1037–1045. [Google Scholar] [CrossRef]
- Lozano, S.; Gutiérrez, E. Non-parametric frontier approach to modelling the relationships among population, gdp, energy consumption and CO2 emissions. Ecol. Econ. 2008, 66, 687–699. [Google Scholar] [CrossRef]
- Mason, C.H.; Perreault, W.D., Jr. Collinearity, power, and interpretation of multiple regression analysis. J. Mark. Res. 1991, 28, 268–280. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E.A.; York, R. Environmentally efficient well-being: Is there a Kuznets curve? Appl. Geogr. 2012, 32, 21–28. [Google Scholar] [CrossRef]
- Stern, D.I. The rise and fall of the environmental Kuznets curve. World Dev. 2004, 32, 1419–1439. [Google Scholar] [CrossRef]
- Song, M.-L.; Zhang, W.; Wang, S.-H. Inflection point of environmental Kuznets curve in mainland China. Energy Policy 2013, 57, 14–20. [Google Scholar] [CrossRef]
- Brajer, V.; Mead, R.W.; Xiao, F. Searching for an environmental Kuznets curve in China’s air pollution. China Econ. Rev. 2011, 22, 383–397. [Google Scholar] [CrossRef]
- Anselin, L.; Rey, S.J. Perspectives on Spatial Data Analysis. 2010. Available online: http://link.springer.com/book/10.1007%2F978-3-642-01976-0 (accessed on 18 November 2015).
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Tiefelsdorf, M. Modelling Spatial Processes: The Identification and Analysis of Spatial Relationships in Regression Residuals by Means of Moran’s I (Germany). Ph.D. Thesis, Wilfrid Laurier University, Waterloo and Brantford, ON, Canada, May 1998. [Google Scholar]
- Anselin, L. Local indicators of spatial association-lisa. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Arribas-Bel, D.; Sanz-Gracia, F. The validity of the monocentric city model in a polycentric age: US metropolitan areas in 1990, 2000 and 2010. Urban Geogr. 2014, 35, 980–997. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, L.; Xu, W.; Ledwith, V. Use of local Moran’s I and GIS to identify pollution hotspots of Pb in urban soils of galway, ireland. Sci. Total Environ. 2008, 398, 212–221. [Google Scholar] [CrossRef] [PubMed]
- Fischer, M.M.; Getis, A. Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Ali, K.; Partridge, M.D.; Olfert, M.R. Can geographically weighted regressions improve regional analysis and policy making? Int. Reg. Sci. Rev. 2007, 30, 300–329. [Google Scholar] [CrossRef]
- Anselin, L.; Bera, A.K. Spatial dependence in linear regression models with an introduction to spatial econometrics. Stat. Textb. Monogr. 1998, 155, 237–290. [Google Scholar]
- Kelejian, H.H.; Prucha, I.R. Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances. J. Econom. 2010, 157, 53–67. [Google Scholar] [CrossRef] [PubMed]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Yu, D.-L. Spatially varying development mechanisms in the greater Beijing area: A geographically weighted regression investigation. Ann. Reg. Sci. 2006, 40, 173–190. [Google Scholar] [CrossRef]
- Lo, C. Population estimation using geographically weighted regression. GIScience Remote Sens. 2008, 45, 131–148. [Google Scholar] [CrossRef]
- Chang, H.-S.; Chen, T.-L. Decision making on allocating urban green spaces based upon spatially-varying relationships between urban green spaces and urban compaction degree. Sustainability 2015, 7, 13399–13415. [Google Scholar] [CrossRef]
- Gao, J.; Li, S. Detecting spatially non-stationary and scale-dependent relationships between urban landscape fragmentation and related factors using geographically weighted regression. Appl. Geogr. 2011, 31, 292–302. [Google Scholar] [CrossRef]
- Song, W.; Jia, H.; Huang, J.; Zhang, Y. A satellite-based geographically weighted regression model for regional PM 2.5 estimation over the Pearl River delta region in China. Remote Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Tu, J.; Xia, Z.G. Examining spatially varying relationships between land use and water quality using geographically weighted regression I: Model design and evaluation. Sci. Total Environ. 2008, 407, 358–378. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, D.C. Visualizing and diagnosing coefficients from geographically weighted regression models. In Geospatial Analysis and Modelling of Urban Structure and Dynamics; Springer Netherland: Heidelberg, Germany, 2010; pp. 415–436. [Google Scholar]
- Li, G.; Fang, C. Analyzing the multi-mechanism of regional inequality in China. Ann. Reg. Sci. 2014, 52, 155–182. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, C.; Liu, H.; Li, G.; Sun, D.; Miao, Z. Estimating the Impact of Urbanization on Air Quality in China Using Spatial Regression Models. Sustainability 2015, 7, 15570-15592. https://doi.org/10.3390/su71115570
Fang C, Liu H, Li G, Sun D, Miao Z. Estimating the Impact of Urbanization on Air Quality in China Using Spatial Regression Models. Sustainability. 2015; 7(11):15570-15592. https://doi.org/10.3390/su71115570
Chicago/Turabian StyleFang, Chuanglin, Haimeng Liu, Guangdong Li, Dongqi Sun, and Zhuang Miao. 2015. "Estimating the Impact of Urbanization on Air Quality in China Using Spatial Regression Models" Sustainability 7, no. 11: 15570-15592. https://doi.org/10.3390/su71115570
APA StyleFang, C., Liu, H., Li, G., Sun, D., & Miao, Z. (2015). Estimating the Impact of Urbanization on Air Quality in China Using Spatial Regression Models. Sustainability, 7(11), 15570-15592. https://doi.org/10.3390/su71115570








