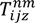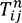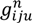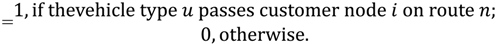Minimizing the Carbon Footprint for the Time-Dependent Heterogeneous-Fleet Vehicle Routing Problem with Alternative Paths
Abstract
:1. Introduction
- This paper proposes a GA for minimizing the carbon footprint for the time-dependent heterogeneous-fleet vehicle routing problem with alternative paths (MTHVRPP).
- In solution representation, time is divided into numerous time steps so that the average vehicle speed on different alternative paths and in different time zones can be expressed.
- Compared with previous VRPs, the factors that influence carbon footprints such as vehicle type, alternative path selection, vehicle load, and time zone speed are considered in this paper, in order to conform to real life situations.
2. Literature Review
2.1. VRP
2.2. Description of VRP
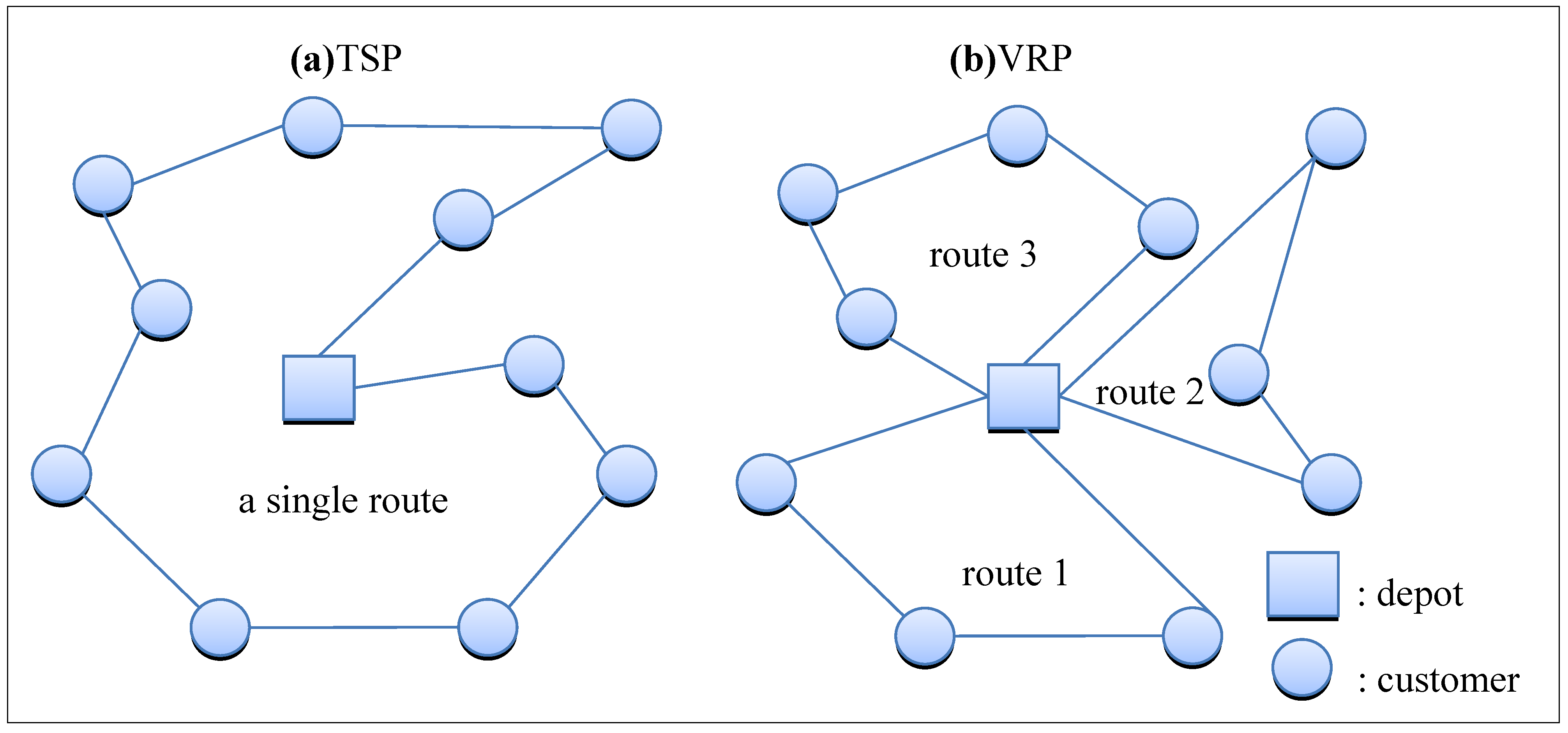
2.3. Approaches for VRP
3. Our Genetic Algorithm Approach for MTHVRPP
3.1. Problem Description
- The objective of the MTHVRPP is to minimize the total carbon footprint, not distance or time.
- The MTHVRPP has more than one vehicle type, and the capacity and basic costs of each vehicle are different.
- In the MTHVRPP, multiple paths exist between customer nodes; the distance of each path and the speed of different time zones of a day and different vehicles are also different.
- Because multiple vehicle types exist, the basic costs for each vehicle are different. The carbon emissions also change based on the load and travel speed during the routing trip.
3.1.1. Problem Assumptions
- (1)
- Route information:
- There is only a single depot, and its location is fixed.
- The distance between customers, the customer locations, the customer demand quantity, and the vehicle speed on routes between customer nodes in different time zones are known and fixed.
- Vehicles leave from the depot and return to the depot after servicing all the customers.
- The capacities for different vehicles are fixed and known.
- The total customer demand requirements on each route cannot exceed the vehicle capacity.
- More than one path between nodes can be selected.
- Each customer node must be visited, and is only visited once.
- Different vehicle types can be used for delivery according to the number of the required routes and the routing distance.
- (2)
- Costs and time:
- There is a positive proportional relationship between the vehicle routing distance and the vehicle carbon emission.
- There is a positive proportional relationship between the vehicle load and the vehicle carbon emission.
- The carbon emission from servicing customers is not considered.
- The vehicle types and vehicle number limitations are not considered.
- The routing time of each vehicle is limited.
- The vehicle fixed costs are not considered.
- The time window limitations are not considered.
3.1.2. Notations
- Node information:
I : I = {V1, V2, V3 ... VS}, where vi is a customer nodes for i ϵ {1, 2, …, S}. v0 : v0 is the depot node. I0 : I0 = I ∪ {v0} - Vehicle information
U : The number of vehicle types. Au : The surface area of each vehicle type. Wu : The empty weight of each vehicle type. - Constant
qi : The cargo demand requirement of node i. Zij : The number of selectable paths from node i to node j. Qu : The maximum load capacity of vehicle type u. : The speed in time zone m on path z between nodes i and j. Dijz : The distance of path z between nodes i and j. S : The total number of customer nodes. N : The number of vehicle routes. Tm : The starting time point for time zone m. L : The vehicle routing time limitation. - Label
i, j, k : Node label. z : Route label. m : Time zone label. u : Vehicle type label. - Variables:
s : The number of customers’ nodes that have already been serviced. : The cargo load of vehicle type u on route n after passing node i. : The time point when the vehicle reaches node i on route n. : The time point when the vehicle leaves node i on route n. : The time consumed by traveling on route n in time zone m on path z between i and j. : The total routing time between nodes i and j on route n. : The routing distance taken on route n in time zone m on path z between nodes i and j. Ln : The time traveling on route n. : The total carbon emission of vehicle u between node i and j on route n. gn : The total carbon emission on route n. TG : The total carbon emission for the entire route. TD : The total routing distance. TT : The total routing time. - Variables:
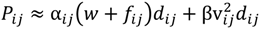
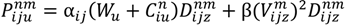
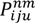 is the energy (J) required by the vehicle type u going from customer node i to node j in time zone m on route n; Wu is the empty weight of vehicle type u (kg);
is the energy (J) required by the vehicle type u going from customer node i to node j in time zone m on route n; Wu is the empty weight of vehicle type u (kg);  is the load (kg) of vehicle type u on route n after passing through node i;
is the load (kg) of vehicle type u on route n after passing through node i; 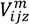 is the vehicle speed (m/s) in time zone m on path z between nodes i and j;
is the vehicle speed (m/s) in time zone m on path z between nodes i and j; 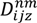 is the distance (m) traveled by the vehicle on route n in time zone m on path z between customer nodes i and j. Furthermore, because the surface area of each vehicle type is different, Equation (3) is modified to:
is the distance (m) traveled by the vehicle on route n in time zone m on path z between customer nodes i and j. Furthermore, because the surface area of each vehicle type is different, Equation (3) is modified to:
3.1.3. Mathematical Model
- Objective equation:
 , which is given as follows:
, which is given as follows:
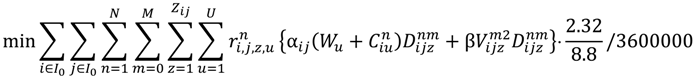
 is one or zero according to the condition whether vehicle type u has passed through path z between nodes i and j on route n. If the condition is true, then
is one or zero according to the condition whether vehicle type u has passed through path z between nodes i and j on route n. If the condition is true, then  = 1; otherwise,
= 1; otherwise,  = 0. Because the result unit obtained by the original objective equation is in J·m2/s2, our requirement is that this unit must be converted to a kilowatt-hour. One liter of gasoline can produce approximately 8.8 kilowatt-hours of energy [9] and approximately 2.32 kg of CO2 [9]. Thus, this objective equation is multiplied with a coefficient of 2.32/8.8/360000.
= 0. Because the result unit obtained by the original objective equation is in J·m2/s2, our requirement is that this unit must be converted to a kilowatt-hour. One liter of gasoline can produce approximately 8.8 kilowatt-hours of energy [9] and approximately 2.32 kg of CO2 [9]. Thus, this objective equation is multiplied with a coefficient of 2.32/8.8/360000.- The constraints of vehicle flow rate conservation:
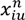 represents whether vehicle type u passes node i on route n. If so, then
represents whether vehicle type u passes node i on route n. If so, then 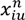 = 1; otherwise,
= 1; otherwise, 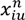 = 0.
= 0.
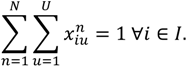
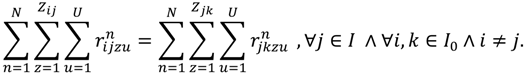
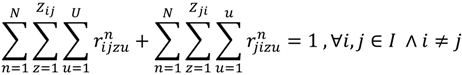

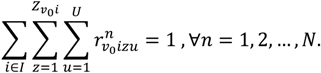
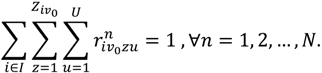
- Vehicle load capacity constraint:
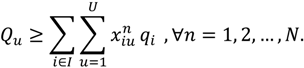
- Vehicle routing time constraint:
- Definition constraint:
 only equals 0 or 1.
only equals 0 or 1.

 only equals 0 or 1. If vehicle u passes through path z between nodes i and j on route n, then
only equals 0 or 1. If vehicle u passes through path z between nodes i and j on route n, then 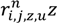 equals 1; otherwise, equals 0.
equals 1; otherwise, equals 0.

- Calculation of parameters:
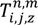 in each situation.
in each situation.

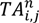 that the vehicle reaches customer node j on route n, where
that the vehicle reaches customer node j on route n, where 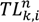 represents the time that the vehicle left node i.
represents the time that the vehicle left node i.
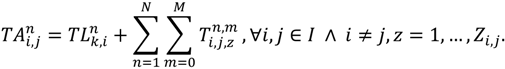
 from node i to j on route n.
from node i to j on route n.
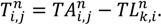
 on route n in time zone m on path z between nodes i and j, where Zi,j is the path selected between i and j.
on route n in time zone m on path z between nodes i and j, where Zi,j is the path selected between i and j.
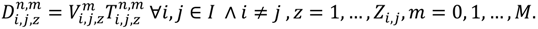
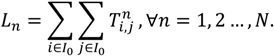
3.1.4. Example Description

3.2. Genetic Algorithm Design
3.2.1. Solution Representation

| Time Zone | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Route | Vehicle type | Path | Distance | Weight | Speed | Routing distance | CO2 | Speed | Routing distance | CO2 | Speed | Routing distance | CO2 | Speed | Routing distance | CO2 | Speed | Routing distance | CO2 | Speed | Routing distance | CO2 | Total | |||
| n = 1 | u = 1 | 0-1 | 20 | 3+3 = 6 | 40 | 6.67 | 0.41 | 50 | 8.33 | 0.60 | 60 | 5 | 0.42 | 1.45 | ||||||||||||
| 1-3 | 10 | 3+1 = 4 | 60 | 5 | 0.35 | 50 | 5 | 0.29 | 0.65 | |||||||||||||||||
| 3-0 | 15 | 3+0 = 3 | 50 | 3.33 | 0.17 | 40 | 6.67 | 0.27 | 50 | 5 | 0.25 | 0.7 | ||||||||||||||
| n = 2 | u = 2 | 0-2 | 15 | 5+6 = 10 | 50 | 8.33 | 0.84 | 50 | 6.67 | 0.67 | 1.52 | |||||||||||||||
| 2-4 | 10 | 5+3 = 8 | 40 | 1.34 | 0.10 | 40 | 6.67 | 0.51 | 40 | 2.00 | 0.15 | 0.77 | ||||||||||||||
| 4-5 | 5 | 5+2 = 7 | 60 | 5 | 0.46 | 0.46 | ||||||||||||||||||||
| 5-0 | 15 | 5+0 = 5 | 45 | 1.33 | 0.08 | 45 | 7.50 | 0.45 | 45 | 6.17 | 0.37 | 0.9 | ||||||||||||||
| n = 3 | u = 2 | 0-6 | 20 | 5+5 = 10 | 60 | 10.00 | 1.14 | 50 | 8.33 | 0.84 | 40 | 1.67 | 0.15 | 2.14 | ||||||||||||
| 6-0 | 20 | 5+0 = 5 | 40 | 5 | 0.27 | 50 | 8.33 | 0.54 | 60 | 6.67 | 0.52 | 1.35 | ||||||||||||||
| Total | 9.95 | |||||||||||||||||||||||||
3.2.2. Our Algorithm

- (1)
- Initial population
- (2)
- Capacity check
- (3)
- Alternative path selection
- (4)
- Fitness evaluation
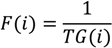
- (5)
- Population selection
- (6)
- Crossover and mutation
- (7)
- Termination condition
4. Experimental Design and Results
4.1. Description of Experimental Problems and Parameter Setting
4.1.1. Parameter Settings



| Vehicle type | Type 1 | Type 2 | Type 3 | Type 4 | Type 5 |
|---|---|---|---|---|---|
| Capacity (ton) | 1 | 1.5 | 2 | 2.5 | 3 |
| Empty vehicle weight (ton) | 0.75 | 1 | 1.5 | 2 | 2.5 |
| Parameter | Value |
|---|---|
| Vehicle acceleration a | 0 |
| Road inclination angle θij | 0.01 |
| Rolling resistance coefficient Cr | 0.7 |
| Road resistance coefficient Cd | 0 |
| Air viscosity coefficient ρ | 1.2041 |
4.1.2. Parameter Setting for our GA
4.2. Influence of Different Objectives on Carbon Footprint Emission
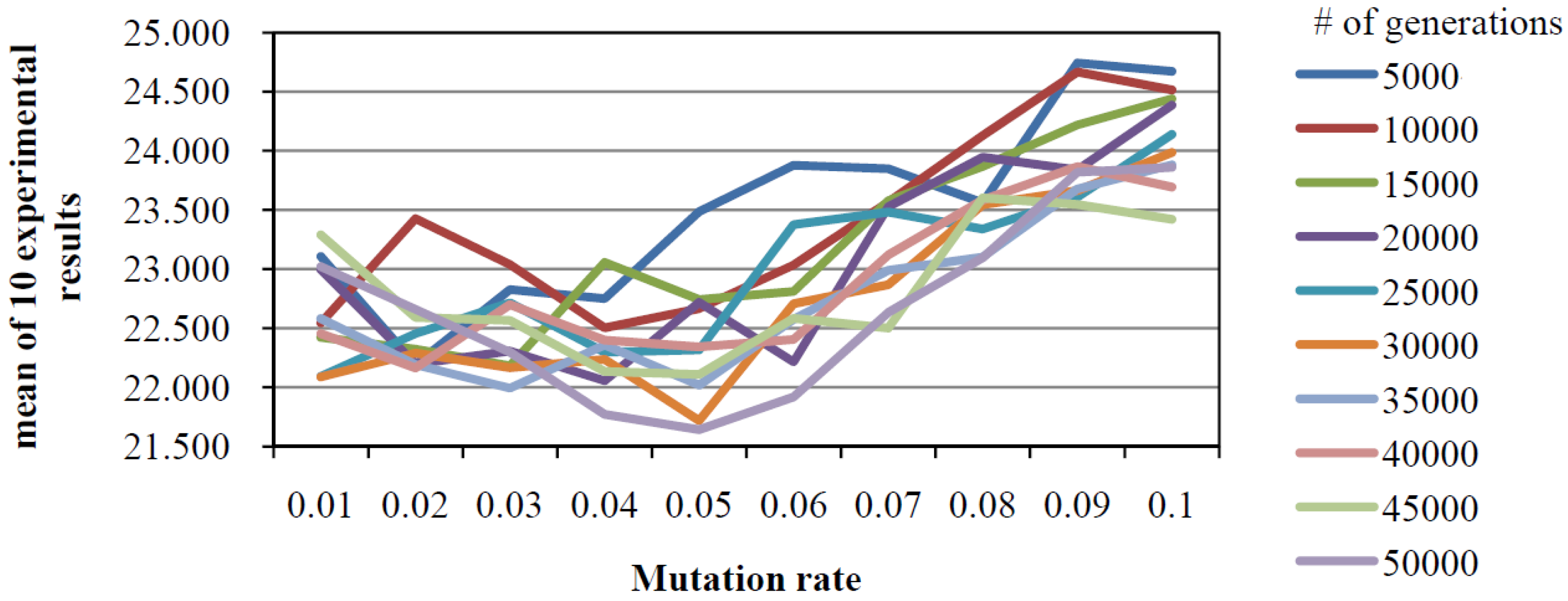
4.2.1. Experimental Results
| Objective | Minimum Carbon Footprint | Minimum Routing Time | Minimum Routing Distance | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Times | Carbon Footprint (kg) | Routing Time (minutes) | Routing Distance (km) | Carbon Footprint (kg) | Routing Time (minutes) | Routing Distance (km) | Carbon Footprint (kg) | Routing Time (minutes) | Routing Distance (km) |
| 1 | 201.39 | 3522.89 | 3466.02 | 221.64 | 3118.71 | 3286.00 | 222.70 | 3045.60 | 3162.49 |
| 2 | 202.85 | 3496.71 | 3454.11 | 210.79 | 2984.85 | 3124.42 | 213.57 | 3121.18 | 3196.92 |
| 3 | 197.75 | 3440.53 | 3385.34 | 240.77 | 3095.69 | 3329.09 | 201.78 | 3217.58 | 3236.93 |
| 4 | 198.05 | 3415.39 | 3355.70 | 224.88 | 3019.47 | 3173.51 | 213.09 | 3215.16 | 3290.20 |
| 5 | 203.92 | 3552.83 | 3498.39 | 233.80 | 3093.27 | 3291.10 | 209.70 | 3249.87 | 3278.01 |
| 6 | 198.69 | 3421.67 | 3363.89 | 231.07 | 3015.33 | 3200.99 | 208.12 | 3147.69 | 3210.50 |
| 7 | 203.42 | 3494.83 | 3484.16 | 219.76 | 3123.51 | 3256.96 | 218.14 | 3156.72 | 3228.00 |
| 8 | 198.72 | 3480.55 | 3409.40 | 236.94 | 3089.65 | 3293.46 | 225.73 | 3141.88 | 3257.11 |
| 9 | 203.53 | 3358.02 | 3353.18 | 249.57 | 3142.63 | 3378.40 | 224.07 | 3125.42 | 3235.01 |
| 10 | 187.91 | 3194.74 | 3130.70 | 231.80 | 3136.67 | 3349.25 | 217.34 | 3092.43 | 3185.39 |
| Average | 199.62 | 3437.82 | 3390.09 | 230.10 | 3081.98 | 3268.32 | 215.42 | 3151.35 | 3228.06 |
| Standard deviation | 4.79 | 102.87 | 106.12 | 11.23 | 55.68 | 80.40 | 7.65 | 61.94 | 40.45 |
4.2.2. Comparison of Results Obtained with and without Alternative Path Selection Considerations
| Instance | c20-3 | c50-3 | c100-3 | c20-5 | c50-5 | c100-5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Route | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No |
| 1 | 22.53 | 22.93 | 82.51 | 89.51 | 195.82 | 202.29 | 21.30 | 23.80 | 83.00 | 88.07 | 201.39 | 212.50 |
| 2 | 20.53 | 23.27 | 80.11 | 90.28 | 193.65 | 206.02 | 20.00 | 23.53 | 84.56 | 91.24 | 202.85 | 210.07 |
| 3 | 21.90 | 24.18 | 84.32 | 87.23 | 196.88 | 207.01 | 20.70 | 23.81 | 84.23 | 87.15 | 197.75 | 210.66 |
| 4 | 21.63 | 24.85 | 82.77 | 85.62 | 197.28 | 207.64 | 20.48 | 22.40 | 79.64 | 89.66 | 198.05 | 212.05 |
| 5 | 22.66 | 23.62 | 83.07 | 88.28 | 197.74 | 207.53 | 20.86 | 24.51 | 82.23 | 89.99 | 203.92 | 210.04 |
| 6 | 20.48 | 25.29 | 83.56 | 85.97 | 196.42 | 208.03 | 19.95 | 22.36 | 80.30 | 88.96 | 198.69 | 209.65 |
| 7 | 22.01 | 24.04 | 82.32 | 90.34 | 196.82 | 207.68 | 21.81 | 22.87 | 83.85 | 91.33 | 203.42 | 203.56 |
| 8 | 22.83 | 25.73 | 82.84 | 89.35 | 199.21 | 210.20 | 20.87 | 23.20 | 86.17 | 88.93 | 198.72 | 208.24 |
| 9 | 21.26 | 24.10 | 79.85 | 88.11 | 192.69 | 204.05 | 21.82 | 21.96 | 83.44 | 90.15 | 203.53 | 210.41 |
| 10 | 21.56 | 24.20 | 79.28 | 87.71 | 197.23 | 201.44 | 21.70 | 22.77 | 81.13 | 91.70 | 187.91 | 211.31 |
| Average | 21.74 | 24.22 | 82.06 | 88.24 | 196.37 | 206.19 | 20.95 | 23.12 | 82.86 | 89.72 | 199.62 | 209.85 |
| Standard deviation | 0.82 | 0.87 | 1.71 | 1.66 | 1.92 | 2.76 | 0.70 | 0.79 | 2.04 | 1.48 | 4.79 | 2.52 |
4.2.3. Analysis of the Experimental Results Parameters for All Sample Problems
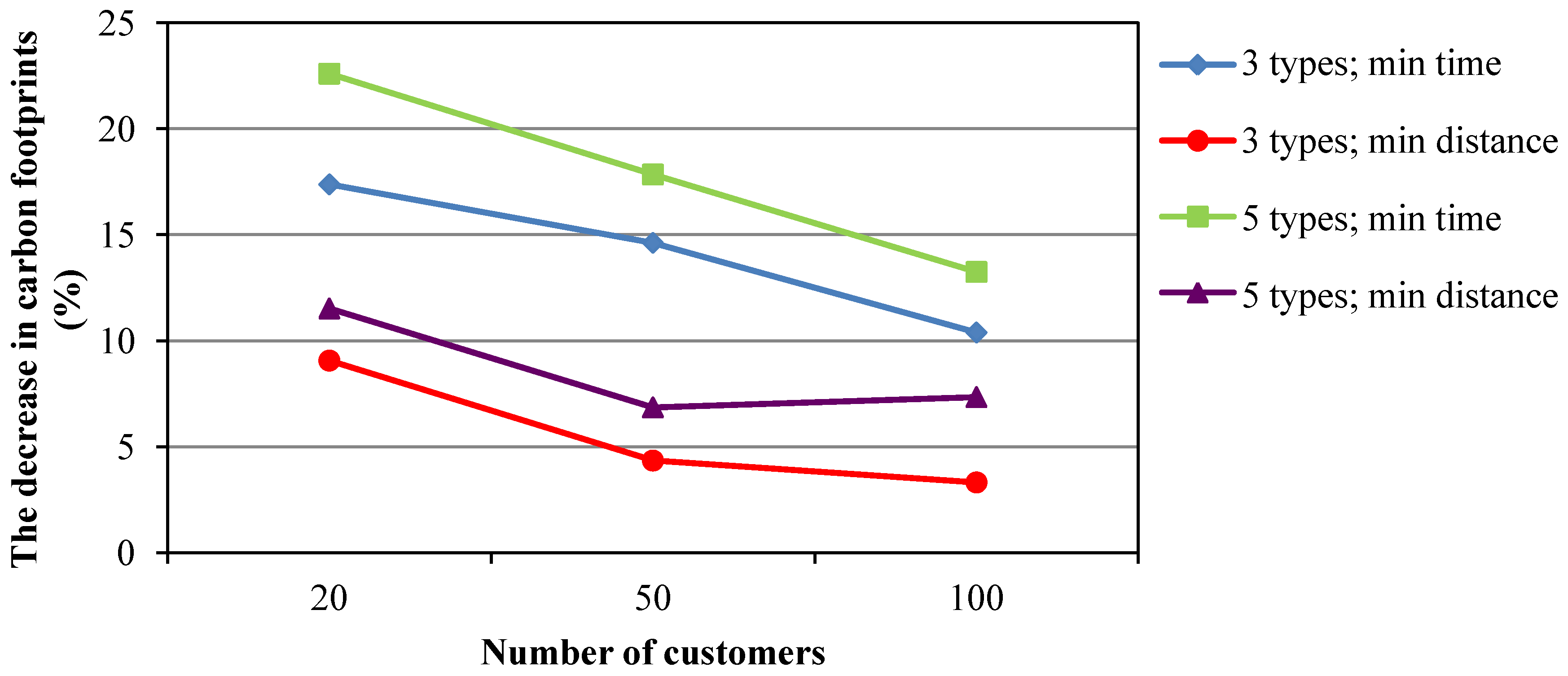
4.2.4. Analysis of the Decreases in the Carbon Footprint Results for All Sample Problems
| Problem Instance | Performance | Using the Objective of Minimal Carbon Footprint | Comparison to the Results with Objective of Minimal Routing Time | Comparison to the Results with Objective of Minimal Routing Distance | ||
|---|---|---|---|---|---|---|
| Mean | Mean | Decrease (%) | Mean | Decrease (%) | ||
| c20-3 | Carbon footprint (kg) | 21.74 | 26.31 | 17.38 | 23.91 | 9.06 |
| Routing time (min) | 564.09 | 484.47 | 16.43 | 513.84 | −9.78 | |
| Routing distance (km) | 465.82 | 454.27 | −2.54 | 445.96 | −4.45 | |
| c50-3 | Carbon footprint (kg) | 82.06 | 96.11 | 14.62 | 85.79 | 4.34 |
| Routing time (min) | 1580.70 | 1439.02 | −9.85 | 1461.75 | −8.14 | |
| Routing distance (km) | 1480.49 | 1476.98 | −0.24 | 1426.82 | −3.76 | |
| c100-3 | Carbon footprint (kg) | 196.37 | 219.13 | 10.39 | 203.09 | 3.31 |
| Routing time (min) | 3441.72 | 3129.40 | −9.98 | 3222.66 | −6.80 | |
| Routing distance (km) | 3401.05 | 3288.08 | −3.44 | 3254.69 | −4.50 | |
| c20-5 | Carbon footprint (kg ) | 20.95 | 27.07 | 22.60 | 23.68 | 11.52 |
| Routing time (min) | 538.85 | 461.29 | −16.81 | 482.37 | −11.71 | |
| Routing distance (km) | 439.12 | 433.76 | −1.23 | 418.20 | −5.00 | |
| c50-5 | Carbon footprint (kg ) | 82.86 | 100.85 | 17.84 | 88.95 | 6.85 |
| Routing time (min) | 1575.54 | 1387.64 | −13.54 | 1433.68 | −9.89 | |
| Routing distance (km) | 1477.79 | 1441.01 | −2.55 | 1398.84 | −5.64 | |
| c100-5 | Carbon footprint (kg) | 199.62 | 230.10 | 13.25 | 215.42 | 7.33 |
| Routing time (min) | 3437.82 | 3081.98 | −11.55 | 3151.35 | −9.09 | |
| Routing distance (km) | 3390.09 | 3268.32 | −3.73 | 3228.06 | −5.02 | |
4.2.5. Analysis of the Computational Time Required for Executing our GA

5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IPCC. Climate Change 2007: Synthesis Report; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2007; pp. 45–54. [Google Scholar]
- Wiedmann, T.; Minx, J. A Definition of ‘Carbon Footprint’. In Ecological Economics Research Trends; Pertsova, C.C., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2008; Chapter 1; pp. 1–11. [Google Scholar]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The pollution-routing problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Golden, B.L.; Assad, A.; Levy, L; Gheysens, F.G. The fleet size and mix vehicle routing problem. Comput. Oper. Res. 1984, 11, 49–66. [Google Scholar] [CrossRef]
- Ichoua, S.; Gendreau, M.; Potvin, J.Y. Vehicle dispatching with time-dependent travel times. Eur. J. Oper. Res. 2003, 144, 379–396. [Google Scholar] [CrossRef]
- Garaix, T.; Artigues, C.; Feillet, D.; Josselin, D. Vehicle routing problems with alternative paths: An application to on-demand transportation. Eur. J. Oper. Res. 2010, 204, 62–75. [Google Scholar] [CrossRef]
- Coe, E. Average Carbon Dioxide Emissions Resulting from Gasoline and Diesel Fuel, Technical Report; United States Environmental Protection Agency: Washington, DC, USA, 2005. [Google Scholar]
- Taillard, E.D. A heuristic column generation method for the heterogeneous fleet. RAIRO Oper. Res. Rech. Opér. 1999, 33, 1–14. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Rinnooy Kan, A.H.G. Complexity of vehicle routing and scheduling problems. Networks 1981, 11, 221–227. [Google Scholar] [CrossRef]
- Fisher, M.L.; Jaikumar, R. Ageneralized assignment heuristic for vehicle routing. Networks 1981, 11, 109–124. [Google Scholar] [CrossRef]
- Bowerman, R.L.; Calamai, P.H.; Hall, G.B. Thespacefilling curve with optimal partitioning heuristic for the vehicle routing problem. Eur. J. Oper. Res. 1994, 76, 128–142. [Google Scholar] [CrossRef]
- Cacchiani, V.; Hemmelmayr, V.C.; Tricoire, F. A set-covering based heuristic algorithm for the periodic vehicle routing problem. Discret. Appl. Math. 2014, 163, 53–64. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J. Scheduling of vehicles from a central depot to a number of delivery points. Oper. Res. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Rosenkrantz, D.; Sterns, R.; Lewis, P. An analysis of several heuristics for the traveling salesman problem. SIAM J. Comput. 1977, 6, 563–581. [Google Scholar] [CrossRef]
- Lin, S. Computer solutions of the traveling salesman problem. Bell Syst. Tech. J. 1965, 44, 2245–2269. [Google Scholar] [CrossRef]
- Baker, B.M.; Sheasby, J. Extensions to the generalized assignment heuristic for vehicle routing. Eur. J. Oper. Res. 1999, 119, 147–157. [Google Scholar] [CrossRef]
- Kontoravdis, G.; Bard, J. Improved Heuristics for the Vehicle Routing Problem with Time Windows; Working Paper; Operations Research Group, Department of Mechanical Engineering, The University of Texas: Austin, TX, USA, 1992. [Google Scholar]
- Potvin, J.; Rousseau, J. An exchange heuristic for routing problems with time windows. J. Oper. Res. Soc. 1995, 46, 1433–1446. [Google Scholar] [CrossRef]
- Russel, R.A. Hybrid heuristics for the vehicle routing problem with time windows. Transp. Sci. 1995, 29, 156–166. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial System; The University of Michigan Press: Ann Arbor, MI, 1975. [Google Scholar]
- Osman, I.H. Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem. Ann. Oper. Res. 1993, 41, 421–451. [Google Scholar] [CrossRef]
- Van Breedam, A. Comparing descent heuristics and metaheuristics for the vehicle routing problem. Comput. Oper. Res. 1995, 28, 289–315. [Google Scholar] [CrossRef]
- Tan, K.C.; Lee, L.H.; Ou, K. Artificial intelligence heuristics in solving vehicle routing problems with time window constraints. Eng. Appl. Artif. Intell. 2001, 14, 825–837. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, W.-Y.; Lin, C.-C.; Chiu, C.-R.; Tsao, Y.-S.; Wang, Q. Minimizing the Carbon Footprint for the Time-Dependent Heterogeneous-Fleet Vehicle Routing Problem with Alternative Paths. Sustainability 2014, 6, 4658-4684. https://doi.org/10.3390/su6074658
Liu W-Y, Lin C-C, Chiu C-R, Tsao Y-S, Wang Q. Minimizing the Carbon Footprint for the Time-Dependent Heterogeneous-Fleet Vehicle Routing Problem with Alternative Paths. Sustainability. 2014; 6(7):4658-4684. https://doi.org/10.3390/su6074658
Chicago/Turabian StyleLiu, Wan-Yu, Chun-Cheng Lin, Ching-Ren Chiu, You-Song Tsao, and Qunwei Wang. 2014. "Minimizing the Carbon Footprint for the Time-Dependent Heterogeneous-Fleet Vehicle Routing Problem with Alternative Paths" Sustainability 6, no. 7: 4658-4684. https://doi.org/10.3390/su6074658
APA StyleLiu, W.-Y., Lin, C.-C., Chiu, C.-R., Tsao, Y.-S., & Wang, Q. (2014). Minimizing the Carbon Footprint for the Time-Dependent Heterogeneous-Fleet Vehicle Routing Problem with Alternative Paths. Sustainability, 6(7), 4658-4684. https://doi.org/10.3390/su6074658