Abstract
In this paper, we present a distributional impact analysis of climate change policies envisaged or implemented to reduce greenhouse gas emissions in Senegal. We consider policies implemented in developed countries and their impact on a developing country. Moreover, we simulate the diminishing productivity of agricultural land as a potential result of climate change (CC) for Senegal. This country is exposed to the direct consequences of CC and is vulnerable to changes in world prices of energy, given its lack of substitution capacity. Past researches have shown that countries with this profile will bear the greatest burden of CC and its mitigation policies. Our results reveal slight increases in poverty when the world price of fossil fuels increases and the negative impact is further amplified with decreases in land productivity. However, subsidizing electricity consumption to protect consumers from world price increases in fossil fuels is shown to provide a weak cushion to poverty increase.
1. Introduction
Policies to reduce global warming are being implemented in many countries that signed the Kyoto Protocol. Other countries are also implementing or considering policies to reduce greenhouse gas emissions. Most of the reforms proposed to achieve the goals of the Kyoto Protocol or reducing greenhouse gasses (GHG) imply internalizing externalities. These policies could directly or indirectly contribute to increasing the production costs of goods that play a part in global warming, as well as the prices of these goods. This increase in cost and price should contribute to modifying consumer and producer behavior, thereby allowing for a reduction in GHG. Moreover, the change in price of these goods relative to other goods produced in the economy will significantly modify factor allocation in the economy and household welfare through a change in consumer prices and factor payments. If these impacts are negative and affect large portions of vulnerable populations, the implementation of environmental policies to reduce GHG could come into conflict with the development goals if appropriate measures are not taken to compensate the losers in this process. In this context and in light of the marginal contribution of some developing countries to GHG, many will chose not to implement GHG reduction policies. However, these countries will not be isolated from the policies implemented in developed countries and will be the first ones affected by global warming, with significant losses in agriculture productivity.
The microeconomic burden of these measures will depend on many factors. Among the important factors are natural resource endowment, factor endowment, structural characteristics of the economies, consumption, and trade patterns of the country. Boccanfuso et al. [1] provide a review of characteristics that will play a role in determining the distributional impact of GHG reduction policies in developing countries. The impact of the policies will not be confined to the country of application. If a country with a large economy or if many countries simultaneously implement similar policies or policies that have the same effect on prices and supply, the impact will be felt on world markets of goods directly or indirectly concerned by the policy. Hence, world demand, supply, and prices will or could be significantly affected.
Most developing countries have been mostly observers with regard to the implementation of policies to tackle global warming. The Kyoto Protocol does not require these countries to contribute to reducing greenhouse gasses. However, they are not observers when it comes to the impact of these reforms. Considering that the sectors most strongly affected by greenhouse gas emission reduction policies are the energy, natural resources, and agricultural sectors and that many developing countries’ economies depend on food and energy imports and export mostly agricultural goods and natural resources, we can assume that they are extremely vulnerable to significant changes in world markets for these goods. In addition, poor and vulnerable groups in developing countries are mostly employed in the agricultural sectors, and agricultural goods constitute a large portion of their total expenditure. Moreover, we are observing increased concern as stated by von Braun [2] and Doornbosch and Steenblik [3] over the negative impact of increasing prices for food staples on the welfare of vulnerable groups in developing countries. Important non-governmental organizations such as OXFAM and Friends of the Earth have taken strong positions against the promotion of biofuels, as their consequences on poor populations of developing countries could be disastrous [4].
One of the most powerful methodologies for analyzing the impact of environmental policies on welfare in order to clearly identify the winners and losers of such reforms is the computable general equilibrium (CGE) model inter alia [5,6,7,8]. Bergman’s [6] pioneering work for analyzing environmental policies in a CGE context illustrated the importance of capturing general equilibrium effects and distinguishing the winners and losers of such policies, even if microeconomic distributional impact is not dealt with in the paper. Winters et al. [5] provide an interesting comparative analysis of economic and welfare aspects of CC via anticipated average yield and price shocks to agriculture on developing countries. Three archetype models representing an Asian, an African, and a Latin American country show that these countries suffer on an aggregate basis, and low substitution possibilities for alternative energy consumption in Africa leads to the worst effects. Once again, this analysis focuses on aggregates and not on micro distributional issues. In a more recent work, O’Ryan et al. [9] analyze national CC mitigation policies in Chile. More specifically they analyze the direct and indirect effects of imposing environmental taxes in Chile for particulate matter (PM-10) as well as taxes on fuels. They show that policies that reduce GHG by 50% can have a significant macroeconomic distributional impact. Dessus and O’Connor [10] use a CGE model both to analyze the reduction of CO2 emissions and health benefits in Chile, and compare with the carbon abatement cost to determine the “no regrets’ CO2 reduction. They find that Chile could reduce their CO2 emissions by 20% from the 2010 baseline with no net welfare lost. Timilsina and Shrestha [11] apply a CGE model to Thailand’s economy and analyze various carbon taxes to reduce GHG and measures about which revenue recycling scheme produces the weakest type of welfare lost.
On the other hand, since the late 1990s a significant body of literature has emerged concerning CGE modeling for poverty and distributional analysis. This line of research includes Decaluwé et al. [12] and Cogneau and Robilliard [13], among others. For an interesting review, the reader can consult Hertel and Reimer [14]. These papers have been followed by a large number of applications. Many analysts have investigated trade reforms (see [14]) and more recently price reforms in utilities with these macro-micro CGE methodologies (see [15]).
Recently, a few authors have combined the two approaches and investigated the poverty and distributional impact of CC using CGE models. We aim to analyze the poverty and distributional impact of CC policies in our application albeit we combine CC policies with the effect of climate change. Let us highlight some of these papers. Most of these applications use dynamic models and have a key objective to measure the loss in growth over the duration of simulation linked to CC. Our objective is not to quantify the growth impact of CC policies of CC as opposed to these authors. First, Thurlow et al. [16] analyze the impact of historical climate variability and future anthropogenic climate change via agricultural productivity changes on growth and poverty in Zambia. Their recursive dynamic model is run over a 10 year period timeframe. They use a household database to compute poverty impact. To achieve this goal, they import changes in real consumption of 15 representative households of the CGE model in a household database applying them to households with the same characteristics. This approach for poverty analysis in CGE modeling context has been strongly criticized by Savard [17] in which he illustrates that poverty changes measured with this approach can lead to biased results. Thurlow et al. [16] find that CC will have a negative impact on growth and that poverty will increase by 1.55% to 7.23% depending on the scenario analyzed.
Ahmed et al. [18] analyze the social impact of CC in developing countries (16 countries) by using the global model known as GTAP model. They use the recursive dynamic model over a 30 year time frame. Their simulations are drawn from a global climate model by designing three distinct agricultural productivity stressors, namely average precipitations, average number of dry days and heat waves. These authors use a micro-simulation model in which household consumption is modeled with an AIDADS demand system. Using such a demand system with a top down approach will lead to important aggregation error that will bias poverty analysis as illustrated in [19]. In this paper Savard [19], illustrates that aggregation of micro household behavior is not equivalent to the demand system included in the CGE model. In order to circumvent this problem, one needs to include the micro-households directly in the CGE model. Only six of the sixteen countries analyzed are part of the least developed countries (LDC) and only five are in Africa (from Southern and Eastern Africa). In the LDC’s, the range of poverty changes for extreme climate scenarios are quite large ranging from a reduction in poverty for agricultural households in Uganda of −0.1 to 110.5% increase in poverty for the urban labor households in Malawi. In general, urban households face much stronger increases in poverty compared to rural households.
Ahmed et al. [20] use a dynamic CGE model to examine the impact of greater volatility of key climate variables on agricultural productivity, and the subsequent effect on poverty and growth in Tanzania. Using a GTAP framework for the Tanzanian economy, they find a range for poverty impact from an increase of 0.26% to an increase of 3.4% in the extreme case scenario over a 30 year time range. They obtained increases in poverty up to 2% over the period in the extreme case scenarios representing up to 700,000 people in Tanzania. They use the same approach as in [19].
Gebreegziabher et al. [21] use a recursive dynamic model to measure the impact on growth and poverty over a 50 year time range. The impacts on agriculture are based on results from a Ricardian model where current and future agricultural productions are analyzed as a function of temperature and precipitation. These authors only analyze change in per capita income for four groups of households classified as rural poor, rural non poor, urban poor and urban non poor. Stricto sensu, they do not analyze poverty changes but only the change in real income of four representative households. With this approach they cannot capture poverty changes for the population as a whole or for parts of the population as is explained in Bourguignon and Savard [22].
All of these papers use a top down approach (also referred to as sequential CGE micro-simulation approach (CGE-SMS)) that will be reviewed below. This approach can lead to problems for measuring poverty changes with the CGE model. An extensive discussion can be found in [22] and in Boeters and Savard [23] on this issue. Moreover, all of these authors assume that there is no dynamic change in the factor endowments of the households in the household data base. This also leads to a strong hypothesis of a uniform distribution of new production factors generated by the growth in the model. To respond to these problems, we applied the CGE-SMS approach but we insured that our functions and data in the microsimulation model were fully coherent with the ones in the CGE model to minimize the aggregation error discussed in [22] and we used a static framework. Given that we do not aim to measure the growth impact of CC changes and CC policies, this reduces the interest in using a dynamic CGE model. The static model will allow capturing of the mechanisms at play between CC and CC policies and poverty changes. Moreover, we extend further from all the reviewed papers by performing a pro-poor growth analysis.
We use a static framework for many reasons. First, since our objective is to sketch out mechanisms it is easier to highlight these with a static framework. Second, one can capture the impact of a policy or external shock with a static model. In many applications of the recursive dynamic model, one only amplifies results obtained after the first run of the model. This type of result can be modified by imposing ad hoc growth hypothesis on certain variables. Our last and most important reason for not using the dynamic approach is linked to difficulties in updating micro-simulation models in a coherent fashion with a CGE module in a dynamic framework. The few applications that attempted to do this imposed a proportional change in the distribution of factors at the end of the simulations. This type of ad hoc approach makes such application irrelevant. Hence, we make the assumption that over the period of our simulation the structure of our micro-simulation model is held constant. In this context of our CC policy simulation (to be discussed below), we are in the strand of work proposed in [9,10,11] who also use static CGE models but in these three cases they do perform a poverty analysis.
The paper is organized as follows. The next section briefly summarizes Senegal’s characteristics in terms of climate and activities, as well as the possible effects of climate change on the country. Section 3 presents the CGE model used in the analysis. A presentation of our distributional impact analysis follows, and concluding remarks are presented in Section 5.
2. Country of Application
Senegal is located at the westernmost part of the African continent. It has a 700 km coastline and benefits from a marine current from the Atlantic Ocean. The maritime current is beneficial for agriculture on the coastline, but the country’s flat topology does not provide a barrier for the harmattan wind coming from the Sahara Desert. This wind brings hot air, dust, and droughts. The country has two main seasons: a dry season from November to May and a rainy season (wet season) from June to October. Senegal was among the countries that signed the United Nations CC agreement in Rio in 1992; the agreement was ratified in Senegal’s parliament in 1994. The country then created the Ministère de l’Environnement et de la Protection de la Nature (MEPN), from which emerged two structures: the Superior Council for the Environment and Natural Resources (CONSERE) and the National Commission for Sustainable Development (NCSD). The country is committed to producing an inventory of all GHG emitted; two such inventories have been produced for 1991–1994, and another for 1995. The MEPN has identified sectoral vulnerability and has worked on adaptation strategies for the future [24].
3. Macro-Micro CGE Model for Distributional Impact Analysis
Since the late 1990s, researchers have been increasingly using CGE in combination with micro-simulation models in developed and developing economies. The impetus for this growing body of research was the recognition of the unsuitability of the CGE representative agents approach (CGE-RA) for analyzing poverty and income distribution. The CGE-RA approach does not allow researchers to take into account within-group changes in income distribution, even though studies ([17,25], as examples) have shown that such changes can be greater than between-group inequality changes. Savard [17] compares the CGE-RA approach to a CGE micro-simulation approach (a top-down/bottom-up approach to be discussed later) and demonstrates that the results of poverty and income distribution analysis can be completely reversed by taking into account within-group distributional effects.
The CGE-RA approach divides households into groups, choosing a representative household for each group and using that representative household in the CGE model. Changes in the income of all households in each group are then inferred from the change of income of the representative household. However, as noted, ignoring within-group income redistribution can lead to misleading conclusions. A second approach, proposed by [12] and applied by [13,26], is the CGE integrated multi-household approach (CGE-IMH). This method incorporates a large number of households from a household survey (sometimes all of them) into the CGE model. The approach takes into account within-group distributional effects and has the further advantage of providing coherence between the micro and macro parts of the model.
The third approach is referred to as the CGE sequential micro-simulation (CGE-SMS) method and can be subdivided into two variants. The first one, micro-accounting, is formally presented by Chen and Ravallion [27] and has been extensively applied in recent years (among early applications of this approach are [28,29]). The second one, proposed by Bourguignon et al. [30], consists in integrating at an individual level, rich micro behaviour observed at a household level such as consumption or labor supply. The general idea of the CGE-MSS approach is that a CGE module feeds market and factor price changes into a micro-simulation household module. The main criticism levelled at this approach is that the micro-feedback effect is not fully taken into account; the question has been raised in two literature reviews of macro-micro modeling for poverty analysis ([14,31]). Bourguignon and Savard [22] perform a comparative analysis of the CGE-IMH and CGE-SMS approaches and discuss the pros and cons of each approach in detail. The CGE-SMS approach is used for our application.
Before describing the model in detail, we consider it important to highlight some potential links between CC mitigation policies and CC impact on household welfare. The policies will essentially be captured by price increases and external shocks on agricultural production. These simulations will be transmitted to household incomes through mechanisms such as variations in market prices of consumer goods and services and, more significantly, on factor payments for production factors (wages, rate of return on capital and land). Between the simulation and price changes, many interactions take place between production sectors as factors relocate. The structure of the economy, behaviour of economic actors, and rules of macroeconomic closure also play important roles. To capture the impact of these simulations on the welfare of individual households, it is important to incorporate details of the question at hand, in this case Senegal’s economic structure and the functioning of the nation’s overall economy.
The model we used is an adaptation of the model used by Boccanfuso et al. [32] to assess the reforms of the electricity sector in Senegal. In order to capture the impact of simulations on individual household welfare, we integrated a detailed view of the electricity sector, with an equally detailed view of the Senegalese economy, given the importance of the use of fossil fuels to produce electricity in Senegal. To begin, we isolated electricity production from the electricity, gas, and waters sector found in the original input/output table and in the household survey (Enquête Sénégalaise Auprès des Ménages-1-ESAM-1) data. Access to Senelec’s financial accounts allowed us to do this. The rest of this section provides a detailed presentation of the model we used.
For all sectors except electricity, total production of a sector is made up of fixed shares (Leontief shares) of value added and intermediate consumptions. Value added is a combination of composite labor and capital related using a Cobb-Douglas function. Producers minimize their cost of producing value added subject to the Cobb-Douglas function. Optimal labor demand equations are derived from this process. Labor is then decomposed into skilled and unskilled labor, with combinations of the two factors determined by the constant elasticity of the substitution function (CES). This assumption allows for sector-specific elasticity of substitution between skilled and unskilled workers [33]. We have assumed that capital is not mobile between sectors, as it is difficult in the medium term to convert capital for use in another sector in Senegal.
The structure of the electricity market is modelled with rigidities of factors (capital and labor are exogenous for this sector) and market price. Consistent with the reality faced by utilities in Senegal, we assume that the electrical utility is subject to price controls, so that the average tariff and tariff structure are givens. This implies that Senelec will produce electricity based on the constraint of a production function and that the quantity of electricity supplied will respond to the demand. Since the factors are fixed, Senelec increases its output by increasing its purchases of the intermediate inputs (such as diesel fuel) that is used to produce electricity. We modeled the Senelec in such a fashion since the productive capital in place is fixed and employment is protected by a strong labor union. For example, in a failed privatization attempt of the company in the late 1990’s, Hydro-Quebec/Elyo failed in its attempt to reduce the number of workers in the company. Moreover, the behavior of the sector over the past fifteen years in light of the major increase in oil price supports this rigid market structure for electricity production in Senegal. Sustained high prices for oil have not reduced oil dependency of Senegal over the last ten years. The output of the sector is therefore demand driven, given a fixed price on the market. In the model, production sectors consume electricity as an intermediate input, and households consume it as final consumption; these quantities are drawn from the household surveys.
Our model is of a small open economy to which world prices of imports and exports are exogenous. We used the Armington [34] hypothesis for import demand, whereby domestic consumers can substitute domestically produced goods with imports (imperfectly) according to an elasticity of substitution that is sector specific. Where local consumers have no preference between imported and local goods, we have a high elasticity of substitution; inversely, the elasticity of substitution is low where consumers prefer one good over the other. The relative price of the two goods is the other determinant of the ratio of demand for imported goods vs. demand for local goods. On the export side, producers can sell the goods on the local market or export their production, and are influenced by relative prices in each market and by their capacity to sell their produced goods on local and foreign markets. This capacity is captured by the elasticity of transformation.
We include in the model all 3,278 households covered in ESAM-1 in order to capture intra-group changes in the distribution of income. Because we use all households of the survey, there is no need to specify household groups within the CGE model. Household decomposition can be done independently of the modeling exercise after policy simulations. Our household income equations are consistent with the structure observed in ESAM-1.
The initial factor endowments for labor and capital, as well as the endogenous transfers between agents, are important determinants of how household welfare changes under various policy simulations. In this model, factor allocations are exogenous; factor payments, endogenous. The other important element is the consumption structure of households, which will be affected by the price changes in the policy simulations. As capital is fixed by sector, we generate 18 endogenous capital payments and two wages (skilled and unskilled). Dividends paid to households are also endogenous and depend on a firm’s income after taxes. Inter-agent transfers are considered endogenous. The transfers paid are a fixed share of household income and the transfers received are a fixed share of total household transfers. We use this approached proposed in [32] since we cannot construct a complete mapping of inter-household transfers for all 3278 households in the survey. Transfers of all households a pooled into a lump sum and the contribution of each household to this pool is a fixed share of the households disposable income. Receiver households will receive a fixed share of this total lump sum transfer. In general, modelers assume that intra-household transfers are fixed for simplification. However, if a household received more than half of its income from this source of revenue and the household which pays this transfer suffers a drop in income, it is unrealistic to assume that the payer household will maintain its transfers exogenous. In a context of strong decline in household income, the fixed transfer assumption would amplify the negative welfare impact on the paying household and attenuate the negative welfare impact on the receiving household. The households that are heavily dependent on those transfers turn out to be very vulnerable to fluctuations in this variable. The other sources of income are exogenous transfers from the government and the rest of the world, which are the last two agents in the model.
The income of private firms is computed as income less dividends plus government subsidies and transfers from the rest of the world. We consider Senelec as an agent in the model, apart from the government and private firms. In the baseline period, we used information from before the first privatization to reflect the situation at Senelec. In 1998, one year before the privatization and for one year after the first privatization, the government provided annual subsidies to Senelec of roughly 4 billion CFA francs [35]. In fact, it varied from 4 to 6 billion CFA francs during the period. We used 4 billion in our model for the reference period. An increase in the price of electricity would help reduce the subsidy, which is endogenous in the model and determined by the difference between the revenues generated from sales of electricity and the cost of producing it.
Government revenue is made up of taxes on producers, customs duties, individual and business income and sales taxes, and transfers from the rest of the world (budgetary assistance and other foreign grants). The government spends its budget on public goods, transfers to households, subsidies to private firms, transfers to the rest of the world, and subsidies to public utilities, such as Senelec.
The household demand system is slightly different in the two modules. This is done to capture a specific feature of household behavior in Senegal for a petroleum sub-product and because we did not have information to disaggregate the demand of households in the CGE module for this item. Let us first describe the behavior modeled in the CGE module before describing the difference in the micro-simulation household module. The demand function is derived from a utility maximization process (Cobb-Douglas utility function), which produces demand functions in which each good has a fixed value share. Households have specific marginal share parameters based on observed data in the household survey. At the micro-simulation household model level, we integrate a behavior observed for household energy consumption. Two main modes of energy are used, as is observed in household survey data. Butane/propane gas is used for cooking and heating and is the main source of energy for cooking, and the other source of energy is wood charcoal. This charcoal is produced by the forestry sector and comprises 56% of energy use [36]. An increase in the use of this source of energy contributes to a significant deforestation problem in Senegal, with a total forest degradation rate of 0.56% per year and increasing over time [37]. Hence, change in the relative price for these two goods will induce a substitution in energy consumption, given the low cost of moving from one source to the other for energy needs. The two sources of energy can also be used for heating during the coldest months of the year (January and February). We model this substitution behavior with a CES function from which we derive optimal demand for these two goods to constitute a composite energy good. The trade-off between the two goods depends on the elasticity of substitution, the relative price of the two goods, and initial shares [38]. The welfare changes are computed by taking this consumption behavior into account with the equivalent variation to capture the price effect and the income effect of each simulation. Given this substitution possibility, the household will be able to attenuate the impact of changing energy prices.
Investment demand is also specified with a fixed value share function. Our price equations are standard. We used the GDP deflator as a price index, and, as stated earlier, international prices (imports and exports) are exogenous. Accordingly, the country has no control over the prices applied on the world market. The only specific item in terms of prices, as mentioned earlier, is that prices for utility services are exogenous to reflect the observed facts.
Our model’s equilibrium conditions for non-utility markets are also standard. The commodity market is balanced by an adjustment of the market price of each commodity. The labor market is segmented and balances out with an adjustment of the nominal wage on each of the respective markets (skilled and unskilled). It is therefore possible for workers to move from one sector to another, but not from one market to another. Labor supply in each of the markets is fixed, and there is no unemployment. This assumption does not mean that we assume zero unemployment in the economy, but rather that unemployment is exogenous to the model. The price index and nominal exchange rate are fixed, and hence the current-account balance is left endogenous [39]. With regard to the equilibrium of savings and investment, total investment adjusts to the sum of the savings of all agents in the model [40].
The diagnosis of poverty and inequality changes is based on indices commonly used in macro-micro modeling. The poverty indices are the Pa index of Foster et al. [41]. Their poverty indices are additively decomposable; as such, they are useful for this type of analysis because they allow us to measure not only the proportion of the poor among the population, but also the depth and severity of poverty. For detailed information on this family of indices, see [42]. The CGE-SMS model generates post-simulation changes in welfare for each household in the model. The changes in welfare are then used to compute changes in poverty. The Gini index is used for the distributional impact analysis. Target groups are defined independently of the CGE modeling exercise, and poverty analysis can be performed for the reference period and after simulations. This approach has the advantage of taking into account price and income effects simultaneously. Finally we perform pro-poor growth analysis with four different approaches.
4. Simulation and Distributional Impact
We analyze three simulations in this paper. It is important to reiterate the objective of this paper. Our goal is not to predict the future outcome of climate change but to understand the mechanisms at play between CC policies and CC on income distribution and poverty in a developing economy namely Senegal. Hence, the size of the simulation is not critical in the process given the fact that performing a 5%, 10% or 20% change in an exogenous variable will generate the same types of mechanisms in the model. Moreover, estimations of impact of indirect CC policies and loss in agricultural productivity exhibit a very broad range of effects in the medium to long term in the literature. Our first simulation is related to CC policies applied in developed countries that would result in an increase in the price of fossil fuels. This indirect effect of CC policy could lead to an increase in energy price as cost of production of fossil fuels could increase with CC policies implemented in developed countries. Two examples of such policies would be the removal of subsidies to sectors involved in the production of fossil fuels and a second example could be the implementation of a carbon tax on producers or other policies such as cap and trade. In the literature, some assume a falling price of fossil fuels given the increase in price induced by CC policies in developed countries based on the fact that this would lead to a decrease in demand in these countries. This is a possible scenario but given the past trends in fossil fuel demand and evolution of fossil fuel prices, combined with decreasing stocks of fossil fuels (namely oil), one can reasonably assume that applying CC policies to shale oil and gas producers as well as oil producers from tar sands could lead to important increases in cost of production. Given the growing share of these two sources of fossil fuel production, a rising price of oil is also a plausible outcome. Moreover, non-conventional oil producers and conventional oil producers benefit from large implicit or explicit subsidies for production in many countries (subsidies can also be on consumption). Removing these subsidies would also lead to increase in prices. We also consider the trend observed in the world for fossil fuel demand in the last ten years in our design of simulations. During the 2001–2008 period, world prices for oil increased by close to 250% and during the same period demand increased by 10%. Moreover, according to the International Energy Outlook [43] present projections for oil price for 2017 from 2010 prices ranges from −23%, to +131% and their reference scenario. The lower bound assumes stringent CC policies, increasing supply and sluggish demand due to prolong world recession. The reference scenario assumes that all policies favoring renewable energies are maintained. For example, Bakker et al [44] are very critical of oil price levels used in IPCC assessment reports and provide a sensitivity analysis by using oil price range from 37$ per barrel to 150$ per barrel. As oil is the main input in energy production in Senegal, it will have direct and indirect effects on the welfare of Senegalese households as well as on production sectors in the economy. In the first simulation, we let the energy price be fixed and the deficit generated by the public utility that produces electricity be absorbed by the government. In the second simulation, we investigate the consequences of increasing the price of energy in Senegal in order to maintain the stability of the balance sheet of Senelec (the public utility producing energy). This simulation can also be interpreted as a CC policy implemented in Senegal where the cost of production of electricity would increase. The last simulation consists in combining simulation 2 with a reduction in agricultural productivity as a direct effect of CC in Senegal. According to MOE [36], loss of agriculture productivity will be the most important impact linked to climate change in the future in Senegal. The range of temperature increase used in Bakker et al. [44], a study supported by the Dutch assistance, uses a range of 1.5 to 4.5 °C increase in temperature over a range of 40 years. By using the lower, bound with the calculation of André and Cloppet [45] for agricultural productivity loss, we obtain a loss in productivity of 13% over 40 years. If we consider the median temperature change of 3 °C with [45] figures for 40 years we have a loss of productivity of 18%. Given that our perspective is much shorter we will use a 10% decrease in agricultural productivity of land and apply in the same fashion as in [21]. In a literature review of impact of CC on agricultural productivity in Senegal, we found a very broad range of productivity loss. In a World Bank [46] report, the present estimates for productivity loss for different crops and for different time span. For most crops, the loss in productivity is much larger than 10% for the 2050 range. For example, maize productivity will decrease by 14.4% by 2050 and cereals by 32% according to this report. Millet and sorghum have a better performance since they are better adapted for warm and dry climate. A BOAD [47] report presents estimates for losses in land productivity by 2050 ranging from 25 to 33%. It is important to keep in mind that these estimates are based on a wide range of assumptions that leads to a fair range of uncertainty. The agriculture sector is an important employer in the country (around 60%) and this is likely to have significant distributional consequences in Senegal. The simulations performed are presented in Table 1. The timeframe for our simulations are also not critical but can be interpreted as being around a 10 year span [48].

Table 1.
Simulations performed in the computable general equilibrium model (CGE).
| Description of Simulations | |
|---|---|
| Simulation 1 | A 50% increase in world price of fossil fuels with fix electricity price |
| Simulation 2 | A 50% increase in world price of fossil fuels with flexible electricity price |
| Simulation 3 | Simulation 2 with a 10% loss in agriculture land productivity |
We briefly describe the macro and sectoral results of our simulations before moving to the distributional analysis. In Table 2, we present a few macroeconomic results and in Table 3 the market price, capital payment and total output by sector as these are the variables affecting the households in the micro-simulation model.

Table 2.
Macro results of CGE Model.
| Macro results (% variations) | ||||
|---|---|---|---|---|
| Senegal | ||||
| Variables | Reference | Sim 1 | Sim 2 | Sim 3 |
| Agg. household income | 177.62 | 0.07 | −0.06 | −1.90 |
| Skilled wage | 1.00 | −0.32 | −0.46 | 0.29 |
| Unskilled wage | 0.50 | −0.24 | −0.41 | −1.02 |
| Government income | 59.41 | 0.70 | 0.58 | −2.67 |
| Firm’s income | 96.73 | 0.39 | 0.23 | −4.01 |
| Total investment | 101.12 | 2.76 | 2.66 | −6.51 |
| GDP | 213.63 | 0.01 | 0.01 | −3.00 |
| Subsidy to Senelec | 0.41 | 76.75 | 0.00 | 0.00 |
| Current account balance | 12.46 | 18.34 | 16.31 | −12.89 |

Table 3.
Sectoral results of CGE Model.
| Branches | Rental rate of capital results | Market price results | Total output | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Variations in % | Variations in % | Variations in % | |||||||
| Sim 1 | Sim 2 | Sim 3 | Sim 1 | Sim 2 | Sim 3 | Sim 1 | Sim 2 | Sim 3 | |
| Agriculture | 0.37 | 0.29 | 18.62 | 0.32 | 0.24 | 12.69 | 0.15 | 0.16 | −16.84 |
| Forestry | 1.65 | 1.55 | 3.87 | 0.87 | 0.75 | −5.33 | 0.59 | 0.61 | 1.43 |
| Livestock | 1.93 | 1.82 | −3.63 | 1.55 | 1.45 | −5.27 | 0.01 | 0.01 | −0.01 |
| Fishing | 0.00 | −0.06 | 6.15 | 1.52 | 1.37 | −10.03 | 0.19 | 0.26 | 4.52 |
| Edible oil industry | −1.89 | −1.65 | −31.39 | 0.36 | 0.25 | 6.59 | −1.00 | −0.75 | −20.09 |
| Other food industry | −0.53 | −0.61 | −1.83 | 0.83 | 0.73 | −2.50 | −0.07 | −0.05 | −0.35 |
| Mining industries | 27.43 | 26.40 | 31.13 | 46.45 | 46.04 | 46.51 | 1.80 | 1.75 | 2.04 |
| Other manufacturing | −3.13 | −3.28 | 6.64 | 0.61 | 0.57 | −1.62 | −0.71 | −0.71 | 1.69 |
| Oil industries | 58.90 | 54.62 | 64.20 | 30.04 | 29.47 | 28.47 | 28.01 | 26.29 | 30.64 |
| Construction | 1.72 | 1.51 | −12.64 | 2.40 | 2.25 | −4.46 | 0.34 | 0.33 | −2.16 |
| Hotel and Restaurants | 0.08 | −0.25 | −5.58 | 1.11 | 1.03 | −1.57 | 0.17 | 0.08 | −2.44 |
| Gas and Water | 0.11 | −16.52 | −18.21 | 11.14 | 10.83 | 9.61 | −0.73 | −0.73 | −0.80 |
| Transport | −3.51 | −3.56 | −5.47 | 1.67 | 1.55 | −1.08 | −0.93 | −0.90 | −1.34 |
| Electricity | −12.37 | 0.00 | 0.00 | 0.00 | 6.39 | 5.59 | 0.00 | 6.39 | 5.59 |
| Commerce | 0.15 | −0.06 | −30.58 | 0.52 | 0.39 | −17.55 | 0.05 | 0.04 | −3.66 |
| Other services | −0.48 | −0.66 | −1.75 | −0.16 | −0.31 | −1.41 | −0.03 | −0.03 | −0.17 |
The first two simulations produce limited impact on the aggregate household income and the last one produces a 1.9% decrease in income. The government income increases in the first two simulations since the higher price for fossil fuel prices increase the revenues from import duties since these are a function of world prices. GDP does not change significantly in the first two simulations given the fixed factor assumption but decreases by 3% in the last simulation. We note that the subsidy to Senelec increases by 76.8% to fund the fixed price of electricity but this subsidy represents half of 1% of the government budget. The unskilled wage and the skilled wage decrease for the first two simulations. This is linked inter alia to the expansion of sectors that are more capital intensive such as the mining industries, construction sector and the forestry sectors as is reflected in Table A1 in the appendix. In this table we present various shares or ratios for the different sectors represented in the model. These shares help understand the origins of variations and mechanisms at play for the three simulations. For the third simulation, the skilled wage increases and the unskilled wage decreases. The expansion of the other manufacturing sector and its relative importance in the GDP are the main factors that explain the changes in wages but the decline in production in the agricultural sector produces a downward pressure on the unskilled wage. The decrease in output of sectors that are intensive in unskilled workers (construction and transport sectors) also contribute to this effect. The total investment increases mainly through the increase in government income in the first two simulations and to a lesser extent with the increase in current account deficit. This in turn contributes to an upward pressure on market prices for sectors supplying a high proportion to investment demand. Sectors concerned here are manufacturing (28%), construction (20%) and agriculture (12%) as is shown in Table A1 in the appendix. This is an important factor putting pressure on market prices for the first two simulations. Other variables influencing total savings and hence total investment do not move as much (firm savings and aggregate household savings) and therefore do not play an important role in market price variations. In the third simulation, the government income decreases (−2.67%), the household income decreases (−1.90%) as well as the current account balance (−12.89%). All these variables push the total investment downwards and this also has a strong effect on market prices in sectors intensively supplying investment goods.
For the distributional analysis, the variations in the rental rates of capital are also a key element since capital income represents 31% of the household’s income. Once again, this ratio and others that constitute the structure of income of the aggregate household is presented in Table A2 of the appendix. Moreover, many poor households are active in agriculture, commerce and other service sectors and therefore these sectors play an important role for the distributional analysis. For the agricultural sector, the increase in price of fossil fuel (simulations 1 and 2) is positive for agriculture since very few farmers use motorized tractors for production. The commerce sector benefits for the first simulation and experience a slight decrease of simulation 2. The commerce sector variation is influenced by the agricultural sector and other manufacturing sector performance since both consume a large share of commerce as an intermediate input (around 30% for the two sectors). In the service sector (other services), the rental rate of capital decreases for the three simulations. This effect is driven by the reduction in intermediate input demand by other sectors (it represents 52% of the total demand). Overall, the last simulation is the one producing the strongest changes in rental rate of capital. Interestingly, agriculture supply is reduced and therefore this increases the market price of this good as well as its rental rate of capital. On the other hand, the commerce sector faces a strong drop in market price and rental rate of capital. This is directly linked with the fact that the agricultural sector is the largest consumer of this service (as an intermediate input) and the drop in agricultural production produces a strong reduction in demand for the commercial services and hence the drop in the two prices (rental rate of capital and market price). As for market prices, the first simulation produces upward movements on most prices but only slight price increases for goods consumed by poor households (agriculture, fishing, food industries and other services). For the second simulation where the price of electricity is flexible, we have weaker price increases for most goods and electricity price increases by 6.4%. In the last simulation, the prices for food industries, fishing, other services and transport prices go down. These are all goods and services consumed by poor households in the country. The market price and factor payment variations play a key role in the change in welfare of individual households in the model as we stated previously. We follow our brief macro and sectoral analysis with this distributional impact analysis.
We present our results for the national level but also divide the population into three sub-groups, namely the Dakar households, other urban households, and rural households. The results of our poverty analysis are presented in Table 4, Table 5, Table 6, Table 7.

Table 4.
Poverty and inequality analysis for Senegal.
| Poverty headcount (FGT0) | Depth of poverty (FGT1) | Severity of poverty (FGT2) | Inequality (Gini index) | ||
|---|---|---|---|---|---|
| Senegal | Reference | 0.6141 | 0.2738 | 0.1537 | 0.4825 |
| Sim 1 | 0.6152 | 0.2742 | 0.1540 | 0.4824 | |
| ∆% | 0.18% | 0.16% * | 0.18% * | −0.03% * | |
| Sim 2 | 0.6154 | 0.2744 | 0.1542 | 0.4824 | |
| ∆% | 0.21% | 0.23% * | 0.28% * | −0.03% * | |
| Sim 3 | 0.6264 | 0.2827 | 0.1598 | 0.4854 | |
| ∆% | 2.00% * | 3.27% * | 3.94% * | 0.58% * |
* Significant results at the 5% rejection level are presented in italic character in the table with an *.
First, at national level, the first two simulations produce the expected results insofar as the increases in world prices of fossil fuels and increase in price of electricity generate an increase in poverty. However, the impact is relatively small given the scale of the simulations performed. The first explanation for these results is that electricity and fossil fuels are not a major staple in the Senegalese poor households’ consumption basket. In fact, these two goods represent less than 3% of the total expenditure on goods and services for households. Hence, the households are not directly affected by these two price changes. The impact on household transits essentially through indirect effects such as changes in factor payments and changes in prices of other goods. As for the poverty changes, inequality is barely modified by the first two simulations, although these changes are significant. We observe a very slight reduction in inequality. Given the small size of the changes, we could say that the simulations have little impact on inequality in Senegal. On the other hand, the reduction in land productivity has a stronger distributional impact. This is observed by an increase of the three poverty indices with the severity index increasing most (3.94%). In this case, we also have an increase in inequality where the poorest households are found in the rural areas and this simulation affects them the most. It is important to note that the reduction in land productivity is accompanied by a relatively strong increase in factor payment for land, as it becomes relatively scarce compared to labor and given the reduction in supply of agricultural goods on the market. Let us see how the national results compare with the regional division. Results for Dakar are found in Table 5 below:

Table 5.
Poverty and inequality analysis for Dakar.
| Poverty headcount (FGT0) | Depth of poverty (FGT1) | Severity of poverty (FGT2) | Inequality (Gini index) | ||
|---|---|---|---|---|---|
| Dakar | Reference | 0.4970 | 0.2148 | 0.1201 | 0.4786 |
| Sim 1 | 0.4981 | 0.2155 | 0.1206 | 0.4787 | |
| ∆% | 0.223% | 0.33% * | 0.41% * | 0.03% * | |
| Sim 2 | 0.4981 | 0.2158 | 0.1208 | 0.4788 | |
| ∆% | 0.23% | 0.46% * | 0.57% * | 0.04% * | |
| Sim 3 | 0.5068 | 0.2218 | 0.1256 | 0.4831 | |
| ∆% | 1.97% * | 3.29% * | 4.56% * | 0.93% * |
* Significant results at the 5% rejection level are presented in italic character in the table with an *.
We note that for simulations 1 and 2, the increase in poverty headcount is not significant in Dakar, but the depth and severity indices increase more than at the national level. This is consistent with the fact that the Dakar households are the ones consuming the most fossil fuels and electricity and are the most directly affected. In contrast with the national inequality changes, we now have a small but significant increase in inequality in Dakar. Simulation 2 reveals a stronger negative impact in Dakar compared to national results and simulation 1. We also reverse the sign of the Gini coefficient compared to the national level. For simulation 3, the negative results for poverty headcount are the same as those at the national level, but the depth and severity indices decrease more. This can be explained by the fact that urban households do not benefit from the increase in factor payment of land, but have to pay more for food staples due to the increase in market prices caused by the reduction in supply of agricultural goods. Moreover, the reduction of the unskilled wage amplifies this negative effect. For this simulation, we have a relatively strong effect on inequality, which increases by almost 1% and variations are significant. These results show that indirect general equilibrium effects play an important role, as indicated by the relatively strong negative impact in Dakar with the loss of land productivity.
In other urban centers (OUC) as shown in Table 6, the situation is somewhat different compared to Dakar for the first and second simulation. The headcount index increases but this change is insignificant. In terms of depth and severity, the increase in poverty is much smaller compared to Dakar and the national level. In the case of the Gini coefficient, it is the same as that observed at the national level. Finally, the impact of the third simulation is negative but weaker compared to the national and Dakar levels for all indices. As for the Gini coefficient, the variation is not significant. The results for the rural areas are presented in Table 7 below.

Table 6.
Poverty and inequality analysis for other urban centres (OUC).
| Poverty headcount (FGT0) | Depth of poverty (FGT1) | Severity of poverty (FGT2) | Inequality (Gini index) | ||
|---|---|---|---|---|---|
| Other Urban Centers | Reference | 0.6589 | 0.2799 | 0.151 | 0.4187 |
| Sim 1 | 0.6595 | 0.2801 | 0.1512 | 0.4186 | |
| ∆% | 0.09% | 0.07% * | 0.12% * | −0.03% * | |
| Sim 2 | 0.6595 | 0.2802 | 0.1513 | 0.4186 | |
| ∆% | 0.09% | 0.14% * | 0.20% * | −0.03% * | |
| Sim 3 | 0.6695 | 0.2879 | 0.1565 | 0.4195 | |
| ∆% | 1.61% * | 2.87% * | 3.62% * | 0.19% |
* Significant results at the 5% rejection level are presented in italic character in the table with an *.

Table 7.
Poverty and inequality analysis for rural areas.
| Poverty headcount (FGT0) | Depth of poverty (FGT1) | Severity of poverty (FGT2) | Inequality (Gini index) | ||
|---|---|---|---|---|---|
| Rural Areas | Reference | 0.6265 | 0.2788 | 0.1596 | 0.439 |
| Sim 1 | 0.6285 | 0.2798 | 0.1602 | 0.4391 | |
| ∆% | 0.31% | 0.36% * | 0.40% * | 0.01% | |
| Sim 2 | 0.6285 | 0.2802 | 0.1604 | 0.4391 | |
| ∆% | 0.31% | 0.48% * | 0.54% * | 0.02% | |
| Sim 3 | 0.6333 | 0.2939 | 0.17 | 0.4438 | |
| ∆% | 1.07% | 5.39% * | 6.55% * | 1.09% * |
* Significant results at the 5% rejection level are presented in italic character in the table with an *.
The results of the first simulation are quite interesting insofar as we have similar impact for rural households and the Dakar households and the poverty increases are higher compared to the other urban households. Similar results are observed for simulation 2. This is somewhat surprising since the rural households are not directly affected by the fuel and electricity price increases. They are indirectly affected through various mechanisms. Some of the elements contributing to this poverty increase for poor rural households are the reduction in unskilled wage and the reduction in the rental rate of capital for other services where many rural households are active. However, more importantly on the consumption side, almost all prices that constitute a large part of the consumption bundle increase. In fact the only positive element for rural households is the rental rate for land (+0.37% for simulation 1 and +0.29% for simulation 2) and given the fact that endowment of land for poor households or agricultural capital is relatively small this price increase has a limited positive impact.
The changes in inequality index are insignificant for the first two simulations. For the last simulation, the impact is negative (+1.09%) which is higher compared to other sub groups or for the national results. The rural households are the clear losers of this CC policy impact and it could be quite dramatic for this group in Senegal if this impact materializes relatively quickly with limited capacity of the poor to adapt.
5. Pro-Poor Growth Analysis
In what follows, the impact of the three simulations is described by the growth incidence curve (GIC) developed by Ravallion and Chen [49]. This curve shows the changes in real income by percentile of households before and after the simulation. We do not present all curves at the national level and for selected sub-groups, nor do we present all curves for all simulations; rather, we present a few cases with specific features. To complete the pro-poor analysis, three indices have been computed: the pro-poor growth index (PPGI) of Kakwani and Pernia [50], the poverty equivalent growth rate (PEGR) of Kakwani and Son [51], and the absolute rate of pro-poor growth of Ravallion and Chen [49] derived from the GIC. For a detailed presentation of these indices, see [52].
We start with simulation 2, at the national level. In Figure 1 above, no pro-poor or pro-rich trend can be observed. A pro-poor trend is represented by a negatively sloped GIC and a pro-rich simulation, by a positively sloped GIC. However, using the three pro-poor indices, we observe a pro-poor simulation with these three indices, although the only significant one is the PPGI index. The results for the three pro-poor indices are presented in Table A3 of the appendix.
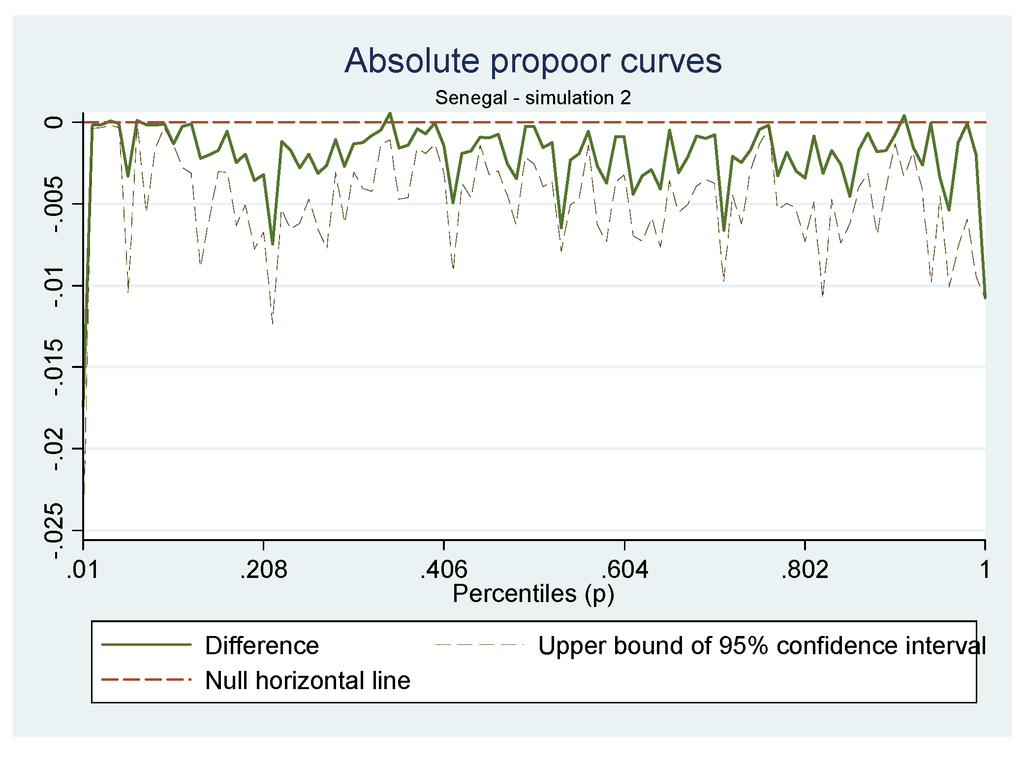
Figure 1.
GIC of Senegal for Simulation 2.
We note that the most negatively affected households are those in the poorest percentile and in the richest one. We also see that the least affected households are between the second or third percentile up to the 15th and between the 35th and 40th. For Dakar (Figure 2), we observe a similar situation with the most negatively affected households found between the 10th and 25th percentile. The group of households between the 35th and 40th percentile seem to either benefit or have little or no negative impact. In this case, our pro-poor indices lead to the conclusion of a pro-rich recession for Dakar households for two indices, but only one is significant.
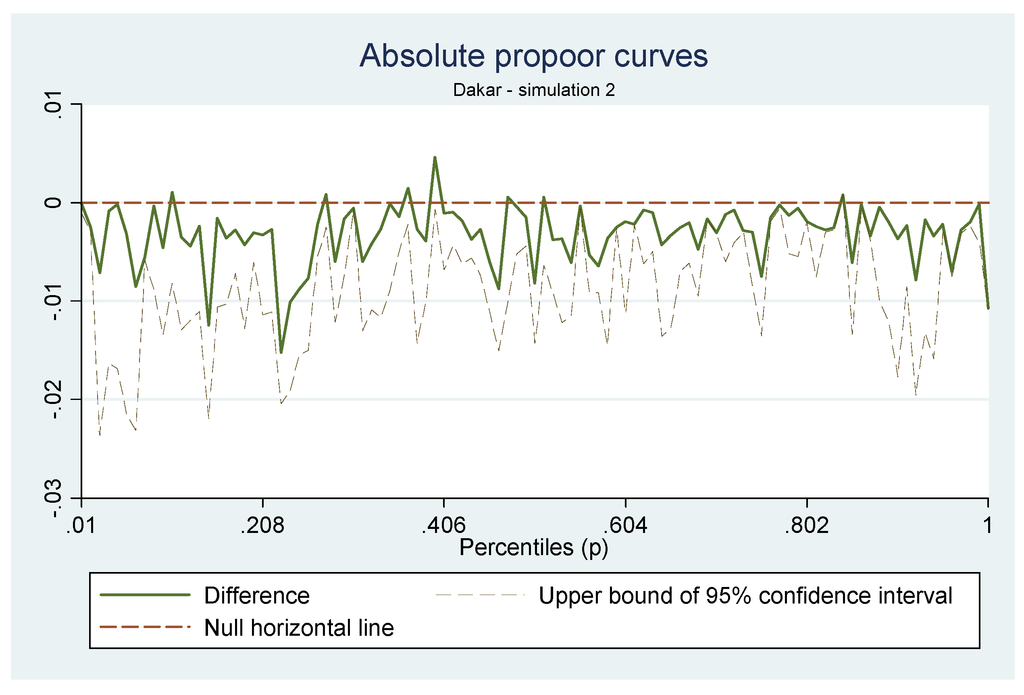
Figure 2.
GIC of Dakar households for Simulation 2.
Finally for this simulation, we see little impact on the rural households (Figure 3) with the exception of two pockets of losers, namely households between the 15th and 40th percentile and those between the 70th and 80th percentile. We observe practically no impact on the poorest 10% of households. The small impact from the GIC is confirmed by the fact that no significant results from our three pro-poor indices are obtained, although the reduction in income seems to be pro-poor.
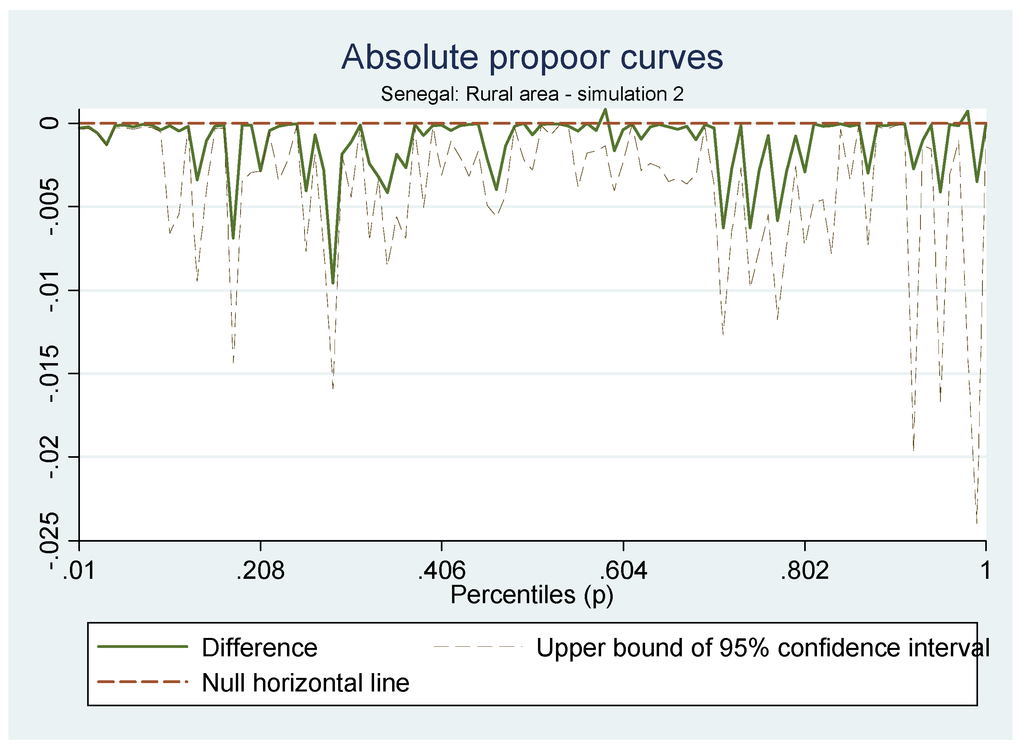
Figure 3.
GIC of rural households for Simulation 2.
In the case of simulation 3, we see stronger effects and sloping trends on some of the GIC. At the national level (Figure 4), this trend is very slight, but we see that the impact of the drop in land productivity is regressive or pro-rich. These results drawn from the GIC are confirmed by our indices. In fact, two provide pro-rich results but only one is significant. The third is pro-poor but not significant.
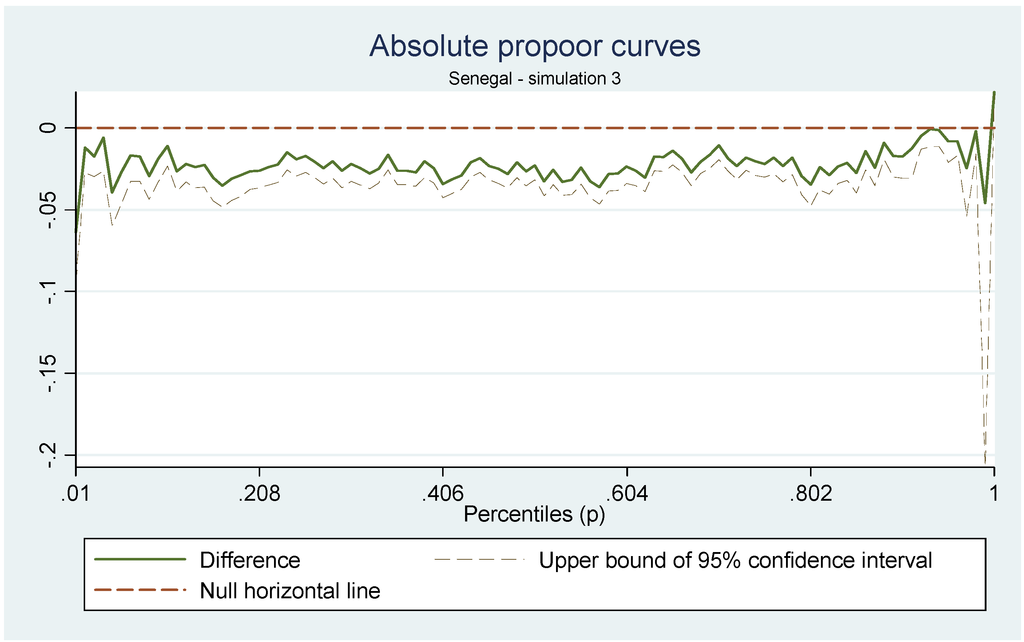
Figure 4.
GIC of Senegal for Simulation 3.
This trend is stronger when looking at sub-groups of households. For the Dakar households (Figure 5), we clearly observe a pro-rich trend with a positive slope to our GIC computed where the richest households gain from the external shock. The first three percentiles are not strongly affected but those following up to the 40th percentile are the one which suffer the most in the simulation. At the national level, the positive slope is confirmed by two indicators that suggest that the shock is pro-rich, but none are significant.
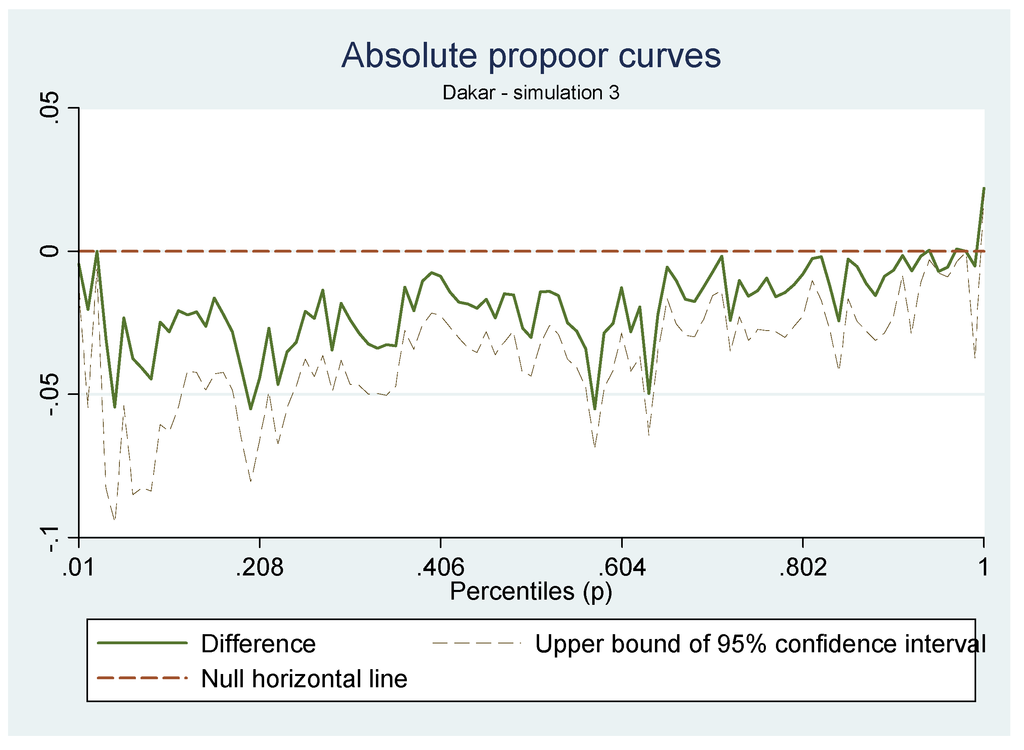
Figure 5.
GIC of Dakar households for Simulation 3.
For this simulation, the rural GIC (Figure 6) does not exhibit the same positive slope; however, we can see that winners are in the top 5 percentile while the biggest losers seem to be around the 20th percentile, but with another negative peak around the 95th percentile. In this case, as for the Dakar households, two indices identify this third simulation as being pro-rich and one index identifies it as being pro-poor, but none of the indices are significant.
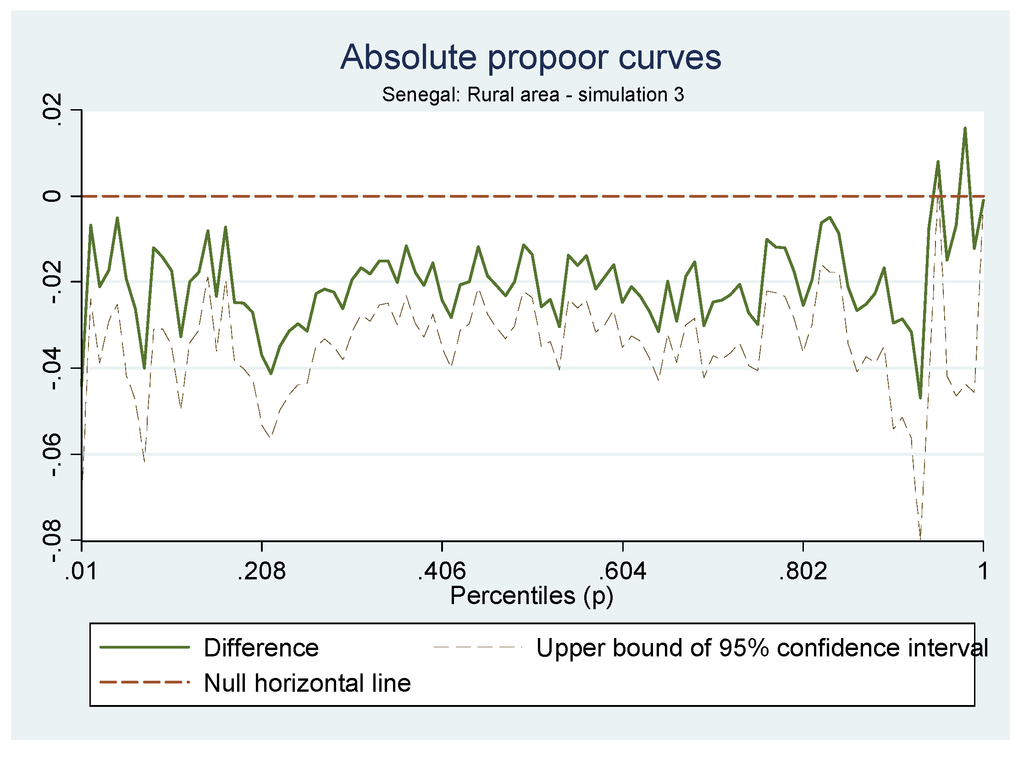
Figure 6.
GIC of rural households for Simulation 3.
This pro-poor analysis can be used as a basis to identify the main losers from CC policies or CC. This would require further investigation in the micro-simulation model to isolate losing households and find the origins of the negative impact for each of the households. It is important to highlight that 38 endogenous variables (16 goods and services market price and 22 endogenous variables on the income side) can have a positive or negative impact on micro households in the model and hence this task of identifying the origin of the negative effect would be a possible but heavy one to implement.
6. Conclusions
In this study, we applied a macro-micro CGE model to analyze possible consequences of GEG mitigation policies in developed countries, and the direct negative impact of CC on a developing country, namely Senegal. As many authors have demonstrated, this methodology is the only one available that allows the analyst to link policy reforms, fiscal policies, and world price changes to income distribution in a country. Our application contributes to the literature by providing an in depth distributional impact analysis with pro-poor measures. Our results show the importance of taking into account indirect general equilibrium effects, since some groups are not directly affected by a policy or external shock but experience negative general equilibrium effects, as we found in our simulated reduction in land productivity for the Dakar households as well as for rural households when energy prices increased. The model also revealed relatively weak negative impact of increases in the world price of fossil fuels, as this good represents a small direct or indirect share of the consumption basket for poor households in the country. More importantly, we show that maintaining electricity prices constant with a subsidy to an electric public utility provides little protection to poor households, since flexible prices generate poverty increases that are only slightly higher compared to the fixed electricity price scenario. Our negative results can in part be attributed to the rigidities of the electricity sector. An important policy response by the government would be to help to reduce these rigidities in this sector. Moreover, efforts should be made to reduce the country’s dependency on oil imports. Our results also highlight the importance of designing adaptation policies for the agricultural sector in Senegal. This sector is likely to be the most negatively impacted by CC and a large part of the population is dependent on this sector. In the design of such policy, this instrument can be useful to identify households to be targeted by interventions.
It is important to highlight that our objective was to identify the linkages between CC policies and CC impact on poverty in a developing country. Our simulations represent the potential impact of CC policies and CC in Senegal but these are based on assumptions with much uncertainty as with many other researches in the ambit. Simulations with qualitative differences would lead to different results but the mechanism at play would be the same and in this context we provide clear evidence of the complexity of these mechanisms and the importance of taking into account the intricacy of the economy in a macro-micro modeling framework for policy responses and adaptation programs in the future.
In this paper, as we have stated, we did not apply a dynamic CGE model given the difficulty in updating the structure of the micro-simulation model. Our comparative static analysis provides important and substantial information of the mechanisms at play following CC policies or agricultural productivity losses. We do not aim to measure the growth effects of CC policies of CC in this model. This would require a dynamic framework but in order to perform credible distributional impact analysis with a micro-simulation model, one needs to capture the evolution in the income and expenditure structure at the household level. This has not been done in a CGE micro-simulation context and is the object of our research agenda to extend the findings of this paper.
Appendix

Table A1.
Shares and ratios found in the SAM of Senegal.
| Ratio drawn from Social Accounting Matrix (SAM) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Branches | Ex/Xs | Ld/Kd | Ldq/Ldnq | M/Q | D/Q | Inv/IT | Cm/Q | Inv/Q | CI/Q | Cm/Ctm |
| Agriculture | 0.01 | 0.29 | 0.83 | 0.24 | 0.76 | 0.12 | 0.56 | 0.20 | 0.25 | 0.25 |
| Forestry | 0.03 | 0.45 | 0.25 | 0.10 | 0.90 | 0.04 | 0.19 | 0.70 | 0.12 | 0.01 |
| Livestock | 0.00 | 0.00 | 0.25 | 0.01 | 0.99 | 0.09 | 0.25 | 0.33 | 0.42 | 0.05 |
| Fishing | 0.18 | 2.20 | 0.75 | 0.07 | 0.93 | 0.08 | 0.02 | 0.47 | 0.51 | 0.00 |
| Edible oil industry | 0.56 | 1.54 | 0.33 | 0.39 | 0.61 | 0.00 | 0.40 | 0.03 | 0.57 | 0.02 |
| Other food industry | 0.24 | 0.38 | 0.48 | 0.16 | 0.84 | 0.17 | 0.36 | 0.29 | 0.35 | 0.14 |
| Mining industries | 0.53 | 0.08 | 0.43 | 0.62 | 0.38 | 0.02 | 0.03 | 0.18 | 0.79 | 0.00 |
| Other manufacturing | 0.34 | 0.32 | 0.85 | 0.49 | 0.51 | 0.28 | 0.22 | 0.25 | 0.53 | 0.15 |
| Oil industries | 0.48 | 1.13 | 0.21 | 0.39 | 0.61 | −0.03 | 0.12 | −0.50 | 1.38 | 0.01 |
| Construction | 0.01 | 0.21 | 0.25 | 0.00 | 1.00 | 0.20 | 0.00 | 0.99 | 0.01 | 0.00 |
| Hotel and Restaurants | 0.29 | 0.89 | 0.67 | 0.09 | 0.91 | 0.06 | 0.32 | 0.55 | 0.13 | 0.03 |
| Gas and Water | 0.28 | 0.55 | 1.82 | 0.01 | 0.99 | 0.00 | 0.41 | 0.00 | 0.59 | 0.05 |
| Transport | 0.00 | 0.39 | 0.14 | 0.19 | 0.81 | 0.00 | 0.18 | 0.00 | 0.82 | 0.03 |
| Electricity | 0.48 | 0.08 | 4.74 | 0.00 | 1.00 | 0.00 | 0.64 | 0.00 | 0.36 | 0.02 |
| Commerce | 0.00 | 0.11 | 1.50 | 0.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 |
| Other services | 0.20 | 0.17 | 0.53 | 0.12 | 0.88 | −0.04 | 0.55 | −0.06 | 0.52 | 0.23 |

Table A2.
Share of income source for aggregate household.
| Branches | Aggregate Household income shares |
|---|---|
| Skilled labor | 0.17 |
| Unskilled Labor | 0.14 |
| Capital income | 0.31 |
| Inter household tranfers | 0.16 |
| Government transfers | 0.05 |
| Dividends | 0.09 |
| Remmittences | 0.08 |

Table A3.
Pro-poor growth indices.
| SENEGAL | |||||
|---|---|---|---|---|---|
| Country | Dakar | Other urban centers | Rural area | ||
| Sim 1 | Growth rate of incomes, g | - | - | - | - |
| Ravaillion & Chen [49] - g | Pro-poor recession* | Pro-rich recession | Pro-rich recession | Pro-poor recession | |
| Kakwani & Son [51] - g | Pro-rich recession | Pro-poor recession | Pro-poor recession | Pro-poor recession | |
| Kakwani & Pernia [50] | Pro-poor recession | Pro-poor recession | Pro-rich recession | Non strictly pro-poor recession | |
| Sim 2 | Growth rate of incomes, g | - | - | - | - |
| Ravaillion & Chen [49] - g | Pro-poor recession* | Pro-rich recession* | Pro-rich recession | Pro-poor recession | |
| Kakwani & Son [51] - g | Pro-poor recession | Pro-rich recession | Pro-rich recession | Pro-poor recession | |
| Kakwani & Pernia [50] | Non strictly pro-poor recession | Pro-poor recession | Pro-poor recession | Non strictly pro-poor recession | |
| Sim 3 | Growth rate of incomes, g | - | - | - | - |
| Ravaillion & Chen [49] - g | Pro-rich recession* | Pro-rich recession | Pro-rich recession* | Pro-rich recession | |
| Kakwani & Son [51] - g | Pro-rich recession | Pro-rich recession | Pro-poor recession | Pro-rich recession | |
| Kakwani & Pernia [50] | Pro-poor recession | Pro-poor recession | Non strictly pro-poor recession | Pro-poor recession | |
Significant results at the 5% rejection level are presented with an * in the table.
References and Notes
- Boccanfuso, D.; Estache, A.; Savard, L. Intra-Country distributional impact of policies to fight climate change: A survey. J. Dev. Stud. 2011, 47, 97–117. [Google Scholar] [CrossRef]
- Von Braun, J. The World Food Situation: New Driving Forces and Required Actions; Food Policy Report No. 18; IFPRI: Washington, DC, USA, 2007. [Google Scholar]
- Doornbosch, R.; Steenblik, R. Biofuels: Is the Cure Worse Than the Disease? OECD, 2007. Available online: http://www.oecd.org/sd-roundtable/39411732.pdf (accessed on 21 May 2013).
- Oxfam, Bio-Fuelling Poverty: Why the EU renewable-fuel target may be disastrous for poor people. Available online: http://oxfamilibrary.openrepository.com/oxfam/bitstream/10546/114092/1/bn-biofuelling-poverty-011107-en.pdf (accessed on 21 May 2013).
- Winters, P.; Murgai, R.; Sadoulet, E.; de Janvry, A.; Frisvold, G. Economic and welfare impacts of climate change on developing countries. ERE 1998, 12, 1–24. [Google Scholar]
- Bergman, L. General equilibrium effects of environmental policy: A CGE-Modeling approach. Environ. Resour. Econ. 1991, 1, 43–61. [Google Scholar]
- Fullerton, D.; Heutel, G. The general equilibrium incidence of environmental taxes. J. Pub. Econ. 2007, 91, 571–591. [Google Scholar] [CrossRef]
- Araar, A.; Dissou, Y.; Duclos, J.-Y. Household Incidence of Pollution Control Policies: A Robust Welfare Analysis Using General Equilibrium Effects; Working paper CIRPEE #08–09; Université Laval: Québec, Canada, 2008. [Google Scholar]
- O’Ryan, R.; Miller, S.; de Miguel, C.J. A CGE framework to evaluate policy options for reducing air pollution emissions in Chile. Environ. Dev. Econ. 2003, 8, 285–309. [Google Scholar]
- Dessus, S.; O’Connor, D. Climate policy without tears: CGE-Based ancillary benefits estimates for chile. Environ. Resour. Econ. 2003, 25, 287–317. [Google Scholar] [CrossRef]
- Timilsina, G.R.; Shrestha, R.M. Atmospheric Stabilization of CO2 Emissions: Near-Term Reductions and Intensity-based Targets; Policy Research Working Paper Series 4352; The World Bank: Washington, DC, USA, 2007. [Google Scholar]
- Decaluwé, B.; Dumont, J.C.; Savard, L. How to Measure Poverty and Inequality in General Equilibrium Framework; Working Paper 9920; CREFA, University of Laval: Québec, Canada, 1999. [Google Scholar]
- Cogneau, D.; Robilliard, A.S. Income Distribution, Poverty and Growth in Madagascar: Micro Simulations in a General Equilibrium Framework; IFPRI TMD Discussion Paper series 61; International Food Policy Research Institute: Washington, DC, USA, 2000. [Google Scholar]
- Hertel, T.; Reimer, J. Predicting the poverty impacts of trade reform. J. Int. Trade Econ. Dev. 2005, 14, 377–405. [Google Scholar] [CrossRef]
- Boccanfuso, D.; Estache, A.; Savard, L. Impact analysis of electricity reforms in mali: A macro-micro analysis. S. Afr. J. Econ. 2009, 77, 127–147. [Google Scholar] [CrossRef]
- Thurlow, J.; Zhu, T.; Diao, X. Current climate variability and future climate change: Estimated growth and poverty impact for zambia. Rev. Dev. Econ. 2012, 16, 394–411. [Google Scholar] [CrossRef]
- Savard, L. Poverty and inequality analysis within a CGE framework: A comparative analysis of the representative agent and microsimulation approaches. Dev. Policy Rev. 2005, 23, 313–332. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Diffenbaugh, N.S.; Hertel, T.W. Climate volatility deepens poverty vulnerability in developing countries. Environ. Res. Lett. 2009, 4, 1–8. [Google Scholar]
- Savard, L. Un système de demandes AIDS dans un contexte EGC microsimulation pour l’analyse de pauvreté et des inégalités (in French); GREDI Working paper no. 04–10; Université de Sherbrooke: Sherbrooke, Canada, 2004. [Google Scholar]
- Ahmed, S.A.; Diffenbaugh, N.S.; Hertel, T.W.; Ramankutty, N.; Rios, A.R.; Rowhani, P. Climate volatility deepens poverty vulnerability in Tanzania. Global Environ. Change 2011, 21, 46–55. [Google Scholar]
- Gebreegziabher, Z.; Stage, J.; Mekonnen, A.; Alemu, A. Climate Change and the Ethiopian Economy; RFF Discussion Paper EfD 11–09; Ressources For the Future: Washington, DC, USA, 2011. [Google Scholar]
- Bourguignon, F.; Savard, L. A CGE Integrated Multi-Household Model with Segmented Labor Markets and unemployment. In The Impact of Macroeconomic Policies on Poverty and Income Distribution: Macro-Micro Evaluation Techniques and Tools; Bourguignon, F., Bussolo, M., da Silva, L.A.P., Eds.; Palgrave-Macmillan Publishers Limited: Houndmills, UK, 2008; pp. 177–211. [Google Scholar]
- Boeters, S.; Savard, L. The Labor Market in Computable General Equilibrium Models. In Handbook of Computable General Equilibrium Modeling; Dixon, P.B., Jorgenson, D.W., Eds.; Elsevier B.V.: Oxford, UK, 2013; pp. 1645–1718. [Google Scholar]
- Ministère de l’environnement et de la protection de la nature du Sénégal (MOE) (in French); Rapport sur l’état de l’environnement au Sénégal; Government of Senegal: Dakar, Sénégal, 2005.
- Huppi, M.; Ravallion, M. The sectoral structure of poverty during an adjustment period: Evidence for indonesia in the mid 1980s. World Dev. 1991, 19, 1653–1678. [Google Scholar] [CrossRef]
- Gørtz, M.; Harrison, G.; Neilsen, C.; Rutherford, T. Welfare gains of extending opening hours in Denmark; Economic working paper B0003; Darla Moore School of Business, University of South Carolina: Columbia, SC, USA, 2000. [Google Scholar]
- Chen, S.; Ravallion, M. Welfare Impacts of China’s Accession to the World Trade Organization. World Bank Econ. Rev. 2004, 18, 29–57. [Google Scholar] [CrossRef]
- Vos, R.; de Jong, N. Trade liberalization and poverty in Ecuador: A CGE macro-microsimulation analysis. Econ. Syst. Anal. 2003, 15, 211–232. [Google Scholar]
- King, D.; Handa, S. The welfare effects of balance of payments reforms: A macro-micro simulation of the cost of rent-seeking? J. Dev. Stud. 2003, 39, 101–128. [Google Scholar]
- Bourguignon, F.; Robilliard, A.S.; Robinson, S. Representative versus Real Households in the Macroeconomic Modeling of Inequality. In Frontiers in Applied General Equilibrium Modeling; Kehoe, T.J., Srinivasan, T.N., Whalley, J., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 219–254. [Google Scholar]
- Bourguignon, F.; Spadaro, A. Microsimulation as a tool for evaluating redistribution policies. J. Econ. Inequal. 2006, 4, 77–106. [Google Scholar] [CrossRef]
- Boccanfuso, D.; Estache, A.; Savard, L. Impact analysis of electricity reforms in senegal: A macro-micro analysis. J. Dev. Stud. 2009, 45, 351–375. [Google Scholar] [CrossRef]
- In our model we assume that unemployment is exogenous to the model. Assuming endogenous labor supply in a micro-simulation model requires one to estimate a micro-econometric labor supply model and no database was available for such an extension in Senegal.
- Armington, P.S. A theory of demand for products distinguished by place of production. IMF Staff Papers 1969, 16, 159–176. [Google Scholar] [CrossRef]
- Commission de Régulation du Secteur de l’Électricité du Sénégal (CRSE), Lettre de Politique de Développement du secteur de l’Energie (in French); Government of Senegal: Dakar, Sénégal, 2003.
- Ministère de l’environnement et de la protection de la nature du Sénégal (MOE), Plan d’action national pour l’adaptation aux changements climatiques (in French); Government of Senegal: Dakar, Senegal, 2006.
- Mongabay homepage. Available online: http://rainforests.mongabay.com/deforestation/2000/Senegal.htm (accessed on 12 December 2009).
- We use a relatively high elasticity of substitution of 5, but performed sensitivity analysis on this parameter and our results were robust to these changes.
- This does not mean that we assume zero unemployment in the economy, but rather that unemployment is exogenous to the model.
- We simulated the policies with other macroeconomic closures. The general trends of the results were maintained, although we observed some slight changes in results. A complete set of equations, variables, and parameters can be obtained from the authors.
- Foster, J.; Greer, J.; Thorbecke, E. A class of decomposable poverty measures. Econometrica 1984, 52, 761–766. [Google Scholar] [CrossRef]
- Ravallion, M. Poverty Comparisons; Harwood Academic Publisher: Reading, UK, 1994. [Google Scholar]
- International Energy Outlook, Annual Energy Outlook 2012; U.S. Energy Information Administration: Washington, DC, USA, 2012.
- Bakker, S.J.A.; Beurskens, L.W.M.; Grafakos, S.; Jansen, J.C.; de Joode, J.; van Ruijven, B.J.; van Vuuren, D.P. Oil Price and Climate Change Mitigation: Sensitivity of Cost of Mitigation Options for Energy Price Changes; Report ECN-B—09008; Netherlands Environmental Assessment Agency: The Hague, The Netherlands, 2009. [Google Scholar]
- André, J.C.; Cloppet, E. Quel Climat fera-t-il demain? Les Cahier de l’Université des Lycéens, Lycée Beauregard (in French); Université des Lycéens Beauregard: Villefranche de Rouergue, France, 2003. [Google Scholar]
- World Bank, Vulnerability, Risk Reduction and Adaptation to Climate Change: Senegal, Climate Risk and Adaptation Country Report, 2011; World Bank: Washington, DC, USA, 2011.
- Banque Ouest Africaine de Développement (BOAD), Changements Climatiques et Sécurité Alimentaire dans la zone UEMOA: Défis, Impacts et Enjeux Actuels et Futurs: Rapport Final (in French); BOAD: Lomé, Togo, 2010.
- In this paper we do not perform an application of a dynamic CGE microsimulation model as this technique has not been applied in the literature yet. Many challenges remain and this constitutes our future research agenda but such an analysis is beyond the scope of this paper. We recall that we aim to highlight the linkages at play and the model was constructed to take into account the 10 to 15 year timeframe of our impact analysis albeit in a comparative static framework.
- Ravallion, M.; Chen, S. Measuring pro-poor growth. Econ. Lett. 2003, 78, 93–99. [Google Scholar] [CrossRef]
- Kakwani, N.; Pernia, E. What is pro-poor growth? Asian Dev. Rev. 2000, 18, 1–16. [Google Scholar]
- Kakwani, N.; Son, H. Pro-Poor growth: Concept, measurement with country case studies. Pak. Dev. Rev. 2003, 42, 417–444. [Google Scholar]
- Boccanfuso, D.; Ménard, C. La croissance pro-pauvre: Un apperçu exhaustif de la boîte à outils (in French); GREDI, Working paper no. 09–06; Université de Sherbrooke: Sherbrooke, Canada, 2009. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).