Household Solar Photovoltaics: Supplier of Marginal Abatement, or Primary Source of Low-Emission Power?
Abstract
:Abbreviations
| AUD | Australian dollar |
| g CO2-e | grams of carbon dioxide-equivalent |
| GJ | energy, 109 joules |
| GW | power, 109 watts (joules per second) |
| GWh | energy, 109 watt-hours |
| kVA | apparent power, 103 volt-amperes |
| kW | power, 103 watts |
| kWh | energy, 103 watt-hours equal to 3.6 megajoules |
| MW | power, 106 watts |
| MWh | energy, 106 watt-hours |
| PJ | energy, 1015 joules |
| TWh | energy, 1012 watt-hours |
| USD | US dollar |
| Wh | watt-hour, unit of energy equal to 3,600 joules |
1. Introduction
2. Household Reliance on a “Less than Green” Electricity Grid
2.1. Solar Energy Available
2.2. Modeled Household Demand and Solar PV
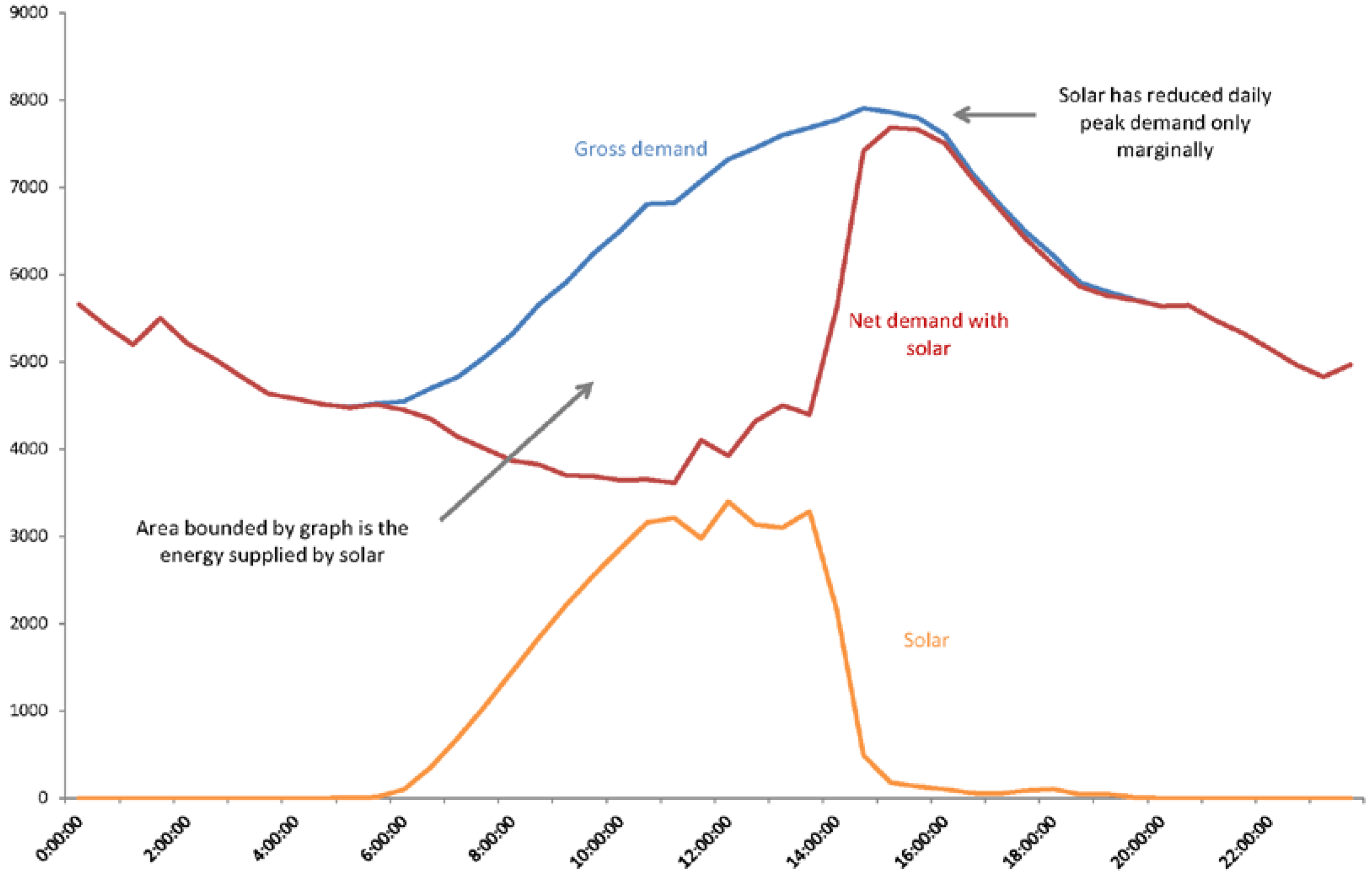
2.3. Temporal Profile of Available Solar Energy
| Solar capacity (kW) | Proportion of annual energy consumption that is imported from the grid (%) | Proportion of annual hours that power is being imported (%) |
|---|---|---|
| 0.0 | 100 | 100 |
| 1.0 | 79 | 92 |
| 2.0 | 70 | 80 |
| 4.4 | 63 | 70 |
| 8.8 | 58 | 63 |
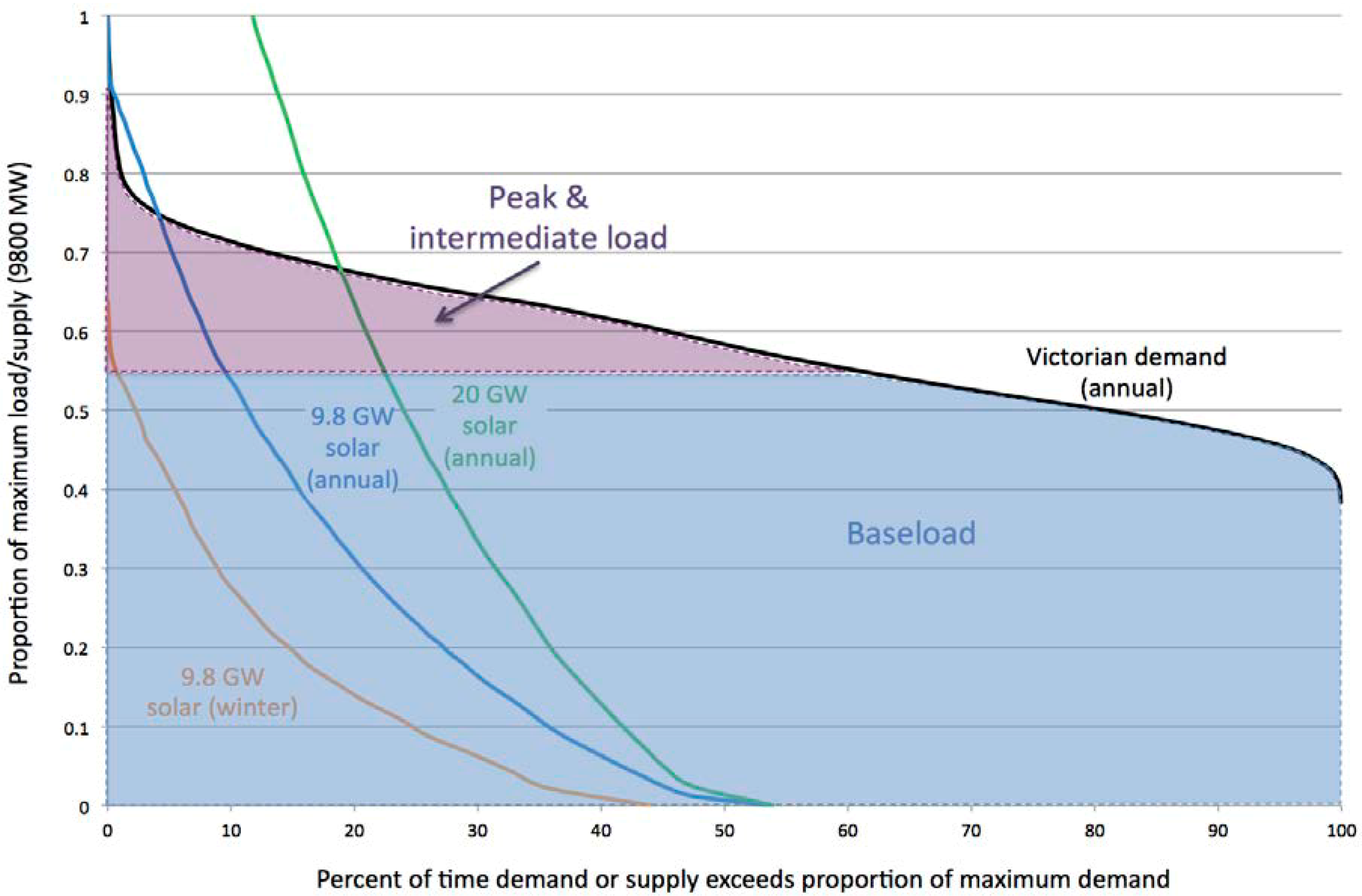
2.4. Quantity of Household PV Practically Available in Victoria
2.5. Contribution to System Energy with Increased System Flexibility
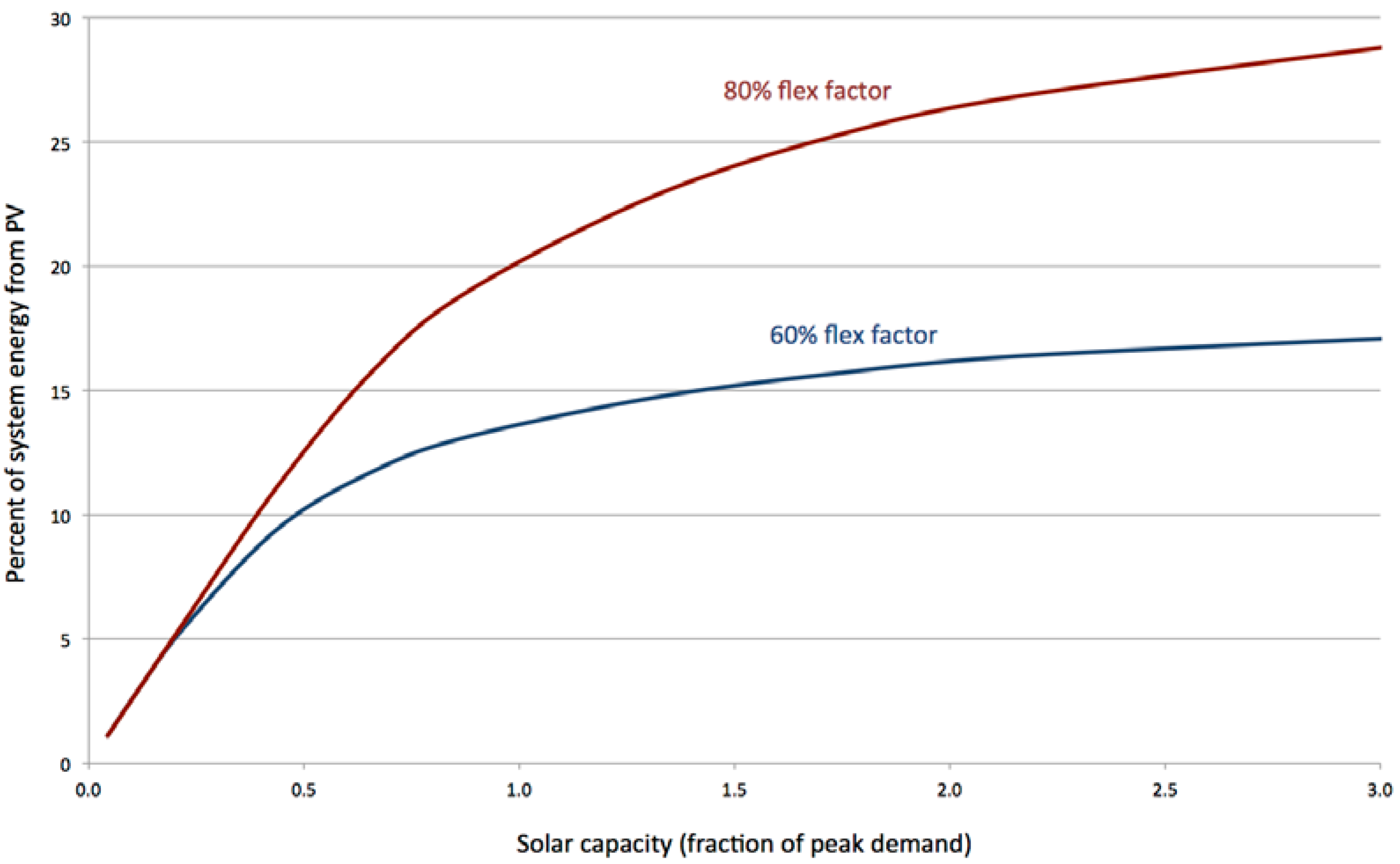
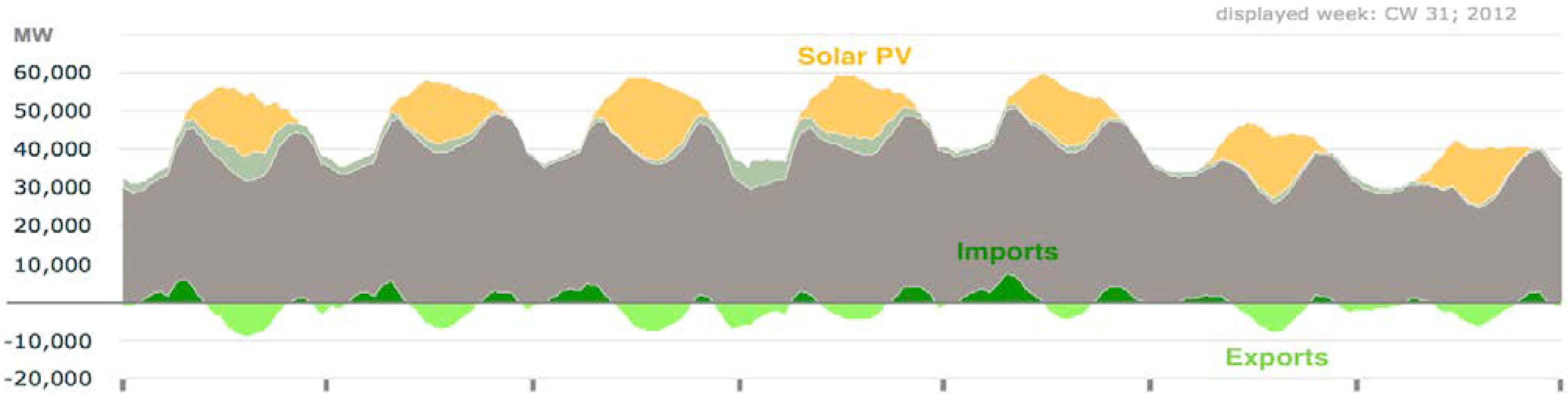
3. Network Support with PV
3.1. Reliance on the Distribution Network

| Peak gross demand | Peak net demand [north/west] | Relative reduction (%) [north/west] | |
|---|---|---|---|
| 11 Jan | 9858 | 9168/8948 | 35/45 |
| 8 Feb | 9465 | 8596/8281 | 43/59 |
| 9 Feb | 9463 | 9025/9025 | 22/22 |
| 12 Jan | 9301 | 7607/7784 | 85/76 |
| 10 Feb | 9100 | 9051/9051 | 2/2 |
| 2 Feb | 8966 | 8356/8300 | 31/33 |
| 3 Feb | 8920 | 8671/8671 | 12/12 |
| 11 Feb | 8604 | 8457/8457 | 7/7 |
| 26 Feb | 8405 | 7934/7909 | 24/25 |
| 19 Feb | 8236 | 7605/7505 | 32/37 |
3.2. Battery Storage to Improve PV Capacity Credit
- (1)
- The orange curve is the actual Victorian demand for the day, with daily peak P1.
- (2)
- The red curve describes the net Victorian demand with 2,000 MW of Melbourne-based solar without storage, with resulting daily peak P2.
- (3)
- The green curve/line describes the net Victorian demand with solar, and with storage assuming the storage is operated with perfect hindsight, with resulting daily peak P3.
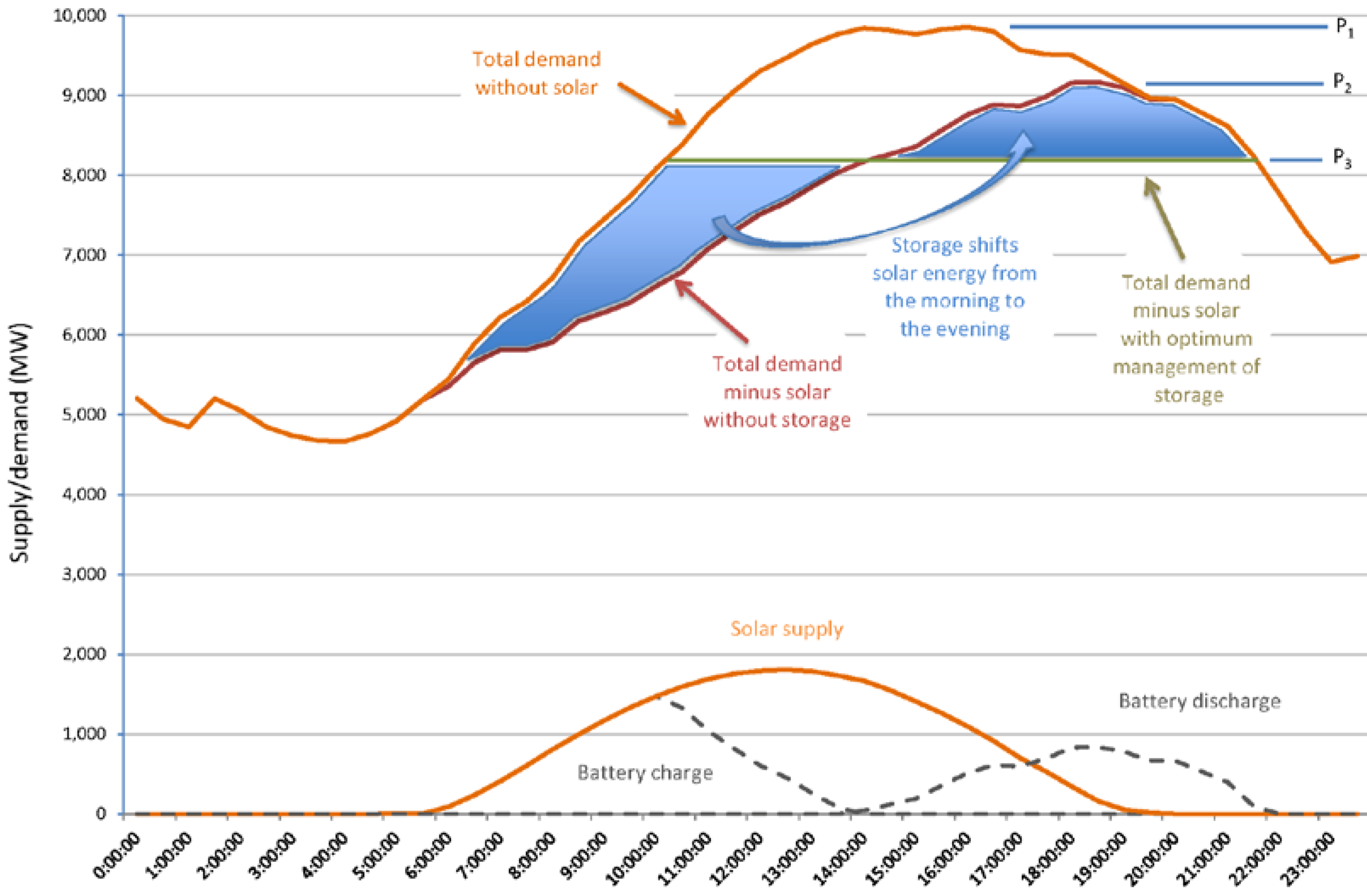
- (1)
- All of the solar is diverted to storage until 10:00 in the morning.
- (2)
- From 10:00 until 13:30, an increasing proportion of solar is fed directly into the grid with a decreasing proportion diverted to storage.
- (3)
- From 13:30 in the early afternoon to 19:00 in the early evening, all of the solar is delivered directly to the grid, with support from the battery storage.
- (4)
- From 19:00 to 22:00, there is no solar generation, but the battery continues to discharge.
3.3. Household PV with Storage to Improve Network Utilization
3.4. Vehicle to Grid Storage (V2G)
3.5. Network Support Summary
4. Assessing the Value of PV for Greenhouse Abatement
4.1. Review of Australian Abatement Cost Estimates
4.2. Abatement Cost Calculation Methodology
4.3. Assumed Life of PV System
4.4. Loss of Abatement through Cycling and Sub-Optimal Operation of Thermal Generators
4.5. Abatement Cost Estimate
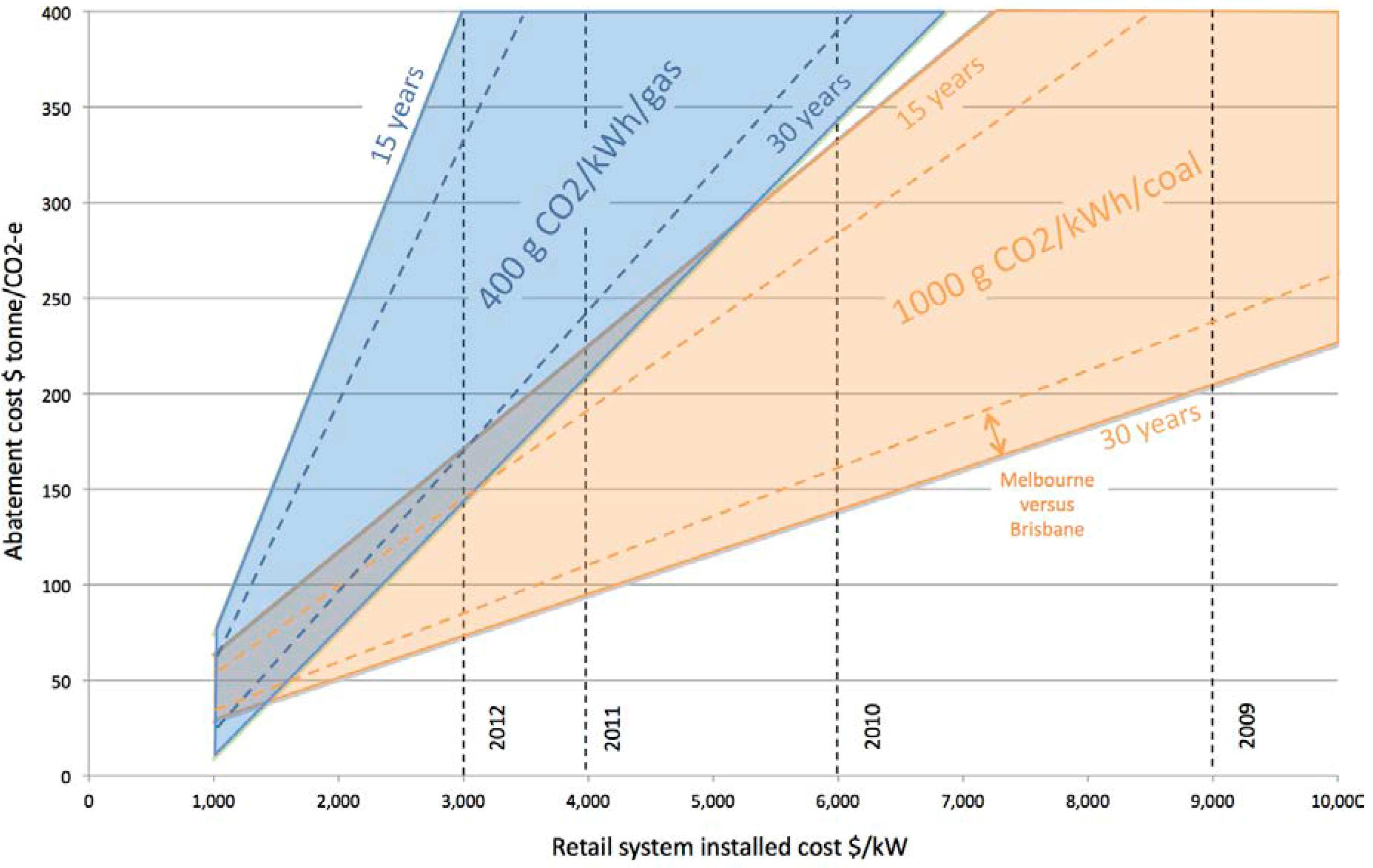
4.6. PV in Relation to Other Abatement Opportunities
5. Practical Constraints on Grid Integration
5.1. Redefining Baseload
5.2. Reduced Load Factor of Electricity Systems with PV
| NEM | Elliston et al. | |
|---|---|---|
| Capacity without reserve [GW] | 84.5 | |
| Reserve margin @ 20% [GW] | 16.9 | |
| Capacity including reserve [GW] | 43 | 101.4 |
| Peak demand [GW] | 33.6 | 33.6 |
| Annual generation [TWh] | 204.4 | 204.4 |
| Calculated load factor [%] | 54 | 23 |
5.3. Comparison of Reliability Measures for Conventional Versus PV
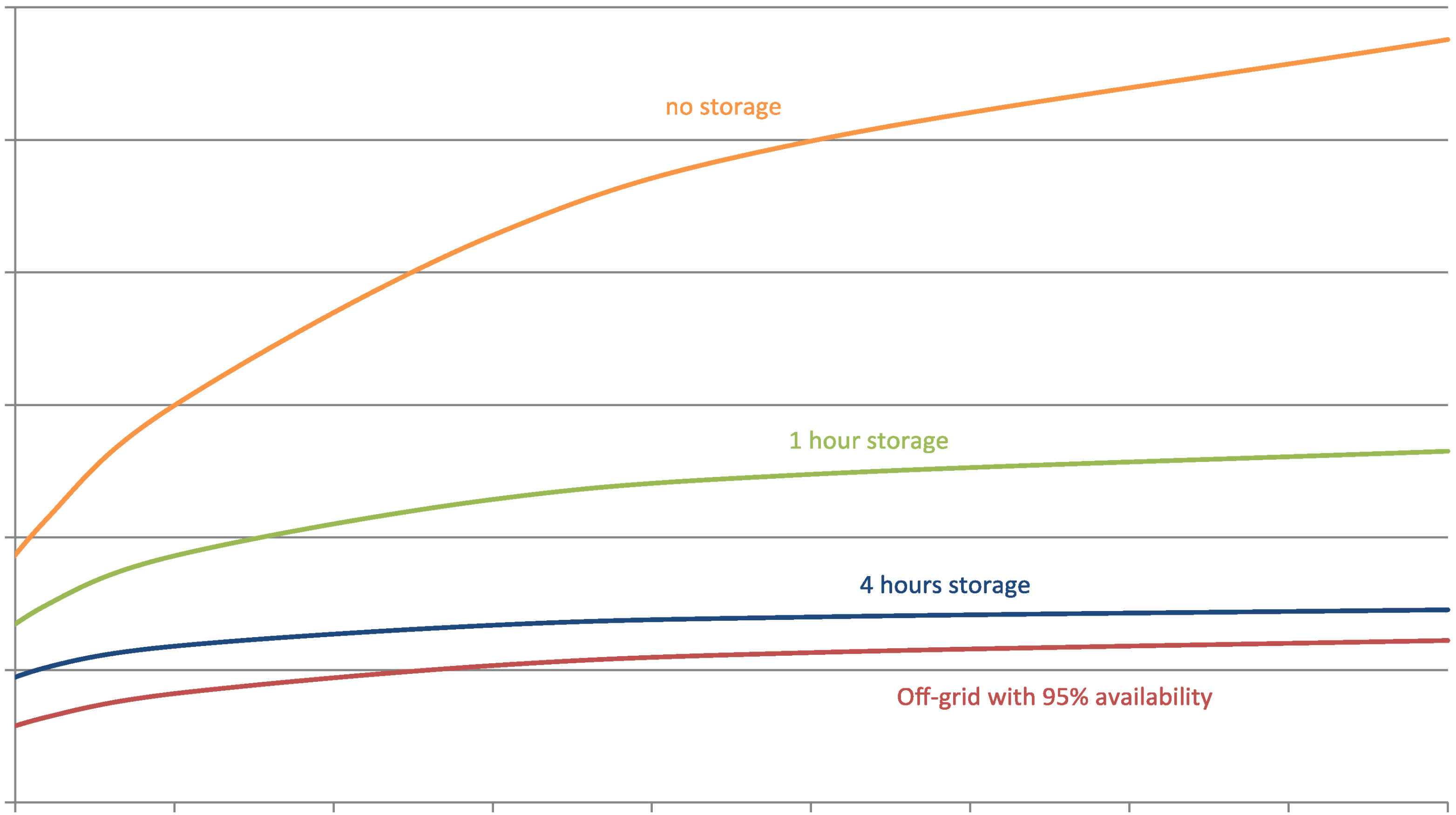
5.4. Comparison of Cost for Conventional Versus PV
5.5. Synchronous Generation, Inertia, and Grid Stability
5.6. Voltage Regulation
- (1)
- Converting households to a three-phase connection with the associated wiring, metering and switchgear, and installing a three-phase inverter. A typical home will cost $500 to $1,000 to upgrade to three phase plus additional inverter costs.
- (2)
- The replacement of OLTC transformers with automatic tap-changing transformers, which require control systems and voltage monitoring within the network to alter the voltage in near real-time in response to prevailing load and supply voltage [101]. At, say $120 to $200 per kVA, the per-household cost of a transformer will be of the order of $500 to $1,000 plus control and monitoring cost.
- (3)
- The commissioning of “smart grid” components to permit active control of solar inverters, storage devices, and loads in response to network operator directives [102].
- (4)
- The use of bi-directional (four-quadrant) inverters to dynamically provide reactive power support and voltage regulation on feeders with high reactance (typically rural feeders) [103].
- (5)
- Augmenting customer service and feeder mains to reduce the impedance seen by solar inverters.
5.7. Solar Ramp Rate Driving a Need for Flexible Generation

6. High Penetration PV Forcing a Sub-Optimal Generation Mix
6.1. Risks and Uncertainties of Future Energy Technologies and Carbon Policies
6.2. Intermittent Generation Forcing a Sub-Optimal Generation Mix
6.3. Low-Emission Baseload Undermined by Intermittent Generation
6.4. Solar PV Competing with Concentrated Solar Thermal and Wind
7. Embodied Energy
7.1. Embodied Energy of PV Systems
7.2. Recent LCA Review
| Mono-c Si (rooftop) | Ribbon Si (rooftop) | |
|---|---|---|
| Insolation [kWh/(m2 yr)] | 1,700 | 1,700 |
| Performance ratio | 0.75 | 0.75 |
| Module efficiency | 14% | 13% |
| Eout,yr [kWhel/(m2 yr)] | 179 | 166 |
| T [yr] | 30 | 30 |
| Eout [kWhel/(m2)] | 5,355 | 4,973 |
| Epp [MJPE/m2] | 3,257 | 1,907 |
| Epp [kWhPE/m2] | 905 | 530 |
| Solar EROIel = Eout/Epp (refer [122]) | 5.9 | 9.4 |
7.3. Primary Energy Equivalent
7.4. Reduction of EROI Due to Storage or Energy Spilling at High Penetration
| Mono-c Si (rooftop) | Ribbon Si (rooftop) | |
|---|---|---|
| Assumed power of solar [kwmax/m2] | 0.14 | 0.13 |
| Assumed battery depth-of-discharge [%] | 50 | 50 |
| Hours of capacity at full power [hours] (refer [34]) | 4 | 4 |
| Storage capacity [Wh] | 1120 | 1040 |
| Sets of batteries over 30 years @ 7.5 yr life | 4 | 4 |
| Lead-acid (recycled) embodied energy [MJ/Wh] (refer pg. 21 [127]) | 0.87 | 0.87 |
| Ebatt [MJ/m2] | 3898 | 3619 |
| Ebatt [kWh/m2] | 1108 | 1005 |
7.5. Embodied Energy with an Off-Grid System
| Daily energy used [kWh] | 15.5 |
|---|---|
| Solar capacity [kW] | 11.1 |
| Battery capacity [kWh] | 63 |
| Ebatt [MJ] @ 4 sets over 30 yrs | 219,240 |
| Solar area [m2] | 79 |
| Epp [MJPE/m2] | 3,257 |
| Esolar = solar area x Epp [MJ] | 258,234 |
| Esystem = Epp + Ebatt | 477,474 |
| Eused @ 15.5 kWh/day over 30 yrs [MJ] | 611,010 |
| System EROIel = Eused/(Esolar + Ebatt) | 1.3 |
7.6. Embodied Energy of the Distribution Network and Retailing
| Industry value added (%) | Employment (%) | Net capital expenditure (%) | |
|---|---|---|---|
| Generation | 35 | 22 | 30 |
| Transmission | 11 | 6 | 18 |
| Distribution | 47 | 62 | 48 |
| On selling and market operation | 7 | 11 | 4 |
| 100 | 100 | 100 |

7.7. Employment in Australian PV-Related Industries
7.8. Extended EROI
| Mono-c Si (rooftop) | Ribbon Si (rooftop) | |
|---|---|---|
| Basic EROIel = Eout/Epp (Table 4) | 5.9 | 9.4 |
| Eout [kWhel/(m2)] (Table 4) | 5355 | 4973 |
| Epp [kWh/m2] (Table 4) | 905 | 530 |
| Ebatt [kWh/m2] (for 4 hours, Table 5) | 1108 | 1005 |
| Ebatt_loss = 5% x Eout [kWh/m2] (Section 7.4) | 268 | 249 |
| Edist = 4% x Eout [kWh/m2] (Section 7.6) | 214 | 199 |
| Elabor = [kWh/m2] (Section 7.7) | 155 | 144 |
| Extended EROIel = Eout/(Epp + Ebatt + Ebatt_loss + Edist + Elabor) | 2.0 | 2.3 |
| Extended energy payback time = life / EROI [yrs] | 15 | 13 |
8. Conclusions
Conflict of Interest
References
- Garnaut, R. The Garnaut Climate Change Review—Final Report; Department of Climate Change and Energy Efficiency: Canberra, Australia, 2008; Figure 20.11. [Google Scholar]
- Department of Climate Change and Energy Efficiency, National Greenhouse Accounts Factors; DCCEE: Canberra, Australia, 2011; Table 5.
- Australian Productivity Commission, Electricity Network Regulatory Frameworks, Draft Report; Productivity Commission: Canberra, Australia, 2012.
- Independent Pricing and Regulatory Tribunal of New South Wales (IPART), Solar Feed-In Tariffs—Setting a Fair and Reasonable Value for Electricity Generated by Small-Scale Solar PV Units in NSW; IPART: Sydney, Australia, 2012.
- Fthenakis, V.; Frischknecht, R.; Raugei, M.; Kim, H.; Alsema, E.; Held, M.; de Wild-Scholten, M. Methodology Guidelines on Life Cycle Assessment of Photovoltaic Electricity; IEA-PVPS: Upton, MA, USA, 2011. [Google Scholar]
- Prieto, P.A.; Hall, C.A.S. Spainʼs Photovoltaic Revolution: The Energy return on Investment; Springer: New York, NY, USA, 2013. [Google Scholar]
- Trainer, T. Can Renewable Energy Sustain Consumer Societies? A Negative Case; Simplicity Institute Report, 12e; Simplicity Institute: Melbourne, Australia, 2012. [Google Scholar]
- Sayeef, S.; Heslop, S.; Cornforth, D.; Moore, T.; Percy, S.; Ward, J.K.; Berry, A.; Rowe, D. Solar Intermittency: Australia’s Clean Energy Challenge: Characterising the Effect of High Penetration Solar Intermittency on Australian Electricity Networks; CSIRO: Sydney, Australia, 2012. [Google Scholar]
- Denholm, P.; Margolis, R.M. Evaluating the limits of solar photovoltaics (PV) in traditional electric power systems. Energ. Pol. 2007, 35, 2852–2861. [Google Scholar] [CrossRef]
- Delucchi, M.A.; Jacobson, M.Z. Providing all global energy with wind, water, and solar power, Part II: Reliability, system and transmission costs, and policies. Energ. Pol. 2011, 39, 1170–1190. [Google Scholar] [CrossRef]
- WWF, The Energy Report: 100% Renewable Energy by 2050; WWF: Gland, Switzerland, 2011.
- Wright, M.; Hearps, P. Australian Sustainable Energy: Zero carbon Australia Stationary Energy Plan; Melbourne Energy Research Institute: Melbourne, Australia, 2010. [Google Scholar]
- Reedman, L.J. High Penetration Renewables Studies: A Review of the Literature, Report prepared for the Australian Energy Market Operator (AEMO); CSIRO: Newcastle, Australia, 2012. [Google Scholar]
- MacKay, D. Sustainable Energy-without the Hot Air; UIT Cambridge: Cambridge, UK, 2008. [Google Scholar]
- Moriarty, P.; Honnery, D. Rise and Fall of the Carbon Civilisation: Resolving Global Environmental and Resource Problems; Springer: London, UK, 2010. [Google Scholar]
- Smil, V. Energy at the Crossroads: Global Perspectives and Uncertainties; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Trainer, T. 100% Renewable supply? Comments on the reply by Jacobson and Delucchi to the critique by Trainer. Energ. Pol. 2013. [Google Scholar] [CrossRef]
- Smil, V. Energy in Nature and Society: General Energetics of Complex Systems; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Deloitte Australia, Advanced Metering Infrastructure Customer Impacts Study, Vol.1; Department of Primary Industries: Melbourne, Australia, 2011; p. xvi.
- Earth System Research Laboratory. NOAA (National Oceanic and Atmospheric Administration) -solar calculation details. 2012. Available online: http://www.esrl.noaa.gov/gmd/grad/solcalc/calcdetails.html (accessed on 1 January 2013).
- Australian Bureau of Statistics (ABS), 1301.0 Year Book of Australia, 2012; ABS: Canberra, Australia, 2012.
- Australian Energy Market Operator (AEMO), Rooftop PV Information Paper; AEMO: Melbourne, Australia, 2012.
- Myers, K.S.; Klein, S.A.; Reindl, D.T. Assessment of High Penetration of Photovoltaics on Peak Demand and Annual Energy Use; Public Service Commission of Wisconsin & The Statewide Energy Efficiency and Renewables Administration: Madison, WI, USA, 2010; p. 150. [Google Scholar]
- Myers, K.S.; Klein, S.A.; Reindl, D.T. Assessment of high penetration of solar photovoltaics in Wisconsin. Energ. Pol. 2010, 38, 7338–7345. [Google Scholar] [CrossRef]
- Auer, J. The German Feed-in Tariff: Recent Policy Changes; Deutsche Bank Group: New York, NY, USA, 2012. [Google Scholar]
- Burger, B. Electricity Production from Solar and Wind in Germany in 2012; Fraunhofer Institute for Solar Energy Systems ISE: Freiburg, Germany, 2013. [Google Scholar]
- Watt, M.; Partlin, S.; Oliphant, M.; MacGill, I.; Spooner, T. The value of PV in summer peaks. Available online: http://www.ergo.ee.unsw.edu.au/value%20of%20PV%20in%20summer%20/peaks.pdf (accessed on 21 March 2013).
- Endeavour Energy, Review of Solar Feed-in Tariffs; Endeavour Energy: Sydney, Australia, 2011.
- Australian PV Association (APVA), APVA Submission to the IPART Energy Issues Paper on Solar Feed-in Tariffs, August 2011; APVA: Liberty Grove, Australia, 2011.
- Ausgrid. Effect of Small Solar Photovoltaic Systems on Network Peak Demand. Available online: http://www.ausgrid.com.au/Common/About-us/Newsroom/Discussions/~/media/Files/About%20Us/Newsroom/Discussions/Solar%20PV%20Research%20Paper.ashx (accessed on 20 March 2013).
- Nelson, T.; Simshauser, P.; Nelson, J. Queensland solar feed-in tariffs and the merit-order effect: economic benefit, or regressive taxation and wealth transfers? AGL App. Econ. Pol. Res. 2012, 42, 277–301. [Google Scholar]
- International Energy Agency (IEA), Technology Roadmap—Solar Photovoltaic Energy; IEA: Paris, France, 2010.
- Wilson, I.A.G.; McGregor, P.G.; Hall, P.J. Energy storage in the UK electrical network: Estimation of the scale and review of technology options. Energ. Pol. 2010, 38, 4099–4106. [Google Scholar] [CrossRef]
- Denholm, P.; Hand, M. Grid flexibility and storage required to achieve very high penetration of variable renewable electricity. Energ. Pol. 2011, 39, 1817–1830. [Google Scholar] [CrossRef]
- Outhred, H. Review of MMA Report “Greenhouse Gas Abatement from Wind and Solar in the Victorian Region of the NEMˮ for Sustainability Victoria; UNSW Global Pty Ltd: Sydney, Australia, 2010. [Google Scholar]
- Electric Power Research Institute, Electricity Energy Storage Technology Options : A White Paper Primer on Applications, Costs, and Benefits; EPRI: Palo Alto, CA, USA, 2010.
- Blackburn, T.R. Distribution Transformers: Proposal to Increase MEPS Levels; Prepared for Energy Efficiency Program: Sydney, Australia, 2007. [Google Scholar]
- International Energy Agency (IEA), Modelling Load Shifting Using Electric Vehicles in a Smart Grid Environment; IEA: Paris, France, 2010.
- Australian Energy Market Operator (AEMO), National Transmission Network Development Plan 2011; AEMO: Melbourne, Australia, 2011.
- Lund, H.; Kempton, W. Integration of renewable energy into the transport and electricity sectors through V2G. Energ. Pol. 2008, 36, 3578–3587. [Google Scholar]
- Trainer, T. A critique of Jacobson and Delucci's proposals for a world renewable energy supply. Energ. Pol. 2012, 44, 476–481. [Google Scholar] [CrossRef]
- Kemp, M. Zero Carbon Britain 2030: a new energy strategy. The second report of the Zero Carbon Britain project.; Centre for Alternative Technology: Powys, UK, 2010; p. 111. [Google Scholar]
- Simshauser, P.; Downer, D. Dynamic Pricing and the Peak Electricity Load Problem. Austral. Econ. Rev. 2012, 45, 305–324. [Google Scholar] [CrossRef]
- Palmer, G. Does Energy Efficiency Reduce Emissions and Peak Demand? A Case Study of 50 Years of Space Heating in Melbourne. Sustainability 2012, 4, 1525–1560. [Google Scholar] [CrossRef]
- Langham, E.; Dunstan, C.; Walgenwitz, G.; Denvir, P. Reduced Infrastructure Costs from Improving Building Energy Efficiency; Institute for Sustainable Future, University of Technology, Sydney: Sydney, Australia, 2010. [Google Scholar]
- Palmer, G. Submission DR046—Electricity Network Regulatory Frameworks Draft,2012; Productivity Commission: Canberra, Australia, 2012. [Google Scholar]
- Department of Climate Change and Energy Efficiency, Estimating the Cost of Abatement, Framework and Practical Guidance; DCCEE: Canberra, Australia, 2011.
- Macintosh, A.; Wilkinson, D. Searching for Public Benefits in Solar Subsidies: A case study on the Australian government’s residential photovoltaic rebate program. Energ. Pol. 2011, 39, 3199–3209. [Google Scholar] [CrossRef]
- Watt, M.; Passey, R.; Johnston, W. PV in Australia 2011: Prepared for the IEA Cooperative Programmme on PV Power Systems; Australian PV Association: Liberty Grove, Australia, 2011. [Google Scholar]
- Australian Productivity Commission, Carbon Emission Policies in Key Economies; Productivity Commission: Canberra, Australia, 2011.
- Oliver, M.; Jackson, T. The evolution of economic and environmental cost for crystalline silicon photovoltaics. Energ. Pol. 2000, 28, 1011–1021. [Google Scholar] [CrossRef]
- Sherwani, A.F.; Usmani, J.A. Life cycle assessment of solar PV based electricity generation systems: A review. Renew. Sust. Energ. Rev. 2010, 14, 540–544. [Google Scholar] [CrossRef]
- Department of Climate Change and Energy Efficiency, National Greenhouse Accounts Factors; DCCEE: Canberra, Australia, 2009.
- Lenzen, M. Life cycle energy and greenhouse gas emissions of nuclear energy: A review. Energ. Convers. Manage. 2008, 49, 2178–2199. [Google Scholar] [CrossRef]
- SKM MMA, Garnaut Climate Change Review Update 2011: Advice on Change in Merit Order of Brown Coal Fired Stations. SKM MMA: Melbourne, Australia, 2011.
- ACIL Tasman, Fuel Resource, New Entry and Generation Costs in the NEM, 0419-0035; AEMO: Melbourne, Australia, 2009.
- Australian PV Association (APVA), APVA Response to PV Costs and Abatement in the Productivity Commission Research Report: Carbon Emission Policies in Key Countries; APVA: Liberty Grove, Australia, 2011.
- Australian Government, Renewable Energy (Electricity) Act 2000, Act No. 174 of 2000 as Amended including Amendments up to Act No. 78 of 2009; Attorney-General’s Department: Canberra, Australia, 2009.
- Australian Greenhouse Office (AGO), Renewable Opportunities: A Review of the Operation of the Renewable Energy (Electricity) Act 2000; AGO: Canberra, Australia, 2003.
- Australian Climate Change Authority, Renewable Energy Target Review: Issues Paper; Australian Climate Change Authority: Canberra, Australia, 2012; p. 37.
- SKM MMA, Greenhouse Gas Abatement from wind and solar in the Victorian Region of the NEM; Sustainability Victoria: Malvern, Australia, 2010.
- Inhaber, H. Why wind power does not deliver the expected emissions reductions. Renew. Sust. Energ. Rev. 2011, 15, 2557–2562. [Google Scholar]
- Bazilian, M.; Onyeji, I.; Liebreich, M.; MacGill, I.; Chase, J.; Shah, J.; Gielen, D.; Arent, D.; Landfear, D.; Zhengrong, S. Re-considering the Economics of Photovoltaic Power. Bloomberg NEF: New York, NY, USA, 2012. [Google Scholar]
- Solarbuzz. Module pricing. Solarbuzz. 2012. Available online: http://www.solarbuzz.com/facts-and-figures/retail-price-environment/module-prices (accessed on 1 January 2013).
- Ekins, P.; Kesicki, F.; Smith, A.Z.P. Marginal Abatement Cost Curves: A Call for Caution; University College London: London, UK, 2011. [Google Scholar]
- Nicholson, M.; Biegler, T.; Brook, B.W. How carbon pricing changes the relative competitiveness of low-carbon baseload generating technologies. Energy 2011, 36, 305–313. [Google Scholar] [CrossRef]
- McKinsey & Company, An Australian Cost Curve for Greenhouse Gas Reduction, Sydney, Australia, 2008.
- Ashworth, P.; Hobman, E. The Australian Public’s Preference for Energy Sources and Related Technologies; CSIRO: Pullenvale, Australia, 2011. [Google Scholar]
- Alcott, B. Impact Caps: Why population, affluence and technology strategies should be abandoned. J. Clean. Prod. 2009, 18, 552–560. [Google Scholar] [CrossRef]
- Institute for Energy Research. Levelized cost of new electricity generating technologies. 2012. Available online: http://www.instituteforenergyresearch.org/2011/02/01/levelized-cost-of-new-electricity-generating-technologies/ (accessed on 1 January 2013).
- Anderson, G. Dynamics and Control of Electric Power Systems; Swiss Federal Institute of Technology: Zurich Switzerland, 2012. [Google Scholar]
- Department of Resources, Energy and Tourism, Energy White paper 2012 : Australiaʼs energy transformation; DRET: Canberra, Australia, 2012.
- Hannahan, B. Can interconnected windfarms replace baseload power plants? 2010. Available online: http://www.nucleargreen.blogspot.com.au/2010/01/review-comment-on-stanford-wind.html/ (accessed on 1 January 2013).
- Sovacool, B.K. The intermittency of wind, solar, and renewable electricity generators: Technical barrier or rhetorical excuse? Utili. Pol. 2009, 17, 288–296. [Google Scholar] [CrossRef]
- Archer, C.L.; Jacobson, M.Z. Supplying baseload power and reducing transmission requirements by interconnecting wind farms. J. Appl. Meteorol. Climatol. 2007, 46, 1701–1717. [Google Scholar] [CrossRef]
- Diesendorf, M. Greenhouse Solutions with Sustainable Energy; UNSW Press: Sydney, Australia, 2007. [Google Scholar]
- Elliston, B.; Diesendorf, M.; MacGill, I. Simulations of scenarios with 100% renewable electricity in the Australian National Electricity Market. Energ. Pol. 2012, 45, 606–613. [Google Scholar] [CrossRef]
- OʼSullivan, J.N. The Burden of Durable Asset Acquisition in Growing Populations. Econ. Aff. 2012, 32, 31–37. [Google Scholar] [CrossRef]
- North American Electric Reliability Corporation, Accommodating high levels of variable generation; NAERC: NJ, USA, 2009.
- Clean Energy Council, Consumer guide to buying household solar panels; Clean Energy Council: Melbourne, Australia, 2011.
- Lang, P. Renewable electricity for Australia - the cost. Critique of “Simulations of scenarios with 100% renewable electricity in the Australian National Electricity Market”. Brave New Climate. 2012. Available online: http://bravenewclimate.files.wordpress.com/2012/02/lang_renewable_energy_australia_cost.pdf (accessed on 1 January 2013).
- North American Electric Reliability Corporation, 2012 State of Reliability; NAERC: Atlanta, GA, USA, 2012.
- TRU Energy, Investor Presentation, March 2011; TRU Energy: Melbourne, Australia, 2011.
- Gross, R.; Heptonstall, P.; Anderson, D.; Green, T.; Leach, M.; Skea, J. The Costs and Impacts of Intermittency: An assessment of the evidence on the costs and impacts of intermittent generation on the British electricity network; UK Energy Research Centre: London, UK, 2006. [Google Scholar]
- US Energy Information Administration (EIA), Levelized Cost of New Generation Resources in the Annual Energy Outlook 2012; EIA: Washington, DC, USA, 2012.
- Electric Power Research Institute, Australian Electricity Generation Technology Costs—Reference Case 2010; Australian Department of Resources, Energy and Tourism: Canberra, Australia, 2010.
- United Nations, Multi Dimensional Issues in International Electric Power Grid Interconnections; New York, NY, USA, 2006.
- Australian Energy Market Operator (AEMO), Technical Guide to the Wholesale Market-0000-0264; AEMO: Melbourne, Australia, 2010.
- Electricity Supply Industry Expert Panel, Technical Parameters of the Tasmanian Electricity Supply System - Information paper; Tasmanian Government: Hobart, Australia, 2011.
- International Energy Agency (IEA), Key World Energy Statistics—2012; IEA: Paris, France, 2012.
- Smil, V. Creating the Twentieth Century: Technical Innovations of 1867–1914 and Their Lasting Impact; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Rouco, L.; Azpiri, I.; de Olea, I.G.; Tabernero, J. Increasing Penetration of Renewals in Isolated Power Systems Using Energy Storage Systems; University Pontificia Comillas: Madrid, Spain, 2009. [Google Scholar]
- Tielens, P.; van Hertem, D. Grid Inertia and Frequency Control in Power Systems with High Penetration of Renewables; KU Leuven: Leuven, Belgium, 2012. [Google Scholar]
- Friedrich, L.; Gautschi, M. Grid stabilization control and frequency regulation for inverter-connected distributed renewable energy sources. Master Thesis, Department of Electrical and Computer Engineering, University of Wisconsin-Madison, 2009. [Google Scholar]
- Tasmania Department of Infrastructure Energy and Resources, Submission to National Electricity Amendment (Network Support and Control Ancillary Services) Rule 2010 (ERC 0108); Tasmania DIER: Hobart, Australia, 2010.
- Halliday, C.; Urquart, D. Voltage and Equipment Standards Misalignment; The Electric Energy Society of Australia: Canberra, Australia, 2011. [Google Scholar]
- Essential Energy, Supply Standards: Electricity Supply Standard AS60038, Essential Energy: Queanbeyan, Australia; 2011.
- Bindner, H. Power Control for Wind Turbines in Weak Grids: Concepts Development; Risø: Roskilde, Denmark, 1999. [Google Scholar]
- Woyte, A.; van Thong, V.; Belmans, R.; Nijs, J. Voltage fluctuations on distribution level introduced by photovoltaic systems. IEEE Transactions Energ. Conv. 2006, 21, 202–209. [Google Scholar] [CrossRef]
- Zahedi, A. Maximizing solar PV energy penetration using energy storage technology. Renew. Sust. Energ. Rev. 2011, 15, 866–870. [Google Scholar] [CrossRef]
- Kadurek, P.; Cobben, J.F.G.; Kling, W.L. Smart MV/LV transformer for future grids. In Proceedings of Power Electronics Electrical Drives Automation and Motion (SPEEDAM), 2010 International Symposium on, Pisa, Italy, 14–16 June 2010.
- Bower, W.; Gonzalez, S.; Akhil, A.; Kuszmaul, S.; Sena-Henderson, L.; David, C.; Reedy, R. Solar Energy Grid Integration Systems: Final Report of the Florida Solar Energy Center Team; Sandia National Laboratories: Albuquerque, NM, USA, 2012. [Google Scholar]
- Essential Energy. Inverter Trial, ENA Smart Networks Summit. 2011. Available online: www.ena.asn.au/udocs/2011/05/Michael-Lysaght.ppt (accessed on 1 January 2013).
- International Energy Agency (IEA), Technology Roadmap—Smart Grids; IEA: Paris, France, 2011.
- ABC News. Smart meters here to stay despite cost blow-out. 2011. Available online: http://www.abc.net.au/news/2011-12-14/smart-meter-roll-out-continues-despite-cost-blowout/3730522/ (accessed on 1 January 2013).
- Huang, X.; Mills, G.A. Objective identification of wind change timing from single station observations Part 1: methodology and comparison with subjective wind change timings. Aust. Met. Mag. 2006, 55, 261–274. [Google Scholar]
- Curtright, A.E.; Apt, J. The character of power output from utility-scale photovoltaic systems. Prog. Photovoltaics: Res. App. 2007, 16, 241–247. [Google Scholar] [CrossRef]
- Lang, P. Pumped-hydro energy storage—cost estimates for a feasible system. Brave New Climate. 2010. Available online: http://bravenewclimate.com/2010/04/05/pumped-hydro-system-cost/ (accessed on 1 January 2013).
- Wood, T.; Edis, T. No Easy Choices: Which Way for Australiaʼs Energy Future? Grattan Institute: Melbourne, Australia, 2011. [Google Scholar]
- McKibbin, W.; Wilcoxen, P. Managing Price and Why a Hybrid Policy Is Better for Australia; Committee for Economic Development of Australia: Melbourne, Australia, 2007. [Google Scholar]
- Ergas, H. Policy Forum: Designing a Carbon Price Policy: Using Market Based Mechanisms for Emission Abatement: Are the Assumptions Plausible? Austral. Econ. Rev. 2012, 45, 86–95. [Google Scholar] [CrossRef]
- Montgomery, D.W.; Smith, A.E. Price, quantity, and technology strategies for climate change policy. In Human Induced Climate Change: An Interdisciplinary Assessment; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Wood, T. The future of gas power: stepping stone or snare? The Conversation. 2012. Available online: http://theconversation.edu.au/the-future-of-gas-power-stepping-stone-or-snare-4575/ (accessed on 1 January 2013).
- Simshauser, P.; Nelson, T. The Energy Market Death Spiral - Rethinking Customer Hardship. AGL App. Econ. Pol. Res. 2012. Available online: http://www.aglblog.com.au/wp-content/uploads/2012/07/No-31-Death-Spiral1.pdf (accessed on 20 March 2013).
- ROAM Consulting, Solar Generation Australian Market Modelling, ROAM: Brisbane, Australia, 2012.
- Sandiford, M. Whoʼs afraid of solar PV? The Conversation. 2012. Available online: http://theconversation.edu.au/whos-afraid-of-solar-pv-8987 (accessed on 1 January 2013).
- Gupta, A.K.; Hall, C.A.S. A review of the past and current state of EROI Data. Sustainability 2011, 3, 1796–1809. [Google Scholar] [CrossRef]
- Alsema, E.A. Energy requirements of thin-film solar cell modules—a review. Renew. Sust. Energ. Rev. 1998, 2, 387–415. [Google Scholar] [CrossRef]
- Crawford, R.H.; Treloar, G.J.; Fuller, R.J.; Bazilian, M. Life-cycle energy analysis of building integrated photovoltaic systems (BiPVs) with heat recovery unit. Renew. Sust. Energ. Rev. 2006, 10, 559–575. [Google Scholar] [CrossRef]
- Trainer, T. Can renewables etc. solve the greenhouse problem? The negative case. Energ. Pol. 2010, 38, 4107–4114. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Balogh, S.; Murphy, D.J.R. What is the minimum EROI that a sustainable society must have? Energies 2009, 2, 25–47. [Google Scholar] [CrossRef]
- Raugei, M.; Fullana-i-Palmer, P.; Fthenakis, V. The energy return on energy investment (EROI) of photovoltaics: Methodology and comparisons with fossil fuel life cycles. Energ. Pol. 2012, 45, 576–582. [Google Scholar] [CrossRef]
- Murphy, D.J.; Hall, C.A.S.; Dale, M.; Cleveland, C. Order from chaos: A preliminary protocol for determining the EROI of fuels. Sustainability 2011, 3, 1888–1907. [Google Scholar] [CrossRef]
- Smil, V. Prime Movers of Globalization: The History and Impact of Diesel Engines and Gas Turbines; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Shinnar, R. The hydrogen economy, fuel cells, and electric car. Technol. Soc. 2003, 25, 455–476. [Google Scholar] [CrossRef]
- Bossel, U. The hydrogen ʻillusionʼ: why electrons are a better energy carrier. Cogen. on-site power prod. Mar-Apr 2004, 55–59. [Google Scholar]
- Alstone, P. Embodied Energy and Off-Grid Lighting; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2012. [Google Scholar]
- Wenham, S.R.; Green, M.A.; Watt, M.E.; Corkish, R. Applied photovoltaics; UNSW Centre for Photovoltaic Engineering: Sydney, Australia, 2006. [Google Scholar]
- Pavlov, D. Lead-Acid Batteries: Science and Technology: Science and Technology; Elsevier Science: Oxford, UK, 2011. [Google Scholar]
- Eisler, M.N. “A Modern Philosopherʼs Stone”: Techno-Analogy and the Bacon Cell. Technol. Cult. 2009, 50, 345–365. [Google Scholar] [CrossRef]
- Han, S.; Han, S. Economic Feasibility of V2G Frequency Regulation in Consideration of Battery Wear. Energies 2013, 6, 748–765. [Google Scholar] [CrossRef]
- Productivity Commission, Productivity in Electricity, Gas and Water: Measurement and Interpretation; PC: Canberra, Australia, 2012.
- Australian Bureau of Statistics (ABS), 5206.0 Australian National Accounts: National Income, Expenditure and Product. ABS: Canberra, Australia, 2012.
- Department of Resources Energy and Tourism, Energy in Australia 2012; DRET: Canberra, Australia, 2012.
- Australian Bureau of Statistics (ABS), 4604.0 Energy Account Australia 2010–11; ABS: Canberra, Australia, 2012.
- Jorge, R.S.; Hawkins, T.R.; Hertwich, E.G. Life cycle assessment of electricity transmission and distribution—part 1: Power lines and cables. Int. J. Life Cycle Assess. 2012, 17, 9–15. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Palmer, G. Household Solar Photovoltaics: Supplier of Marginal Abatement, or Primary Source of Low-Emission Power? Sustainability 2013, 5, 1406-1442. https://doi.org/10.3390/su5041406
Palmer G. Household Solar Photovoltaics: Supplier of Marginal Abatement, or Primary Source of Low-Emission Power? Sustainability. 2013; 5(4):1406-1442. https://doi.org/10.3390/su5041406
Chicago/Turabian StylePalmer, Graham. 2013. "Household Solar Photovoltaics: Supplier of Marginal Abatement, or Primary Source of Low-Emission Power?" Sustainability 5, no. 4: 1406-1442. https://doi.org/10.3390/su5041406
APA StylePalmer, G. (2013). Household Solar Photovoltaics: Supplier of Marginal Abatement, or Primary Source of Low-Emission Power? Sustainability, 5(4), 1406-1442. https://doi.org/10.3390/su5041406




