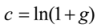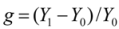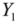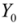The Economic Value of Mangroves: A Meta-Analysis
Abstract
:1. Introduction
2. Mangrove Ecosystem Services and Valuation Methods
| Ecological function | Economic goods and services | Value type | Commonly used valuation method(s) * |
|---|---|---|---|
| Flood and flow control | Flood protection | Indirect use | RCM MP |
| Storm buffering/ sediment retention | Storm protection | Indirect use | RCM PF |
| Water quality maintenance/nutrientretention | Improved water quality | Indirect use | CVM |
| Waste disposal | Direct use | RCM | |
| Habitat and nursery for plant and animalspecies | Commercial fishing and hunting | Direct use | MP NFI |
| Recreational fishing and hunting | Direct use | TCM CVM | |
| Harvesting of natural materials | Direct use | MP NFI | |
| Energy resources | Direct use | MP NFI | |
| Biodiversity | Appreciation of species existence | Non-use | CVM |
| Carbon sequestration | Reduced global warming | Indirect use | RCM |
| Natural environment | Recreation, tourism | Direct use | CVM TCM |
| Existence, bequest, option values | Non-use | CVM |
3. Methods
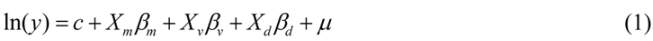
| Variable | Definition and units | Mean(St. dev.) | N |
|---|---|---|---|
| Study characteristics b | |||
| Average value | Baseline category.a It depicts when the value is taken as an average over the entire area of mangroves. | 0.74 (0.44) | 108 |
| Marginal value | 1 if the value was calculated per hectare and 0 otherwise | 0.260 (0.44) | 38 |
| Publication year | Year of publication | 2000 (7.13) | 146 |
| MP | Baseline category a | 0.411 (0.494) | 60 |
| Static PF | 1 if a static production function was used and 0 otherwise | 0.014 (0.117) | 2 |
| Dynamic PF | 1 if a dynamic production function was used and 0 otherwise | 0.068 (0.253) | 10 |
| Mangrove characteristics c | |||
| Other regressions | 1 if other regressions were used and 0 otherwise | 0.034 (0.182) | 4 |
| NFI | 1 if the net factor income method was used and 0 otherwise | 0.192 (0.395) | 28 |
| RC | 1 if the replacement cost method was used and 0 otherwise | 0.212 (0.410) | 31 |
| CV | 1 if the contingent valuation method was used and 0 otherwise | 0.068 (0.253) | 10 |
| Mangrove characteristics c | |||
| Area | Area of the mangrove site in logarithm form | 8.65 (2.937) | 146 |
| Local | Baseline category | ||
| Global | 1 if exports or the contribution of foreign visitors represents a significant portion of value and zero otherwise | ||
| Thailand | Baseline category a | 0.219 (0.415) | 32 |
| Asia (excl. Thailand) | 1 if in Asia but not Thailand and 0 otherwise | 0.514 (0.502) | 75 |
| Middle East & Africa | 1 if in the Middle East and Africa and 0 otherwise | 0.075 (0.265) | 11 |
| Americas | 1 if in the Americas and 0 otherwise | 0.123 (0.33) | 18 |
| Other continent | 1 if in Fiji or Micronesia and 0 otherwise | 0.068 (0.253) | 10 |
| Protected | 1 if site is designated as RAMSAR or provided any other legal protection by the state and 0 otherwise | 0.486 (0.502) | 71 |
| Fisheries | Baseline category a | 0.349 (0.478) | 51 |
| Forestry | 1 if a forestry product and 0 otherwise | 0.24 (0.43) | 35 |
| Recreation | 1 if tourism, recreation, or research and 0 otherwise | 0.096 (0.295) | 14 |
| Coastal protection | 1 if coastal protection and stabilization or flood control and 0 otherwise | 0.197 (0.40) | 29 |
| Carbon sequestration | 1 if carbon sequestration and 0 otherwise | 0.048 (0.214) | 7 |
| Nonuse | 1 if a nonuse value and 0 otherwise | 0.041 (0.199) | 6 |
| Water & air quality | 1 if water and air purification or waste assimilation and 0 otherwise | 0.027 (0.164) | 4 |
| GDP per capita | GDP per capita in logarithmic form | 6.71 (2.345) | 146 |
4. Data
| Variable | Obs. | Mean | Std. Dev. | Min | Max | Median |
|---|---|---|---|---|---|---|
| Fish, shellfish, molluscs (Kg) * | 29 | 539 | 748 | 10 | 2,500 | 126 |
| Shrimp (Kg) | 22 | 146 | 119 | 6 | 349 | 109 |
| Timber (Kg) | 3 | 5,976 | 6,658 | 289 | 13,300 | 4,340 |
| Timber (m3) | 13 | 6 | 4 | 1 | 13 | 5 |
| Fuel wood, charcoal (Kg) | 6 | 5,140 | 11,393 | 6 | 28,370 | 511 |
| Fuel wood, charcoal (m3) | 7 | 102 | 102 | 2 | 230 | 92 |
| Carbon (Mg)** | 34 | 5.27 | 15.41 | 0.02 | 90.5 | 1.69 |
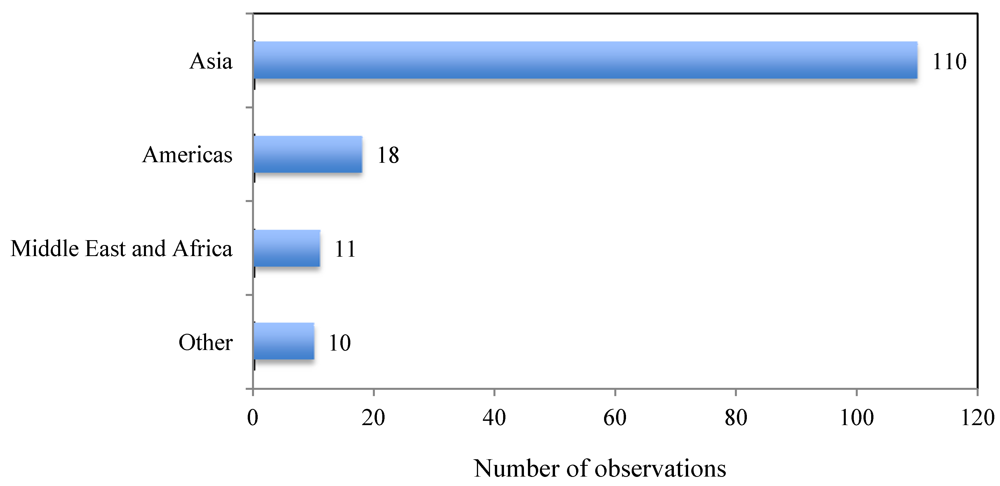
| Service | Obs. | Mean | Min | Max | Median |
|---|---|---|---|---|---|
| Fisheries | 51 | 23,613 | 10.05 | 555,168 | 627 |
| Forestry | 35 | 38,115 | 18.00 | 1,287,701 | 576 |
| Coastal protection | 29 | 3,116 | 10.45 | 8,044 | 3,604 |
| Recreation & tourism | 14 | 37,927 | 1.74 | 507,368 | 1,079 |
| Nutrient retention | 1 | 44 | - | - | - |
| Carbon sequestration | 7 | 967 | 39.89 | 4,265 | 211 |
| Nonuse | 6 | 17,373 | 3.77 | 50,737 | 15,212 |
| Biodiversity | 1 | 52 | - | - | - |
| Water and air purification/ waste assimilation | 4 | 4,748 | 12.43 | 7,379 | 5,801 |
| Traditional uses | 1 | 114 | - | - | - |
| Total | 149 |
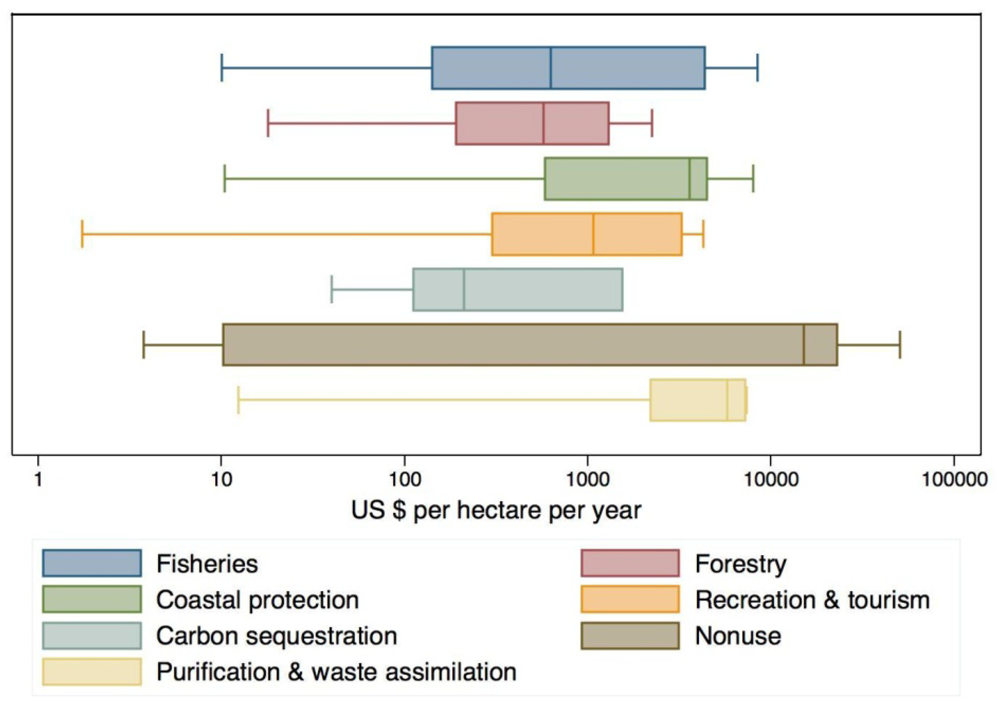
| Method | Obs. | Mean | Min | Max | Median |
|---|---|---|---|---|---|
| Static PF | 2 | 2,975 | 120 | 5,830 | 2,975 |
| Dynamic PF | 10 | 209 | 10 | 1,334 | 53 |
| Other regressions | 4 | 257,905 | 4,377 | 555,168 | 236,037 |
| Market prices | 62 | 31,990 | 2 | 1,287,701 | 768 |
| Net factor income | 28 | 1,545 | 18 | 11,341 | 342 |
| Replacement cost | 32 | 3,390 | 12 | 8,044 | 3,889 |
| Contingent valuation | 10 | 10,691 | 4 | 50,737 | 1,082 |
| Travel cost | 1 | 8,094 | |||
| Total | 149 |

5. Results and Discussion
| Variable | Model 1 | Model 2 |
|---|---|---|
| Marginal value | −1.066 ** (0.491) | −1.274*** (0.4) |
| Static PF | −0.437 (1.019) | −0.328 (0.802) |
| Dynamic PF | 1.148 * (0.682) | 1.344 ** (0.544) |
| Other regressions | 3.705 *** (0.871) | 2.880 *** (0.704) |
| NFI | −0.618 * (0.327) | −0.614 ** (0.264) |
| RC | −0.791 (0.881) | 3.103 *** (0.819) |
| CV | −2.421 (1.944) | 4.199 *** (1.532) |
| Log (area) | −0.0774 (0.056) | −0.018 (0.0463) |
| Global | 0.674 * (0.377) | −0.278 (0.311) |
| Asia (excl. Thailand) | −0.833 * (0.427) | −0.0462 (0.355) |
| Middle East & Africa | 1.043 (1.008) | 2.175 *** (0.804) |
| Americas | −0.581 (0.635) | 0.197 (0.533) |
| Other continent | 0.977 (0.896) | 0.941 (0.73) |
| Protected | 0.845 ** (0.37) | 0.520 * (0.304) |
| Forestry | −0.455 (0.342) | 0.294 (0.412) |
| Recreation | −0.263 (0.766) | −0.00449 (0.732) |
| Coastal protection | 2.059 ** (0.949) | −5.492 *** (1.062) |
| Carbon sequestration | 1.342 ** (0.543) | −3.123 *** (1.064) |
| Nonuse | 5.809 ** (2.266) | 6.403 ** (2.533) |
| Water & air quality | 3.027 ** (1.502) | 7.869 (11.19) |
| Log (GDP) | 0.866 *** (0.0794) | 0.792 *** (0.0664) |
| Forestry_GDP per capita | −9.72 × 10−5 ** (4.06 × 10−5) | |
| Recreation_GDP per capita | −2.07 × 10−5 (2.79 × 10−5) | |
| Coastal protection_GDP per capita | 0.000563 *** (0.00013) | |
| Carbon sequestration_GDP per capita | 0.000288 *** (8.37 × 10−5) | |
| Nonuse_GDP per capita | −0.00119 *** (0.00023) | |
| Water & air quality _GDP per capita | −0.00204 (0.003) | |
| Constant | −0.0787 (0.101) | −0.0881 (0.081) |
| No. of observations | 143 | 142 |
| Adjusted R2 | 0.6 | 0.7 |
| F | 45.85*** | 59.45*** |
| Performance Measure | Model 1 | Model 2 |
|---|---|---|
| In-sample MAPE | 0.402 | 0.35 |
| Transfer MAPE | 0.488 | 0.54 |
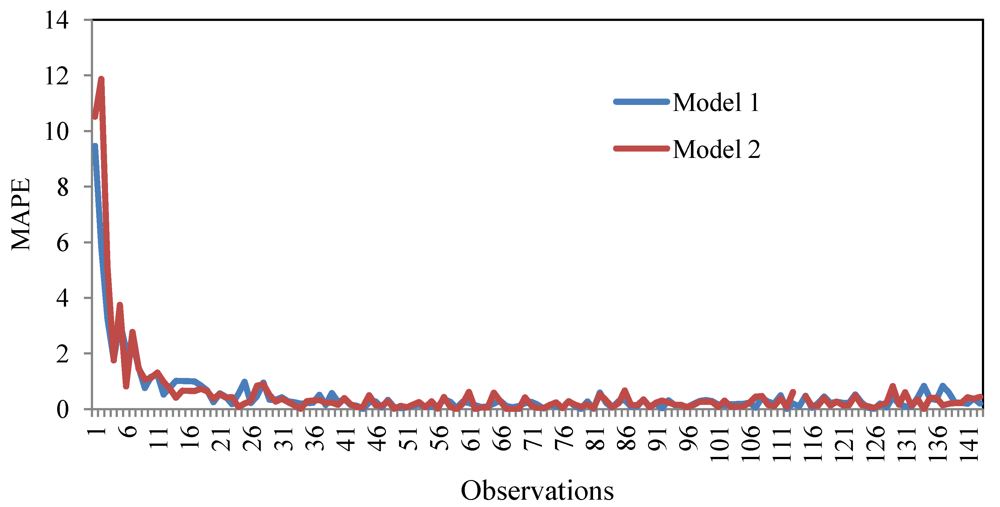
5.1. Robustness Checks
6. Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- Warne, K. Forests of the tides. National Geographic Magazine. February 2007. Available online: http://ngm.nationalgeographic.com/2007/02/mangroves/warne-text (accessed on 27 December 2011).
- Stedman, S.; Dahl, T.E. Status and Trends of Wetlands in the Coastal Watersheds of the Eastern United States 1998 to 2004; National Oceanic and Atmospheric Administration, National Marine Fisheries Service and U.S. Department of the Interior, Fish and Wildlife Service: Charleston, SC, USA, 2008; p. 32. [Google Scholar]
- Sathirathai, S. Economic Valuation of Mangroves and the Roles of Local Communities in the Conservation of Natural Resources: Case Study of Surat Thani, South of Thailand; Research Report no. rr1998061; Economy and Environment Program for Southeast Asia (EEPSEA): Bangkok, Thailand, 1997. [Google Scholar]
- Mitsch, W.J.; Gosselink, J.G. Wetlands; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- For a review of mangroves, see William J. Mitsch and James G. Gosselink. Wetlands; John Wiley & Sons, Inc.: New York, NY, USA, 2000.
- Dahdouh-Guebas, F.; Jayatissa, L.P.; di Nitto, D.; Bosire, J.O.; Lo Seen, D.; Koedam, N. How effective were mangroves as a defence against the recent tsunami. Curr. Biol. 2005, 15, 443–447. [Google Scholar]
- Barbier, E. Valuing ecosystem services as productive inputs. Econ. Policy 2007, 22, 177–230. [Google Scholar] [CrossRef]
- Blaber, S.J. Mangroves and fishes: Issues of diversity, dependence, and dogma. Bull. Mar. Sci. 2007, 80, 457–472. [Google Scholar]
- Bann, C. An Economic Analysis of Alternative Mangrove Management Strategies in Koh Kong Province, Cambodia; EEPSEA Research Report; Environment and Economics Program for South East Asia, International Development Research Centre: Ottawa, Canada, 1997; p. 58. [Google Scholar]
- Chong, J. Protective Values of Mangrove and Coral Ecosystems: A Review of Methods and Evidence; IUCN: Gland, Switzerland, 2005. [Google Scholar]
- Badola, R.; Hussain, S.A. Valuing ecosystem functions: An empirical study on the storm protection function of Bhitarkanika mangrove ecosystem, India. Environ. Conserv. 2005, 32, 85–92. [Google Scholar] [CrossRef]
- Spalding, M. The global distribution and status of mangrove ecosystems. Int. Newsl. Coast. Manag. Intercoast Netw. 1997, 1, 20–21. [Google Scholar]
- Untawale, A.G. Asia Country Reports: India. In Mangroves of Asia and the Pacific: Status and Management; Natural Resources Management Center and National Mangrove Committee, Ministry of Natural Resources: Quezon City, Philippines, 1986; pp. 51–87, Technical Report, UNDP/UNESCO Research and Training Pilot Programme on Mangrove Ecosystems in Asia and the Pacific. [Google Scholar]
- Ruitenbeek, J. Mangrove Management: An Economic Analysis of Management Options with a Focus on Bintuni Bay, Irian Jaya; Dalhousie University Printing Centre: Halifax, Nova Scotia, Canada, 1992; Volume 8, p. 51, Environmental Management Development in Indonesia Project (EMDI) Environmental Reports; School for Resource and Environmental Studies, Dalhousie University, Halifax, Nova Scotia, Canada and the Ministry of State for Population and Environment, Jakarta, Indonesia. [Google Scholar]
- Hirway, I.; Goswami, S. Valuation of Coastal Resources: The Case of Mangroves in Gujarat; Academic Foundation/ Centre for Development Alternatives: Ahmedabad, India, 2007; p. 49. [Google Scholar]
- Ronnback, P. The ecological basis for economic value of seafood production supported by mangrove ecosystems. Ecol. Econ. 1999, 29, 235–252. [Google Scholar] [CrossRef]
- Brander, L.; Florax, R.; Vermaat, J. The empirics of wetland valuation: A comprehensive summary and a meta-analysis of the literature. Environ. Resour. Econ. 2006, 33, 223–250. [Google Scholar] [CrossRef]
- Mangroves are highly susceptible to oil exposure due to the fact that they, where present, are a boundary between land and sea and are hence prime locations for oil accumulation after spills. Past oil spills have resulted in both lethal and sub-lethal effects to mangrove forests. Furthermore, once a spill has occurred, the forests are difficult to protect and clean up due to the convoluted nature of the trees and the fact that the forests are relatively hard to access by humans (Hoff, R. Oil Spills in Mangroves: Planning & Response Considerations; National Oceanic and Atmospheric Administration, NOAA Ocean Service, Office of Response and Restoration: Seattle, WA, USA, 2002. Available Online: http://response.restoration.noaa.gov/book_shelf/34_mangrove_complete.pdf (accessed on 12/5/2010). Added to this are the burrowing activities of crustaceans, which are typically found in mangrove forests. Increasingly high quantities of oil are entering the marine environment through three main routes: Natural seeps, offshore drilling and production and transportation losses. Together, these factors lead to persistent and high levels of oil pollution both on the surface and deep within the soil (Lewis, R. Impact of oil spills on mangrove forests. In Biology and Ecology of Mangroves, Tasks for Vegetation Science; Teas, H.J., Junk, W., Eds.; Springer: Hague, the Netherlands, 1983).
- National Oceanic and Atmospheric Administration (NOAA). Available online: http://response.restoration.noaa.gov/topic_subtopic_entry (accessed on 12 March 2011).
- Bennett, E.; Reynolds, C. The value of a mangrove area in sarawak. Biodivers. Conserv. 1993, 2, 359–375. [Google Scholar] [CrossRef]
- Costanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–261. [Google Scholar]
- Barbier, E.; Strand, I. Valuing mangrove-fishery linkages. Environ. Resour. Econ. 1998, 12, 151–166. [Google Scholar] [CrossRef]
- Bann, C. A Contingent Valuation of the Mangroves of Benut, Johor State, Malaysia; Johor State Forestry Dapartment/ DANCED/ Darudec: Johor, Malaysia, 1999; p. 79, Preparation of an Integrated Management Plan for the Sustainable Use of the Johor Mangrove Forest. [Google Scholar]
- Cooper, E.; Burke, L.; Bood, N. Coastal Capital: Belize the Economic Contribution of Belize’s Coral Reefs and Mangroves; World Resources Institute: Washington, DC, USA, 2009; p. 54. [Google Scholar]
- Brower, R.; Langford, I.; Bateman, I.; Crowards, T.; Turner, R. A Meta-Analysis of Wetland Contingent Valuation Studies; CSERGE Working Paper GEC 97–20; the Centre for Social and Economic Research on the Global Environment (CSERGE): Norwich, UK, 1997. [Google Scholar]
- Heimlich, R.; Wiebe, K.; Claassen, R.; Gadsby, D.; House, R. Wetlands and agriculture: Private interests and public benefits. In Agricultural Economic Report; Resource Economic Division, Economic Research Service, USDA: Washington, DC, USA, 1998; p. 94. [Google Scholar]
- Woodward, R.; Wui, Y. The economic value of wetland services: A meta-analysis. Ecol. Econ. 2001, 257–270. [Google Scholar] [CrossRef]
- Chen, D.-R. Essays on Improving the Econometric Estimation of Wetlands Values via Meta-Analysis.
- Ghermandi, A.; van den Bergh, J.C.J.M.; Brander, L.; de Groot, H.; Nunes, P.A.L.D. The Values of Natural and Constructed Wetlands: A Meta-Analysis; Tinbergen Institute: Amsterdam, Holland, 2009; p. 22, Tinbergen Institute Discussion Paper. [Google Scholar]
- Hamilton, L.S.; Snedaker, R.E. Handbook for Mangrove Area Management; UNEP and East West Center, Environment and Policy Institute: Honolulu, HI, USA, 1984; p. 126. [Google Scholar]
- Martosubroto, P.; Naamin, N. Relationship between tidal forests (mangroves) and commercial shrimp production in Indonesia. Mar. Res. Indones. 1977, 18, 81–86. [Google Scholar]
- Turner, R.E. Intertidal vegetation and commercial yields of penaeid shrimp. Trans. Am. Fish. Soc. 1977, 106, 411–416. [Google Scholar] [CrossRef]
- Pauly, D.; Ingles, J. The relationship between shrimp yields and intertidal vegetation (mangrove) areas: A reassessment. In Ecosistemasde Manglar en América Tropical. Instituto de Ecología A.C. México; Yáñez-Arancibia, A., Lara-Domínguez, A.L., Eds.; UICN/ORMA, Costa Rica, NOAA/NMFS: Silver Spring, MD, USA, 1999; pp. 311–318. [Google Scholar]
- National Research Council of the National Academies, Valuing Ecosystem Services: Toward Better Environmental Decision-Making; Committee on Assessing and Valuing the Services of Aquatic and Related Terrestrial Ecosystems, Water Science and Technology Board, Division on Earth and Life Studies, The National Academies Press: Washington, DC, USA, 2005.
- Barbier, E.B. Valuing the environment as input: Review of applications to mangrove-fishery linkages. Ecol. Econ. 2000, 35, 47–61. [Google Scholar] [CrossRef]
- Freeman, A.M. The Measurement of Environmental & Resource Values: Theory and Methods, 2nd ed; Resources for the Future Press: Washington, DC, USA, 2003. [Google Scholar]
- Barbier, E.B. An approach to economic evaluation of tropical wetlands: With examples from Guatemala and Nicaragua. In Caribbean Ecology and Economics; Girvan, N.P., Simons, D., Eds.; Caribbean Conservation Association: St. Michael, Barbados, 1991; pp. 207–231. [Google Scholar]
- Barbier, E.B.; Acreman, M.; Knowler, D. Economic Valuation of Wetlands: A Guide for Policy Makers and Planners; Ramsar Convention Bureau: Gland, Switzerland, 1997. [Google Scholar]
- Brouwer, R. Environmental value transfer: State of the art and future prospects. Ecol. Econ. 2000, 32, 137–152. [Google Scholar] [CrossRef]
- Carson, R.T.; Hanemann, W.M. Contingent Valuation. In the Handbook of Environmental Economics: Valuing Environmental Changes; Maler, K.-G., Vincent, J.R., Eds.; Elsevier: Amsterdam, the Netherlands, 2005; Volume 2. [Google Scholar]
- For more details about conducting a proper CV study, see Carson, R.T.; Hanemann, W.M. Contingent Valuation. In the Handbook of Environmental Economics: Valuing Environmental Changes; Maler, K.-G., Vincent, J.R., Eds.; Elsevier: Amsterdam, the Netherlands, 2005; Volume 2.or Boyle, K. Contingent valuation in practice. In A Primer on Nonmarket Valuation; Champ, P., Boyle, K., Brown, T., Eds.; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2003.
- Parsons, G.R. The travel cost model. In A Primer on Nonmarket Valuation; Champ, P., Boyle, K., Brown, T., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Phaneuf, D.J.; Smith, V.K. Recreation demand models. In Handbook of Environmental Economics: Valuing Environmental Changes; Maler, K.-G., Vincent, J.R., Eds.; Elsevier: Amsterdam, the Netherlands, 2005; Volume 2. [Google Scholar]
- The proper definition involves the use of the compensated demand curve, but it may not be observable, so the ordinary demand curve is used (Brouwer, R. Environmental value transfer: State of the art and future prospects. Ecol. Econ. 2000, 32, 137–152).
- Stanley, T.D.; Jarrell, S.B. Meta-regression analysis: A quantitative method of literature surveys. J. Econ. Surv. 1989, 3, 161–170. [Google Scholar] [CrossRef]
- Stanley, T.D. Wheat from chaff: Meta-analysis as quantitative literature review. J. Econ. Perspect. 2001, 15, 131–150. [Google Scholar] [CrossRef]
- Mangroves generally occur in the region confined by 30° north and south of the equator. The exceptions to this are a few areas in the North (Japan and Bermuda) and South (New Zealand, Australia and the east coast of South Africa) (Spalding, M. The global distribution and status of mangrove ecosystems. Int. Newsl. Coast. Manag. Intercoast Netw. 1997, 1, 20-21). However, none of these countries are included in our valuations.
- Bennett, E.M.; Peterson, G.D.; Gordon, L.J. Understanding relationships among multiple ecosystem services. Ecol. Lett. 2009, 12, 1394–1404. [Google Scholar] [CrossRef]
- Barbier, E.B. Progress and challenges in valuing coastal and marine ecosystem services. Rev. Environ. Econ. Policy. 2012, 6, 1–19. [Google Scholar] [CrossRef]
- Guerrya, A.D.; Ruckelshausa, M.H.; Arkemaa, K.K.; Bernhardta, J.R.; Guannela, G.; Kima, C.-K.; Marsikb, M.; Papenfusa, M.; Tofta, J.E.; Verutesa, G.; et al. Modeling benefits from nature: Using ecosystem services to inform coastal and marine spatial planning. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2012, iFirst, 1–15. [Google Scholar]
- Ong, P.; Padilla, J. Assessment of fisheries-related functions of the Pagbilao experimental mangrove forest. In Mangroves or Fishponds? Valuation and Evaluation of Alternative uses of a Mangrove Forest in the Philippines; Janssen, R., Padilla, J.E., Eds.; Institute for Environmental Studies (IVM), Vrije Universiteit: Amsterdam, the Netherlands, 1996. [Google Scholar]
- Gammage, S. Estimating the Returns to Mangrove Conversion: Sustainable Management or Short Term Gain? Environmental Economics Programme, Discussion Paper; International Institute for Environment and Development: London, UK, 1997; p. 48, cited in Spaninks, F.; Beukering, P. Economic Valuation of Mangrove Ecosystems: Potential and Limitations; CREED Working Paper Series; International Institute for Environment and Development, Vrije Universiteit: Amsterdam, The Netherlands, 1997; Working paper No. 14, p. 53. [Google Scholar]
- Sanchirico, J.N.; Mumby, P. Mapping ecosystem functions to the valuation of ecosystem services: Implications of species-habitat associations for coastal land-use decisions. Theor. Ecol. 2009, 2, 67–77. [Google Scholar] [CrossRef]
- Sanchirico, J.N.; Springborn, M. How to get there from here: Ecological and economic dynamics of ecosystem service provision. Environ. Resource Econ. 2011, 48, 243–267. [Google Scholar] [CrossRef]
- OLS estimates in meta-analyses should only be used for hypothesis-testing if robust standard errors are used (Nelson, J.P.; Kennedy, P.E. The use (and abuse) of meta-analysis in environmental and natural resource economics: An assessment. Pennsylvania State University, unpublished paper, 2008. Available online: http://ssrn.com/abstract=1117490 (accessed on 12 November 2011). Nevertheless, we ran the OLS regression with standard errors, but got results that were very similar to those with robust standard errors..
- We also ran the regression while manually excluding outliers that lie outside of logical cutoff points revealed by the data. Hence, we excluded observations representing the 3 lowest values and 4 highest values of annual per hectare values. The results were very similar to the those obtained by the robust regression, with the only difference being that in the former the estimated coefficient of per capita GDP was significant. Consequently, we have not reported the results of the OLS regression.
- The robust regression process is one whereby a regression is first run and the observations with a Cook’s D (Cook, R.D. Detection of influential observation in linear regression. Technometrics 1977, 19, 15-18) greater than 1 are excluded to eliminate gross outliers. An iterative process then proceeds where case weights from absolute residuals are generated in each step and used for the regression in the following step. The process continues until the maximum change in weights falls below a pre-determined tolerance threshold.
- Mrozek, J.R.; Taylor, L.O. What determines the value of life? A meta-analysis. J. Policy Anal. Manag. 2002, 21, 253–270. [Google Scholar] [CrossRef]
- Nelson, J.P.; Kennedy, P.E. Available online: http://ssrn.com/abstract=1117490 (accessed on 12 November 2011), The use (and abuse) of meta-analysis in environmental and natural resource economics: An assessment. Pennsylvania State University, unpublished paper, 2008..
- We also ran the regression while clustering the observations of each to study to allow correlations between them while maintaining independence across studies. The results were very similar to those reported for OLS with robust standard errors, with the only exception that the estimated coefficient for area became insignificant. Consequently, we have not reported the results of the cluster regression.
- Another consideration taken into account when choosing the studies to be included is that the valuations be measured in the absence of mangrove conversion into other uses. For example, aquaculture is only considered if the existing mangrove swamps are used for this activity, but not if the mangroves are cleared for the purposes of aquaculture.
- Costanza, R.; Farber, S.; Maxwell, J. Valuation and management of wetland ecosystems. Ecol. Econ. 1989, 1, 335–361. [Google Scholar] [CrossRef]
- The first approach was used by Barbier, E.; Strand, I. Valuing mangrove-fishery linkages. Environ. Resour. Econ. 1998, 12, 151–166., the second and third were used by Gammage, S. Estimating the Returns to Mangrove Conversion: Sustainable Management or Short Term Gain? Environmental Economics Programme, Discussion Paper; International Institute for Environment and Development: London, UK, 1997; p. 48 (Spaninks, F.; Beukering, P. Economic Valuation of Mangrove Ecosystems: Potential and Limitations; CREED Working Paper Series; International Institute for Environment and Development, Vrije Universiteit: Amsterdam, The Netherlands, 1997; Working paper No. 14, p. 53) and the fourth was used by Aburto-Oropeza, O.; Ezcurra, E.; Danemann, G.; Valdez, V.; Murray, J.; Sala, E. Mangroves in the Gulf of California increase fishery yields. Proc. Natl. Acad. Sci. USA 2008, 105, 10456–10459.
- Engle, V. Estimating the provision of ecosystem services by gulf of mexico coastal wetlands. Wetlands. 2011, 31, 179–193. [Google Scholar] [CrossRef]
- This fact also holds for the original number of observations before exclusion of studies.
- Brander, L.; Florax, R.; Vermaat, J. The empirics of wetland valuation: A comprehensive summary and a meta-analysis of the literature. Environ. Resour. Econ. 2006, 33, 223–250, Note that the their study includes all types of wetlands and not just mangroves. [Google Scholar] [CrossRef]
- Halvorsen, R.; Palmquist, R. The interpretation of dummy variables in semilogarithmic equations. Am. Econ. Rev. 1980, 70, 474–475. [Google Scholar]
- The relationship between the coefficient and the relative effect of the categorical variable on the dependent variable is given by
where c is the estimated coefficient and
where
and
denote the value of the dependent variable when the categorical variable takes the value of 1 and 0, respectively (Halvorsen, R.; Palmquist, R. The interpretation of dummy variables in semilogarithmic equations. Am. Econ. Rev. 1980, 70, 474–475 ).
- Barbier, E.; Strand, I.; Sathirathai, S. Do open access conditions affect the valuation of an externality? Estimating the welfare effects of mangrove-fishery linkages in Thailand. Environ. Resour. Econ. 2002, 21, 343–367. [Google Scholar] [CrossRef]
Supplementary Files
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Salem, M.E.; Mercer, D.E. The Economic Value of Mangroves: A Meta-Analysis. Sustainability 2012, 4, 359-383. https://doi.org/10.3390/su4030359
Salem ME, Mercer DE. The Economic Value of Mangroves: A Meta-Analysis. Sustainability. 2012; 4(3):359-383. https://doi.org/10.3390/su4030359
Chicago/Turabian StyleSalem, Marwa E., and D. Evan Mercer. 2012. "The Economic Value of Mangroves: A Meta-Analysis" Sustainability 4, no. 3: 359-383. https://doi.org/10.3390/su4030359
APA StyleSalem, M. E., & Mercer, D. E. (2012). The Economic Value of Mangroves: A Meta-Analysis. Sustainability, 4(3), 359-383. https://doi.org/10.3390/su4030359