Advancing Sustainable Development and the Net-Zero Emissions Transition: The Role of Green Technology Innovation, Renewable Energy, and Environmental Taxation

Abstract

In the macro context of promoting sustainable development and achieving net zero emissions, the role of green technology innovation, renewable energy utilization and environmental policy is crucial. However, there is still a lack of consistent empirical evidence regarding the combined emission reduction effect of these three factors in OECD countries. This study aims to empirically examine the combined impact of green technology innovation (GTI), renewable energy consumption (REC), and environmental taxes (ETAX) on carbon dioxide emissions. We expect that the former two will effectively reduce emissions, while the effect of environmental taxes depends on their design. Based on the panel data of 35 OECD economies from 1990 to 2019, this study adopts the augmented mean group (AMG) as the main estimation method, and uses the common correlation mean group (CCEMG) for the robustness test. To control potential endogenous issues, the difference generalized method of moments (GMM) is also employed for estimation. The causal relationship between variables is tested using the Dumitrescu–Herlin method. The results show that, as expected, GTI and REC have a significant negative impact on carbon dioxide reduction. However, ETAX is positively correlated with carbon emissions and does not have statistical significance, which deviates from the ideal policy effect and suggests that there may be efficiency bottlenecks in the current tax design. The causality test further reveals that there is a significant two-way causal relationship between CO₂ emissions and GTI, REC, ETAX, GDP, and fossil fuel consumption (FEC). Therefore, it is recommended that OECD countries give priority to expanding investment in green technologies and renewable energy infrastructure and re-evaluate and optimize environmental tax policies to effectively promote the transition to a low-carbon economy.

1. Introduction

Pursuing sustainable development and transitioning towards net-zero emissions are central to addressing climate change, environmental degradation, and resource depletion. IPCC [1] emphasizes that urgent action is required to limit global warming to within 1.5 °C above pre-industrial levels, which is a critical threshold for avoiding catastrophic climate impacts. As both major contributors to global emissions and leaders in climate action, OECD countries aim to balance economic growth with environmental sustainability. In this context, green technology innovation (GTI), renewable energy consumption (REC), and environmental taxes (ETAX) are considered three key strategies for reducing emissions.

Green technology innovation serves as a fundamental driver of the transition to a low-carbon economy, encompassing a range of technologies from energy efficiency improvements to carbon capture and storage (CCS) [2]. Renewable energy sources such as solar and wind are now cost-competitive and contribute to lower carbon intensity [3]. Environmental taxes aim to internalize the social costs of carbon emissions and thereby stimulate the shift toward cleaner energy [4]. However, each of these strategies faces implementation challenges: GTI often confronts adoption barriers; REC poses issues related to system integration and grid stability; and the effectiveness of ETAX depends heavily on specific design features, such as tax rate calibration and revenue recycling [5,6]. Therefore, OECD policymakers should prioritize increasing investment in green research and development and expanding renewable energy infrastructure. Concurrently, environmental tax frameworks could be redesigned to incorporate revenue recycling mechanisms. Together, these measures offer a methodologically sound approach to decarbonization for developed economies.

Despite OECD countries’ disproportionate share of global emissions (Figure 1 and Figure 2) and their binding climate commitments, empirical analyses on the integrated impact of these three drivers remain scarce. To address this crucial gap, this study establishes the following objectives: within a robust analytical framework that accounts for both cross-sectional dependence and heterogeneity, we aim to empirically examine the combined impact and relative effectiveness of GTI, REC, and ETAX on carbon dioxide emissions in OECD countries. To this end, this study employs panel data from 35 OECD economies spanning 1990–2019 and adopts advanced second-generation econometric techniques—specifically the Augmented Mean Group (AMG) estimator with Common Correlated Effects Mean Group (CCEMG) robustness checks. This approach overcomes limitations related to cross-sectional dependence and heterogeneity that limited prior studies. It also enhances the generalizability of the results.

The paper proceeds as follows: Section 2 reviews the extant literature; Section 3 describes the data and methodology; Section 4 presents and discusses the results; and Section 5 concludes and outlines the policy implications.

2. Review of the Literature

2.1. Green Technology Innovation and CO₂ Emissions

The relationship between green technology innovation (GTI) and CO₂ emissions is essential for climate change mitigation. Although most research suggests that GTI reduces emissions, significant nuances and contextual dependencies exist. Empirical studies across different regions consistently show a generally negative association between GTI and emissions. Popp [7] illustrates this negative relationship in OECD countries by using patent data as an innovation proxy. Similarly, cross-country analyses by Dechezleprêtre et al. [8] and Aghion et al. [9] further establish that economies with higher numbers of green patent filings tend to experience slower CO₂ growth and lower per capita emissions. Regional studies support these findings: Zhou et al. [10] report that GTI reduces emissions in Europe. Liu et al. [11] observe that its effectiveness is stronger in Chinese regions with stringent environmental regulations. However, this relationship is not a simple linear correlation. Its effectiveness depends substantially on the stage of economic development, the maturity of the technological system, and the supporting policies.

Firstly, the emission reduction effect of GTI demonstrates a clear income threshold and regional heterogeneity. Research indicates that the resulting improvement in carbon productivity is significant only in economies above a certain income level, whereas its impact remains limited in low-income countries [12]. This discovery suggests that within the OECD economies, although they all belong to the developed group, the internal development differences among them may also lead to the heterogeneity of the GTI emission reduction effect. Moreover, a disaggregated analysis across European countries reveals that GTI significantly lowers emissions in Eastern and Southern Europe, while potentially increasing them in Western and Northern Europe due to structural rebound effects [13]. This outcome underscores the importance of contextual dependence.

Secondly, the relationship between GTI and carbon emissions can involve complex nonlinearities and rebound effects. Not only in Europe, but also based on provincial panel data from China, evidence shows that the impact of GTI on local and adjacent regions’ carbon intensity follows an “inverted U-shaped” relationship [14]. That is, in the early stage of development, it may push up emissions due to the technology lock-in effect, and only after reaching the critical point can it truly play a role in reducing emissions. More notably, research indicates that even in technologically mature transportation sector, total emissions can rise despite lower per-unit emissions, owing to increased overall usage [15]. Together, these counter-intuitive findings suggest that the net emission-reduction effect of GTI is not guaranteed; rather, it depends strongly on a comprehensive policy framework capable of mitigating rebound effects.

In summary, the existing literature reveals a central tension in the relationship between GTI and CO₂ emissions: while macro-level evidence broadly supports GTI’s role in reducing emissions, micro-level analyses show that its effectiveness depends heavily on development levels, regional context, technology types, and supporting policies, and can be undermined by rebound effects. This underscores the importance of using rigorous methods that control for cross-country heterogeneity and common shocks when assessing the overall impact of GTI.

2.2. Renewable Energy Consumption and CO₂ Emissions

Renewable energy plays a pivotal role in decarbonization and the achievement of net-zero targets, thereby directly contributing to Sustainable Development Goals (SDGs) 7 and 13 [16,17]. Replacing fossil fuels improves energy security, promotes sustainable economic growth, and lowers CO₂ emissions. Empirical evidence confirms this inverse relationship across OECD countries [18], and in the U.S., where renewable energy supports carbon neutrality [19]. However, the strength and significance of this relationship are far from consistent. In-depth studies of OECD or similar developed economies reveal that the abatement effect of renewable energy is moderated by a complex set of factors.

Firstly, the institutional and policy context serves as a crucial moderating variable. A sound policy framework and high-quality institutions can significantly enhance the emission reduction effect of renewable energy. The research indicates that in OECD countries with a sound policy framework, the emission reduction effect of renewable energy is more pronounced. On the contrary, in an environment with weak regulations, the environmental benefits may be greatly reduced [20]. Furthermore, macroeconomic factors, such as financial market deepening and research and development (R&D) investment, have also been shown to indirectly strengthen the emission reduction pathway of renewable energy. They do so by promoting clean energy consumption [21].

Secondly, the challenges in integrating technical systems may reduce their net emission reduction contribution. The inherent intermittency of wind and solar power means that, without adequate energy storage or flexible backup capacity, fossil fuel-based generation may still be required for grid balancing and peak shaving. This reliance can partially offset the emission reduction potential of renewables. Consequently, transitioning to a power system with a high share of renewable energy requires not only greater installed capacity but also systemic infrastructure upgrades. These include the development of smart grids, demand-side management, and sector coupling [22].

Finally, the “rebound effect” and the hidden costs of the upstream supply chain constitute significant constraints. Energy efficiency improvements and the decline in energy costs may stimulate additional energy consumption, thereby eroding some of the emission reduction gains [23]. Studies have shown that for every 1% increase in the penetration rate of renewable energy, the resulting reduction in emissions may be relatively limited [24]. Furthermore, the production of renewable energy equipment (such as photovoltaic panels and wind turbines) relies on key minerals like rare earths. The mining and processing of these minerals themselves have high energy consumption and pollution characteristics, which constitute hidden environmental costs from a full life cycle perspective.

In conclusion, while theoretical and empirical evidence supports the emission reduction effect of renewable energy consumption (REC), the realization of its net environmental benefits is conditional and heterogeneous. The OECD countries examined in this study generally possess relatively complete institutional frameworks, advanced technological capabilities, and clear emission reduction commitments. This macro environment is favorable for REC to contribute significantly to emission reductions. However, the internal differences among countries in terms of energy structure, policy depth, level of globalization, and technological integration capabilities may also lead to heterogeneity in the effectiveness of REC emission reduction.

2.3. Environmental Tax and CO₂ Emissions

Environmental taxes (ETAX), including carbon levies, internalize pollution’s social costs to incentivize cleaner energy use. Empirical research generally supports their efficacy in reducing CO₂ emissions and accelerating renewable adoption, as demonstrated by meta-analyses [25], cross-national studies [26,27], and successful implementations like Sweden’s carbon tax achieving 25% emission reductions alongside growth [28]. However, there is a growing consensus that the effectiveness of environmental taxes is not unconditional, and that their effects are highly constrained by the specific design, implementation environment, and macroeconomic context of the policy [29]. Recent studies based on nonlinear models reveal that there may be a critical threshold effect on the abatement effect of environmental taxes. For example, Ulucak et al. (2020) found in the study of BRICS countries that the emission reduction effect of environmental tax is highly dependent on a country’s level of globalization; In the low stage of globalization, environmental taxes may even exacerbate emissions by triggering a “green paradox” [30]. This suggests that the theoretical efficacy of environmental taxes may be weakened or reversed in practice when certain preconditions are not met.

First, inadequate tax rates and coverage are seen as core constraints. The case study shows that the carbon tax in British Columbia, Canada, failed to bring about a significant decrease in the total emissions of the province due to its low tax rate and exemption of key emitting sectors [31]. Chile [32] also pointed out that its symbolic low-tax carbon tax had a limited effect on emission reduction. This strongly implies that the level of environmental taxes in the OECD countries in the sample of this study may not reach the threshold to effectively motivate the transition.

Secondly, the signal of an isolated environmental tax will be diluted without a coordinated policy and reasonable revenue reuse. Studies in G7 countries [33] show that improving energy efficiency can reduce carbon emissions more directly than environmental taxes. Without complementary measures such as energy efficiency standards, subsidies for renewable energy, and channeling tax revenues into green investment, a single price signal may struggle to drive systemic change.

Finally, macro background and institutional quality play a moderating role. Paradoxical outcomes emerge in weak enforcement regimes where taxes trigger fossil fuel smuggling [34]. Financial factors may also offset the effect of taxes, for example, unguided financial inclusion may stimulate high-carbon consumption [35]. This highlights the key context dependence.

Overall, the effectiveness of environmental taxes in actual emission reduction is constrained by multiple factors. Their ineffectiveness may stem from the following aspects: Firstly, the tax rate is insufficient or the coverage is limited, failing to reach the threshold for stimulating behavioral changes; Secondly, the tax design lacks complementary policies and revenue recycling mechanisms; Thirdly, the differences in macroeconomic structure and institutional quality may affect it, such as in high-carbon locked-in industries or regions with weak law enforcement, environmental taxes may trigger the “green paradox” or evasion behavior; Fourthly, political and economic resistance in policy implementation, such as industry lobbying, exemption clauses, etc., weaken the tax signal. These mechanisms collectively explain why environmental taxes have not shown significant emission reduction effects.

2.4. Gap in the Literature

Green technology innovation (GTI), renewable energy consumption (REC) and environmental taxes (ETAX) have been widely regarded as key tools to promote sustainable development. Although the existing literature has separately explored their relationship with carbon dioxide emissions, there are still two limitations on the whole, which provide the entry point for this study.

First, existing studies fail to provide consistent and comprehensive comparative evidence on the abatement effectiveness of GTI, REC and ETAX, especially within the important group of OECD countries. Secondly, from a methodological perspective, many multi-country panel data studies fail to adequately account for cross-sectional dependence and heterogeneity. This omission can produce biased estimates, thereby undermining the robustness and generalizability of the findings. In addition, the current application of the second generation of panel measurement methods is still limited to a single country, a specific region, or only focuses on bivariate relationships.

Based on this, this study aims to systematically bridge the aforementioned gaps through a unified framework. To this end, we select 35 OECD economies as samples, and adopt the second-generation panel econometric methods with Augmented Mean Group (AMG) estimation as the core, supplemented by Common Correlated Effects Mean Group (CCEMG) for robustness test, to overcome the limitations of the previous methodology. Through empirical analysis, this paper systematically examines the combined impact of these factors on carbon neutrality in OECD countries, and provides clear and targeted decision-making basis for OECD countries to optimize their green policy mix.

3. Materials and Methods

3.1. Theoretical Rationale

To explore the comprehensive impact of green technology innovation, renewable energy consumption, and environmental tax on carbon dioxide emissions, this study has constructed a cross-disciplinary analytical framework that integrates perspectives of technology, energy, and economy. This framework mainly relies on the following three core theories, which jointly explain the internal mechanisms by which different driving factors affect carbon emissions.

Firstly, the theory of technological change and environmental efficiency provides the foundation for this study to examine the role of green technology innovation. This theory emphasizes that targeted technological progress is a key way to enhance environmental performance and resource efficiency [36]. Specifically, green technology innovation encompasses a series of technologies ranging from improving energy efficiency to carbon capture and storage. Its essence lies in significantly reducing carbon emissions generated by unit economic output or energy consumption through improvements in production processes and the development of low-carbon products and services. Therefore, this theory anticipates that green technology innovation can become the fundamental driving force for achieving deep emission reduction without restricting economic growth.

Secondly, the theory of energy transition provides fundamental support for understanding the role of renewable energy consumption in reducing emissions. This theory states that the structural transformation of the global energy system from being dominated by fossil fuels to being dominated by renewable energy is the core for addressing climate change and achieving sustainability [37]. The direct substitution of renewable energy sources (such as solar, wind, and hydro power) for carbon-intensive energy sources like coal, oil, and natural gas can significantly reduce greenhouse gas emissions at the source. This transition process is directly linked to the United Nations’ Sustainable Development Goals, particularly ensuring universal access to affordable, reliable, and sustainable modern energy (SDG 7) and taking urgent action to address climate change and its impacts (SDG 13).

Finally, Pigouvian tax theory serves as the economic foundation for evaluating the effectiveness of environmental taxation policies. This theory posits that by using tax tools to internalize the negative external costs of environmental pollution, it can provide economic incentives for polluters to reduce emissions [38]. A well-designed environmental tax can guide enterprises and households to adopt cleaner production and consumption patterns through price signals, and may use the collected revenue to fund green technology research and development or for fair transition, thereby forming a virtuous cycle of “innovation—emission reduction” [39]. However, the full theoretical potential of environmental taxes is highly dependent on specific design details such as tax rate setting, coverage scope, income utilization methods, and coordination with other policies.

Based on the above theoretical analysis, this study proposes the following core hypotheses:

H1: 

Green technology innovation (GTI) has a significant negative impact on carbon dioxide emissions in OECD countries.

H2: 

Renewable energy consumption (REC) has a significant negative impact on carbon dioxide emissions in OECD countries.

H3: 

Under the current prevailing policy framework, the environmental tax (ETAX) has no significant impact on carbon dioxide emissions in OECD countries.

3.2. Empirical Model Building

Considering the afore-discussed theoretical foundations, this extant study proposes a panel model in a multivariate framework to estimate the impact of green technology innovation, renewable energy consumption, and environmental taxes on CO₂ emissions in OECD economies. Importantly, all variables are transformed into natural logarithms to mitigate potential heteroscedasticity. Thus, our proposed method transforms log-linear model in a panel multivariate context specified as follows:

$${lnCO}_{2it}={\alpha }_i+ {\beta }_{1}ln{GTI}_{it}+{\beta }_2{lnREC}_{it}+{\beta }_{3}ln{ETAX}_{it}+{\epsilon }_{it}$$

(1)

where lnCO₂, lnGTI, lnREC, and lnETAX, respectively, represent the natural logarithm transformations of carbon dioxide emissions, green technology innovation, renewable energy consumption, and environmental taxes. Given the log-linear specification, the coefficients β1, β2, and β3 represent elasticities, indicating the percentage change in CO₂ emissions resulting from a 1% change in the respective explanatory variable, holding other factors constant. ${\epsilon }_{it}$ is the error term, while $i$ and $t$ indicate the country cross-sections and time.

In particular, to control for socioeconomic conditions in nations and time-varying factors that may influence changes in the dependent variable, the study incorporates control variables such as income. Thus, the specified model in Equation (2) is extended as follows:

$${lnCO}_{2it}={\alpha }_i+ {\beta }_{1}ln{GTI}_{it}+{\beta }_2{lnREC}_{it}+{\beta }_{3}ln{ETAX}_{it}+{\sum }_{j=1}^2{\varnothing }_j{Z}_{it}+{\epsilon }_{it}$$

(2)

where ${\alpha }_i$ is a constant term for the individual cross-sections, ${\beta }_1$, ${\beta }_2$ and ${\beta }_3$ are the parameter estimates of capturing the effect of green technology innovation, renewable energy consumption and environmental taxes correspondingly, ${\varnothing }_j$ is $k\times 1$ vector of parameters that accounts for the respective effect of the control variables, whereas $Z_{it}$ is also a vector containing the control variables (economic growth (GDP) and fossil fuel energy consumption (FEC)), where $i$ and $t$ represent individual countries within a panel at a specific time correspondingly and ${\epsilon }_{it}$ represents the error term.

Controlling for GDP and fossil fuel consumption is essential to isolate the impact of green policies on CO₂ emissions, as their confounding effects distort findings. GDP fluctuations conflate cyclical economic effects with policy outcomes—expansions increase emissions irrespective of green advancements, while downturns may falsely suggest policy-driven reductions. Furthermore, omitting fossil fuel consumption risks misattributing emission declines to renewables when they are actually driven by fluctuations in fossil fuel use or prices, inducing omitted variable bias given the interdependencies within energy systems [40]. Environmental tax efficacy further depends on economic/energy contexts [41], while rebound effects necessitate GDP controls to quantify green innovation’s net impact. Fossil fuel controls prevent overstatement of renewables’ displacement effects [42], collectively mitigating biases and clarifying decarbonization pathways.

3.3. Estimation Approach

Prior to estimating the effect of environmental tax, renewable energy consumption, and green technology innovation on CO₂ emissions whilst controlling for economic growth and fossil fuel energy consumption, the following standard panel econometric procedures are carried out steadily. First, the existence of cross-section CSD is examined. CSD arises when unobserved common factors such as global economic shocks, shared policies, or spatial spillovers induce correlations in residuals across units (countries), violating independence assumptions. Ignoring this can lead to biased standard errors and invalid inferences. Based on this, the Pesaran CSD (PCSD) test is employed to examine the issues relating to cross-sectional dependence. The test statistics of the PCSD test were derived from the pairwise correlation coefficients of residuals obtained from individual regressions for each cross-sectional unit. Specifically, for a panel with $N$ cross-sectional units and $T$ periods, the PCSD test calculates the average of all pairwise correlations of residuals between units $i$ and $j$ (denoted as ${\widehat{\rho }}_{ij}$), then standardizes this average to form a statistic that asymptotically follows the standard normal distribution under the null hypothesis of no cross-sectional dependence. The test equation is formulated as follows:

$$PCSD=\sqrt{{\displaystyle \frac{2T}{N(N-1)}}}{\sum }_{i=1}^N{\sum }_{j=i+1}^N{\widehat{\rho }}_{ij}$$

(3)

where ${\widehat{\rho }}_{ij}$ is the sample of the correlation coefficient between the residuals of the units $i$ and $j$. Under the null hypothesis of cross-sectional independence, CSD converges to a normal distribution with mean 0 and variance 1. A significant PCSD test value rejects the null hypothesis, indicating the presence of cross-sectional dependence.

Bearing in mind the potential existence of cross-sectional dependence in panel data settings, it would not be econometrically meaningful to use conventional unit root tests such as the ADF test, PP test and IPS test, since they do not produce robust and reliable outcomes in the presence of cross-sectional dependence issues. In line with this, the study employs a second-generation unit root test by Pesaran [43] known as the cross-section Im, Pesaran and Shin (CIPS) test, in the second phase of the estimation procedure to examine the stationarity properties of the study variables. The CIPS explicitly models dependence by augmenting the standard Dickey–Fuller (DF) regressions with cross-sectional averages of lagged levels and the first differences in the series. For a panel dataset with $N$ cross-sectional units (countries) and $T$ time periods, the CIPS test estimates the cross-sectional augmented DF regression for each unit $i$:

$$∆y_{it}={\alpha }_i+{\beta }_i{y}_{i,t-1}+{\gamma }_i∆{\overline{y}}_{i,t-1}+{\delta }_i{\overline{y}}_{t-1}+{\epsilon }_{it}$$

(4)

where $∆y_{it}$ is the first difference in the variable $y_{it}$, $y_{it-1}$ is the lagged level of $y_{it}$, $∆{\overline{y}}_{i,t-1}={\displaystyle \frac{1}{N}}\sum _{i=1}^N∆y_{i,t-1}$ is the cross-sectional average of lagged first differences, ${\overline{y}}_{t-1}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{y}_{i,t-1}$ is the cross-sectional difference in the lagged levels, whereas ${\alpha }_i$, ${\gamma }_i$ and ${\delta }_i$ are unit-specific coefficients. The inclusion of $∆{\overline{y}}_{i,t-1}$ and ${\overline{y}}_{t-1}$ accounts for common factors affecting all units, mitigating cross-sectional dependence. The CIPS statistics are, thus, estimated as the cross-sectional averages of the $t-$ statistics ($t_i$) for the null hypothesis of $H_0:{\beta }_i=0$ (unit root exists) from each cross-section augmented DF regression:

$$CIPS={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{t}_i$$

(5)

Having confirmed the integration order of the utilized variables, the study further examined the existence of cointegration or long-run liaison among variables within the proposed empirical model using the Westerlund [44] (WE) cointegration test. The test employs an error correction model framework. Thus, for a panel with $N$ cross-section units and $T$ time periods, the error correction model for unit $i$ is specified as follows:

$$\mathsf{\Delta }{y}_{i,t}={\delta }_i\left(y_{i,t-1}+{\pi }_i^{\prime }{x}_{i,t-1}\right)+{\sum }_{j=1}^p{\theta }_{ij}\mathsf{\Delta }{y}_{i,t-j}+{\sum }_{j=1}^q{\gamma }_{ij}\mathsf{\Delta }{x}_{i,t-j}+{\epsilon }_{i,t}$$

(6)

where ${\delta }_i\left(y_{i,t-1}+{\pi }_i^{\prime }{x}_{i,t-1}\right)$ captures the cointegration relationship (speed of adjustment towards the long-run equilibrium) with $y_{i,t-1}$ being the lagged dependent variable, $x_{i,t-1}$ the lagged independent variable(s), ${\pi }_i^{\prime }$ the vector of cointegration coefficients, $\sum _{j=1}^p{\theta }_{ij}\mathsf{\Delta }{y}_{i,t-j}$ represents the lags of the dependent variable’s first difference, capturing the short-term effect and $\sum _{j=1}^q{\gamma }_{ij}\mathsf{\Delta }{x}_{i,t-j}$ denotes the lags of the independent variable(s)’s first difference, capturing the short-term dynamics of $x$’s. The test computes four statistics: two group-mean statistics ($G_{\tau }$ and $G_{\alpha }$), which explore the alternate theory of cointegration of the whole group and two-panel statistics ($P_{\tau }$ and $P_{\alpha }$), which, on the other hand, note that at least one cross-section of the panel is cointegrated. The group-mean statistics aggregate individual unit results, with $G_{\tau }$ averaging the $t-$ statistics of ${\delta }_i$ and $G_{\alpha }$ averages normalized adjustment speeds as follows:

$$G_{\tau }={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\displaystyle \frac{{\delta }_i}{SE\left({\delta }_i\right)}}, G_{\alpha }={\displaystyle \frac{1}{N}}{\sum }_{i=1}^{N}T{\delta }_i$$

(7)

where $SE\left({\delta }_i\right)$ is the standard error of ${\delta }_i$. The panel statistics pools data across units, with $P_{\tau }$ and $P_{\alpha }$ derived from pooled estimates of $\delta$ as follows:

$$P_{\tau }={\displaystyle \frac{\delta }{SE\left(\delta \right)}}, P_{\alpha }=T\delta$$

(8)

The WE cointegration test relies on the null hypothesis, $H_o:{\delta }_i=0 for all i$, which posits no cointegration across units, while the alternative $H_o:{\delta }_i<0 for some i$, suggests cointegration in at least one unit. Critical values are generated via a sieve bootstrap procedure to address cross-sectional dependence. This method resamples residuals while preserving their cross-unit correlation structure, ensuring robustness to shared trends or shocks.

Further, heterogeneity -where parameters vary across cross-sectional units -reflects divergent responses to variables due to institutional, cultural or economic differences. Specifically, the presence or absence of slope heterogeneity leads to the selection of an appropriate estimator for estimating the slope coefficients with respect to the variables specified in the study’s proposed model. Thus, to determine whether slope heterogeneity is an issue of concern, the Pesaran and Yamagata [43] (PY) test is employed prior to finally estimating the relationship among the study variables. The PY test extends Swamy’s method by addressing small-sample bias and cross-sectional dependence. Under the null hypothesis $H_o:{\beta }_i=\beta for all i$, slope coefficients are identical across units (homogeneity), while the alternative allows heterogeneity ($H_o:{\beta }_i={\beta }_j for some i,j$). The test employs two test statistics, which include the delta tilde ($\widetilde{∆}$) and adjusted delta tilde (${\widetilde{∆}}_{adj}$) which modify Swamy’s statistic to correct for bias in finite samples. The statistics are thus estimated as follows:

$$\widetilde{∆}=\sqrt{N}\left({\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left({\widehat{\beta }}_i-{\tilde{\beta }}_{WFE}\right)}^{\prime }\left({\displaystyle \frac{X_i^{\prime }{M}_T{X}_i}{{\widehat{\sigma }}_i^2}}\right)\left({\widehat{\beta }}_i-{\tilde{\beta }}_{WFE}\right)-k\right)/\sqrt{2k}$$

(9a)

$${\widetilde{∆}}_{adj}=\sqrt{N}\left({\displaystyle \frac{S-k\sqrt{\frac{T}{T-1}}}{\sqrt{2k}}}\right)$$

(9b)

where ${\widehat{\beta }}_i$ represent the unit-specific ordinary least square estimates, ${\tilde{\beta }}_{WFE}$ is a weighted fixed-effects pooled estimator, $X_i$ is the matrix of regressors, $M_T$ is the within-group matrix, ${\widehat{\sigma }}_i^2$ is the error variance estimate for unit $i$, $k$ is the number of regressors, $N$ and $T$ are cross-sectional and time dimensions, and $S$ is the Swamy’s original statistic. Under the null hypothesis, $\widetilde{∆}$ and ${\widetilde{∆}}_{adj}$ converge to a standard normal distribution for large $N$ and $T$. Rejection of the null hypothesis thus implies slope heterogeneity, necessitating the implementation of estimators like the AMG, CCEMG, just to mention a few.

Addressing cross-sectional dependence and slope heterogeneity, this study estimates cointegration between CO₂ emissions, environmental taxes, and renewable energy—controlling for GDP and fossil fuels—using AMG [45] and CCEMG [46]. Unlike traditional FE methods imposing homogeneity assumptions, AMG incorporates common dynamic effects (θₜ), capturing unobserved time-varying factors across units, thereby correcting for heterogeneity biases while averaging unit-specific coefficients. This approach ensures robust estimation where conventional methods fail. The AMG model for unit $i$ at time $t$ is thus expressed as follows:

$$y_{it}={\alpha }_i+{\beta }_i{x}_{it}+{\gamma }_i{\theta }_t+{\epsilon }_{it,}$$

(10)

where $y_{it}$ is the dependent variable, $x_{it}$ is a vector of independent variables, ${\alpha }_i$ is a unit-specific intercept, ${\beta }_i$ represents unit-specific slopes, and ${\theta }_t$ is a common term (often proxied by the cross-sectional average of $\Delta y_{i,t}$ or time dummies). By specifying or reformulating Equation (10) with the study variables, the AMG model to be estimated in this study thus becomes

$${lnCO}_{2it}={\alpha }_i+{\beta }_{1}ln{GTI}_{it}+{\beta }_2{lnREC}_{it}+{\beta }_{3}ln{ETAX}_{it}+{\sum }_{j=1}^2{\varnothing }_j{Z}_{it}+{\gamma }_i{\theta }_t+{\epsilon }_{it}$$

(11)

From Equation (11), the AMG estimates for the coefficients or parameters with respect to the explanatory variables and control variables are thus determined by using the cross-sectional means of ${\beta }_i$’s and ${\varnothing }_j$’s as follows:

$${\beta }_{i, AMG}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\widehat{\beta }}_i , {\varnothing }_{i, AMG}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\widehat{\varnothing }}_i$$

(12)

where ${\beta }_{i, AMG}$ and ${\varnothing }_{i, AMG}$ are the AMG estimators of the explanatory variables of interest and control variables for each cross-sectional unit in the panel, ${\widehat{\beta }}_i$ and ${\widehat{\varnothing }}_i$ are the parameter estimates concerning the explanatory variables of interest and the control variables utilized in this study.

On the other hand, the CCEMG estimation method accounts for cross-sectional dependence by including cross-sectional averages of the dependent and independent variables as proxies for unobserved common factors. Using the cross-section averages of the regressors together with those of the response variable, the CCEMG approach approximates latent common factors, allowing the model to filter out cross-unit correlations. Thus, for a cross-sectional unit $i$ at time $t$, the CCEMG model is theoretically expressed as

$$y_{it}={\alpha }_i+{\beta }_i{x}_{it}+{\lambda }_i{\overline{y}}_t+{\mu }_i{\overline{x}}_t+{\epsilon }_{it,}$$

(13)

where ${\overline{y}}_t={\displaystyle \frac{1}{N}}\sum _{i=1}^N{y}_{it}$ and ${\overline{x}}_t={\displaystyle \frac{1}{N}}\sum _{i=1}^N{x}_{it}$ are the cross-sectional averages of the response and regressors at time $t$, whereas ${\lambda }_i$ and ${\mu }_i$ respectively denotes specific unit coefficients of the cross-sectional means of the response and explanatory variables. By specifying the theoretical model in Equation (14) with the study variables, the CCEMG model is empirically expressed as follows:

$$\begin{array}{r}{lnCO}_{2it}={\alpha }_i+ {\beta }_{1}ln{GTI}_{it}+{\beta }_2{lnREC}_{it}+{\beta }_{3}ln{ETAX}_{it}+{\sum }_{j=1}^2{\varnothing }_j{Z}_{it}+{\lambda }_i{\overline{{lnCO}_2}}_t+{\mu }_1\overline{ln{GTI}_t}+{\mu }_2\overline{ln{REC}_t}+\\ {\mu }_3\overline{ln{ETAX}_t}{+{\sum }_{j=1}^2{\psi }_j\overline{Z_t}+\epsilon }_{it}\end{array}$$

(14)

where ${\overline{{lnCO}_2}}_t$, $\overline{ln{GTI}_t}$, $\overline{ln{REC}_t}$, $\overline{ln{ETAX}_t}$ and $\overline{Z_t}$ represents the cross-sectional averages ${lnCO}_{2it}$, $ln{GTI}_{it}$, ${lnREC}_{it}$ and ${lnETAX}_{it}$ together with the control variables $Z_{it}=[{lnGDP}_{it},{lnFEC}_{it}]$ and ${\psi }_j$ is the slope coefficient of the $jth$ control variable.

Similar to the AGM estimator, the CCEMG estimates for the coefficients or parameters with respect to the explanatory variables and control variables are thus determined by the following relations:

$${\beta }_{ CCEMG}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\widehat{\beta }}_i , {\varnothing }_{CCEMG}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\hat{\varnothing }}_i$$

(15)

where ${\beta }_{CCEMG}$ and ${\varnothing }_{ CCEMG}$ are the CCEMG estimators for the explanatory variables and control variables for each cross-sectional unit in the panel, ${\widehat{\beta }}_i$ and ${\widehat{\varnothing }}_i$ are the parameter estimates concerning the explanatory variables of interest and the control variables utilized in this study.

Since the recommended estimation approaches (AMG and CCEMG) only give elasticity inference, the direction of causal relationships between the employed study variables is examined by employing the panel causality approach of Dumitrescu and Hurlin [47] (henceforth, DH test). Unlike conventional tests assuming homogeneous causality, the DH test explicitly accommodates heterogeneity—allowing causal relationships to exist in some cross-sectional units but not others—making it ideal for contexts where structural or institutional differences cause varying effects across economies. The test implements a panel vector autoregressive (VAR) framework to determine if lagged values of variable X improve predictions of variable Y beyond Y’s own history, thereby robustly identifying causal pathways amid unit-specific variations. Thus, for each cross-section unit $i$ and time $t$, the model is specified as

$$Y_{i,t}={\alpha }_i+{\sum }_{k=1}^K{{\gamma }_i}^{\left(k\right)}{Y}_{i,t-k}+{\sum }_{k=1}^K{{\beta }_i}^{\left(k\right)}{X}_{i,t-k}+{ϵ}_{i,t},$$

(16)

where ${\alpha }_i$ represents unit-specific fixed effects, ${{\gamma }_i}^{\left(k\right)}$ and ${{\beta }_i}^{\left(k\right)}$ are the lag coefficients specific to unit $i$ and ${ϵ}_{i,t}$ is the error term. The null hypothesis posits that $X$ does not Granger-cause $Y$ in any unit $(H_o:{{\beta }_i}^{\left(k\right)}=0 \forall i,k)$, while the alternative hypothesis allows for causality in at least some units $(H_o:{{\beta }_i}^{\left(k\right)}\ne 0 for some i)$. This formulation explicitly acknowledges heterogeneity as a causal effect (${{\beta }_i}^{\left(k\right)}$) as being permitted to differ across units. The test statistics are constructed in two stages. First, individual Wald statistics $\left(W_i\right)$ are computed for each unit $i$ to test the null hypothesis ${{\beta }_i}^{\left(k\right)}=0$. These statistics are then averaged across units to form the panel statistic $\overline{W}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{W}_i$. To address cross-sectional dependence and ensure asymptotic normality, the standardized statistic $Z_{\overline{W}}=\sqrt{{\displaystyle \frac{N}{K}}}\left(\overline{W}-K\right)$ is derived, where $N$ is the number of cross-sectional units, and $K$ is the number of lags. Under the null, $Z_{\overline{W}}$ converges to a standard normal distribution, enabling hypothesis testing.

In summary, the analytical roadmap is pictorially illustrated in Figure 3 as

3.4. Data and Descriptive Analysis

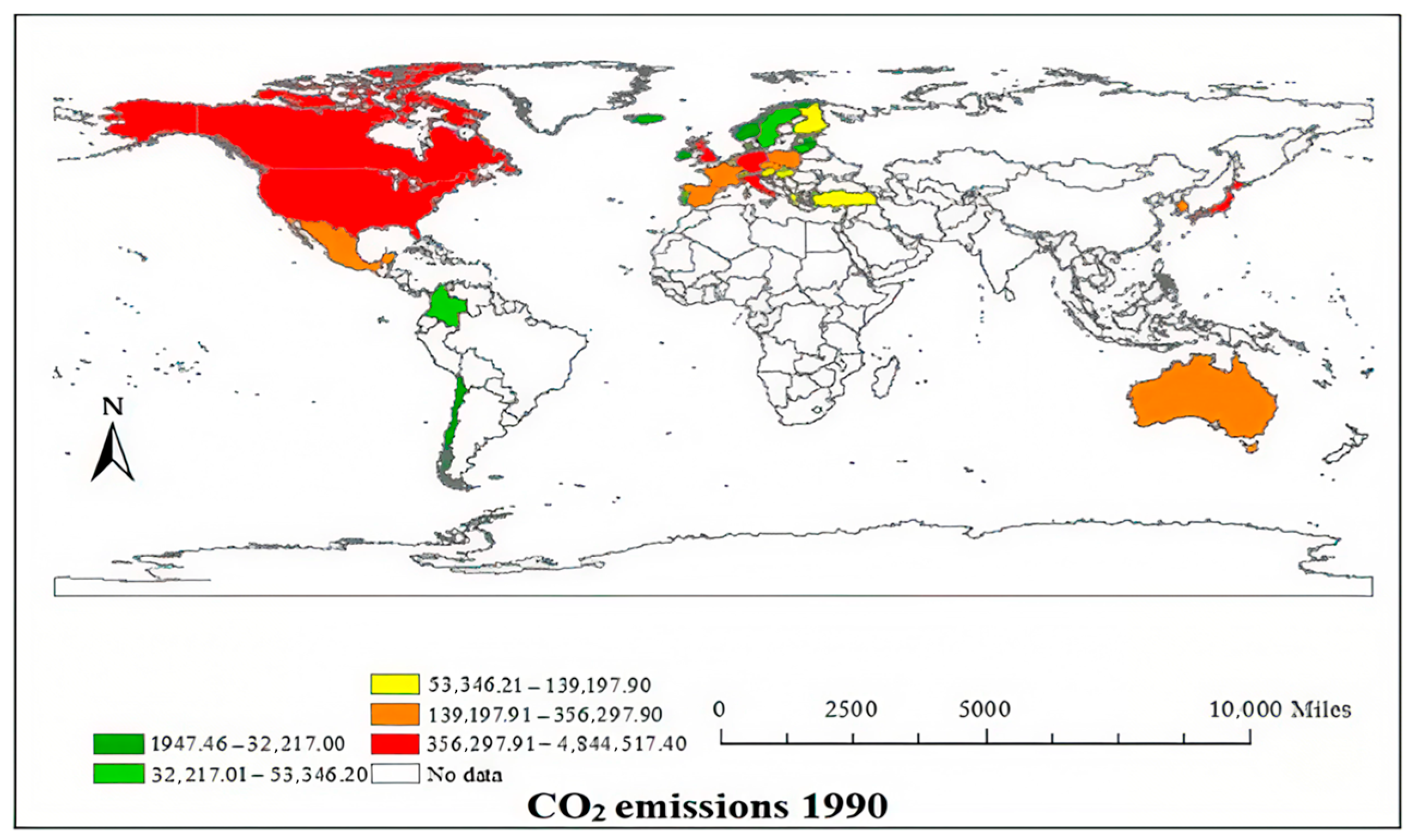
Based on data availability, this study uses annual data of 35 OECD economies from 1990 to 2019. Data on green technology innovation and environmental taxes are sourced from the OECD statistics database. Renewable energy consumption, fossil fuel energy consumption, and GDP were sourced from the World Development Indicators (WDIs). Based on previous literature [48,49,50], the selected variables are based on the United Nations Sustainable Development Goals (7, 8, 9, and 13):

Carbon dioxide emissions (CO₂): The total amount of carbon dioxide emissions (in thousands of tons) sourced from the World Development Indicators (WDI) database. This indicator is a direct result variable for measuring the impact of human activities on climate change and is the core dependent variable for evaluating the ultimate effectiveness of various emission reduction policies and technologies.

Green Technology Innovation (GTI): The “number of environmental-related technology patents” from the OECD statistical database is used as the proxy variable. Patent data is an internationally recognized indicator for measuring the output of technological innovation and the stock of knowledge, and can effectively capture the invention and creation activities in the green technology field. This indicator operationalizes the core concepts in the “Theory of Technological Change and Environmental Efficiency”, and is used to test the contribution of green knowledge creation to emission reduction.

Renewable Energy Consumption (REC): Utilizing the “percentage of renewable energy consumption in the total final energy consumption” from the World Development Indicators (WDI) database. This indicator directly quantifies the extent to which clean energy replaces traditional fossil fuels, and is the core metric for measuring the process of the energy system’s transition towards a low-carbon model.

Environmental Taxes (ETAX): Utilizes “environmental taxes revenue” from the OECD statistical database. It is usually measured as a percentage of GDP or total taxes for cross-country comparisons. This indicator aims to capture the overall policy intensity of countries in using price-based tools for environmental regulation.

GDP: The per capita GDP (in constant 2010 US dollars) is used as a control variable to account for the fundamental impact of economic development stage, economic scale, and related energy demand levels on emissions.

Fossil Fuel Energy Consumption (FEC): The “percentage of fossil fuel energy consumption in the total final energy consumption” (WDI) is used as a control variable to control the carbon intensity of the energy structure itself. This is crucial for isolating the effect of renewable energy (REC) substitution, avoiding mistakenly attributing the decline in fossil fuel energy consumption due to market or technological factors to policy variables.

Table 1. Description of study variables and databases.

Variable	Definition	Unit	Database
CO2	Carbon dioxide emission	Kiloton (kt)	WDI
GTI	Green technology innovation	Number of patents for environmental-related technologies	OECD statistics
REC	Renewable energy consumption	% of total final energy	WDI
ETAX	Environmental taxes	Environmental taxes	OECD statistics
GDP	Gross domestic product per capita	Constant US 2010	WDI
FEC	Fossil fuel energy consumption	% of total final energy	WDI

contains definitions of the variables and data sources.

Table 2. Descriptive statistics of variables.

Variables	CO2	GTI	REC	ETAX	FEC	GDP
Mean	11.531	4.168	2.375	0.766	4.248	10.111
Median	11.197	4.265	2.402	0.874	4.379	10.371
Max.	15.569	9.249	4.348	1.681	4.590	14.027
Min.	7.528	−1.772	−0.817	−4.200	2.328	7.431
Std. Dev.	1.558	2.380	1.054	0.471	0.386	0.834
Skewness	0.020	−0.021	−0.480	−2.639	−2.510	−0.521
Kurtosis	3.216	2.399	2.801	19.172	10.229	3.730
Jarque–Bera	2.111	15.868	42.030	12,660.510	3388.843	70.795
Probability	0.348	0.000	0.000	0.000	0.000	0.000
N	1050	1050	1050	1050	1050	1050
VIF	/	2.29	1.68	1.08	1.55	2.17

summarizes descriptive statistics for the study variables using their respective means, median, maximum and minimum values, standard deviations, skewness and kurtosis, Jarque–Bera test, and Variance Inflation Factor (VIF) outcomes. Specifically, the mean values indicate the average level of each variable across 1050 observations, with CO₂ emissions averaging 11.531, GTI at 4.168, REC at 2.375, ETAX at 0.766, FEC at 4.248, and GDP at 10.111. Further, the maximum and minimum values highlight the range of variations within the dataset. Evidently, CO₂ emissions range from 7.528 to 15.569, GTI varies significantly from −1.722 to 9.429, and ETAX shows a particularly large spread from −4.200 to 1.681, indicating substantial differences in environmental tax policies. The standard deviation values also suggest the extent of variability in each variable, with GTI exhibiting relatively higher variability at 2.380, reflecting the unbalanced development of green technology innovation; while ETAX and FEC show lower dispersion at estimated values of 0.471 and 0.386, respectively. Overall, the standard deviation suggests that while some variables, such as GTI, have substantial fluctuations, others, like ETAX and FEC, display more stability within the dataset.

On the other hand, the median values are close to their respective means, indicating that most variables have approximately symmetric distributions. However, the skewness and kurtosis values of ETAX and FEC show that their distributions deviate from normality (negative skew, high kurtosis), and the Jarque–Bera test further confirms the non-normality. These distribution characteristics suggest that there may be cross-sectional heterogeneity in the data, which needs to be considered in the subsequent modeling. The VIF values are all below 5 (the maximum is 2.29), indicating that severe multicollinearity is not present among the explanatory variables. This supports the reliability of the subsequent regression estimates, a conclusion further corroborated by the correlation matrix presented in Figure 4.

Moreover, Figure 5 presents combined boxplot and violin plots for CO₂ emissions, GTI, REC, ETAX, GDP, and FEC, offering a visual summary of their distributions and dispersion. For CO₂ emissions, the interquartile range indicates a moderate variability in emission levels, with the median positioned centrally, reflecting balanced dispersion. GTI also exhibits a compact interquartile range, suggesting clustered data around the median, which may imply limited but consistent adoption of sustainable technologies. REC also exhibits a similar narrow spread, highlighting regional similarities in OECD economies’ renewable energy usage, although the median levels may reflect modest overall adaptation. Moreover, ETAX displays a tilted distribution, with the median closer to the lower quartile, indicating that most regions in the OECD economies implement relatively low tax policies. Conversely, FEC has a wide interquartile range, underscoring significant variability in reliance on non-renewable energy sources, with the median indicating a moderate overall dependence. GDP finally demonstrates a right-skewed distribution, where the median is closer to the lower end of the scale, indicating economic disparities, as most nations in the OECD community exhibit lower GDP levels. These visual results further emphasize the existence of cross-national heterogeneity.

Figure 6’s scatter plots reveal critical bivariate relationships: CO₂ emissions exhibit a counterintuitive positive correlation with GTI, suggesting innovations may coexist with carbon-intensive processes or exhibit delayed mitigation effects. Conversely, REC shows a clear negative correlation, confirming cleaner energy’s decarbonization role. ETAX displays no discernible trend, indicating that effectiveness depends on enforcement rigor, rate calibration, and complementary policies. FEC demonstrates a strong positive relationship, reinforcing carbon-intensive energy’s environmental impact. GDP exhibits a weak positive correlation, with data dispersion reflecting heterogeneous growth-emissions linkages across economies due to varying efficiency and policies. These visual patterns align with Figure 6’s correlation matrix, collectively highlighting the complex, variable-specific dynamics governing emission drivers in OECD nations.

4. Results and Discussions

4.1. Preliminary Analysis

The results from the Pesaran [51] PCSD test and the test of slope homogeneity are presented in

Table 3. Cross-sectional dependence test and homogeneity test.

Variable		CSD-Test	Correlation
CO2		13.91 ***	0.51
GTI		105.88 ***	0.79
REC		42.72 ***	0.70
ETAX		17.53 ***	0.62
GDP		95.41 ***	0.79
FEC		36.17 ***	0.62
Slope heterogeneity test
$\overline{∆}$	Adjusted $\overline{∆}$
35.220 (0.000) ***	40.225 (000) ***

Note: *** indicates statistical significance at 1%.

.

Specifically, the PCSD test is based on the null hypothesis that there is no residual cross-section correlation across the cross-sections with the panel of OECD economies, as opposed to the alternative hypothesis, which states vice versa. Evidently, the findings from the PCSD test led to the rejection of the null hypothesis since all test values for each utilized variable are statistically significant at 1%. This thus points out the interconnectedness of these economies regarding the study’s variables and further explains why the fight against CO₂ emissions requires unanimous action. Further, the slope homogeneity test is evaluated using the delta tilde ($\widetilde{∆}$) and adjusted delta tilde (${\widetilde{∆}}_{adj}$) test statistics of Pesaran and Yamagata, assuming homogenous slopes across cross-sectional units as the null hypothesis. From the results in Table 3, the null hypothesis of slope homogeneity is rejected since the estimated test values for both delta tilde ($\widetilde{∆}$) and adjusted delta tilde (${\widetilde{∆}}_{adj}$) tests are statistically significant. This implies that there is slope variability or heterogeneity among variables across the cross-sectional unit with the study’s panel of OECD countries. With the evidence concerning the presence of residual cross-sectional dependence and slope heterogeneity, a conclusion can be drawn that adopting conventional unit root tests and cointegration methods could render the conclusions biased.

Addressing cross-sectional dependence and slope heterogeneity, this study employs the CIPS unit root test (

Table 4. Results of the stationarity test.

Variable	CIPS		Remarks
	Level	1st Difference
CO2	−1.524	−4.712 ***	Stationary
GTI	−2.606	−5.042 ***	Stationary
REC	−2.209	−5.023 ***	Stationary
ETAX	−1.291	−4.944 ***	Stationary
GDP	−1.888	−3.210 ***	Stationary
FEC	−2.406	−5.272 ***	Stationary

Note: *** indicates statistical significance at 1%.

), confirming all variables are integrated of order one [I(1)]—non-stationary at levels but stationary when first-differenced. This common integration order [52] enables cointegration testing. The Westerlund–Edgerton approach (selected for robustness to cross-dependence per Dauda et al.) [53] rejects the null hypothesis of no cointegration across all four statistics ($G_{\tau }$, $G_{\alpha }$, $P_{\tau }$ and $P_{\alpha }$) in

Table 5. Cointegration test results.

Statistics	Value	Z-Value	Robust p-Value
Gt	−2.581 ***	−3.508	0.000
Ga	−11.625 **	−2.358	0.009
Pt	−14.616 ***	−4.339	0.000
Pa	−10.433 ***	−4.833	0.000

Note: *** and ** indicate statistical significance at 1% and 5%.

. This provides robust evidence of a significant long-run equilibrium relationship among variables, warranting subsequent estimation of cointegrating vectors.

The Westerlund cointegration test results in Table 5 show that all the statistics significantly reject the null hypothesis of no cointegration relationship. This confirms the existence of a long-term statistical equilibrium between the core variables and carbon emissions, providing a quantitative basis for subsequent tests of theoretical hypotheses. At the same time, the existence of cross-sectional dependence and heterogeneity (Table 3) demonstrates the necessity of using second-generation panel estimation methods such as AMG and CCEMG. Therefore, the subsequent long-term estimation will directly be used to test the hypotheses: to assess whether GTI and REC will significantly reduce emissions as expected, and whether the impact of ETAX will be as expected to be insignificant.

4.2. Long Run Estimation Results

Addressing cross-sectional dependence and slope heterogeneity, this study employs the AMG estimator (with CCEMG robustness checks) to quantify long-run elasticities.

Table 6. Long-run results based on AMG and CCEMG.

Variable	AMG	CCEMG
GTI	−0.019 **	−0.023 *
	(0.018)	(0.051)
REC	−0.210 ***	−0.195 ***
	(0.000)	(0.000)
ETAX	0.033	0.016
	(0.401)	(0.586)
GDP	0.404 ***	0.337 ***
	(0.000)	(0.000)
FEC	0.835 ***	0.632 **
	(0.001)	(0.037)
Wald-Test	62.34 ***	49.55 ***
	(0.000)	(0.000)

Note: ***, **, and * indicate statistical significance at 1%, 5% and 10%. Values in parentheses are probability values.

displays the long-run findings for AMG and CCEMG estimators.

Results confirm that the coefficients of green technology innovation are negative and statistically significant under both estimation methods (AMG: p < 0.05; CCEMG: p < 0.1), indicating that green technology innovation significantly reduces CO₂ emissions. For every 1% increase, emissions decrease by 0.019%, which is in line with the expectation of hypothesis H1. While this marginal effect appears modest relative to Paris Agreement targets requiring 40–50% reductions, it demonstrates innovation’s cumulative decarbonization potential when scaled. Crucially, achieving deep emissions cuts necessitates integrating green innovation within a broader policy mix—including accelerated renewable adoption, strengthened environmental taxation, and enhanced energy efficiency—rather than relying on incremental technological advances alone.

The significant negative coefficient for green technology innovation confirms its efficacy in mitigating CO₂ emissions across OECD economies. This outcome reflects stringent environmental policies—subsidies, tax incentives, and emissions standards—that incentivize firms to adopt innovations, creating a positive feedback loop enhancing sustainability.

Similarly, renewable energy consumption exhibits a statistically significant adverse relationship with emissions: AMG estimations indicate a 0.210% emissions reduction per 1% renewable increase. This result supports Hypothesis H2. This demonstrates renewables’ capacity to displace fossil fuels within OECD energy matrices, particularly where supportive regulatory frameworks enhance economic viability. The transition bolsters energy security through supply diversification while aligning with net-zero objectives, corroborating studies emphasizing renewables as prerequisites for carbon neutrality [18,54,55]. Critically, these findings underscore that technological advancement and renewable deployment—reinforced by policy mechanisms—collectively drive emission reductions in advanced economies. Consequently, OECD nations must prioritize scaling R&D investments in green technologies and expanding renewable infrastructure to accelerate decarbonization.

Regression analysis shows a statistically insignificant positive relationship between environmental taxes and CO₂ emissions in OECD countries. This result supports Hypothesis H3. This conclusion suggests current tax designs fail due to suboptimal rates, extensive exemptions, and weak enforcement, allowing cost-passing rather than green innovation. Sectoral resistance and Ayin and Esen’s threshold theory indicate environmental taxes only reduce emissions above critical behavioral-change levels, implying OECD rates are sub-threshold. Firstly, the environmental tax rates in most OECD countries in the sample may be lower than the critical level required for the transformation of the energy structure, and there are industry exemptions, which weaken the overall emission reduction incentives. Secondly, if the environmental taxes revenue is not directed towards green investment or compensation for affected groups, it is difficult to achieve the “dual dividend” effect, and it may even suppress the adoption of clean technologies due to cost shifting. Moreover, in the absence of complementary policies, a single tax tool is difficult to overcome the path dependence and rebound effects of the energy system. Effective decarbonization requires recalibrating environmental taxes with fewer exemptions, higher thresholds, and strategic revenue recycling. These findings are in line with studies on the threshold effect of the “green paradox”, emphasizing that environmental taxes can only be effective when integrated into a broader policy framework.

Regression analysis confirms robust positive relationships: a 1% GDP increase elevates CO₂ emissions by 0.404% (AMG), reflecting industrialization’s scale effects that amplify fossil fuel demand despite efficiency gains. Fossil fuel consumption shows an even stronger impact (0.835% emissions rise per 1% increase), underscoring thermodynamic realities and the OECD’s structural carbon dependency. These persistent linkages—aligning with environmental Kuznets curve dynamics [56,57,58]—reveal decarbonization efforts are insufficient to offset growth-driven emissions momentum. OECD nations must therefore accelerate structural transitions via aggressive renewable integration, fossil subsidy reallocation, and systemic innovations to disrupt the entrenched growth-emissions trajectory and achieve meaningful decoupling.

OECD economies’ persistent fossil fuel dependence demonstrably elevates CO₂ emissions, validating established ecological impacts and aligning with prior findings [59]. Summarily, the graphic of the long-term results is shown in Figure 7.

Methodologically, the AMG estimator’s robustness was confirmed through Wald tests, indicating strong predictive validity and cross-validated via CCEMG estimation. Although coefficient weights varied slightly (Ref. second column of Table 6), both approaches produced consistent directional results—attributable to their shared capacity for addressing cross-sectional dependence and heterogeneity through distinct factor modeling (AMG directly estimates common factors; CCEMG incorporates cross-sectional averages). This methodological convergence underscores the reliability of the emissions drivers identified in our analysis.

Given that carbon emissions exhibit path dependence and inertia, current emission levels are influenced by previous periods. Model (2) may suffer from endogeneity issues. Therefore, this paper constructs the following dynamic panel data model.

$${lnCO}_{2it}={\alpha }_i+{\gamma }_1{lnCO}_{2i(t-1)}+{\beta }_{1}ln{GTI}_{it}+{\beta }_2{lnREC}_{it}+{\beta }_{3}ln{ETAX}_{it}+{\sum }_{j=1}^2{\varnothing }_j{Z}_{it}+{\epsilon }_{it}$$

(17)

Equation (17) is estimated using the Difference GMM method, with results presented in

Table 7. Estimation Results Based on the Difference GMM Method.

Variable	GMM
L.CO2	0.926 ***
	(0.023)
GTI	−0.012 ***
	(0.003)
REC	0.054 *
	(0.011)
ETAX	0.012 ***
	(0.010)
GDP	0.045 ***
	(0.010)
FEC	0.437
	(0.035)
Constant	−1.508 ***
	(0.269)
AR(1)	p-value = 0.000
AR(2)	p-value = 0.710
Hansen test	chi2(50) = 33.94 Prob > chi2 = 0.975

Note: *** and * indicate statistical significance at 1% and 10%. Values in parentheses are probability values.

. The over-identification test for the model yields a Hansen test p-value of 0.960, indicating the validity of the instruments. The AR(2) test p-value is 0.567, suggesting no serial correlation in the error terms. These results confirm the appropriateness of employing the Difference GMM method to estimate Equation (2). At the 1% significance level, the coefficient of L.CO₂ is significantly positive, confirming the presence of path dependence in carbon emissions. The effects of other variables on carbon emissions are consistent with the conclusions reported in Table 6.

4.3. Causality Test

Table 8. Results of causality test.

Null Hypothesis	$\mathbf{W}-$ Stats	$\overline{\mathsf{{\rm Z}}}-$ Stats	$\mathbf{P}\mathbf{r}\mathbf{o}\mathbf{b}.$	Direction of Causality
GTI $\ne$ CO2	3.279 ***	7.953	0.000	$\leftrightarrow$
CO2 $\ne$ GTI	3.574 ***	9.023	0.000
REC $\ne$ CO2	4.274 ***	11.556	0.000	$\leftrightarrow$
CO2 $\ne$ REC	4.592 ***	12.712	0.000
ETAX $\ne$ CO2	1.945 ***	3.122	0.002	$\leftrightarrow$
CO2 $\ne$ ETAX	3.602 ***	9.125	0.000
GDP $\ne$ CO2	3.610 ***	9.154	0.000	$\leftrightarrow$
CO2 $\ne$ GDP	3.053 ***	7.134	0.000
FEC $\ne$ CO2	2.769 ***	6.106	0.000	$\leftrightarrow$
CO2 $\ne$ FEC	2.625 ***	5.584	0.000

Note: *** indicates statistical significance at 1%.

’s panel causality test reveals bidirectional causation between CO₂ emissions and key explanatory variables—green technology innovation, renewables, environmental taxes, fossil fuels, and GDP—in OECD countries. This highlights a complex, interdependent system where economic, technological, and policy factors both drive and are driven by carbon emissions. Such feedback loops mean progress in one area can lower emissions, yet persistent emissions or slow transitions can hinder decarbonization efforts and reinforce emissions, complicating the energy transition.

First, the results indicate a significant bidirectional causal relationship between GTI and CO₂ emissions. This finding supports and extends the logic of induced technological change. Specifically, causality from GTI to CO₂ emissions confirms that green innovation is an effective driver of long-term emission reduction, thereby supporting Hypothesis H1. In the reverse direction, causality from CO₂ emissions to GTI reveals that mounting emission pressures themselves stimulate the development and adoption of green technologies, creating a dynamic “pressure–innovation–mitigation” feedback loop. This underscores the critical role of stringent emission targets or carbon pricing in continuously inducing innovation.

Second, a significant bidirectional causal relationship is also found between REC and CO₂ emissions. The causality from REC to CO₂ emissions confirms the direct decarbonization mechanism central to energy transition theory. Conversely, causality from CO₂ emissions to REC suggests that rising emission levels or stringent climate policies can accelerate the shift toward renewable energy. This mutually reinforcing relationship implies that proactively advancing the energy transition not only reduces emissions directly but also, by establishing a cleaner energy infrastructure, lowers the long-term cost of future decarbonization.

The bidirectional relationship between environmental taxes and CO₂ emissions is complex: The Granger causality test indicates a significant predictive relationship from ETAX to CO₂ emissions. In the reverse direction, there is also significant causality from CO₂ emissions to ETAX, suggesting a policy-response mechanism whereby rising emissions may trigger stricter taxation. However, when this bidirectional statistical linkage is interpreted in light of the long-run estimation results—which show an economically small and statistically insignificant positive coefficient for ETAX—a critical insight emerges. While a policy intent and feedback loop exist statistically, the current design and implementation of environmental taxes in OECD countries appear insufficient to translate this into a measurable, negative long-run impact on emissions. This is likely due to well-documented design flaws such as sub-optimal tax rates, extensive exemptions, and political economy constraints that dilute the price signal.

Similarly, GDP and CO₂ emissions exhibit reciprocal causality, reflecting the tension between economic growth and climate-related economic risks. Critically, the persistent causality between fossil fuel use and emissions underscores structural path dependence in OECD energy systems, requiring systemic interventions like accelerated phaseouts and carbon adjustments to overcome inertia. These findings align with prior literature [60] and are visualized in Figure 8.

5. Conclusions and Policy Recommendations

Realizing sustainable development and net-zero emission goals remain a central challenge of this century, given escalating global climate change. Developing and deploying sustainable innovations and implementing clean environmental taxation policies are imperative to abate emissions. This study examines the role of green technology innovation, renewable energy consumption, environmental taxes, GDP, and fossil energy consumption in accelerating the carbon neutrality transition of 35 OECD countries, using data from 1990 to 2019. Preliminary econometric tests were used to establish the fundamental association among the indicators. The primary estimations were conducted using the AMG and CCEMG long-term methodologies, and potential endogeneity issues were controlled through the difference generalized method of moments (GMM). The causal relationship was evaluated using the Dumitrescu–Hurling technique. The long-run estimates indicate that green technology innovation and renewable energy consumption significantly reduce CO₂ emissions, thereby contributing positively to sustainable development and net-zero emissions. However, environmental taxes, GDP, and fossil fuel energy have a positive influence on CO₂ emissions. The results suggest that accelerating efforts to achieve net-zero emissions will be aided by green technology innovations and increased renewable energy consumption, which can help curb CO₂ emissions in OECD economies. Conversely, the pursuit of economic growth coupled with continued reliance on fossil fuel energy will hinder progress toward this goal. Finally, the causality test outcomes established bidirectional causal relationships between each explanatory variable and CO₂ emissions, respectively. Based on the outlined outcomes from the long-run estimation and causality test, stringent actions and policies are required to achieve an equitable emissions level and accelerate the shift to carbon neutrality.

Based on this study’s findings, policymakers in OECD countries should prioritize a comprehensive strategy that focuses on accelerating green technology innovation, refining environmental tax policies, and systematically phasing out fossil fuel subsidies. First, given that REC has the greatest emission reduction flexibility, OECD countries should set more ambitious renewable energy targets and overcome integration obstacles through investments in grid modernization, research and development of energy storage technologies, and simplification of administrative procedures. Regarding the “marginal but significant” impact of GTI, policies should aim to expand its scale and diffusion rate. The governments must enhance financial support for green technology development and renewable energy adoption by implementing targeted fiscal incentives such as tax credits and grants and establishing public–private partnerships to boost research and development. Second, environmental tax policies must be reformed to ensure they are sufficiently strong and well-targeted to discourage carbon-intensive activities. This may involve raising tax rates to the effective threshold and gradually expanding the coverage, reducing exempted industries; establishing a “tax-subsidy” linkage mechanism, using the environmental tax revenue specifically to fund green technology innovation, renewable energy infrastructure, and the transformation of affected communities; strengthening the synergy with policies such as energy efficiency standards and carbon emission trading systems to avoid the limitations of a single tool; and enhancing cross-border coordination and institutional enforcement to prevent carbon leakage and tax avoidance. To reduce the harmful impact of fossil fuel consumption on CO₂ emissions, policymakers within OECD economies should phase out fossil fuel subsidies and adopt stringent carbon pricing mechanisms to facilitate the shift toward low-carbon alternatives. Collectively, these measures—bolstering green innovation, optimizing policy, and curbing fossil fuel dependence—offer a clear, actionable pathway for OECD countries to accelerate sustainable development and achieve net-zero emissions.

This study has certain limitations, which also point to directions for future research. Firstly, the measurement of core variables (such as green technology innovation) can still be further improved. In the future, more detailed indicators such as R&D expenditure and technology application data can be adopted to more comprehensively capture their actual impacts. Secondly, in this study, environmental taxes are analyzed as a whole, without distinguishing their specific types (such as carbon taxes and energy taxes) and design details (such as tax rates, coverage, and revenue usage methods). Future research can delve deeper into the heterogeneity of emission reduction effects resulting from different tax system designs. Furthermore, in the future, the sample can be expanded to include non-OECD countries, and additional variables such as institutional quality and financial structure can be introduced to more systematically reveal the specific transmission mechanisms of various policy tools in different socio-economic contexts. Finally, due to the limited availability of complete comparable data for the core variables, the time range of this study is up to 2019. Subsequent research can extend the time range to recent years when the data is complete to further verify the dynamic applicability of the conclusions.