Sector-Specific Carbon Emission Forecasting for Sustainable Urban Management: A Comparative Data-Driven Framework
Abstract
1. Introduction
2. Materials and Methods
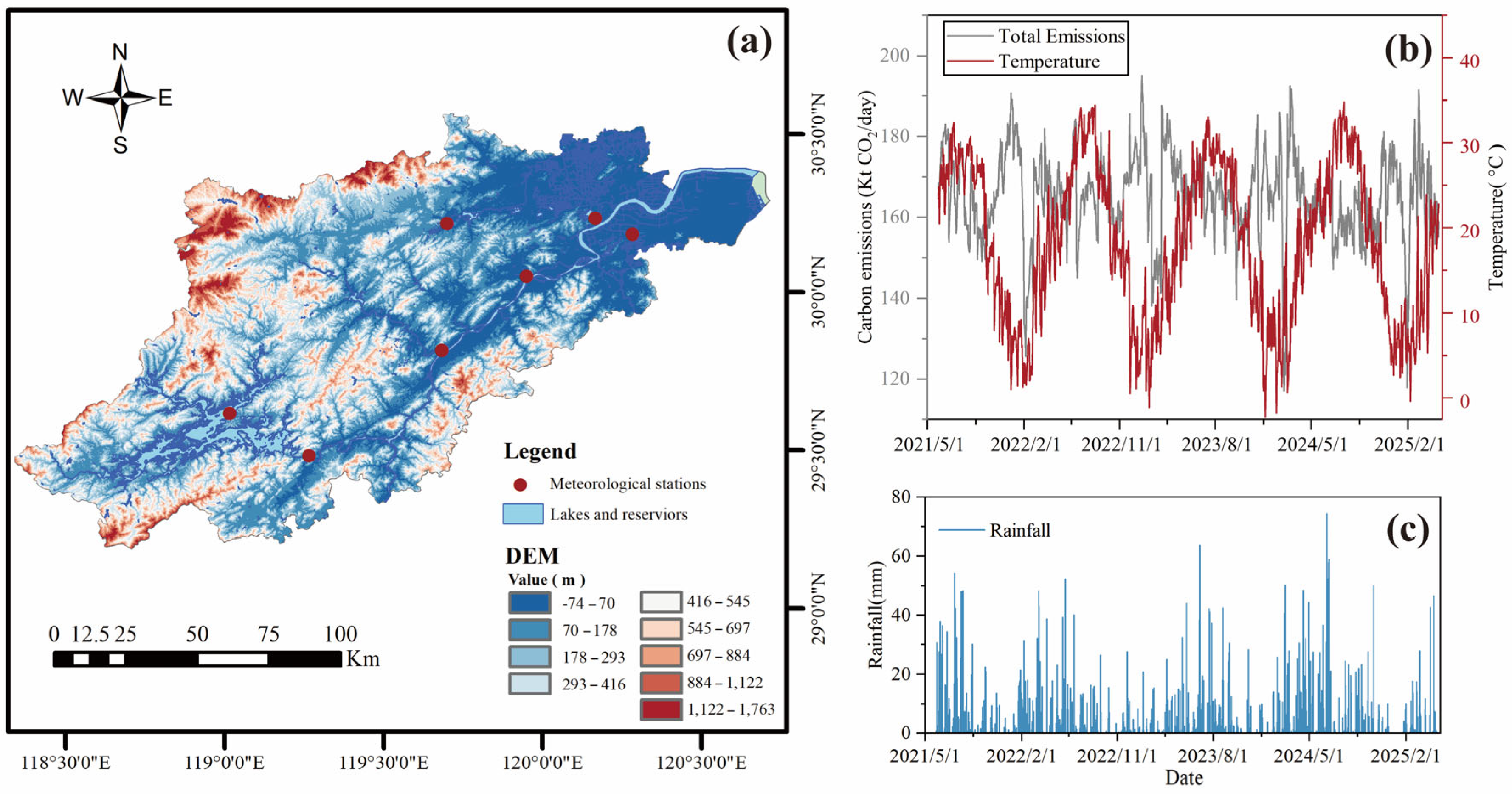
2.1. Study Area
2.2. Data Sources and Preprocessing
2.3. Correlation Analysis Between Meteorological Factors and Carbon Emissions
2.4. Model Building
2.5. Experimental Design and Performance Evaluation
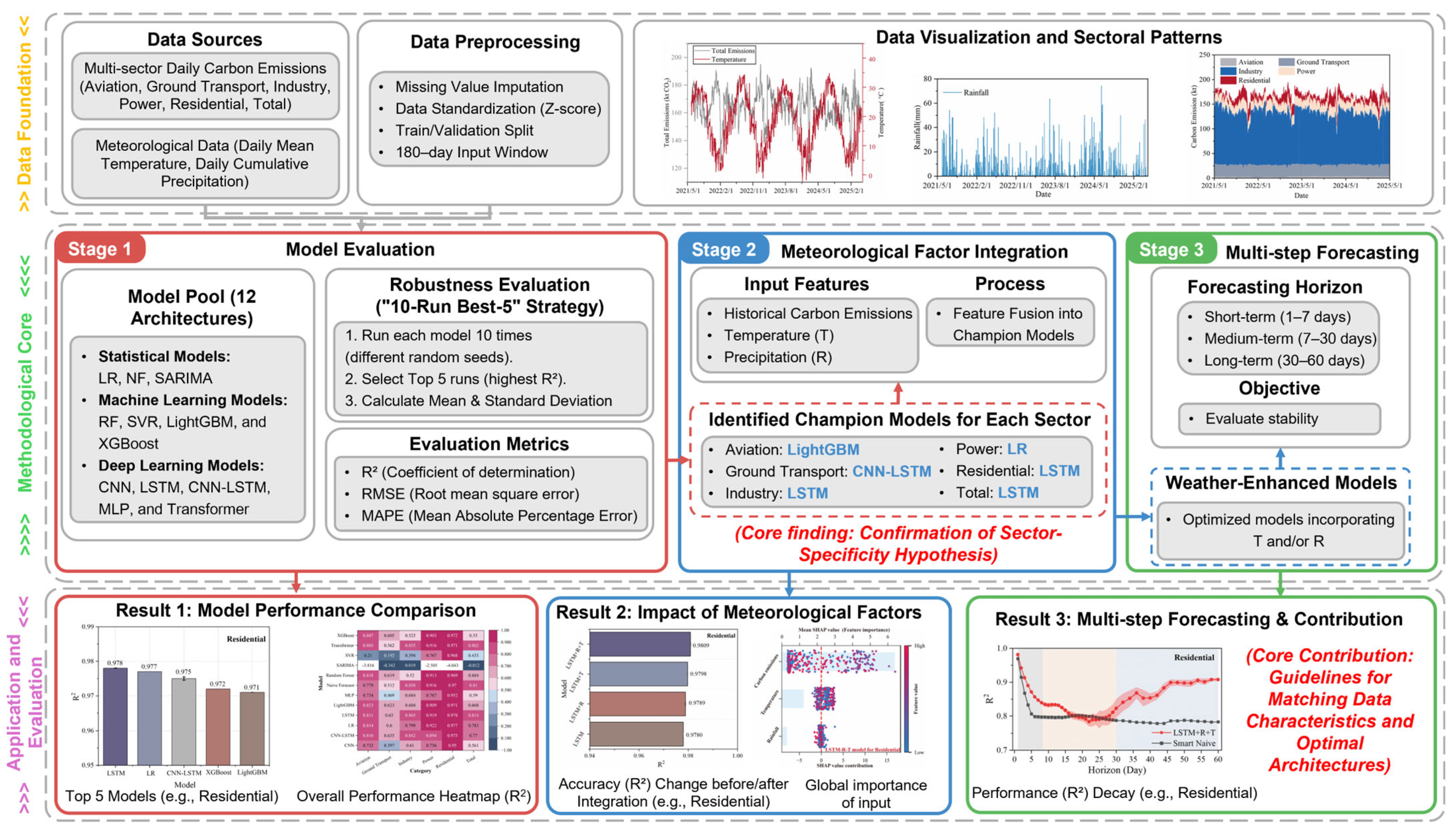
2.5.1. Three-Stage Experimental Framework
2.5.2. Data Partitioning and Preprocessing
2.5.3. Model Training and Performance Evaluation
3. Results
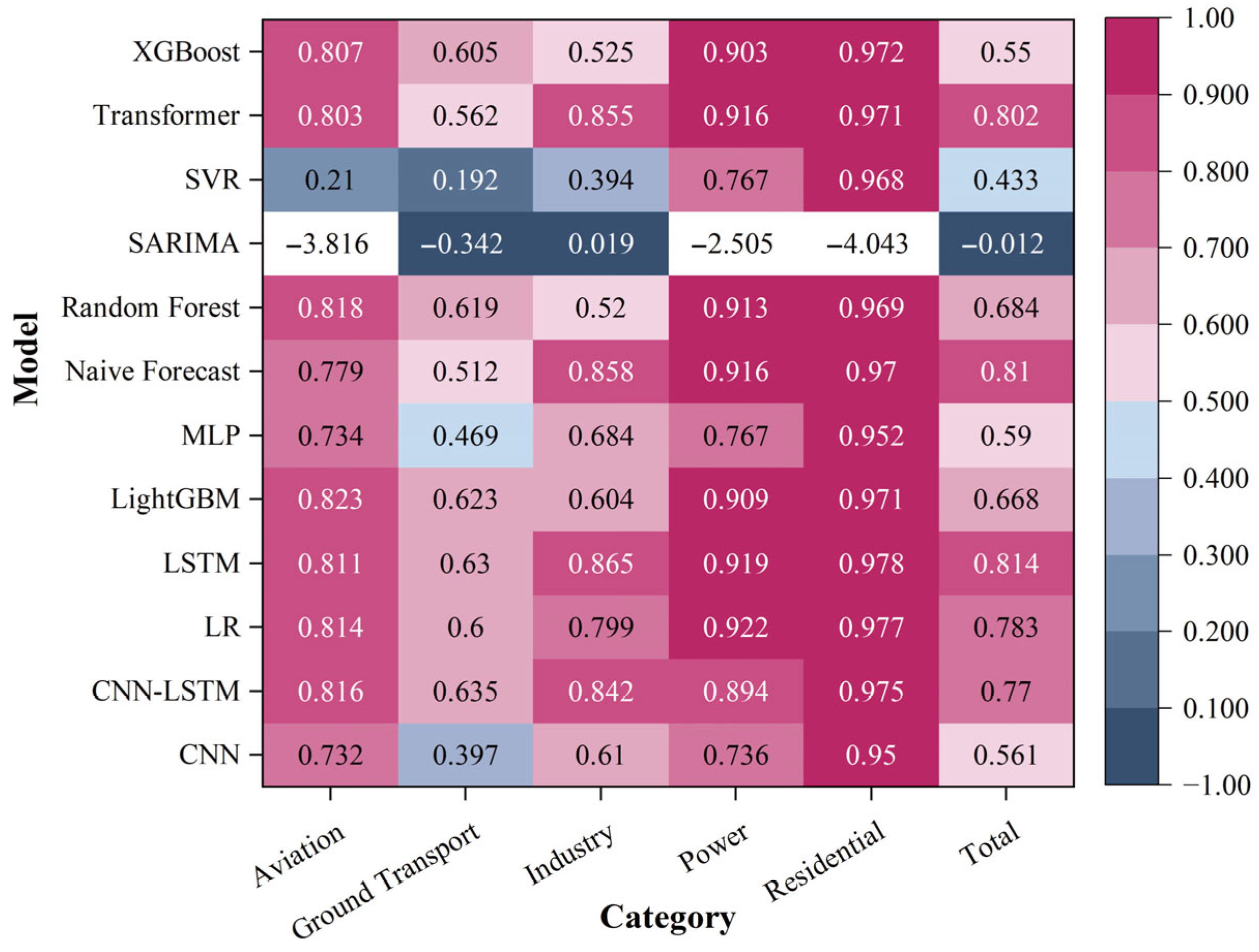
3.1. Model Performance Comparison
3.2. Comprehensive Evaluation of Meteorological Influences
3.2.1. Lagged Correlation Analysis
3.2.2. Effect of Meteorological Factor Integration
3.2.3. Feature Contribution Analysis (SHAP)
3.3. Multi-Step Forecast Performance
4. Discussion
4.1. Heterogeneity in Sector-Specific Model Selection
4.2. The Role of Meteorological Drivers
4.3. Physical Interpretability of Data-Driven Models
4.4. Stability in Long-Horizon Forecasting
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, X.; Wang, L.; Chen, W.; Robiou Du Pont, Y.; Clarke, L.; Yang, L.; Wang, H.; Lu, X.; He, J. Decarbonizing China’s Energy System to Support the Paris Climate Goals. Sci. Bull. 2022, 67, 1406–1409. [Google Scholar] [CrossRef] [PubMed]
- Shan, Y.; Guan, Y.; Hang, Y.; Zheng, H.; Li, Y.; Guan, D.; Li, J.; Zhou, Y.; Li, L.; Hubacek, K. City-Level Emission Peak and Drivers in China. Sci. Bull. 2022, 67, 1910–1920. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Jia, J.; Guo, Y.; Wu, B.; Chen, C. Scenario of Carbon Dioxide (CO2) Emission Peaking and Reduction Path Implication in Five Northwestern Provinces of China by the Low Emissions Analysis Platform (LEAP) Model. Front. Energy Res. 2022, 10, 983751. [Google Scholar] [CrossRef]
- Hou, L.; Chen, H. The Prediction of Medium- and Long-Term Trends in Urban Carbon Emissions Based on an ARIMA-BPNN Combination Model. Energies 2024, 17, 1856. [Google Scholar] [CrossRef]
- Yang, L.-H.; Ye, F.-F.; Hu, H.; Lu, H.; Wang, Y.-M.; Chang, W.-J. A Data-Driven Rule-Base Approach for Carbon Emission Trend Forecast with Environmental Regulation and Efficiency Improvement. Sustain. Prod. Consum. 2024, 45, 316–332. [Google Scholar] [CrossRef]
- Ding, L.; Zhang, R.; Zhao, X. Forecasting Carbon Price in China Unified Carbon Market Using a Novel Hybrid Method with Three-Stage Algorithm and Long Short-Term Memory Neural Networks. Energy 2024, 288, 129761. [Google Scholar] [CrossRef]
- Sun, Y.; Qu, Z.; Liu, Z.; Li, X. Hierarchical Multi-Scale Decomposition and Deep Learning Ensemble Framework for Enhanced Carbon Emission Prediction. Mathematics 2025, 13, 1924. [Google Scholar] [CrossRef]
- Han, Z.; Cui, B.; Xu, L.; Wang, J.; Guo, Z. Coupling LSTM and CNN Neural Networks for Accurate Carbon Emission Prediction in 30 Chinese Provinces. Sustainability 2023, 15, 13934. [Google Scholar] [CrossRef]
- Ji, R. Research on Factors Influencing Global Carbon Emissions and Forecasting Models. Sustainability 2024, 16, 10782. [Google Scholar] [CrossRef]
- Liu, W.; Cai, D.; Nkou Nkou, J.; Liu, W.; Huang, Q. A Survey of Carbon Emission Forecasting Methods Based on Neural Networks. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23 March 2023; pp. 1546–1551. [Google Scholar]
- Tan, J.; Wang, J.; Wang, H.; Liu, Z.; Zeng, N.; Yan, R.; Dou, X.; Wang, X.; Wang, M.; Jiang, F.; et al. Influence of Extreme 2022 Heatwave on Megacities’ Anthropogenic CO2 Emissions in Lower-Middle Reaches of the Yangtze River. Sci. Total Environ. 2024, 951, 175605. [Google Scholar] [CrossRef]
- Dou, X.; Hong, J.; Ciais, P.; Chevallier, F.; Yan, F.; Yu, Y.; Hu, Y.; Huo, D.; Sun, Y.; Wang, Y.; et al. Near-Real-Time Global Gridded Daily CO2 Emissions 2021. Sci. Data 2023, 10, 69. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Ciais, P.; Deng, Z.; Davis, S.J.; Zheng, B.; Wang, Y.; Cui, D.; Zhu, B.; Dou, X.; Ke, P.; et al. Carbon Monitor, a near-Real-Time Daily Dataset of Global CO2 Emission from Fossil Fuel and Cement Production. Sci. Data 2020, 7, 392. [Google Scholar] [CrossRef] [PubMed]
- Morakinyo, T.E.; Ren, C.; Shi, Y.; Lau, K.K.-L.; Tong, H.-W.; Choy, C.-W.; Ng, E. Estimates of the Impact of Extreme Heat Events on Cooling Energy Demand in Hong Kong. Renew. Energy 2019, 142, 73–84. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y.; Hu, W.; Deng, N.; He, W. Exploring the Impact of Temperature Change on Residential Electricity Consumption in China: The ‘Crowding-out’ Effect of Income Growth. Energy Build. 2021, 245, 111040. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, K.; Hu, W.; Zhu, B.; Wang, P.; Wei, Y.-M. Exploring the Climatic Impacts on Residential Electricity Consumption in Jiangsu, China. Energy Policy 2020, 140, 111398. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y. Modeling and Predicting City-Level CO2 Emissions Using Open Access Data and Machine Learning. Environ. Sci. Pollut. Res. 2021, 28, 19260–19271. [Google Scholar] [CrossRef]
- Shan, Y.; Guan, D.; Hubacek, K.; Zheng, B.; Davis, S.J.; Jia, L.; Liu, J.; Liu, Z.; Fromer, N.; Mi, Z.; et al. City-Level Climate Change Mitigation in China. Sci. Adv. 2018, 4, eaaq0390. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, H.; Bao, M.; Li, Z.; Fan, G. Climatic Characteristics of Centennial and Extreme Precipitation in Hangzhou, China. Environ. Res. Commun. 2024, 6, 85015. [Google Scholar] [CrossRef]
- Xia, C.; Xiang, M.; Fang, K.; Li, Y.; Ye, Y.; Shi, Z.; Liu, J. Spatial-Temporal Distribution of Carbon Emissions by Daily Travel and Its Response to Urban Form: A Case Study of Hangzhou, China. J. Clean. Prod. 2020, 257, 120797. [Google Scholar] [CrossRef]
- Liu, Z.; Ciais, P.; Deng, Z.; Lei, R.; Davis, S.J.; Feng, S.; Zheng, B.; Cui, D.; Dou, X.; Zhu, B.; et al. Near-Real-Time Monitoring of Global CO2 Emissions Reveals the Effects of the COVID-19 Pandemic. Nat. Commun. 2020, 11, 5172. [Google Scholar] [CrossRef]
- Hsiang, S. Climate Econometrics. Annu. Rev. Resour. Econ. 2016, 8, 43–75. [Google Scholar] [CrossRef]
- Bloom, A.A.; Bowman, K.W.; Liu, J.; Konings, A.G.; Worden, J.R.; Parazoo, N.C.; Meyer, V.; Reager, J.T.; Worden, H.M.; Jiang, Z.; et al. Lagged Effects Regulate the Inter-Annual Variability of the Tropical Carbon Balance. Biogeosciences 2020, 17, 6393–6422. [Google Scholar] [CrossRef]
- Stenseth, N.C.; Mysterud, A.; Ottersen, G.; Hurrell, J.W.; Chan, K.-S.; Lima, M. Ecological Effects of Climate Fluctuations. Science 2002, 297, 1292–1296. [Google Scholar] [CrossRef] [PubMed]
- Kour, M. Modelling and Forecasting of Carbon-Dioxide Emissions in South Africa by Using ARIMA Model. Int. J. Environ. Sci. Technol. 2023, 20, 11267–11274. [Google Scholar] [CrossRef]
- Kumari, S.; Singh, S.K. Machine Learning-Based Time Series Models for Effective CO2 Emission Prediction in India. Environ. Sci. Pollut. Res. 2022, 30, 116601–116616. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Feda, A.K.; Agyekum, E.B.; Mbasso, W.F.; Kamel, S. Towards Greener Futures: SVR-Based CO2 Prediction Model Boosted by SCMSSA Algorithm. Heliyon 2024, 10, e31766. [Google Scholar] [CrossRef]
- Zhang, H.; Peng, J.; Wang, R.; Zhang, M.; Gao, C.; Yu, Y. Use of Random Forest Based on the Effects of Urban Governance Elements to Forecast CO2 Emissions in Chinese Cities. Heliyon 2023, 9, e16693. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.A.; Lee, H.-J. A Review on Deep Learning Models for Forecasting Time Series Data of Solar Irradiance and Photovoltaic Power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Özmen, E.S. Time Series Performance and Limitations with SARIMAX: An Application with Retail Store Data. Turk. Stud. 2021, 16, 1583–1592. [Google Scholar] [CrossRef]
- Ramachandram, D.; Taylor, G.W. Deep Multimodal Learning: A Survey on Recent Advances and Trends. IEEE Signal Process. Mag. 2017, 34, 96–108. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Ben Taieb, S.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A Review and Comparison of Strategies for Multi-Step Ahead Time Series Forecasting Based on the NN5 Forecasting Competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef]
- Cerqueira, V.; Torgo, L.; Mozetič, I. Evaluating Time Series Forecasting Models: An Empirical Study on Performance Estimation Methods. Mach. Learn. 2020, 109, 1997–2028. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2019, arXiv:1711.05101. [Google Scholar] [CrossRef]
- Sun, W.; Ren, C. Short-Term Prediction of Carbon Emissions Based on the EEMD-PSOBP Model. Environ. Sci. Pollut. Res. 2021, 28, 56580–56594. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Xiao, F.; Guo, F.; Yan, J. Interpretable Machine Learning for Building Energy Management: A State-of-the-Art Review. Adv. Appl. Energy 2023, 9, 100123. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Luo, X.; Zhao, H. Diagnosis of Parkinson’s Disease Based on SHAP Value Feature Selection. Biocybern. Biomed. Eng. 2022, 42, 856–869. [Google Scholar] [CrossRef]
- Owen, B.; Lee, D.S.; Lim, L. Flying into the Future: Aviation Emissions Scenarios to 2050. Environ. Sci. Technol. 2010, 44, 2255–2260. [Google Scholar] [CrossRef]
- Shobana Bai, F.J.J. A Machine Learning Approach for Carbon Di Oxide and Other Emissions Characteristics Prediction in a Low Carbon Biofuel-Hydrogen Dual Fuel Engine. Fuel 2023, 341, 127578. [Google Scholar] [CrossRef]
- Wu, Y.; Luo, M.; Ding, S.; Han, Q. Using a Light Gradient-Boosting Machine–Shapley Additive Explanations Model to Evaluate the Correlation between Urban Blue–Green Space Landscape Spatial Patterns and Carbon Sequestration. Land 2024, 13, 1965. [Google Scholar] [CrossRef]
- Esfandi, T.; Sadeghnejad, S.; Jafari, A. Effect of Reservoir Heterogeneity on Well Placement Prediction in CO2-EOR Projects Using Machine Learning Surrogate Models: Benchmarking of Boosting-Based Algorithms. Geoenergy Sci. Eng. 2024, 233, 212564. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, R.; Liu, Z.; Liu, L.; Wang, J.; Liu, W. A Review of Macroscopic Carbon Emission Prediction Model Based on Machine Learning. Sustainability 2023, 15, 6876. [Google Scholar] [CrossRef]
- Mekouar, Y.; Saleh, I.; Karim, M. GreenNav: Spatiotemporal Prediction of CO2 Emissions in Paris Road Traffic Using a Hybrid CNN-LSTM Model. Network 2025, 5, 2. [Google Scholar] [CrossRef]
- Xiang, J.; Ghaffarpasand, O.; Pope, F.D. Assessing the Impact of Calendar Events upon Urban Vehicle Behaviour and Emissions Using Telematics Data. Smart Cities 2024, 7, 3071–3094. [Google Scholar] [CrossRef]
- Rajalakshmi, V.; Ganesh Vaidyanathan, S. Hybrid CNN-LSTM for Traffic Flow Forecasting. In Proceedings of 2nd International Conference on Artificial Intelligence: Advances and Applications; Springer: Singapore, 2022. [Google Scholar]
- Ajala, A.A.; Adeoye, O.L.; Salami, O.M.; Jimoh, A.Y. An Examination of Daily CO2 Emissions Prediction through a Comparative Analysis of Machine Learning, Deep Learning, and Statistical Models. Environ. Sci. Pollut. Res. 2025, 32, 2510–2535. [Google Scholar] [CrossRef] [PubMed]
- Radha, C.; Elangovan, D. A Big Data-Driven LSTM Approach for Accurate Carbon Emission Prediction in Low-Carbon Economies. Nanotechnol. Percept. 2024, 20, 2017–2030. [Google Scholar]
- Wei, X.; Xu, Y. Research on Carbon Emission Prediction and Economic Policy Based on TCN-LSTM Combined with Attention Mechanism. Front. Ecol. Evol. 2023, 11, 1270248. [Google Scholar] [CrossRef]
- Kim, H.; Park, S.; Kim, S. Time-Series Clustering and Forecasting Household Electricity Demand Using Smart Meter Data. Energy Rep. 2023, 9, 4111–4121. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical Load Forecasting Models: A Critical Systematic Review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Sosa, G.R.; Falah, M.Z.; Dika Fikri, L.; Wibawa, A.P.; Handayani, A.N.; Hammad, J.A.H. Forecasting Electrical Power Consumption Using ARIMA Method Based on kWh of Sold Energy. Sci. Inf. Technol. Lett. 2021, 2, 9–15. [Google Scholar] [CrossRef]
- Nematirad, R.; Pahwa, A.; Natarajan, B. SPDNet: Seasonal-Periodic Decomposition Network for Advanced Residential Demand Forecasting. arXiv 2025, arXiv:2503.22485. [Google Scholar] [CrossRef]
- Martínez Comesaña, M.; Febrero-Garrido, L.; Troncoso-Pastoriza, F.; Martínez-Torres, J. Prediction of Building’s Thermal Performance Using LSTM and MLP Neural Networks. Appl. Sci. 2020, 10, 7439. [Google Scholar] [CrossRef]
- Moreno-Carbonell, S.; Sánchez-Úbeda, E.F.; Muñoz, A. Time Series Decomposition of the Daily Outdoor Air Temperature in Europe for Long-Term Energy Forecasting in the Context of Climate Change. Energies 2020, 13, 1569. [Google Scholar] [CrossRef]
- Chen, X.; Yang, L. Temperature and Industrial Output: Firm-Level Evidence from China. J. Environ. Econ. Manag. 2019, 95, 257–274. [Google Scholar] [CrossRef]
- Lehr, J.; Rehdanz, K. The Effect of Temperature on Energy Use, CO2 Emissions, and Economic Performance in German Industry. Energy Econ. 2022, 138, 107818. [Google Scholar] [CrossRef]
- Wang, B.; Ding, Q. Global Monsoon: Dominant Mode of Annual Variation in the Tropics. Dyn. Atmos. Ocean. 2008, 44, 165–183. [Google Scholar] [CrossRef]
- Liu, Y.; Song, W. Influences of Extreme Precipitation on China’s Mining Industry. Sustainability 2019, 11, 6719. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A Survey on Feature Selection Methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Huo, Z.; Zha, X.; Lu, M.; Ma, T.; Lu, Z. Prediction of Carbon Emission of the Transportation Sector in Jiangsu Province-Regression Prediction Model Based on GA-SVM. Sustainability 2023, 15, 3631. [Google Scholar] [CrossRef]
- Batterman, S.; Cook, R.; Justin, T. Temporal Variation of Traffic on Highways and the Development of Accurate Temporal Allocation Factors for Air Pollution Analyses. Atmos. Environ. 2015, 107, 351–363. [Google Scholar] [CrossRef]
- Afshar, M.; Usefi, H. Optimizing Feature Selection Methods by Removing Irrelevant Features Using Sparse Least Squares. Expert Syst. Appl. 2022, 200, 116928. [Google Scholar] [CrossRef]
- Ali, L.; Rahman, A.; Khan, A.; Zhou, M.; Javeed, A.; Khan, J.A. An Automated Diagnostic System for Heart Disease Prediction Based on χ2 Statistical Model and Optimally Configured Deep Neural Network. IEEE Access 2019, 7, 34938–34945. [Google Scholar] [CrossRef]
- Zhang, B.; Ling, L.; Zeng, L.; Hu, H.; Zhang, D. Multi-Step Prediction of Carbon Emissions Based on a Secondary Decomposition Framework Coupled with Stacking Ensemble Strategy. Environ. Sci. Pollut. Res. 2023, 30, 71063–71087. [Google Scholar] [CrossRef] [PubMed]
- Le Quéré, C.; Jackson, R.B.; Jones, M.W.; Smith, A.J.P.; Abernethy, S.; Andrew, R.M.; De-Gol, A.J.; Willis, D.R.; Shan, Y.; Canadell, J.G.; et al. Temporary Reduction in Daily Global CO2 Emissions during the COVID-19 Forced Confinement. Nat. Clim. Change 2020, 10, 647–653. [Google Scholar] [CrossRef]
- Wang, C.; Huang, X.-F.; Zhu, Q.; Cao, L.-M.; Zhang, B.; He, L.-Y. Differentiating Local and Regional Sources of Chinese Urban Air Pollution Based on the Effect of the Spring Festival. Atmos. Chem. Phys. 2017, 17, 9103–9114. [Google Scholar] [CrossRef]
- Zheng, B.; Geng, G.; Ciais, P.; Davis, S.J.; Martin, R.V.; Meng, J.; Wu, N.; Chevallier, F.; Broquet, G.; Boersma, F.; et al. Satellite-Based Estimates of Decline and Rebound in China’s CO2 Emissions during COVID-19 Pandemic. Sci. Adv. 2020, 6, eabd4998. [Google Scholar] [CrossRef]
- Mideksa, T.K.; Kallbekken, S. The Impact of Climate Change on the Electricity Market: A Review. Energy Policy 2010, 38, 3579–3585. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A Review of Methods to Deal with It and a Simulation Study Evaluating Their Performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Bessec, M.; Fouquau, J. The Non-Linear Link between Electricity Consumption and Temperature in Europe: A Threshold Panel Approach. Energy Econ. 2008, 30, 2705–2721. [Google Scholar] [CrossRef]
- Santamouris, M.; Papanikolaou, N.; Livada, I.; Koronakis, I.; Georgakis, C.; Argiriou, A.; Assimakopoulos, D.N. On the Impact of Urban Climate on the Energy Consumption of Buildings. Sol. Energy 2001, 70, 201–216. [Google Scholar] [CrossRef]
- Eggleston, H.S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; IPCC National Greenhouse Gas Inventories Programme, Intergovernmental Panel on Climate Change (IPCC): Hayama, Kanagawa, Japan, 2006. [Google Scholar]
- Khaniya, B.; Priyantha, H.G.; Baduge, N.; Azamathulla, H.M.; Rathnayake, U. Impact of Climate Variability on Hydropower Generation: A Case Study from Sri Lanka. ISH J. Hydraul. Eng. 2020, 26, 301–309. [Google Scholar] [CrossRef]
- Hasan, A.; Baroudi, B.; Elmualim, A.; Rameezdeen, R. Factors Affecting Construction Productivity: A 30 Year Systematic Review. Eng. Constr. Archit. Manag. 2018, 25, 916–937. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current Status and Future Directions. Int. J. Forecast. 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are Transformers Effective for Time Series Forecasting? Proc. AAAI Conf. Artif. Intell. 2023, 37, 11121–11128. [Google Scholar] [CrossRef]
- Blazakis, K.; Katsigiannis, Y.; Stavrakakis, G. One-Day-Ahead Solar Irradiation and Windspeed Forecasting with Advanced Deep Learning Techniques. Energies 2022, 15, 4361. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]









| Models | Type | Suitability | Advantages | Disadvantages | Refs. |
|---|---|---|---|---|---|
| 1. Seasonal AutoRegressive Integrated Moving Average (SARIMA) | Traditional Statistical | Suitable for univariate time series with linear trends and seasonality. | Effectively handles seasonality and linear trends. | Fails to capture non-linear relationships; performance drops significantly on non-stationary data like CO2 emissions compared to AI models. | [26,30] |
| 2. Naive Forecast (NF) | Used as a benchmark for evaluating the skill of advanced models, assuming future values equal current ones. | Simple implementation; zero computational cost. | Cannot handle trends, seasonality, or sudden changes; accuracy degrades rapidly with longer horizons. | [29] | |
| 3. Linear Regression (LR) | Best for scenarios where variables have clear linear relationships; often used as a baseline. | Simple structure; high interpretability; low computational cost. | Cannot capture complex non-linear characteristics of carbon emission data; prediction accuracy is generally lower than deep learning models. | [26,28] | |
| 4. Random Forest (RF) | Machine Learning | Suitable for high-dimensional data and analyzing the importance of driving factors (e.g., urban governance elements). | Robust against overfitting; provides interpretability via feature importance. | In some univariate forecasting contexts, it may perform worse than LSTM or SARIMAX; limited ability to extrapolate trends outside training range. | [26,28] |
| 5. Support Vector Regression (SVR) | Applicable to small samples, non-linear, and high-dimensional data. | Strong generalization ability; handles non-linearity via kernel functions. | Highly sensitive to hyper-parameters (penalty C, kernel functions) requiring optimization algorithms (e.g., SCMSSA); computationally demanding for large datasets. | [27] | |
| 6. Light Gradient Boosting Machine (LightGBM) | Suitable for large-scale datasets and capturing non-linear regression patterns. | Fast training speed and high efficiency. | Often treats time-series observations as independent instances, failing to adequately model sequential/temporal dependencies. | [7] | |
| 7. eXtreme Gradient Boosting (XGBoost) | Used for structured data prediction, often combined with decomposition techniques for carbon prices or emissions. | High prediction accuracy; includes regularization to prevent overfitting. | Complex parameter tuning; like other tree-based models, it struggles to capture long-range temporal dependencies naturally compared to RNNs. | [7] | |
| 8. Long Short-Term Memory (LSTM) | Deep Learning | Designed for sequential data with long-term dependencies (e.g., historical emission trends). | Solves the vanishing gradient problem of RNNs; excellent for capturing long-term temporal relationships. | Large number of parameters; longer training time compared to GRU or simple ML models; difficulty in extracting spatial features. | [6,26,29] |
| 9. Convolutional Neural Network (CNN) | Applicable for extracting local patterns and features from spatial or grid-structured data. | Excellent at feature extraction and dimensionality reduction. | Lacks memory for long-term temporal dependencies; usually needs to be combined with LSTM for time-series forecasting. | [6,7,8] | |
| 10. Hybrid CNN-LSTM | Best for complex data requiring both local feature extraction and temporal modeling. | Combines CNN’s feature extraction with LSTM’s temporal memory; generally outperforms standalone models in accuracy. | Complex model structure; high computational resource consumption; longer training times. | [9,29] | |
| 11. Multilayer Perceptron (MLP) | Suitable for modeling non-linear mapping relationships. | Better than linear regression for non-linear data. | Weaker than LSTM in capturing time-series memory; prone to getting trapped in local optima; lower accuracy than hybrid models. | [6,29] | |
| 12. Transformer | Suitable for capturing long-range dependencies and multi-scale patterns in complex emission data. | Self-attention mechanism captures global dependencies better than RNNs; supports parallel computing. | Data-hungry; complex architecture requires significant tuning; risk of overfitting on small datasets. | [7] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Zhang, P.; Xu, D.; Hu, J.; Yuan, Y. Sector-Specific Carbon Emission Forecasting for Sustainable Urban Management: A Comparative Data-Driven Framework. Sustainability 2026, 18, 19. https://doi.org/10.3390/su18010019
Huang W, Zhang P, Xu D, Hu J, Yuan Y. Sector-Specific Carbon Emission Forecasting for Sustainable Urban Management: A Comparative Data-Driven Framework. Sustainability. 2026; 18(1):19. https://doi.org/10.3390/su18010019
Chicago/Turabian StyleHuang, Wanyi, Peng Zhang, Dong Xu, Jianyong Hu, and Yuan Yuan. 2026. "Sector-Specific Carbon Emission Forecasting for Sustainable Urban Management: A Comparative Data-Driven Framework" Sustainability 18, no. 1: 19. https://doi.org/10.3390/su18010019
APA StyleHuang, W., Zhang, P., Xu, D., Hu, J., & Yuan, Y. (2026). Sector-Specific Carbon Emission Forecasting for Sustainable Urban Management: A Comparative Data-Driven Framework. Sustainability, 18(1), 19. https://doi.org/10.3390/su18010019







