Modeling the Process of Crop Yield Management in Hydroagro-Landscape Saline Soils
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Materials
2.2. Principles of Constructing Mathematical Models of Agricultural Crop Yield
2.3. Construction of Mathematical Models of Crop Yields
2.4. Methodology and Materials for Mathematical Modeling of Crop Yields
3. Results
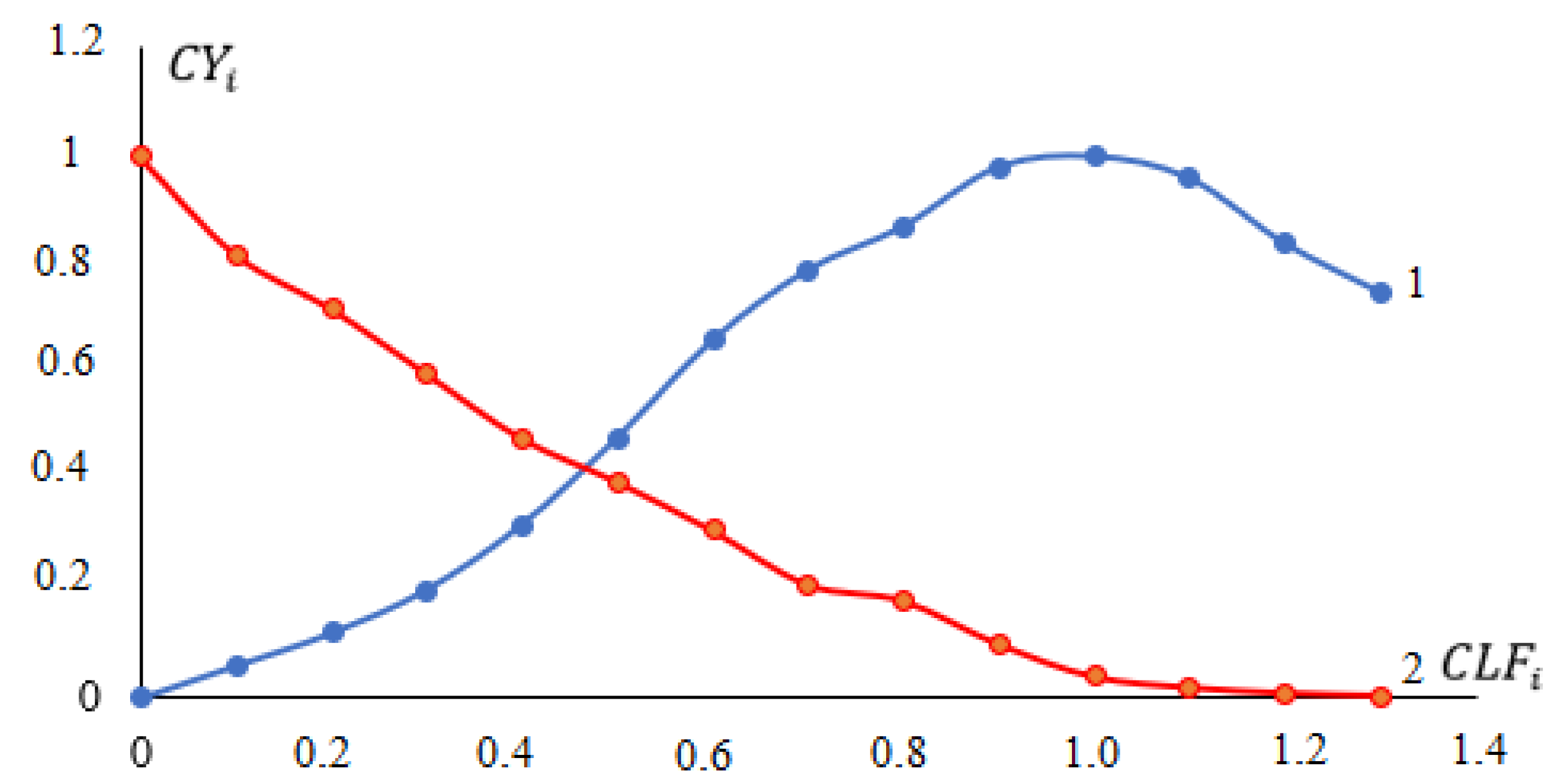
3.1. Dynamic Models of Crop Yields
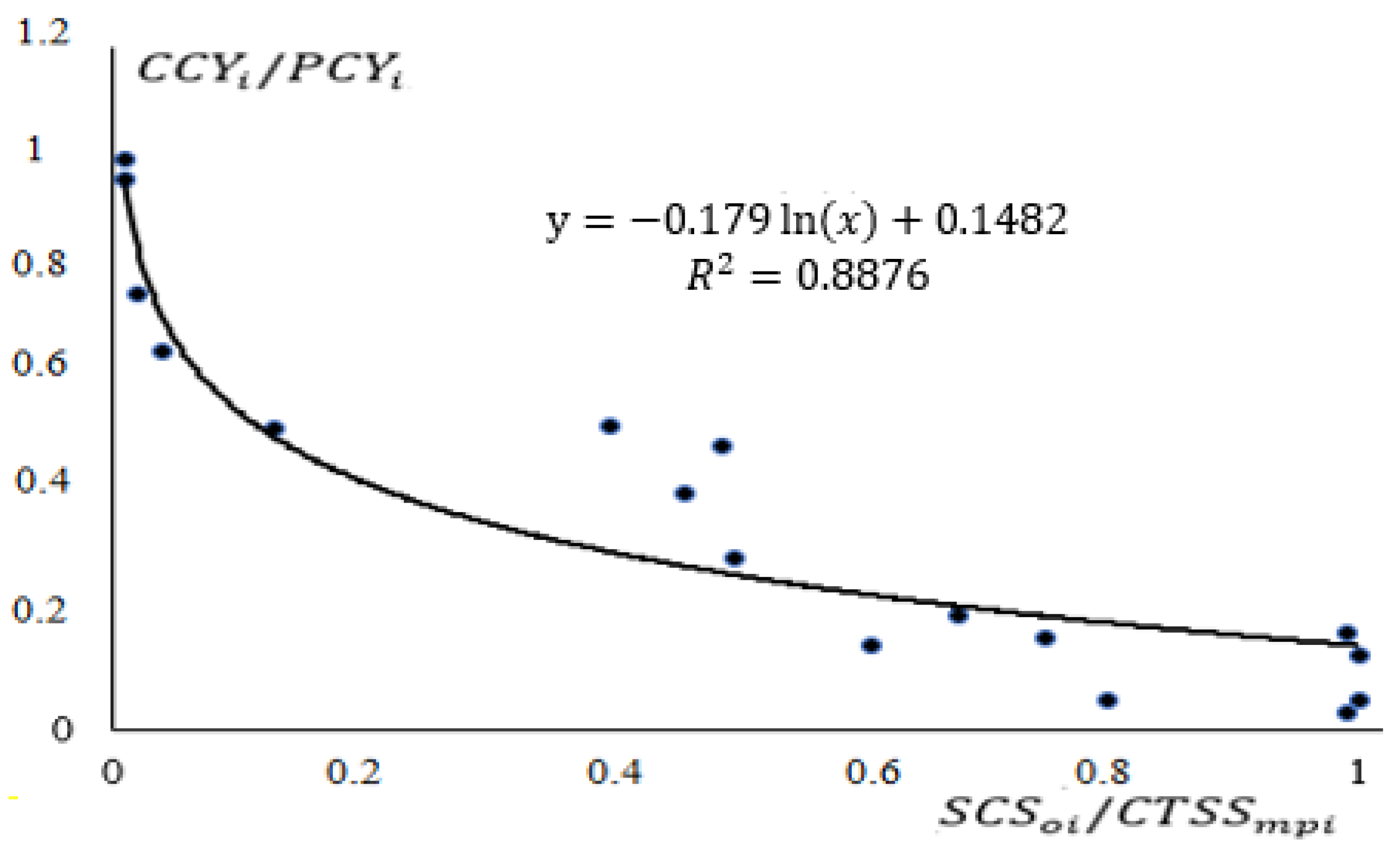
3.2. Linear Correlation Model of Crop Yields on Saline Lands
4. Discussion of Research Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FAO. Global Network on Integrated Soil Management for Sustain-Able Use of SaltAffected Soils; FAO: Rome, Italy, 2000; Available online: http://www.fao.org/ag/agl/agll/spush (accessed on 6 March 2025).
- Ghassemi, F.; Jakeman, A.J.; Nix, H.A. Salinisation of Land and Water Resources: Human Causes, Management and Case Studies; University of New South Wales Press: Sydney, Australia, 1995. [Google Scholar]
- Munns, R. Genes and salt tolerance: Bringing them together. New Phytol. 2005, 167, 645–663. [Google Scholar] [CrossRef]
- Pessarakli, M.; Szabolics, I. Soil salinity and sodicity as particular plant/crop stress factors. In Handbook of Plant and Crop Stress, 2nd ed.; Pessarakli, M., Ed.; Marcel Dekker: New York, NY, USA, 1999; pp. 1–16. [Google Scholar]
- FAO. FAO Statistical Year Book 2012, World Food and Agriculture; Food and Agriculture Organization of the United Nation: Rome, Italy, 2012; p. 366. Available online: http://www.fao.org/docrep/015/i2490e/i2490e00.htm (accessed on 6 March 2025).
- Kijne, J.W. Aral Sea Basin Initiative: Towards a Strategy for Sustainable Irrigated Agriculture with Feasible Nvestment in Drainage; Synthesis Report; IPTRID/FAO: Rome, Italy, 2005; p. 72. [Google Scholar]
- Tokbergenova, A.; Skorintseva, I.; Ryskeldiyeva, A.; Kaliyeva, D.; Salmurzauly, R.; Mussagaliyeva, A. Assessment of Anthropogenic Disturbances of Landscapes: West Kazakhstan Region. Sustainability 2025, 17, 573. [Google Scholar] [CrossRef]
- Mustafayev, Z.; Medeu, A.; Skorintseva, I.; Bassova, T.; Aldazhanova, G. Improvement of the methodology for the assessment of the agro-resource potential of agricultural landscapes. Sustainability 2024, 16, 419. [Google Scholar] [CrossRef]
- Qadir, M.; Noble, A.D.; Qureshi, A.S.; Gupta, R.K.; Yuldashev, T.; Karimov, A. Salt-induced land and water degradation in the Aral Sea basin: A challenge to sustainable agriculture in Central Asia. Nat. Resour. Forum 2009, 33, 134–149. [Google Scholar] [CrossRef]
- Khachaturyan, V.K.; Aydarov, I.P. Conceptual Approaches to Improving the Ecological and Meliorative Situation in the Aral Sea Basin. J. Land Reclam. Water Econ. 1991, 5–12. [Google Scholar]
- Reimers, N.F. Ecology. Theory, Laws, Rules, Principles, and Hypotheses; Russia Molodaya: Moscow, Russia, 1994; 367p. [Google Scholar]
- Kovda, V.A.; Mamayeva, P.Y. The Limits of Salt Toxicity in Soils of the Pakhte-Aral Region for Alfalfa and Cotton. Soil Sci. 1939, 80–98. [Google Scholar]
- Puruzyan, S.S. Influence of Soil Salinization on the Growth and Development of Corn. Soil Sci. 1959, 45–50. [Google Scholar]
- Rabochev, I.S.; Burdygina, V.S. Influence of Soil Solution Concentration on Cotton Yield. In A Collection of Articles; Ylym: Ashgabat, Turkmenistan, 1968; pp. 125–145. [Google Scholar]
- Tsyvilev, M.N. Influence of Solonetz on Southern Chernozem on Cereal Crop Yield. Soil Sci. 1975, 61–65. [Google Scholar]
- Gorbachyov, R.M. Development of Issues Related to the Efficiency of Hydro-Melioration in the Lower Amu Darya River. In Proceedings of the SANIRRI, Tashkent, Uzbekistan, 16–18 September 1980; pp. 54–68. [Google Scholar]
- Schmidt, S.M. Statistical Relationship Between Cotton Yield and Soil Salinization. In Collection of Scientific Papers of SANIRRI Principles of Regulating Reclamation Soil Regimes; Sugorish: Tashkent, Uzbekistan, 1982; Volume 166, pp. 132–143. [Google Scholar]
- Dukhony, V.A.; Umardzhanov, D. Methodology for Evaluating the Efficiency of Irrigation System Reconstruction. In Collection of Scientific Papers of SANIRRI/Improvement of Hydro-Reclamation Systems; Sugorish: Tashkent, Uzbekistan, 1982; Volume 167, pp. 41–80. [Google Scholar]
- Aidarov, I.P.; Pestov, L.F.; Korolyov, T.P. Influence of Soil Salinization Type and Degree on Crop Yield. In Collection of Scientific Papers of MGMI/Integrated Reclamation Regulation of Soil Processes; Moscow Hydrometeorological Institute: Moscow, Russia, 1982; pp. 120–131. [Google Scholar]
- Usmanov, A.U. Influence of Irrigation Water Quality on Crop Yield. Reclamation of Lands in the Lower Reaches of the Amu Darya River. In Proceedings of the SANIRRI; Sugorish: Tashkent, Uzbekistan, 1988; pp. 38–42. [Google Scholar]
- Nerpin, S.V.; Chudnovsky, A.F. Energy and Mass Exchange in the Plant-Soil-Air System; Gidrometeoizdat: Leningrad, Russia, 1975; 357p. [Google Scholar]
- Mitcherlikha, E.A. Soil Science; Foreign Literature: Moscow, Russia, 1957; 146p. [Google Scholar]
- Tang, J.; Riley, W.J. Finding Liebig’s law of the minimum. Ecol. Appl. 2021, 31, 02458. [Google Scholar] [CrossRef]
- Ramamoorthy, B.; Velayutham, M. The Law of Optimum and soil test-based fertiliser use for targeted yield of crops and soil fertility management for sustainable agriculture. Madras Agric. J. 2011, 98, 295–307. [Google Scholar]
- Mitscherlich, E.A.; Merrec, E. Eine guantitatire Stiekstoftanalyse für sehr geringe Mengen. Landwirtchaftliche Jahrbücher Z. Wiss. Landwirtsch. 1909, 7, 537–552. [Google Scholar]
- Griguletsky, V.G. Generalization of the law of action of growth factors and plant productivity of E.A. Mitscherlich. Oilseed Crops 2022, 2, 18–29. [Google Scholar] [CrossRef]
- Shelford, V.E. Some concepts of bioecology. Ecology 1931, 12, 455–467. [Google Scholar] [CrossRef]
- Ross, Y.K. Radiation Regime and Architecture of the Plant Cover; Gidrometeoizdat: Leningrad, Russia, 1975; 342p. [Google Scholar]
- Tooming, H.G. Solar Radiation and Crop Formation; Gidrometeoizdat: Leningrad, Russia, 1977; 200p. [Google Scholar]
- Moldau, H.A. Optimal Distribution of Assimilates Under Water Deficit (Mathematical Model). In Proceedings of the Academy of Sciences of the USSR, Biological Series; Consultants Bureau Enterprises: Moscow, Russia, 1975; Volume 24, pp. 3–9. [Google Scholar]
- Laisk, A.; Moldau, X.; Nielson, T.; Ross, Y.; Tooming, H. Modeling the Productivity Process of the Plant Cover. Bot. J. 1971, 56, 761–776. [Google Scholar]
- Sirotenko, O.D. Mathematical Modeling of the Water-Heat Regime and Productivity of Agroecosystems; Gidrometeoizdat: Leningrad, Russia, 1981; 167p. [Google Scholar]
- Khvalinsky, Y.A.; Sirotenko, O.D. Method for Calculating Photosynthesis of Agricultural Crops Based on Standard Meteorological Data. Proc. Inst. Meteorol. 1973, 3, 32–42. [Google Scholar]
- Polevoy, A.N.; Florya, L.V. Modeling of Agroclimatic Resources, Crop Yield Productivity, and Formation of Agricultural Crop Productivity. Hydrometeorol. Ecol. 2015, 31, 36–49. [Google Scholar]
- Mustafayev, Z.S.; Kozykeeva, A.T.; Zhidekulova, G.E. Model of Crop Productivity Formation in Hydroagrolandscape Systems. Int. Tech. Econ. J. 2017, 100–120. [Google Scholar]
- Paudel, D.; Boogaard, H.; de Wit, A.; Janssen, S.; Osinga, S.; Pylianidis, C.; Athanasiadis, I.N. Machine learning for large-scale crop yield forecasting. Agric. Syst. 2021, 187, 103016. [Google Scholar] [CrossRef]
- Ju, W.; Gao, P.; Zhou, Y.; Chen, J.M.; Chen, S.; Li, X. Prediction of summer grain crop yield with a process-based ecosystem model and remote sensing data for the northern area of the Jiangsu Province, China. Int. J. Remote Sens. 2010, 31, 1573–1587. [Google Scholar] [CrossRef]
- Kakabouki, I.; Roussis, I.; Mavroeidis, A.; Stavropoulos, P.; Kanatas, P.; Pantaleon, K.; Folina, A.; Beslemes, D.; Tigka, E. Effects of Zeolite Application and Inorganic Nitrogen Fertilization on Growth, Productivity, and Nitrogen and Water Use Efficiency of Maize (Zea mays L.) Cultivated Under Mediterranean Conditions. Sustainability 2025, 17, 2178. [Google Scholar] [CrossRef]
- Ullah Khan, F.; Zaman, F.; Qu, Y.; Wang, J.; Darmorakhtievich, O.H.; Wu, Q.; Fahad, S.; Du, F.; Xu, X. Long-Term Effects of Crop Treatments and Fertilization on Soil Stability and Nutrient Dynamics in the Loess Plateau: Implications for Soil Health and Productivity. Sustainability 2025, 17, 1014. [Google Scholar] [CrossRef]
- Fischetti, E.; Beni, C.; Santangelo, E.; Bascietto, M. Agroecology and Precision Agriculture as Combined Approaches to Increase Field-Scale Crop Resilience and Sustainability. Sustainability 2025, 17, 961. [Google Scholar] [CrossRef]
- de Freitas Cunha, R.L.; Silva, B.; Avegliano, P.B. Comprehensive Modeling Approach for Crop Yield Forecasts using AI-Based Methods and Crop Simulation Models. 2024. Available online: https://www.researchgate.net/publication/371727905 (accessed on 22 May 2024).
- Shabanov, V.V. Bioclimatic Justification of Reclamation; Gidrometeoizdat: Leningrad, Russia, 1975; pp. 342p. [Google Scholar]
- Misle, E. Allometric determination between mineral absorption and biomass in different cultivated species. Lat Am. J. Agric. Environ. Sci. 2006, 33, 67–71. [Google Scholar] [CrossRef]
- Misle, E. Simulating the accumulation of mineral nutrients by crops: An allometric proposal for fertigation. J. Plant Nutr. 2013, 36, 1327–1343. [Google Scholar] [CrossRef]
- Misle, E.; Garrido, E. Determination of crop nutrient accumulation under water or saline stress through an allometric model. In Proceedings of the 17 th International Symposium of the International Scientific Centre for Fertilizers (CIEC), Shenyang, China, 3–7 September 2018. [Google Scholar]
- Niklas, K.J. Plant Allometry: The Scaling of Form and Process; University of Chicago Press: Chicago, IL, USA, 1994; 395p. [Google Scholar]
- Enquist, B. Universal scaling in tree and vascular plant allometry: Toward a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol. 2002, 22, 1045–1064. [Google Scholar] [CrossRef] [PubMed]
- Misle, E.; Kahlaoui, B. Nonlinear Allometric Equation for Crop Response to Soil Salinity. J. Stress Physiol. Biochem. 2015, 11, 49–63. [Google Scholar]
- Bloemberg, G.V.; Lugtenberg, B.J.J. Molecular basis of plant growth promotion and biocontrol by rhizobacteria. Curr. Opin. Plant Biol. 2001, 4, 343–350. [Google Scholar] [CrossRef]
- Bartels, D.; Sunkar, R. Drought and salt tolerance in plants. Crit. Rev. Plant Sci. 2005, 24, 23–58. [Google Scholar] [CrossRef]
- Manchanda, G.; Garg, N. Salinity and its effects on the functional biology of legumes. Acta Physiol. Plant 2008, 30, 595–618. [Google Scholar] [CrossRef]
- Dimkpa, C.; Weinand, T.; Asch, F. Plant– rhizobacteria interactions alleviate abiotic stress conditions. Plant Cell. Environ. 2009, 32, 1682–1694. [Google Scholar] [CrossRef]
- Bano, A.; Fatima, M. Salt tolerance in Zea mays (L). following inoculation with Rhizobium and Pseudomonas. Biol. Fertil. Soils 2009, 45, 405–413. [Google Scholar] [CrossRef]
- Yang, J.; Kloepper, J.W.; Ryu, C.M. Rhizosphere bacteria help plants tolerate abiotic stress. Trends Plant Sci. 2009, 14, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Egamberdieva, D. Pseudomonas chlororaphis: A salt-tolerant bacterial inoculant for plant growth stimulation under saline soil conditions. Acta Physiol. Plant 2012, 34, 751–756. [Google Scholar] [CrossRef]
- Setia, R.; Gottschalk, P.; Smith, P.; Marschner, P.; Baldock, J.; Setia, D.; Smith, J. Soil salinity decreases global soil organic carbon stocks. Sci. Total Environ. 2013, 465, 267–272. [Google Scholar] [CrossRef]
- Panhwar, Q.A.; Naher, U.A.; Radziah, O.; Shamshuddin, J.; Mohd Razi, I. Bio-fertilizer, ground magnesium limestone and basalt applications may improve chemical properties of Malaysian acid sulfate soils and rice growth. Pedosphere 2014, 24, 827–835. [Google Scholar] [CrossRef]
- Qin, Y.; Druzhinina, I.S.; Pan, X.; Yuan, Z. Microbially mediated plant salt tolerance and microbiome-based solutions for saline agriculture. Biotechnol. Adv. 2016, 34, 1245–1259. [Google Scholar] [CrossRef]
- Yadav, A.N. Plant Microbiomes for Sustainable Agriculture: Current Research and Future Challenges; Yadav, A.N., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 475–482. [Google Scholar]
- Zamora Re, M.; Tomasek, A.; Hopkins, B.G.; Sullivan, D.; Brewer, L. Managing Salt-affected Soils for Crop Production (Revised 2022). Available online: https://extension.oregonstate.edu/catalog/pub/pnw-601-managing-salt-affected-soils-crop-production (accessed on 6 March 2025).
- Daba, A.W.; Qureshi, A.S. Review of Soil Salinity and Sodicity Challenges to Crop Production in the Lowland Irrigated Areas of Ethiopia and Its Management Strategies. Land 2021, 10, 1377. [Google Scholar] [CrossRef]
- Tukhtashev, B.B.; Norkulov, U.; EIzbasarov, B. The Role of Salt-Tolerant Crops in the Proper Use of Saline Soils. E3S Web Conf. 2024, 477, 00101. [Google Scholar] [CrossRef]
- Mishra, A.K.; Das, R.; George Kerry, R.; Biswal, B.; Sinha, T.; Sharma, S.; Arora, P.; Kumar, M. Promising management strategies to improve crop sustainability and to amend soil salinity. Front. Environ. Sci. 2023, 10, 962581. [Google Scholar] [CrossRef]
- Mustafayev, Z.S.; Abdeshev, K.B. Modeling of Soil Salinization and Desalinization Processes; LAP LAMBERT Academic Publishing: Chisinau, Moldova, 2023; 185p. [Google Scholar]
- McElgunn, J.D.; Lawrence, T. Salinity tolerance of Altai wild ryegrass and other forage grasses. Can. J. Plant Sci. 1973, 53, 303–307. [Google Scholar] [CrossRef]
- van Genuchten, M.T. Analyzing Crop Salt Tolerance Data: Model Description and User’s Manual; Research Report No. 120; U.S. Salinity Laboratory, USDA, ARS: Riverside, CA, USA, 1983. [Google Scholar]
- Munns, R.; Tester, M. Mechanisms of salinity tolerance. Annu. Rev. Plant Biol. 2008, 59, 651–681. [Google Scholar] [CrossRef] [PubMed]
- Grieve, C.M.; Grattan, S.R.; Maas, E.V. Plant salttolerance. In ASCE Manual and Reports on Engineering Practice No. 71 Agricultural Salinity Assessment and Management, 2nd ed.; Wallender, W.W., Tanji, K.K., Eds.; ASCE: Reston, VA, USA, 2012; Chapter 13; pp. 405–459. [Google Scholar]

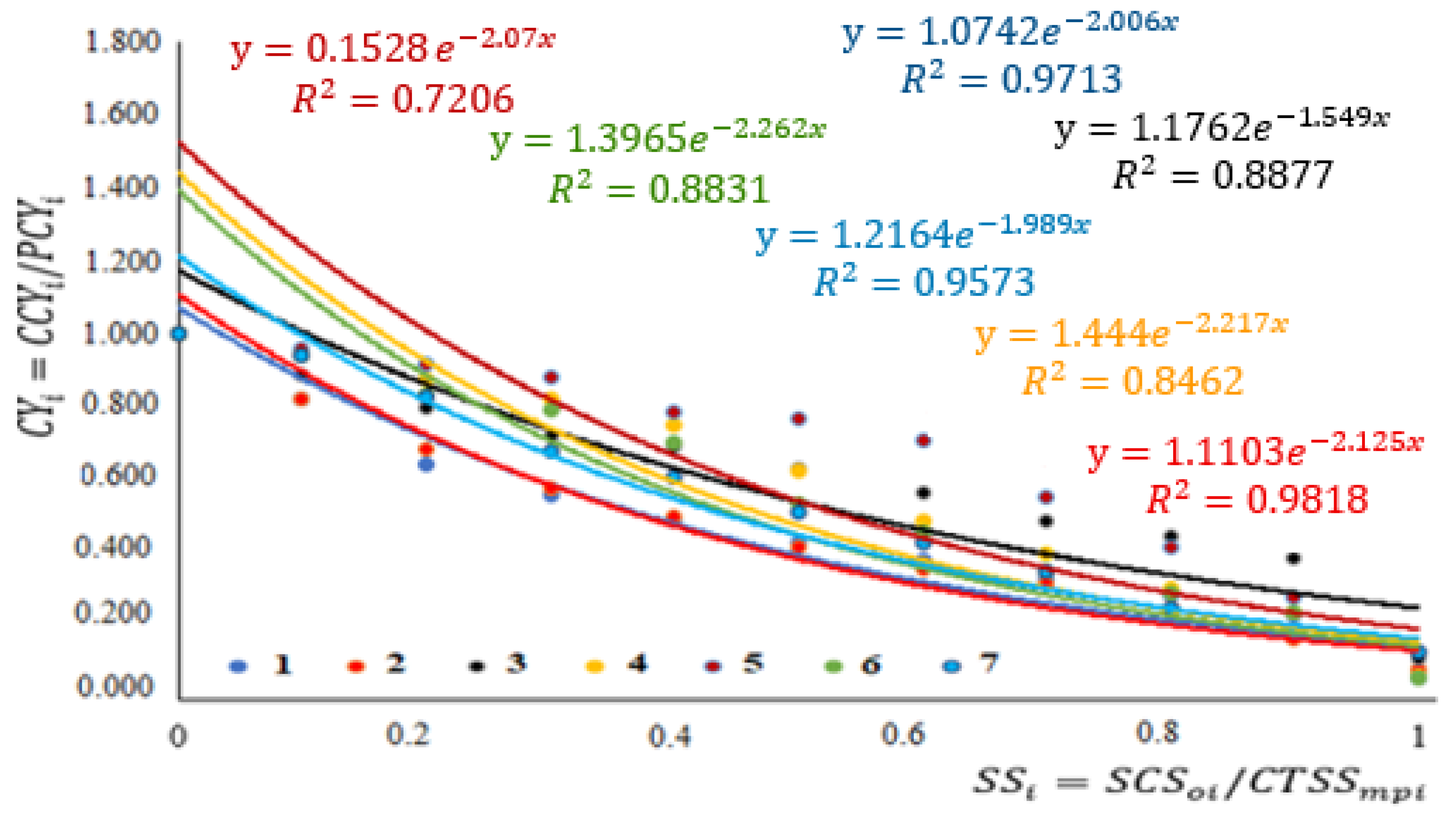
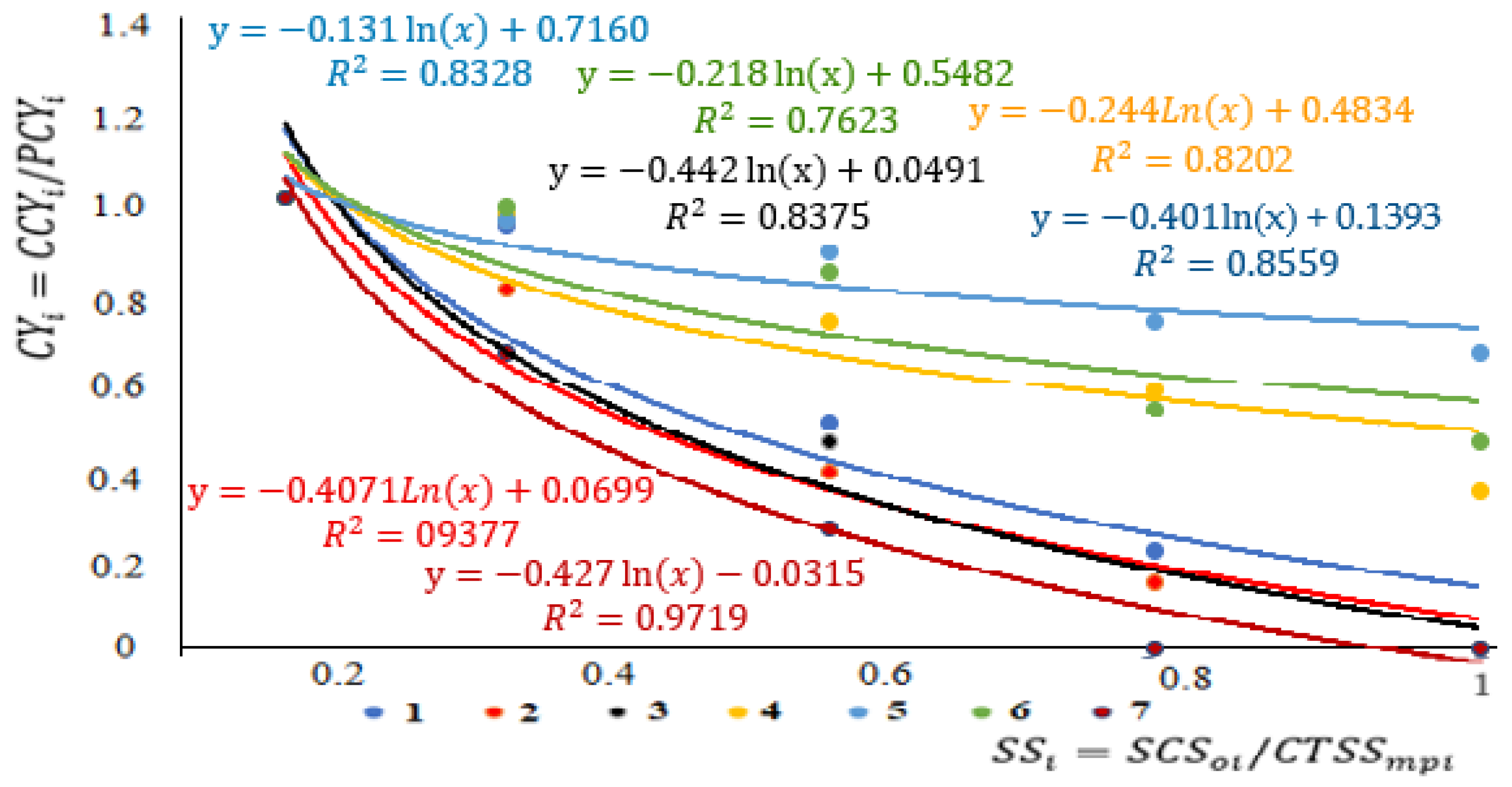
| Agricultural Crop | Equation | |
|---|---|---|
| Cotton | 0.9671 | |
| 0.8559 | ||
| Winter wheat | 0.9818 | |
| 0.9377 | ||
| Grain corn | 0.8877 | |
| 0.8375 | ||
| Silage corn | 0.8627 | |
| 0.8184 | ||
| Alfalfa | 0.8462 | |
| 0.8328 | ||
| Sugar beet | 0.7206 | |
| 0.8328 | ||
| Sunflower | 0.8831 | |
| 0.7623 | ||
| Potato | 0.7674 | |
| 0.7712 | ||
| Tomato | 0.8398 | |
| 0.8119 | ||
| Pea | 0.9573 | |
| 0.9719 | ||
| Sweet pepper | 0.8737 | |
| 0.9125 | ||
| Eggplant | 0.8737 | |
| 0.8389 |
| Plant Species | . mg/1000 | ||||
|---|---|---|---|---|---|
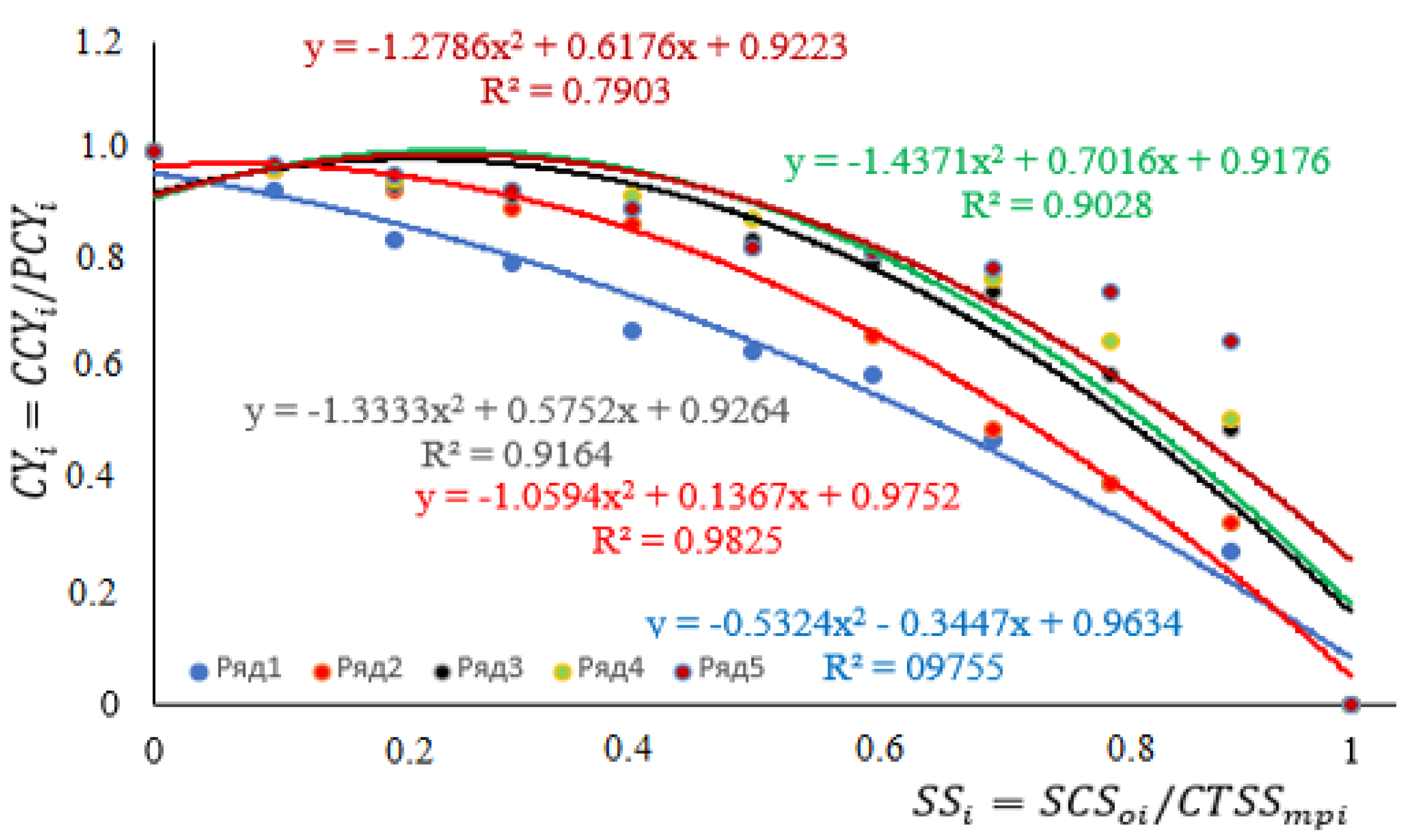
| Sugar beet | −0.5324 | −0.3447 | 0.9634 | 0.9755 | 5.00 |
| Alfalfa | −1.0694 | 0.1367 | 0.9752 | 0.9825 | 6.00 |
| Red clover | −1.1744 | 0.4251 | 0.9309 | 0.8998 | 8.00 |
| Buckwheat | −1.3333 | 0.5752 | 0.9264 | 0.9154 | 10.00 |
| Corn | −1.4371 | 0.7061 | 0.9176 | 0.9076 | 10.00 |
| Barley | −1.4371 | 0.7061 | 0.9176 | 0.9076 | 10.00 |
| Forage beans | −1.4371 | 0.7061 | 0.9176 | 0.9076 | 10.00 |
| Flax | −1.2786 | 0.6175 | 0.9223 | 0.7903 | 12.50 |
| Oats | −1.4793 | 0.7561 | 0.9108 | 0.8945 | 18.00 |
| Forage crops | |||||
| ) | −0.6379 | −0.3150 | 0.9711 | 0.9964 | 0.3 мг/кг |
| ) | −0.2016 | −0.7104 | 0.9700 | 0.9859 | 0.5 мг/кг |
| ) | −0.1955 | −0.8098 | 0.9886 | 0.9922 | 100 мг/кг |
| On Slightly Saline Soils (0.3–0.5%) | On Moderately Saline Soils (0.7–0.9%) | On Strongly Saline Soils (1.0–2.0%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Yield | Difference in Yield Depending on the Predecessor | Yield | Difference in Yield Depending on the Predecessor | Yield | Difference in Yield Depending on the Predecessor | |||
| centners/ha | centners | centners/ha | centners | centners/ha | centners | % | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| On rotation with perennial grasses for 1–10 years | ||||||||
| N60–90 | P2O590–100 | - | N90 | P2O590–110 | - | N120 | P2O5125 | - |
| 57.8 | - | - | 53.1 | - | - | 48 | - | - |
| Under the plasticity of perennial grass Rotation for rice field 2–10 years | ||||||||
| N90–120 | P2O5110 | - | N120 | P2O5110 | - | N130 | P2O5130 | - |
| 53.1 | 4.7 | 8.1 | 47.8 | 5.3 | 10.0 | 41.8 | 6.2 | 13.0 |
| On rice field 3–10 years | On rice field 3–10 years | |||||||
| N120 | P2O5120 | - | N120–150 | P2O5120 | - | N150 | P2O5140 | - |
| 48.3 | 9.5 | 16.4 | 42.3 | 10.8 | 20.3 | 35.3 | 12.7 | 26.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umirzakov, S.; Mustafayev, Z.; Tokhetova, L.; Baimanov, Z.; Akylbayev, K.; Koldasova, L. Modeling the Process of Crop Yield Management in Hydroagro-Landscape Saline Soils. Sustainability 2025, 17, 4214. https://doi.org/10.3390/su17094214
Umirzakov S, Mustafayev Z, Tokhetova L, Baimanov Z, Akylbayev K, Koldasova L. Modeling the Process of Crop Yield Management in Hydroagro-Landscape Saline Soils. Sustainability. 2025; 17(9):4214. https://doi.org/10.3390/su17094214
Chicago/Turabian StyleUmirzakov, Serikbay, Zhumakhan Mustafayev, Laura Tokhetova, Zhanuzak Baimanov, Kairat Akylbayev, and Lazzat Koldasova. 2025. "Modeling the Process of Crop Yield Management in Hydroagro-Landscape Saline Soils" Sustainability 17, no. 9: 4214. https://doi.org/10.3390/su17094214
APA StyleUmirzakov, S., Mustafayev, Z., Tokhetova, L., Baimanov, Z., Akylbayev, K., & Koldasova, L. (2025). Modeling the Process of Crop Yield Management in Hydroagro-Landscape Saline Soils. Sustainability, 17(9), 4214. https://doi.org/10.3390/su17094214







