3.1.1. Game Model Analysis of the Participant
Based on the income matrix in
Table 2, the expected income from strict government supervision was
, as shown in Equation (1).
The expected benefit that the government chooses not to supervise strictly was
, as shown in Equation (2).
The government’s average expected return was
, as expressed in Equation (3).
The government’s replication dynamic equation (a dynamic differential equation that describes the frequency or frequency with which a particular strategy is adopted by species in a population) [
30,
31] was
, as shown in Equation (4).
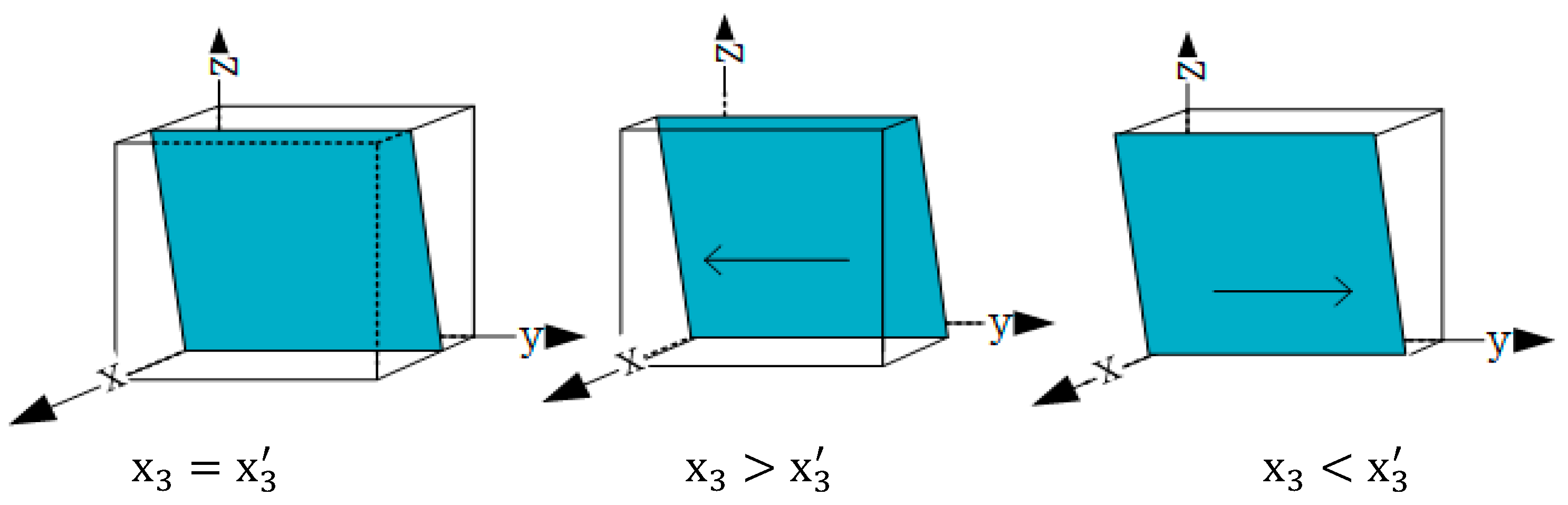
To analyze the equilibrium conditions for the government to achieve the stability strategy from the perspective of a single game player, the following analysis was conducted. Let determine the stability of the government’s choice strategy. Since was positively or negatively uncertain, the following assumption was made:
When , suppose , the following was true:
When , then , all were in the evolutionary stable state.
When , with , two possible evolutionary stability points were and .
According to the stability theorem of the replication dynamic equation, the probability of the government choosing supervision to be in a stable state must satisfy two conditions:
and
. Therefore, by taking the derivative of
, Equation (5) was obtained.
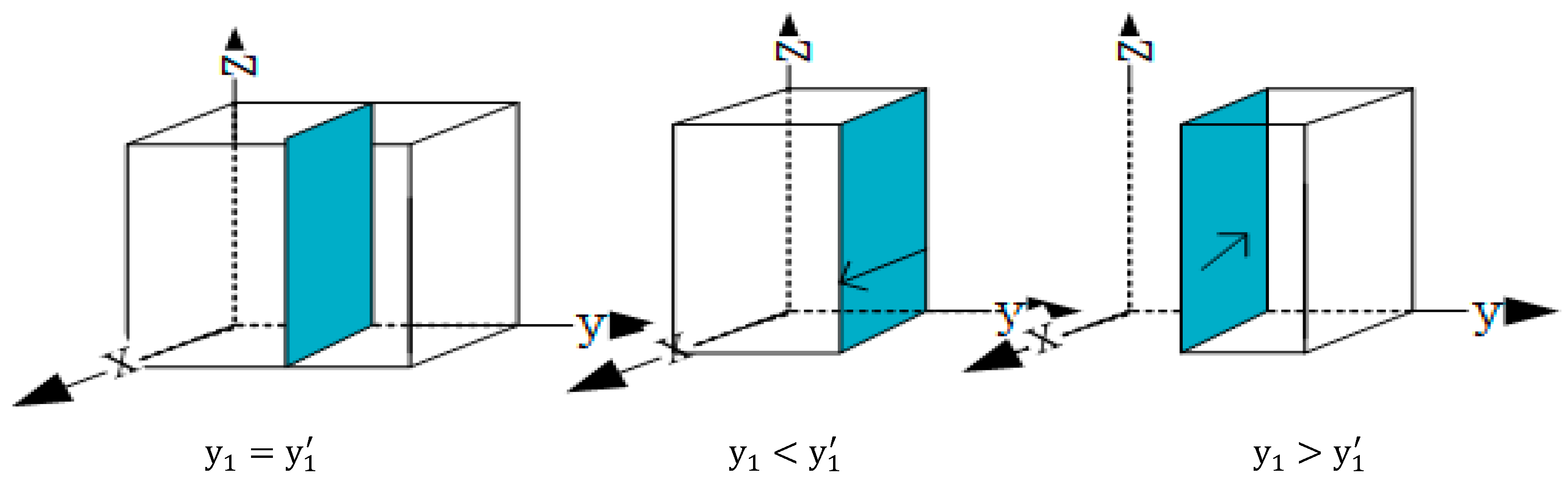
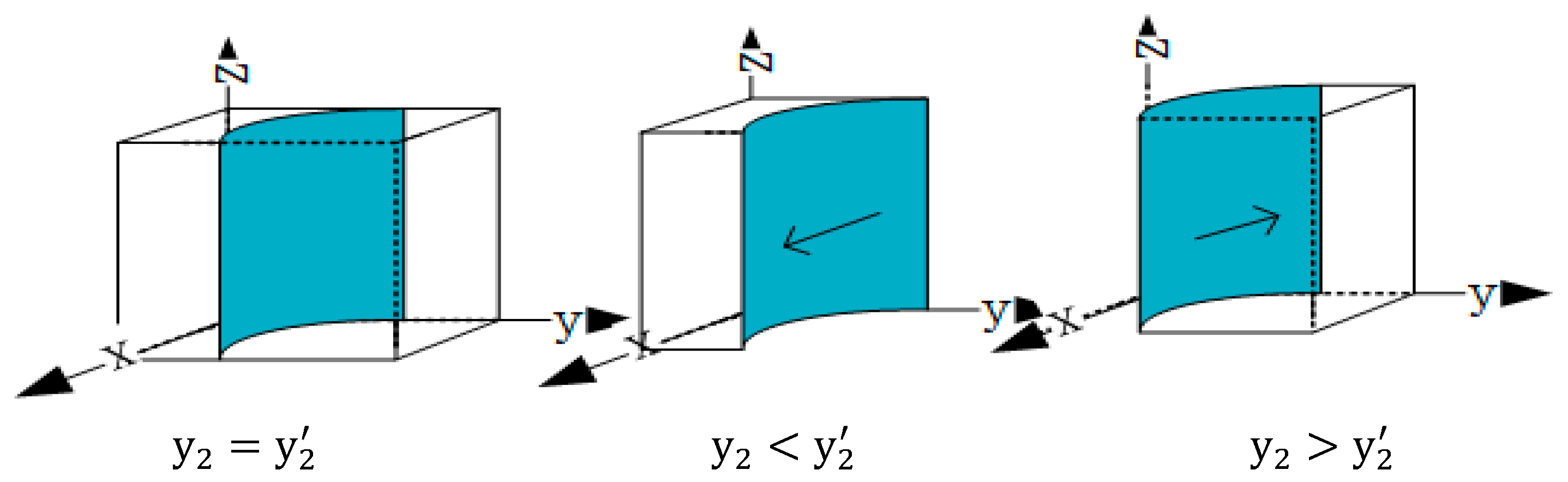
When , the two conditions for reaching a steady state were satisfied, and in this case, meant the government evolved a stable strategy.
When
,
, the two conditions for achieving a stable state were met, where
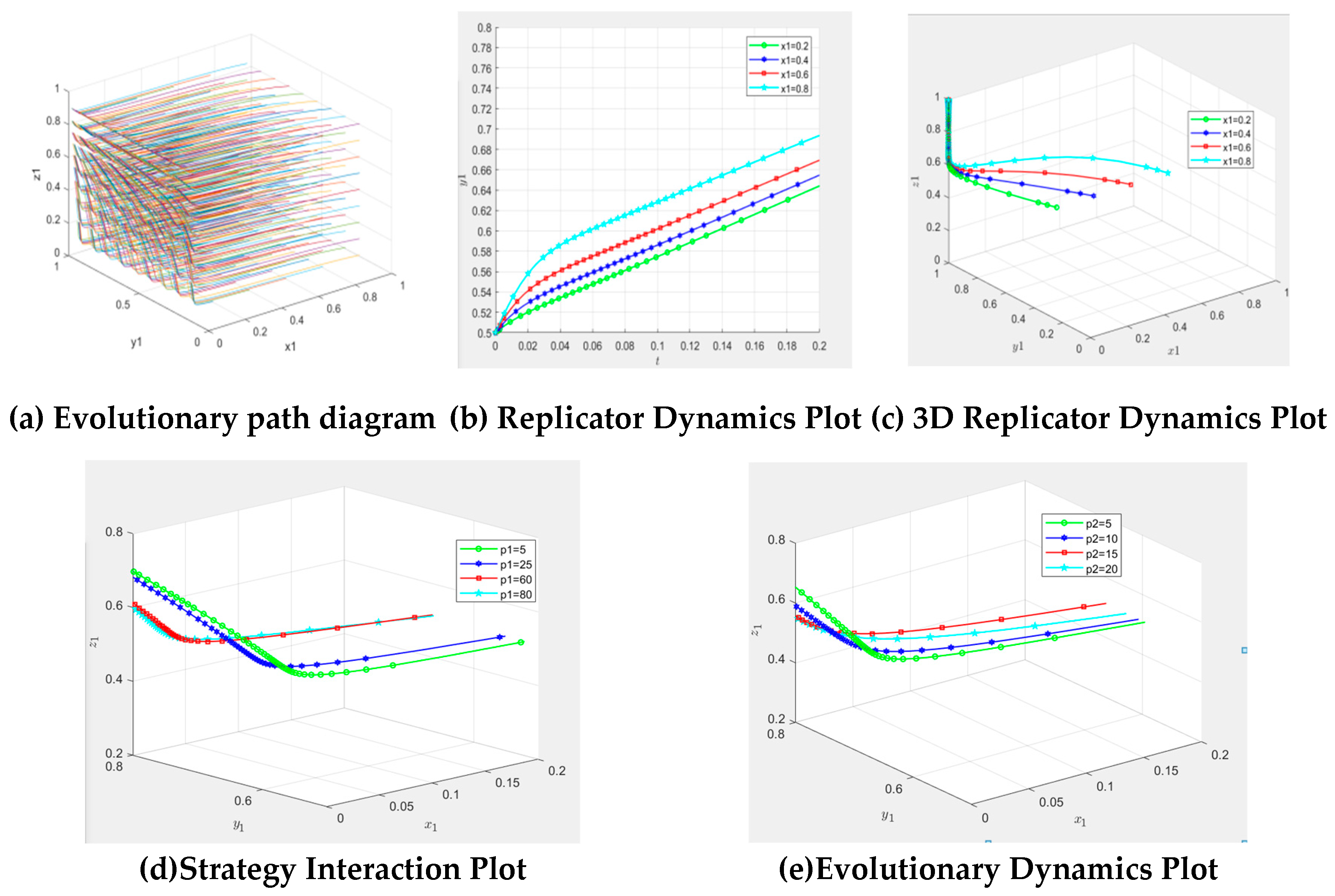
was the government’s evolution stability strategy. To demonstrate the above conclusions more intuitively, the evolutionary trend of government strategy was plotted (
Figure 2).
Based on the return matrix in
Table 2, the expected return of heavy-pollution enterprises that opt for emission reduction was
, and it was expressed as Equation (6).
The expected return of the heavy-pollution enterprise group was
, which was expressed s Equation (7).
The average expected return of heavily polluting enterprises was
, which was given by Equation (8).
The replication dynamic equation for the policy selection of heavily polluting enterprises is shown in Equation (9).
To analyze the equilibrium conditions for heavily polluting enterprises to achieve the stability strategy from the perspective of an individual game subject and to achieve for the stability of heavily polluting enterprises’ strategy because reflected positive and negative uncertainty, the following was assumed:
When , set , and the following was true:
When , then , all was in an evolutionary stable state.
When , make , and two possible evolutionary stability points were and .
According to the stability theorem of the replication dynamic equation, the probability that the heavily polluting enterprises were in a stable state must meet two conditions:
and
. Therefore, by taking the derivative of
, Equation (10) was obtained.
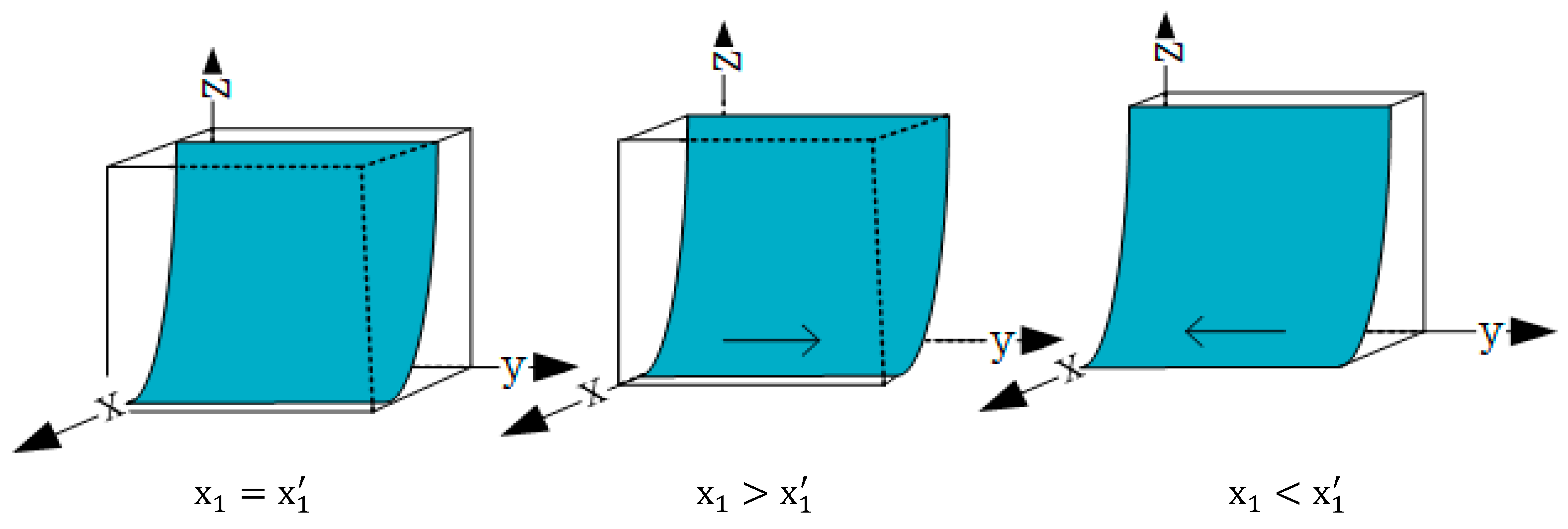
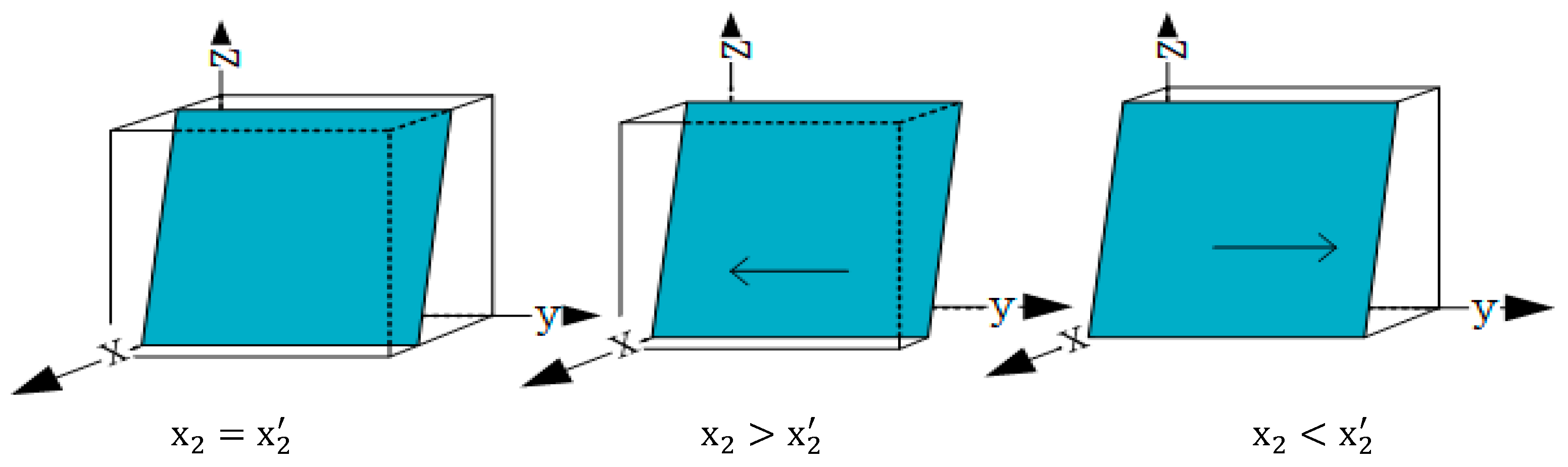
When , the two conditions to becoming a stable state were met. Where denotes the evolutionary stability strategy of the heavily polluting enterprises.
When
, the two conditions to becoming a stable state were met. Where
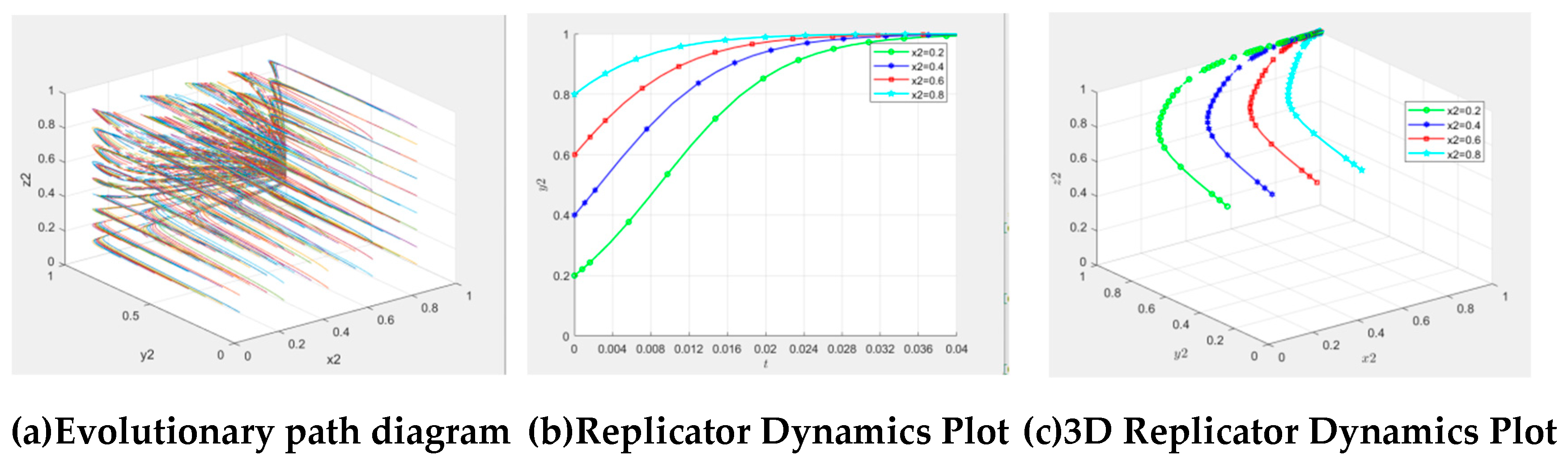
denotes the evolutionary stability strategy of the heavily polluting enterprises. To demonstrate the above conclusions more intuitively, the strategic evolution trend of heavily polluting enterprises was plotted (
Figure 3).
Based on the income matrix in
Table 2, the expected return of the public from choosing supervised enterprises was
, as shown in Equation (11).
The expected return of the public choosing not to supervise the enterprise was
, as shown in Equation (12).
The average expected return for the public was
, as shown in Equation (13).
The replication dynamic equation for public strategy selection is shown in Equation (14):
To analyze the equilibrium conditions for the public to reach a stable strategy from the perspective of a single game player, was used to seek the stability of the public choice strategy. Since reflected positive and negative uncertainty, the following was performed:
When , set , the following situations exist:
When , then , was in an evolutionary stable state.
When , set , evolutionary stability was true for and .
According to the stability theorem of the replication dynamic equation, the probability of the public choosing supervision to be in a stable state must satisfy two conditions:
and
. By taking the derivative of
, Equation (15) was obtained.
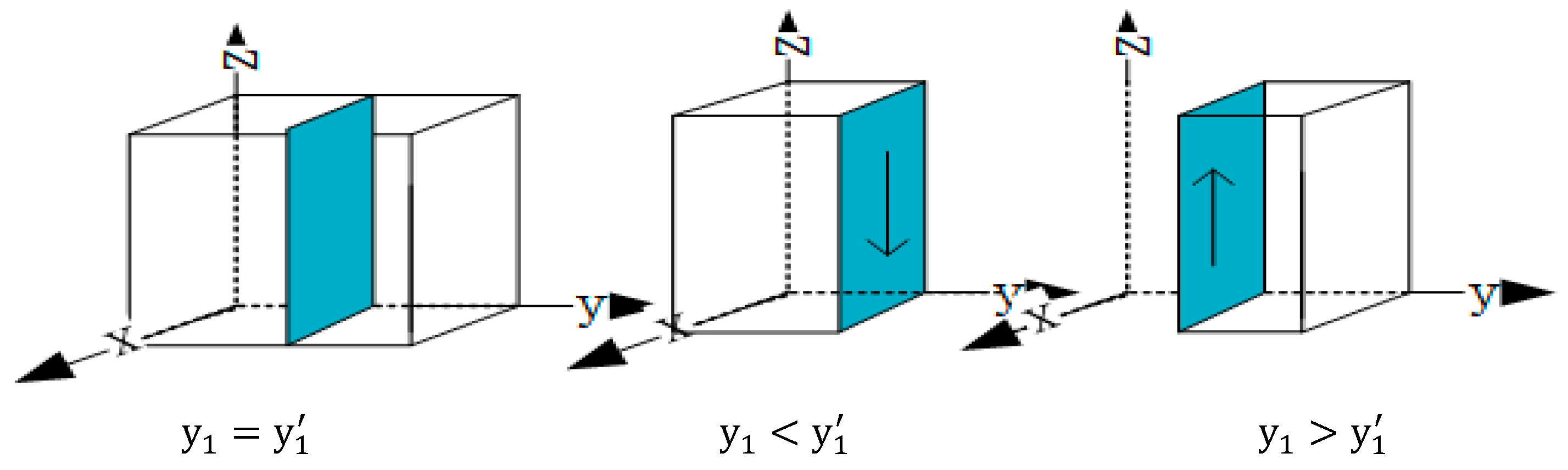
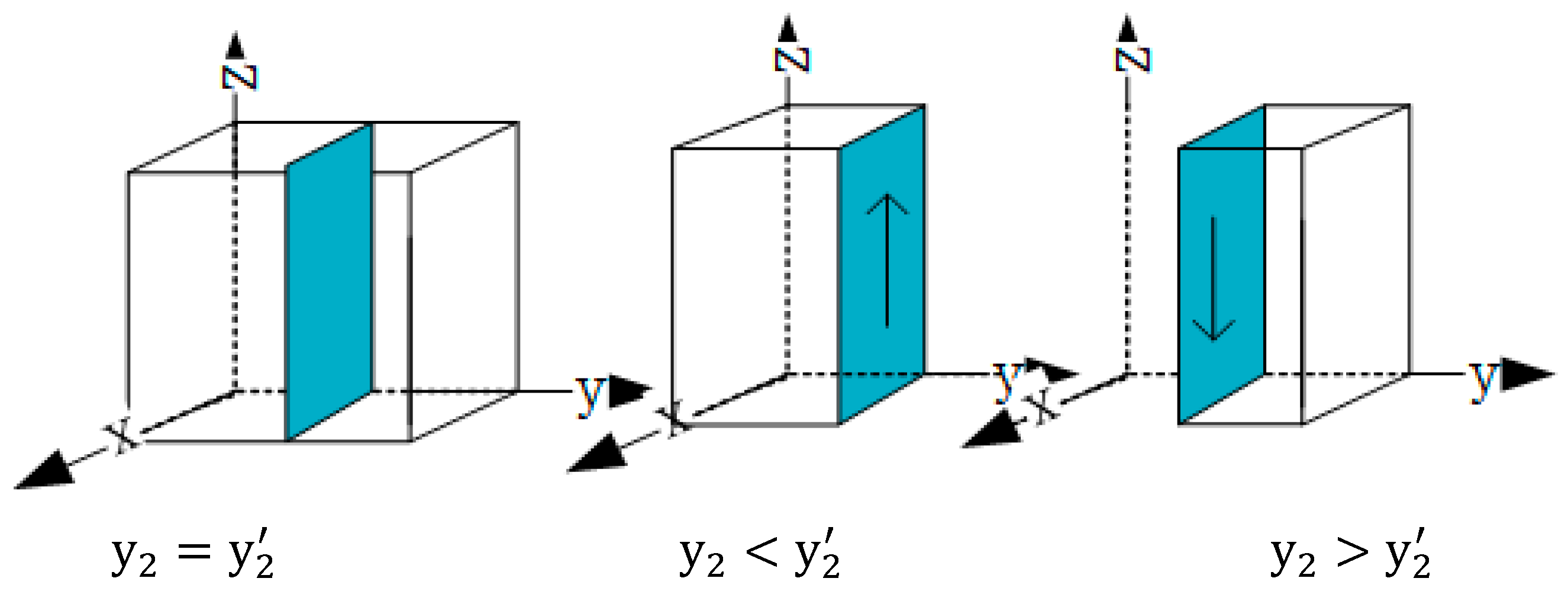
When and , the two conditions for achieving a stable state were satisfied, where was the mass evolution stability strategy.
When
,
, the two conditions were satisfied, and
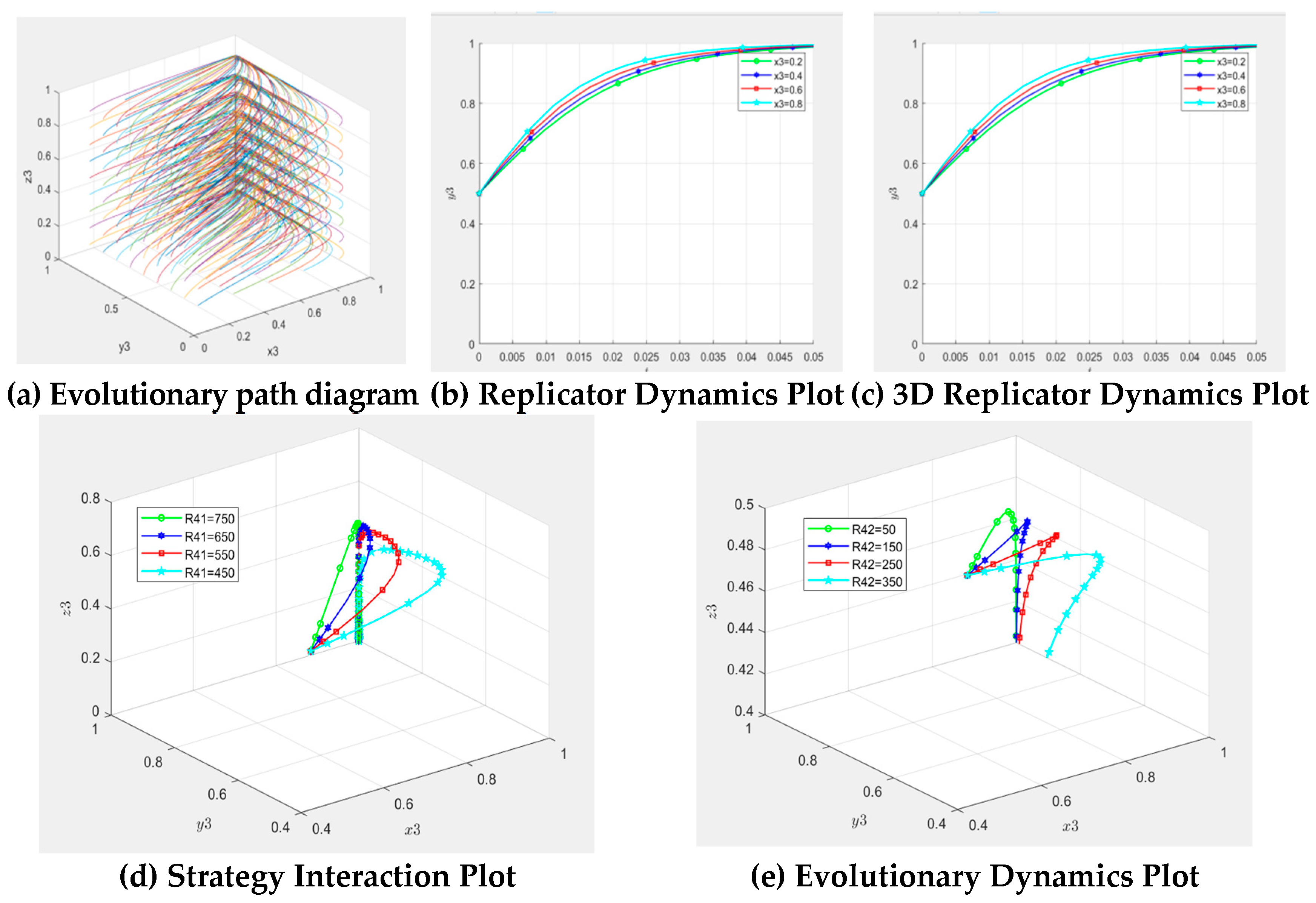
denotes the mass evolution stability strategy. To illustrate the above conclusions more intuitively, the evolutionary trends of public strategies were plotted (
Figure 4).
3.1.2. System Stability Analysis
The replication dynamic system was built according to Equations (4), (9) and (14).
It was assumed that , and eight pure strategy equilibria were obtained:
and .
By constructing a Jacobian matrix,
where T =
In the analysis of the stability of the replication dynamic system using Lyyanov’s first method (If the eigenvalues of the Jacobian matrix corresponding to the local equilibrium point were all negative, then the equilibrium point was the evolutionary stability point. If at least one eigenvalue was positive, the equilibrium point was unstable), and the resulting eight pure strategy equilibrium points were substituted into the Jacobian matrix to find the eigenvalues of each equilibrium point, as shown in
Table 3 [
32,
33].
When and , that is, the net income of government supervision was less than that of public supervision, reflected the stable evolution strategy, the system was the evolution trend of government supervision, emission reduction from heavily polluting enterprises, and the state of public supervision. In this ideal social state, enterprises were weakly constrained by the masses through independent governance and actively reduced pollution emissions. Moreover, the promotion of public education enhanced social awareness of environmental protection. The government does not directly supervise but ensures the transparency of environmental action and the possibility of public participation by formulating incentive policies, improving the legal system, and providing a platform for information disclosure. With the joint efforts of the government, enterprises, and the public, society formed a self-regulated and self-supervised environmental protection ecosystem that promoted the green transformation and sustainable development of the economy.
When and , that is, the net income of the government choice of supervision is greater than the net income of choosing no supervision, and the net income of mass choice of supervision is less than the net income of choosing no supervision was the stability point, and the evolution trend of system stability was government supervision, emission reduction by heavily polluting enterprises, and no public supervision. In this state, government supervision becomes key in promoting the emission reduction from heavily polluting enterprises. To further enhance the sustainability of this state, governments should continue to strengthen regulations and standards while encouraging businesses to invest in clean technologies through economic incentives such as tax incentives and subsidies. Support for technological innovation is also crucial, and governments can fund research and development projects to help companies adopt more environmentally friendly production methods, as well as raise public awareness through environmental education. Establishing public participation mechanisms, such as online reporting systems, and ensuring the transparency of corporate environmental information can gradually stimulate public enthusiasm for participation.
When , , and , was the stability point of system evolution. The evolution trend was supervision from the government, emission reduction, and public supervision, which reflected the most unsatisfactory state. In this situation, the government’s regulatory efforts failed to effectively promote the emission reduction actions of enterprises, and the supervision of the masses failed to produce the expected positive impact, leading to difficulties in achieving environmental protection. This suggested the need for reassessment and adjustment of regulatory strategies as well as enhancing the effectiveness of public participation to achieve better environmental protection.
When , , and , was the stability point of system evolution. Here, the strategy of the system was government supervision, emission reduction, and public supervision. This joint effort constituted a comprehensive environmental protection framework. The government must establish and implement strict environmental laws and regulations, encourage enterprises to reduce emissions through incentive and punishment mechanisms, and increase the research, development, and promotion of environmental protection technologies. Moreover, public awareness of environmental protection must be increased, and people should be encouraged to implement energy conservation and emission reduction practices in their daily lives through education and media.