Abstract
This study examines the impact of housing price increases on income inequality using the dynamic system GMM for OECD countries (2010–2021). We test the hypothesis that housing price appreciation affects income distribution differently based on economic development levels and homeownership patterns. The analysis is conducted both for the entire sample and by dividing countries into two groups based on per capita income, Group 1 (16 countries) with below-median per capita GDP and Group 2 (17 countries) with above-median per capita GDP, to account to account for structural differences in housing markets, financial systems, and wealth accumulation mechanisms. The findings show that rising housing prices help reduce income inequality, especially in countries that are relatively low-income and where more low-income households own their homes. Specifically, our estimates indicate that a one-point increase in the housing price index leads to a statistically significant (p < 0.05) 0.21 percentage point reduction in the Gini change rate in lower-income countries. However, in higher-income countries, the effect of housing prices on inequality is statistically insignificant, suggesting that the relationship between housing markets and income inequality varies across different economic contexts. This insignificance likely stems from countervailing forces: while housing appreciation increases wealth for homeowners, higher housing costs may disproportionately burden lower-income households through rental markets in these economies. The findings highlight the importance of country-specific housing programs that consider homeownership patterns and financial market access in tackling inequality, along with comprehensive public social policies. Our study has implications for policymakers seeking to address inequality through housing market interventions, particularly during the post-2008 recovery period and into the early pandemic phase.
1. Introduction
Although globalization has led to a narrowing of the income gap between countries, income inequality within countries has continued to rise over the past three decades [1,2,3]. This trend contradicts Kuznets’ (1955) hypothesis that income inequality would decrease after countries reach a certain level of economic development [4,5,6,7,8,9,10,11,12]. The persistence of income inequality demands a rigorous analysis of its underlying drivers to inform effective policy interventions.
Given the persistence of inequality, it is crucial to accurately track its evolution over time. Among various scientifically accepted indicators, the Gini coefficient is the most widely applied due to its simplicity, interpretability, and broad international coverage. While measurement approaches may differ, this study follows the conventional practice of using the Gini index, which offers reliable cross-country comparability.
In recent years, sharp increases in housing prices—particularly in metropolitan areas—have raised important questions about their distributional consequences. As housing represents a significant form of wealth for most households, changes in housing prices can affect inequality by shifting the relative advantages of homeowners and non-homeowners. However, the empirical evidence on this relationship remains limited and often contradictory.
The existing literature on the link between rising housing prices and income inequality presents two competing perspectives. The first argues that housing price increases exacerbate income inequality by creating a wealth effect that primarily benefits high-income households who are more likely to own multiple properties, thereby widening the wealth gap between homeowners and non-homeowners, intensifying existing inequalities. The second perspective suggests that, under certain conditions, housing price increases may actually reduce income inequality rather than widen it.
The underlying mechanism through which housing prices may reduce income inequality primarily relates to the wealth-building potential of homeownership. In economies where low-income households have relatively higher access to homeownership, rising housing prices can generate capital gains for these groups, thereby narrowing the wealth gap. This wealth accumulation may serve as a cushion against income volatility, reduce reliance on informal credit markets, and enhance long-term financial resilience. In contrast, in contexts where homeownership is concentrated among high-income groups, housing price increases may exacerbate inequality by concentrating asset appreciation in already wealthy households. Therefore, the direction and magnitude of the effect largely depend on how equitably homeownership is distributed across income groups.
This study examines three key questions:
- How do housing price dynamics influence income inequality trends in OECD countries?
- Does the relationship between housing prices and inequality differ across economies with varying levels of economic development?
- What role do homeownership patterns, particularly among lower-income households, play in mediating this relationship?
To address these questions, we investigate the effect of housing prices on income inequality in 33 OECD countries between 2010 and 2021 using a dynamic panel data approach with the system GMM. This methodological approach effectively addresses endogeneity concerns while capturing the dynamic nature of the relationship between housing markets and inequality.
To account for structural differences across economies, we divide our sample into two groups based on per capita GDP: countries below the median (Group 1) and countries above the median (Group 2). This classification allows us to examine how the distributional effects of housing price changes may vary across different economic contexts. While alternative groupings based on pre-existing inequality levels or housing market structures were considered, GDP per capita provides a robust proxy that correlates with multiple relevant structural characteristics including financial market development, homeownership rates, and redistributive capacity.
The contributions of this study are threefold. First, this study is one of the few that empirically examines the impact of rising housing prices on income inequality in OECD countries using a dynamic panel data approach. Unlike existing studies that primarily focus on the negative effects of housing price appreciation on inequality, our study provides evidence that, under certain conditions, rising housing prices may lead to more equitable wealth distribution.
Second, our two-group classification based on per capita GDP enables a comparative analysis between economies with relatively lower and higher income levels. This distinction is critical in understanding how the role of housing in wealth accumulation differs across different economic structures.
Third, this study contributes to the discussion on sustainable urban development by examining how housing price increases influence income inequality, a key factor in social and economic sustainability. Understanding this relationship is crucial for designing equitable and sustainable housing policies aligned with the principles of inclusive growth and sustainable cities [13].
The rest of this paper is structured as follows: Section 2 reviews the empirical literature on housing prices and income inequality; Section 3 outlines the data, sample, model, and methodology; Section 4 reports the empirical findings; Section 5 offers a discussion of the results; and Section 6 presents the conclusions and policy implications.
2. Theoretical Discussions on the Relationship Between Income Inequality and Housing Prices
Income inequality refers to how income generated in a certain time is distributed unequally among a population. When comparing the level of welfare between countries, the way income is distributed domestically is at least as important as the country’s income level and per capita income measurements. Indeed, studies have shown that increases in income inequality disrupt social peace and tranquility [14] and cause or deepen various economic problems. A growing body of literature suggests that inequality can be detrimental to sustainable long-term growth [15,16,17] and contribute to the deepening of the poverty problem [18,19]. Following the 2008 global financial crisis, academic interest in income inequality has intensified. Some authors have argued that income inequality may play a significant role in deepening economic crises [20,21,22,23,24,25]. Moreover, authors have shown that income inequality causes many social problems in terms of health [26,27], education [28], and psychology [29], in addition to its economic, political, and financial consequences. Recent findings also indicate that inequality affects tax systems and fiscal structures [30,31,32,33].
The global rise in income inequality over the past three decades has raised concerns about its root causes. While some scholars emphasize innovation and technological change as primary drivers [34,35,36], others point to globalization and liberalization as direct or indirect sources of rising inequality [8,12,37]. Additionally, findings in the literature indicate that international trade [38], labor market conditions [39,40], economic crises [41], political interventions [42], and other inequalities (e.g., wealth, gender, race, regional inequalities) [43,44] affect income inequality. However, relatively few studies disentangle the respective impacts of market forces and public policy on redistributive outcomes [23,45,46,47,48].
Recent studies highlight the bidirectional relationship between housing prices and income inequality by illustrating how inequality affects housing markets and how housing price changes, in turn, reshape income distribution through mechanisms such as wealth accumulation, affordability constraints, or spatial segregation. Building on these insights, the literature has evolved in two main directions, focusing either on how inequality shapes housing markets or on how housing affects inequality.
The argument that rising income inequality leads to higher housing prices is based on the notion that high-income households use their growing purchasing power in the housing market, thereby further driving price increases [49,50,51]. This idea is supported by evidence showing that income concentration among the wealthy fuels demand for premium housing in desirable neighborhoods. This is often referred to as the “superstar city” effect, where affluent individuals raise property prices in sought-after areas, contributing to broader increases in housing costs [52,53]. Moreover, various forms of inequality—such as differences in family structure, female labor force participation, race, and occupational status—also influence households’ access to both new and existing housing markets. While the market serves certain segments of the population, it fails to serve the majority of lower-income households [54]. However, this view is not without contradiction. Some studies have shown that increases in income inequality may suppress housing prices [55,56,57,58]. According to these findings, as inequality increases, low-income households struggle to access housing, and their weakened demand cannot be offset by higher-income groups. Simultaneously, wealth accumulation among upper-income households may lead to oversupply in certain market segments [58].
In recent years, there has been a growing number of studies examining the impact of housing prices on income inequality, yet the findings remain far from conclusive. While a significant body of research supports the inequality-exacerbating effects of housing price increases, a growing number of studies point to conditions under which the opposite may occur (Table 1). The following paragraphs explore both strands in turn.
Several empirical studies demonstrate that increasing housing-related costs—whether through rising prices, rents, or housing expenditures—contribute to growing income inequality, especially among lower-income households. In their time-series analysis for Iran between 1982 and 2012, Gholipour et al. (2016) [59] revealed that a 1% increase in housing costs increased income inequality by 0.125%. Similarly, Sun-Hee and Seong-Min (2019) [60], using panel VAR analysis of Korean regional data from 2003 to 2016, found that rent prices significantly affected income inequality before the global financial crisis, while both rent and housing sales prices had a significant impact in the post-crisis period. Dustmann et al. (2022) [61] show that between 1993 and 2013, income inequality in Germany increased much more sharply when housing expenditures are taken into account. For example, the 50/10 ratio of net household income rose by 22 percentage points before housing, but by 62 percentage points after housing expenditure. Margalef Jordà and Villarroya Pascua (2020:7) [62] argued that increasing housing prices will increase inequality at different levels. Indeed, rising housing prices intensify “economic inequality”, as it creates wealth for some people through capital accumulation while requiring others to spend more; “social inequality”, as it reshapes social classes and social structures; and “spatial inequality”, by creating regional “gentrification”, as it directly affects the spatial appearance of cities.
Conversely, some studies in the literature suggest that the housing market may alleviate income inequality. In their study of Canadian metropolitan areas between 2006 and 2016, Sopchokchai and Zhou (2020) [63] found that a 1% increase in the average sales price decreased the Gini index calculated by the gross income method by 6% and the Gini index calculated by the net income method by 4.5%. Similarly, Woloszko and Causa (2020) [64] concluded in their analysis of OECD countries that an increase in homeownership strengthens the middle class with the wealth effect and reduces wealth inequality. Moreover, some recent studies emphasize the importance of contextual factors such as redistribution policies or structural market differences. Kim and Rhee (2022) [65] reveal that in countries with strong redistribution mechanisms, the inequality-exacerbating effect of asset prices is muted. Conversely, in countries with weak social safety nets, housing price increases tend to aggravate inequality. This insight supports the argument that housing markets alone do not determine inequality outcomes—public policies and structural differences play a crucial role.

Table 1.
Current literature about the “Effects of Housing Market on Income Inequality” (“POSITIVE” or “NEGATIVE” is meaning regression direction).
Table 1.
Current literature about the “Effects of Housing Market on Income Inequality” (“POSITIVE” or “NEGATIVE” is meaning regression direction).
| Authors | Topic/Title | Model/Period/Countries | Main Finding |
|---|---|---|---|
| Yin et al. (2019) [66] | Spatial Justice of a Chinese Metropolis: A Perspective on Housing Price-to-Income Ratios in Nanjing, China | Geostatistical Analysis, Spatial Modeling and Interpolation Techniques 2009–2017, Nanjing | The rising housing price-to-income ratio has exacerbated spatial inequality, displacing vulnerable groups to urban fringes and reinforcing class stratification (POSITIVE) |
| Margalef Jordà and Villarroya Pascua (2020) [62] | Housing Price Inflation and Inequality: Assessment of the housing market in the city of Barcelona | Assessment Analysis, Barcelona | It has been argued that increasing housing prices will increase inequality at different levels. Indeed, while the increase in housing prices creates wealth for some people through capital accumulation, it increases economic inequality as it requires others to spend more; social inequality as it reshapes social classes and structures; and spatial inequality by creating regional “gentrification” by shaping the landscape of cities. (POSITIVE) |
| Sopchokchai and Zhou (2020) [63] | House Price and Income Inequality in Canada: the Instrumental Variable Approach | Panel Data Analysis, 2006–2016, Canada Metropolitan Areas (CMA) | They consider Gini coefficients calculated from both total income and residual income, and they find that an increase of 1% in median sale price reduces the Gini index by about 6% and by 4.5%, respectively. (NEGATIVE) |
| Fuller et al. (2020) [67] | Housing Prices and Wealth Inequality in Western Europa | Panel Data Analysis, wealth-to-income ratios, 1970 to 2003 13 Western European and OECD countries, | The increase in wealth–income ratios is not due to homeownership or national savings rates but rather to rising housing prices and price changes in other financial assets. (POSITIVE) |
| Woloszko and Causa (2020) [64] | Housing and wealth inequality: A story of policy trade-offs | Microsimulation Analysis, OECD countries | The increase in homeownership strengthens the middle class through the wealth effect and reduces wealth inequality. (An elementary illustrative microsimulation study shows that if the value of all homes suddenly fell to zero, the Gini coefficients of the net wealth distribution would be 1.24 times higher on average across countries.) (NEGATIVE) |
| Dustmann vd. (2022) [61] | Housing Expenditure and Income Inequality | Panel Data Analysis, 1993–2013, Germany | This study contributes to the inequality literature by demonstrating that changes in the housing market may be the main driving force behind the increasing income inequality after housing expenditures and may lead to differentiation in consumption and savings patterns among income groups. (POSITIVE) |
| Kim and Rhee (2022) [65] | The effects of asset prices on income inequality: Redistribution policy does matter | Panel Data Analysis, 1980–2018, 32 developed countries | After conducting empirical analyses on 32 developed countries between 1980 and 2018, they concluded that the stance of countries in redistribution policies significantly affects the impact of asset prices on income inequality. The results indicate that housing prices worsen inequality in countries with weak redistribution, but have no effect where redistribution is strong. (POSITIVE) |
In line with the second strand of the existing literature, this study empirically investigates the impact of rising housing prices on income inequality across economies that exhibit structural heterogeneity with respect to income levels. While much of the existing work relies on single-country analyses or static estimation techniques, this study employs a dynamic panel approach using the system GMM estimator. By distinguishing countries based on income level, it offers new insights into how housing markets affect inequality under varying structural conditions. This study offers novel empirical insights, demonstrating that the inequality effects of housing prices are deeply shaped by structural and contextual differences.
3. Data, Sample, Methodology, and Models
3.1. Research Data and Sample
Panel data for OECD countries were compiled from annual observations spanning the period from 2000 to 2021. The dependent variable, the percentage change in the Gini coefficient, is calculated using data from the OECD database. The first lag of the dependent variable was computed for inclusion in the GMM model. The real house price index and the percentage of owner-occupied households in the first- and fifth-income quintiles are obtained from the OECD Affordable Housing Database (AHD). Additionally, the ratio of the percentage of homeowner households in the fifth-income quintile to that in the first-income quintile is derived from the same source.
As control variables, the domestic consumer price index is obtained from the OECD database, while the natural logarithm of GDP (PPP) is computed using data from the World Bank. The Gross Domestic Product per capita is also sourced from the World Bank database.
We collected data for 33 OECD countries during the period 2010–2021. However, OECD countries are heterogeneous in terms of housing ownership structure. Therefore, we also divided the OECD countries into two groups based on their per capita income for the same period. The country list is presented in Table 2. Countries below the median were classified as relatively low-income (Group 1), while those above the median were categorized as high-income (Group 2).

Table 2.
Sources and definitions of variables.
3.2. Methodology and Models
In this study, whether the consumer price index, real housing price index, the ratio of the shares of homeownership among the richest and poorest income groups, the shares of homeowners of the poorest income groups in the total population, and the increases in real GDP have a significant effect on income inequality were investigated using the dynamic panel data analysis method. For this purpose, annual data for 33 OECD countries were used in this study, and the years 2010–2021 were examined. Then, we divided the 33 countries into two groups (Group 1: 16 countries, and Group 2: 17 countries) according to their per capita income. Those above the median have relatively higher per capita income than other countries and vice versa for low-income countries. For this purpose, analysis was carried out with the two-stage system generalized moments estimator (system GMM), one of the dynamic panel data methods. The Stata-17 econometric analysis package program was used in all analyses.
We chose the dynamic system GMM approach for several reasons. First, traditional panel data methods such as fixed effects or random effects estimators become inconsistent when lagged dependent variables are included in models with relatively short time dimensions [68]. Second, the system GMM effectively addresses the endogeneity concerns in our model, where housing prices and inequality likely exhibit bidirectional causality. Third, this method is more efficient than the difference GMM when variables are highly persistent, as is the case with many macroeconomic variables, including inequality measures. Finally, the system GMM allows us to incorporate both time-invariant and slowly changing variables, which is crucial when analyzing structural differences across countries.
In the time-series regression models, it is common practice to include lagged values of the dependent variable. However, in panel data models where the period is short, a small sample bias occurs in coefficient estimation and hypothesis testing. This is because of the endogeneity problems originating from the dynamic structure, fixed effects, or random effects estimation, which are inference methods based on least squares, and are biased and inconsistent. Therefore, it has become a standard practice today to use instrumental variable (IV) methods or the Generalized Method of Moments (GMM), which produce consistent parameter estimates for a finite number of time periods (T) and a large cross-section size (N) [69]. The general dynamic panel data model is discussed as follows.
Here, denotes the unobserved heterogeneity that varies only from unit to unit. is the idiosyncratic error component. and are the observed variables. The dynamic panel data model in (1) distinguishes between long-run or equilibrium relationships and short-run dynamics. Usually, the unit-specific effect is associated with . Furthermore, the lagged dependent variable is associated with the individual-specific effect, i.e., E(|) = 0. This endogeneity problem implies that least squares-based estimators may be inconsistent. For this purpose, dynamic panel-specific estimators have been proposed. These estimators obey the following conditional moment restriction of the errors.
Based on assumption (1), the model can be expressed in first differences as follows:
In Equation (3), the lagged value of the dependent variable is related to . Lagged levels of endogenous variables can be used as instruments for current changes. Simple IV estimators of this type were first proposed by Anderson and Hsiao (1981, 1982) [70,71]. Since is related to but not to , it can be used as an instrumental variable instead of . The instrumental variable proposed by Anderson and Hsiao (1981, 1982) [70,71] is provided with the moment conditions = 0 and = 0. However, the Anderson and Hsiao (AH) estimator does not consider all moment conditions. Arellano and Bond (1991) [72] proposed the Generalized Method of Moments (GMM), which considers all moment conditions. In the literature before Arellano and Bond, the first difference estimator defined the instrumental variable. Blundell and Bond (1998) also defined the instrumental variable for the undifferentiated Equation (1) and developed the system GMM estimator [73]. The estimation of the dynamic error components model in Blundell and Bond (1998) was designed to improve the properties of the standard first-differenced GMM estimator and is handled using two alternative linear estimators [73]. Later, with the improvements made by Bun and Windmeijer (2010), a finite sample correction was provided to the two-stage covariance matrix; it was shown that the two-stage estimator would give more consistent results than the single-stage estimator [74].
In this study, the effect of key economic and housing market variables on income inequality dynamics is examined using the dynamic system GMM method. Given the short time dimension of the panel dataset, unit root tests were not performed to avoid unreliable results. Instead, we employ a progressive modeling approach with three distinct econometric model variants to examine how various factors influence income inequality and to assess the consistency of our key findings under alternative variable configurations. Specifically, we begin with a parsimonious baseline equation capturing core macroeconomic relationships, then systematically incorporate additional housing market variables in subsequent model iterations to evaluate the stability of coefficient estimates across different functional representations. In all models, the dependent variable represents changes in income inequality, indicating whether inequality increases or decreases. As is known, the Gini Coefficient, developed by the Italian statistician Corrado Gini (1884–1965), is frequently used in income inequality measurements and provides a quantifiable measure of inequality [75]. In this study, the Gini index is scaled from 0 to 100, rather than the conventional 0 to 1 range. This scaling choice affects the interpretation of all coefficients in our models—changes that would represent a 0.01-point movement on the 0–1 scale correspond to a 1-point movement on our 0–100 scale. This distinction is particularly important when comparing our results with other studies that may use the traditional 0–1 scaling. The coefficient approaches to 1, indicating an increased inequality, while as it approaches to 0, income is distributed more fairly [76]. In this study, the Gini index is scaled from 0 to 100, rather than the conventional 0 to 1 range. Accordingly, all interpretations of changes in the Gini index should be understood in this context. The percentage change in the Gini Index (), also referred to as the growth rate of the Gini Index, measures the relative variation in income inequality over time. A positive indicates that income inequality has increased compared to the previous period, while a negative () suggests a reduction in income inequality.
The models are structured progressively, with each new specification building upon the previous one to provide deeper insights into income inequality dynamics:
This initial model examines the fundamental relationship between income inequality and key macroeconomic indicators. The inclusion of GDP per capita (), is grounded in the Kuznets hypothesis, which posits an inverted U-shaped relationship between economic development and inequality. As countries develop, inequality initially rises but eventually declines as growth benefits spread more widely. Consumer prices (, are included to analyze inflation’s distributional effects, as inflation typically affects income groups asymmetrically, with lower-income households being more vulnerable due to their higher propensity to consume and limited financial hedging capabilities. Real housing prices () represent a critical wealth component based on wealth–income inequality transmission mechanisms, as housing constitutes the largest asset for many households and price fluctuations significantly impact wealth distribution. Together, these theoretically justified variables provide the economic context that is essential for understanding broader inequality patterns.
Building on Model 1, this specification introduces two critical housing market dimensions: the homeownership rate among the poorest-income quintile () and the price-to-rent ratio (). The homeownership rate of the bottom quintile serves as a direct measure of housing accessibility for vulnerable populations. The homeownership rate of the bottom quintile serves as a direct measure of housing accessibility for vulnerable populations, inspired by prior research from Woloszko and Causa (2020), who found that homeownership strengthens the middle class and reduces wealth inequality [64]. Additionally, Kim and Rhee (2022) demonstrated that redistribution policies interact with housing markets to impact inequality outcomes—an insight that motivated our examination of whether housing ownership patterns among low-income groups could have similar mediating effects [65]. When this rate decreases, it suggests that lower-income households face greater barriers to acquiring property assets, potentially widening wealth disparities that subsequently affect income inequality. The price-to-rent ratio complements this by measuring housing market affordability—a high ratio indicates expensive purchasing relative to renting, which may force lower-income households to remain renters, preventing wealth accumulation through property ownership. These variables’ impact varies across economic contexts: during periods of rapid housing price appreciation, limited homeownership among lower-income groups can accelerate inequality, while during economic contractions, these effects may become even more pronounced as vulnerable homeowners face a greater risk of property loss. This model helps reveal whether housing market dynamics may disproportionately affect lower-income households, potentially exacerbating or mitigating income disparities beyond what general economic indicators suggest.
Our most comprehensive specification replaces the bottom quintile homeownership variable with the “Housing Inequality Ratio” (), which directly captures the homeownership gap between the richest and poorest income groups. Defined as the ratio of homeownership rates between the top (Q5) and bottom (Q1)-income quintiles, this variable reflects the structural distribution of housing wealth across society. This ratio was inspired by Margalef Jordà and Villarroya Pascua (2020), who argued that housing markets create multiple forms of inequality—economic, social, and spatial—when wealth accumulation through property ownership is unevenly distributed [62]. This ratio behaves differently across economic contexts: during economic expansions, especially those with strong housing market growth, the gap tends to widen as wealthier households leverage existing assets to acquire more property. Conversely, during economic downturns, this gap may either expand further (if lower-income homeowners face disproportionate foreclosures) or temporarily contract (if high-end property markets experience sharper corrections). By examining this alongside housing affordability measures, we assess whether disparities in asset ownership between income extremes significantly drive broader income inequality patterns, potentially identifying a wealth-based mechanism through which housing markets influence overall economic inequality.
These models collectively provide insights into how macroeconomic conditions, housing market dynamics, and the distribution of homeownership contribute to changes in income inequality across OECD countries. The progressive structure allows us to isolate and understand the specific channels through which housing markets may exacerbate or mitigate income disparities beyond what standard economic indicators suggest.
While our methodological approach offers several advantages, we acknowledge certain limitations. First, despite system GMM’s ability to address endogeneity, the complex bidirectional relationship between housing markets and inequality may not be fully captured. Second, our relatively short time dimension (2010–2021) may not adequately reflect long-term structural changes or complete market cycles. Third, the heterogeneity across OECD housing markets—including various regulatory frameworks, taxation systems, and cultural preferences for ownership—introduces complexity that simplified models cannot entirely address. Finally, our results may be sensitive to the period studied, which includes the aftermath of the global financial crisis and part of the COVID-19 pandemic, both of which significantly impacted housing markets and inequality in ways that vary across countries.
4. Findings
Table 3 presents the descriptive statistics of the selected variables, covering the period from 2010 to 2021, in line with the scope of the study. The mean Gini coefficient is higher in low-income countries (Group 1) than in high-income countries (Group 2), indicating greater income inequality in lower-income economies. However, the homeownership inequality ratio (Q5/Q1) is higher in Group 2, suggesting a greater disparity in homeownership rates across income quintiles in wealthier countries. The mean homeownership rate in the first-income quintile (Q1) is significantly higher in low-income countries (69.076) compared to high-income countries (39.424), implying that economic conditions or policies in lower-income countries may support homeownership among low-income households.

Table 3.
Summary statistics for selected variables used models. (a) Statistical significance of mean differences between Group 1 and Group 2 countries.
Regarding macroeconomic indicators, GDP per capita is expectedly higher in Group 2, with an average of 56,329 compared to 29,646 in Group 1. Additionally, the consumer price index is slightly higher in low-income countries. These findings highlight significant differences in inequality, homeownership, and macroeconomic indicators across OECD countries.
As shown in Table 3, the average homeownership rate among the lowest quintile (Q1) in Group 1 countries is 69.1%, significantly higher than in Group 2 (39.4%). This descriptive finding aligns with the empirical result from Model 2 (β5 = −0.017), which shows that greater homeownership among low-income households reduces inequality. Similarly, the Q5/Q1 ratio—significantly higher in Group 2—correlates with Model 3 findings, where an increase in this disparity leads to greater inequality (β5 = 0.532). Therefore, Table 3 does not only describe structural differences but provides the essential context for understanding the estimated effects in subsequent models.
To assess whether the observed differences in means between Group 1 and Group 2 countries are statistically significant, we conducted two-sample t-tests for each variable of interest. Table 3 presents the results of these tests. The differences between the two groups are statistically significant across all key variables. Notably, the Gini coefficient difference (t = 7.533, p < 0.001) confirms that income inequality is systematically higher in Group 1 countries. The homeownership inequality ratio difference (t = −22.017, p < 0.001) exhibits an extremely large effect size (Cohen’s d = −2.214), indicating a fundamental structural difference in how housing wealth is distributed across income groups in the two country clusters. Similarly, the homeownership rate in the bottom quintile shows a highly significant difference (t = 28.899, p < 0.001), with an extraordinarily large effect size (Cohen’s d = 2.906). These findings provide robust statistical evidence of the structural differences in housing markets and inequality patterns between lower and higher-income OECD countries, supporting the theoretical premise that homeownership distribution patterns may mediate the relationship between housing prices and income inequality.
Figure 1 shows the average housing ownership rate of the first and last 20% income quantile in selected OECD countries (Group 1 and Group 2) for the period of 2010 to 2021. It highlights a significant distinction between the two groups in terms of housing ownership rates among lower-income households. In Group 1 countries, which have a per capita GDP below the median, the homeownership rate of the bottom 20% income quantile (Q1OWN) is relatively higher compared to Group 2. This suggests that, in these economies, lower-income households have greater access to homeownership, potentially due to lower entry barriers in the housing market or historical policy incentives.
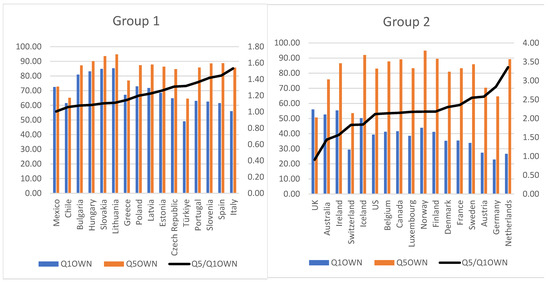
Figure 1.
Housing ownership rate by first and last 20% income wuantile (Q5/Q1OWN). (Group 1: countries with below-median GDP per capita; Group 2: countries with above-median GDP per capita; Q1OWN: the homeownership rate of the bottom 20% income quantile; Q5OWN: the homeownership rate of the last 20% income quantile).
While Figure 1 visually confirms the descriptive statistics in Table 3, its added value lies in highlighting the disparity between income groups more intuitively. The visibly narrower gap between Q1 and Q5 in Group 1 underscores the relative equity in homeownership distribution, whereas the stark difference in Group 2 suggests a more concentrated housing wealth. These visual patterns reinforce the empirical results from Model 3, where greater Q5/Q1 inequality correlates with increased income inequality.
In more developed economies, a greater variety of financial instruments allows investors to diversify into non-housing alternative markets. This, in turn, may be an additional factor contributing to the relatively higher homeownership rates among lower-income groups. Therefore, the Q5/Q1 homeownership ratio, indicating the disparity in housing ownership between the highest and lowest income groups, is lower in Group 1 than in Group 2. This implies that homeownership is more evenly distributed across income groups in these countries.
As it is known, there are three essential conditions for the reliability of the system GMM estimator [68]: (i) The GMM estimator must provide the condition that the error term does not have a second-degree autocorrelation. When the autocorrelation test results in all models are examined at the 5% significance level, it is concluded that there is a first-degree autocorrelation but no second-degree autocorrelation. In this case, the system GMM estimation results are effective and consistent. (ii) Since the system GMM produces many “weak” instrumental variables that may lead to deviant estimators, the number of instrumental variables should not exceed the number of observations. The fact that the probability value of the Hansen test statistic is less than 1 and more significant than 0.05 or 0.10 indicates that the null hypothesis of the validity of the over-identification restrictions indicating the suitability of the instrumental variables cannot be rejected and the model is correctly identified. According to the Sargan test result, “Instrumental variables are valid. Over-identification restrictions are valid”. The null hypothesis is rejected. Therefore, the over-identification restrictions are not valid. According to the difference-Hansen test results, the null hypothesis cannot be rejected; the instruments used in the instrumental variables regression are valid. (iii) In the model, the coefficient of the lagged value of the dependent variable should be less than 1 as an indicator of convergence of the system GMM [68]. In addition, the fact that this coefficient is between the coefficients obtained with the Pooled OLS and fixed effects model estimators shows that the estimator is not biased upwards or downwards due to weak instruments and that the model is good.
When examining the results across all observations (Table 4), the first model serves as a baseline, incorporating the GDP (), consume price index (), and HPI () as key explanatory variables. The results indicate that the lagged dependent variable is (β₁ = −0.304) significantly negative across all estimations, suggesting a mean-reverting process in income inequality changes. This coefficient implies that approximately 30.4% of a deviation from the equilibrium level of inequality is corrected in the subsequent period, indicating moderate persistence in inequality dynamics.

Table 4.
Dynamic panel estimates, models based on all available observations.
GDP growth exhibits a negative and significant coefficient (β2 = −0.139), indicating that economic expansion contributes to reductions in income inequality. Specifically, a 1% increase in GDP is associated with a 0.139 percentage point decrease in the rate of change in the Gini coefficient. Inflation, on the other hand, demonstrates a consistently positive and significant effect (β3 = 0.037), confirming its adverse impact on income inequality by eroding the purchasing power of lower-income households. For every 1-point increase in the consumer price index, the Gini change rate increases by 0.037 percentage points, widening the income gap.
The negative and significant coefficient of the HPI (β4 = −0.033) suggests that rising housing prices contribute to reductions in income inequality, possibly through capital gains or wealth effects favoring middle- and lower-income homeowners. In quantitative terms, a 1-unit increase in the house price index leads to a 0.033 percentage point decrease in the Gini change rate in the short run and a 0.025 percentage point decrease in the long-term forecast (LTF). This effect, while modest, indicates that housing price appreciation may have redistributive effects that benefit income equality under certain conditions.
The second model extends the baseline specification by incorporating the share of the poorest 20% in homeownership () and the price-to-rent ratio (). The introduction of homeownership among the lowest-income quintile provides additional insight into the redistributive effects of property ownership. The coefficient for (β5 = −0.017) is negative and statistically significant, suggesting that increased homeownership among the poorest segments of society helps mitigate income inequality. Specifically, a 1 percentage point increase in homeownership rates among the bottom-income quintile is associated with a 0.017 percentage point decrease in inequality growth. This finding aligns with the argument that facilitating access to property ownership can serve as a tool for wealth accumulation among lower-income households.
Conversely, the price-to-rent ratio has a positive and significant impact (β6 = 0.078) on changes in income inequality. This indicates that an increase in housing costs relative to rental prices exacerbates inequality, as lower-income households face higher barriers to homeownership and increased financial strain due to rising rental costs. For each 1-point increase in the price-to-rent ratio, the Gini change rate increases by 0.078 percentage points in the short run and 0.060 percentage points in the long run, highlighting the importance of housing affordability in inequality dynamics.
In this model, the effect of housing prices (β4) strengthens to −0.093, nearly triple the magnitude observed in Model 1. This enhanced effect suggests that when controlling for homeownership distribution and affordability, the equalizing impact of housing price increases becomes more pronounced. According to the results of Model 2, a 1-point increase in the HPI leads to a 0.093 percentage point decrease in the Gini change rate in the short run and a 0.072 percentage point decrease in the long term.
The third model replaces the share of the poorest 20% in homeownership with a measure of the homeownership gap (), which reflects disparities in property ownership between the wealthiest and poorest quintiles. The results reveal a positive and significant coefficient for (β5 = 0.532), indicating that an increase in the disparity between high- and low-income homeownership rates exacerbates income inequality. Specifically, a 1-unit increase in the homeownership gap ratio is associated with a 0.532 percentage point increase in the Gini change rate in the short run and a 0.405 percentage point increase in the long run. This substantial effect suggests that when housing markets become more concentrated in upper-income groups, wealth accumulation benefits are disproportionately captured by wealthier households, reinforcing existing inequalities.
Model 3 results offer a more nuanced view of how different housing and macroeconomic variables interact with income inequality. Specifically, the positive association between the Q5/Q1 homeownership ratio and Gini changes indicates that greater disparities in ownership patterns directly exacerbate income inequality. In contrast, the negative effect of housing prices (HPI) suggests that, under certain conditions, asset appreciation may reduce inequality—particularly when homeownership is accessible to lower-income groups. Additionally, the consistent positive impact of the consumer price index (CPI) across models underscores the regressive nature of inflation, which tends to disproportionately burden lower-income households and widen inequality.
In this model, the housing price coefficient (β4 = −0.092) remains strongly negative and similar in magnitude to Model 2. This consistency across specifications reinforces the robustness of our finding that, controlling for other factors, housing price increases tend to have an equalizing effect on income distribution. According to Model 3, a 1-point increase in the HPI leads to a 0.092 percentage point decrease in the Gini change rate in the short run and a 0.070 percentage point decrease in the long term.
The empirical results reveal also distinct effects of housing price dynamics on income inequality across different income groups (Table 5 and Table 6). In countries with a below-average GDP per capita (Group 1), an increase in housing prices has a statistically significant and negative impact (β4 = −0.069 in Model 1) on the Gini change rate, suggesting that rising housing prices in lower-income economies contribute to reducing income inequality. This effect becomes substantially stronger in Models 2 and 3 (β4 = −0.353 and −0.322, respectively), indicating that housing price appreciation may play a crucial role in wealth redistribution in these economies.

Table 5.
Dynamic panel estimates, models based on countries with below-average GDP per capita (Group 1).

Table 6.
Dynamic panel estimates, models based on countries with above-average GDP per capita (Group 2).
For this group, according to Model 1, every 1-point increase in HPI corresponds to an approximate 0.041 percentage point reduction in the Gini index change rate in the long term. In Models 2 and 3, the long-term effects are even more substantial, with decreases of approximately 0.216 and 0.194 percentage points, respectively. These magnitudes suggest that in lower-income countries, housing price appreciation can significantly contribute to reducing income inequality, particularly when considering the role of homeownership patterns and affordability.
In addition, the price-to-rent ratio—often seen as a key indicator of housing affordability—emerges as statistically significant only in Group 1 models (e.g., Model 2: β = 0.330, p < 0.1), but not in Group 2. This suggests that in lower-income contexts, rental market pressures meaningfully drive inequality, likely due to limited access to ownership and more vulnerable tenant populations. The absence of significance in Group 2 may reflect broader financial protections, greater regulatory control, or alternative housing options for low-income renters.
Although rising housing prices appear to reduce inequality in Group 1 countries, the positive and significant effect of the price-to-rent ratio suggests that rental affordability remains a key driver of inequality for low-income households who are unable to access homeownership. This highlights a dual mechanism: while owner-occupiers benefit from capital gains, tenants may experience increased vulnerability—indicating that housing market dynamics produce heterogeneous effects across socioeconomic strata.
However, in countries with above-average GDP per capita (Group 2), the impact of housing prices on income inequality diminishes and becomes statistically insignificant across all models (β4 = −0.029, −0.038, and −0.026 in Models 1, 2, and 3, respectively). This suggests that in higher-income countries, housing price increases do not translate into improved income distribution. The lack of a significant relationship could indicate that housing price appreciation primarily benefits higher-income households rather than fostering equitable wealth distribution. Additionally, the homeownership inequality ratio (Q5/Q1) is higher in this group, reinforcing the notion that wealthier households gain disproportionately from rising property values.
It is worth noting that in Group 2, the coefficient for homeownership among the lowest-income quintile (β5 = −0.028 in Model 2) remains negative and marginally significant, suggesting that even in high-income countries, policies that expand homeownership among low-income households may help mitigate inequality. However, the overall insignificance of housing price effects suggests that other structural factors dominate inequality dynamics in these advanced economies.
These findings highlight the importance of considering structural economic differences and housing market characteristics when analyzing the relationship between housing prices and income inequality.
Although our analysis is not structured around year-by-year trends, the panel covers a critical decade shaped by post-crisis recovery and early pandemic shocks. To capture dynamics implicitly, our model incorporates lagged dependent variables and long-term forecasts, which reflect convergence patterns in inequality over time. In Group 1 countries, these results suggest a gradual narrowing of inequality, particularly when homeownership among lower-income groups is sustained. In contrast, Group 2 countries show stagnation in distributional improvements, consistent with structurally rigid housing markets. Future research could incorporate time-fixed effects or period-specific interactions to explicitly capture temporal shifts.
The substantial differences in coefficient magnitudes between Group 1 and Group 2 underscore how the redistributive effects of housing markets are contingent upon underlying socioeconomic conditions, particularly the distribution of homeownership across income groups.
5. Discussion
While previous studies in the literature often emphasize the inequality-worsening effects of housing price increases [51,60,62,67], this study takes a different perspective by examining the conditions under which rising housing prices may contribute to improving income distribution.
For lower-income OECD countries, our results reveal that under certain conditions, rising housing prices may contribute to reducing income inequality. A key factor explaining this outcome is the relatively high rate of homeownership among lower-income households. In many such countries—especially post-socialist transition economies in Eastern Europe—historical and institutional factors, such as the large-scale privatization of public housing in the 1990s, enabled broad-based access to homeownership [77]. Additional contributing factors include historically lower housing prices relative to income, government-subsidized housing programs, weakly developed rental markets, and a cultural preference for ownership.
In these contexts, widespread homeownership allows capital gains from housing price increases to be more evenly distributed across income groups. This diffusion of the wealth effect can soften the inequality-enhancing impacts of housing market dynamics. Our findings support the notion of housing’s “equalizing power”, as described by Causa et al. (2019) [77], which suggests that when housing is broadly owned, it acts as a leveling force in the distribution of wealth.
Historical experiences reinforce this view. For instance, Zhang et al. (2021) [78] show that the expansion of homeownership in China during the 1990s contributed to a significant reduction in wealth inequality. However, they also note that after 2008, as housing became increasingly unaffordable for new low-income buyers, wealth inequality began to rise again. Similarly, Yin et al. (2019) [66] demonstrate how soaring housing prices in rapidly developing economies can lead to new forms of exclusion, particularly for youth and low-income households. These examples highlight a critical point: the inequality-reducing effect of housing appreciation is contingent upon sustained affordability and accessibility for lower-income groups.
In contrast, our results show no statistically significant relationship between rising housing prices and inequality in high-income OECD countries. This lack of effect suggests a more complex interaction between housing markets and income distribution in advanced economies. While previous studies [61,65,67] provide evidence of rising inequality due to housing price inflation, our empirical findings suggest that institutional structures such as mature housing systems, redistributive fiscal policies, and strong welfare regimes may have dampened or offset such effects.
A particularly illuminating case is that of Sopchokchai and Zhou (2020) [63], who found that despite significant increases in housing prices across Canadian cities, income inequality appeared to decline. However, this decline was not a result of real improvements in the income distribution. Instead, the observed reduction was driven by the displacement of low-income households, who could no longer afford to remain in or move to these urban areas. This compositional effect highlights the importance of distinguishing between city-level and national-level inequality dynamics and underscores the need to critically examine the mechanisms behind observed statistical changes.
Overall, our findings suggest that housing market policies should be tailored to the specific economic and institutional context of each country. In lower-income economies, where homeownership among disadvantaged groups is more common, policies that improve access to affordable housing and mortgage credit can reinforce wealth accumulation and reduce inequality. In higher-income countries, where homeownership is more exclusive, rising housing prices may not generate the same redistributive benefits. In such contexts, progressive property taxation, housing subsidies for low-income households, and regulatory frameworks to curb speculative real estate investment may be necessary to mitigate distributional concerns.
Beyond its implications for income distribution, equitable access to housing markets also plays a pivotal role in advancing urban cohesion and spatial justice—core elements of sustainable urban development. As emphasized by the United Nations’ Sustainable Development Goal 11 (Sustainable Cities and Communities), affordable housing and inclusive homeownership are key to building resilient and just urban environments. Policies that enhance housing affordability while discouraging speculative behavior can help reduce socio-spatial disparities and foster more inclusive growth.
Ultimately, a one-size-fits-all approach is insufficient. Policymakers must design housing strategies that account for variations in homeownership access, financial market alternatives, and redistributive capacities in order to ensure that housing markets become instruments of equitable and sustainable development.
6. Study Limitations and Directions for Future Research
Despite its empirical strengths, this study has several limitations that should be acknowledged.
First, the possibility of reverse causality cannot be entirely ruled out. While our dynamic system GMM approach mitigates endogeneity concerns, it does not fully isolate the direction of causality between housing prices and income inequality. Recent studies have explored how inequality may influence housing prices through mechanisms such as aggregate demand shifts or investment concentration. However, a major limitation in the existing literature is that most studies adopt a unidirectional perspective—either from inequality to housing prices or vice versa—often neglecting potential feedback effects. This study, like many others, focuses on the effect of housing prices on inequality. We encourage future research to address this gap by modeling bidirectional dynamics using structural frameworks or simultaneous equation systems.
Second, although rent is a critical component of housing-related costs, our attempts to include rental variables in the models resulted in panel instability and multicollinearity issues due to limited and inconsistent data availability. As a result, we focused on housing prices as a more robust and interpretable measure. Nevertheless, the exclusion of rent may lead to an incomplete assessment of income distribution dynamics, particularly by overlooking the redistributive effects of rental income flows between different socioeconomic groups.
Third, the relatively short time span of our dataset (2010–2021) may limit the detection of long-term or lagged structural effects. Extending the temporal coverage—either through historical data or higher-frequency observations—could improve future research on slow-moving inequality dynamics and housing market cycles.
Fourth, our empirical design does not explicitly account for extraordinary external shocks such as the 2008 global financial crisis or the COVID-19 pandemic, both of which significantly disrupted housing markets and income structures in many OECD countries. While our panel starts after the 2008 crisis and includes part of the pandemic period, these shocks are not modeled separately due to data and identification constraints. Further studies may incorporate dummy variables, interaction terms, or time-varying controls to better capture these events’ impacts.
7. Conclusions
This study has examined the impact of rising housing prices on income inequality in 33 OECD countries from 2010 to 2021 using the system GMM approach. The empirical findings show that in countries with a below-median GDP per capita (Group 1), a 1-point increase in the house price index (HPI) is associated with a long-term reduction of approximately 0.21 points in the rate of change in income inequality (Gini index). In contrast, for higher-income countries (Group 2), the effect of housing prices on inequality is statistically insignificant, indicating heterogeneity in how housing markets shape income distribution.
A key contribution of this research lies in revealing that where lower-income households have relatively higher homeownership rates, rising housing prices can have an equalizing effect. This finding challenges the dominant narrative in the literature, which typically frames housing price increases as inequality-worsening. Unlike studies emphasizing the regressive nature of asset appreciation, our results suggest that under specific structural conditions—particularly a more equitable distribution of housing ownership—rising housing prices may enhance wealth accumulation among vulnerable groups.
While our empirical findings offer novel insights, they should be interpreted in light of the study’s methodological and data-related limitations, as discussed in detail in Section 6.
In terms of policy implications, the findings emphasize the importance of country-specific strategies. In relatively lower-income economies, measures that enhance housing access for low-income groups—such as social housing programs or mortgage support—may strengthen inclusive wealth accumulation. Conversely, in higher-income countries where homeownership is predominantly concentrated among upper-income groups, instruments such as progressive property taxation, targeted subsidies, or rental market regulations may be more effective in mitigating rising wealth inequality.
Finally, future research should explore the bidirectional dynamics between income inequality and housing markets using structural equation models or extended time-series datasets. Further studies could also differentiate the effects of ownership and rental structures more clearly and investigate the generational or spatial dimensions of housing inequality, particularly in the context of long-term urban transformation.
Author Contributions
Conceptualization, G.Ü. and Ö.Ç.; methodology, Ö.Ç.; software, G.Ü. and Ö.Ç.; validation, H.H.Y.; formal analysis, G.Ü. and H.H.Y.; investigation, G.Ü. and Ö.Ç.; resources, G.Ü.; data curation, G.Ü.; writing—original draft preparation, G.Ü. and Ö.Ç.; writing—review and editing, G.Ü., Ö.Ç. and H.H.Y.; visualization, G.Ü.; supervision, H.H.Y.; project administration, G.Ü.; funding acquisition, G.Ü., Ö.Ç. and H.H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sandmo, A. The Principal Problem in Political Economy. In Handbook of Income Distribution; Atkinson, A.B., Bourguignon, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 2B, pp. 3–65. [Google Scholar]
- Flaherty, T.M.; Rogowski, R. Rising Inequality As a Threat to the Liberal International Order. Int. Organ. 2021, 75, 495–523. [Google Scholar] [CrossRef]
- Hung, H.-F. Recent Trends in Global Economic Inequality. Annu. Rev. Sociol. 2021, 47, 349–367. [Google Scholar] [CrossRef]
- Kuznets, S. Economic Growth and Income Inequality. In The Economic Growth and Income Inequality; American Economic Association: Nashville, TN, USA, 1955; Volume 45, pp. 1–28. [Google Scholar]
- Alvaredo, F.; Chancel, L.; Piketty, T.; Saez, E.; Zucman, G. World Inequality Report 2018; Belknap Press: Berlin, Germany, 2018. [Google Scholar]
- Atkinson, A.B.; Piketty, T.; Saez, E. Top Incomes in the Long Run of History. J. Econ. Lit. 2011, 49, 3–71. [Google Scholar] [CrossRef]
- IMF The IMF and Income Inequality. Available online: https://www.imf.org/en/Topics/Inequality (accessed on 12 February 2023).
- Piketty, T. Capital in the Twenty-First Century; President and Fellows of Harvard College: London, UK, 2014; ISBN 2013036024. [Google Scholar]
- Piketty, T.; Saez, E. Income Inequality in The United States, 1913–1998. Q. J. Econ. 2003, 118, 1–41. [Google Scholar] [CrossRef]
- Roser, M.; Ortiz-Ospina, E. Income Inequality. Available online: https://ourworldindata.org/income-inequality (accessed on 12 February 2023).
- Saez, E.; Berkeley, U. Striking It Richer: The Evolution of Top Incomes in the United States (Updated with 2018 Estimates); University of California: Berkeley, CA, USA, 2020. [Google Scholar]
- Stiglitz, J. The Price of Inequality: How Today’s Divided Society Endangers Our Future; W. W. Norton & Company: New York, NY, USA, 2012. [Google Scholar]
- United Nations Sustainable Development Goals: 17 Goals to Transform Our World. Available online: https://sdgs.un.org/goals (accessed on 18 March 2025).
- Agnello, L.; Castro, V.; Jalles, J.T.; Sousa, R.M. Income Inequality, Fiscal Stimuli and Political (in)Stability. Int. Tax Public Financ. 2017, 24, 484–511. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Tang, X. Understanding the Economic Dynamics behind Growth–Inequality Relationships. J. Macroecon. 2011, 33, 14–32. [Google Scholar] [CrossRef]
- Berg, A.; Ostry, J.D.; Tsangarides, C.G.; Yakhshilikov, Y. Redistribution, Inequality, and Growth: New Evidence. J. Econ. Growth 2018, 23, 259–305. [Google Scholar] [CrossRef]
- Tsounta, E.; Suphaphiphat, N.; Ricka, F.; Dabla-Norris, E.; Kochhar, K. Causes and Consequences of Income Inequality. Staff Discuss. Notes 2015, 2015, 1. [Google Scholar] [CrossRef]
- IMF Income Distribution and Sustainable Growth: The Perspective from the IMF at Fifty—Opening Remarks by Michel Camdessus. Available online: https://www.imf.org/en/News/Articles/2015/09/28/04/53/spmds9509 (accessed on 10 June 2024).
- Kakwani, N.C. Income Inequality and Poverty; A World Bank Research Publication: Washington, DC, USA, 1980; ISBN 019520126. [Google Scholar]
- Bordo, M.D.; Meissner, C.M. Does Inequality Lead to a Financial Crisis? J. Int. Money Financ. 2012, 31, 2147–2161. [Google Scholar] [CrossRef]
- Kumhof, M.; Rancière, R.; Winant, P. Inequality, Leverage, and Crises. Am. Econ. Rev. 2015, 105, 1217–1245. [Google Scholar] [CrossRef]
- Rajan, R.G. Fault Lines; Princeton University Press: Princeton, NJ, USA, 2011; ISBN 9781400839803. [Google Scholar]
- Rhee, D.-E.; Kim, H. Does Income Inequality Lead to Banking Crises in Developing Countries? Empirical Evidence from Cross-Country Panel Data. Econ. Syst. 2018, 42, 206–218. [Google Scholar] [CrossRef]
- Stockhammer, E. Rising Inequality as a Cause of the Present Crisis. Camb. J. Econ. 2015, 39, 935–958. [Google Scholar] [CrossRef]
- van Treeck, T.; Sturn, S. Income Inequality as a Cause of the Great Recession? A Survey of Current Debates; ILO, Conditions of Work and Employment Branch: Geneva, Switzerland, 2012. [Google Scholar]
- Kawachi, I.; Subramanian, S. Income Inequality. In Social Epidemiology; Oxford University Press: New York, NY, USA, 2014; pp. 126–152. [Google Scholar]
- Wilkinson, R.G.; Pickett, K.E. Income Inequality and Social Dysfunction. Annu. Rev. Sociol. 2009, 35, 493–511. [Google Scholar] [CrossRef]
- Reardon, S.F. The Widening Academic Achievement Gap Between the Rich and the Poor. In Inequality in the 21st Century; Routledge: Abingdon, UK, 2018; pp. 177–189. [Google Scholar]
- Oishi, S.; Kesebir, S.; Diener, E. Income Inequality and Happiness. Psychol. Sci. 2011, 22, 1095–1100. [Google Scholar] [CrossRef]
- Adam, A.; Kammas, P.; Lapatinas, A. Income Inequality and the Tax Structure: Evidence from Developed and Developing Countries. J. Comp. Econ. 2015, 43, 138–154. [Google Scholar] [CrossRef]
- Alesina, A.; La Ferrara, E. Preferences for Redistribution in the Land of Opportunities. J. Public Econ. 2005, 89, 897–931. [Google Scholar] [CrossRef]
- Delestre, I.; Kopczuk, W.; Miller, H.; Smith, K. NBER Working Paper Series Top Income Inequality and Tax Policy; National Bureau of Economic Research: Cambridge, MA, USA, 2022. [Google Scholar]
- Kuziemko, I.; Norton, M.I.; Saez, E.; Stantcheva, S. How Elastic Are Preferences for Redistribution? Evidence from Randomized Survey Experiments. Am. Econ. Rev. 2015, 105, 1478–1508. [Google Scholar] [CrossRef]
- Aghion, P.; Akcigit, U.; Bergeaud, A.; Blundell, R.; Hemous, D. Innovation and Top Income Inequality. Rev. Econ. Stud. 2019, 86, 1–45. [Google Scholar] [CrossRef]
- Chu, A.C.; Furukawa, Y.; Mallick, S.; Peretto, P.; Wang, X. Dynamic Effects of Patent Policy on Innovation and Inequality in a Schumpeterian Economy. Econ. Theory 2021, 71, 1429–1465. [Google Scholar] [CrossRef]
- Harari, Y.N. Homo Deus: A Brief History of Tomorrow; Harper Collins Publishers: London, UK, 2017. [Google Scholar]
- Palma, J.G. The Revenge of the Market on the Rentiers.: Why Neo-Liberal Reports of the End of History Turned out to Be Premature. Camb. J. Econ. 2009, 33, 829–869. [Google Scholar] [CrossRef]
- Huang, K.; Yan, W.; Sim, N.; Guo, Y.; Xie, F. Can Trade Explain the Rising Trends in Income Inequality? Insights from 40 Years of Empirical Studies. Econ. Model. 2022, 107, 105725. [Google Scholar] [CrossRef]
- Card, D.; Lemieux, T.; Riddell, W.C. Unions and Wage Inequality. J. Labor Res. 2004, 25, 519–559. [Google Scholar] [CrossRef]
- Lemieux, T.; MacLeod, W.B.; Parent, D. Performance Pay and Wage Inequality. Q. J. Econ. 2009, 124, 1–49. [Google Scholar] [CrossRef]
- Nguyen, T.C. The Effects of Financial Crisis on Income Inequality. Dev. Policy Rev. 2022, 40, e12600. [Google Scholar] [CrossRef]
- Lenza, M.; Slacalek, J. How Does Monetary Policy Affect Income and Wealth Inequality? Evidence from Quantitative Easing in the Euro Area. SSRN Electron. J. 2018, 2018, 2190. [Google Scholar] [CrossRef]
- Bertrand, M.; Mullainathan, S. Are Emily and Greg More Employable Than Lakisha and Jamal? A Field Experiment on Labor Market Discrimination. Am. Econ. Rev. 2004, 94, 991–1013. [Google Scholar] [CrossRef]
- Blau, F.D.; Kahn, L.M. The Gender Wage Gap: Extent, Trends, and Explanations. J. Econ. Lit. 2017, 55, 789–865. [Google Scholar] [CrossRef]
- Agnello, L.; Sousa, R.M. How Does Fiscal Consolidation Impact on Income Inequality? Rev. Income Wealth 2014, 60, 702–726. [Google Scholar] [CrossRef]
- Furceri, D.; Loungani, P.; Zdzienicka, A. The Effects of Monetary Policy Shocks on Inequality. J. Int. Money Financ. 2018, 85, 168–186. [Google Scholar] [CrossRef]
- Albanesi, S. Inflation and Inequality. J. Monet. Econ. 2007, 54, 1088–1114. [Google Scholar] [CrossRef]
- Yilmaz, H.H.; Ozyer, M.A.; Ozyer, S.I. Redistribution Effects of Taxes on Expenditure: The Case of Turkey (2002–2013); Hacienda Publica Espanola-Review of Public Economics: Madrid, Spain, 2019; Volume 230, ISBN 0000000171830. [Google Scholar]
- Goda, T.; Stewart, C.; Torres García, A. Absolute Income Inequality and Rising House Prices. Socio-Econ. Rev. 2020, 18, 941–976. [Google Scholar] [CrossRef]
- Zhang, C.; Jia, S.; Yang, R. Housing Affordability and Housing Vacancy in China: The Role of Income Inequality. J. Hous. Econ. 2016, 33, 4–14. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, F. Effects of Housing Prices on Income Inequality in Urban China. Crit. Hous. Anal. 2015, 2, 1. [Google Scholar] [CrossRef]
- Fligstein, N.; Hastings, O.P.; Goldstein, A. Keeping up with the Joneses: How Households Fared in the Era of High Income Inequality and the Housing Price Bubble, 1999–2007. Socius Sociol. Res. Dyn. World 2017, 3, 2378023117722330. [Google Scholar] [CrossRef]
- Gyourko, J.; Mayer, C.; Sinai, T. Superstar Cities. Am. Econ. J. Econ. Policy 2013, 5, 167–199. [Google Scholar] [CrossRef]
- Whiting, C. Income Inequality, the Income Cost of Housing, and the Myth of Market Efficiency: “Optimal” for Whom? Am. J. Econ. Sociol. 2004, 63, 851–879. [Google Scholar] [CrossRef]
- Hailemariam, A.; Awaworyi Churchill, S.; Smyth, R.; Baako, K.T. Income Inequality and Housing Prices in the Very Long-run. South. Econ. J. 2021, 88, 295–321. [Google Scholar] [CrossRef]
- Lin, Y.C.; Kang, C.W.; Chang, Y.C.; Lin, C.F.; Huang, C.W. The Relationship Between Housing Price and Income Inequality—A Case Study of Taipei City. Res. Rep. 2010, 2010, 1–13. [Google Scholar]
- Määttänen, N.; Terviö, M. Income Distribution and Housing Prices: An Assignment Model Approach. SSRN Electron. J. 2014, 151, 381–410. [Google Scholar] [CrossRef]
- Özmen, M.U.; Kalafatcılar, M.K.; Yılmaz, E. The Impact of Income Distribution on House Prices. Cent. Bank Rev. 2019, 19, 45–58. [Google Scholar] [CrossRef]
- Gholipour, H.F.; Nguyen, J.; Farzanegan, M.R. Higher Property Prices Linked to Income Inequality: Study. Available online: https://theconversation.com/higher-property-prices-linked-to-income-inequality-study-68664 (accessed on 20 June 2024).
- Sun-Hee, K.; Seong-Min, H. Analysis of the Relationship between House Price, Income Inequality and Macroeconomic Variables. J. Digit. Converg. 2019, 17, 55–62. [Google Scholar] [CrossRef]
- Dustmann, C.; Fitzenberger, B.; Zimmermann, M. Housing Expenditure and Income Inequality. Econ. J. 2022, 132, 1709–1736. [Google Scholar] [CrossRef]
- Margalef Jordà, A.M.; Villarroya Pascua, M. Housing Price Inflation and Inequality: Assessment of the Housing Market in the City of Barcelona. Universitat Pompei Fabra Barcelona: Barcelona, Spain, 2020. [Google Scholar]
- Sopchokchai, D.; Zhou, C. Housing Research Report House Price and Income Inequality in Canada: The Instrumental Variable Approach. 2020. Available online: https://assets.cmhc-schl.gc.ca/sf/project/archive/research_5/69676_rr.pdf (accessed on 26 February 2025).
- Woloszko, N.; Causa, O. Housing and Wealth Inequality: A Story of Policy Trade-Offs. Available online: https://cepr.org/voxeu/columns/housing-and-wealth-inequality-story-policy-trade-offs (accessed on 5 July 2024).
- Kim, H.; Rhee, D.E. The Effects of Asset Prices on Income Inequality: Redistribution Policy Does Matter. Econ. Model. 2022, 113, 105899. [Google Scholar] [CrossRef]
- Yin, S.; Ma, Z.; Song, W.; Liu, C. Spatial Justice of a Chinese Metropolis: A Perspective on Housing Price-to-Income Ratios in Nanjing, China. Sustainability 2019, 11, 1808. [Google Scholar] [CrossRef]
- Fuller, G.W.; Johnston, A.; Regan, A. Housing Prices and Wealth Inequality in Western Europe. West Eur. Polit. 2020, 43, 297–320. [Google Scholar] [CrossRef]
- Roodman, D. How to Do Xtabond2. In Proceedings of the North American Stata Users Group Meetings, Boston, MA, USA, 24–25 July 2006; pp. 1–30. [Google Scholar]
- Baltagi, B.H. The Oxford Handbook of Panel Data; Oxford Unicersity Press: New York, NY, USA, 2015. [Google Scholar]
- Anderson, T.W.; Hsiao, C. Estimation of Dynamic Models with Error Components. J. Am. Stat. Assoc. 1981, 76, 598. [Google Scholar] [CrossRef]
- Anderson, T.W.; Hsiao, C. Formulation and Estimation of Dynamic Models Using Panel Data. J. Econom. 1982, 18, 47–82. [Google Scholar] [CrossRef]
- Arellano, M.; Bond, S. Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations. Rev. Econ. Stud. 1991, 58, 277. [Google Scholar] [CrossRef]
- Blundell, R.; Bond, S. Initial Conditions and Moment Restrictions in Dynamic Panel Data Models. J. Econom. 1998, 87, 115–143. [Google Scholar] [CrossRef]
- Bun, M.J.G.; Windmeijer, F. The Weak Instrument Problem of the System GMM Estimator in Dynamic Panel Data Models. Econom. J. 2010, 13, 95–126. [Google Scholar] [CrossRef]
- Campano, F.; Salvatore, D. Income Distribution; Oxford University Press: New York, NY, USA, 2006; ISBN 0195300912. [Google Scholar]
- Atkinson, A.B.; Bourguignon, F. Introduction: Income Distribution Today. In Handbook of Income Distribution; Atkinson, A.B., Bourguignon, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 2A, ISBN 9780444594280. [Google Scholar]
- Causa, O.; Woloszko, N.; Leite, D. Housing, Wealth Accumulation and Wealth Distribution: Evidence and Stylized Facts; OECD Economics Department Working Papers: Paris, France, 2019; Volume 1588. [Google Scholar]
- Zhang, P.; Sun, L.; Zhang, C. Understanding the Role of Homeownership in Wealth Inequality: Evidence from Urban China (1995–2018). China Econ. Rev. 2021, 69, 101657. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).