Freeway Curve Safety Evaluation Based on Truck Traffic Data Extracted by Floating Car Data

Abstract

Due to complex traffic conditions, freeway curves are associated with higher crash rates, particularly for trucks, which poses significant safety risks. Predicting truck crash rates on curves is essential for enhancing freeway safety. However, geometric design consistency indicators (GDCIs) are limited in terms of their ability to evaluate safety levels. To address this, this study identifies key factors influencing truck crash rates on curves and proposes a new safety evaluation indicator, the mean speed change rate (MSCR). A vague set, as an extension of the fuzzy set, was employed to integrate the MSCR and GDCI to identify high-risk curves. The factors contributing to differences in crash rates between the curves to the left and right are also analyzed. To assess the proposed approach, a case study was conducted using truck traffic data extracted from floating car data (FCD) collected on 32 freeway curves. The results demonstrate that the deflection angle, radius, and deflection direction are key contributions to truck crash risks. Importantly, the recognition accuracy of the MSCR indicator for crash risks on curves to the left and right is improved by 11.8% and 18.2% compared with GDCIs. Combining the proposed MSCR indicator with GDCIs can more comprehensively evaluate the safety of curves, with recognition accuracy rates of 88.2% and 27.3%, respectively. The indicator change value of the curves to the left are always larger, and the difference is more obvious as the geometric indicator changes. The MSCR indicator provides a more comprehensive curve safety assessment method than existing indicators, which is expected to promote the formulation of curve safety management strategies and further achieve sustainable development goals.

1. Introduction

In the realm of highway research, the correlation between crash rates and various road design elements has garnered significant attention. Prior research has demonstrated that truck crash rates are three to four times higher on horizontal curves than on similar tangent segments [1,2]. Moreover, in traffic crash analysis, it has been observed that trucks traveling on curves to the left tend to have more significant speed fluctuations than those traveling on curves to the right, indicating that there are differences in driving behavior and risk perception in the two scenarios and the crash rates on curves to the left are also relatively high. During a turn, the driver’s line of sight may be directed to the inside of the curve [3], and the driver’s speed choice is also related to the spatial position of the truck on the road. Studies have shown that curves to the right have a better adjustment effect on the driver’s subjective perception than curves to the left [4]. In addition, scholars who have suggested higher crash rates on curves to the left are more likely to come from countries with left-hand drive, where the driver’s turning trajectory in the innermost lane of the curves to the left will deviate more than expected due to the “sidewall effect,” resulting in a smaller trajectory radius and increased centrifugal forces. Although various safety management strategies for circular curves are required in many countries, such as Singapore [5], China [6], and the United States [7], many crashes still occur on the curve every year. According to statistics, 19% of traffic crash deaths in China are related to trucks [8], and 44% of truck traffic crashes occur on curves [9]. Therefore, analyzing the reasons for the difference in truck collision crashes between curves to the left and right from the speed perspective and proposing different safety assurance measures for curves with different deflection directions is crucial to improving the effectiveness of safety management strategies.

The crash rate for trucks on curves of freeways remains high. The fundamental reason is that the geometric design indicators of the curve are not consistent with the driving characteristics of the trucks. This includes the poor matching of design indicators such as the length and radius of the curve with the speed adjustment requirements of the trucks. The limiting values of the geometric design indicators of some curves cannot fully guarantee the smooth turning of trucks, and the transition of horizontal and vertical indicators is relatively frequent. Compared with passenger cars, trucks have lower braking ability, worse steering stability, and more complex dynamic force states, making them prone to rear-end collisions, side collisions, rollovers, and other crashes on curves [10]. Due to the limited quality and quantity of crash analysis reports on curved segments of freeways, researchers used speed analysis indicators to investigate traffic safety on curved segments. Through a series of data collection methods such as radar speed measurement, video data extraction, and simulation [11], indicators such as speed variability, acceleration, and speed consistency are proposed to analyze the speed changes of trucks on curves to evaluate the degree of speed change and speed uniformity, thereby gaining a deep understanding of the risks that may be caused by speed mutations and evaluating the safety level of the curve. However, using traditional indicators and data to evaluate the safety level of curves brings the following challenges: (a) it is difficult to obtain continuous and universal data through cross-sectional data collection and simulation; (b) existing research mainly focuses on the combination of horizontal curves and vertical curves on low-grade highways. For high-grade freeways, the effect of the deflection angle on the safety is often ignored; (c) traditional indicators make it difficult to comprehensively evaluate the safety level of the entire curve.

Driving characteristics such as speed, acceleration, and speed difference can truly reflect the adaptability of trucks on the curve. A comprehensive and accurate grasp of the speed behavior of trucks on curves is the key basis for solving the above difficulties [12]. A variety of speed behavior collection methods have been proposed, mainly including FCD, simulated driving, real truck driving, drone aerial photography, road video monitoring, etc. Among the many data collection technologies, the full-time domain and full-road section high-precision speed data obtained regarding freight floating trucks have a series of significant advantages [13]. 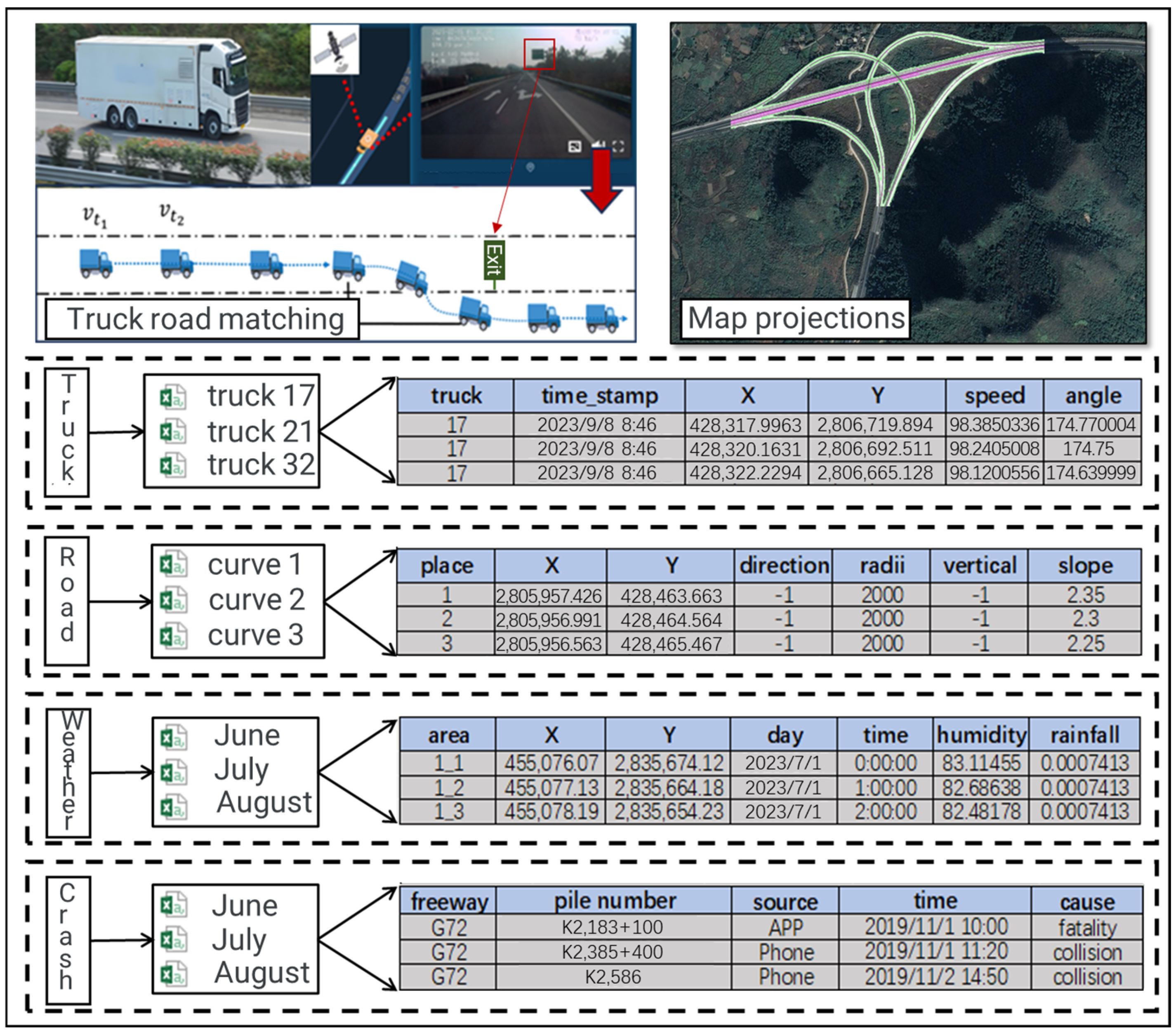Compared with general trajectory data, these data have multiple characteristics such as full-time domain, large range, high precision, high frequency, and no environmental and human interference, which is conducive to comprehensively and accurately grasping the continuous driving characteristics of trucks on different segments of curves [14]. In the early stage of this study, the real-time trajectories of more than 5000 trucks from the Guangxi region of China was obtained. The driving skills of the drivers were similar, and all of them drove left-hand drive. About 110 million trajectory data points were generated every day, with a speed measurement accuracy of 1 km/h and a timing accuracy of 1 s. In addition, the geometric design data for two freeways, including deflection angles from 20 to 65 degrees and radii from 763 to 2500 m, were obtained. Using the truck traffic data extracted from FCD and freeway geometric design data can effectively expand the research sample size and allowed us to obtain continuous trajectory data on curves at the second level. This lays the foundation for exploring the differences in truck crash rates on curves and evaluating the safety level of curves.

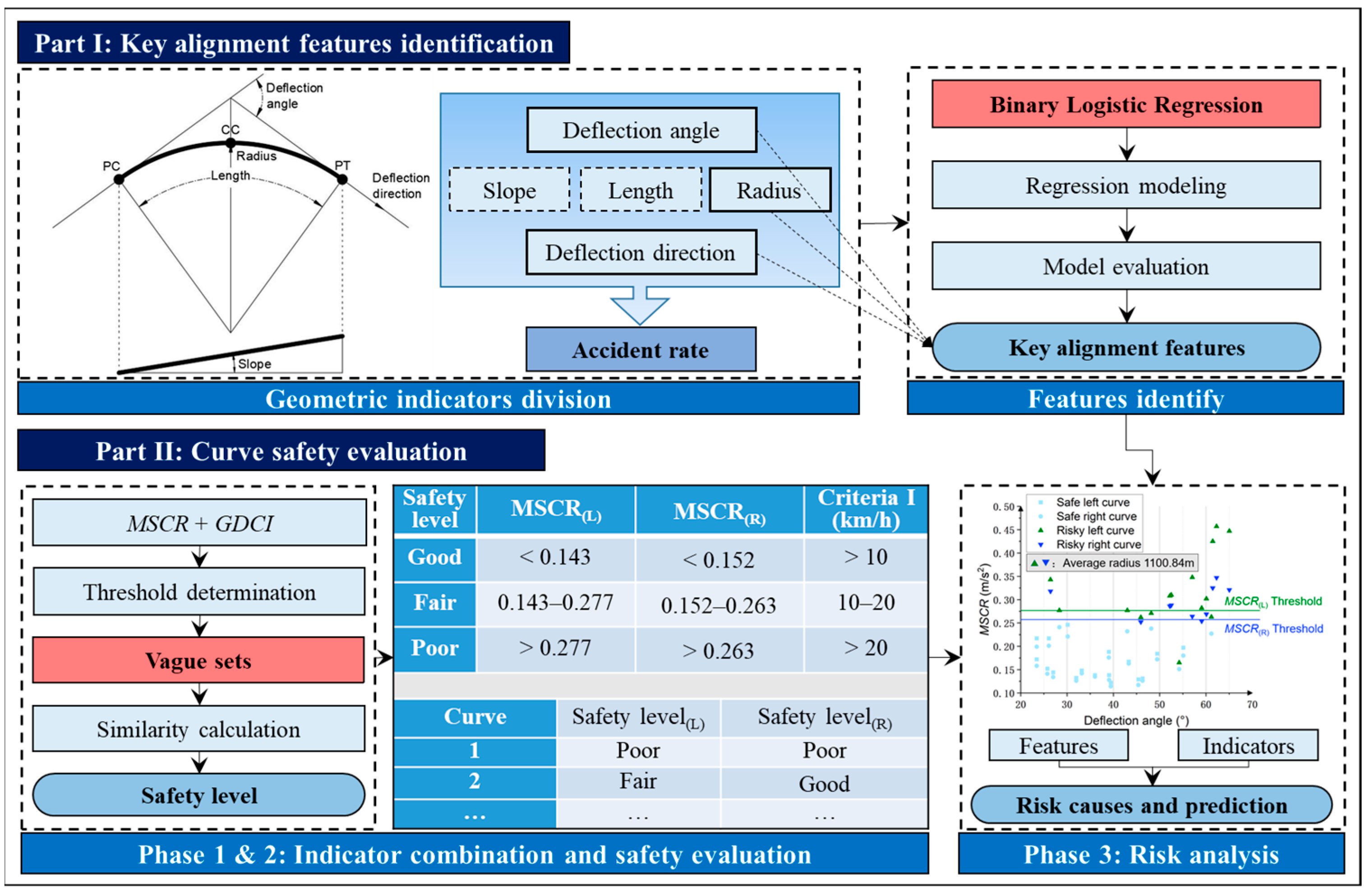
To summarize, in this study, a safety evaluation indicator—an MSCR indicator based on GDCIs—is proposed to evaluate the safety level of curves and to analyze the difference in crash rates between curves to the left and right. This MSCR indicator can further combine GDCIs to complete the safety evaluation of curves to the left and right. After identifying key features and determining the indicator threshold, the vague sets are used to assess the safety level of the curve, and the difference in crash rates between curves to the left and right is analyzed. As a case study, the truck traffic data extracted from FCD for the 32 circular curve segments on freeways are used to verify and evaluate the proposed method. This study offers two key contributions. First, at the methodological level, we employed binary logistic regression (BLR) to identify the key features influencing the crash rate of curves and introduce the MSCR as a novel safety evaluation indicator. This methodological advancement not only enhances the precision of crash-rate assessments but also aligns with sustainability goals by promoting safer road designs that reduce crash-related environmental impacts and resource consumption. By integrating the GDCIs, a more practical and comprehensive analysis of crash-rate differences between curves to the left and right is possible, thereby supporting sustainable transportation infrastructure development. Secondly, at the analytical application level, the research findings on safety indicators elucidate the underlying causes of crash-rate disparities between curves to the left and right. This insight is crucial for freeway management departments to evaluate the safety levels of curves more effectively. By implementing targeted safety management strategies for curves with different deflection directions, the crash rate can be significantly reduced, further reducing emissions from traffic congestion, reducing material waste from vehicle maintenance, and minimizing medical costs related to injuries, thereby contributing to the achievement of sustainable development goals.

2. Literature Review

2.1. Truck Characteristics on Curves

The geometric design indicators of the curved sections of freeways will affect the driving characteristics of trucks. Most scholars have mainly considered the impact of the road’s horizontal and vertical alignments on truck speed [15,16,17,18]. We utilized methods such as regression analysis, fuzzy theory, neural network, and other methods to analyze the relationship between single or multiple indicators of vehicle speed and road alignment. The key characteristic of a curve is the radius, and since the driving task relies heavily on vision, the driver needs to perceive the radius. However, from the driver’s perspective, the perception of radius is distorted on two-lane curved roads. Moreover, freeways on plains tend to have higher horizontal and vertical indicators, and many curves’ radii are within the range that does not require superelevation. Drivers are less likely to feel changes in centrifugal force when driving on such curves, which means they are speed sensitive. Therefore, it has been suggested that other factors, such as the deflection angle of the curve, also affect curve perception and speed selection [19]. The application of curve deflection angle in driving risk analysis has attracted widespread attention in recent years. By quantifying the degree of curvature encountered by the driver, researchers can identify potential hazards and develop mitigation strategies. Godumula and Shanker [20] found that the level of road geometric consistency was significantly affected by the deflection angle, which was negatively correlated with the level of inconsistency. Goyani et al. [21] conclude that geometric variables such as curve radius, deflection angle, curve length, and tangent length significantly affect the driver’s speed selection behavior through curves. Goyani et al. [22] also found that the number of crashes of cars and heavy commercial vehicles (HCVs) is related to the curve radius and the deflection angle. Maji et al.’s [23] experimental results show that the 85th percentile speed of a car on a curve depends on the length of the curve and the deflection angle.

The geometric indicators of the curve and the vehicle dynamics of the truck are the bases for the changes in the speed behavior of the truck when driving on the curve. In addition, factors such as the driver’s age, occupation, and perception of the curve can also lead to inconsistencies in the speed behavior of the truck when driving on the curve [24]. Drivers’ reaction times on curves are always higher than their reaction times on straight sections [25], and if the available sight distance at any point on a highway is less than the distance required to come to a complete stop after seeing a hazard, the driver will not be able to stop in time to avoid a collision [26]. Calvi [27] investigated drivers’ perception of road curves and behavior and found that on curves with smaller radii, drivers had greater difficulty following the road axis and experienced higher levels of pathological discomfort. Elvik et al. [28] investigated the relationship between driver age and gender and crashes and found that males under 30 years old and females over 64 years old had higher crash rates. Furthermore, drivers need to adjust their speed and lane position to accommodate curves, which requires better control of the pedals and steering to safely maneuver the vehicle. When driving on a curve, fast and reliable analysis of the spatiotemporal parameters required to keep the vehicle on the road is required. Drivers need to allocate more attention resources to gather information and more brain resources to make decisions when driving on a curve. To safely navigate a curve, drivers must correctly perceive traffic objects (e.g., road signs), stay alert, make decisions, and perform driving actions at the right time [29]. Othman et al. [30] mentioned that the curve radius has an effective regulatory effect on the driver’s emotional perception during driving. Under the same curve radius conditions, the values of driver fatigue, tension, awareness, attention, thinking, and workload are greater on curves to the left than on curves to the right, while relaxation and comfort are more significant on curves to the right. The curves to the right bring drivers more positive and stable emotional perception than the curve to the left.

The deflection angle is considered a key variable for understanding truck movement and behavior [31]. The deflection angle of a curve represents the degree of rotation of the driver’s field of view and is also related to the driver’s perception of the curve shape. Existing research mainly focuses on traditional horizontal and vertical indicators, making it difficult to fully characterize the driving characteristics of trucks on curves by only considering indicators such as the radius and longitudinal slope. Analysis based on geometric indicators such as deflection angle and radius are also more suitable for high-index plain freeways.

2.2. Curve Safety Evaluation Indicators

Studies on driving on curved sections of road primarily examine scenarios where drivers navigate through curves, with a predominant focus on the driver’s line of sight within the lane, as well as on their chosen lateral position and speed during curve negotiation [32]. The analysis of curve speeds, which dates back to research interests in the 1960s, has subsequently become a crucial indicator in road safety studies, significantly impacting the field of transportation research [33].

Yotsutsuji et al. [34] used driving simulation software to determine the probability of a crash being caused by speeding on a curve and described this as the speeding crash risk indicator (Pr). Pr is defined as the probability that the actual speed of a car entering a curved section exceeds the maximum safe speed for the curve based on the driver’s perceived speed. This indicator is used for crash prediction. De Almeida et al. [35] selected some volunteers and collected data on the volunteers’ actual truck experimental speeds. They proposed a profile based on operating speed to quantify road design consistency, aiming to minimize the difference between predicted and observed speed profiles. Zhao et al. [36] used the traffic order indicator (TOI) of driving behavior and speed changes to assess the road safety risk level based on driving behavior data collected from users’ mobile phones. Cai et al. [37] used LiDAR to collect truck driving behavior data and established a road traffic safety risk assessment index system with road traffic safety entropy (RTSE) as the primary indicator and sudden acceleration frequency, sudden deceleration frequency, speeding frequency, etc. as secondary indicators.

Numerous scholars have proposed various indicators to evaluate driver safety, predominantly relying on average speed, acceleration, and other pertinent metrics. Existing traditional indicators are advantageous due to their simplicity and their capacity to rapidly capture driver behavior on curved road segments. However, these studies are generally constrained by limited data samples and low data collection accuracy. In addition, indicator analysis often limits analysis to specific curve breakpoints, making it difficult to accurately characterize the continuous speed change trend of the truck throughout the curve. Therefore, it is difficult to comprehensively and accurately identify high-risk curves, which highlights a key flaw in the current understanding of safety level assessment. The truck traffic data-based MSCR indicator aims to provide a more comprehensive and accurate assessment by: (a) capturing the continuous speed trend of trucks throughout the curve; (b) improving data accuracy and expanding sample size to ensure more reliable and representative analysis; and (c) more effectively identifying high-risk curves to improve road safety assessment and intervention.

3. Data Processing and Preliminary Analysis

The following subsections describe the data processing and preliminary analysis in two steps: first, the acquisition and processing of vehicle data, road data, and crash data are outlined (Section 3.1); then, the speed variation trends of trucks on curves to the left and right with the same radius are preliminarily analyzed (Section 3.2).

3.1. Data Collection and Processing

3.1.1. Road Data

The study chose the G72 freeway (53.389 km) and G65 freeway (66.655 km) for collecting high-frequency GPS floating truck speed data, specifically on curves. The design speed of the G72 and G65 freeways is 120 km/h, with four lanes in both directions and a total roadbed width of 28.0 m. The key technical specifications of the tested segments are summarized in Figure 1, and a total of 32 curves were selected for data processing. The curves of the survey segment have radii ranging from 763 m to 2500 m. The longitudinal slope of the road varies between −2.22% and 3.9%. Additionally, approximately 90% of the road segment has an absolute value of slope of less than 3%, and both the horizontal and vertical linear indicators exhibit high standards.

The construction of the road database includes the following steps: (a) research road section orthogonalization. The north–south direction of the road is used as the primary classification standard, and the circular curve is used as the secondary classification standard. Each circular curve is numbered separately in orthogonal order. (b) Geometric information restoration. The plane and longitudinal section alignment of the circular curve are restored based on the design file. (c) Road database construction. The road pile number, coordinates, curve direction, radius, average longitudinal slope, and other data are extracted to construct the road database.

3.1.2. Trajectory Data

The term floating trucks typically refers to trucks equipped with on-board GPS positioning devices [38]. In this study, the acquired truck traffic data extracted from FCD pertains to truck driving records from a Chinese express delivery company. Leveraging its high-frequency data transmission capabilities, detailed information such as truck number, time, position, speed, and heading angle is logged every second during operation.

Although GPS technology captures the speed value at each point, extracting speed data specific to the curve areas of freeways necessitates a series of procedures, including framing, screening, and cleansing of the raw data, to yield reliable and relevant speed data. The process is divided into two parts: trajectory—road data matching and data cleaning.

The construction of the trajectory database includes the following steps: (a) trajectory data cleaning. This includes removing structurally anomalous and driving anomaly data from the trajectory records. A driving recorder is used to eliminate trajectories influenced by surrounding trucks, ensuring that only those under free-flow conditions are retained in the database. (b) Clean the structural anomaly data and driving anomaly data in the trajectory dataset. Use dashcam footage to remove trajectories influenced by surrounding trucks. Use the trajectory timestamps to determine the sunrise and sunset times of each day, and filter out trajectories that occur entirely during daytime. Obtain weather data from the local metrological department, match the weather conditions to each trajectory date based on the timestamp, and remove trajectories affected by rainstorms, snowy days, and other adverse weather conditions, to ensure that the trucks in the database are operating under free-flow conditions. (c) Matching. The trajectory coordinates are aligned with the road’s design coordinates to accurately position the trajectory along the roadway.

3.1.3. Crash Data

This section includes the collision event data for the test section highway over the past five years, which includes a total of 4645 crashes. These data are manually entered into the system by traffic police, road management departments, or company personnel, recording the time of the crash, road pile number, severity, cause of the crash, etc. The collision event data for most sections have a positioning accuracy of 1 km, and the crash data positioning accuracy for a few sections reaches 100 m. According to the definition of high-incidence points for highway traffic crashes written by the Traffic Management Bureau of the Ministry of Public Security of China, sections with 3–5 traffic crashes in the past three years and sections with frequent traffic crashes within a certain period of time are defined as high-crash-rate sections. The specific database construction process is shown in Figure 2.

3.2. Preliminary Analysis

Using the database constructed in Section 3.1, the data for all trucks traveling on a circular curve with a radius of 600 m are extracted. A graph is then plotted with the mileage of the trucks along the road on the horizontal axis and the actual speed values of all trucks on the vertical axis. Since the freeway is a two-way four-lane freeway, we extracted the data for trucks in the left and right directions of the circular curve with the same radius, and the results are shown in Figure 3.

The speed selection of drivers is fundamentally influenced by their perception of curves, directly affecting the stability and safety of navigating these curves. Underestimating the appropriate entry speed significantly increases the risk associated with curve driving [39]. Prior to entering a curve, there is considerable variance in truck speeds. However, once within the curve, speed distribution becomes more concentrated, and it disperses again upon exiting, indicating that the linear conditions significantly impact speed selection behavior.

A comparative analysis of truck speeds on curves to the left and right reveals that drivers can more easily detect the curve to the right and, thus, apply braking measures earlier to negotiate the curve at a safer speed. Conversely, drivers often fail to anticipate the curve to the left well in advance, leading to a more abrupt deceleration upon entry. The speed curve of trucks entering the curve to the left shows a steeper deceleration trend, with a slower acceleration trend post-curve, suggesting higher deceleration rates when entering the curve compared to the acceleration rates upon exiting.

The deceleration rate for the curve to the right is more gradual, and the overall cornering speed of the truck is lower compared to the curve to the left. By analyzing the shapes of the speed curves at various percentile levels, it becomes evident that deceleration on the curves to the left exceeds that on curves to the right, indicating a more complex and potentially hazardous braking pattern. These observations indicate that the speed behavior of trucks on curves deviates from the current assumptions about driving behavior on curved roads. Current research generally assumes that trucks will completely decelerate before entering a curve and pass through the curve at a constant speed [40]. In fact, the deceleration behavior extends to the inside of the curve, at which time the truck will be subjected to a combination of lateral and longitudinal traction, making the driving state even more unstable.

4. Methods

To analyze the crash-rate difference between curves to the left and right, this study proposed a new curve safety evaluation method, which used truck traffic data to calculate the speed indicator and applied vague sets to determine the safety level of the curves. Figure 4 illustrates the overall approach framework, which consists of two main parts: key alignment features identification and construction of curve safety evaluation indicator. The first part uses BLR to determine the geometric indicators that impact the crash rate of curves most. The second part first compares the safety evaluation capabilities of the MSCR indicator and the geometric design consistency indicators and, further, uses vague sets to determine the comprehensive similarity of the safety level of the combined indicators to identify high-risk segments. Finally, the causes of high-risk curves are analyzed based on features and indicators, and the risk is predicted.

4.1. Binary Logistic Regression

While driving on the freeway, a truck’s speed varies based on road alignment, roadside environment, weather conditions, and the driver’s state [41], with each factor exerting a distinct influence on speed. Due to the joint action of various factors on speed, it is impossible to accurately reflect the relationship between these factors and speed without controlling other influencing elements. Hence, BLR was used to explain the variability in crash rates as a function of several factors. Different curves and different deflection directions of the curve have high/low crash rates (0 represents low and 1 represents high).

Table 1. Variables Considered for the Model.

Symbol	Types	Description
Direction	Categorical	The same curve is divided into left and right directions (0 represents left and 1 means right)
Radius	Continuous	The same curve segment is divided into left and right directions, and the radius is large. It is believed that the radius of the curve to the left is approximately equal to the curve to the right.
Deflection angle	Continuous	Using the deflection angle to indicate the magnitude of the driver’s field of vision deflection
Average slope	Continuous	The weighted average of the longitudinal slope in the chosen segment.
Length	Continuous	Varying lengths offer differing amounts of time and distance for the driver to adapt to curve changes.

shows the factors that were considered in this study.

A BLR model was developed to analyze the reasons for the differences in crash rates for different deflection directions of the curve. Before modeling, a t-test should be used for continuous variables, and a χ² test should be used for categorical variables to determine the model’s independent variables. The crash-rate probability is modeled using a logistic distribution, as shown in Equation (1), where the logit of the logistic regression model is provided in the same equation.

$$\pi \left(x\right)={\displaystyle \frac{e^{g\left(x\right)}}{1+e^{g\left(x\right)}}}$$

(1)

$$g\left(x\right)=\ln {\displaystyle \frac{\pi (x)}{1-\pi (x)}}={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_{\alpha }{x}_{\alpha }+\dots \dots +{\beta }_{\mathrm{n}}{x}_n$$

(2)

where the $\pi \left(\mathrm{x}\right)$ represents the conditional probability of crash, and the $x_1$, $x_2$, and …$x_n$ represents the independent variables that can be either categorical or continuous. The logit procedure was adopted to determine the variables in the model.

4.2. Curve Safety Evaluation Indicator

4.2.1. Basic Indicators

Regarding geometric design consistency, operating speed (V₈₅) is widely considered a key and straightforward geometric design consistency measure [42]. The change in speed of trucks is a visible indicator of inconsistency in geometric design. Several interpretations of operating speed as a geometric design consistency measure have been made in the literature. The operating speed can be used in consistency evaluation by examining the variation between the design speed (V_d) and V₈₅ on a particular freeway segment or examining the differences between V₈₅ on consecutive freeway elements (ΔV₈₅). The design speed is the primary basis for establishing speed limit standards. The operating speed is a variable in the truck driving process and is the reference range value of the road speed limit. The speed limit should be formulated based on the design speed, operating speed, and relevant safety regulations and adjusted promptly after sorting and analyzing the data reflected in the road operation and safety management process. The research object of the design speed usually considers small passenger cars. The research object of this article is a large truck with relatively poor power performance. Therefore, the speed limit (V_L) is used for geometric design consistency analysis instead of the design speed. The fixed-point data collection is mostly concentrated at point of curvature (PC), midpoint of curve (MC), and point of tangency (PT) breakpoints. According to Equations (3) and (4), the speed is analyzed using Criteria I and Criteria II values:

$$Criteria I=\left|V_{85\left(i\right)}-V_{L\left(i\right)}\right|$$

(3)

$$Criteria II=\left|V_{85\left(i\right)}-V_{85(i+1)}\right|$$

(4)

where $V_{L\left(i\right)}$ represents the limit speed at breakpoint i (m/s), and $V_{85\left(i\right)}$ represents 85% percentile of speed at breakpoint i (m/s).

4.2.2. Indicator Improvements

In order to comprehensively analyze the speed differences of trucks on curves to the left and right, a new safety evaluation indicator, termed the MSCR, is proposed based on Criteria II values of GDCI. MSCR analyses the speed variation rate of a segment based on the speed difference and length of the segment (PC to MC and MC to PT). Equation (5), that defines the described indicator, is as follows:

$$MSCR={\displaystyle \frac{\left|V_{85(n)}-V_{85(n+1)}\right|\times {\overline{V}}_{s(n)}}{L_{s(n)}}}$$

(5)

where $MSCR$ represents the Mean Speed Change Rate (m/s²), ${\overline{V}}_{s(n)}$ represents the mean speed at segment n (m/s), and $L_{s(n)}$ represents the length of segment n (m).

MSCR_(L) represents the MSCR value of the curves to the left, and MSCR_(R) represents the MSCR value of the curves to the right. MSCR surpasses traditional geometric design consistency indicators by considering both speed differences and average speed across specific road segments. The length of the road segment plays a fundamental role in influencing vehicular dynamics. Combined with the segment length, it can more realistically reflect the speed differences of trucks in different segments. Therefore, it is not comprehensive enough to use the safety level at the breakpoints to represent the safety level of the entire curve. In contrast, the MSCR proposed based on continuous trajectory data can evaluate the curve safety in a more detailed and continuous manner. Multiplying speed differences with average speed provides a comprehensive view of vehicular behavior, accounting for acceleration, deceleration, and steady-state motion.

4.2.3. Safety Evaluation and Risk Prediction

The purpose of this section is to use vague sets to determine the safety level of the curve based on MSCR and GDCI. Vague sets surpass fuzzy sets when dealing with uncertain information [43]. Thus, vague sets are applied in this study to estimate the safety level of speed at curve segments. The comprehensive material element can be calculated as per Equation (6). In our study, all the indicators are supposed to be as more minor as they can, thus, $t_{ij}$ and $f_{ij}$ are calculated as per Equations (7) and (8), respectively:

$$V_{ij}=\left[t_{ij},1-f_{ij}\right]$$

(6)

$$t_{ij}=\left(x_j^{\max }-x_{ij}\right)/\left(x_j^{\max }-x_j^{\min }\right)$$

(7)

$$f_{ij}=\left(x_{ij}-x_j^{\min }\right)/\left(x_j^{\max }-x_j^{\min }\right)$$

(8)

where $V_{ij}$ represents the vague value of object i with indicator j, $t_{ij}$ represents the true membership function, $f_{ij}$ represents the false membership function, $x_{ij}$ represents the values of object i with indicator j, $x_j^{\max }$ represent the maximum value of indicator j of all objects, and $x_j^{\min }$ represents the minimum value of indicator j of all objects.

The essence of this process is normalization. Similarities between the matter element under test and the indicator of standard are computed as per Equation (9) [44]:

$$M_z\left(\mathrm{x},y_j\right)=1-{\displaystyle \frac{\left|\left(t_x-t_{yj}\right)-\left(f_x-f_{yj}\right)\right|}{2}}$$

(9)

where $\mathrm{x}$ represents the indicator value for the matter element under test, $y_j$ represents the indicator value for different levels, and $M_z\left(\mathrm{x},y_j\right)$ denotes the similarity between the matter element under test and the standard indicator. The similarity values of each security level are calculated, and the larger the similarity value is, the higher the probability that the curve is at the security level.

5. Results and Discussion

The mentioned method is applied to the experimental section of the highway: first, we obtained the road geometry variables that have an impact on crashes (Section 5.1), then, we verifyed the effectiveness of the MSCR indicator and vague sets, analyzed the impact of geometric indicators on safety evaluation indicators, and predicted safety evaluation indicators (Section 5.2).

5.1. Key Contribution Alignment Features for Curve Safety

5.1.1. Modeling and Assessment

After testing single indicators, the significance of length is 0.357, and the significance of average longitudinal slope is 0.498. The p-values are greater than 0.05, so length and average longitudinal slope are eliminated during modeling.

Table 2. Modeling Results for Coefficients of Variables.

Variables	B	S.E.	Wald	Dof	Significant	Exp(B)	95% Confidence Interval
							Lower Limit	Higher Limit
Deflection angle	0.091	0.039	5.384	1	0.020	1.095	1.014	1.183
Radius	−0.004	0.001	9.908	1	0.002	0.996	0.994	0.998
Deflection direction	−2.235	0.942	5.631	1	0.018	0.107	0.017	0.678
p-value for Hosmer–Lemeshow test: 0.915

provides the modeling results from the BLR method. Eventually, after setting the significance level at 0.05 (p-value < 0.05), three variables among all varied variables were found to be significantly related to crash-rate probability, as presented in the results table. Then, the model from BLR can be presented using Equations (10) and (11):

$$X=\left(\mathit{deflection} \mathit{angle}, \mathit{radius}, \mathit{deflection} \mathit{direction}\right)$$

(10)

$$\beta =\left(2.519, 0.091,-0.004,-2.235\right)$$

(11)

To use BLR in crash-rate prediction, a threshold of 50% in the probability of a crash was set: a crash is predicted if $\pi \left(x\right)$ > 50%; otherwise, if $\pi \left(x\right)$ < 50%, a non-crash event is predicted. The BLR from the trained set was applied to test its prediction performance using the test set data. The confusion matrix was applied, and the results are provided in

Table 3. Results for Crash Prediction based on BLR.

		Predicted Class		Prediction Accuracy
		False	True
True class	False	31	6	83.8
	True	4	23	85.2
Overall Percentage				84.4

. From the Table, the global accuracy of using the BLR model to predict crashes reached 84.4%. Additionally, the recall for crash prediction reached 85.2%.

5.1.2. Features’ Determination

According to the analysis results of the BLR, the curve deflection direction, deflection angle, and radius have a strong correlation with the crash rate, which is consistent with the conclusions of some scholars’ research [45,46].

Since the length of the curve can be obtained from the curve radius and the deflection angle, there may be a collinear relationship between the three variables, and the features (length) with the same contribution are eliminated. Moreover, it was found that the crash-rate sensitivity to the longitudinal slope of curves was reduced on freeways in high-index plain areas. Scholars who use variables such as longitudinal slope to analyze speed indicators mainly focus on the combined curved and sloped segments of low-grade highways with lower technical indicators [47,48]. This study aimed to include only variables that are easily extracted from a geometric design, namely the deflection angle, radius, and start and end position of curves. Other, more complex variables [49] might improve the models further but are difficult to implement in design evaluations.

5.2. Curve Safety Evaluation

5.2.1. Threshold Determination

The Criteria I and MSCR values of the most unfavorable position of the curve are calculated using Equations (3) and (5), and the results are shown in

Table 4. MSCR and Criteria I indicator calculation results for the curve.

Curve	Deflection Angle	Radius	MSCR(L)	MSCR(R)	Criteria I (L)	Criteria I (R)
1	62.27417	763	0.457	0.347	18.547	13.127
2	23.44736	2000	0.217	0.199	6.319	5.879
3	55.11104	1538.406	0.197	0.18	9.775	8.758
……
31	45.93267	1300	0.262	0.252	9.213	7.465
32	52.189	1000	0.328	0.286	9.813	7.526

. The range of the MSCR_(L) is 0.122~0.457 m/s², the range of the MSCR_(R) is 0.114~0.347 m/s², the range of Criteria I _(L) values is 4.193~18.547 m/s², and the range of Criteria I _(R) values is 4.032~13.127 m/s². The data show a relatively discrete trend.

(1) Acc

The effects of traditional acceleration index and MSCR on curve safety assessment are compared, and the threshold of the traditional acceleration index is determined. AASHTO defines the comfortable braking acceleration and uncomfortable truck braking acceleration based on the main line design speed [7]. When the main line design speed is 120 km/h, the corresponding comfortable deceleration and uncomfortable deceleration thresholds are 0.5 m/s² and 1.0 m/s², respectively.

(2) Criteria I

Safety Criteria I is the most common set of criteria used to determine the level of consistency of a highway segment in relation to operating speed. Lamm [17] classified highway segments into three categories. In this classification, “Good” indicates that no highway alignment correction is necessary; “Fair” suggests that while alignment correction is not required, improvements to elements such as signage or road camber may be beneficial; and “Poor” signifies that alignment redesign is recommended. This set of criteria is among the most widely recognized safety assessment standards.

(3) MSCR

The determination of indicator thresholds is an important basis for safety level classification, and the indicator thresholds of the curves to the left and right are determined using the interquartile range method. Other threshold determination methods were also considered in this paper. For example, the area under the ROC curve (AUC), which summarizes the trade-off between true positive rate and false positive rate under different threshold settings, is particularly useful for distinguishing the overall accuracy of the threshold. However, considering the specific context of this study, the interquartile range method is favored for its simplicity and ability to be directly related to the percentile-based MSCR threshold. The interquartile range method was chosen because it can reduce the impact of outliers and more accurately reflect the central tendency of the data. Since the circular curves handled in this paper are mostly large-radius sections, the MSCR for section of the curve is mainly concentrated in a smaller range. The interquartile range method is particularly useful when dealing with such skewed data distributions because it focuses on the middle 50% of the data and is less susceptible to extreme values that may distort the results. The 75% quantile value of the MSCR_(L) is 0.277 m/s², and the 25% quantile is 0.143 m/s². Therefore, when the MSCR_(L) is less than 0.143 m/s², the security level is “Good”, when it is between 0.143 m/s² and 0.277 m/s², the security level is “Fair”, and when it is greater than 0.277 m/s², the security level is “Poor”. Similarly, the MSCR_(R) is calculated to determine the corresponding safety level.

Finally, the indicator safety classification of this study is shown in

Table 5. Design Evaluation Criteria.

Safety Level	MSCR(L) (m/s2)	MSCR(R) (m/s2)	Criteria I (km/h)	Acc (m/s2)
Good	MSCR ≤ 0.143	MSCR ≤ 0.152	|V85 − VL| < 10	Acc < 0.5
Fair	0.143 < MSCR ≤ 0.277	0.152 < MSCR ≤ 0.263	10 < |V85 − VL| ≤ 20	0.5 < Acc ≤ 1.0
Poor	MSCR > 0.277	MSCR > 0.263	|V85 − VL| > 20	Acc > 1.0

.

5.2.2. Safety Evaluation Indicators’ Comparison

Table 6. Indicator Determination Accuracy.

Indicators	Left Direction			Right Direction
	Judgment Value	Actual Value	Accuracy (%)	Judgment Value	Actual Value	Accuracy (%)
Acc	5	17	29.4	3	11	27.3
Criteria I	9		52.9	6		54.5
MSCR	11		64.7	8		72.7
MSCR+ Criteria I	15		88.2	9		81.8

compares the results of different indicators for determining the curve safety level. The accuracy of using acceleration to identify the left and right directions is less than 30%, which is significantly lower than the other indicators. The recommended braking acceleration value is based on passenger cars, not trucks. In addition, since the design speed of the road is high and the truck drivers are employees of freight companies with rich driving experience, they rarely take drastic deceleration measures when driving trucks through curves. The braking acceleration thresholds proposed in Table 5 are relatively redundant, and the safety level of the identified curves is mostly “Good”, which cannot truly reflect the crash risk.

The results of the analysis of the safety level of the curves to the left and right using Criteria I show that the effectiveness of this standard is not ideal. The accuracy of the safety level evaluation for curves to the left is 52.9%, while the accuracy of the safety level evaluation for curves to the right is only 54.5%. One possible explanation for the limited effectiveness of Criteria I is that it does not consider other relevant factors that affect the safety of curves, and the speed changes at only two points cannot fully analyze driving safety.

Using the MSCR indicator, a total of 11 high-risk curves to the left and 8 high-risk curves to the right were identified, with accuracy rates of 64.7% and 72.7%, respectively, which is an improvement over Criteria I and Acc. However, it still cannot comprehensively evaluate the safety level. Therefore, we considered using vague sets, combined with the MSCR and Criteria I, to jointly determine the safety level of the curves.

The use of vague sets to determine the safety level of a curve is divided into several steps. First, the comprehensive material element can be calculated by Equation (6). Furthermore, the similarity between the matter element under evaluation and the standard indicator is calculated using Equation (9). Finally, the comprehensive similarity is calculated by Equation (10), and the safety level of the curve is confirmed. A curve of the G65 freeway in the same area is selected as the supporting project to evaluate the safety level. The speed limit on this segment is 60 km/h. The radius of the selected curve is 1000 m, the average longitudinal slope is 0.2%, and the deflection angle is 52.5°. Analyzing the most unfavorable position of this curve, in the left direction, the MSCR_(L) is 0.337 m/s², which is rated as “Poor”, and Criteria I value is 11.57 m/s, which is rated as “Fair”. In the right direction, the MSCR_(R) is 0.281 m/s², which is rated as “Poor”, and Criteria I value is 9.34 m/s, which is rated as “Good”.

The comprehensive material units and the vague sets are calculated by Equation (6), as shown in

Table 7. The Comprehensive Material units.

Indicators	Good	Fair	Poor	Indicators Under Test
Left direction
MSCR(L)	(0, 0.143)	(0.143, 0.277)	(0.277, 0.457)	0.337
Criteria I	(0, 10)	(10, 20)	(20, 60)	11.57
Right direction
MSCR(D, R)	(0, 0.152)	(0.152, 0.263)	(0.263, 0.35)	0.281
Criteria I	(0, 10)	(10, 20)	(20, 60)	9.34

and

Table 8. The Comprehensive Vague Sets of Material units.

Indicators	Good	Fair	Poor	Indicators Under Test
Left direction
MSCR(L)	(0, 0.313)	(0.313, 0.606)	(0.606, 1)	(0.737, 0.737)
Criteria I	(0, 0.167)	(0.167, 0.333)	(0.333, 1)	(0.193, 0.193)
Right direction
MSCR(R)	(0, 0.434)	(0.434, 0.751)	(0.751, 1)	(0.803, 0.803)
Criteria I	(0, 0.167)	(0.167, 0.333)	(0.333, 1)	(0.156, 0.156)

, respectively.

The similarities between the matter element under test and the indicator of standard are computed by Equation (9). The results are shown below.

• The indicator’s similarity (left direction)

$$\left[\begin{array}{ccc}0.420& 0.723& 0.934\\ 0.891& 0.943& 0.527\end{array}\right]$$

• The indicator’s similarity (right direction)

$$\left[\begin{array}{ccc}0.414& 0.790& 0.928\\ 0.928& 0.906& 0.490\end{array}\right]$$

The information about the comprehensive similarity is computed by Equation (10). The similarities of the safety levels “Good”, “Fair”, and “Poor” in the left direction are 0.561, 0.789, and 0.812, respectively, and those in the right direction are 0.568, 0.824, and 0.796, respectively. This indicates that the speed safety level of the left direction of the curve is “Poor”, and the safety level of the right direction is “Fair”. Based on this method, the safety level of some segments was evaluated, and the results are shown in Figure 5. It can be seen that the safety level of some curves is not optimal, and the speed safety levels in the left and right directions are inconsistent. The safety level of the curve is determined based on vague sets. The accuracy of the curves to the left is 88.2%, and the accuracy of the curves to the right is 81.8%, which are 35.3% and 18.2% higher than those for Criteria I, respectively. Although this combined method has significantly improved the evaluation of curve safety levels, for newly built freeways, it is impossible to directly obtain truck speed data, that is, it is impossible to calculate the MSCR and GCDIs of the road. Therefore, this study is more suitable for freeways that are already in operation, and safety improvement measures such as speed limits and sign updates are proposed.

5.2.3. Risk Analysis and Prediction

Figure 6 presents the analysis results for the MSCR and Criterion I for the high-risk curves identified in Section 5.2.2. It can be seen that considering only one indicator cannot accurately identify high-risk curves. Furthermore, features and indicators are integrated to analyze the causes of high risk on the curve.

Figure 6a,b show the analysis results of the MSCR and features. Evidently, at the same deflection angle or radius, the MSCR_(L) is greater than the MSCR_(R). On the curves to the left, drivers tend to apply the brakes more frequently over short distances, resulting in a steeper decrease in truck speed. The difference in speed variations offers a plausible explanation for the comparatively higher crash rate observed on the curves to the left. Furthermore, when the deflection angle is less than 40°, the difference between the MSCR_(L) and MSCR_(R) remains relatively stable at approximately 0.02. The disparity between the two increases as the deflection angle surpasses 40°. When the deflection angle reaches 65°, this difference jumps to 0.13. The results of the analysis of radii show a more concentrated trend. The data suggest a phenomenon where the effect of curve radius on drive safety is relatively muted for larger radii (1300 m to 2500 m), whereas a more pronounced difference in speed behavior is observed for smaller radii (below 1300 m). As the curve radius decreases, the MSCR_(L) and MSCR_(R) gradually increase, indicating that the deceleration effect is more obvious on narrower curves. However, in the 1300 m to 2500 m range, the changes in the MSCR_(L) and MSCR_(R) values are small, with the maximum difference being 0.04 m/s². Because freeways in plain areas usually have higher surface indicators, for trucks passing through curves with a radius of more than 1300 m, it may not be necessary to make large speed adjustments.

Several notable trends emerge when analyzing the speed differential between the curves to the left and right, particularly when considering the different features. Figure 6d shows the analysis results between Criteria I and the radius. It can be seen intuitively that there is a negative growth trend between the two, but it is relatively discrete. In contrast, the Criterion I analysis based on the deflection angle presents a more complex situation. As shown in Figure 6c, although the Criteria I values for both left and right curves increase significantly with the increase of the deflection angle, their changing trends show a nonlinear pattern. The difference is relatively small at lower angles but significantly larger between 40° and 65°. This suggests that the driver’s speed preference differs more between curve directions at smaller deflection angles, whereas at smaller deflection angles, the driver’s behavior becomes more similar. This difference may be related to factors such as visual cues, driver expectations, and corner geometry. It is worth noting that for a curve with a deflection angle of 62.27° and a radius of 763 m, the Criteria I value at the curves to the left reached 18.547 km/h. Considering the effect of the deflection angle on truck speed in curve design plays an important role in ensuring safe and efficient driving. China’s route design specifications recommend a radius of 1000 m for circular curve sections with a design speed of 120 km/h, and do not specify the deflection angle of the circular curve [6]. According to the analysis results for the MSCR and Criteria I value for such curve sections, when the radius is less than 1300 m or the deflection angle is greater than 40 degrees, there will be a certain risk of conflict when trucks are driving on the curve. Therefore, in the design stage of new roads, when conditions permit, the radius of the circular curve should be increased, or the deflection angle of the circular curve should be reduced.

The increased differentials in both the MSCR and Criteria I values suggest that design considerations for curve geometry, including deflection angle, radius, and deflection direction, become more critical in ensuring safe and efficient truck speeds on freeways. Previous studies demonstrate that changes in driver speed directly correlate with road safety [7,50], with excessive speed variations being linked to elevated driving risks. Other studies indicate truck speed fluctuations are influenced by road alignment [51], revealing a higher driving risk on curves to the left compared to curves to the right. The present study reinforces these observations. Furthermore, the findings of this paper regarding the deflection angle align with previous scholarly research [40], indicating that an increase in angle negatively impacts truck speed. Based on the indicator analysis results, we recommend that the curves with different deflection directions be studied separately in order to be given separate attention in design guidelines. The discrepancy in the indicators between curves to the left and right could potentially explain the variance in crash rates, particularly considering the left-hand driving configuration of Chinese trucks. Drivers’ visual field factors lead to distinct behavioral patterns for trucks navigating curves in different deflection directions. This is in contrast to the conclusions of the Society of Osaka Traffic Scientific Research [52] and the National Police Agency [53], who reported more crashes on curves to the right. This is because Japanese trucks are right-hand driven, thus providing a contrasting perspective to validate the relationship between curve deflection direction and drive safety.

Using the analysis results shown in Figure 6, taking the curves to the left as the more unfavorable section, the deflection angle and radius are used as independent variables to construct the best fitting subset of the MSCR and Criteria I. Then, the geometric index can be inputted to predict the evaluation index value of a new curve and determine the safety level of the curve. The best fitting subsets of the MSCR and Criteria I values are shown in Equations (12) and (13), with R-square values of 0.725 and 0.78, respectively, which have relatively good fitting accuracy and can be used as the prediction of the indicators.

$$MSCR=1.853+0.0004D-0.224\ln \left(R\right)$$

(12)

$$Criteria I=-3+0.194D+{\displaystyle \frac{5026.031}{R}}$$

(13)

where D represents the deflection angle of the curve and R represents the radius of the curve.

6. Conclusions

In this study, based on a series of indicators, the reasons for the difference in crash rates between trucks on curves to the left and right were analyzed from the perspective of speed, and the safety level of curves was evaluated. The primary contributions are summarized as follows. First, the features that lead to crashes on curved roads are identified at the methodological level, and a new safety evaluation indicator based on geometric design consistency, the MSCR indicator, is proposed. Through multi-angle analysis, the MSCR indicator is seen to be more practical than traditional acceleration indicators. Combined with geometric consistency indicators, it is more suitable for evaluating the safety level of curves. Secondly, at the analytical application level, we used floating trucks to collect a large amount of truck speed data from 32 curves with different corners on the freeway. On this basis, the accuracy of the MSCR indicator and GDSI in identifying high-risk curves was compared, and the analysis indicators were used to evaluate the safety level of the curves through examples to find out the reasons for the difference in crash rates between the curves to the left and right. The conclusions are as follows:

(1) BLR was used to comprehensively analyze the relationship between the geometric indicators of the test segments (including radius, length, average longitudinal slope, deflection angle, and deflection direction) and crash-rates’ analysis. The study found that there may be a collinear relationship between the length and other features. Because the test segments are mainly a freeway in a plain area, the geometric indicators value is relatively high. The average longitudinal slope has no significant impact on crash rates. BLR analysis further found that curve radius, deflection angle, and deflection direction significantly impact crash rates, so this study selected the above influencing factors for analysis.

(2) Vague sets can express fuzzy information more comprehensively. Based on this, the safety level of curves with different deflection directions is considered by combining the MSCR and GDSI. The combination of indicators can significantly improve the accuracy of curve safety level evaluation.

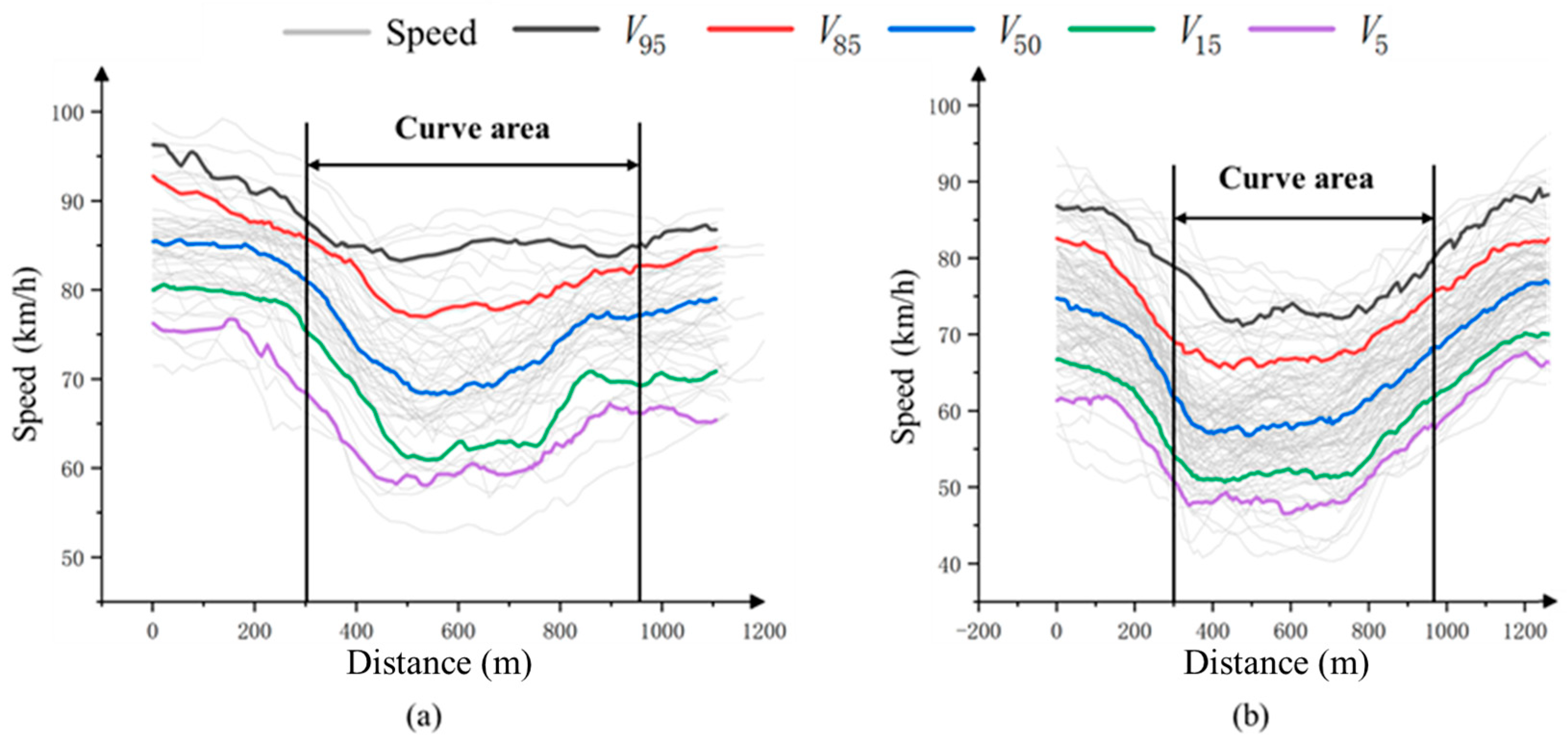
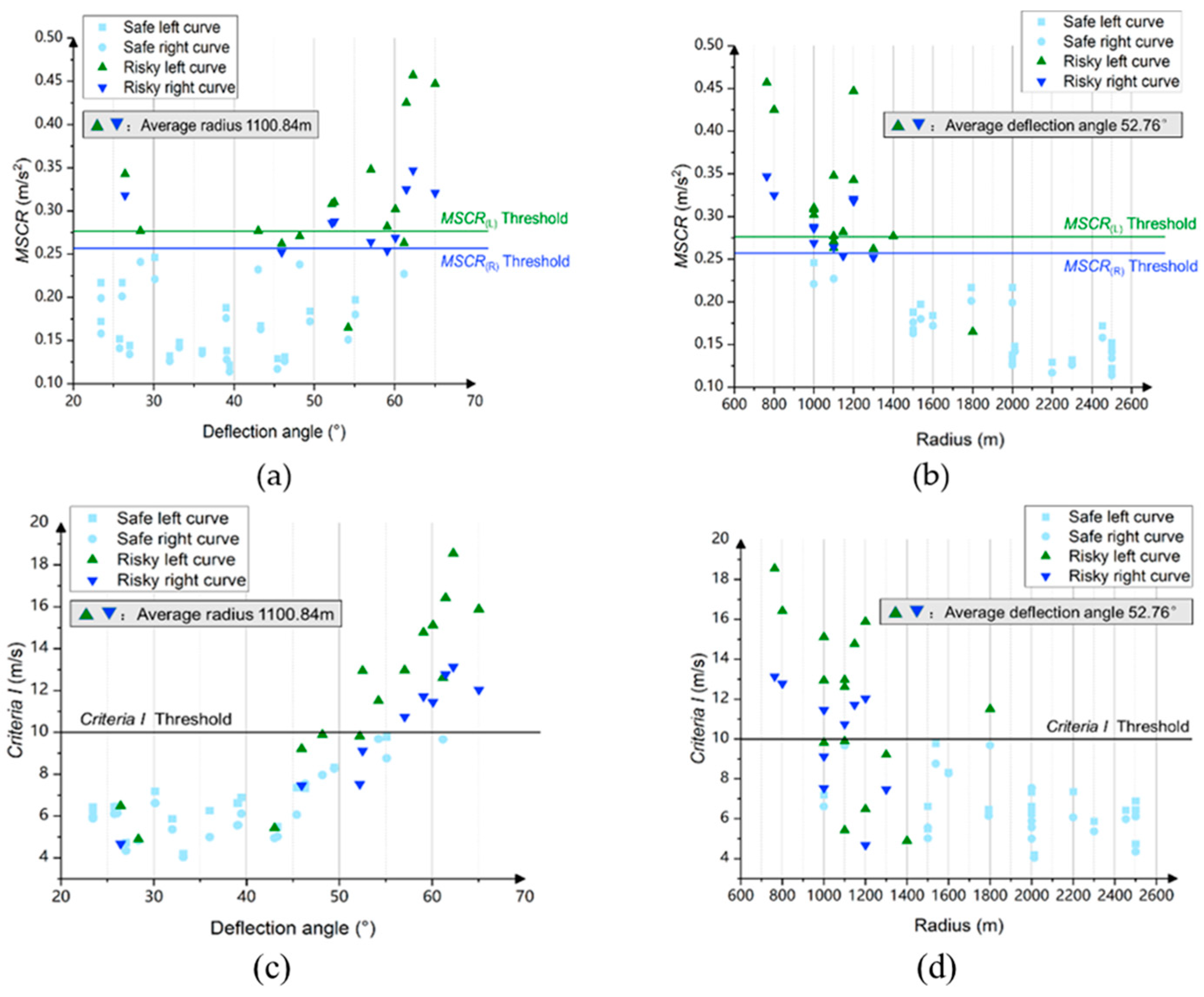
(3) Whether considering the MSCR or Criteria I values, the change value of the curves to the left consistently surpasses that of the curves to the right at the same deflection angle and radius. Furthermore, as the deflection angle increases or the radius decreases, the divergence between the curves to the left and right becomes progressively more pronounced. The disparity in safety indicators may constitute one of the underlying factors contributing to the variation in crash rates between curves to the left and right.

However, this article only extracts the features of a single curve and analyses its safety level. It is impossible to effectively evaluate the safety level of trucks on special forms of curves, such as oval curves and S-shaped curves. Furthermore, the operating environment of the freeway is highly complex, with factors such as road alignment conditions, the driver’s physiological characteristics (such as handedness, gender, age, etc.), weather, traffic volume, and cross-segmental elements all exerting some influence on driving safety. The research results of this paper can be applied to the safety evaluations of highways that have been put into operation, but the factors considered in the fitting subset are relatively few. In the future, it is necessary to further expand the sample size and consider more factors affecting truck driving, improve the accuracy and applicability of the evaluation, build a more accurate collision risk prediction model, and use geometric design indicators to predict collision risks, so as to provide stronger theoretical support for highway driving safety research, contributing to the sustainable development goals.