Drivers’ Welfare and Pollutant Emission Induced by Ride-Hailing Platforms’ Pricing Strategies
Abstract
1. Introduction
2. Literature Review
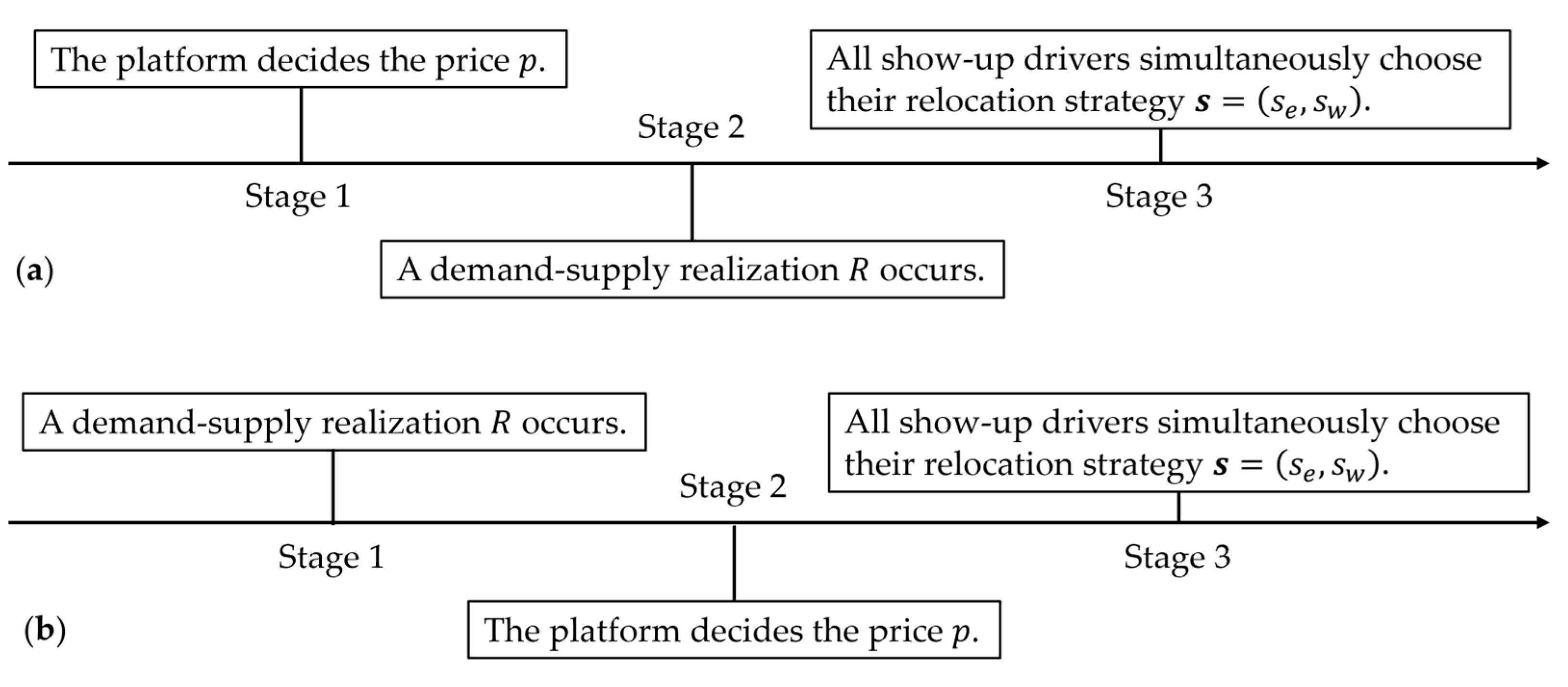
3. Model
4. Equilibrium
4.1. Show-Up Drivers’ Equilibrium Responses
- (i)
- If , the strategy profile satisfying the following conditions is the unique Nash equilibrium: if and , and otherwise.
- (ii)
- If , the strategy profile satisfying the following conditions is the unique Nash equilibrium: if and otherwise.
- (iii)
- If , then
- (iii-i)
- When , the strategy profile given in (ii) is a Nash equilibrium.
- (iii-ii)
- When , the strategy profile satisfying the following conditions is the unique Nash equilibrium: if and. otherwise.
- (iii-iii)
- When , the strategy profile such that is a Nash equilibrium.
- (iv)
- If , then
- (iv-i)
- When , the strategy profile given in (ii) is a Nash equilibrium.
- (iv-ii)
- When , the strategy profile given in (iii-ii) is the unique Nash equilibrium.
- (iv-iii)
- When , the strategy profile satisfying the following conditions is the unique Nash equilibrium: (iv-iii-i) if , (iv-iii-ii) if , , and .
4.2. Platform’s Ex-Ante Pricing Strategy
4.3. Platform’s Ex-Post Pricing Strategy
5. Managerial Implications
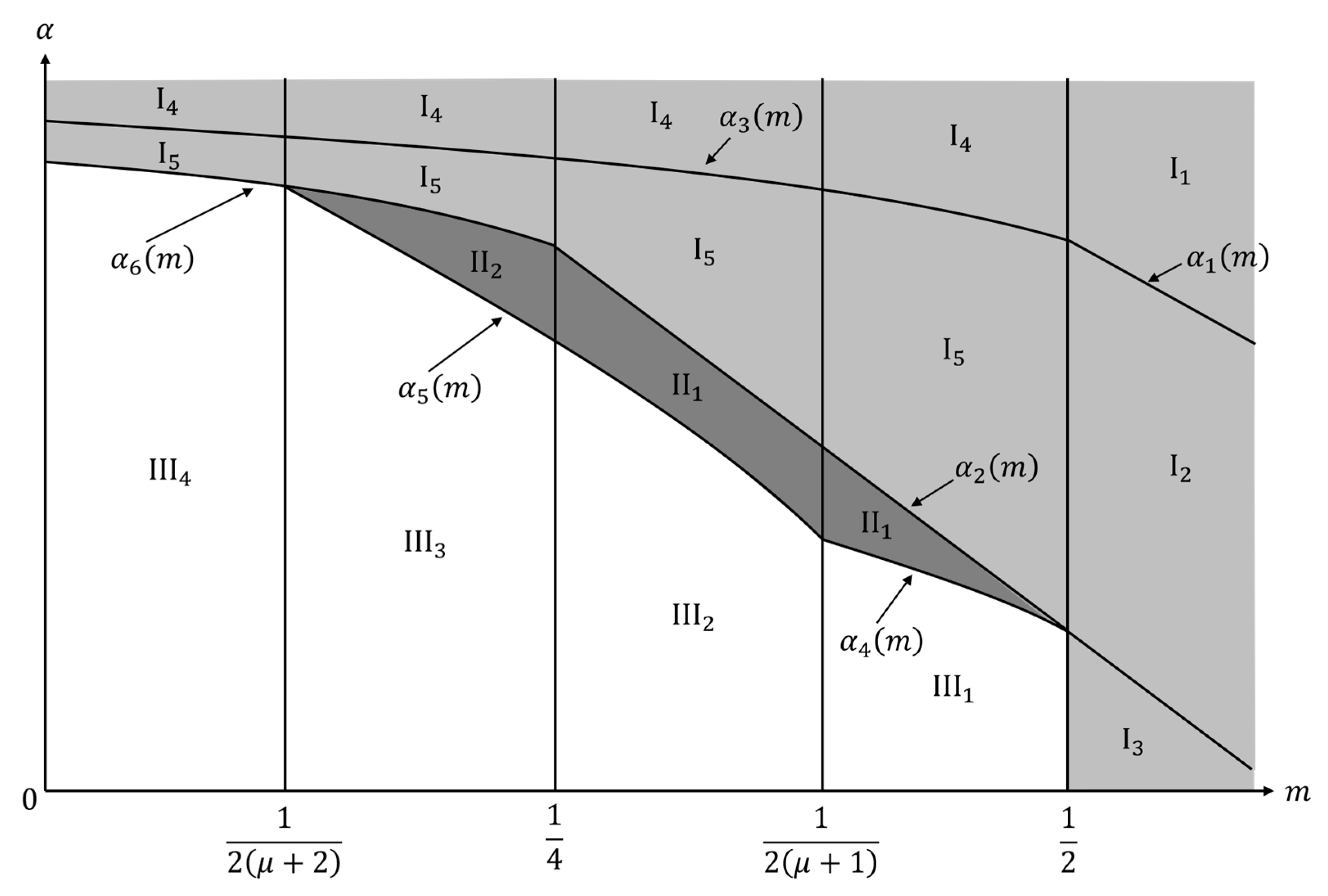
5.1. The Impact of the Commission Rate Under the Ex-Ante Pricing Strategy
- (i)
- When , drops downwards at , and jumps upwards at , and drops downwards at both and .
- (ii)
- When , drops downwards at jumps upwards , and drops downwards at and .
- (iii)
- When , and drop downwards at and , and jumps upwards at .
- (iv)
- When , and drop downwards at and , and jumps upwards at .
5.2. The Impact of the Commission Rate Under Ex-Post Pricing Strategy
- (i)
- When , drops downwards at , and jumps upwards at , and drops downwards at both and .
- (ii)
- When , and drop downwards at and , and jumps upwards at .
- (iii)
- When , and drop downwards at and , and jumps upwards at .
5.3. The Impact of Ex-Post Pricing Strategy
- (i)
- When falls in Regions –, we have , , and .
- (ii)
- When falls in Regions and , we have , , and for where
- (iii)
- When falls in Regions –, we have , , and .
6. Discussion
6.1. A Numerical Case Study
6.2. Actionable Recommendations
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. Proof of Proposition 3
Appendix A.4. Proof of Proposition 4
Appendix A.5. Proof of Proposition 5
| Conditions | ||||
|---|---|---|---|---|
| (i) | ||||
| (ii) | ||||
| (iii) | ||||
| (iv) | ||||
Appendix A.6. Proof of Proposition 6
| Conditions | ||||
|---|---|---|---|---|
| (i) | ||||
| (ii) | ||||
| (iii) | ||||
Appendix A.7. Proof of Proposition 7
References
- Yan, C.; Zhu, H.; Korolko, N.; Woodard, D. Dynamic pricing and matching in ride-hailing platforms. Nav. Res. Logist. 2020, 67, 705–724. [Google Scholar] [CrossRef]
- Feng, G.; Kong, G.; Wang, Z. We are on the way: Analysis of on-demand ride-hailing systems. M&SOM-Manuf. Serv. Oper. Manag. 2021, 23, 1237–1256. [Google Scholar]
- Tirachini, A.; Del Río, M. Ride-hailing in Santiago de Chile: Users’ characterisation and effects on travel behaviour. Transp. Policy 2019, 82, 46–57. [Google Scholar] [CrossRef]
- Tirachini, A. Ride-hailing, travel behaviour and sustainable mobility: An international review. Transportation 2020, 47, 2011–2047. [Google Scholar] [CrossRef]
- Khaloei, M.; Ranjbari, A.; Laberteaux, K.; MacKenzie, D. Analyzing the effect of autonomous ridehailing on transit ridership: Competitor or desirable first-/last-mile connection? Transp. Res. Rec. 2021, 2675, 1154–1167. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, K.; Xiao, Y.; Fan, R. Does Online Ride-Hailing Service Improve the Efficiency of Taxi Market? Evidence from Shanghai. Sustainability 2022, 14, 8872. [Google Scholar] [CrossRef]
- Brown, A.; LaValle, W. Hailing a change: Comparing taxi and ridehail service quality in Los Angeles. Transportation 2021, 48, 1007–1031. [Google Scholar] [CrossRef]
- Meng, S.; Brown, A.; Barajas, J.M. Complements or competitors? Equity implications of taxis and ride-hail use in Chicago. J. Transp. Geogr. 2024, 120, 103973. [Google Scholar] [CrossRef]
- Hall, J.V.; Krueger, A.B. An analysis of the labor market for Uber’s driver-partners in the United States. ILR Rev. 2018, 71, 705–732. [Google Scholar] [CrossRef]
- Uber, Lyft Drivers Protest Across the US, Overseas|The Seattle Times. Available online: https://www.seattletimes.com/business/uber-lyft-drivers-plan-to-strike-in-cities-across-the-us/ (accessed on 10 March 2025).
- Drivers Are Rising Up Against Uber’s ‘Opaque’ Pay System|WIRED. Available online: https://www.wired.com/story/drivers-are-rising-up-against-ubers-opaque-pay-system/ (accessed on 10 March 2025).
- Lee, Y.; Chen, G.Y.H.; Circella, G.; Mokhtarian, P.L. Substitution or complementarity? A latent-class cluster analysis of ridehailing impacts on the use of other travel modes in three southern US cities. Transport. Res. Part D-Transport. Environ. 2022, 104, 103167. [Google Scholar] [CrossRef]
- Ban, X.J.; Dessouky, M.; Pang, J.S.; Fan, R. A general equilibrium model for transportation systems with e-hailing services and flow congestion. Transp. Res. Pt. B-Methodol. 2019, 129, 273–304. [Google Scholar]
- Giller, J.; Young, M.; Circella, G. Correlates of modal substitution and induced travel of Ridehailing in California. Transp. Res. Rec. 2024, 2678, 2046–2059. [Google Scholar] [CrossRef]
- Qian, X.; Lei, T.; Xue, J.; Lei, Z.; Ukkusuri, S.V. Impact of transportation network companies on urban congestion: Evidence from large-scale trajectory data. Sust. Cities Soc. 2020, 55, 102053. [Google Scholar] [CrossRef]
- Fageda, X. Measuring the impact of ride-hailing firms on urban congestion: The case of Uber in Europe. Pap. Reg. Sci. 2021, 100, 1230–1254. [Google Scholar] [CrossRef]
- Li, Z.; Liang, C.; Hong, Y.; Zhang, Z. How do on-demand ridesharing services affect traffic congestion? The moderating role of urban compactness. Prod. Oper. Manag. 2022, 31, 239–258. [Google Scholar] [CrossRef]
- Agarwal, S.; Mani, D.; Telang, R. The impact of ride-hailing services on congestion: Evidence from indian cities. M&SOM-Manuf. Serv. Oper. Manag. 2023, 25, 862–883. [Google Scholar]
- Guda, H.; Subramanian, U. Your uber is arriving: Managing on-demand workers through surge pricing, forecast communication, and worker incentives. Manag. Sci. 2019, 65, 1995–2014. [Google Scholar] [CrossRef]
- Afèche, P.; Liu, Z.; Maglaras, C. Ride-hailing networks with strategic drivers: The impact of platform control capabilities on performance. M&SOM-Manuf. Serv. Oper. Manag. 2023, 25, 1890–1908. [Google Scholar]
- Feng, X.; Wang, M. Strategic driver’s acceptance-or-rejection behavior and cognitive hierarchy in on-demand platforms. Transp. Res. Pt. E-Logist. Transp. Rev. 2023, 176, 103175. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, S.; Luo, X.; Li, J.; Zhang, C. Optimal pricing strategy of an on-demand platform with cross-regional passengers. Omega-Int. J. Manag. Sci. 2024, 122, 102947. [Google Scholar] [CrossRef]
- Zha, L.; Yin, Y.; Xu, Z. Geometric matching and spatial pricing in ride-sourcing markets. Transp. Res. Pt. C-Emerg. Technol. 2018, 92, 58–75. [Google Scholar] [CrossRef]
- Sun, L.; Teunter, R.H.; Babai, M.Z.; Hua, G. Optimal pricing for ride-sourcing platforms. Eur. J. Oper. Res. 2019, 278, 783–795. [Google Scholar] [CrossRef]
- Özkan, E. Joint pricing and matching in ride-sharing systems. Eur. J. Oper. Res. 2020, 287, 1149–1160. [Google Scholar] [CrossRef]
- Besbes, O.; Castro, F.; Lobel, I. Surge pricing and its spatial supply response. Manag. Sci. 2021, 67, 1350–1367. [Google Scholar] [CrossRef]
- Megantara, T.R.; Supian, S.; Chaerani, D. Strategies to Reduce Ride-Hailing Fuel Consumption Caused by Pick-Up Trips: A Mathematical Model under Uncertainty. Sustainability 2022, 14, 10648. [Google Scholar] [CrossRef]
- Li, T.; Xu, M.; Sun, H.; Xiong, J.; Dou, X. Stochastic ridesharing equilibrium problem with compensation optimization. Transp. Res. Pt. E-Logist. Transp. Rev. 2023, 170, 102999. [Google Scholar] [CrossRef]
- Xu, Y.; Ling, L.; Wu, J.; Xu, S. On-demand ride-hailing platforms under green mobility: Pricing strategies and government regulation. Transp. Res. Pt. E-Logist. Transp. Rev. 2024, 189, 103650. [Google Scholar] [CrossRef]
- Taylor, T.A. On-demand service platforms. M&SOM-Manuf. Serv. Oper. Manag. 2018, 20, 704–720. [Google Scholar]
- Bai, J.; So, K.C.; Tang, C.S.; Chen, X.; Wang, H. Coordinating supply and demand on an on-demand service platform with impatient customers. M&SOM-Manuf. Serv. Oper. Manag. 2019, 21, 556–570. [Google Scholar]
- Wu, T.; Zhang, M.; Tian, X.; Wang, S.; Hua, G. Spatial differentiation and network externality in pricing mechanism of online car hailing platform. Int. J. Prod. Econ. 2020, 219, 275–283. [Google Scholar] [CrossRef]
- Dong, Z.; Leng, M. Managing on-demand ridesharing operations: Optimal pricing decisions for a ridesharing platform. Int. J. Prod. Econ. 2021, 232, 107958. [Google Scholar] [CrossRef]
- Zhong, Y.; Yang, T.; Cao, B.; Cheng, T.C.E. On-demand ride-hailing platforms in competition with the taxi industry: Pricing strategies and government supervision. Int. J. Prod. Econ. 2022, 243, 108301. [Google Scholar] [CrossRef]
- Zhao, D.; Yuan, Z.; Chen, M.; Yang, S. Differential pricing strategies of ride-sharing platforms: Choosing customers or drivers? Int. Trans. Oper. Res. 2022, 29, 1089–1131. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Li, L.; Wu, J. Bilateral pricing of ride-hailing platforms considering cross-group network effect and congestion effect. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1721–1740. [Google Scholar] [CrossRef]
- Zhao, C.L.; Sun, Y.; Wu, H.; Niu, D. Pricing model of ride-hailing platform considering rationally inattentive passengers. Transp. Lett. 2024, 1–11, in press. [Google Scholar] [CrossRef]
- Chen, Q.; Lei, Y.; Jasin, S. Real-time spatial–intertemporal pricing and relocation in a ride-hailing network: Near-optimal policies and the value of dynamic pricing. Oper. Res. 2024, 72, 2097–2118. [Google Scholar] [CrossRef]
- Bai, J.; Tang, C.S. Can two competing on-demand service platforms be profitable? Int. J. Prod. Econ. 2022, 250, 108672. [Google Scholar] [CrossRef]
- Siddiq, A.; Taylor, T.A. Ride-hailing platforms: Competition and autonomous vehicles. M&SOM-Manuf. Serv. Oper. Manag. 2022, 24, 1511–1528. [Google Scholar]
- Sun, Z.; Liu, J. Impacts of differentiated services and competition on the pricing strategies of ride-hailing platforms. Manag. Decis. Econ. 2023, 44, 3604–3624. [Google Scholar] [CrossRef]
- Cachon, G.P.; Daniels, K.M.; Lobel, R. The role of surge pricing on a service platform with self-scheduling capacity. M&SOM-Manuf. Serv. Oper. Manag. 2017, 19, 368–384. [Google Scholar]
- Chen, Y.; Hu, M. Pricing and matching with forward-looking buyers and sellers. M&SOM-Manuf. Serv. Oper. Manag. 2020, 22, 717–734. [Google Scholar]
- Hu, B.; Hu, M.; Zhu, H. Surge pricing and two-sided temporal responses in ride hailing. M&SOM-Manuf. Serv. Oper. Manag. 2022, 24, 91–109. [Google Scholar]
- Garg, N.; Nazerzadeh, H. Driver surge pricing. Manag. Sci. 2022, 68, 3219–3235. [Google Scholar] [CrossRef]
- Tripathy, M.; Bai, J.; Heese, H.S. Driver collusion in ride-hailing platforms. Decis. Sci. 2023, 54, 434–446. [Google Scholar] [CrossRef]
- Sui, Y.; Zhang, H.; Song, X.; Shao, F.; Yu, X.; Shibasaki, R.; Sun, R.; Yuan, M.; Wang, C.; Li, S.; et al. GPS data in urban online ride-hailing: A comparative analysis on fuel consumption and emissions. J. Clean Prod. 2019, 227, 495–505. [Google Scholar] [CrossRef]
- Barnes, S.J.; Guo, Y.; Borgo, R. Sharing the air: Transient impacts of ride-hailing introduction on pollution in China. Transport. Res. Part D-Transport. Environ. 2020, 86, 102434. [Google Scholar] [CrossRef]
- Naumov, S.; Keith, D. Optimizing the economic and environmental benefits of ride-hailing and pooling. Prod. Oper. Manag. 2023, 32, 904–929. [Google Scholar] [CrossRef]
- Chen, J.; Li, W.; Zhang, H.; Cai, Z.; Sui, Y.; Long, Y.; Song, X.; Shibasaki, R. GPS data in urban online ride-hailing: A simulation method to evaluate impact of user scale on emission performance of system. J. Clean Prod. 2021, 287, 125567. [Google Scholar] [CrossRef]
- Tikoudis, I.; Martinez, L.; Farrow, K.; Bouyssou, C.G.; Petrik, O.; Oueslati, W. Ridesharing services and urban transport CO2 emissions: Simulation-based evidence from 247 cities. Transport. Res. Part D-Transport. Environ. 2021, 97, 102923. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Wang, L.; Fan, F. Has ridesourcing reduced haze? An analysis using the Didi app. Environ. Sci. Pollut. Res. 2021, 28, 45571–45585. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L.; Tang, J.; Xie, B.; Ge, J. Effect of ride sharing on air quality: Evidence from Shenzhen, China. J. Appl. Econ. 2022, 25, 197–219. [Google Scholar] [CrossRef]
- Zhao, Y.; Wen, Y.; Wang, F.; Tu, W.; Zhang, S.; Wu, Y.; Hao, J. Feasibility, economic and carbon reduction benefits of ride-hailing vehicle electrification by coupling travel trajectory and charging infrastructure data. Appl. Energy 2023, 342, 121102. [Google Scholar] [CrossRef]
- Gao, W.; Zhao, C.; Zeng, Y.; Tang, J. Exploring the Spatio-Temporally Heterogeneous Impact of Traffic Network Structure on Ride-Hailing Emissions Using Shenzhen, China, as a Case Study. Sustainability 2024, 16, 4539. [Google Scholar] [CrossRef]
- Vives, X. Oligopoly Pricing; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Shin, H.; Tunca, T.I. Do firms invest in forecasting efficiently? The effect of competition on demand forecast investments and supply chain coordination. Oper. Res. 2010, 58, 1592–1610. [Google Scholar] [CrossRef]
- Eslamipoor, R. Contractual Mechanisms for Coordinating a Sustainable Supply Chain with Carbon Emission Reduction. Bus. Strateg. Environ. 2025; in press. [Google Scholar] [CrossRef]
- Cook, C.; Diamond, R.; Hall, J.V.; List, J.A.; Oyer, P. The gender earnings gap in the gig economy: Evidence from over a million rideshare drivers. Rev. Econ. Stud. 2021, 88, 2210–2238. [Google Scholar] [CrossRef]
- Tracking Your Earnings|Driver App|Uber Ghana. Available online: https://www.uber.com/gh/en/drive/basics/tracking-your-earnings/ (accessed on 10 April 2025).
- Bimpikis, K.; Candogan, O.; Saban, D. Spatial pricing in ride-sharing networks. Oper. Res. 2019, 67, 744–769. [Google Scholar] [CrossRef]
- Tirole, J. The Theory of Industrial Organization; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- DiDi Global-Financials-Corporate Report. Available online: https://ir.didiglobal.com/financials/annual-reports/default.aspx (accessed on 10 April 2025).
- Jenn, A. Emissions benefits of electric vehicles in Uber and Lyft ride-hailing services. Nat. Energy 2020, 5, 520–525. [Google Scholar] [CrossRef]
- Qiao, Q.; Zhao, F.; Liu, Z.; Hao, H.; He, X.; Przesmitzki, S.V.; Amer, A.A. Life cycle cost and GHG emission benefits of electric vehicles in China. Transport. Res. Part D-Transport. Environ. 2020, 86, 102418. [Google Scholar] [CrossRef]
- Ku, Y.; Wu, P.; Ren, Q.; Wang, Y. The sequential pricing of ride-hailing system with rental service in the context of fleet electrification. J. Syst. Sci. Syst. Eng. 2024, 33, 77–105. [Google Scholar] [CrossRef]
- Du, M.; Cheng, L.; Li, X.; Yang, J. Acceptance of electric ride-hailing under the new policy in Shenzhen, China: Influence factors from the driver’s perspective. Sust. Cities Soc. 2020, 61, 102307. [Google Scholar] [CrossRef]
- Sepehriar, A.; Eslamipoor, R. An economical single-vendor single-buyer framework for carbon emission policies. J. Bus. Econ. 2024, 94, 927–945. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Jenn, A. Evaluating the emission benefits of shared autonomous electric vehicle fleets: A case study in California. Appl. Energy 2022, 323, 119638. [Google Scholar] [CrossRef]

| Symbol | Description |
|---|---|
| The probability that riders show up in each area, and [0, 1]. | |
| The probability that drivers show up in each area, and [0, 1]. | |
| The demand–supply realization. | |
| The commission rate and [0, 1]. | |
| The service price and [0, 1]. | |
| The demanded quantity induced by the price . | |
| The supply size. | |
| The probability that realization occurs. | |
| The relocation strategy of show-up drivers in area . | |
| The relocation strategy profile of all drivers. | |
| The pollutant emission caused by a show-up driver’s relocation. | |
| The ex-post no-relocation-cost utility of a show-up driver. | |
| The ex-post relocation-cost-subtracted utility of a show-up driver in area . | |
| The ex-post total pollutant emission. | |
| The platform’s ex-post profit. | |
| Drivers’ ex-ante expected total relocation-cost-subtracted utility. | |
| The ex-ante expected total pollutant emission. | |
| The platform’s ex-ante expected profit. |
| Conditions | Realization | Show-Up Drivers’ Relocation Strategies | ||
|---|---|---|---|---|
| (i) | (i-i) | |||
| (i-ii) | ||||
| () | ||||
| (i-iii) | ||||
| () | ||||
| if and () if | ||||
| (ii) | (ii-i) | |||
| (ii-ii) | ||||
| () | ||||
| (ii-iii) | ||||
| () | ||||
| if and () if | ||||
| (iii) | (iii-i) | |||
| (iii-ii) | ||||
| () | ||||
| (iii-iii) | ||||
| () | ||||
| if and () if | ||||
| (iv) | (iv-i) | |||
| (iv-ii) | ||||
| () | ||||
| (iv-iii) | ||||
| () | ||||
| if and () if | ||||
| Conditions | Realization | Show-Up Drivers’ Relocation Strategies | ||
|---|---|---|---|---|
| (i) | (i-i) | |||
| (i-ii) | ||||
| () | ||||
| (i-iii) | ||||
| () | ||||
| if and () if | ||||
| (ii) | (ii-i) | |||
| (ii-ii) | ||||
| () | ||||
| (ii-iii) | ||||
| () | ||||
| if and () if | ||||
| (iii) | (iii-i) | |||
| (iii-ii) | ||||
| () | ||||
| (iii-iii) | ||||
| () | ||||
| if and () if | ||||
| The Relocation Cost | The Percent Change | The Percent Change | The Percent Change |
|---|---|---|---|
| The Relocation Cost | The Percent Change | The Percent Change | The Percent Change |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhang, G.; Ni, D. Drivers’ Welfare and Pollutant Emission Induced by Ride-Hailing Platforms’ Pricing Strategies. Sustainability 2025, 17, 3896. https://doi.org/10.3390/su17093896
Li J, Zhang G, Ni D. Drivers’ Welfare and Pollutant Emission Induced by Ride-Hailing Platforms’ Pricing Strategies. Sustainability. 2025; 17(9):3896. https://doi.org/10.3390/su17093896
Chicago/Turabian StyleLi, Jiayang, Guoyin Zhang, and Debing Ni. 2025. "Drivers’ Welfare and Pollutant Emission Induced by Ride-Hailing Platforms’ Pricing Strategies" Sustainability 17, no. 9: 3896. https://doi.org/10.3390/su17093896
APA StyleLi, J., Zhang, G., & Ni, D. (2025). Drivers’ Welfare and Pollutant Emission Induced by Ride-Hailing Platforms’ Pricing Strategies. Sustainability, 17(9), 3896. https://doi.org/10.3390/su17093896






