Abstract
Rapid urbanization has intensified pressure on transport infrastructures, with urban bus networks playing a crucial role in promoting sustainable mobility. However, managing operational costs while minimizing environmental impacts remains a major challenge. This study investigates the innovative “Tire-as-a-Service” (TaaS) model applied to bus fleets, incorporating regrooving and retreading techniques to improve tire durability and efficiency. The TaaS model shifts the focus from purchasing tires to a service-based approach, where users pay according to usage (i.e., kilometers driven), promoting proactive maintenance and waste reduction. Solving this problem is based on a discrete-event simulation algorithm to optimize tire inspection schedules and, consequently, minimize total costs while guaranteeing a minimum level of service and reducing environmental impact. A robustness analysis will validate the model developed, thus contributing to a more sustainable urban transport system.
1. Introduction
1.1. Urban Transports Needs for Sustainability and Profitability
Urban transport systems are at the core of modern cities, facilitating mobility while influencing economic and environmental outcomes. However, rapid urbanization has intensified issues like congestion, air pollution, and inefficiencies in energy use. This urbanization and growing population in cities have led to increased demand for efficient and sustainable urban transport systems. These challenges necessitate a dual focus on sustainability and profitability to create systems that not only minimize environmental impacts but also sustain economic growth. Traditional transport models, heavily reliant on fossil fuels, significantly contribute to greenhouse gas emissions and urban pollution. Road transport accounts for approximately 95% of CO2 emissions from the transport sector in Europe, highlighting its substantial role in greenhouse gas emissions and urban pollution [1]. In 2022, transport-related greenhouse gas emissions represented about one-quarter of the total emissions in the European Union, underlining the critical impact of fossil fuel dependence on urban pollution [2]. Furthermore, according to the World Health Organization, ambient air pollution is responsible for an estimated 4.2 million premature deaths annually, largely attributed to emissions from fossil fuel-powered vehicles [3]. As cities strive to meet climate goals and improve the quality of urban life, there is a pressing need to transition towards more sustainable transport solutions. Emerging approaches, such as the integration of shared micro-mobility, electrification of transit fleets, and optimized pricing strategies, have demonstrated potential in balancing these dual objectives [4]. In particular, business models like dynamic fleet management and renewable energy-powered transit systems have contributed to aligning urban mobility with circular economy principles [5].
The integration of public transport systems and their impact on sustainable smart cities has been extensively studied. Kraus and Proff (2021) [6] conducted a systematic review to define criteria and indicators for sustainable urban transportation. Their study highlights the need for balancing social, economic, and environmental dimensions in urban transport projects. They emphasize that well-defined sustainability metrics are essential for aligning transportation initiatives with global climate goals, such as those outlined in the Paris Agreement. Synchronization of public transport services is crucial for efficient urban mobility. A bi-objective model has been developed to maximize synchronization while minimizing operational costs in bus timetables, demonstrating the effectiveness of smart transport planning approaches [7]. Effective public transport planning is essential for reducing traffic congestion and lowering emissions, contributing to the overall sustainability of urban areas [8]. Furthermore, rational planning strategies that incorporate various modes of transport, such as metro systems and shared mobility solutions, can significantly improve urban transport efficiency and sustainability [9]. Holistic planning models for shared vehicle systems have also demonstrated improvements in fleet utilization and revenue generation [5]. Policy measures also play a critical role. The adoption of road pricing mechanisms, as modeled in recent studies, highlights the potential to align financial incentives with environmental goals, fostering sustainable urban development [10].
Recent advancements in urban transport optimization have been driven by a combination of technological and policy innovations. Shared micro-mobility solutions, for instance, are reshaping urban transport dynamics, promoting sustainability through reduced vehicular congestion and lower emissions [11]. At the same time, electrification of transport systems is gaining traction, with studies demonstrating the economic and environmental benefits of integrating electric buses and vehicles into urban fleets [12]. Mobility-as-a-Service (MaaS) is emerging as a key paradigm for integrating urban transport systems under uncertain conditions. Recent studies highlight the role of MaaS in fostering seamless mobility solutions and enhancing transportation resilience [13]. User preferences are central to the success of MaaS frameworks. A recent study investigates how preference modeling can enhance MaaS adoption through a case study, providing insights into user-centric transport solutions [14]. Recent studies have also explored the role of digitalization, including big data and artificial intelligence, which can significantly enhance the efficiency and sustainability of urban transport systems by enabling better planning and management of transport resources. Creutzig et al. found in 2019 that AI-driven approaches and shared mobility systems can significantly reduce car dependency, urban congestion, and emissions [15]. However, they also noted potential rebound effects, such as increased travel demand, which could offset environmental gains. A novel AI-based scheduling system has been proposed for public transport in smart cities, enabling more efficient and adaptive scheduling [16]. Sauvey et al. recently puclished a paper helping to model an induction motor in a spreadsheet software, thus allowing them to understand energy consumption in electric propulsion motors [17].
1.2. Bus Fleet Tire Maintenance
Bus fleets play a vital role in urban mobility, but maintaining their operational efficiency while minimizing costs and environmental impact remains a challenge. Tires, as a significant cost factor and environmental concern, require innovative life-cycle management techniques such as regrooving and retreading.
1.2.1. Current Practices and Available Data
Currently, traditional tire management practices involve frequent replacements, leading to increased operational costs and environmental burdens. In Europe, the adoption of regrooving and retreading has demonstrated significant resource savings and reduced carbon footprints in public transportation fleets [18]. The integration of automated systems for tire inspection and regrooving has further streamlined these processes, ensuring consistency and quality [19].
Research highlights the efficiency of retreading and regrooving as cost-effective solutions. A study by Bareket (2000) demonstrated that bus tires with a sound carcass could undergo multiple retreading cycles, significantly reducing operational costs [20]. Similarly, advancements in regrooving equipment have enabled precise tread restoration, extending tire lifespan without compromising safety [19]. Retreading and regrooving contribute to circular economy principles, achieving up to 60% savings in raw material consumption compared to new tires, with significant reductions in energy use and carbon emissions [21].
1.2.2. Challenges and Limitations
Despite their benefits, these techniques face challenges, including public perception and regulatory barriers. Retreaded and regrooved tires are often misperceived as less safe, despite evidence to the contrary [22]. Moreover, the effectiveness of these techniques depends on proper carcass inspection and adherence to quality standards. Bischoff and Maciejewski (2016) analyzed case studies in cities such as Lisbon and Berlin, demonstrating how car-sharing strategies could reduce the number of vehicles in urban areas by more than 90%, thereby saving space and improving environmental conditions [23].
1.2.3. Tire-as-a-Service (TaaS) as an Alternative Solution to the Traditional Model
To address these challenges, the ‘Tire-as-a-Service’ (TaaS) model has emerged as a sustainable and economically viable solution. This model shifts the traditional approach from purchasing tires to a service-based framework, where users pay according to usage, promoting proactive maintenance and waste reduction. The TaaS model leverages advanced tire technologies and digital tools to monitor tire performance, ensuring optimal usage and timely maintenance.
Regrooving and retreading are key components of this model, significantly enhancing the lifespan of bus tires and reducing the need for new tire production. Regrooving involves cutting new tread patterns into worn tires, while retreading replaces the worn tread with a new layer, with both processes contributing to material savings and lower carbon emissions, as stated by major tire manufacturing companies and specialized actors.
Recent studies have demonstrated the environmental and economic benefits of the TaaS model. For instance, Michelin’s implementation of this model has shown substantial reductions in raw material consumption and CO2 emissions, alongside cost savings for fleet operators [24]. Additionally, the European Tyre & Rubber Manufacturers’ Association discusses the benefits of the TaaS model in driving sustainable change within the tire industry, highlighting how digital tools and service-based frameworks can improve tire performance and reduce environmental impacts [25]. They found that the integration of digital technologies in tire management enhances the efficiency and effectiveness of tire maintenance practices.
A recent paper published in Autocar Professional explores the potential of retreading and regrooving to extend the usable life of tires, thereby reducing the demand for new tires and associated waste generation [26]. Another report by Market Research Intellect emphasizes that retreading reduces the number of tires ending up in landfills and requires less energy and fewer raw materials, resulting in a smaller carbon footprint [27].
Each element of a system has an influence on the global efficiency of the system. This is true not only for reliability calculation, as modeled by Schutz and Sauvey [28], but also for security and sustainability purposes. Additionally, modeling of the electric supply of the wheels’ electric drives could be of interest [29].
1.2.4. Potential of Tire Management Digitilizing in Public Transport
While various sustainable transport solutions have been explored, limited research has focused on optimizing operational models that extend the lifecycle of key transport assets such as bus tires. This study introduces a novel approach by integrating the Tire-as-a-Service (TaaS) model, which shifts from a traditional ownership-based structure to a performance-based framework, ensuring both economic viability and sustainability.
TaaS builds upon established principles of servitization in the automotive sector, where manufacturers and fleet operators prioritize usage-based models over direct ownership [30]. This concept has gained traction in various industries, including aviation and heavy machinery, demonstrating its potential for reducing costs while enhancing resource efficiency [31].
By applying the TaaS model to bus fleets, this study contributes to filling this research gap by assessing how digital monitoring, retreading, and regrooving strategies can optimize operational costs while reducing waste and carbon emissions. Unlike traditional fleet management approaches, the proposed model integrates predictive maintenance and real-time performance tracking, ensuring optimal tire usage and extending service life. The combination of IoT-enabled sensors and advanced analytics for tire wear prediction further strengthens the case for TaaS in urban mobility [32].
The concept of servitization has gained increasing attention in the automotive sector, where transitioning from product ownership to service-oriented models has proven to enhance sustainability and economic efficiency [30]. Tire-as-a-Service (TaaS) embodies this paradigm by shifting from traditional tire purchasing to a usage-based service framework. This transition enables proactive maintenance strategies, extends tire lifespans, and reduces material waste, aligning with circular economy principles.
Recent real-world implementations of predictive maintenance in urban bus fleets highlight the effectiveness of digital tools in optimizing operational efficiency. For instance, Singapore’s SBS Transit has successfully integrated predictive analytics into its fleet management, significantly reducing unexpected breakdowns and improving sustainability [33,34]. Such advancements underscore the relevance of the TaaS model as a data-driven approach to tire management.
1.3. Paper Outline
This paper addresses the dual challenge of optimizing urban transport systems to enhance sustainability while ensuring profitability of public transport companies. We propose a model of the problem of regrooving and retreading for bus tires. An optimization algorithm based on this model gives then the optimal inspection frequency to reduce environmental impacts and operational costs. The avoid–shift–improve paradigm, which has been recognized as a crucial framework for reducing transport emissions and promoting sustainable mobility [35], serves as the foundation for our approach, avoiding unnecessary tires changes, shifting to more sustainable modes of transport, and improving vehicle maintenance technologies.
2. Technologies for Bus Tire Life Extension
2.1. Tire Components
The structure of a bus tire incorporates several essential technical components designed to withstand heavy loads and intensive use conditions. Readers are invited to consult the Continental Tires website [36] foran illustration of the cross-section of a tire. In this figure, the tread pattern (number ①), the outer element in contact with the road consists of three distinct areas: the cap layer providing grip and wear resistance, the base layer protecting the internal structure, and the shoulder ensuring transition to the sidewalls. Beneath this tread, the cap ply (number ②), made of nylon cords embedded in rubber, and the belt package (number ③) provide rigidity and directional stability. The internal tire structure includes the carcass ply (number ④), which controls internal pressure and maintains the tire’s shape; the inner-liner (number ⑤), which ensures air-tightness; and the sidewalls (number ⑥), which are made of natural rubber and protect against external damage. The assembly is secured to the rim by the bead area, featuring bead reinforcement (number ⑦) made of nylon or aramid for enhanced directional stability and steering precision. This complex structure is similar for all types of tires dedicated to rolling vehicles, with the exception of handling equipment or other specific equipment. Maintenance operations, particularly tread regrooving and complete retreading, as mentioned in [37], can be performed on certain models whose tread patterns are about 1.5 times thicker than those of standard tires, which is about 10 mm.
2.2. Tire Maintenance Operations
Regrooving is the first significant intervention in a bus tire’s life-cycle. This technique involves deepening existing grooves in the tread pattern when the groove depth reaches approximately 2–3 mm, utilizing an additional layer of rubber specifically provided during manufacturing. This operation, performed with specialized tools, restores optimal groove depth, thus improving water evacuation and grip. Regrooving can extend tire life by 20 to 30% while maintaining optimal performance, directly contributing to resource conservation by reducing the need for new tire production.
When wear reaches a critical level after regrooving, retreading becomes the preferred alternative. This more complex technology involves the complete replacement of the tread pattern. The process begins with a thorough inspection of the carcass for potential structural defects. The residual tread is then removed via mechanical buffing until reaching the protective layer of the carcass. A new pre-molded tread is applied to the prepared carcass, followed by vulcanization in an autoclave to ensure optimal molecular bonding between components. Vulcanization conditions, particularly temperature and pressure, are strictly controlled to warrant retreading quality. This process consumes approximately 70% less oil and requires significantly less energy compared to manufacturing a new tire, making it an environmentally sustainable choice.
The effectiveness of these technologies depends on implementing a rigorous inspection program. Tires must be regularly checked to identify the optimal time for intervention, thus avoiding excessive wear that would compromise the possibility of regrooving or retreading. The quality of inspection directly influences the potential tire life and its ability to undergo multiple maintenance cycles, ultimately determining the ecological footprint of the tire throughout its life-cycle.
The economic and environmental benefits of these technologies are substantial. Regrooving represents a minimal investment for substantial mileage gain, while retreading allows for reuse of the carcass, whose production accounts for approximately 80% of a new tire’s energy cost. From an environmental perspective, these practices significantly reduce:
- Carbon emissions: Each retreaded tire saves approximately 68 kg of CO2 emissions compared to producing a new tire
- Raw material consumption: Retreading saves about 40 kg of rubber compounds and other raw materials per tire
- Energy usage: The retreading process requires only about 30% of the energy needed to manufacture a new tire
- Waste reduction: Each retreaded tire keeps approximately 40 kg of solid waste out of landfills
- Water consumption: The process uses significantly less water compared to new tire production, contributing to water conservation efforts
- Fuel efficiency: Regrooving a tire can save approximately 2 L of fuel per 100 km, reducing overall fuel consumption and emissions
These practices exemplify circular economy principles in action, transforming what was traditionally a linear consumption model into a circular one. By extending tire life through multiple cycles, these technologies help to address the growing challenge of tire waste management, which is particularly crucial given that end-of-life tires can take over 500 years to decompose naturally. Furthermore, reducing the demand for new rubber production helps to preserve natural rubber plantations and their ecosystems, thereby contributing to the conservation of biodiversity.
Beyond their environmental advantages, these maintenance operations also have implications for road safety and travel comfort. While regrooving and retreading do not negatively affect travel comfort, regrooving provides a tangible safety benefit by improving grip and traction by approximately 10% [37]. This enhanced performance contributes to better vehicle control, particularly in challenging road conditions.
To fully harness these advantages, the implementation of structured maintenance programs is essential. Regular inspections ensure that tires undergo regrooving and retreading at the optimal time, thereby maximizing both economic and environmental benefits. In this process, predictive maintenance approaches play a crucial role. Mathematical modeling helps to better understand the factors influencing tire life—such as usage conditions, load, pressure, temperature, and road surface—enabling precise optimization of maintenance cycles. Recent studies have also explored the use of machine learning techniques to refine decision-making by integrating environmental impact assessments [38]. While such advanced data-driven methods fall outside the scope of the present research, they represent a promising avenue for fleet managers aiming to balance operational efficiency with sustainability.
The environmental benefits of these practices are further amplified when considering the entire fleet perspective. Large-scale adoption of regrooving and retreading by bus and truck fleets can lead to substantial cumulative environmental savings, contributing significantly to transportation sector sustainability goals and reducing overall environmental impact. This systemic approach to tire maintenance and renewal, supported by advanced predictive techniques, represents a crucial step towards more sustainable transportation systems. By optimizing tire lifecycles on a larger scale, these practices contribute to a significant reduction in tire waste and resource consumption, helping to build a more circular and eco-efficient transport infrastructure.
3. Modeling and Results
3.1. Discrete-Event Simulation Methodology
The optimal management of bus tires in an urban transport context represents a complex challenge involving strategic decisions related to preventive maintenance. This optimization requires a rigorous methodological approach, where discrete-event simulation emerges as a particularly suitable tool for modeling and analyzing different maintenance strategies.
The developed model revolves around three main decision variables.
- The first decision variable concerns the periodic inspection frequency, defining the time interval between successive tire condition assessments. This variable is crucial, as it directly influences maintenance costs and the ability to detect potential problems early.
- The second variable corresponds to the safety tread depth, an intervention threshold set above the legal limit of 1.6 mm. This safety margin ensures that necessary actions are taken before the tire reaches a critical non-compliance state. At this threshold, the tire is either retreaded—provided that the maximum number of retreads has not been reached and the casing is in suitable condition—or completely replaced.
- The third decision variable is the retread success rate, which represents the probability that a tire meeting the retreading conditions is successfully retreaded. This factor is essential, as it impacts both the overall life-cycle of the tire and the cost-effectiveness of maintenance strategies.
The originality of our approach lies in the explicit integration of the inherent variability in tire wear processes. This variability, stemming from multiple factors such as road conditions, driving style, weather conditions, and tire-specific characteristics, significantly influences wear dynamics. The simulation model incorporates this variability through a stochastic approach, thus enabling the evaluation of its impact on optimal inspection strategies and the assessment of regulatory non-compliance risk.
Discrete-event simulation allows for modeling the temporal evolution of tire conditions and various maintenance interventions. Each event (inspection, regrooving, retreading, replacement) is processed sequentially, taking into account the interactions between different system components. This approach enables detailed analysis of maintenance decision consequences on overall system performance, both in economic terms and safety aspects.
The primary objective of this modeling is to determine the optimal values for inspection frequency and safety limit that minimize total maintenance costs while ensuring satisfactory service and safety levels. The consideration of variability also allows us to evaluate the robustness of the proposed strategies and identify the most resilient configurations in the face of operational uncertainties.
3.2. Role of Variability in the Simulation Model
The integration of variability in discrete event simulation plays a fundamental role in accurately representing real-world tire wear dynamics. The corresponding MATLAB R2024b code is provided in Listing A3. While deterministic models can provide baseline predictions, they fail to capture the inherent uncertainties and fluctuations present in actual operating conditions. These variations stem from multiple sources: environmental factors (temperature, road conditions, precipitation), operational parameters (driving patterns, load distribution, tire pressure), and intrinsic tire characteristics (manufacturing tolerances, material properties). By incorporating these stochastic elements, our simulation model provides a more realistic and robust framework for decision-making in tire maintenance strategies.
In the sub-figures of Figure 1, the green areas represent the results of multiple simulations (10,000 iterations for each variability) conducted with a variability of around the evolution of the nominal tread wear, depicted by the straight black line. The blue area (which includes the green area) represents a variability of , while the red area (encompassing both the green and blue areas) corresponds to a variability of .
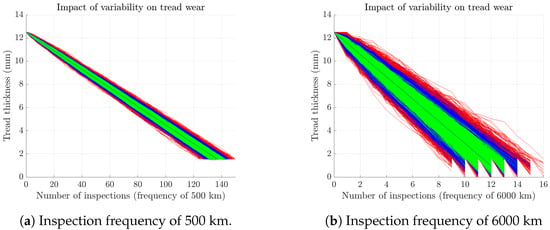
Figure 1.
Impact of variability on tread wear.
These different levels of variability highlight how real-world uncertainties can significantly impact maintenance planning and decision-making. The simulation results demonstrate that considering only the nominal case would lead to suboptimal maintenance strategies, as it would ignore the substantial probability of accelerated or delayed wear patterns. This stochastic approach enables maintenance planners to develop more resilient strategies that can accommodate the full spectrum of possible wear scenarios, ultimately leading to more effective and economically viable maintenance policies.
The main difference between Figure 1a,b lies in the inspection frequencies of 500 km and 6000 km, respectively. The 500 km frequency is based on statistical analysis and reflects a typical inspection interval observed in industry practices. With a wear rate of 0.00016 mm/km and no variability, the total tread wear of the tire—i.e., 10.9 mm (the nominal thickness of 12.5 mm minus the legally required minimum thickness of 1.6 mm)—is reached after 68,125 km (10.9/0.00016). This corresponds to approximately 136 inspections at a 500 km frequency, or 11 inspections at a 6000 km frequency.
The 6000 km inspection frequency was chosen to highlight the effects of less frequent inspections on tread wear variability. As the inspection interval increases, wear variability also increases, which may result in the tread depth exceeding the safety threshold between inspections. For a 500 km inspection frequency, the wear threshold is typically reached after 125 to 150 inspections (62,500 km to 75,000 km), whereas for a 6000 km frequency, it is reached between 9 and 15 inspections (from 54,000 km to 90,000 km).
With lower inspection frequencies, the tread wear between successive inspections can become significant. As shown in Figure 1b, wear can exceed 1.6 mm, potentially causing the tread to reach 0 mm after the tenth inspection. Conversely, very frequent inspections allow for maximum tread utilization but entail an economic trade-off due to the associated inspection costs.
Thus, it is necessary to strike a balance between maximizing tread usage and ensuring cost-effective maintenance operations through an optimal inspection frequency.
3.3. Parameters and Simulation Algorithm
The modeling of the tire maintenance system requires precise identification and characterization of parameters influencing wear dynamics and associated decisions. The tire wear rate, a central parameter of the model, is modeled as a random variable following a normal distribution, with the mean and standard deviation estimated from historical data. This approach captures the natural variability of the wear process while maintaining a tractable mathematical representation. The costs associated with different operations constitute a set of critical model parameters. These costs include periodic inspections (labor, downtime), regrooving and retreading operations, as well as potential penalties related to regulatory non-compliance. The integration of these various costs enables a comprehensive economic evaluation of maintenance strategies.
Figure 2 presents the state diagram representing the simulation algorithm based on discrete event logic. The states represent the different ‘lives’ of the tire, while the arrows indicate the transitions between these states. Dashed arrows indicate retreading operations, dotted arrows represent regrooving operations, and solid arrows denote inspections.
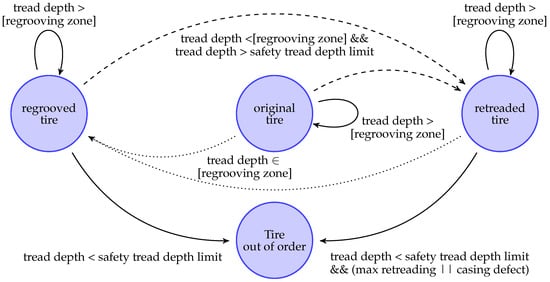
Figure 2.
State diagram representing maintenance operations for a multi-use tire.
Using this state diagram, the simulation algorithm can be developed in MATLAB R2024b, with the corresponding code provided in Listing A1. In this case, the algorithm evaluates the tire condition at each inspection. It is important to note that the tread wear accumulated since the previous inspection is not constant.
To model this variability, the funcVariability function—developed in MATLAB R2024b and detailed in Listing A3—was implemented. This function introduces stochastic wear variability based on a Gaussian distribution, as described in Section 3.2.
At each inspection, several scenarios may occur:
- If the tread depth is above the regrooving threshold, no maintenance action is required.
- If the tread depth falls within the regrooving zone, two cases are possible:
- -
- If the tire has never been regrooved, a regrooving operation is performed, extending its service life.
- -
- If the tire has already been regrooved, inspections continue until the tread depth reaches the retreading zone.
- If the tread depth falls within the retreading zone (between the safety tread depth limit and the legal safety limit), three cases are possible:
- -
- The maximum number of retread cycles has not been reached and the casing is in good condition: the tire is retreaded, effectively granting it a new service life.
- -
- The maximum number of retread cycles has not been reached, but the casing is damaged: the tire is considered to have reached the end of its service life.
- -
- The maximum number of retread cycles has been reached: the tire is also considered at the end of its service life.
The simulation continues until one of the following stop conditions is reached:
- The tread depth becomes inferior to the safety limit
- The maximum number of authorized retreadings is reached
- A casing defect is detected during the retreading process
This approach allows us to evaluate the effectiveness of different inspection and maintenance strategies throughout the tire’s useful life cycle. Through this simulation algorithm, three decision variables are used:
- The inspection frequency
- The safety tread depth
- The success rate of retreading
3.4. Input Data, Results, and Discussion
In this section, we detail the parameters used in the simulation model, including fixed parameters and decision variables, summarized in Table 1. The chosen values for these parameters reflect real-world data, based on statistical studies gathered from multiple sources, such as tire manufacturers, vendors, and garages available on the Internet. Each simulation is repeated 10,000 times to ensure robustness, allowing for reliable average estimates and trend identification with greater confidence.

Table 1.
Fixed parameters and decision variables used in the simulation.
Table 1 is structured into two main categories: fixed parameters and decision variables.
Fixed parameters define the fundamental characteristics of the system, such as tire wear behavior and dynamics, such as the initial tread depth, wear rate per kilometer, and the legal safety limit. The input parameters also include cost-related parameters such as tire prices, inspection costs, and regrooving costs, as well as legal constraints. These directly impact the economic analysis of different maintenance strategies.
Decision variables, on the other hand, represent the parameters that can be adjusted within the simulation to optimize performance. They are key factors in determining optimal inspection and maintenance strategies. For instance, the inspection frequency and safety tread depth limit influence the trade-off between tire longevity and operational safety. The retread success rate further affects the economic and environmental impact of tire reuse. These decision variables enable scenario analysis and policy evaluation.
By structuring the table in this manner, we aim to provide clarity on the distinction between input parameters and decision levers. The detailed values and ranges ensure that the reader can fully grasp the scope of the simulation model.
To establish a baseline for comparison, an initial simulation model is designed to represent the case of single-use tires, where no maintenance actions such as regrooving or retreading are considered. This simplified model focuses solely on periodic inspections until the tread depth reaches the legal safety limit. It provides a reference scenario to evaluate the potential benefits of extending tire life through additional maintenance strategies.
3.4.1. Results for Single-Use Tires
The objective of the single-use tire model is to determine the inspection frequency and the safety tread depth that minimize the cost per kilometer while ensuring compliance with legal requirements. Specifically, the goal is to maintain a maximum proportion of tires exceeding the legal wear limit, thereby balancing cost efficiency with regulatory constraints.
Table 2 and Table 3 are structured as matrices, with each cell representing the intersection of an inspection frequency and a legal tread depth. These two tables display, respectively, the percentage of tires below the legal tread thickness and the average cost per kilometer, based on 10,000 simulations. By setting a threshold of 2 % non-compliant tires, all values exceeding this threshold are highlighted with a red background, thus excluding these combinations in order to identify the one that yields the minimal cost. In this case, the best solution is achieved with an inspection frequency of 500 km and a safety threshold of 1.7 mm.

Table 2.
Percentage of tires below legal tread thickness.

Table 3.
Average cost per km.
3.4.2. Results for Multi-Use Tires
In the case of multi-life tires, the two main maintenance operations are regrooving and retreading. These interventions take place when the tread reaches the manufacturer’s recommended thresholds, which generally remain constant. The key difference lies in the probability of successful retreading, which is heavily influenced by the condition of the casing. This, in turn, depends on its design and operating conditions. The MATLAB code for simulating the multi-life tire model is provided in Listing A2.
Assuming that the decision variables d_SafetyTreadDepth and d_RetreadSuccessRate are set to 2 mm and 97%, respectively, Figure 3 illustrates the distribution of tire end-of-life causes. This figure provides a detailed breakdown of the different failure modes observed across various inspection intervals. This can result from one of three events described in Section 3.3: Casing Defect, Maximum Number of Retreads, or Wear Beyond the Legal Limit.
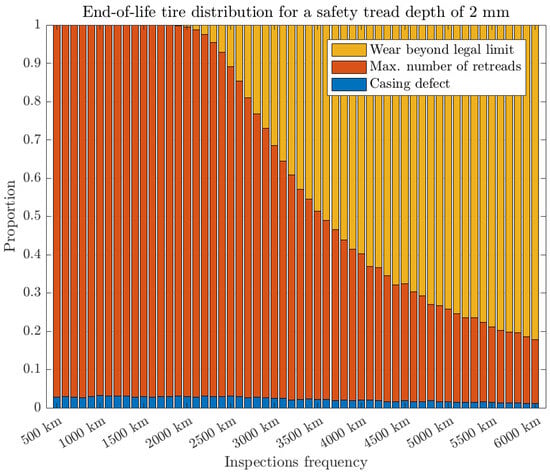
Figure 3.
End-of-life tire distribution by cause: wear limit, max retreads, casing defect.
When inspection intervals are relatively short, only two stopping criteria emerge: the maximum number of retreads and, consequently, carcass anomalies. The occurrence of these anomalies is directly correlated with the number of retreads through the decision variable d_RetreadSuccessRate, which explains the decrease in this criterion with the increase in inspection intervals.
As the inspection interval increases, a shift occurs in the distribution of failure causes. Initially dominated by casing defects and the maximum number of retreads, tire failures progressively become more influenced by wear exceeding the legal limit. For this chosen value of safety thickness, i.e., 2 mm, we note in Figure 3 the appearance of the “wear beyond legal limit” criterion from inspections carried out every 2000 km and beyond. This trend suggests that while shorter inspection intervals ensure a higher probability of maintaining retreadable casings, they may also lead to more frequent maintenance interventions, which could increase operational costs.
If a strong constraint is imposed, such as limiting the proportion of tires exceeding the legal wear limit to a maximum of x%, an upper bound on the inspection frequency can be established as a function of the decision variable d_SafetyTreadDepth. By defining this threshold, maintenance strategies can be adjusted to balance safety compliance with economic efficiency.
Figure 4 is particularly informative, as it depicts the Pareto fronts illustrating the probabilities of exceeding the legal limit as a function of inspection frequency and the specified safety tread depth limit, but for a single retread with a success rate set at 97%. The contour plot provides further insights into this relationship in the context of optimizing maintenance strategies. It enables a more nuanced understanding of the trade-offs involved in different parameter selections, aiding in the development of targeted maintenance policies. It represents the probability of exceeding the legal wear threshold, with different levels indicated by the color scale: warmer colors (red/yellow) correspond to a higher probability of exceeding the limit, while cooler colors (blue/green) indicate a lower risk.
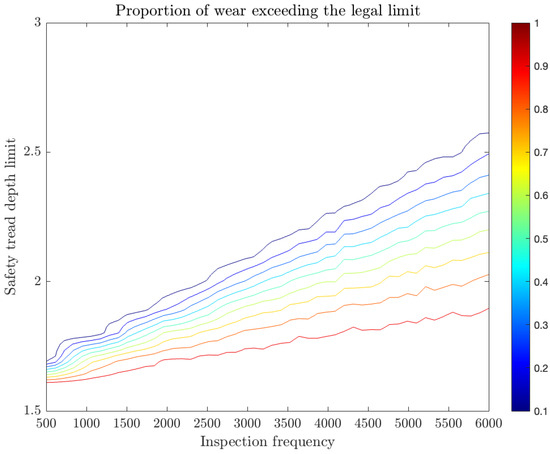
Figure 4.
Pareto fronts show the proportion of tires exceeding the legal safety limit as a function of inspection frequency and safety tread depth.
The Pareto front highlights the trade-off between inspection frequency and tread depth limit: optimizing these two parameters can help maintain compliance with safety standards while minimizing unnecessary maintenance costs. Specifically, we observe that lower safety tread depth limits require more frequent inspections to keep the probability of exceeding legal wear low, whereas higher limits allow for more extended inspection intervals at the cost of increased material consumption.
Overall, this figure supports decision-making by providing a structured approach to determining an optimal balance between inspection schedules and tread depth thresholds, ensuring both safety and cost efficiency. Such visual representations are instrumental in guiding fleet managers toward selecting the most appropriate strategies based on their operational constraints and risk tolerance.
The retreading operation allows for a multi-life tire to have its existing tread replaced with a new one, provided that the tire’s casing is suitable. The complexity of tire life optimization emerges from the intricate interactions between multiple decision variables. Key factors—including inspection frequency, safety tread depth limit, and retread success rate—do not operate in isolation but form a sophisticated, interconnected system where variations in one parameter substantially impact the overall performance and cost-effectiveness. According to various suppliers, casings generally offer a high probability (typically greater than 95 %) for successful retreading operations. However, it is important to account for the risk that a casing may no longer be suitable for retreading, further impacting the average cost per km.
In this regard, Figure 5 presents a scatterplot based on the values from Table 4, limited here to the top 1% of the best solutions, i.e., 48 solutions out of a total of 4800 combinations. Each point represents a triplet based on the three previously mentioned decision variables. The selected solutions are only those for which the tread band meets the safety threshold by at least 98%. Colder colors represent solutions with the lowest costs, reinforcing their relative economic advantage.
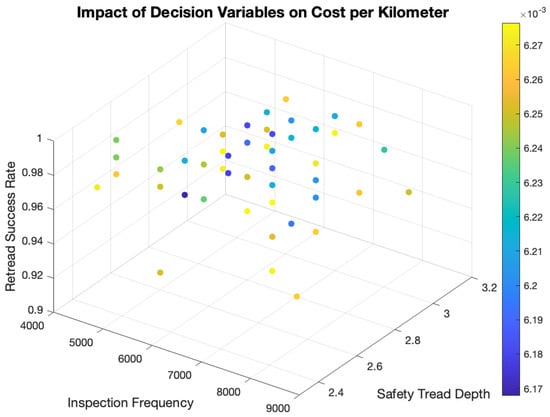
Figure 5.
Impact of inspection frequency, retread success rate, and safety tread depth on cost per kilometer.

Table 4.
The ten best solutions.
We observe that these solutions only start appearing for periodic inspections set at 4000 km, meaning that the safety threshold is at least 2 mm, as recalled by the Pareto front in Figure 4. Already, we can see that these solutions contrast with the single-lifetime tire, where the best solution was obtained for the lowest inspection frequency, namely 500 km.
A deeper analysis of Figure 5 reveals that the most cost-effective solutions tend to cluster within specific ranges of decision variables. First, higher retread success rates (above 96%) are a common feature among the best solutions, confirming the strong impact of retreading on cost reduction. Second, the inspection frequency appears to have a nonlinear effect: while too frequent inspections increase maintenance costs without significant performance gains, excessively long intervals lead to greater wear beyond the legal limit. The optimal balance seems to lie between 5500 km and 7500 km, where the lowest cost values are observed.
Regarding safety tread depth, values around 2.60 mm to 2.70 mm are particularly favorable, offering an efficient trade-off between durability and material consumption. Interestingly, solutions with deeper treads (above 2.80 mm) do not necessarily lead to better cost performance, likely due to increased material use and higher replacement frequency. Conversely, shallower treads (below 2.50 mm) tend to be associated with higher wear beyond the legal limit, emphasizing the importance of staying within a narrow optimal range.
These findings highlight the complexity of optimizing tire management under the TaaS model. Unlike the single-use tire scenario, where minimizing inspection frequency was a dominant strategy, the interplay between retread success rate, inspection intervals, and tread depth creates a multidimensional decision problem. The results suggest that small adjustments in one variable can have cascading effects on cost, safety, and sustainability, underscoring the need for a carefully balanced approach.
Table 4 presents the 10 best solutions. While the differences between these solutions remain small, the cost advantage of the TaaS model becomes particularly evident when compared to the single-use tire scenario. Specifically, the best single-use tire solution results in an average cost per kilometer of EUR 0.0103, whereas the TaaS model achieves EUR 6.1285 , leading to a cost reduction of approximately 40.5%. In addition, the results reveal several key insights into the relationship between inspection frequency, safety tread depth, retread success rate, and overall performance. First, maximizing the retread success rate significantly reduces costs, as demonstrated by the strong presence of high success rates (above 96%) in the best solutions. Additionally, inspection frequency plays a crucial role, with most optimal solutions falling between 5500 km and 7500 km, suggesting that intermediate intervals strike a balance between maintenance expenses and tire longevity.
Finally, while the total cost per kilometer varies only slightly across the best solutions (ranging from to ), the impact on safety is much more pronounced. These results suggest that minor adjustments to inspection frequency, tread depth, or retread success rate can significantly influence cost performance, but they may also have critical consequences on tire wear compliance and safety, especially when it comes to the overall durability of the tires. Moreover, the cost advantage of the TaaS model becomes particularly evident when compared to the single-use tire scenario. In this case, the best solution for the single-life tire yields an average cost per kilometer estimated at 0.0103, whereas the TaaS model achieves , representing a cost reduction of approximately 40.5%. This cost advantage not only contributes to economic efficiency but also promotes the long-term sustainability of tire maintenance strategies. Therefore, selecting the optimal maintenance strategy requires careful consideration of both economic and regulatory factors to ensure a well-balanced approach between cost efficiency and safety.
4. Conclusions and Perspectives
Urban transport systems are evolving to meet the demands of sustainability and profitability through innovative technologies and policies. The integration of shared mobility, electrification, and optimized logistics offers promising directions, on which current research is focused. Regrooving and retreading represent sustainable and economical solutions for bus tire management. By addressing challenges such as public perception and scaling adoption through policy support, these practices can contribute significantly to more sustainable urban transport systems. Future research should focus on advancing automated technologies and establishing standardized protocols to maximize their potential.
This study has explored the implementation of the ‘Tire-as-a-Service’ (TaaS) model for urban bus fleets, focusing on the integration of regrooving and retreading techniques to enhance tire durability and efficiency. The TaaS model shifts the traditional approach from purchasing tires to a service-based framework, where users pay according to usage, promoting proactive maintenance and waste reduction.
The primary purpose of this research was to address the dual challenges of managing operational costs and minimizing environmental impacts in urban bus fleets. Traditional tire management practices often lead to frequent tire replacements, resulting in high costs and significant environmental burdens due to increased raw material consumption and waste generation. The mathematical model developed in this dissertation optimizes tire inspection schedules, aiming to minimize total costs while ensuring a minimum level of service and reducing environmental impact. By adopting the TaaS model, this study aims to provide a sustainable and economically profitable solution that extends tire life and reduces the need for new tire production.
Key findings from this research include:
- The successful implementation of the TaaS model demonstrates a viable alternative to conventional tire procurement strategies, offering both economic and environmental benefits.
- The TaaS model significantly reduces operational costs and environmental impacts by extending tire life through regrooving and retreading.
- Proactive maintenance strategies, supported by digital technologies, enhance the efficiency and effectiveness of tire management practices.
- A detailed optimization framework is proposed for determining the optimal inspection frequency, tailored to the specific characteristics of the bus fleet, ensuring both cost-effectiveness and service reliability.
- The robustness analysis confirms the model’s reliability and effectiveness under various scenarios, demonstrating its practical applicability in real-world settings.
The implementation of the TaaS model offers a sustainable and economically viable solution for urban bus fleets, contributing to the broader goals of sustainable urban transport. By shifting the focus from tire ownership to a service-based approach, fleet operators can benefit from reduced costs, improved tire performance, and lower environmental impacts. This model also encourages the adoption of proactive maintenance practices, which are essential for maximizing tire lifespan and minimizing waste.
In addition to the economic and environmental advantages, this research highlights the importance of policy incentives and industry collaboration in facilitating the large-scale adoption of the TaaS model. Aligning regulatory frameworks with sustainability goals can further enhance its impact.
Future research could explore the integration of additional digital tools and technologies to further enhance the model’s capabilities and address emerging challenges in tire management. For instance, the use of advanced sensors and predictive analytics could provide more accurate and timely data on tire conditions, enabling even more effective maintenance strategies.
In conclusion, the TaaS model, supported by advanced optimization techniques and proactive maintenance strategies, represents a significant step towards achieving sustainable and efficient urban transport systems. By reducing costs and environmental impacts, this model not only benefits fleet operators but also contributes to the overall sustainability of urban environments. The findings of this study underscore the transformative potential of service-based models, demonstrating how innovative approaches can drive sustainability in traditional industries.
Author Contributions
Conceptualization, J.S. and C.S.; Methodology, J.S. and C.S.; Software, J.S. and C.S.; Validation, J.S. and C.S.; Writing—original draft, J.S. and C.S.; Writing—review & editing, J.S. and C.S. All the authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The executable files for the project are available, on demand, at the authors address. This ensures the reproducibility of the results. However, it remains the exclusive property of the authors of this paper, and commercial use is not permitted without the explicit consent of the authors. A reference to this paper will be greatly appreciated both by the authors and the editor of this original and open access research work.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. MATLAB Code for the Simulation Model
Appendix A.1
| Listing A1. MATLAB code for the “taas” function. |
  |
Appendix A.2
| Listing A2. MATLAB code for the “funcTaaSMultiUse” function. |
  |
Appendix A.3
| Listing A3. MATLAB code for the “funcVariability” function. |
  |
References
- ODYSSEE-MURE. Emissions from Transport in Europe. Available online: https://www.odyssee-mure.eu/publications/efficiency-by-sector/transport/emissions-from-transport.html (accessed on 26 March 2025).
- European-Environment-Agency. Sustainability of Europe’s Mobility Systems; European-Environment-Agency: Copenhagen, Denmark, 2024.
- World-Health-Organization. Ambient Air Pollution: A Global Assessment of Exposure and Burden of Disease; Technical Report; World Health Organization: Geneva, Switzerland, 2016.
- Fuady, S.; Pfaffenbichler, P.; Susilo, Y. Bridging the gap: Toward a holistic understanding of shared micromobility fleet development dynamics. Commun. Transp. Res. 2024, 4, 100149. [Google Scholar] [CrossRef]
- Golalikhani, M. An Integrated Decision-Support Framework Towards Incorporating Practical Pricing Decisions into Carsharing Systems. Ph.D. Thesis, Universidade do Porto, Porto, Portugal, 2024. [Google Scholar]
- Kraus, L.; Proff, H. Sustainable urban transportation criteria and measurement—A systematic literature review. Sustainability 2021, 13, 7113. [Google Scholar] [CrossRef]
- Risso, C.; Nesmachnow, S.; Rossit, D. Smart Public Transport: A Bi-Objective Model for Maximizing Synchronizations and Minimizing Costs in Bus Timetables. Appl. Sci. 2023, 13, 13032. [Google Scholar] [CrossRef]
- Rivera, R.; Amorim, M.; Reis, J. Public Transport Systems and its Impact on Sustainable Smart Cities: A Systematic Review. In Industrial Engineering and Operations Management; Tavares Thomé, A.M., Barbastefano, R.G., Scavarda, L.F., Gonçalves dos Reis, J.C., Amorim, M.P.C., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 33–47. [Google Scholar] [CrossRef]
- Baek, S.H.; Chen, Z.; Zuo, J. Rational planning strategies of urban structure, metro, and car use for sustainable cities. Environ. Dev. Sustain. 2023, 25, 6987–7010. [Google Scholar] [CrossRef]
- Wei, Q.; Gou, X.; Zhang, B. Urban Sharing Logistics Strategies against Epidemic Outbreaks: Its Feasibility and Sustainability. Sustainability 2024, 16, 7628. [Google Scholar] [CrossRef]
- Zhou, F.; Arvidsson, A.; Wu, J.; Kulcsár, B. Collaborative electric vehicle routing with meet points. Commun. Transp. Res. 2024, 4, 100135. [Google Scholar] [CrossRef]
- Assolie, A.A.; Imam, R.; Khliefat, I.; Alobeidyeen, A. Modeling of Applying Road Pricing to Airport Highway Using VISUM Software in Jordan. Sustainability 2024, 16, 8079. [Google Scholar] [CrossRef]
- Chmiel, B.; Pawlowska, B.; Szmelter-Jarosz, A. Mobility-as-a-Service as a Catalyst for Urban Transport Integration in Conditions of Uncertainty. Energies 2023, 16, 1828. [Google Scholar] [CrossRef]
- Franco, A.; Vitetta, A. Preference Model in the Context of Mobility as a Service: A Pilot Case Study. Sustainability 2023, 15, 4802. [Google Scholar] [CrossRef]
- Creutzig, F.; Franzen, M.; Moeckel, R.; Heinrichs, D.; Nagel, K.; Nieland, S.; Weisz, H. Leveraging digitalization for sustainability in urban transport. Glob. Sustain. 2019, 2, e14. [Google Scholar] [CrossRef]
- Rosca, C.M.; Stancu, A.; Neculaiu, C.F.; Gortoescu, I.A. Designing and Implementing a Public Urban Transport Scheduling System Based on Artificial Intelligence for Smart Cities. Appl. Sci. 2024, 14, 8861. [Google Scholar] [CrossRef]
- Sauvey, C.; Schutz, J.; Gillet, Y. Practical Work of Three-Phased Induction Motor Modeling in a Classical Spreadsheet Software. Appl. Sci. 2025, 15, 1015. [Google Scholar] [CrossRef]
- Van Beukering, P.; Hess, S. Improving markets for secondary materials: Case study report on rubber. Used/Post-Consum. Tyres 2004, 1, 269–296. [Google Scholar]
- Zukanović, M. Development and Analysis of Productivity, Quality, and Cost-Effectiveness of an Automated Tire Regrooving Machine. Master’s Thesis, Lappeenranta–Lahti University of Technology LUT, Lappeenranta, Finland, 2002. [Google Scholar]
- Bareket, Z.; Blower, D.; MacAdam, C. Blowout Resistant Tire Study for Commercial Highway Vehicles. Technical Report, The University of Michigan Transportation Research Institute. 2000. Available online: https://deepblue.lib.umich.edu/bitstream/handle/2027.42/1309/94093.0001.001.pdf (accessed on 26 March 2025).
- Lonca, G.; Muggéo, R.; Imbeault-Tétreault, H.; Bernard, S.; Margni, M. Does material circularity rhyme with environmental efficiency? Case studies on used tires. J. Clean. Prod. 2018, 183, 424–435. [Google Scholar] [CrossRef]
- Woodrooffe, J.; Page, O.; Blower, D.F.; Green, P.E. Commercial Medium Tire Debris Study; Technical Report; National Highway Traffic Safety Administration: Washington, DC, USA, 2008; Available online: https://deepblue.lib.umich.edu/handle/2027.42/61517 (accessed on 26 March 2025).
- Bischoff, J.; Maciejewski, M. Simulation of City-wide Replacement of Private Cars with Autonomous Taxis in Berlin. Procedia Comput. Sci. 2016, 83, 237–244. [Google Scholar] [CrossRef]
- Michelin-Group. Tire as a Service: Reinventing Our Way of Working to Meet Today’s Challenges. 2023. Available online: https://www.movinonconnect.com/en/nos-actualites/economie-fonctionnalite-tire-service-reinventer/ (accessed on 25 February 2025).
- European Tyre; Rubber Manufacturers’ Association. Tyre-As-A-Service: How the Tyre Industry Drives Sustainable Change. ETRMA News. 2023. Available online: https://www.etrma.org/wp-content/uploads/2022/12/Tyre-As-A-Service-brochure.pdf (accessed on 26 March 2025).
- Sharda, J. Reimagining Tyre Waste Management in the Circular Economy. 2024. Available online: https://www.autocarpro.in/news/-reimagining-tyre-waste-management-in-the-circular-economy-122053 (accessed on 25 February 2025).
- Market-Research-Intellect. Retread Tyres: The Future of Sustainable and Cost-Effective Driving. 2024. Available online: https://www.marketresearchintellect.com/blog/retread-tyres-the-future-of-sustainable-and-cost-effective-driving/ (accessed on 25 February 2025).
- Schutz, J.; Sauvey, C. Teaching of system reliability based on challenging practical works using a spreadsheet software. Aims Math. 2023, 8, 24764–24785. [Google Scholar] [CrossRef]
- Sauvey, C. Mathematical Modeling of Electrical Circuits and Practical Works of Increasing Difficulty with Classical Spreadsheet Software. Modelling 2022, 3, 445–463. [Google Scholar] [CrossRef]
- Baines, T.; Lightfoot, H.; Evans, S.; Neely, A.; Greenough, R.; Peppard, J.; Roy, R.; Shehab, E.; Braganza, A.; Tiwari, A.; et al. State-of-the-art in product-service systems. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2007, 221, 1543–1552. [Google Scholar] [CrossRef]
- Tukker, A. Product services for a resource-efficient and circular economy—A review. J. Clean. Prod. 2015, 97, 76–91. [Google Scholar] [CrossRef]
- Ingemarsdotter, E.; Diener, D.; Andersson, S.; Jonasson, C.; Mellquist, A.C.; Nyström, T.; Jamsin, E.; Balkenende, R. Quantifying the net environmental impact of using IoT to support circular strategies—The case of heavy-duty truck tires in sweden. Circ. Econ. Sustain. 2021, 1, 613–650. [Google Scholar] [CrossRef]
- Stratio Automotive. SBS Transit Rolls Out Predictive Maintenance for its Entire Bus Fleet Including Electric Buses. 2024. Available online: https://stratioautomotive.com/stratio-sbst-collaboration/ (accessed on 26 March 2025).
- Sustainable Bus. Singaporean SBS Transit Enters Deal with Stratio to Implement Predictive Maintenance Fleet-Wide. 2024. Available online: https://www.sustainable-bus.com/its/sbs-transit-stratio-predictive-maintenance/ (accessed on 26 March 2025).
- Turan, B.; Hemmelmayr, V.; Larsen, A.; Puchinger, J. Transition towards sustainable mobility: The role of transport optimization. Cent. Eur. J. Oper. Res. 2023, 32, 435–456. [Google Scholar] [CrossRef]
- Continental Tires. Tire Components—An Inside Look at the Components that Make Up Modern Car Tires. 2024. Available online: https://www.continental-tires.com/fr/fr/tire-knowledge/tire-components/ (accessed on 25 February 2025).
- Michelin. Retreading and Regrooving: White Paper. 2015. Available online: https://b2b.middle-east.michelin.com/tyres/regrooving (accessed on 25 February 2025).
- Karkaria, V.; Chen, J.; Siuta, C.; Lim, D.; Radulescu, R.; Chen, W. A Machine Learning–Based Tire Life Prediction Framework for Increasing Life of Commercial Vehicle Tires. J. Mech. Des. 2023, 146, 020902. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).