Abstract
This study developed an integrated approach for estimating tropical forest aboveground biomass (AGB) by combining UAV–LiDAR structural metrics and Sentinel-2B spectral data, optimized through successive projections algorithm (SPA) feature selection and random forest (RF) regression. Field surveys across three tropical forest sites in Hainan Province (49 plots) provided ground-truth AGB measurements, while UAV–LiDAR (1 m resolution) and Sentinel-2B (10 m) data were processed to extract 98 and 69 features, respectively. The results showed that LiDAR-derived elevation metrics (e.g., percentiles and kurtosis) correlated strongly with the AGB measurements (r = 0.652–0.751), outperforming Sentinel-2B vegetation indices (max r = 0.520). SPA–RF models with selected features significantly improved accuracy compared to full-feature RF, achieving R2 = 0.670 (LiDAR), 0.522 (Sentinel-2B), and 0.749 (coupled data), with the fusion model reducing errors by 46–54% in high-biomass areas. Despite Sentinel-2B’s spectral saturation limitations, its integration with LiDAR enhanced spatial heterogeneity representation, particularly in complex canopies. The 200-iteration randomized validation ensured a robust performance, with mean absolute relative errors of ≤0.071 for fused data. This study demonstrates that strategic multi-sensor fusion, coupled with SPA-optimized feature selection, significantly improves tropical AGB estimation accuracy, offering a scalable framework for carbon stock assessments in support of Reducing Emissions from Deforestation and Forest Degradation (REDD+) and climate mitigation initiatives.
1. Introduction
Quantifying carbon stocks in tropical forests is of critical importance, as these ecosystems serve as vital carbon sinks and play a key role in global carbon cycle regulation [1]. Forest carbon stocks are primarily stored in the following two main reservoirs: aboveground biomass (AGB), which includes all living vegetation above the soil surface, and belowground biomass (BGB), comprising root systems and other subterranean organic matter. While BGB quantification can be achieved through intense labor, this approach becomes impractical for large-scale assessments due to its destructive sampling requirements and substantial manpower investment [2]. In contrast, AGB estimation offers a more feasible pathway for carbon stock assessment in rainforests [3]. The carbon content of rainforests can be reliably estimated by applying species-specific or ecosystem-level carbon conversion factors to AGB measurements, with studies demonstrating consistent carbon concentrations across tropical forest types [4]. This relationship underscores why accurate AGB quantification serves as the fundamental basis for Reducing Emissions from Deforestation and Forest Degradation (REDD+) program implementation and climate change mitigation strategy development.
Traditional methods for estimating AGB rely on allometric equations that correlate tree parameters (e.g., tree size, shape, volume, height, etc.) with biomass [5,6,7]. However, developing these equations requires intensive fieldwork, including destructive sampling, which limits their scalability and regional applicability [3]. Remote sensing technology has emerged as a more economical and efficient alternative, enabling large-scale and temporally dynamic AGB monitoring [8]. Recent advances in remote sensing—particularly LiDAR and multispectral satellite data—have significantly improved spatial and temporal carbon stock assessments. Nevertheless, key challenges remain, including signal saturation in dense, high-biomass forests and the need for regionally adapted allometric models that account for structural variability across tropical forests [9]. These limitations underscore the importance of continued methodological innovation to enhance the accuracy and operational feasibility of AGB estimation, especially in support of global climate mitigation initiatives such as REDD+.
Optical high-spatial-resolution imagery, including SPOT, IKONOS, and Quick-Bird, has been extensively employed for assessing AGB in forests [10,11,12,13]. For example, Hirata et al. [10] used high-resolution satellite imaging (Quick-Bird) to estimate the AGB of forests in southern Ranong Province, Thailand, with an R2 of 0.65. Pham and Brabyn [12] integrated spectral, textural, and vegetative indices derived from SPOT 4 and 5 imagery to model and map forest biomass with an adjusted R2 of 0.73. Although studies have demonstrated a moderate estimation accuracy through various analytical approaches, this technology faces fundamental challenges in forest environments. Canopy complexity frequently leads to signal saturation, while the absence of shortwave infrared bands in most high-resolution systems impedes robust AGB estimation [14]. The recently launched Sentinel-2B optical sensor offers enhanced capabilities for estimating forest AGB through its improved spectral and spatial resolution. While studies utilizing Sentinel-2A, such as those conducted by Luo et al. [15] and Baloloy et al. [16] in the Philippines, have demonstrated its potential for regional-scale AGB assessment, the application of Sentinel-2B remains notably under-explored, particularly for species-level AGB estimation [8]. This research gap highlights the need for further investigation into the sensor’s capabilities for detailed forest AGB mapping.
Light detection and ranging (LiDAR) technology has emerged as a powerful tool for characterizing three-dimensional vegetation structure with unprecedented detail [17]. For the past two decades, airborne LiDAR systems have been extensively used to derive critical forest biophysical metrics, including diameter at breast height (DBH) [18], crown height [19], stand density [20], basal area, and timber volume [19,21]. Compared to optical remote sensing, LiDAR obtained a higher accuracy in AGB estimation due to its direct measurement of vertical forest structure [22]. Nevertheless, the widespread adoption of airborne LiDAR has been constrained by several operational limitations, including substantial acquisition costs, mission safety consideration, and stringent flight requirements [23]. Recent advancements in unmanned aerial vehicle (UAV) platforms and miniaturized LiDAR sensors have addressed these challenges, leading to the rapid proliferation of UAV–LiDAR systems for forestry inventory applications [24,25].
Recent advances in remote sensing have highlighted the synergistic benefits of multi-source data fusion for accurately estimating forest AGB. While a recent study by Vaglio Laurin et al. [26] found that hyperspectral data alone showed a limited predictive capability for AGB assessment, their integration with LiDAR-derived structural metrics has been shown significantly enhance estimation accuracy. This complementary approach capitalizes on the spectral information from hyperspectral imagery and the three-dimensional structural data from LiDAR to overcome the limitations of single-sensor systems [15]. However, given the practical challenges associated with hyperspectral data acquisition—including limited availability, high costs, and complex processing requirements—researchers have increasingly turned to more accessible alternatives. The combination of LiDAR with freely available multispectral data, particularly from Sentinel-2B, presents a viable and cost-effective solution for large-scale AGB estimation. This integrated approach leverages Sentinel-2B’s high spatial resolution and spectral bands while benefiting from LiDAR’s precise structural measurements, offering a balanced compromise between accuracy and practicality for operational forest monitoring applications.
The estimation of forest AGB using LiDAR and optical remotely sensed data has been approached using various regression techniques. Conventional methods range from linear regression and logarithmic polynomial (second-degree) regression models [16,27,28] to more sophisticated machine learning approaches, including partial least squares regression (PLSR) [22], support vector regression (SVR) [29,30,31], artificial neural network analysis (ANN) [30,31], and the random forest method (RF) [12]. Additionally, allometric regression models remain widely used for their biological interpretability [32,33]. A critical challenge in these modeling approaches is the inherent collinearity among the optical and LiDAR metrics, which can compromise model performance through overfitting and a reduced generalizability. The successive projections algorithm (SPA) offers a robust solution to this issue by systematically selecting optimal variable combinations while minimizing multicollinearity effects [25]. This feature selection capability makes the SPA particularly valuable for enhancing the accuracy and reliability of AGB estimation models. Consequently, exploring the SPA’s efficacy in metrics selection represents an important research direction for improving optical and LiDAR-based forest AGB estimation.
This study addresses the critical need for accurate forest AGB mapping by developing an integrated remote sensing approach across the following three representative tropical forest sites in Hainan Province: Diaoluoshan forest park, Qingpilin reserve, and Fengmu forest farm. The research pursues the following two primary objectives: (1) to quantitatively evaluate the synergistic potential of combining Sentinel-2B spectral data and UAV–LiDAR structural metrics for enhancing the estimation of rainforest AGB and (2) to systematically assess the performance of SPA-optimized RF modeling in feature selection and AGB prediction. The findings are expected to advance current methodologies by establishing a robust framework for multi-source remote-sensing-based AGB estimation in complex tropical ecosystems, while contributing new insights into the optimal integration of optical and LiDAR data for forest carbon stock assessment.
2. Materials and Methods
2.1. Field Sampling
Field investigations were conducted during 10–30 May 2020 across three representative tropical forest ecosystems in Hainan Province, China (Figure 1), which collectively embody the full spectrum of Hainan’s tropical rainforest characteristics. As China’s southernmost tropical region, these study areas experience a typical monsoon climate with mean annual temperature of 20.8–23.5 °C and precipitation range of 1870–2760 mm. The study areas were strategically selected to capture the complete ecological gradient of Hainan’s tropical forests, from the pristine ecosystems of Diaoluoshan forest park, with its intact vertical vegetation zonation and characteristic monsoon rain forest formations, to Qingpilin reserve’s unique old-growth stands dominated by the endemic Green husk tree (Excentrodendron hsienmu) and Fengmu forest farm’s human-modified landscapes, featuring commercial plantations alongside regenerating secondary forests dominated by Rubber forest, Betelnut forest, and Acacia mangium forest. This comprehensive representation of undisturbed, endemic, and managed tropical forest types ensures that the study encompasses the full range of structural complexity, successional stages, and management regimes characteristic of Hainan’s tropical rainforest ecosystems, thereby providing a robust basis for AGB estimation across the region’s diverse forest landscapes.
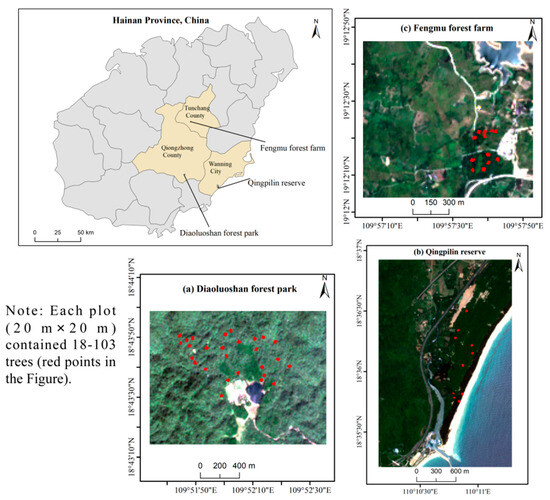
Figure 1.
Spatial distribution of 49 sampling plots in three study areas.
A total of 27, 10, and 12 plots (20 m × 20 m) were randomly set in Diaoluoshan forest park, Qingpilin reserve, and Fengmu forest farm, respectively (Figure 1). In each plot, the geographic location, diameter at breast height, and canopy height were obtained using a differential GPS, leather measuring tape, and laser altimeter, respectively. The AGB (unit: t/ha) was calculated according to the following method by Chen et al. [34]:
where i is the ith tree; n is the total number of trees in each plot; 400 is the plot area; and the value of 10 is the conversion coefficient from the unit of kg/m2 to t/ha (1 ha = 10,000 m2).
This study employed one-way analysis of variance (ANOVA) to evaluate the differences in AGB among the three sampling regions. As a robust parametric method, ANOVA partitions total variability into systematic between-group variation and random within-group variation, quantified by the between-group sum of squares (SSB) and within-group sum of squares (SSW), respectively [35]. The significance of regional differences was determined using the F-statistic, calculated as the ratio of the mean square between groups (MSB) to the mean square within groups (MSW). Statistical significance was assessed at the conventional threshold of p < 0.05, with significant results suggesting notable regional disparities in AGB [36].
2.2. UAV–LiDAR and Sentinel-2 Image Acquisition
During field surveys, UAV–LiDAR point cloud data acquisition was conducted during optimal weather conditions using a DJI M600 Pro (DJI, Shenzhen, China) drone equipped with an ARS-100 sensor (spectral band: 903 nm, GreenValley International, Ltd., Beijing, China). The system operated at a consistent flight altitude of 100 m, achieving an average point density of approximately 80 points/m2 across all three study areas. Data processing was performed using LiDAR 360 software (version 4.1, GreenValley International, Ltd., Beijing, China) through a rigorous six-step workflow, as follows: (1) outlier removal was applied to reduce noise influence in subsequent analyses by analyzing the distribution of average distances between each point and its k nearest neighbors (default k = 10–20 within a search radius of 0.5 m) and removing points that deviated beyond the standard deviation range; (2) point cloud classification separated ground from non-ground returns using an improved progressive TIN (triangulation irregular network) densification filtering algorithm; (3) this classification enabled the generation of essential surface models, a digital elevation model (DEM), a digital surface model (DSM), and a canopy height model (CHM); (4) CHM segmentation isolated individual tree crowns, extracting precise structural metrics including tree height and crown diameter; (5) point cloud normalization relative to the DEM ensured accurate vertical referencing; and (6) the normalized data generated 98 comprehensive metrics (56 elevation and 42 intensity features) at a 1 m spatial resolution, providing a robust foundation for AGB estimation modeling.
We acquired Sentinel-2B (MSI) Level-1C products covering the three study areas, obtained on 7 May 2020 through the USGS EarthExplorer platform (https://earthexplorer.usgs.gov/, accessed on 19 February 2025). The initial preprocessing phase employed the Sen2cor v2.8 atmospheric correction processor (https://step.esa.int/main/snap-supported-plugins/sen2cor/, accessed on 19 February 2025) to perform radiometric calibration and atmospheric correction and convert the Level-1C top-of-atmosphere reflectance data into Level-2A bottom-of-atmosphere surface reflectance products. Subsequently, we performed spatial resolution enhancement using the software SNAP 8.0 (https://step.esa.int/main/download/, accessed on 19 February 2025) and plug-in Sen2Res (https://step.esa.int/main/snap-supported-plugins/sen2res/, accessed on 19 February 2025), which harmonized all 12 spectral bands to a consistent 10 m resolution while preserving radiometric fidelity. The enhanced dataset maintained the original spectral characteristic by band-to-band registration, minimizing resampling artifacts [37]. The three Sentinel-2 images were subjected to geometric correction based on the high-accuracy LiDAR-derived CHM image as reference data, and the co-registration achieved sub-pixel accuracy with registration errors of less than 0.5 pixels.
2.3. UAV–LiDAR and Sentinel-2 Image-Derived Feature Selection Using SPA
The derived LiDAR metrics comprised the following two distinct categories of features for forest characterization: elevation-based structural parameters and intensity-based return signal features. A total of 98 metrics were extracted from the normalized point cloud data, consisting of 56 elevation statistics capturing vertical structural distribution and 42 intensity features analyzing the return signal intensity of the vegetation surface. These metrics were computed following standardized protocols for terrestrial LiDAR analysis. The complete mathematical definitions and computational formulas for all metrics are systematically presented in Table 1. The parallel derivation of elevation and intensity metrics enabled a synergistic analysis of both structural and spectral forest properties, providing a robust basis for AGB estimation. The Sentinel-2 imagery was processed in ENVI 5.6 using the Spectral Indices Batch tool (https://envi.geoscene.cn/appstore/, accessed on 19 February 2025) to generate 57 vegetation indices (VIs). A comprehensive list of these VIs, along with their corresponding equations and descriptions, is provided in Table 2.

Table 1.
LiDAR-derived feature metrics and their mathematical formulations.

Table 2.
The descriptions and mathematical formulas of the vegetation indices (VIs).
Due to the high dimensionality of the features derived from UAV–LiDAR and Sentinel-2 imagery, we used the SPA to select the most important features for accurate AGB estimation. The SPA is an efficient feature selection method widely used in chemometrics, spectroscopy, and remote sensing applications, owing to its computational efficiency, simplicity, and ability to produce robust results [38,39]. The algorithm operates by iterating with a single feature and selecting new features through projection operators in vector space until reaching a predefined number of features [38,39].
The SPA was implemented using a SPA_GUI tool (https://eigenvector.com/software/pls-toolbox/, accessed on 19 February 2025), with the dataset partitioned into training and test subsets. Notably, when randomly splitting a dataset multiple times, the SPA tends to select different combinations of important features. To ensure robust and reliable feature selection for AGB estimation, we performed the SPA procedure 200 times in Matlab 2019 using the following protocol:
- (1)
- For the 98 UAV LiDAR-derived features, 69 Sentinel-2 image-derived features (12 bands and 57 VIs), and their coupled data (167 features), the 49 sample plots were randomly divided into training (70%) and test (30%) subsets through 200 stratified sampling iterations. Each training subset maintained a consistent distribution, containing data from 19 plots in Diaoluoshan forest park, 7 plots in Qingpilin reserve, and 8 plots in Fengmu forest farm.
- (2)
- The SPA was executed for each of the 200 training and test subset pairs, resulting in 200 distinct sets of selected features.
- (3)
- We subsequently analyzed the frequency of feature selection across all iterations. Features with higher selection frequencies were considered as more sensitive and reliable for accurate AGB estimation.
2.4. RF Model Development and Evaluation
To determine how many features improved the model performance, we conducted a random forest (RF) regression with 200 repeated operations. RF regression is an ensemble learning method that operates by constructing multiple decision trees during training and outputting the mean prediction for the regression of individual trees [40]. The RF algorithm utilizes the following two key techniques to enhance model performance: bagging (bootstrap aggregating) and random feature selection. In the bagging process, each decision tree is trained on a different bootstrap sample of the original dataset, which helps to reduce variance and improve generalization. The random feature selection mechanism further decorrelates the trees by limiting each split to a random subset of features, typically the square root of the total number of features for classification problems or one-third of the features for regression problems [41]. This dual randomization approach enables RF to demonstrate a better performance than other multivariate regression methods, particularly in handling high-dimensional data with complex feature interactions. Our comprehensive procedure for selecting the optimal combination of sensitive features consisted of the following three main steps:
- (1)
- The features were first ranked based on their selection frequency in the SPA from highest to lowest. The regression model then sequentially selected the top k features (k = 1, 2, 3, …, n, where n is the total number of features selected by the SPA across the 200 iterations) as the new independent variables, resulting in n combinations of independent variables. This step-wise approach allowed us to systematically evaluate how incremental additions of features affected the model performance.
- (2)
- For each combination of independent variables, we paired the selected features with the AGB measurements from the 49 sampling plots. Each dataset was randomly divided into training (70%) and testing (30%) subsets, repeating this partitioning 200 times following the methodology described in Section 2.3. The RF models were trained with 500 trees, as this number typically ensures prediction error stabilization while maintaining computational efficiency.
- (3)
- An RF model was established and cross-validated with a training subset in Matlab 2019 using the following specifications: a minimum leaf size of 5 observations to prevent overfitting and an unlimited tree depth to ensure complete node purity. Each model was independently validated with the corresponding test set. The determination coefficient of cross-validation and independent validation (R2CV and R2Val) and residual prediction deviation (RPD) values were calculated to evaluate the performance of each model. Hence, a total of 200 R2CV, R2Val, and RPD values were generated for each combination of independent variables.
By a comparative analysis of validation performance (mean R2Val) across all n feature combinations, the top k features that produced the highest mean R2Val were considered as the features most sensitive to AGB estimation.
3. Results
3.1. Statistics of Aboveground Biomass
The DBH of the trees across the three sites exhibited distinct size distributions, as follows: Diaoluoshan forest park (range 3.0 to 89.8 cm; mean: 15.60 cm), Qingpilin reserve (range 5.0 to 77 cm; mean: 14.99 cm), and Fengmu forest farm (range 5.0 to 88.6; mean: 17.71 cm). Similarly, tree height varied significantly among sites, with Diaoluoshan (1.01–25.40 m; mean: 11.99 m), Qingpilin (1.14–19.36 m; mean: 7.93 m), and Fengmu (1.29–29.23 m; mean: 12.91 m) displaying contrasting vertical structures. Crown diameter also differed regionally, averaging 4.250 m (range: 1.129–43.364 m) in Diaoluoshan; 8.366 m (range: 1.128–37.864 m) in Qingpilin reserve; and 6.583 m (range: 1.420–30.024 m) in Fengmu (Figure 2).
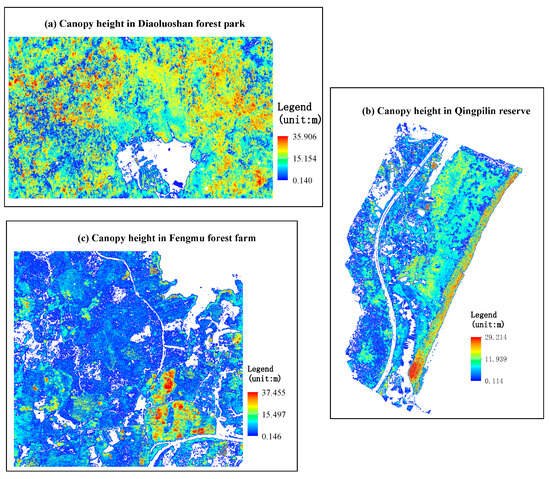
Figure 2.
Canopy height model (CHM, spatial resolution: 1 m) derived from UAV–LiDAR data of the three study areas. The CHM image was clipped by the polygon derived from the merge of single tree polygons, which could be generated by CHM segmentation.
Statistical descriptions of the AGB in the three sampling sites are displayed in Table 3. Overall, the combined dataset (n = 49 plots) revealed an average AGB of 141.372 t/ha across all sites, with values ranging from 89.162 to 185.878 t/ha and a moderate variability (CV = 17.30%). The AGB across the three study sites showed notable variations, with Fengmu forest farm exhibiting both the highest mean (153.010 t/ha) and maximum (185.878 t/ha) values, along with the greatest variability (CV = 23.94%). Diaoluoshan forest park demonstrated more consistent AGB levels (mean = 144.135 t/ha, CV = 9.91%), while Qingpilin reserve had the lowest mean biomass (119.946 t/ha) among the protected areas. The results of the ANOVA showed that there were significant AGB differences among the three study areas (F = 4.555, p = 0.016). Among the three areas (Table 1), the plots in Fengmu forest farm had the highest mean AGB (153.010 t/ha) and CV value (23.94%), suggesting that the biomass of this area had larger intraspecific variation. The plots in Diaoluoshan forest park had the lowest CV value (9.91%).

Table 3.
Statistics of aboveground biomass of 49 plots (20 m × 20 m).
3.2. Relationship Between UAV–LiDAR/Sentinel-2B Image-Derived Features and Aboveground Biomass
The UAV–LiDAR-derived features demonstrated significantly stronger absolute correlations with AGB compared to the Sentinel-2B image-derived features, with absolute correlation coefficients of 0.496 and 0.285, respectively (Figure 3).
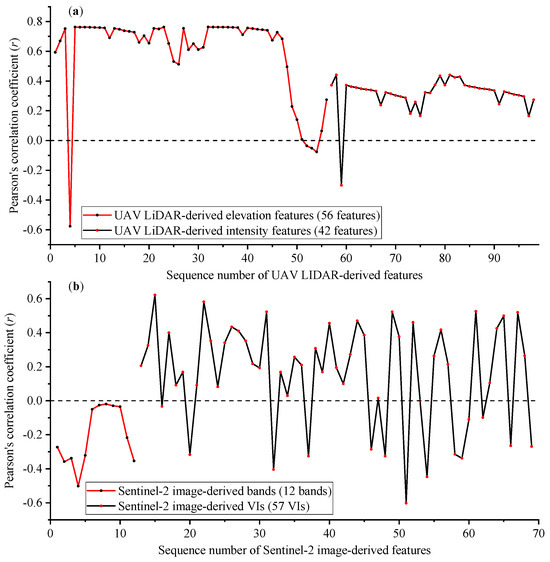
Figure 3.
(a) Pearson’s correlation coefficient of aboveground biomass (49 plots) against 98 UAV–LiDAR-derived features and (b) 69 Sentinel-2B image-derived features.
Analysis of the UAV–LiDAR data revealed distinct performance differences between feature types. Elevation features showed a markedly higher correlation with AGB (mean absolute correlation coefficient |r| = 0.621) than intensity features (mean |r| = 0.328). Among these features, 31 elevation features exhibited a relatively high correlation with AGB (r > 0.7, p < 0.01). The feature ID-32 of elev_AIH_x showed the strongest biomass relationship (r = 0.763, p < 0.01). In contrast, all 42 intensity features displayed relatively weak correlations (r < 0.5) with AGB.
Analysis of the Sentinel-2B imagery revealed consistently weak negative correlations between all 12 spectral bands and AGB (|r| < 0.5). The mean absolute correlation coefficient for spectral bands (0.210) was significantly lower than that of the 57 vegetation indices (0.301). Among the 12 spectral bands, Band 4 (Red, 650–680 nm) showed the strongest negative correlation with AGB (r = −0.499, p < 0.01). In contrast, several bands demonstrated negligible correlations, as follows: Band 6 (Red Edge2, 733–748 nm), Band 7 (Red Edge3 band, 773–793 nm), Band 8 (NIR, 785–900 nm), Band 9 (NIR2, 858–880 nm), and Band 10 (Water Vapor, 935–955 nm), which displayed almost no correlation with AGB. Among all vegetation indices, VI_3 of the Atmospherically Resistant Vegetation Index (ARVI) demonstrated the maximum positive correlation with AGB (r = 0.614, p < 0.01), while VI_39 of the Plant Senescence Reflectance Index (PSRI) showed the strongest negative correlation (r = −0.596, p < 0.01).
3.3. Sensitive Features for Aboveground Biomass Estimation
With the UAV–LiDAR data, the combination of five elevation features (elev_median_z, elev_kurtosis, elev_AIH-IQ, density_metrics [1], and density_metrics [9]) and one intensity feature (int_variance) exhibited the best model performance compared to all other combinations (Figure 4a; Table 1). The SPA selected a total of 54 features, among which intensity features constituted a minority (14 features, 25.9%) and appeared with a relatively low selection frequency. The six most frequently selected features had statistically significant correlations (p < 0.01) with AGB, with correlation coefficients ordered by strength of density_metrics [1] (elevation_47: r = 0.684), elev_median_z (elevation_20: r = 0.655), elev_kurtosis (elevation_24: r = 0.652), elev_AIH-IQ (elevation_30: r = 0.612), int_variance (intensity_1: r = 0.372), and density_metrics [9] (elevation_56: r = 0.274), respectively (Figure 3a).
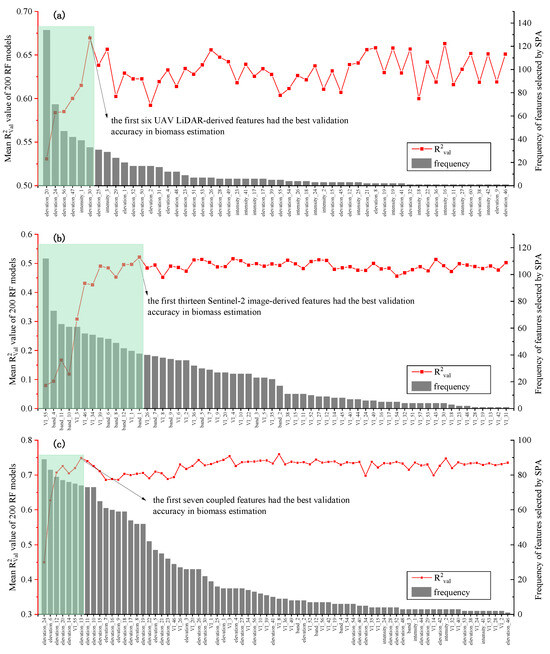
Figure 4.
The mean R2Val value of 200 random forest models in AGB estimation using the first n features, n = 1, 2, 3, …) derived from (a) UAV–LiDAR, (b) Sentinel-2B imagery, and (c) their coupled data. The features were selected using the SPA method 200 times, hence the highest selection frequency of the features was no more than 200.
With the Sentinel-2B imagery, the optimal feature combination for AGB estimation consisted of the first 13 features—including 6 VIs (Atmospherically Resistant VI, Normalized Difference Built-Up Index, Plant Senescence Reflectance Index, Structure Insensitive Pigment Index, and WorldView Improved VI) and 7 bands (Band 1, 4, 6, 8, 10, 11, and 12)—which outperformed all other feature combinations in model accuracy (Figure 4b; Table 2). Among these features, Worldview Improved VI (VI_55) and Band 4 emerged as the most frequently selected features, exhibiting statistically significant correlations with AGB (r = 0.520 and r = −0.499, respectively; Figure 3b).
Using the coupled data, the first seven most influential features (selection frequency of >70) for AGB estimation included six elevation features (elev_percentile_5, elev_percentile_50, elev_percentile_60, elev_percentile_70, elev_median_z, and elev_kurtosis) derived from UAV–LiDAR and one VI (Worldview Improved VI) obtained from Sentinel-2B (Figure 4c; Table 1 and Table 2). The most frequently selected features demonstrated statistically significant correlations with AGB (Figure 3a,b), with correlation coefficients ranked as follows: elev_percentile_5 (elevation_5: r = 0.743), elev_percentile_50 (elevation_12: r = 0.697), elev_percentile_60 (elevation_13: r = 0.751), elev_percentile_70 (elevation_14: r = 0.739), elev_median_z (elevation_20: r = 0.655), and elev_kurtosis (elevation_24: r = 0.652).
3.4. Model Performance for Aboveground Biomass Estimation
SPA–RF models employing selected features showed a superior performance in AGB estimation compared to RF models using all features (Table 4). For UAV–LiDAR data, the 6-feature SPA–RF model demonstrated a superior accuracy (mean R2CV = 0.628 and R2Val = 0.670) and stability (lower SD values: R2CV SD = 0.149 and R2Val SD = 0.230) compared to the full 98-feature RF model (mean R2CV = 0.585 and R2Val = 0.617). The RPD values further supported this trend (SPA–RF: 1.752 vs. RF: 1.701), indicating a better predictive capability with feature selection. Similar improvements were observed with the 13-feature SPA–RF model using Sentineal-2B imagery, which achieved higher mean R2 values (R2CV = 0.466 and R2Val = 0.522) and a lower variability (R2CV SD = 0.128 and R2Val SD = 0.174) than the 69-feature RF model (R2CV = 0.439 and R2Val = 0.507). The RPD metric (SPA–RF: 1.416 vs. RF: 1.376) also reflected an enhanced performance, though both configurations exhibited the weakest results among all datasets.

Table 4.
Model performance of aboveground biomass estimation with selected and all features.
Figure 5 presents the measured versus predicted AGB relationships for the SPA–RF (left panels) and full-RF (right panels) models employing the following: (a) UAV–LiDAR, (b) Sentinel-2B, and (c) combined features. Most data points clustered closely around the 1:1 reference line, demonstrating a good agreement between the predicted and observed values. While both the SPA and full models exhibited similar distribution patterns in scatter plots, the SPA model achieved a comparable predictive performance using significantly fewer input features for modeling.
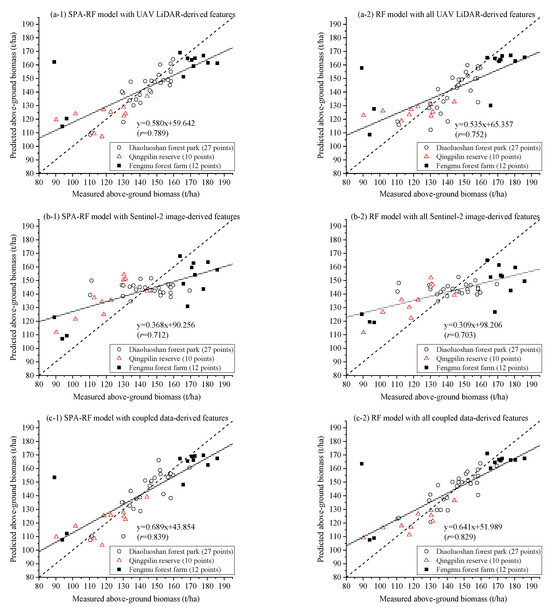
Figure 5.
Scatter plots of measured versus predicted aboveground biomass with (a) UAV–LiDAR; (b) Sentinel-2B imagery; and (c) their coupled data-derived features. Each predicted value was the average of aboveground biomass derived from 200 SPA–RF.
The SPA–RF model incorporating seven selected features from the coupled UAV–LiDAR and Sentinel-2B dataset demonstrated the highest stability, with the lowest standard deviation (SD) value for both the cross-validated and independent validation R2 values R2CV and R2Val (SD = 0.095 and 0.154, respectively). This consistency across 200 randomized iterations underscores the model’s reliability in AGB estimation. Further validation was provided by the strong agreement between the measured and predicted AGB, as evidenced by the scatter plot (Figure 5(c-1)), which yielded a high correlation coefficient (r = 0.839, p < 0.01). The near-ideal slope and minimal intercept of the regression line further confirm the SPA–RF model’s robustness. Additionally, this configuration achieved the lowest mean absolute relative error (0.071) among all tested models (Table 3), solidifying its superior predictive accuracy across all study plots.
Comprehensive evaluation demonstrated that the integrated UAV–LiDAR and Sentinel-2B model (R2Val = 0.749 ± 0.154 and RPD = 2.101 ± 0.661) achieved a significantly higher accuracy than models using either UAV–LiDAR (R2Va = 0.670 ± 0.230 and RPD = 1.752 ± 0.432) or Sentinel-2B (R2Val = 0.522 ± 0.174 and RPD = 1.416 ± 0.214) alone. Notably, the full-variable RF model incorporating all 69 Sentinel-2B features showed the weakest performance (R2Val = 0.507 ± 0.209 and RPD = 1.376 ± 0.228), with its predictive capability being markedly inferior to all other model configurations.
The AGB estimation results showed distinct variations, with Fengmu forest farm exhibiting significant overestimation (mean absolute relative error, MARE > 0.70) when using either UAV–LiDAR alone or the coupled dataset (Table 5). The points in Diaoluoshan park were more accurately estimated than those in Qingilin reserve and Fengmu forest farm. With UAV–LiDAR and Sentinel-2B imagery, the SPA–RF model provided less accurate results in Qingpilin reserve than it did in the other two areas. The evaluation revealed distinct spatial patterns in estimation accuracy across the study areas, with Fengmu forest farm showing systematic overestimation (MARE: 0.095–0.171 across models) and Diaoluoshan forest park demonstrating the highest accuracy, particularly for UAV–LiDAR SPA–RF (MARE = 0.042). Qingpilin reserve exhibited the largest performance variations, where the UAV–LiDAR SPA–RF (MARE = 0.158) underperformed compared to its RF counterpart (MARE = 0.099), while the coupled-data SPA–RF achieved a 46% error reduction (MARE = 0.079) compared to Sentinel-2B-only models. The coupled-data SPA–RF showed the best overall performance (MARE = 0.071), though its effectiveness varied spatially—improving its accuracy in Diaoluoshan (ΔMARE = −0.007) but degrading it in Qingpilin (ΔMARE = +0.059) for UAV–LiDAR. The Sentinel-2B RF models consistently showed the highest errors in Fengmu (MARE = 0.171), confirming their overall weakest performance, while data fusion proved particularly valuable in challenging environments like Qingpilin, where it reduced errors by 54% compared to the UAV–LiDAR SPA–RF.

Table 5.
Mean absolute relative error of three study areas based on 200 SPA–RF or RF models.
Although UAV–LiDAR data provided a higher spatial resolution (1 m) than Sentinel-2B imagery (10 m), the SPA–RF model using LiDAR-derived features alone showed a limited capability to accurately estimate high AGB values (Figure 6). By contrast, the SPA–RF model incorporating fused LiDAR and Sentinel-2B data demonstrated a superior performance across the full AGB spectrum, effectively characterizing both low- and high-biomass regions. Comparative analysis of the AGB mapping results across the three study regions revealed that the integrated data approach better captured the spatial heterogeneity in biomass distribution, as evidenced by its wider dynamic range of AGB values and improved representation of fine-scale spatial patterns compared to single-source datasets. These findings highlight the synergistic value of combining structural (LiDAR) and spectral (Sentinel-2B) data for comprehensive AGB assessment, particularly in areas with complex biomass gradients.
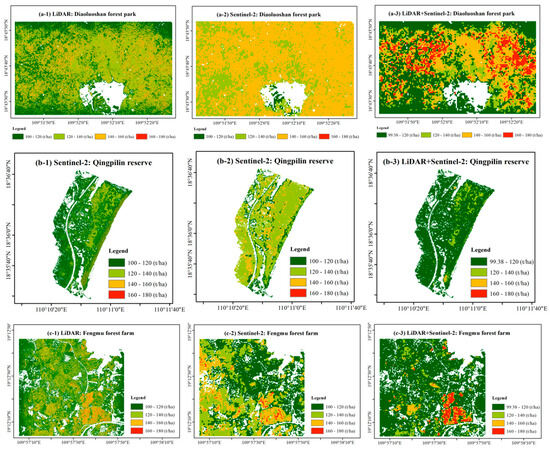
Figure 6.
Spatial distribution of AGB in (a) Diaoluoshan forest park; (b) Qingpilin reserve; and (c) Fengmu forest farm using the SPA–RF model. Each pixel value is the average of the aboveground biomass derived from 200 SPA–RF model.
4. Discussion
The accuracy of LiDAR-based AGB estimation exhibits considerable variability across different forest ecosystems, as evidenced by comparative studies. While Feliciano et al. [3] demonstrated successful applications of airborne LiDAR in the western Everglades National Park, subsequent research has revealed substantial performance differences tied to environmental conditions and methodological approaches. Notably, Gobakken et al. [42] achieved an exceptional forest AGB estimation accuracy with an R2 of 0.95 and RMSE of 19.02 Mg/ha in Scandinavian boreal forests, whereas Hansen et al. [43] reported more moderate results (R2 = 0.71 and RMSE = 158.02 Mg/ha) in temperate forest and Luo et al. [15] obtained a strong performance (R2 = 0.874 and RMSE = 16.545 Mg/ha) in subtropical environments. Our study’s UAV–LiDAR results (R2 = 0.628) reflect these documented variations while accounting for the unique challenges of tropical forest ecosystems. The observed differences stem from multiple interacting factors, including forest structural complexity, where our study area’s multi-layered canopies and high species diversity present greater challenges than the simpler boreal systems studied by Gobakken et al. [42].
Additionally, the typically higher biomass levels in tropical forests often approach or exceed the saturation points for LiDAR metrics, limiting their sensitivity in upper biomass ranges. Methodological variations in regression approaches and sampling designs further contribute to accuracy differences across studies. Importantly, our results align with the expected performance thresholds for tropical forest applications, where structural complexity and biomass density inherently constrain estimation precision. The moderate accuracy achieved represents a meaningful ecological signal given these challenges, rather than indicating methodological limitations. This performance context underscores the importance of ecosystem-specific calibration when applying LiDAR for tropical forest AGB estimation.
The performance of optical remote sensing for forest AGB estimation varies significantly depending on sensor characteristics and forest conditions, as evidenced by comparative studies. While Castillo et al. [30] achieved a strong correlation (r = 0.75) using Sentinel-2A in Philippines forests, our Sentinel-2B results (R2 = 0.522) reflect the additional challenges posed by mature tropical ecosystems, where high biomass levels frequently lead to spectral saturation. This difference likely stems from their study area containing more secondary growth forests with linear spectral–biomass relationships compared to our focus on dense, high-biomass stands that push optical sensors to their detection limits. Notably, the marginal improvements shown by hyperspectral systems (r = 0.60 and 0.738 by Laurin et al. [26] and Luo et al. [15], respectively) validate our finding that Sentinel-2B’s multispectral bands provide sufficient spectral information while offering substantial operational advantages. The limited gains from hyperspectral data, despite their narrower bands, underscore the fundamental constraints in the optical remote sensing of tropical forests, where canopy complexity and biomass saturation diminish the value of additional spectral resolution. Our results align with the known limitations of optical systems in high-biomass environments, where several factors converge to a moderate estimation accuracy, as follows: heterogeneous canopy structures create complex spectral mixtures, atmospheric interference introduces noise, and persistent cloud cover limits ideal image acquisition. The achieved accuracy represents a realistic expectation given these challenges, particularly when compared to studies in less complex forest systems.
A comparative analysis between and optical remote sensing for forest AGB estimation reveals consistent patterns across multiple studies, including our current research. Our findings demonstrate that Sentinel-2B-derived metrics yield a lower AGB estimation accuracy compared to LiDAR data, results that align with previous work by Luo et al. [15] showing that LiDAR data had a higher prediction ability than hyperspectral images. This performance gap is further corroborated by Laurin et al. [26], who reported a substantially higher estimation accuracy for LiDAR (R2 = 0.64) compared to hyperspectral data alone (R2 = 0.36). These observed differences stem from fundamental limitations in the optical remote sensing of forest AGB. As demonstrated by Mutanga and Skidmore [44], VIs derived from spectral data exhibit asympotic saturation behavior beyond certain biomass thresholds, a phenomenon particularly pronounced in the dense canopies typical of mature forests [45]. This saturation effect explains why our Sentinel-2B results, while scientifically valid for lower biomass ranges, show a reduced sensitivity in high-biomass conditions compared to LiDAR. The three-dimensional structural information captured by LiDAR proves more robust in these scenarios, as it directly measures canopy architecture rather than relying on spectral reflectance properties that become less responsive at higher biomass levels.
This study demonstrated that integrating LiDAR- and Sentinel-2B-derived metrics could improve the estimation accuracy for forest AGB compared with either source alone. Our findings align with but also extend previous research on multi-sensor fusion for biomass estimation. Kulawardhana et al. [45] achieved a superior accuracy (R2 = 0.70) by combining LiDAR and hyperspectral data compared to individual sensors (LiDAR R2 = 0.64; hyperspectral R2 = 0.36); Luo et al. [15] found that, compared with LiDAR metrics alone, fused LiDAR and hyperspectral data improved R2 by 2.2%, and decreased RMSE by 7.9% for AGB. Our study revealed an even more substantial enhancement through LiDAR and Sentinel-2B integration. This is likely the result of LiDAR providing the three-dimensional canopy structure of a forest, while hyper- or multispectral data can provide only the spectral characteristics of the forest [15]. Other studies showed that the fusion LiDAR and hyperspectral data only marginally increased the estimation accuracy for AGB compared with using LiDAR data alone [20,46,47]. These reports demonstrate that LiDAR metrics alone can be strongly correlated with AGB, while spectral data make a small contribution to improving estimation accuracy. However, in this study, the fusion of LiDAR and Sentinel-2B metrics improved R2 by 11.79% compared with LiDAR metrics alone. The random sampling of calibration and validation datasets might reduce the credibility of the results. Therefore, as this study repeated 200 randomly separated datasets to train the regression models, the AGB inversion results can be more robust and reliable and avoid the overfitting encountered when fused LiDAR and Sentinel-2B metrics were used.
While some studies have shown only minor accuracy gains from sensor fusion, our results suggest that the integration approach and forest type significantly influence outcomes. The stronger performance improvement observed in our study may reflect the following: (1) optimized feature selection from each sensor type, (2) the particular sensitivity of Sentinel-2B bands to vegetation characteristics in our study area, and (3) more sophisticated modeling techniques that better exploit complementary information. Importantly, our repeated random sampling approach provides greater statistical confidence in these findings compared to the single-split validation methods used in some previous studies.
Our study demonstrates that the successive projections algorithm (SPA) effectively identifies the most informative metrics for accurate AGB estimation, with SPA-based RF models consistently improving prediction accuracy across all tested combinations of LiDAR and Sentinel-2B metrics. These findings corroborate and extend previous work by Shi et al. [25], confirming the SPA’s ability to enhance model performance by eliminating redundant variables while retaining biologically meaningful predictors. The robust performance of our SPA–RF approach across different sensor combinations stems from the following several key advantages: (1) effective reduction in multicollinearity among high-dimensional input features, (2) synergistic combination with RF’s inherent feature importance weighting, and (3) optimized parameterization for tropical forest applications, where canopy complexity amplifies the benefits of careful feature selection. Our results show particularly strong improvements, likely due to the comprehensive integration of structural and spectral metrics, which provides the SPA with richer feature combinations to optimize. This application of SPA feature selection prior to RF modeling offers an efficient solution to prevent overfitting while maintaining accuracy, especially valuable for AGB monitoring programs.
The selected LiDAR elevation features (percentiles, median, and kurtosis) and Worldview VI demonstrate a strong ecological rationale for AGB estimation, consistent with previous studies [9,48]. The high correlations (r = 0.652–0.751) align with findings that lower/mid-canopy metrics best predict tropical forest biomass. Elevation percentiles characterize vertical distribution, while kurtosis captures structural heterogeneity—both critical for biomass estimation [49]. The sole optical index’s inclusion, though less frequent than LiDAR metrics, reflects its known performance in high-biomass conditions, while supporting observations that structural features generally outweigh spectral data in dense canopies due to saturation effects [50].
The UAV–LiDAR data could accurately reflect information regarding the canopy structure of forests. However, because of the limitation of battery power, the UAV–LiDAR data could not cover a large spatial distribution. Our study demonstrated that the fusion of LiDAR and Sentinel-2B imagery improved the accuracy of forest AGB estimation. This approach provides a technique for integrating satellite-based LiDAR and multispectral images to map biomass over a large area. In future studies, the variation coefficient of AGB can be increased by integrating different regions and different communities, which would likely improve model accuracy.
5. Conclusions
This study presents a comprehensive approach for estimating forest AGB in tropical regions through the integration of UAV–LiDAR and Sentinel-2B data, employing the successive projections algorithm (SPA) for feature selection and random forest (RF) for regression modeling. The key findings demonstrate the following:
- (1)
- UAV–LiDAR data served as a reliable foundation for tropical forest AGB estimation, capturing crucial structural information;
- (2)
- LiDAR-derived metrics consistently outperformed Sentinel-2B data in estimation accuracy, highlighting the importance of three-dimensional canopy characterization;
- (3)
- The SPA proved highly effective in identifying optimal metric combinations by minimizing collinearity while retaining biologically meaningful predictors;
- (4)
- The sensor fusion strategy yielded superior results, with the combined LiDAR and Sentinel-2B approach outperforming either dataset used independently.
These conclusions collectively underscore the value of integrating structural and spectral remote sensing data through optimized feature selection and machine learning techniques for accurate tropical forest biomass mapping, while also confirming the particular advantages of LiDAR technology in high-biomass ecosystems, where optical data alone face saturation limitations. The methodological framework developed in this study provides an effective solution for operational AGB monitoring in tropical forests, balancing accuracy requirements with practical implementation considerations.
Author Contributions
Methodology, Z.C., T.W. and Y.C.; Validation, X.P. and X.C.; Investigation, X.P. and J.L.; Resources, X.Y.; Data curation, Y.L.; Writing—original draft, Z.C.; Writing—review & editing, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the Hainan Provincial Science and Technology Program (ZDKJ202008).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Twilley, R.; Chen, R.; Hargis, T. Carbon sinks in mangroves and their implications to carbon budget of tropical coastal ecosystems. Water Air Soil Pollut. 1992, 64, 265–288. [Google Scholar] [CrossRef]
- Mokany, K.; Raison, R.J.; Prokushkin, A.S. Critical analysis of root: Shoot ratios in terrestrial biomes. Glob. Change Biol. 2006, 1, 84–96. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D. Assessing mangrove above-ground biomass and structure using terrestrial laser scanning: A case study in the Everglades National Park. Wetlands 2014, 34, 955–968. [Google Scholar] [CrossRef]
- Locatelli, T.; Binet, T.; Kairo, J.G.; King, L.; Madden, S.; Patenaude, G.; Upton, C.; Huxham, M. Turning the tide: How blue carbon and payments for ecosystem services (pes) might help save mangrove forests. Ambio 2014, 43, 981–995. [Google Scholar] [CrossRef]
- Coronado-Molina, C.; Day, J.W.; Reyes, E.; Perez, B.C. Standing crop and abovegound biomass partitioning of a dwarf mangrove forest in Taylor River Slough, Florida. Wetl. Ecol. Manag. 2004, 3, 157–164. [Google Scholar] [CrossRef]
- Komiyama, A.; Ong, J.E.; Poungparn, S. Allometry, biomass, and productivity of mangrove forests: A review. Aquat. Bot. 2008, 89, 128–137. [Google Scholar] [CrossRef]
- Komiyama, A.; Poungparn, S.; Kato, S. Common allometric equations for estimating the tree weight of mangroves. J. Trop. Ecol. 2005, 21, 471–477. [Google Scholar] [CrossRef]
- Pham, T.D.; Yokoya, N.; Bui, D.T.; Yoshino, K.; Friess, D.A. Remote sensing approaches for monitoring mangrove species, structure, and biomass: Opportunities and challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Hirata, Y.; Tabuchi, R.; Patanaponpaiboon, P.; Poungparn, S.; Yoneda, R.; Fujioka, Y. Estimation of aboveground biomass in mangrove forests using high-resolution satellite data. J. Forest Res. 2014, 19, 34–41. [Google Scholar] [CrossRef]
- Manna, S.; Nandy, S.; Chanda, A.; Akhand, A.; Hazra, S.; Dadhwal, V.K. Estimating aboveground biomass in Avicennia marina plantation in Indian Sundarbans using high-resolution satellite data. J. Appl. Remote Sens. 2014, 8, 3700–3721. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, K.; Liu, L.; Wang, S.; Liu, H. Retrieval of Mangrove Aboveground Biomass at the Individual Species Level with WorldView-2 Images. Remote Sens. 2015, 7, 12192–12214. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation medthods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Pan, F.; Peng, D.; Zou, J.; Nie, S.; Qin, H. Fusion of airborne lidar data and hypersepctral imagery for aboveground and belowground forest biomass estimation. Ecol. Indic. 2017, 73, 378–387. [Google Scholar] [CrossRef]
- Baloloy, A.B.; Blanco, A.C.; Candido, C.G.; Agramosa, R.J.L.; Dumalag, J.B.L.C.; Dimapilis, L.L.C.; Paringit, E.C. Estimation of mangrove forest aboveground biomass using multispectral bands, vegetation indices and biophysical variabels derived from optical satellite imageries: Rapideye, planetscope and sentinel-2. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 29–36. [Google Scholar]
- Næsset, E.; Gobakken, T. Estimation of above- and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-footprint lidar estimation of sub-canopy elevation and tree height in a tropical rain forest landscape. Remote Sens. Environ. 2004, 1, 68–69. [Google Scholar] [CrossRef]
- Maltamo, M.; Peuhkurinen, J.; Malinen, J.; Vauhkonen, J.; Packalen, P.; Tokola, T. Predicting tree attributes and quality characteristics of Scots pine using airborne laser scanning data. Silva Fenn. 2009, 3, 507–521. [Google Scholar] [CrossRef]
- Latifi, H.; Fassnacht, F.; Koch, B. Forest structure modeling with combined airborne hyperspectral and LiDAR data. Remote Sens. Environ. 2012, 121, 10–25. [Google Scholar] [CrossRef]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning lidar. Photogramm. Eng. Remote Sens. 2000, 11, 1367–1372. [Google Scholar]
- de Souza Pereira, F.R.; Kampel, M.; Gomez, S.M.; Estrada, G.; Bentz, C.; Vincent, G. Reducing uncertainty in mapping of mangrove aboveground biomass using airborne discrete return lidar data. Remote Sens. 2018, 10, 637. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 6, 1519–1543. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Shi, T.Z.; Chen, Y.; Liu, H.; Wang, J.J.; Wu, G. Soil organic carbon content estimation with laboratory-based visible-near-infrared reflectance spectroscopy-Feature selection. Appl. Spectrosc. 2014, 68, 831–837. [Google Scholar] [CrossRef] [PubMed]
- Vaglio Laurin, G.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Frate, F.D.; Guerriero, L.; Pirotti, F.; Valentini, R. Above ground biomass estimation in an african tropical forest with lidar and hyperspectral data. Isprs J. Photogramm. 2014, 89, 49–58. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Simard, M. Height and biomass of mangroves in Africa from ICESat/GLAS and SRTM. Int. J. Remote Sens. 2013, 34, 668–681. [Google Scholar] [CrossRef]
- Pandey, P.C.; Anand, A.; Srivastava, P.K. Spatial distribution of mangrove forest species and biomass assessment using field inventory and earth observation hyperspectral data. Biodivers Conserv. 2019, 28, 2143–2162. [Google Scholar] [CrossRef]
- Navarro, J.A.; Algeet, N.; Fernandez-Landa, A.; Esteban, J.; Rodriguez-Noriega, P.; Guillen-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Castillo, J.A.A.; Apan, A.A.; Maraseni, T.N.; Salmo, S.G. Estimation and mapping of above-ground biomass of mangrove forests and their replacement land uses in the Philippines using sentinel imagery. ISPRS J. Photogramm. 2017, 134, 70–85. [Google Scholar] [CrossRef]
- Pham, T.D.; Yoshino, K.; Le, N.; Bui, D. Estimating aboveground biomass of a mangrove plantation on the northern coast of vietnam using machine learning techniques with an integration of alos-2 palsar-2 and sentinel-2a data. Int. J. Remote Sens. 2018, 39, 7761–7788. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Feliciano, E.A.; Lagomasino, D.; Lee, S.K.; Trettin, C. Estimating mangrove aboveground biomass from airborne LiDAR data: A case study from the Zambezi River delta. Environ. Res. Lett. 2018, 13, 25012–25023. [Google Scholar] [CrossRef]
- Fatoyinbo, T.; Simard, M.; Washington-Allen, R.A.; Shugart, H.H. Landscape-scale extent, height, biomass, and carbon estimation of Mozambique’s mangrove forests with Landsat ETM+ and Shuttle Radar Topography Mission elevation data. J. Geophys. Res. 2008, 113, G2S–G6S. [Google Scholar] [CrossRef]
- Chen, D.; Li, Y.; Luo, T.; Lin, M.; Sun, Y. Study on biomass and net primary productivity of Podocarpus imbricatus plantation in Jianfenglin, Hainan Island. For. Res. 2004, 17, 598–604. (In Chinese) [Google Scholar]
- Field, A. Discovering Statistics Using IBM SPSS Statistics; Sage Publications Limited: London, UK, 2024. [Google Scholar]
- Quinn, G.P.; Keough, M.J. Experimental Design and Data Analysis for Biologists; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Li, F.; Jupp, D.L.B.; Thankappan, M.; Lymburner, L.; Mueller, N.; Lewis, A.; Held, A. A physics-based atmospheric and BRDF correction for Landsat data. Int. J. Remote Sens. 2019, 124, 8079–8105. [Google Scholar]
- Araújo, M.C.U.D.; Saldanha, T.C.B.; Galvão, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemometr. Intell. Lab. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Wang, J.J.; Shi, T.Z.; Liu, H.; Wu, G.F. Successive projections algorithm-based three-band vegetation index for foliar phosphorus estimation. Ecol. Indic. 2016, 67, 12–20. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Wang, J.J.; Chen, Y.Y.; Chen, F.; Shi, T.Z.; Wu, G. Wavelet-based coupling of leaf and canopy reflectance spectra to improve the estimation accuracy of foliar nitrogen concentration. Agric. Forest Meteorol. 2018, 248, 306–315. [Google Scholar] [CrossRef]
- Gobakken, T.; Næsset, E.; Nelson, R.; Bollandsas, O.; Gregoire, T.; Stahl, G.; Holm, S.; Orka, H.; Astrup, R. Estimating biomass in Hedmark County, Norway using national forest inventory field plots and airborne laser scanning. Remote Sens. Environ. 2012, 123, 443–456. [Google Scholar] [CrossRef]
- Hansen, E.; Gobakken, T.; Bollandsas, O.; Zahabu, E.; Næsset, E. Modeling aboveground biomass in dense tropical submontane rainforest using airborne laser scanner data. Remote Sens. 2015, 7, 788–807. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 19, 3999–4014. [Google Scholar] [CrossRef]
- Kulawardhana, R.; Popescu, S.; Feagin, R. Fusion of lidar and multispectral data to quantify salt marsh carbon stocks. Remote Sens. Environ. 2014, 154, 345–357. [Google Scholar] [CrossRef]
- Anderson, J.E.; Plourde, L.C.; Martin, M.E.; Braswell, B.H.; Smith, M.L.; Dubayah, R.O.; Hofton, M.A.; Blair, B.J. Integrating waveform lidar with hyperspectral imagery for inventory of a northern temperate forest. Remote Sens. Environ. 2008, 112, 1856–1870. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Ewel, J.; Clark, D.B. Estimation of tropical rain forest aboveground biomass with small-footprint lidar and hypersepctral sensors. Remote Sens. Environ. 2011, 115, 2931–2942. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Boardman, J.; Green, R.O.; Kennedy-Bowdoin, T.; Eastwood, M.; Martin, R.E.; Anderson, C.; Field, C.B. Carnegie Airborne Observatory-2: Increasing science data dimensionality via high-fidelity multi-sensor fusion. Remote Sens. Environ. 2012, 115, 454–465. [Google Scholar] [CrossRef]
- Saatchi, S.; Asefi-Najafabady, S.; Malhi, Y.; Aragão, L.E.; Anderson, L.O.; Myneni, R.B.; Nemani, R. Persistent effects of a severe drought on Amazonian forest canopy. Proc. Natl. Acad. Sci. USA 2013, 110, 565–570. [Google Scholar] [CrossRef]
- Meyer, V.; Saatchi, S.S.; Chave, J.; Dalling, J.W.; Bohlman, S.; Fricker, G.A.; Robinson, C.; Neumann, M.; Hubbell, S. Detecting tropical forest biomass dynamics from repeated airborne lidar measurements. Biogeosciences 2013, 10, 5421–5438. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).