Real-Time Modeling of a Solar-Driven Power Plant with Green Hydrogen, Electricity, and Fresh Water Production: Techno-Economics and Optimization
Abstract
1. Introduction
1.1. Background
1.2. Rationale for Study
- How does the performance of the thermal storage tank vary across different months of the year, and how does this influence the overall system performance?
- How do seasonal variations affect the rates of electricity, hydrogen, and fresh water production?
- Which components of the system contribute most to exergy destruction, and how can this information guide future improvements?
- How do changes in key parameters—such as solar radiation intensity, turbine inlet temperature, and electricity allocation strategy—affect system efficiencies and product outputs?
- What are the trade-offs between cost and efficiency in the system, and how can multi-objective optimization help identify the best balance?
- Proposing an integrated energy system that utilizes solar energy and thermal storage to ensure uninterrupted generation of electricity, hydrogen, and clean water, even in the absence of sunlight.
- Examining the impact of electricity allocation strategies on system efficiency and economic feasibility by studying scenarios in which electricity is allocated for hydrogen production, fresh water generation, or direct grid sales.
- Performing extensive thermodynamic and economic evaluations via parametric studies and multi-objective optimization to determine the trade-offs between efficiency and cost.
- Conducting a real-time case study in Antalya, Turkey, to analyze system performance hourly over the course of a year, thereby offering insights into its practical application under actual operational settings.
- Employing multi-objective optimization methods to address energy, exergy, and economic factors, for achieving an ideal balance between efficiency and cost.
2. System Description
Assumptions and Input Data
- -
- The proposed system is presumed to function at steady-state conditions [4].
- -
- All turbomachinery is presumed to operate as adiabatic devices [19].
- -
- Pressure losses are assumed to be negligible throughout the system [19].
- -
- Heat exchange with the environment is disregarded for all system components, except for the solar collector and thermal storage tank, owing to its minimal impact [4].
- -
- Variations in kinetic and potential energy are considered negligible and hence are disregarded [19].
3. System Modeling and Analysis
3.1. Thermodynamic Analysis
3.1.1. RO Unit
3.1.2. Proton Exchange Membrane Electrolyzer (PEME)
3.1.3. PTSC
3.1.4. Thermal Storage Tank
3.2. Exergy Analysis
3.3. Techno-Economic Analysis
3.4. System Performance Indicators
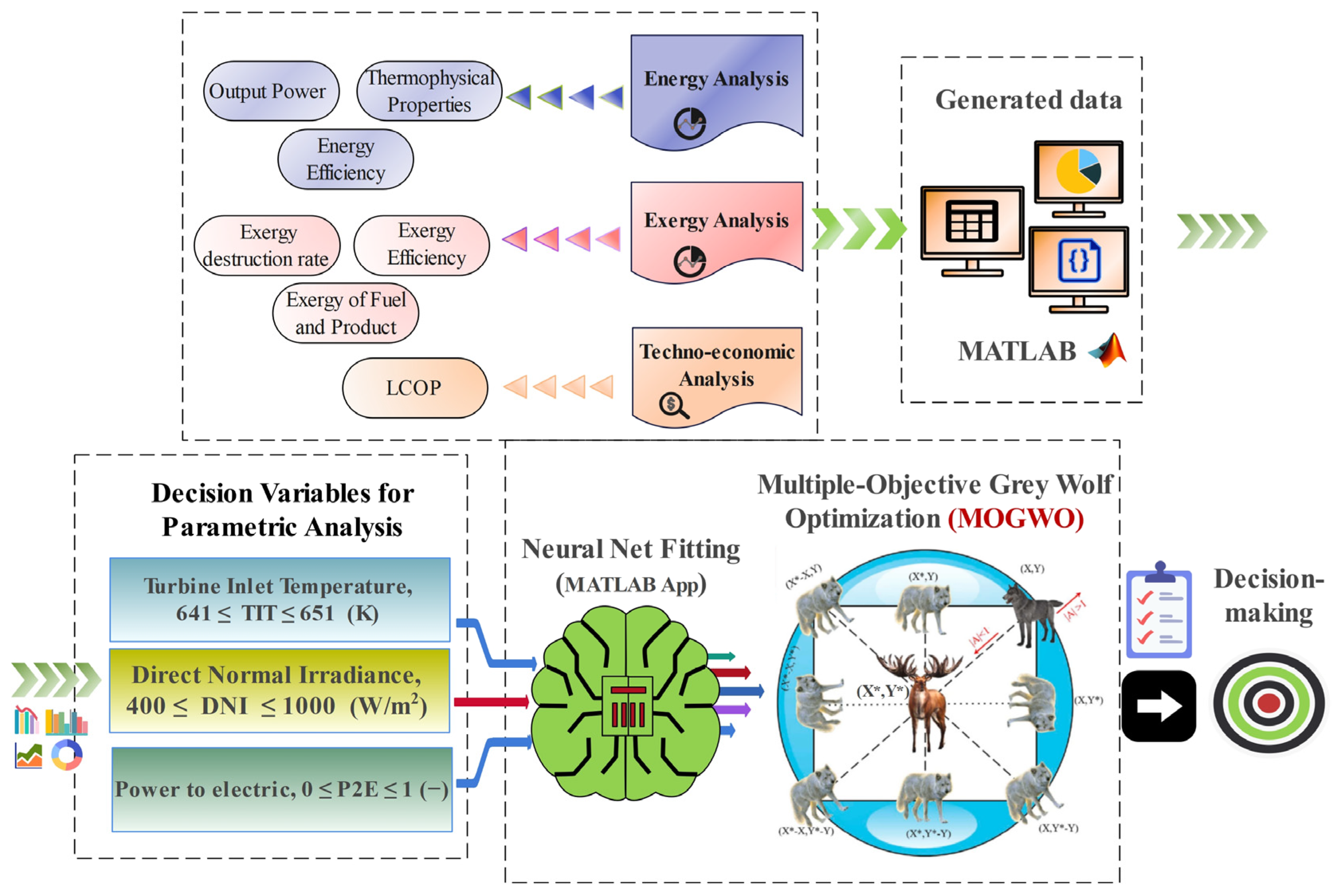
3.5. Multi-Objective Optimization
3.6. Validation
3.6.1. ORC
3.6.2. PTSC
3.6.3. Thermal Storage Tank
4. Results and Discussion
4.1. Application Considered
4.2. System Performance and Efficiency
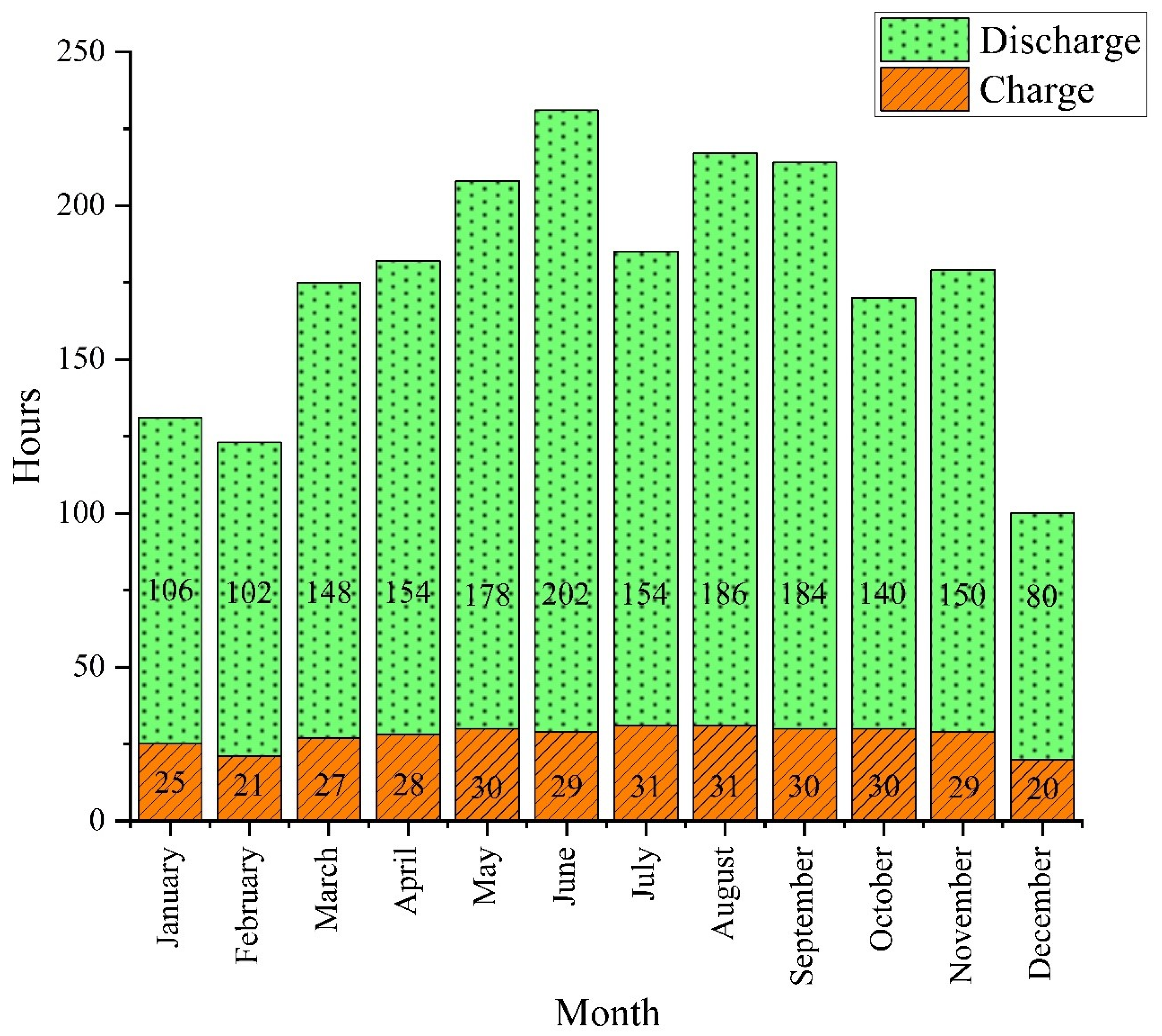
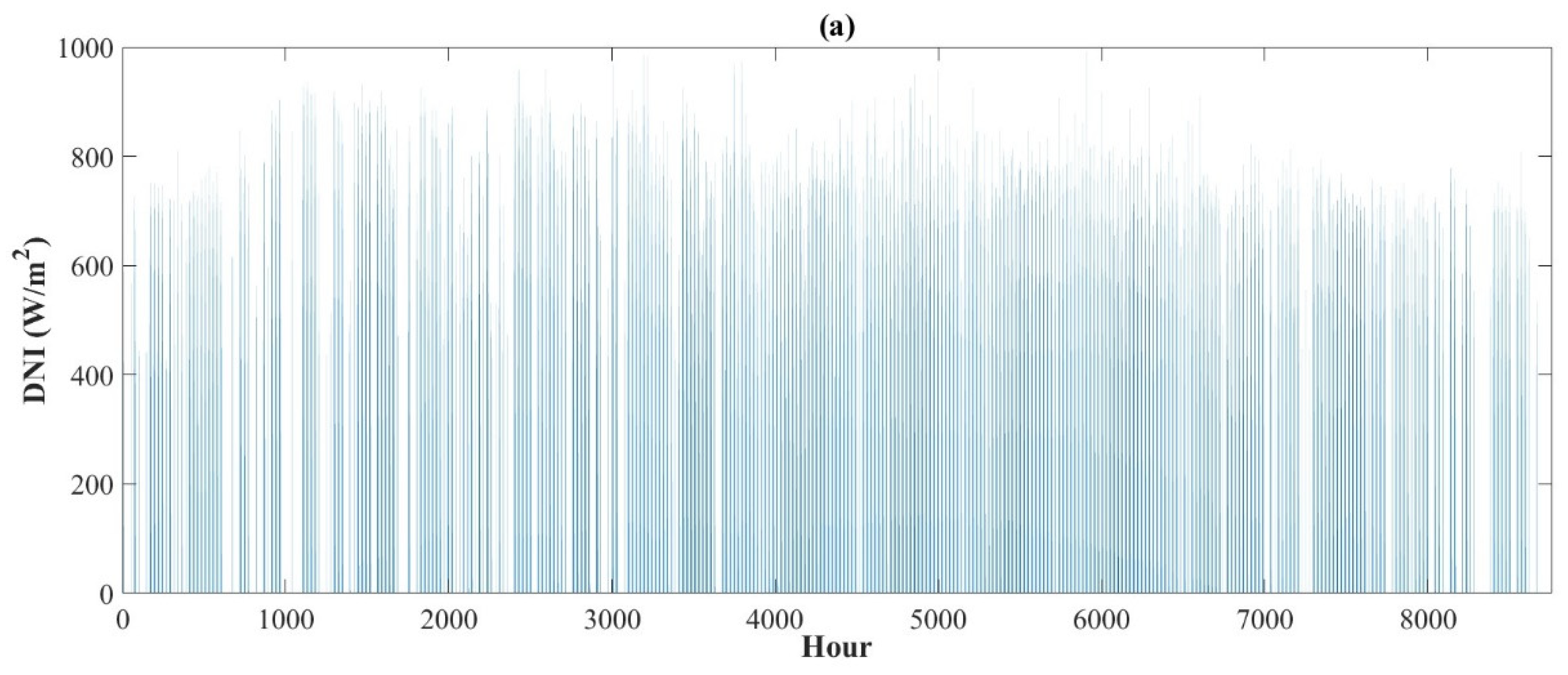
4.2.1. Solar Reservoir
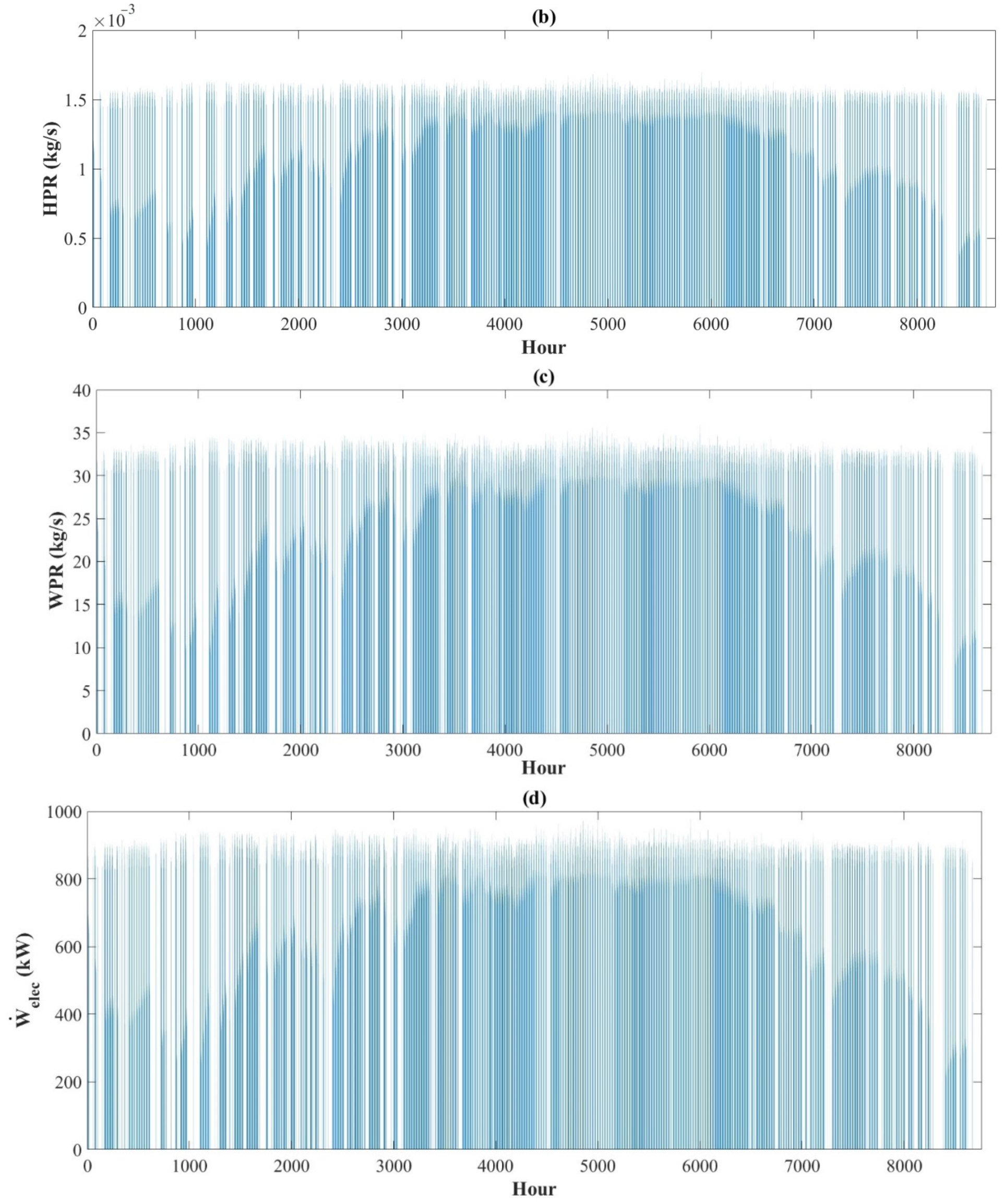
4.2.2. Hourly Distribution of System Production
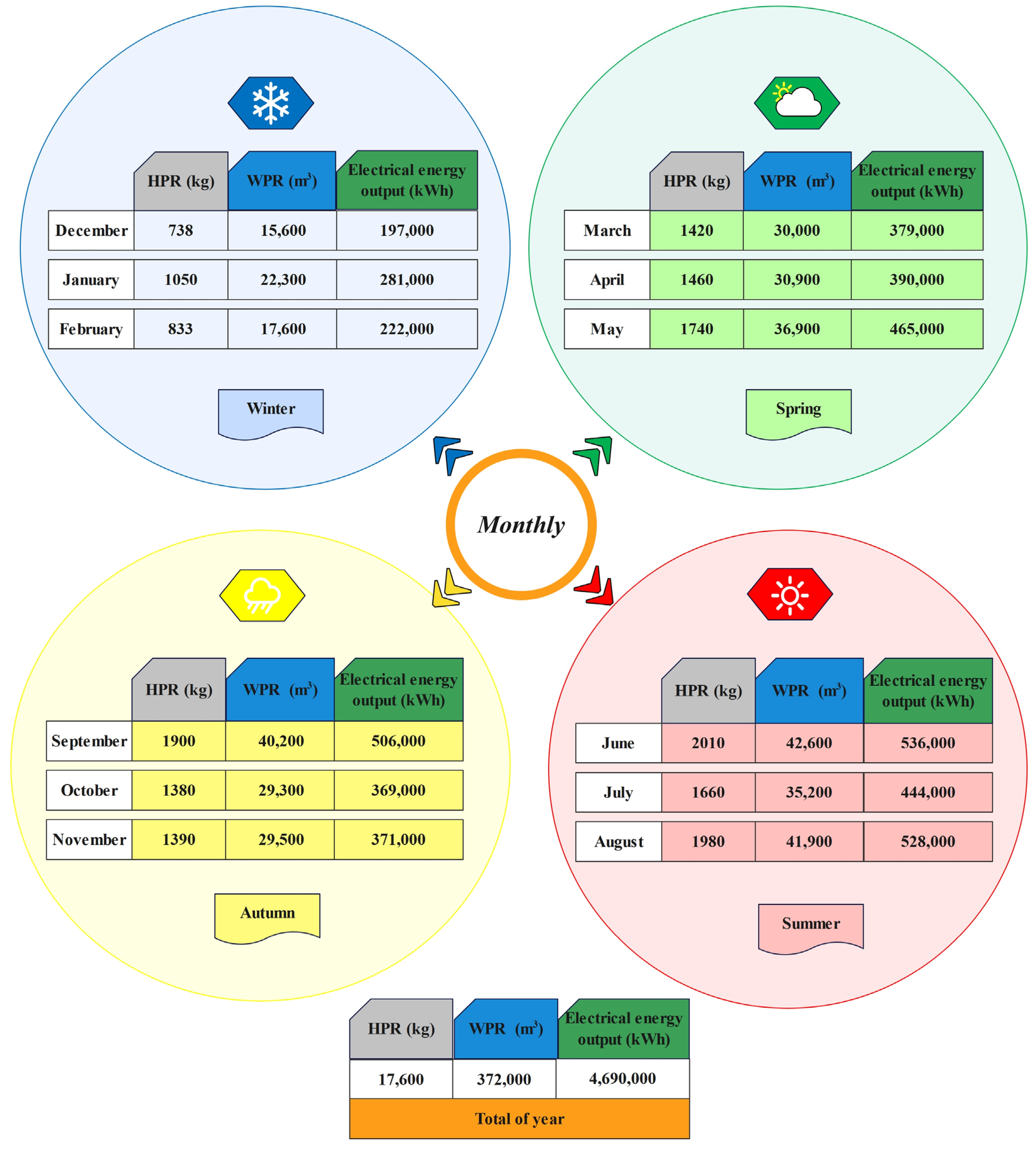
4.2.3. Monthly Distribution of System Products
4.2.4. Economic Study of the System
4.2.5. Sankey Diagram of the Multigeneration System
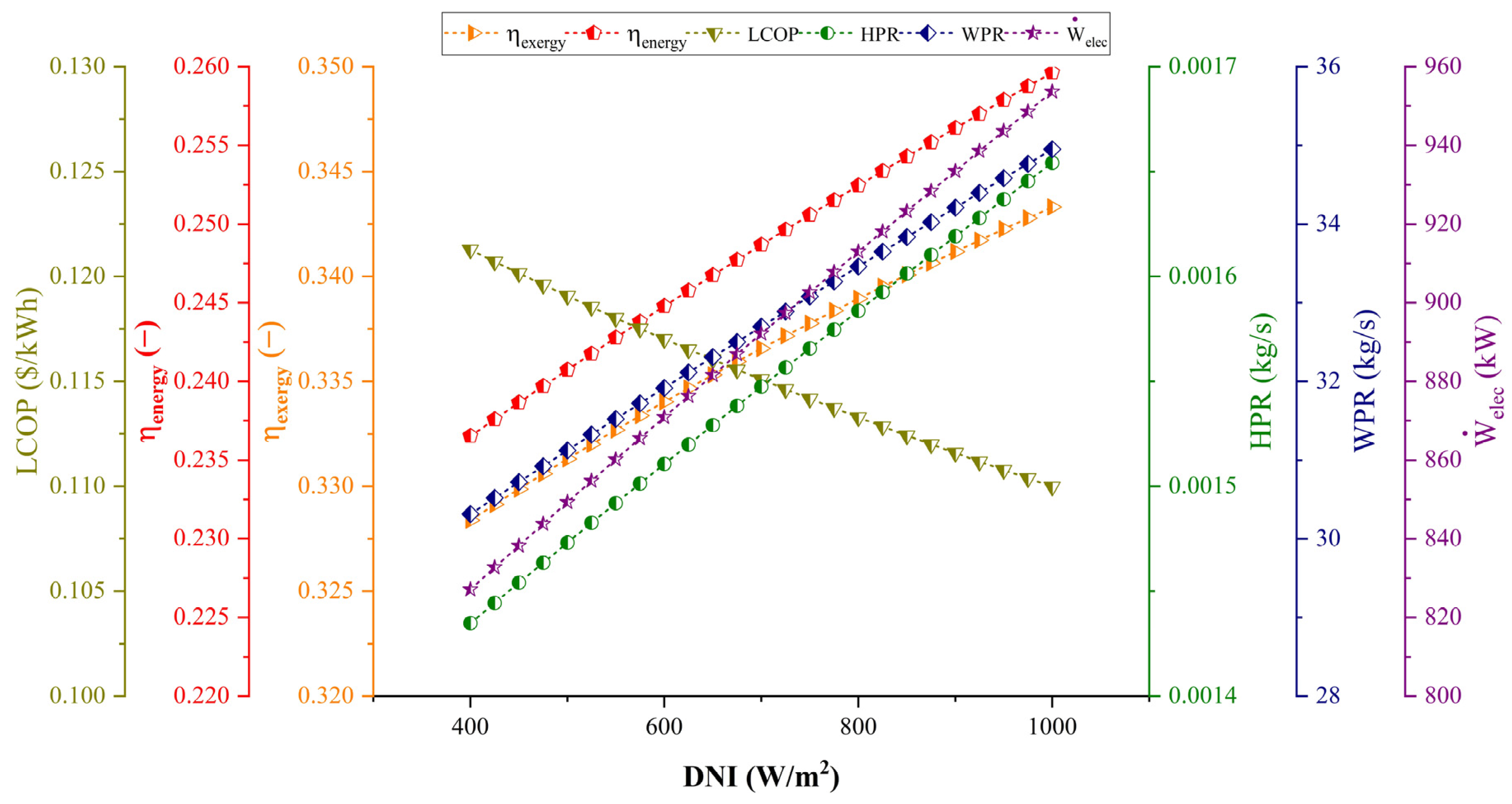
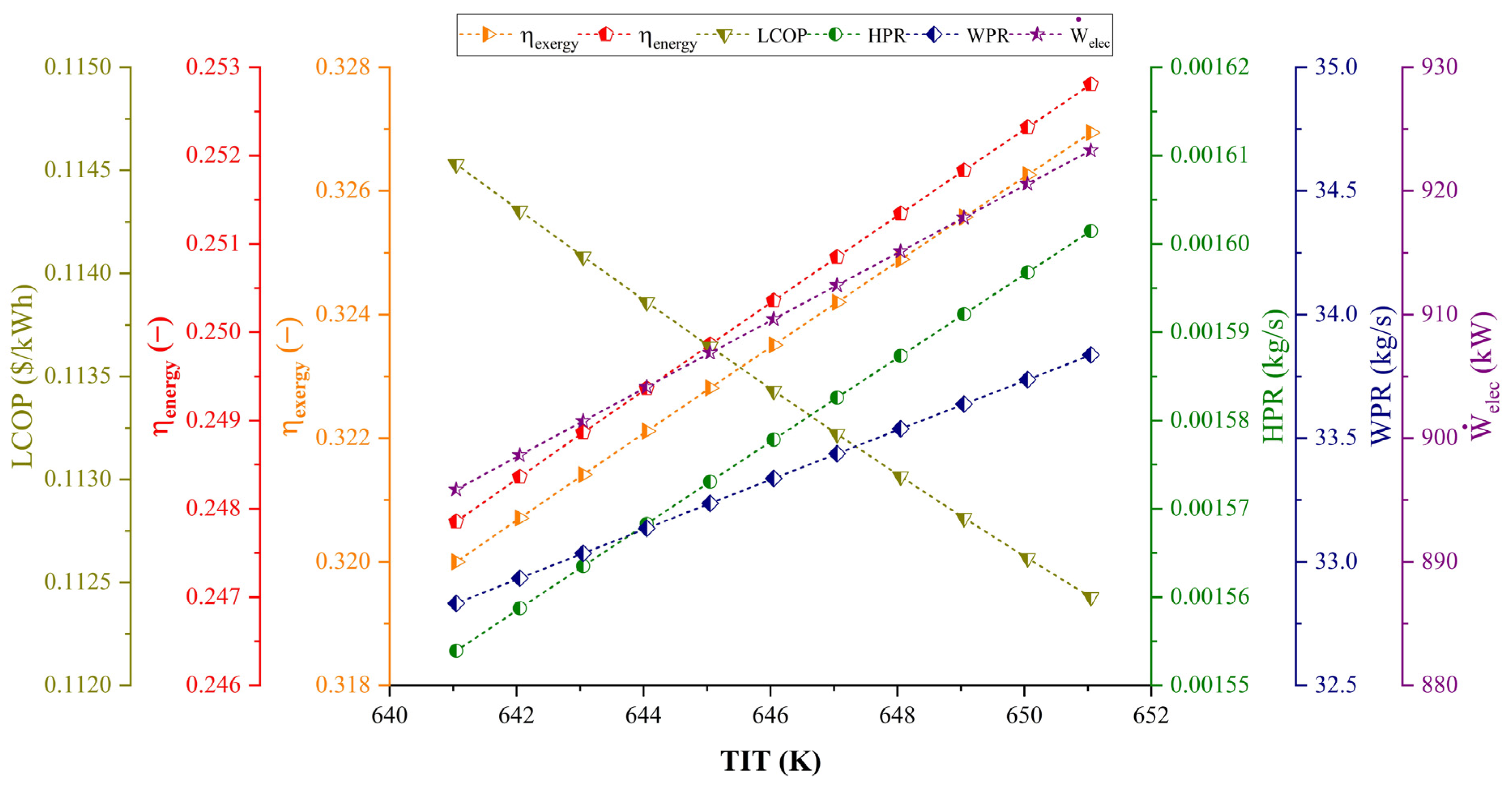
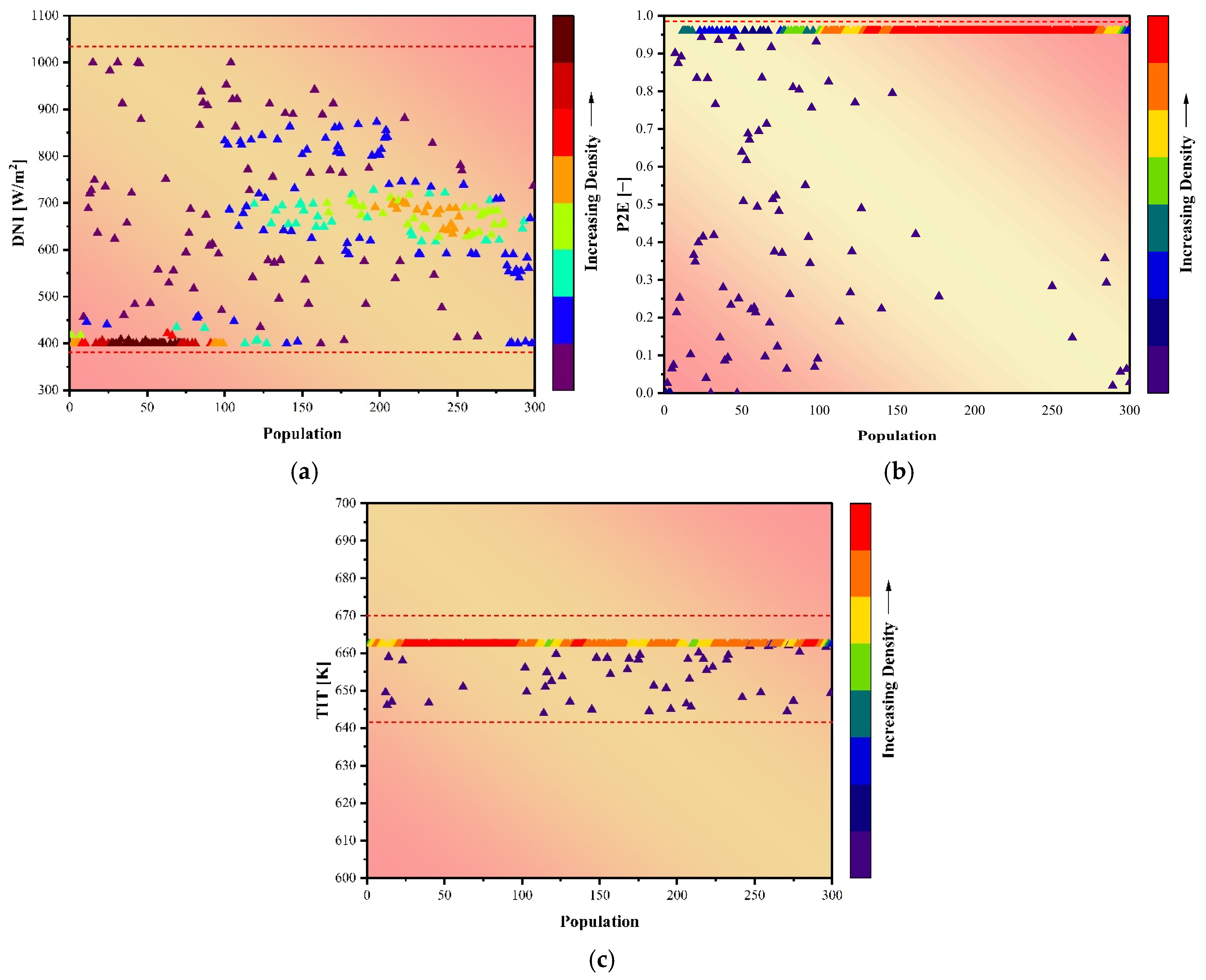
4.3. Parametric Study
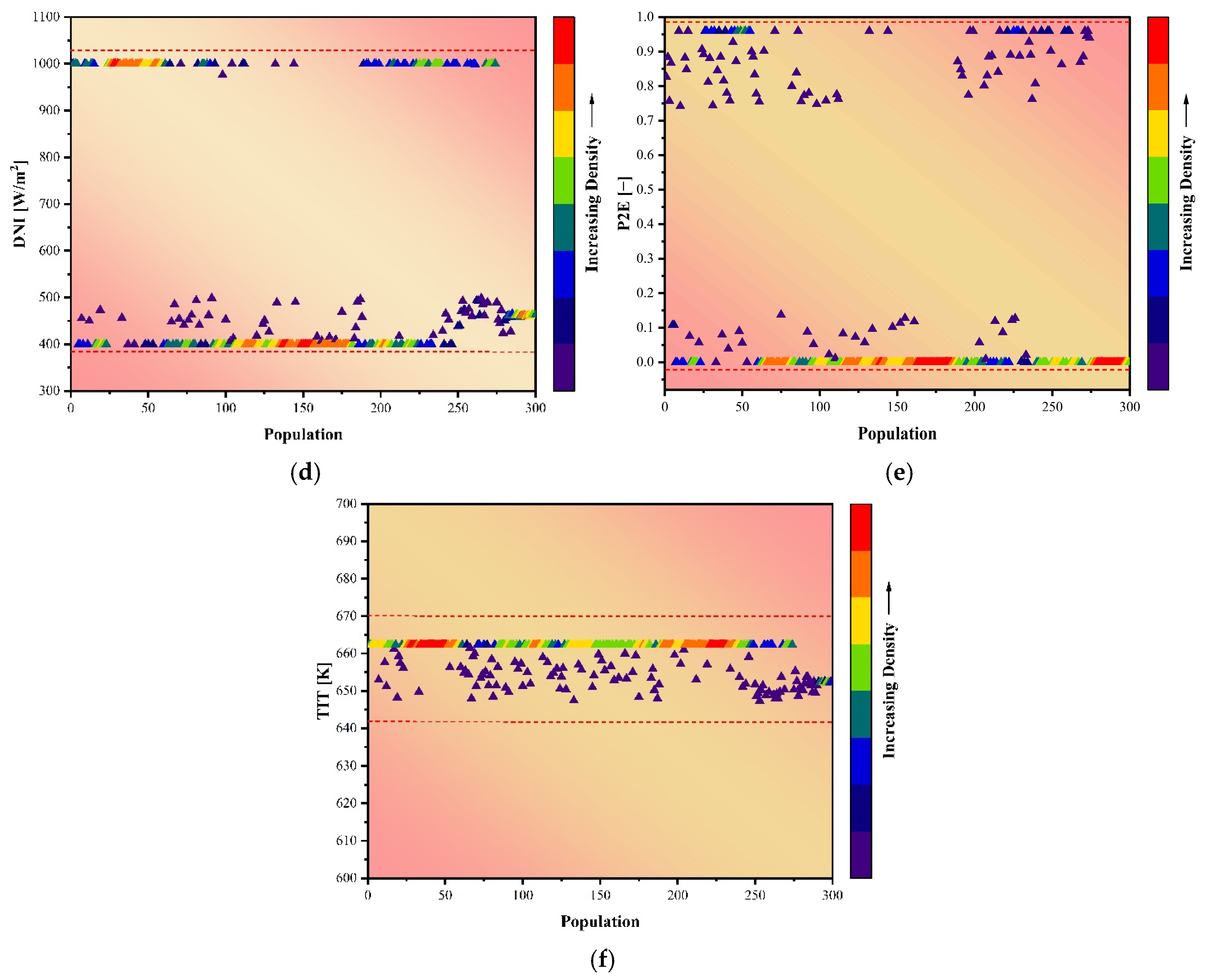
4.4. Optimization Procedure
5. Conclusions
- Reduced LCOP and enhanced energy and exergy efficiencies, as well as elevated rates of power, hydrogen, and water generation, are attained with increasing values of DNI and TIT. Also, allocating more electricity to the PEME and RO units decreases the system’s energy and exergy efficiencies and increases LCOP.
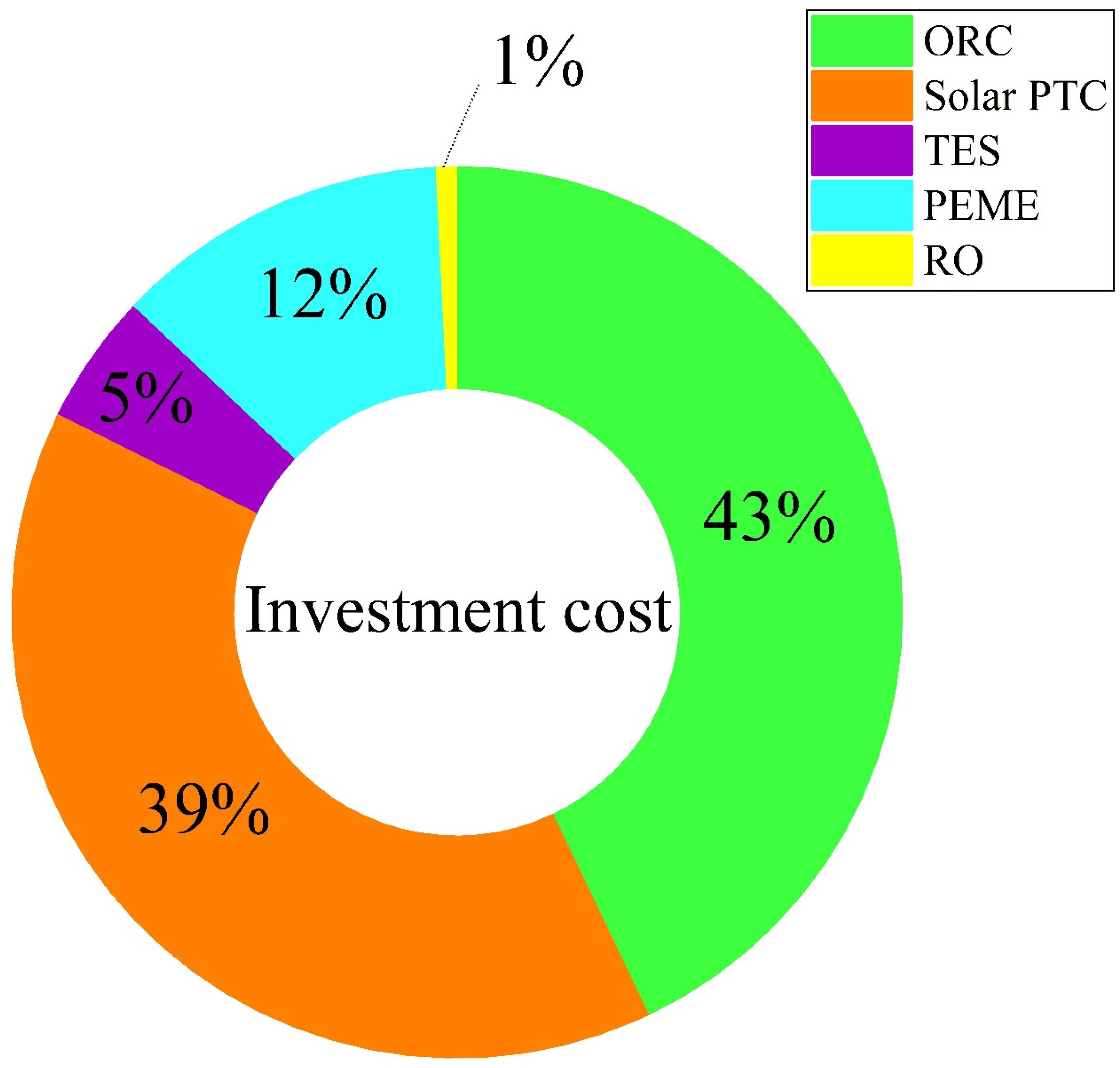
- The analysis of the system’s investment costs indicates that the ORC has the highest capital cost. Also, the thermal storage tank constitutes a relatively significant portion of the total costs.
- Under optimal conditions for optimizing production rates and lowering product costs through multi-objective system optimization, the values attained are 89.9 kg/s for WPR, 0.006 kg/s for HPR, and 0.11 $/kWh for LCOP.
- Future work could focus on addressing the practical feasibility of the proposed system, including detailed economic analyses, engineering constraints, and optimization strategies for large-scale implementation. Additionally, incorporating real-world factors such as energy storage, system integration, and operational flexibility could enhance the overall performance and viability of the system. Exploring hybrid configurations or alternative energy sources to complement the existing system could also lead to more sustainable and economically viable solutions in the long term.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Aperture area [] | |
| Area of receiver cover [] | |
| Area of receiver [] | |
| Specific heat at constant pressure [ | |
| Total number of collectors per row | |
| Total number of solar collector rows | |
| Cost index | |
| Capital recovery factor | |
| Control volume | |
| Diameter | |
| Exergy rate [] | |
| Exergy destruction rate [] | |
| Activation energy | |
| Faraday constant [C/mole] | |
| Heat removal factor | |
| Collector efficiency factor | |
| Beam solar irradiance | |
| Specific enthalpy [] | |
| Convection heat coefficient [] | |
| Radiative heat transfer coefficient [] | |
| Interest rate | |
| Current density [A/m2] | |
| J ref | Reference current density [A/m2] |
| Thermal conductivity [W/m] | |
| Collector length [ | |
| Levelized cost of products | |
| Mass flow rate [] | |
| Mass of oil in the tank [] | |
| Plant lifetime [years] | |
| Yearly operational duration [hours] | |
| Nusselt number | |
| Pressure [] | |
| Purchase equipment cost | |
| Pinch point temperature difference | |
| Heat | |
| Heat transfer rate [] | |
| R | Ohmic resistance [Ω] |
| Specific entropy [] | |
| Radiation absorbed by receiver | |
| Temperature [] | |
| Product of overall heat transfer coefficient and area [kW/K] | |
| Overall heat loss coefficient of solar collector | |
| Heat loss coefficient between ambient and receiver of solar collector | |
| Voltage | |
| Collector width [] | |
| Power [] | |
| Investment cost rate [] | |
| Absorbance of receiver | |
| Change in time | |
| Emittance of receiver cover | |
| Efficiency [%] | |
| Intercept factor | |
| Incidence angle modifier | |
| Stefan–Boltzmann constant ] | |
| Density [] | |
| Reflectance of mirror | |
| Transmittance of glass cover | |
| Thickness of insulation material [m] | |
| Water content at location x of membrane | |
| Reference condition | |
| Exit | |
| Cond | Condenser |
| Energy | |
| Exergy | |
| Evaporator | |
| Expansion valve | |
| Turbine | |
| Heat exchanger | |
| Inlet | |
| Isentropic | |
| Net | |
| Outlet | |
| Physical | |
| r | Receiver |
Appendix A. Balances for Components
| Component | Energy Rate Balances and Relations | Exergy Rate Balance |
|---|---|---|
| ORC | ||
| Recuperator | ||
| ORC pump | ||
| Tur | ||
| Cond | ||
| Evap | ||
| RO unit | ||
| FP | ||
| HPP | ||
| BP | ||
| Pelton turbine | ||
| RO1 | ||
| RO2 | ||
| PTC and TES | ||
| Solar pump | ||
| PTC field | ||
| Storage tank—charge mode | ||
| Storage tank—discharge mode | ||
| PEME | ||
| PEME HEX | ||
| PEME |
| Component | Purchased Equipment Cost Function | Ref. Year | Cost Index |
|---|---|---|---|
| Turbine | 2005 | 468.2 | |
| Condenser | 1968 | 113.7 | |
| HEX | 1986 | 318.4 | |
| Tank | 2005 | 468.2 | |
| Solar | 2010 | 550.8 | |
| ORC and solar pump | 2011 | 585.7 | |
| Recuperator | |||
| PEME | |||
| H2 storage tank | |||
| FP | |||
| HPP | |||
| BP | |||
| Pelton turbine |
References
- Gul, E.; Baldinelli, G.; Bartocci, P.; Shamim, T.; Domenighini, P.; Cotana, F.; Wang, J.; Fantozzi, F.; Bianchi, F. Transition toward net zero emissions—Integration and optimization of renewable energy sources: Solar, hydro, and biomass with the local grid station in central Italy. Renew. Energy 2023, 207, 672–686. [Google Scholar] [CrossRef]
- Zabat, L.H.; Sadaoui, N.A.; Abid, M.; Sekrafi, H. Threshold effects of renewable energy consumption by source in U.S. economy. Electr. Power Syst. Res. 2022, 213, 108669. [Google Scholar] [CrossRef]
- Akan, T. Can renewable energy mitigate the impacts of inflation and policy interest on climate change? Renew. Energy 2023, 214, 255–289. [Google Scholar] [CrossRef]
- Sarabchi, N.; Mahmoudi, S.M.S.; Yari, M.; Farzi, A. Exergoeconomic analysis and optimization of a novel hybrid cogeneration system: High-temperature proton exchange membrane fuel cell/Kalina cycle, driven by solar energy. Energy Convers. Manag. 2019, 190, 14–33. [Google Scholar] [CrossRef]
- Wang, T.; Cao, X.; Jiao, L. PEM water electrolysis for hydrogen production: Fundamentals, advances, and prospects. Carbon Neutrality 2022, 1, 21. [Google Scholar] [CrossRef]
- Laleh, S.S.; Safarpour, A.; Shahrak, A.S.; Alavi, S.H.F.; Soltani, S. Thermodynamic and exergoeconomic analyses of a novel biomass-fired combined cycle with solar energy and hydrogen and freshwater production in sports arenas. Int. J. Hydrogen Energy 2024, 59, 1507–1517. [Google Scholar] [CrossRef]
- Raninga, M.; Mudgal, A.; Patel, V.; Patel, J. Zeotropic mixture as a working fluid for cascade Rankine cycle-based reverse osmosis: Energy, exergy, and economic analysis. Int. J. Thermofluids 2024, 24, 100890. [Google Scholar] [CrossRef]
- Batista, N.E.; Carvalho, P.C.M.; Fernández-Ramírez, L.M.; Braga, A.P.S. Optimizing methodologies of hybrid renewable energy systems powered reverse osmosis plants. Renew. Sustain. Energy Rev. 2023, 182, 113377. [Google Scholar] [CrossRef]
- Kolathur, S.; Khatiwada, D.; Khan, E.U. Life cycle assessment and life cycle costing of a building-scale, solar-driven water purification system. Energy Nexus 2023, 10, 100208. [Google Scholar] [CrossRef]
- Zheng, N.; Zhang, H.; Duan, L.; Wang, Q.; Bischi, A.; Desideri, U. Techno-economic analysis of a novel solar-driven PEMEC-SOFC-based multi-generation system coupled parabolic trough photovoltaic thermal collector and thermal energy storage. Appl. Energy 2023, 331, 120400. [Google Scholar] [CrossRef]
- Zheng, N.; Zhang, H.; Duan, L.; Wang, X.; Liu, L. Energy, exergy, exergoeconomic and exergoenvironmental analysis and optimization of a novel partially covered parabolic trough photovoltaic thermal collector based on life cycle method. Renew. Energy 2022, 200, 1573–1588. [Google Scholar] [CrossRef]
- Bedakhanian, A.; Maleki, A.; Haghighat, S. Utilizing the multi-objective particle swarm optimization for designing a renewable multiple energy system on the basis of the parabolic trough solar collector. Int. J. Hydrogen Energy 2022, 47, 36433–36447. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, S.; Yue, W.; Tian, Z.; Yang, C.; Gao, W. Energy; exergy, economic and environmental (4E) evaluation of a solar-integrated energy system at medium–high temperature using CO2 as the parabolic trough collector (PTC) working medium. Energy Convers. Manag. 2023, 296, 117683. [Google Scholar] [CrossRef]
- Maya, J.C.; Chejne, F.; Gómez, C.A.; Montoya, J.; Chaquea, H.; Pecha, B. Analysys of the performance a PEM-type electrolyzer in variable energy supply conditions. Chem. Eng. Res. Des. 2023, 196, 526–541. [Google Scholar] [CrossRef]
- Abdollahipour, A.; Sayyaadi, H. Optimal design of a hybrid power generation system based on integrating PEM fuel cell and PEM electrolyzer as a moderator for micro-renewable energy systems. Energy 2022, 260, 124944. [Google Scholar] [CrossRef]
- Astriani, Y.; Tushar, W.; Nadarajah, M. Optimal planning of renewable energy park for green hydrogen production using detailed cost and efficiency curves of PEM electrolyzer. Int. J. Hydrogen Energy 2024, 79, 1331–1346. [Google Scholar] [CrossRef]
- Abedi, M.; Tan, X.; Klausner, J.F.; Bénard, A. Solar desalination chimneys: Investigation on the feasibility of integrating solar chimneys with humidification–dehumidification systems. Renew. Energy 2023, 202, 88–102. [Google Scholar] [CrossRef]
- Kianfard, H.; Khalilarya, S.; Jafarmadar, S. Exergy and exergoeconomic evaluation of hydrogen and distilled water production via combination of PEM electrolyzer, RO desalination unit and geothermal driven dual fl uid ORC. Energy Convers. Manag. 2018, 177, 339–349. [Google Scholar] [CrossRef]
- Dashtizadeh, E.; Darestani, M.M.; Rostami, S.; Ashjaee, M.; Houshfar, E. Comparative optimization study and 4E analysis of hybrid hydrogen production systems based on PEM, and VCl methods utilizing steel industry waste heat. Energy Convers. Manag. 2024, 303, 118141. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Hamdullahpur, F.; Dincer, I. Performance assessment of a novel system using parabolic trough solar collectors for combined cooling, heating, and power production. Renew. Energy 2012, 48, 161–172. [Google Scholar] [CrossRef]
- Okonkwo, E.C.; Essien, E.A.; Akhayere, E.; Abid, M.; Kavaz, D.; Ratlamwala, T.A.H. Thermal performance analysis of a parabolic trough collector using water-based green-synthesized nanofluids. Sol. Energy 2018, 170, 658–670. [Google Scholar] [CrossRef]
- Blanco-Marigorta, A.M.; Masi, M.; Manfrida, G. Exergo-environmental analysis of a reverse osmosis desalination plant in Gran Canaria. Energy 2014, 76, 223–232. [Google Scholar] [CrossRef]
- Abbasi, H.R.; Pourrahmani, H. Multi-criteria optimization of a renewable hydrogen and freshwater production system using HDH desalination unit and thermoelectric generator. Energy Convers. Manag. 2020, 214, 112903. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Dincer, I.; Hamdullahpur, F. Exergy modeling of a new solar driven trigeneration system. Sol. Energy 2011, 85, 2228–2243. [Google Scholar] [CrossRef]
- Wang, J.; Dai, Y.; Gao, L.; Ma, S. A new combined cooling, heating and power system driven by solar energy. Renew. Energy 2009, 34, 2780–2788. [Google Scholar] [CrossRef]
- Gao, Z.; Miao, J.; Zhao, J.; Mesri, M. Comprehensive economic analysis and multi-objective optimization of an integrated gasification power generation cycle. Process Saf. Environ. Prot. 2021, 155, 61–79. [Google Scholar] [CrossRef]
- Meng, F.; Wang, E.; Zhang, B.; Zhang, F.; Zhao, C. Thermo-economic analysis of transcritical CO2 power cycle and comparison with Kalina cycle and ORC for a low-temperature heat source. Energy Convers. Manag. 2019, 195, 1295–1308. [Google Scholar] [CrossRef]
- Dudley, V.E.; Kolb, J.; Mahoney, A.R.; Mancini, T.R.; Matthews, C.W. Test Results of SEGS LS-2 Solar Collector; USDOE: Washington, DC, USA, 1994.
- Ashouri, M.; Vandani, A.M.K.; Mehrpooya, M.; Ahmadi, M.H.; Abdollahpour, A. Techno-economic assessment of a Kalina cycle driven by a parabolic Trough solar collector. Energy Convers. Manag. 2015, 105, 1328–1339. [Google Scholar] [CrossRef]
- Kurşun, B.; Ökten, K. Comprehensive energy; exergy, and economic analysis of the scenario of supplementing pumped thermal energy storage (PTES) with a concentrated photovoltaic thermal system. Energy Convers. Manag. 2022, 260, 115592. [Google Scholar] [CrossRef]
- Boyaghchi, F.A.; Chavoshi, M. Multi-criteria optimization of a micro solar-geothermal CCHP system applying water/CuO nanofluid based on exergy, exergoeconomic and exergoenvironmental concepts. Appl. Therm. Eng. 2017, 112, 660–675. [Google Scholar] [CrossRef]
- Hai, T.; Kumar, A.; Aminian, S.; Al-Qargholi, B.; Soliman, N.F.; El-Shafai, W. Improved efficiency in an integrated geothermal power system including fresh water unit: Exergoeconomic analysis and dual-objective optimization. Process Saf. Environ. Prot. 2023, 180, 305–323. [Google Scholar] [CrossRef]
- Fan, G.; Yang, B.; Guo, P.; Lin, S.; Farkoush, S.G.; Afshar, N. Comprehensive analysis and multi-objective optimization of a power and hydrogen production system based on a combination of flash-binary geothermal and PEM electrolyzer. Int. J. Hydrogen Energy 2021, 46, 33718–33737. [Google Scholar] [CrossRef]
- Khodaei, E.; Yari, M.; Nami, H.; Goravanchi, F. Techno-economic Assessment and Optimization of a Solar-Driven Power and Hydrogen Co-generation Plant Retrofitted with Enhanced Energy Storage. Energy Convers. Manag. 2024, 301, 118004. [Google Scholar] [CrossRef]





| Parameter | Unit | Value | Ref. |
|---|---|---|---|
| Reference pressure, | |||
| Reference temperature, | |||
| Solar unit | |||
| Collector width, | [20] | ||
| Collector length, | [21] | ||
| Focal length, | [21] | ||
| Receiver efficiency, | [20] | ||
| Beam solar irradiance (during times of low availability), | [20] | ||
| Beam solar irradiance (during times of high availability), | [20] | ||
| Emittance of receiver cover, | [20] | ||
| Total number of collectors per single row, | |||
| Total number of solar collector rows, | |||
| Mass of oil in the tank, | |||
| Diameter, | [20] | ||
| Reflectance of mirror, | [20] | ||
| Intercept factor, | [20] | ||
| Transmittance of glass cover, | [20] | ||
| Absorbance of receiver, | [20] | ||
| Incidence angle modifier, | [20] | ||
| Storage unit | |||
| Diameter of storage tank, | |||
| Height of storage tank, | |||
| Number of storage tanks | 3 | ||
| Rankine cycle | |||
| Isentropic efficiency of turbine, | [18] | ||
| Isentropic efficiency of pump, | [18] | ||
| PPTD of evaporator, | 5 | [18] | |
| PPTD of recuperator, | 15 | [18] | |
| PPTD of condenser, | 10 | [18] | |
| PEME | |||
| Oxygen output pressure, | 1 | ||
| Hydrogen output pressure, | 1 | ||
| Operating temperature of PEME, | °C | 80 | [19] |
| Activation energy for anode reaction, | 76 | [19] | |
| Activation energy for cathode reaction, | 18 | [19] | |
| Stoichiometric coefficient or air–fuel ratio at anode, | 14 | [19] | |
| Stoichiometric coefficient or air–fuel ratio at cathode, | 10 | [19] | |
| Reference current density at anode, | [19] | ||
| Reference current density at cathode, | [19] | ||
| Reverse osmosis unit | |||
| Isentropic efficiency of pumps, | 76.7 | [22] | |
| Isentropic efficiency of Pelton turbine, | 79 | [22] | |
| Water inlet temperature of RO unit, | 298 | [22] | |
| Desalination rate of RO-1 | 0.55 | [22] | |
| Desalination rate of RO-2 | 0.6 | [22] | |
| Item | Value |
|---|---|
| Fixed capital investment (FCI) | |
| |
| Total purchased equipment costs | |
| Installation costs | |
| Electrical equipment and materials | |
| Piping costs | |
| Civil, structural, and architectural work | |
| Land | |
| Service facilities | |
| |
| Construction costs | |
| Engineering and supervision | |
| Contingencies |
| Test | |||||
|---|---|---|---|---|---|
| Cases | Present Study | Okonkwo et al. [21] | Error (%) | Experiment of Dudley et al. [28] | Error (%) |
| 1 | 0.722 | 0.707 | 2.0 | 0.725 | 0.48 |
| 2 | 0.716 | 0.695 | 3.0 | 0.709 | 0.95 |
| 3 | 0.711 | 0.686 | 3.6 | 0.702 | 1.3 |
| 4 | 0.703 | 0.668 | 5.2 | 0.703 | 0.057 |
| 5 | 0.699 | 0.664 | 5.3 | 0.680 | 2.9 |
| 6 | 0.695 | 0.653 | 6.5 | 0.689 | 0.89 |
| 7 | 0.689 | 0.636 | 8.3 | 0.638 | 7.9 |
| 8 | 0.687 | 0.633 | 8.5 | 0.633 | 8.4 |
| Test | |||||
|---|---|---|---|---|---|
| Cases | Present Study | Okonkwo et al. [21] | Error (%) | Experiment of Dudley et al. [28] | Error (%) |
| 1 | 398.4 | 397.2 | 0.30 | 397.2 | 0.30 |
| 2 | 447.8 | 446.4 | 0.32 | 446.5 | 0.29 |
| 3 | 493.9 | 492.7 | 0.24 | 492.7 | 0.24 |
| 4 | 542.9 | 541.4 | 0.28 | 542.6 | 0.062 |
| 5 | 590.2 | 589.9 | 0.059 | 589.6 | 0.11 |
| 6 | 590.1 | 589.6 | 0.091 | 590.4 | 0.044 |
| 7 | 647.1 | 646.9 | 0.03 | 647.2 | 0.016 |
| 8 | 670.83 | 670.6 | 0.034 | 671.2 | 0.055 |
| Hour | Present Study | Ashouri et al. [30] | Error (%) |
|---|---|---|---|
| 10 | 109 | 110 | 1.0 |
| 11 | 116 | 115 | 0.52 |
| 12 | 123 | 124 | 0.98 |
| 13 | 133 | 132 | 1.3 |
| 14 | 140 | 139 | 0.65 |
| 15 | 146 | 145 | 0.65 |
| 16 | 150 | 148 | 1.0 |
| 17 | 150 | 150 | 0.18 |
| 18 | 148 | 152 | 2.5 |
| 19 | 145 | 149 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arashrad, P.; Sharafi Laleh, S.; Rabet, S.; Yari, M.; Soltani, S.; Rosen, M.A. Real-Time Modeling of a Solar-Driven Power Plant with Green Hydrogen, Electricity, and Fresh Water Production: Techno-Economics and Optimization. Sustainability 2025, 17, 3555. https://doi.org/10.3390/su17083555
Arashrad P, Sharafi Laleh S, Rabet S, Yari M, Soltani S, Rosen MA. Real-Time Modeling of a Solar-Driven Power Plant with Green Hydrogen, Electricity, and Fresh Water Production: Techno-Economics and Optimization. Sustainability. 2025; 17(8):3555. https://doi.org/10.3390/su17083555
Chicago/Turabian StyleArashrad, Paniz, Shayan Sharafi Laleh, Shayan Rabet, Mortaza Yari, Saeed Soltani, and Marc A. Rosen. 2025. "Real-Time Modeling of a Solar-Driven Power Plant with Green Hydrogen, Electricity, and Fresh Water Production: Techno-Economics and Optimization" Sustainability 17, no. 8: 3555. https://doi.org/10.3390/su17083555
APA StyleArashrad, P., Sharafi Laleh, S., Rabet, S., Yari, M., Soltani, S., & Rosen, M. A. (2025). Real-Time Modeling of a Solar-Driven Power Plant with Green Hydrogen, Electricity, and Fresh Water Production: Techno-Economics and Optimization. Sustainability, 17(8), 3555. https://doi.org/10.3390/su17083555








