Two-Stage Optimization on Vessel Routing and Hybrid Energy Output for Marine Debris Collection

Abstract

The harm of marine debris (MD) to the environment and human beings has been paid more and more attention. At present, the most effective way to collect macro-MD floating on the sea is to send vessels. We employ vessels equipped with a hybrid energy system (HES) composed of photovoltaic (PV), battery and diesel to carry out MD cleanup. We propose a two-stage optimization approach for vessel routing and energy management strategy. In the first stage, the vessel routing problem with a drifting time window is modeled to minimize the vessel travel time considering continuous speed. The drifting time window means that multiple time windows are set on the MD trajectory, which is used to depict its dynamic nature. An adaptive large neighborhood search algorithm considering an elitist strategy coupled with speed optimization is designed to solve this problem. In the second stage, a mixed integer linear programming model for energy management strategy is established to minimize the total cost, including the power generation cost of diesel and PV, the battery charge, and discharge and carbon tax costs. The model takes the power load balance, the power limit of each part of the hybrid energy system and the battery charge and discharge state as constraints. The correctness of the proposed models and the effectiveness of the proposed algorithm are verified by a numerical example. The results not only show the advantages of hybrid energy vessels in energy saving and emission reduction but also show that the drifting time window can provide a rich and effective route selection solution. Some suggestions for rational utilization of hybrid energy vessels with long and short trips are put forward.

1. Introduction

At present, marine plastic debris, as the main part of marine debris (MD), is considered to be one of the fastest-growing pollutants [1]. According to the report of the United Nations Environment Programme [2], there are about 75 million to 199 million tons of plastic debris in the ocean, accounting for 85% of MD, and about 1100 tons of plastic debris flow into the ocean every year. MD poses a serious threat to marine organisms, such as sea turtles [3], seabirds [4], sea lions [5], crabs [6], cetaceans [7], marine phytoplankton [8], etc. The most obvious effects include ingestion, suffocation and entanglement. Moreover, it not only harms the marine ecosystem, but also affects human health and social and economic activities. The annual negative impact of marine plastic waste is estimated to be at least USD 8 billion [9]. MD leads to the accumulation of toxins in seafood, which may cause health hazards to humans if they ingest MD through seafood [10].

Due to wind and currents, MD will drift around in the ocean, which is the difficulty of MD cleanup compared to land-based garbage collection. Additionally, plastic debris will be degraded into microplastics (less than 5 mm) in the ocean over time. Microplastics can easily enter the marine food chain and pose a greater threat to marine organisms and human beings than macroplastics [10]. Therefore, vessels should be dispatched to collect MD as soon as possible. A logistics network method can be employed to optimize the vessel routing problem (VRP) with a time window [11,12]. To reflect the mobility nature of MD, we introduce the concept of a drifting time window, that is, multiple different time windows are set on the drifting trajectory of each MD, and each time window corresponds to a different MD location (MDL). In this way, the problem is defined on a logistics space–time network. We name the problem VRP with drifting time window (VRPDTW).

Pollutants emitted by vessels will cause environmental deterioration in coastal areas, and particles such as nitrogen oxides in the air will affect human health [13]. Therefore, how to reduce the economic cost and environmental pollution as much as possible while dispatching vessels to collect MD is our research motivation and goal. In order to reduce carbon emissions, Duan et al. [14] set a carbon emission cap constraint, but the results are limited. The use of traditional fossil fuels to power vessels inevitably produces a large amount of carbon emissions. Moreover, due to the depletion of global energy, the development and utilization of renewable or clean energy technology with extremely low carbon emissions has become the focus of vessel development. As a representative, photovoltaic (PV) has been widely used in vessels [15]. However, as the output power of PV is affected by weather conditions and is unstable, there may be insufficient power or excessive power generation. Using diesel generators as an auxiliary can provide a supplement when the PV power is small, and the energy storage system can adjust the excess power [16]. Therefore, PV can be combined with diesel generators and batteries to form a hybrid energy system (HES), which will always meet the vessel’s load requirements. In order to achieve the best energy management of the PV/diesel/battery hybrid energy system, it is necessary to adopt effective energy management strategies (EMSs) for PV, diesel generators and batteries, that is, to regulate the energy flow between various parts and minimize the power cost and carbon tax cost of vessels [17].

The problem studied in this paper is the cleaning of MD by hybrid solar vessels, aiming to combine VRPDTW for MD cleanup and EMS for HES. The vessels we use are powered by HES composed of PV, batteries and diesel generators. Since the power flow distribution of each part of HES must be carried out on the basis of the power demand of vessels in each period after all routes’ determination, it is too difficult to optimize the route and power flow distribution of vessels simultaneously [12]. Therefore, we employ a two-stage optimization method for VRPDTW and optimal power flow (OPF) of HES. In the first stage, we establish a mixed integer linear programming (MILP) model for VRPDTW as well as vessel speed on each arc to minimize the total travel time, whose constraints consider the weight and volume capacity of the vessel and the drifting time window of MDL. An adaptive large neighborhood search (ALNS) embedded with an elitist strategy, namely the ALNSES algorithm, is proposed to optimize vessel route and speed, which includes the design of eight removal operators and four insertion operators and combines a speed optimization algorithm (SOA). The optimal route and speed obtained in the first stage are then used as inputs for the second stage to optimize the power flow for the HES. In the second stage, we also propose an MILP model, whose objective is to minimize the total cost, including the depreciation cost of PV and battery, diesel power generation cost and carbon tax. The constraints are the power load balance, the rated power of each part of HES and the charge and discharge state of the storage battery. Due to the small amount of data at this stage, we use MATLAB to call CPLEX Solver to solve the OPF. The overall framework of the research is shown in Figure 1.

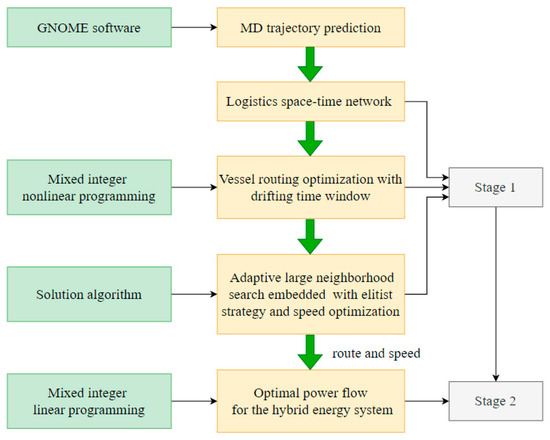
Figure 1. Overall framework of the research.

The main contributions of this paper are as follows. First of all, we adopt the logistics space–time network to optimize VRPDTW by introducing a drifting time window, which can depict the mobility more accurately during MD drifting process. To the best of our knowledge, this is the first time VRP has been used for MD cleanup. Secondly, vessel speed has a critical impact on travel time and carbon emissions. In order to make better use of hybrid energy vessels, we propose the VRPDTW model to optimize the route and speed simultaneously. Thirdly, we show that drifting time windows are superior to single time windows. It is not only related to the number of time windows but also related to the combination of time windows. This advantage is not only reflected in the number of time windows but also in their combination.

The organization of the remainder is as follows. The Section 2 introduces the literature review related to the routing problem and HES vessels. In the Section 3, we establish two MILP models for VRPDTW and OPF, respectively. In the Section 4, we design a novel algorithm ALNSES with speed optimization for the first stage problem. In the Section 5, we conduct some numerical experiments and report the analytical results and the proposed algorithm performance. Finally, the Section 6 gives our conclusions and future study directions.

2. Literature Review

2.1. Vessel Routing Problem

The VRP needs to consider the marine meteorological conditions, which have a crucial impact on the vessel route and speed. Gkerekos and Lazakis [18] proposed a data-driven decision-making framework, which considered the vessel performance and weather conditions. By inputting the weather forecast and historical vessel voyage data, the route with the minimum carbon emissions can be obtained and the carbon emissions of alternative routes can be calculated. Wei et al. [19] established a joint optimization model of vessel route and speed with the goal of minimum fuel consumption, which considered the voluntary and involuntary loss of speed caused by the marine environment and time window constraint. And they designed a heuristic method based on the difference algorithm to solve the model. Zis et al. [20] reviewed the main methods to solve the problem of weather route and voyage optimization and constructed a classification method to classify the relevant papers.

In order to control the greenhouse gas emissions from vessels, the International Maritime Organization has set up four emission control areas (ECAs) in which the greenhouse gas emissions from vessels are strictly restricted. Weng et al. [21] discussed the impact of ECA policies on vessel routes and emissions, and the results showed that the number and emissions of vessels in strict ECA waters were reduced by 9.44% and 42.67%, respectively. Ma et al. [22] established and solved the route and speed optimization model considering ECA and weather conditions. The results showed that the establishment of ECA could reduce the sailing distance and pollutant emissions of vessels in ECA but might increase the total distance and total emissions of the whole shipping process. Li et al. [23] studied the coping strategies of ECA. They found that the longer the sailing distance and the higher the fuel price ratio, the greater amount of vessels that would choose the strategy of avoiding ECA, which was the reason for the increase in total pollution emissions. Ma et al. [24] established a multi-objective model considering ECA to optimize the vessel route and speed to minimize the total cost and CO₂ and SO_x emissions. The method could effectively balance the internal and external emissions of ECA and avoid a significant increase in the total cost caused by the rise in the price of low-sulfur fuel.

2.2. Vessels with HES

In order to cope with global energy depletion and reduce the pollution caused by the shipping industry, the best method is to adopt clean energy and green technology. However, due to costs and technical reasons, clean energy cannot completely replace fossil fuels nowadays. HES composed of fossil fuels and clean energy is widely used in vessels. The choice of clean energy is an important issue. Ghenai et al. [25] presented the optimal design and performance analysis of HES with PV. Ballini et al. [26] analyzed the health costs and economic impacts of wind-assisted vessels. Pan et al. [27] pointed out that solar energy, wind energy, fuel cell and wave energy can all be used in the vessel’s power system. They summarized the vessel names, principal data, types of new energy sources, hybrid power system structures and benefits of current hybrid new energy vessels. Wen et al. [28] established a mathematical model of a PV power generation system for a vessel, taking into account the effects of vessel rolling. They proposed a new method based on Fourier analysis to optimize the size of the energy storage system to smooth the fluctuation of PV power. Lan et al. [16] employed multi-objective particle swarm optimization to determine the size of a hybrid PV/diesel/energy storage system, which can minimize the capex, fuel cost and carbon emissions, and tested it on the route from Dalian in China to Aden in Yemen.

For the HES of vessels, the current research mainly focuses on the EMS. Tang et al. [29] proposed a power flow scheduling model for a PV/battery/diesel/cold-ironing hybrid system to minimize power cost. They designed an adaptive multi-context cooperatively coevolving particle swarm optimization algorithm, which can obtain the best OPF while saving a lot of power costs. Haseltalab et al. [30] presented a scheme using a solid oxide fuel cell, gas engine, and battery as HES and proposed a novel approach to optimize component size and EMS. The results showed that the scheme could reduce the carbon dioxide emissions by 53% and improve the fuel efficiency by 21% compared with the traditional diesel electric vessel. For HES composed of fuel cells, batteries and supercapacitors, Chen et al. [31] developed a joint optimization method to simultaneously optimize EMS design and HES size to improve the performance of hybrid electric vessels.

2.3. Cross-Research on VRP and EMS

In order to make full use of the energy system and achieve the purpose of emission reductions and efficiency increases, some researchers conduct joint optimization of VRP and EMS. Ma et al. [32] designed a multi-objective vessel energy efficiency optimization model using engine speed as the variable to reduce fuel consumption and sailing time, incorporating sea condition clustering for route segmentation. Results demonstrated significant improvements, with potential reductions of up to 25.28% in fuel consumption or 17.08% in sailing time, while ideal solutions offered more balanced trade-offs. Öztürk and Başar [33] developed fuel oil consumption prediction models using multiple linear regression analysis and artificial neural networks based on voyage data to optimize vessel efficiency and reduce emissions. The models achieved 76–90% accuracy in fuel oil consumption prediction and analyzed the impact of factors on energy efficiency, showing potential savings of 6–37% through optimization.

Koumaniotis and Kanellos [34] employed a two-stage approach to minimize operational costs and emissions by modeling routing and power generation for large electric-powered ships. Particle swarm optimization is used for route planning based on sea resistance and energy efficiency, followed by power scheduling with a steepest descent algorithm to reduce emissions. Zhu et al. [35] enhanced the traditional level set algorithm by incorporating ocean current dynamics to plan fuel-efficient vessel routes in complex sea conditions, optimizing paths based on energy consumption gradients and flow field models. Case studies showed the algorithm reduced energy consumption by 2.1% in open waters and 1.4% in obstacle-rich environments compared to conventional shortest-path methods. Pan et al. [36] optimized the HES composed of diesel generators, batteries, fuel cells, PV, and shore power, using a bi-level tri-objective differential evolution algorithm, with route planning and component sizing in the upper level and power dispatch in the lower level. The three objectives were investment costs, operating expenses and greenhouse gas emissions. Case studies on the Dalian–Singapore route showed the approach effectively reduced operational costs and emissions.

3. Two-Stage Optimization Approach

3.1. Problem Description

In order to reduce environmental pollution, we employ hybrid energy vessels equipped with PV/diesel/battery to collect macro-MD floating on the sea surface. Considering the mobile characteristics of MD, by introducing the drifting time window and using the method of logistics space–time network, we establish mathematical models to optimize the vessel collection routing and speed, and reasonably arrange the power output of PV, battery banks and diesel generators to minimize the total cost. However, energy output is determined by demand, which in turn is determined according to the vessel’s operating condition. The operating conditions here include cruising and MD collection. In a period of time, the vessel may be in different combinations of operating conditions, which is completely determined by the vessel route and speed.

We use Figure 2 as an example to illustrate the influence of route and speed on energy output. Assume that there are two MDs, and the collection time of each MD is 1 h. In Figure 2, the number in the circle (vertex) represents MD, where 0 is the depot, the numbers in brackets above the circle are the time window (in hours), the number above the directed arc indicates the distance between two points, and the number below indicates the speed. Given route 0-1-2-0 and speed 10, 30 and 40 km/h, as shown in Figure 2a, if the departure time of 0 is set to 0 h, the arrival time and departure time of vertex 1 are 2 and 3 h, respectively, while they are 4 and 5 h for vertex 2, respectively, and the return time of 0 is 6 h. The arrival time of each vertex meets the time window requirement. If the energy output is optimized for a period of one hour, under the route and speed, there is only one working condition in each period, that is, the vessel is in a sailing state in periods 1, 2, 4 and 6, while MD is collected in periods 3 and 5. When the route is changed to 0-2-1-0 and the corresponding speeds are 40/3, 30 and 40 km/h, as shown in Figure 2b, the time to return 0 is 6.5 h. During periods 1, 2, 3 and 5, the vessel is under sail, and period 7 is under sail for only half an hour; Periods 4 and 6 are MD collection states. If the speed of arc 2-1 is changed to 40 km/h shown in Figure 2c, the vessel has two working conditions in period 5, the first 0.75 h is the sailing state, and the second 0.25 h is the MD collection state. Period 6 also has two working conditions. Changes in route and speed directly affect the calculation of energy output, and it is very difficult to optimize them simultaneously.

Figure 2. Different routes and speeds. (a) Route 0-1-2-0; (b) route 0-2-1-0; (c) route 0-2-1-0 and different speeds.

Therefore, to simplify, we solve the problem in two stages. In the first stage, the VRPDTW model is established to optimize the vessel routing and speed with the objective function of minimizing the total travel time. After the route and speed of each vessel are obtained, the power demand of each vessel in each period is determined. With the power demand of the first stage as the input parameter in the second stage, the OPF model of energy output is established with the goal of minimizing the total cost.

3.2. First Stage

3.2.1. Drifting Time Window

MD is not fixed, and it drifts around under the action of currents and winds, which is the biggest difference from land garbage collection. In order to determine MDL, we first obtain the initial MDL through remote sensing. Then, the initial MD location and meteorological data, such as wind direction, wind speed, and ocean current, can be entered into GNOME software (https://www.gnome.org/) to predict the trajectory. A location on the trajectory is selected as MDL. Finally, the drifting time window is set according to the actual situation [12,37].

GNOME is a software for predicting the diffusion trajectory of spilled crude oil, and it has been successfully applied to predict the trajectories of floating MD [38,39]. It uses the Lagrangian particle tracking method to simulate the diffusion path of MD. By inputting the initial position and time of MD, as well as marine meteorological data (such as wind, current, temperature, etc.), and combining with real-time or forecasted environmental conditions, it calculates the dynamic trajectory of MD. The model outputs the movement trajectory, affected area, and time evolution of debris and generates visual charts. For detailed use of the software, the reader is referred to Maximenko et al. [38] and Purba et al. [39].

Although the above method transforms the dynamic problem into a static one by setting a time window for MDL, the choice of location is too subjective. If the location is not chosen well, the optimization result will be very poor. To avoid this situation, we introduce the concept of a drifting time window. We choose multiple locations on each MD trajectory and set a time window for each location, which is called the drifting time window. Each drifting time window corresponds to a different MDL, which can better reflect the dynamic properties of MD. We take Figure 3 as an example to illustrate how to determine the drifting time window on each MD trajectory. The red dotted arrow represents the MD trajectory from 7:00 a.m. to 8:00 p.m. on a given day, as predicted by GNOME. On this trajectory, we can select three locations (represented by a circle) from each of the three periods in the morning, midday and evening.

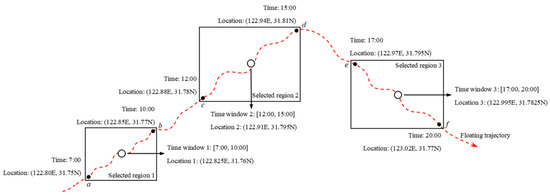
Figure 3. Drifting time window diagram.

There are three square or rectangular regions along the trajectory, called selected regions, each covering a non-overlapping segment of the trajectory. The black solid dot indicates the starting or ending point within each selected region, while the hollow circle is the midpoint of the line between the starting and ending points of each selected region. The location of each point is expressed by longitude and latitude coordinates, which is determined by GNOME software. We take the circle as the inference point of MD for the selected region, namely an MDL. Its coordinates and time window are determined by the starting and ending points in the selected region. There are three drifting time windows (MDLs) in Figure 3. For example, in selected region 1, the time and location of the starting point $a$ and ending point $b$ are 7:00 a.m. (122.80 E, 31.75 N) and 10:00 a.m. (122.85 E, 31.77 N), respectively. Therefore, the time window and location of the inference point in selected region 1 are [7:00, 10:00] and (122.825 E, 31.76 N), respectively.

3.2.2. Logistics Space–Time Network

Since each MD has multiple MDLs along its drifting trajectory, each MDL corresponding to an inference point, we can define a logistics space–time network through it. Each inference point of each MD in a selected region is taken as a vertex in a network. Figure 4 shows an example of a logistics space-time network with two MD and eight vertices, including six inference points (circles), an origin (square) and a destination (square). There are two numbers on each vertex, of which the first represents the time window and the second MD. For example, (1, 2) is the location of MD 2 in the first time window. Each column of vertices belongs to the same MD, indicating its different time and location, and their first number is sorted by the time window from small to large. For example, (1, 1), (2, 1) and (3, 1), respectively, represent the location of MD 1 in three time windows. Each row of vertices has the same time window range, reflecting the distribution of different MD in the same time window. For example, (1, 1) and (1, 2) represent the locations of the two MD in the first time window. For the sake of modeling, a port is divided into two vertices, an origin and a destination, labeled (0, 0) and (4, 3), respectively.

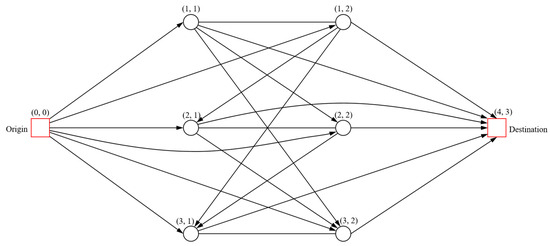
Figure 4. Logistics space–time network of MD.

Only vertices between different columns have edges. Since the vertices in the same column all belong to the same MD, there are no edges between them. There are two types of edges in Figure 4, where undirected edges exist between vertices in the same row and directed edges exist between vertices in different rows. Also, in a directed edge, the first number of the starting vertex must be smaller than that of the ending vertex, which is limited by time. Our model is based on the logistics space–time network.

3.2.3. VRPDTW and Speed Optimization Model

In the first stage, we will model the VRPDTW and speed with the goal of minimizing the total travel time. The model follows the following assumptions. 1. There is one port, which is divided into two vertices. 2. A homogeneous fleet of the same maximum deadweight and volume. 3. The weight and volume of each MD shall not exceed the maximum deadweight and volume of the vessel. 4. The mass and volume of MD do not change, i.e., the decomposition and sinking of MD during floating are not considered. 5. Each MD has the same number of time windows. If the time window corresponds to the same number, the time range is also the same. With the same numbered time window, they also have the same time range.

Based on the above logistics space–time network, a group of appropriate mathematical notations used in the VRPDTW and speed model can be defined, whose descriptions are shown in Table 1.

Table 1. Mathematical notations and descriptions in the VRPDTW and speed optimization model.

Sets:
$T_0$	Set of time window for origin, $T_0=\left\{0\right\}$
$T_1$	Set of time windows of MDs, $T_1=\left\{\mathrm{1,2}\dots ..m\right\}$
$T_2$	Set of time window for destination, $T_2=\left\{m+1\right\}$
$N$	Set of all vertices, $N=N_0\cup N_1\cup N_2$
$N_0$	Set of origin, $N_0=\left\{0\right\}$
$N_1$	Set of MDs, $N_1=\left\{\mathrm{1,2}\dots ..n\right\}$
$N_2$	Set of destination, $N_2=\left\{n+1\right\}$
$\left(T,N\right)$	Set of edges, $\left(T,N\right)=\left(T_0,N_0\right)\cup \left(T_1,N_1\right)\cup \left(T_2,N_2\right)$
$\left(T_0,N_0\right)$	Set of origin with time window, $\left(T_0,N_0\right)=\left\{\left(\mathrm{0,0}\right)\right\}$
$\left(T_1,N_1\right)$	Set of MDLs, $\left(T_1,N_1\right)=\left\{\right(h,i\left)\right|h\in T_1,i\in N_1\}$
$\left(T_2,N_2\right)$	Set of destination with time window, $\left(T_2,N_2\right)=\left\{\right(m+1,n+1\left)\right\}$
$E$	Set of all edges, $E=E_0\cup E_1\cup E_2$
$E_0$	Set of edges from origin with time window to an MDL, $E_0=\left\{\left(\mathrm{0,0},k,j\right)|\left(\mathrm{0,0}\right)\in \left(T_0,N_0\right),(k,j)\in \left(T_1,N_1\right)\right\}$
$E_1$	Set of edges from one MDL to another, $E_1=\left\{\left(h,i,k,j\right)|\left(h,i\right),(k,j)\in \left(T_1,N_1\right),h\le k,i\ne j\right\}$
$E_2$	Set of edges from an MDL to destination with time window, $E_2=\left\{\left(h,i,m+1,n+1\right)|\left(h,i\right)\in \left(T_1,N_1\right),(m+1,n+1)\in \left(T_2,N_2\right)\right\}$
$P$	Set of vessels
Parameters:
$r_i$	MD collection time at vertex $i\in N$
$o_i$	MD volume at vertex $i\in N$
${\rho }_i$	MD density at vertex $i\in N$
$\left[t_{hi}^e,t_{hi}^l\right]$	Time window of vertex $\left(h,i\right)\in \left(T,N\right)$, $t_{hi}^e$ and $t_{hi}^l$ are the earliest time and the latest time, respectively
$V_{\mathrm{m}\mathrm{a}\mathrm{x}}$	Maximum design speed of the vessel
$C_p^w$	Weight capacity of vessel $p\in P$
$C_p^o$	Volume capacity of vessel $p\in P$
$d_{hikj}$	Distance of edge $\left(h,i,k,j\right)\in E$
Decision variables:
$x_{hikjp}$	1 if vessel $p\in P$ transfers edge $(h,i,k,j)\in E$; 0 otherwise
$Q_{phi}^o$	Cumulative loaded volume of vessel $p\in P$ at vertex $(h,i)\in \left(T,N\right)$
$Q_{phi}^w$	Cumulative loaded weight of vessel $p\in P$ at vertex $(h,i)\in \left(T,N\right)$
$v_{hikjp}$	The speed of vessel $p\in P$ on edge $(h,i,k,j)\in E$
$t_{phi}^a$	Arrival time of vessel $p\in P$ at vertex $(h,i)\in \left(T,N\right)$

The first MILP model for VRPDTW including speed optimization is proposed below.

$$\min F_1=\sum _{p\in P}\left(t_{m+1,n+1,p}^a-t_{\mathrm{0,0},p}^a\right)$$

(1)

Subject to

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\left(k,j\right)\in \left(T_1,N_1\right)}}{x}_{\mathrm{0,0},k,j,p}=1\hfill & \hfill p\in P\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}h\le k\\ \left(h,i\right)\in \left(T_0,N_0\right)\cup \left(T_1,N_1\right)\end{array}}}{x}_{hikjp}={\displaystyle \sum _{\begin{array}{c}g\ge k\\ \left(g,l\right)\in \left(T_1,N_1\right)\cup \left(T_2,N_2\right)\end{array}}}{x}_{kjglp}\hfill & \hfill p\in P,(k,j)\in \left(T_1,N_1\right)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\left(k,j\right)\in \left(T_1,N_1\right)}}{x}_{\mathrm{0,0},k,j,p}={\displaystyle \sum _{\left(h,i\right)\in \left(T_1,N_1\right)}}{x}_{h,i,m+1,n+1,p}\hfill & \hfill p\in P\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\displaystyle \sum _{p\in P}}{\displaystyle \sum _{\begin{array}{c}h\le k\\ \left(h,i\right)\in \left(T_0,N_0\right)\cup \left(T_1,N_1\right),k\in T_1\end{array}}}{x}_{hikjp}=1\hfill & \hfill j\in N_1\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill t_{phi}^a+r_i+{\displaystyle \frac{d_{hikj}}{v_{hikjp}}}{x}_{hikjp}\le t_{pkj}^a+\left(1-x_{hikjp}\right)M_{hikjp}\hfill & \hfill p\in P,\left(h,i,k,j\right)\in E\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill t_{kj}^e{\displaystyle \sum _{\begin{array}{c}h\le k\\ \left(h,i\right)\in \left(T_0,N_0\right)\cup \left(T_1,N_1\right)\end{array}}}{x}_{hikjp}\le t_{pkj}^a\le t_{kj}^l{\displaystyle \sum _{\begin{array}{c}h\le k\\ \left(h,i\right)\in \left(T_0,N_0\right)\cup \left(T_1,N_1\right)\end{array}}}{x}_{hikjp}\hfill & \hfill p\in P,\left(k,j\right)\in \left(T,N\right)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill Q_{phi}^o+o_i\le Q_{pkj}^o+\left(1-x_{hikjp}\right)C_p^o\hfill & \hfill p\in P,\left(h,i,k,j\right)\in E\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill Q_{phi}^w+{\rho }_i{o}_i\le Q_{pkj}^w+\left(1-x_{hikjp}\right)C_p^w\hfill & \hfill p\in P,\left(h,i,k,j\right)\in E\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill Q_{p,m+1,n+1}^o\le C_p^o\hfill & \hfill p\in P\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill Q_{p,m+1,n+1}^{\mathrm{w}}\le C_p^w\hfill & \hfill p\in P\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill v_{hikjp}\le V_{\mathrm{m}\mathrm{a}\mathrm{x}}\hfill & \hfill p\in P,\left(h,i,k,j\right)\in E\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill Q_{p,\mathrm{0,0}}^o=0\hfill & \hfill p\in P\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill Q_{p,\mathrm{0,0}}^w=0\hfill & \hfill p\in P\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill t_{p,\mathrm{0,0}}^{\mathrm{a}}=t_{\mathrm{0,0}}^{\mathrm{e}}\hfill & \hfill p\in P\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill x_{hikjp}\in \left\{\mathrm{0,1}\right\}\hfill & \hfill p\in P,\left(h,i,k,j\right)\in E\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill v_{hikjp}\ge 0\hfill & \hfill p\in P,\left(h,i,k,j\right)\in E\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill Q_{phi}^{\mathrm{u}},Q_{phi}^{\mathrm{w}},t_{phi}^{\mathrm{a}}\ge 0\hfill & \hfill p\in P,\left(h,i\right)\in \left(T,N\right)\hfill \end{array}$$

(18)

The objective function (1) minimizes the total travel time of all vessels, which is equal to the sum of the difference between the return time and the departure time of each vessel. Constraint (2) ensures that all vessels depart from the port only once. Constraint (3) requires the equilibrium flow at each MDL to reach the conservation state. Constraint (4) ensures that all vessels return to port. Constraint (5) guarantees that for the same MD, one and only one MDL will be collected by one vessel. Constraint (6) calculates the arrival time of each vessel at each vertex, where $M_{hikjp}=t_{hi}^l+r_i+{\displaystyle \frac{d_{hikj}}{v_{hikjp}}}$. Constraint (7) is a time window constraint. Constraints (8) and (9) are used to calculate the cumulative volume and weight of MD collected when the vessel reaches each MDL on its route. Constraints (10) and (11) ensure that the cumulative volume and weight of MD loaded by each vessel do not exceed the maximum volume and weight capacity. Constraint (12) ensures that vessel speed on each edge does not exceed the maximum designed speed. Constraints (13) and (14) ensure that each vessel is empty when it leaves the port. Constraint (15) initializes vessel departure time. Constraints (16), (17) and (18) are variable declarations.

3.3. Second Stage

3.3.1. Power Demand

In the second stage, the OPF model will be proposed to optimize the power output of HES for each vessel. After obtaining the route and speed in the first stage, we can easily determine the power requirements of each vessel in each period. For the convenience of calculation, we take one hour as a time period to calculate the power demand of each vessel and take it as the input parameter of the second stage. The power demand of each vessel is related to its working condition, speed and working time. There are two working conditions in the MD cleaning process, navigation and collection. When there is only one working condition in a period, its power demand is easy to calculate. Since vessels remain at a low speed or stationary during MD collection, its power demand is relatively fixed and is set to a fixed value. In the sailing state, its power demand is proportional to the speed curve, which is specifically calculated by Equation (19).

$$\begin{array}{c}Powerdemandperhourduringsailing\hfill \\ ={\left({\displaystyle \frac{actualspeed}{maximumdesignedspeed}}\right)}^3\hfill \\ \times \left(thepowerdemandperhouratmaximumdesignedspeed\right)\hfill \end{array}$$

(19)

When there are multiple combinations of working conditions in a period, the total power demand in the period is equal to the sum of the duration of each working condition multiplied by the respective power demand per hour.

3.3.2. PV Output

In order to optimize the power flow distribution of HES, we also need to predict the PV output power in each period. The PV output power is not only related to the parameters of the module but is also affected by the ambient temperature and illumination intensity. We use the calculation method for PV output power introduced by Tang et al. [29], as shown in Equations (20) and (21).

$$\left\{\begin{array}{l}I=I_{SC}\left\{1-D_1\left[\exp \left({\displaystyle \frac{V}{D_2{V}_{OC}}}\right)-1\right]\right\}\\ D_1=\left(1-{\displaystyle \frac{I_m}{I_{SC}}}\right)\exp \left({\displaystyle \frac{-V_m}{D_2{V}_{OC}}}\right)\\ D_2=\left({\displaystyle \frac{V_m}{V_{OC}}}-1\right){\left[\mathrm{l}\mathrm{n}\left(1-{\displaystyle \frac{I_m}{I_{SC}}}\right)\right]}^{-1}\end{array}\right.$$

(20)

$$\left\{\begin{array}{l}{I}_{SC}=I_{SCr}{\displaystyle \frac{S}{S_r}}\left[1+a\left(T-T_r\right)\right]\\ \begin{array}{l}{V}_{OC}=V_{OCr}\mathrm{l}\mathrm{n}\left[e+b\left(S-S_r\right)\right]\left[1-c\left(T-T_r\right)\right]\\ I_m=I_{mr}{\displaystyle \frac{S}{S_r}}\left[1+a\left(T-T_r\right)\right]\\ V_m=V_{mr}\mathrm{l}\mathrm{n}\left[e+b\left(S-S_r\right)\right]\left[1-c\left(T-T_r\right)\right]\end{array}\end{array}\right.$$

(21)

In the above two equations, $S_r$ and $T_r$ are the reference irradiation and temperature, which are 1000 $\mathrm{W}/{\mathrm{m}}^2$ and 25 °C, respectively. $S$ and $T$ are the actual irradiation and temperature, respectively. $I_{SCr}$, $V_{OCr}$, $I_{mr}$ and $V_{mr}$ are the parameters of the PV panel. The parameters, $a$, $b$ and $c$, are compensation coefficients, and take values of 0.0025/°C, 0.0005 $\mathrm{W}/{\mathrm{m}}^2$ and 0.00288/°C, respectively. $e$ is the base of the natural logarithm. Obviously, in order to calculate the PV output power, the actual data of irradiation must be obtained. We will describe a specific method for improving prediction accuracy according to historical data in Section 5.

3.3.3. OPF Model

We abide by the following assumptions for the OPF model. 1. The routes and speeds solved in the first stage are taken as input parameters in the second stage. 2. The parameters of the HES for each vessel are the same. 3. In order to protect the battery, it cannot be charged and discharged at the same time, and the state of charge (SOC) has upper and lower limits. 4. We consider the loss of electric quantity in the charging and discharging process. 5. Both PV and diesel generators can feed load and charge the battery at the same time.

Table 2 lists the sets, parameters, and variables used in the OPF model.

Table 2. Mathematical notations and descriptions in the OPF model.

Set:
$\overline{T}$	Set of all periods, $\overline{T}=\left\{\mathrm{1,2},\cdots ,\overline{n}\right\}$
Parameters:
$C_1$	Loss cost of PV power generation
$C_2$	Cost of diesel
$C_3$	Loss cost of battery charging and discharging
$f^{\mathrm{ct}}$	Carbon tax rate
$e$	Carbon emission factor
$\alpha$	Diesel intercept coefficient
$\beta$	Diesel slope coefficient
$W_{pt}^{\mathrm{l}}$	Power required for load of vessel $p\in P$ in period $t\in \overline{T}$
$W_t^{\mathrm{p}}$	Maximum output power of PV in period $t\in \overline{T}$
${\eta }^{\mathrm{c}}$	Battery charging efficiency
${\eta }^{\mathrm{d}}$	Battery discharge efficiency
$S^{\mathrm{m}\mathrm{a}\mathrm{x}}$	Maximum value of battery SOC
$S^{\mathrm{m}\mathrm{i}\mathrm{n}}$	Minimum value of battery SOC
$W^{\mathrm{p}\mathrm{r}}$	Rated power of PV power
$W^{\mathrm{d}\mathrm{r}}$	Rated power of diesel generator
$W_1$	Maximum power of PV to vessel load
$W_2$	Maximum power of PV to battery
$W_3$	Maximum power of diesel generator to vessel load
$W_4$	Maximum power of diesel generator to battery
$W_5$	Maximum power of storage battery to vessel load
Decision Variables:
$X_{pt}^1$	Power of PV to load of vessel $p\in P$ in period $t\in \overline{T}$
$X_{pt}^2$	Power of PV to battery of vessel $p\in P$ in period $t\in \overline{T}$
$X_{pt}^3$	Power of diesel generator to load of vessel $p\in P$ in period $t\in \overline{T}$
$X_{pt}^4$	Power of diesel generator to battery in period $t\in \overline{T}$
$X_{pt}^5$	Power of storage battery to load of vessel $p\in P$ in period $t\in \overline{T}$
$S_{pt}$	Battery SOC of vessel $p\in P$ at the beginning of period $t\in \overline{T}$
$Y_{pt}^1$	1 if the battery of vessel $p\in P$ is charged in period $t\in \overline{T}$; 0 otherwise
$Y_{pt}^2$	1 if the battery of vessel $p\in P$ is discharged in period $t\in \overline{T}$; 0 otherwise
$Y_{pt}^3$	1 if the diesel generator of vessel $p\in P$ is on in period $t\in \overline{T}$; 0 otherwise

The objective is to minimize the total cost consisting of four costs. The first is the diesel generation cost of vessel $p$, $f_p^1$, defined by Equation (22). The diesel consumption of the diesel generator depends on its rated power and actual power, including the fixed consumption of diesel when the diesel generator is started and the consumption of diesel used to supply power to the vessel load and charge the battery.

$$f_p^1=C^2\sum _{t\in \overline{T}}\left(\alpha W^{\mathrm{d}\mathrm{r}}{Y}_{pt}^3+\beta (X_{pt}^3+X_{pt}^4)\right)$$

(22)

There is a fixed investment when installing PV equipment on a vessel. We take it as the PV generation cost in the form of depreciation loss and divide it by the power generation within its service life as the power generation cost per kWh, $f_p^2$. It includes two parts, power supply for vessel load and battery charging, which is designed by Equation (23).

$$f_p^2=C^1\sum _{t\in \overline{T}}(X_{pt}^1+X_{pt}^2)$$

(23)

Similarly, batteries also require a fixed investment. We take it as the charge and discharge cost $f_p^3$ in the form of the depreciation of charge and discharge, defined by Equation (24).

$$f_p^3=C^3\sum _{t\in \overline{T}}\left(X_{pt}^5+{\eta }^{\mathrm{c}}\left(X_{pt}^2+X_{pt}^4\right)\right)$$

(24)

Since the diesel generator generates carbon dioxide when consuming diesel for power generation, we consider the carbon tax cost $f_p^4$, which is determined by Equation (25) definitions. The amount of diesel consumed has been defined in Equation (22).

$${f_p^4=f}^{\mathrm{ct}}e\sum _{t\in \overline{T}}\left(\alpha W^{\mathrm{d}\mathrm{r}}{Y}_{pt}^3+\beta (X_{pt}^3+X_{pt}^4)\right)$$

(25)

The second MILP model for OPF is proposed below.

$$\mathrm{m}\mathrm{i}\mathrm{n}{F}_2=\sum _{p\in P}\sum _{q=1}^4{f}_p^q$$

(26)

Subject to

$$\begin{array}{cc}\hfill X_{pt}^1+X_{pt}^3+X_{pt}^5=W_{pt}^{\mathrm{l}}\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill S_{pt}=S_{p,t-1}+{\eta }^{\mathrm{c}}\left(X_{p,t-1}^2+X_{p,t-1}^4\right)-{\displaystyle \frac{1}{{\eta }^{\mathrm{d}}}}{X}_{p,t-1}^5\hfill & \hfill t\in \overline{T}\backslash \left\{1\right\},p\in P\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill S^{\mathrm{m}\mathrm{i}\mathrm{n}}\le S_{pt}\le S^{\mathrm{m}\mathrm{a}\mathrm{x}}\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{{\eta }^{\mathrm{d}}}}{X}_t^5\le S_{pt}-S^{\mathrm{m}\mathrm{i}\mathrm{n}}\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill S_{p,m+1}\ge S_{p1}\hfill & \hfill p\in P\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill X_{pt}^1+X_{pt}^2\le W_t^{\mathrm{p}}\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill X_{pt}^1+X_{pt}^2\le W^{\mathrm{p}\mathrm{r}}\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill X_{pt}^3+X_{pt}^4\le W^{\mathrm{d}\mathrm{r}}\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill Y_{pt}^1+Y_{pt}^2\le 1\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill X_{pt}^2+X_{pt}^4\le M{Y}_{pt}^1\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill X_{pt}^2+X_{pt}^4\ge Y_{pt}^1/M\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill X_{pt}^5\le M{Y}_{pt}^2\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill X_{pt}^5\ge Y_{pt}^2/M\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill X_{pt}^3+X_{pt}^4\le M{Y}_{pt}^3\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill X_{pt}^3+X_{pt}^4\ge Y_{pt}^3/M\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill X_{pt}^i\le W_i\hfill & \hfill t\in \overline{T},i=1,\dots ,5,p\in P\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill X_{pt}^1,X_{pt}^2,X_{pt}^3,X_{pt}^4,X_{pt}^5\ge 0\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill Y_{pt}^1,Y_{pt}^2,Y_{pt}^3\in \left\{\mathrm{0,1}\right\}\hfill & \hfill t\in \overline{T},p\in P\hfill \end{array}$$

(44)

The objective function (26) minimizes the total cost, which is the sum of four costs of all vessels used. Constraint (27) refers to the power load balance. The vessel load demand is supplied by PV, diesel generators and batteries. The constraint (28) represents the SOC of the battery at the end of each period, considering the loss of charge and discharge. Constraint (29) represents the SOC range of the battery in each period. Constraint (30) means the power limitation for the battery to power the load. Constraint (31) indicates that the battery charge in the end of the last period shall not be less than the one in the initial period. Constraints (32) and (33) indicate that the PV output power in each period shall not be higher than its maximum output power and rated power in that period. Constraint (34) indicates that the output power of the diesel generator shall not be higher than its rated power. Constraint (35) indicates that the battery cannot be charged and discharged at the same time. Constraints (36)–(39) are logic constraints, which represent the relationship between battery charging and discharging, where $M$ is a big positive number. Constraints (40) and (41) refer to the switching state of the diesel generator. Constraint (42) includes the maximum power limits of each energy transformation. Constraints (43) and (44) are variable declarations.

Since the above model is vessel independent and there are few time periods, resulting in few variables, we use YALMIP in MATLAB to use the CPLEX 12.10 solver to solve the model.

4. Solution Algorithm for VRPDTW

We propose a heuristic method, ALNSES algorithm, based on an ALNS algorithm coupled with an elitist strategy and SOA to solve the SRPDTW and speed model in the first stage. The ALNS algorithm proposed by Ropke and Pisinger [40] for the vehicle routing problem is based on the large neighborhood search algorithm. It adds a variety of removal operators and insertion operators, and assigns weights to them respectively, which is the basis of the probability of being selected. In the iterative process of the algorithm, the weight of each operator is dynamically adjusted according to the quality of the new solution generated by the operator. This algorithm has been successfully applied to combinatorial optimization, especially to routing and scheduling problems [41,42,43]. Interested readers can refer to the thorough summary of ALNS algorithms by Mara et al. [44].

After the ALNS algorithm is executed, we optimize the speed to obtain the minimum travel time. To improve the solution quality, we also take advantage of the population optimization method and introduce the elite strategy, that is, the parent and child populations are merged into a large population and the best individuals are selected from it to form a new population.

4.1. Removal Operators

The removal operators select one or more MDLs according to a certain rule and remove them from a feasible solution (routes), so as to destroy the original feasible solution and prepare for the construction of a new solution. We design eight removal operators, some of which remove $num$ MDLs at a time from a feasible solution, and others remove one MDL at a time by repeating the operation $num$ times. After removing an MDL, its corresponding MD is added to the set $\Omega$.

1. Random removal. The operator takes the distance between MDLs as the removal rule, selects an MDL at random and calculates its distance from other MDLs in the feasible solution. Then, it removes the num MDLs nearest to it. Note that the initially selected MDL will not be removed.

2. Regional Removal. The operator takes the vessel loading rate as the removal criterion, randomly selects an MDL, calculates the distance from other MDLs in the feasible solution, and removes the nearest $num$ MDLs. Note that the initially randomly selected MDL will not be removed.

3. Vessel Removal. The operator takes the distance between MDLs as the removal rule. The vessel loading rate $R_p^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ is related to the loading volume and weight, which can be calculated according to Equation (44).

$$R_p^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}={\displaystyle \frac{Q_{p,m+1,n+1}^o}{C_p^o}}\times {\displaystyle \frac{Q_{p,m+1,n+1}^w}{C_p^w}}$$

(45)

In Equation (44), $C_p^o$ and $C_p^w$ are the volume and weight capacities of vessel $p$, respectively; $Q_{p,m+1,n+1}^o$ and $Q_{p,m+1,n+1}^w$ are the accumulated volume and weight when vessel $p$ returns to port. The larger $R_p^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}$ is, the higher the vessel loading rate is. The loading rates of all ships are calculated. All MDLs on the vessel with the smallest loading rate are removed. Note that the number of MDLs removed by this operator can be different from $num$.

4. Similarity Removal. This operator takes the similarity between MDLs as the removal criterion. The similarity $\Phi \left((h,i),(k,j)\right)$ of two MDLs $(h,i)$ and $(k,j)$, including the following information: location, time window, volume and weight of MD and route, is specifically defined by Equation (46).

$$\Phi \left((h,i),(k,j)\right)={\displaystyle \frac{1}{{\omega }_1{d}_{hikj}+{\omega }_2\left(\left|t_{hi}^e-t_{kj}^e\right|+\left|t_{hi}^l-t_{kj}^l\right|\right)+{\omega }_3\left|u_i-u_j\right|+{\omega }_4\left|{\rho }_i{u}_i-{{\rho }_{j}u}_j\right|+{\omega }_5{a}_{hikj}}}$$

(46)

In Equation (45), ${\omega }_q$ is the weight coefficient and satisfies $\sum _{q=1}^5{\omega }_q=1$. $d_{hikj}$ is the distance between $(h,i)$ and $(k,j)$. $\left|t_{hi}^e-t_{kj}^e\right|+\left|t_{hi}^l-t_{kj}^l\right|$ is the absolute value of the difference between the time windows of two MDLs. $\left|u_{hi}-u_{kj}\right|$ and $\left|{\rho }_{hi}{u}_{hi}-{{\rho }_{kj}u}_{kj}\right|$ are the absolute values of the difference between the volume and weight of two MDLs, respectively. The last term in the denominator $a_{hikj}$ is 0–1 variable, which takes the value 1 when two MDLs are on the same route, and 0 otherwise. Obviously, the larger $\Phi \left((h,i),(k,j)\right)$ is, the higher is the similarity between $(h,i)$ and $(k,j)$. With roulette, the higher the similarity of MDL, the higher the probability of being selected. Note that an MDL is randomly selected as the first one to be removed.

5. Partial Similarity Removal. This operator is a special version of Similarity Removal, considering only volume and weight, i.e., ${\omega }_3+{\omega }_4=1$ in Equation (45).

6. Distance Removal. Removing an MDL from a route will reduce the route distance. This operator removes the MDL with the largest distance reduction each time, and a total of $num$ MDLs are removed.

7. Sailing Time Removal. Similar to Distance Removal, this operator is based on the most reduced sailing time in a route.

8. Average Sailing Time Removal. This operator takes the average sailing time per edge as the removal rule. The average sailing time per edge in a route is the total sailing time excluding debris collection time divided by the number of edges. After an MDL is removed, the new average sailing time per edge will change. The MDL with the largest change is removed sequentially.

4.2. Insertion Operators

The insertion operators reinsert an MDL belonging to an MD in set $\Omega$ into a route and satisfiy all the constraints. Then remove the MDL from set $\Omega$ until the set is empty. Four insertion operators are designed.

1. Greedy Insertion. The operator is based on the distance increment after an MDL is inserted into a route. According to the greedy principle, insert an MDL at the location with the smallest distance increment among all routes.

2. Random Number Based Greedy Insertion. Based on Distance-Based Greedy Insertion, we multiply the maximum distance increment by a random number in the interval [−0.1, 0.1], and then add the product to each distance increment. The selection of insertion position is the same as Greedy Insertion.

3. Regret Value Insertion. The operator takes the difference between the second smallest value and the minimum value of the distance increment as the regret value. The regret value is calculated for the MDLs belonging to each MD in $\Omega$, and then the MDL with the largest regret value is successively selected to be inserted into the position with the smallest distance increment.

4. Random Number-Based Regret Value Insertion. Combining Regret Value Insertion and Random Number-Based Greedy Insertion, add the regret value of each MDL of MD in $\Omega$ to the product of the maximum distance increment and a random number in the interval [−0.1, 0.1].

4.3. Speed Optimization

After each removal and insertion operation, the speed of each edge in each route needs to be optimized to obtain a new descendant solution. Since the objective function is the shortest travel time, the idea of speed optimization is to make the vessel arrive at each vertex as early as possible without violating the time window. The pseudo code of the speed optimization algorithm is described in Appendix A.

4.4. Adaptive Operator Selection Mechanism

4.4.1. Selection Probability

The selection probability of each operator in each iteration of the ALNS algorithm is determined by its weight. The smaller the objective function value, the higher the operator weight is. In this way, the operator with a smaller objective function value can be selected more easily. When adjusting the operator weight, we divide the algorithm iteration process into multiple cycles and adjust the weight periodically.

Taking the removal operator as an example, the weight $w_{ms}$ of the removal operator $s$ in the m-th update cycle is calculated by Equation (47).

$$w_{ms}=\left\{\begin{array}{c}{\theta w}_{m-1,s}+\left(1-\theta \right){\displaystyle \frac{S_{m-1,s}}{t_{m-1,s}}},t_{m-1,s}>0\\ \theta w_{m-1,s},t_{m-1,s}=0\end{array}\right.$$

(47)

In Equation (47), $w_{m-1,s}$ is the weight of the removal operator $s$ in the $(m-1)$-th cycle. $\theta \in \left(\mathrm{0,1}\right)$ is the transfer factor, which represents the influence degree of the weight in the last cycle on the current weight. $t_{m-1,s}$ is the number of times operator $s$ is selected in the $\left(m-1\right)$-th cycle. And $S_{m-1,s}$ means the cumulative score of operator $s$ in the $\left(m-1\right)$-th cycle (see next subsection for details).

The probability $P_{ms}$ of operator $s$ being selected in the $m$-th cycle is calculated by Equation (48), where $RO$ is the set of removal operators. Note that in the first cycle, the weight of each operator is set to 1, so the selection probability of each operator is the same.

$$P_{ms}={\displaystyle \frac{w_{ms}}{\sum _{s^{\prime }\in RO}{w}_{{ms}^{\prime }}}}$$

(48)

4.4.2. Operator Score

After an iteration, including removal, insertion and speed optimization, we will score each operator according to its performance. If the child solution is better than the parent solution and the current best solution at the same time, the operator’s score is ${\zeta }_1$. If the child solution is better than the parent solution but inferior to the current best solution, the operator’s score is ${\zeta }_2$. If the child solution is worse than the parent solution and the current best solution at the same time, the operator’s score is ${\zeta }_3$. And ${\zeta }_1>{\zeta }_2>{\zeta }_3$ is satisfied. Each time an operator is selected, its number of uses is increased by 1. In a cycle, the cumulative score of each operator is the sum of each score. Initialize the cumulative score and usage times of all operators before each cycle.

4.4.3. Elitist Strategy

In the ALNS algorithm, if the child solution is inferior to its parent solution, it is directly discarded. Although this comparison is intuitive, it is not comprehensive, which may lead to the rejection of the better child solution and the retention of the worse child solution. For this reason, we introduce the elitist strategy, which can preserve excellent solutions in the parent and child generations, thus improving the solution quality. Let the population size be $N$. In the iteration, the parent and child populations are combined to form a $2N$ population, and the first $N$ individuals with the shortest total travel time are selected as a new population.

In summary, Algorithm 1 shows the pseudo code of the proposed ALNSES algorithm.

Algorithm 1 ALNSES algorithm

Input: population size $N$, maximum iterations $Maxlter$, weight update cycle $M$, removal operator set $RO$, insertion operator set $IO$, removal operator weight set $W_{RO}$, insertion operator weight set $W_{IO}$, removal operator score set $S_{RO}$, insertion operator score set $S_{IO}$, score ${\zeta }_1$, ${\zeta }_2$, ${\zeta }_3$, transfer factor $\theta$, removal operator probability set $P_{RO}$, insertion operator probability set $P_{IO}$. Output: $x^{best}$

Generate an initial feasible solutions population $X=\left\{x_1,\dots ,x_N\right\}$ Find the best solution $x^{best}\in X$ $C=0$

$gen=1$ Initialize $W_{RO}$ and $W_{IO}$

while $gen<Maxlter$

for $i=1,\dots ,N$

Select removal operator $\overline{r}\in RO$ and insertion operator $\overline{i}\in IO$ according to $P_{\overline{r}}\in P_{RO}$ and $P_{\overline{i}}\in P_{IO}$, respectively

Perform operators $\overline{r}$ and $\overline{i}$ on a feasible solution $x_i$ to obtain $x_i^{new}$

Perform SO algorithm on $x_i^{new}$ to obtain ${\overline{x}}_i^{new}$

if ${\overline{x}}_i^{new}<x_i$

if ${\overline{x}}_i^{new}<x^{best}$

$x^{best}={\overline{x}}_i^{new}$

$S_{RO}\left(\overline{r}\right)=S_{RO}\left(\overline{r}\right)+{\zeta }_1$

$S_{IO}\left(\overline{r}\right)=S_{IO}\left(\overline{r}\right)+{\zeta }_1$

else

$S_{RO}\left(\overline{r}\right)=S_{RO}\left(\overline{r}\right)+{\zeta }_2$

$S_{IO}\left(\overline{r}\right)=S_{IO}\left(\overline{r}\right)+{\zeta }_2$

end

else

$S_{RO}\left(\overline{r}\right)=S_{RO}\left(\overline{r}\right)+{\zeta }_3$

$S_{IO}\left(\overline{r}\right)=S_{IO}\left(\overline{r}\right)+{\zeta }_3$

end

$C=C+1$

if $C$ mod $M$ = 0

Update $W_{RO}$ and $W_{IO}$ according to Equation (46)

Update $P_{RO}$ and $P_{IO}$ according to Equation (47)

end

end

Merge parent population $X$ and offspring population ${\overline{X}}^{new}$ to obtain population $X^{all}$

Update population $X$: Perform Elite strategy on $X^{all}$ to obtain new parent population $X$

$gen=gen+1$

end

Print $x^{best}$

5. Numerical Experiment

5.1. Experiment Data

In order to verify our proposed two models and the ALNSES algorithm, this section takes a set of MD data from the estuary of the Yangtze River to the East China Sea as a case study, where Yangshan Port is the round-trip port. The parameters including weight capacity, volume capacity, and the maximum sailing speed used for vessels are 12.5 tons, 16 m³ and 40 km/h, respectively. The number of time windows for each MD is set to 3. After using remote sensing to obtain the initial locations of all MDs, we employ the diagnostic mode of GNOME software to predict the drifting trajectory of MDs. Figure 5 shows the drifting trajectory and distribution of 30 MDs in one day, where Figure 5a, Figure 5b and Figure 5c, respectively, draw three groups of MDLs in three time windows [7, 10], [13, 15], and [17.5, 19.5]. The red dot indicates the MDL, and the size indicates the volume information of the MD. The number in the red dot indicates its corresponding serial number. The black five-pointed star is the location of Yangshan port. Information on MDs, including weight, volume, and collection time, as well as the locations of the port and MDs are provided in Table 3 and Table 4, respectively. The experiment is carried out on a laptop equipped with a Windows 10 operating system, 1.8 GHz AMD Ryzen 7 processor and 16 GB memory. The software used for the algorithm is MATLAB R2018b. Table 5 lists the parameters defined in the proposed algorithm.

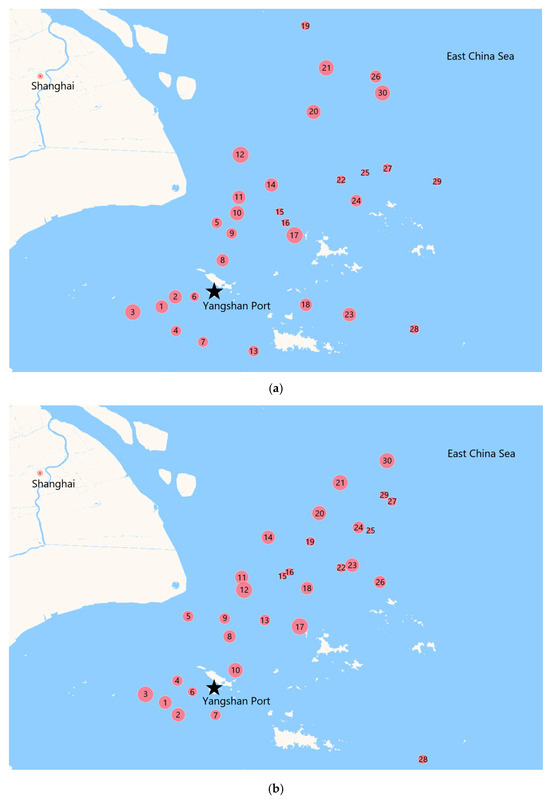
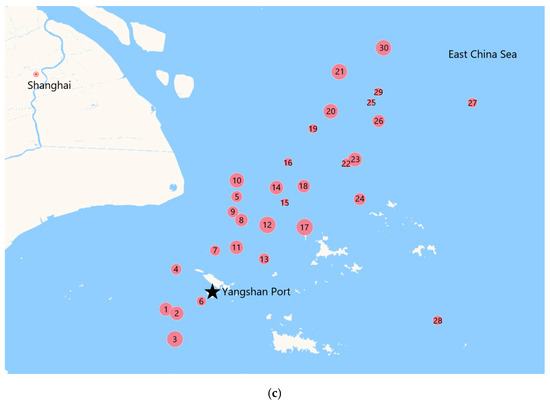
Figure 5. The distribution of MDs. (a) MDLs in time window [7, 10]; (b) MDLs in time window [13, 15]; (c) MDLs in time window [17.5, 19.5].

Table 3. MD information.

Debris No.	1	2	3	4	5	6	7	8	9	10
Weight (tons)	1.91	2.16	2.55	1.27	1.59	1.01	1.13	2.07	1.37	2.64
Volume (m3)	2.67	2.81	3.57	1.78	1.91	1.31	1.69	2.48	1.92	3.17
Collection time (h)	1.1	1.1	1.5	0.9	0.9	0.8	0.9	1.0	0.9	1.3
Debris No.	11	12	13	14	15	16	17	18	19	20
Weight (tons)	2.15	2.52	1.24	1.87	0.53	0.71	2.92	2.09	0.97	2.07
Volume (m3)	2.80	3.78	1.86	2.81	0.69	0.92	3.8	2.51	1.26	3.1
Collection time (h)	1.1	1.6	0.9	1.1	0.6	0.9	1.6	1.0	0.8	1.2
Debris No.	21	22	23	24	25	26	27	28	29	30
Weight (tons)	2.67	1.09	1.91	1.60	0.33	1.83	1.01	1.12	0.66	2.87
Volume (m3)	3.47	1.31	2.87	2.24	0.39	2.38	1.31	1.35	0.98	3.45
Collection time (h)	1.5	0.8	1.1	1.0	0.5	1.0	0.8	0.8	0.7	1.4

Table 4. Location information.

Time Window	[7, 10]		[13, 15]		[17.5, 19.5]
Debris No.	Latitude	Longitude	Latitude	Longitude	Latitude	Longitude
0	30.5922	122.0746	30.5922	122.0746	30.5922	122.0746
1	30.5443	121.8925	30.5497	121.9043	30.5403	121.9154
2	30.5735	121.9392	30.5130	121.9491	30.5280	121.9523
3	30.5284	121.7923	30.5736	121.8362	30.4521	121.9460
4	30.4722	121.9415	30.6140	121.9462	30.6576	121.9503
5	30.7940	122.0825	30.8051	121.9833	30.8706	122.1567
6	30.5745	122.0054	30.5816	121.9981	30.5639	122.0362
7	30.4397	122.0351	30.5124	122.0778	30.7127	122.0831
8	30.6824	122.1027	30.7435	122.1245	30.8020	122.1727
9	30.7625	122.1340	30.7987	122.1095	30.8261	122.1435
10	30.8226	122.1530	30.6455	122.1468	30.9182	122.1572
11	30.8695	122.1593	30.9207	122.1681	30.7218	122.1558
12	30.9958	122.1649	30.8834	122.1763	30.7876	122.2613
13	30.4125	122.2102	30.7941	122.2481	30.6881	122.2506
14	30.9061	122.2715	31.0390	122.2595	30.8971	122.2920
15	30.8272	122.3001	30.9263	122.3102	30.8544	122.3215
16	30.7945	122.3210	30.9369	122.3321	30.9719	122.3321
17	30.7571	122.3516	30.7753	122.3685	30.7811	122.3885
18	30.5500	122.3907	30.8887	122.3936	30.9011	122.3853
19	31.3781	122.3890	31.0267	122.4047	31.0695	122.4168
20	31.1228	122.4172	31.1103	122.4354	31.1205	122.4775
21	31.2529	122.4611	31.2005	122.5079	31.2359	122.5070
22	30.9215	122.5127	30.9489	122.5108	30.9687	122.5315
23	30.5210	122.5411	30.9569	122.5488	30.9795	122.5605
24	30.8596	122.5648	31.0681	122.5711	30.8633	122.5767
25	30.9438	122.5957	31.0588	122.6106	31.1471	122.6150
26	31.2275	122.6325	30.9067	122.6451	31.0919	122.6411
27	30.9562	122.6721	31.1450	122.6862	31.1455	122.9609
28	30.4777	122.7659	30.3808	122.7931	30.5073	122.8421
29	30.9171	122.8444	31.1642	122.6592	31.1774	122.6399
30	31.1789	122.6554	31.2654	122.6695	31.3057	122.6574

Table 5. The parameter values used in ALNSES algorithm.

Parameter	Value	Parameter	Value	Parameter	Value
${\omega }_1$	0.2	${\omega }_5$	0.2	$\theta$	0.7
${\omega }_2$	0.2	${\zeta }_1$	6	$N$	100
${\omega }_3$	0.2	${\zeta }_2$	3	$MaxIter$	300
${\omega }_4$	0.2	${\zeta }_3$	1	$M$	200

5.2. Algorithm Performance

The ALNSES algorithm for VRPDTW is run ten times, and the average running time of each time is 119.91 s. Six vessels are used with the total travel time of 53.52 h in the best solution we found. Table 6 lists the best solution we found, including route, speed on each edge, travel time, loaded weight and volume of each vessel. In the route column, 0 represents the port, and the subscript represents the time window number, where subscripts 1, 2 and 3 in route column, respectively, represent time windows [7, 10], [13, 15] and [17.5, 19.5]. In the speed column, since the speed is on the edge, it is one less than the number of vertices in the route column of the same row. Figure 6 depicts the best route of each vessel, with different colors representing different routes.

Table 6. Best solution for VRPDTW.

Vessel No.	Route	Speed (km/h)	Travel Time (h)	Loading Weight (tons)	Loading Volume (m3)
1	0-231-281-262-202-153-123-0	40, 40, 17.6946, 40, 16.8217, 40, 40	13.56	9.98	14.17
2	0-221-301-272-292-212-183-143-0	40, 40, 2.4726, 40, 40, 29.6628, 40, 40	13.72	12.26	15.84
3	0-81-161-171-192-252-242-133-113-0	40, 40, 40, 16.8198, 40, 40, 29.7806, 40, 40	13.11	11.99	15.75
4	0-61-41-71-0	40, 40, 40, 40	3.68	3.41	4.78
5	0-91-101-51-0	40, 40, 40, 40	4.35	5.6	7
6	0-21-11-31-0	40, 40, 40, 40	5.1	6.62	9.05

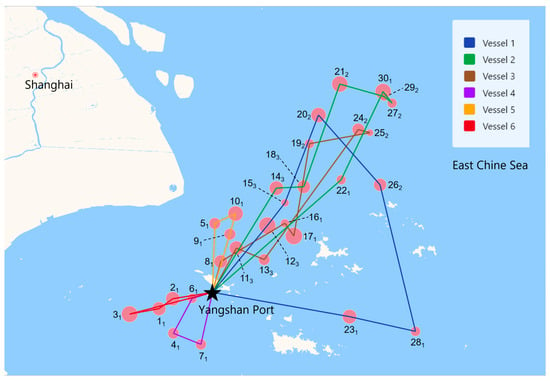
Figure 6. Best routes.

To show the convergence process of the proposed algorithm, we recorded the best total travel time in each iteration, as shown in Figure 7. It can be seen from Figure 7 that at the beginning, from 64.99 h in the first generation to 57.02 h in the 17th generation, the algorithm converges quickly. From 57.02 h in the 18th generation to 54.01 h in the 94th generation, the convergence rate is much slower than that of the previous 17 generations. From 54.01 h in the 95th generation to 53.68 h in the 163rd generation, the convergence speed slows down significantly. After that, there is no change in 97 iterations until the 260th generation dropped to 53.52 h and remains unchanged. This shows that the ALNSES algorithm has good convergence in solving the small-scale VRPDTW with 30 MDs and three time windows (90 vertices in total).

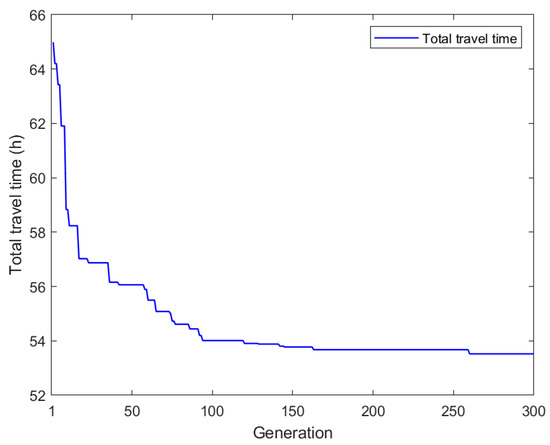
Figure 7. Convergence diagram.

We compare the ALNSES algorithm with the ALNS algorithm proposed by Duan et al. [11] under the same computer configuration conditions. Table 7 lists the results of running the two algorithms for ten times, respectively, including the total travel time and algorithm running time. The maximum, minimum and average running time of the ALNSES algorithm are 4.29%, 1.3% and 3% less than those of the ALNS algorithm, respectively, while the maximum, minimum and average total travel time of the ALNSES algorithm are 2.68%, 3.56% and 3.9% less than those of the ALNS algorithm, respectively. This shows that our proposed algorithm is superior to the ALNS algorithm in terms of running time and results. We evaluate the stability of the solution by two criteria: range (the difference between the maximum value and the minimum value) and variance. The range of the two algorithms is 1.08 and 2.82 h, respectively, while the variance is 0.3579 and 1.0081, respectively. The range and variance of the ALNSES algorithm are 61.79% and 64.40% smaller than those of the ALNS algorithm, respectively. Therefore, the ALNSES algorithm is obviously better than the ALNS algorithm in solving stability.

Table 7. Algorithm comparison.

Algorithm		Total Travel Time (h)	Running Time (s)
ALNSES	Min	53.52	114.23
	Max	54.6	124.4
	Average	53.81	119.91
ALNS	Min	54.22	117.37
	Max	57.04	128.99
	Average	55.48	124.77

In order to further verify the performance of ALNSES algorithm, we also tested problems of different scales, from 90 to 300 MDLs (vertices), and the calculation results are summarized in Table 8. We use quadratic polynomial, cubic polynomial and exponential functions to fit them, respectively. The corresponding fitting functions of the running time as shown in Figure 8 are $0.0346n^2-6.7037n+468.34$, $0.0001n^3-0.0271n^2+4.4376n-141.82$ and $40.701e^{0.0124n}$, respectively, where $n$ is the number of MDLs. The goodness-of-fit of the three functions are 0.9973, 0.9998 and 0.9977, respectively. It is obvious that the fitting effect of cubic polynomial function is the best. Therefore, the ALNSES algorithm has the characteristic of approximate cubic polynomial time when solving medium- and large-scale VRPDTW.

Table 8. Computation results of different scales.

MDL Scale	Total Travel Time (h)	Running Time (s)
90	53.81	119.91
120	74.73	172.58
150	98.9	270.15
180	118.7	407.84
210	134.61	570.98
240	160.28	811.16
270	179.09	1162.41
300	202.74	1598.78

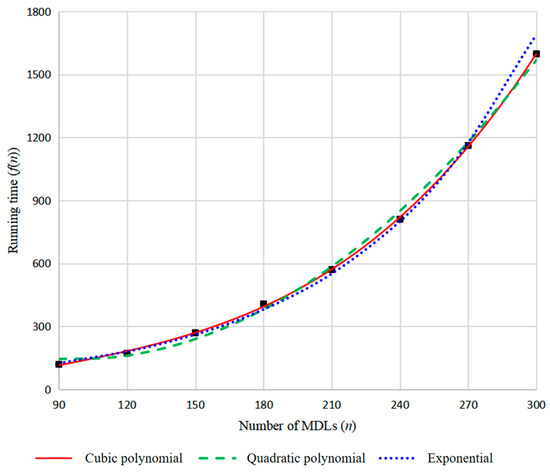
Figure 8. Fitting curve.

5.3. HES

5.3.1. Data

After obtaining the best route as well as speed in the first stage, the power demand of each vessel is determined. The power demand is taken as the input parameter in the second stage, and YALMIP in MATLAB to use CPLEX Solver software is employed to optimize the power flow allocation of HES for each vessel. We first introduce how to determine the power demand according to route and speed and then analyze the computational results of the OPF model. We set the initial SOC of the battery to 130 kW. Table 9 shows the information related to the OPF model. Among them, the PV power generation loss $C^{\mathrm{P}\mathrm{V}}$, and battery charge and discharge loss $C^{\mathrm{B}}$ come from the official website of Trinasolar Energy Co., LTD (https://www.trinasolar.com/en-apac), headquartered in Shanghai, China, accessed on 10 January 2022.

Table 9. The information related to the OPF model.

Parameter	Value
Rated power of PV $W^{\mathrm{p}\mathrm{r}}$	180 kW
Rated power of diesel generator $W^{\mathrm{d}\mathrm{r}}$	200 kW
Maximum value of battery SOC $S^{\mathrm{m}\mathrm{a}\mathrm{x}}$	400 kWh
Minimum value of battery SOC $S^{\mathrm{m}\mathrm{i}\mathrm{n}}$	120 kWh
Loss cost of PV power generation $C_1$	0.3 CNY/kWh
Cost of diesel $C_2$	6.4 CNY/L
Loss cost of battery charging and discharging $C_3$	0.3 CNY/kWh
Carbon tax rate $f^{\mathrm{ct}}$	0.14 CNY/kg
Carbon emission factor $e$	3.315
Diesel intercept coefficient $\alpha$	0.01609
Diesel slope coefficient $\beta$	0.2486
Battery charging efficiency ${\eta }^{\mathrm{c}}$	85%
Battery discharge efficiency ${\eta }^{\mathrm{d}}$	100%

Since the travel time of the six vessels does not exceed 14 h, we divide the whole process into 14 periods, with one hour as one period. We take vessel 1 as an example to analyze the computational results, where its route and the speed on each edge are 0-23₁-28₁-26₂-20₂-15₃-12₃-0 with the time window as the subscript, and (40, 40, 17.69, 40, 16.82, 40, 40), respectively. Figure 9 shows the space–time diagram of vessel 1, in which the horizontal and the vertical axes are period and debris number, respectively. The red, blue and green solid lines indicate that the vessel is in the sailing state with the speeds of 40, 17.69 and 16.82 km/h, respectively. The black dotted line means the working state. The number on the vertex is the arrival or completion time. The duration of each vessel under different conditions in each period is also listed in Table 10, where sailing 1, 2, and 3 in the column of condition represent speeds of 16.82, 17.69 and 40 km/h, respectively. According to Equation (19), we can compute the load demand of each vessel in each period, as shown in Table 11.

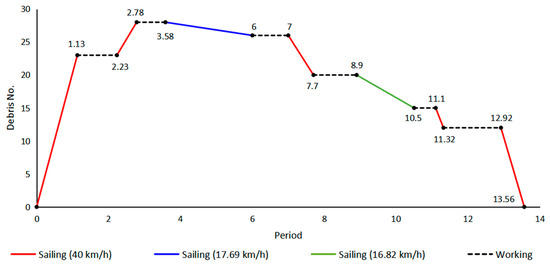
Figure 9. Space–time diagram of vessel 1.

Table 10. Duration of vessel 1 under different conditions in each period (h).

Condition	Period
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Sailing 1	0	0	0	0	0	0	0	0	0.1	1	0.5	0	0	0
Sailing 2	0	0	0	0.42	1	1	0	0	0	0	0	0	0	0
Sailing 3	1	0.13	0.55	0	0	0	0	0.7	0	0	0	0.22	0.08	0.56
Working	0	0.87	0.45	0.58	0	0	1	0.3	0.9	0	0.5	0.78	0.92	0

Table 11. Vessel load demand in each period (Kw).

Vessel No.	Period
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	160	73.26	114.94	48.35	32.12	32.12	60	130.15	57.08	30.41	45.21	81.58	68.42	90.31
2	160	91.53	130.63	60	28.89	20.03	67.95	97.34	60	69.35	68.55	82.41	77.59	115.66
3	82.67	118.9	71.6	60	43.18	30.41	80	99.75	61.82	77.78	68.89	84.15	85.85	17.36
4	80	86.09	83.78	78.41	0	0	0	0	0	0	0	0	0	0
5	103.29	75.13	78.26	73.33	56.23	0	0	0	0	0	0	0	0	0
6	92.8	73.22	84.35	60	119.63	15.73	0	0	0	0	0	0	0	0

We can calculate the output power of PV according to Equations (20) and (21). Among the many factors, the most important is the illumination intensity. The historical illumination intensity data used for predicting future illumination intensity are obtained from the NASA’s official website (https://power.larc.nasa.gov/data-access-viewer/), accessed on 15 January 2022. Due to the drastic changes in the weather at sea, the illumination intensity is also unstable. In order to reflect this situation more objectively, we divide the PV output power into three scenarios.

• Scenario A: maximum likely output. In the historical data greater than the most likely one, the illumination intensity that occurs the most is selected, and the PV output calculated from this is the maximum likely output.
• Scenario B: most likely output. In all historical data, the illumination intensity with the highest occurrence is taken as the most likely one, and the PV output calculated is thus regarded as the most likely output. This scenario is used as the baseline for further analysis.
• Scenario C: minimum likely output. In the historical data less than the most likely one, the illumination intensity with the most occurrence times is selected, and the PV output calculated from this is the minimum possible PV output.

Table 12 shows the PV output under scenarios A, B and C. We use YALMIP in MATLAB to call CPLEX Solver to solve the minimum cost under the three scenarios, with an average time of 6.54 s each time. Table 13 shows the optimal cost under three scenarios. Obviously, the higher the illumination intensity, the more PV power, and the lower the cost. Scenario A with the highest illumination intensity has the lowest cost, which is 10.94% and 45.29% lower than Scenarios B and C, respectively. Therefore, it is helpful to save costs by sending vessels to collect MDs at the time of high illumination intensity. Since Scenario B is the most likely output, we conduct a subsequent analysis based on it.

Table 12. PV output under three scenarios (kW).

Scenario	Period
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
A	80	90	100	140	160	180	150	120	90	80	60	35	20	0
B	70	80	90	120	140	160	130	100	80	70	50	30	15	0
C	40	50	60	90	110	130	100	70	50	40	30	15	5	0

Table 13. Optimal cost under three scenarios (CNY).

Scenario	Vessel No.						Total
	1	2	3	4	5	6
A	572.17	680.93	445.89	98.49	163.17	166.28	2126.93
B	634.59	739.67	514.24	137.43	181.83	180.35	2388.1
C	918.93	1127.79	820.8	344.94	343.62	331.5	3887.58

5.3.2. OPF Analysis

Under Scenario B, the OPF can be solved. There are five energy output forms in the model of stage 2. Let PV-Load, PV-Battery, Diesel-Load, Battery-Load and Diesel-Battery indicate PV supply load and charge the battery, diesel and the battery supply load, and diesel charge the battery, respectively. However, no Diesel-Battery appears in OPF. The former four energy outputs account for 63.16%, 16.56%, 6.2% and 14.08% of the total energy output, respectively. All PV outputs, including PV-Load and PV-Battery, are close to 80%, indicating that PV is the main energy output in HES. The optimal total cost is CNY 2388.10, among which the diesel power generation cost ($f^1$), PV generation cost ($f^2$), battery loss ($f^3$) and carbon tax ($f^4$) are CNY 672.88, CNY 1231.51, CNY 434.92 and CNY 48.79, respectively. The PV generation cost is more than half (51.57%) of the total cost. Although diesel output only accounts for 6.2% of the total energy output, its cost accounts for 38.16% of the total cost. This suggests that increasing the proportion of PV generation or decreasing the proportion of diesel output can significantly reduce costs.

Next, we take vessel 1 as an example to explain the results shown in Table 14. In period 1, the load demand (160 kW) is supplied by PV (59.16 kW) and diesel (100.84 kW), respectively. PV also charges the battery at 10.84 kW. Since the initial SOC of the battery is 130 kW, minus 15% of the charging loss (1.63 kW), the SOC at the end of the first period is 139.21 kW. In other words, in period 1, PV generates a total of 70 kW. From period 2, diesel no longer powers the load. The battery starts powering the load from period 3. The load demand in the last period is provided entirely by the battery, and the SOC of the battery is returned to its initial level (130 kW).

Table 14. OPF of vessel 1.

Item (kW)	Period
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Load demand	160	73.26	114.94	48.35	32.12	32.12	60	130.15	57.08	30.41	45.21	81.58	68.42	90.31
PV-Load	59.16	73.26	90	48.35	32.12	32.12	60	100	57.08	30.41	45.21	30	15	0
PV-Battery	10.84	6.74	0	71.65	100	100	5.35	0	0	0	0	0	0	0
Diesel-Load	100.84	0	0	0	0	0	0	0	0	0	0	0	0	0
Battery-Load	0	0	24.94	0	0	0	0	30.15	0	0	0	51.58	53.42	90.31
SOC	139.21	144.94	120	180.91	265.91	350.91	355.46	325.31	325.31	325.31	325.31	273.73	220.31	130

In order to further analyze the results, we also make statistics on the energy output composition of each vessel in each period, as shown in Figure 10. We can draw the following conclusions.

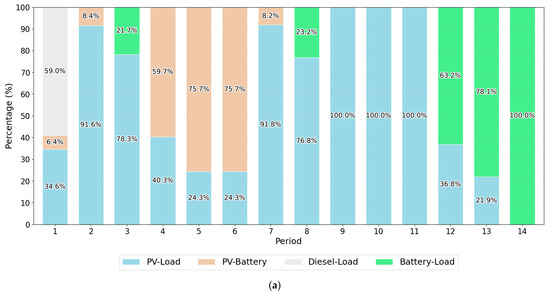
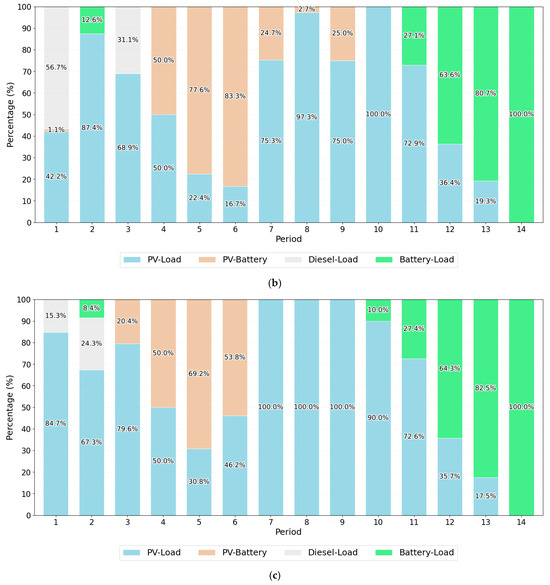
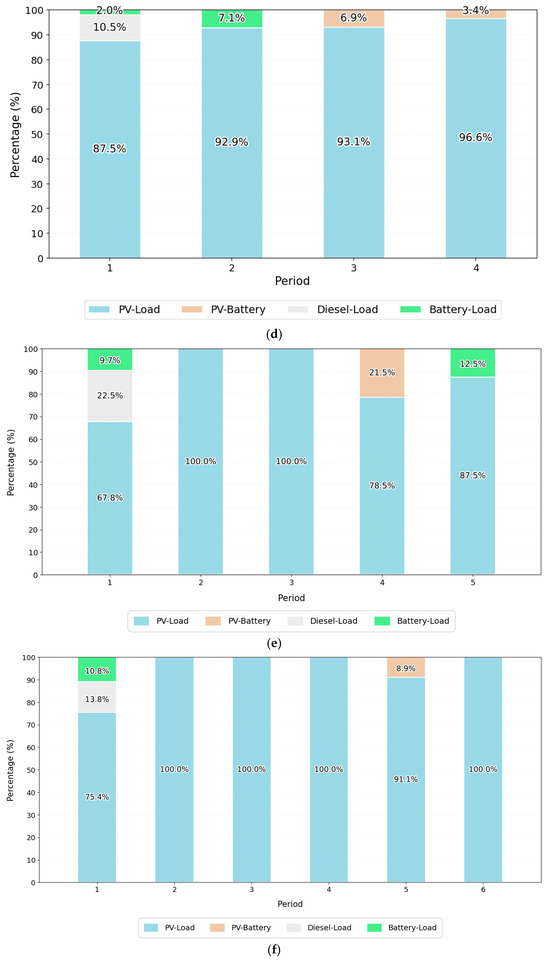
Figure 10. Energy output composition of each vessel in each period. (a) vessel 1; (b) vessel 2; (c) vessel 3; (d) vessel 4; (e) vessel 5; (f) vessel 6.

• The reason there is no Diesel-Battery in the OPF is that the cost of the battery powering load after diesel has charged the battery is higher than if diesel powers the load directly. Thus, to save costs, diesel does not charge the battery.
• According to the length of the travel time, all vessels can be divided into two categories, the first three vessels with 14 periods (Category 1) and the last three vessels with no more than 6 periods (Category 2). On the one hand, the two categories share some characteristics. (1) There is no separate output of diesel at any period; (2) there are only three kinds of energy output at most, i.e., Diesel-Load, PV-Load, and PV-Battery, which only occurs in the first two periods; (3) PV-Battery and Battery-Load do not occur in the same period; and (4) PV-Battery must occur simultaneously with PV-Load, which indicates that the condition for PV to charge the battery is when PV supplies power to the load and there is surplus. On the other hand, each category presents different characteristics.
• In Category 1, due to the long trip, PV-Battery and Battery-Load have more outputs except PV-Load. PV-Load runs through almost all of the periods except the last period where the load is completely powered by battery. It is easy to see from Table 14 that PV output in the last period is 0. Diesel-Load occurs in the first three periods, ranging from 15.33% to 59.03%. PV-Battery appears in the front and middle periods (from 1 to 9), reaching a maximum of 83.31%. Battery-Load is mainly located in the later period (from 10 to 14), and the later the period, the higher the proportion.
• In Category 2, the short-trip results in the load being mostly supplied by PV, and the other energy outputs are extremely low. Diesel-Load only appears in period 1, ranging from 3.45% to 21.46%. PV-Battery and Battery-Load are, respectively, no more than 22% and 13% in each period.

Obviously, increasing PV output or reducing diesel output can effectively reduce costs. For short trip vessels, we can deploy them during periods of high illumination intensity. For long-trip vessels, we can appropriately increase the initial SOC of the battery.

5.3.3. Carbon Emissions

In cloudy or rainy weather, the PV output power is 0, and the vessel load is completely provided by a diesel generator. We name this Scenario D, whose carbon emissions and total cost are 4148.84 kg and CNY 8590.65, respectively. In Scenario B, they are 348.53 kg and CNY 2388.10, decreased by 91.60% and 72.20%, respectively. This shows that vessels with HES have overwhelming superiority in terms of carbon emissions and cost compared with conventional diesel-powered vessels.

The manufacturing process of the battery and the mining, refining and transportation process of diesel all produce carbon emissions. The energy and materials needed to manufacture the PV equipment itself will consume a lot of electricity. If the electricity comes from fossil fuels, it will also cause some carbon emissions. Because it is difficult to calculate accurately, this part of the emissions is not considered in this paper. For a more comprehensive comparison, we also consider their full life cycle carbon emissions. According to Emilsson and Dahlf [45], the carbon emissions of a lithium-ion battery during its life cycle are between 0.07 and 0.3 kg/kWh. The carbon emissions of diesel in crude oil exploitation and transportation, production and product oil transportation are 0.246 kg/L [46]. After adding 3.315 kg/L of carbon emission from combustion, the life cycle carbon emissions of diesel are 3.561 kg/L. Based on the above data, the carbon emissions in Scenario B are between 475.88 to 809.31 kg, while those in Scenario D are 4456.71 kg. By comparison, the reduction rate is still 81.84% to 89.32%. Compared with the results without considering the life cycle, the reduction in carbon emissions is no more than 10%. This suggests that vessels with HES still have an overwhelming advantage in terms of carbon emissions.

5.4. Time Windows

Compared to a single time window, the drifting time window can depict the debris trajectory, provide more location information, and obtain better optimization results. In this subsection, we will analyze the impact of the time windows on the results. There are three time windows, [7, 10], [13, 15] and [17.5, 19.5] in the first stage. According to the quantity and combination of time windows, we divide them into seven cases, as shown in Table 15, in which Case 3, including three time windows, is taken as the baseline. Cases 1.1, 1.2, and 1.3 each have only one time window, while Cases 2.1, 2.2, and 2.3 each contain two time windows. In Scenario B, the results including the total cost, travel time and number of vessels used under various cases are shown in Figure 11.

Table 15. Combination of time windows.

Case	Time Windows
1.1	[7, 10]
1.2	[13, 15]
1.3	[17.5, 19.5]
2.1	[13, 15], [17.5, 19.5]
2.2	[7, 10], [17.5, 19.5]
2.3	[7, 10], [13, 15]
3 (baseline)	[7, 10], [13, 15], [17.5, 19.5]

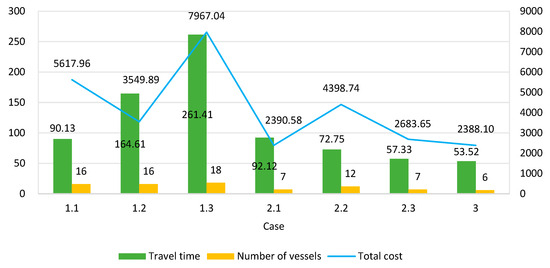
Figure 11. Comparison under different cases.

Obviously, Case 3 has the least total cost, travel time and number of vessels (6) of all cases. Although the more time windows, the fewer vessels are used, the total cost and travel time do not conform to this rule. For example, the total cost of Case 2.2 (CNY 4398.74) is higher than that of Case1.2 (CNY 3549.89), and the travel time of Case 2.1 (92.12 h) is higher than that of Case 1.1 (90.13 h). However, the total cost, travel time and vessels used in Case 2.1 are all less than those in Cases 1.2 and 1.3, respectively. This is because both time windows for Cases 1.2 and 1.3 are included in Case 2.1. The same is true for Case 2.2 and Cases 1.1 and 1.3. Because the results of Cases 1.1 and 1.2 are the best in all the cases with one time window, the results of Case 2.3 including both time windows of the above case, are also the best in all the cases with two time windows. Similarly, Case 3 is the best in all cases since it includes all time windows. This indicates that the optimization results are not only related to the number of time windows but also to the combination of time windows. Therefore, the selection of the number and combination of time windows is crucial to the optimization results.

6. Conclusions

We use hybrid energy vessels with PV/diesel/battery to clean up MDs floating on the ocean. The problem is divided into two stages. In the first stage, the logistics space–time network is established by a drifting time window to optimize VRPDTW with speed, and the ALNSES algorithm is proposed. The second stage optimizes the output of hybrid energy with the goal of minimizing the cost. The correctness of the models and the effectiveness of the proposed algorithm are verified by numerical examples. This would not only effectively remove MDs but also dramatically reduce carbon emissions and protect the environment. Some valuable conclusions are drawn.

(1) The drifting time window can make full use of the trajectory information of MD, allowing more MDLs to be selected, so as to construct the logistics space–time network, and model VRPDTW and speed optimization. The results show that the drifting time window is significantly better than the single time window in terms of the number of vessels used, the total travel time and the total cost. In the combination of two time windows, if the two time windows are far apart, the optimization result is poor. This indicates that the combination of different time windows also has an important effect on the optimization results.

(2) The ALNSES algorithm we proposed for the VRPDTW is superior to the ALNS algorithm in terms of computational efficiency and stability. The fitting results show that the running time of the proposed algorithm is a cubic polynomial of the problem size.

(3) With the cooperation of PV and battery, the HES has an overwhelming advantage in cost saving and emission reduction over the pure diesel system, and the results show that the maximum reduction is 72.20% and 91.60%, respectively. Even taking full life cycle carbon emissions into account, vessels with HES can still reduce carbon emissions by more than 80% compared to pure diesel vessels. Different strategies should be adopted for vessels with different trips to improve the efficiency of HES. The initial SOC of the battery should be increased for long-range vessels, while it should be deployed during periods of high illumination intensity for short-range vessels.

It will be our future research to establish a comprehensive optimization model for cleaning MDs by vessels with HES. To achieve the goal of carbon neutrality, we will further explore how to utilize HES composed of other clean and renewable energy sources, such as PV, batteries, wind, and liquefied natural gas.