Clustering-Based Urban Driving Cycle Generation: A Data-Driven Approach for Traffic Analysis and Sustainable Mobility Applications in Ecuador
Abstract
1. Introduction
2. Methodology
2.1. Acquisition of Experimental Data
2.1.1. Route Selection
2.1.2. Sample Size
2.1.3. Data Collection
2.2. Data Processing
2.2.1. Extraction of Microtrips
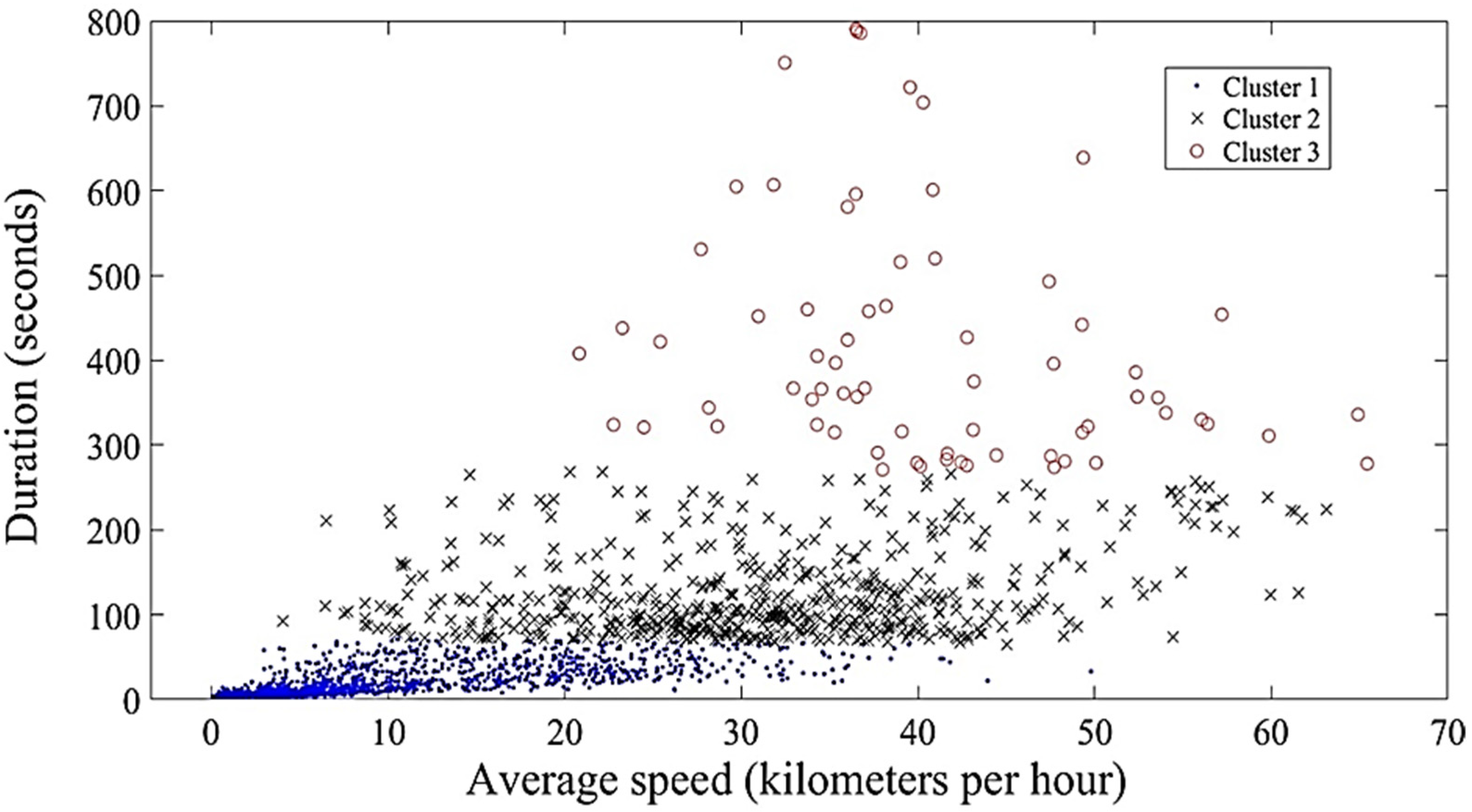
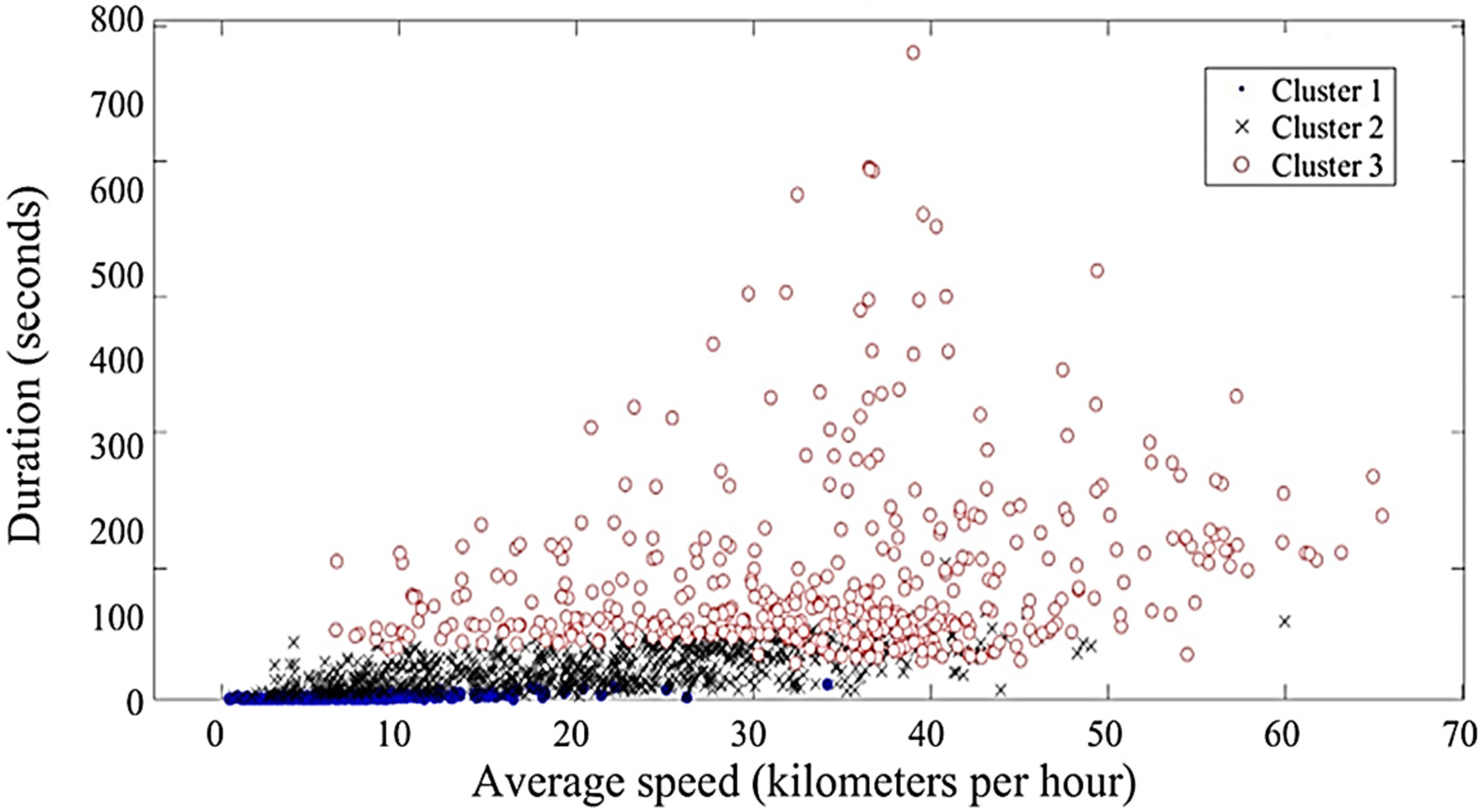
2.2.2. K-Means Clustering Method for Driving Cycle Construction
2.2.3. Elbow Method for Determining K, the Optimal Number of Clusters
2.3. Construction of Driving Cycles with Microtrips
3. Results
Comparison Between Quito Cycle and International Cycles
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECE 15 | European Driving Cycle |
| FTP 72 | Federal Test Procedure 1972 (USA) |
| FTP 75 | Federal Test Procedure 1975 (USA) |
| HK | Hong Kong Driving Cycle |
| IM 240 | Inspection and Maintenance 240 Seconds (USA) |
| J10-15 | Japanese 10–15 Mode Cycle (JAPON) |
| LA 92 | Los Angeles 92 Driving Cycle (USA) |
| NEDC | New European Driving Cycle (Europa) |
| RDC | Representative Driving Cycle |
| SFTP-SC03 | Supplemental Federal Test Procedure-SC03 (USA) |
| SSE | Sum of Squared Errors |
| WLTC | Worldwide harmonized light vehicles test cycle |
References
- Padam, S.; Singh, S.K. Urbanization and Urban Transport in India: The Search for a Policy. SSRN 2004, 50. [Google Scholar] [CrossRef]
- Bishop, J.D.; Stettler, M.E.; Molden, N.; Boies, A.M. Engine maps of fuel use and emissions from transient driving cycles. Appl. Energy 2016, 183, 202–217. [Google Scholar] [CrossRef]
- Tamsanya, S.; Chungpaibulpatana, S.; Limmeechokchai, B. Development of a driving cycle for the measurement of fuel consumption and exhaust emissions of automobiles in Bangkok during peak periods. Int. J. Automot. Technol. 2009, 10, 251–264. [Google Scholar] [CrossRef]
- Galgamuwa, U.; Perera, L.; Bandara, S. Developing a General Methodology for Driving Cycle Construction: Comparison of Various Established Driving Cycles in the World to Propose a General Approach. J. Transp. Technol. 2015, 5, 191–203. [Google Scholar] [CrossRef]
- Mudgal, A. Modeling Driving Behavior at Traffic Control. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2011. [Google Scholar]
- Barlow, T.; Latham, S.; McCrae, I.S.; Boulter, P. A Reference Book of Driving Cycles for Use in the Measurement of Road Vehicle Emissions; TRL: Berkshire, UK, 2009; Report No. 354. [Google Scholar]
- EUR-Lex. Regulation (EU) 2019/631 of the European Parliament and of the Council of 17 April 2019 setting CO2 emission performance standards for new passenger cars and for new light commercial vehicles. EUR-Lex 2019, OJ L 111, 13–53. [Google Scholar]
- Ministerio de Energía. Establishment of the Vehicle Energy Efficiency Standard of Light Motor Vehicles; Technical Report; Ministerio de Energía: Santiago, Chile, 2022.
- Soares de Andrade, G.M.; Cavalcanti de Araujo, F.; Magalhaes de Novaes Santos, M.P.; dos Anjos Garnes, S.J.; Santana Magnani, F. Simple Methodology for the Development and Analysis of Local Driving Cycles Applied in the Study of Cars and Motorcycles in Recife, Brazil. Transp. Res. Rec. 2021, 2675, 213–224. [Google Scholar] [CrossRef]
- Barbero, D.A.; Barraza, M.A.; Santos, J.; Castronuovo, M.; Álvarez, G.B.; Uría, L. Methodology for estimating air pollution caused by fuel consumption in vehicular traffic. Estud. Del Hábitat 2010, 11, 109–119. [Google Scholar]
- Cuisano, J.C.; Basagoitia, J.S.; Quirama, L.F. Development of an urban driving cycle in the Lima Metropolitan Area, Peru. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Giraldo-Galindo, M.D.; Quirama-Londoño, L.F.; Huertas-Cardozo, J.I. Protocol to evaluate methods designed for the construction of representative driving cycles. Rev. Fac. Ing. Univ. Antioq. 2024, 114, 40–50. [Google Scholar] [CrossRef]
- Ho, S.H.; Wong, Y.D.; Wei-Chung, V. Developing Singapore Driving Cycle for passenger cars to estimate fuel consumption and vehicular emissions. Atmos. Environ. 2014, 97, 353–362. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, Z.; Yu, F.; Liao, S.; Luo, H.; Zhong, Z.; Zhu, M.; Li, Z.; Cui, X.; Yan, M.; et al. Road type-based driving cycle development and application to estimate vehicle emissions for passenger cars in Guangzhou. Atmos. Pollut. Res. 2021, 12, 101138. [Google Scholar] [CrossRef]
- Duque Sarmiento, D.A.; Rocano Yunda, J.A. Determination of the Autonomy of the Electric Vehicle by Means of Controlled Cycles. Bachelor’s Thesis, Universidad Politécnica Salesiana, Cuenca, Ecuador, 2018. [Google Scholar]
- Vega, D.; Parra Narváez, R. Characterization of the average daily intensity and hourly profiles of vehicular traffic in the Metropolitan District of Quito. ACI Av. En Cienc. E Ing. 2014, 6. [Google Scholar] [CrossRef]
- Llanes-Cedeño, E.; Rodriguez-Munive, M.; López-Villada, J.; Bustamante-Villagómez, D.; Pino-Tarragó, J. Definition of Urban, Highway and Combined Driving Cycles for the city of Quito—Ecuador. Int. J. Membr. Sci. Technol. 2023, 10, 3114–3127. [Google Scholar] [CrossRef]
- Urgilés, P.; Urgilés, S. Aplicación del método de diferencias mínimas ponderadas para la obtención de un ciclo de conducción en una ruta urbana de un autobús. Caso de estudio: Azogues, Ecuador. INCITEC 2021, 1, 48–52. [Google Scholar]
- Castillo-Calderón, J.; Carrión, R.; Díaz, D.; Panchana, B. Estimation of Traction Energy Consumption of Urban Service Buses in an Intermediate Andean City. IOP Conf. Ser. Earth Environ. Sci. 2023, 1141, 012001. [Google Scholar] [CrossRef]
- Rivera, N.; Molina, J.; Idrovo, D.; Narvaez, J.; Botto-Tobar, M.; Zambrano, M.; Montes, S.; Torres-Carrion, P.; Durakovic, B. Influence Analysis of Driving Style on the Energy Consumption of an Electric Vehicle Through PID Signals Study. In Proceedings of the International Conference on Applied Technologies, Quito, Ecuador, 20–22 November 2024; Springer: Berlin/Heidelberg, Germany, 2024; Volume 2049, pp. 194–205. [Google Scholar]
- Espinoza, F.; Tacuri, F.; Contreras, W.; Vázquez, J. Algorithm for predicting fuel consumption for anhydrous ethanol mixtures in high-altitude cities. Ingenius 2020, 25, 41–49. [Google Scholar] [CrossRef]
- Selim, S.Z.; Ismail, M.A. K-Means-Type Algorithms: A Generalized Convergence Theorem and Characterization of Local Optimality. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 81–87. [Google Scholar] [CrossRef] [PubMed]
- Aubaidan, B.; Mohd, M.; Albared, M. Comparative Study of K-Means and K-Means++ Clustering Algorithms on Crime Domain. J. Comput. Sci. 2014, 10, 1197–1206. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.; Netanyahu, N.; Piatko, C.; Silverman, R.; Wu, A. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Desineedi, R.M.; Mahesh, S.; Ramadurai, G. Developing driving cycles using k-means clustering and determining their optimal duration. Transp. Res. Procedia 2020, 48, 2083–2095. [Google Scholar] [CrossRef]
- Anida, I.N.; Salisa, A.R. Driving cycle development for Kuala Terengganu city using k-means method. Int. J. Electr. Comput. Eng. 2019, 9, 1780–1787. [Google Scholar] [CrossRef]
- Espinoza, J.; Pantoja, D.; Castro, C.; Sangovalin, J.; Villamarin, J. Fuel consumption vs. eco-driving and traffic on a mixed route in the city of Quito. Rev. Cient. Tecnol. UPSE 2022, 9, 85–96. [Google Scholar]
- Moreno, G.; Macias, B. Design of a Datalogger for Route Testing in Automobiles. Bachelor’s Thesis, SEK International University, Quito, Ecuador, 2021. [Google Scholar]
- Oppenlander, J.; Bunte, W.F.; Kadakia, P.L. Sample Size Requirements for Vehicular Speed Studies. Highw. Res. Board Bull. 1961, 281, 68–86. [Google Scholar]
- Federal Highway Administration (FHWA). Procedures for Setting Advisory Speeds on Curves; U.S. Department of Transportation: Washington, DC, USA, 2011; No. HWA-SA-11-22; p. 44.
- Ibrahim, N.A.; Jabar, S.N.; Yu, W. KT driving cycle data collection and development using MATLAB mobile application. AIP Conf. Proc. 2024, 2898, 030001. [Google Scholar]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Zandbergen, P.A. Accuracy of iPhone Locations: A Comparison of Assisted GPS, WiFi and Cellular Positioning. Trans. GIS 2009, 13, 5–25. [Google Scholar] [CrossRef]
- Bone, E.; Almachi, J.C.; Montenegro, J.; Fajardo, C.; Simbana, J.; Gutiérrez, L.; Vargas, D. Cálculo y Análisis de la Incertidumbre del Valor de Fuerza Centrífuga Adquirido del Equipo Zentrolkraftgerat 11008-001 PHYWE del Laboratorio de Física General de la EPN. In Proceedings of the 1st Latin American Congress on Engineering (CLADI), Salta, Argentina, 12–15 July 2017; pp. 325–327, ISBN 978-987-1896-84-4. [Google Scholar]
- He, Y. Research on the construction method of vehicle driving cycle based on Mean Shift clustering. arXiv 2020, arXiv:2008.05070. [Google Scholar]
- Silva, M.I.; Henriques, R. TripMD: Driving patterns investigation via Motif Analysis. Expert Syst. Appl. 2021, 184, 115527. [Google Scholar] [CrossRef]
- Moosavi, S.; Nandi, A.; Ramnath, R. Discovery of Driving Patterns by Trajectory Segmentation. In Proceedings of the 3rd ACM SIGSPATIAL PhD Workshop, San Francisco, CA, USA, 31 October–3 November 2016. [Google Scholar]
- Olszewski, D. Asymmetric K-Means Algorithm; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–10. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1967; Volume 1, pp. 281–297. [Google Scholar]
- Salvador, S.; Chan, P. Determining the number of clusters/segments in hierarchical clustering/segmentation algorithms. In Proceedings of the 16th IEEE International Conference on Tools with Artificial Intelligence, Boca Raton, FL, USA, 15–17 November 2004; pp. 576–584. [Google Scholar]
- Sugar, C.A.; James, G.M. Finding the Number of Clusters in a Dataset. J. Am. Stat. Assoc. 2003, 98, 750–763. [Google Scholar] [CrossRef]
- Maximilian, Z.; Svenja, K.; Markus, L. Compressed Driving Cycles Using Markov Chains for Vehicle Powertrain Design. World Electr. Veh. J. 2020, 11, 52. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, Q.; Yu, Y.; Ye, M.; Yu, M. Development of a representative urban driving cycle construction methodology for electric vehicles: A case study in Xian. Transp. Res. Part D Transp. Environ. 2020, 81, 102279. [Google Scholar] [CrossRef]
- Patel, E.; Kushwaha, D.S. Clustering Cloud Workloads: K-Means vs Gaussian Mixture Model. Procedia Comput. Sci. 2020, 171, 158–167. [Google Scholar] [CrossRef]
- Castillo, J.; Restrepo, Á.; Tibaquirá, J.; Quirama, L. Energy efficiency strategies for light duty vehicles in Colombia. Rev. UIS Ing. 2019, 18, 129–140. [Google Scholar] [CrossRef]
- Ma, Z.; Nørregaard-Jørgensen, B.; Ma, Z. A Scoping Review of Energy-Efficient Driving Behaviors and Applied State-of-the-Art AI Methods. Energies 2024, 17, 500. [Google Scholar] [CrossRef]
- Mohd, A.; Yahaya, N.; Syed-Abd, S. Air pollution from motor vehicles: A mathematical model analysis—Case study in Ipoh City, Perak, Malaysia. J. East. Asia Soc. Transp. Stud. 2003, 5, 2367–2391. [Google Scholar]
- Zhang, L.; Peng, K.; Zhao, X.; Khattak, A. New fuel consumption model considering vehicular speed, acceleration, and jerk. J. Intell. Transp. Syst. 2023, 27, 174–186. [Google Scholar] [CrossRef]
- Fafoutellis, P.; Mantouka, E.G.; Vlahogianni, E.I. Eco-Driving and Its Impacts on Fuel Efficiency: An Overview of Technologies and Data-Driven Methods. Sustainability 2021, 13, 226. [Google Scholar] [CrossRef]
- Vaca-Ramírez, F. Robustness of urban road networks based on spatial topological patterns. arXiv 2019, arXiv:1904.03546. [Google Scholar]
- Rivera, J.; Molina, J.; Zambrano, M. Investigating Traffic Flow in High-Altitude Urban Areas: A Study in Quito. Traffic Flow J. 2022, 16, 101–120. [Google Scholar]
- Treiber, M.; Kesting, A.; Thiemann, C. How Much Does Traffic Congestion Increase Fuel Consumption and Emissions? Applying Fuel Consumption Model to NGSIM Trajectory Data. In Proceedings of the 87th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 2008. [Google Scholar]
- Totev, V.; Gueorgiev, V. Efficiency of Regenerative Braking in Electric Vehicles. In Proceedings of the 21st International Symposium on Electrical Apparatus & Technologies (SIELA 2020), Bourgas, Bulgaria, 3–6 June 2020; Volume 9, pp. 1–4. [Google Scholar]







| ID | Vehicle Make and Model | Vehicle Technical Specifications | GPS Device (Smartphone) | Phone Technical Specifications | GPS Sampling | Additional Comments |
|---|---|---|---|---|---|---|
| 1 | Sedan JAC-S3 2019 | 1.6 L engine, gasoline, manual transmission | Redmi Note 9 | MediaTek Helio G85 octa-core 2 GHz, Mali-G52 MC2, Android 10, Dual-Band GPS | 2 Hz | Dense traffic route, nighttime conditions |
| 2 | Pickup Truck Mitsubishi L200 2009 | 2.5 L engine, diesel, 4 × 4 drive | Redmi Note 12 | Snapdragon 4 Gen 1, 2 GHz, 128 GB, Android 10, Dual-Band GPS | 2 Hz | Dense traffic route, nighttime conditions |
| 3 | Hatchback Chevrolet Aveo 2010 | 1.5 L engine, gasoline, manual transmission | Huawei Y9 | Kirin 710, Octa-core, 12 nm, Mali-G51 MP4 GPU | 2 Hz | Dense traffic route, nighttime conditions |
| 4 | Pickup Truck Mazda BT50 2019 | 3.0 L engine, diesel, rear-wheel drive, manual transmission | Huawei Mate 40 Pro | Kirin 9000, 8 GB RAM, Android 11, Dual-Frequency GPS | 1 Hz | Dense traffic route, nighttime conditions |
| 5 | Hatchback Corza Wind 2002 | 1.4 L engine, gasoline, manual transmission | OnePlus 11 | Snapdragon 8 Gen 2, 16 GB RAM, Android 13, Multi-Frequency GNSS | 2 Hz | Dense traffic route, nighttime conditions |
| Criteria | Abbreviation | Unit |
|---|---|---|
| Distance | D | |
| Cycle time | T | |
| Average speed for entire trip | V | |
| Average running speed | Vr | |
| Standard deviation of speed | V sd | |
| Standard deviation of acceleration | A sd | |
| Average acceleration of all acceleration phases | aa | |
| Average deceleration of all acceleration phases | ad | |
| Root mean square acceleration | arms | |
| Positive acceleration kinetic energy | PKE | |
| Percentage of idle time (speed = 0) | Pi | % |
| Percentage of time spent in acceleration mode (a > 0.1 m·s−2) | Pa | % |
| Percentage of time spent in deceleration mode (d < −0.1 m·s−2) | Pd | % |
| Percentage of time spent in cruise mode (Pc) (−0.1 m/s2 < acceleration < 0.1 m/s2, speed > 5 kmph) | Pc | % |
| Initial Cluster | Rear Cluster 1 | Rear Cluster 2 | Rear Cluster 3 |
|---|---|---|---|
| 1 | 0.7933 | 0.188 | 0.0209 |
| 2 | 0.5300 | 0.4408 | 0.0292 |
| 3 | 0.4746 | 0.4407 | 0.0847 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| V (km/h) | 23.21 | (%) | 24.07 |
| Vr (km/h) | 30.03 | (%) | 13.79 |
| A | 0.55 | (%) | 23.55 |
| ad | −0.57 | (%) | 23.50 |
| (%) | 36.97 | 0.63 | |
| (%) | 35.02 | PKE | 0.20 |
| Driving Cycle | Objective Evaluation Parameters | Developed Driving Cycle | Difference |
|---|---|---|---|
| D (km) | 18.24 | 18.08 | 0.16 |
| T(s) | 2948 | 2870 | 78 |
| V (km/h) | 23.21 | 22.68 | 0.53 |
| Vr (km/h) | 30.03 | 28.34 | 1.69 |
| Aa (m/s2) | 0.55 | 0.47 | 0.08 |
| Ad (m/s2) | −0.57 | −0.44 | −0.13 |
| PKE (m/s2) | 0.2 | 0.18 | 0.02 |
| Pad (%) | 23.5 | 24.74 | −1.24 |
| Pi (%) | 24.07 | 20 | 4.07 |
| Pa(%) | 36.97 | 33.31 | 3.66 |
| Pd (%) | 35.02 | 35.54 | −0.52 |
| Pc (%) | 13.79 | 12.07 | 1.72 |
| Arms (m/s2) | 0.63 | 0.59 | 0.04 |
| Driving Cycle | Quito | FTP 75 | FTP 72 | HK | NYCC | LA 92 | SFTP-SC03 | ECE 15 | 10 Mode | 10–15 Mode | IM 240 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Origin | Ecu. | USA | USA | China | USA | USA | USA | Europe | Japan | Japan | USA |
| Distance (km) | 18.08 | 17.99 | 11.99 | 10.33 | 1.9 | 15.8 | 5.76 | 0.99 | 0.66 | 4.17 | 3.15 |
| Duration (s) | 2870 | 1874 | 1369 | 1548 | 599 | 1436 | 596 | 195 | 136 | 660 | 240 |
| Average running speed (km/h) | 28.34 | 41.6 | 38.3 | 30.4 | 17.9 | 46.7 | 42.3 | 26.5 | 24.1 | 33.1 | 49.1 |
| Maximum speed (km/h) | 69.84 | 91.3 | 91.3 | 77.7 | 44.6 | 108.2 | 88.2 | 50 | 40 | 70 | 91.3 |
| Average acceleration (m/s2) | 0.47 | 0.607 | 0.597 | 0.593 | 0.712 | 0.673 | 0.603 | 0.642 | 0.673 | 0.569 | 0.516 |
| Average deceleration (m/s2) | −0.44 | 0.7 | 0.695 | 0.595 | 0.704 | 0.754 | 0.717 | 0.748 | 0.654 | 0.647 | 0.795 |
| Root mean square acceleration (m/s2) | 0.59 | 0.76 | 0.744 | 0.734 | 0.909 | 0.846 | 0.795 | 0.661 | 0.692 | 0.612 | 0.664 |
| Positive acceleration kinetic energy (m/s2) | 0.18 | 0.384 | 0.382 | 0.395 | 0.554 | 0.409 | 0.411 | 0.565 | 0.577 | 0.427 | 0.337 |
| Proportion of idle (Pi) | 19.97 | 17.9 | 17.6 | 17.8 | 36.2 | 15.2 | 17.8 | 30.8 | 27.2 | 31.4 | 3.8 |
| Percentage of time spent in acceleration mode (Pa) | 33.31 | 32.4 | 32.8 | 34.5 | 27.9 | 38.2 | 34.7 | 21.5 | 24.3 | 25.2 | 46.3 |
| Percentage of time spent in deceleration mode (Pd) | 35.02 | 28.2 | 28.3 | 34.2 | 28.2 | 34.1 | 29.4 | 18.5 | 25 | 22.1 | 30.4 |
| Proportion of cruise (Pc) | 12.07 | 21.2 | 20.9 | 12 | 6.3 | 12.2 | 18 | 29.2 | 23.5 | 21.4 | 19.6 |
| Driving Cycle | FTP 75 | FTP 72 | HK | NYCC | LA 92 | SFTP-SC03 | ECE 15 | 10 Mode | 10–15 Mode | IM 240 |
|---|---|---|---|---|---|---|---|---|---|---|
| Performance Value PV | 0.543 | 0.567 | 0.44 | 0.816 | 0.591 | 0.631 | 0.861 | 0.805 | 0.646 | 0.719 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almachi, J.C.; Saguay, J.; Anrango, E.; Cando, E.; Reina, S. Clustering-Based Urban Driving Cycle Generation: A Data-Driven Approach for Traffic Analysis and Sustainable Mobility Applications in Ecuador. Sustainability 2025, 17, 3353. https://doi.org/10.3390/su17083353
Almachi JC, Saguay J, Anrango E, Cando E, Reina S. Clustering-Based Urban Driving Cycle Generation: A Data-Driven Approach for Traffic Analysis and Sustainable Mobility Applications in Ecuador. Sustainability. 2025; 17(8):3353. https://doi.org/10.3390/su17083353
Chicago/Turabian StyleAlmachi, Juan Carlos, Jonathan Saguay, Edwin Anrango, Edgar Cando, and Salvatore Reina. 2025. "Clustering-Based Urban Driving Cycle Generation: A Data-Driven Approach for Traffic Analysis and Sustainable Mobility Applications in Ecuador" Sustainability 17, no. 8: 3353. https://doi.org/10.3390/su17083353
APA StyleAlmachi, J. C., Saguay, J., Anrango, E., Cando, E., & Reina, S. (2025). Clustering-Based Urban Driving Cycle Generation: A Data-Driven Approach for Traffic Analysis and Sustainable Mobility Applications in Ecuador. Sustainability, 17(8), 3353. https://doi.org/10.3390/su17083353








