Research on Online Energy Management Strategy for Hybrid Energy Storage Electric Vehicles Under Adaptive Cruising Conditions
Abstract
1. Introduction
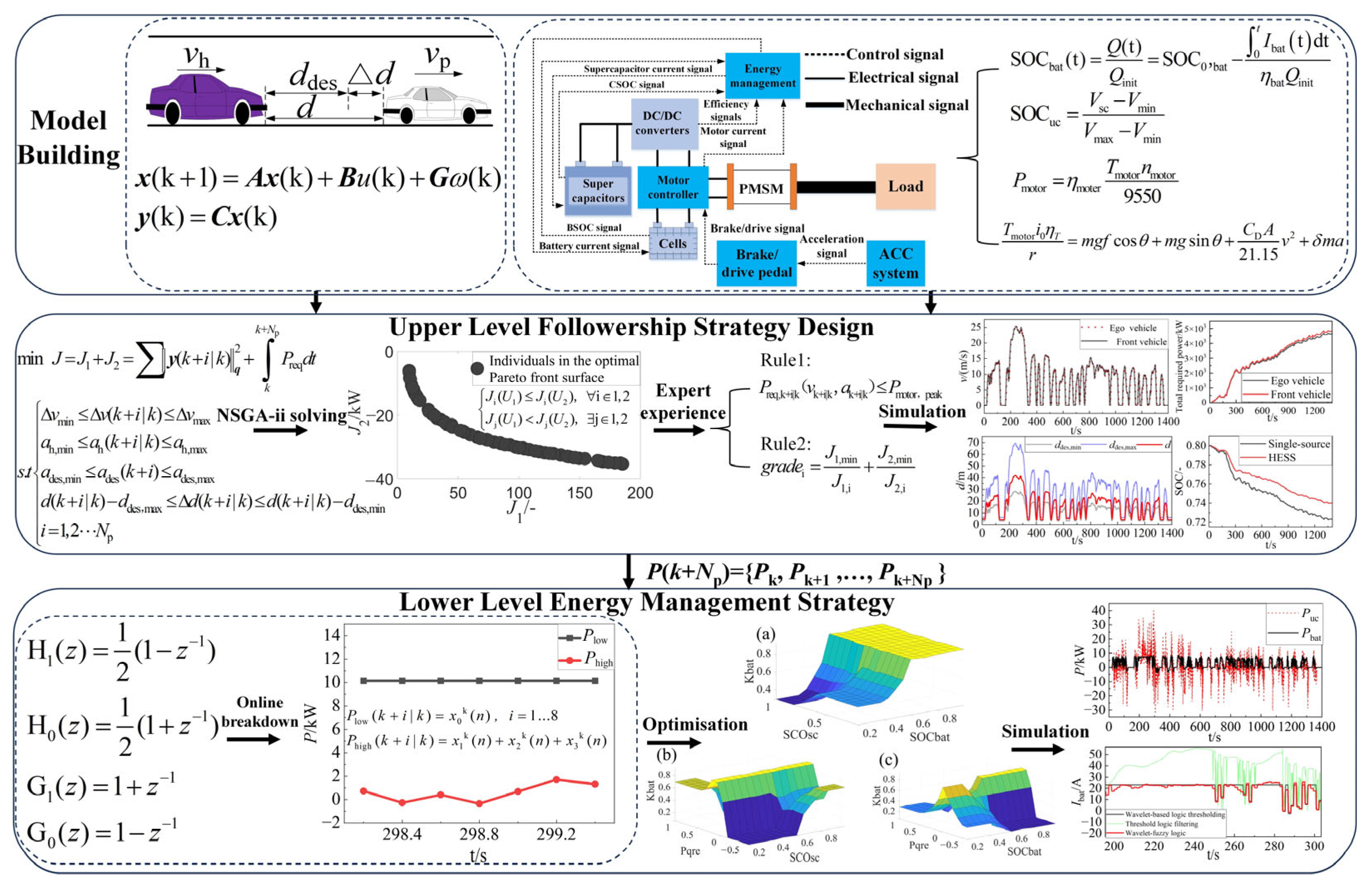
2. System Model
2.1. Car-Following Model
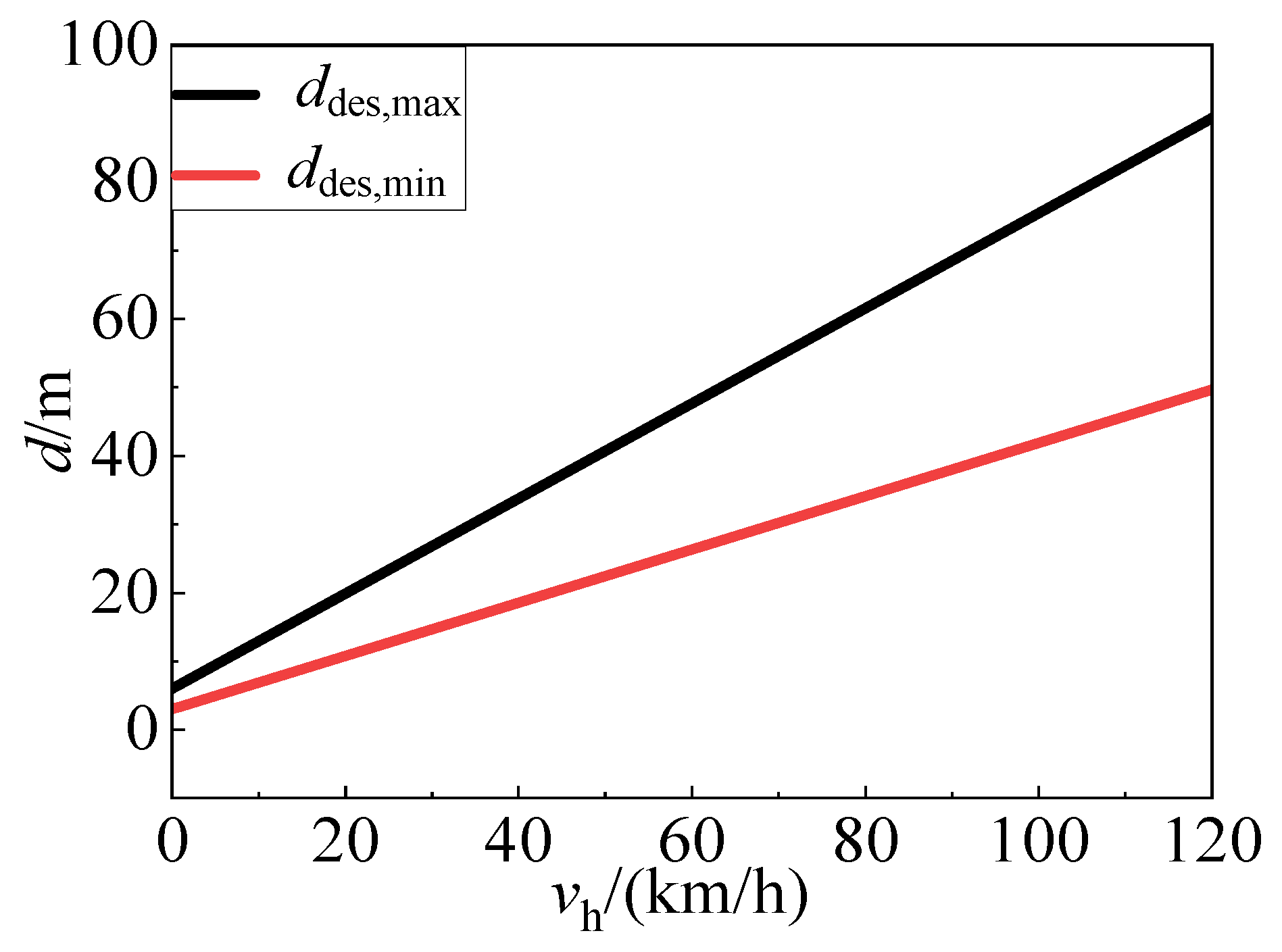
2.1.1. Expected Distance Model
2.1.2. Car-Following Model Based on Longitudinal Kinematics
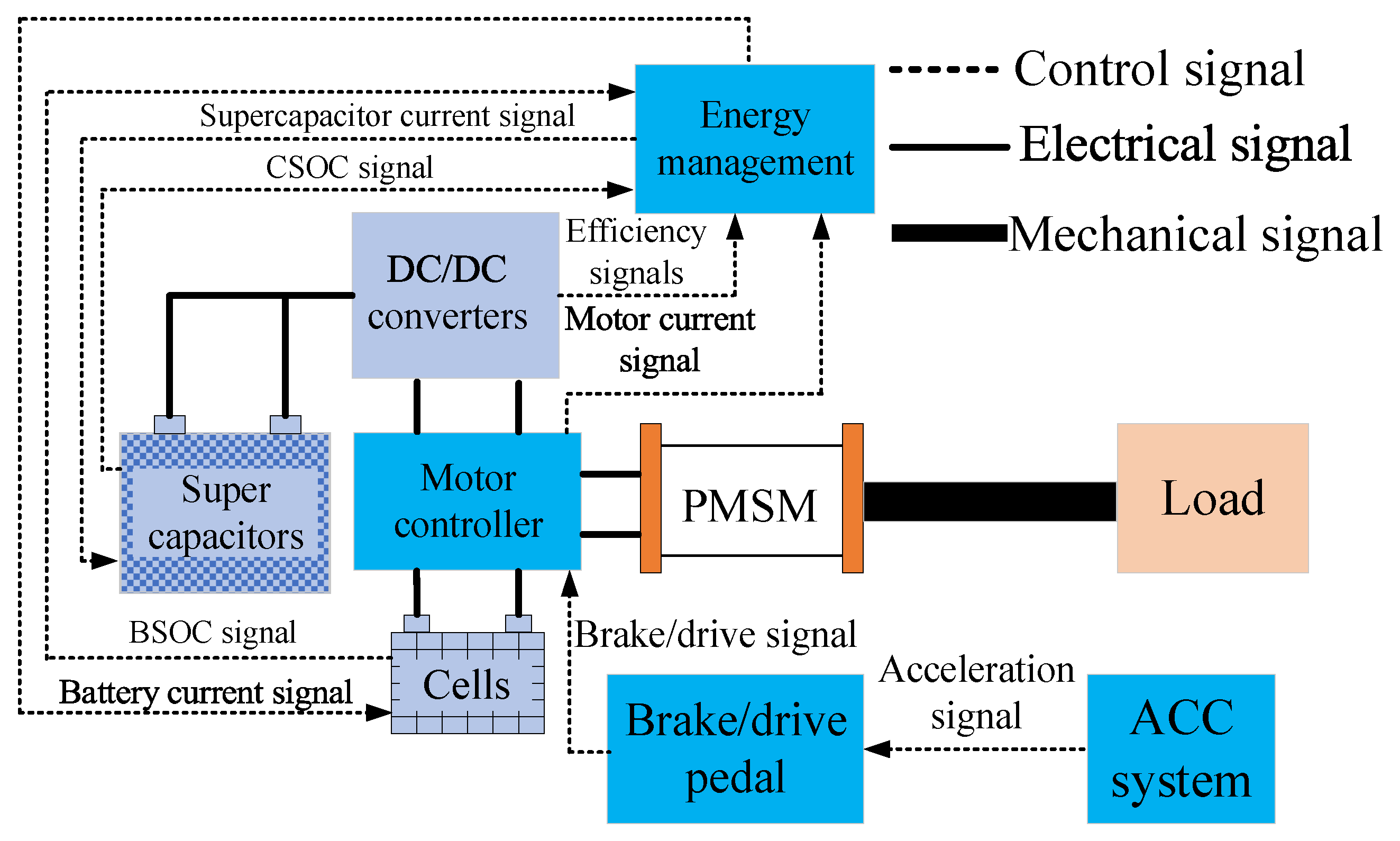
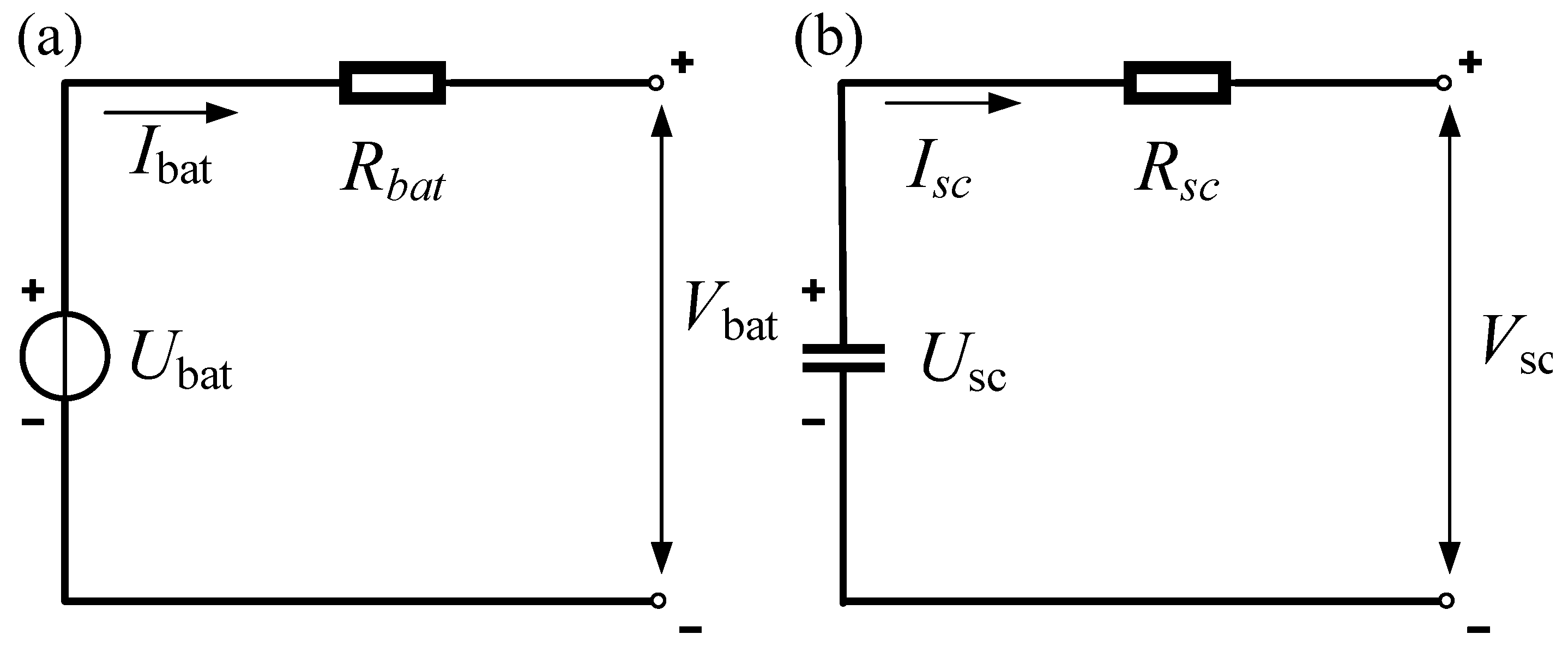
2.2. HESS Model
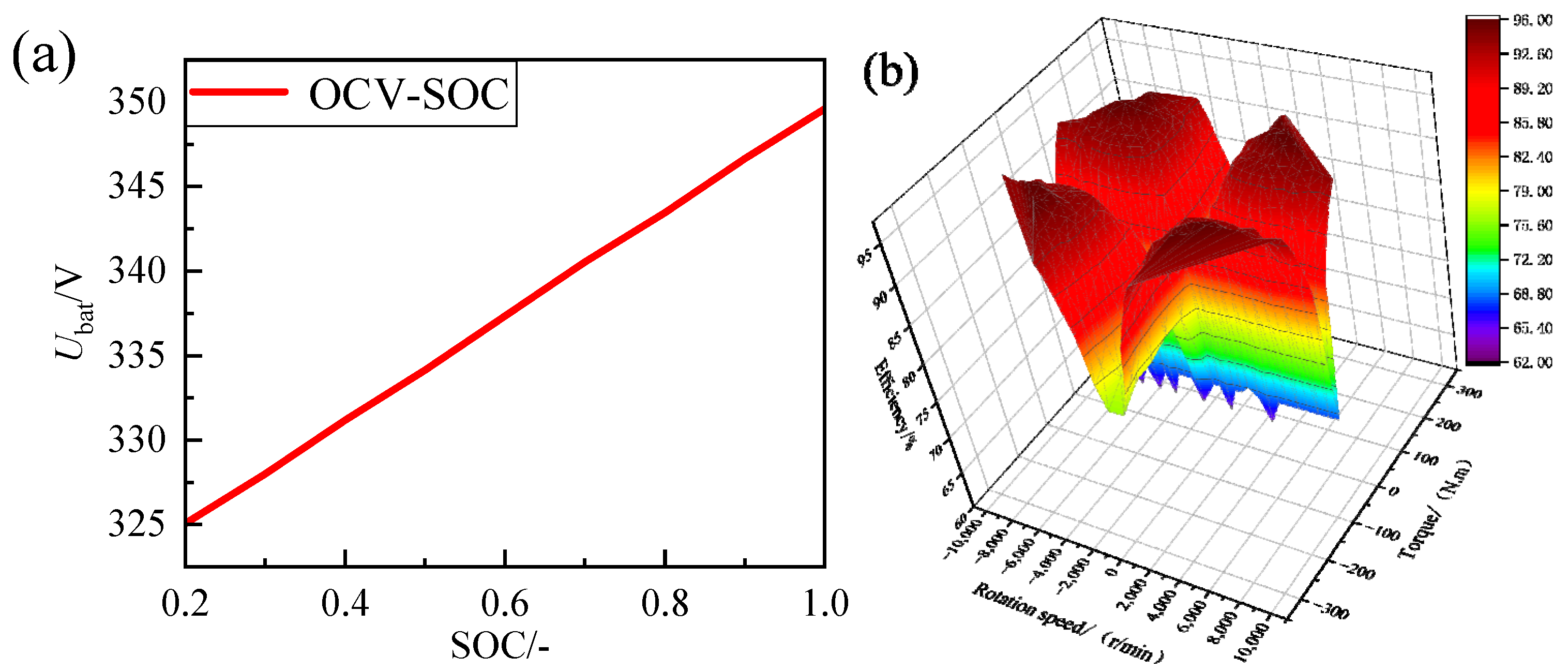
2.2.1. Lithium-Ion Battery Model
2.2.2. Supercapacitor Model
2.2.3. Motor Model
3. Design of Adaptive Cruise Algorithm Based on Vehicle Speed Prediction
3.1. Establishment of Multi-Objective Function
3.1.1. Longitudinal Tracking Performance
3.1.2. Energy Economy
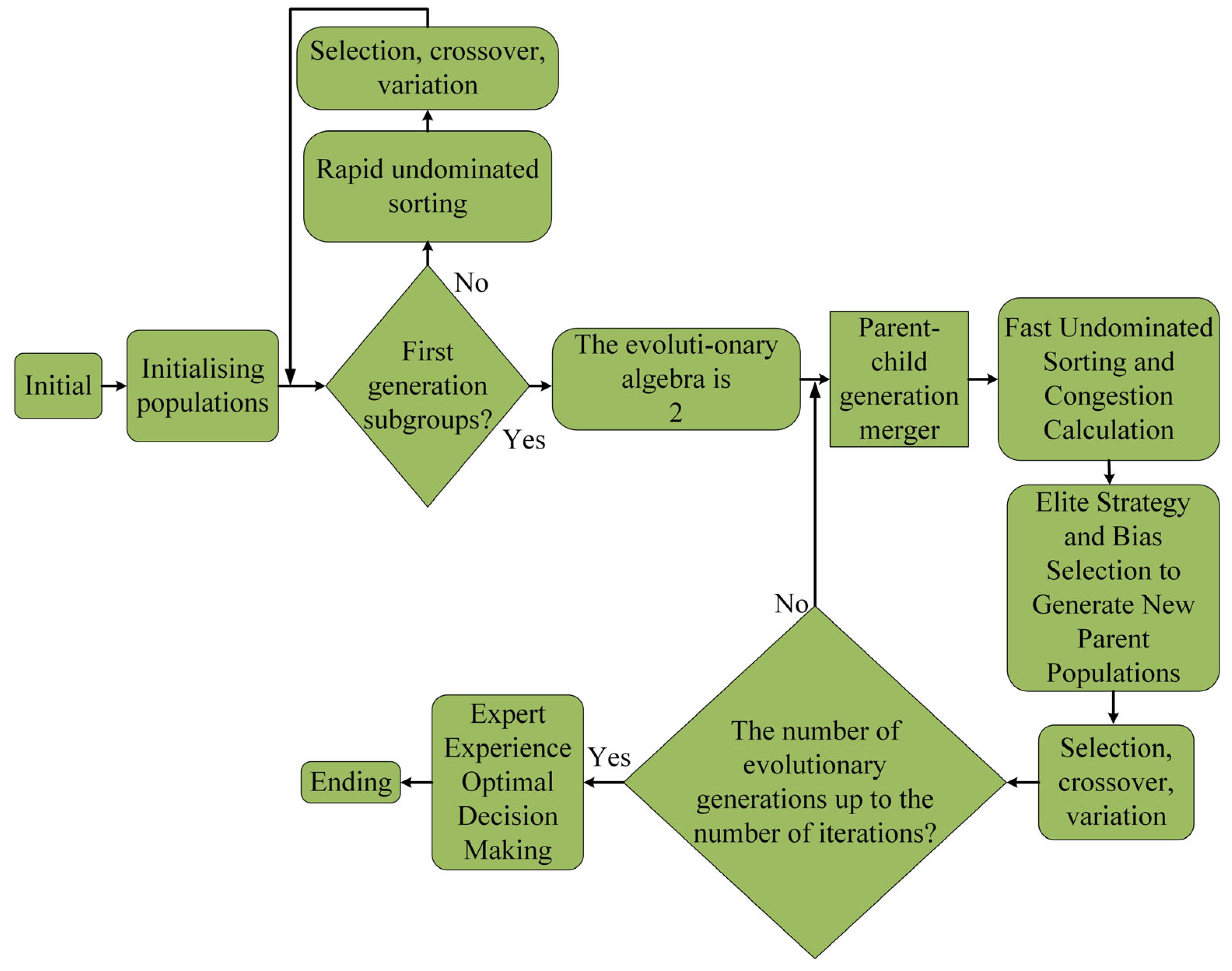
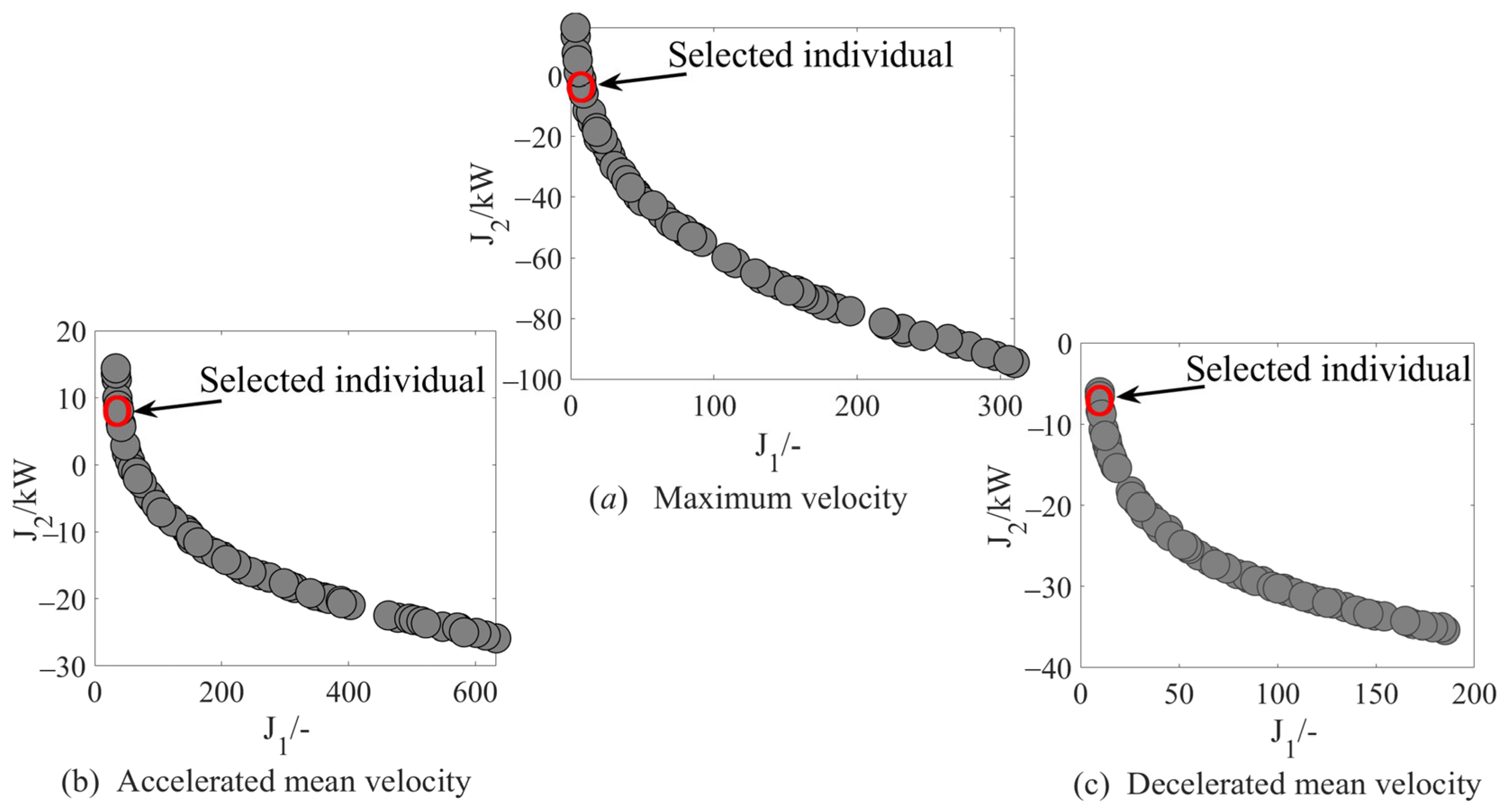
3.2. Fast Non-Dominated Sorting Genetic Algorithm NSGA-II Optimisation Solution
3.2.1. Fast Non-Dominated Sorting
3.2.2. Crowding Distance and Bias Sequence
3.2.3. Elite Selection Strategy
3.2.4. Optimal Individual Decision
- (1)
- The time-domain predicted power demand must be constrained below the motor’s peak power output capacity throughout the driving cycle. This critical operational constraint guarantees the electric machine’s dynamic response capability to deliver the required tractive effort.
- (2)
- The primary concern is the capacity for longitudinal tracking performance, a matter that is addressed through a combination of energy economy considerations.
4. Design of Energy Management Strategy for HESS
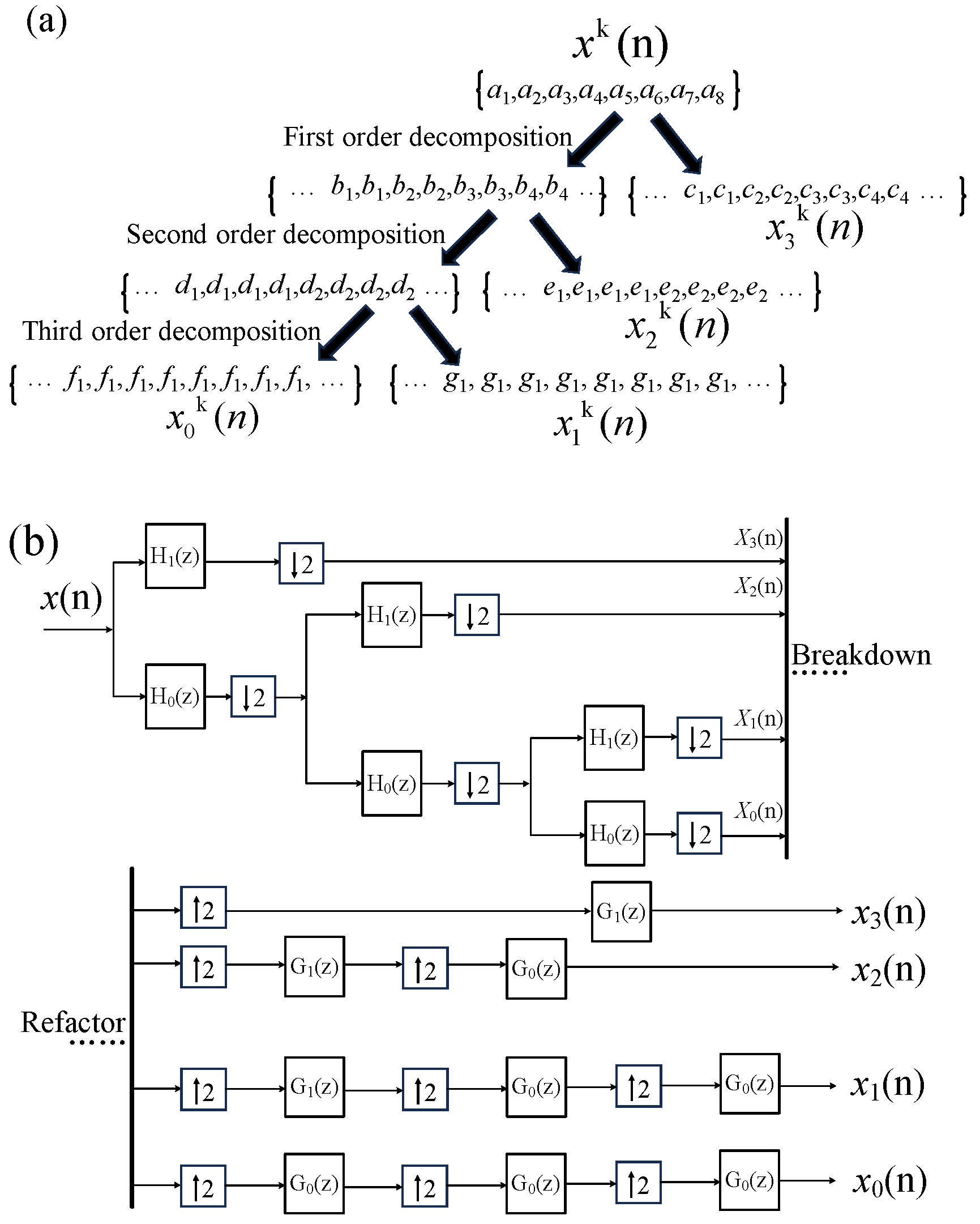
4.1. Haar Wavelet Decomposition of Demand Power
| Algorithm 1: ACC-WT Hierarchical Control Algorithm |
| Input: Ego vehicle: vh, ah Front vehicle: vp, ap Vehicle distance: d Output: Power Components: Phigh, Plow 1: Initialize weight vector q1, q2, q3 Initialize ego vehicle parameters 2: Define cost functions and constraints 3: // ====== NSGA-II Optimization ====== 4: Generate P₀ ← Random population (size=200) 5: for gen ← 1 to 200 do: 6: Apply genetic operators: Simulated binary crossover (η = 0.8) Polynomial mutation (pm = 0.2) 7: Fast non-dominated sorting → {rank1, …, rankn} 8: Calculate crowding distance dj and bias sequence 9: Select Pt+1 using Elite selection strategy 10: end for 11: // ====== Optimal individual decision ====== 12: H₁ ← { U∈ P200 | Preq ≤ Pmotor,peak} 13: H₂ ← Top 10% solutions in H₁ by J₁ 14: Compute score: gradei = (J₁,min/J₁,i) + (J2,min/J2,i) 15: Ubest(k + Np) ← max(gradei) 16: // ====== Online Haar Decomposition ====== 17: Preq = {Preq,k, Preq,k+1, …, Preq,k+7} ← Vehicle driving power calculation 18: [Phigh, Plow] ← 3-level Haar(Preq) Decomposition: H₁(z) = 0.5(1 − z−1), H₀(z) = 0.5(1 + z−1) Reconstruction: G₁(z) = (1 + z−1), G₀(z) = (1 − z−1) |
4.2. Low-Frequency Steady-State Power Quadratic Optimal Decomposition Based on Fuzzy Logic Control
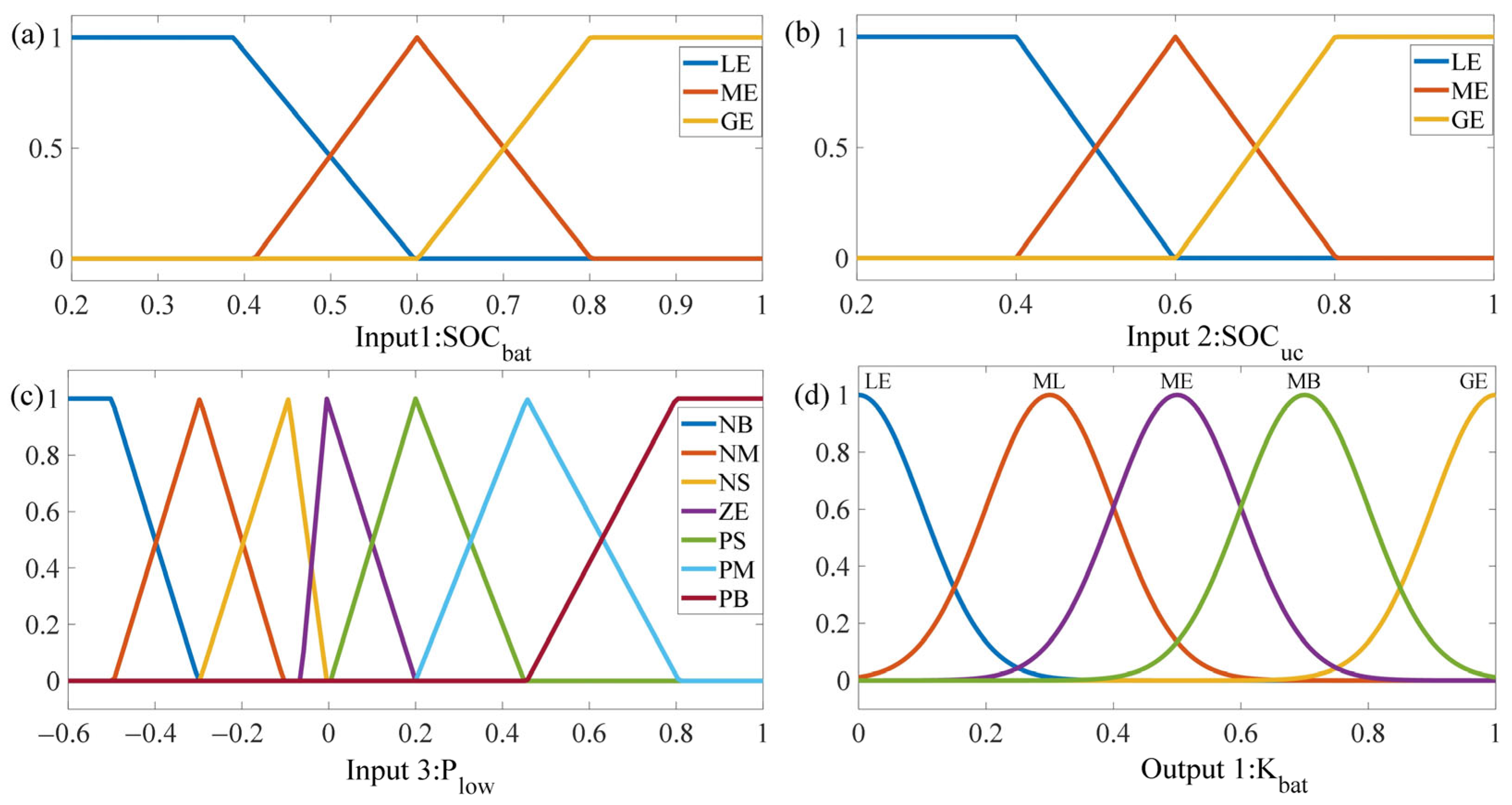
4.2.1. Control Variable Setting and Fuzzy Subset Delineation
4.2.2. Control Variable Affiliation Function Design
4.2.3. Fuzzy Rule Design
- (1)
- In circumstances where demand power is minimal, the demand power is matched by the lithium-ion battery.
- (2)
- Under moderate traction power demand conditions, the lithium-ion battery exclusively handles the power demand when its SOCbat is sufficiently high, regardless of the supercapacitor’s SOCuc. Conversely, If SOCbat is relatively low, coordinated power allocation between the supercapacitor and lithium-ion battery is activated to fulfill the operational requirements.
- (3)
- During high traction power demand, the supercapacitor solely supplies power when its SOCuc is sufficient, independent of the lithium-ion battery’s SOCbat. When SOCuc becomes insufficient, both energy storage units jointly provide power to meet the demand.
- (4)
- Under braking conditions, the supercapacitor recycles the energy converted from larger and medium braking power. The lithium-ion battery recycles the energy converted from smaller braking power.
5. Simulation Verification
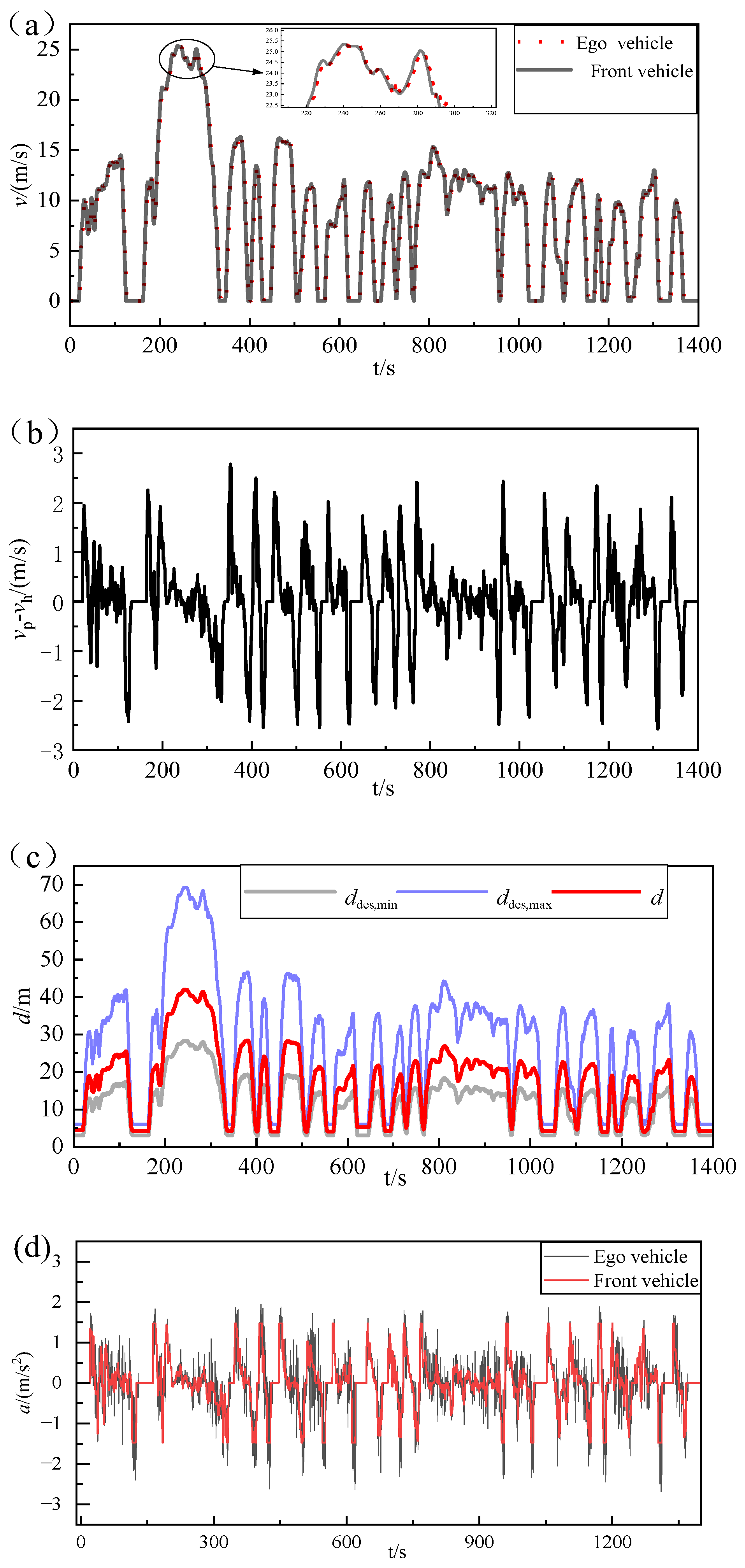
5.1. Simulation Verification of Followership Algorithm
5.2. Simulation Verification of EMS
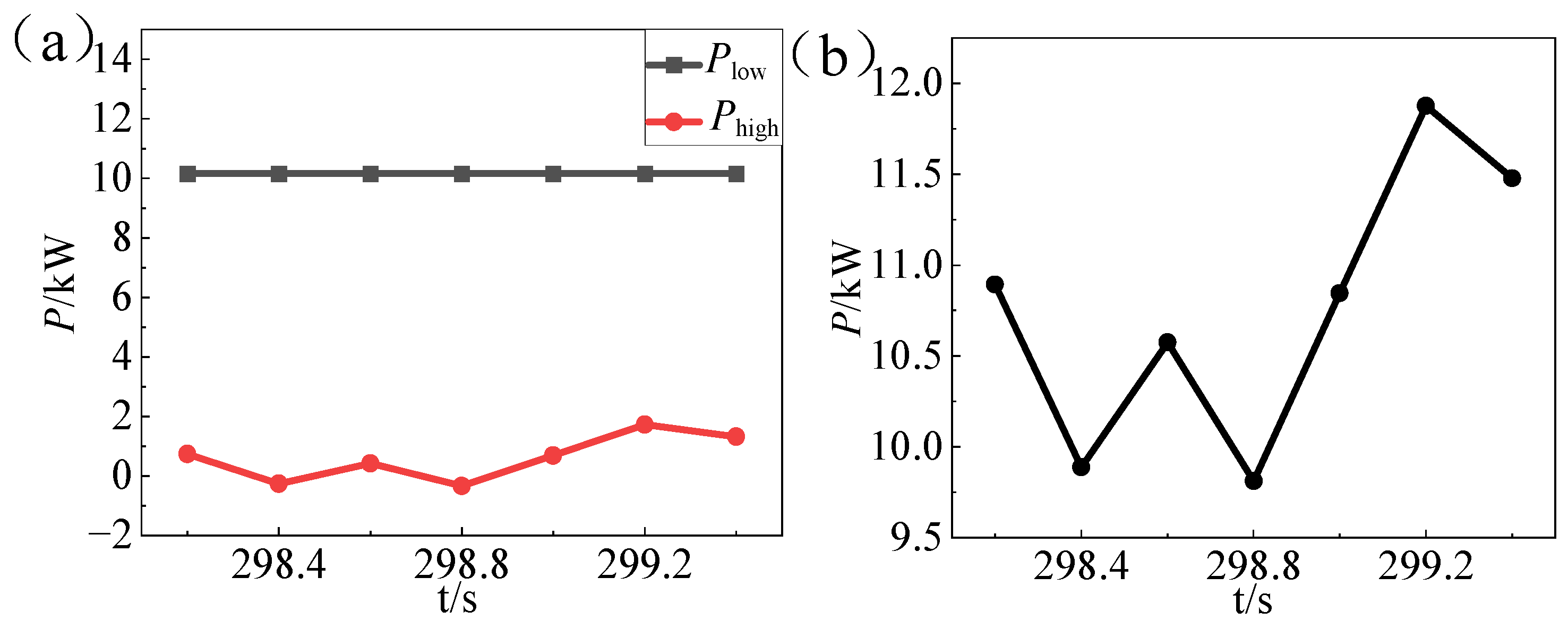
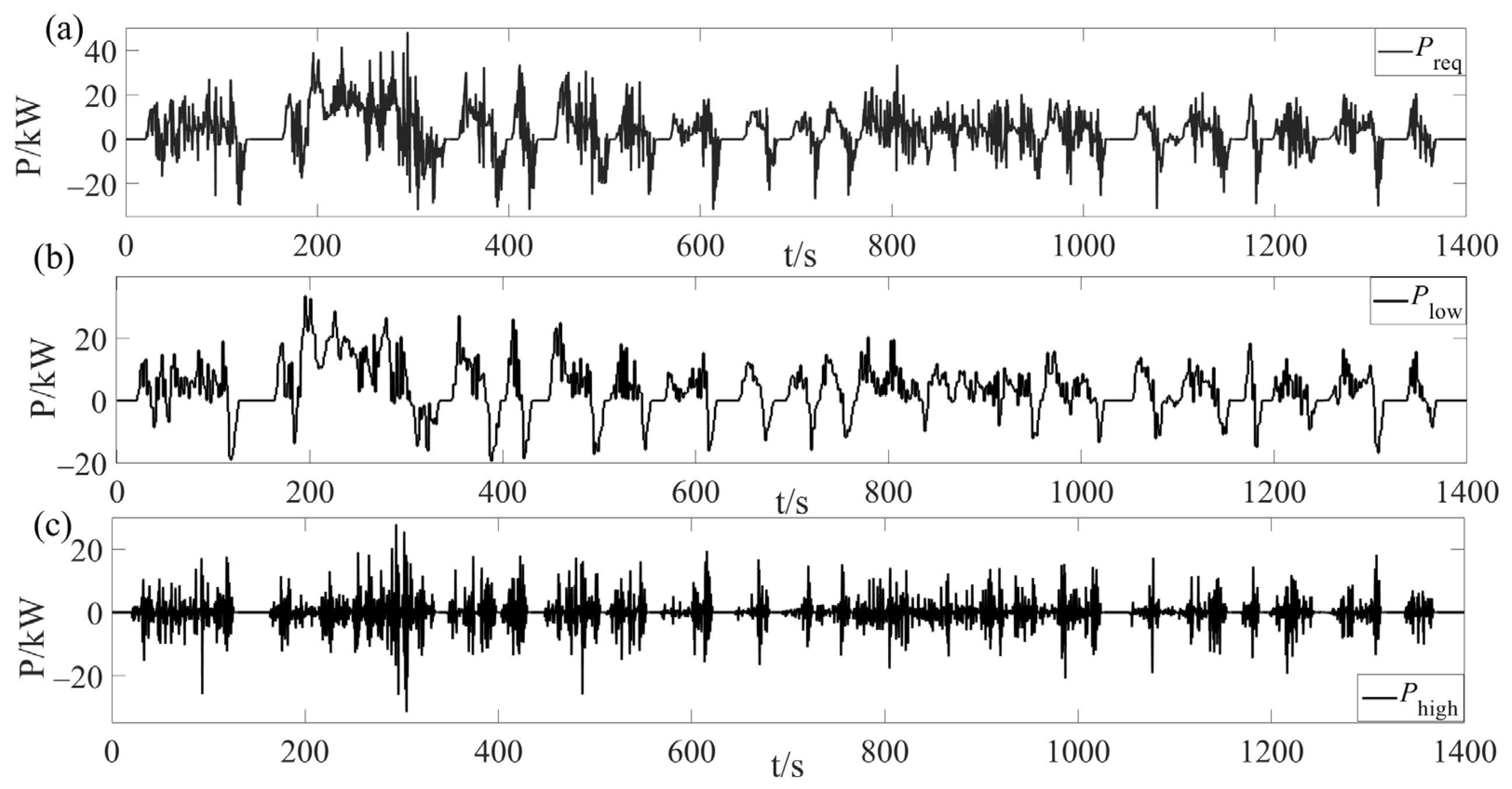
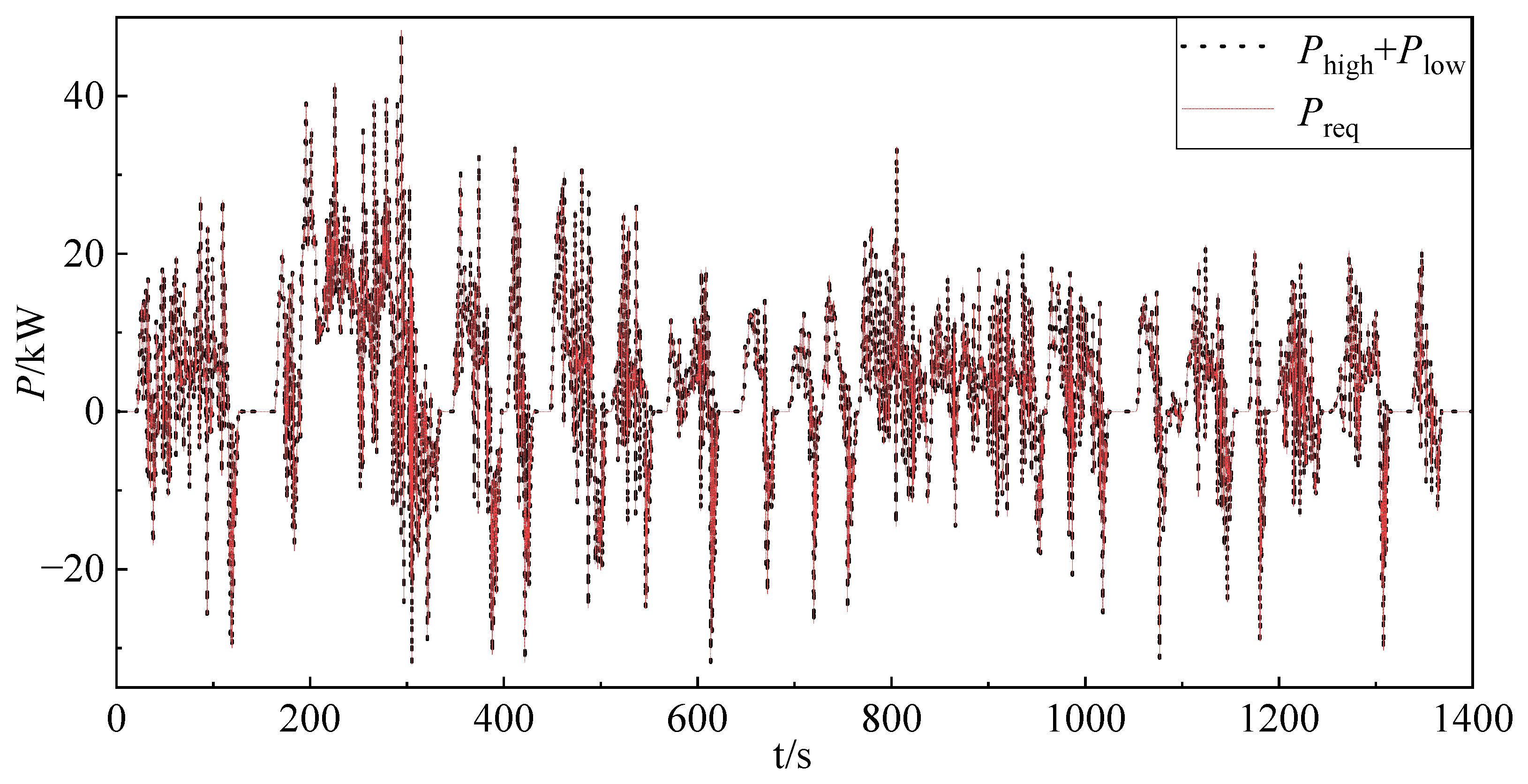
5.2.1. Haar Wavelet Simulation Verification
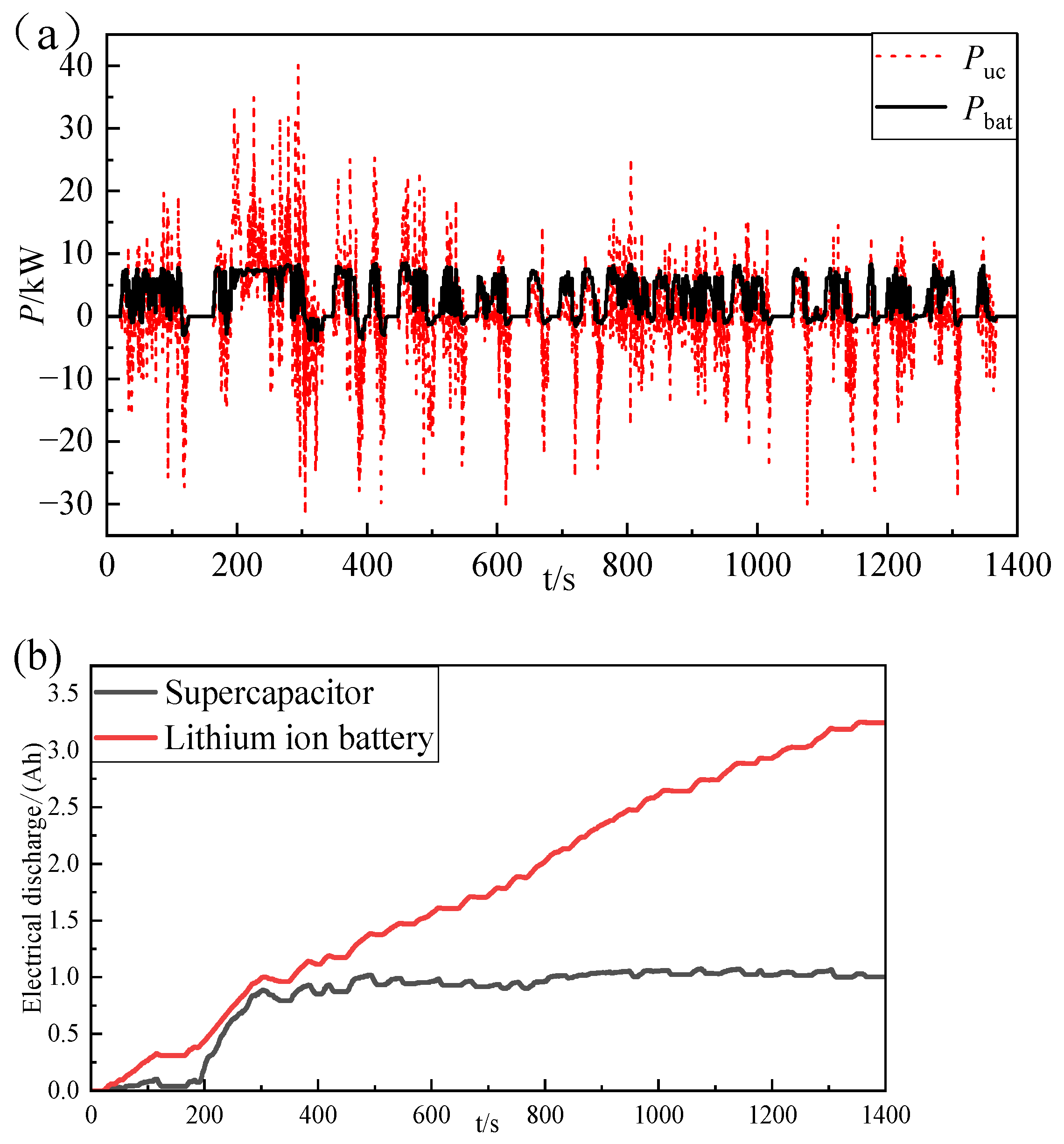
5.2.2. Fuzzy Logic Control Simulation Verification and Comparison
6. Conclusions
- (1)
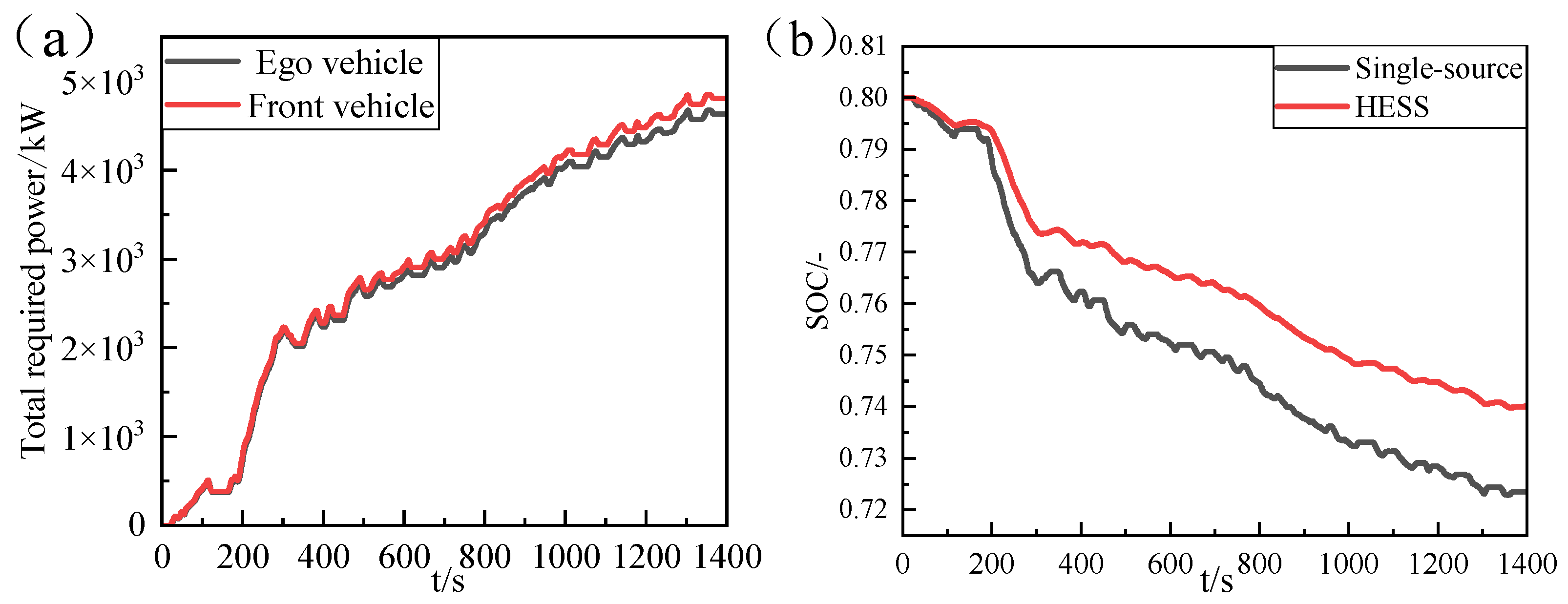
- After multi-objective optimization using NSGA-II for optimal tracking quality and energy economy, the maximum relative speed between vehicles is 2.7 m/s with an average relative speed of 0.56 m/s. The relative distance remains within the desired range, accompanied by a 3.71% reduction in total power demand. The ego vehicle demonstrates stable following capability with improved energy economy. The SOC of the lithium-ion battery in the dual-source system decreases more gradually compared to single-source configurations.
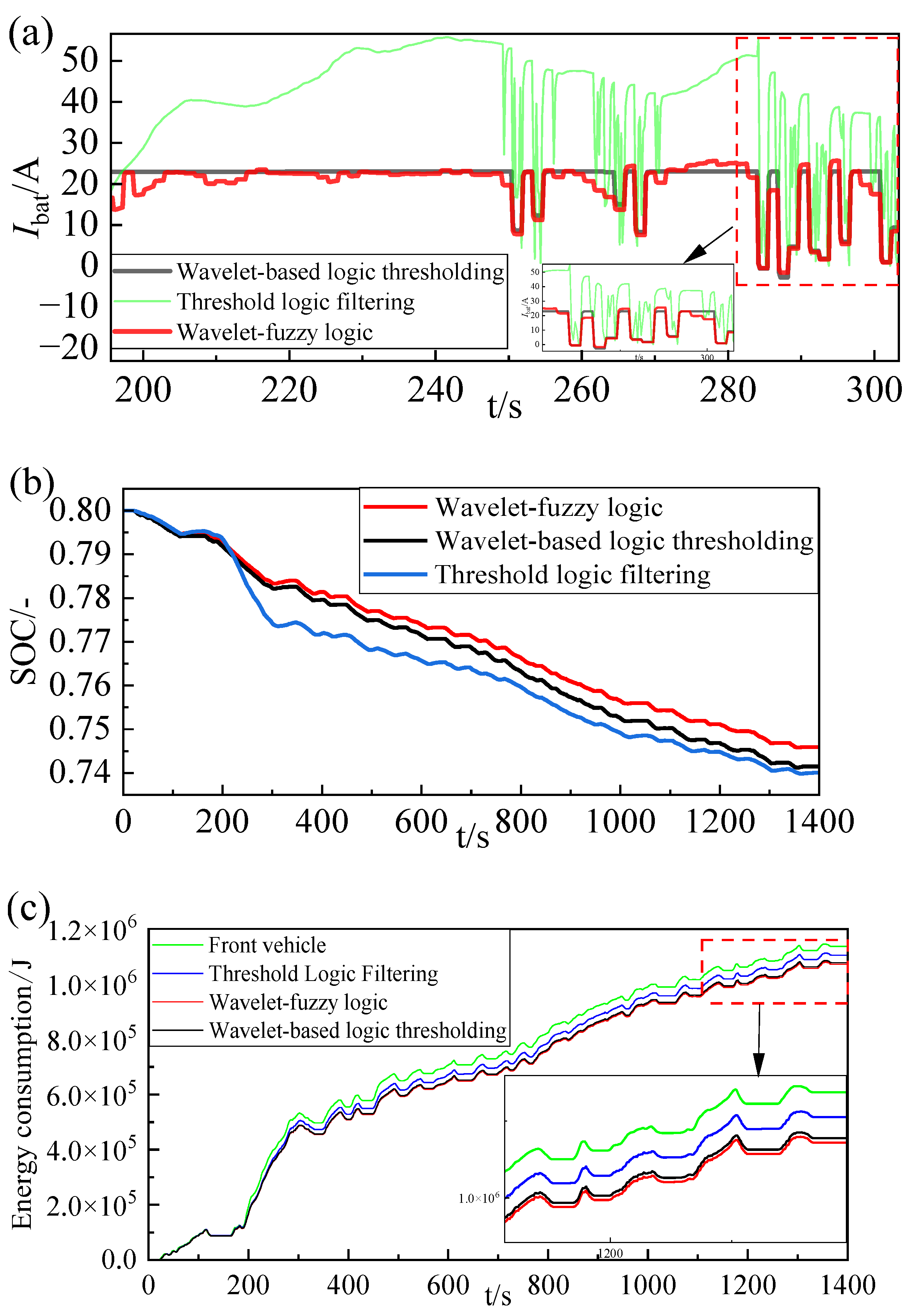
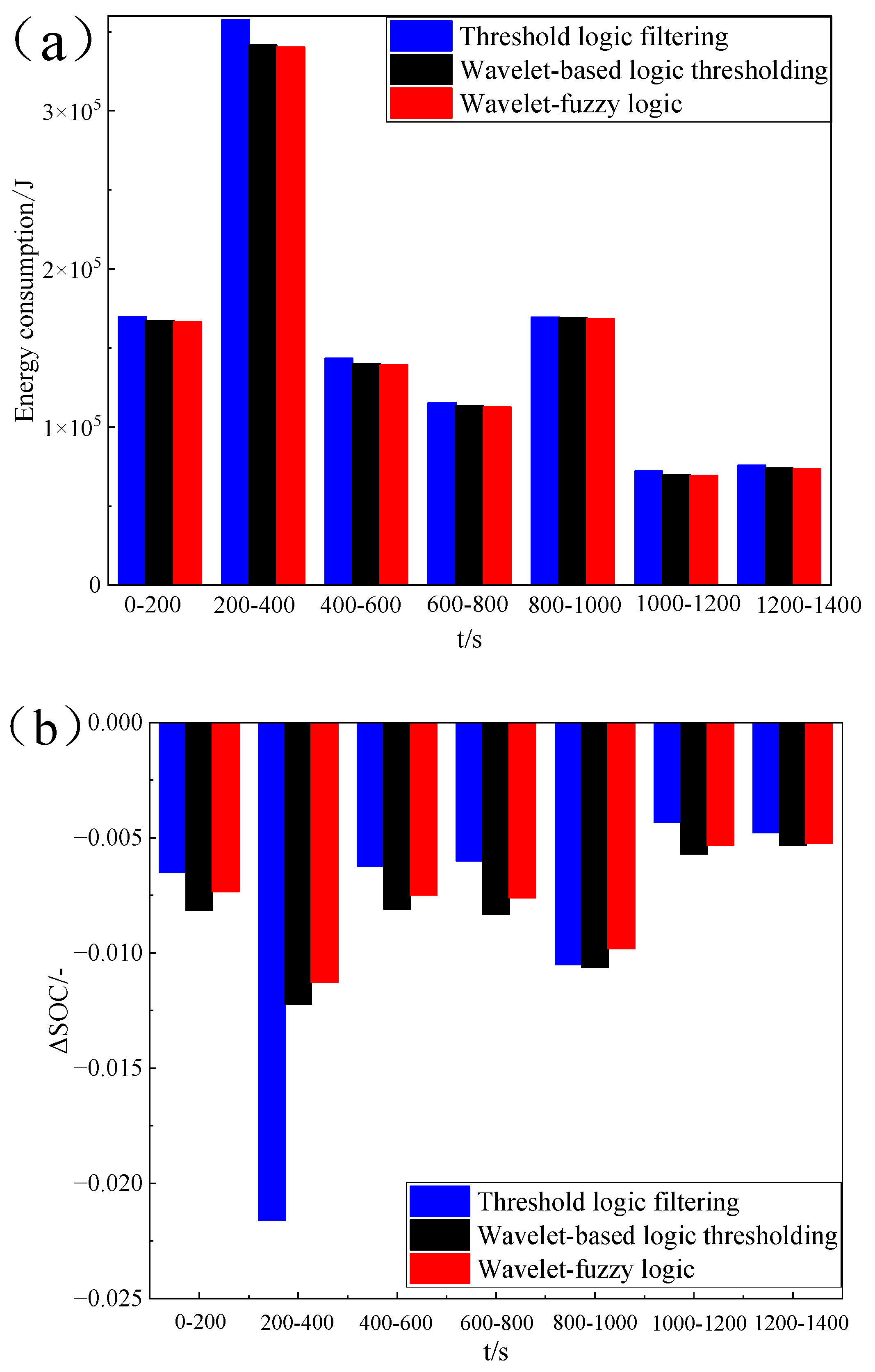
- (2)
- The high-frequency transient power of lithium-ion batteries is significantly reduced after online rolling decomposition based on third-order Haar theory. The wavelet-based logic thresholding is demonstrably superior in terms of control when compared with threshold logic filtering. This is evidenced by a more uniform current, a substantial decrease in peak current, and a 2.51% reduction in energy consumption.
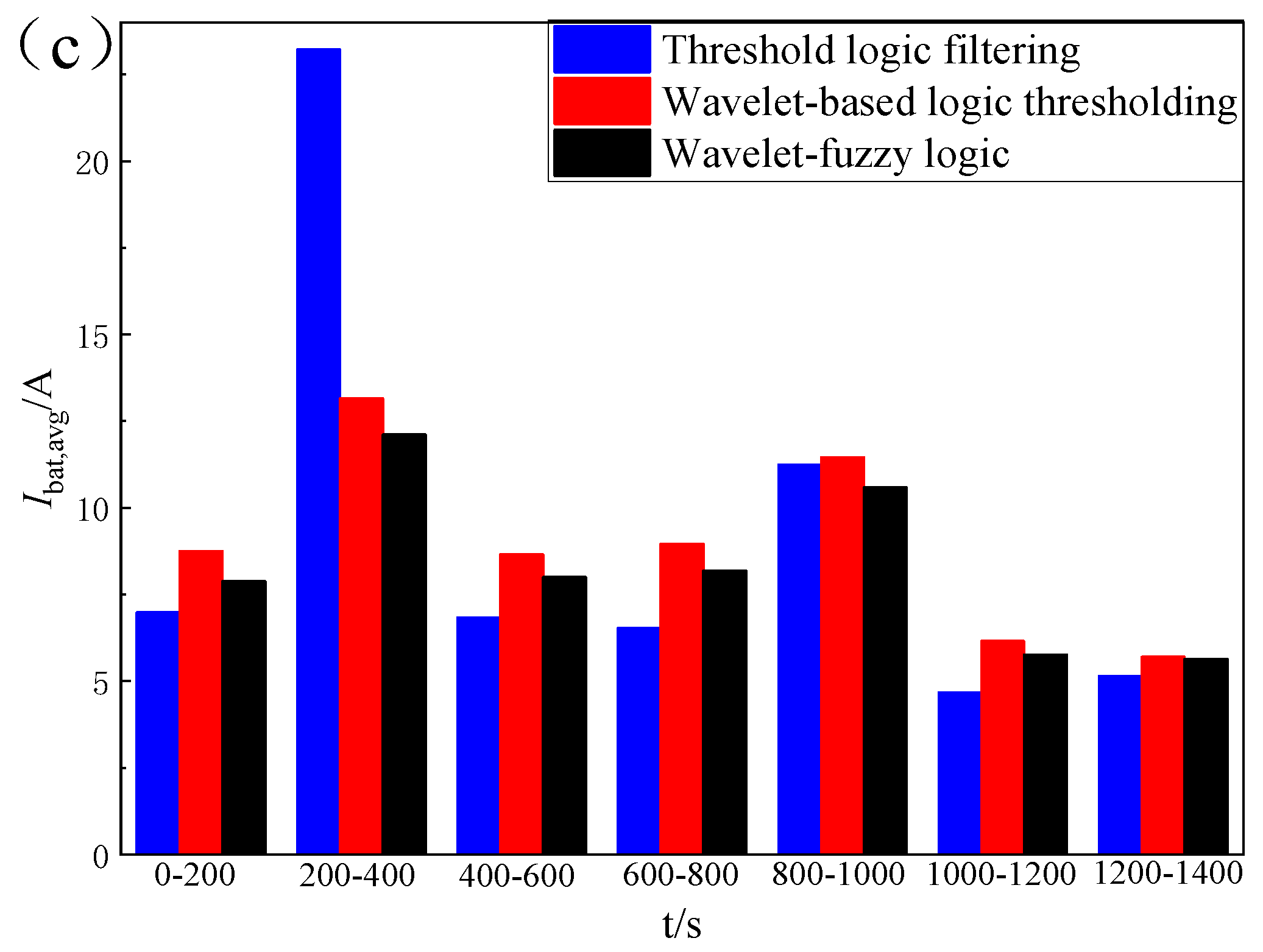
- (3)
- Compared to the wavelet-based logic threshold, the wavelet-fuzzy logic approach demonstrates superior adaptability to operational condition variations and lower energy consumption. These improvements are validated by an 8.1% reduction in average battery current and a 0.59% increase in SOC of the lithium-ion battery.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, J.; Fan, Y.; Yin, G.; Jiang, R. Collaborative Optimization of Energy Management Strategy and Adaptive Cruise Control Based on Deep Reinforcement Learning. IEEE Trans. Transp. Electrif. 2022, 9, 34–44. [Google Scholar]
- Li, J.; Chen, C.; Yang, B.; He, J.; Guan, X. Energy-Efficient Cooperative Adaptive Cruise Control for Electric Vehicle Platooning. IEEE Trans. Intell. Transp. Syst. 2023, 25, 4862–4875. [Google Scholar]
- Zhu, L.; Tao, F.; Fu, Z.; Wang, N.; Ji, B.; Dong, Y. Optimization Based Adaptive Cruise Control and Energy Management Strategy for Connected and Automated FCHEV. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21620–21629. [Google Scholar]
- Kural, E.; Güvenç, B.A. Integrated Adaptive Cruise Control for Parallel Hybrid Vehicle Energy Management. IFAC-PapersOnLine 2015, 48, 313–319. [Google Scholar]
- He, Y.; Zhou, Q.; Makridis, M.; Mattas, K.; Li, J.; Williams, H.; Xu, H. Multiobjective Co-Optimization of Cooperative Adaptive Cruise Control and Energy Management Strategy for PHEVs. IEEE Trans. Transp. Electrif. 2020, 6, 346–355. [Google Scholar]
- Li, S.; Chu, L.; Fu, P.; Pu, S.; Wang, Y.; Li, J.; Guo, Z. Energy-Oriented Hybrid Cooperative Adaptive Cruise Control for Fuel Cell Electric Vehicle Platoons. Sensors 2024, 24, 5065. [Google Scholar] [CrossRef]
- Aljohani, T.M.; Ebrahim, A.; Mohammed, O. Real-Time Metadata-Driven Routing Optimization for Electric Vehicle Energy Consumption Minimization Using Deep Reinforcement Learning and Markov Chain Model. Electr. Power Syst. Res. 2021, 192, 106962. [Google Scholar]
- Aslan Yıldız, Ö.; Sarıçiçek, İ.; Yazıcı, A. A Reinforcement Learning-Based Solution for the Capacitated Electric Vehicle Routing Problem from the Last-Mile Delivery Perspective. Appl. Sci. 2025, 15, 1068. [Google Scholar] [CrossRef]
- Lu, C.; Dong, J.; Hu, L. Energy-Efficient Adaptive Cruise Control for Electric Connected and Autonomous Vehicles. IEEE Intell. Transp. Syst. Mag. 2019, 11, 42–55. [Google Scholar]
- Li, G.; Görges, D. Ecological Adaptive Cruise Control and Energy Management Strategy for Hybrid Electric Vehicles Based on Heuristic Dynamic Programming. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3526–3535. [Google Scholar]
- Zhang, R.; Wu, N.; Wang, Z.; Li, K.; Song, Z.; Chang, Z.; Chen, X.; Yu, F. Constrained Hybrid Optimal Model Predictive Control for Intelligent Electric Vehicle Adaptive Cruise Using Energy Storage Management Strategy. J. Energy Storage 2023, 65, 107383. [Google Scholar]
- Yu, S.; Pan, X.; Georgiou, A.; Chen, B.; Jaimoukha, I.M.; Evangelou, S.A. A Real-Time Robust Ecological-Adaptive Cruise Control Strategy for Battery Electric Vehicles. IEEE Trans. Transp. Electrif. 2023, 10, 7389–7404. [Google Scholar]
- Wang, C.; Xiong, R.; He, H.; Zhang, Y.; Shen, W. Comparison of Decomposition Levels for Wavelet Transform Based Energy Management in a Plug-in Hybrid Electric Vehicle. J. Clean. Prod. 2019, 210, 1085–1097. [Google Scholar]
- Ibrahim, M.; Jemei, S.; Wimmer, G.; Hissel, D. Nonlinear Autoregressive Neural Network in an Energy Management Strategy for Battery/Ultra-Capacitor Hybrid Electrical Vehicles. Electr. Power Syst. Res. 2016, 136, 262–269. [Google Scholar]
- Yan, M.; Li, M.; He, H.; Peng, J.; Sun, C. Rule-Based Energy Management for Dual-Source Electric Buses Extracted by Wavelet Transform. J. Clean. Prod. 2018, 189, 116–127. [Google Scholar]
- Zhang, Z.; Tang, J.; Zhang, J.; Zhang, T. Research on Energy Hierarchical Management and Optimal Control of Compound Power Electric Vehicle. Energies 2024, 17, 1359. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, W.; Liang, J.; Zhang, Y.; Wu, Y. Layered Control of Compound Power Loader Based on Fuel Cell. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48, 2165–2176. [Google Scholar]
- Liu, Y. Research on Energy-saving Adaptive Cruise Control for Pure electric Vehicles. Master’s Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
- Huan, J.; Wei, W.; Zou, D. Research on Mode Switching Strategy of Adaptive Cruise System based on Personalized Spacing Strategy. Automot. Eng. 2020, 42, 1302–1311. [Google Scholar]
- Li, S.; Li, K.; Rajamani, R.; Wang, J. Model Predictive Multi-objective Vehicular Adaptive Cruise Control. IEEE Trans. Control Syst. Technol. 2010, 19, 556–566. [Google Scholar]
- Santhanakrishnan, K.; Rajamani, R. On Spacing Policies for Highway Vehicle Automation. IEEE Trans. Intell. Transp. Syst. 2003, 4, 198–204. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zhang, Q.; Hou, J.; Hu, X.; Yuan, L.; Jankowski, Ł.; An, X.; Duan, Z. Vehicle Parameter Identification and Road Roughness Estimation Using Vehicle Responses Measured in Field Tests. Measurement 2022, 199, 111348. [Google Scholar] [CrossRef]
- Lv, Y.-M.; Yuan, H.-W.; Liu, Y.-Y.; Wang, Q.-S. Fuzzy Logic based Energy Management Strategy of Battery-ultracapacitor single power supply for HEV. In Proceedings of the 2010 First International Conference on Pervasive Computing, Signal Processing and Applications, Harbin, China, 17–19 September 2010; pp. 1209–1214. [Google Scholar]
- Hemmati, R.; Saboori, H. Emergence of Hybrid Energy Storage Systems in Renewable Energy and Transport Applications–A Review. Renew. Sustain. Energy Rev. 2016, 65, 11–23. [Google Scholar] [CrossRef]
- Yuan, Z.; Tian, T.; Hao, F. A Hybrid Neural Network Based on Variational Mode Decomposition Denoising for Predicting State-of-Health of Lithium-Ion Batteries. J. Power Sources 2024, 609, 234697. [Google Scholar] [CrossRef]
- Li, Y.; Wu, Y.; Huang, H. Neural Network-Based Modeling of Diffusion-Induced Stress in a Hollow Cylindrical Nano-Electrode of Lithium-Ion Battery. J. Electrochem. Energy Convers. Storage 2025, 22, 011011. [Google Scholar] [CrossRef]
- Hoque, M.A.; Hassan, M.K.; Hajjo, A.; Tokhi, M.O. Neural Network-Based Li-Ion Battery Aging Model at Accelerated C-Rate. Batteries 2023, 9, 93. [Google Scholar] [CrossRef]
- Sarkar, S.; Halim, S.Z.; El-Halwagi, M.M. Electrochemical Models: Methods and Applications for Safer Lithium-Ion Battery Operation. J. Electrochem. Soc. 2022, 169, 100501. [Google Scholar] [CrossRef]
- Bhat, C.; Channegowda, J. An Improved Electrochemical-Based Model to Estimate Battery Equivalent Circuit Parameters for Pulsed Discharge Scenarios. Energy Storage 2022, 4, e294. [Google Scholar] [CrossRef]
- Lagnoni, M.; Scarpelli, C.; Lutzemberger, G. Critical Comparison of Equivalent Circuit and Physics-Based Models for Lithium-Ion Batteries: A Graphite/Lithium-Iron-Phosphate Case Study. J. Energy Storage 2024, 94, 112326. [Google Scholar] [CrossRef]
- Cheng, Y.S. Identification of Parameters for Equivalent Circuit Model of Li-Ion Battery Cell with Population Based Optimization Algorithms. Ain Shams Eng. J. 2024, 15, 102481. [Google Scholar] [CrossRef]
- Graule, A.; Oehler, F.F.; Schmitt, J. Development and Evaluation of a Physicochemical Equivalent Circuit Model for Lithium-Ion Batteries. J. Electrochem. Soc. 2024, 171, 020503. [Google Scholar] [CrossRef]
- Hussein, H.M.; Esoofally, M.; Donekal, A.; Rafin, S.M.S.H.; Mohammed, O. Comparative Study-Based Data-Driven Models for Lithium-Ion Battery State-of-Charge Estimation. Batteries 2024, 10, 89. [Google Scholar] [CrossRef]
- Mu, G.; Wei, Q.; Xu, Y. State of Health Estimation of Lithium-Ion Batteries Based on Feature Optimization and Data-Driven Models. Energy 2025, 314, 134578. [Google Scholar] [CrossRef]
- Zheng, X.; Wu, F.; Tao, L. Degradation Trajectory Prediction of Lithium-Ion Batteries Based on Charging-Discharging Health Features Extraction and Integrated Data-Driven Models. Qual. Reliab. Eng. Int. 2024, 40, 1833–1854. [Google Scholar] [CrossRef]
- Zhang, W.; Xie, Y.; He, H. Multi-Physics Coupling Model Parameter Identification of Lithium-Ion Battery Based on Data Driven Method and Genetic Algorithm. Energy 2025, 314, 134120. [Google Scholar] [CrossRef]
- Shi, J. Research on Adaptive Cruise Control Algorithm considering Road Conditions. Master’s Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Aljohani, T.M.; Mohammed, O. A Real-Time Energy Consumption Minimization Framework for Electric Vehicles Routing Optimization Based on SARSA Reinforcement Learning. Vehicles 2022, 4, 1176–1194. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, T.; Zhang, S.; Li, K. Intelligent Hybrid Electric Vehicle ACC with Coordinated Control of Tracking Ability, Fuel Economy, and Ride Comfort. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2303–2308. [Google Scholar] [CrossRef]
- Pan, C.; Huang, A.; Wang, J.; Chen, L.; Liang, J.; Zhou, W.; Wang, L.; Yang, J. Energy-optimal Adaptive Cruise Control Strategy for Electric Vehicles based on Model Predictive Control. Energy 2022, 241, 122793. [Google Scholar]
- Yan, W. Research on Improved Genetic Algorithm Based on Multi-objective optimization Problem. Master’s Thesis, Tianjin Polytechnic University, Tianjin, China, 2019. [Google Scholar]
- Zhang, X.; Mi, C. Vehicle Energy Management: Modeling, Control and Optimization; Zhang, X.; Mi, C., Translators; China Machine Press: Beijing, China, 2013; pp. 113–140. [Google Scholar]
- Kakouche, K.; Oubelaid, A.; Mezani, S.; Rekioua, D.; Rekioua, T. Different Control Techniques of Permanent Magnet Synchronous Motor with Fuzzy Logic for Electric Vehicles: Analysis, Modelling, and Comparison. Energies 2023, 16, 3116. [Google Scholar] [CrossRef]
- Wang, B. Research on Parameter Matching and Control Strategy of New Energy Vehicle Power System. Master’s Thesis, Hunan University, Changsha, China, 2018. [Google Scholar]
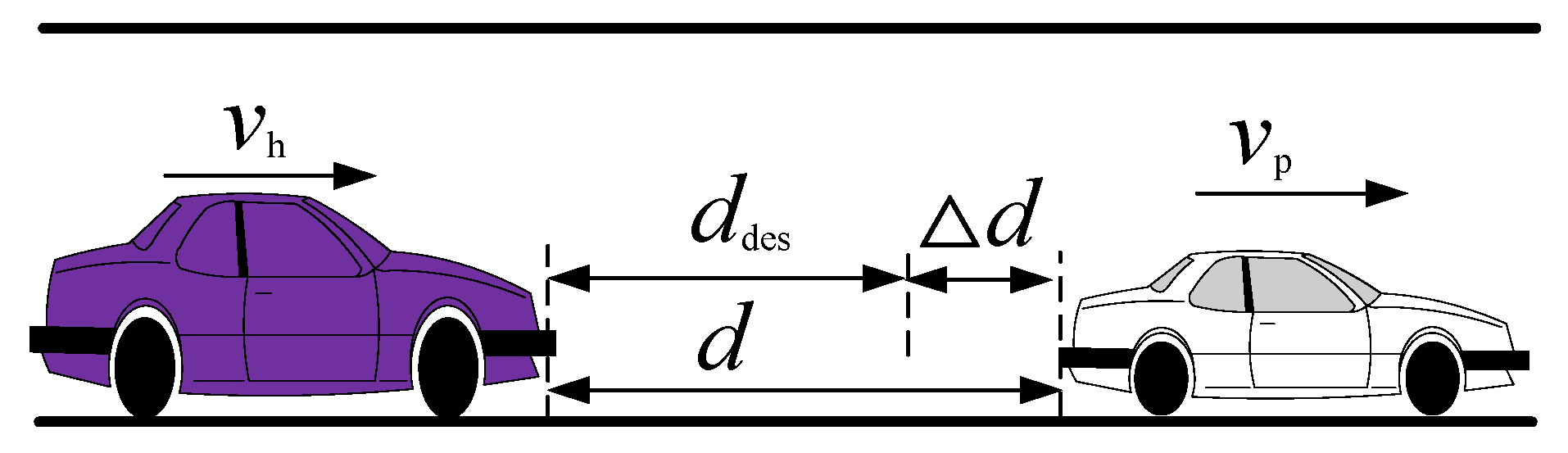

| Parameter Type | Parameter Name | Value |
|---|---|---|
| Whole vehicle | Curb weight/kg | 1370 |
| Windward area/m2 | 2.4 | |
| Rolling resistance coefficient | 0.02 | |
| Wind resistance | 0.342 | |
| Rotating mass conversion factor | 1.05 | |
| Tyre rolling radius/m | 0.325 | |
| Transmission efficiency | 0.96 | |
| Motor | Rated speed/(r/min) | 3000 |
| Maximum speed/(r/min) | 9000 | |
| Rated torque/(N.m) | 88 | |
| Maximum torque/(N.m) | 264 | |
| Peak power/kW | 83 | |
| Rated power/kW | 46 | |
| Lithium-ion battery | Quantity | 1 |
| Unit capacity/Ah | 60 | |
| Maximum voltage/V | 349.6 | |
| Minimum voltage/V | 320 | |
| Internal resistance/Ω | 0.8 | |
| Supercapacitor | Quantity | 4 |
| Peak voltage/V | 432 | |
| Minimum voltage/V | 250 | |
| Unit capacity/F | 23.6 | |
| Internal resistance/Ω | 0.045 | |
| DC/DC efficiency | 0.9 |
| Kbat | Plow | |||||||
|---|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZE | PS | PM | PB | ||
| SOCbat SOCuc = LE | LE | ML | ML | GE | GE | ME | ME | ML |
| ME | LE | LE | LE | GE | GE | MB | MB | |
| GE | LE | LE | LE | GE | GE | MB | GE | |
| SOCbat SOCuc = ME | LE | ML | ME | GE | GE | ME | ML | ML |
| ME | LE | LE | LE | GE | GE | ME | LE | |
| GE | LE | LE | LE | GE | GE | ME | ML | |
| SOCbat SOCuc = GE | LE | GE | GE | GE | GE | ML | LE | LE |
| ME | MB | MB | ML | GE | GE | ML | LE | |
| GE | LE | LE | LE | GE | GE | ME | LE | |
| Parameter | Δv/(m/s) | d/m | a/(m/s2) |
|---|---|---|---|
| Maximum values | 2.7 | 41.95 | 1.94 |
| Minimum value | −2.57 | 3.97 | −2.67 |
| Average value | 0.56 | 16.92 | - |
| Parameter | Pmax/kW | Pdrive,avg/kW | Pbrake,avg/kW | Q/Ah |
|---|---|---|---|---|
| Battery | 8.53 | 4.66 | −0.77 | 3.25 |
| Supercapacitor | 40.1 | 4.34 | −4.37 | 1 |
| Parameter | SOC/% | Ibat,max/A | Ibat,avg/A | Energy Consumption/J |
|---|---|---|---|---|
| Front vehicle | 0.7231 | 167.06 | 18.9 | 1137275 |
| Threshold logic filtering | 0.74 | 55.71 | 11.01 | 1105196 |
| Wavelet-based logic thresholding | 0.7415 | 23.06 | 10.2 | 1077475 |
| Wavelet-fuzzy logic | 0.7459 | 26.49 | 9.37 | 1071748 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Tang, J.; Zhang, J.; Li, T.; Chen, H. Research on Online Energy Management Strategy for Hybrid Energy Storage Electric Vehicles Under Adaptive Cruising Conditions. Sustainability 2025, 17, 3232. https://doi.org/10.3390/su17073232
Zhang Z, Tang J, Zhang J, Li T, Chen H. Research on Online Energy Management Strategy for Hybrid Energy Storage Electric Vehicles Under Adaptive Cruising Conditions. Sustainability. 2025; 17(7):3232. https://doi.org/10.3390/su17073232
Chicago/Turabian StyleZhang, Zhiwen, Jie Tang, Jiyuan Zhang, Tianyu Li, and Hao Chen. 2025. "Research on Online Energy Management Strategy for Hybrid Energy Storage Electric Vehicles Under Adaptive Cruising Conditions" Sustainability 17, no. 7: 3232. https://doi.org/10.3390/su17073232
APA StyleZhang, Z., Tang, J., Zhang, J., Li, T., & Chen, H. (2025). Research on Online Energy Management Strategy for Hybrid Energy Storage Electric Vehicles Under Adaptive Cruising Conditions. Sustainability, 17(7), 3232. https://doi.org/10.3390/su17073232







