The Efficiency Measurement and Spatial Spillover Effect of Green Technology Innovation in Chinese Industrial Enterprises

Abstract

Green technology innovation (GTI) is the core force driving the sustainable and advanced progression of the economy. Accurately assessing the green technology innovation efficiency (GTIE) of Chinese industrial firms will help promote the green transformation and development of industrial firms. Based on the three-stage DEA(3S-DEA) model, the article measures the GTIE of Chinese industrial firms from 2013 to 2022. Then, its spatial distribution characteristics and spatial spillover effects were analyzed using the spatial Durbin model (SDM). The study shows that after excluding environmental elements and stochastic interference, the value of GTIE of industrial firms shows the trend of east > central > northeast > west; the GTIE of industrial firms has significant spatial correlation, and there are differences in direct and spillover effects under different spatial weight matrices. The level of economic development, industrialization, openness, and information infrastructure has a remarkable positive influence on the GTIE of industrial firms, while government support does not show a significant effect.

1. Introduction

In the new era of green advancement led by the construction of ecological civilization, it has become a social consensus to pursue the harmonious advancement of the economy with population, resources, and the environment. Environmental protection and green advancement have been prioritized by the Chinese Government as a national roadmap. As the meeting point of the two main ideas of “innovation-propelled” and “green advancement”, GTI will undoubtedly become a crucial route to maximize environmental quality and address resource and environmental issues in the current new normal of slowing economic growth and progressively more noticeable resource and environmental constraints [1]. Although technological advancement is a core driver of economic prosperity and social evolution, the traditional model of technological innovation has led to continued environmental degradation while creating economic benefits. In the practice of industrial firms, “green advancement” and “technological innovation” have not yet realized effective synergy. Therefore, it is essential to overcome the constraints of the conventional paradigm of technological innovation to tackle the problem of the disparity between economic and environmental benefits. This is why ecological concepts must be incorporated into industry transformation and upgrading, and GTI must be used to encourage the growth of the innovation system, economic system, and environmental system in a coordinated manner and with benign interaction [2,3].

Currently, GTI has emerged as a crucial avenue for industrial firms to achieve efficiency and quality [4]. At the “quantitative” level, Chinese industrial enterprises’ expenses regarding GTI have shown a consistent annual increase. However, at the “qualitative” level, they face the outstanding problem of inefficiency in innovation input and output. Resources will be wasted, and innovation efficiency will stagnate if we only concentrate on increasing “quantity” and ignore improving “quality” [5]. As a matter of fact, GTI in the field of industrial manufacturing is characterized by high cost, high risk, and uncertain benefit. This causes the innovation’s main body to lack motivation for carrying out GTI activities, which require a long study and development cycle and are associated with significant challenges in promotion. This is also the main reason for the current lack of willingness of Chinese industrial firms in green innovation. Thus, in addition to considering the total amount of innovation input, we should also focus more on increasing innovation efficiency when enhancing the GTI capacity of industrial firms [6]. The authorities have implemented several complementary guidelines, including fiscal and tax subsidies as well as environmental control, to incentivize industrial firms to actively engage in GTI [7,8]. Mandatory measures, like environmental regulations, can compel businesses to innovate in a green way, but it takes time and resources to conduct professional monitoring to determine whether businesses are actually adhering to green standards. Furthermore, even though non-mandatory measures like government subsidies can offer financial assistance, it is challenging to guarantee the ongoing enhancement of businesses’ GTIE. Once government support is weakened, enterprises may again face a decline in innovation efficiency due to insufficient incentives.

The primary study questions of this article are as follows: How efficient is the GTI of Chinese industrial firms? Is there a spatial spillover effect? What is its direction and intensity? To test the above study questions, the following hypotheses are proposed in this article. H1: The GTIE of Chinese industrial firms varies significantly by region. H2: GTIE has spatial spillover effects, meaning that businesses in nearby areas will have an impact on one another’s efficiency. H3: The spatial spillover effect is affected by geographic distance and economic level.

Thus, a reasonable and scientific assessment of Chinese industrial firms’ GTIE and the identification of the major factors influencing its improvement can yield theoretical guidance for the future development and green transformation of industrial firms, which is a valuable area of study. The following are this article’s marginal contributions. Firstly, the GTIE index system has been enhanced and refined. Secondly, the impact of random and environmental elements is effectively eliminated by introducing a 3S-DEA model, which enhances the precision of measuring the true level of GTIE of Chinese industrial firms. Finally, the spatial distribution features of the GTIE of Chinese industrial firms and their spatial spillover effects are thoroughly examined using the SDM.

The following is the article’s primary structure. The Section 2 of this study is devoted to the compilation of the literature review; the Section 3 is devoted to the study design and data description; the Section 4 is devoted to the empirical analysis; and the Section 5 is devoted to the results and discussion.

2. Literature Review

2.1. Study on the Connotation of GTI

The term “GTI” was proposed by foreign scholars Braun et al. [9]. It describes the creative actions firms take to boost commitment to the development of green technology, procedures, or goods in an effort to lower energy consumption and environmental degradation. According to some academics, GTI is a model of technological advancement that prioritizes environmental benefits. For instance, Fernando et al. [10] characterize GTI as an economic advancement process that prioritizes environmental sustainability, with energy efficiency and emission control serving as fundamental requirements. The exploration of GTI in China started relatively late. Tong et al. [11] defined GTI as a form of innovative management and an improvement strategy that integrates environmental considerations into the production process from the firm’s point of view. Zeng et al. [12] classified GTI into two categories: green product and process innovation, which further integrated environmental elements into GTI activities. To achieve the strategic goal of sustainable advancement, this article argues that GTI can achieve the synergistic advancement of the economy and environment by combining the opinions of pertinent studies from the perspectives of resource allocation and ecological preservation. Specifically, in the process of promoting green technological progress, enterprises should give full play to knowledge capital, attract talents, and invest funds to promote technological innovation through the study strategy of excellence to advance eco-friendly technological solutions that comply with ecological preservation criteria, secure corresponding intellectual property rights, and, consequently, realize a mutually beneficial outcome balancing fiscal gains with environmental conservation.

2.2. Study on the Measurement of GTIE

The studies of efficiency evaluation mainly use the SFA model with a parametric approach and the DEA model with a non-parametric approach. For instance, Zhang et al. [13] employed the SFA to assess the GTIE and its two elements—technical efficiency and technical progress—in 33 nations that collaborate to construct the “Belt and Road”. Chen et al. [14] applied the SFA model to study how technological advancement, technical efficiency, and scale change dynamically in China at the provincial level. However, since SFA requires the specific functional form of the production frontier to be determined in advance, most scholars tend to prefer DEA for measuring the GTIE. Liu et al. [15] have examined the GTIE in high-technology sectors across China, revealing an overall upward trend in efficiency. Zhang et al. [16] measured the GTIE in architectural firms using the EBM model and came to the conclusion that environmental regulation would greatly increase the GTIE in architectural firms. Adopting the innovation value chain framework, Liu et al. [17,18] categorized GTIE into two phases, R&D efficiency and efficiency of transforming achievements, and used the Super-SBM to evaluate the GTIE across 30 provinces in China. Wang et al. [19] evaluated the two-stage GTIE of 38 Chinese new energy firms using the non-radial DEA method. Wu et al. [20] applied a two-stage network DEA with common inputs to appraise the GTIE in 30 industrial firms in China and to explore the characteristics of their regional differences. Qin et al. [21] appraised the innovation efficiency of 80 Chinese industrial research institutes using a 3S-DEA model. Zhong et al. [22] evaluated the GTIE of publicly listed lithium-ion battery firms in China between 2009 and 2018 using a 3S-DEA and Tobit model.

2.3. Study on the Influencing Factors of GTIE

In a study on the major determinants of GTIE, Fu et al. [23] focused on Chinese-listed manufacturing enterprises and found that regional innovation ability is the direct reason affecting the GTIE, while human resources and government finance belong to the category of indirect influence. Focusing on the regional level, Wang et al. [24] assessed the GTIE across 30 Chinese provinces and empirically proved that the coordination of bilateral foreign direct investment (FDI) can highly enhance the performance of GTI through the regression model. Through an in-depth analysis of China’s heavily polluting firms, Li et al. [25] conducted a thorough analysis of China’s heavy pollution sectors and found that government subsidies can effectively encourage companies to pursue innovations in green technology. The study conducted by Fan et al. [26] examines the determinants of the external environment affecting enterprises. The authors assert that while environmental regulation can favorably impact the GTIE, the provision of government subsidies may further amplify this beneficial effect. However, they also acknowledge that environmental regulation may have adverse consequences. Chen et al. [27] posited that foreign direct investment, organizational size, and advancements in technology positively influence GTIE.

2.4. Literature Evaluation

In summary, existing studies have focused on the connotation definition, measurement methods, and analysis of influencing factors of GTI. Firstly, in terms of connotation definition, scholars have interpreted GTI in multiple dimensions from different perspectives (e.g., corporate practice, environmental benefit priority, and economic-environmental synergistic development), and emphasized its strategic value in resource optimization and ecological protection. Secondly, in terms of measurement methods, scholars have widely adopted parametric (e.g., SFA) and non-parametric (e.g., DEA and its derivative models) methods, among which DEA is preferred because it does not need to preset the form of a production function. Recent studies have refined the assessment dimensions of GTI efficiency through two-stage or three-stage models, enhancing the scientific nature of the measurement. Finally, regarding the influencing factors, the study identifies key variables such as government subsidies, environmental regulations, FDI, and human resources, and reveals the heterogeneity of direct and indirect effects.

In conclusion, the current study has made great strides in understanding the meaning of GTI, measuring efficiency, and determining its impact factors; however, the following issues remain. Firstly, studies on the GTIE in industrial firms are scarcer. Secondly, the conventional DEA is mostly used, and the application of the 3S-DEA model is not yet widespread. Thirdly, a thorough examination of the features of the spatial distribution of efficiency and spillover effects is lacking. Therefore, this article will use a 3S-DEA to assess the GTIE of Chinese industrial firms and analyze their spatial distribution characteristics and spatial spillover effects using the SDM.

This article’s innovations primarily fall into the following three categories. Firstly, taking Chinese industrial firms as the study target expands the coverage of the study field of GTIE and enriches the empirical analysis of related topics. Secondly, in terms of study methodology, a 3S-DEA model is implemented, combining the non-parametric advantages of DEA with the parametric advantages of SFA, effectively eliminating the influence of environmental and random disturbances, and thus more accurately reflecting the real GTIE of industrial firms. Finally, by introducing the SDM, the spatial distribution characteristics of GTIE of industrial firms and their spatial spillover effects are analyzed in depth, which provides a new perspective for understanding the inter-regional efficiency differences and their interactions.

3. Study Design and Data Description

3.1. Data Sources and Processing

This article collects panel data from 31 Chinese provinces from 2013 to 2022. As much as possible, data from industrial firms at the large-scale level are used in the data selection process to accurately analyze the innovation characteristics of industrial firms; in certain situations, data at the provincial level are used as a substitute for data that is difficult to obtain [28,29]. Specifically, data on input and output variables are derived from the China Science and Technology Statistical Yearbook and the China Industrial Statistical Yearbook for the years 2014–2023. The China Statistical Yearbook and the National Bureau of Statistics’ official website provide the environmental variable data for the years 2014–2023. The data on GTIE were calculated from the 3S-DEA model.

3.2. Variable Selection

In this article, the GTIE of Chinese industrial firms is measured using a 3S-DEA model. Based on this study goal, this article will use the study of Liu et al. [15] and Zhang et al. [30] to build an indicator system from three perspectives: input variables, output variables, and environmental variables. Specifically, input variables reflect the resource input of industrial firms in GTI, which is the basis of efficiency measurement; output variables measure the direct results of innovation activities, reflecting economic and environmental benefits; and environmental variables are utilized to control the impact of external elements on efficiency. Specific indicators are selected as follows.

(1)

Input Variables Selection

The input of labor and capital is the basic element of production. Combined with related literature, this article selects R&D personnel, R&D investment, and fixed assets as input indicators of GTI in industrial firms. Among them, R&D personnel is labor investment, which is generally indicated by the full-time equivalent of R&D personnel (I1); R&D input and fixed assets belong to capital input, which is expressed by R&D funds’ internal expenses (I2), the new product advancement funds’ expenses (I3), and total enterprise assets (I4), respectively [31,32,33,34,35].

(2)

Output Variables Selection

Drawing on relevant studies, this article selects patents and new products as output indicators of industrial firms’ GTI. Among them, green patents serve as an indicator of GTI output. This is typically measured by the quantity of green patent applications (O1) and the quantity of effective green invention patents (O2). Meanwhile, new products reflect the economic outcomes of industrial firms, which are assessed through the count of new product advancement projects (O3) and the revenue generated from the sale of new products (O4) [31,32,33,34,35].

(3)

Environment Variables Selection

The GTIE measured by the Phase 1 DEA model is affected by the external environment. The impact of environmental elements must be eliminated in order to conduct a more thorough analysis of the GTIE of Chinese industrial firms. Therefore, this article chooses five indicators—economic advancement (pgdp), industrialization (ind), opening to the outside world (open), government support (gov), and information infrastructure (int)—to investigate the environmental elements affecting the GTIE based on the existing study and the characteristics of GTI of industrial firms [31,32,33,34,35]. Among them, the level of economic advancement is represented by GDP per capita; the level of industrialization is represented by the ratio of industrial added value to regional GDP; the extent of external openness is represented by the proportion of total imports and exports to regional GDP; the government support is measured as the ratio of government R&D expense to local R&D expense; and the information infrastructure is represented by the Internet penetration rate. Input, output, and environmental variables are defined as shown in

Table 1. Definition of variables.

Variable Type	Variable Name	Variable Symbols	Description of Variables	Unit (of Measure)
Input variable	Staffing inputs	I1	R&D staff full-time equivalent	man-year
	capital investment	I2	Internal investment in R&D funds	billions
		I3	Expenses for new product advancement	billions
	Asset investment	I4	Total business assets	billions
Output variables	Scientific and technical outputs	O1	Number of green patent applications	piece
		O2	Number of effective green invention patents	piece
	Economic output	O3	Number of new product advancement projects	term
		O4	Revenue from sales of new products	billions
Environment variable	Level of economic development	pgdp	GDP per capita	Yuan/person
	Industrialization level	ind	Industrial value added/regional GDP	%
	Egypt’s open-door policy towards the outside world	open	Total exports and imports/regional GDP	%
	Government support	gov	Government funded R&D expense/regional R&D expense	%
	Information infrastructure	int	Internet penetration	%

.

3.3. Study Methods

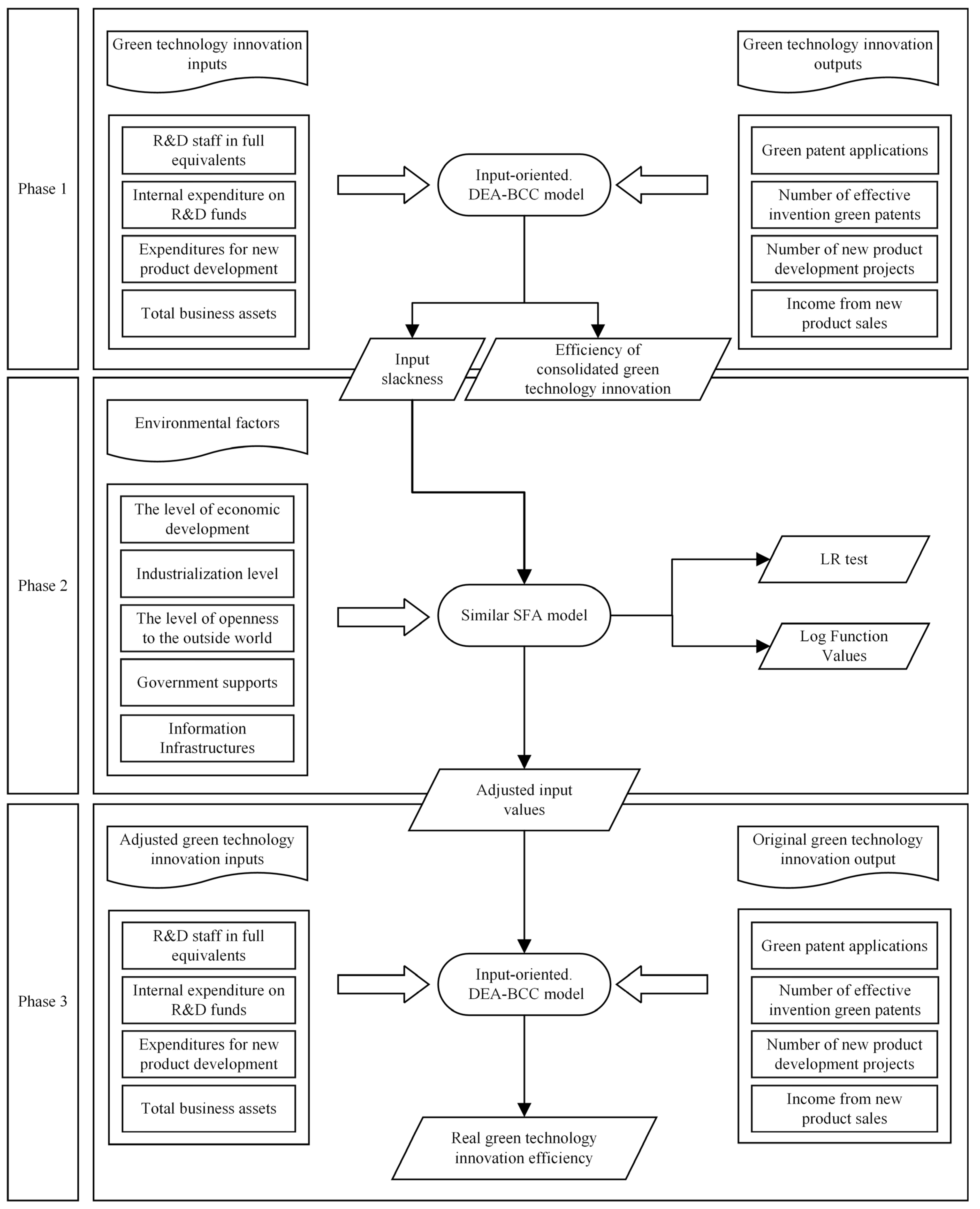
3.3.1. Three-Stage DEA Model

On the basis of constant returns to scale, the traditional DEA model functions. When evaluating the effectiveness of decision-making units that encounter variable returns to scale, this assumption is insufficient. Additionally, the model ignores how stochastic disturbances and environmental elements affect GTI activities, which could lead to skewed efficiency assessments. Therefore, this study adopts the 3S-DEA model advanced by Fried et al. [36] to measure the GTIE of industrial firms. Figure 1 displays the theoretical framework.

Phase 1: Traditional DEA Modeling

Efficiency measurements of original input–output data use classical DEA modeling. Innovation inputs are simpler to manage than output uncertainty, especially considering the intricacy of GTI activities. Therefore, the input-oriented BCC model with variable returns to scale is chosen to assess the GTIE (crste), pure technology efficiency (vrste), and scale efficiency (scale) of industrial firms. The set model is shown in Equation (1).

$$\begin{array}{c}\min \left[\theta -\epsilon \left({\stackrel{⌢}{e}}^T{S}^{-}+e^T{S}^{+}\right)\right]\\ s.t.\left\{\begin{array}{c}{\displaystyle \sum _{i=1}^n{X}_i{\lambda }_i+S^{-}=\theta X_0}\\ {\displaystyle \sum _{i=1}^n{Y}_i{\lambda }_i-S^{+}=Y_0}\\ {\displaystyle \sum _{i=1}^n{\lambda }_i=1}\\ {\lambda }_i\ge 0,S^{-}\ge 0,S^{+}\ge 0\end{array}\right.\end{array}$$

(1)

where i = 1, 2, …, n is the decision entity; X represents the input variables I1, I2, I3, I4; Y represents the output variables O1, O2, O3, O4; λ_i is the weight coefficient of the decision entity; θ denotes the initial value of GTIE; S⁻, S⁺ are the input and output slack variables, respectively.

Phase 2: Similar SFA Models

The input slack variable derived in the initial stage is primarily composed of three components: environmental elements, management inefficiency, and statistical noise. The SFA regression model is employed to eliminate the influences of environmental elements and statistical noise. The input-oriented (SFA) regression model is formulated as Equation (2), utilizing input slack as the dependent variable and environmental variables as independent variables.

$$S_{ni}=f\left(Z_i;{\beta }_n\right)+v_{ni}+{\mu }_{ni}\left(n=1,2,\cdots ,N;i=1,2,\cdots ,I\right)$$

(2)

where S_ni denotes the input slack variable; Z_i represents the environmental variable pgdp, ind, open, gov, int; β_n is the coefficient’s value for the environmental variable; v_ni and μ_ni are the statistical noise and managerial inefficiency, respectively; v_ni + μ_ni denotes the hybrid error term.

From the results obtained in the SFA regression, the adjusted formula is set as Equation (3). Filter out the influence of environmental and stochastic variables on the efficiency measure and place all input quantities within a uniform environmental context.

$${X^A}_{ni}=X_{ni}+\left[\max \left(f\left(Z_i;{\beta }_n\right)\right)-f\left(Z_i;{\stackrel{⌢}{\beta }}_n\right)\right]+\left[\max \left(v_{ni}\right)-v_{ni}\right]\left(n=1,2,\cdots ,N;i=1,2,\cdots ,I\right)$$

(3)

where X_ni, X^A_ni are the pre- and post-adjustment inputs, respectively; $\max \left(\mathrm{f}\left(Z_i;{\beta }_n\right)\right)-\mathrm{f}\left(Z_i;{\stackrel{⌢}{\beta }}_n\right)$ refers to the modification of environmental variables; and $\max \left(v_{ni}\right)-v_{ni}$ is to place all the decision-making units in the same stochastic disturbance condition.

Phase 3: Adjusted DEA Modeling

After removing stochastic and environmental elements, the DEA model is once more used to account for the above adjusted inputs and raw outputs, resulting in a more reliable GTIE of industrial firms.

3.3.2. Spatial Self-Relation

The Global Moran Index and the Local Moran Index are two different versions of the Moran Index. The former examines the spatial correlation of the entire study area, whereas the latter shows the agglomeration within the study area [37,38], as in Equations (4) and (5).

$$Moran’s I={\displaystyle \frac{n{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{W}_{ij}\left(y_i-\overline{y}\right)\left(y_j-\overline{y}\right)}}}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{W}_{ij}{\displaystyle \sum _{i=1}^n{\left(y_j-\overline{y}\right)}^2}}}}}$$

(4)

$$Moran’s I_i={\displaystyle \frac{Z_i}{S^2}}{\displaystyle \sum _{j\ne i}^n{W}_{ij}}{Z}_j$$

(5)

where Moran’s I and Moran’s I_i denote the global and local spatial auto-correlation indices, respectively; W_ij is the matrix of spatial weights; y_i and y_j indicate the value of GTIE for area i and j, respectively; n is the number of provinces, $Z_i=y_i-\overline{y}$, $Z_j=y_j-\overline{y}$, $S^2={\displaystyle \frac{1}{n}}{{\displaystyle \sum \left(y_i-\overline{y}\right)}}^2$.

To investigate the spatial relevance of GTIE of industrial companies, the neighbor weight matrix (W₁), geographic distance weight matrix (W₂), and economic distance weight matrix (W₃) are chosen from the matrix of spatial weights. Meanwhile, in order to avoid the island effect, it is assumed that Guangdong and Hainan are neighboring, as in Equations (6)–(8).

$$W_{ij}=\left\{\begin{array}{ll}1& if i,j are adjacent\\ 0& if i,j are not adjacent\end{array}\right.$$

(6)

$$W_{ij}=\left\{\begin{array}{ll}{\displaystyle \frac{1}{d_{ij}}}& i\ne j\\ 0& i=j\end{array}\right.$$

(7)

$$W_{ij}=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\left|\overline{G_{pi}}-\overline{G_{pj}}\right|}}& i\ne j\\ 0& i=j\end{array}\right.$$

(8)

where d_ij is the distance from the two areas; and $\overline{G_{pi}}$ is the GDP value of a year in province i in the study period.

3.3.3. Spatial Measurement Models

(1)

Spatial Lag Model (SAR)

$$Y_{it}=\rho W_{ij}{Y}_{jt}+\beta x_{it}+{\mu }_i+{\gamma }_t+{\epsilon }_{it}$$

(9)

(2)

Spatial Error Model (SEM)

$$\begin{array}{c}{Y}_{it}=\beta x_{it}+{\mu }_i+{\gamma }_t+{\epsilon }_{it}\\ {\epsilon }_{it}=\lambda W_{ij}{\epsilon }_{jt}+{\upsilon }_{it}\end{array}$$

(10)

(3)

Spatial Durbin Model (SDM)

$$Y_{it}=\rho W_{ij}{Y}_{it}+\beta x_{it}+\delta W_{ij}{x}_{jt}+{\mu }_i+{\gamma }_t+{\epsilon }_{it}$$

(11)

where Y denotes the GTIE; W is the matrix of spatial weights; x is the explanatory variable pgdp, ind, open, gov, int; μ_i is the spatial effect; γ_t is the time effect; ε_it is the stochastic error term; and ρ, δ, and λ denote the parameter of the lagged spatial terms of the explanatory variables, the explained variables, and the random errors, respectively.

4. Empirical Analysis

When using the DEA model for measurement, the input and output variables should satisfy the principle of homogeneity.

Table 2. The results of the Pearson correlation analysis.

	O1	O2	O3	O4	I1	I2	I3	I4
O1	1
O2	0.951 ***	1
O3	0.964 ***	0.881 ***	1
O4	0.966 ***	0.883 ***	0.961 ***	1
I1	0.954 ***	0.847 ***	0.941 ***	0.972 ***	1
I2	0.941 ***	0.868 ***	0.920 ***	0.975 ***	0.965 ***	1
I3	0.982 ***	0.940 ***	0.951 ***	0.980 ***	0.957 ***	0.975 ***	1
I4	0.877 ***	0.802 ***	0.868 ***	0.921 ***	0.918 ***	0.952 ***	0.918 ***	1

Note: *** represent statistically significant at 1%.

displays the results of the analysis conducted using Stata17 software to determine the sample data’s Pearson correlation coefficient. According to the model’s homogeneity requirement, the input and output variables have a strong and favorable correlation at the 1% level.

4.1. Phase 1: Traditional DEA Results Analysis

The traditional DEA-BCC model was used to evaluate the GTIE of Chinese industrial firms from 2013 to 2022 using DEAP2.1 software. This evaluation did not account for the impacts of environmental elements or stochastic errors. Due to space limitations, only four years of data for 2013, 2016, 2019, and 2022 are shown, and the findings are presented in

Table 3. GTIE values of industrial firms at stages 1 and 3 in 31 provinces of China.

Area	Province	2013		2016		2019		2022		Average
		Pre-Adjustment	Adjusted	Pre-Adjustment	Adjusted	Pre-Adjustment	Adjusted	Pre-Adjustment	Adjusted	Pre-Adjustment	Adjusted
East area	Beijing	1.000	0.887	1.000	0.758	1.000	0.857	1.000	1.000	0.999	0.844
	Tianjin	1.000	1.000	1.000	0.941	1.000	0.827	1.000	0.814	0.967	0.876
	Anhui	0.723	0.679	0.647	0.666	0.761	0.728	0.877	0.787	0.749	0.713
	Shanghai	1.000	1.000	1.000	0.719	1.000	0.762	0.951	0.805	0.995	0.812
	Jiangsu	0.978	1.000	0.902	1.000	0.799	1.000	0.901	1.000	0.897	1.000
	Zhejiang	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	Fujian	0.766	0.732	0.728	0.901	0.723	0.802	0.775	0.876	0.756	0.830
	Shandong	0.809	1.000	0.707	0.920	0.651	0.757	1.000	1.000	0.764	0.916
	Guangdong	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	Hainan	1.000	0.097	1.000	0.133	1.000	0.117	1.000	0.202	1.000	0.137
	average	0.928	0.840	0.898	0.804	0.893	0.785	0.950	0.848	0.913	0.813
Central area	Shanxi	0.487	0.379	0.432	0.324	0.888	0.572	0.924	0.619	0.692	0.462
	Anhui	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	Jiangxi	0.703	0.480	0.896	0.536	1.000	0.765	1.000	0.849	0.928	0.658
	Henan	0.628	0.634	0.802	1.000	0.874	0.860	0.861	0.900	0.811	0.865
	Hubei	0.698	0.794	0.736	0.813	1.000	0.872	0.970	0.925	0.826	0.836
	Hunan	1.000	0.982	1.000	0.997	0.925	0.792	1.000	0.783	0.982	0.892
	average	0.753	0.712	0.811	0.778	0.948	0.810	0.959	0.846	0.873	0.785
West area	Inner Mongolia	0.448	0.280	0.394	0.282	0.595	0.382	0.811	0.475	0.581	0.349
	Guangxi	0.738	0.471	0.808	0.501	1.000	0.470	1.000	0.572	0.909	0.520
	Chongqing	1.000	0.745	1.000	0.852	0.809	0.629	0.942	0.724	0.957	0.736
	Sichuan	1.000	0.989	0.827	0.792	0.972	0.794	0.918	0.857	0.938	0.851
	Guizhou	0.765	0.294	0.946	0.356	0.956	0.426	0.906	0.503	0.909	0.394
	Yunnan	0.634	0.261	1.000	0.395	0.677	0.408	0.847	0.545	0.827	0.419
	Tibet	1.000	0.009	1.000	0.008	1.000	0.010	1.000	0.017	1.000	0.010
	Shaanxi	0.817	0.666	0.524	0.506	0.684	0.581	0.659	0.681	0.655	0.599
	Gansu	0.952	0.283	0.554	0.243	0.783	0.266	0.982	0.352	0.746	0.272
	Qinghai	0.599	0.030	0.354	0.034	0.885	0.083	0.993	0.133	0.746	0.073
	Ningxia	1.000	0.188	0.916	0.165	1.000	0.239	0.903	0.320	0.966	0.215
	Xinjiang	0.562	0.169	0.863	0.222	1.000	0.263	1.000	0.405	0.847	0.253
	average	0.793	0.365	0.766	0.363	0.863	0.379	0.913	0.465	0.840	0.391
Northeast area	Liaoning	0.702	0.791	0.598	0.568	0.882	0.695	0.732	0.751	0.762	0.687
	Jilin	1.000	0.819	0.946	0.544	0.763	0.395	1.000	0.630	0.962	0.620
	Heilongjiang	0.604	0.388	0.581	0.375	0.675	0.351	0.913	0.485	0.741	0.408
	average	0.769	0.666	0.708	0.496	0.773	0.480	0.882	0.622	0.822	0.572
Overall average		0.826	0.617	0.813	0.603	0.883	0.608	0.932	0.681	0.869	0.625

.

(1)

Nationally, from 2013 to 2022, the GTIE values of Chinese industrial firms are all greater than 0.8, with an overall trend of steady growth. Over the ten-year period, the mean GTIE stood at 0.869, which suggests that the GTIE of industrial firms in China remains at a relatively high level. This has been driven by a combination of policy support, technological advances, market demand, environmental regulations, and regional synergies.

(2)

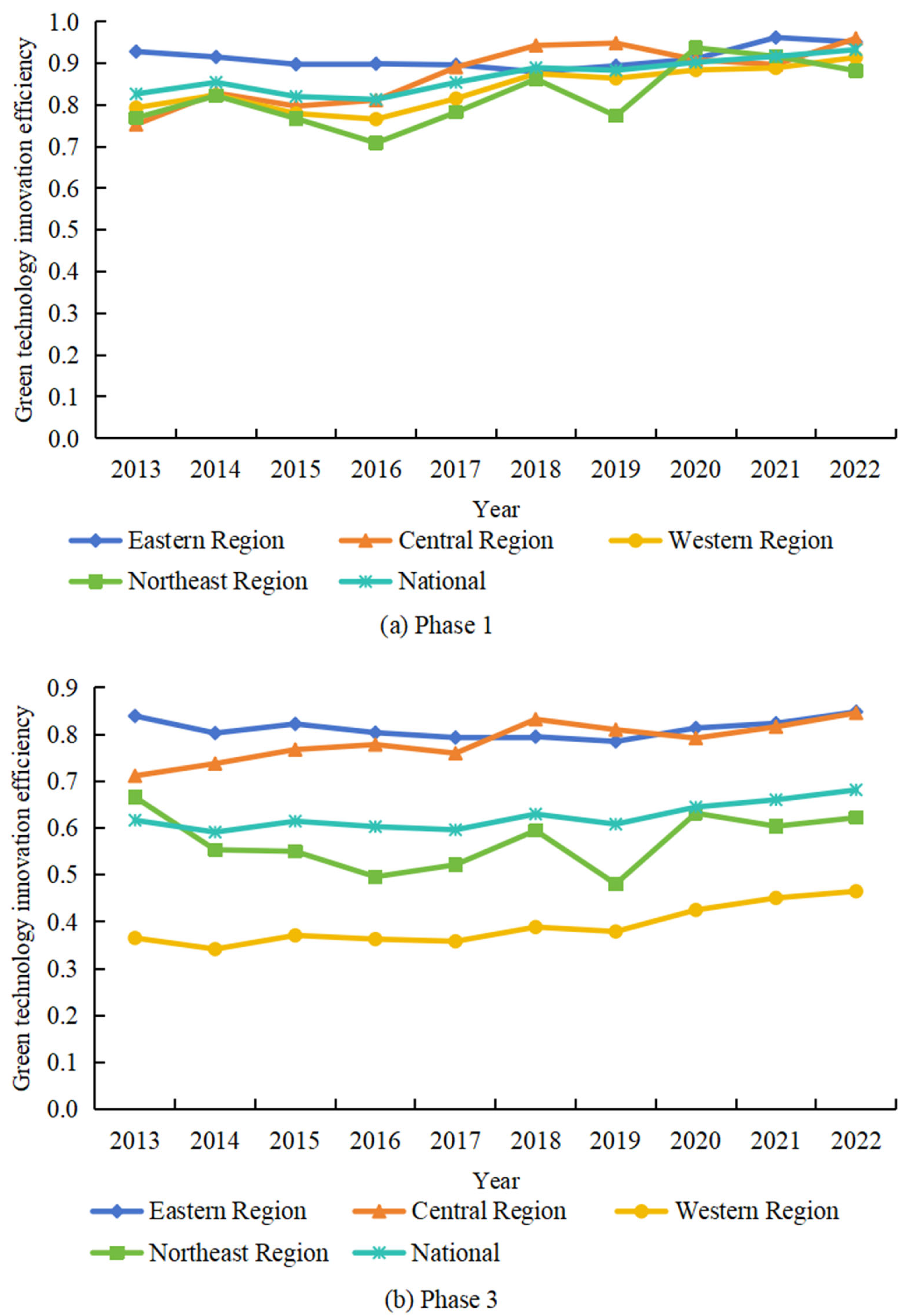
In the four major areas, from 2013 to 2022, the GTIE averages of China’s east, central, west, and northeast areas are generally on an upward trend, and the gap between areas is gradually narrowing. In the decade, the GTIE averages were 0.913, 0.873, 0.840, and 0.822, revealing a trend of east > central > west > northeast. Possible reasons for this are as follows: the eastern area has a developed economy, abundant innovation resources and strong policy support, and has a better foundation for GTI. The central area has benefited from industrial transfer and policy support, and its innovation capacity has gradually improved. The western area shows advantages in resource endowment, but is constrained by infrastructure and talent shortage. The northeast area is relatively inefficient due to the high proportion of traditional industries and the pressure of transformation and upgrading. Overall, regional coordinated advancement policies and the promotion of GTI have contributed to the gradual narrowing of inter-regional disparities.

(3)

By province, the GTIE of Zhejiang, Guangdong, Hainan, Anhui, and Tibet between 2013 and 2022 is one, while that of Beijing, Tianjin, Shanghai, Hunan, and Jilin is one or close to one in most years, which does not reflect the change in efficiency over the 10 years. The GTIE means of Hebei, Fujian, and Shandong are 0.749, 0.756, and 0.764, respectively, which is not consistent with our perception that the eastern area has high innovation capacity. This is due to the fact that Hebei, Fujian, and Shandong, although located in the east part of the country, may be affected by industrial structure (e.g., a high proportion of heavy industry), unequal distribution of resources, or differences in the implementation of policies, resulting in a relatively low GTIE.

4.2. Phase 2: SFA Regression Results

The results shown in

Table 4. Stage 2 SFA regression analysis.

Environment Variables	R&D Staff Full-Time Equivalent Slack Variable	R&D Staff Costs Internal Expense Slack Variables	New Product Advancement Expense Slack Variable	Enterprise Asset Total Slack Variables
pgdp	0.143 ***	0.000996 ***	0.000691 ***	0.049423 ***
	(7.031)	(3.034)	(3.583)	(3.727)
ind	45,189.461 ***	24.050	20.182	27,120.685 ***
	(45,188.035)	(0.344)	(0.478)	(26,916.620)
open	−12,871.431 ***	−59.371 **	−36.419 **	−12,408.272 ***
	(−12,870.531)	(−2.141)	(−2.133)	(−11,591.177)
gov	−7202.369 ***	48.710	37.250	−9669.647 ***
	(−7202.280)	(0.348)	(0.455)	(−9630.417)
int	−3410.786 ***	−81.535	−69.687 *	4758.096 ***
	(−3410.684)	(−1.183)	−1.672	(4756.231)
_cons	−22,010.006 ***	−21.526	−8.593	−12,500.454 ***
	(−22,007.086)	(−0.469)	(−0.308)	(−11,711.694)
σ2	396,514,760 ***	14,780.068 ***	4852.250 ***	161,887,270 ***
	(396,514,760)	(1635.493)	(4.566)	(161,887,270)
γ	0.72 ***	0.62 ***	0.60 ***	0.70 ***
	(29.948)	(19.771)	(6.476)	(28.113)
Log Function Values	−3342.547	−1805.820	−1639.876	−3214.305
LR One-sided Test	145.638 ***	104.557 ***	67.355 ***	128.002 ***

Note: ***, **, * represent statistically significant at 1%, 5%, 10%, respectively.

were obtained by using Frontier 4.1 software, taking each input slack obtained in the first stage as the explanatory variable of the SFA model and the five environmental variables defined in the previous section as the explanatory variables, respectively. The sign direction of the regression coefficients of the environmental variables reflects their effect on input slack. When the regression coefficients are positive, it indicates that environmental elements are unfavorable for input slack reduction. It means that the higher the number of inputs, the more serious the waste problem is, and vice versa.

Table 4 shows that the one-tailed test for each input slack LR passes the 1% significance level. γ values are 0.72, 0.62, 0.60, and 0.70, respectively, and all of them are greater than 0.6. The results show that the input redundancy of GTI in industrial firms is mainly affected by managerial inefficiency, which suggests that the SFA model is set up reasonably. The details are as follows.

4.2.1. The Level of Economic Development

The significance test was successfully completed by the input relaxation variables [39,40]. At the 1% level, the slack variables for R&D funding internal expenses, R&D staff full-time equivalent, new product advancement expense, and total enterprise assets are all highly positive. This suggests that higher levels of economic development are associated with greater redundancy in their input factors. This is most likely due to redundant R&D investment in areas with high economic development in terms of people, money, and assets. Excessive inputs do not result in GTI outcomes, leading to inefficient GTI.

4.2.2. Industrialization Level

The slack variables for internal R&D expenses and new product advancement expenses did not pass the significance test. Both the full-time equivalent of R&D personnel slack variable and the total enterprise assets slack variable are highly positive at the 1% level, indicating that an increase in the level of industrialization will increase the input redundancy of both. This is due to the fact that as industrialization progresses, firms’ demand for R&D personnel and assets increases, but the inefficient allocation of resources or inadequate management capacity leads to redundant inputs.

4.2.3. The Extent of External Openness

All input relaxation variables are negatively significant, indicating that increasing the extent of external openness can effectively reduce the input redundancy of the R&D personnel full-time equivalent relaxation variable, the internal expense relaxation variable of R&D funds, the expense relaxation variable of new product advancement funds, and the relaxation variable of the total enterprise assets. Mostly because the more open an area is, the more money will be taken in, and more people and money will be put into R&D. This encourages the transfer of technological innovations and improves the GTIE.

4.2.4. Government Supports

The R&D funding internal expense slack variable failed the significance test [41]. The R&D personnel full-time equivalent relaxation variable, the new product advancement expense relaxation variable, and the enterprise asset total relaxation variable are all highly negative at the 1% level. This indicates that as the degree of government support for industrial firms increases, the government’s ability to coordinate personnel, funds, and assets is enhanced, thereby facilitating a reduction in their input cost redundancy.

4.2.5. Information Infrastructures

The R&D internal expense slack variable failed the significance test. The R&D personnel full-time equivalent slack variable and the new product advancement expense slack variable are negatively significant, indicating that the better the information infrastructure, the less redundant the inputs [42]. At the 1% level, the total firm assets slack variable is highly positive, suggesting that input redundancy increases with the quality of the information infrastructure. This shows that in areas with good infrastructure, there are still unreasonable structures in the allocation of personnel inputs and expenses, which restrain the enhancement of the GTIE.

4.3. Phase 3: DEA Results Analysis with Adjusted Input Factors

(1)

Nationally, after barring environmental and random elements, the average value of GTIE for the period 2013–2022 is 0.625, which is 0.244 lower than that of the first stage, as shown in Table 3. It demonstrates how the GTIE value of Chinese industrial firms is overestimated as a result of stochastic disturbances and environmental elements. Meanwhile, Chinese industrial firms have a low GTIE value, and much more can be done to improve it. Therefore, firms should focus on the optimization of the external environment and the advancement of the internal management level in the process of GTI.

(2)

Regionally, for the years 2013–2022, the first stage’s GTIE value is greater than the third stage in each of the four areas, as seen in Figure 2. Of these, the GTIE value of the western area decreased the most in the third stage, suggesting that external environmental elements have a greater impact on the western area’s GTIE. This is a result of resource-based industries dominating the western area’s industrial structure and the relative lack of enthusiasm for GTI, which has increased resistance to technology transfer and application. In addition, the GTIE value’s change trend remains constant throughout the first and third phases. Of these, the GTIE value for the eastern area declines and then rises, the central and western areas show an annual increase, and the northeastern area fluctuates and changes over a specific time period. Figure 2a shows that the inter-regional differences are negligible and the gap between the GTIE values of the four areas in the first stage is small. Figure 2b shows that the GTIE values of the four areas in the third stage differ significantly after stochastic and environmental disturbances are eliminated. It reveals the trend of east > central > northeast > west. Meanwhile, the eastern and central areas’ GTIE values are above the national mean, while the areas of the northeast and west are below the national average.

(3)

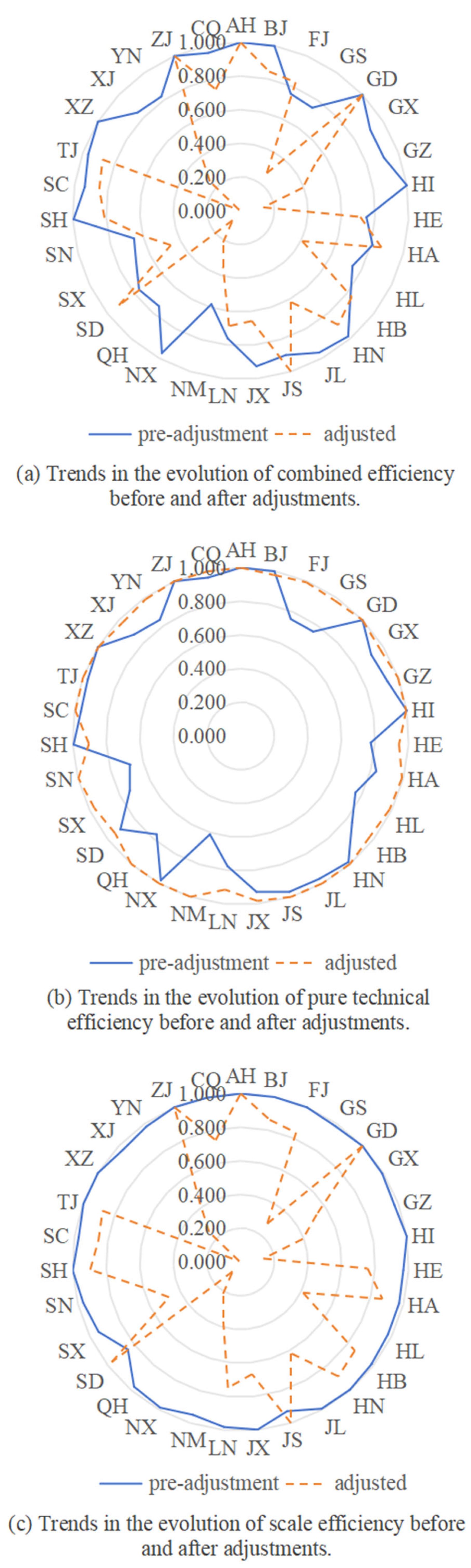
In terms of provinces, the GTIE in the first and third stages is decomposed as follows. As shown in Figure 3a, the crste values before and after adjustment in Zhejiang and Guangdong are both one, which are both in the effective frontier, while the crste values of the rest of the provinces have obvious differences before and after adjustment. Most of the provinces have decreased crste values after adjustment, among which the crste differences before and after adjustment in Tibet, Hainan, Ningxia, Qinghai, Xinjiang, and Guizhou are all greater than 0.5; they are 0.990, 0.863, 0.750, 0.673, 0.594, and 0.515, respectively. It indicates that environmental elements lead to a serious overstatement of the efficiency of GTI. The opposite is true for Jiangsu, Fujian, Shandong, Henan, and Hubei, where the difference in crste before and after adjustment is less than zero. As shown in Figure 3b, the adjusted vrste values are generally higher than those before adjustment, and the adjusted vrste values of the provinces are all greater than 0.9, which is at a higher level. Among them, 24 provinces have higher vrste values after adjustment, four provinces have lower vrste values after adjustment, and the vrste values before and after adjustment of three provinces, Zhejiang, Guangdong, and Anhui, are all one, which are all at the effective frontier. A comparison of vrste values before and after adjustment shows that the vrste values of most provinces will be underestimated if the influence of environmental elements is not excluded. As shown in Figure 3c, the scale values of all provinces are close to one before adjustment. After the adjustment, only Zhejiang and Guangdong scale values remain unchanged and reach the effective frontier, Jiangsu and Shandong scale values increase, and the remaining provinces’ scale values decrease. Among them, the adjusted scale values of Tibet, Qinghai, Hainan, Ningxia, Xinjiang, and Gansu decrease rapidly, and the difference between the pre- and post-adjustment values is greater than 0.7, which is 0.9899, 0.8999, 0.8624, 0.771, 0.7075, and 0.7063, respectively. It demonstrates how stochastic disturbances and environmental elements greatly affect scale, and that future resource allocation should be greatly expanded.

(4)

Taking 2013 and 2022 as the time nodes, we use the natural break point method to categorize the GTIE of Chinese industrial firms and their decomposition efficiency into five grades: low, sub-low, medium, sub-high, and high. ArcGIS 10.8 software was used to map the spatial and temporal evolution of GTIE of Chinese industrial firms, excluding environmental and stochastic disturbances, as depicted in Figure 4.

The GTIE in China’s 31 provinces showed a “high in the east and low in the west” distribution structure when viewed from the standpoint of spatial and temporal evolution. In other words, the eastern area has a central distribution of high-value areas, whereas the western area is primarily composed of low-value and second-low-value areas. As time goes by, a gradual shift towards higher values of technology transfer efficiency in industrial firms takes place. Among them, the hierarchical leap in vrste is the most significant. Thirteen provinces leap to higher tiers. Qinghai, Gansu, Ningxia, Guangdong, Hunan, Zhejiang, Anhui, Jiangsu, Shandong, Chongqing, Jilin, and Tianjin are the 12 provinces that remain within the original high-value zone. There are also a few provinces that have fallen in vrste values. As far as crste is concerned, 19 provinces increased their crste values between 2013 and 2022. Among them, Henan, Hubei, Jiangxi, and Yunnan are four provinces that realize high-level jumps, and Jiangsu, Zhejiang, Anhui, Shandong, and Guangdong have crste values that are on the effective frontier surface and always remain within the high-value zone. The scale value is consistent with the crste value change. When the scale of the same province increases, its crste also increases accordingly; the reverse is also true. Due to the fact that the vrste of each province is close to one, which has less influence on the crste value, while the scale value is the main influencing factor of the crste value.

4.4. Spatial Metrics Analysis

4.4.1. Spatial Correlation Test

As indicated in

Table 5. Spatial correlation test of GTIE of Chinese industrial firms, between 2013 and 2022.

Year	(W1)		(W2)		(W3)
	Moran’s I	Geary’s c	Moran’s I	Geary’s c	Moran’s I	Geary’s c
2013	−0.094 ***	1.071 ***	0.289 ***	0.646 ***	0.118 **	0.864 **
2014	−0.111 ***	1.085 ***	0.316 ***	0.629 ***	0.097 **	0.889 *
2015	−0.113 ***	1.083 ***	0.306 ***	0.631 ***	0.101 **	0.901 *
2016	−0.123 ***	1.093 ***	0.301 ***	0.639 ***	0.092 **	0.904
2017	−0.132 ***	1.104 ***	0.327 ***	0.603 ***	0.072 *	0.912
2018	−0.129 ***	1.102 ***	0.324 ***	0.594 ***	0.048	0.957
2019	−0.131 ***	1.107 ***	0.371 ***	0.565 ***	0.100 **	0.899 *
2020	−0.126 ***	1.105 ***	0.324 ***	0.596 ***	0.084 **	0.909
2021	−0.128 ***	1.105 ***	0.334 ***	0.586 ***	0.085 **	0.909
2022	−0.128 ***	1.106 ***	0.334 ***	0.582 ***	0.090 **	0.914

Note: ***, **, * represent statistically significant at 1%, 5%, 10%, respectively.

, the Stata17 software was used to calculate Moran’s I and Geary’s c of GTIE of Chinese industrial firms from 2013 to 2022 using various spatial weight matrices, including W₁, W₂, and W₃.

Moran’s I is less than 0, and Geary’s c is greater than 1 with the W₁, and both are significant at the 1% level from 2013 to 2022. It indicates that the GTIE of Chinese industrial firms shows negative spatial correlation. As far as the W₂ is concerned, both Moran’s I and Geary’s c fall between 0 and 1 and are substantial at the 1% level. It reveals that the GTIE of industrial firms presents a spatial positive correlation. That is, provinces that are close to each other have smaller differences in the GTIE of industrial firms. When using the W₃, the spatial correlation is weak because, in most years, Geary’s c is close to one and Moran’s I is low. Comparing the W₁, W_2, and W₃ matrices, it is found that W₂ has the strongest spatial correlation of the GTIE of industrial firms, suggesting a greater dependence on the geographical distance aspect. This is due to the fact that geographically close provinces have higher similarity and convenience in terms of resource endowment, policy environment, and technological exchanges, which makes it easier to form technological spillovers and synergistic innovation effects.

The Moran’s I scatter plot of W₂ is plotted according to the results of the measurements in 2013, 2016, 2019, and 2022, as displayed in Figure 5. As observed in the figure, most provinces are distributed in the first and third quadrants. A few provinces exhibit a high-low and low-high clustering effect, while the majority of provinces’ industrial firms’ GTIE display a high-high and low-low clustering effect. The first quadrant, which is far from the origin, contains Jiangsu, Anhui, and Zhejiang. It indicates that industrial firms in these provinces have a demonstration effect and a GTIE at the top of the country. It can highly promote the improvement of GTIE of industrial firms in the neighboring areas. Qinghai, Gansu, and Tibet are located in the third quadrant, which is further away from the origin. The GTIE of industrial firms lies at a low level, with a weak driving effect on the neighboring areas. Therefore, inter-regional technological cooperation and resource sharing among industrial firms should be further strengthened in the future to promote the radiation drive from high-performance areas to low-performance areas and to narrow the inter-regional GTIE gap.

4.4.2. Spatial Durbin Regression Analysis

Table 6. Influence factor regression results under different spatial weight matrices and spatial regression models.

Variables	OLS	W1				W2				W3
		SEM	SAR		SDM	SEM	SAR		SDM	SEM	SAR		SDM
pgdp	2.85 × 10−6 ***	4.94 × 10−7	1.37 × 10−7		1.77 × 10−6 **	−9.44 × 10−7 *	−2.54 × 10−7		−6.57 × 10−8	−2.12 × 10−9	−7.66 × 10−8		1.13 × 10−6 *
	(7.09 × 10−7)	(6.46 × 10−7)	(5.57 × 10−7)		(7.59 × 10−7)	(5.62 × 10−7)	(5.82 × 10−7)		(6.02 × 10−7)	(5.73 × 10−7)	(5.7 × 10−7)		(6.25 × 10−7)
ind	1.607 ***	0.728 ***	0.713 ***		0.643 ***	0.856 ***	0.799 ***		0.778 ***	0.772 ***	0.776 ***		0.754 ***
	(0.129)	(0.140)	(0.133)		(0.151)	(0.132)	(0.136)		(0.129)	(0.136)	(0.135)		(0.138)
open	0.282 ***	0.199 ***	0.180 ***		0.249 ***	0.231 ***	0.197 ***		0.287 ***	0.193 ***	0.192 ***		0.192 ***
	(0.0594)	(0.0716)	(0.0673)		(0.0835)	(0.0679)	(0.0692)		(0.0684)	(0.0690)	(0.0694)		(0.0716)
gov	−0.467 *	0.183	0.183		0.114	0.259 *	0.220		0.191	0.192	0.193		0.270 *
	(0.268)	(0.142)	(0.139)		(0.142)	(0.146)	(0.143)		(0.142)	(0.144)	(0.144)		(0.146)
int	0.289 **	0.255 ***	0.207 **		0.399 ***	0.121	0.189 **		0.0972	0.230 **	0.208 **		0.281 **
	(0.146)	(0.0989)	(0.0907)		(0.117)	(0.0933)	(0.0930)		(0.0918)	(0.0986)	(0.0943)		(0.110)
W × pgdp					1.71 × 10−5 **				−3.77 × 10−6 ***				3.62 × 10−6
					(6.07 × 10−6)				(1.02 × 10−6)				(2.39 × 10−6)
W × ind					−0.735				0.622 **				−0.199
					(1.492)				(0.286)				(0.531)
W × open					−0.528				0.338 **				0.161
					(0.975)				(0.146)				(0.259)
W × gov					−1.212				0.224				−0.0564
					(2.006)				(0.282)				(0.716)
W × int					3.374 ***				−0.504 **				1.479 ***
					(1.271)				(0.244)				(0.361)
_cons	−0.294 ***
	(0.0886)
ρ		−1.193 ***	−1.091 ***		−0.829 **	−0.378 ***	−0.161		−0.234 **	−0.159	−0.124		−0.209
		(0.412)	(0.380)		(0.379)	(0.123)	(0.104)		(0.109)	(0.141)	(0.135)		(0.137)
σ2		0.00342 ***	0.00344 ***		0.00325 ***	0.00348 ***	−0.161		0.00316 ***	0.00363 ***	0.00364 ***		0.00340 ***
		(0.000285)	(0.000284)		(0.000266)	(0.000284)	(0.104)		(0.000255)	(0.000292)	(0.000293)		(0.000273)
N	310	310	310		310	310	310		310	310	310		310
R2	0.537	0.504	0.564		0.094	0.352	0.447		0.100	0.486	0.480		0.345
LM-error		7.087 ***				11.770 ***				6.523 **
RobustLM-error		10.818 ***				0.911				7.881 ***
LM-lag		47.325 ***				40.686 ***				0.056
RobustLM-lag		51.055 ***				29.827 ***				1.414
Hausman test		23.93 ***				157.50 ***				−7.07
Wald test		22.08 ***		20.57 ***		44.01 ***		37.16 ***		21.68 ***		21.15 ***
LR test		21.60 ***		21.37 ***		40.96 ***		34.91 ***		20.82 ***		20.34 ***

Note: ***, **, * represent statistically significant at 1%, 5%, 10%, respectively.

reveals that the spatial regression parameter ρ passed the 1% significance level test using either the SEM or the SAR using W₁. Using the model of W₂, the parameter ρ passed the 1% significance level test for the SEM, while the SAR failed the test. Both SEM and SAR failed the test using W₃. Therefore, the SDM should be chosen in combination with the LM test. The hypothesis that the SDM is transformed into the SAR or the SEM was found to fail by the Wald and LR tests. Finally, the SDM is best suited to handle dual fixed effects in both time and space, according to the Hausman test.

The coefficients of pgdp, ind, open, gov, and int are positively correlated with the GTIE under W₁, W_2, and W₃. However, the significance level is different under different weight matrices, and, also, some influencing elements are not significant. This demonstrates that they influence the enhancement of industrial firms’ GTIE in terms of economic development, industrialization, opening to the outside world, government assistance, and information infrastructure.

In terms of spatial spillover effects, the coefficient of spatial autoregression ρ for the SDM is negative. It also passed the 5% degree of significance for W₁ and W₂. It indicates that the GTIE in industrial firms has a negative spatial spillover impact, and it fails the significance test under W₃. The level of economic development and information infrastructure among the influencing elements show positive spillover effects under W₁, and the remaining three influencing elements show negative spillover effects. The industrialization level, openness level, and government support under W₂ show positive spillover effects, and the remaining two items express negative spillover effects. With W₃, the openness level exhibits the same spillover effect as W₂, and the remaining four items exhibit inverse spillover effects.

4.4.3. Spatial Impact Effects Analysis

To clarify the spatial effects of the influences mentioned above on the GTIE in industrial firms, the total effect is decomposed into direct and indirect effects [43]. While the indirect effect shows that explanatory variables have an average effect on the explained variables in the neighboring area, the direct effect indicates that explanatory variables have an impact on the explained variables in the area. The GTIE of industrial firms in neighboring areas is boosted by the strengthening of explanatory variables in the area and vice versa, according to the positive indirect effect. Specific results are shown in

Table 7. Decomposition of spatial effects of the SDM.

Variables	W1		W2		W3
	Direct Effect	Indirect Effect	Direct Effect	Indirect Effect	Direct Effect	Indirect Effect
pgdp	1.48 × 10−6 **	9.59 × 10−6 **	8.96 × 10−8	−3.17 × 10−6 ***	1.08 × 10−6 *	3.03 × 10−6
	(7.18 × 10−7)	(4.52 × 10−5)	(6.18 × 10−7)	(9.63 × 10−7)	(6.42 × 10−7)	(2.07 × 10−6)
ind	0.661 ***	−0.799	0.756 ***	0.368	0.756 ***	−0.316
	(0.136)	(0.954)	(0.125)	(0.248)	(0.134)	(0.477)
open	0.271 ***	−0.410	0.283 ***	0.228 *	0.197 ***	0.100
	(0.0728)	(0.569)	(0.0675)	(0.123)	(0.0694)	(0.225)
gov	0.134	−0.684	0.181	0.170	0.270 *	−0.0518
	(0.137)	(1.185)	(0.136)	(0.228)	(0.138)	(0.597)
int	0.341 ***	1.859 **	0.115	−0.443 **	0.250 **	1.229 ***
	(0.107)	(0.915)	(0.0919)	(0.211)	(0.108)	(0.317)
N	310	310	310	310	310	310
R2	0.094	0.094	0.100	0.100	0.345	0.345

Note: ***, **, * represent statistically significant at 1%, 5%, 10%, respectively.

.

In terms of direct effects, the estimated coefficients of pgdp, ind, open, gov, and int are all positive under W₁, W₂, and W₃, among which the coefficients of the level of industrialization and the level of opening up to the outside world are all beneficial with a significance level of 1%. The improvement of industrial firms’ GTIE is facilitated by the aforementioned explanatory variables, with the facilitating effect of industrialization and opening-up levels being more significant. The level of industrialization is the principal engine of economic expansion and the main battlefield of technological innovation. The improvement of the industrialization level helps industrial firms to develop high-end intelligent green advancement and constantly break through the core technology in order to accelerate the transfer of technological achievements. Increasing the extent of external openness encourages the growth of international trade in terms of scale, quality, and efficiency. This helps local industrial firms use external resources, conduct cooperation and exchanges, and improve the GTIE.

With low significance levels, the indirect effect demonstrates that the explanatory variables have diverse spatial effects on the GTIE in industrial firms under various spatial weight matrices [40,44]. As for W₁, the indirect effect values of economic development level and information infrastructure are 0.00000959 and 1.859, respectively, which are larger than the direct effect values and passed the 5% significance test. This suggests that the level of local economic advancement and the quality of information infrastructure exert beneficial spillover effects on enhancing the GTIE among industrial firms in adjacent areas. The GTIE in industrial firms in nearby areas is expected to increase by 0.00000959% and 1.859%, respectively, with a 1% increase in both variables. Areas with relatively low levels of economic development and information infrastructure should accelerate their economic development, improve their information infrastructure, take the initiative to strengthen transmission and exchange with economically developed areas, and enhance the local digitization level, which can better receive the spillover dividend effect of economic advancement and information infrastructure in the neighboring areas.

5. Results and Discussion

5.1. Results

By using the 3S-DEA model and the SDM, this article measures and analyzes the GTIE, spatial distribution characteristics, and spatial spillover effects of industrial firms in 31 Chinese provinces from 2013 to 2022. The results are as follows.

Firstly, before removing stochastic disturbances and environmental influences from the GTIE values of industrial firms, they were principally caused by changes in vrste. The inter-regional gap in the value of GTIE of industrial firms is relatively small, presenting the trend of east > central > west > northeast. This phenomenon might be explained by the fact that the eastern area is highly marketized, economically developed, and rich in scientific and technological resources, whereas the central, western, and northeastern areas are comparatively inefficient in GTI because of their underdeveloped economies and inadequate technological accumulation.

Secondly, environmental and random interference elements must be eliminated. When the two influences are eliminated, industrial companies’ GTIE values show an increasing annual trend, with scale being the primary influencing factor. There is a significant difference in the value of GTIE of industrial firms between areas, showing the trend of east > center > northeast > west. At the same time, the eastern and central areas’ crste values are higher than the national average, while the northeastern and western areas are lower than the national average. This is because the eastern area has a strong economic base, a concentration of scientific and technological talent, and a leading GTIE. The central area has steadily improved its efficiency by undertaking industrial transfer and policy support from the east. On the other hand, the northeastern and western areas are less efficient in GTI due to their heavy industrial structure and weak infrastructure. The disparity in development between areas is highlighted by the fact that the GTIE values of the eastern and central areas are above the national mean, while those of the northeastern and western areas are lower.

Thirdly, under various spatial weight matrices, the direct and spillover effects differ, and the GTIE of industrial companies exhibits a strong spatial correlation. Comparing the three weight matrices, it was found that industrial firms’ GTIE based on W₂ was highly positive and had the strongest spatial correlation. The SDM utilizing W₁ demonstrates more pronounced spillover effects than those based on geographic or economic distance weight matrices. The GTIE of regional industrial firms is greatly improved by openness, industrialization, economic development, and information infrastructure. However, government support had no significant effect, which may be related to poor policy implementation or inefficient resource allocation. Simultaneously, economic development and information infrastructure highly boost the GTIE of industrial firms in adjacent areas.

5.2. Recommendations

The following recommendations are made in this article based on the results of the above empirical analysis.

Firstly, area-specific policies should be developed to enhance the allocation efficiency of GTI resources. Significant variations exist in the GTIE values of industrial firms across the four areas when random interference and environmental elements are taken out, and each province should develop unique solutions based on its unique circumstances. For example, provinces with “high input and low efficiency” should appropriately control the scale of input, reduce input redundancy, and improve the internal management level of enterprises to rationally allocate resources. On the other hand, for provinces with “low input and low efficiency”, the government can give an appropriate policy inclination, increase support, create a favorable environment for the transformation of technological accomplishments of enterprises, and motivate local enterprises to increase the scale of investment in GTI.

Secondly, we should rapidly improve the information infrastructure and stage for the conversion of technological accomplishments. The state and all levels of government should work together to support the development of the database and data service platform for technological accomplishments, enhance the mechanism for sharing information about these accomplishments, and realize the interdependence of these data resources. Sharing through the platform will provide scientific and technological talents with more innovative thinking, which will in turn promote the conversion and application of technological accomplishments in the fields of agriculture, medical and health care, ecological and environmental protection, and so on.

Thirdly, GTI talents should be cultivated, and GTI services should be strengthened. A high-level team of GTI talents is of great significance in enhancing the GTIE. Every province should set up a thorough system for developing GTI talent, encouraging and regulating the participation of qualified professionals from study institutes, universities, and businesses. In order to create a skilled group of GTI brokers and achieve the synergistic growth of “universities, study institutes, and enterprises”, they should also collaborate with global GTI organizations to develop global GTI talent.

5.3. Study Limitations and Future Perspectives

While identifying the direction for future scholarly study, this article still has certain limitations despite measuring the GTIE of Chinese industrial firms and analyzing the spatial spillover effects.

Firstly, this article primarily examines data from 2013 to 2022, which may not accurately represent the long-term evolution of GTIE and does not account for the trend of change over a longer time period. Future studies can integrate data from more varied sources and for a longer duration to more fully capture the dynamic trend of GTIE.

Secondly, even though the study removed some random interferences and environmental elements, the selection of environmental variables might not have been thorough enough. For instance, policy changes, the market environment, international competition, and other elements might not have been adequately included in the analysis, which could have biased the estimation of efficiency values. In the future, the selection of environmental variables should be further refined to include elements such as policy support, market environment, and international technological competition into the analytical framework to improve the accuracy and practicality of the study.

Finally, this article primarily examines the GTIE of various industries at the regional level, omitting a detailed discussion of the variations in technological features and stages of development. To provide a foundation for the development of distinct policies, future studies on the GTIE of various industries should be enhanced to highlight the variations among regional industries and their causes.