Optimization of Renewable Energy Sharing for Electric Vehicle Integrated Energy Stations and High-Rise Buildings Considering Economic and Environmental Factors
Abstract
1. Introduction
- (1)
- A detailed system model was developed, integrating wind power, photovoltaics, energy storage, EV charging/discharging, and building electricity loads. This model enables the coordination and optimization of energy flow between the EVIES, high-rise building wind-solar-storage sharing system, and power grid, providing a theoretical foundation and technological framework for optimizing capacity allocation.
- (2)
- A multi-objective capacity allocation optimization model was established, and the entropy-TOPSIS (ETOPSIS) method was applied to optimize the installed capacities of photovoltaic, wind power, and energy storage systems. This optimization significantly improves the system’s economic efficiency, reduces carbon emissions, stabilizes power grid load fluctuations, and achieves a multi-dimensional balance of economy, environmental protection, and stability.
- (3)
- An MSCSO based on a mutation-dominated selection strategy was proposed to effectively solve the optimization model. The simulation results show that MSCSO outperforms existing algorithms in terms of solution efficiency, convergence speed, and solution set diversity, verifying its advantages in multi-objective optimization.
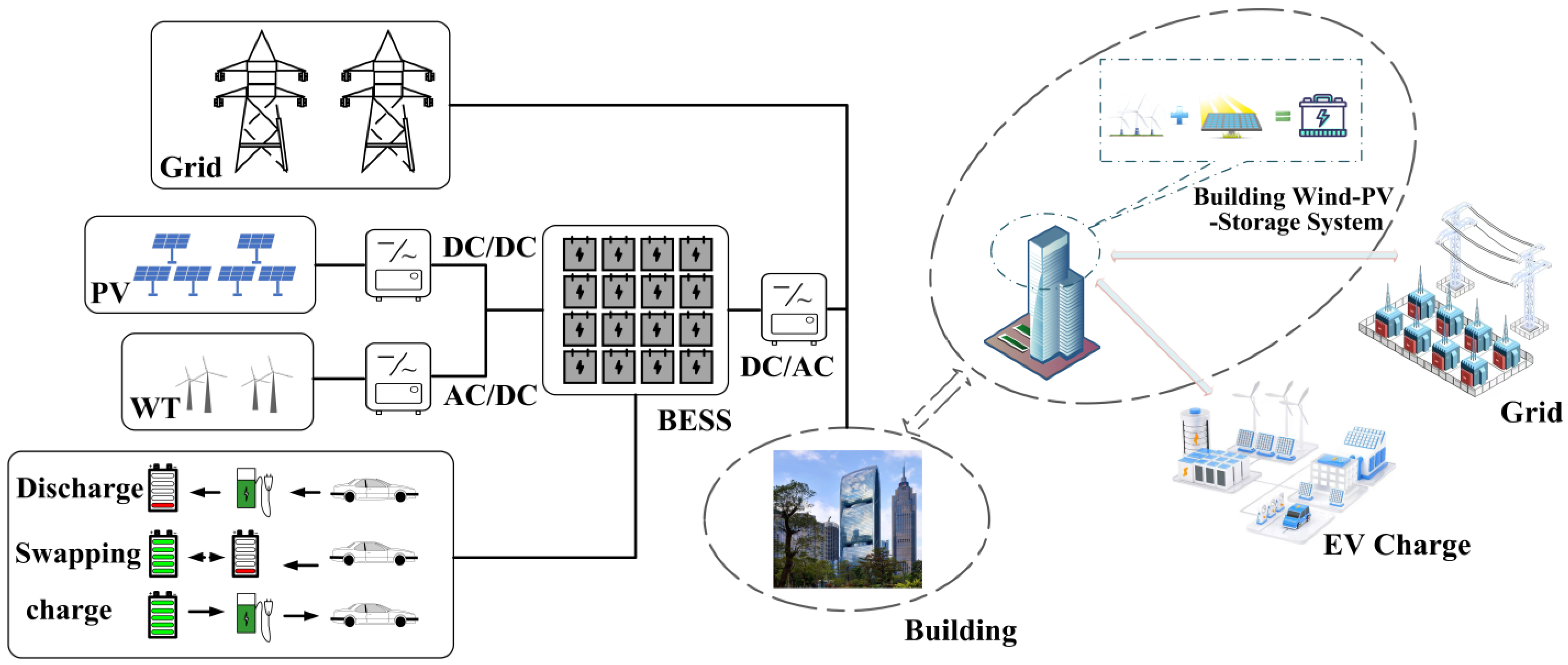
2. System Description
3. System Model
3.1. Wind Power Generation Model
3.2. Photovoltaic Power Generation Model
3.3. Battery Storage System
3.4. Energy Storage System Loss Rate Model
4. Multi-Objective Optimization Problem Formulation
4.1. Objective Functions
4.1.1. Maximizing the Daily Economic Revenue of EVIES
- Revenue from the EVIES, as shown in Equation (9), is given by:
- b.
- Calculation of wind turbine PV costs, as shown in Equation (10), is given by:
- c.
- Penalty function, as shown in Equations (13) and (14), are given by:
4.1.2. Minimizing the Load Variance on the Building’s Grid Side
4.1.3. Minimizing Overall Carbon Emissions
4.2. Constraints
4.2.1. EVIES Battery Storage System Constraints
- Battery State Change Balance Constraints for Battery Energy Storage Systems, as shown in Equation (19), are given by:
- b.
- State Mutually Exclusive Constraints for Battery Energy Storage Systems, as shown in Equation (20), is given by:
- c.
- Charging and Discharging Constraints for Battery Energy Storage Systems, as shown in Equations (21) and (22), are given by:
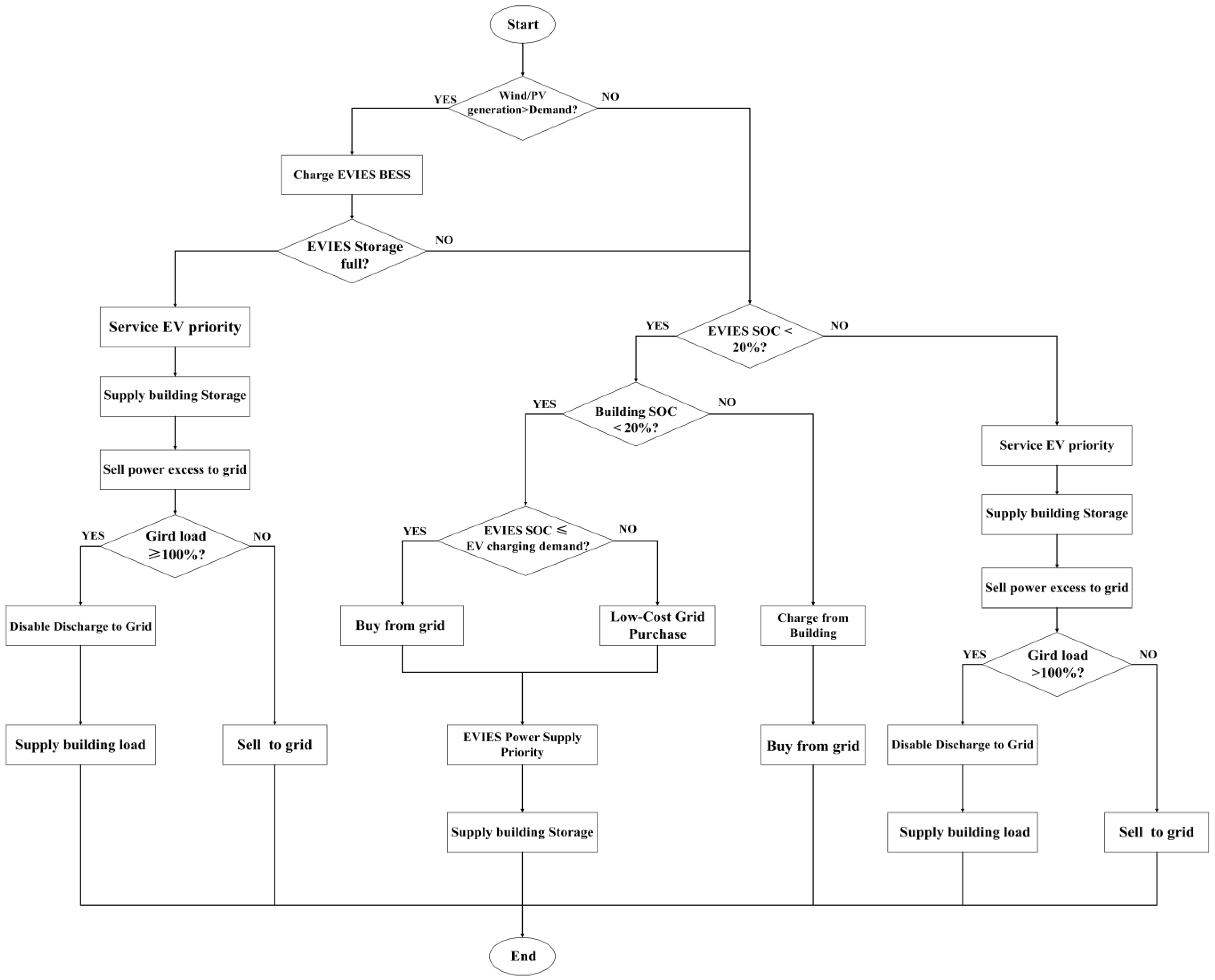
4.2.2. User Charging, Discharging, and Swapping Priority Constraints
4.2.3. High-Rise Building Load Constraints
4.2.4. System Equipment Capacity Constraints
4.2.5. Overall System Power Balance Constraints
- High-rise building power balance constraint:
- b.
- Electricity balance constraint for integrated electric vehicle refueling stations:
- c.
- Grid power balance constraints:
- d.
- overall electrical balance constraint equation:
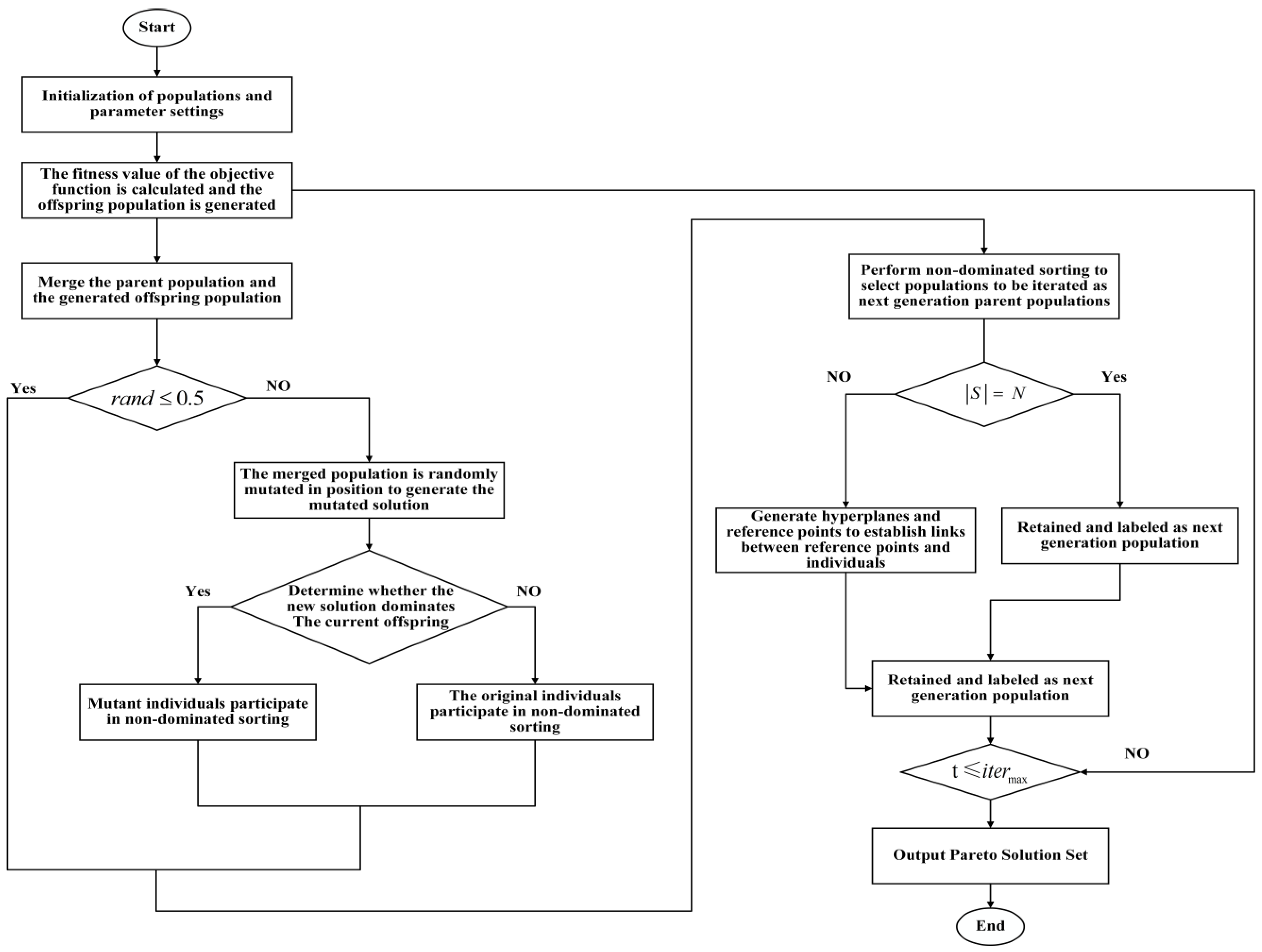
5. Multi-Objective Sand Cat Swarm Optimization Algorithm
5.1. MSCSO Based on Mutation-Dominated Selection Strategy
| Algorithm 1 Pseudo-code of the MSCSO Algorithm. |
| Input: Specify the starting number of individuals in the population , Set the upper limit on the number of iterations for the optimization process , the first-generation sand cat population and the offspring population after iterations 1. for then 2. % Combine the SCSO algorithm with a dominance-based local mutation strategy to replace the GA algorithm in NSGA-III 3. for : do 4. % Sensitivity Range Setting 5. % is the balance parameter between exploration and exploitation in SCSO 6. Obtain a random angle using the Roulette Wheel Selection method () 7. if () do % Refresh the entire population of individuals 8. 9. else 10. 11. end if 12. % Calculate the fitness of the population 13. % Identify the individual with the highest fitness in the population , and log the position of the top-performing individual 14. end for 15. After is done, , 16. , 17. 18. % Perform a random mutation on the current position 19. After is done, , 20. , 21. 22. else 23. 24. Point to be chosen from , 25. Normalize the objective functions and create a reference set , 26. Associate member of with the reference point 27. Choose members one at a time from to construct 28. end if 29. end for |
5.2. Benchmark Test Functions (DTLZ1~DTLZ7) and Simulation Results
5.2.1. Experimental Setup and Evaluation Metrics
5.2.2. Simulation Results
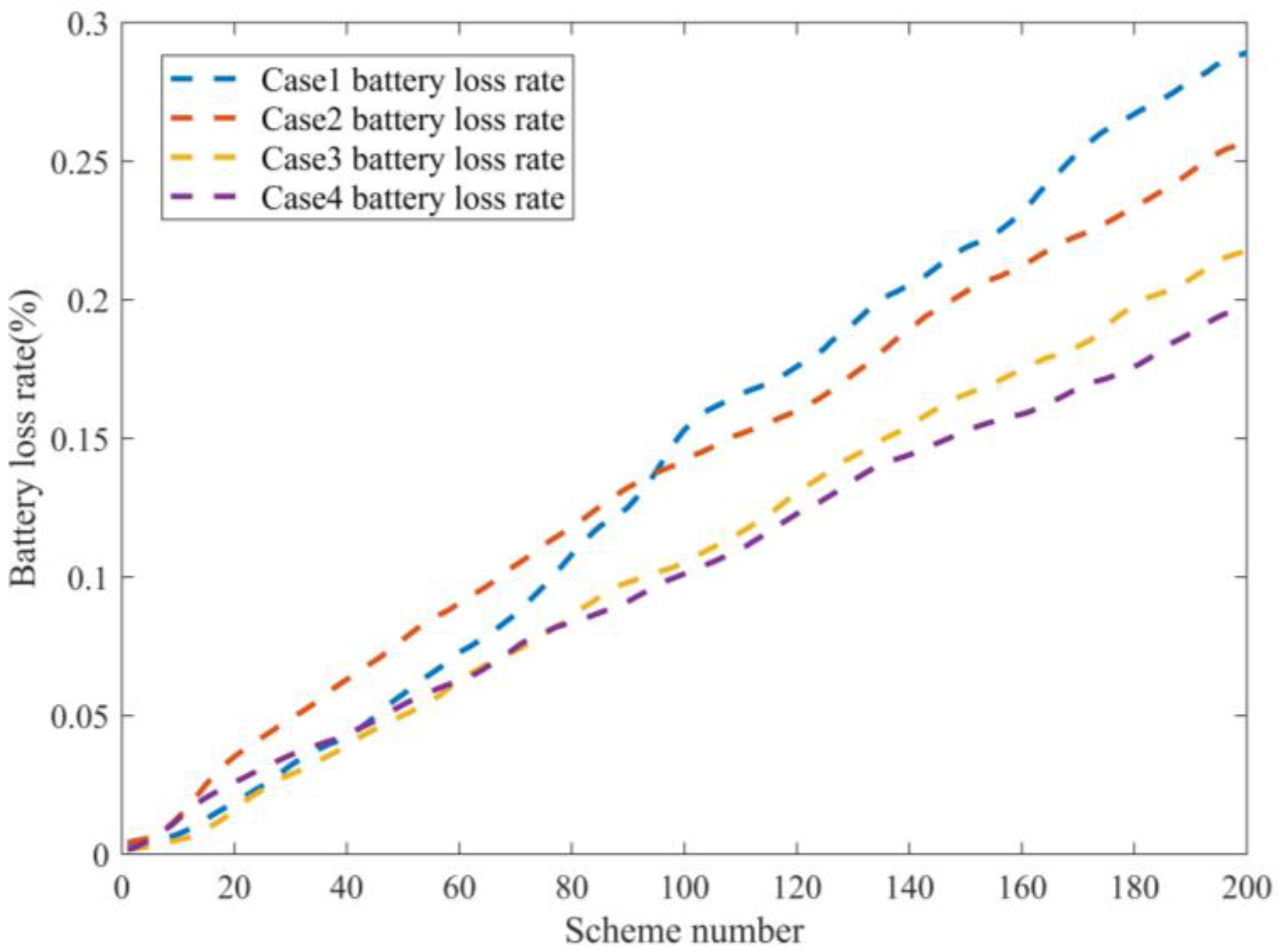
6. Case Study
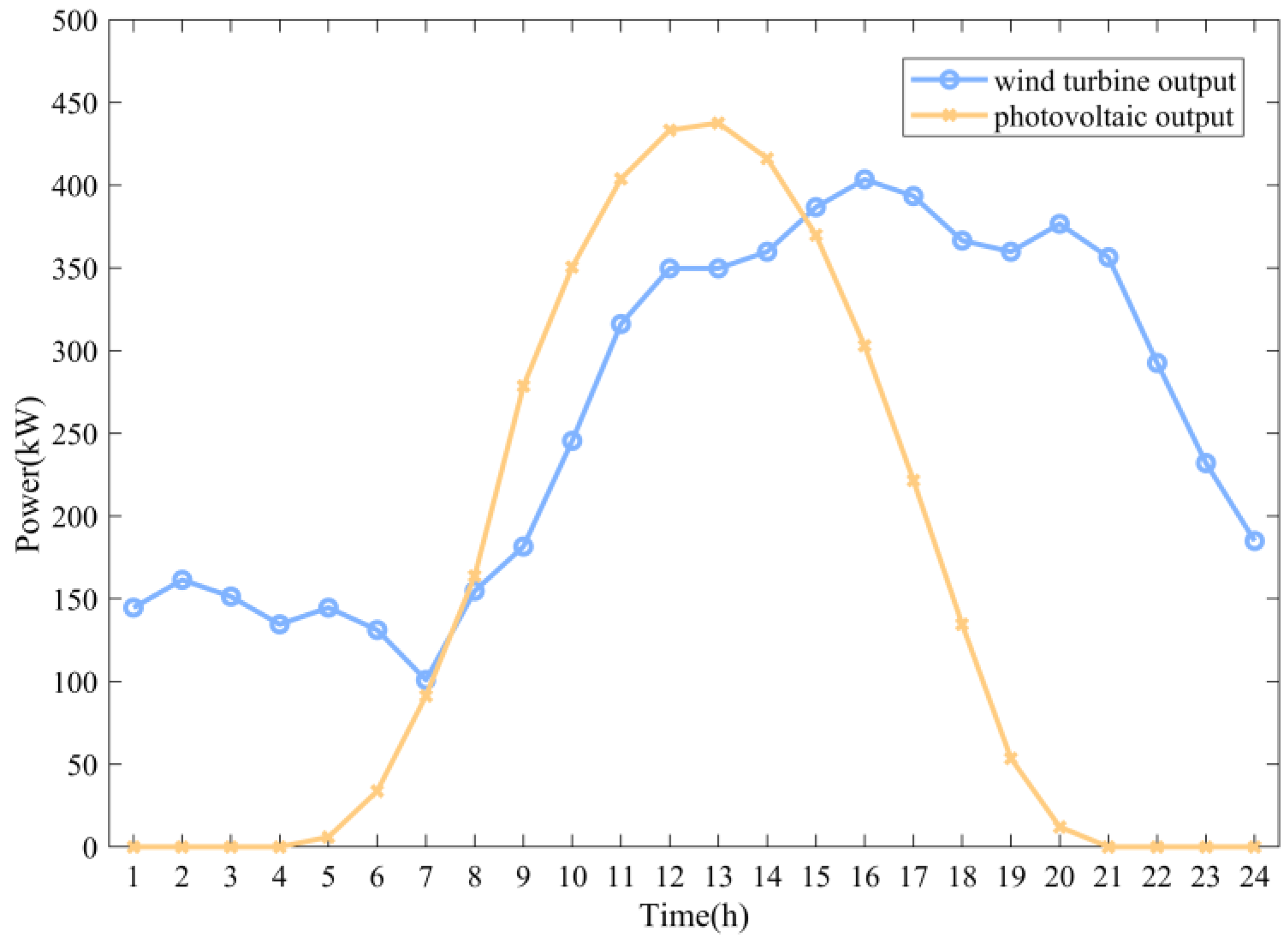
6.1. Experimental Data
6.2. Model Solution Algorithm Comparison
6.3. Experimental Results Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Function | M | MaxGen | MOPSO | MOCell | D × 10AL | NSGAIII | MSCSO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | |||
| DTLZ1 | 3 | 300 | 4.23 × 100 | 5.27 × 10−1 | 3.32 × 10−4 | 6.93 × 10−5 | 3.34 × 100 | 1.25 × 100 | 1.43 × 10−4 | 1.22 × 10−5 | 1.37 × 10−4 | 1.53 × 10−5 |
| 5 | 500 | 3.39 × 100 | 2.84 × 10−1 | 5.15 × 10−2 | 3.29 × 10−2 | 3.04 × 100 | 2.49 × 10−1 | 1.37 × 10−3 | 1.31 × 10−5 | 1.45 × 10−3 | 1.07 × 10−4 | |
| 8 | 800 | 4.77 × 100 | 1.44 × 100 | 1.93 × 101 | 5.30 × 100 | 2.36 × 100 | 3.71 × 10−1 | 4.19 × 10−3 | 6.99 × 10−5 | 3.85 × 10−3 | 8.58 × 10−5 | |
| DTLZ2 | 3 | 300 | 3.58 × 10−3 | 1.37 × 10−3 | 1.50 × 10−3 | 1.15 × 10−4 | 1.47 × 10−3 | 2.55 × 10−4 | 3.58 × 10−4 | 6.60 × 10−6 | 3.57 × 10−4 | 4.38 × 10−6 |
| 5 | 500 | 4.13 × 10−2 | 2.85 × 10−2 | 1.63 × 10−2 | 2.72 × 10−3 | 7.53 × 10−3 | 1.36 × 10−3 | 4.36 × 10−3 | 2.62 × 10−6 | 4.31 × 10−3 | 1.82 × 10−5 | |
| 8 | 800 | 2.98 × 10−2 | 1.31 × 10−2 | 1.80 × 10−1 | 3.22 × 10−3 | 2.44 × 10−2 | 7.69 × 10−3 | 1.42 × 10−2 | 3.65 × 10−5 | 1.35 × 10−2 | 2.61 × 10−4 | |
| DTLZ3 | 3 | 300 | 3.30 × 101 | 9.75 × 100 | 1.33 × 10−1 | 3.54 × 10−1 | 1.72 × 101 | 1.47 × 101 | 1.07 × 10−3 | 4.19 × 10−4 | 1.91 × 10−3 | 1.73 × 10−3 |
| 5 | 500 | 2.27 × 101 | 4.94 × 100 | 1.21 × 101 | 6.40 × 100 | 1.89 × 101 | 9.36 × 10−1 | 3.50 × 10−2 | 4.34 × 10−3 | 1.34 × 10−4 | 4.29 × 10−3 | |
| 8 | 800 | 2.77 × 101 | 8.25 × 100 | 1.38 × 102 | 2.38 × 100 | 1.83 × 101 | 1.48 × 100 | 1.22 × 100 | 1.41 × 10−2 | 4.87 × 10−4 | 1.33 × 10−2 | |
| DTLZ4 | 3 | 300 | 1.42 × 10−2 | 1.10 × 10−2 | 1.36 × 10−3 | 3.17 × 10−4 | 1.51 × 10−2 | 2.93 × 10−2 | 3.58 × 10−4 | 4.02 × 10−6 | 3.55 × 10−4 | 5.60 × 10−6 |
| 5 | 500 | 1.10 × 10−1 | 2.56 × 10−2 | 1.70 × 10−2 | 3.47 × 10−3 | 2.23 × 10−2 | 1.82 × 10−2 | 4.34 × 10−3 | 1.54 × 10−5 | 4.29 × 10−3 | 4.00 × 10−5 | |
| 8 | 800 | 1.50 × 10−1 | 1.69 × 10−2 | 1.75 × 10−1 | 2.27 × 10−3 | 2.73 × 10−2 | 9.55 × 10−3 | 1.41 × 10−2 | 1.65 × 10−3 | 1.33 × 10−2 | 8.91 × 10−5 | |
| DTLZ5 | 3 | 300 | 1.78 × 10−4 | 8.40 × 10−5 | 2.13 × 10−4 | 4.24 × 10−5 | 1.17 × 10−2 | 3.41 × 10−3 | 1.19 × 10−4 | 2.22 × 10−5 | 3.29 × 10−6 | 1.46 × 10−7 |
| 5 | 500 | 1.15 × 10−1 | 1.88 × 10−2 | 1.38 × 10−1 | 1.33 × 10−2 | 2.27 × 10−1 | 1.07 × 10−2 | 1.13 × 10−1 | 1.03 × 10−2 | 1.45 × 10−1 | 1.81 × 10−2 | |
| 8 | 800 | 8.34 × 10−2 | 2.00 × 10−2 | 1.83 × 10−1 | 4.69 × 10−3 | 2.55 × 10−1 | 1.49 × 10−2 | 1.03 × 10−1 | 5.90 × 10−3 | 1.25 × 10−1 | 8.24 × 10−3 | |
| DTLZ6 | 3 | 300 | 1.56 × 10−1 | 1.03 × 10−1 | 3.50 × 10−6 | 7.91 × 10−8 | 9.73 × 10−6 | 8.26 × 10−7 | 3.40 × 10−6 | 1.59 × 10−7 | 3.29 × 10−6 | 1.46 × 10−7 |
| 5 | 500 | 6.67 × 10−1 | 7.56 × 10−3 | 7.67 × 10−1 | 3.14 × 10−2 | 3.29 × 10−1 | 3.67 × 10−2 | 2.96 × 10−1 | 3.50 × 10−2 | 2.77 × 10−1 | 2.77 × 10−1 | |
| 8 | 800 | 6.61 × 10−1 | 3.80 × 10−3 | 8.05 × 10−1 | 6.80 × 10−3 | 4.14 × 10−1 | 7.02 × 10−2 | 3.60 × 10−1 | 4.77 × 10−2 | 2.17 × 10−1 | 4.11 × 10−2 | |
| DTLZ7 | 3 | 300 | 1.06 × 10−1 | 6.83 × 10−2 | 2.28 × 10−3 | 3.91 × 10−4 | 1.83 × 10−2 | 9.31 × 10−3 | 1.16 × 10−3 | 1.28 × 10−4 | 6.95 × 10−4 | 2.16 × 10−4 |
| 5 | 500 | 1.06 × 100 | 2.40 × 10−1 | 2.59 × 10−2 | 1.71 × 10−3 | 1.83 × 10−2 | 7.39 × 10−4 | 1.11 × 10−2 | 5.28 × 10−4 | 9.03 × 10−3 | 1.74 × 10−3 | |
| 8 | 800 | 2.38 × 100 | 4.45 × 10−2 | 1.04 × 100 | 1.63 × 10−1 | 6.91 × 10−2 | 1.64 × 10−2 | 1.91 × 10−2 | 5.06 × 10−4 | 1.64 × 10−2 | 8.02 × 10−3 |
| Function | M | MaxGen | MOPSO | MOCell | D × 10AL | NSGAIII | MSCSO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | |||
| DTLZ1 | 3 | 300 | 6.48 × 100 | 1.80 × 100 | 1.98 × 10−2 | 8.78 × 10−4 | 7.72 × 100 | 3.72 × 100 | 1.42 × 10−2 | 3.77 × 10−5 | 1.37 × 10−2 | 2.51 × 10−5 |
| 5 | 500 | 1.40 × 101 | 1.28 × 101 | 4.78 × 10−1 | 2.92 × 10−1 | 5.93 × 100 | 4.95 × 100 | 6.34 × 10−2 | 3.24 × 10−5 | 6.30 × 10−2 | 1.86 × 10−4 | |
| 8 | 800 | 2.47 × 101 | 1.13 × 101 | 1.34 × 101 | 6.28 × 100 | 2.93 × 100 | 1.90 × 100 | 1.02 × 10−1 | 1.26 × 10−2 | 9.74 × 10−2 | 4.23 × 10−4 | |
| DTLZ2 | 3 | 300 | 6.38 × 10−2 | 8.41 × 10−3 | 5.19 × 10−2 | 1.36 × 10−3 | 4.40 × 10−2 | 1.74 × 10−3 | 3.64 × 10−2 | 4.18 × 10−6 | 3.52 × 10−2 | 1.16 × 10−5 |
| 5 | 500 | 6.87 × 10−1 | 1.18 × 10−1 | 2.55 × 10−1 | 1.02 × 10−2 | 2.10 × 10−1 | 6.38 × 10−3 | 1.95 × 10−1 | 9.66 × 10−6 | 1.85 × 10−1 | 1.34 × 10−5 | |
| 8 | 800 | 9.53 × 10−1 | 2.24 × 10−1 | 2.03 × 100 | 3.21 × 10−1 | 3.75 × 10−1 | 2.76 × 10−2 | 3.15 × 10−1 | 1.66 × 10−4 | 3.07 × 10−1 | 4.23 × 10−4 | |
| DTLZ3 | 3 | 300 | 7.74 × 101 | 4.72 × 101 | 5.58 × 10−2 | 6.05 × 10−3 | 3.46 × 101 | 4.26 × 101 | 4.38 × 10−2 | 7.43 × 10−3 | 6.43 × 10−2 | 3.25 × 10−2 |
| 5 | 500 | 1.51 × 102 | 8.37 × 101 | 8.75 × 100 | 8.28 × 100 | 7.18 × 101 | 2.53 × 101 | 1.96 × 10−1 | 4.23 × 10−4 | 2.23 × 10−1 | 4.71 × 10−2 | |
| 8 | 800 | 1.35 × 102 | 6.30 × 101 | 8.22 × 102 | 2.19 × 102 | 3.31 × 101 | 2.10 × 101 | 3.24 × 10−1 | 5.95 × 10−3 | 3.37 × 10−1 | 9.63 × 10−3 | |
| DTLZ4 | 3 | 300 | 2.15 × 10−1 | 8.55 × 10−2 | 5.17 × 10−2 | 1.86 × 10−3 | 9.30 × 10−2 | 9.53 × 10−2 | 3.64 × 10−2 | 2.68 × 10−5 | 3.59 × 10−2 | 9.89 × 10−6 |
| 5 | 500 | 1.39 × 100 | 5.21 × 10−1 | 2.49 × 10−1 | 9.36 × 10−3 | 2.80 × 10−1 | 5.36 × 10−2 | 2.23 × 10−1 | 8.02 × 10−2 | 1.95 × 10−1 | 7.29 × 10−5 | |
| 8 | 800 | 2.23 × 100 | 3.14 × 10−1 | 2.01 × 100 | 1.26 × 10−1 | 4.14 × 10−1 | 2.15 × 10−2 | 3.84 × 10−1 | 9.74 × 10−2 | 3.16 × 10−1 | 1.82 × 10−4 | |
| DTLZ5 | 3 | 300 | 6.63 × 10−3 | 1.11 × 10−3 | 3.57 × 10−3 | 2.50 × 10−4 | 3.85 × 10−2 | 6.15 × 10−3 | 5.96 × 10−3 | 5.96 × 10−4 | 8.20 × 10−3 | 4.33 × 10−4 |
| 5 | 500 | 1.19 × 100 | 2.11 × 10−1 | 1.00 × 10−1 | 1.66 × 10−2 | 1.27 × 10−1 | 2.24 × 10−2 | 1.23 × 10−1 | 2.45 × 10−2 | 9.85 × 10−2 | 1.97 × 10−2 | |
| 8 | 800 | 9.93 × 10−1 | 3.42 × 10−1 | 2.66 × 10−1 | 2.09 × 10−1 | 2.15 × 10−1 | 3.12 × 10−2 | 2.24 × 10−1 | 2.84 × 10−2 | 1.67 × 10−1 | 3.93 × 10−2 | |
| DTLZ6 | 3 | 300 | 1.92 × 100 | 1.17 × 100 | 2.83 × 10−3 | 8.89 × 10−5 | 2.90 × 10−2 | 7.95 × 10−3 | 9.44 × 10−3 | 1.72 × 10−3 | 1.07 × 10−2 | 1.64 × 10−3 |
| 5 | 500 | 8.97 × 100 | 5.13 × 10−1 | 5.35 × 100 | 7.05 × 10−1 | 2.99 × 10−1 | 4.10 × 10−1 | 3.55 × 10−1 | 2.06 × 10−1 | 1.44 × 10−1 | 3.14 × 10−2 | |
| 8 | 800 | 9.29 × 100 | 3.22 × 10−1 | 7.26 × 100 | 9.04 × 10−1 | 1.81 × 10−1 | 5.79 × 10−2 | 6.82 × 10−1 | 2.89 × 10−1 | 2.32 × 10−1 | 6.82 × 10−2 | |
| DTLZ7 | 3 | 300 | 1.89 × 100 | 7.43 × 10−1 | 5.62 × 10−2 | 1.71 × 10−3 | 1.78 × 10−1 | 7.65 × 10−2 | 5.10 × 10−2 | 6.51 × 10−4 | 5.06 × 10−2 | 7.94 × 10−4 |
| 5 | 500 | 1.25 × 101 | 3.56 × 100 | 4.21 × 10−1 | 1.05 × 10−2 | 5.93 × 10−1 | 1.14 × 10−2 | 3.42 × 10−1 | 7.20 × 10−3 | 3.38 × 10−1 | 6.89 × 10−3 | |
| 8 | 800 | 3.58 × 101 | 4.39 × 100 | 1.37 × 100 | 9.58 × 10−2 | 1.58 × 100 | 1.50 × 10−1 | 7.82 × 10−1 | 2.92 × 10−2 | 7.98 × 10−1 | 3.18 × 10−2 |
| Function | M | MaxGen | MOPSO | MOCell | D × 10AL | NSGAIII | MSCSO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | |||
| DTLZ1 | 3 | 300 | 0.00 × 100 | 0.00 × 100 | 8.35 × 10−1 | 4.90 × 10−3 | 5.77 × 10−2 | 7.90 × 10−2 | 8.51 × 10−1 | 3.92 × 10−4 | 8.63 × 10−1 | 3.49 × 10−4 |
| 5 | 500 | 0.00 × 100 | 0.00 × 100 | 4.25 × 10−1 | 4.19 × 10−1 | 0.00 × 100 | 0.00 × 100 | 9.71 × 10−1 | 2.08 × 10−3 | 9.75 × 10−1 | 1.62 × 10−4 | |
| 8 | 800 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 9.77 × 10−3 | 2.39 × 10−2 | 9.95 × 10−1 | 1.23 × 10−3 | 9.98 × 10−1 | 7.63 × 10−5 | |
| DTLZ2 | 3 | 300 | 5.12 × 10−1 | 1.57 × 10−2 | 5.44 × 10−1 | 1.54 × 10−3 | 5.54 × 10−1 | 2.25 × 10−3 | 5.71 × 10−1 | 3.19 × 10−5 | 5.76 × 10−1 | 1.02 × 10−4 |
| 5 | 500 | 1.27 × 10−1 | 1.36 × 10−1 | 5.85 × 10−1 | 1.58 × 10−2 | 7.38 × 10−1 | 1.57 × 10−2 | 7.89 × 10−1 | 4.54 × 10−4 | 7.95 × 10−1 | 3.73 × 10−4 | |
| 8 | 800 | 6.89 × 10−2 | 6.61 × 10−2 | 2.08 × 10−3 | 5.88 × 10−3 | 7.96 × 10−1 | 3.13 × 10−2 | 9.22 × 10−1 | 4.07 × 10−4 | 9.29 × 10−1 | 3.21 × 10−4 | |
| DTLZ3 | 3 | 300 | 0.00 × 100 | 0.00 × 100 | 5.36 × 10−1 | 1.31 × 10−2 | 0.00 × 100 | 0.00 × 100 | 5.55 × 10−1 | 9.52 × 10−3 | 5.41 × 10−1 | 3.16 × 10−2 |
| 5 | 500 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 7.77 × 10−1 | 6.40 × 10−3 | 7.83 × 10−1 | 7.86 × 10−3 | |
| 8 | 800 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 8.06 × 10−1 | 3.26 × 10−1 | 9.24 × 10−1 | 2.41 × 10−3 | |
| DTLZ4 | 3 | 300 | 4.43 × 10−1 | 4.18 × 10−2 | 5.46 × 10−1 | 1.43 × 10−3 | 5.53 × 10−1 | 5.75 × 10−3 | 5.72 × 10−1 | 1.22 × 10−4 | 5.75 × 10−1 | 9.46 × 10−5 |
| 5 | 500 | 3.03 × 10−2 | 6.11 × 10−2 | 6.27 × 10−1 | 1.73 × 10−2 | 7.09 × 10−1 | 3.69 × 10−2 | 7.74 × 10−1 | 5.97 × 10−2 | 7.95 × 10−1 | 3.55 × 10−4 | |
| 8 | 800 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 8.49 × 10−1 | 1.41 × 10−2 | 9.16 × 10−1 | 2.13 × 10−2 | 9.24 × 10−1 | 2.73 × 10−4 | |
| DTLZ5 | 3 | 300 | 1.95 × 10−1 | 2.75 × 10−3 | 2.00 × 10−1 | 1.48 × 10−4 | 1.77 × 10−1 | 6.55 × 10−4 | 1.98 × 10−1 | 8.32 × 10−4 | 1.97 × 10−1 | 6.44 × 10−4 |
| 5 | 500 | 0.00 × 100 | 0.00 × 100 | 1.06 × 10−1 | 6.09 × 10−3 | 1.12 × 10−1 | 5.65 × 10−4 | 9.95 × 10−2 | 2.54 × 10−2 | 1.06 × 10−1 | 3.50 × 10−3 | |
| 8 | 800 | 7.46 × 10−6 | 2.11 × 10−5 | 3.79 × 10−2 | 3.40 × 10−2 | 9.51 × 10−2 | 5.39 × 10−4 | 9.18 × 10−2 | 2.73 × 10−3 | 9.06 × 10−2 | 3.70 × 10−3 | |
| DTLZ6 | 3 | 300 | 2.50 × 10−2 | 7.08 × 10−2 | 2.01 × 10−1 | 4.75 × 10−5 | 1.63 × 10−1 | 5.09 × 10−2 | 1.96 × 10−1 | 9.94 × 10−4 | 1.96 × 10−1 | 6.99 × 10−4 |
| 5 | 500 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 9.05 × 10−2 | 5.06 × 10−2 | 9.13 × 10−2 | 1.07 × 10−3 | 9.73 × 10−2 | 5.87 × 10−3 | |
| 8 | 800 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 9.48 × 10−2 | 2.01 × 10−3 | 7.69 × 10−2 | 2.59 × 10−2 | 9.44 × 10−2 | 2.48 × 10−3 | |
| DTLZ7 | 3 | 300 | 4.18 × 10−2 | 5.83 × 10−2 | 2.70 × 10−1 | 8.78 × 10−4 | 2.25 × 10−1 | 2.86 × 10−2 | 2.79 × 10−1 | 6.01 × 10−4 | 2.82 × 10−1 | 5.44 × 10−4 |
| 5 | 500 | 0.00 × 100 | 0.00 × 100 | 1.58 × 10−1 | 1.13 × 10−2 | 1.17 × 10−1 | 5.95 × 10−3 | 2.36 × 10−1 | 7.94 × 10−3 | 2.44 × 10−1 | 3.57 × 10−3 | |
| 8 | 800 | 0.00 × 100 | 0.00 × 100 | 8.51 × 10−4 | 4.65 × 10−4 | 9.17 × 10−2 | 1.39 × 10−3 | 2.02 × 10−1 | 3.07 × 10−3 | 2.17 × 10−1 | 4.69 × 10−3 |
References
- Lu, Q.; Liu, M. A multi-criteria compromise ranking decision-making approach for analysis and evaluation of community-integrated energy service system. Energy 2024, 306, 132439. [Google Scholar] [CrossRef]
- Talihati, B.; Tao, S.; Fu, S.; Zhang, B.; Fan, H.; Li, Q.; Lv, X.; Sun, Y.; Wang, Y. Energy storage sharing in residential communities with controllable loads for enhanced operational efficiency and profitability. Appl. Energy 2024, 373, 123880. [Google Scholar] [CrossRef]
- Sun, B. A multi-objective optimization model for fast electric vehicle charging stations with wind, PV power and energy storage. J. Clean. Prod. 2021, 288, 125564. [Google Scholar] [CrossRef]
- Liao, X.; Qian, B.; Jiang, Z.; Fu, B.; He, H. Integrated Energy Station Optimal Dispatching Using a Novel Many-Objective Optimization Algorithm Based on Multiple Update Strategies. Energies 2023, 16, 5126. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, H.; Xu, Y.; Chen, H.; Zhu, Y.; Zhang, Z.; Li, W. Multi-objective capacity configuration optimization of an integrated energy system considering economy and environment with harvest heat. Energy Convers. Manag. 2022, 269, 116116. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Li, Y.; Zheng, Y.; Liu, J. A green-fitting dispatching model of station cluster for battery swapping under charging-discharging mode. Energy 2023, 276, 127600. [Google Scholar] [CrossRef]
- Yang, J.; Liu, W.; Ma, K.; Yue, Z.; Zhu, A.; Guo, S. An optimal battery allocation model for battery swapping station of electric vehicles. Energy 2023, 272, 127109. [Google Scholar] [CrossRef]
- Linjuan, Z.; Han, F.; Zhiheng, Z.; Shangbing, W.; Jinbin, Z. Site selection and capacity determination of charging stations considering the uncertainty of users’ dynamic charging demands. Front. Energy Res. 2024, 11, 1295043. [Google Scholar] [CrossRef]
- Ang, Y.Q.; Polly, A.; Kulkarni, A.; Chambi, G.B.; Hernandez, M.; Haji, M.N. Multi-objective optimization of hybrid renewable energy systems with urban building energy modeling for a prototypical coastal community. Renew. Energy 2022, 201, 72–84. [Google Scholar]
- Çiçek, A. Multi-Objective Operation Strategy for a Community with RESs, Fuel Cell EVs and Hydrogen Energy System Considering Demand Response. Sustain. Energy Technol. 2023, 55, 102957. [Google Scholar] [CrossRef]
- Ge, J.; Shen, C.; Zhao, K.; Lv, G. Energy production features of rooftop hybrid photovoltaic–wind system and matching analysis with building energy use. Energy Convers. Manag. 2022, 258, 115485. [Google Scholar] [CrossRef]
- Xie, Y.; Li, J.; Li, Y.; Zhu, W.; Dai, C. Two-stage evolutionary algorithm with fuzzy preference indicator for multimodal multi-objective optimization. Swarm Evol. Comput. 2024, 85, 101480. [Google Scholar]
- Shen, J.; Wang, P.; Dong, H.; Wang, W.; Li, J. Surrogate-assisted evolutionary algorithm with decomposition-based local learning for high-dimensional multi-objective optimization. Expert Syst. Appl. 2024, 240, 122575. [Google Scholar] [CrossRef]
- Hadikhani, P.; Lai, D.T.C.; Ong, W.H. Human Activity Discovery with Automatic Multi-Objective Particle Swarm Optimization Clustering with Gaussian Mutation and Game Theory. IEEE Trans. Multimed. 2024, 26, 420–435. [Google Scholar] [CrossRef]
- Yang, W.; Liu, S.; Yang, J. An optimized surrogate model and algorithm with rapid multi-parameter processing capability for antenna design. Measurement 2025, 241, 115719. [Google Scholar]
- Wei, L.; Li, E. A Grey Prediction-Based Reproduction Strategy for Many-Objective Evolutionary Algorithm. Int. J. Intell. Syst. 2024, 2024, 8994938. [Google Scholar]
- Gao, X.; Song, S. A switching competitive swarm optimizer for multi-objective optimization with irregular Pareto fronts. Expert Syst. Appl. 2024, 255, 124641. [Google Scholar]
- Jameel, M.; Abouhawwash, M. Multi-objective Mantis Search Algorithm (MOMSA): A novel approach for engineering design problems and validation. Comput. Methods Appl. Mech. Eng. 2024, 422, 116840. [Google Scholar]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Jia, J.; Li, H.; Wu, D.; Guo, J.; Jiang, L.; Fan, Z. Multi-objective optimization study of regional integrated energy systems coupled with renewable energy, energy storage, and inter-station energy sharing. Renew. Energy 2024, 225, 120328. [Google Scholar]
- Zhang, X.; Gao, W.; Zhong, J. Decentralized Economic Dispatching of Multi-Micro Grid Considering Wind Power and Photovoltaic Output Uncertainty. IEEE Access 2021, 9, 104093–104103. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, S.; Ge, B.; Li, Y. Design optimization and uncertainty analysis of multi-energy complementary system for residential building in isolated area. Energy Convers. Manag. 2021, 241, 114310. [Google Scholar]
- Deltenre, Q.; De Troyer, T.; Runacres, M.C. Performance assessment of hybrid PV-wind systems on high-rise rooftops in the Brussels-Capital Region. Energy Build. 2020, 224, 110137. [Google Scholar]
- Asdrubali, F.; Baldinelli, G.; Scrucca, F.; D Alessandro, F. Life Cycle Assessment of electricity production from renewable energies: Review and results harmonization. Renew. Sustain. Energy Rev. 2015, 42, 1113–1122. [Google Scholar]
- Coello, C.A.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; pp. 1051–1056. [Google Scholar]
- Nebro, A.J.; Durillo, J.J.; Luna, F.; Dorronsoro, B.; Alba, E. MOCell: A cellular genetic algorithm for multiobjective optimization. Int. J. Intell. Syst. 2009, 24, 726–746. [Google Scholar]
- Vu, C.C.; Bui, L.T.; Abbass, H.A. DEAL: A Direction-Guided Evolutionary Algorithm; Bui, L.T., Ong, Y.S., Hoai, N.X., Ishibuchi, H., Suganthan, P.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 148–157. [Google Scholar]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems with Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable Test Problems for Evolutionary Multiobjective Optimization. In Evolutionary Multiobjective Optimization: Theoretical Advances and Applications; Abraham, A., Jain, L., Goldberg, R., Eds.; Springer: London, UK, 2005; pp. 105–145. [Google Scholar]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable multi-objective optimization test problems. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; pp. 825–830. [Google Scholar]
- van Veldhuizen, D.A. Evolutionary Computation and Convergence to a Pareto Front. In Late Breaking Papers at the Genetic Programming 1998 Conference; Stanford University Bookstore: Stanford, CA, USA, 1998. [Google Scholar]
- Coello, C.A.C.; Cortés, N.C. Solving Multiobjective Optimization Problems Using an Artificial Immune System. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar]
- Liao, X.; Ma, J.; Jiang, Z.; Zhou, J. Many-objective optimization based mutual feed scheduling for energy system of integrated energy station. Appl. Soft Comput. 2024, 161, 111803. [Google Scholar]
- Häder, D.; Cabrol, N.A. Monitoring of Solar Irradiance in the High Andes. Photochem. Photobiol. 2020, 96, 1133–1139. [Google Scholar]
- Li, Q.S.; Shu, Z.R.; Chen, F.B. Performance assessment of tall building-integrated wind turbines for power generation. Appl. Energy 2016, 165, 777–788. [Google Scholar] [CrossRef]
- Fagiano, L.; Milanese, M.; Piga, D. High-Altitude Wind Power Generation. IEEE Trans. Energy Convers. 2010, 25, 168–180. [Google Scholar] [CrossRef]
- Blumthaler, M.; Ambach, W.; Ellinger, R. Increase in solar UV radiation with altitude. J. Photochem. Photobiol. B Biol. 1997, 39, 130–134. [Google Scholar] [CrossRef]
- Murakami, S.; Uehara, K.; Komine, H. Amplification of wind speed at ground level due to construction of high-rise building in urban area. J. Wind Eng. Ind. Aerodyn. 1979, 4, 343–370. [Google Scholar] [CrossRef]
- Quddus, M.A.; Shahvari, O.; Marufuzzaman, M.; Usher, J.M.; Jaradat, R. A collaborative energy sharing optimization model among electric vehicle charging stations, commercial buildings, and power grid. Appl. Energy 2018, 229, 841–857. [Google Scholar] [CrossRef]
- Wang, R.; Mu, J.; Sun, Z.W.; Wang, J.; Hu, A. NSGA-II multi-objective optimization regional electricity price model for electric vehicle charging based on travel law. Energy Rep. 2021, 7, 1495–1503. [Google Scholar] [CrossRef]
- Roslan, M.F.; Ramachandaramurthy, V.K.; Mansor, M.; Mokhzani, A.S.; Jern, K.P.; Begum, R.A.; Hannan, M.A. Techno-economic impact analysis for renewable energy-based hydrogen storage integrated grid electric vehicle charging stations in different potential locations of Malaysia. Energy Strategy Rev. 2024, 54, 101478. [Google Scholar] [CrossRef]
- Abid, M.S.; Ahshan, R.; Al Abri, R.; Al-Badi, A.; Albadi, M. Techno-economic and environmental assessment of renewable energy sources, virtual synchronous generators, and electric vehicle charging stations in microgrids. Appl. Energy 2024, 353, 122028. [Google Scholar] [CrossRef]
- Khan, S.; Sudhakar, K.; Bin Yusof, M.H. Building integrated photovoltaics powered electric vehicle charging with energy storage for residential building: Design, simulation, and assessment. J. Energy Storage 2023, 63, 107050. [Google Scholar] [CrossRef]
- Salek, F.; Resalati, S.; Morrey, D.; Henshall, P.; Azizi, A. Technical Energy Assessment and Sizing of a Second Life Battery Energy Storage System for a Residential Building Equipped with EV Charging Station. Appl. Sci. 2022, 12, 11103. [Google Scholar] [CrossRef]
- Liu, G.; Xue, Y.; Chinthavali, M.S.; Tomsovic, K. Optimal Sizing of PV and Energy Storage in an Electric Vehicle Extreme Fast Charging Station. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar]
- Mazzeo, D. Solar and wind assisted heat pump to meet the building air conditioning and electric energy demand in the presence of an electric vehicle charging station and battery storage. J. Clean. Prod. 2019, 213, 1228–1250. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A Reference Vector Guided Evolutionary Algorithm for Many-Objective Optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar]
- Yuan, J.; Liu, H.L.; Ong, Y.S.; He, Z. Indicator-Based Evolutionary Algorithm for Solving Constrained Multiobjective Optimization Problems. IEEE Trans. Evol. Comput. 2022, 26, 379–391. [Google Scholar]
- Corne, D.W.; Knowles, J.D.; Oates, M.J. The Pareto Envelope-Based Selection Algorithm for Multiobjective Optimization; Schoenauer, M., Deb, K., Rudolph, G., Yao, X., Lutton, E., Merelo, J.J., Schwefel, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 839–848. [Google Scholar]
- Li, M.; Zheng, J. Spread Assessment for Evolutionary Multi-Objective Optimization; Ehrgott, M., Fonseca, C.M., Gandibleux, X., Hao, J., Sevaux, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 216–230. [Google Scholar]
- Huang, W.; Shuai, B.; Sun, Y.; Wang, Y.; Antwi, E. Using entropy-TOPSIS method to evaluate urban rail transit system operation performance: The China case. Transp. Res. Part A Policy Pract. 2018, 111, 292–303. [Google Scholar]

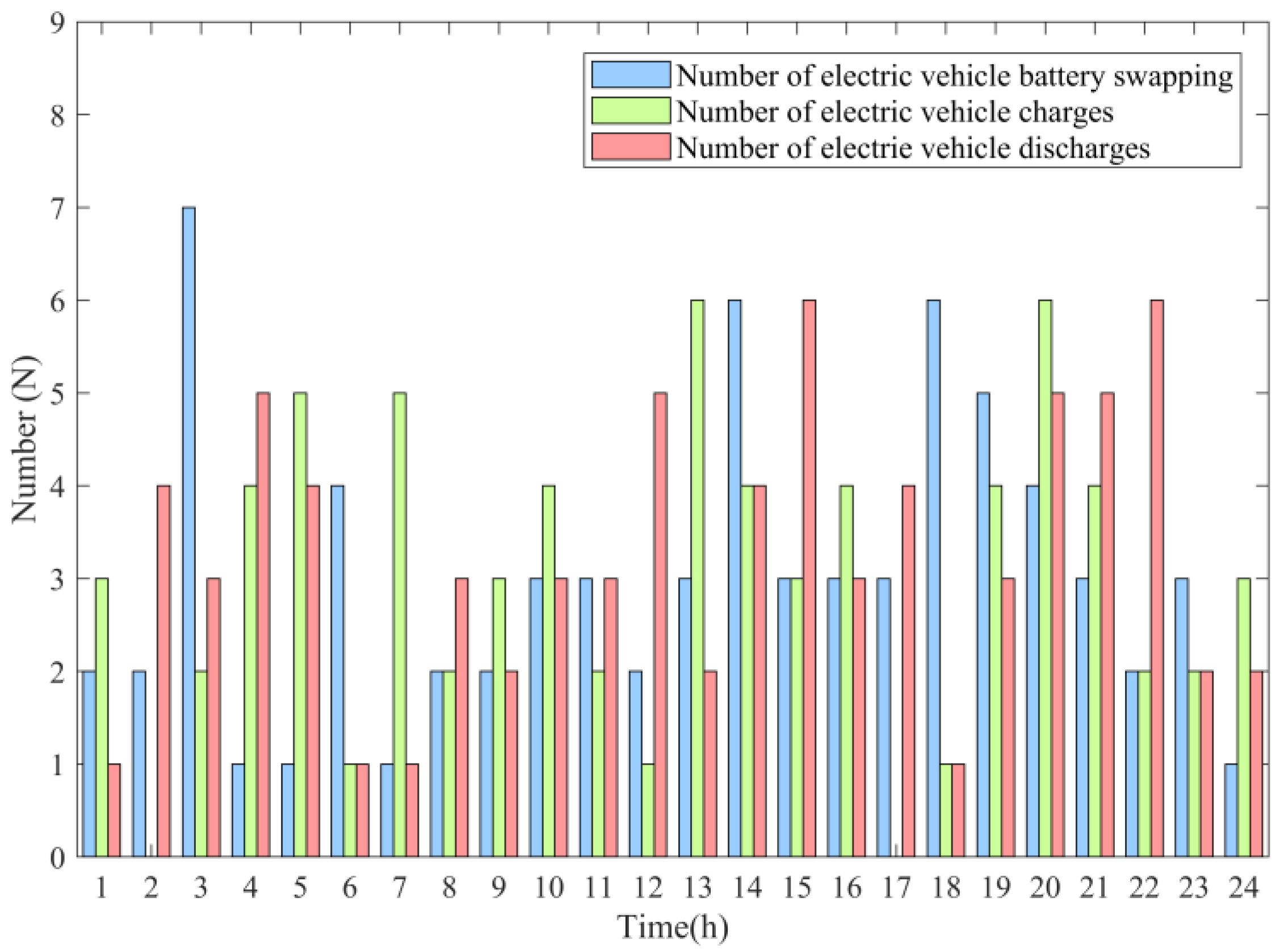
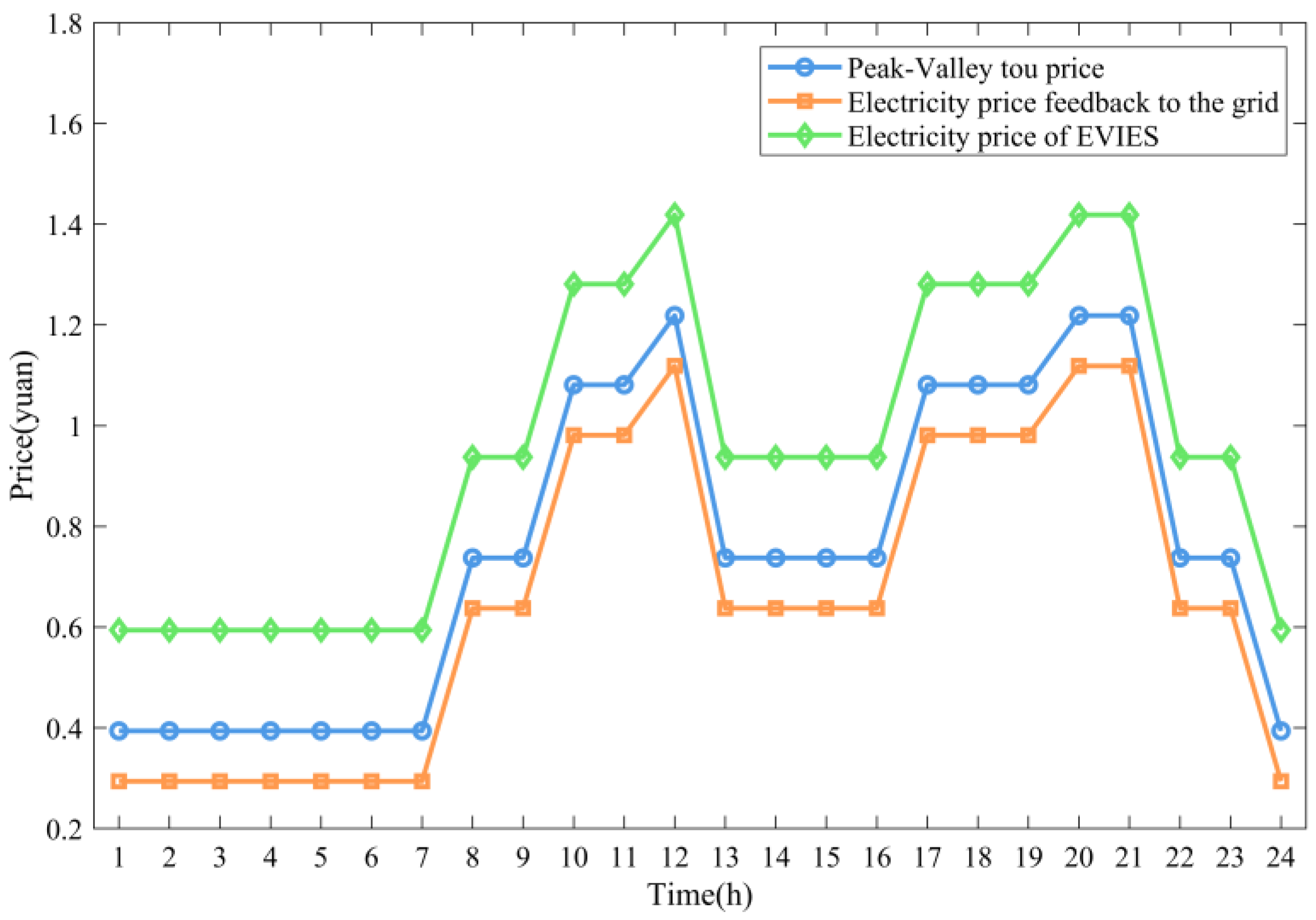
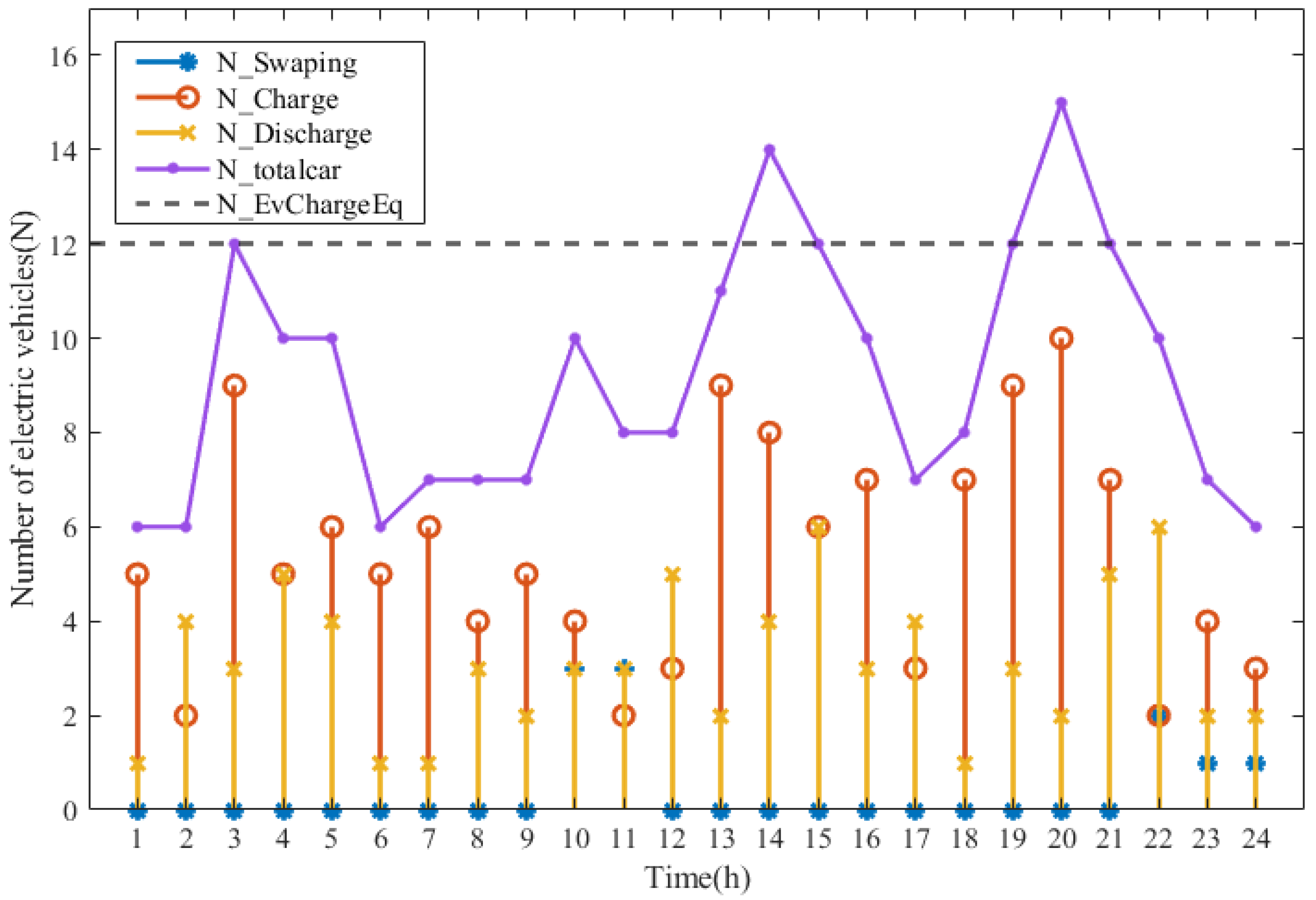

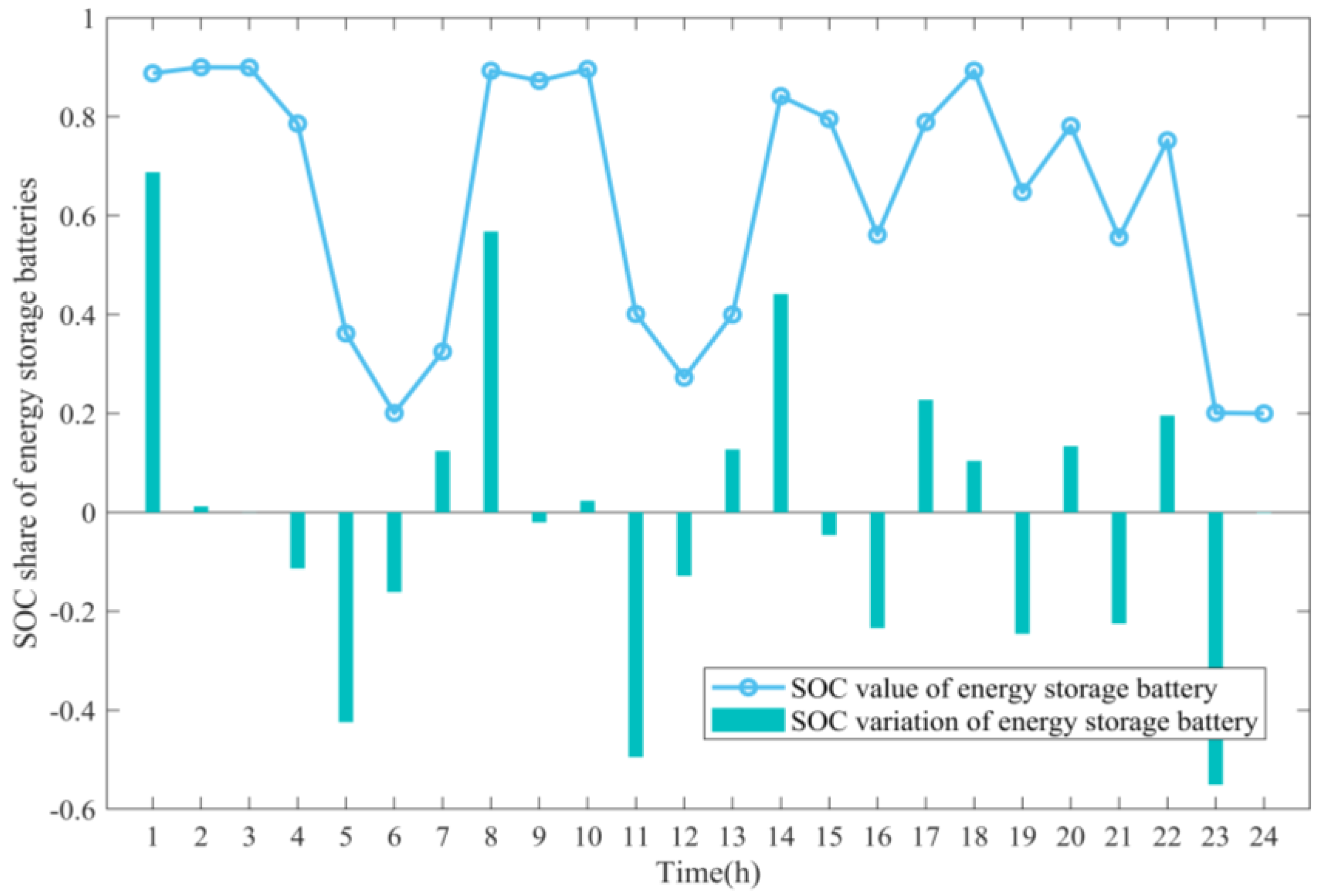
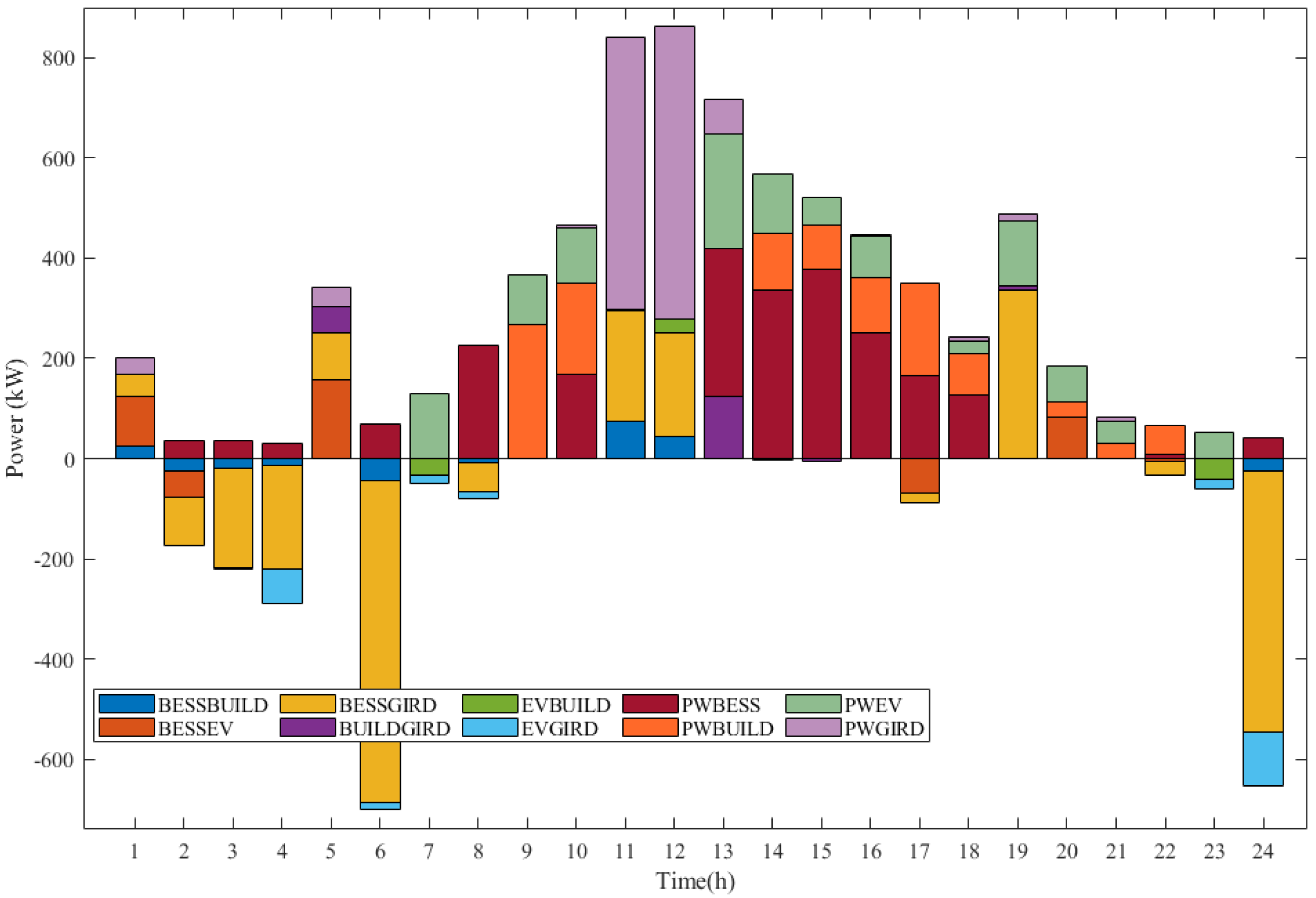
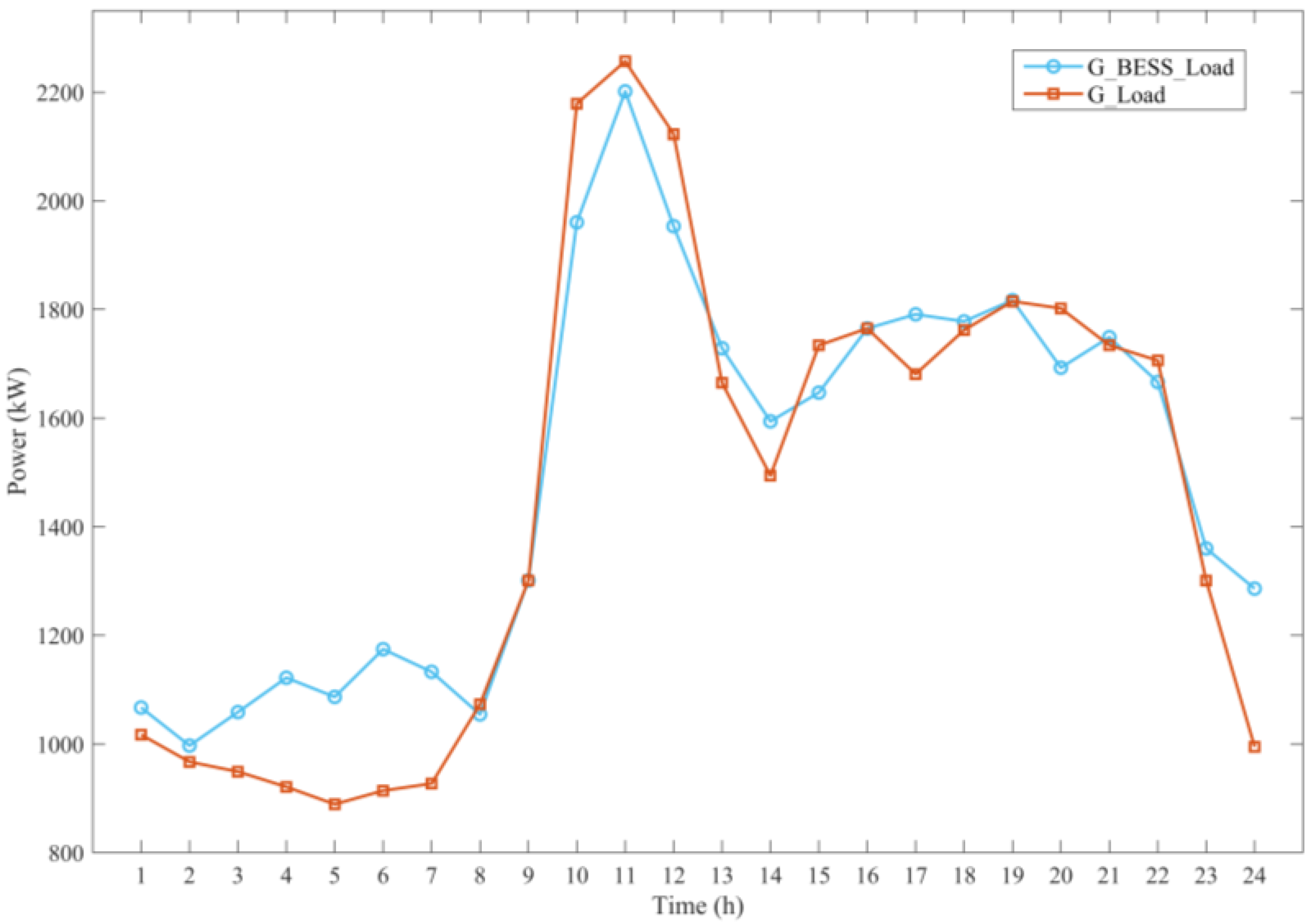
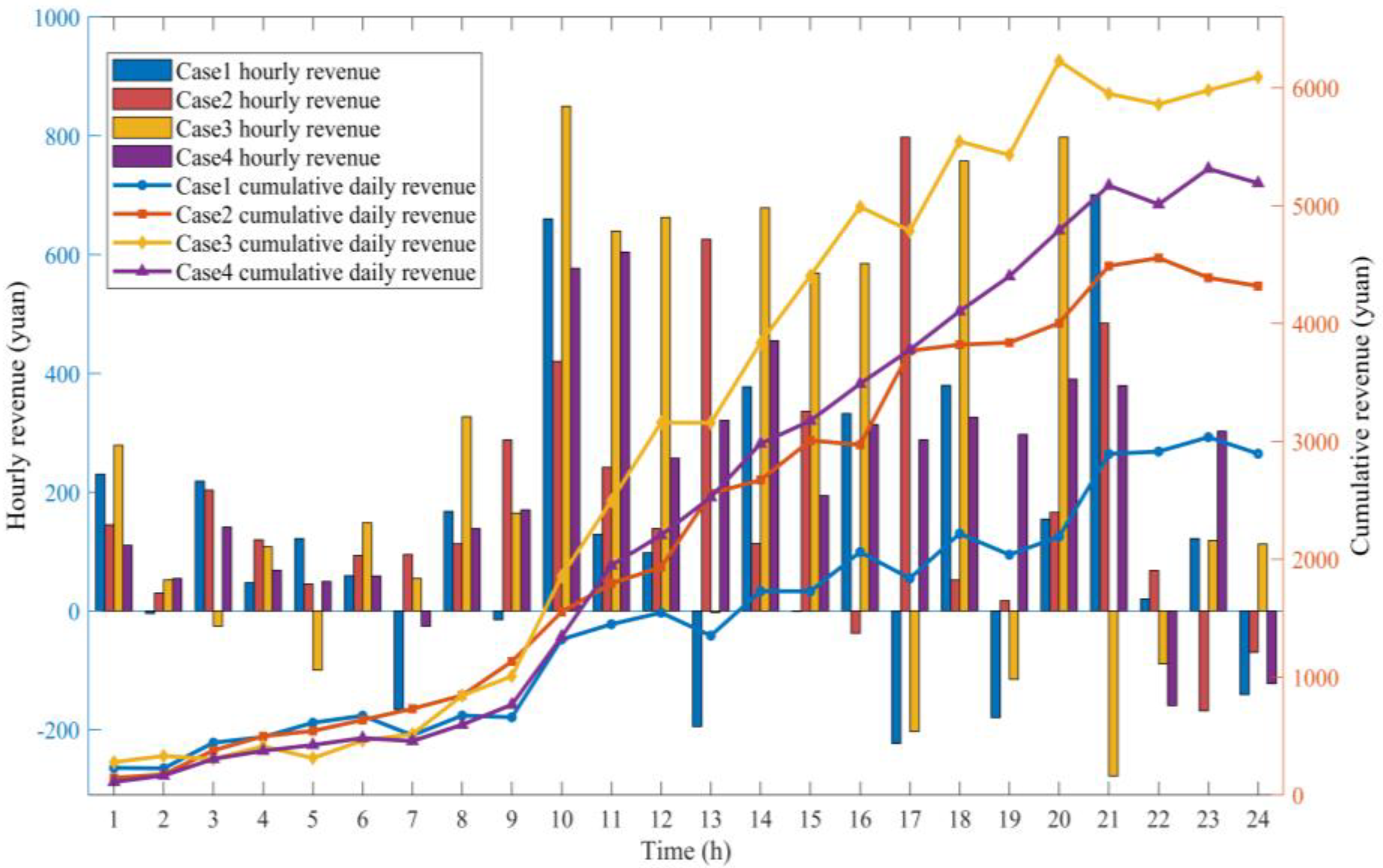
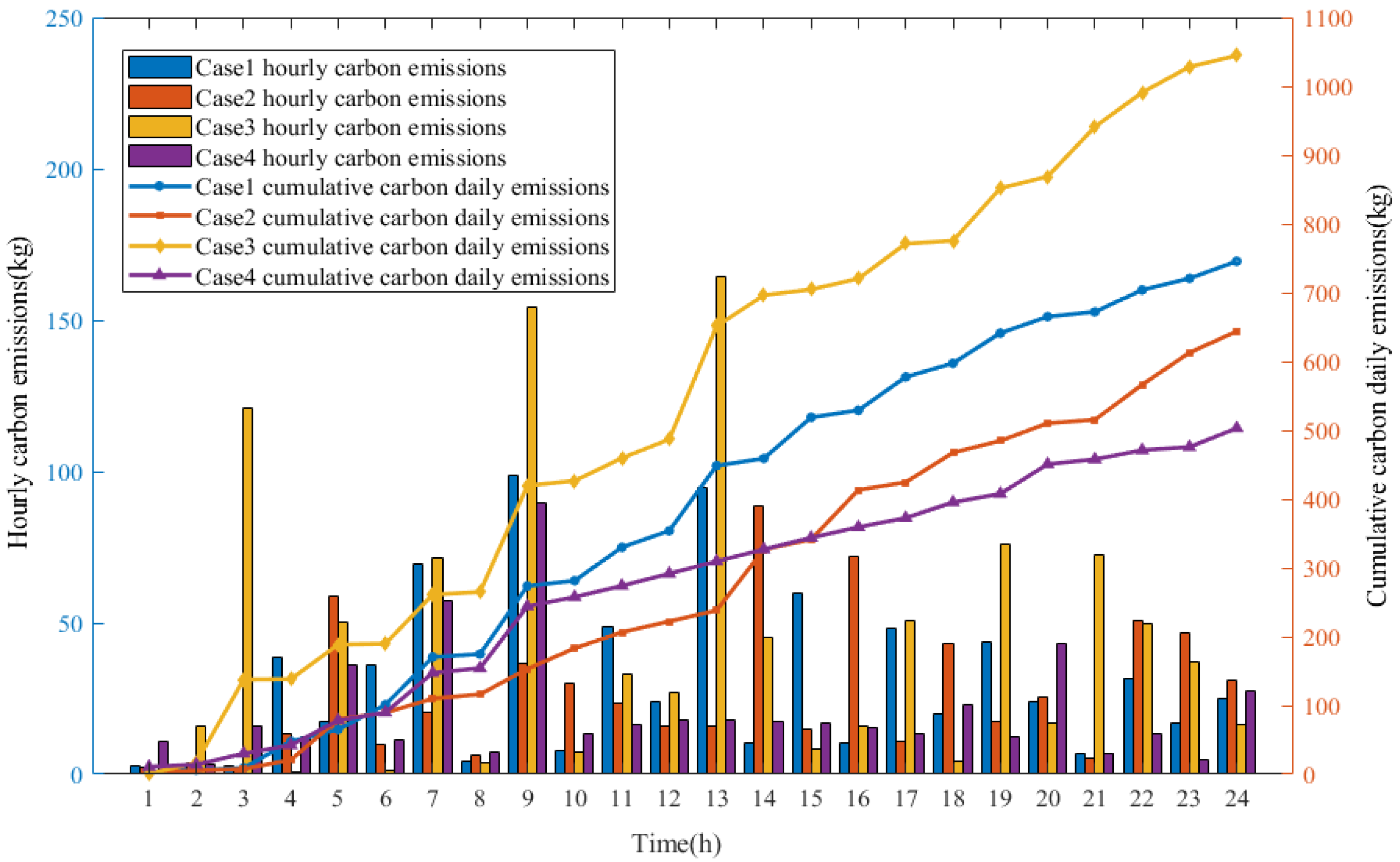

| Parameters | Conditions | |
|---|---|---|
| < 0.45 | ≥ 0.45 | |
| 152.5 | 152.5 | |
| 0.57 | 0.57 | |
| 2.8978 × 103 | 2.6943 × 103 | |
| 7.4131 × 103 | 6.0256 × 103 | |
| 3.15 × 104 | 3.15 × 104 | |
| 8.314 | 8.314 | |
| Parameter | Carbon Emission Factor (kg/kWh) | Value |
|---|---|---|
| Grid Power Consumption | 0.556 | |
| Photovoltaic Panel Production | 0.029 | |
| Wind Turbine Production | 0.048 | |
| Energy storage battery production | 0.250 |
| Parameter | Parameter Descriptions | Value |
|---|---|---|
| . | Penalty Coefficient | 5% |
| Depreciation Rate | 10% | |
| Electric Vehicle Battery Capacity | 60 | |
| Service Life of WT/PV Panels | 20 | |
| Cost per Storage Unit | 3.8 × 104 | |
| Cost per Photovoltaic Unit | 2.5 × 105 | |
| Cost per Wind Turbine | 4.0 × 105 | |
| PV Operation and Maintenance Cost | 350 | |
| WT Operation and Maintenance Cost | 400 |
| Parameter | Value |
|---|---|
| Population size | 200 |
| Iteration limit | 800 |
| WT capacity range | [0, 20] |
| PV capacity range | [0, 20] |
| BESS capacity range | [5, 35] |
| Gird configuration boundary | [−800, 800] |
| Algorithm | Best | Mean | Worst |
|---|---|---|---|
| RVEA | 8.7119 × 10−2 | 7.5150 × 10−2 | 5.5996 × 10−2 |
| IBEA | 1.3131 × 10−1 | 8.6035 × 10−2 | 6.4770 × 10−2 |
| MOPSO | 1.4139 × 10−1 | 1.0032 × 10−1 | 6.7300 × 10−2 |
| PESAII | 1.8204 × 10−1 | 1.1071 × 10−1 | 7.6691 × 10−2 |
| NSGAIII | 1.4477 × 10−1 | 9.0994 × 10−2 | 7.3874 × 10−2 |
| MSCSO | 2.1749 × 10−1 | 1.3622 × 10−1 | 1.0153 × 10−1 |
| Algorithm | Best | Mean | Worst |
|---|---|---|---|
| RVEA | 4.2080 × 10−1 | 5.0864 × 10−1 | 6.8773 × 10−1 |
| IBEA | 5.7496 × 10−1 | 7.2864 × 10−1 | 8.4125 × 10−1 |
| MOPSO | 4.7153 × 10−1 | 6.6695 × 10−1 | 7.7536 × 10−1 |
| PESAII | 4.6206 × 10−1 | 6.0788 × 10−1 | 7.1299 × 10−1 |
| NSGAIII | 4.8062 × 10−1 | 5.9100 × 10−1 | 1.0572 × 100 |
| MSCSO | 4.3778 × 10−1 | 4.9216 × 10−1 | 5.8144 × 10−1 |
| Algorithm | Best | Mean | Worst |
|---|---|---|---|
| RVEA | 6.6068 × 101 | 6.8773 × 101 | 7.2733 × 101 |
| IBEA | 7.6709 × 101 | 8.0941 × 101 | 8.9851 × 101 |
| MOPSO | 6.2577 × 101 | 6.3508 × 101 | 6.5675 × 101 |
| PESAII | 6.1712 × 101 | 6.6480 × 101 | 7.2818 × 101 |
| NSGAIII | 6.5148 × 101 | 6.6747 × 101 | 6.9045 × 101 |
| MSCSO | 5.8144 × 10−1 | 6.1741 × 101 | 6.2913 × 101 |
| Algorithm | Functions1 | |
|---|---|---|
| Min | Max | |
| RVEA | −3655.6730 | −3411.3412 |
| IBEA | −4558.7595 | −4350.4675 |
| MOPSO | −4326.8892 | −3604.3204 |
| PESAII | −4463.7385 | −3651.7192 |
| NSGAIII | −4378.6923 | −4293.6201 |
| MSCSO | −4884.1325 | −4533.8327 |
| Algorithm | Functions2 | |
|---|---|---|
| Min | Max | |
| RVEA | 138,347.4705 | 147,149.2357 |
| IBEA | 136,205.4731 | 155,717.2408 |
| MOPSO | 157,058.4080 | 205,616.7163 |
| PESAII | 164,521.5865 | 181,832.5745 |
| NSGAIII | 139,623.6120 | 155,724.9789 |
| MSCSO | 134,676.4628 | 141,107.6105 |
| Algorithm | Functions3 | |
|---|---|---|
| Min | Max | |
| RVEA | 833.4063 | 968.3241 |
| IBEA | 703.9207 | 1071.4816 |
| MOPSO | 606.8311 | 1131.7989 |
| PESAII | 563.0736 | 741.2197 |
| NSGAIII | 915.3269 | 1093.5630 |
| MSCSO | 580.6526 | 698.1306 |
| CASE | EVIES-PV | EVIES-WT | Building-WT/PV |
|---|---|---|---|
| Case 1 | √ | √ | |
| Case 2 | √ | √ | |
| Case 3 | √ | √ | |
| Case 4 | √ | √ | √ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; He, H.; Liao, X.; Zou, F.; Huang, W.; Li, C. Optimization of Renewable Energy Sharing for Electric Vehicle Integrated Energy Stations and High-Rise Buildings Considering Economic and Environmental Factors. Sustainability 2025, 17, 3142. https://doi.org/10.3390/su17073142
Liu K, He H, Liao X, Zou F, Huang W, Li C. Optimization of Renewable Energy Sharing for Electric Vehicle Integrated Energy Stations and High-Rise Buildings Considering Economic and Environmental Factors. Sustainability. 2025; 17(7):3142. https://doi.org/10.3390/su17073142
Chicago/Turabian StyleLiu, Ke, Hui He, Xiang Liao, Fuyi Zou, Wei Huang, and Chaoshun Li. 2025. "Optimization of Renewable Energy Sharing for Electric Vehicle Integrated Energy Stations and High-Rise Buildings Considering Economic and Environmental Factors" Sustainability 17, no. 7: 3142. https://doi.org/10.3390/su17073142
APA StyleLiu, K., He, H., Liao, X., Zou, F., Huang, W., & Li, C. (2025). Optimization of Renewable Energy Sharing for Electric Vehicle Integrated Energy Stations and High-Rise Buildings Considering Economic and Environmental Factors. Sustainability, 17(7), 3142. https://doi.org/10.3390/su17073142







