Composite Triple Activation Function: Enhancing CNN-BiLSTM-AM for Sustainable Financial Risk Prediction in Manufacturing
Abstract
1. Introduction
- (1)
- How effective are different deep learning architectures (such as CNNs, BiLSTM, CNN-AM, BiLSTM-AM, and CNN-BiLSTM-AM) in predicting financial risks in the manufacturing industry?
- (2)
- Can composite activation functions (such as CTAFs) outperform traditional activation functions regarding prediction accuracy and stability?
- (1)
- A CTAF (composite triple activation function) is proposed, the activation strategy is optimized, gradient propagation efficiency is improved, and the nonlinear expression ability is modeled.
- (2)
- A deep model structure that integrates a CNN, BiLSTM, and an AM and that fully leverages the advantages of multi-network collaborative feature extraction by using the CTAF is built.
- (3)
- Empirical research is conducted on a manufacturing financial dataset, revealing that the model performs excellently in accuracy and stability and has strong cross-industry applicability.
2. Literature Review
2.1. The Application of Deep Learning in Financial Risk Prediction
2.2. Optimization Application of Activation Function in Deep Learning
3. Methodology
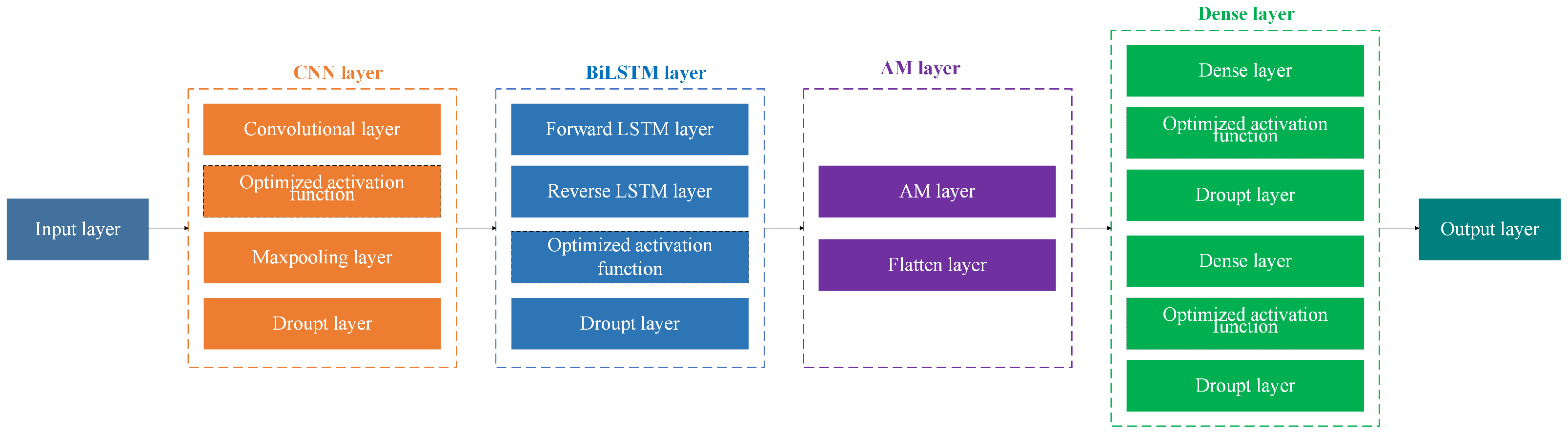
3.1. CNN-BiLSTM-AM Model Architecture
- (1)
- Data Preprocessing and Feature Extraction: Preprocessed financial indicators are first passed through a fully connected layer to extract global features.
- (2)
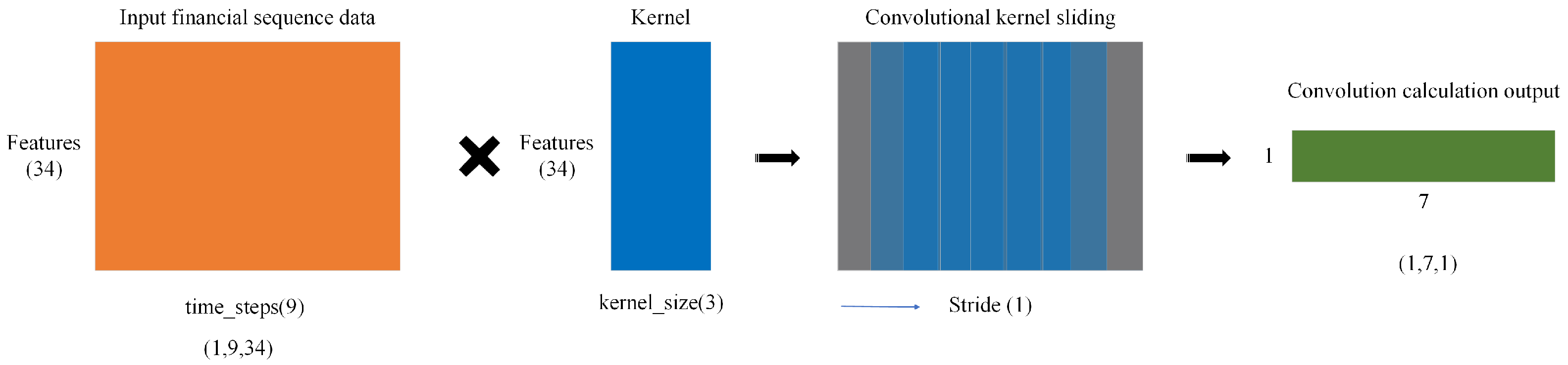
- CNN Layer: Local patterns are captured via convolution and max pooling, reducing dimensionality while retaining essential information.
- (3)
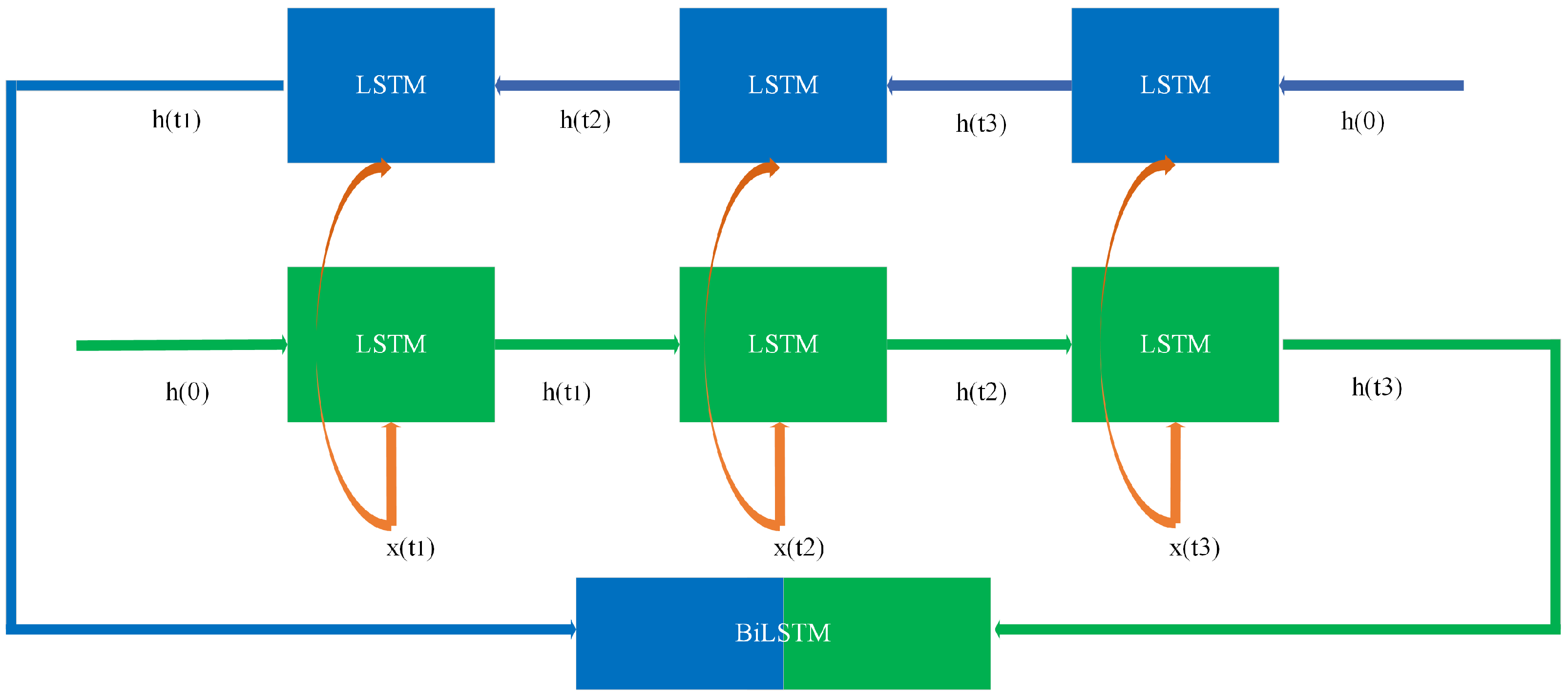
- BiLSTM Layer: Outputs from the CNN are processed by forward and backward LSTM units to capture contextual dependencies in both directions.
- (4)
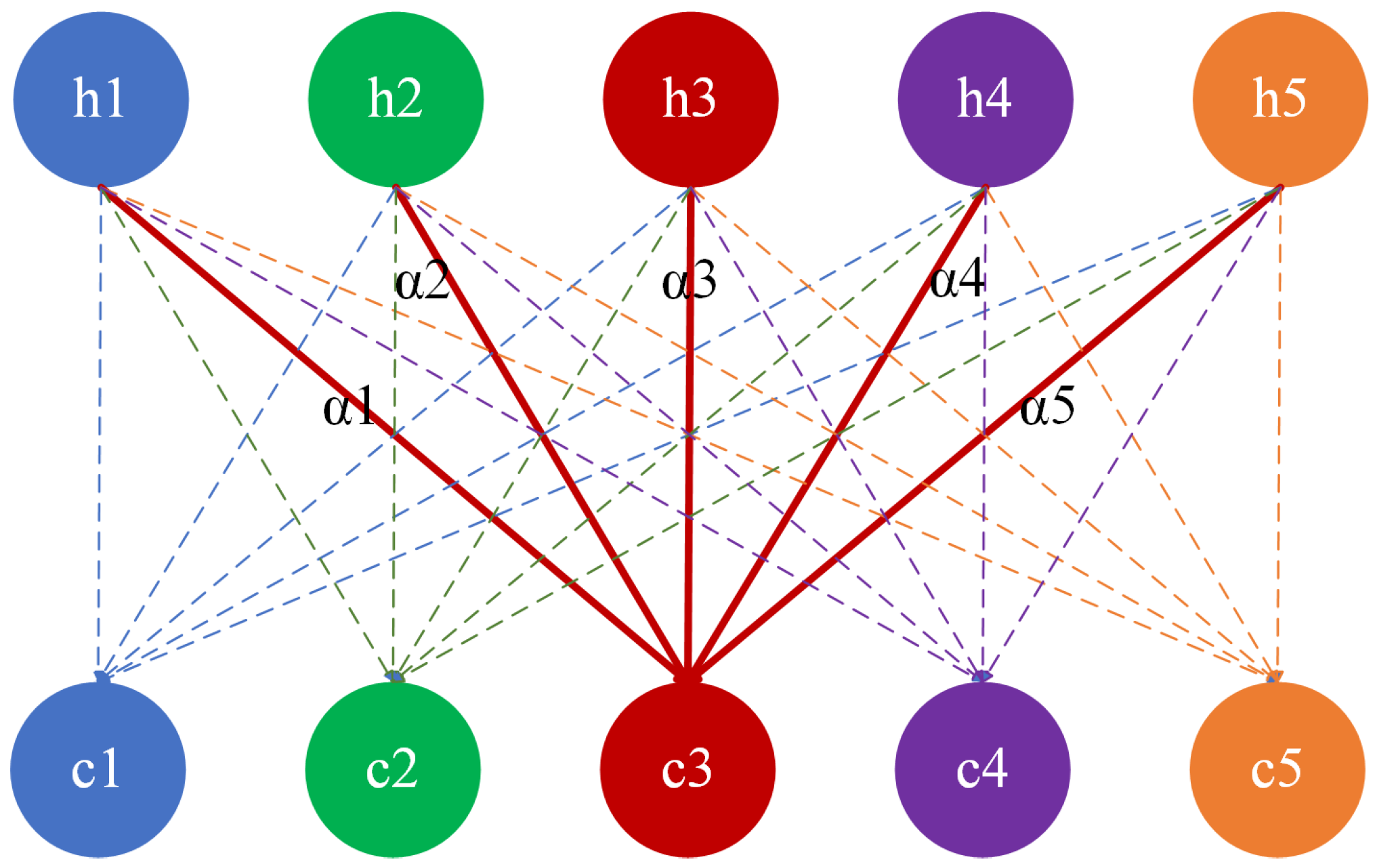
- AM Layer: The attention layer highlights key temporal dependencies, allowing the model to focus on informative parts of the sequence.
- (5)
- Activation Function Optimization: Optimized activation functions are applied throughout the network to improve nonlinearity, generalization, and robustness.
- (6)
- Dense Output Layer: High-level features are mapped to prediction outputs via the final Dense layer.
3.1.1. Convolutional Neural Network (CNN)
3.1.2. Bidirectional Long Short-Term Memory (BiLSTM)
3.1.3. Attention Mechanism (AM)
3.2. Composite Triple Activation Function (CTAF)
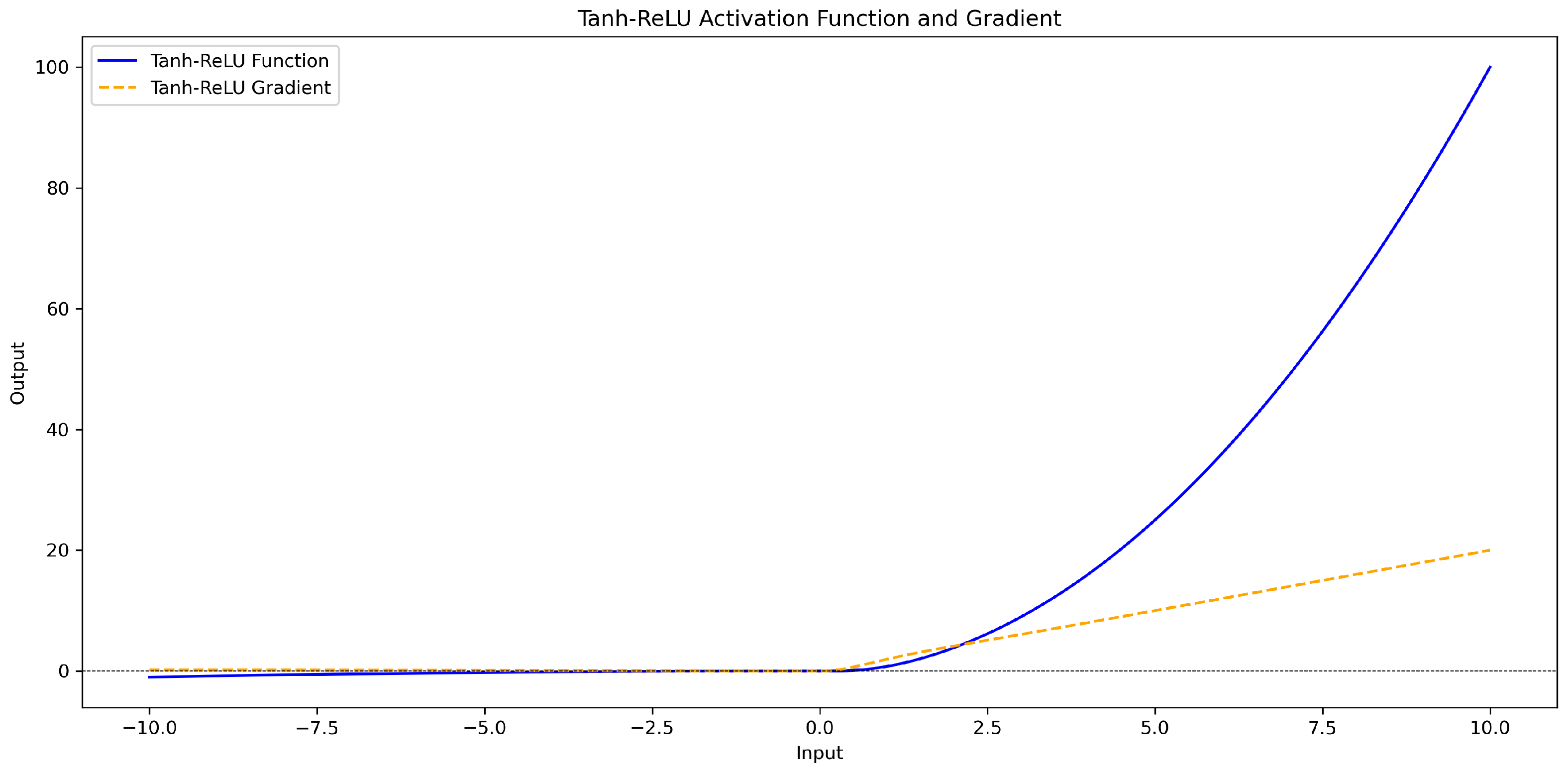
3.2.1. Tanh_Relu Activation Function
3.2.2. Tanh_Sig Activation Function
3.2.3. Relu_Sig Activation Function
4. Experiment
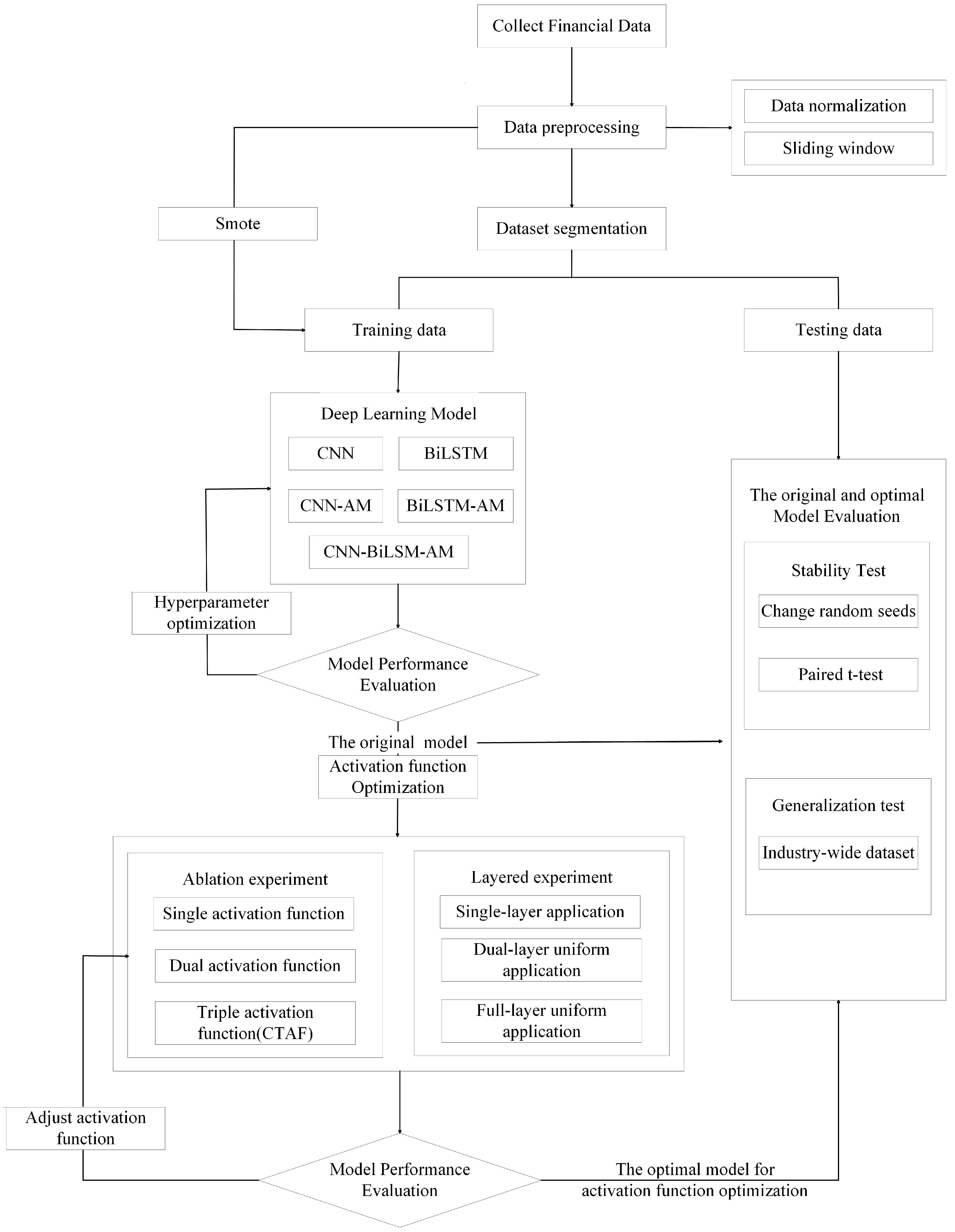
4.1. Overview of Experimental Process
- (1)
- Data Preprocessing: Financial indicator data were collected and preprocessed through normalization and a sliding window approach to convert the raw time series data into structured input samples. We then split the dataset into training and testing sets. To address the class imbalance in the training set, we employed the SMOTE (Synthetic Minority Oversampling Technique), generating synthetic samples for the minority class to ensure balanced training.
- (2)
- Model Construction and Comparison: Multiple deep learning models, including a CNN, BiLSTM, CNN-AM, BiLSTM-AM, and CNN-BiLSTM-AM, were constructed using the training data. These models were evaluated under the same experimental conditions to compare their performance. We conducted hyperparameter optimization to identify the best-performing model architecture.
- (3)
- Activation Function Optimization: CNN-BiLSTM-AM, which was determined to be the optimal structure, was further enhanced through the optimization of the activation function. In this process, we systematically explored different activation function configurations, including single, double, and composite triple activation functions (CTAFs), to evaluate their impact on model performance. In addition, the CTAFs and current activation functions were applied to different layers, such as single-layer, double-layer uniform, and full-layer uniform applications, to examine the influence of layer-by-layer activation distribution. We evaluated the models under each configuration and determined the most effective activation function strategy to improve the model’s nonlinear learning ability.
- (4)
- Stability and Generalization Evaluation: To verify the stability of the optimized model, we conducted additional testing under various conditions. Statistical tests, such as paired t-tests, confirmed the significance of the performance improvements. Additionally, to assess the optimized model’s generalizability, it was tested on a broader industry-wide dataset without industry-specific segmentation.
4.2. Sample Selection
- (1)
- ST companies, which were initially designated as “Special Treatment” (ST) due to abnormal financial conditions, such as two consecutive years of losses.
- (2)
- Non-ST companies, which remained financially stable and were not marked for ST designation during the observation period. To ensure comparability between the two groups, non-ST companies were selected from the same industry and year as the ST companies, with comparable asset scales (within ±20%) and no ST designation in that year.
4.3. Indicator Selection
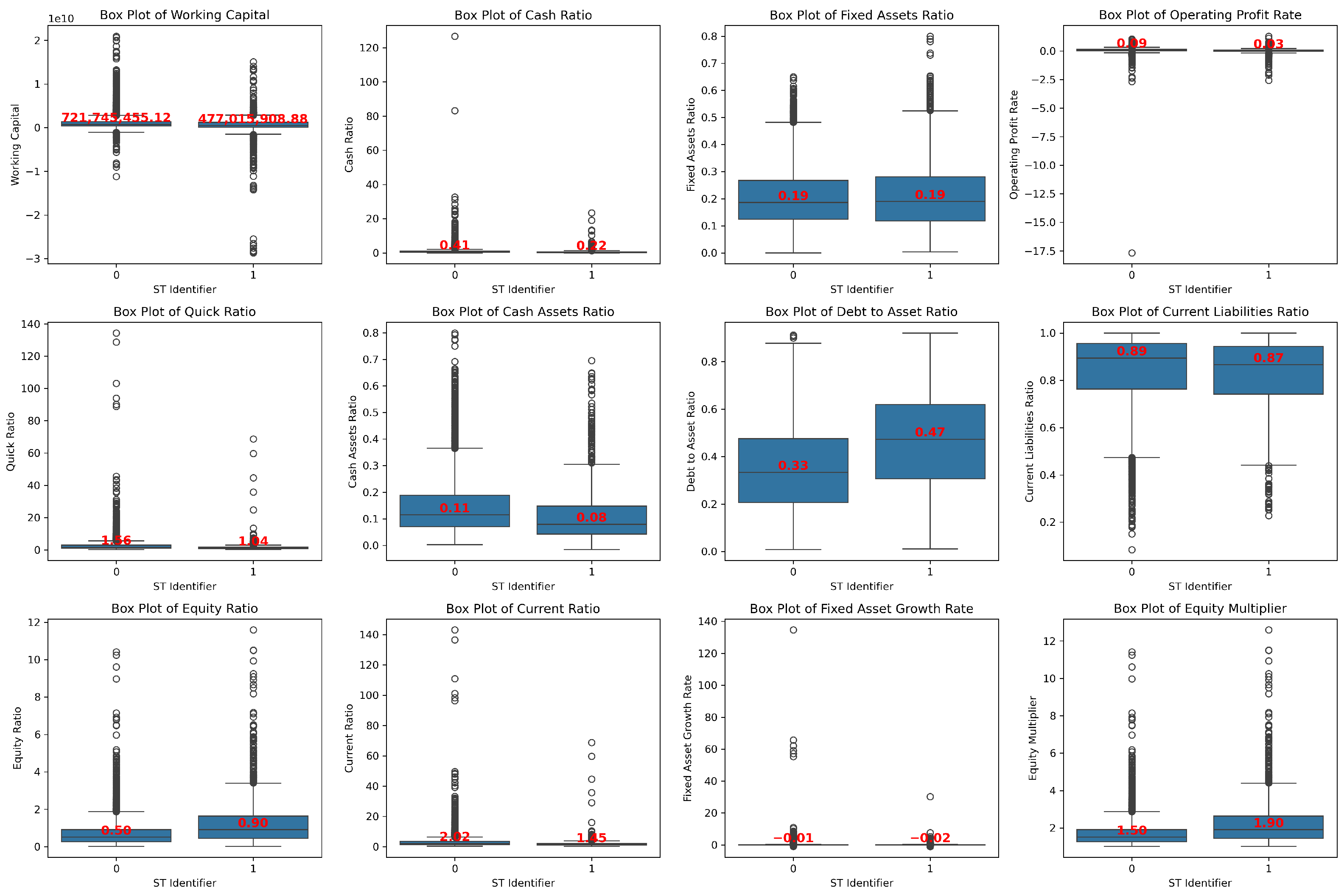
- (1)
- Debt-paying ability, including current ratio, quick ratio, cash ratio, working capital, debt-to-asset ratio, equity multiplier, and equity ratio;
- (2)
- Ratio structure, including current assets ratio, cash assets ratio, working capital ratio, non-current assets ratio, current liabilities ratio, fixed assets ratio, and operating profit margin;
- (3)
- Operating ability, including accounts receivable turnover, inventory turnover, accounts payable turnover, current asset turnover, fixed asset turnover, and total asset turnover;
- (4)
- Profitability, including return on assets, net profit margin on total assets, net profit margin on current assets, net profit margin on fixed assets, return on equity, and operating profit rate;
- (5)
- Cash flow ability, including the operating index;
- (6)
- Development ability, including capital preservation and appreciation rate, fixed asset growth rate, revenue growth rate, sustainable growth rate, and owners’ equity growth rate;
- (7)
- Per share, including earnings per share and earnings before interest and taxes per share.
4.4. Data Preprocessing
4.4.1. Sliding Window
4.4.2. SMOTE Oversampling
5. Results
5.1. Model Construction and Comparison
5.1.1. Prediction Results of Different Models at Different Time Steps
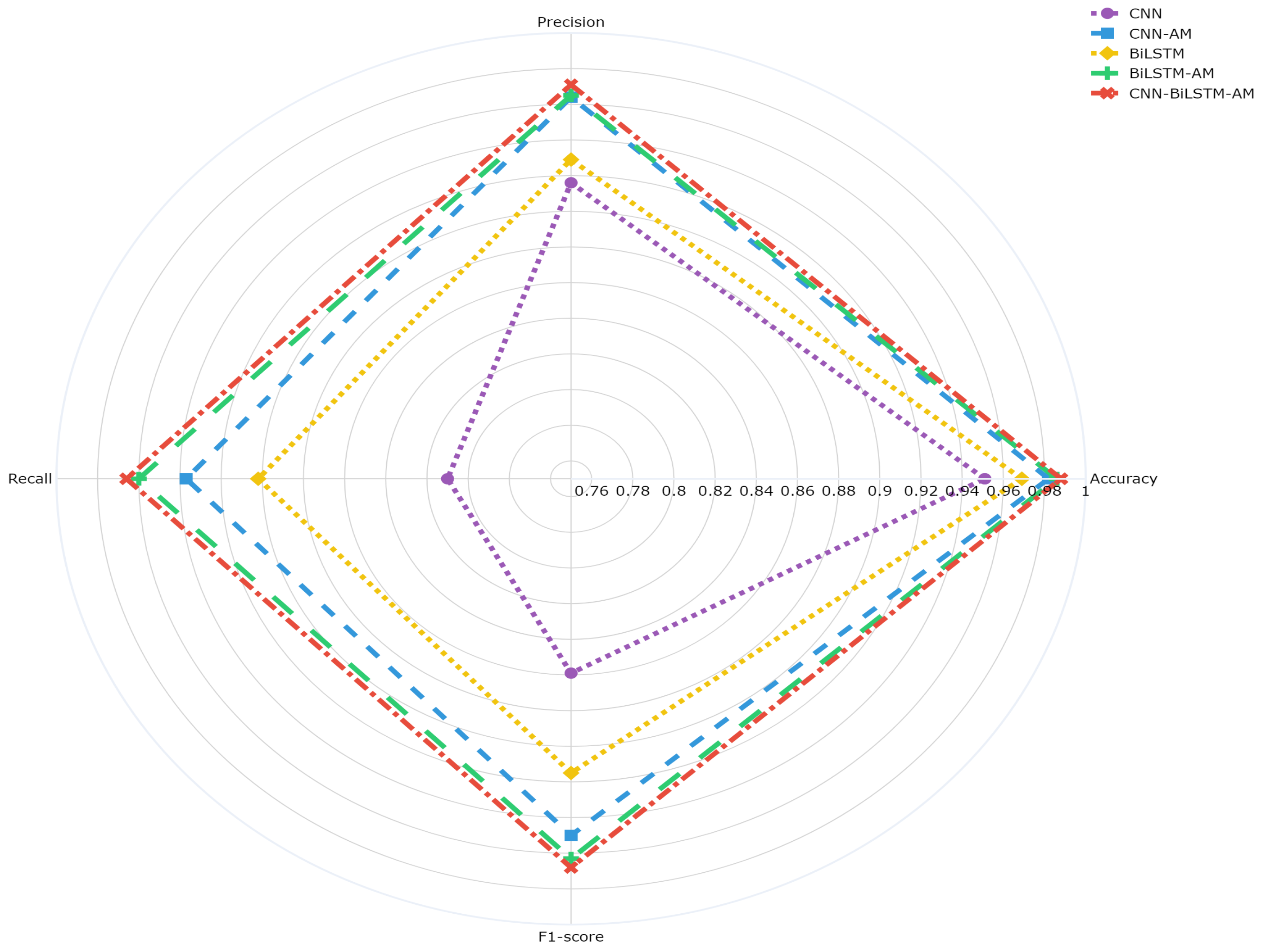
5.1.2. Comparison of Different Model Results at w = 8
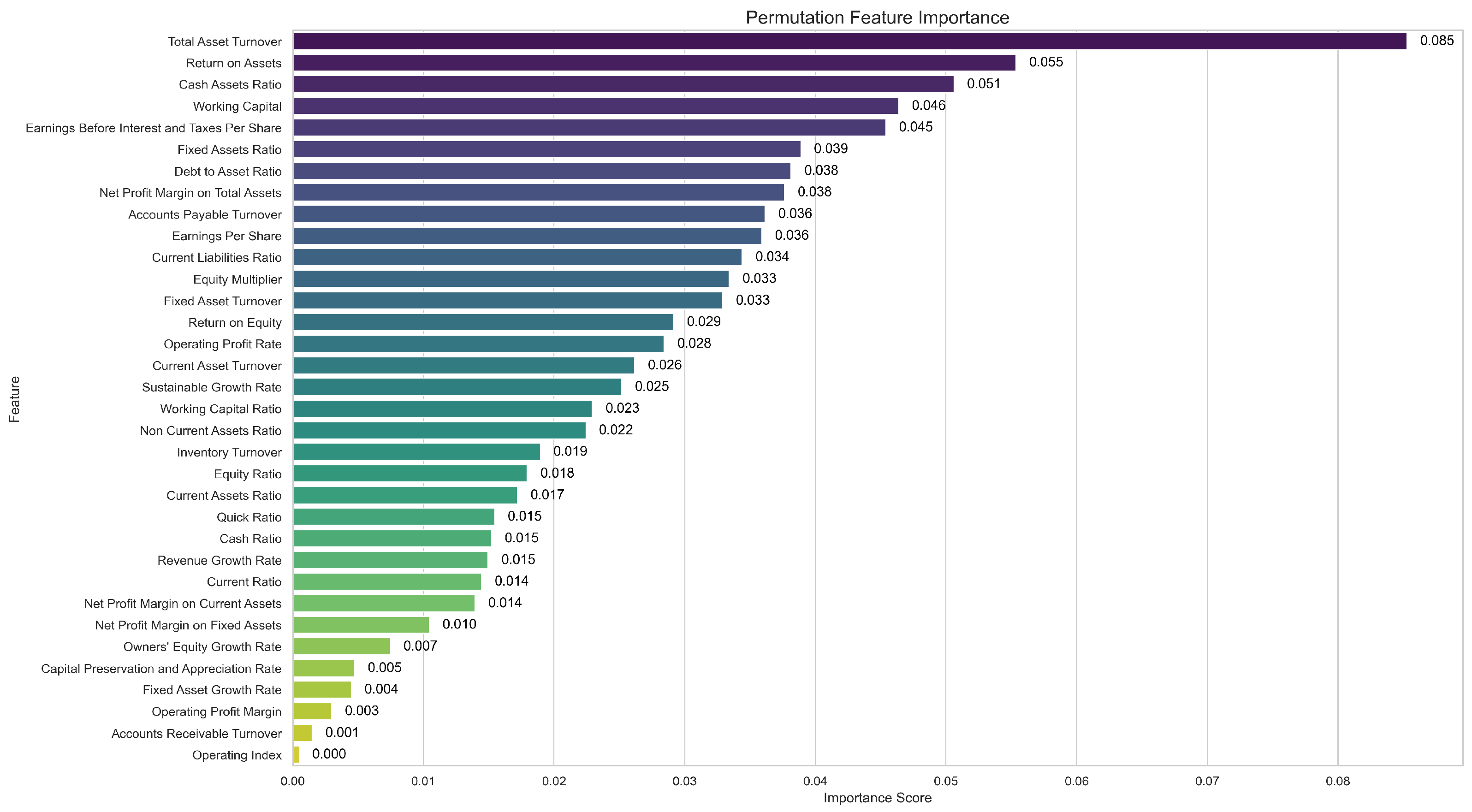
5.1.3. Feature Importance Analysis of the CNN-BiLSTM-AM Model
5.2. Comparison of CNN-BiLSTM-AM Results Under Different Activation Functions
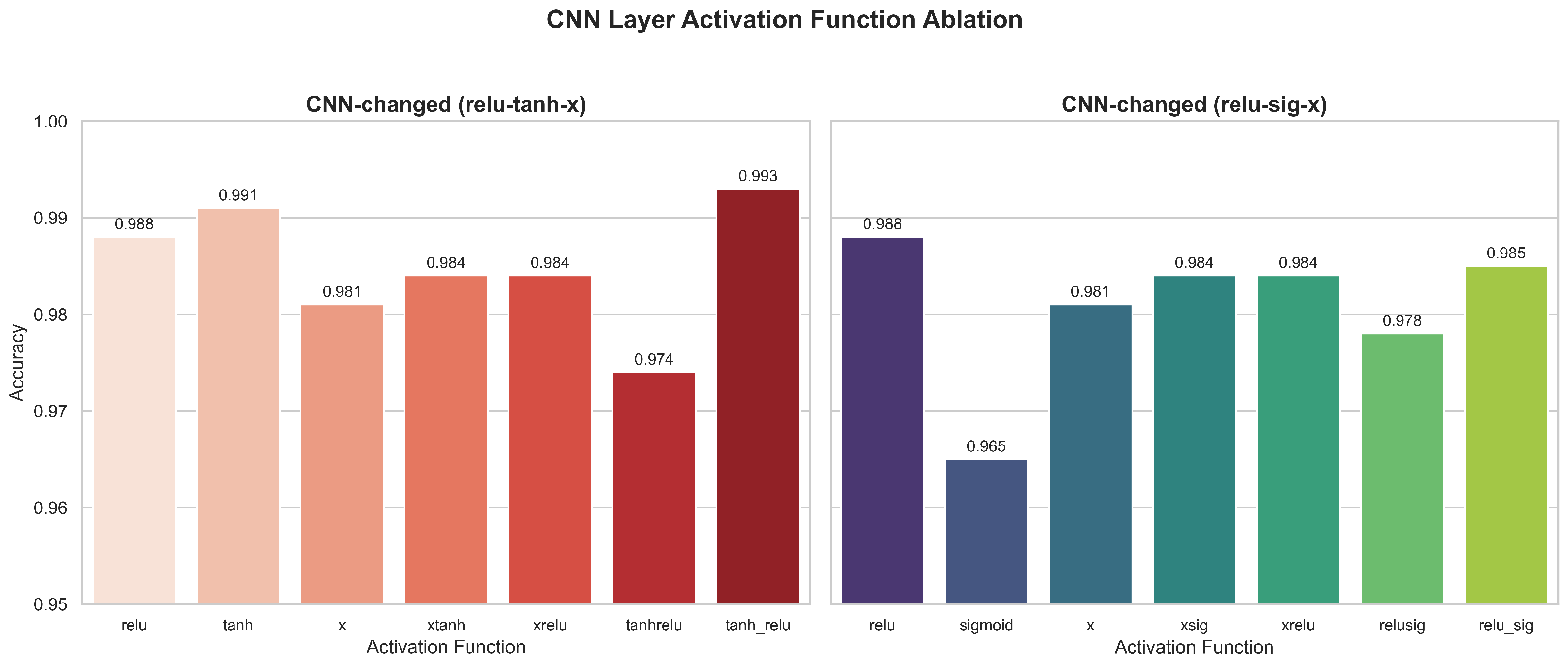
5.2.1. Ablation Experiment Results
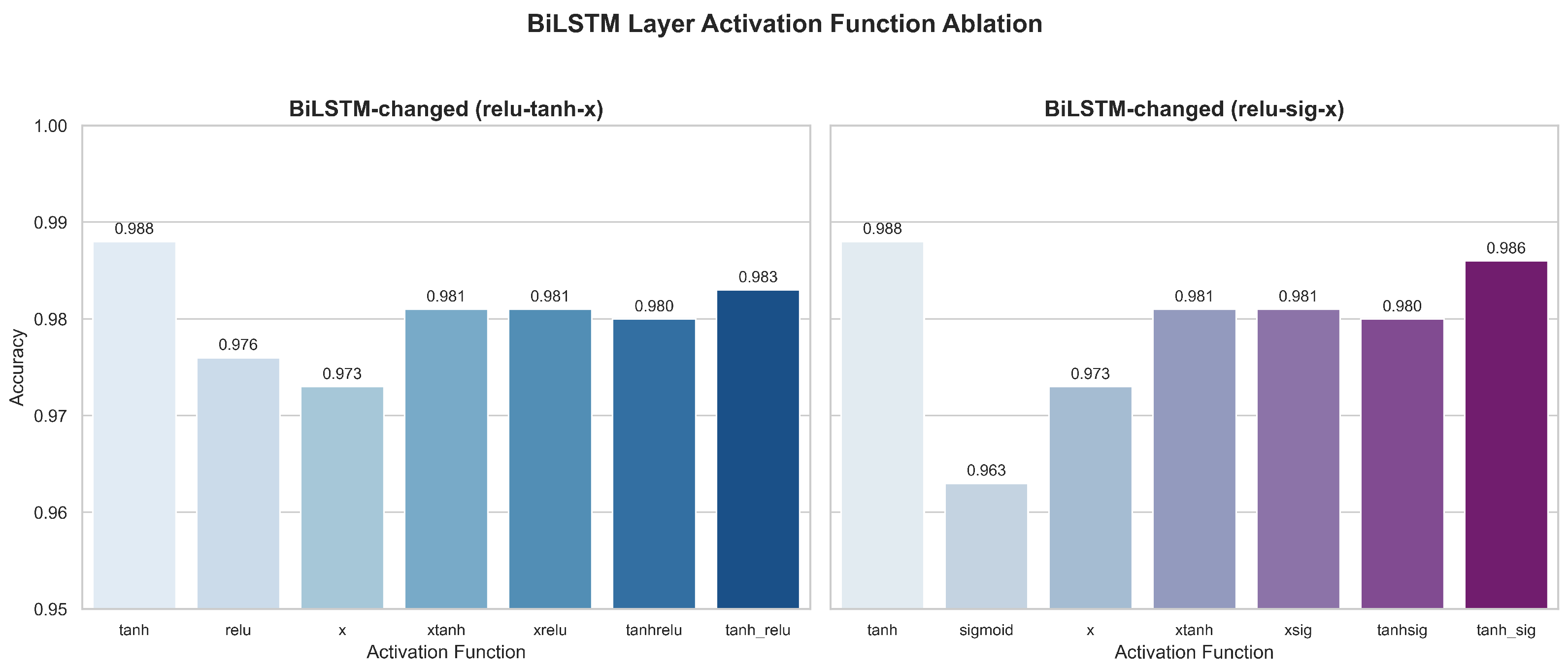
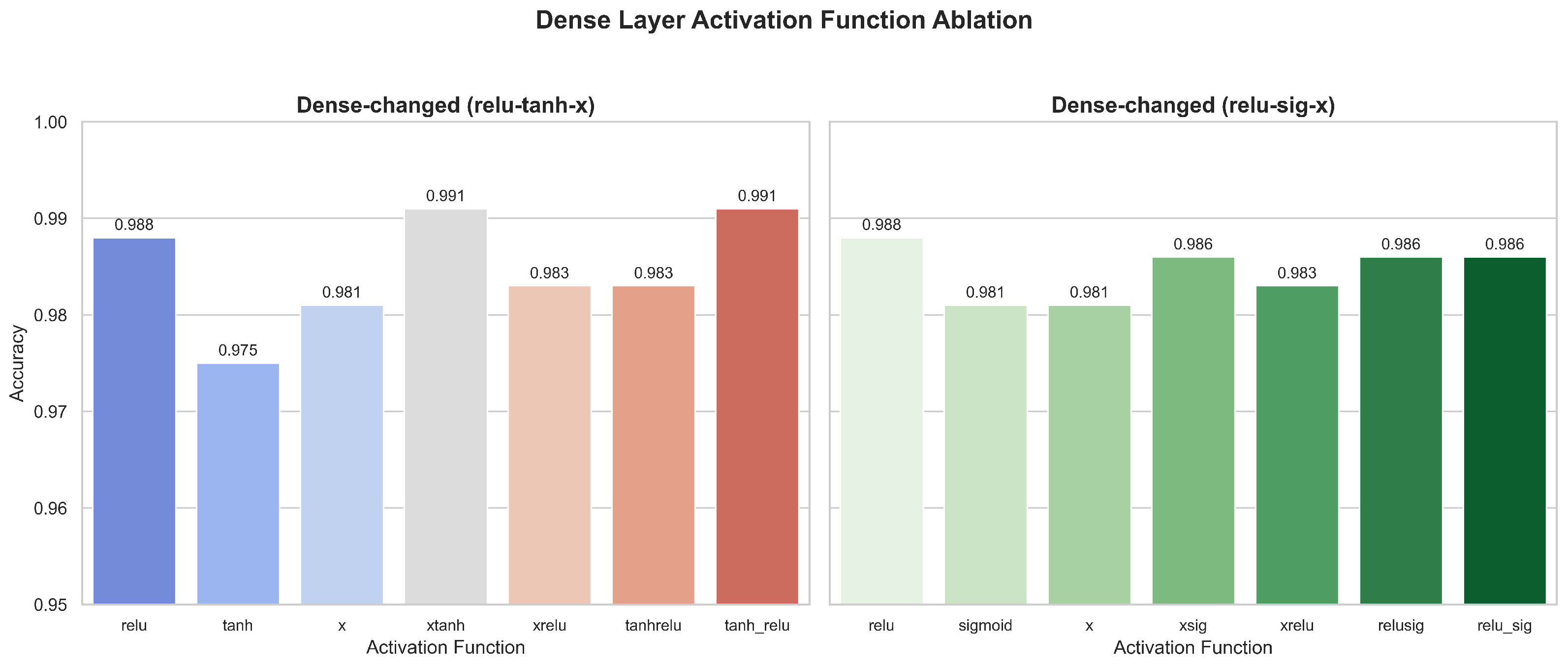
5.2.2. Layered Experiment Results
- (1)
- Activation Strategies in the BiLSTM LayerTwo fine-grained strategies adapted specifically for the BiLSTM layer were used to further investigate how activation functions influence sequence modeling:
- (i)
- Direct replacement of the BiLSTM main activation function: The default main activation function (usually tanh) in the BiLSTM layer is modified, and its impact on sequence feature extraction and overall model performance is observed.
- (ii)
- Post-processing activation via Lambda layer: After the BiLSTM layer output its results, the model applies the activation function through a Lambda layer while keeping the BiLSTM layer’s default activation function unchanged. Then, it adds a Lambda layer after its output and performs further nonlinear transformations on the output (applying activation functions) to achieve finer control.
- (2)
- Activation Function Deployment Strategies Across Network Layers
- (i)
- Single-layer application: A specific activation function is applied to only one single layer, keeping the other layers unchanged. This isolates the influence of each activation function within a single network component.
- (ii)
- Dual-layer uniform application: The same activation function is applied to both the CNN and flattened Dense layers while varying the activation function in the BiLSTM or BiLSTM-Lambda layer. This setup allows for an evaluation of how the recurrent layer interacts with fixed nonlinear transformations in the non-recurrent layers and how this affects overall model performance.
- (iii)
- Full-layer uniform application: The same activation function is uniformly applied across all key layers. This strategy allows for an evaluation of the global effect of consistent nonlinearity throughout the network hierarchy.
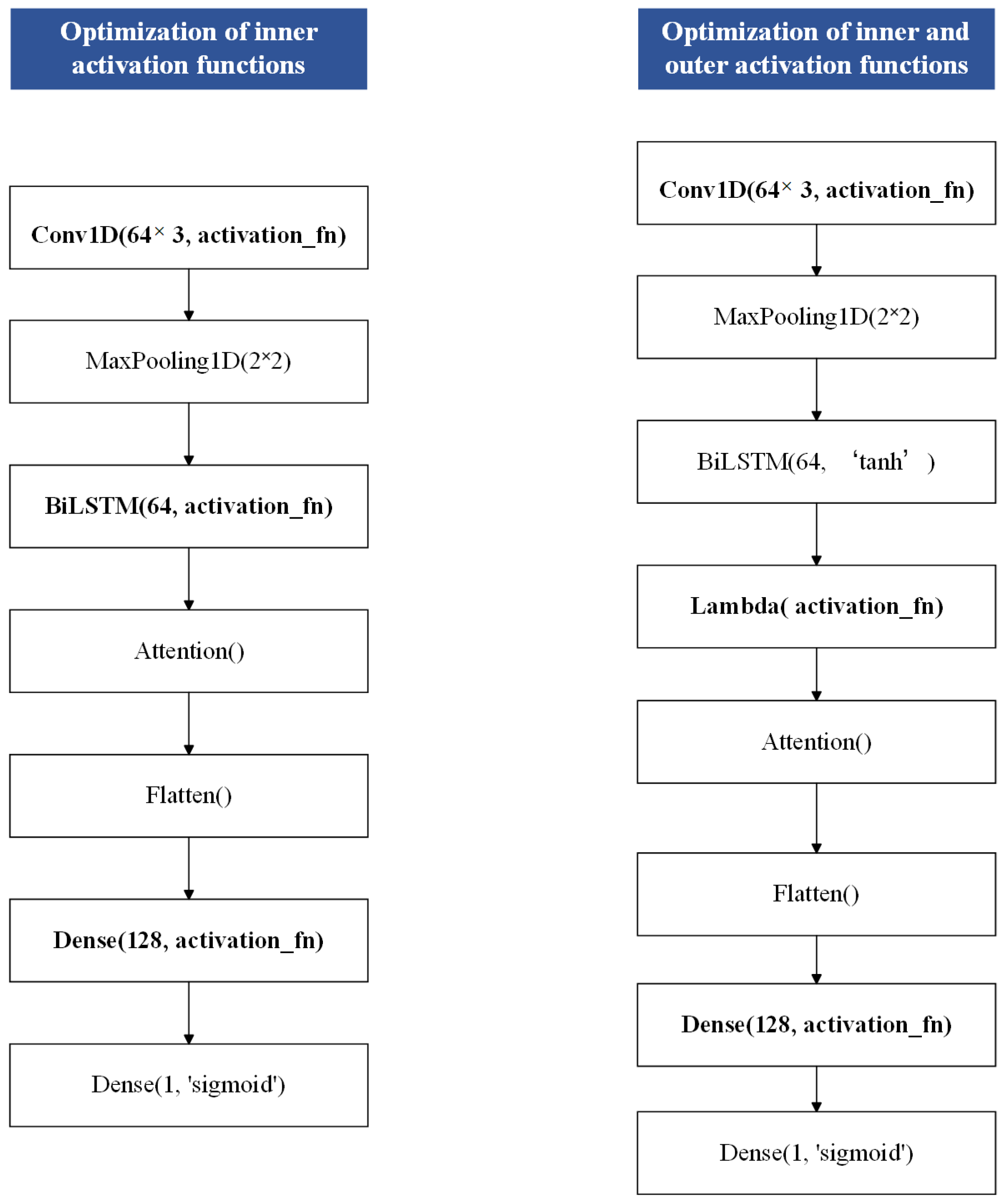
5.3. Performance of CNN-BiLSTM-AM Model with CTAF
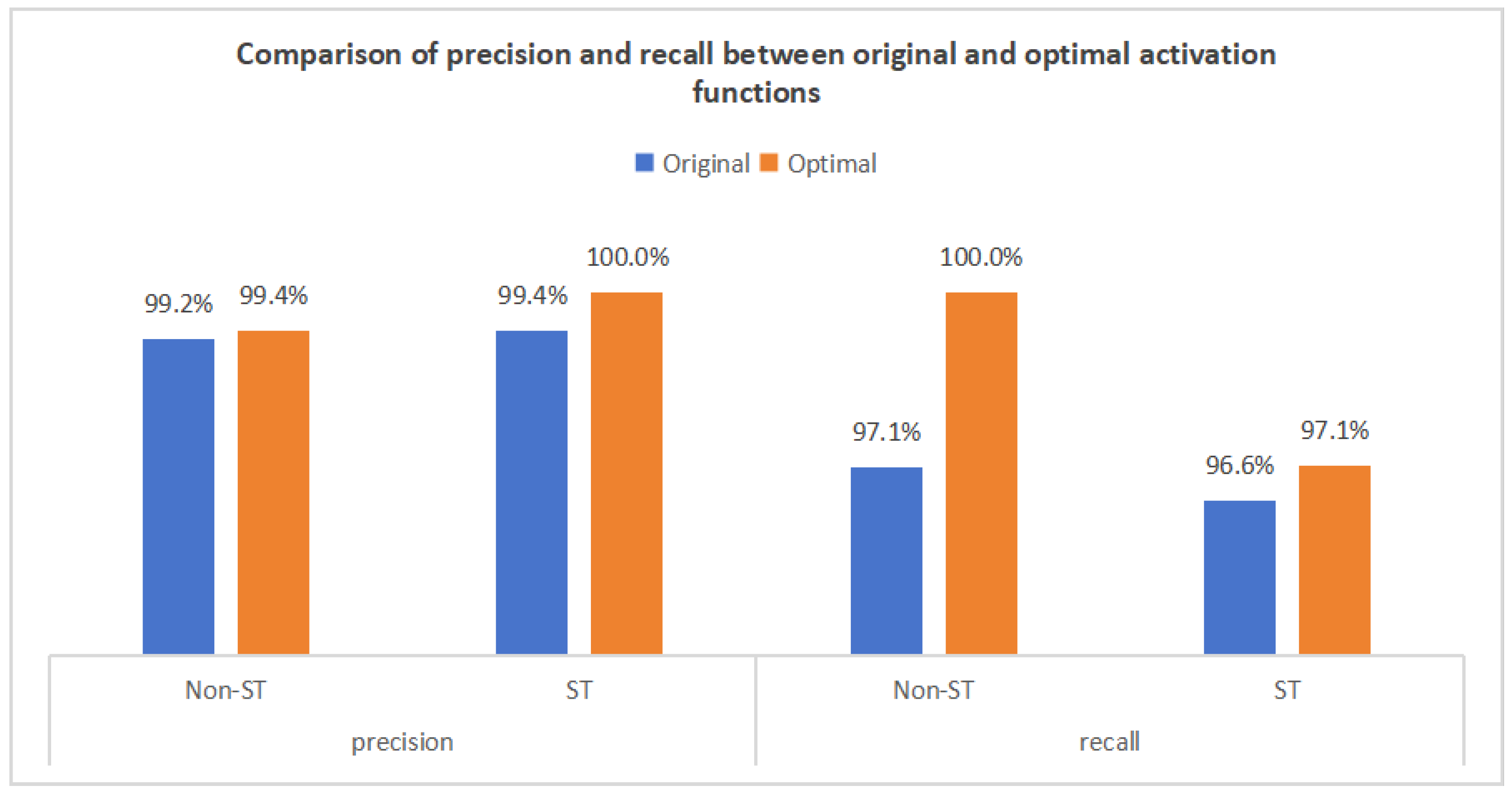
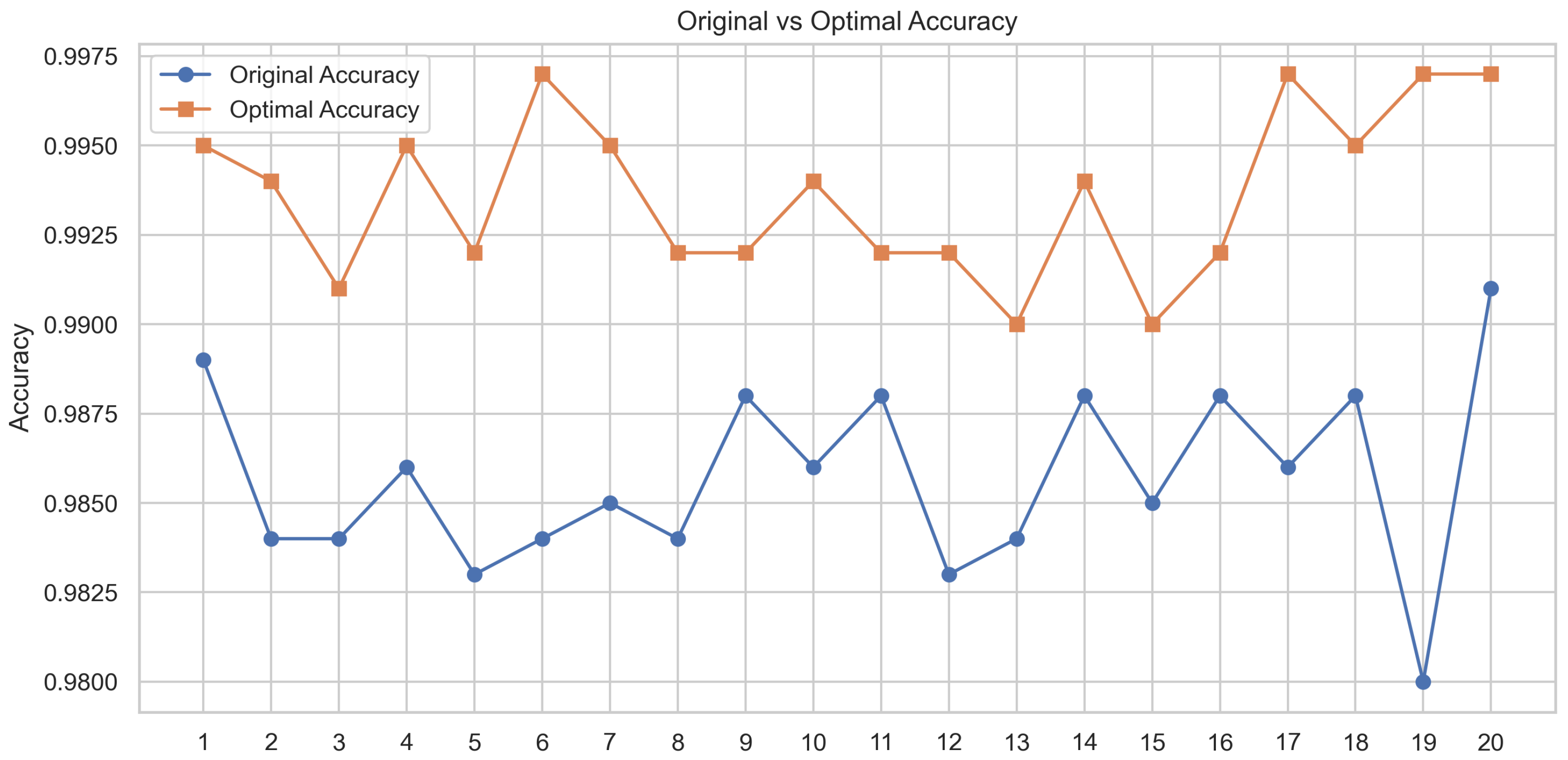
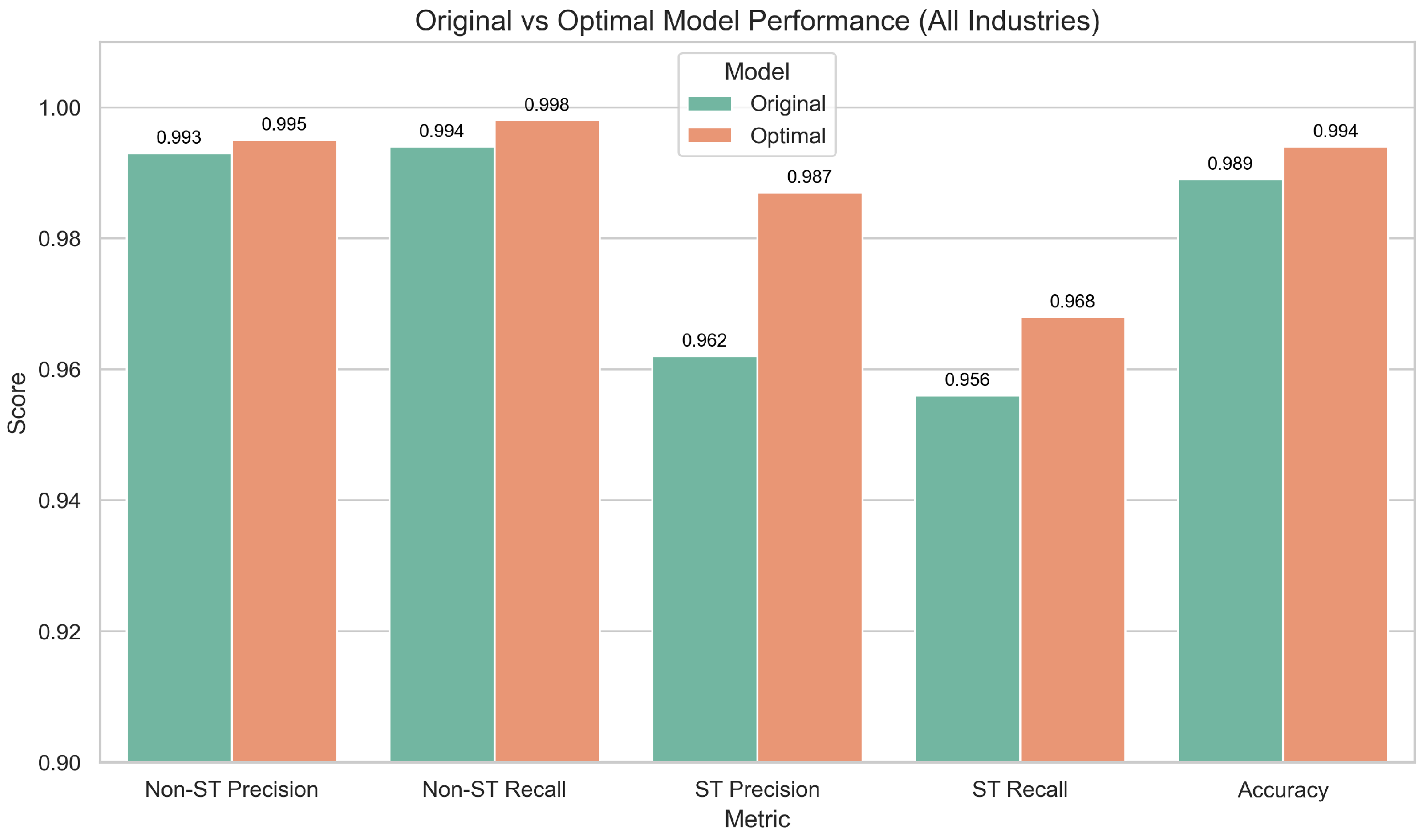
5.3.1. Comparison of Performance of the Original and Optimal Models
- (1)
- Non-ST Company Recall: Increased from 97.1% to 100%, correctly identifying all 772 non-ST companies without omission, demonstrating improved recognition of majority-class samples.
- (2)
- ST Company Accuracy: Improved from 99.4% to 100%, indicating no false positives among the 169 predicted ST companies.
- (3)
- ST Company Recall: Increased from 96.6% to 97.1%, reducing missed ST identifications from six to five among 174 true ST samples.
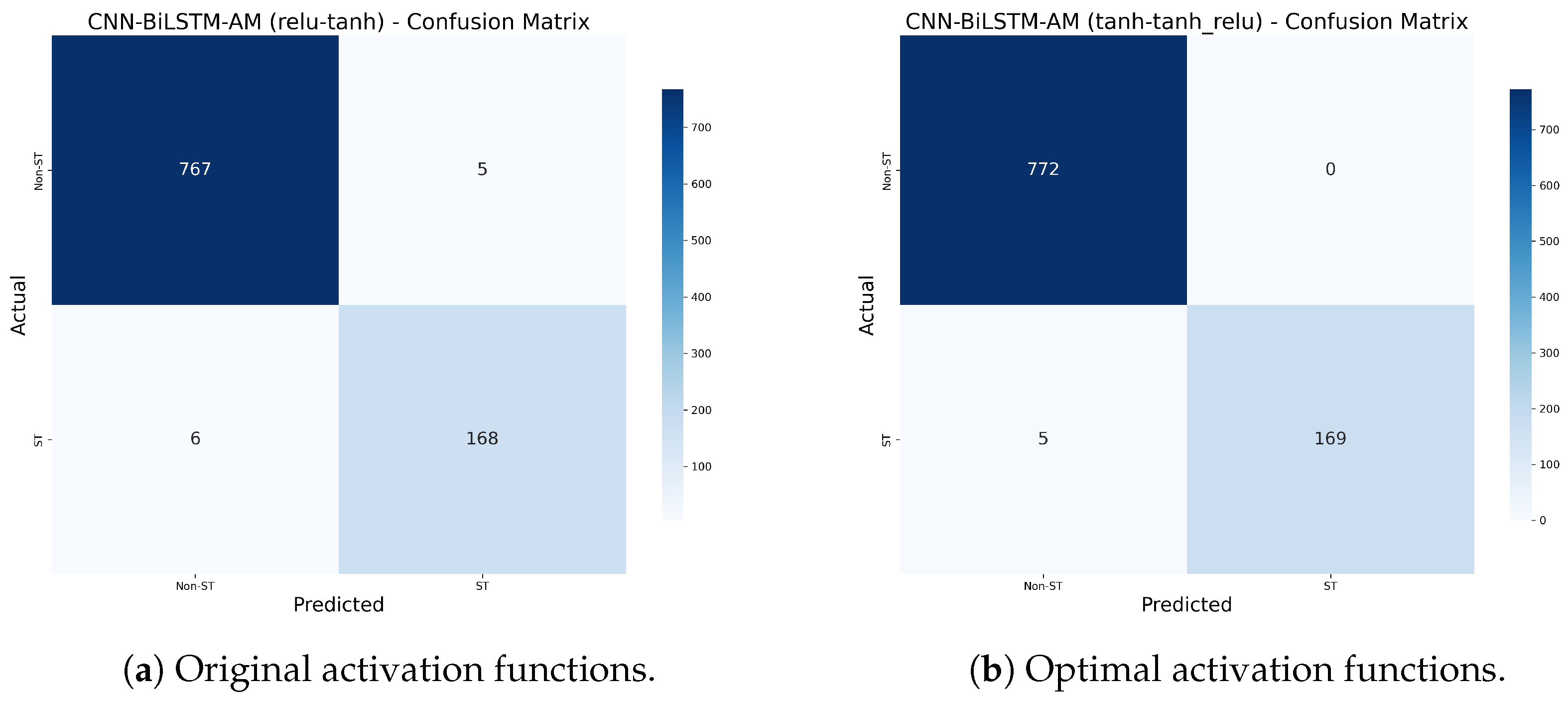
5.3.2. Stability Test Between the Original and Optimal Models
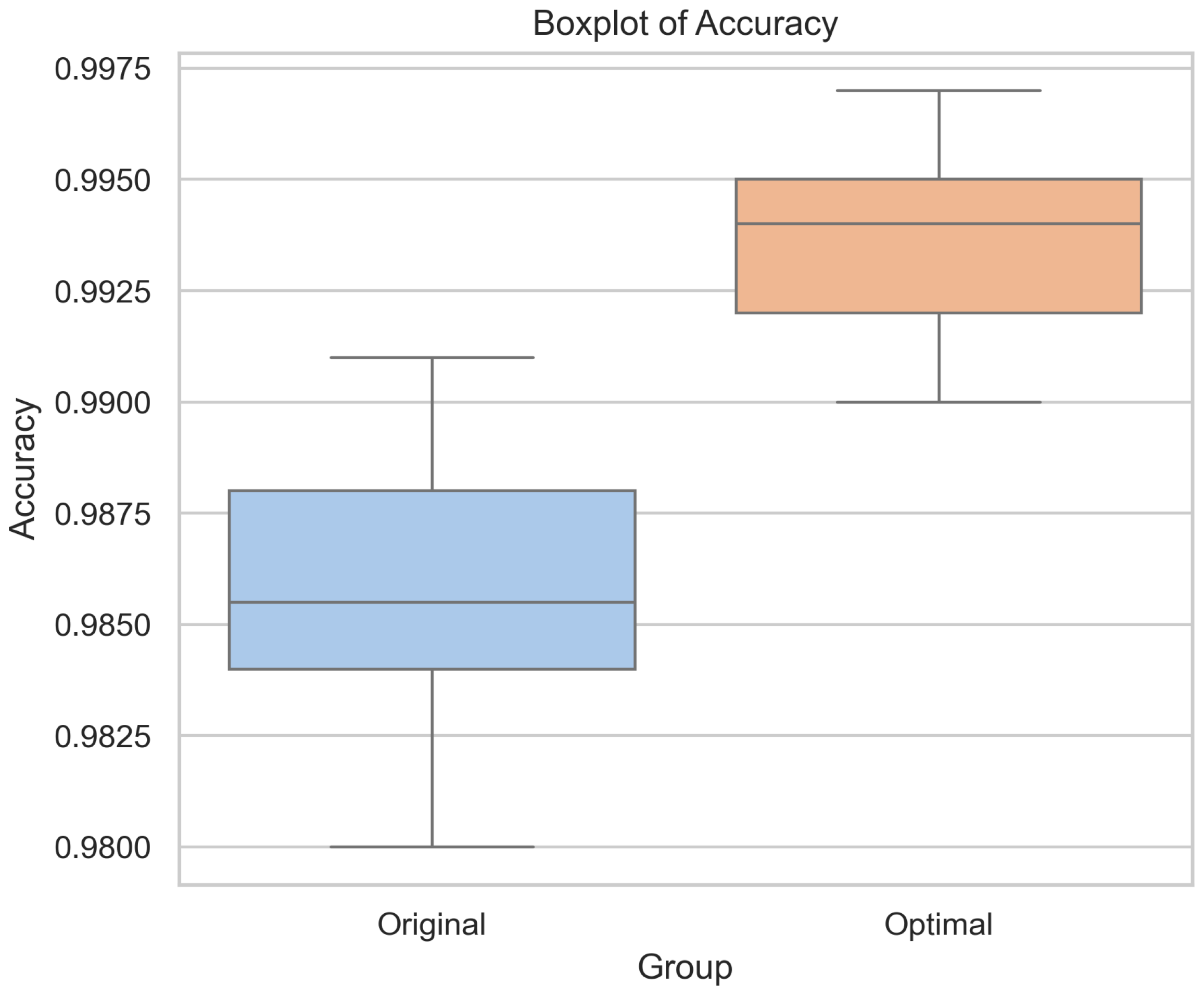
5.3.3. Generalization Test Between the Original and Optimal Models
5.4. Summary of Results
- (1)
- Model construction and comparison: When the time step is w = 8, CNN-BiLSTM-AM achieves the best performance (0.988), outperforming the other models.
- (2)
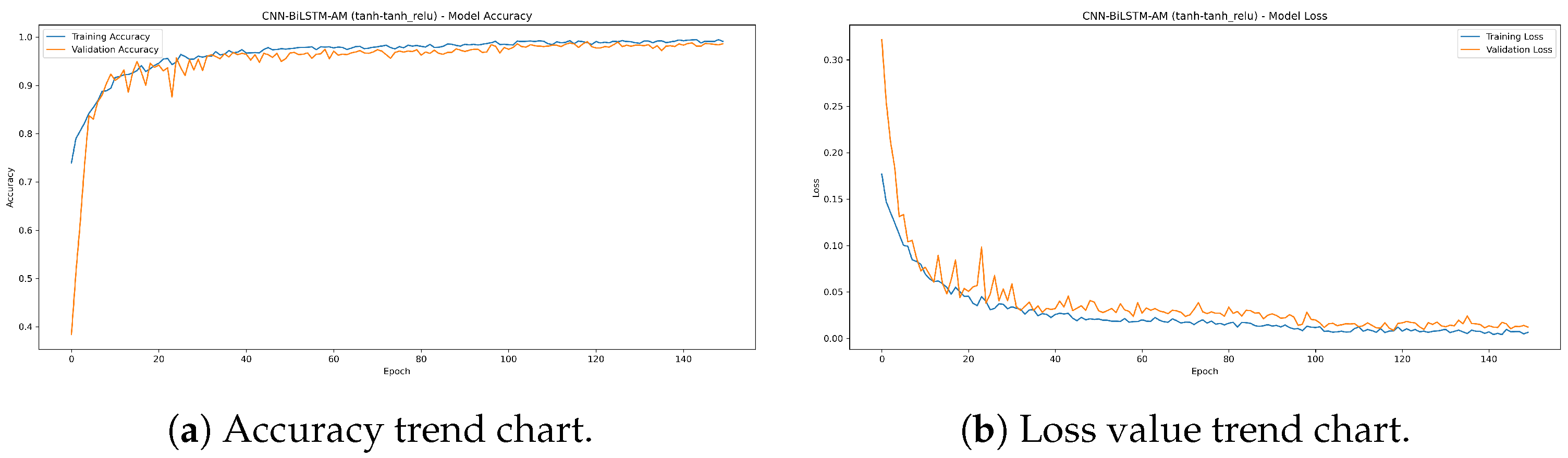
- Comparison of CNN-BiLSTM-AM results under different activation functions: In the ablation and layered experiments, the CTAF shows the best application effect in the single-layer CNN, Dense layer, and Lambda layer, with corresponding model accuracies of 0.993, 0.991, and 0.993, respectively. However, in the BiLSTM layer, the performance of the CTAF is poor, and the original tanh activation function performs better. When the CNN, BiLSTM, and Dense layers use tanh and the CTAF (tanh_relu) is applied in the Lambda layer after BiLSTM, the model’s accuracy reaches its highest level (0.995). However, the model performance decreases when the CTAF is applied to all layers.
- (3)
- Performance of CNN-BiLSTM-AM model with the CATF: The paired t-test and industry-wide data expansion experiment verify that the optimal model consistently outperforms the original model.
6. Conclusions
6.1. Research Conclusions
- (1)
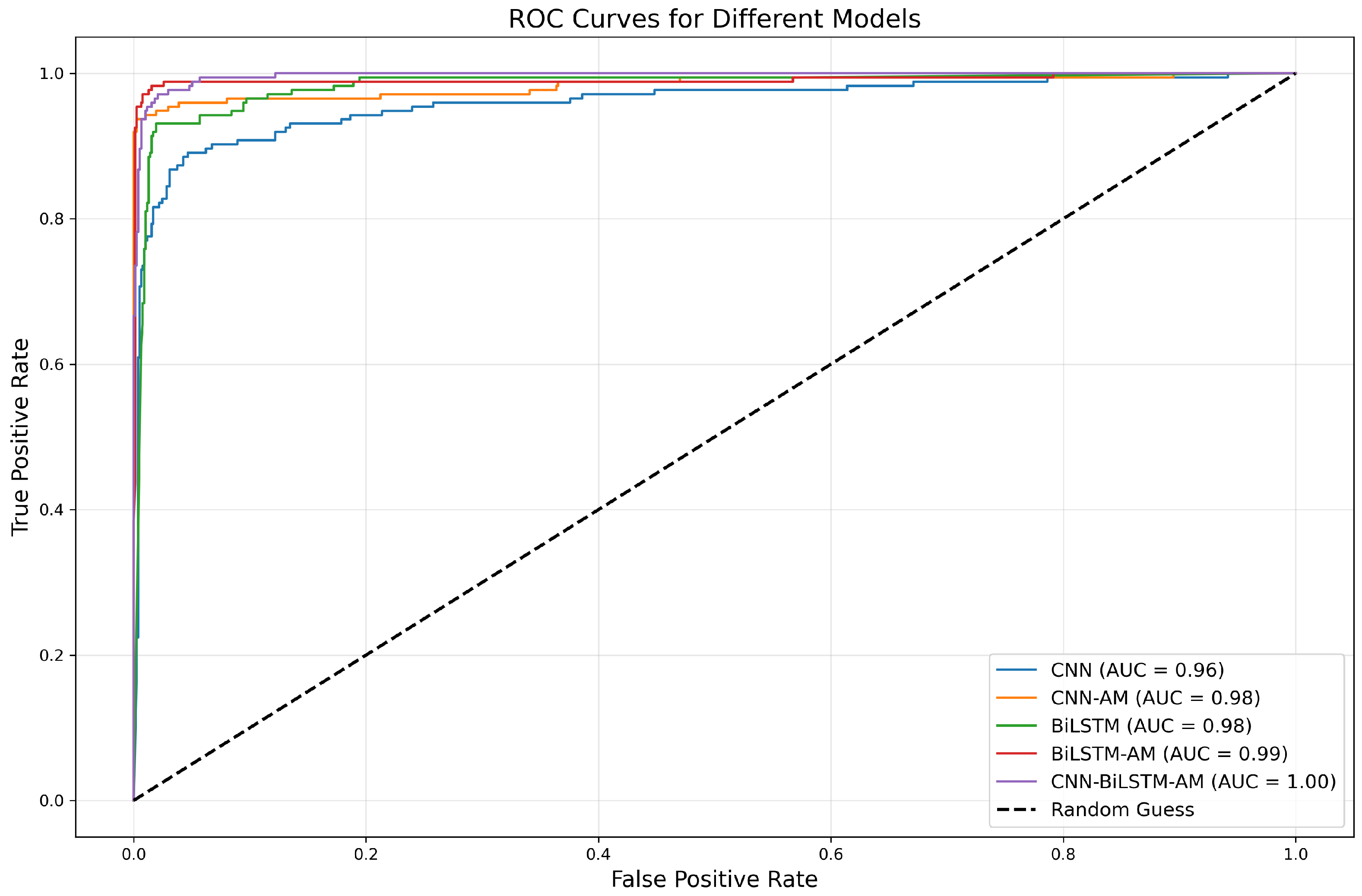
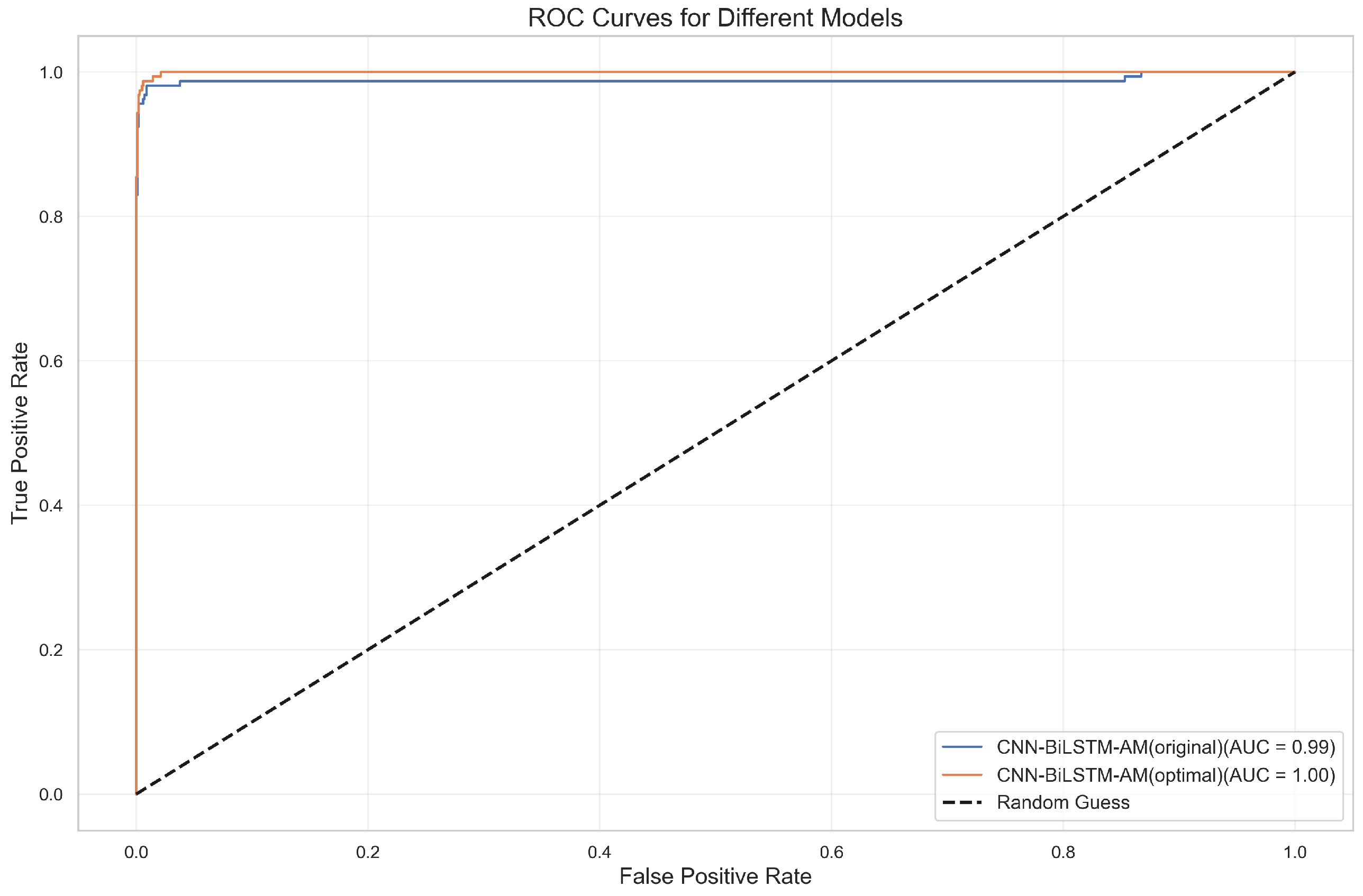
- The comprehensive advantages of the CNN-BiLSTM-AM model: Under the default activation function configuration, the predictive performance of the CNN-BiLSTM-AM model is superior to that of single or partial combination models such as CNNs, CNN-AM, BiLSTM, and BiLSTM AM, with an optimal accuracy (98.8%) and AUC value (1.00). This indicates that the model effectively combines the local feature extraction ability of the CNN, the temporal modeling ability of BiLSTM, and the feature selection ability of the attention mechanism, demonstrating excellent prediction performance.
- (2)
- The effectiveness of the attention mechanism: Introducing an attention mechanism significantly enhances the model’s ability to select key features. A comparative analysis shows that models with attention mechanisms, such as CNN-AM and BiLSTM-AM, perform significantly better in terms of accuracy and AUC values than models without attention mechanisms, further confirming the important role of attention mechanisms in modeling complex temporal data.
- (3)
- The identification of key financial indicators: Using permutation importance, it is found that the CNN-BiLSTM-AM model relies mostly on key financial indicators such as total asset turnover, return on assets, cash assets ratio, working capital, and earnings before interest and taxes per share, as permuting these indicators causes the most significant drop in performance.
- (4)
- Layer-wise ablation validates the superiority of the CTAF: Through structured ablation and comparative experiments involving single activation functions (e.g., relu and tanh), dual combinations (e.g., tanhrelu), and composite triple activation functions (CTAFs, e.g., tanh_relu), the proposed CTAF demonstrates clear performance advantages. Particularly in the CNN and Dense layers, the CTAF (tanh_relu) consistently achieves the highest accuracy, highlighting its superior nonlinear feature extraction and gradient propagation capabilities. Even in the BiLSTM layer, which is sensitive due to its gating mechanisms, the CTAF maintains competitive stability, confirming its generalizability across different layer types.
- (5)
- Activation functions exhibit heterogeneous performance in different network layers: The experimental results show that composite triple activation functions (CTAFs) are particularly effective in the CNN and Dense layers, where deep feature extraction and nonlinear decision boundaries are essential. In contrast, recurrent layers such as BiLSTM achieve better stability and performance with traditional tanh, benefiting from its balanced gradient flow and temporal memory capabilities. Furthermore, applying CTAFs in a Lambda layer after the BiLSTM output enhances sequential feature representation, revealing that activation efficiency is not only layer specific but also influenced by positional deployment within the architecture.
- (6)
- Significant effect and stability of the CTAF: The optimized model achieves the best performance when using tanh in the CNN and Dense layers and the CTAF tanh_relu in the Lambda layer after the BiLSTM output, increasing the accuracy from 98.8% to 99.5%. Repeated experiments under 20 random seeds confirmed that the improvement is stable and statistically significant (paired t-test), verifying both the effectiveness and robustness of the CTAF.
- (7)
- The CTAF demonstrates robust generalizability across industries: The effectiveness of the proposed composite triple activation function (CTAF) is not limited to the manufacturing sector. When applied to an industry-wide dataset covering a diverse set of ST and non-ST companies, the optimized model maintains superior performance, improving accuracy from 98.9% to 99.4%. The enhanced recognition of ST companies and improved ROC characteristics confirm that the CTAF retains its predictive advantages in broader real-world scenarios.
6.2. Discussion
6.2.1. Discussion of Model and CTAF Validity
6.2.2. Practical Implications and Application of the Model
6.2.3. Research Limitations and Plans
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Term |
| CNN | Convolutional Neural Network |
| BiLSTM | Bidirectional Long Short-Term Memory |
| AM | Attention Mechanism |
| SVM | Support Vector Machine |
| XGBoost | Extreme Gradient Boosting |
| RNN | Recurrent Neural Network |
| ROC | Receiver Operating Characteristic |
| AUC | Area Under the Curve |
| LSTM | Long Short-Term Memory |
| ST | Special Treatment |
| SMOTE | Synthetic Minority Oversampling Technique |
| CTAF | Composite Triple Activation Function |
| ReLU | Rectified Linear Unit Activation Function |
| Tanh | Hyperbolic Tangent Activation Function |
| Sigmoid | Sigmoid Activation Function |
| Swish | Swish Activation Function |
| Mish | Mish Activation Function |
| Leaky ReLU | Leaky Rectified Linear Unit Activation Function |
| LUTanh | Linear Unit Hyperbolic Tangent Activation Function |
| PReLU | Parametric Rectified Linear Unit Activation Function |
| SoftPlus | SoftPlus Activation Function |
| SPReLU | S-Shaped Rectified Linear Unit |
References
- Beaver, W.H. Financial ratios as predictors of failure. J. Account. Res. 1966, 4, 71–111. [Google Scholar]
- Chaiyawat, T.; Samranruen, P. Delisting Risk Analysis: Empirical Evidence from the Thai Listed Companies. Adv. Econ. Bus. 2016, 4, 461–467. [Google Scholar]
- Gottlieb, O.; Salisbury, C.; Shek, H.; Vaidyanathan, V. Detecting Corporate Fraud: An Application of Machine learning; American Institute of Computing: Chicago, IL, USA, 2006; pp. 100–215. [Google Scholar]
- Aydin, N.; Sahin, N.; Deveci, M.; Pamucar, D. Prediction of financial distress of companies with artificial neural networks and decision trees models. Mach. Learn. Appl. 2022, 10, 100432. [Google Scholar]
- Rustam, Z.; Saragih, G.S. Predicting bank financial failures using random forest. In Proceedings of the 2018 International Workshop on Big Data and Information Security (IWBIS), Jakarta, Indonesia, 12–13 May 2018; IEEE: New York, NY, USA, 2018; pp. 81–86. [Google Scholar]
- Yang, H.; Li, E.; Cai, Y.F.; Li, J.; Yuan, G.X. The extraction of early warning features for predicting financial distress based on XGBoost model and SHAP framework. Int. J. Financ. Eng. 2021, 8, 2141004. [Google Scholar] [CrossRef]
- Petrică, A.C.; Stancu, S.; Tindeche, A. Limitation of ARIMA models in financial and monetary economics. Theor. Appl. Econ. 2016, 23, 19–42. [Google Scholar]
- Sekhar, S.C.; Kovvuri, S.B.R.; Vyshnavi, K.S.S.; Uppalapati, S.; Yaswanth, K.; Teja, R.K. Risk Modelling and Prediction of Financial Management in Macro Industries using CNN Based Learning. In Proceedings of the 2023 International Conference on Disruptive Technologies (ICDT), Greater Noida, India, 11–12 May 2023; IEEE: New York, NY, USA, 2023; pp. 297–300. [Google Scholar]
- Tan, Y.; Chen, J.; Sun, J. On financial crisis warning of listed companies based on CNN. J. Southwest China Norm. Univ. (Nat. Sci. Ed.) 2021, 46, 73–80. [Google Scholar]
- Nong, X. Construction and Simulation of Financial Risk Prediction Model Based on LSTM. In Proceedings of the 2022 6th Asian Conference on Artificial Intelligence Technology (ACAIT), Changzhou, China, 9–11 December 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar]
- Wei, Y.; Xu, K.; Yao, J.; Sun, M.; Sun, Y. Financial Risk Analysis Using Integrated Data and Transformer-Based Deep Learning. J. Comput. Sci. Softw. Appl. 2024, 4, 1–8. [Google Scholar]
- Liu, Z.; Liu, X.; Zhou, L. A Hybrid CNN and LSTM Based Model for Financial Crisis Prediction. Teh. Vjesn. 2024, 31, 185–192. [Google Scholar]
- Huang, Y.; Wan, X.; Zhang, L.; Lu, X. A novel deep reinforcement learning framework with BiLSTM-Attention networks for algorithmic trading. Expert Syst. Appl. 2024, 240, 122581. [Google Scholar]
- Su, J.; Liang, J.; Zhu, J.; Li, Y. HCAM-CL: A Novel Method Integrating a Hierarchical Cross-Attention Mechanism with CNN-LSTM for Hierarchical Image Classification. Symmetry 2024, 16, 1231. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Y.; Wang, M. An Attention-Based Logistic-CNN-BiLSTM Hybrid Neural Network for Credit Risk Prediction of Listed Real Estate Enterprises. Expert Syst. 2024, 41, e13299. [Google Scholar]
- Haykin, S.; Network, N. A Comprehensive Foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 30, p. 3. [Google Scholar]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for activation functions. arXiv 2017, arXiv:1710.05941. [Google Scholar]
- Misra, D. Mish: A self-regularized non-monotonic activation function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Wu, T.; Xu, X.; Wu, Y. Research on optimization of SPReLU activation function in convolutional neural network. Comput. Digit. Eng. 2021, 49, 1637–1641. [Google Scholar]
- Shidik, G.F.; Pramunendar, R.A.; Kusuma, E.J.; Saraswati, G.W.; Winarsih, N.A.; Rohman, M.S.; Saputra, F.O.; Naufal, M.; Andono, P.N. LUTanh Activation Function to Optimize BI-LSTM in Earthquake Forecasting. Int. J. Intell. Eng. Syst. 2024, 17, 572–583. [Google Scholar]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar]
- Hochreiter, S. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Bahdanau, D. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Highway networks. arXiv 2015, arXiv:1505.00387. [Google Scholar]
- Jayakumar, S.M.; Czarnecki, W.M.; Menick, J.; Schwarz, J.; Rae, J.; Osindero, S.; Teh, Y.W.; Harley, T.; Pascanu, R. Multiplicative interactions and where to find them. In Proceedings of the International Conference on Learning Representations, Virtual, 26–30 April 2020. [Google Scholar]
- Li, M.; Zhang, Z.; Lu, M.; Jia, X.; Liu, R.; Zhou, X.; Zhang, Y. Internet financial credit risk assessment with sliding window and attention mechanism LSTM model. Teh. Vjesn. 2023, 30, 1–7. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
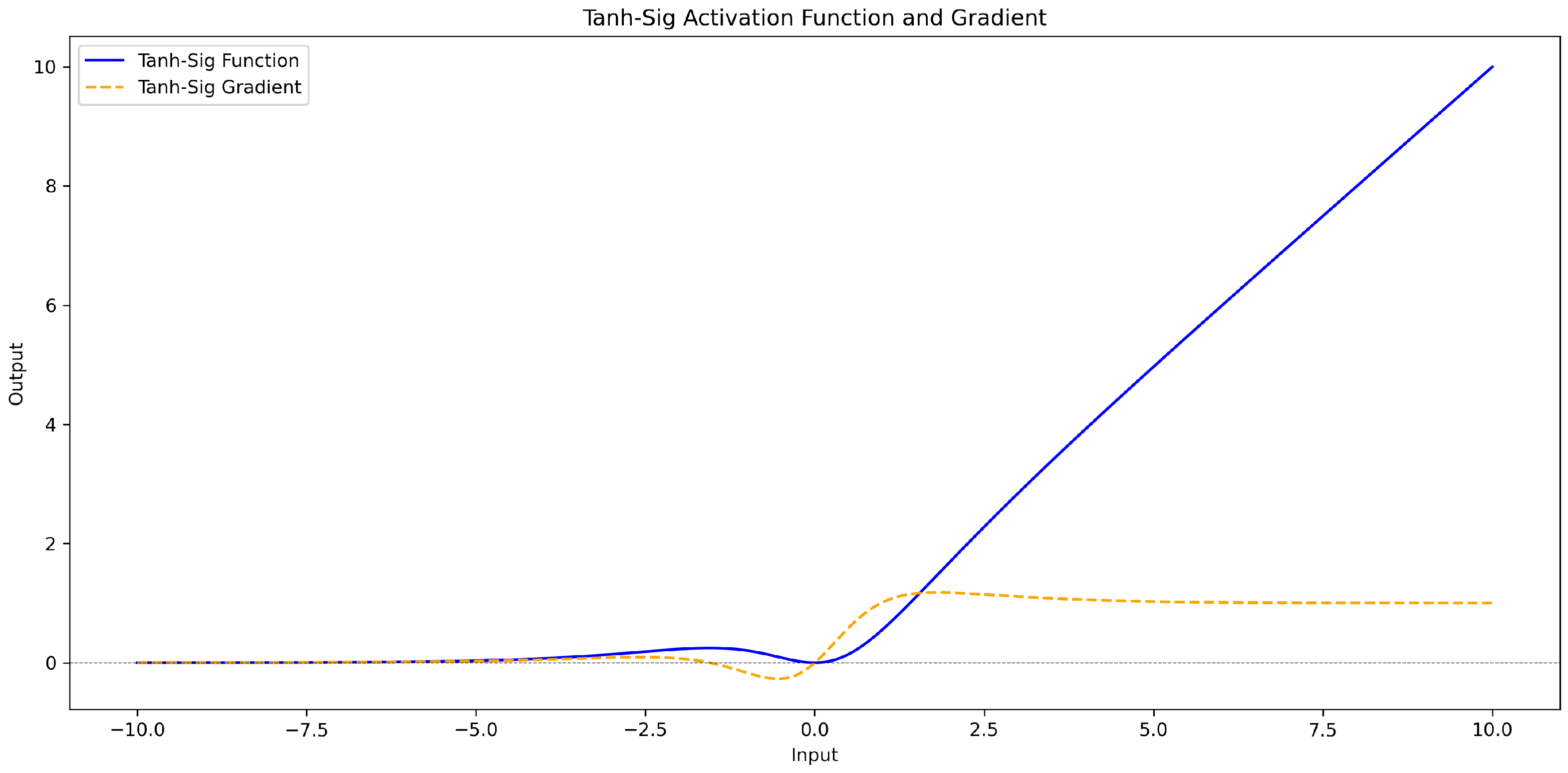
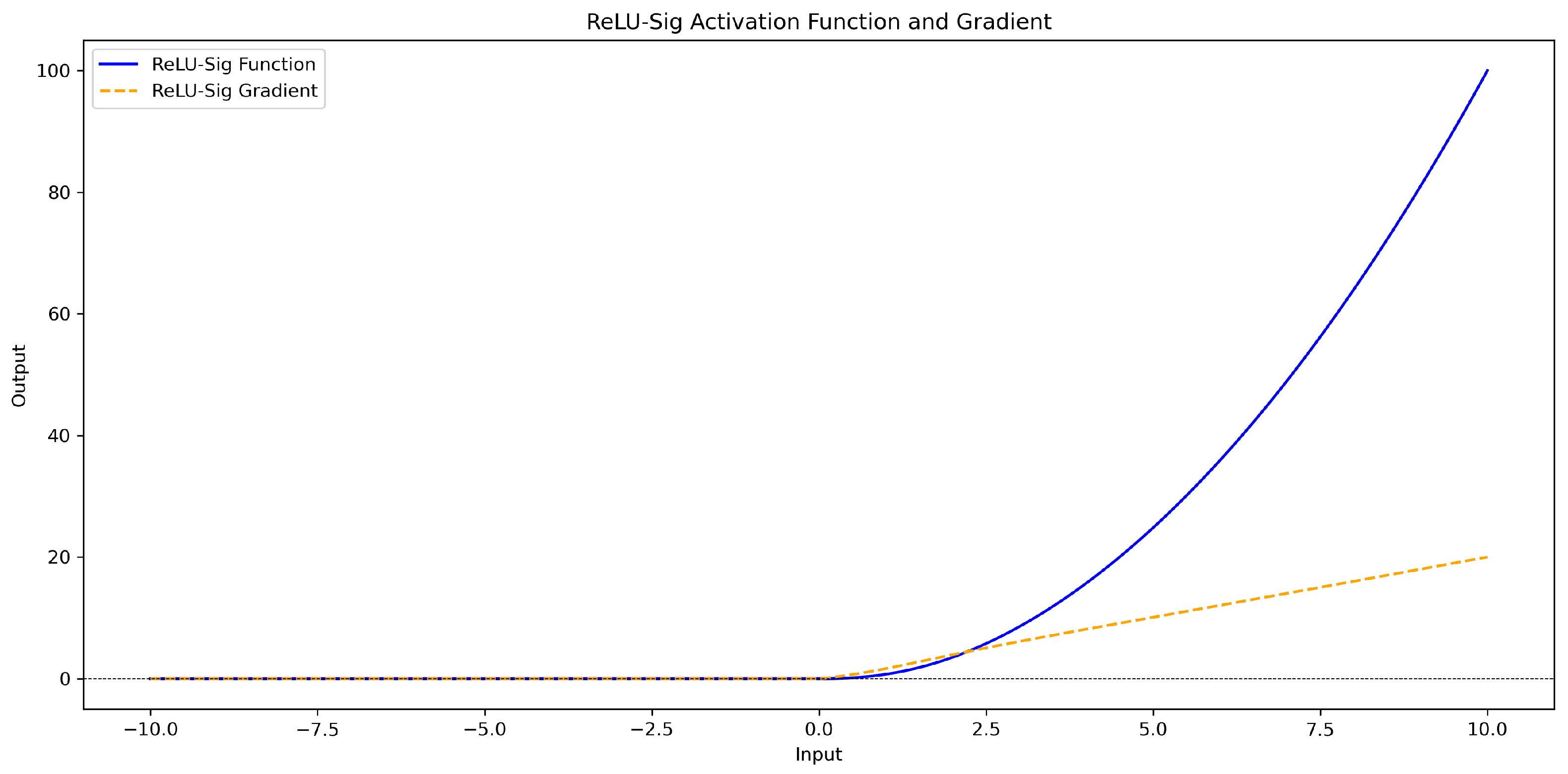

| Activation Function | Mathematical Formula | Advantages | Disadvantages | References |
|---|---|---|---|---|
| Sigmoid | Smooth, simple, widely used in early models | Non-zero centered, vanishing gradient | [17] | |
| Tanh | Zero centered, better convergence than sigmoid | Still suffers from vanishing gradients | [18] | |
| ReLU | Efficient computation, alleviates vanishing gradient | Dying ReLU problem (inactive neurons) | [19] | |
| Leaky ReLU | Avoids dying neurons, small gradient in negative part | Requires choosing/learning slope | [20] | |
| Swish | Nonmonotonic, smooth gradient, improves deep network performance | Higher computation than ReLU | [21] | |
| Mish | Smooth, strong generalization and performance | Slightly more expensive computation | [22] | |
| SPReLU | Composite of ReLU, PReLU and Softplus | Combines advantages of multiple functions, alleviates gradient vanishing | Complex, more parameters | [23] |
| LUTanh | Combines linearity and nonlinearity, robust | Task specific, not yet general | [24] |
| Company Type | Number of Company Samples | Number of Time Series Data Points |
|---|---|---|
| ST | 115 | 1380 |
| Non-ST | 512 | 6144 |
| Total | 627 | 7524 |
| Time Step | Training Data | Testing Data | ||||
|---|---|---|---|---|---|---|
| Non-ST | ST | Total | Non-ST | ST | Total | |
| w = 12 | 343 | 95 | 438 | 169 | 20 | 189 |
| w = 11 | 713 | 164 | 877 | 311 | 66 | 377 |
| w = 10 | 1082 | 238 | 1320 | 457 | 110 | 567 |
| w = 9 | 1437 | 318 | 1755 | 611 | 142 | 753 |
| w = 8 | 1797 | 410 | 2207 | 772 | 174 | 946 |
| w = 7 | 2155 | 495 | 2650 | 929 | 207 | 1136 |
| w = 6 | 2547 | 546 | 3093 | 1052 | 274 | 1326 |
| w = 5 | 2887 | 649 | 3536 | 1277 | 289 | 1566 |
| w = 4 | 3241 | 738 | 3979 | 1388 | 318 | 1706 |
| Hyperparameter | Search Range | Best Value |
|---|---|---|
| filters | [32, 64, 128] | 64 |
| kernel_size | [2, 3, 5] | 3 |
| dropout_cnn | [0.1, 0.2, 0.3, 0.4, 0.5] | 0.5 |
| lstm_units | [32, 64, 128] | 64 |
| dropout_lstm | [0.1, 0.2, 0.3, 0.4, 0.5] | 0.2 |
| dense_units_1 | [32, 64, 128] | 128 |
| dropout_dense_1 | [0.1, 0.2, 0.3, 0.4, 0.5] | 0.1 |
| dense_units_2 | [32, 64, 128] | 128 |
| dropout_dense_2 | [0.1, 0.2, 0.3, 0.4, 0.5] | 0.3 |
| batch_size | [32, 64] | 32 |
| epochs | [100, 150, 200] | 150 |
| Model Structure | CNN | CNN-AM | BiLSTM | BiLSTM-AM | CNN-BiLSTM-AM |
|---|---|---|---|---|---|
| Conv1D | 3 × 64 (ReLU) | 3 × 64 (ReLU) | - | - | 3 × 64 (ReLU) |
| MaxPool | 2 × 2 | 2 × 2 | - | - | 2 × 2 |
| BiLSTM | - | - | 64 (Tanh) | 64 (Tanh) | 64 (Tanh) |
| Attention | - | ✓ | - | ✓ | ✓ |
| Dense | 128 (ReLU) | 128 (ReLU) | 128 (ReLU) | 128 (ReLU) | 128 (ReLU) |
| Time Step | CNN | CNN-AM | BiLSTM | BiLSTM-AM | CNN-BiLSTM-AM |
|---|---|---|---|---|---|
| w = 12 | 0.857 | 0.825 | 0.820 | 0.783 | 0.794 |
| w = 11 | 0.915 | 0.883 | 0.905 | 0.912 | 0.939 |
| w = 10 | 0.928 | 0.963 | 0.956 | 0.952 | 0.968 |
| w = 9 | 0.940 | 0.962 | 0.968 | 0.959 | 0.959 |
| w = 8 | 0.951 | 0.987 | 0.969 | 0.986 | 0.988 |
| w = 7 | 0.947 | 0.978 | 0.968 | 0.974 | 0.977 |
| w = 6 | 0.957 | 0.974 | 0.960 | 0.965 | 0.974 |
| w = 5 | 0.937 | 0.950 | 0.948 | 0.956 | 0.948 |
| w = 4 | 0.909 | 0.931 | 0.937 | 0.942 | 0.935 |
| Layer Change Method | Unchanged Layers and Settings | Changed Layer | Activation Functions |
|---|---|---|---|
| CNN layer changes | BiLSTM-tanh, Dense-relu | CNN | relu, tanh, x, xtanh, xrelu, tanhrelu, tanh_relu, sigmoid, xsig, relusig, relu_sig |
| Dense layer changes | CNN-relu, BiLSTM-tanh | Dense | relu, tanh, x, xtanh, xrelu, tanhrelu, tanh_relu, sigmoid, xsig, relusig, relu_sig |
| BiLSTM layer changes | CNN-relu, Dense-relu | BiLSTM | tanh, relu, x, xtanh, xrelu, tanhrelu, tanh_relu |
| Activation Functions | Formula |
|---|---|
| relu | |
| tanh | |
| sigmoid | |
| x | x |
| xtanh | |
| xrelu | |
| xsig | |
| tanhrelu | |
| relusig | |
| tanhsig | |
| tanh_relu | (CTAF) |
| relu_sig | (CTAF) |
| tanh_sig | (CTAF) |
| Model | Relu | Sigmoid | Tanh | Swish | Mish | Leaky Relu | Relu_Sig | Tanh_Relu | Tanh_Sig |
|---|---|---|---|---|---|---|---|---|---|
| CNN | 0.988 | 0.965 | 0.984 | 0.985 | 0.985 | 0.983 | 0.985 | 0.993 | 0.993 |
| Dense | 0.988 | 0.981 | 0.980 | 0.989 | 0.983 | 0.981 | 0.986 | 0.991 | 0.988 |
| BiLSTM | 0.976 | 0.964 | 0.988 | 0.983 | 0.973 | 0.980 | 0.979 | 0.983 | 0.978 |
| BiLSTM-Lambda | 0.984 | 0.973 | 0.993 | 0.989 | 0.976 | 0.990 | 0.989 | 0.993 | 0.986 |
| CNN/Dense | BiLSTM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Relu | Sigmoid | Tanh | Swish | Mish | Leaky Relu | Relu_Sig | Tanh_Relu | Tanh_Sig | |
| relu | 0.976 | 0.970 | 0.988 | 0.983 | 0.967 | 0.952 | 0.985 | 0.987 | 0.981 |
| sigmoid | 0.934 | 0.918 | 0.950 | 0.942 | 0.946 | 0.944 | 0.939 | 0.941 | 0.937 |
| tanh | 0.980 | 0.974 | 0.989 | 0.979 | 0.973 | 0.961 | 0.983 | 0.989 | 0.985 |
| swish | 0.976 | 0.953 | 0.984 | 0.985 | 0.984 | 0.959 | 0.975 | 0.975 | 0.985 |
| mish | 0.984 | 0.971 | 0.989 | 0.984 | 0.988 | 0.967 | 0.983 | 0.987 | 0.975 |
| leaky relu | 0.989 | 0.957 | 0.983 | 0.958 | 0.964 | 0.968 | 0.956 | 0.948 | 0.963 |
| relu_sig | 0.873 | 0.968 | 0.977 | 0.952 | 0.952 | 0.944 | 0.958 | 0.973 | 0.964 |
| tanh_relu | 0.913 | 0.979 | 0.980 | 0.950 | 0.967 | 0.964 | 0.971 | 0.966 | 0.967 |
| tanh_sig | 0.961 | 0.978 | 0.990 | 0.964 | 0.970 | 0.963 | 0.967 | 0.959 | 0.975 |
| CNN/Dense | BiLSTM-Lambda | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Relu | Sigmoid | Tanh | Swish | Mish | Leaky Relu | Relu_Sig | Tanh_Relu | Tanh_Sig | |
| relu | 0.985 | 0.970 | 0.972 | 0.980 | 0.984 | 0.986 | 0.992 | 0.984 | 0.990 |
| sigmoid | 0.943 | 0.929 | 0.949 | 0.947 | 0.940 | 0.940 | 0.936 | 0.939 | 0.941 |
| tanh | 0.979 | 0.974 | 0.978 | 0.980 | 0.977 | 0.989 | 0.980 | 0.995 | 0.984 |
| swish | 0.985 | 0.968 | 0.986 | 0.986 | 0.986 | 0.978 | 0.987 | 0.983 | 0.986 |
| mish | 0.988 | 0.965 | 0.976 | 0.974 | 0.979 | 0.984 | 0.982 | 0.982 | 0.984 |
| leaky relu | 0.974 | 0.973 | 0.976 | 0.970 | 0.963 | 0.989 | 0.979 | 0.988 | 0.986 |
| relu_sig | 0.973 | 0.974 | 0.973 | 0.969 | 0.973 | 0.943 | 0.958 | 0.965 | 0.967 |
| tanh_relu | 0.974 | 0.978 | 0.961 | 0.969 | 0.972 | 0.978 | 0.975 | 0.976 | 0.963 |
| tanh_sig | 0.987 | 0.980 | 0.989 | 0.990 | 0.983 | 0.973 | 0.985 | 0.986 | 0.984 |
| Model | Relu | Sigmoid | Tanh | Swish | Mish | Leaky_Relu | Relu_Sig | Tanh_Relu | Tanh_Sig |
|---|---|---|---|---|---|---|---|---|---|
| CNN-BiLSTM-Dense | 0.976 | 0.918 | 0.989 | 0.985 | 0.988 | 0.968 | 0.958 | 0.966 | 0.975 |
| CNN-BiLSTM-Lambda-Dense | 0.990 | 0.924 | 0.993 | 0.988 | 0.992 | 0.989 | 0.966 | 0.966 | 0.986 |
| Test | Statistic | p-Value |
|---|---|---|
| Shapiro–Wilk | 0.911 | 0.067 |
| Paired t-test | −10.932 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Chiangpradit, M.; Busababodhin, P. Composite Triple Activation Function: Enhancing CNN-BiLSTM-AM for Sustainable Financial Risk Prediction in Manufacturing. Sustainability 2025, 17, 3067. https://doi.org/10.3390/su17073067
Song Y, Chiangpradit M, Busababodhin P. Composite Triple Activation Function: Enhancing CNN-BiLSTM-AM for Sustainable Financial Risk Prediction in Manufacturing. Sustainability. 2025; 17(7):3067. https://doi.org/10.3390/su17073067
Chicago/Turabian StyleSong, Yingying, Monchaya Chiangpradit, and Piyapatr Busababodhin. 2025. "Composite Triple Activation Function: Enhancing CNN-BiLSTM-AM for Sustainable Financial Risk Prediction in Manufacturing" Sustainability 17, no. 7: 3067. https://doi.org/10.3390/su17073067
APA StyleSong, Y., Chiangpradit, M., & Busababodhin, P. (2025). Composite Triple Activation Function: Enhancing CNN-BiLSTM-AM for Sustainable Financial Risk Prediction in Manufacturing. Sustainability, 17(7), 3067. https://doi.org/10.3390/su17073067


_Li.png)




