Ridesharing Methods for High-Speed Railway Hubs Considering Path Similarity
Abstract
1. Introduction
2. Literature Review
3. Model Formulation
3.1. Problem Description and Modeling Assumptions
- (1)
- Cars reach the pick-up area before the passengers and depart the hub only after boarding.
- (2)
- All passengers arrive at the specified location before the earliest scheduled departure time.
- (3)
- Each car maintains a constant speed throughout the journey.
- (4)
- Once passengers receive their ridesharing details, they do not cancel their trips.
- (5)
- The road network is assumed to be free of traffic congestion, and other random disruptions are not considered.
3.2. Mathematical Model
3.2.1. Symbols and Parameters
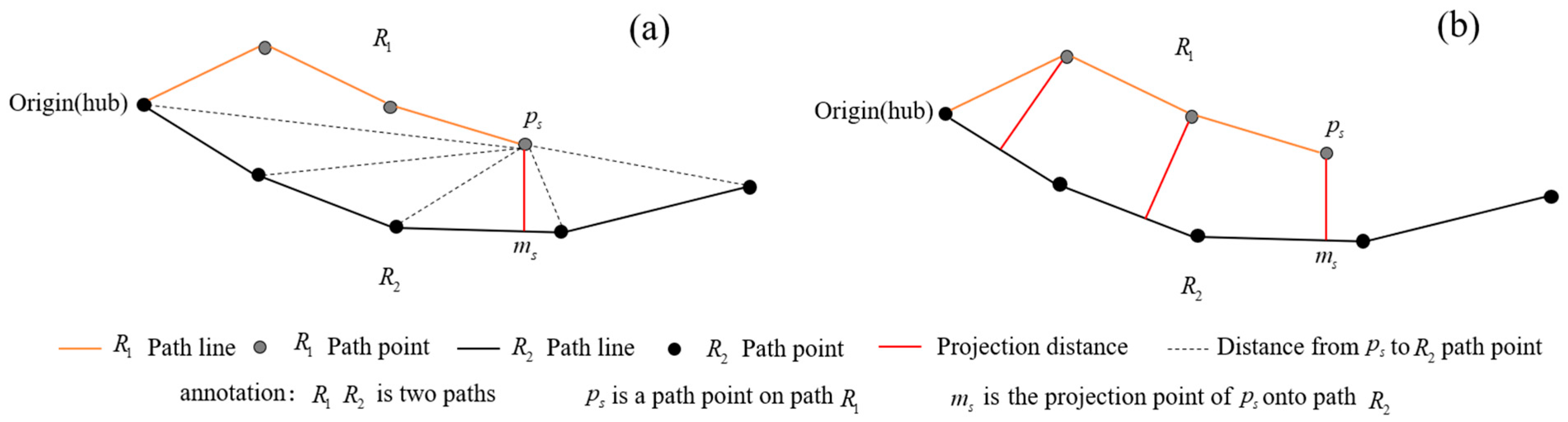
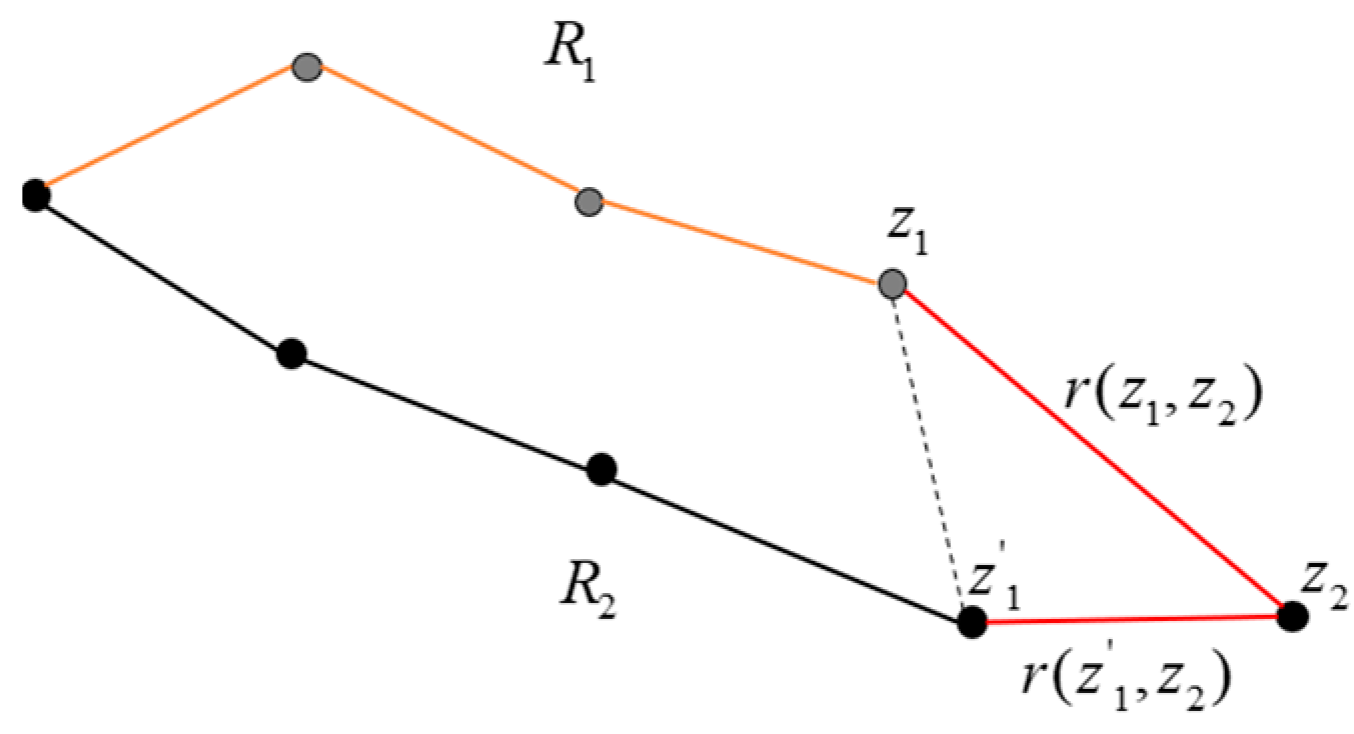
3.2.2. Measurement of Path Similarity
- (1)
- Measurement of spatial proximity of paths
- (2)
- Measurement of directional similarity of paths
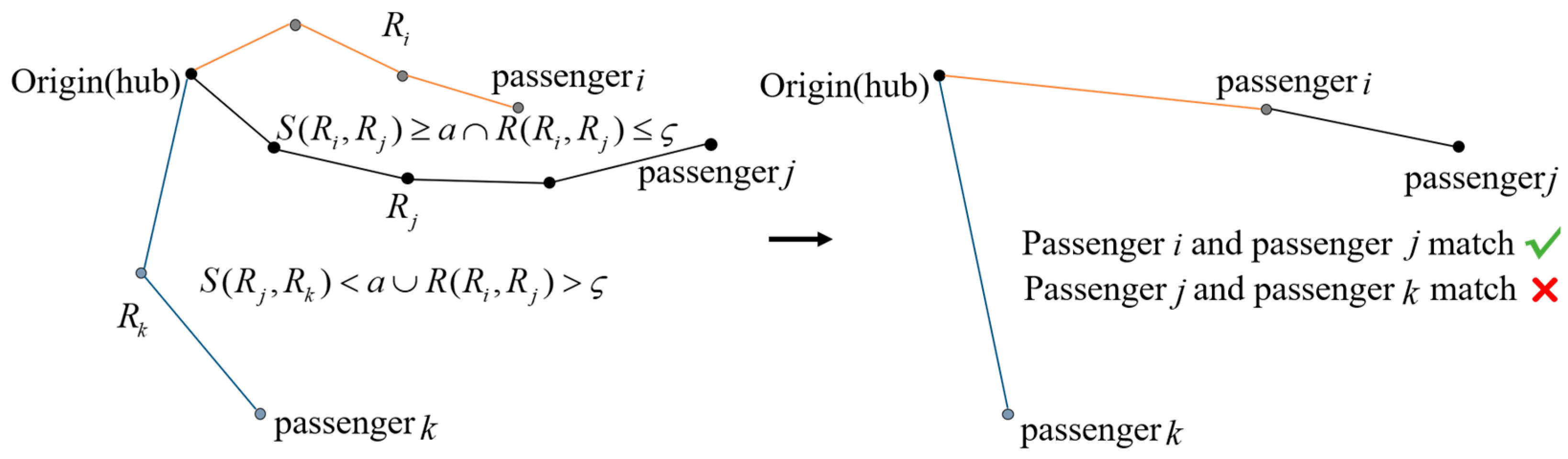
- (3)
- Measurement of path similarity—DSPD
- 1)
- , where passenger and passenger achieve a successful match, ;
- 2)
- , where passenger and passenger fail to match.
3.2.3. Mathematical Model
4. Solution Algorithm
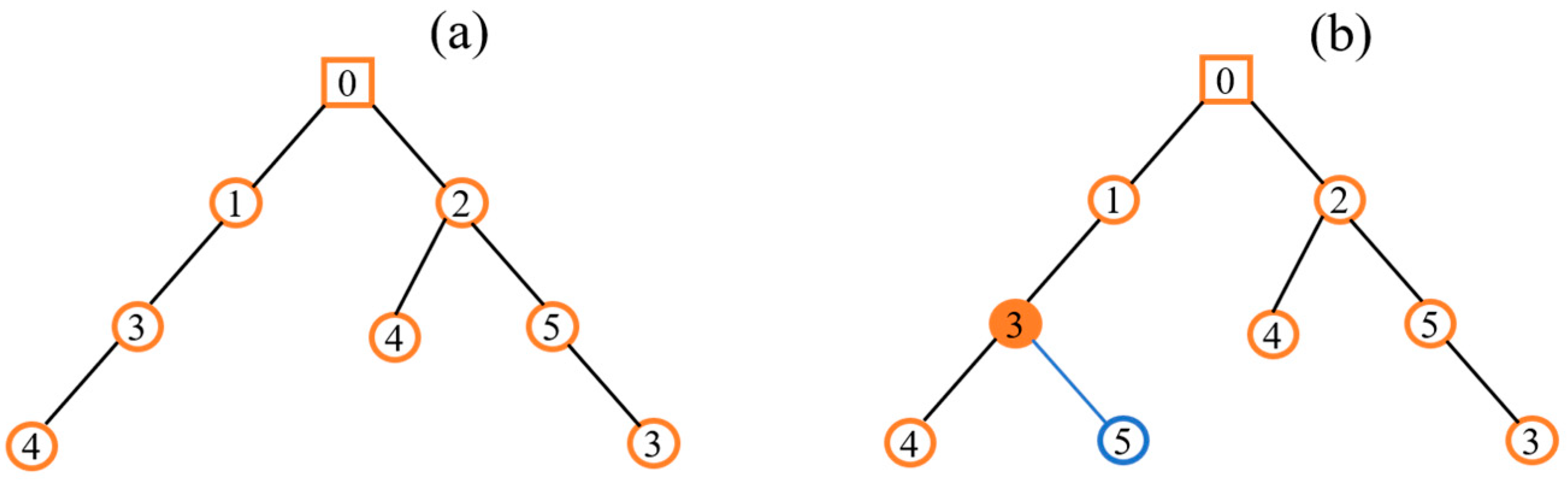
4.1. Request Clustering Based on Path Vector Similarity
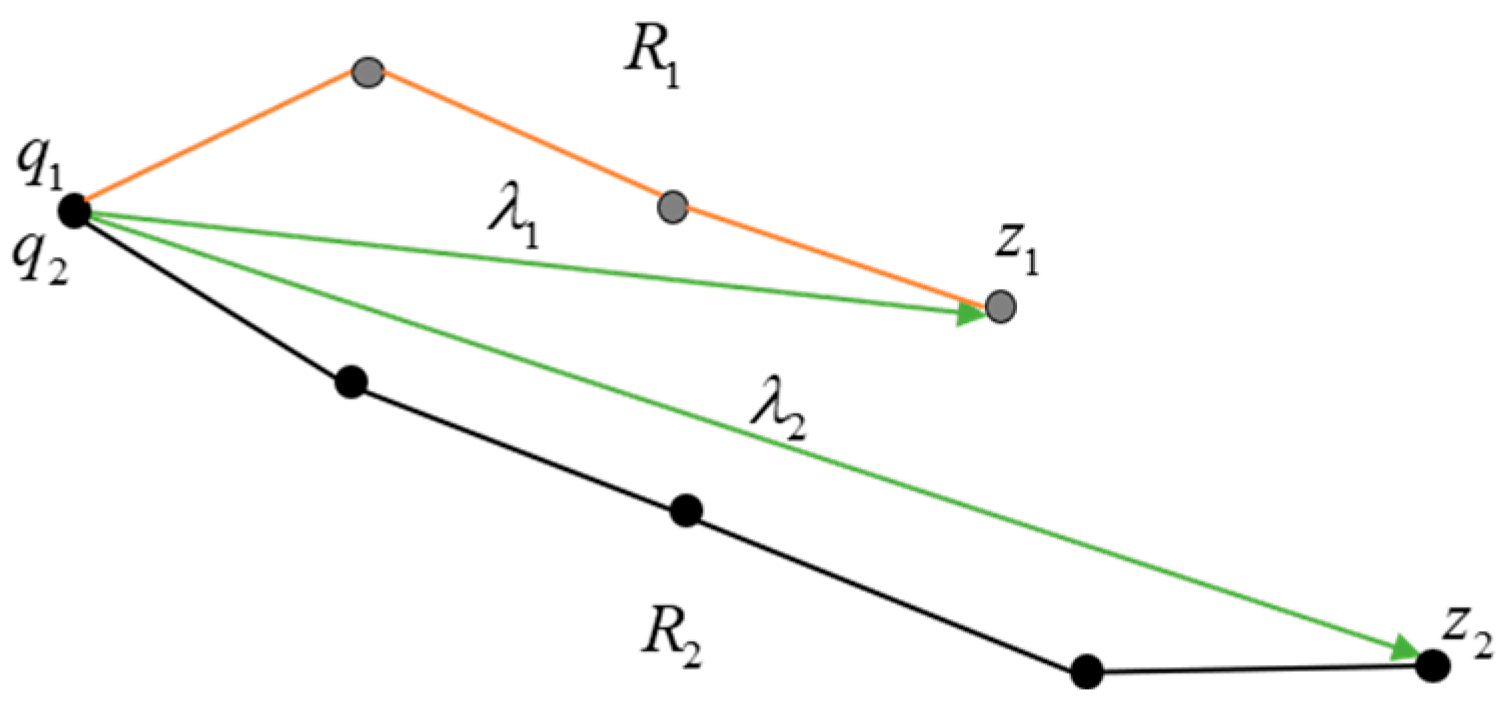
4.1.1. Definition of Path Vector Similarity
- (1)
- Vector similarity in direction
- (2)
- Vector similarity in temporal
4.1.2. Clustering Based on a Greedy Heuristic Algorithm
4.2. Adaptive Large Neighborhood Search Algorithm
| Algorithm 1: Outline of ALNS | |
| 01 | Input: similarity data, removal and repair operators, other algorithm |
| 02 | ) |
| 03 | current an initial solution by Insert algorithm |
| 04 | , iter ← 0; |
| 05 | while termination criteria are not met do |
| 06 | select removal & repair operators by roulette selection |
| 07 | ) |
| 08 | ) |
| 09 | |
| 10 | ) |
| 11 | |
| 12 | ) but accepted by the Metropolis criterion then |
| 13 | |
| 14 | else |
| 15 | |
| 16 | update T, scores, and weights of removal & repair operators |
| 17 | |
4.2.1. Initial Solution
| Algorithm 2: Insert algorithm | |
| 01 | Input: requests, cars |
| 02 | Output: set of routes |
| 03 | uninserted requests ← all requests |
| 04 | while |uninserted requests| > 0 do |
| 05 | generate a new empty route (r) |
| 06 | for each request do |
| 07 | for each possible insertion position in the route do |
| 08 | new route ← insert the request at the current position |
| 09 | check the feasible of the new route; |
| 10 | if the new route is feasible then |
| 11 | delete this uninserted requests, r ← new route and break |
| 12 | else |
| 13 | try inserting in the next position |
| 14 | add r to routes |
| 15 | return routes |
4.2.2. Removal and Repair Operators
- (1)
- Random Removal: This operator randomly removes a certain number of requests from the current vehicle route at a specific rate of destruction.
- (2)
- Worst removal: This operator removes the request, saving the most considerable routing cost. First, the routing cost savings are calculated for each request removed. Then, the request that results in the most significant cost savings is removed from the current route. Finally, the first two steps are repeated until the number of removals is satisfied.
- (3)
- Shaw Removal: We define the similarity of two requests in a route, obtain the two requests with the highest similarity, and remove one request from it to increase the diversity of the scheme. The similarity of two requests i and j for a route is defined as SM(i,j), as shown in Equation (25).
- (1)
- Random Repair: Each request can be randomly inserted into a feasible location. An empty route is created to insert this request if no feasible position exists.
- (2)
- Greedy Repair: This operator first calculates the insertion cost of inserting each request into each available location and then selects the request–location pair that results in the smallest increase in routing cost, which means this request will be inserted into this position. If there is no feasible insertion location for a given request, an empty route is generated for storage.
- (3)
- Regret-2 Repair: This operator includes a forward-looking message when selecting a customer to insert. We use to denote the minimum insertion cost of placing a request into route . This operator calculates the insertion costs of placing the request into the first-best and second-best routes. represents the maximum regret value for inserting the request . The request with the highest regret value is inserted into the first-best position.
4.2.3. Adaptive Mechanism
4.2.4. Parallel Computing and Acceleration Strategies
- (1)
- When a complete route is successfully retrieved, return the total cost of the route directly.
- (2)
- When a complete route is not retrieved, assess its feasibility, calculate the total cost, and store it in the trie structure.
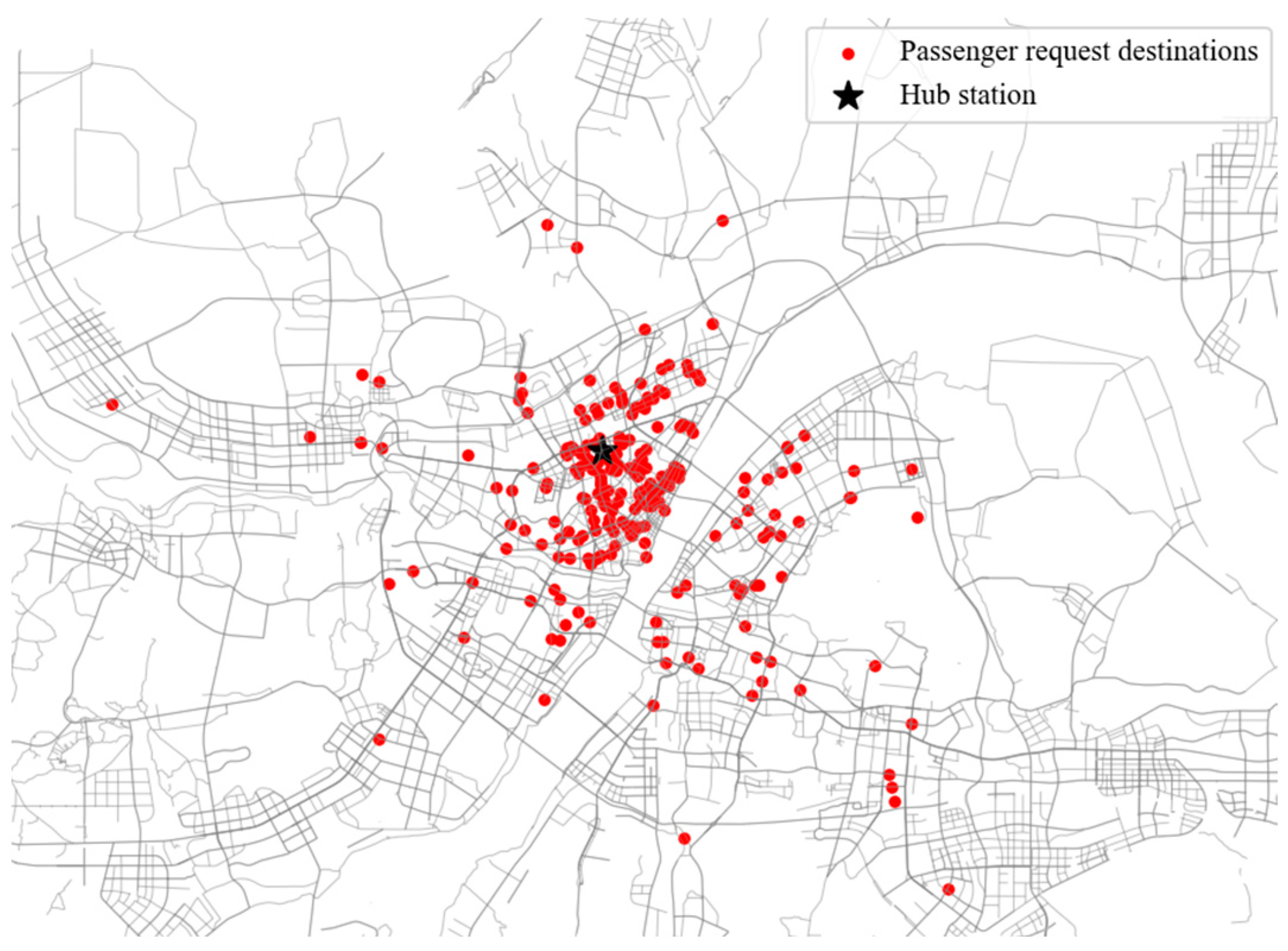
5. Case Study
5.1. Parameter Configuration and Instance Generation
5.2. Analysis of the Effects of Heuristic Clustering Based on Path Vector Similarity
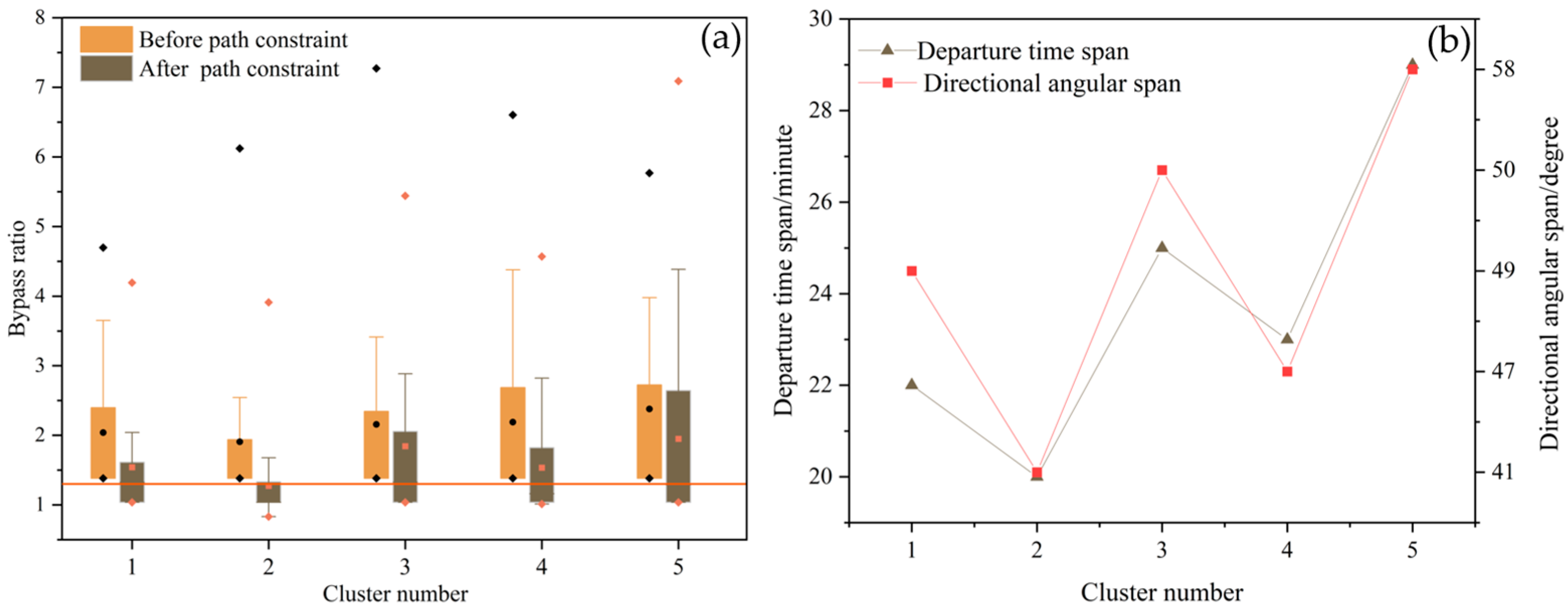
5.3. Analysis of the Effects of Path Similarity
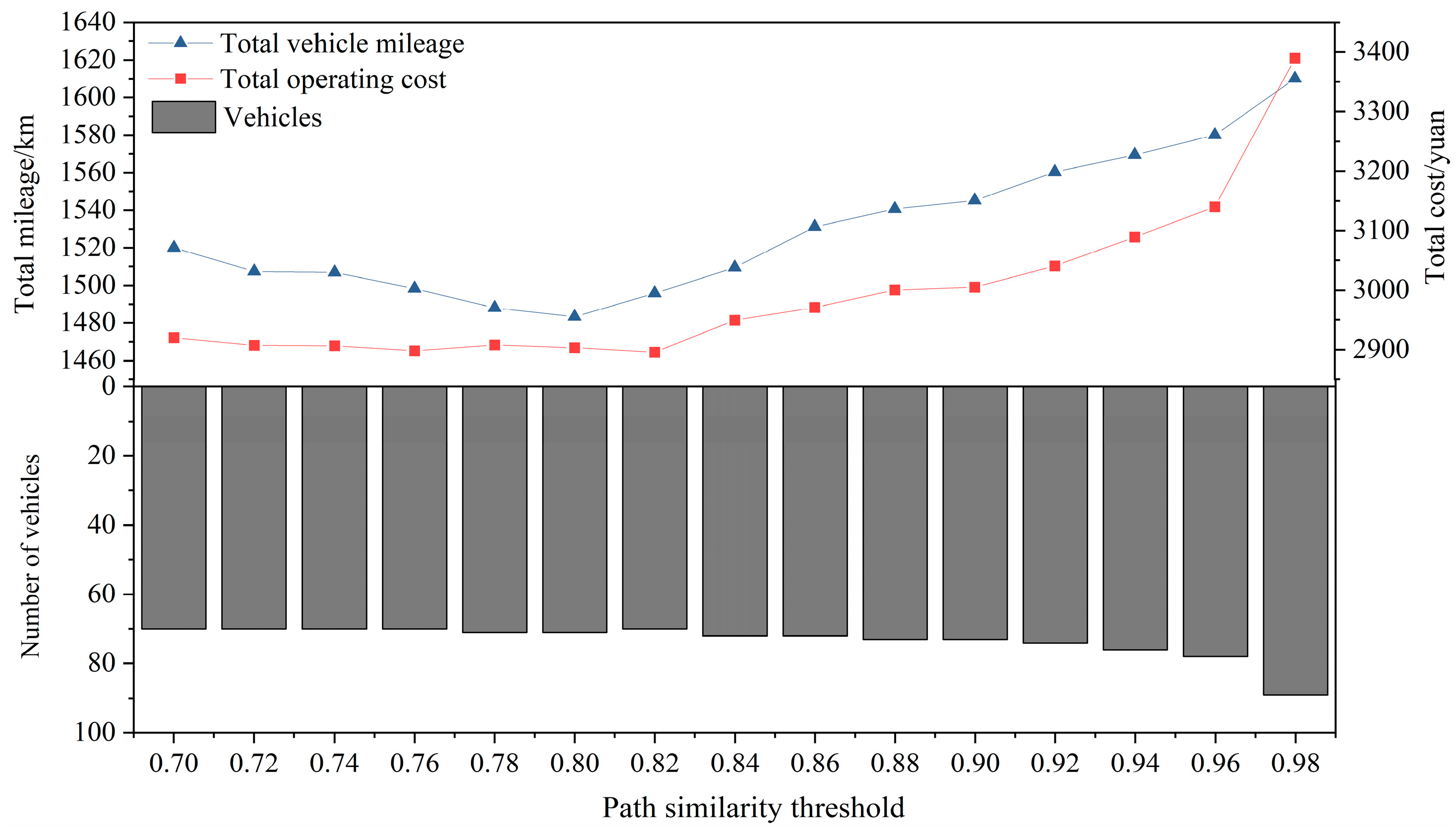
5.4. Sensitivity Analysis of Path Similarity Threshold
5.5. Analysis of the Impact of Large Luggage on Route Feasibility
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, P.; Jin, J.G.; Schulte, F.; Trépanier, M. Optimizing first-mile ridesharing services to intercity transit hubs. Transp. Res. Part C-Emerg. Technol. 2023, 150, 104082. [Google Scholar]
- Nourinejad, M.; Roorda, M.J. Agent based model for dynamic ridesharing. Transp. Res. Part C-Emerg. Technol. 2016, 64, 117–132. [Google Scholar]
- Bian, Z.Y.; Liu, X. Mechanism design for first-mile ridesharing based on personalized requirements part I: Theoretical analysis in generalized scenarios. Transp. Res. Part B-Methodol. 2019, 120, 147–171. [Google Scholar]
- Li, Y.Y.; Liu, Y.; Xie, J. A path-based equilibrium model for ridesharing matching. Transp. Res. Part B-Methodol. 2020, 138, 373–405. [Google Scholar] [CrossRef]
- Du, M.Q.; Zhou, J.K.; Li, G.Y.; Tan, H.Q.; Chen, A.T.Y. A stochastic ridesharing user equilibrium model with origin-destination-based ride-matching strategy. Transp. Res. Part E-Logist. Transp. Rev. 2024, 189, 103688. [Google Scholar]
- Hosni, H.; Naoum-Sawaya, J.; Artail, H. The shared-taxi problem: Formulation and solution methods. Transp. Res. Part B-Methodol. 2014, 70, 303–318. [Google Scholar]
- Yin, R.Y.; Lu, P.X. A Cluster-First Route-Second Constructive Heuristic Method for Emergency Logistics Scheduling in Urban Transport Networks. Sustainability 2022, 14, 2301. [Google Scholar] [CrossRef]
- Nitter, J.; Yang, S.S.; Fagerholt, K.; Ormevik, A.B. The static ridesharing routing problem with flexible locations: A Norwegian case study. Comput. Oper. Res. 2024, 167, 106669. [Google Scholar]
- Fielbaum, A. Optimizing a vehicle’s route in an on-demand ridesharing system in which users might walk. J. Intell. Transp. Syst. 2022, 26, 432–447. [Google Scholar]
- Najmi, A.; Waller, T.; Liu, W.; Rashidi, T.H. Integration of ridesharing and activity travel pattern generation. Transp. A-Transp. Sci. 2023. [Google Scholar] [CrossRef]
- Agatz, N.A.H.; Erera, A.L.; Savelsbergh, M.W.P.; Wang, X. Dynamic ride-sharing: A simulation study in metro Atlanta. Transp. Res. Part B-Methodol. 2011, 45, 1450–1464. [Google Scholar]
- Ramezani, M.; Valadkhani, A.H. Dynamic ride-sourcing systems for city-scale networks- Part I: Matching design and model formulation and validation. Transp. Res. Part C-Emerg. Technol. 2023, 152, 104158. [Google Scholar]
- Miller, J.; How, J.P. Predictive Positioning and Quality Of Service Ridesharing for Campus Mobility On Demand Systems. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1402–1408. [Google Scholar]
- Ma, J.; Xu, M.; Meng, Q.; Cheng, L. Ridesharing user equilibrium problem under OD-based surge pricing strategy. Transp. Res. Part B-Methodol. 2020, 134, 1–24. [Google Scholar]
- Li, M.; Di, X.; Liu, H.X.; Huang, H.J. A restricted path-based ridesharing user equilibrium. J. Intell. Transp. Syst. 2020, 24, 383–403. [Google Scholar]
- Hsieh, F.S. Trust-Based Recommendation for Shared Mobility Systems Based on a Discrete Self-Adaptive Neighborhood Search Differential Evolution Algorithm. Electronics 2022, 11, 776. [Google Scholar] [CrossRef]
- Huang, Y.T.; Kockelman, K.M.; Garikapati, V. Shared automated vehicle fleet operations for first-mile last-mile transit connections with dynamic pooling. Comput. Environ. Urban Syst. 2022, 92, 101730. [Google Scholar]
- Stiglic, M.; Agatz, N.; Savelsbergh, M.; Gradisar, M. Enhancing urban mobility: Integrating ride-sharing and public transit. Comput. Oper. Res. 2018, 90, 12–21. [Google Scholar]
- Ma, T.Y.; Rasulkhani, S.; Chow, J.Y.J.; Klein, S. A dynamic ridesharing dispatch and idle vehicle repositioning strategy with integrated transit transfers. Transp. Res. Part E-Logist. Transp. Rev. 2019, 128, 417–442. [Google Scholar]
- Shen, R.G.; Pei, Y.L. Research on Effect of Passenger Behavior to Transfer Demand of Comprehensive Transport Hub: A Case of High-speed Railway Station. In Proceedings of the 2012 2nd International Conference on Applied Robotics for the Power Industry (CARPI), Zurich, Switzerland, 11–13 September 2012; pp. 456–459. [Google Scholar]
- Deloukas, A.; Georgiadis, G.; Papaioannou, P. Shared Mobility and Last-Mile Connectivity to Metro Public Transport: Survey Design Aspects for Determining Willingness for Intermodal Ridesharing in Athens. In Proceedings of the 20th International Conference on Computational Science and Its Applications (ICCSA), Cagliari, Italy, 1–4 July 2020; pp. 819–835. [Google Scholar]
- Li, H.J.; Zhou, H.C.; Feng, J.R.; Chen, X.H.; Zhang, W. Railway passengers travel behavior based on bounded rationality by rough set weight. Clust. Comput.-J. Netw. Softw. Tools Appl. 2019, 22, S10019–S10029. [Google Scholar]
- Wu, Y.L.; Poon, M.; Yuan, Z.Z.; Xiao, Q.Y. Time-dependent customized bus routing problem of large transport terminals considering the impact of late passengers. Transp. Res. Part C-Emerg. Technol. 2022, 143, 103859. [Google Scholar]
- Peng, Z.X.; Feng, R.; Wang, C.Y.; Jiang, Y.L.; Yao, B.Z. Online bus-pooling service at the railway station for passengers and parcels sharing buses: A case in Dalian. Expert Syst. Appl. 2021, 169, 114354. [Google Scholar]
- Bian, Z.Y.; Liu, X.; Asme. Planning the ridesharing route for the first-mile service linking to railway passenger transportation. In Proceedings of the 2017 Joint Rail Conference, American Society of Mechanical Engineers Digital Collection, Philadelphia, PA, USA, 19 July 2017; pp. 1–11. [Google Scholar]
- Tamannaei, M.; Irandoost, I. Carpooling problem: A new mathematical model, branch-and-bound, and heuristic beam search algorithm. J. Intell. Transp. Syst. 2019, 23, 203–215. [Google Scholar]
- He, P.; Jin, J.G.; Trépanier, M.; Schulte, F. A column-generation matheuristic approach for optimizing first-mile ridesharing services with publicly- and privately-owned autonomous vehicles. Transp. Res. Part C-Emerg. Technol. 2024, 160, 104516. [Google Scholar]
- Hua, S.J.; Zeng, W.J.; Liu, X.L.; Qi, M.Y. Optimality-guaranteed algorithms on the dynamic shared-taxi problem. Transp. Res. Part E-Logist. Transp. Rev. 2022, 164, 102809. [Google Scholar]
- Montemanni, R.; Gambardella, L.M.; Rizzoli, A.E.; Donati, A. Ant colony system for a dynamic vehicle routing problem. J. Comb. Optim. 2005, 10, 327–343. [Google Scholar]
- Lin, Y.; Bian, Z.Y.; Liu, X. Developing a dynamic neighborhood structure for an adaptive hybrid simulated annealing—Tabu search algorithm to solve the symmetrical traveling salesman problem. Appl. Soft Comput. 2016, 49, 937–952. [Google Scholar]
- Hou, L.W.; Li, D.; Zhang, D.L. Ride-matching and routing optimisation: Models and a large neighbourhood search heuristic. Transp. Res. Part E-Logist. Transp. Rev. 2018, 118, 143–162. [Google Scholar]
- Santos, D.O.; Xavier, E.C. Taxi and Ride Sharing: A Dynamic Dial-a-Ride Problem with Money as an Incentive. Expert Syst. Appl. 2015, 42, 6728–6737. [Google Scholar]
- Li, Y.L.; Chung, S.H. Ride-sharing under travel time uncertainty: Robust optimization and clustering approaches. Comput. Ind. Eng. 2020, 149, 106601. [Google Scholar]
- Dondo, R.; Cerdá, J. A cluster-based optimization approach for the multi-depot heterogeneous fleet vehicle routing problem with time windows. Eur. J. Oper. Res. 2007, 176, 1478–1507. [Google Scholar]
- Alisoltani, N.; Ameli, M.; Zargayouna, M.; Leclercq, L. Space-time clustering-based method to optimize shareability in real-time ride-sharing. PLoS ONE 2022, 17, e0262499. [Google Scholar]
- Besse, P.C.; Guillouet, B.; Loubes, J.M.; Royer, F. Review and Perspective for Distance-Based Clustering of Vehicle Trajectories. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3306–3317. [Google Scholar]
- Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Comput. Oper. Res. 2007, 34, 2403–2435. [Google Scholar]
- Zhang, Y.; Zhang, Z.Z.; Lim, A.; Sim, M. Robust Data-Driven Vehicle Routing with Time Windows. Oper. Res. 2021, 69, 469–485. [Google Scholar]
- Wei, L.J.; Zhang, Z.Z.; Zhang, D.F.; Lim, A. A variable neighborhood search for the capacitated vehicle routing problem with two-dimensional loading constraints. Eur. J. Oper. Res. 2015, 243, 798–814. [Google Scholar]
- Jaccard, P. The distribution of the flora in the alpine zone. New Phytol. 1912, 11, 37–50. [Google Scholar]



| Symbols | Description |
|---|---|
| Set of all cars | |
| Set of passenger destinations | |
| Set of all nodes, including the railway hub (denoted as 0) | |
| Fixed usage cost per car | |
| Operational cost per unit distance for each car | |
| Number of seats in each car | |
| Number of passengers of request | |
| Number of large luggage items of request | |
| Number of pieces of luggage that can be placed on the trunk of each car | |
| Number of pieces of luggage that can be placed on a seat | |
| Vehicle speed | |
| Drop-off time for each passenger (service time) | |
| Departure time window for passenger | |
| Desired arrival time window for passenger | |
| 0–1 variable, when vehicle travels from node to node = 0 |
| Scale | Index | PVS-ALNS | ALNS | Gap (%) |
|---|---|---|---|---|
| 60 | Objective function/USD | 131.87 | 131.87 | 0 |
| Number of cars/vehicles | 28 | 28 | 0 | |
| Total car mileage/km | 381.92 | 381.92 | 0 | |
| Average solution time/s | 28.31 | 139.85 | 79.8 | |
| Average passenger waiting time/minute | 3.07 | 3.07 | 0 | |
| 120 | Objective function/USD | 304.40 | 308.16 | 1.2 |
| Number of cars/vehicles | 52 | 52 | 0 | |
| Total car mileage/km | 989.35 | 1014.37 | 2.5 | |
| Average solution time/s | 42.23 | 711.65 | 94 | |
| Average passenger waiting time/minute | 2.87 | 4.14 | 30.6 | |
| 230 | Objective function/USD | 401.45 | 406.35 | 1.2 |
| Number of cars/vehicles | 71 | 71 | 0 | |
| Total car mileage/km | 1483.38 | 1526.71 | 2.8 | |
| Average solution time/s | 86.24 | 1882.40 | 95 | |
| Average passenger waiting time/minute | 2.90 | 4.16 | 30.2 |
| Index | Before Ridesharing | With Path Constraints | Without Path Constraints |
|---|---|---|---|
| Objective function/USD | 880.73 | 401.45 | 411.35 |
| Total car mileage/km | 1772.24 | 1483.38 | 1577.35 |
| Number of cars/vehicles | 230 | 71 | 70 |
| Total mileage saving rate/% | — | 16% | 11% |
| Average passenger diversions ratio | — | 1.56 | 1.84 |
| Ridesharing success rate/ % | — | 97% | 100% |
| JAC value | — | 0.63 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, W.; Xu, L.; Zhu, D.; Liu, W.; Li, Y. Ridesharing Methods for High-Speed Railway Hubs Considering Path Similarity. Sustainability 2025, 17, 2975. https://doi.org/10.3390/su17072975
Qin W, Xu L, Zhu D, Liu W, Li Y. Ridesharing Methods for High-Speed Railway Hubs Considering Path Similarity. Sustainability. 2025; 17(7):2975. https://doi.org/10.3390/su17072975
Chicago/Turabian StyleQin, Wendie, Liangjie Xu, Di Zhu, Wanheng Liu, and Yan Li. 2025. "Ridesharing Methods for High-Speed Railway Hubs Considering Path Similarity" Sustainability 17, no. 7: 2975. https://doi.org/10.3390/su17072975
APA StyleQin, W., Xu, L., Zhu, D., Liu, W., & Li, Y. (2025). Ridesharing Methods for High-Speed Railway Hubs Considering Path Similarity. Sustainability, 17(7), 2975. https://doi.org/10.3390/su17072975






