Enhanced TSMixer Model for the Prediction and Control of Particulate Matter
Abstract
1. Introduction
- (1)
- The E-TSMixer with a fully connected output layer is proposed to enhance the predictive capability of complex spatiotemporal dependencies for minute-level particulate matter prediction.
- (2)
- The various time-series data, including air quality and traffic flow, are fused to achieve high-precision predictions of particulate matter in the proposed model.
- (3)
- An intelligent dual-threshold decision-support system that integrates fixed and dynamic thresholds derived from E-TSMixer prediction is proposed for the dynamic decision-making of water truck operation.
2. Literature Review
2.1. Existing Methods
2.2. TSMixer and Its Applications
3. Enhanced TSMixer Model
3.1. Basic Framework and Mathematical Foundation
3.1.1. Mixer Layer Mathematics
3.1.2. The Temporal Projection Layer
3.2. Enhanced Model
3.2.1. Fully Connected Output Layer
3.2.2. Optimization of the Loss Function
4. Empirical Analysis
4.1. Experimental Data
4.2. Experimental Setup and Hyperparameter Configuration
4.3. Model Comparison
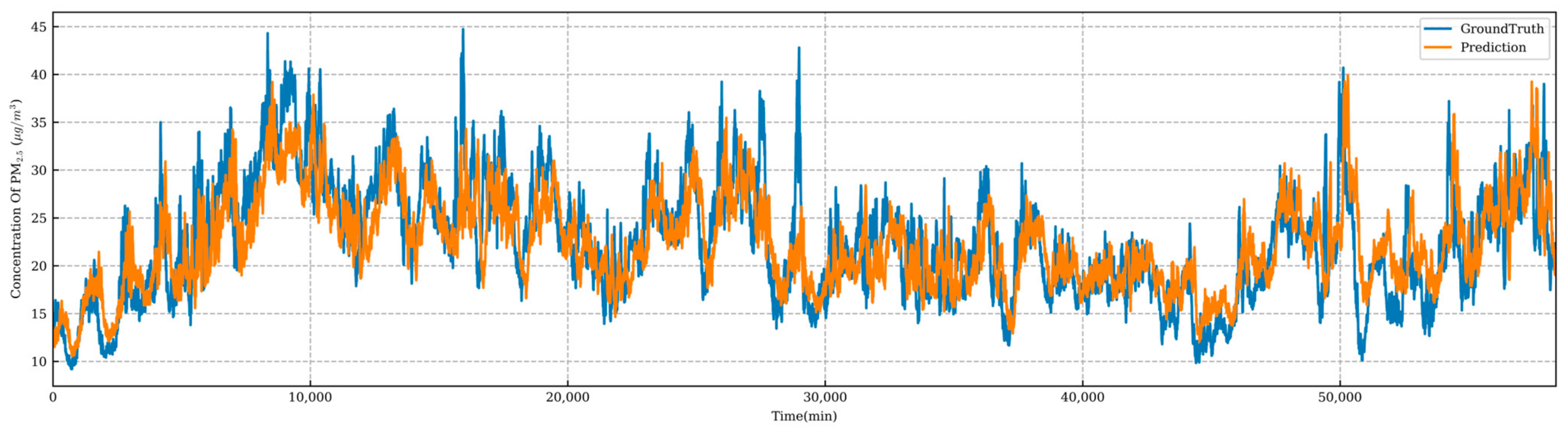
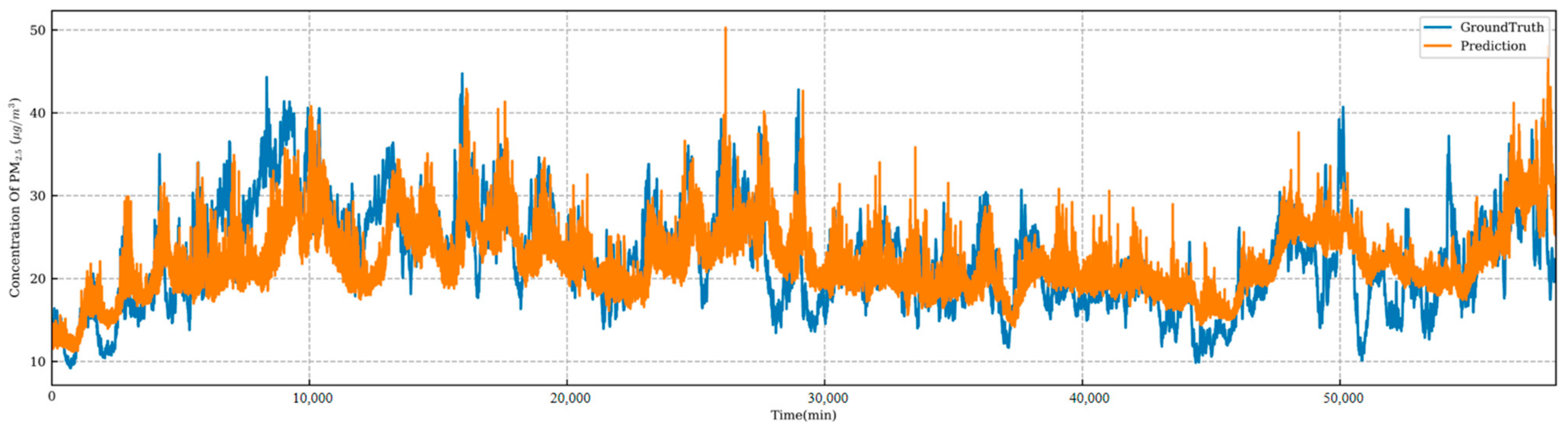
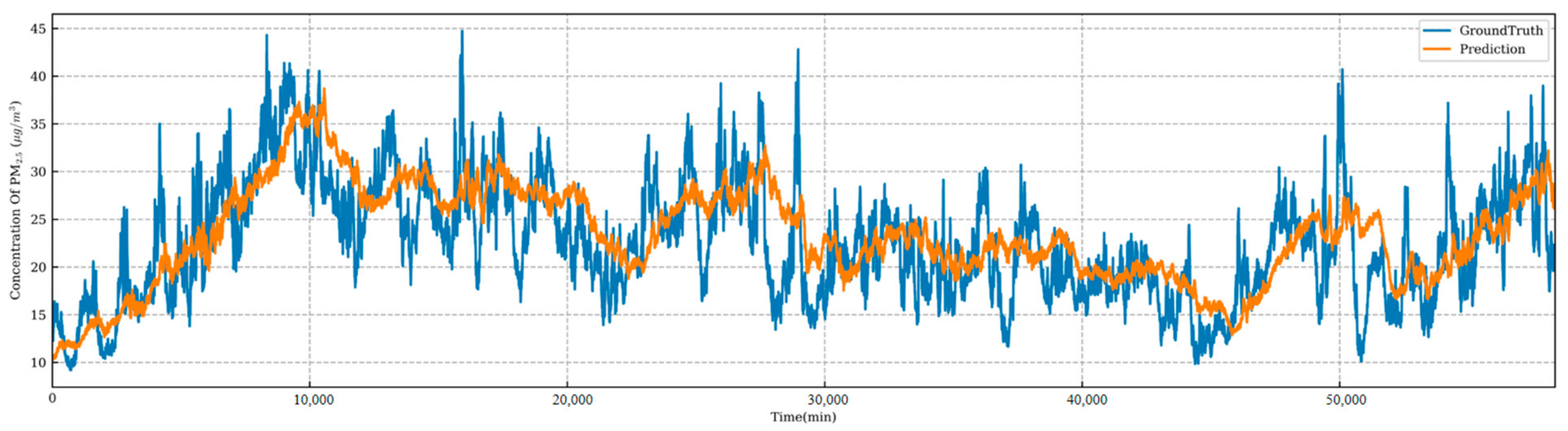
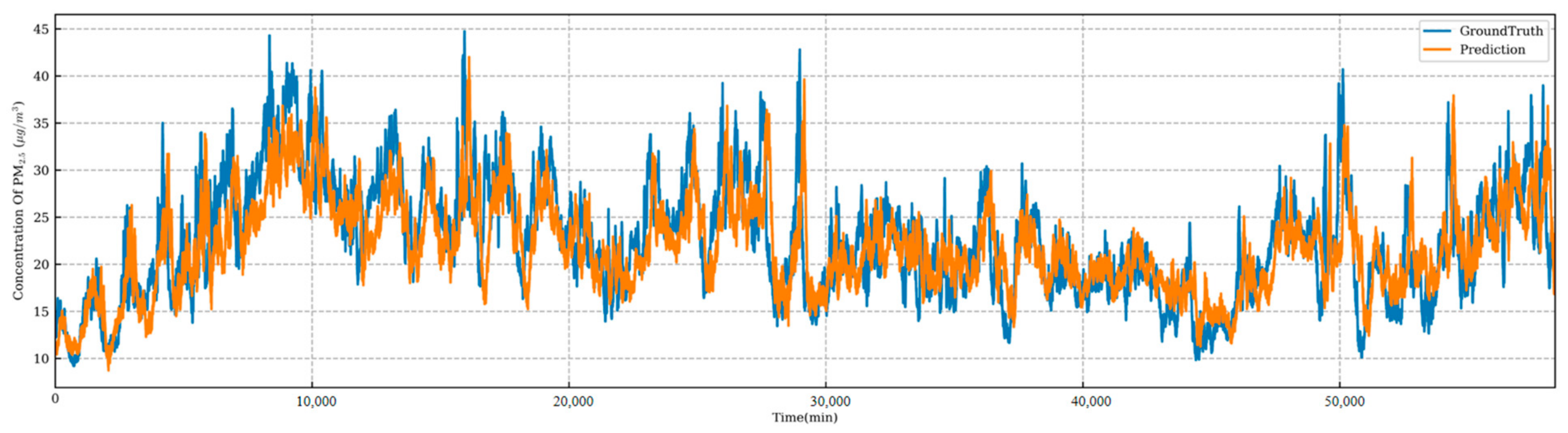
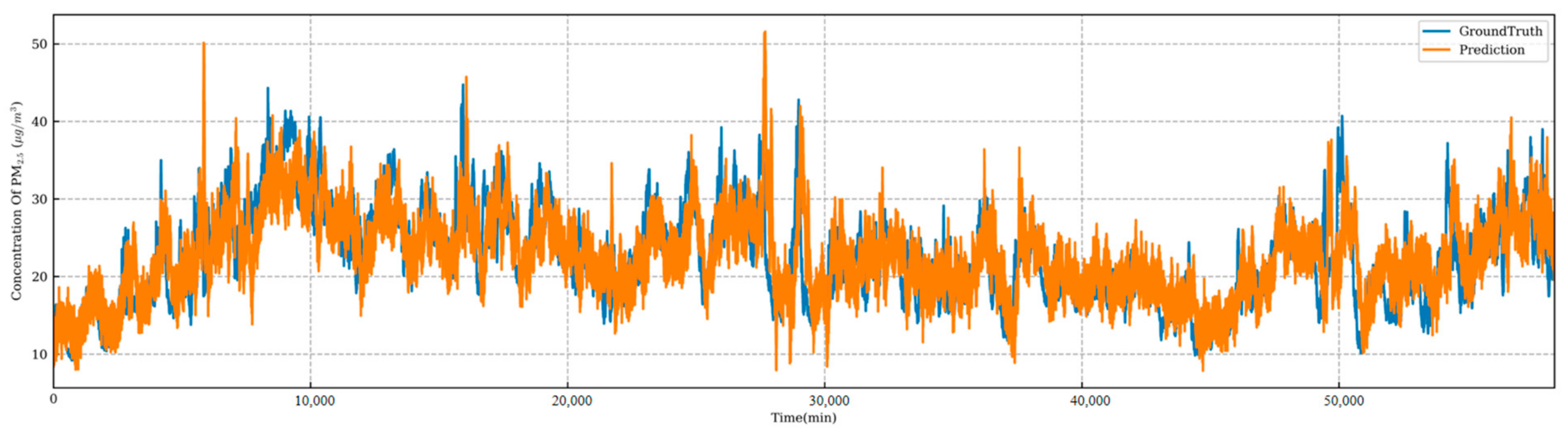
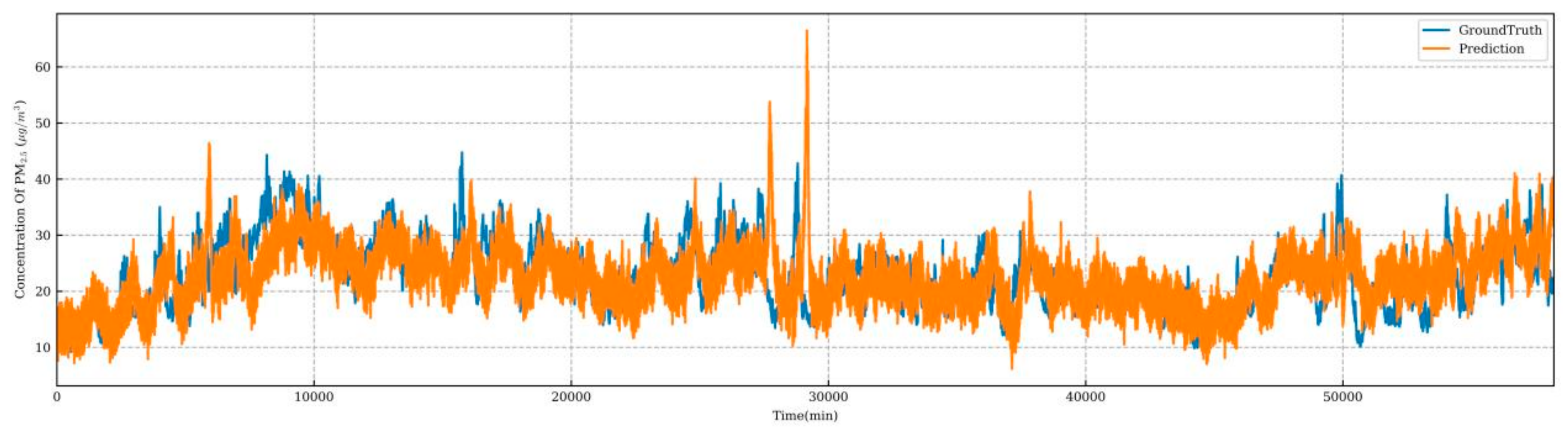
4.4. Predictive Model Performance
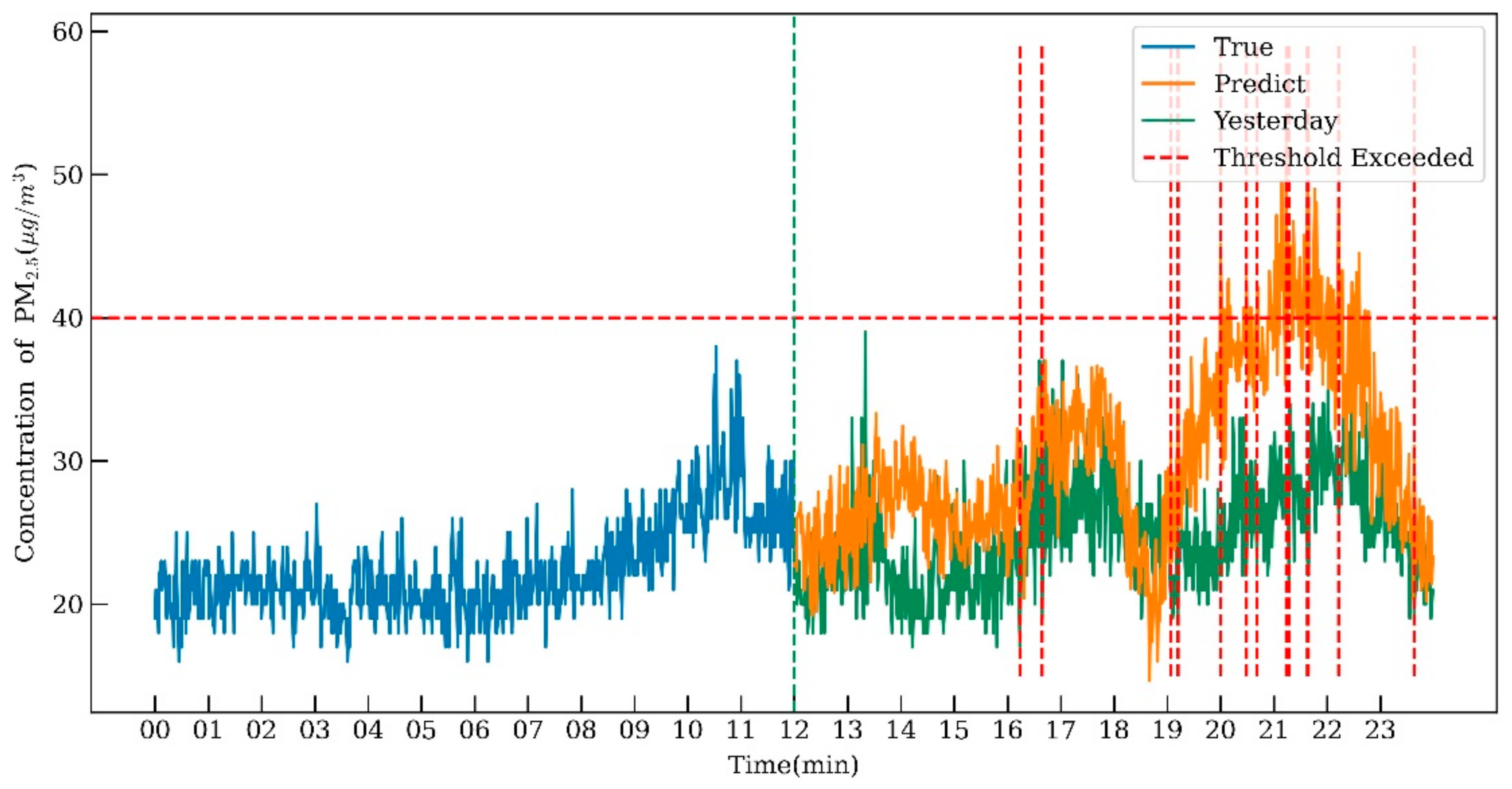
4.5. Intelligent Decision-Making Model Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.; Choi, J.; Kim, M.; Cho, Y.; Kim, J.; Cho, P. Verification of On-Site Applicability of Rainwater Road Surface Spraying for Promoting Rainwater Utilization and Analyzing the Fine Dust Reduction Effect. Sustainability 2024, 16, 8756. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Kamruzzaman, M. Planning, Development and Management of Sustainable Cities: A Commentary from the Guest Editors. Sustainability 2015, 7, 14677–14688. [Google Scholar] [CrossRef]
- Amato, F.; Querol, X.; Johansson, C.; Nagl, C.; Alastuey, A. A Review on the Effectiveness of Street Sweeping, Washing and Dust Suppressants as Urban PM Control Methods. Sci. Total Environ. 2010, 408, 3070–3084. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, L.; Wang, H.; Han, H.; Zhu, Z.; Zhao, X.; Wang, Y. A Review of Physical and Chemical Methods to Improve the Performance of Water for Dust Reduction. Process Saf. Environ. Prot. 2022, 166, 86–98. [Google Scholar] [CrossRef]
- Alavi, A.H.; Jiao, P.; Buttlar, W.G.; Lajnef, N. Internet of Things-Enabled Smart Cities: State-of-The-Art and Future Trends. Measurement 2018, 129, 589–606. [Google Scholar] [CrossRef]
- Chamoso, P.; González-Briones, A.; Rodríguez, S.; Corchado, J.M. Tendencies of technologies and platforms in smart cities: A state-of-the-art review. Wirel. Commun. Mob. Comput. 2018, 2018, 3086854. [Google Scholar] [CrossRef]
- Uyanık, G.K.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia-Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Box, G.E.P.; Pierce, D.A. Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models. J. Am. Stat. Assoc. 1970, 65, 1509. [Google Scholar] [CrossRef]
- Hurd, H.L.; Miamee, A. Periodically Correlated Random Sequences: Spectral Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 9780470182826. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Chodakowska, E.; Nazarko, J.; Nazarko, Ł. ARIMA Models in Electrical Load Forecasting and Their Robustness to Noise. Energies 2021, 14, 7952. [Google Scholar] [CrossRef]
- Byun, D.; Schere, K.L. Review of the Governing Equations, Computational Algorithms, and Other Components of the Models-3 Community Multiscale Air Quality (CMAQ) Modeling System. Appl. Mech. Rev. 2006, 59, 51. [Google Scholar]
- Stohl, A.; Forster, C.; Frank, A.; Seibert, P.; Wotawa, G. Technical Note: The Lagrangian Particle Dispersion Model FLEXPART Version 6.2. Atmos. Chem. Phys. 2005, 5, 2461–2474. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar] [CrossRef]
- Stockie, J.M. The Mathematics of Atmospheric Dispersion Modeling. SIAM Rev. 2011, 53, 349–372. [Google Scholar] [CrossRef]
- Joachims, T. Making Large-Scale SVM Learning Practical. In RePEc: Research Papers in Economics; Universität Dortmund: Dortmund, Germany, 1998. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, P.; Zhao, L.; Wang, G.; Zhang, W.; Liu, J. Air Quality Predictions with a Semi-Supervised Bidirectional LSTM Neural Network. Atmos. Pollut. Res. 2021, 12, 328–339. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1998; pp. 255–258. [Google Scholar]
- Chen, S.A.; Li, C.L.; Yoder, N.; Arik, S.O.; Pfister, T. Tsmixer: An all-mlp architecture for time series forecasting. arXiv 2023, arXiv:2303.06053. [Google Scholar]
- Xayasouk, T.; Lee, H.; Lee, G. Air Pollution Prediction Using Long Short-Term Memory (LSTM) and Deep Autoencoder (DAE) Models. Sustainability 2020, 12, 2570. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, X.; Luo, B.; Yang, C.; Gui, W.; Dubljevic, S. Accelerated MPC: A real-time model predictive control acceleration method based on TSMixer and 2D block stochastic configuration network imitative controller. Chem. Eng. Res. Des. 2024, 208, 837–852. [Google Scholar] [CrossRef]
- Seng, D.; Zhang, Q.; Zhang, X.; Chen, G.; Chen, X. Spatiotemporal Prediction of Air Quality Based on LSTM Neural Network. Alex. Eng. J. 2021, 60, 2021–2032. [Google Scholar] [CrossRef]
- Pinkus, A. Approximation Theory of the MLP Model in Neural Networks. Acta Numer. 1999, 8, 143–195. [Google Scholar] [CrossRef]
- GB 3095-2012; Ambient Air Quality Standard. Ministry of Environmental Protection of the People’s Republic of China: Beijing, China; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China; China Environmental Science Press: Beijing, China, 2012.
- Zhao, J.; Deng, F.; Cai, Y.; Chen, J. Long Short-Term Memory—Fully Connected (LSTM-FC) Neural Network for PM2.5 Concentration Prediction. Chemosphere 2019, 220, 486–492. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2023, arXiv:1706.03762. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Wen, Q.; Sun, L.; Yao, T.; Yin, W.; Jin, R. Film: Frequency improved legendre memory model for long-term time series forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 12677–12690. [Google Scholar]
- Campos, D.; Zhang, M.; Yang, B.; Kieu, T.; Guo, C.; Jensen, C.S. LightTS: Lightweight Time Series Classification with Adaptive Ensemble Distillation. Proc. ACM Manag. Data 2023, 1, 1–27. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar]
- Karunasingha, D.S.K. Root Mean Square Error or Mean Absolute Error? Use Their Ratio as Well. Inf. Sci. 2021, 585, 609–629. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar]


| No. | Metric | Unit |
|---|---|---|
| 1 | PM2.5 | μg/m3 |
| 2 | PM10 | μg/m3 |
| 3 | Temperature | °C |
| 4 | Humidity | %RH |
| 5 | Atmospheric Pressure | kPa |
| 6 | Wind Speed | m/s |
| 7 | Wind Direction | ° |
| 8 | Nitrogen Dioxide | μg/m3 |
| 9 | Carbon Monoxide | mg/m3 |
| 10 | Ozone | mg/m3 |
| 11 | Illumination | Lux |
| 12 | Total Radiation | W/m2 |
| 13 | Rainfall | mm/min |
| 14 | Sulfur Dioxide | μg/m3 |
| No. | Metric | Unit |
|---|---|---|
| 1 | Lane | - |
| 2 | Average Speed | km/h |
| 3 | Traffic Volume | vehicles |
| 4 | Average Occupancy | % |
| 5 | Headway Distance | meters |
| 6 | Headway Time | seconds |
| 7 | Buses | vehicles |
| 8 | Cars | vehicles |
| 9 | Trucks | vehicles |
| 10 | Motorcycles | vehicles |
| 11 | Bicycles | vehicles |
| 12 | Fleet Length | vehicles |
| Method | Epoch | Learning Rate | Batch Size | No. Workers |
|---|---|---|---|---|
| LSTM-FC | 100 | 0.0001 | 32 | 8 |
| Transformer | 100 | 0.0001 | 32 | 8 |
| FilM | 100 | 0.0001 | 32 | 8 |
| LightTS | 100 | 0.0001 | 32 | 8 |
| TSMixer | 100 | 0.0001 | 32 | 8 |
| E-TSMixer | 100 | 0.0001 | 32 | 8 |
| Method | RMSE | MAE | SMAPE | Training Time per Epoch (s) | Inference Time per Data (ms) |
|---|---|---|---|---|---|
| LSTM-FC | 4.12 | 3.17 | 14.16 | 153.16 | 3.61 |
| Transformer | 5.02 | 3.86 | 17.20 | 2186.55 | 6.31 |
| FilM | 4.51 | 3.56 | 15.95 | 2062.10 | 3.09 |
| LightTS | 4.28 | 3.23 | 14.36 | 121.01 | 11.35 |
| TSMixer | 4.02 | 3.02 | 13.41 | 25.97 | 1.98 |
| E-TSMixer | 4.57 | 3.42 | 15.17 | 48.76 | 2.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Li, H.; Ma, Y.; Huang, Y.; Chu, X. Enhanced TSMixer Model for the Prediction and Control of Particulate Matter. Sustainability 2025, 17, 2933. https://doi.org/10.3390/su17072933
Yang C, Li H, Ma Y, Huang Y, Chu X. Enhanced TSMixer Model for the Prediction and Control of Particulate Matter. Sustainability. 2025; 17(7):2933. https://doi.org/10.3390/su17072933
Chicago/Turabian StyleYang, Chaoqiong, Haoru Li, Yue Ma, Yubin Huang, and Xianghua Chu. 2025. "Enhanced TSMixer Model for the Prediction and Control of Particulate Matter" Sustainability 17, no. 7: 2933. https://doi.org/10.3390/su17072933
APA StyleYang, C., Li, H., Ma, Y., Huang, Y., & Chu, X. (2025). Enhanced TSMixer Model for the Prediction and Control of Particulate Matter. Sustainability, 17(7), 2933. https://doi.org/10.3390/su17072933





