Sustainable CO2 Storage Assessment in Saline Aquifers Using a Hybrid ANN and Numerical Simulation Model Across Different Trapping Mechanisms
Abstract
1. Introduction
2. Carbon Capture and Storage (CCS) in Saline Aquifers

2.1. Trapping Mechanisms in CCS
2.1.1. Structural and Stratigraphic Trapping
2.1.2. Residual Trapping
2.1.3. Solubility Trapping
2.1.4. Mineral Trapping
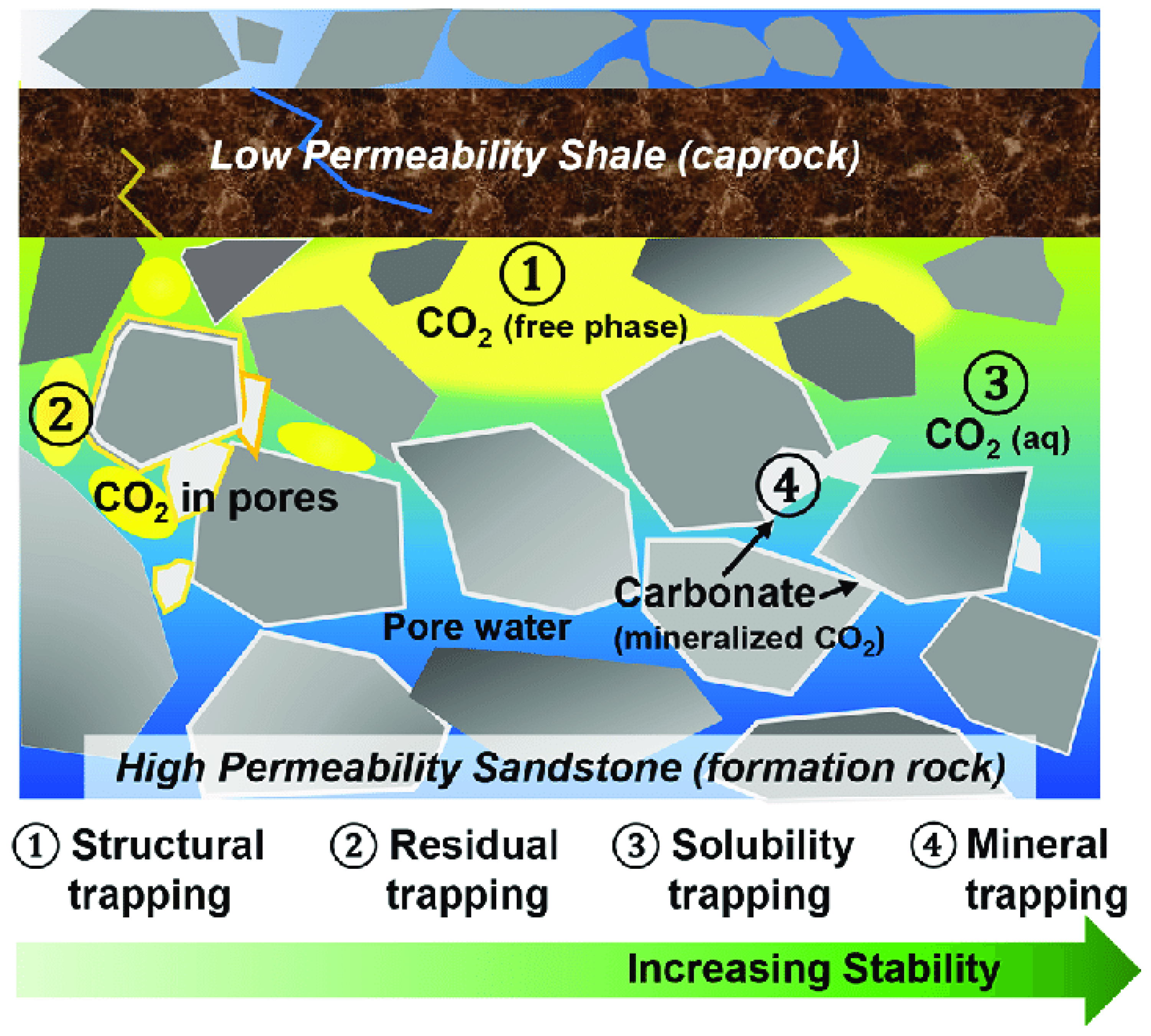
2.2. Importance of Integrated Trapping Mechanisms
2.3. Utilizing CMG-GEM for CO2 Storage Simulations
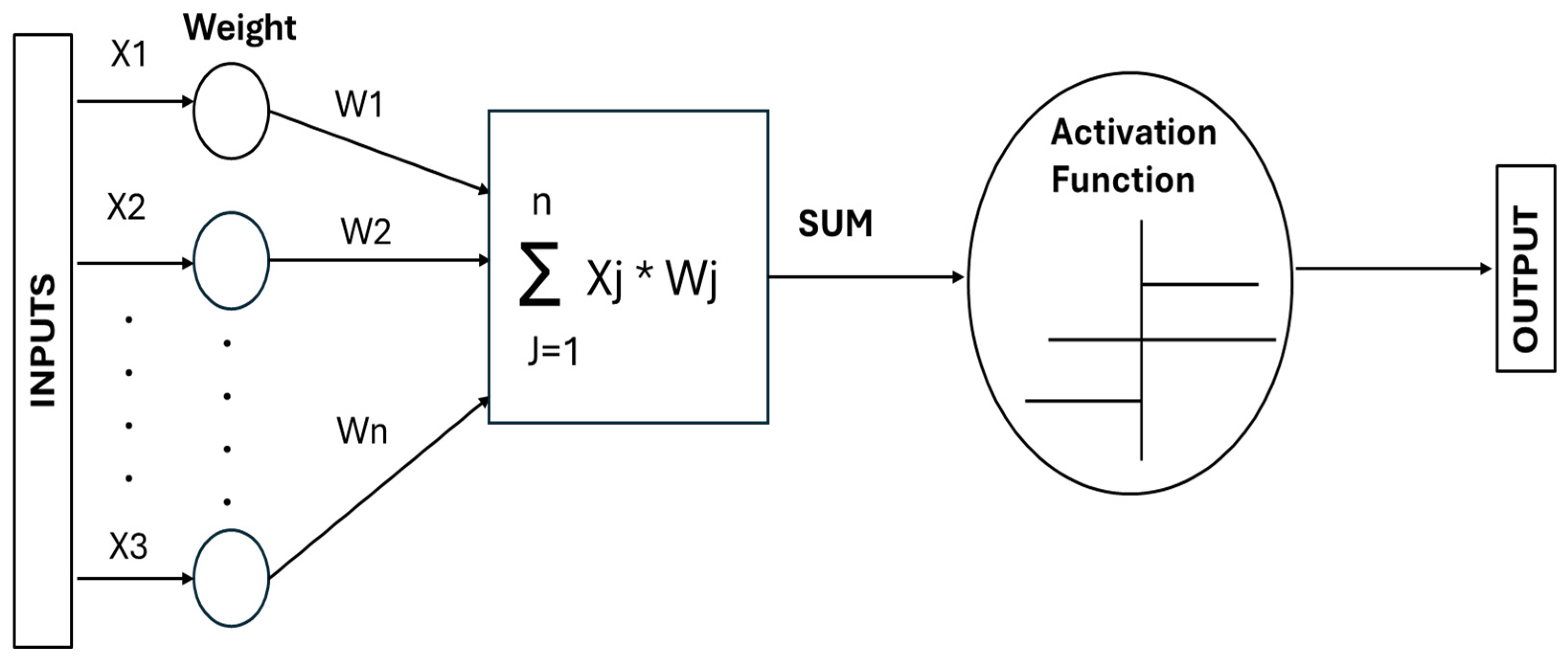
2.4. Predictive Modeling Using Artificial Neural Networks (ANNs)
2.5. Integration of Simulation Data with ANNs in CCS
| Paper Title | Description | Input Parameters | Output Parameters | Key Advantages | Limitations |
|---|---|---|---|---|---|
| Physics-Based Proxy Modeling of CO2 Sequestration in Deep Saline Aquifers | This study uses physics-based proxy modeling with machine learning (ML) to predict CO2 trapping mechanisms’ residual, solubility, and mineral trapping. An expansive dataset generated using a compositional reservoir simulator was used to train and validate four ML models: multilayer perceptron (MLP), random forest (RF), support vector regression (SVR), and extreme gradient boosting (XGB) [12]. | Basic petrophysical and fluid properties | Residual, solubility, and structural traps | Uses physics-based proxy modeling | Limited parameter selection and requires further field-scale validation |
| Multi-Objective Optimization of CO2 Enhanced Oil Recovery Projects Using a Hybrid Artificial Intelligence Approach | This study develops a hybrid optimization workflow for CO2—EOR projects considering multiple objective functions. The robustness of the development is confirmed via a field case study. Moreover, this work investigates the relationship between the solutions of the aggregative objective function and the Pareto front, which helps define constraints and reduces the uncertainties involved in the multi-objective optimization process [27]. | EOR-specific parameters (pressure, injection rates) | CO2-EOR-related trapping mechanisms | Optimizes CO2-EOR efficiency | Not focused on sequestration |
| Real-time High-resolution CO2 Geological Storage Prediction using Nested Fourier Neural Operators | The study introduces the Nested Fourier Neural Operator (FNO), a machine learning framework designed for the high-resolution, dynamic 3D modeling of CO2 storage at the basin level. This approach uses a hierarchy of FNOs to produce forecasts at varying levels of refinement and accelerates flow predictions by nearly 700,000 times compared to traditional methods. By learning the solution operator for the governing partial differential equations, Nested FNO acts as a versatile alternative to numerical simulators, accommodating diverse reservoir conditions, geological heterogeneity, and injection schemes [28]. | Geological heterogeneity, injection schemes | CO2 flow dynamics (not trapping-specific) | faster than traditional simulation models | Requires significant computational power and requires further field-scale validation |
| Deep learning-based coupled flow–geomechanics surrogate model for CO2 sequestration | This study presents a deep-learning-based surrogate model, the recurrent R-U-Net, for predicting flow and geomechanical responses in CO2 storage operations. Combining convolutional and recurrent neural networks, the model captures the spatial and temporal evolution of CO2 saturation, pressure, and surface displacement fields. Trained on 2000 high-fidelity simulations of storage aquifer realizations, it accurately predicts 3D aquifer dynamics and 2D surface displacement maps, reducing computational demands [29]. | Flow and geomechanical parameters | Pressure, saturation, and surface displacement | Predicts both subsurface and surface deformation | High-fidelity training required |
| Application of machine learning to predict CO2 trapping performance in deep saline aquifers | This study applies machine learning (ML) models—Gaussian Process Regression (GPR), Support Vector Machine (SVM), and random forest (RF) to predict CO2 trapping efficiency in saline formations. A training dataset was developed using uncertainty variables, including geological, petrophysical, and physical parameters, to analyze residual trapping, solubility trapping, and cumulative CO2 injection [30]. | Geological and petrophysical properties | Residual, solubility, and cumulative injection | Incorporates uncertainty analysis | Lacks real-time dynamic modeling and requires further field-scale validation |
| Sustainable CO2 Storage Assessment in Saline Aquifers Using a Hybrid ANN and Numerical Simulation Model Across Different Trapping Mechanisms (Current Paper) | This study employs the Levenberg–Marquardt backpropagation algorithm to develop an artificial neural network (ANN) model for predicting total CO2 storage capacity and its distribution across different trapping mechanisms. The ANN is trained using a wide range of geological and operational parameters, derived from extensive reservoir simulation runs, ensuring that the model captures the complex interactions governing CO2 sequestration. | Includes the parameters of the other models plus extra input sets not included in previous models (aquifer volume, hysteresis coefficient, reservoir pressure, and CO2 injection pressure) | All four major mechanisms (residual, solubility, mineral, and structural) in addition to CO2 supercritical volume; these outputs are only included in this study | ✔ Fully conclusive predictions (total CO2 volume + full trapping breakdown) ✔ Balances accuracy and computational efficiency ✔ Real-time adaptability and easy to use | Requires further field-scale validation |
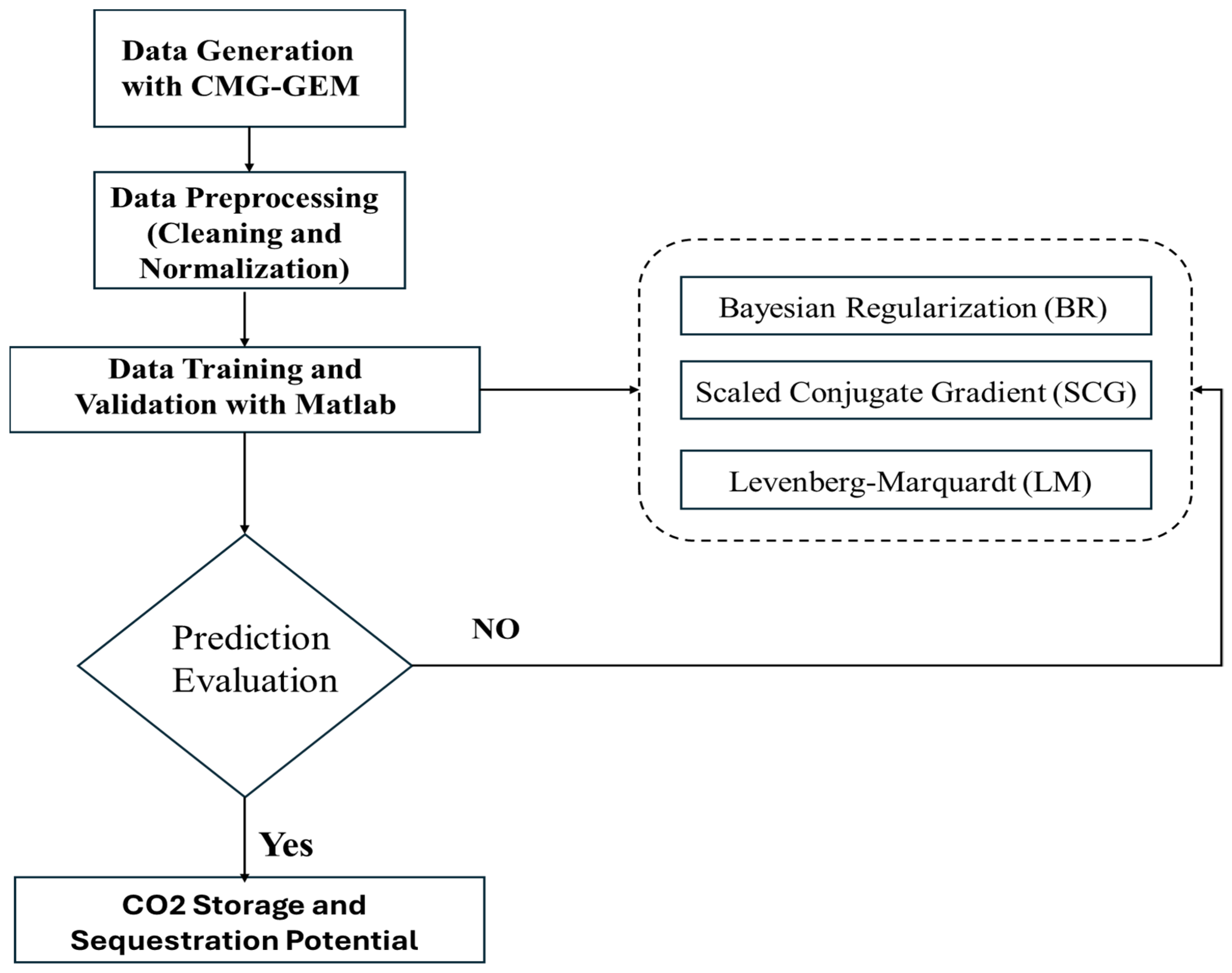
3. Methodology
3.1. Data Generation Using 3D Simulation
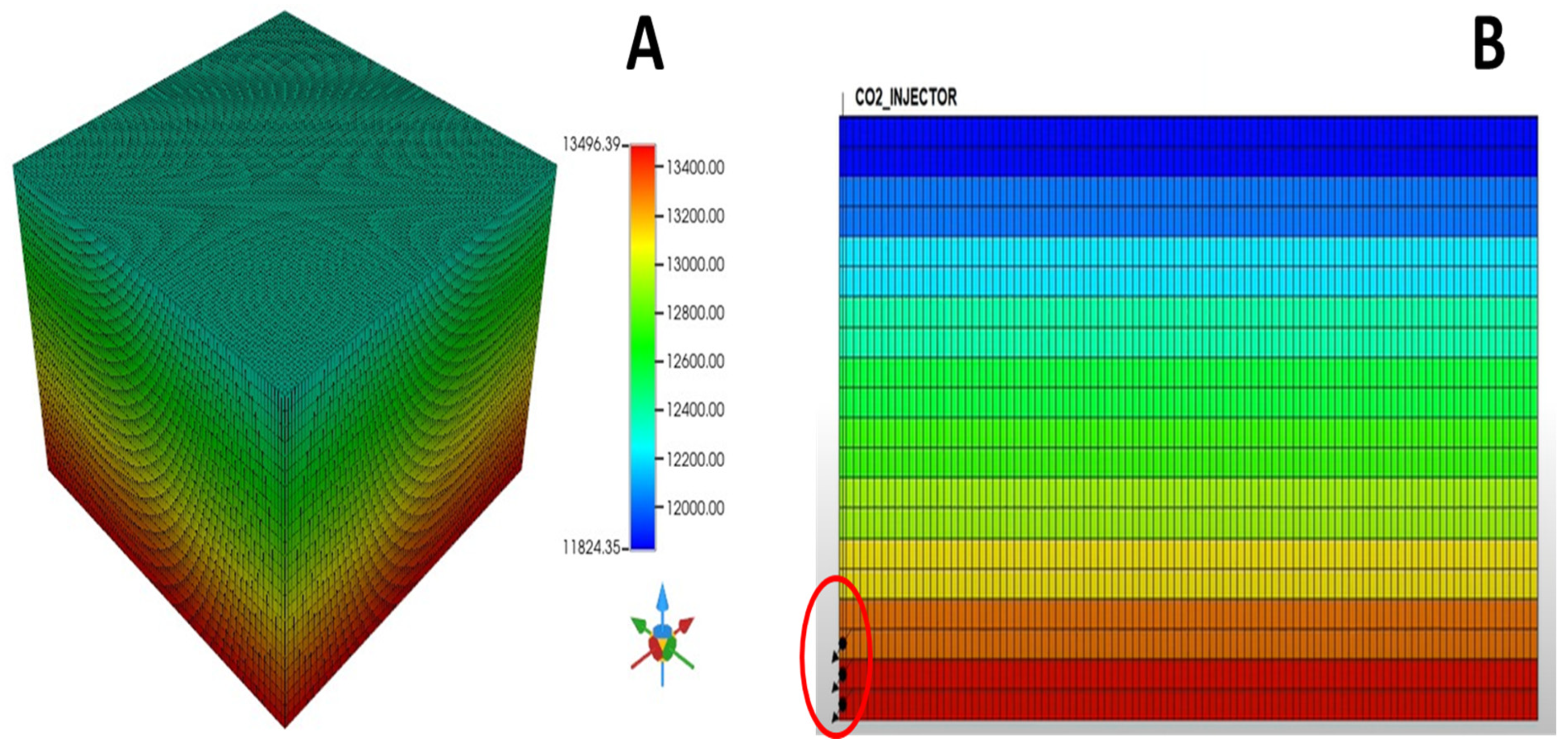

3.2. ANN Model Development
3.3. Different ANN Algorithms in MATLAB
| Parameters | Highest Value | Lowest Value |
|---|---|---|
| Thickness (m) | 10 | 3 |
| Hysteresis factor | 0.6 | 0.1 |
| Injector BHP, KPa | 50,000 | 30,000 |
| Injection Rate (m3/day) | 12,000 | 7000 |
| Horizontal Permeability (md) | 1000 | 50 |
| Vertical Permeability (md) | 0.5 | 0.1 |
| Porosity (%) | 0.3 | 0.08 |
| Reservoir Pressure, KPa | 11,800 | 8000 |
| Aquifer Volume, m3 | 10,000 | 1000 |
| Thickness (m) | 10 | 3 |
| Hysteresis factor | 0.6 | 0.1 |
4. Results and Discussion
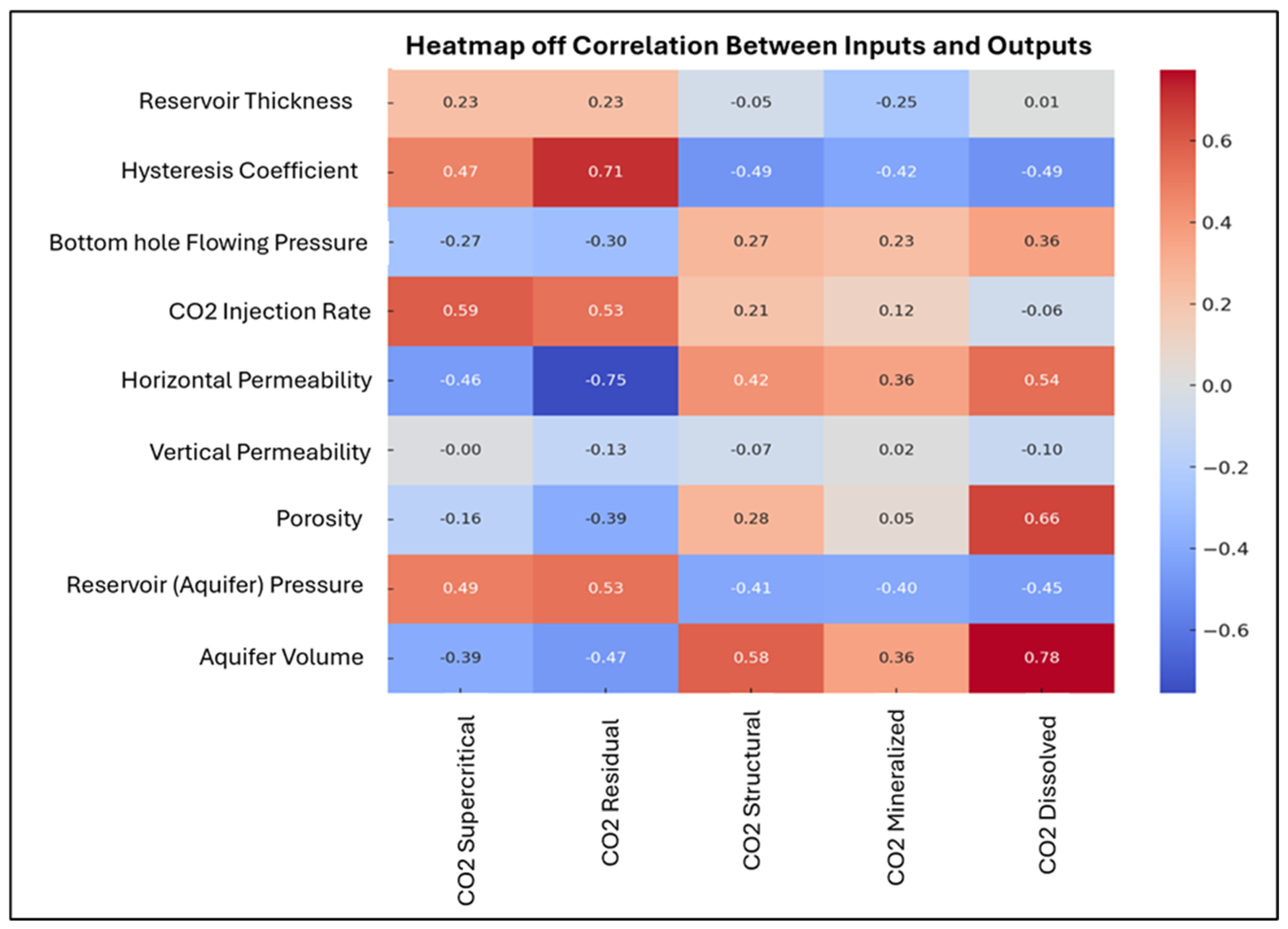
4.1. Impact of Different Parameters on Different Traps
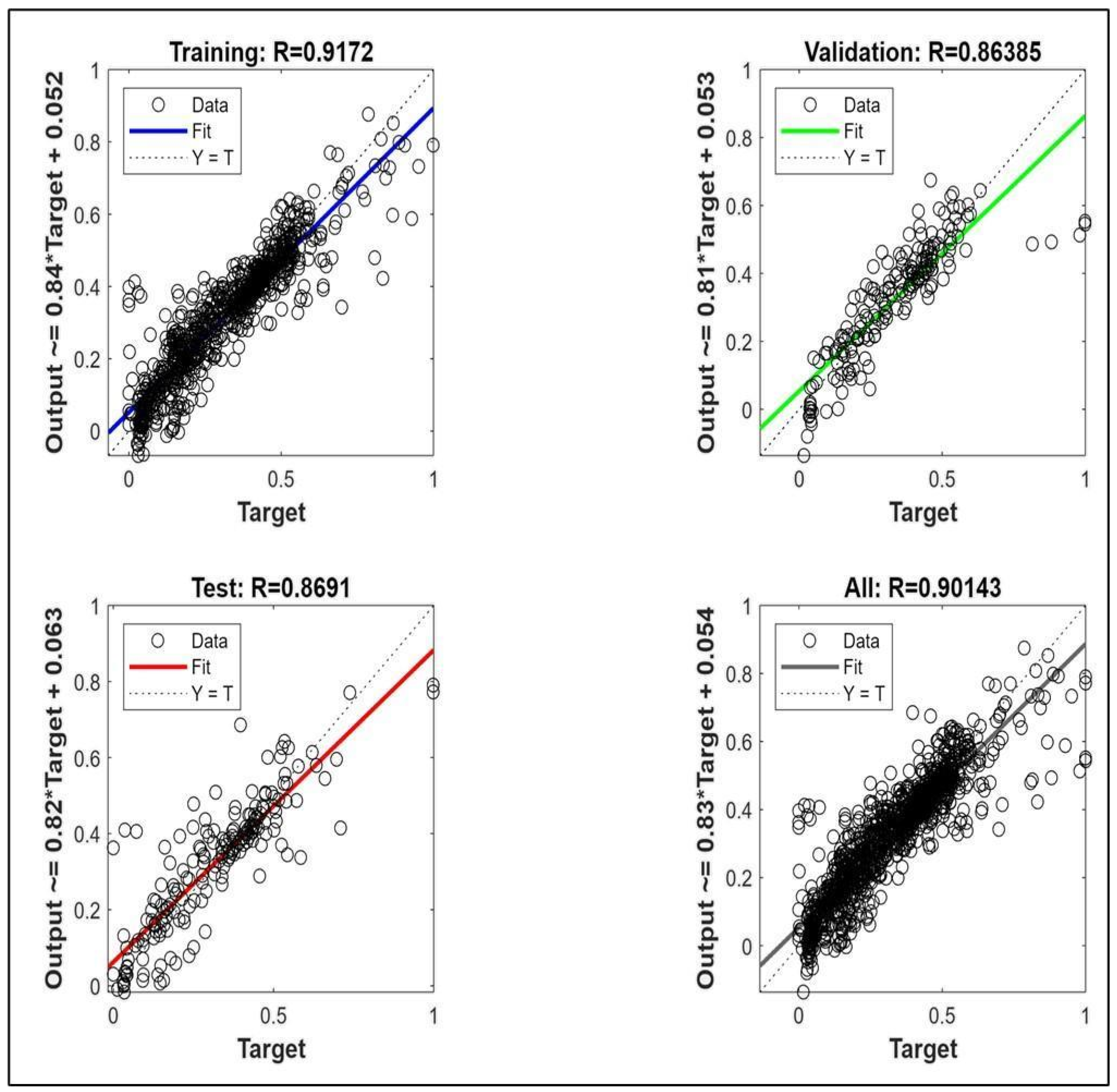
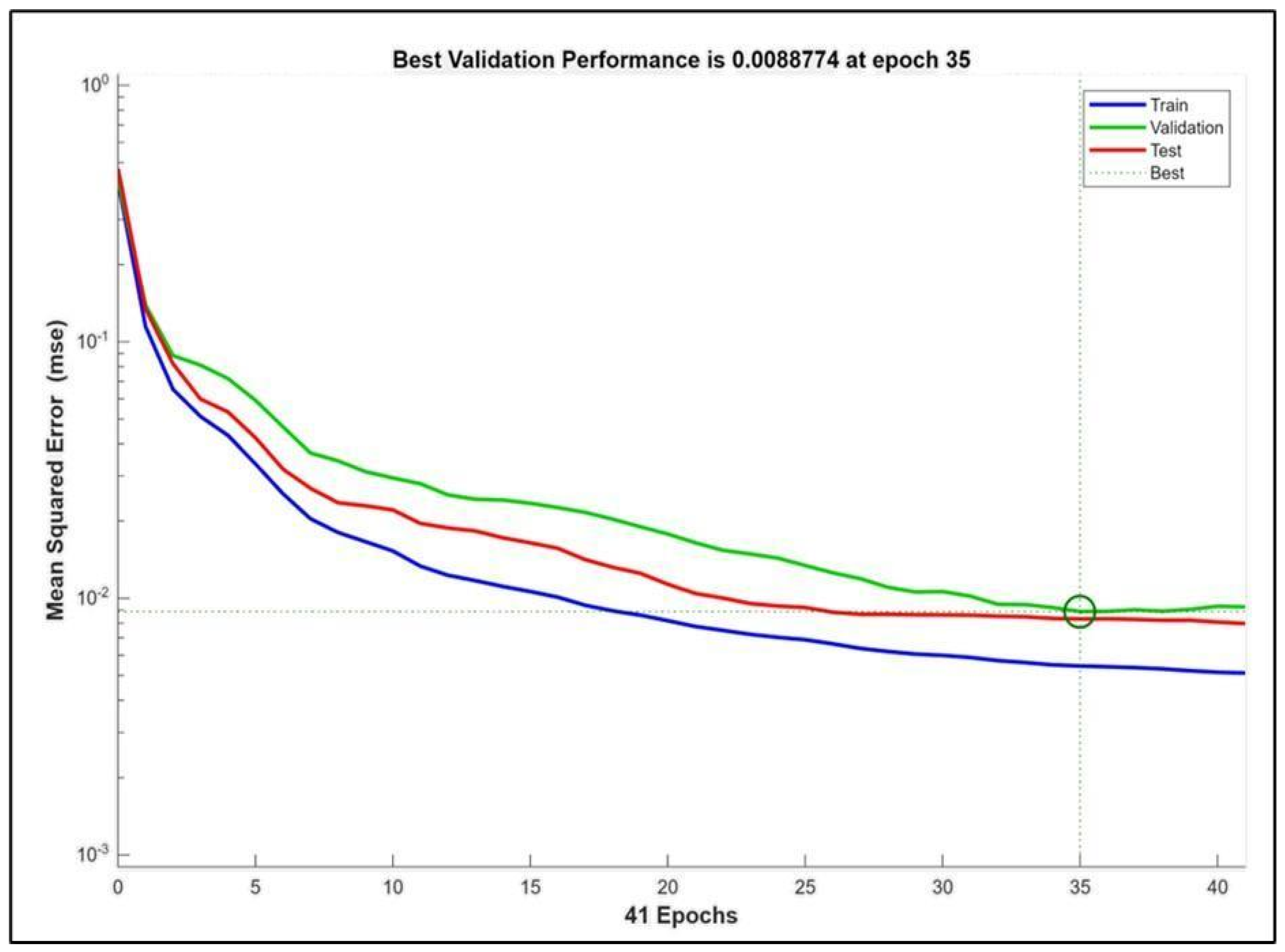
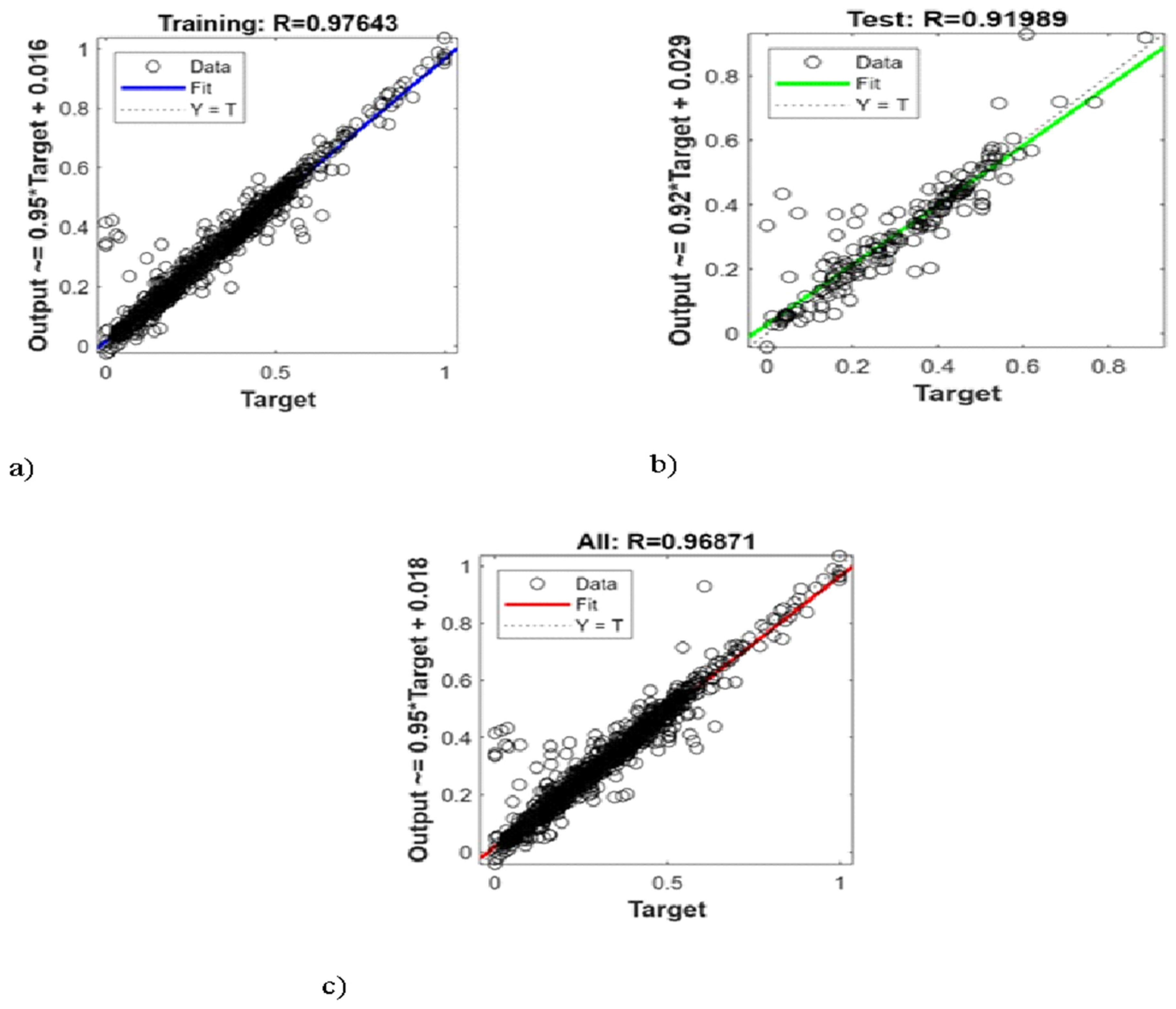
4.2. Evaluating the Reliability and Accuracy of the Models

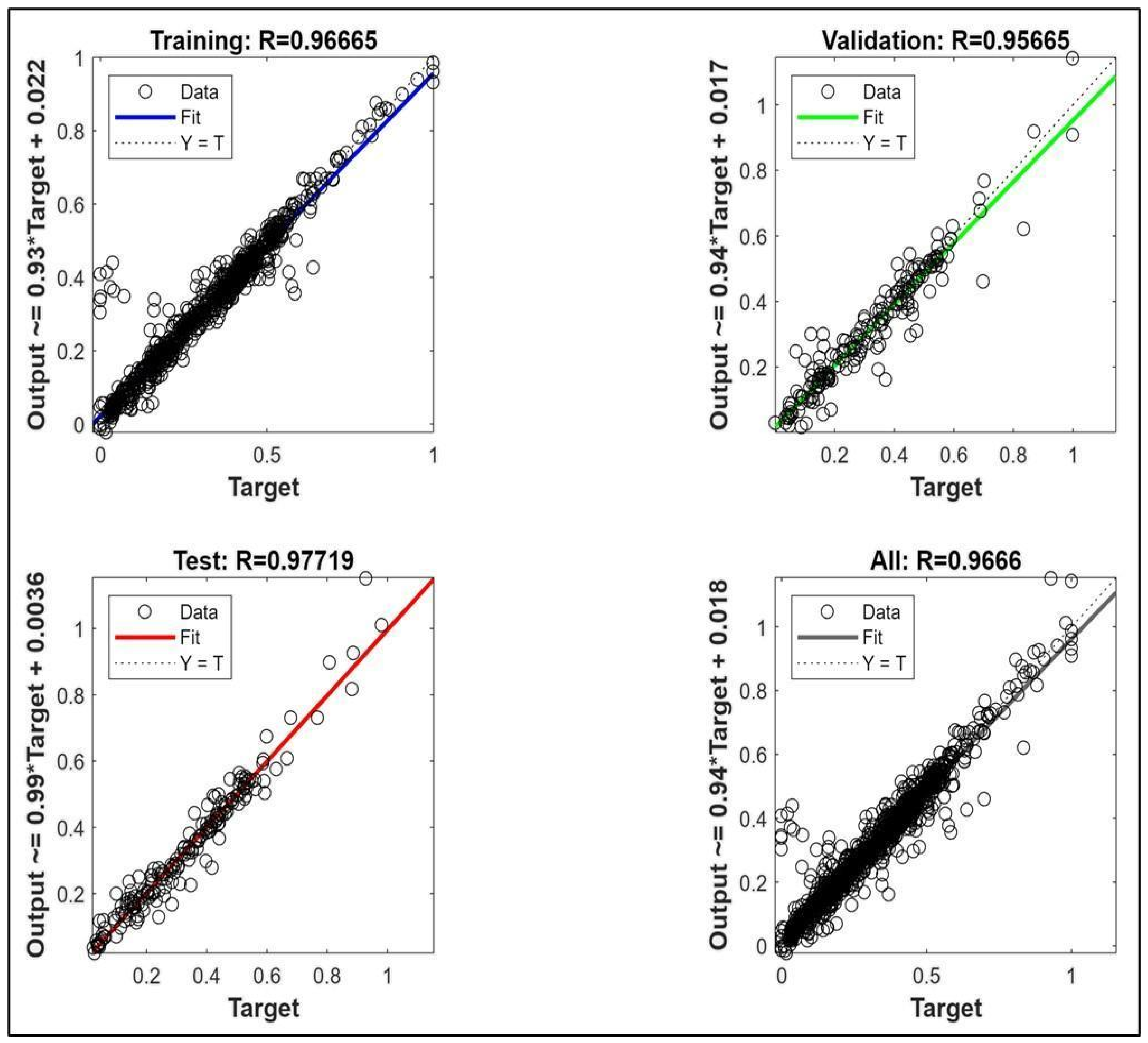
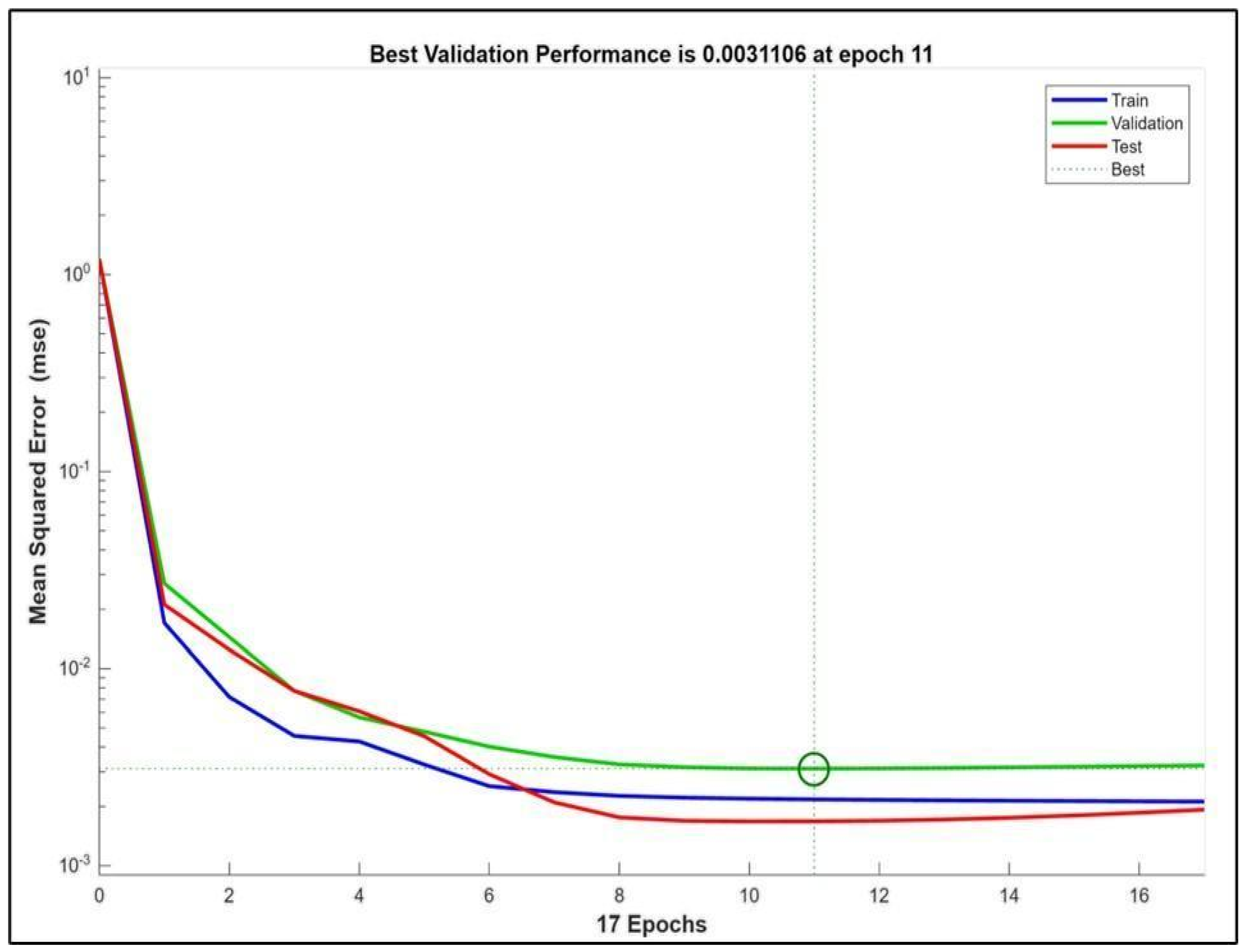
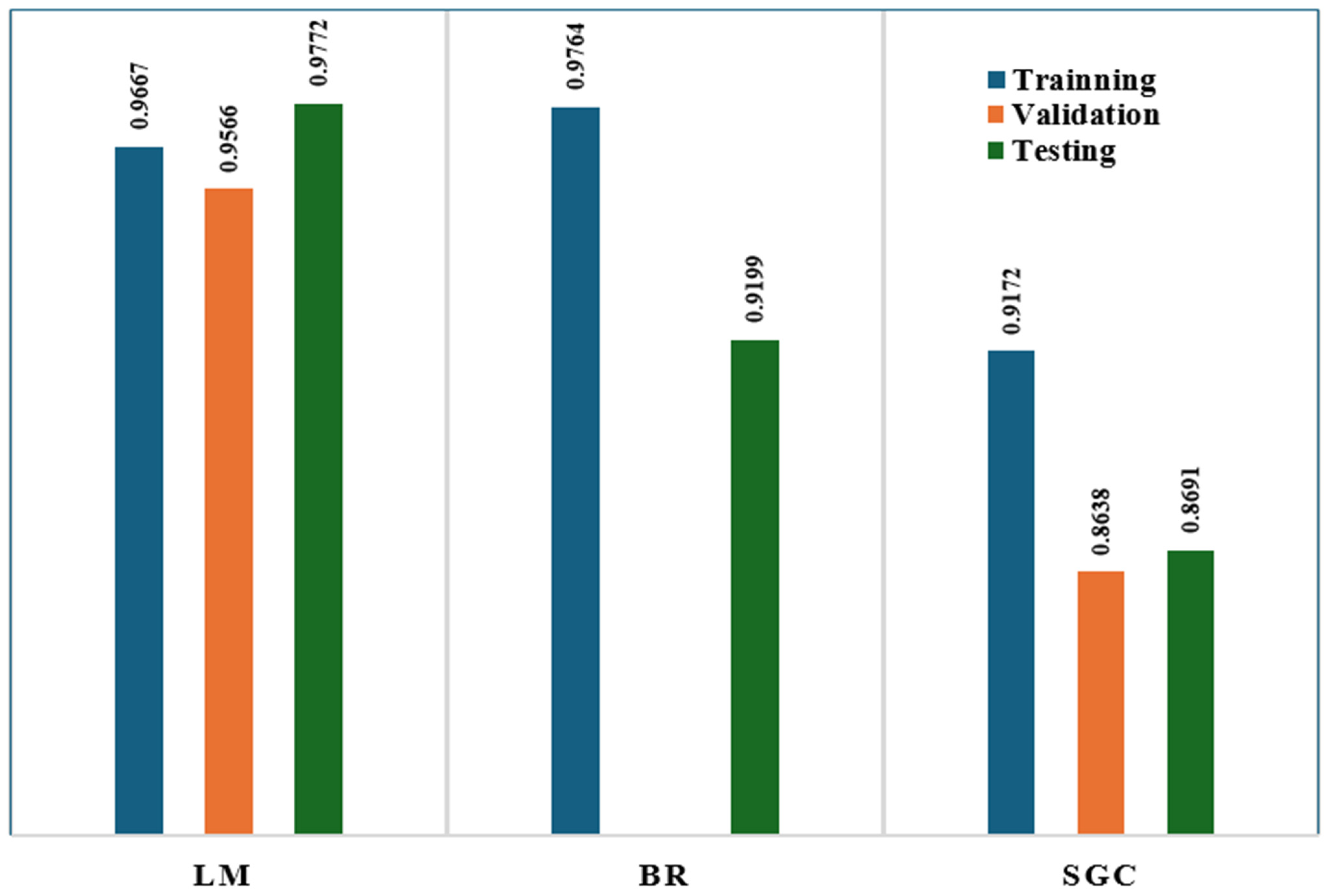
4.3. Strengths, Limitations and Future Work
5. Conclusions
- The generation of the diverse dataset from 250 CMG-GEM simulations using detailed sensitivity analysis in the development of ANN models yielded a diverse dataset covering several subsurface and operation scenarios.
- This generated dataset is used to develop different ANN models with different algorithms while including the optimization of the number of inputs, outputs, and hidden layers.
- Then, based on the results, the final ANN was chosen to encompass 9 inputs with 10 hidden layers and 5 outputs.
- The inputs represented in the geological and operational parameters include the porosity, grid thickness, both horizontal and vertical permeability, injection rate, bottom hole flowing pressure, hysteresis factor, aquifer volume, and reservoir pressure.
- The outputs included the CO2 trapping states, including structural, residual, dissolved, mineralized, and total (supercritical).
- The Levenberg–Marquardt (LM) algorithm is selected as it showed higher stability and efficiency compared to the other algorithms, with an impressive coefficient of determination (R2) of 0.977 in forecasting CO2 sequestration.
- The methodology deployed in the research provides a scalable framework that leverages sophisticated simulation tools alongside machine learning techniques, thereby enriching our comprehension of CCS processes. A sensitivity analysis integral to the simulation phase was instrumental in pinpointing pivotal parameters that influence CO2 sequestration, which in turn guided the development of the ANN model and ensured its applicability to practical scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aminu, M.; Nabavi, S.; Rochelle, C.; Manović, V. A review of developments in carbon dioxide storage. Appl. Energy 2017, 208, 1389–1419. [Google Scholar] [CrossRef]
- Umrani, R.; Jones, R.; Ware, C.; Janise, D.; Ozah, R.; Joshi, N. Evaluating an Area of Review for CO2 Sequestration and Storage: A Subsurface Modelling Workflow Tied to Regulatory Guidelines. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2023. [Google Scholar] [CrossRef]
- Leung, D.; Caramanna, G.; Maroto-Valer, M. An overview of current status of carbon dioxide capture and storage technologies. Renew. Sustain. Energy Rev. 2014, 39, 426–443. [Google Scholar] [CrossRef]
- McLaughlin, H.; Littlefield, A.A.; Menefee, M.; Kinzer, A.; Hull, T.; Sovacool, B.K.; Bazilian, M.D.; Kim, J.; Griffiths, S. Carbon capture utilization and storage in review: Sociotechnical implications for a carbon reliant world. Renew. Sustain. Energy Rev. 2023, 177, 113215. [Google Scholar] [CrossRef]
- Xu, S.; Baslaib, M.; Keebali, A.; Para, H.; BinAmro, A. Potential for Permanent CO2 Geological Storage, an Onshore Abu Dhabi Large Scale Assessment. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 31 October 2022. [Google Scholar] [CrossRef]
- Yusuf, M.; Ibrahim, H. A comprehensive review on recent trends in carbon capture, utilization, and storage techniques. J. Environ. Chem. Eng. 2023, 11, 111393. [Google Scholar] [CrossRef]
- Peter, K.; Sally, M.B.; Hélène, P.; Peter, P.; Jennifer, W. An Overview of the Status and Challenges of CO2 Storage in Minerals and Geological Formations. Front. Clim. 2019, 1, 9. [Google Scholar] [CrossRef]
- Mwenketishi, G.T.; Benkreira, H.; Rahmanian, N. A Comprehensive Review on Carbon Dioxide Sequestration Methods. Energies 2023, 16, 7971. [Google Scholar] [CrossRef]
- Benson, S.; Orr, F. Carbon Dioxide Capture and Storage. MRS Bull. 2008, 33, 303–305. [Google Scholar] [CrossRef]
- Bashir, A.; Ali, M.; Patil, S.; Aljawad, M.S.; Mahmoud, M.; Al-Shehri, D.; Hoteit, H.; Kamal, M.S. Comprehensive review of CO2 geological storage: Exploring principles, mechanisms, and prospects. Earth-Sci. Rev. 2024, 249, 104672. [Google Scholar] [CrossRef]
- Kamashev, A.; Amanbek, Y. Reservoir Simulation of CO2 Storage Using Compositional Flow Model for Geological Formations in Frio Field and Precaspian Basin. Energies 2021, 14, 8023. [Google Scholar] [CrossRef]
- Application of artificial neural networks for reservoir characterization with limited data. J. Pet. Sci. Eng. 2005, 49, 212–222. [CrossRef]
- Bachu, S. CO2 Storage in Geological Media: Role, Means, Status and Barriers to deployment. Prog. Energy Combust. Sci. 2008, 34, 254–273. [Google Scholar] [CrossRef]
- Bachu, S.; Bonijoly, D.; Bradshaw, J.; Burruss, R.; Holloway, S.; Christensen, N.P.; Mathiassen, O.M. CO2 storage capacity estimation: Methodology and gaps. Int. J. Greenh. Gas Control 2007, 1, 430–443. [Google Scholar] [CrossRef]
- Song, Y.; Sung, W.; Jang, Y.; Jung, W. Application of an artificial neural network in predicting the effectiveness of trapping mechanisms on CO2 sequestration in saline aquifers. Int. J. Greenh. Gas Control 2020, 98, 103042. [Google Scholar] [CrossRef]
- Khanal, A.; Shahriar, M.F. Physics-Based Proxy Modeling of CO2 Sequestration in Deep Saline Aquifers. Energies 2022, 15, 4350. [Google Scholar] [CrossRef]
- Bourg, I.; Beckingham, L.; DePaolo, D. The Nanoscale Basis of CO2 Trapping for Geologic Storage. Environ. Sci. Technol. 2015, 49, 10265–10284. [Google Scholar] [CrossRef] [PubMed]
- Saadatpoor, E.; Bryant, S.L.; Sepehrnoori, K. New Trapping Mechanism in Carbon Sequestration. Transp. Porous Media 2010, 82, 3–17. [Google Scholar] [CrossRef]
- Novak Mavar, K.; Gaurina-Medimurec, N.; Hrnčević, L. Significance of Enhanced Oil Recovery in Carbon Dioxide Emission Reduction. Sustainability 2021, 13, 1800. [Google Scholar] [CrossRef]
- Burnside, N.; Naylor, M. Review and implications of relative permeability of CO2/brine systems and residual trapping of CO2. Int. J. Greenh. Gas Control 2014, 23, 1–11. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H.; Green, C.P.; Ennis-King, J. Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments. Int. J. Greenh. Gas Control 2015, 40, 238–266. [Google Scholar] [CrossRef]
- Iglauer, S. Dissolution Trapping of Carbon Dioxide in Reservoir Formation Brine—A Carbon Storage Mechanism; INTECH Open Access Publisher: London, UK, 2011; pp. 233–262. [Google Scholar] [CrossRef]
- Dumitrache, L.N.; Suditu, S.; Ghețiu, I.; Pană, I.; Brănoiu, G.; Eparu, C. Using Numerical Reservoir Simulation to Assess CO2 Capture and Underground Storage, Case Study on a Romanian Power Plant, and Its Surrounding Hydrocarbon Reservoirs. Processes 2023, 11, 805. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Salimi, H.; Zitha, P.L.J.; Bruning, J. Numerical Simulation of Density-Driven Natural Convection in Porous Media with Application for CO2 Injection Projects. Int. J. Heat Mass Transf. 2007, 50, 5054–5064. [Google Scholar] [CrossRef]
- Muradkhanli, L. Neural Networks for Prediction of Oil Production. IFAC-Pap. Online 2018, 51, 415–417. [Google Scholar] [CrossRef]
- Khan, C.; Ge, L.; Rudolph, V. Reservoir Simulation Study for CO2 Sequestration in Saline Aquifers. Int. J. Appl. Sci. Eng. 2015, 5, 30–45. [Google Scholar]
- You, J.; Ampomah, W.; Sun, Q.; Kutsienyo, E.J.; Balch, R.S.; Cather, M. Multi-Objective Optimization of CO Enhanced Oil Recovery Projects Using a Hybrid Artificial Intelligence Approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar] [CrossRef]
- Wen, G.; Li, Z.; Long, Q.; Azizzadenesheli, K.; Anandkumar, A.; Benson, S.M. Real-time High-resolution CO2 Geological Storage Prediction using Nested Fourier Neural Operators. Energy Environ. Sci. 2023, 16, 1732–1741. [Google Scholar] [CrossRef]
- Tang, M.; Ju, X.; Durlofsky, L.J. Deep-learning-based coupled flow-geomechanics surrogate model for CO2 sequestration. Int. J. Greenh. Gas Control 2022, 118, 103692. [Google Scholar] [CrossRef]
- Thanh, H.V.; Lee, K.-K. Application of machine learning to predict CO2 trapping performance in deep saline aquifers. Energy 2022, 239, 122457. [Google Scholar] [CrossRef]
- Ranganathan, P.; van Hemert, P.; Rudolph, E.S.J.; Zitha, P.Z. Numerical modeling of CO2 mineralisation during storage in deep saline aquifers. Energy Procedia 2011, 4, 4538–4545. [Google Scholar] [CrossRef]
- Shokir EM, E.M.; Hamed, M.M.; Ibrahim AE, S.; Mahgoub, I. Gas lift optimization using artificial neural network and integrated production modeling. Energy Fuels 2017, 31, 9302–9307. [Google Scholar] [CrossRef]
- Bahaa, M.; Shokir, E.; Mahgoub, I. Soft Computation Application: Utilizing Artificial Neural Network to Predict the Fluid Rate and Bottom Hole Flowing Pressure for Gas-lifted Oil Wells. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 12–15 November 2018. [Google Scholar] [CrossRef]
- Ibrahim, A.F.; Elkatatny, S. Data-driven models to predict shale wettability for CO2 sequestration applications. Sci. Rep. 2023, 13, 10151. [Google Scholar] [CrossRef]
- The MathWorks Inc. MATLAB, version 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022; Available online: https://www.mathworks.com (accessed on 15 April 2024).





| Aquifer Parameters | Values |
|---|---|
| Grid number | 300,000 (100 × 100 × 30) |
| Length (m) | 1000 |
| Width (m) | 1000 |
| Depth at the top (m) | 1400 |
| Thickness (m) | 30 |
| Permeability (md) | 150 |
| Porosity (%) | 0.23 |
| Salinity (M) | 1.7 |
| Component | CO2 |
| Critical Pressure (atm) | 72.8 |
| Critical Temperature (K) | 304.2 |
| Algorithm | Performance and Accuracy | Use Cases |
|---|---|---|
| Bayesian Regularization (BR) |
| Well-suited for regression problems and complex pattern recognition tasks where model generalization was crucial. |
| Scaled Conjugate Gradient (SCG) |
| It is advantageous for training large neural networks and handling datasets where computational resources are limited. |
| Levenberg–Marquardt (LM) |
| It is effective for function approximation, pattern recognition, and time-series prediction problems where the dataset size is not excessively large. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamed, M.; Shirif, E. Sustainable CO2 Storage Assessment in Saline Aquifers Using a Hybrid ANN and Numerical Simulation Model Across Different Trapping Mechanisms. Sustainability 2025, 17, 2904. https://doi.org/10.3390/su17072904
Hamed M, Shirif E. Sustainable CO2 Storage Assessment in Saline Aquifers Using a Hybrid ANN and Numerical Simulation Model Across Different Trapping Mechanisms. Sustainability. 2025; 17(7):2904. https://doi.org/10.3390/su17072904
Chicago/Turabian StyleHamed, Mazen, and Ezeddin Shirif. 2025. "Sustainable CO2 Storage Assessment in Saline Aquifers Using a Hybrid ANN and Numerical Simulation Model Across Different Trapping Mechanisms" Sustainability 17, no. 7: 2904. https://doi.org/10.3390/su17072904
APA StyleHamed, M., & Shirif, E. (2025). Sustainable CO2 Storage Assessment in Saline Aquifers Using a Hybrid ANN and Numerical Simulation Model Across Different Trapping Mechanisms. Sustainability, 17(7), 2904. https://doi.org/10.3390/su17072904





