Surface Energy Balance of Green Roofs Using the Profile Method: A Case Study in South Korea During the Summer
Abstract
1. Introduction
2. Materials and Methods
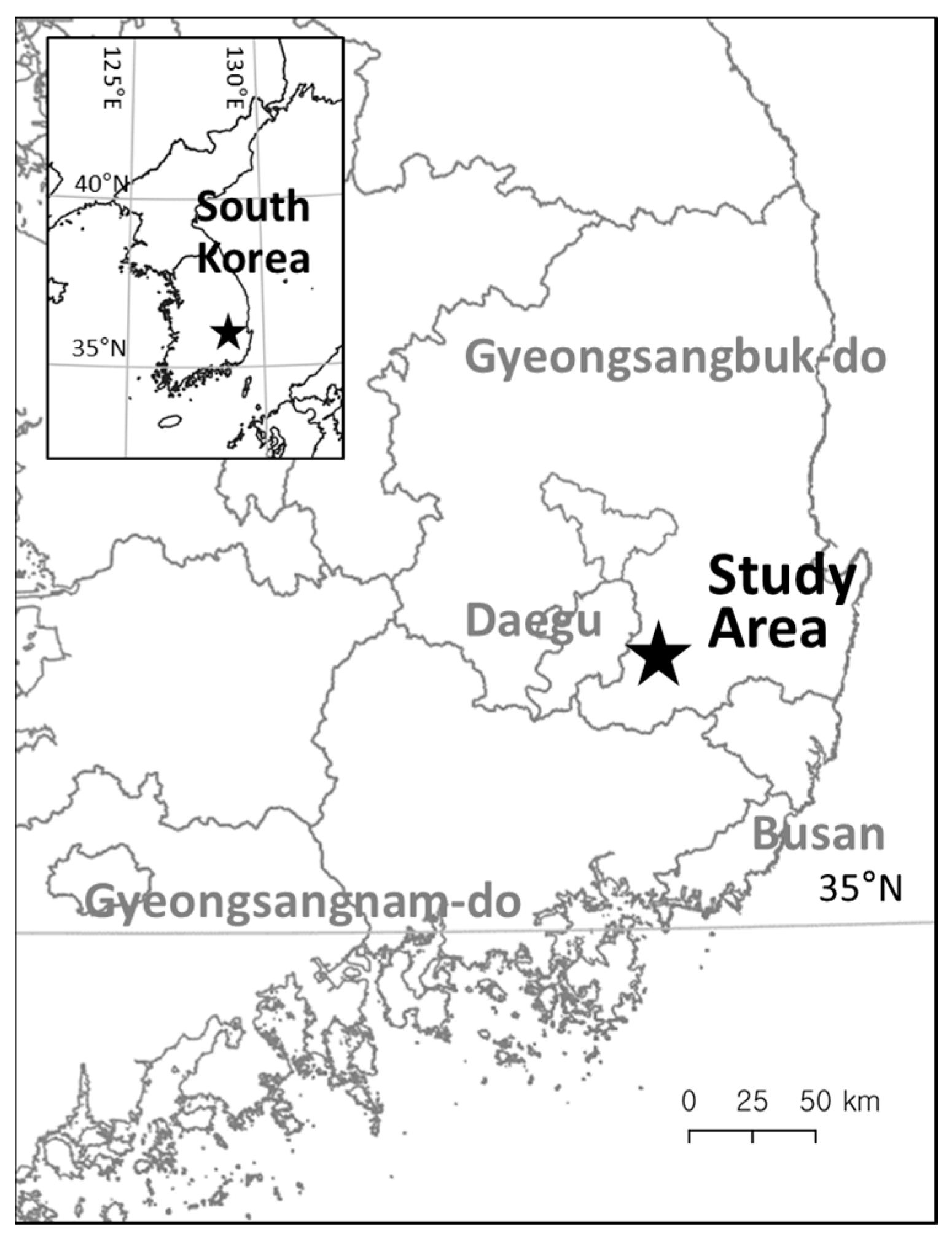
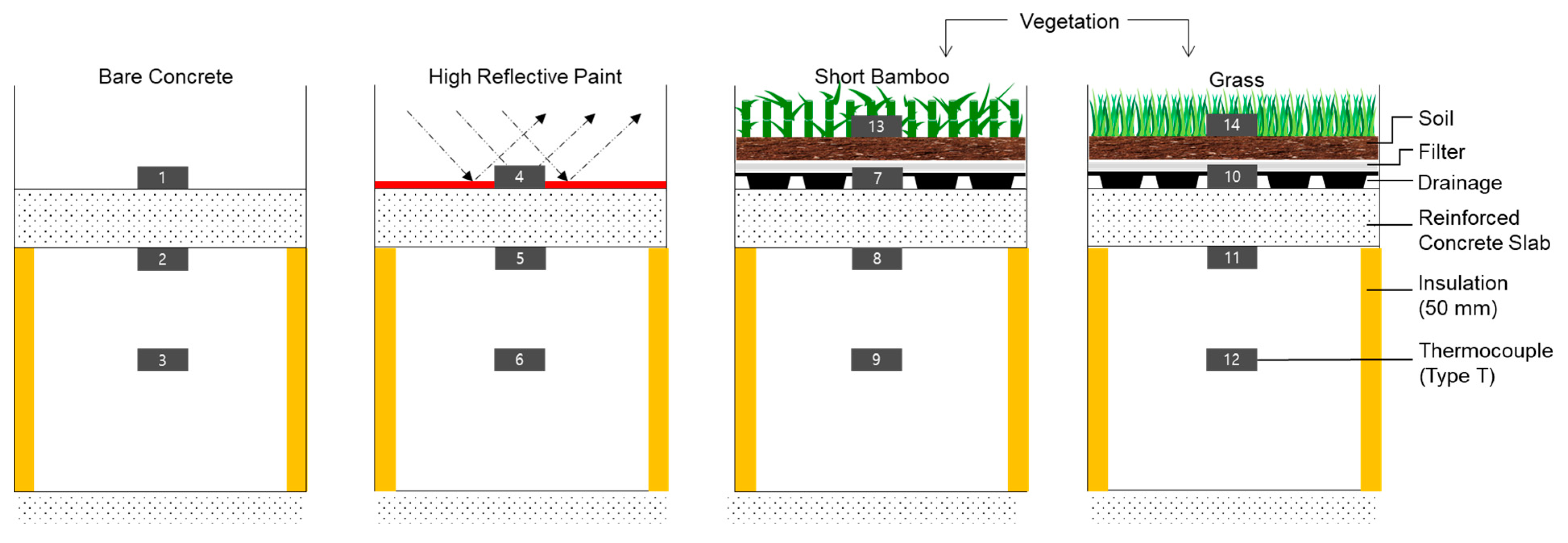
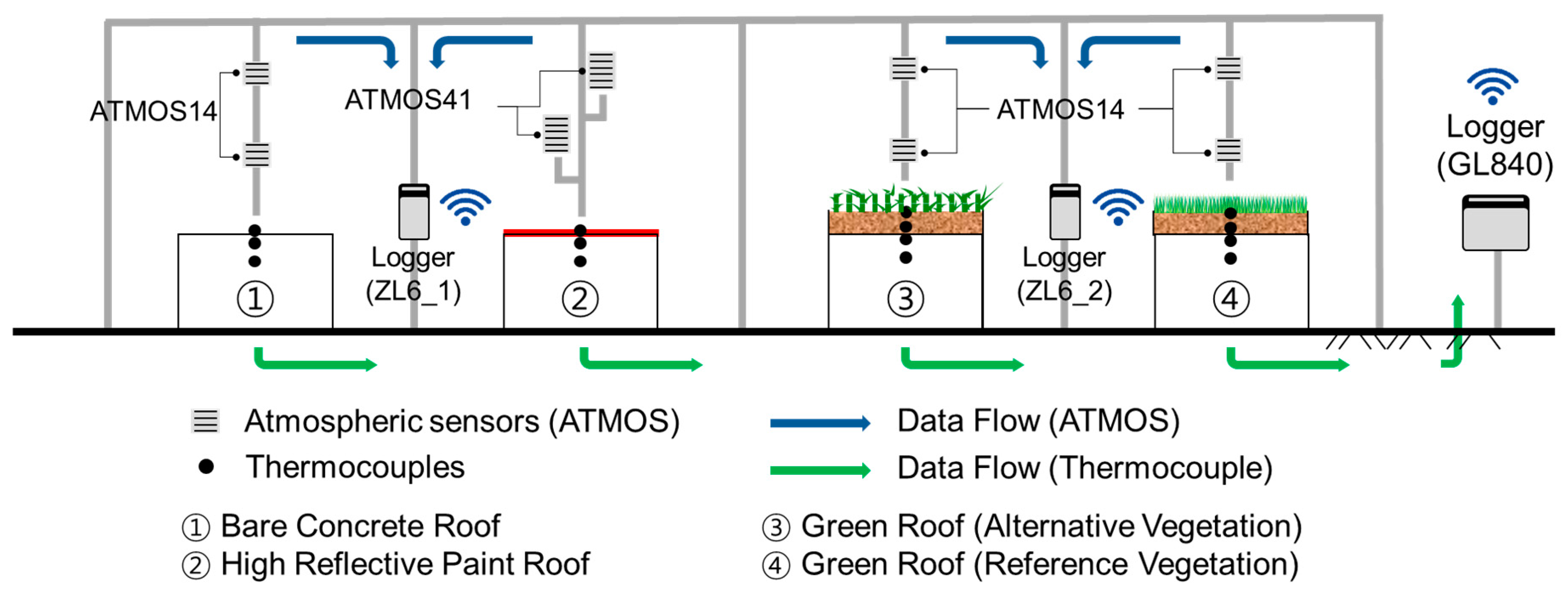
2.1. Study Area and Experimental Setup
2.2. Net Radiation and Flux Profile Method
3. Results
3.1. Concrete Roof and Highly Reflective Painted Roof
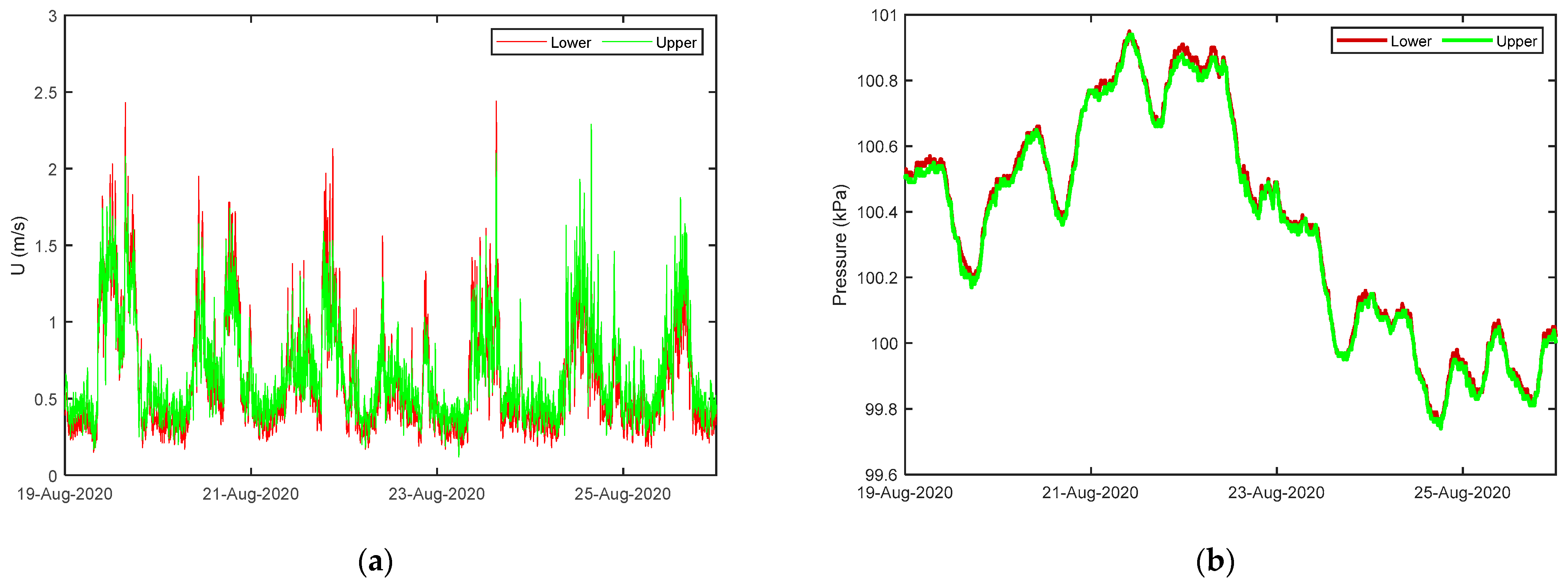
3.1.1. Wind Speed and Pressure Measurements
3.1.2. Temperature Measurements
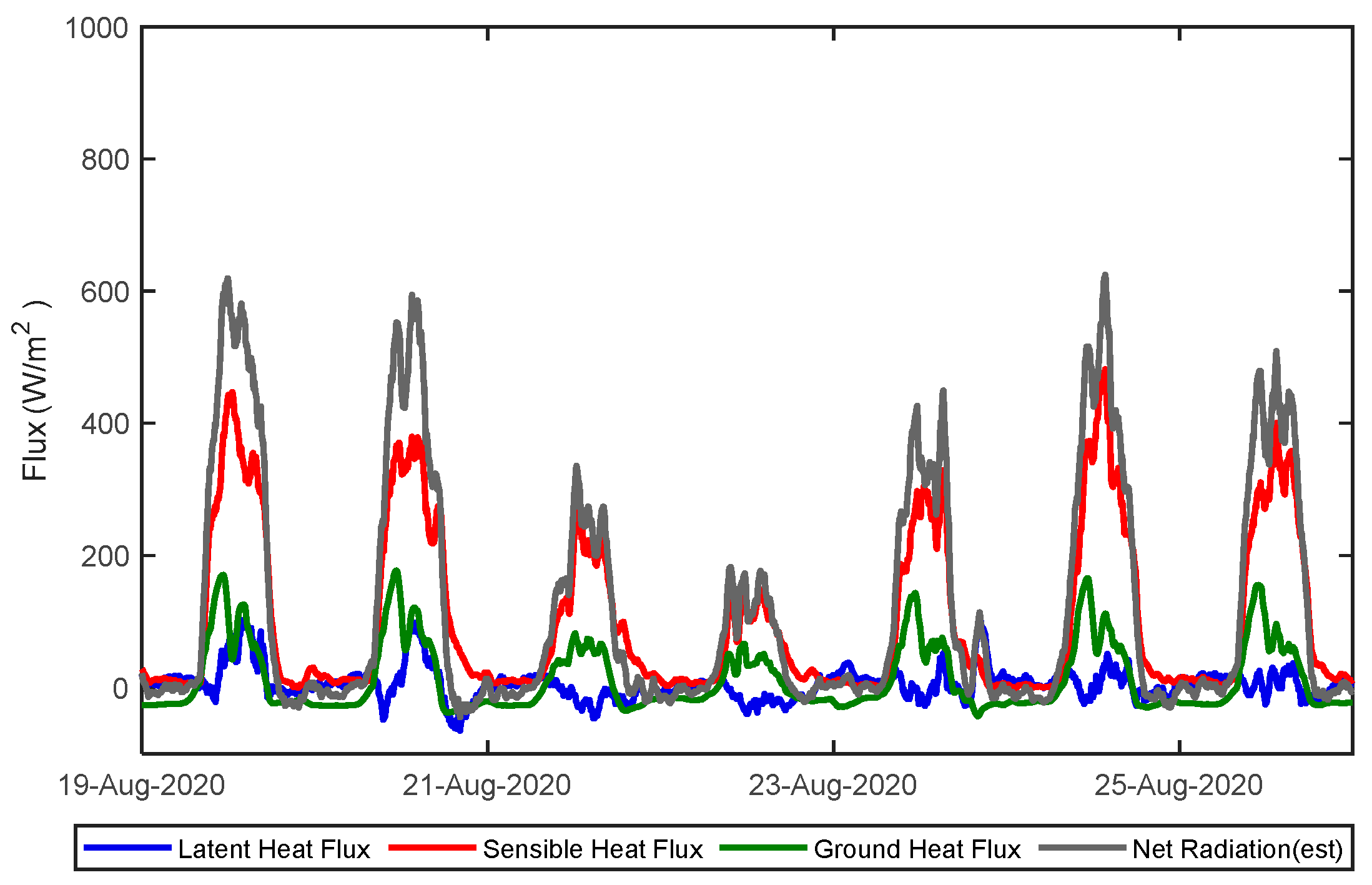
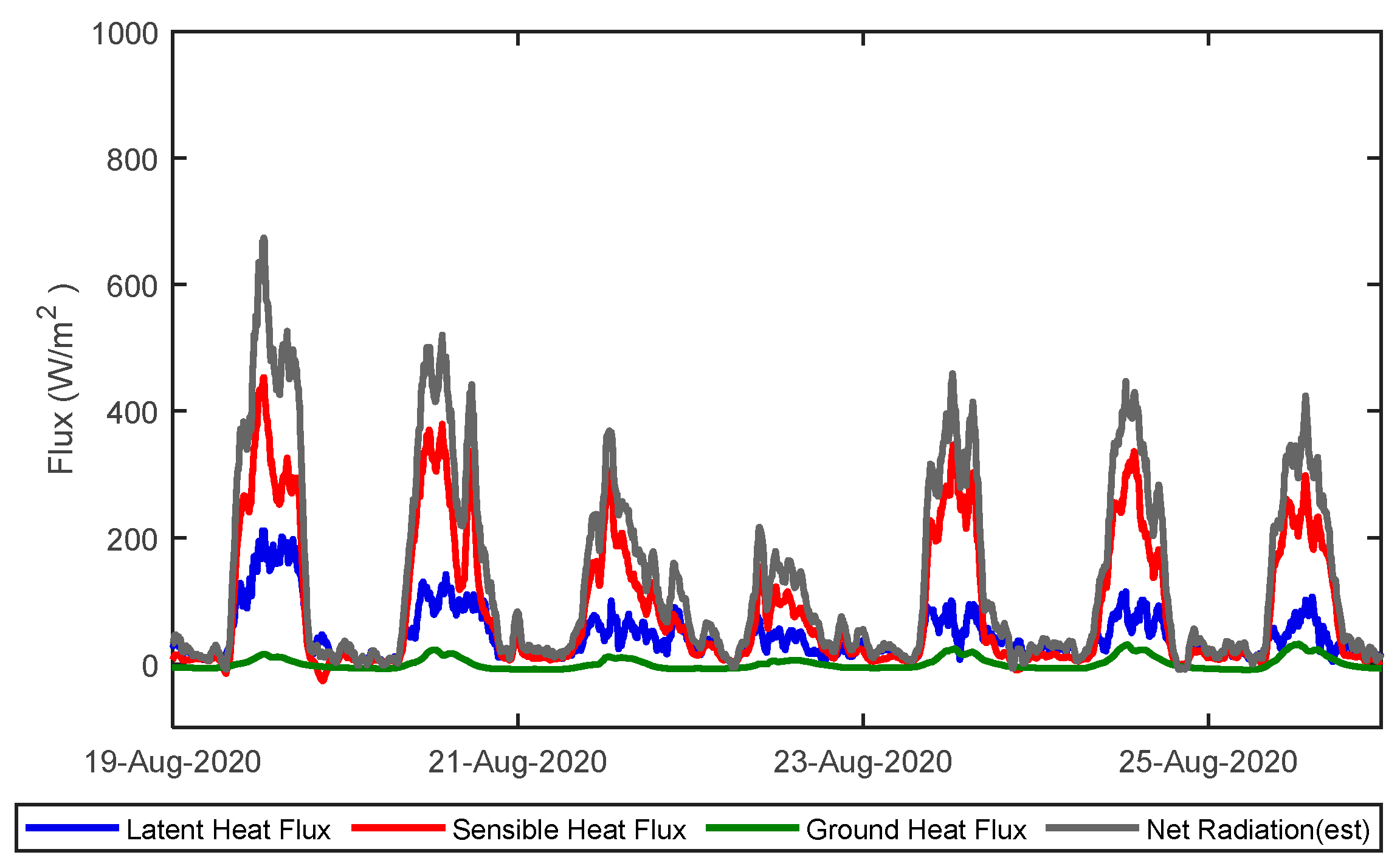
3.1.3. Estimation of Surface Energy Balance
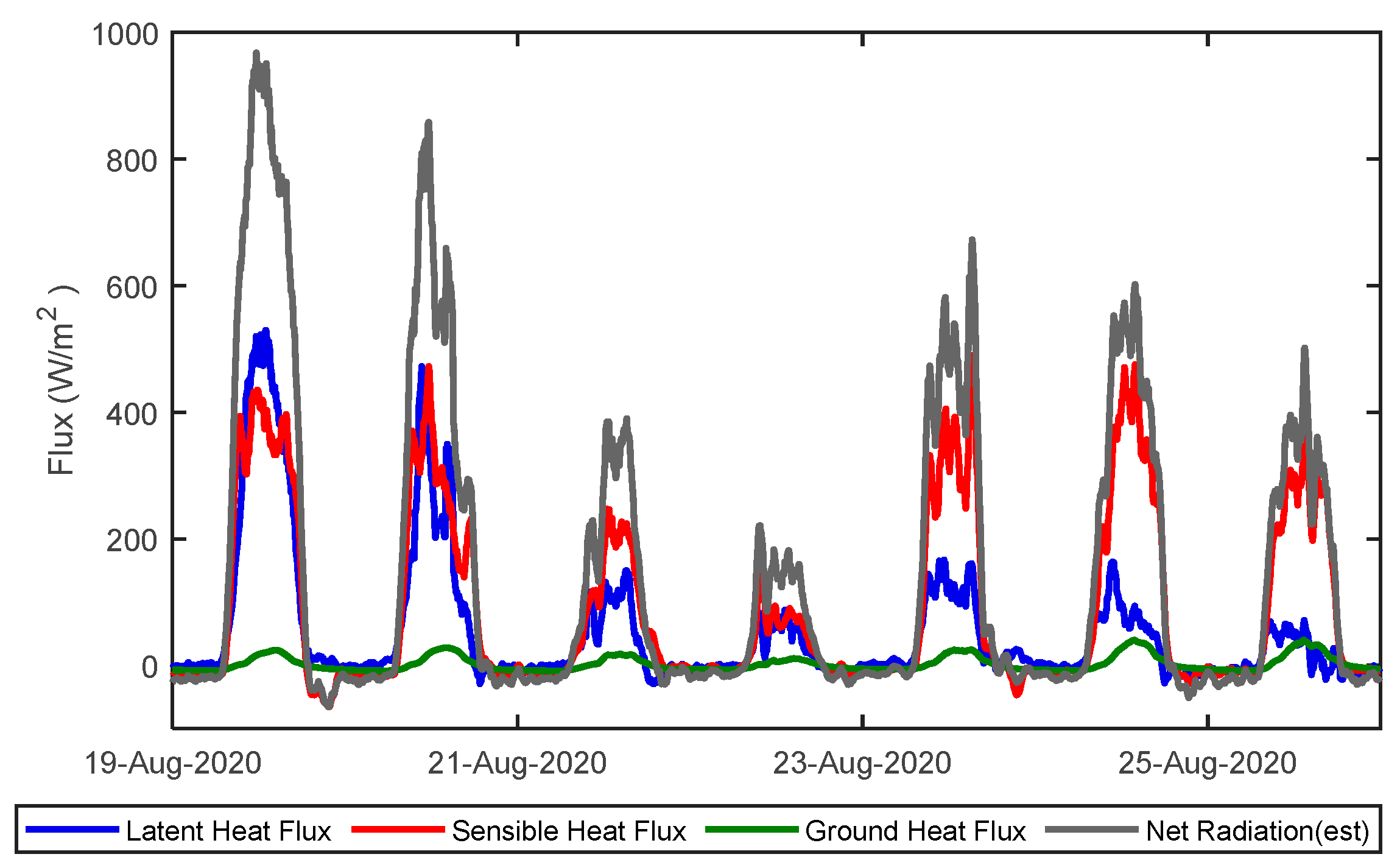
3.2. Green Roofs
3.2.1. Temperature and Pressure Measurements
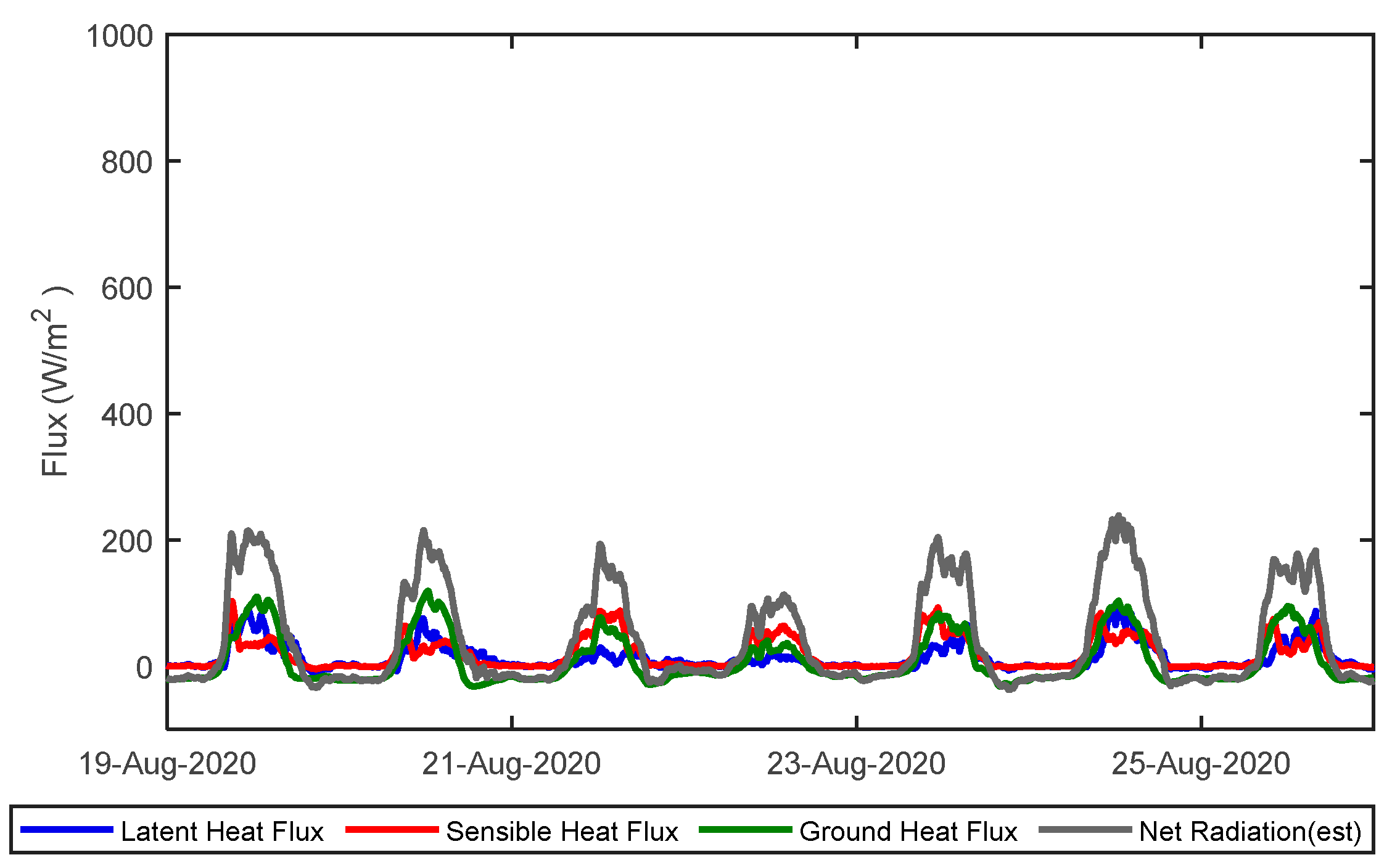
3.2.2. Estimation of Surface Energy Balance
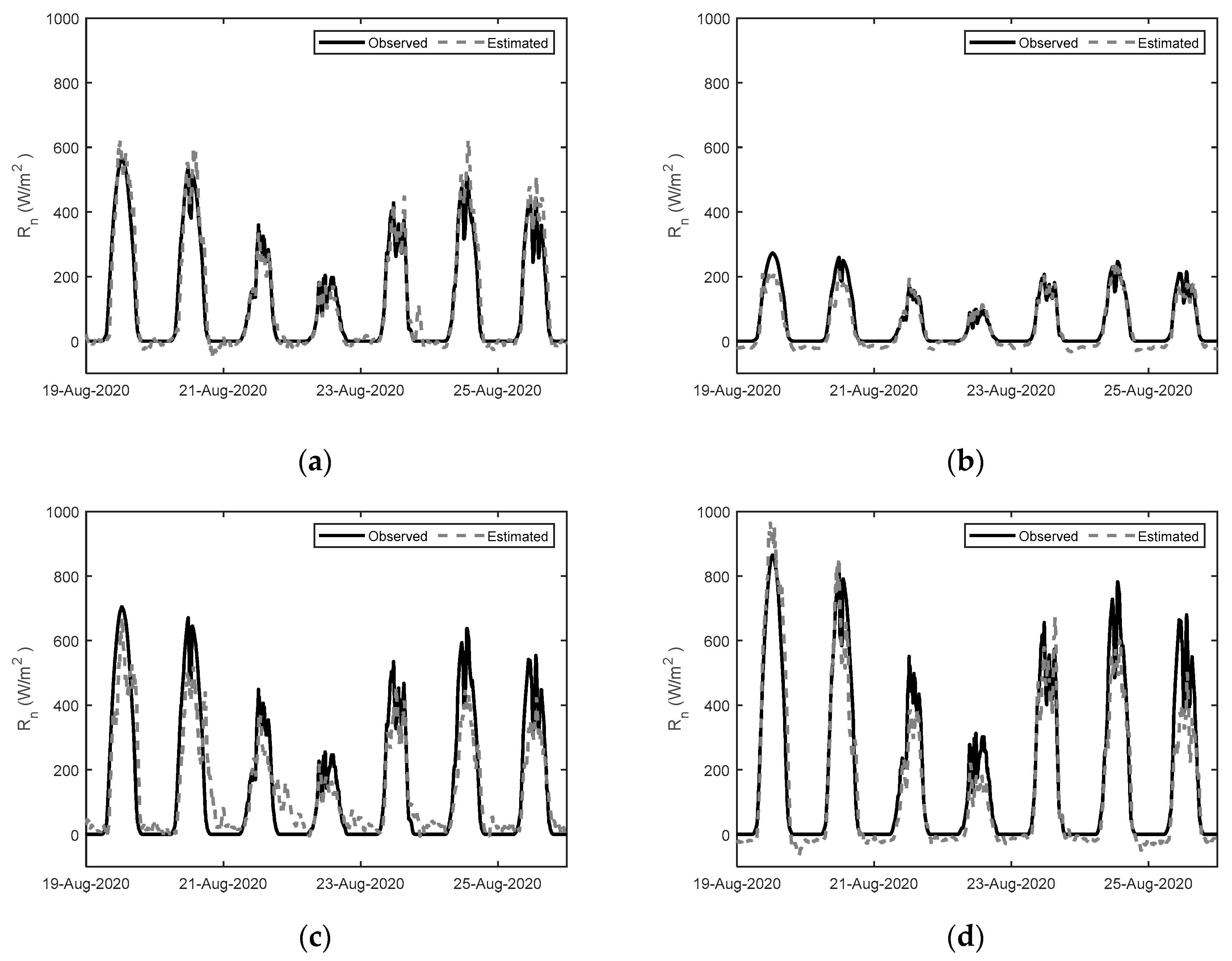
3.3. Comparison with the Observed Net Radiation
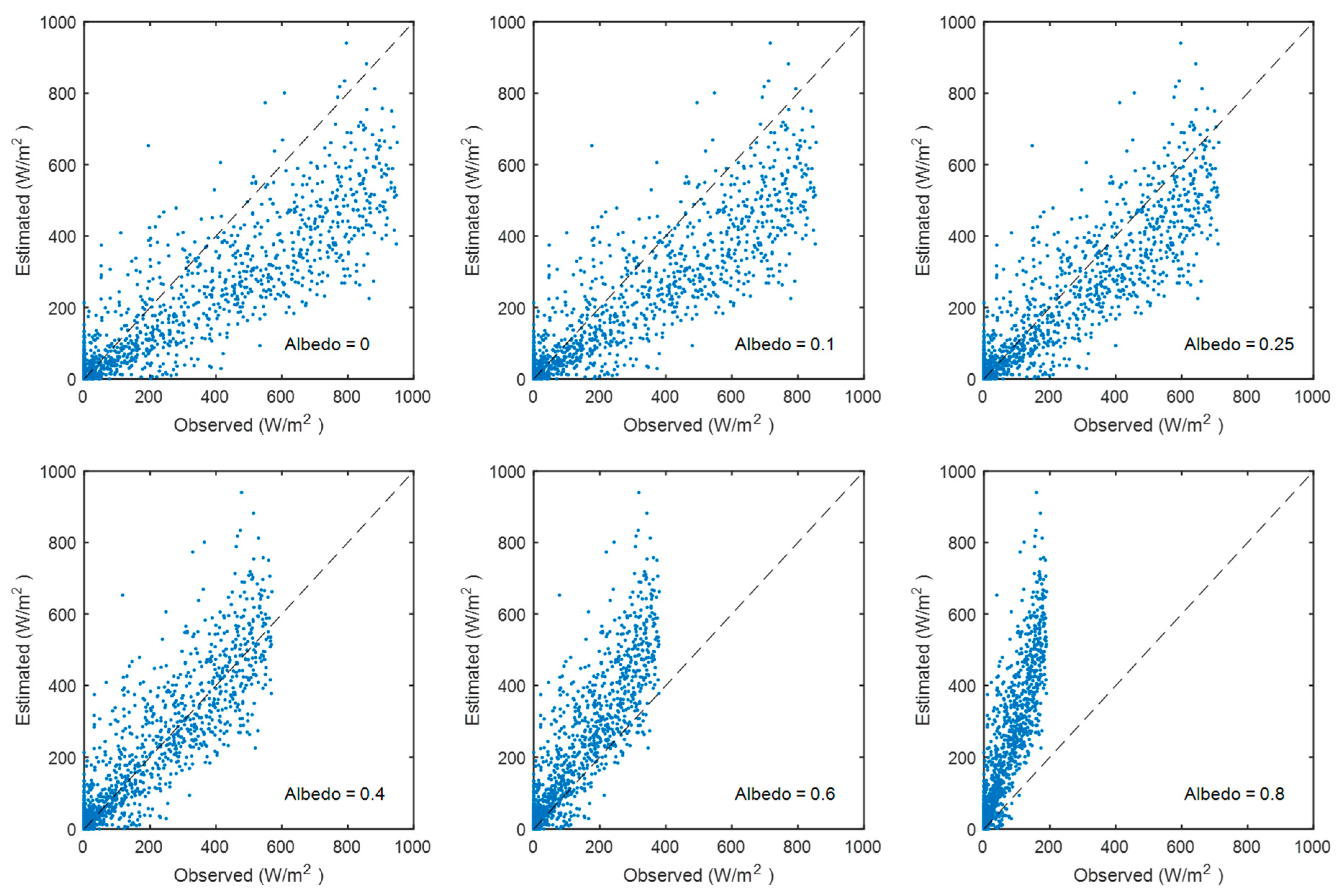
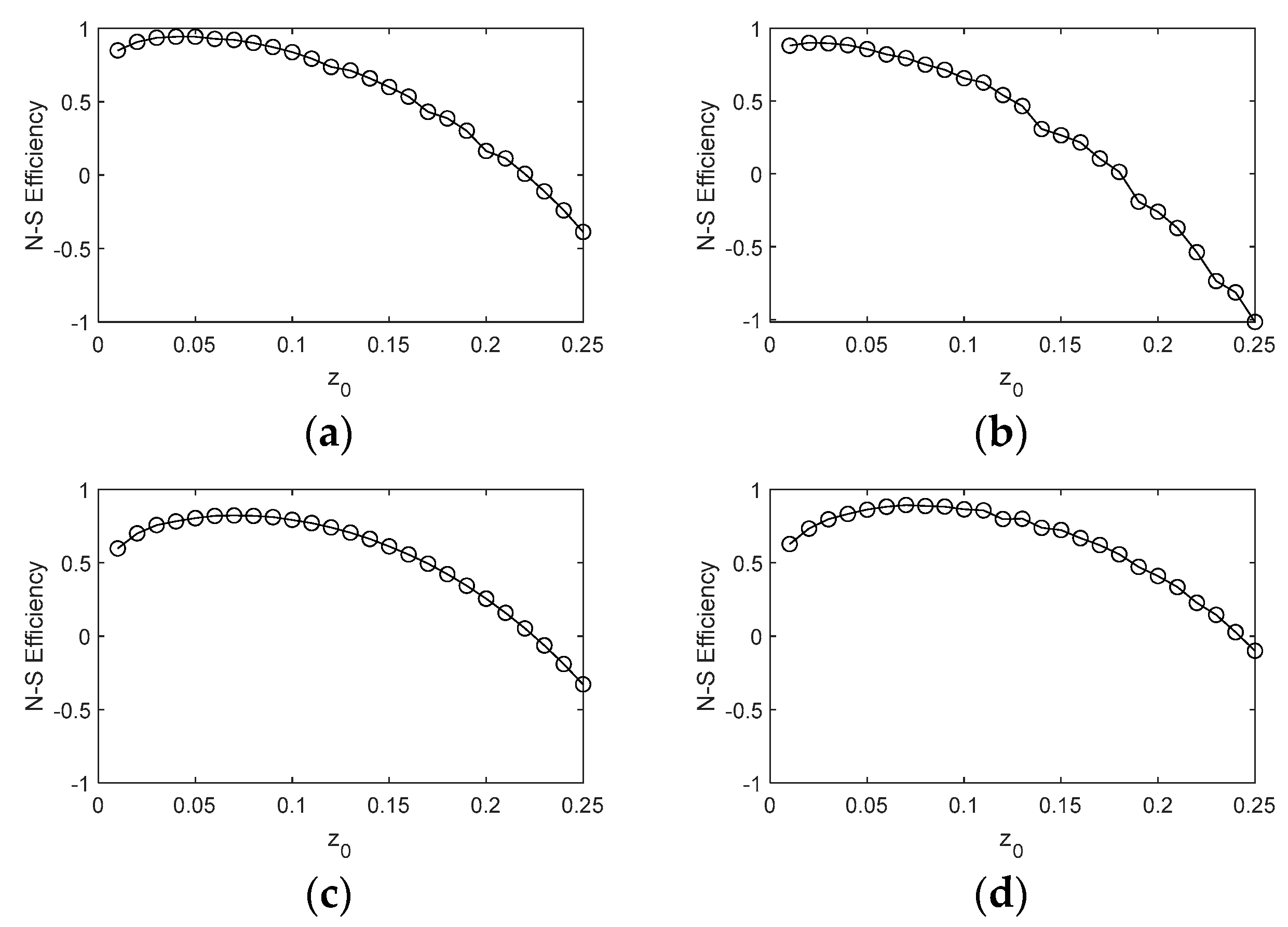
4. Discussion
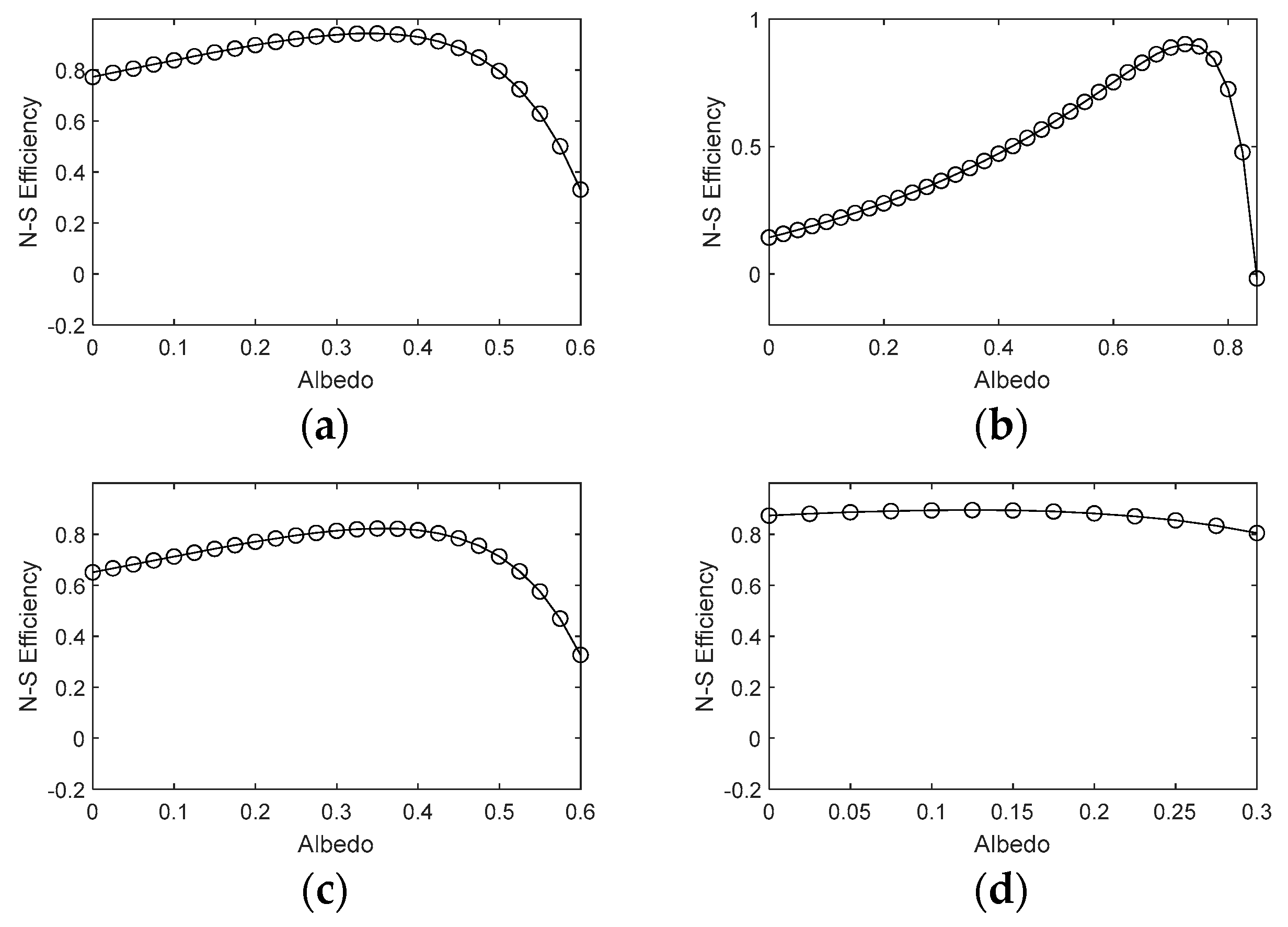
Sensitivity Analysis of the Albedo
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Slaney, S. Stormwater Management for Sustainable Urban Environments; Images Publishing Group Pty Limited: Chadstone, VIC, Australia, 2016. [Google Scholar]
- Ascione, F.; Bianco, N.; de’ Rossi, F.; Turni, G.; Vanoli, G.P. Green roofs in European climates. Are effective solutions for the energy savings in air-conditioning? Appl. Energy 2013, 104, 845–859. [Google Scholar] [CrossRef]
- Ávila-Hernández, A.; Simá, E.; Xamán, J.; Hernández-Pérez, I.; Téllez-Velázquez, E.; Chagolla-Aranda, M.A. Test box experiment and simulations of a green-roof: Thermal and energy performance of a residential building standard for Mexico. Energy Build. 2020, 209, 109709. [Google Scholar] [CrossRef]
- Baraldi, R.; Neri, L.; Costa, F.; Facini, O.; Rapparini, F.; Carriero, G. Ecophysiological and micromorphological characterization of green roof vegetation for urban mitigation. Urban For. Urban Green. 2019, 37, 24–32. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere: Theory, History, and Applications; Springer: Dordrecht, The Netherlands, 1982; 299p. [Google Scholar]
- Businger, J.A.; Yaglom, A.M. Introduction to Obukhov’s paper on ‘turbulence in an atmosphere with a non-uniform temperature’. Bound.-Layer Meteorol. 1971, 2, 3–6. [Google Scholar] [CrossRef]
- Cai, L.; Feng, X.-P.; Yu, J.-Y.; Xiang, Q.-C.; Chen, R. Reduction in Carbon Dioxide Emission and Energy Savings Obtained by Using a Green Roof. Aerosol Air Qual. Res. 2019, 19, 2432–2445. [Google Scholar] [CrossRef]
- Castiglia Feitosa, R.; Wilkinson, S. Modelling green roof stormwater response for different soil depths. Landsc. Urban Plan. 2016, 153, 170–179. [Google Scholar] [CrossRef]
- Collins, S.; Kuoppamäki, K.; Kotze, D.J.; Lü, X. Thermal behavior of green roofs under Nordic winter conditions. Build. Environ. 2017, 122, 206–214. [Google Scholar] [CrossRef]
- Costa-Filho, E.; Chávez, J.L.; Zhang, H.; Andales, A.A. An optimized surface aerodynamic temperature approach to estimate maize sensible heat flux and evapotranspiration. Agric. For. Meteorol. 2021, 311, 108683. [Google Scholar] [CrossRef]
- Gregoire, B.G.; Clausen, J.C. Effect of a modular extensive green roof on stormwater runoff and water quality. Ecol. Eng. 2011, 37, 963–969. [Google Scholar] [CrossRef]
- Hathaway, M.A.; Hunt, F.W.; Jennings, D.G. A Field Study of Green Roof Hydrologic and Water Quality Performance. Trans. ASABE 2008, 51, 37–44. [Google Scholar] [CrossRef]
- Heusinger, J.; Weber, S. Surface energy balance of an extensive green roof as quantified by full year eddy-covariance measurements. Sci. Total Environ. 2017, 577, 220–230. [Google Scholar] [CrossRef]
- Kotsiris, G.; Androutsopoulos, A.; Polychroni, E.; Souliotis, M.; Kavga, A. Carbon footprint of green roof installation on school buildings in Greek Mediterranean climatic region. Int. J. Sustain. Energy 2019, 38, 866–883. [Google Scholar] [CrossRef]
- Li, Y.; Babcock, R.W. Green roofs against pollution and climate change. A review. Agron. Sustain. Dev. 2014, 34, 695–705. [Google Scholar] [CrossRef]
- Lin, B.-S.; Yu, C.-C.; Su, A.-T.; Lin, Y.-J. Impact of climatic conditions on the thermal effectiveness of an extensive green roof. Build. Environ. 2013, 67, 26–33. [Google Scholar] [CrossRef]
- Liu, K.; Bass, B. Performance of green roof systems. In Proceedings of the Cool Roofing Symposium, Toronto, ON, Canada, 12–13 May 2005; pp. 1–18. [Google Scholar]
- Mehdi, R.; Nyirumuringa, E.; Juyeon, K.; Doo Hwan, K. Analyzing the Impact of Green Roof Functions on the Citizens’ Mental Health in Metropolitan Cities. Iran. J. Public Health 2021, 50, 900. [Google Scholar] [CrossRef]
- Moghbel, M.; Erfanian Salim, R. Environmental benefits of green roofs on microclimate of Tehran with specific focus on air temperature, humidity and CO2 content. Urban Clim. 2017, 20, 46–58. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Tr. Akad. Nauk SSSR Geophiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Peng, L.L.H.; Jim, C.Y. Economic evaluation of green-roof environmental benefits in the context of climate change: The case of Hong Kong. Urban For. Urban Green. 2015, 14, 554–561. [Google Scholar] [CrossRef]
- Peng, Z.J.; Stovin, V. Independent Validation of the SWMM Green Roof Module. J. Hydrol. Eng. 2017, 22, 04017037. [Google Scholar] [CrossRef]
- Prueger, J.H.; Kustas, W.P. Aerodynamic Methods for Estimating Turbulent Fluxes; Micrometeorology in Agricultural Systems Agricultural Research Service: Lincoln, NE, USA, 2005; pp. 407–436. [Google Scholar]
- Qin, X.; Wu, X.; Chiew, Y.; Li, Y. A green roof test bed for stormwater management and reduction of urban heat island effect in Singapore. Br. J. Environ. Clim. Change 2013, 2, 410–420. [Google Scholar] [CrossRef]
- Sailor, D.J. A green roof model for building energy simulation programs. Energy Build. 2008, 40, 1466–1478. [Google Scholar] [CrossRef]
- Santamouris, M. Cooling the cities—A review of reflective and green roof mitigation technologies to fight heat island and improve comfort in urban environments. Sol. Energy 2014, 103, 682–703. [Google Scholar] [CrossRef]
- Speak, A.F.; Rothwell, J.J.; Lindley, S.J.; Smith, C.L. Urban particulate pollution reduction by four species of green roof vegetation in a UK city. Atmos. Environ. 2012, 61, 283–293. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1988; 666p. [Google Scholar]
- Fortuniak, K.; Pawlak, W.; Siedlecki, M. Integral Turbulence Statistics Over a Central European City Centre. Bound.-Layer Meteorol. 2013, 146, 257–276. [Google Scholar] [CrossRef]
- Montgomery, R.B. Vertical Eddy Flux of Heat in the Atmosphere. J. Atmos. Sci. 1948, 5, 265–274. [Google Scholar] [CrossRef]
- Swinbank, W.C. The Measurement of Vertical Transfer of Heat and Water Vapor by Eddies in the Lower Atmosphere. J. Atmos. Sci. 1951, 8, 135–145. [Google Scholar] [CrossRef]
- Wyngaard, J.C.; Clifford, S.F. Estimating Momentum, Heat and Moisture Fluxes from Structure Parameters. J. Atmos. Sci. 1978, 35, 1204–1211. [Google Scholar] [CrossRef]
- Gawuc, L.; Łobocki, L.; Strużewska, J. Application of the profile method for the estimation of urban sensible heat flux using roadside weather monitoring data and satellite imagery. Urban Clim. 2022, 42, 101098. [Google Scholar] [CrossRef]
- USEPA. Green Roofs for Stormwater Runoff Control; EPA/600/R-09/026; United States Environmental Protection Agency: Washington, DC, USA, 2009. [Google Scholar]
- Van der Meulen, S.H. Costs and Benefits of Green Roof Types for Cities and Building Owners. J. Sustain. Dev. Energy Water Environ. Syst. 2019, 7, 57–71. [Google Scholar] [CrossRef]
- VanWoert, N.D.; Rowe, D.B.; Andresen, J.A.; Rugh, C.L.; Fernandez, R.T.; Xiao, L. Green Roof Stormwater Retention. J. Environ. Qual. 2005, 34, 1036–1044. [Google Scholar] [CrossRef]
- William, R.; Goodwell, A.; Richardson, M.; Le, P.V.V.; Kumar, P.; Stillwell, A.S. An environmental cost-benefit analysis of alternative green roofing strategies. Ecol. Eng. 2016, 95, 1–9. [Google Scholar] [CrossRef]



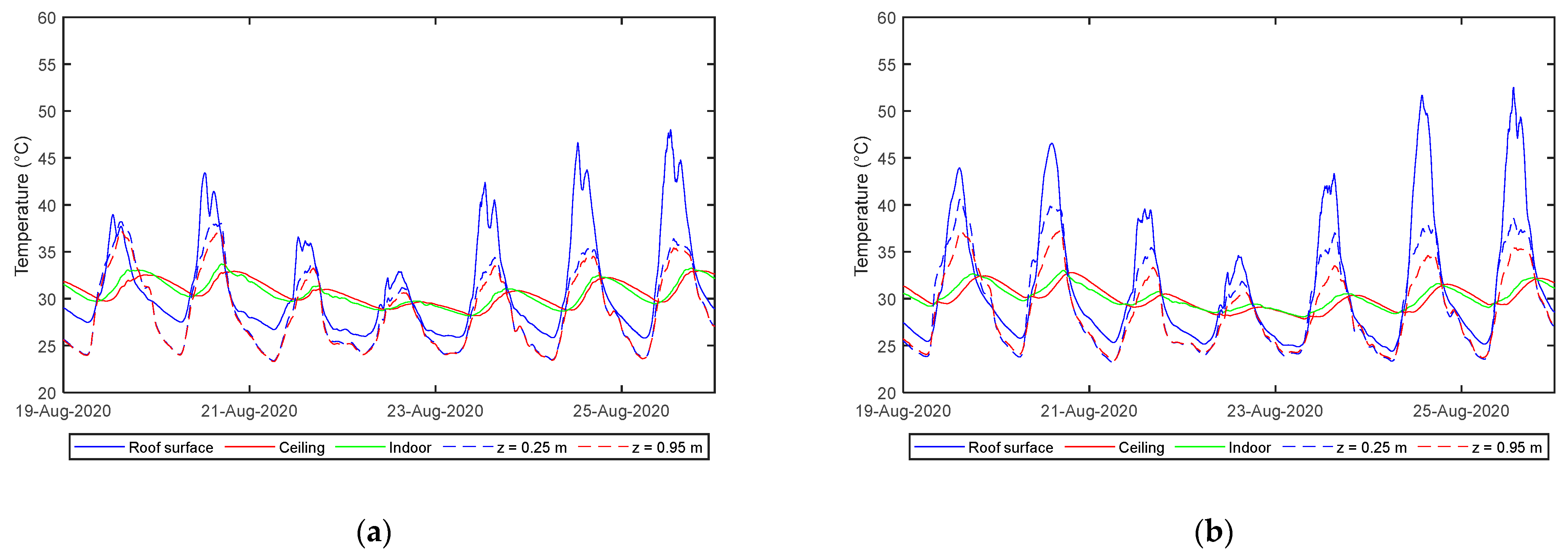
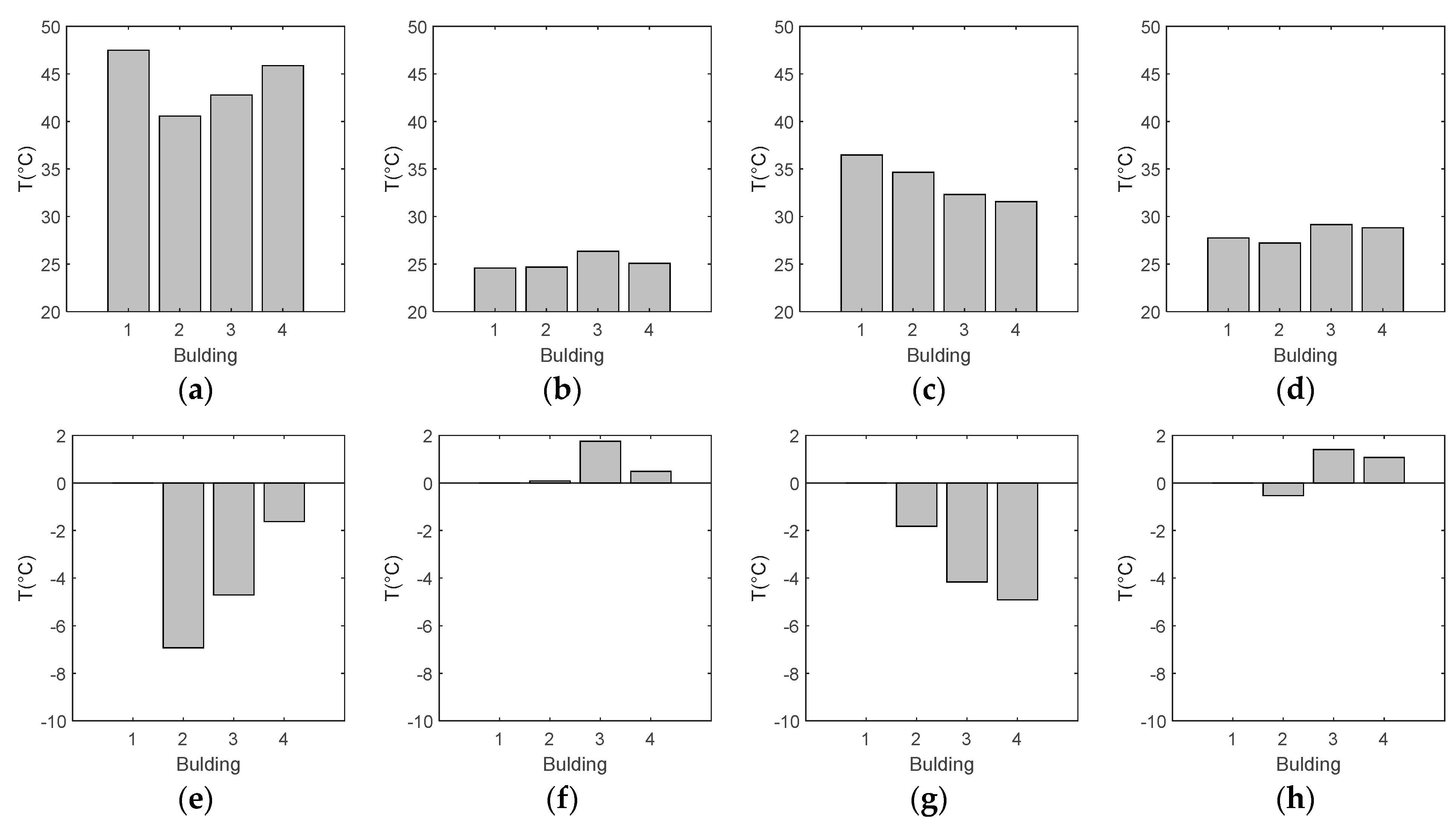
| Temperature Sensor Location | Mean Temperature (°C) | Building | |
|---|---|---|---|
| Bare Concrete Roof (Building 1) | Highly Reflective Painted Roof (Building 2) | ||
| Roof surface | Total | 32.74 | 30.87 |
| Daytime | 37.33 | 33.96 | |
| Nighttime | 28.15 | 27.78 | |
| Daily Maximum | 47.50 | 40.57 | |
| Daily Minimum | 24.60 | 24.69 | |
| Ceiling | Total | 32.02 | 30.38 |
| Daytime | 34.62 | 31.97 | |
| Nighttime | 29.42 | 28.79 | |
| Daily Maximum | 42.21 | 37.20 | |
| Daily Minimum | 25.67 | 25.44 | |
| Indoor | Total | 31.56 | 30.48 |
| Daytime | 32.45 | 31.13 | |
| Nighttime | 30.68 | 29.83 | |
| Daily Maximum | 36.49 | 34.67 | |
| Daily Minimum | 27.75 | 27.22 | |
| Lower point above the roof surface | Total | 29.54 | 28.77 |
| Daytime | 32.28 | 30.83 | |
| Nighttime | 26.80 | 26.71 | |
| Daily Maximum | 37.55 | 34.98 | |
| Daily Minimum | 23.90 | 23.84 | |
| Upper point above the roof surface | Total | 28.76 | 28.42 |
| Daytime | 30.91 | 30.14 | |
| Nighttime | 26.61 | 26.70 | |
| Daily Maximum | 35.28 | 34.08 | |
| Daily Minimum | 23.77 | 23.82 | |
| Temperature Sensor Location | Mean Temperature (°C) | Building | |
|---|---|---|---|
| Green Roof (Grass) (Building 4) | Green Roof (Short Bamboo) (Building 3) | ||
| Roof surface | Total | 31.23 | 31.52 |
| Daytime | 34.28 | 35.38 | |
| Nighttime | 28.19 | 27.65 | |
| Daily Maximum | 42.79 | 45.88 | |
| Daily Minimum | 26.36 | 25.09 | |
| Ceiling | Total | 30.64 | 30.05 |
| Daytime | 30.09 | 29.53 | |
| Nighttime | 31.19 | 30.57 | |
| Daily Maximum | 32.10 | 31.59 | |
| Daily Minimum | 29.29 | 28.87 | |
| Indoor | Total | 30.60 | 30.13 |
| Daytime | 30.29 | 30.01 | |
| Nighttime | 30.91 | 30.24 | |
| Daily Maximum | 32.33 | 31.58 | |
| Daily Minimum | 29.16 | 28.83 | |
| Lower point above the roof surface | Total | 28.96 | 29.54 |
| Daytime | 31.32 | 32.62 | |
| Nighttime | 26.61 | 26.46 | |
| Daily Maximum | 35.81 | 37.97 | |
| Daily Minimum | 23.77 | 23.61 | |
| Upper point above the roof surface | Total | 28.58 | 28.67 |
| Daytime | 30.65 | 30.71 | |
| Nighttime | 26.50 | 26.63 | |
| Daily Maximum | 34.82 | 34.88 | |
| Daily Minimum | 23.70 | 23.80 | |
| Building | Rn | QH | QE | QG |
|---|---|---|---|---|
| Bare concrete roof | 123.18 | 103.81 (84%) | 5.73 (5%) | 13.63 (11%) |
| Highly reflective painted roof | 42.99 | 19.40 (45%) | 14.35 (33%) | 9.23 (22%) |
| Grass roof | 136.99 | 91.54 (67%) | 44.38 (32%) | 1.05 (1%) |
| Short bamboo roof | 149.48 | 93.58 (63%) | 53.28 (36%) | 2.61 (1%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, Y.; Kwon, Y.; Hwang, J. Surface Energy Balance of Green Roofs Using the Profile Method: A Case Study in South Korea During the Summer. Sustainability 2025, 17, 2725. https://doi.org/10.3390/su17062725
Seo Y, Kwon Y, Hwang J. Surface Energy Balance of Green Roofs Using the Profile Method: A Case Study in South Korea During the Summer. Sustainability. 2025; 17(6):2725. https://doi.org/10.3390/su17062725
Chicago/Turabian StyleSeo, Yongwon, Youjeong Kwon, and Junshik Hwang. 2025. "Surface Energy Balance of Green Roofs Using the Profile Method: A Case Study in South Korea During the Summer" Sustainability 17, no. 6: 2725. https://doi.org/10.3390/su17062725
APA StyleSeo, Y., Kwon, Y., & Hwang, J. (2025). Surface Energy Balance of Green Roofs Using the Profile Method: A Case Study in South Korea During the Summer. Sustainability, 17(6), 2725. https://doi.org/10.3390/su17062725





