Optimization Scheduling of Hydro–Wind–Solar Multi-Energy Complementary Systems Based on an Improved Enterprise Development Algorithm
Abstract
1. Introduction
2. Generation of Typical Wind and Solar Scenarios
2.1. Calculation of Wind and Solar Power Output
- (1)
- Wind power output calculation [27]
- (2)
- Solar Power Output Calculation
2.2. Scenario Generation and Reduction
3. Short-Term Optimal Scheduling Model for Hydropower–Wind–Solar Complementarity
3.1. Objective Function
3.2. Constraints
- (1)
- Water Balance Constraints
- (2)
- Water Level Constraints
- (3)
- Output Constraints
- (4)
- Generation Flow Constraints
- (5)
- Water Level Fluctuation Constraints
- (6)
- Boundary Constraints
4. Model Solution Based on the TGED Algorithm
4.1. Improvement Strategy
- (1)
- Chaos Initialization
- (2)
- Gaussian Walk
4.2. TGED Algorithm
4.2.1. Population Initialization
4.2.2. Gaussian Walk Optimization
4.2.3. Update Mechanism
- (1)
- Task Update
- (2)
- Structure Update
- (3)
- Technology Update
- (4)
- Personnel Update
4.2.4. Update Switching Mechanism
4.3. Model Solving Process
| Algorithm 1: TGED for Solving the Hydro-Wind-Solar Multi-Energy Complementary Optimization Scheduling Problem. |
| Input: Inflow runoff sequence for the scheduling period, wind–solar output scenarios, boundary conditions for scheduling operation, and various operational constraints. Initialization: Generate the initial population based on Tent mapping and calculate the fitness values of each particle. Main Program: while (iter <= iteration) Perform Gaussian random walk optimization Calculate c(t) value for i = 0 to popSize = 0.1) Task update: For the worst fitness individual, regenerate based on Tent mapping else switch c(t) case c(t) = 1 Structure update case c(t) = 2 Technology update case c(t) = 3 Personnel update end of switch end of if end of for Update iteration count: iter++ if iter = iteration end Output: Optimal solution and corresponding water level, outflow, and output processes. |
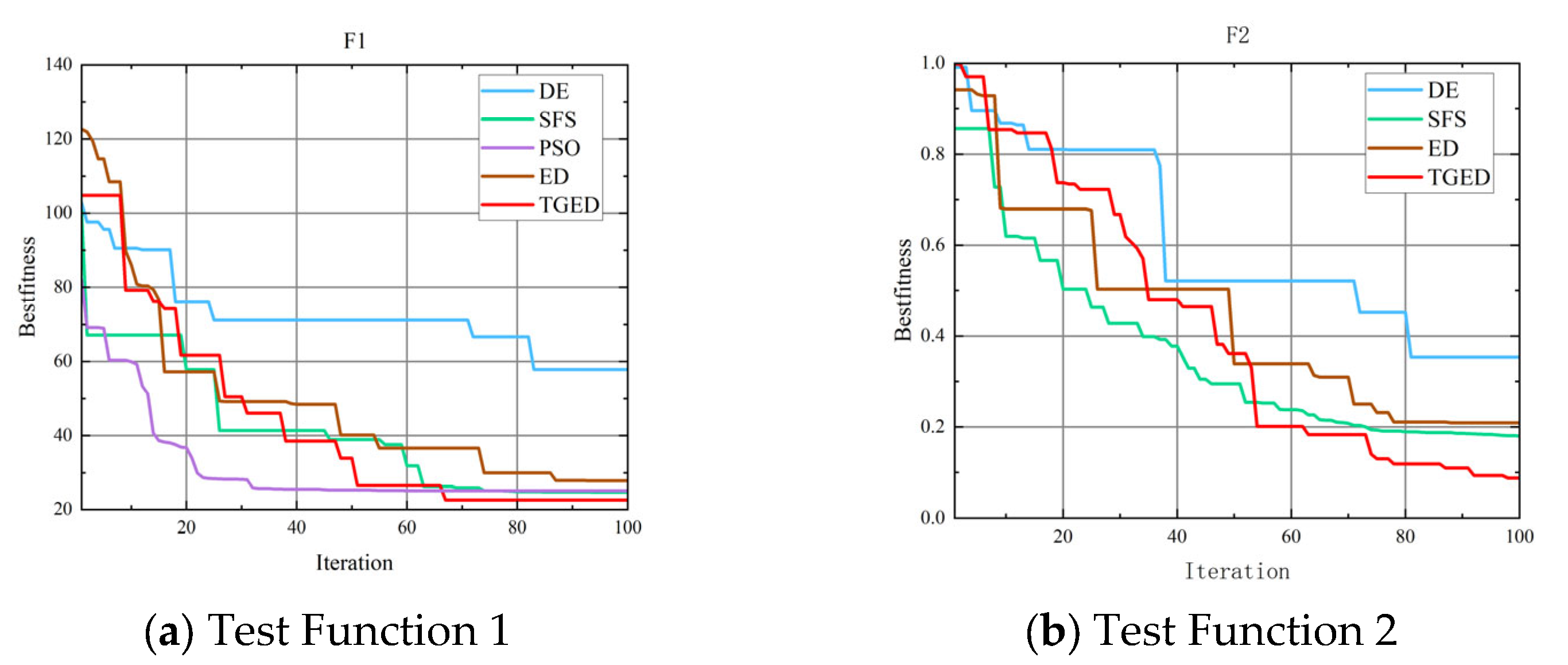
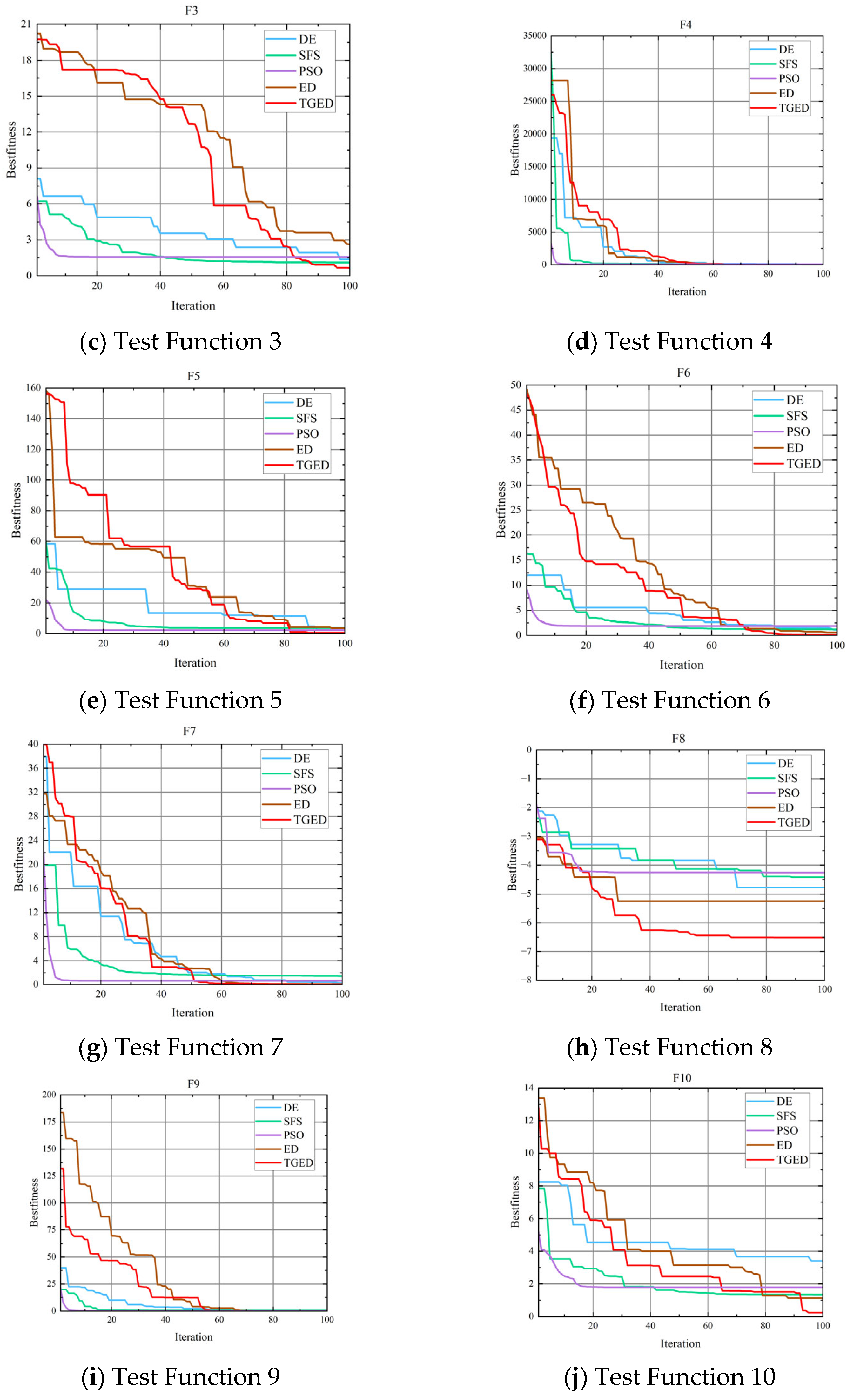
4.4. Function Testing and Analysis
5. Case Study
5.1. Engineering Background
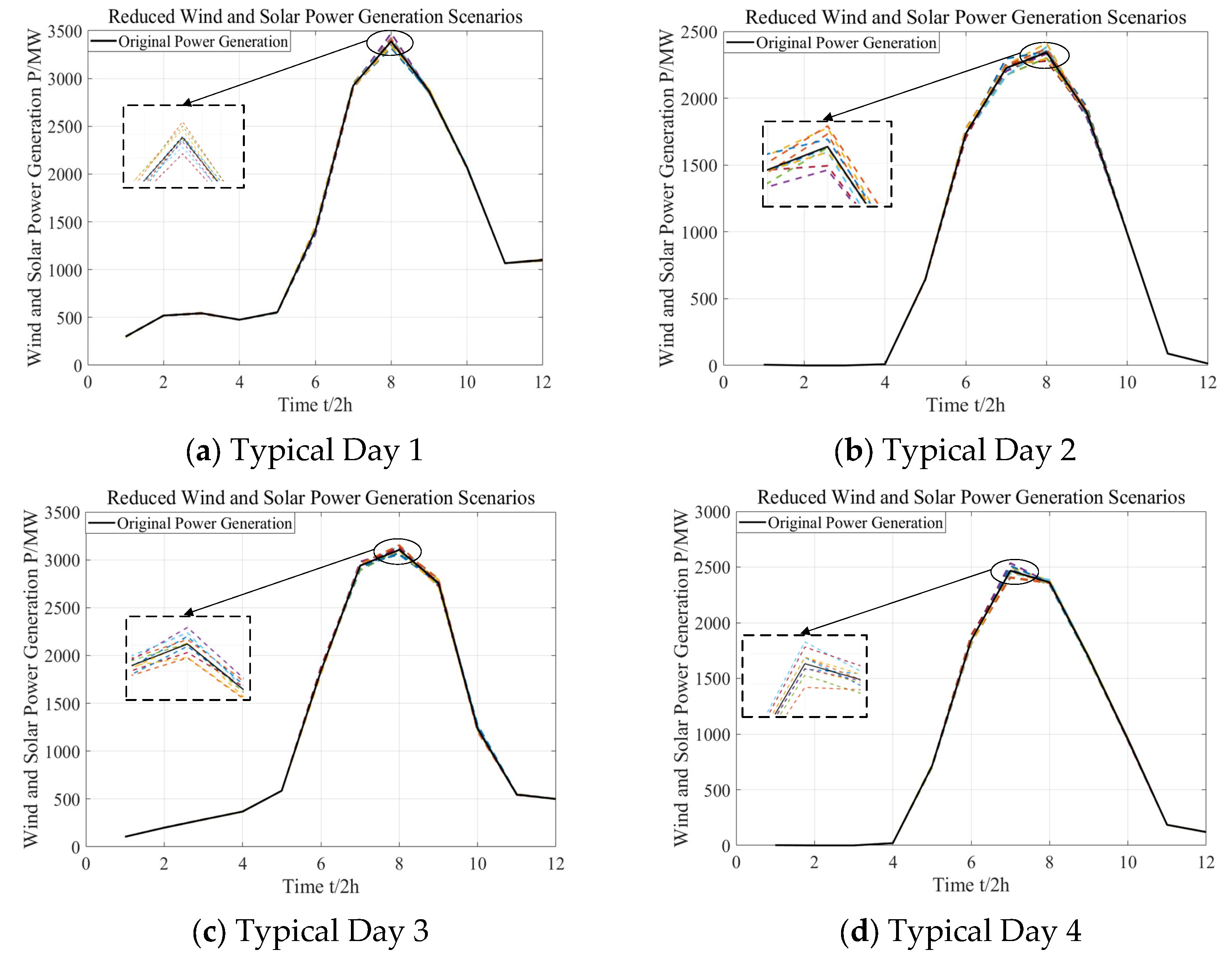
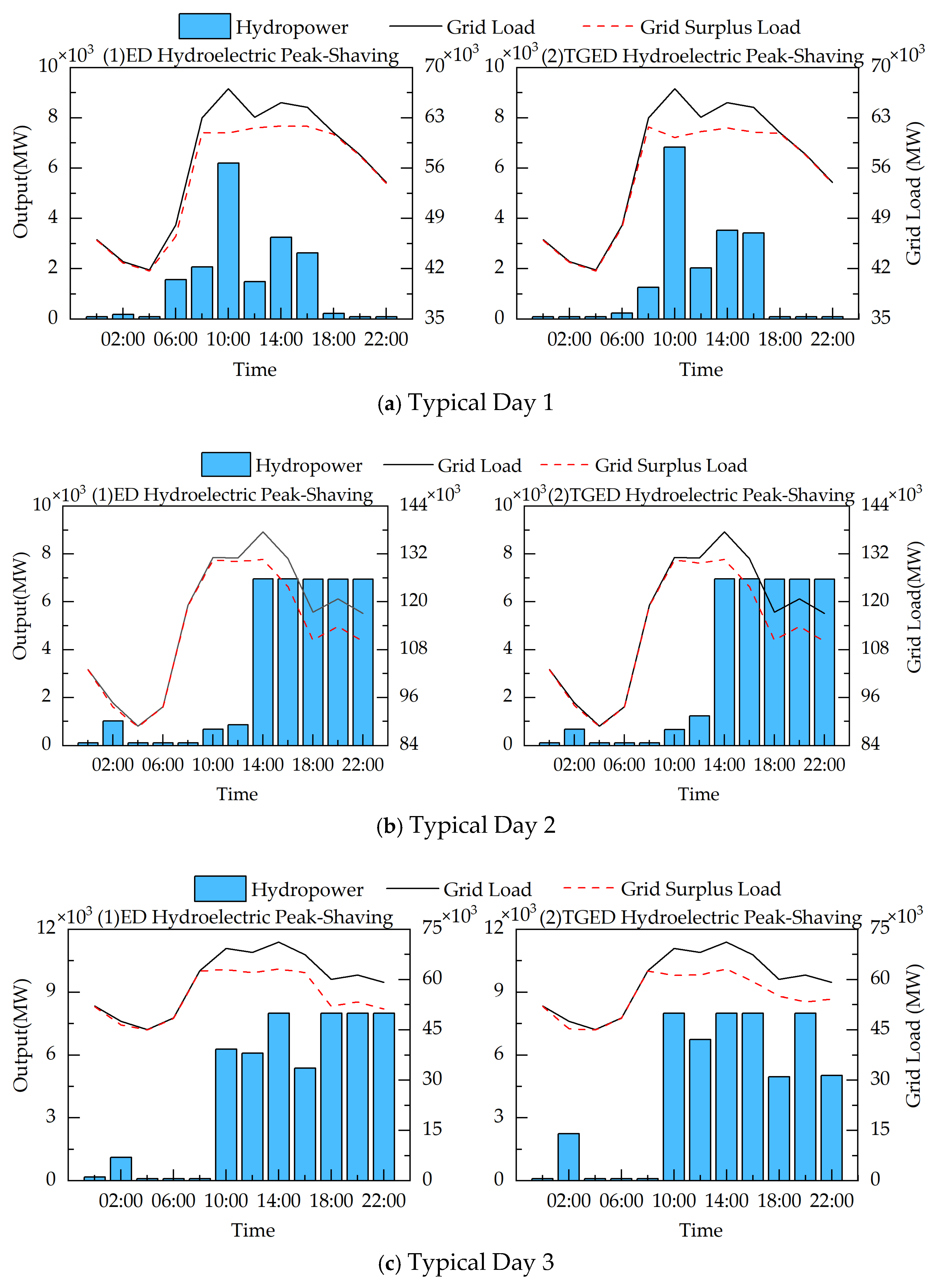
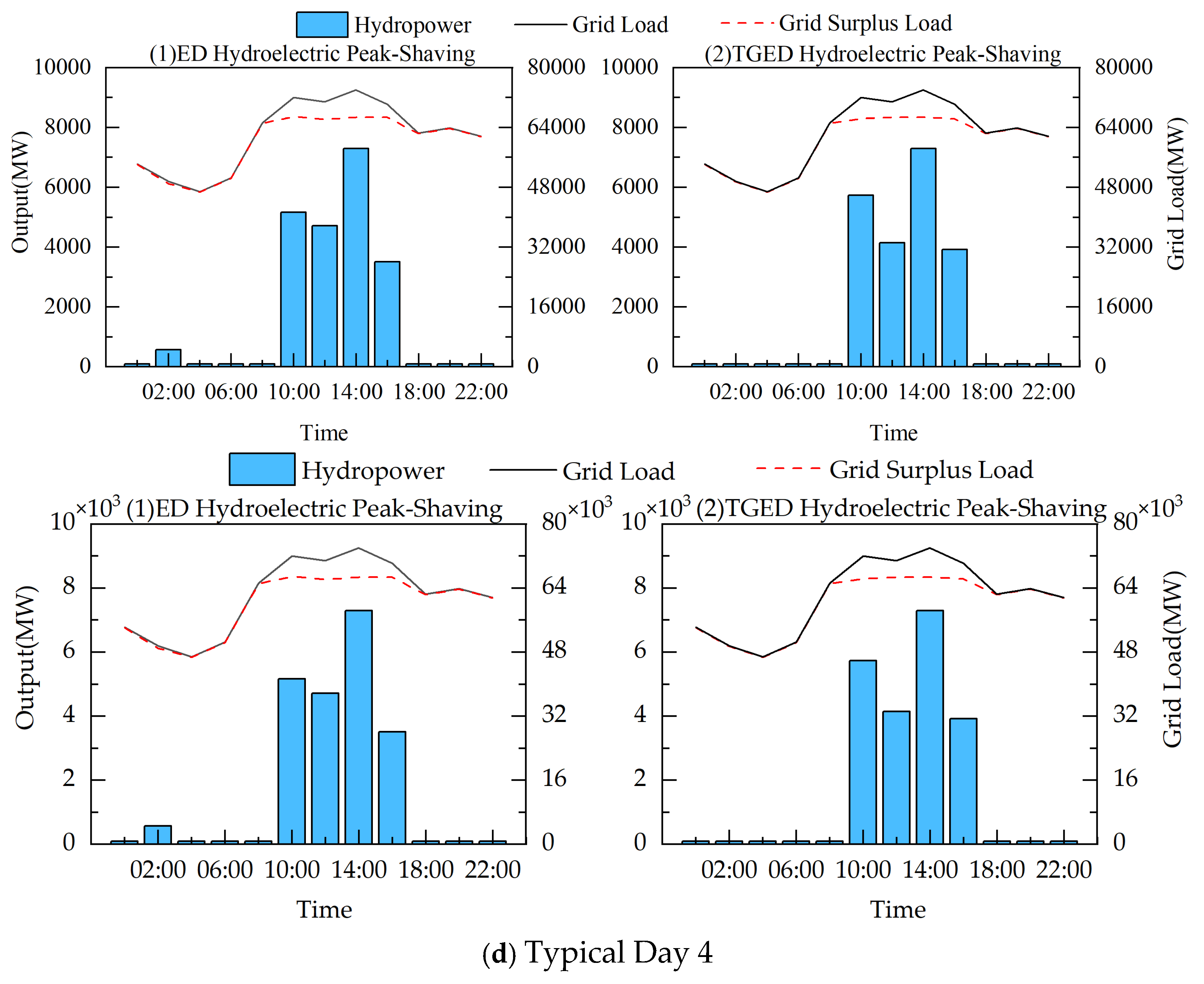
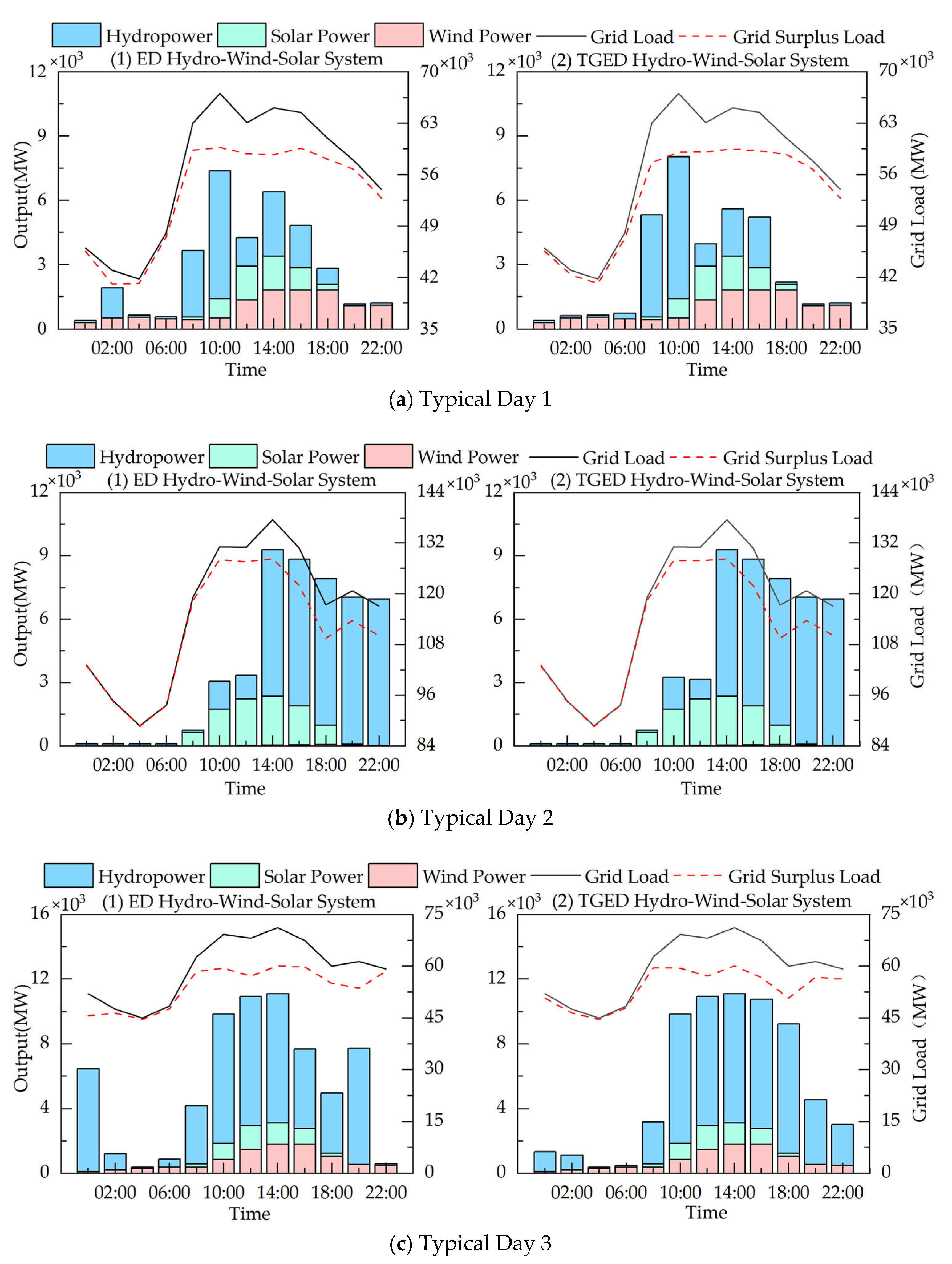
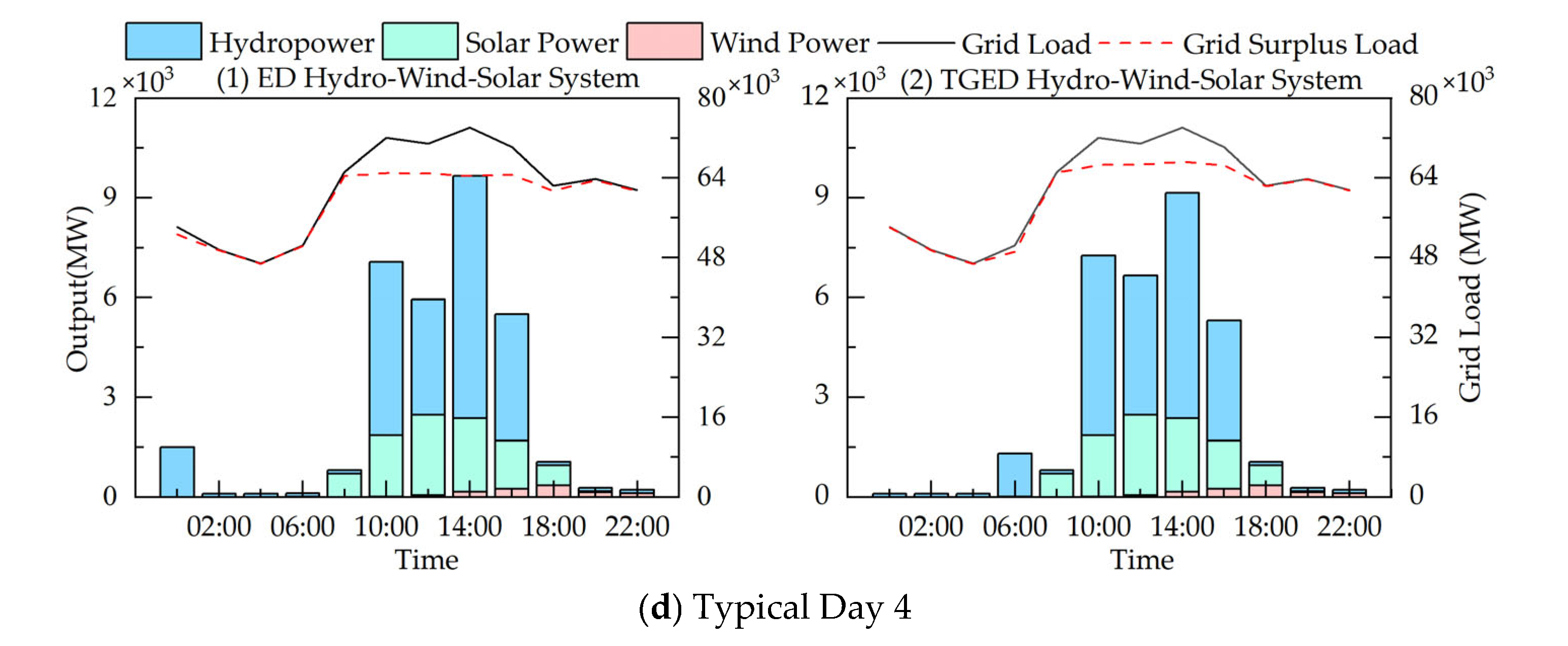
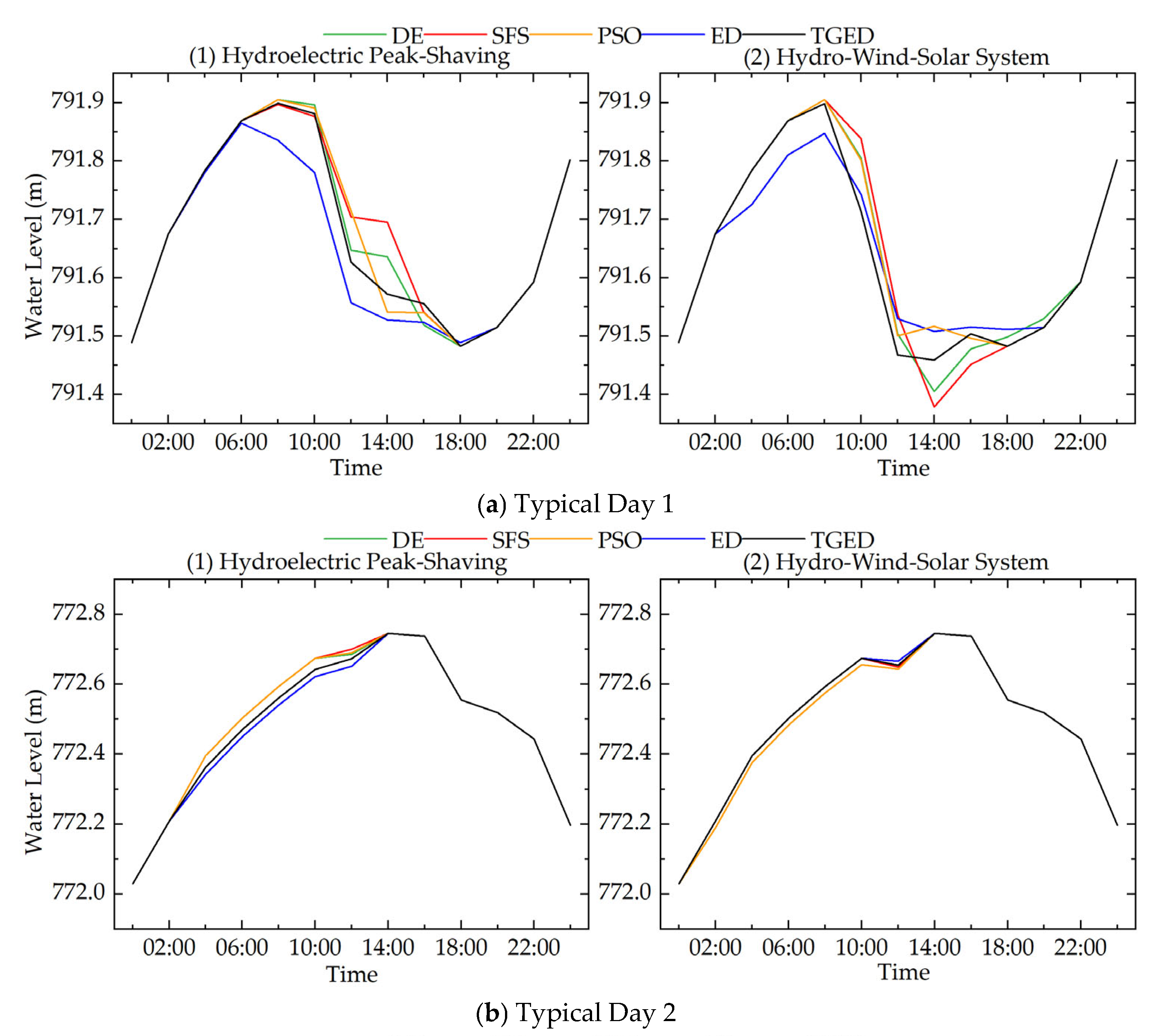
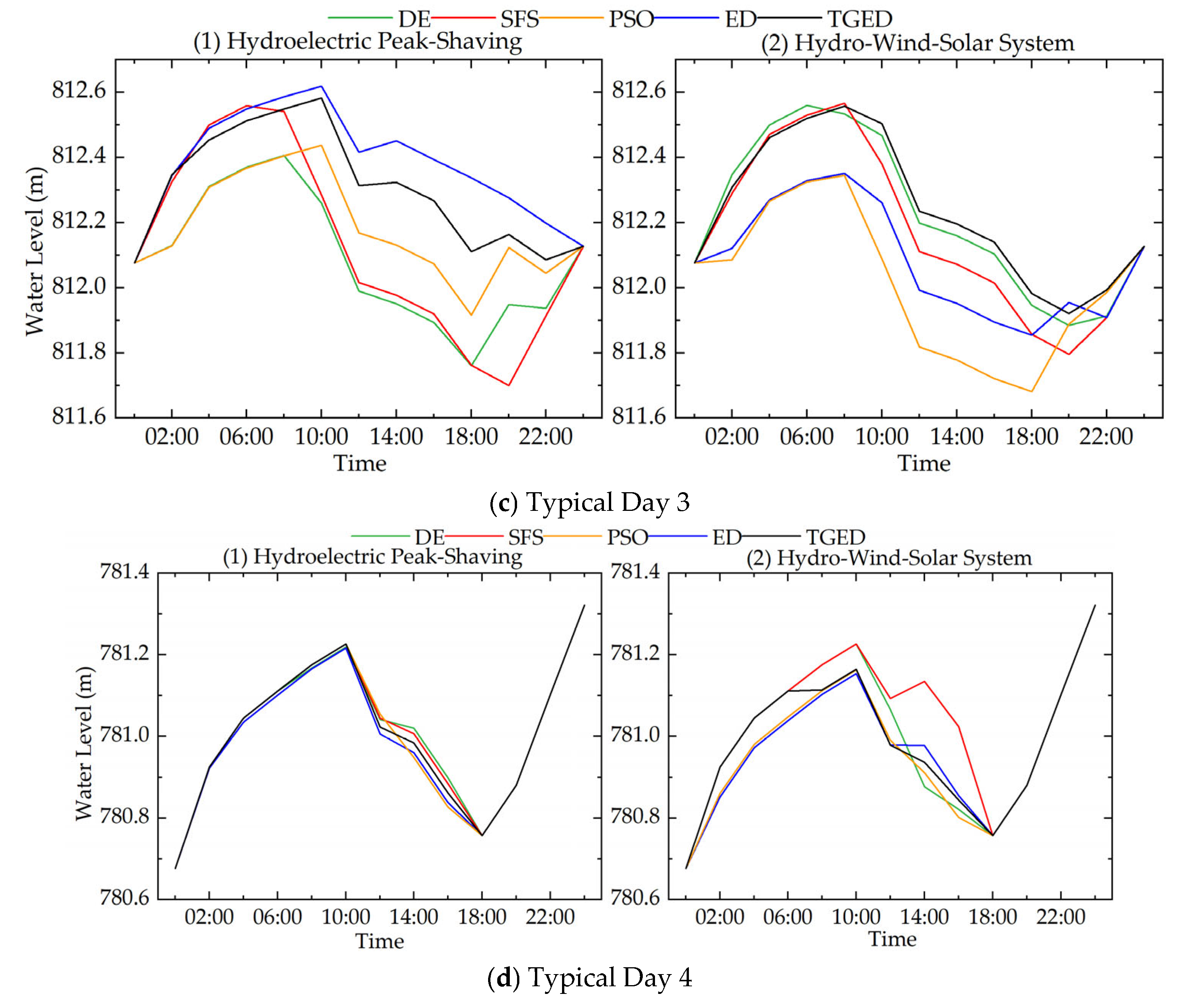
5.2. Analysis of Typical Days
6. Conclusions and Summary
- (1)
- Effectiveness of the Improved Algorithm: This paper improves the Enterprise Development Optimization (ED) algorithm by combining chaotic initialization and Gaussian random walk with the standard algorithm. A new ED algorithm is proposed that enhances the solving accuracy and reduces the likelihood of falling into local optima. Preliminary validation through ten test functions shows that the TGED algorithm achieves high accuracy, faster convergence, and better optimization capabilities compared to other algorithms.
- (2)
- Peak-Shaving Performance Improvement: The TGED algorithm has optimized grid load peak-shaving across multiple typical day scenarios, demonstrating excellent optimization performance. Its adaptive update mechanism can rapidly respond to fluctuations in load and output, further smoothing the residual load process. Compared with the standard DE, SFS, PSO, and ED algorithms, the TGED algorithm exhibits superior peak-shaving results, further confirming its applicability in complex multi-energy scheduling environments.
- (3)
- Advantages of Hydro–Wind–Solar Complementarity: In multi-energy complementary operation, hydro–wind–solar complementarity uses the flexible regulation capability of hydropower to effectively suppress the fluctuations of wind and solar output, achieving a more stable grid load output, which facilitates efficient consumption of renewable energy. Typical day analysis shows that the hydro–wind–solar complementary optimization scheduling model based on TGED can effectively reduce the system’s load peak–valley difference under various meteorological conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TGED | Tent–Gaussian Enterprise Development Optimization |
| ED | Enterprise Development Optimization |
| DE | Differential Evolution |
| SFS | Stochastic Fractal Search |
| PSO | Linear dichroism |
References
- Yang, G.; Kong, D.; He, X.; Yu, X.; Jiang, K. Prediction of hydrogen leakage location and intensity in hydrogen refueling stations based on deep learning. Int. J. Hydrogen Energy 2024, 68, 209–220. [Google Scholar] [CrossRef]
- Yogeswari, M.K.; Dharmalingam, K.; Mullai, P. Implementation of artificial neural network model for continuous hydrogen production using confectionery wastewater. J. Environ. Manag. 2019, 252, 8. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Ma, X.; Chen, B.; Shang, Y.; Song, M. Challenges toward carbon neutrality in china: Strategies and countermeasures. Resour. Conserv. Recycl. 2022, 176, 9. [Google Scholar] [CrossRef]
- Yuan, K.; Zhang, T.; Xie, X.; Du, S.; Xue, X.; Abdul-Manan, A.F.N.; Huang, Z. Exploration of low-cost green transition opportunities for china’s power system under dual carbon goals. J. Clean. Prod. 2023, 414, 15. [Google Scholar] [CrossRef]
- Babay, M.; Adar, M.; Chebak, A.; Mabrouki, M. Forecasting green hydrogen production: An assessment of renewable energy systems using deep learning and statistical methods. Fuel 2025, 381, 31. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Feng, L. Transient analysis of a green hydrogen production and storage system using alkaline electrolyzer. Fuel 2022, 324, 10. [Google Scholar] [CrossRef]
- Qing, X.; Niu, Y. Hourly day-ahead solar irradiance prediction using weather forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Li, J.; Liu, Y.; Yao, L.; Wang, Y.; Wang, C.; Pei, S.; Zhou, J. Short-term optimal operation of wind-solar-hydro hybrid system considering uncertainties. Energy Convers. Manag. 2020, 205, 16. [Google Scholar] [CrossRef]
- Babay, M.; Adar, M.; Chebak, A.; Mabrouki, M. Comparative sustainability analysis of serpentine flow-field and straight channel PEM fuel cell designs. Int. J. Syst. Assur. Eng. Manag. 2024, 15, 3954–3970. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, H.X.; Yu, D.; Wang, Y.T.; Ling, D.; Ming, X. Short-term optimal operation of hydro-wind-solar hybrid system with improved generative adversarial networks. Appl. Energy 2019, 250, 389–403. [Google Scholar] [CrossRef]
- Liu, Z.; Mo, L.; Lou, S.; Zhu, Y.; Liu, T. An ecology-oriented single—Multi-objective optimal operation modeling and decision-making method in the case of the ganjiang river. Water 2024, 16, 970. [Google Scholar] [CrossRef]
- Fu, K.; Sun, X.; Chen, K.; Mo, L.; Xiao, W.; Liu, S. Monthly runoff prediction based on stochastic weighted averaging-improved stacking ensemble model. Water 2024, 16, 3580. [Google Scholar] [CrossRef]
- Hart, E.K.; Jacobson, M.Z. A monte carlo approach to generator portfolio planning and carbon emissions assessments of systems with large penetrations of variable renewables. Renew. Energy 2011, 36, 2278–2286. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Z.; Hu, W.; Wang, Y.; Dong, L.; Zhang, J. Coordinated optimal operation of hydro-wind-solar integrated systems. Appl. Energy 2019, 242, 883–896. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Yong, K.P.; Lee, H.W.; Zhang, J.H. Probabilistic load flow evaluation with hybrid latin hypercube—Sampling and cholesky decomposition. IEEE Trans. Power Syst. 2009, 24, 661–667. [Google Scholar] [CrossRef]
- Heitsch, H.; Römisch, W. Scenario reduction algorithms in stochastic programming. Comput. Optim. Appl. 2003, 24, 187–206. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Kirschen, D.S. Scenario reduction with submodular optimization. IEEE Trans. Power Syst. 2017, 32, 2479–2480. [Google Scholar] [CrossRef]
- Dupacová, J.; Gröwe-Kuska, N.; Römisch, W. Scenario reduction in stochastic programming: An approach using probability metrics. Math. Program. 2003, 95, 493–511. [Google Scholar] [CrossRef]
- Lv, S.; Wang, H.; Meng, X.; Yang, C.; Wang, M. Optimal capacity configuration model of power-to-gas equipment in wind-solar sustainable energy systems based on a novel spatiotemporal clustering algorithm: A pathway towards sustainable development. Renew. Energy 2022, 201, 240–255. [Google Scholar] [CrossRef]
- Li, F.; Chen, S.; Ju, C.; Zhang, X.; Ma, G.; Huang, W. Research on short-term joint optimization scheduling strategy for hydro-wind-solar hybrid systems considering uncertainty in renewable energy generation. Energy Strateg. Rev. 2023, 50, 17. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, Y.; Fang, G.; Ding, Z. Research on short-term optimal scheduling of hydro-wind-solar multi-energy power system based on deep reinforcement learning. J. Clean. Prod. 2023, 385, 12. [Google Scholar] [CrossRef]
- Wang, X.; Chang, J.; Meng, X.; Wang, Y. Hydro-thermal-wind-photovoltaic coordinated operation considering the comprehensive utilization of reservoirs. Energy Convers. Manag. 2019, 198, 15. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, M.; Jia, T.; Ma, X.; Song, Q.; Zhou, Q.; Yang, X.; Liu, J.; Guo, A. A heat-resistant glass-modified multi-component phosphate adhesive for repair and connection of superalloy in extreme environment. J. Alloys Compd. 2018, 745, 868–873. [Google Scholar] [CrossRef]
- Jin, X.; Liu, B.; Liao, S.; Cheng, C.; Li, G.; Liu, L. Impacts of different wind and solar power penetrations on cascade hydroplants operation. Renew. Energy 2022, 182, 227–244. [Google Scholar] [CrossRef]
- Huang, S.J. Enhancement of hydroelectric generation scheduling using ant colony system based optimization approaches. IEEE Trans. Energy Convers. 2001, 16, 296–301. [Google Scholar] [CrossRef]
- Truong, D.; Chou, J. Metaheuristic algorithm inspired by enterprise development for global optimization and structural engineering problems with frequency constraints. Eng. Struct. 2024, 318, 25. [Google Scholar] [CrossRef]
- Daneshvar, M.; Mohammadi-Ivatloo, B.; Zare, K. Two-stage optimal robust scheduling of hybrid energy system considering the demand response programs. J. Clean. Prod. 2020, 248, 13. [Google Scholar] [CrossRef]
- Mazidi, M.; Zakariazadeh, A.; Jadid, S.; Siano, P. Integrated scheduling of renewable generation and demand response programs in a microgrid. Energy Convers. Manag. 2014, 86, 1118–1127. [Google Scholar] [CrossRef]
- Shu, Z.; Jirutitijaroen, P. Latin hypercube sampling techniques for power systems reliability analysis with renewable energy sources. IEEE Trans. Power Syst. 2011, 26, 2066–2073. [Google Scholar] [CrossRef]
- Lu, L.; Yuan, W.; Su, C.; Wang, P.; Cheng, C.; Yan, D.; Wu, Z. Optimization model for the short-term joint operation of a grid-connected wind-photovoltaic-hydro hybrid energy system with cascade hydropower plants. Energy Convers. Manag. 2021, 236, 12. [Google Scholar] [CrossRef]
- Shatrevich, V. Industrial structures as competitive factor in organization development. In Proceedings of the 2nd International Scientific Conference—Contemporary Issues in Business, Management and Education, Vienna, Austria, 13–14 May 2013; Volume 110, pp. 871–878. [Google Scholar] [CrossRef]
- Glasauer, C. The PREVENT-model: Human and organizational factors fostering engineering of safe and secure robotic systems. J. Syst. Softw. 2023, 195, 17. [Google Scholar] [CrossRef]
- Chen, M.S.; Gu, Y.L. The mechanism and measures of adjustment of industrial organization structure: The perspective of energy saving and emission reduction. In Proceedings of the 2010 International Conference on Energy, Environment and Development (Iceed2010), Kuala Lumpur, Malaysia, 8–9 December 2010; Volume 5, pp. 2562–2567. [Google Scholar] [CrossRef]
- Shao, S.; Peng, Y.; He, C.; Du, Y. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 2020, 97, 415–430. [Google Scholar] [CrossRef] [PubMed]
- Xu, A.; Mo, L.; Wang, Q. Research on operation mode of the yalong river cascade reservoirs based on improved stochastic fractal search algorithm. Energies 2022, 15, 7779. [Google Scholar] [CrossRef]
- Qin, A.K.; Suganthan, P.N. Self-adaptive differential evolution algorithm for numerical optimization. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Proceedings, Scotland, UK, 2–5 September 2005; Volumes 1–3, pp. 1785–1791. [Google Scholar] [CrossRef]
| No. | Type | Test Function | Value Range | Optimal Value | ||||
|---|---|---|---|---|---|---|---|---|
| TGED | ED | DE | SFS | PSO | ||||
| 1 | Multimodal | [−5.12,5.12] | 22.561 | 27.829 | 57.790 | 24.682 | 25.095 | |
| 2 | Multimodal | [−6,6] | 0.088 | 0.209 | 0.353 | 0.180 | 0.229 | |
| 3 | Multimodal | [−32.768,32.768] | 0.666 | 2.612 | 1.359 | 1.124 | 1.560 | |
| 4 | Unimodal | [−5,5] | 9.376 | 10.127 | 43.587 | 32.298 | 36.535 | |
| 5 | Multimodal | [−5,10] | 0.555 | 3.533 | 2.203 | 3.742 | 2.157 | |
| 6 | Unimodal | [−10,10] | 0.050 | 0.583 | 1.109 | 1.235 | 1.884 | |
| 7 | Unimodal | [−5,5] | 0.001 | 0.035 | 0.265 | 1.453 | 0.623 | |
| 8 | Multimodal | [0,π] | −6.512 | −5.246 | −4.775 | −4.418 | −4.263 | |
| 9 | Multimodal | [−10,10] | 0 | 0.039 | 0.169 | 0.823 | 0.272 | |
| 10 | Multimodal | [−10,10] | 0.246 | 1.126 | 3.411 | 1.348 | 1.797 | |
| Typical Day | Typical Day 1 (5 February 2022) | Typical Day 2 (4 August 2021) | Typical Day 3 (19 October 2021) | Typical Day 4 (10 May 2022) |
|---|---|---|---|---|
| Initial Water Level (m) | 791.489 | 772.029 | 812.076 | 780.676 |
| Final Water Level (m) | 791.802 | 772.196 | 812.127 | 781.322 |
| Average Inflow Rate (m3/s) | 2229.450 | 4175.667 | 4392.786 | 3279.863 |
| Upper Water Level Limit (m) | 794.489 | 775.029 | 815.076 | 783.676 |
| Lower Water Level Limit (m) | 789.489 | 770.029 | 810.076 | 778.676 |
| Peak-Shaving Scheme | Algorithm | Typical Day 1 (5 February 2022) | Typical Day 2 (4 August 2021) | Typical Day 3 (19 October 2021) | Typical Day 4 (10 May 2022) |
|---|---|---|---|---|---|
| Hydro Peak-Shaving (MW) | DE | 20,305.056 | 41,933.288 | 18,253.657 | 20,312.989 |
| SFS | 20,348.814 | 41,933.281 | 18,253.659 | 20,211.558 | |
| PSO | 20,218.028 | 41,933.288 | 18,253.657 | 20,125.865 | |
| ED | 20,166.453 | 41,933.273 | 18,253.657 | 20,137.728 | |
| TGED | 20,054.825 | 41,933.273 | 18,253.657 | 20,010.942 | |
| Hydro–Wind–Solar Peak-Shaving (MW) | DE | 18,986.451 | 39,591.004 | 15,434.336 | 18,787.417 |
| SFS | 19,214.943 | 39,591.004 | 15,434.332 | 18,730.139 | |
| PSO | 18,537.146 | 39,591.004 | 15,434.332 | 18,887.543 | |
| ED | 18,639.182 | 39,591.004 | 15,434.335 | 18,237.425 | |
| TGED | 18,353.094 | 39,591.004 | 15,434.332 | 18,153.789 |
| Peak-Shaving Scheme | Algorithm | Typical Day 1 (5 February 2022) | Typical Day 2 (4 August 2021) | Typical Day 3 (19 October 2021) | Typical Day 4 (10 May 2022) |
|---|---|---|---|---|---|
| Hydro Peak-Shaving (MW) | DE | 7586.221 | 14,296.914 | 6270.719 | 7296.032 |
| SFS | 7621.973 | 14,298.937 | 6166.487 | 7264.329 | |
| PSO | 7594.924 | 14,297.350 | 6543.328 | 7268.999 | |
| ED | 7790.163 | 14,486.555 | 6709.961 | 7353.426 | |
| TGED | 7581.350 | 14,413.551 | 6286.271 | 7262.861 | |
| Hydro–Wind–Solar Peak-Shaving (MW) | DE | 6872.589 | 14,062.395 | 5410.825 | 6644.506 |
| SFS | 6911.993 | 13,506.207 | 5131.845 | 6648.868 | |
| PSO | 6839.797 | 13,556.159 | 5806.627 | 6759.444 | |
| ED | 7086.412 | 13,506.064 | 5835.296 | 6770.382 | |
| TGED | 6853.253 | 13,505.933 | 5218.572 | 6794.697 |
| Peak-Shaving Scheme | Runtime (min) | ||||
|---|---|---|---|---|---|
| TGED | ED | DE | SFS | PSO | |
| Hydro Peak-Shaving | 0.023 | 0.016 | 0.026 | 0.028 | 0.027 |
| Hydro–Wind–Solar Peak-Shaving | 12.330 | 11.541 | 12.898 | 13.302 | 12.248 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, G.; Yu, C.; Huang, H.; Yu, Y.; Zou, L.; Mo, L. Optimization Scheduling of Hydro–Wind–Solar Multi-Energy Complementary Systems Based on an Improved Enterprise Development Algorithm. Sustainability 2025, 17, 2691. https://doi.org/10.3390/su17062691
Zhao G, Yu C, Huang H, Yu Y, Zou L, Mo L. Optimization Scheduling of Hydro–Wind–Solar Multi-Energy Complementary Systems Based on an Improved Enterprise Development Algorithm. Sustainability. 2025; 17(6):2691. https://doi.org/10.3390/su17062691
Chicago/Turabian StyleZhao, Guohan, Chuanyang Yu, Haodong Huang, Yi Yu, Linfeng Zou, and Li Mo. 2025. "Optimization Scheduling of Hydro–Wind–Solar Multi-Energy Complementary Systems Based on an Improved Enterprise Development Algorithm" Sustainability 17, no. 6: 2691. https://doi.org/10.3390/su17062691
APA StyleZhao, G., Yu, C., Huang, H., Yu, Y., Zou, L., & Mo, L. (2025). Optimization Scheduling of Hydro–Wind–Solar Multi-Energy Complementary Systems Based on an Improved Enterprise Development Algorithm. Sustainability, 17(6), 2691. https://doi.org/10.3390/su17062691






