Abstract
Spanning China’s eastern, central, and western regions, the Yangtze River Economic Belt (YREB) is a pivotal area for economic growth and carbon emissions, with its three major urban agglomerations serving as key hubs along the upper, middle, and lower reaches of the Yangtze River. Understanding the driving factors of carbon emissions and simulating carbon peak scenarios in these regions are critical for informing low-carbon development strategies across China’s diverse geographical zones. This study employs Grey Relational Analysis to identify key drivers and applies the Logarithmic Mean Divisia Index (LMDI) decomposition method to quantify the contributions of various factors to carbon emissions from 2005 to 2021. Furthermore, the STIRPAT (Stochastic Impacts by Regression on Population, Affluence, and Technology) model is utilized to project future emission trends under multiple scenarios. The results indicate that (1) the growth rate of carbon emissions in the three urban agglomerations has generally decelerated during the study period; (2) the influence of driving factors varies significantly across regions, with economic development, urbanization, and population size positively correlating with carbon emissions, while energy structure and energy intensity exhibit mitigating effects; and (3) tailored emission reduction strategies for each urban agglomeration—namely, the Yangtze River Delta Urban Agglomeration (YRD), the Middle Reaches of the Yangtze River Urban Agglomeration (TCC), and the Chengdu-Chongqing Urban Agglomeration (CCA)—can enable all three to achieve carbon peaking by 2030. These findings provide a robust foundation for region-specific policy-making to support China’s carbon neutrality goals.
1. Introduction
Currently, China faces the dual challenge of sustaining economic growth while mitigating carbon emissions, as its total carbon output continues to escalate. In a significant commitment to global climate efforts, the Chinese government announced in September 2020 its ambitious targets to peak CO2 emissions by 2030 and achieve carbon neutrality by 2060. These Carbon Peaking and Carbon Neutrality Goals have been formally embedded as binding indicators within China’s long-term socio-economic development frameworks, steering the nation’s strategic initiatives in energy conservation and emission reduction to address climate change. However, the vast geographical expanse of China, coupled with pronounced regional disparities in natural geography, economic development, industrial structures, and stages of industrial evolution, complicates the attainment of a uniform carbon emissions trajectory across regions. Urban agglomerations, which function as critical engines of regional economic growth and major hubs of energy consumption and carbon emissions, are at the forefront of energy conservation and emission reduction endeavors. Notably, urban clusters centered around megacities or large cities contribute 77.8% of the national GDP and 71.7% of the country’s carbon emissions. Projections indicate that by 2030 these proportions are expected to rise to 90% and 83%, respectively [1]. This underscores the pivotal role of urban agglomerations in achieving China’s carbon mitigation objectives.
The YREB, strategically centered along the Yangtze River’s navigation corridor, spans both riverbanks and traverses China’s eastern, central, and western regions. Covering 11 provinces and municipalities, it accounts for approximately 21.4% of the nation’s total land area and supports around 43% of the national population. In 2020, the YREB contributed 46.5% to China’s GDP, highlighting its critical role in the country’s economic framework. As such, the sustainable and healthy development of the YREB is of immense strategic significance to China’s overall growth and stability. Geographically, the YREB is characterized by three major urban agglomerations extending from east to west: the YRD, the TCC, and the CCA (Figure 1). Recent analyses reveal a consistent upward trajectory in carbon emissions across these regions, although the average annual growth rate of emissions has shown a significant slowdown in recent years (Figure 2). As a linchpin of rapid economic development across China’s diverse geographical and economic zones, the YREB also serves as a pivotal region for advancing low-carbon and green development initiatives. This dual role makes it an exemplary and highly relevant area for research on sustainable development. Therefore, a comprehensive investigation into the drivers of carbon emissions, their evolutionary trends, and effective emission reduction strategies within these urban agglomerations is essential for promoting high-quality development in the YREB and, more broadly, across China. Such research carries profound implications for achieving sustainable economic growth, mitigating environmental impacts, and enhancing ecological governance, thereby contributing to China’s long-term development goals and global environmental commitments.
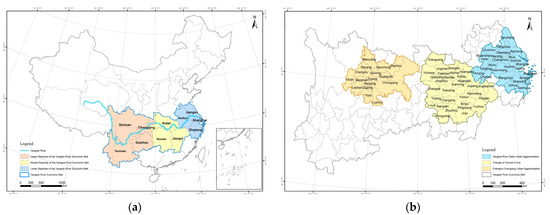
Figure 1.
Geographic distribution and scope of the study area. (a) Spatial position of the YREB within China. (b) Delineation and spatial extent of the three major urban agglomerations within the YREB.
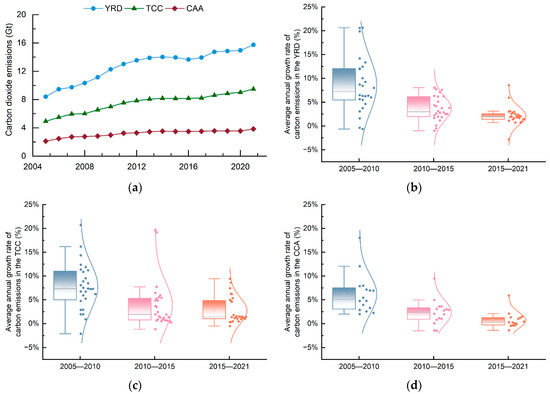
Figure 2.
Temporal trends in carbon emissions across the three urban agglomerations (2005–2021). (a) Cumulative carbon emissions growth in the three urban agglomerations from 2005 to 2021. (b) Average annual growth rate of carbon emissions in the YRD. (c) Average annual growth rate of carbon emissions in the TCC. (d) Average annual growth rate of carbon emissions in the CCA.
Scholars worldwide have conducted extensive and in-depth research on the factors influencing carbon emissions, utilizing a diverse array of analytical models. Among the most widely adopted methodologies for factor identification are SDA, LMDI, and the GDIM, all of which fall under the broader framework of IDA. Additionally, the IPAT model and its extended version, the STIRPAT model, have been extensively employed to explore the drivers of carbon emissions. Advanced statistical techniques, such as Lasso regression, have further enhanced the precision of these analyses. Collectively, these models provide a robust and comprehensive toolkit for elucidating the complex determinants of carbon emissions and their underlying dynamics.
Among the various factors influencing carbon emissions, economic growth is consistently recognized as the predominant driver of carbon emission increases [2,3]. Notably, Du et al. [4] demonstrated that the digital economy’s impact on carbon emission efficiency in urban agglomerations follows a U-shaped pattern, characterized by initial suppression followed by subsequent enhancement, leading to short-term energy rebound effects during the early stages of digital economic development. Simultaneously, the combustion of fossil fuels, such as coal and oil, constitutes the largest source of carbon dioxide emissions, establishing a strong correlation between carbon emission growth and energy consumption [5]. Li et al. [6] utilized the LMDI model to investigate the drivers of carbon emissions across Chinese provinces, concluding that economic development and energy structure serve as key accelerators and inhibitors, respectively, of carbon emission growth. Similarly, Jiang et al. [7] analyzed data from 30 Chinese provinces spanning 1995 to 2013, employing a combination of multilayer LMDI decomposition and hierarchical clustering. Their findings revealed that changes in energy intensity significantly contributed to emission reductions in most provinces, positioning it as a dominant factor in China’s carbon mitigation efforts. Studies on the Yangtze River Delta urban agglomeration emphasize prioritizing energy conservation and alternative energy technologies to reduce fossil fuel dependence through lowering energy intensity and enhancing clean energy utilization, thereby achieving carbon mitigation [8]. Research in the Pearl River Delta [9] corroborates these findings, demonstrating that improved energy efficiency and industrial restructuring effectively curb carbon emissions in urban agglomerations. With the growing global focus on carbon emissions, scholarly investigations into their drivers have expanded substantially, progressively encompassing diverse dimensions of societal systems. For instance, Tarazkar et al. [10] and Du et al. [11] demonstrated that demographic factors—including population size, population structure, household size, and per capita consumption—exhibit strong intrinsic linkages with carbon emissions. Emerging scholarly evidence indicates that reduced population density may alleviate environmental pressures through synergistic mechanisms. These include diminished per capita energy consumption, attenuated industrial production intensity, enhanced transportation system efficiency, and improved residential energy utilization efficacy, which collectively facilitate low-carbon transition trajectories [12,13]. Liu et al. [14], through an analysis of China’s industrial energy consumption structure, highlighted the substantial impact of economic activities, particularly the export of energy-intensive products, on carbon emissions. They identified exports as a major driver of the rapid rise in China’s total carbon emissions. Furthermore, studies by Wu et al. [15] and Dong et al. [16] established a long-term equilibrium relationship between carbon emissions and factors such as economic growth and industrial structure upgrading. Meanwhile, Wang et al. [17] empirically demonstrated the effects of supply-side structural adjustments on carbon emissions in the Beijing-Tianjin-Hebei region, underscoring the role of institutional interventions in promoting industrial green transformation. Du et al. developed the TEA-IS model by integrating complementary advantages of standalone modeling frameworks, demonstrating that green technology innovation mechanisms under low-carbon pilot city policies significantly enhance eco-efficiency through systemic resource reallocation [12]. Recent years have witnessed increasing scholarly focus on the mechanistic drivers of carbon emissions in urban agglomerations, emphasizing the roles of energy intensity, economic development, urbanization rates, industrial structure, foreign trade, and other factors [18,19]. Concurrently, integrated modeling approaches have been employed to decipher the complex mechanisms and spatiotemporal heterogeneity of emission-driving factors [20]. These studies collectively enhance our understanding of the complex dynamics driving carbon emissions and provide valuable insights for formulating strategies aimed at sustainable development and emission reduction.
A majority of scholars employ an integrated approach combining forecast model and scenario analysis to estimate the timing and magnitude of carbon emission peaks. The methodological frameworks commonly utilized in such studies encompass the Environmental Kuznets Curve (EKC), STIRPAT model, LEAP model [21,22], Grey Forecast Model [23], Logistic Regression Forecast Model, and other classical forecasting approaches, along with system dynamics and machine learning techniques such as Back Propagation Neural Networks. Among these, the STIRPAT model has gained particular prominence in examining the relationship between carbon emissions and various driving factors. This preference stems from its ability to overcome the limitations of the unit elasticity assumption inherent in the traditional IPAT model, offering greater flexibility and stochastic properties [24,25]. Extensive research has been conducted through integrated methodological frameworks combining predictive modeling and scenario analysis, generating comprehensive carbon emission trajectory simulations and peak prediction analyses across geographic scales spanning national to regional levels. For instance, Li et al. [24] applied the STIRPAT model to project that Fujian Province would reach its carbon emission peak between 2030 and 2040. Furthermore, Chen et al. [26] integrated the STIRPAT model with scenario analysis to demonstrate that China could achieve its carbon peak target by 2030 across various scenarios, including low emission reduction, baseline, and high emission reduction scenarios. Analyses by Li et al. [6] delineate substantial interprovincial variations in carbon peaking schedules across China, with eastern and northern provinces likely achieving earlier emission peaks driven by industrial sophistication and economic maturity. Conversely, northwestern regions exhibit delayed peaking trajectories attributable to constrained technological capacity and entrenched fossil fuel reliance. These findings provide robust scientific evidence supporting the feasibility of China’s carbon peak commitment. The extended STIRPAT framework demonstrates methodological rigor in carbon emission forecasting applications, particularly when synergistically integrated with scenario analysis techniques. This coupled analytical paradigm enables systematic projection of regional emission trajectories through concurrent consideration of multidimensional drivers and scenario-specific dynamics.
Current research on regional carbon emissions reveals several critical gaps that require further scholarly attention. First, the existing literature predominantly focuses on national or provincial scales, with limited investigation at the urban agglomeration or city level, particularly within the context of river basin economic zones. [27,28]. Although some studies have examined specific metropolitan regions, such as the YRD, Pearl River Delta, and Beijing-Tianjin-Hebei urban agglomerations, comparative analyses of carbon emission drivers across different urban agglomerations remain scarce [18]. Second, the selection of influencing factors has been overly reliant on qualitative frameworks or theoretical assumptions, lacking rigorous quantitative screening and dynamic contribution assessments. Third, a significant methodological gap exists in the integration of factor decomposition results with scenario-based projections. Current studies often treat these as separate analytical components rather than combining them to provide a more holistic understanding of emission dynamics and their underlying drivers, which limits the practical applicability of research findings.
This study focuses on three major urban agglomerations within the YREB as primary research subjects, with particular emphasis on analyzing the determinants and evolving patterns of carbon emissions within these metropolitan regions. To address these limitations, this study presents innovations in research scope, methodology, and analytical framework as follows (Figure 3): (1) we systematically investigate carbon emission determinants across three strategic urban clusters in the YREB (CCA, TCC, and YRD), filling critical research gaps in comparative analysis of watershed economic zones; (2) by synergizing grey relational analysis for objective factor screening with LMDI decomposition, we overcome the subjectivity limitations of conventional qualitative approaches while precisely quantifying historical emission drivers; and (3) we construct the optimized STIRPAT model based on rigorous factor selection, significantly enhancing forecast accuracy through systematic parameter optimization.
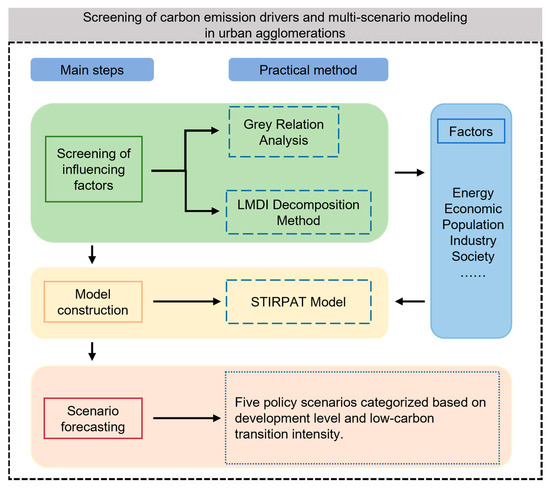
Figure 3.
Research framework.
2. Methods and Data
2.1. Variable Selection
Changes in carbon emissions are driven by a complex interplay of social, economic, and other factors, with varying influences across different regions. Therefore, accurately identifying the key drivers of carbon emission characteristics in urban agglomerations is essential for constructing robust forecast models. Building on previous research [5,19,29,30], this study preliminarily examines factors influencing carbon emissions in urban agglomerations within the YREB (Table 1). These factors include energy intensity, energy structure, economic development, industrial structure, population size, urbanization level, degree of openness, transportation, and government intervention, which serve as the foundation for further analysis.

Table 1.
Preliminary screening impact factors.
2.2. Grey Relational Analysis
Grey relational analysis quantifies associations between independent and dependent variables by assessing geometric similarity across data sequences, with its core mechanism deriving from variable interaction patterns revealed through curve spatial proximity. In this study, grey relational analysis was employed to investigate the existence and magnitude of correlations between various influencing factors and carbon emissions. Variables demonstrating strong correlations were subsequently selected as input parameters for the forecast model of carbon emissions. The analytical procedure comprises the following sequential steps:
- Establishment of reference and comparison sequence.
Reference sequence:
Comparison sequence:
- 2.
- Dimensionless processing of raw data series.
To ensure comparability across indicators, the raw data series were normalized to eliminate dimensional effects through standardized normalization procedures.
- 3.
- Creating difference sequences.
- 4.
- Determination of the resolution factor ρ.
The resolution coefficient, denoted as ρ, is defined within the interval (0, 1), where a decrease in ρ corresponds to an increase in resolution, and conversely, an increase in ρ indicates a decrease in resolution. In this study, drawing upon empirical evidence and prior research [31,32], the range of resolution coefficients [ρ1, ρ2] is established through the following equations:
- 5.
- Correlation size calculation.
2.3. LMDI Decomposition Method
Ang et al. [33] pioneered the development of the LMDI decomposition method, which was established as an extension of the fundamental Kaya identity. This robust analytical framework has gained widespread recognition in carbon emission driver analysis [34,35] and energy systems research [36] owing to its two principal methodological advantages: (1) the capacity to achieve complete decomposition of contributing factors without residual terms, and (2) the generation of decomposition results that are free from residual components. Drawing upon this theoretical foundation and integrating methodological innovations proposed by Li et al. [6] and Huang et al. [37], we have developed an advanced LMDI decomposition framework to systematically quantify the driving forces underlying carbon emissions. Specifically, our analytical model enables the identification and quantification of key drivers and their respective contribution rates across three strategically important urban agglomerations within the YREB, encompassing its upper, middle, and lower reaches. The mathematical formulation of the model is presented as follows:
where C is carbon emissions; E is total energy consumption; GDP is gross domestic product; UP is total urban population; and POP is total resident population.
The additive decomposition equation is as follows:
where ΔC is the change in total carbon emissions; Ct is the carbon emissions in year t; and C0 is the carbon emissions in the base year. ΔCES, ΔCEG, ΔCDUP, ΔCUR, ΔCPOP represent energy structure effect, energy intensity effect, economic development effect, urbanization development effect, and population size effect, respectively.
The contribution of each factor to the change in carbon emissions (CR) is calculated as follows:
2.4. Expanded STIRPAT Model
The STIRPAT model represents an extensible stochastic environmental impact assessment (EIA) framework, which has evolved from the foundational IPAT model. This analytical framework has been widely employed to examine the influence of various driving factors on diverse environmental issues. In the present study, we utilize an extended version of the STIRPAT model to project future carbon emission trajectories and estimate the timing of carbon emission peaks across urban agglomerations. The mathematical formulation of the model is expressed as follows:
where I is the environmental factor; P is the population factor; A is the economic factor; T is the technological factor; a is the model coefficient; b, c, and d are elasticity coefficients reflecting the importance of the corresponding influencing factors; e is the random error term; and i is the different study region.
To eliminate heteroskedasticity, Equation (18) is taken to be logarithmic:
Expand Equation (19) based on the initial screening of influencing factors as follows:
2.5. Data Sources
This study focuses on 26 cities in the YRD, 28 cities in the TCC, and 16 cities in the CCA, covering the period from 2005 to 2021. Urban carbon emissions data were obtained from the EDGAR EU Global Atmospheric Emissions Database. Due to the unavailability of energy balance sheets at the prefecture-level city level, which precludes the direct measurement of energy consumption by type, this study estimates total energy consumption using an inverse approach based on nighttime lighting data, as supported by previous studies [38,39]. Data on the value-added of the secondary and tertiary industries, GDP, POP, UR, TCO, TEV, FDI, and FS were collected from provincial and municipal statistical yearbooks, the China Urban Statistical Yearbook, and municipal statistical bureaus. To account for inflation, all relevant economic data for the period 2005–2021 were adjusted to constant 2005 prices.
3. Variable Screening and Impact Analysis
3.1. Grey Relational Analysis Results
In general, a grey correlation coefficient (GCC) below 0.5 implies a weak correlation between the independent and dependent variables. A GCC within the range of 0.5 to 0.8 reflects a moderate to significant correlation, whereas a GCC above 0.8 denotes a strong correlation.
The results of the grey relational analysis conducted on carbon emissions and their influencing factors across the three urban agglomerations reveal distinct regional patterns (Table 2, Figure 4). In the YRD, the correlation coefficients between carbon emissions and UR as well as RS are 0.4125 and 0.3578, respectively, indicating relatively weak associations. Conversely, the remaining factors exhibit statistically significant correlations, ranked in descending order as follows: FDI > TCO > POP > FS > TEV > ES > RT > DUP > EG. In the TCC, the correlation coefficients between carbon emissions and both RS and RT are below 0.5 (0.3274 and 0.3770, respectively), suggesting that industrial structure is not a primary determinant of carbon emission variations in this region. Among the remaining factors, ES demonstrates the strongest correlation with carbon emissions, with a coefficient of 0.7448. Within the CCA, ES, POP, TEV, FDI, TCO, and FS all exhibit correlation coefficients exceeding 0.5 with carbon emissions. Notably, FS and POP display particularly robust correlations. The ranking of correlation strength is as follows: FS > POP > TCO > TEV > FDI > ES. Given the significant correlation between TEV, FDI, and carbon emissions, and to ensure comparability across urban agglomerations, FDI is employed as a proxy to characterize the degree of external openness.

Table 2.
Correlation degree analysis table.
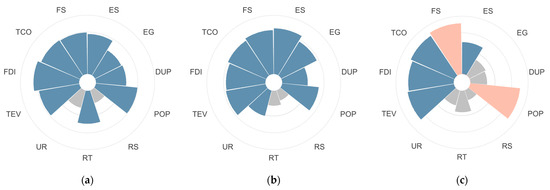
Figure 4.
Comparative analysis of correlation coefficients in (a) YRD, (b) TCC, and (c) CCA. Orange indicates strong correlation (>0.8), blue represents significant correlation (0.5–0.8), and gray denotes weak correlation (<0.5).
3.2. LMDI Decomposition Results
Based on the decomposition analysis of carbon emission drivers across the three urban agglomerations, the results indicate that, overall, economic development, urbanization, and population growth were the primary contributors to carbon emissions during the period from 2005 to 2021. Among these, economic development emerged as the most significant factor, increasing carbon emissions in the YRD, the TCC, and the CCA by 112,507.04 Mt, 78,984.66 Mt, and 322,040.11 Mt, respectively, with contribution rates of 153.14%, 172.64%, and 188.21% (Table 3, Figure 5). In contrast, ES and EG acted as key suppressors of carbon emission growth during the same period, driven by energy structure adjustments, continuous improvements in utilization efficiency, and the implementation of energy-saving and emission-reduction policies. Notably, EG was the most influential carbon suppression factor, contributing to emission reductions in the YRD, TCC, and CCA at rates of 142.10%, 95.38%, and 134.92%, respectively (Figure 5). A comparative analysis of the three urban agglomerations reveals that energy restructuring played a more substantial role in reducing carbon emissions in the TCC and CCA than in the YRD. Conversely, population size contributed the most to carbon emission growth in the YRD, primarily due to its highly developed economy, robust industrial base, rapid urbanization, and strong population absorption capacity. However, the YRD’s relatively low proportion of clean energy sources, such as natural gas and electricity, highlights the need for further adjustments in energy consumption structure and advancements in energy utilization technologies. These remain critical focus areas for future carbon emission reduction efforts in the region [8].

Table 3.
Cumulative effects of different driving factors from 2005 to 2021.
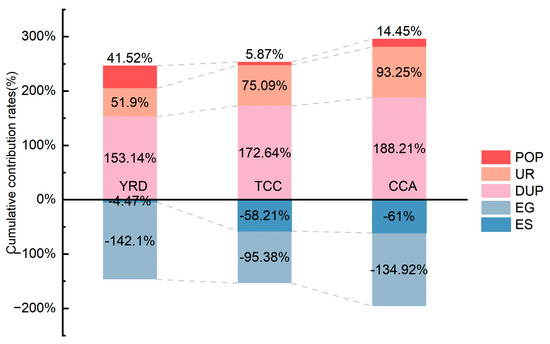
Figure 5.
Cumulative contribution rates of different driving factors from 2005 to 2021.
3.3. STIRPAT Model Construction
By integrating the outcomes of grey relational analysis and the LMDI decomposition method, the YRD region identifies nine principal factors influencing carbon emissions: ES, EG, DUP, UR, POP, RT, TCO, FDI, and FS. Conversely, the TCC and the CAA are characterized by eight major carbon emission determinants, excluding RT. Building upon these findings, this study formulates the STIRPAT forecast model.
Research indicates that variables such as population size, economic expansion, and industrial progression are intricately and closely interrelated. Their concurrent inclusion in the model may introduce multicollinearity issues, potentially skewing the model’s estimation outcomes. To address this, the Variance Inflation Factor (VIF) was calculated using Ordinary Least Squares (OLS) regression. The analysis reveals that the majority of the explanatory variables exhibit VIF values exceeding 5 (refer to Table 4), confirming the presence of multicollinearity.

Table 4.
Mean value of VIF for models in each urban agglomeration.
Significant multicollinearity was detected among the explanatory variables, rendering ordinary least squares (OLS) regression methodologically inappropriate. While multiple approaches exist to mitigate this issue—including ridge regression, principal component analysis (PCA), Lasso regression, and partial least squares (PLS)—our methodological selection was guided by three critical considerations specific to the dataset and research objectives. First, the study encompasses a large-scale panel dataset spanning 2005–2021 with numerous cities and multidimensional indicators, creating a high-dimensional feature space where ridge regression demonstrates particular efficacy in handling substantial sample sizes while preserving variable information. Second, while Lasso regression’s tendency to shrink coefficients to zero would discard potentially valuable predictors, and PCA’s dimensionality reduction sacrifices interpretability of original variables, ridge regression optimally retains all multidimensional indicators through controlled coefficient shrinkage. Finally, the bias-variance trade-off inherent in ridge regression enhances predictive stability—a crucial requirement for scenario simulations of carbon emissions. This combination of methodological strengths ensures robust parameter estimates while maintaining the interpretative capacity essential for policy-relevant modeling. Thus, this study employs ridge regression for parameter estimation.
The ridge regression results (Table 5) demonstrate that when the ridge parameter K is set to 0.143, 0.189, and 0.134 for the YRD, the TCC, and the CCA, respectively, the regression coefficients of the explanatory variables stabilize. This indicates that the model achieves a robust fit and exhibits strong explanatory power.

Table 5.
Results of ridge regression.
In summary, the carbon emission forecast model for the YRD is as follows:
Carbon emission forecast model for the TCC:
Carbon emission forecast model for the CCA:
4. Results and Discussion
4.1. Carbon Emission Scenario Setting
This study develops a two-dimensional framework integrating development level and low-carbon transition intensity to construct five distinct policy scenarios for analyzing pathway evolution. The baseline scenario (BL) extends current policies and societal trajectories without external interventions, capturing autonomous development patterns. Within proactive intervention scenarios, the framework delineates development pathways through two approaches: the high-development scenario prioritizes rapid economic expansion and marked improvements in social welfare, characterized by growth in DUP, UR, POP, TCO, FDI, and FS; and the low-development scenario emphasizes balanced progress between economic growth and qualitative development, focusing on inclusive sustainability through regional coordination, urban-rural integration, and livelihood enhancement. Subsequently, under the carbon mitigation framework, strategic pathways are bifurcated into strong and weak low-carbon intensities. The strong low-carbon scenario enforces stringent emission controls coupled with systematic energy replacement, driven by service sector advancement and disruptive clean technology innovations, whereas the weak low-carbon scenario adopts progressive mitigation approaches centered on phased energy efficiency enhancements and stepwise technological upgrades. Cross-dimensional integration generates four policy scenarios: (1) high development with weak low-carbon transition (HDWC, prioritizing economic growth); (2) high development with strong low-carbon transition (HDSC, driven by green technology innovation); (3) low development with weak low-carbon transition (LDWC, ensuring fundamental emission reduction); and (4) low development with strong low-carbon transition (LDSC, balancing equity considerations with deep decarbonization). This scenario design not only reveals the intricate relationship between development paradigms and low-carbon transitions but also enables systematic evaluation of synergies and trade-offs among multiple objectives—including economic growth, social equity, and climate change mitigation—under different policy combinations.
In accordance with China’s carbon reduction policies, the study defines the forecasting period from 2022 to 2040, using 2021 as the baseline year. The parameters for influencing factors are configured based on the five-year planning framework and the varying degrees of development and low-carbon intensity are represented by the growth rates assigned to each respective indicator (Table 6).

Table 6.
Development scenario setting in each city group.
Based on the socio-economic development status of urban agglomerations and referencing policies including provincial “14th Five-Year Plan” initiatives, we defined annual change rates (2021–2025) for key drivers across three urban agglomerations. The growth targets of DUP followed the 14th Five-Year Plans, while other factors were calibrated using historical annualized change rates. Subsequent growth rates (2026–2030, 2031–2035, 2036–2040) will be gradually adjusted from the 2021–2025 baseline, informed by systematic analysis of historical trends and existing empirical studies [6,40,41,42]. The specific parameter growth rates for each scenario are detailed in Appendix A, Appendix B and Appdedix C.
4.2. Scenario Forecasting Results and Analysis
As depicted in Figure 6, the carbon emissions trajectory of the YRD demonstrates a consistent pattern of initial increase followed by a subsequent decline. Overall, the YRD is projected to achieve its carbon peak target between 2025 and 2035. Specifically, under the BL, HDSC, LDWC, and LDSC scenarios, the YRD is expected to reach its carbon peak by 2030. Notably, the LDSC scenario achieves the earliest peak in 2025, with emissions reaching 16.91 × 108 tons. The HDWC scenario is projected to peak in 2035. These findings indicate that achieving the carbon peak by 2030 is feasible for the YRD. According to the BL scenario, maintaining the current levels of economic development and emission reduction measures will result in a deceleration in the rate of carbon emissions, culminating in a peak in 2030. The implementation of more stringent mitigation and carbon reduction measures under the LDSC and HDSC scenarios can effectively slow the growth rate of carbon emissions, thereby enabling earlier peak attainment or a reduction in peak emissions. As China’s most robust economic hub, characterized by comprehensive strength and rapid economic growth, the YRD’s achievement of the carbon peak under the HDSC scenario aligns more closely with its objective requirements. This scenario represents the optimal strategy for balancing economic development with the goal of achieving carbon peak targets.
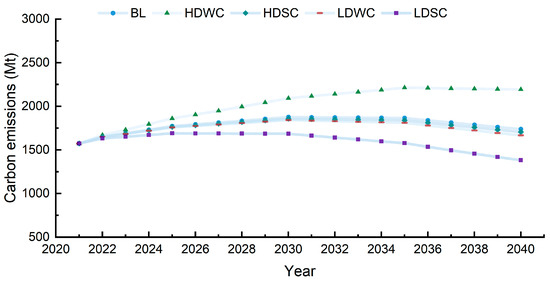
Figure 6.
Projected carbon emission trends in the YRD, 2021–2040.
As illustrated in Figure 7, the carbon emissions trajectory of the TCC region under five distinct scenarios reveals a consistent pattern of peaking between 2030 and 2035. The peak emissions under these scenarios are projected to be 10.01 × 108 tons, 12.07 × 108 tons, 9.84 × 108 tons, 9.74 × 108 tons, and 9.06 × 108 tons, respectively. The forecast results indicate that the current carbon emission control measures in the TCC region have already begun to yield positive effects, and the goal of achieving carbon peak by 2030 is attainable under the existing development trajectory. Moving forward, the TCC region should adopt a comprehensive approach to coordinate various factors, including energy utilization, population dynamics, economic growth, urbanization, and external trade. By doing so, the region can effectively reduce carbon emissions, achieve an earlier peak, and maintain steady economic development. This integrated strategy will be critical for balancing emission reduction targets with sustainable economic progress.
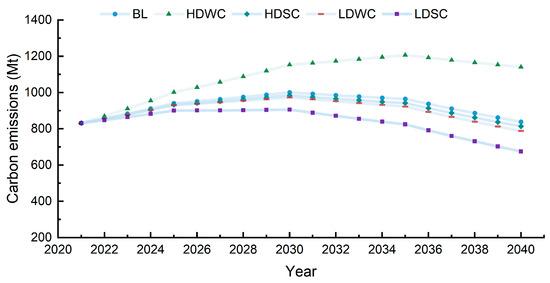
Figure 7.
Projected carbon emission trends in the TCC, 2021–2040.
The CCA demonstrates significant temporal variations in carbon peaking across different scenarios, as depicted in Figure 8. Under the BL scenario, the CCA is projected to achieve carbon peaking by 2035, falling short of the 2030 target. In contrast, under the LDSC and HDSC scenarios, carbon peaking is anticipated to occur in 2025 and 2030, respectively, with peak reductions of 13.20% and 8.60% compared to the BL scenario. Notably, under the HDWC scenario, carbon peaking remains unattainable within the 2021–2040 forecast period. These results highlight the critical need for the CCA to maintain a green development pathway, adopt rigorous emission reduction strategies, and implement targeted policies and initiatives. Specifically, accelerating the transition to green and low-carbon energy systems, promoting energy conservation and carbon reduction measures, establishing a sustainable low-carbon product supply chain, and conducting pilot demonstrations of green development practices are essential steps to achieve the 2030 carbon peaking target.
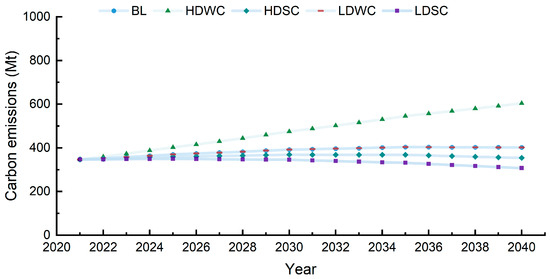
Figure 8.
Projected carbon emission trends in the CCA, 2021–2040.
4.3. Additional Analysis
To assess the impact of variations in key parameter assumptions on the model outcomes, we conducted a sensitivity analysis using the following methodology: Within the framework of comprehensive scenario projections, we systematically altered the rate of change for one influencing factor at a time (low, medium, and high rates), while maintaining constant rates for other factors. This methodology enabled the evaluation of how variations in individual factor change rates affect both the peak timing and magnitude of carbon emissions in urban agglomerations. The results demonstrate that the influence of each factor on both emission peak characteristics remains robust overall, with no anomalous discontinuities observed. Furthermore, this approach facilitates a more precise quantification of the differential impacts exerted by distinct factors on carbon emission patterns. Detailed data can be found in Appendix D, Appendix E and Appendix F.
The YRD analysis revealed that accelerated reduction rates in ES, EG, and RT exerted consistent positive effects on both emission peak magnitude and timing. Specifically, higher mitigation rates correlated with lower peak values and earlier peaking timelines, as evidenced in the BL, HDSC, and LDSC scenarios. Conversely, enhanced growth rates of other factors demonstrated negative correlations, where increased development velocity amplified peak emissions. This pattern delayed peaking timelines in the BL and LDSC scenarios, whereas the HDWC, HDSC, and LDWC scenarios maintained temporally stable peaking schedules. For the TCC, individual factor variation predominantly modulated peak magnitudes without significantly altering peaking chronology across most scenarios. The analysis results of the CCA reveal that rate changes in individual influencing factors exert certain impacts on both the peak timing and peak magnitude of carbon emissions. Specifically, carbon emissions demonstrate high sensitivity to variations in ES and EG under the LDWC and LDSC scenarios. These findings further substantiate that energy-related factors constitute the critical determinants influencing carbon emissions in the CCA.
5. Conclusions and Policy Implications
5.1. Conclusions and Discussion
Utilizing carbon emission data from three urban agglomerations in the YREB spanning 2005–2021, this study systematically investigates the correlation between key drivers and carbon emissions through grey relational analysis. A LMDI decomposition framework is further employed to quantify the contributions of five core factors: ES, EG, DUP, UR, and POP. Integrating findings from grey relational analysis and LMDI decomposition, we developed an extended STIRPAT model to systematically evaluate the efficacy, limitations, and implementation outcomes of carbon mitigation policies across urban agglomerations through multi-scenario simulations. The main findings are as follows:
- Significant disparities in total carbon emissions are observed across various urban agglomerations, with the YRD consistently exhibiting the highest emission levels, followed by the TCC. This pattern is consistent with the relative scale of these urban agglomerations. In terms of emission growth rates, the YRD, TCC, and CCA demonstrated comparable average annual growth rates from 2005 to 2021, at 4.00%, 4.19%, and 3.75%, respectively. Moreover, from the 11th to the 13th Five-Year Plan periods, the average annual growth rates of carbon emissions in these regions exhibited a consistent downward trend. This decline demonstrates the sustained effectiveness of China’s integrated policy framework for climate change mitigation and adaptation, marking a strategic transition in climate governance from reactive response to proactive regulation [25].
- This study employed an integrated analytical framework combining grey relational analysis and LMDI decomposition to identify critical drivers of carbon emissions among 11 variables spanning five distinct categories. The methodology innovatively incorporates social factors (e.g., government intervention and openness level) beyond conventional economic, energy, and industrial determinants [6,7,30]. The grey relational analysis revealed substantial spatial heterogeneity in factor–emission correlations across geographically distinct urban agglomerations. Notably, social factors such as openness level may surpass conventional determinants in impact magnitude, as evidenced by the highest correlation (FS = 0.8138) observed in the CCA. The LMDI decomposition results indicate that DUP, UR, and POP exerted positive driving effects on carbon emissions across all three urban agglomerations during 2005–2021, with contribution rates ranked as DUP > UR > POP. Conversely, ES and EG suppressed emission growth, showing EG > ES in contribution magnitude. While this aligns with the consensus that economic factors dominate emissions growth and energy-related measures serve as primary mitigators in China [6,43], our comparative analysis reveals distinct spatial heterogeneity among the YRD, TCC, and CCA. POP contributed significantly more to carbon emissions in the YRD than in the TCC and CCA, with the TCC exhibiting the lowest population-driven effects. ES demonstrated lower emission suppression efficiency in the YRD compared to the other two urban agglomerations, whereas urbanization rate emerged as the most significant driver of carbon emissions in the CCA.
- Based on the established predictive model, our findings reveal no inverted U-shaped relationship between DUP and carbon emissions in the three urban agglomerations during the observation period, indicating that carbon emission growth rates have not yet significantly slowed in their industrialization and urbanization processes, with no clear inflection point observed. Collectively, these findings suggest that current development patterns in these city clusters sustain a positive correlation between economic activities and carbon output, failing to achieve the decoupling effect expected in advanced urban systems. Meanwhile, the regression analysis of the YRD’s carbon emission forecast model reveals a negative coefficient for the RT, indicating that increasing the proportion of tertiary industries effectively suppresses emission growth. This finding highlights industrial structure optimization as a viable pathway for achieving total carbon emission control in the YRD [8].
- In this study, while we isolated the individual contributions of various factors, a more nuanced discussion is warranted regarding both the direct and indirect impacts of each driving factor, considering potential interactions among them. Energy consumption constitutes the primary source of carbon emissions, with China’s fossil fuel-dominated energy structure creating a direct correlation between energy demand growth and emission escalation. However, such energy-driven emission growth has been effectively mitigated through clean energy deployment and energy efficiency improvements. Overall, ES and EG are projected to exhibit gradual declines, demonstrating accelerated reduction rates under strong low-carbon scenarios. Economic growth, typically driven by energy consumption and large-scale production factor inputs, directly accelerates carbon emission increases. Simultaneously, it indirectly stimulates social dynamics such as rural–urban migration and improvements in living standards, which collectively amplify energy demand. The disparities in DUP growth rates are explicitly incorporated into the scenario design through high-development and low-development frameworks in this study. Population scale operates as a dual emission driver, directly amplifying energy demand and indirectly stimulating production scaling. Industrial restructuring mediates emissions through energy patterns, technological trajectories, and policy instruments, with accelerated tertiary sector growth characterizing strong low-carbon scenarios. Urbanization manifests dual effects: while lifestyle transitions and land-use modifications intensify emissions through elevated energy demands, concentrated urban settlements enhance resource utilization efficiency via shared infrastructure and public services. The sustained growth of national economies, coupled with rising living standards and transportation accessibility, has escalated transport-related energy consumption, driving progressive intensification of environmental burdens across high-development and low-development scenarios. FDI exhibits dual effects: the pollution haven effect through industrial relocation versus the pollution halo effect via technology diffusion. Government intervention reveals phase-dependent efficacy, transitioning from growth-oriented fiscal policies during early industrialization—exacerbating fossil energy dependence—to green fiscal mechanisms prioritizing ecological civilization construction during advanced development stages.
- This study establishes five carbon emission scenarios based on the current developmental status and policy frameworks of respective urban agglomerations, projecting future carbon emission trajectories for the YRD, TCC, and CCA under these scenarios. The findings reveal that under the HDSC and LDSC scenarios, the three urban agglomerations can achieve carbon peaking by 2030 with relatively low peak carbon levels, confirming that stringent low-carbon policies effectively facilitate peak carbon targets. Conversely, HDWC strategies present a primary barrier to regional emission reduction [44], either failing to meet the peaking timeline or inducing significantly higher peak levels.
5.2. Policy Implications
- The findings reveal significant heterogeneity among the YRD, TCC, and CCA in both total carbon emissions and key contributing factors. Our emission forecasts further indicate that achieving carbon peaking targets optimally requires implementing strong low-carbon scenarios across these metropolitan clusters, with region-specific strategies prioritizing dominant emission drivers. The following evidence-based policy recommendations integrate these strategic dimensions to operationalize effective climate governance frameworks. Steadily advancing energy transformation and establishing a clean energy-dominated supply system are critical. Each urban agglomeration should prioritize exploitation of indigenous clean and low-carbon energy resources following the proximity principle. For instance, the YRD can leverage coastal wind resources to advance offshore wind farm development [45], with strategic focus on establishing coastal wind power bases in Yancheng and Nantong, while enhancing the Zhoushan Archipelago offshore wind power operations and maintenance hub. To address current challenges of elevated capital intensity in offshore wind projects, implementation of domestic substitution strategies for critical components and operation systems, coupled with innovative financing mechanisms such as output-contingent financing and negative list approval protocols, merits consideration. The TCC and CCA could capitalize on abundant hydropower potential through cascade hydropower station deployment, thereby displacing incumbent fossil fuel-based energy infrastructure via clean energy capacity expansion. Concurrently, grid modernization initiatives must be accelerated to improve renewable energy accommodation capacity, with particular emphasis on mitigating wind curtailment and hydropower spillage through enhanced transmission infrastructure and smart grid technologies. In synergistic green transportation development, the YRD and CCA have made significant progress in promoting new energy vehicles (NEVs) and building green transportation infrastructure. The TCC, with its well-established automotive industry, can further enhance the development pace and scale of NEVs by capitalizing on its industrial advantages. Regional policymakers must implement dynamic NEV production-tax incentive linkage mechanisms. Through tiered fiscal schemes, these policy instruments can effectively counteract central subsidy reductions, thereby ensuring orderly industrial transitions while sustaining regional market growth trajectories.
- Factor decomposition analysis identifies economic development as the persistent primary driver of carbon emissions across all urban agglomerations. China’s ongoing economic restructuring, characterized by simultaneous optimization of existing industries and strategic development of emerging sectors, underscores the potential to amplify energy-saving effects through targeted industrial structure refinement. The YRD can leverage its robust manufacturing foundation to foster the deep integration of advanced manufacturing with modern service industries. The TCC can leverage its geographical advantages to foster complementary development among cities, rational industrial specialization, and establish comprehensive industrial and supply chains. This strategic positioning enables effective absorption of industrial relocation from advanced regions like the Yangtze River Delta and Greater Bay Area. However, caution is warranted against potential pollution transfer and cost constraints associated with green transition initiatives. The CCA could accelerate industrial upgrading through cluster-oriented transformation of traditional industries, particularly in achieving high-end manufacturing and intelligent production systems. Nonetheless, comparative analysis reveals relatively weaker comprehensive competitiveness in industrial development and the current challenges of significant industrial planning overlap within the region necessitate institutional innovations to establish cross-regional industrial coordination mechanisms, which should be prioritized for synergistic development.
- Research has demonstrated that population size is a significant driver of carbon emission growth in the YRD [43]. Although an increase in population size can stimulate industrial development, scientific and technological innovation, urbanization, and improvements in infrastructure within the YRD, it also generates negative consequences, including increased carbon emissions, heightened pressure on resource scarcity, and environmental pollution. Consequently, the YRD must implement science-based policy frameworks to refine population structure and elevate human capital quality. Critical priorities include leveraging technological innovation, fostering cross-sector industrial coordination, and establishing institutional mechanisms to steer labor redistribution toward low-carbon sectors, thereby aligning decarbonization objectives with sustained economic growth.
- It is imperative to promote urbanization in a systematic and orderly manner while ensuring the scientific planning and development of urban agglomerations. In 2021, the average urbanization rates of the TCC and CCA were 64.65% and 63.42%, respectively, indicating that both regions are at a pivotal stage in their urbanization processes. Both urban agglomerations still possess urbanization potential, but future development should prioritize structural optimization. Establishing a “core cities-sub-nodes-specialized towns” hierarchical system could enhance complementary advantages and coordinated growth. This tiered system enables functional complementarity and coordinated development, achieving synergistic benefits via functional specialization, enhanced resource allocation efficiency, and cross-regional coordination mechanisms.
- Current fiscal allocations in local governments exhibit structural imbalance, prioritizing capital expenditures for economic growth over environmental improvement investments. This expenditure bias constitutes a primary driver of the observed positive correlation between fiscal expansion and carbon emission growth. Environmental projects’ extended payback periods often exceed typical political cycles, creating temporal misalignment that dampens governmental prioritization of ecological investments. To reconcile this, establishing legally mandated environmental expenditure ratios and promoting green bond issuance (as exemplified by Guangdong Province’s pioneering “carbon-neutral” bond issuance in 2021) could mobilize private capital for long-term sustainability projects while alleviating fiscal burdens. Metropolitan clusters should leverage geographic synergies through shared environmental infrastructure (e.g., integrated water management networks in the YRD’s Qingpu-Wujiang-Jiashan demonstration zone) and joint funding mechanisms for cross-jurisdictional environmental governance, particularly targeting transboundary river remediation and regional air quality management systems.
5.3. Future Directions
While our study provides valuable insights, its methodological limitations require rigorous scholarly attention. Future research can identify breakthroughs in the following aspects:
- While nighttime light data offer valuable insights for estimating energy consumption and carbon emissions, several inherent limitations should be acknowledged. First, sensor-specific discrepancies may introduce biases, particularly in highly urbanized areas with overglow or pixel saturation [38]. Second, the linear regression models commonly employed to link nighttime light intensity to energy consumption oversimplify complex nonlinear relationships, potentially neglecting regional heterogeneity in energy structures, industrial activities, and energy efficiency [46]. Third, the reliance on provincial-level energy statistics to downscale estimates to city-level scales may amplify errors due to intra-provincial spatial heterogeneity, such as uneven distribution of energy-intensive industries or consumption patterns across cities within the same province [46]. Future studies could mitigate these issues by integrating multi-source data (e.g., thermal infrared, mobility patterns) and adopting hybrid models that account for spatial autocorrelation and energy transition dynamics.
- This study employs the STIRPAT framework to elucidate the direct contributions of individual drivers to carbon emissions, utilizing a partial equilibrium approach that presumes independence among socioeconomic and technological factors. While this methodological design aligns with our primary objective of isolating direct effects for differentiated policy interventions, it does not account for potential synergistic or antagonistic interactions between drivers. Specifically, urbanization trajectories may simultaneously drive energy demand growth and accelerate renewable technology adoption via agglomeration effects, producing non-linear feedback mechanisms that our analytical framework cannot resolve. Furthermore, rebound effects linking energy efficiency gains to consumption expansion remain unquantified. Future research could explore alternative models, such as machine learning or dynamic systems modeling, and could offer more flexibility in capturing complex and non-linear patterns in emissions data.
- Existing studies on carbon emission drivers predominantly focus on conventional determinants (economic scale, energy structure, industrial transitions, population density), yet lack systematic analysis of non-linear impacts stemming from evolving household behavioral patterns. For instance, while sharing economy initiatives (e.g., ride-sharing platforms) and waste classification policies have significantly altered residential carbon footprints, behavioral elasticity coefficients remain absent from mainstream emission forecasting models. Future research should integrate interdisciplinary methodologies to decode multi-agent interactions (households–enterprises–governments), complemented by causal inference techniques (e.g., difference-in-differences, synthetic controls) to quantify net emission reductions from emerging behavioral interventions.
Author Contributions
Conceptualization, Z.Z., S.C. and P.J.; methodology, Z.Z. and P.J.; software, Z.Z. and S.C.; formal analysis, Z.Z.; resources, P.J. and Z.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z. and P.J.; supervision, P.J.; project administration, P.J.; funding acquisition, P.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Shanghai Science and Technology Commission (23ZR1404100), the Sino-German Center (M-0049), and Fudan Tyndall Centre of Fudan University (IDH6286315).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data presented in this study are available on request from the author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Average annual growth rates of impact factors under different scenarios for the YRD.
Table A1.
Average annual growth rates of impact factors under different scenarios for the YRD.
| Impact Factor | Time Interval | BL | HDWC | HDSC | LDWC | LDSC |
|---|---|---|---|---|---|---|
| ES | 2021–2025 | 0.64% | 1.14% | 0.14% | 0.84% | 0.44% |
| 2026–2030 | −0.36% | 0.14% | −0.86% | −0.16% | −0.56% | |
| 2031–2035 | −1.36% | −0.86% | −1.86% | −1.16% | −1.56% | |
| 2036–2040 | −2.36% | −1.86% | −2.86% | −2.16% | −2.56% | |
| EG | 2021–2025 | −8.18% | −7.18% | −9.18% | −7.68% | −8.68% |
| 2026–2030 | −7.18% | −6.18% | −8.18% | −6.68% | −7.68% | |
| 2031–2035 | −6.18% | −5.18% | −7.18% | −5.68% | −6.68% | |
| 2036–2040 | −5.18% | −4.18% | −6.18% | −4.68% | −5.68% | |
| DUP | 2021–2025 | 5.33% | 5.83% | 5.83% | 4.83% | 4.83% |
| 2026–2030 | 4.33% | 4.83% | 4.83% | 3.83% | 3.83% | |
| 2031–2035 | 3.33% | 3.83% | 3.83% | 2.83% | 2.83% | |
| 2036–2040 | 2.33% | 2.83% | 2.83% | 1.83% | 1.83% | |
| UR | 2021–2025 | 1.58% | 1.78% | 1.78% | 1.38% | 1.38% |
| 2026–2030 | 1.28% | 1.48% | 1.48% | 1.08% | 1.08% | |
| 2031–2035 | 0.98% | 1.18% | 1.18% | 0.78% | 0.78% | |
| 2036–2040 | 0.68% | 0.88% | 0.88% | 0.48% | 0.48% | |
| POP | 2021–2025 | 1.36% | 1.56% | 1.56% | 0.96% | 0.96% |
| 2026–2030 | 0.96% | 1.16% | 1.16% | 0.56% | 0.56% | |
| 2031–2035 | 0.56% | 0.76% | 0.76% | 0.16% | 0.16% | |
| 2036–2040 | 0.16% | 0.36% | 0.36% | −0.24% | −0.24% | |
| RT | 2021–2025 | 2.23% | 1.73% | 2.73% | 1.73% | 2.73% |
| 2026–2030 | 1.73% | 1.23% | 2.23% | 1.23% | 2.23% | |
| 2031–2035 | 1.23% | 0.73% | 1.73% | 0.73% | 1.73% | |
| 2036–2040 | 0.73% | 0.23% | 1.23% | 0.23% | 1.23% | |
| TCO | 2021–2025 | 9.22% | 10.22% | 10.22% | 8.22% | 8.22% |
| 2026–2030 | 7.22% | 8.22% | 8.22% | 6.22% | 6.22% | |
| 2031–2035 | 5.22% | 6.22% | 6.22% | 4.22% | 4.22% | |
| 2036–2040 | 3.22% | 4.22% | 4.22% | 2.22% | 2.22% | |
| FDI | 2021–2025 | 3.03% | 3.53% | 3.53% | 2.53% | 2.53% |
| 2026–2030 | 2.53% | 3.03% | 3.03% | 2.03% | 2.03% | |
| 2031–2035 | 2.03% | 2.53% | 2.53% | 1.53% | 1.53% | |
| 2036–2040 | 1.53% | 2.03% | 2.03% | 1.03% | 1.03% | |
| FS | 2021–2025 | 5.92% | 6.42% | 6.42% | 5.42% | 5.42% |
| 2026–2030 | 4.92% | 5.42% | 5.42% | 4.42% | 4.42% | |
| 2031–2035 | 3.92% | 4.42% | 4.42% | 3.42% | 3.42% | |
| 2036–2040 | 2.92% | 3.42% | 3.42% | 2.42% | 2.42% |
Appendix B

Table A2.
Average annual growth rates of impact factors under different scenarios for the TCC.
Table A2.
Average annual growth rates of impact factors under different scenarios for the TCC.
| Impact Factor | Time Interval | BL | HDWC | HDSC | LDWC | LDSC |
|---|---|---|---|---|---|---|
| ES | 2021–2025 | −2.59% | −2.09% | −3.09% | −2.39% | −2.79% |
| 2026–2030 | −3.59% | −3.09% | −4.09% | −3.39% | −3.79% | |
| 2031–2035 | −4.59% | −4.09% | −5.09% | −4.39% | −4.79% | |
| 2036–2040 | −5.59% | −5.09% | −6.09% | −5.39% | −5.79% | |
| EG | 2021–2025 | −3.56% | −2.56% | −4.56% | −3.06% | −4.06% |
| 2026–2030 | −4.06% | −3.06% | −5.06% | −3.56% | −4.56% | |
| 2031–2035 | −4.56% | −3.56% | −5.56% | −4.06% | −5.06% | |
| 2036–2040 | −5.06% | −4.06% | −6.06% | −4.56% | −5.56% | |
| DUP | 2021–2025 | 6.50% | 7.00% | 7.00% | 6.00% | 6.00% |
| 2026–2030 | 5.50% | 6.00% | 6.00% | 5.00% | 5.00% | |
| 2031–2035 | 4.50% | 5.00% | 5.00% | 4.00% | 4.00% | |
| 2036–2040 | 3.50% | 4.00% | 4.00% | 3.00% | 3.00% | |
| UR | 2021–2025 | 2.23% | 2.43% | 2.43% | 2.03% | 2.03% |
| 2026–2030 | 1.93% | 2.13% | 2.13% | 1.73% | 1.73% | |
| 2031–2035 | 1.63% | 1.83% | 1.83% | 1.43% | 1.43% | |
| 2036–2040 | 1.33% | 1.53% | 1.53% | 1.13% | 1.13% | |
| POP | 2021–2025 | −0.14% | 0.06% | 0.06% | −0.34% | −0.34% |
| 2026–2030 | −0.34% | −0.14% | −0.14% | −0.54% | −0.54% | |
| 2031–2035 | −0.54% | −0.34% | −0.34% | −0.74% | −0.74% | |
| 2036–2040 | −0.74% | −0.54% | −0.54% | −0.94% | −0.94% | |
| TCO | 2021–2025 | 12.05% | 13.05% | 13.05% | 11.05% | 11.05% |
| 2026–2030 | 11.05% | 12.05% | 12.05% | 10.05% | 10.05% | |
| 2031–2035 | 10.05% | 11.05% | 11.05% | 9.05% | 9.05% | |
| 2036–2040 | 9.05% | 10.05% | 10.05% | 8.05% | 8.05% | |
| FDI | 2021–2025 | 9.74% | 11.74% | 11.74% | 7.74% | 7.74% |
| 2026–2030 | 7.74% | 9.74% | 9.74% | 5.74% | 5.74% | |
| 2031–2035 | 5.74% | 7.74% | 7.74% | 3.74% | 3.74% | |
| 2036–2040 | 3.74% | 5.74% | 5.74% | 1.74% | 1.74% | |
| FS | 2021–2025 | 6.52% | 7.02% | 7.02% | 6.02% | 6.02% |
| 2026–2030 | 5.52% | 6.02% | 6.02% | 5.02% | 5.02% | |
| 2031–2035 | 4.52% | 5.02% | 5.02% | 4.02% | 4.02% | |
| 2036–2040 | 3.52% | 4.02% | 4.02% | 3.02% | 3.02% |
Appendix C

Table A3.
Average annual growth rates of impact factors under different scenarios for the CCA.
Table A3.
Average annual growth rates of impact factors under different scenarios for the CCA.
| Impact Factor | Time Interval | BL | HDWC | HDSC | LDWC | LDSC |
|---|---|---|---|---|---|---|
| ES | 2021–2025 | −4.55% | −3.55% | −5.55% | −4.05% | −5.05% |
| 2026–2030 | −3.55% | −2.55% | −4.55% | −3.05% | −4.05% | |
| 2031–2035 | −2.55% | −1.55% | −3.55% | −2.05% | −3.05% | |
| 2036–2040 | −1.55% | −0.55% | −2.55% | −1.05% | −2.05% | |
| EG | 2021–2025 | −4.66% | −3.66% | −5.66% | −4.16% | −5.16% |
| 2026–2030 | −5.66% | −4.66% | −6.66% | −5.16% | −6.16% | |
| 2031–2035 | −6.66% | −5.66% | −7.66% | −6.16% | −7.16% | |
| 2036–2040 | −7.66% | −6.66% | −8.66% | −7.16% | −8.16% | |
| DUP | 2021–2025 | 6.28% | 6.78% | 6.78% | 5.78% | 5.78% |
| 2026–2030 | 5.28% | 5.78% | 5.78% | 4.78% | 4.78% | |
| 2031–2035 | 4.28% | 4.78% | 4.78% | 3.78% | 3.78% | |
| 2036–2040 | 3.28% | 3.78% | 3.78% | 2.78% | 2.78% | |
| UR | 2021–2025 | 2.97% | 3.17% | 3.17% | 2.77% | 2.77% |
| 2026–2030 | 2.67% | 2.87% | 2.87% | 2.47% | 2.47% | |
| 2031–2035 | 2.37% | 2.57% | 2.57% | 2.17% | 2.17% | |
| 2036–2040 | 2.07% | 2.27% | 2.27% | 1.87% | 1.87% | |
| POP | 2021–2025 | 0.68% | 0.88% | 0.88% | 0.48% | 0.48% |
| 2026–2030 | 0.48% | 0.68% | 0.68% | 0.28% | 0.28% | |
| 2031–2035 | 0.28% | 0.48% | 0.48% | 0.08% | 0.08% | |
| 2036–2040 | 0.08% | 0.08% | 0.08% | −0.12% | −0.12% | |
| TCO | 2021–2025 | 9.50% | 10.50% | 10.50% | 9.00% | 9.00% |
| 2026–2030 | 8.50% | 9.50% | 9.50% | 8.00% | 8.00% | |
| 2031–2035 | 7.50% | 8.50% | 8.50% | 7.00% | 7.00% | |
| 2036–2040 | 6.50% | 7.50% | 7.50% | 6.00% | 6.00% | |
| FDI | 2021–2025 | 7.82% | 8.82% | 8.82% | 6.82% | 6.82% |
| 2026–2030 | 6.82% | 7.82% | 7.82% | 5.82% | 5.82% | |
| 2031–2035 | 5.82% | 6.82% | 6.82% | 4.82% | 4.82% | |
| 2036–2040 | 4.82% | 5.82% | 5.82% | 3.82% | 3.82% | |
| FS | 2021–2025 | 13.32% | 14.32% | 14.32% | 12.32% | 12.32% |
| 2026–2030 | 12.32% | 13.32% | 13.32% | 11.32% | 11.32% | |
| 2031–2035 | 11.32% | 12.32% | 12.32% | 10.32% | 10.32% | |
| 2036–2040 | 10.32% | 11.32% | 11.32% | 9.32% | 9.32% |
Appendix D

Table A4.
Impact of rate changes in different factors under various scenarios on carbon peaking time and peak values in the YRD.
Table A4.
Impact of rate changes in different factors under various scenarios on carbon peaking time and peak values in the YRD.
| Impact Factor | Scenario | Low-Rate Peak | Low-Rate Time to Peak | Medium-Rate Peak | Medium-Rate Time to Peak | High-Rate Peak | High-Rate Time to Peak |
|---|---|---|---|---|---|---|---|
| ES | BL | 19.05 | 2035 | 18.77 | 2030 | 18.41 | 2030 |
| HDWC | 22.14 | 2035 | 21.70 | 2035 | 21.05 | 2035 | |
| HDSC | 19.35 | 2035 | 18.96 | 2035 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.19 | 2030 | 17.84 | 2030 | |
| LDSC | 17.42 | 2030 | 17.19 | 2030 | 16.91 | 2025 | |
| EG | BL | 19.56 | 2035 | 18.77 | 2030 | 18.21 | 2030 |
| HDWC | 22.14 | 2035 | 21.12 | 2035 | 20.14 | 2035 | |
| HDSC | 20.21 | 2035 | 19.29 | 2035 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.15 | 2030 | 17.60 | 2030 | |
| LDSC | 17.65 | 2030 | 17.12 | 2030 | 16.80 | 2025 | |
| DUP | BL | 18.52 | 2030 | 18.77 | 2030 | 19.07 | 2035 |
| HDWC | 21.20 | 2035 | 21.66 | 2035 | 22.14 | 2035 | |
| HDSC | 18.09 | 2030 | 18.34 | 2030 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.67 | 2030 | 18.93 | 2030 | |
| LDSC | 16.91 | 2025 | 17.09 | 2030 | 17.32 | 2030 | |
| UR | BL | 18.58 | 2030 | 18.77 | 2030 | 18.97 | 2035 |
| HDWC | 21.42 | 2035 | 21.78 | 2035 | 22.14 | 2035 | |
| HDSC | 18.19 | 2030 | 18.39 | 2030 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.62 | 2030 | 18.82 | 2030 | |
| LDSC | 16.91 | 2025 | 17.04 | 2030 | 17.22 | 2030 | |
| POP | BL | 18.52 | 2030 | 18.77 | 2030 | 18.90 | 2030 |
| HDWC | 21.45 | 2035 | 21.91 | 2035 | 22.14 | 2035 | |
| HDSC | 18.21 | 2030 | 18.46 | 2030 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.68 | 2030 | 18.80 | 2030 | |
| LDSC | 16.91 | 2025 | 17.09 | 2030 | 17.21 | 2030 | |
| RT | BL | 19.05 | 2035 | 18.77 | 2030 | 18.53 | 2030 |
| HDWC | 22.14 | 2035 | 21.69 | 2035 | 21.26 | 2035 | |
| HDSC | 19.15 | 2035 | 18.82 | 2030 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.19 | 2030 | 17.95 | 2030 | |
| LDSC | 17.30 | 2030 | 17.08 | 2030 | 16.91 | 2025 | |
| TCO | BL | 18.57 | 2030 | 18.77 | 2030 | 18.99 | 2035 |
| HDWC | 21.39 | 2035 | 21.76 | 2035 | 22.14 | 2035 | |
| HDSC | 18.18 | 2030 | 18.38 | 2030 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.63 | 2030 | 18.83 | 2030 | |
| LDSC | 16.91 | 2025 | 17.05 | 2030 | 17.23 | 2030 | |
| FDI | BL | 18.65 | 2030 | 18.77 | 2030 | 18.90 | 2030 |
| HDWC | 21.69 | 2035 | 21.91 | 2035 | 22.14 | 2035 | |
| HDSC | 18.34 | 2030 | 18.46 | 2030 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.55 | 2030 | 18.67 | 2030 | |
| LDSC | 16.91 | 2025 | 16.97 | 2030 | 17.08 | 2030 | |
| FS | BL | 18.68 | 2030 | 18.77 | 2030 | 18.86 | 2030 |
| HDWC | 21.81 | 2035 | 21.97 | 2035 | 22.14 | 2035 | |
| HDSC | 18.41 | 2030 | 18.49 | 2030 | 18.58 | 2030 | |
| LDWC | 18.43 | 2030 | 18.51 | 2030 | 18.60 | 2030 | |
| LDSC | 16.91 | 2025 | 16.95 | 2025 | 17.02 | 2030 |
Appendix E

Table A5.
Impact of rate changes in different factors under various scenarios on carbon peaking time and peak values in the TCC.
Table A5.
Impact of rate changes in different factors under various scenarios on carbon peaking time and peak values in the TCC.
| Impact Factor | Scenario | Low-Rate Peak | Low-Rate Time to Peak | Medium-Rate Peak | Medium-Rate Time to Peak | High-Rate Peak | High-Rate Time to Peak |
|---|---|---|---|---|---|---|---|
| ES | BL | 10.35 | 2030 | 10.01 | 2030 | 9.67 | 2030 |
| HDWC | 12.07 | 2035 | 11.44 | 2035 | 10.84 | 2035 | |
| HDSC | 10.54 | 2030 | 10.18 | 2030 | 9.84 | 2030 | |
| LDWC | 9.94 | 2030 | 9.61 | 2030 | 9.28 | 2030 | |
| LDSC | 9.50 | 2030 | 9.18 | 2030 | 8.93 | 2025 | |
| EG | BL | 10.46 | 2030 | 10.01 | 2030 | 9.56 | 2030 |
| HDWC | 12.07 | 2035 | 11.25 | 2035 | 10.54 | 2030 | |
| HDSC | 10.84 | 2035 | 10.30 | 2030 | 9.84 | 2030 | |
| LDWC | 9.96 | 2030 | 9.52 | 2030 | 9.10 | 2030 | |
| LDSC | 9.69 | 2030 | 9.27 | 2030 | 8.92 | 2025 | |
| DUP | BL | 9.74 | 2030 | 10.01 | 2030 | 10.28 | 2030 |
| HDWC | 11.04 | 2035 | 11.54 | 2035 | 12.07 | 2035 | |
| HDSC | 9.32 | 2030 | 9.58 | 2030 | 9.84 | 2030 | |
| LDWC | 9.74 | 2030 | 10.01 | 2030 | 10.28 | 2030 | |
| LDSC | 9.06 | 2030 | 9.31 | 2030 | 9.56 | 2030 | |
| UR | BL | 9.92 | 2030 | 10.01 | 2030 | 10.09 | 2030 |
| HDWC | 11.75 | 2035 | 11.91 | 2035 | 12.07 | 2035 | |
| HDSC | 9.67 | 2030 | 9.75 | 2030 | 9.84 | 2030 | |
| LDWC | 9.74 | 2030 | 9.82 | 2030 | 9.91 | 2030 | |
| LDSC | 9.06 | 2030 | 9.14 | 2030 | 9.22 | 2030 | |
| POP | BL | 10.08 | 2030 | 10.01 | 2030 | 9.93 | 2030 |
| HDWC | 12.07 | 2035 | 11.92 | 2035 | 11.78 | 2035 | |
| HDSC | 9.84 | 2030 | 9.76 | 2030 | 9.69 | 2030 | |
| LDWC | 9.89 | 2030 | 9.82 | 2030 | 9.74 | 2030 | |
| LDSC | 9.20 | 2030 | 9.13 | 2030 | 9.06 | 2030 | |
| TCO | BL | 9.93 | 2030 | 10.01 | 2030 | 10.08 | 2030 |
| HDWC | 11.80 | 2035 | 11.94 | 2035 | 12.07 | 2035 | |
| HDSC | 9.70 | 2030 | 9.77 | 2030 | 9.84 | 2030 | |
| LDWC | 9.74 | 2030 | 9.81 | 2030 | 9.88 | 2030 | |
| LDSC | 9.06 | 2030 | 9.12 | 2030 | 9.19 | 2030 | |
| FDI | BL | 9.92 | 2030 | 10.01 | 2030 | 10.09 | 2030 |
| HDWC | 11.76 | 2035 | 11.91 | 2035 | 12.07 | 2035 | |
| HDSC | 9.68 | 2030 | 9.76 | 2030 | 9.84 | 2030 | |
| LDWC | 9.74 | 2030 | 9.82 | 2030 | 9.90 | 2030 | |
| LDSC | 9.06 | 2030 | 9.13 | 2030 | 9.21 | 2030 | |
| FS | BL | 9.96 | 2030 | 10.01 | 2030 | 10.05 | 2030 |
| HDWC | 11.91 | 2035 | 11.99 | 2035 | 12.07 | 2035 | |
| HDSC | 9.76 | 2030 | 9.80 | 2030 | 9.84 | 2030 | |
| LDWC | 9.74 | 2030 | 9.78 | 2030 | 9.82 | 2030 | |
| LDSC | 9.06 | 2030 | 9.10 | 2030 | 9.13 | 2030 |
Appendix F

Table A6.
Impact of rate changes in different factors under various scenarios on carbon peaking time and peak values in the CCA.
Table A6.
Impact of rate changes in different factors under various scenarios on carbon peaking time and peak values in the CCA.
| Impact Factor | Scenario | Low-Rate Peak | Low-Rate Time to Peak | Medium-Rate Peak | Medium-Rate Time to Peak | High-Rate Peak | High-Rate Time to Peak |
|---|---|---|---|---|---|---|---|
| ES | BL | 4.74 | 2040 | 4.04 | 2035 | 3.62 | 2035 |
| HDWC | 6.04 | 2040 | 5.13 | 2040 | 4.34 | 2040 | |
| HDSC | 4.93 | 2040 | 4.18 | 2040 | 3.69 | 2035 | |
| LDWC | 4.36 | 2040 | 3.80 | 2035 | 3.51 | 2030 | |
| LDSC | 3.98 | 2035 | 3.60 | 2030 | 3.46 | 2025 | |
| EG | BL | 4.45 | 2040 | 4.04 | 2035 | 3.74 | 2035 |
| HDWC | 6.04 | 2040 | 5.46 | 2040 | 4.93 | 2040 | |
| HDSC | 4.34 | 2040 | 3.97 | 2035 | 3.69 | 2030 | |
| LDWC | 4.23 | 2040 | 3.89 | 2035 | 3.65 | 2030 | |
| LDSC | 3.71 | 2030 | 3.54 | 2030 | 3.47 | 2025 | |
| DUP | BL | 3.90 | 2035 | 4.04 | 2035 | 4.22 | 2040 |
| HDWC | 5.50 | 2040 | 5.76 | 2040 | 6.04 | 2040 | |
| HDSC | 3.54 | 2030 | 3.61 | 2030 | 3.69 | 2030 | |
| LDWC | 4.04 | 2035 | 4.21 | 2040 | 4.42 | 2040 | |
| LDSC | 3.50 | 2025 | 3.53 | 2025 | 3.60 | 2030 | |
| UR | BL | 3.99 | 2035 | 4.04 | 2035 | 4.09 | 2040 |
| HDWC | 5.86 | 2040 | 5.95 | 2040 | 6.04 | 2040 | |
| HDSC | 3.64 | 2030 | 3.66 | 2030 | 3.69 | 2030 | |
| LDWC | 4.04 | 2035 | 4.09 | 2035 | 4.15 | 2040 | |
| LDSC | 3.50 | 2025 | 3.51 | 2025 | 3.53 | 2025 | |
| POP | BL | 3.98 | 2035 | 4.04 | 2035 | 4.10 | 2035 |
| HDWC | 5.87 | 2040 | 5.96 | 2040 | 6.04 | 2040 | |
| HDSC | 3.62 | 2030 | 3.65 | 2030 | 3.69 | 2030 | |
| LDWC | 4.04 | 2035 | 4.10 | 2035 | 4.16 | 2035 | |
| LDSC | 3.50 | 2025 | 3.52 | 2025 | 3.53 | 2025 | |
| TCO | BL | 4.00 | 2035 | 4.04 | 2035 | 4.12 | 2040 |
| HDWC | 5.83 | 2040 | 5.90 | 2040 | 6.04 | 2040 | |
| HDSC | 3.63 | 2030 | 3.65 | 2030 | 3.69 | 2030 | |
| LDWC | 4.04 | 2035 | 4.08 | 2035 | 4.17 | 2040 | |
| LDSC | 3.50 | 2025 | 3.51 | 2025 | 3.53 | 2025 | |
| FDI | BL | 4.00 | 2035 | 4.04 | 2035 | 4.08 | 2040 |
| HDWC | 5.88 | 2040 | 5.96 | 2040 | 6.04 | 2040 | |
| HDSC | 3.64 | 2030 | 3.67 | 2030 | 3.69 | 2030 | |
| LDWC | 4.04 | 2035 | 4.08 | 2035 | 4.13 | 2040 | |
| LDSC | 3.50 | 2025 | 3.51 | 2025 | 3.52 | 2025 | |
| FS | BL | 3.96 | 2035 | 4.04 | 2035 | 4.13 | 2040 |
| HDWC | 5.74 | 2040 | 5.89 | 2040 | 6.04 | 2040 | |
| HDSC | 3.60 | 2030 | 3.64 | 2030 | 3.69 | 2030 | |
| LDWC | 4.04 | 2035 | 4.12 | 2040 | 4.23 | 2040 | |
| LDSC | 3.50 | 2025 | 3.52 | 2025 | 3.54 | 2030 |
References
- Liu, Y.; He, S.; Jiang, Y.; Luo, X.; Yuan, J. Spatial-temporal decomposition of carbon emission in China’s four major urban agglomerations. Clim. Change Res. 2024, 20, 231–241. [Google Scholar]
- Du, K.; Xie, C.; Ouyang, X. A Comparison of Carbon Dioxide (CO2) Emission Trends among Provinces in China. Renew. Sustain. Energy Rev. 2017, 73, 19–25. [Google Scholar] [CrossRef]
- Yang, P.; Liang, X.; Drohan, P.J. Using Kaya and LMDI Models to Analyze Carbon Emissions from the Energy Consumption in China. Environ. Sci. Pollut. Res. Int. 2020, 27, 26495–26501. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Liu, X.; Liu, Y.; Xie, J. Digital Economy and Carbon Emission Efficiency in Three Major Urban Agglomerations of China: A U-Shaped Journey towards Green Development. J. Environ. Manag. 2025, 373, 123571. [Google Scholar] [CrossRef]
- Kaya, Y. Impact of Carbon Dioxide Emission Control on GNP Growth: Interpretation of Proposed Scenarios; IPCC Energy and Industry Subgroup, Response Strategies Working Group: Paris, France, 1990; Available online: https://www.researchgate.net/publication/312468754 (accessed on 13 March 2025).
- Li, S.; Yao, L.; Zhang, Y.; Zhao, Y.; Sun, L. China’s Provincial Carbon Emission Driving Factors Analysis and Scenario Forecasting. Environ. Sustain. Indic. 2024, 22, 100390. [Google Scholar] [CrossRef]
- Jiang, J.; Ye, B.; Xie, D.; Tang, J. Provincial-Level Carbon Emission Drivers and Emission Reduction Strategies in China: Combining Multi-Layer LMDI Decomposition with Hierarchical Clustering. J. Clean. Prod. 2017, 169, 178–190. [Google Scholar] [CrossRef]
- Chen, C.; Luo, Y.; Zou, H.; Huang, J. Understanding the Driving Factors and Finding the Pathway to Mitigating Carbon Emissions in China’s Yangtze River Delta Region. Energy 2023, 278, 127897. [Google Scholar] [CrossRef]
- Yu, Y.; Dai, Y.; Xu, L.; Zheng, H.; Wu, W.; Chen, L. A Multi-Level Characteristic Analysis of Urban Agglomeration Energy-Related Carbon Emission: A Case Study of the Pearl River Delta. Energy 2023, 263, 125651. [Google Scholar] [CrossRef]
- Tarazkar, M.H.; Dehbidi, N.K.; Ozturk, I.; Al-Mulali, U. The Impact of Age Structure on Carbon Emission in the Middle East: The Panel Autoregressive Distributed Lag Approach. Environ. Sci. Pollut. Res. 2021, 28, 33722–33734. [Google Scholar] [CrossRef]
- Du, Y.; Huang, T. Impact of Demographic Factors on Carbon Emission in Jiangsu Province. Resour. Environ. Yangtze Basin 2013, 22, 399–404. [Google Scholar]
- Du, M.; Antunes, J.; Wanke, P.; Chen, Z. Ecological Efficiency Assessment under the Construction of Low-Carbon City: A Perspective of Green Technology Innovation. J. Environ. Plan. Manag. 2022, 65, 1727–1752. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, M.; Wang, L.; Liang, Y.; Tang, F.; Li, S.; Wu, C. Impact of Urban Shrinkage on Pollution Reduction and Carbon Mitigation Synergy: Spatial Heterogeneity and Interaction Effects in Chinese Cities. Land 2025, 14, 537. [Google Scholar] [CrossRef]
- Liu, H.; Liu, W.; Tang, Z. The Origin Source and Elasticity Analysis of the CO2 Emission Induced by Fossil Fuel Using Industrial Activities in China. Prog. Geogr. 2010, 29, 670–676. [Google Scholar]
- Wu, Z.; Xie, X.; Wang, S. The Influence of Economic Development and Industrial Structure to Carbon Emission Based on China’s Provincial Panel Data. Chin. J. Manag. Sci. 2012, 20, 161–166. [Google Scholar]
- Dong, B.; Xu, Y.; Fan, X. How to Achieve a Win-Win Situation between Economic Growth and Carbon Emission Reduction: Empirical Evidence from the Perspective of Industrial Structure Upgrading. Environ. Sci. Pollut. Res. 2020, 27, 43829–43844. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhao, Y.; Zhang, W.; Liu, Y. Analysis on Influencing Factors of Carbon Emission and Scenario Forecast of Carbon Peak in Beijing-Tianjin-Hebei—A Perspective of Supply-side Reform. J. Beijing Inst. Technol. (Soc. Sci. Ed.) 2022, 24, 54–66. [Google Scholar]
- Zang, H.; Yang, W.; Zhang, J.; Wu, P.; Cao, L.; Xu, Y. Research on Carbon Dioxide Emissions Peaking in Beijing-Tianjin-Hebei City Agglomeration. Environ. Eng. 2020, 38, 19–24, 77. [Google Scholar]
- Liu, B.; Tian, C.; Li, Y.; Song, H.; Zhanxin, M. Research on the Effects of Urbanization on Carbon Emissions Efficiency of Urban Agglomerations in China. J. Clean. Prod. 2018, 197, 1374–1381. [Google Scholar] [CrossRef]
- Cai, A.; Wang, L.; Zhang, Y.; Wu, H.; Zhang, H.; Guo, R.; Wu, J. Uncovering the Multiple Socio-Economic Driving Factors of Carbon Emissions in Nine Urban Agglomerations of China Based on Machine Learning. Energy 2025, 319, 134859. [Google Scholar] [CrossRef]
- Miao, A.; Yuan, Y.; Wu, H.; Ma, X.; Shao, C. Pathway and Policy for China’s Provincial Carbon Emission Peak. Environ. Sci. 2023, 44, 4623–4636. [Google Scholar]
- Cong, Y.; Cheng, S.; Feng, W. Study on Energy Demand an Carbon Peaking Time Prediction in Jilin Province Based on the LEAP Model. Mod. Chem. Res. 2023, 20, 182–184. [Google Scholar]
- Wang, Y.; Ma, L. Analysis and Forecast of Related Factors of Energy Consumption Carbon Emission in Jilin Province: Baswd on Grey Relational Analysis and GM(1,1) Model. Ecol. Econ. 2016, 32, 65–70. [Google Scholar]
- Li, X.; Su, S.; Zhang, Y.; Zhu, X. Carbon Emission Prediction and Carbon Peak Path Analysis in Fujian Province. Resour. Dev. Mark. 2023, 39, 139–147. [Google Scholar]
- Xie, P.; Liao, J.; Pan, X.; Sun, F. Will China’s Carbon Intensity Achieve Its Policy Goals by 2030? Dynamic Scenario Analysis Based on STIRPAT-PLS Framework. Sci. Total Environ. 2022, 832, 155060. [Google Scholar] [CrossRef]
- Chen, T.; Li, X.; Chen, B. Decomposition of influencing factors and peak prediction of carbon emissions in China. J. Saf. Environ. 2024, 24, 396–406. [Google Scholar]
- Zou, Y.; Huang, M. Carbon Emissions in Urban Agglomerations: Feature Mining, Formation Mechanism and Peak Intervention. J. Beijing Inst. Technol. (Soc. Sci. Ed.) 2023, 25, 56–67. [Google Scholar]
- Han, M.; Xiong, J.; Wang, S.; Yang, Y. Chinese Photovoltaic Poverty Alleviation: Geographic Distribution, Economic Benefits and Emission Mitigation. Energy Policy 2020, 144, 111685. [Google Scholar] [CrossRef]
- Liang, X.; Fan, M.; Huang, X.; Cai, C.; Zhou, L.; Wang, Y. Spatial Distributed Characteristics of Carbon Dioxide Emissions Based on Fossil Energy Consumption and Their Driving Factors at Provincial Scale in China. Energy 2024, 309, 133062. [Google Scholar] [CrossRef]
- Qin, H.; Huang, Q.; Zhang, Z.; Lu, Y.; Li, M.; Xu, L.; Chen, Z. Carbon Dioxide Emission Driving Factors Analysis and Policy Implications of Chinese Cities: Combining Geographically Weighted Regression with Two-Step Cluster. Sci. Total Environ. 2019, 684, 413–424. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, W. Determination of Discriminating Coefficient in Grey Correlation Analysis. Arid Environ. Monit. 1994, 8, 132–135, 190. [Google Scholar]
- Xing, S.M.; Feng, X.X.; Shui, Z.X. Determination of Discrimination Coefficient in Grey Incidence Analysis. J. Air Force Eng. Univ. (Nat. Sci. Ed.) 2003, 4, 68–70. [Google Scholar]
- Ang, B.W.; Liu, N. Handling Zero Values in the Logarithmic Mean Divisia Index Decomposition Approach. Energy Policy 2007, 35, 238–246. [Google Scholar] [CrossRef]
- Ortega-Ruiz, G.; Mena-Nieto, A.; García-Ramos, J.E. Is India on the Right Pathway to Reduce CO2 Emissions? Decomposing an Enlarged Kaya Identity Using the LMDI Method for the Period 1990–2016. Sci. Total Environ. 2020, 737, 139638. [Google Scholar] [CrossRef]
- Yang, J.; Cai, W.; Ma, M.; Li, L.; Liu, C.; Ma, X.; Li, L.; Chen, X. Driving Forces of China’s CO2 Emissions from Energy Consumption Based on Kaya-LMDI Methods. Sci. Total Environ. 2020, 711, 134569. [Google Scholar] [CrossRef]
- Li, J.; Li, H. Analysis of Carbon Emission Factors Decomposition and Emission Reduction Potetial of Beijing-Tianjin-Hebei Regional Petrochemical Industry from the Perspective of Industrial Transfer. Res. Environ. Sci. 2020, 33, 324–332. [Google Scholar]
- Huang, Y.; Wang, Y.; Peng, J.; Li, F.; Zhu, L.; Zhao, H.; Shi, R. Can China Achieve Its 2030 and 2060 CO2 Commitments? Scenario Analysis Based on the Integration of LEAP Model with LMDI Decomposition. Sci. Total Environ. 2023, 888, 164151. [Google Scholar] [CrossRef] [PubMed]
- Jiansheng, W.U.; Yan, N.; Jian, P.; Zheng, W.; Xiulan, H. Research on Energy Consumption Dynamic among Prefecture-Level Cities in China Based on DMSP/OLS Nighttime Light. Geogr. Res. 2014, 33, 625–634. [Google Scholar]
- Li, C.; Zhou, W. Can Digital Economy Development Contribute to Urban Carbon Emission Reduction?—Empirical Evidence from China. J. Environ. Manag. 2024, 357, 120680. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, Y.; Wu, G.L. Chinese Provincial Energy Consumption Intensity Prediction by the CGM (1,1). Energy 2024, 292, 130626. [Google Scholar] [CrossRef]
- Korkmaz, Z. Do Environment-Related Technologies, Urbanization, Trade Openness, and Income Impact Energy Consumption and Intensity? Energy Effic. 2024, 17, 93. [Google Scholar] [CrossRef]
- Liu, D.; Xiao, B. Can China Achieve Its Carbon Emission Peaking? A Scenario Analysis Based on STIRPAT and System Dynamics Model. Ecol. Indic. 2018, 93, 647–657. [Google Scholar] [CrossRef]
- Xiong–tian, S.H.I.; Feng–qing, W.U.; Yang, C.; Li-li, D.A.I. Analysis of Factors Influencing Carbon Emissions in the Yangtze River Delta Region and Projections of Carbon Peak Scenarios. Ecol. Econ. 2024, 20, 2–24. [Google Scholar]
- Chen, P.; Wang, X.; Yang, Z.; Shi, C. Research on Spatial Heterogeneity, Impact Mechanism, and Carbon Peak Prediction of Carbon Emissions in the Yangtze River Delta Urban Agglomeration. Energies 2024, 17, 5899. [Google Scholar] [CrossRef]
- Dong, S.; Gong, Y.; Wang, Z.; Incecik, A. Wind and Wave Energy Resources Assessment around the Yangtze River Delta. Ocean Eng. 2019, 182, 75–89. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, X.; Chen, M. Spatiotemporal Dynamics and Driving Forces of City-Level CO2 Emissions in China from 2000 to 2019. J. Clean. Prod. 2022, 377, 134358. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).