1. Introduction
Globally, complex climate changes and rapid urbanization stand as significant driving factors behind urban flood disasters [
1,
2,
3]. The extensive coverage of impermeable urban surfaces over natural ones inhibits rainwater infiltration, leading to a substantial increase in both total runoff volume and peak flow rates, consequently causing urban flooding [
4,
5]. In order to enhance urban resilience when facing flood events, various countries have successively introduced valuable explorations such as low-impact development (LID), sustainable urban drainage systems (SUDS), sponge cities, best management practices (BMPs), and water-sensitive urban design (WSUD) [
6,
7,
8,
9,
10]. These explorations primarily focus on the rainfall–runoff phase, fully harnessing the water storage and infiltration capabilities of surfaces and soils to significantly reduce the volume of water that could potentially lead to flooding right from the source. As our understanding of urban flood control and drainage deepens, there is an increasing emphasis on addressing flood control, drainage, and dewatering tasks concurrently. This is particularly achieved through interventions facilitated by hydraulic-engineering scheduling schemes, thus elevating urban flood management during heavy rain and flood events.
Frequent water-related disasters have posed challenges to the rationale behind traditional disaster-mitigation strategies such as levees and diversion projects [
11]. In addition to the construction of urban basic hydraulic engineering, it is necessary to complement it with well-considered water engineering joint-scheduling measures to establish a more comprehensive flood control and drainage system, allowing for the reasonable storage, retention, and discharge of stormwater flooding. In recent years, resilience-based urban stormwater management strategies have gained increasing attention [
12]. The combination of green infrastructure (GI), gray infrastructure (GEI), and blue infrastructure (BI) is regarded as a crucial approach to enhance urban resilience [
13]. In practice, a sponge city represents a classic green–gray–blue system, comprising green infrastructure at the source, known as LID, which measures GI, with a drainage network system called GEV addressing the conveyance process, and receiving the water bodies, BI, at the end [
14]. In the process of rainfall–runoff leading to flooding, rainfall–runoff initially undergoes treatment through LID facilities, subsequently enters the drainage network, and ultimately flows into the receiving water bodies [
15]. Therefore, from both a physical process and spatial perspective, GI, GEI, and BI are an integrated whole, collectively forming the flood control and drainage system [
16].
When modeling in highly urbanized flood-prone areas, it is essential to select models that align with the environmental prerequisites [
17]. Urban land surfaces exhibit a significant spatial heterogeneity, with micro-topography and specific land-use characteristics [
18,
19]. Within each catchment unit in the model, there is significant uncertainty associated with model parameters and the interaction of water flow between impervious and pervious areas [
18,
20]. Processes associated with GI are intimately tied to runoff generation and convergence. To effectively address these processes, it is essential to partition the land surface into permeable and impermeable areas, thus distinguishing between various methods for calculating infiltration and runoff. In urban regions that maintain direct hydrological connections with upstream mountainous areas, it is also crucial to incorporate runoff calculations from these mountainous regions [
21,
22]. Processes associated with GEI are the processes of water conveyance through pipelines. Typically, one-dimensional hydraulic models are widely used to assess the hydraulic status of the pipelines at any given moment. When analyzing surface flooding, it becomes essential to couple the pipeline model with inundation processes on the surface. This coupling involves the integration of one-dimensional pipe network models with two-dimensional hydraulic models [
23,
24]. High-resolution two-dimensional hydrodynamic models pose a challenging aspect of research. HLLC (Harten–Lax–van Leer Contact) and Roe formats, which approximate Riemann solutions, find widespread application in numerical flux calculations [
25,
26]. When dealing with complex fluid dynamics, the utilization of specific slope limiters to adjust finite-difference schemes plays a crucial role in reducing numerical dissipation and dispersion [
27]. This enhances the model’s ability to accurately capture the fluid shocks and other intricate fluid behaviors [
28]. Processes associated with BI encompass river network runoff, where river channels serve as lower boundaries for the pipeline network. Interaction with the surface is considered when accounting for river floodplains. The control schemes can be implemented based on river hydrodynamic modeling [
21].
The approach, using hydrological–hydraulic models based on physical processes, is also referred to as a physics-based model (PBM). Recent studies have shown that data-driven models (DDMs) based on machine learning and deep learning are an effective alternative for flood simulation [
29,
30,
31]. These models utilize extensive datasets to improve flood prediction accuracy, without relying on the nonlinear dynamics of multiple urban flood subsystems [
32]. DDMs excel at capturing hidden patterns within rainfall–runoff relationships, enabling precise predictions for complex urban drainage systems [
33,
34,
35]. Urban pluvial-flood models employ various data types, including meteorological, rainfall, and geographical data [
36]. Logistic regression [
37,
38], artificial neural networks [
39,
40], support vector machines [
41,
42], and random forests [
43] have found widespread applications in urban flood risk assessment. As sample sizes increase and problem complexity grows, deep neural networks autonomously learn feature representations layer by layer, extracting abstract features from raw data [
44]. Combining PBMs with DDMs enhances the applicability and computational efficiency of flood models [
45].
In previous studies, analyses of LID performance have often concentrated on the influence of individual factors, such as precipitation and soil permeability. However, uncertainties exist regarding the configuration, design, and operational conditions of LID systems, making it challenging to accurately predict their actual performance in practice. These uncertainties may significantly affect urban flood control and, consequently, the effectiveness of decision making. This study delves into the uncertainties associated with LID performance and, by integrating hydrological and hydrodynamic models, evaluates the effectiveness of LID in urban flood control. The objective of this study is to assess the uncertainty in stormwater control for urban flooding. To achieve this, this paper first constructs an urban flooding model based on hydrological and hydrodynamic models; then, it uses generalized likelihood uncertainty analysis methods to analyze model parameters and simulation uncertainty; finally, it establishes the nonlinear dependencies between surface-flood process characteristic variables under stormwater control. This research not only helps enhance the resilience of urban flood management but also provides support for promoting sustainable urban planning and addressing climate change.
2. Methodology
The current research proposes a framework for evaluating stormwater control uncertainty analysis, which includes: (1) flooding modeling, where an urban-scale flooding model is constructed based on hydrological and hydrodynamic models; (2) uncertainty analysis, where model-parameter uncertainty and runoff-simulation uncertainty are analyzed using parameter heterogeneity and generalized likelihood uncertainty methods; (3) joint probability analysis, where stormwater control characteristics are derived from the prior and posterior distributions of model parameters, and a joint probability distribution reflecting the relationship between surface-runoff reduction rate and peak-flow reduction rate is constructed.
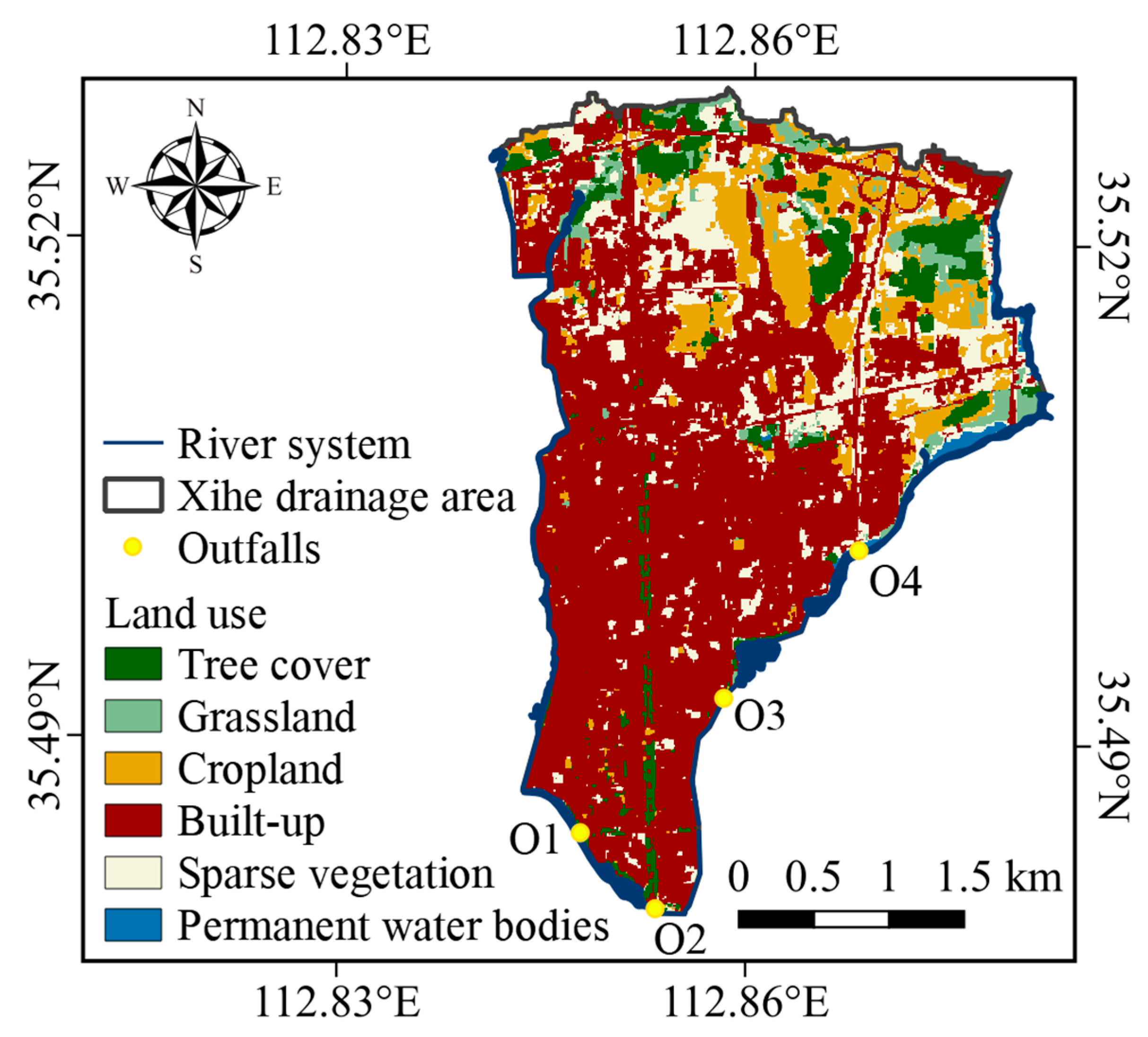
Figure 1 presents the study workflow in the current research.
2.1. Physics-Based Model
The physics-based model transforms real-world issues into mathematical and physical equation-based models for resolution. We use SWMM to simulate the hydrological process in pluvial flooding. Highly urbanized areas feature extensive pipe networks, facilitating the convergence of surface runoff into downstream channels through numerous outlets. The hydrodynamic coupling of watersheds and urban areas primarily encompasses several aspects: the flow generation and convergence at the surface, the flow in pipelines and channels, and the inundation at the ground surface.
The Horton runoff model was used to construct the runoff model for each land-use type in the urban areas:
where
is the stable permeability in Horton’s model (mm/h);
is the initial permeability in Horton’s model (mm/h); and
is the attenuation coefficient (h
−1).
Following the Saint-Venant equations initially introduced by the French scientist B. Saint-Venant in 1871, we utilize Equations (2) and (3) to represent the behavior of unsteady flow within urban river channels. Flow in pipelines and channels were described as:
where
B (m) represents the cross-sectional width;
Z (m) stands for water level;
t (s) denotes time;
Q (m
3/s) signifies the average flow rate across the section;
x (m) represents the longitudinal distance along the channel’s main axis;
A (m
2) denotes the cross-sectional area;
h (m) stands for water depth;
g (m/s
2) represents the acceleration due to gravity; and
S0 and
Sf represent the slope and friction term.
2.2. Uncertainty Analysis of Model
The generalized likelihood uncertainty estimation (GLUE) method is a classic parameter-sensitivity and uncertainty analysis approach introduced by British hydrologist Keith Beven in 1992. Its core concept suggests that different parameter combinations can achieve the same simulation results under the same evaluation criteria, and that parameter combinations with a certain likelihood yield valid simulation results. The higher or lower the value of the evaluation metric (determined by the likelihood function), the greater the likelihood and the higher the confidence level.
The main steps of the GLUE method are as follows: (1) Define the parameter range and prior distribution form, sample a certain number of parameters sets, and input them into the model. (2) Define the likelihood function and calculate the goodness of fit between the simulated and observed values, i.e., the likelihood. (3) Set a likelihood threshold and filter out effective parameter sets. Parameter sets above the threshold are considered invalid, and their likelihood weight is assigned a value of 0. The likelihood values of effective parameters set below the threshold are normalized. This process provides the likelihood function or probability density distribution of the parameter space, allowing for an analysis of parameter sensitivity through the probability density plot. (4) Rank the parameter sets according to their likelihood and estimate the uncertainty range for a given confidence level. Compared to classical Bayesian uncertainty analysis methods (such as SCEM-UA and MCMC), the GLUE method offers greater flexibility, allowing for the subjective selection of the likelihood function and threshold to quantify model uncertainty. It has advantages and good applicability in hydrological simulations.
This study uses six indicators—NSE, MSE, RMSE, Nash-Sutcliffe determination coefficient (N-S), relative error of average runoff depth (REMR), and relative error of average peak flow (REMP)—to evaluate the model performance. The values of these six evaluation indicators are combined using the entropy weight method to calculate a comprehensive uncertainty evaluation index (CUEI) for the overall assessment.
where
N is the total sample size;
and
are the observed and simulated discharge flow at the drainage outlet for the
j-th flood event, respectively, m
3/s;
is the average discharge flow at the drainage outlet, m
3/s;
and
are the variances of the simulated data and the observed data, respectively;
M is the number of extracted parameter combinations;
and
are the observed and simulated average runoff depth for the
j-th flood event, respectively, mm;
and
are the observed and simulated peak flow for the
j-th flood event, respectively, m
3/s.
In interval estimation, there are several methods for evaluating the quality of uncertainty intervals, primarily involving the coverage and bandwidth of the uncertainty intervals. Based on this, to analyze the effectiveness of uncertainty intervals, this section selects four evaluation indicators: the average relative width
Bw, the average offset
D, the coverage rate
CR, and the average symmetry
S, to assess the symmetry of the uncertainty intervals. The formulas for these indicators are as follows:
where
n is the number of flow-process sequence points;
and
are the upper and lower boundary values of the confidence interval for the simulated flow points, respectively;
is the observed flow; and
is the number of observed values that fall within the confidence interval.
For a given confidence level, B indicates a better quality of the predicted uncertainty interval. CR represents the proportion of the observed flow that falls within the prediction interval, usually expressed as a percentage. The closer CR is to 100%, the higher the likelihood that the simulated values are close to the observed values, and the better the simulation performance. S indicates the level of uncertainty in the interval; the larger the value of S, the greater the uncertainty. Due to the high nonlinearity of hydrological phenomena, D quantifies the deviation between the center line of the uncertainty prediction interval and the observed flow-process line. A smaller D indicates better symmetry of the prediction interval and smaller uncertainty.
2.3. Copula-Based Uncertainty Analysis of Stormwater Control
The use of a two-dimensional Copula function to evaluate the effectiveness of LID management is an effective statistical method, as it accurately captures the dependencies between different management factors. In the analysis of LID management effectiveness, the two-dimensional Copula combines the marginal distributions with the dependency structure, effectively describing the complex correlations between variables. Specifically, the two-dimensional Copula function maps the cumulative distribution function (CDF) of the marginal distributions onto a uniform distribution in the [0, 1] interval, eliminating specific numerical information and focusing only on the ranking relationships between variables. In addition, the two-dimensional Copula function involves cumulative probability density (PDF), through which the joint distribution between variables can be further quantified, thereby assessing the strength of their dependencies. This process allows the two-dimensional Copula to flexibly handle nonlinear dependencies and high-dimensional data.
In the application process, selecting an appropriate Copula model allows for capturing the association patterns between different management factors based on the characteristics of the data. These models can reflect the complex interactions in the effectiveness of LID management, helping to accurately assess the performance of different management strategies and providing theoretical support for optimizing LID solutions. Through non-parametric testing methods, the two-dimensional Copula model avoids strong assumptions about the data distribution, enhancing the flexibility and adaptability of the method, thus providing a more reliable analytical tool.
The analysis metrics for LID management effectiveness include joint management effectiveness, synergistic management effectiveness, conditional management effectiveness, and combined management effectiveness, which can be expressed as:
(1) Joint management effectiveness:
(2) Synergistic management effectiveness:
(3) Conditional management effectiveness:
(4) Combined management effectiveness:
4. Results and Discussion
4.1. Model Uncertainty Analysis
Based on the GLUE algorithm, Latin Hypercube Sampling (LHS) is used for random sampling of SWMM parameters, LID parameters, and different rainfall scenarios. A total of 10,000 parameter combinations that meet the criteria are selected using the uncertainty evaluation index, CUEI. The flow process at the drainage outlet is then simulated for each parameter combination.
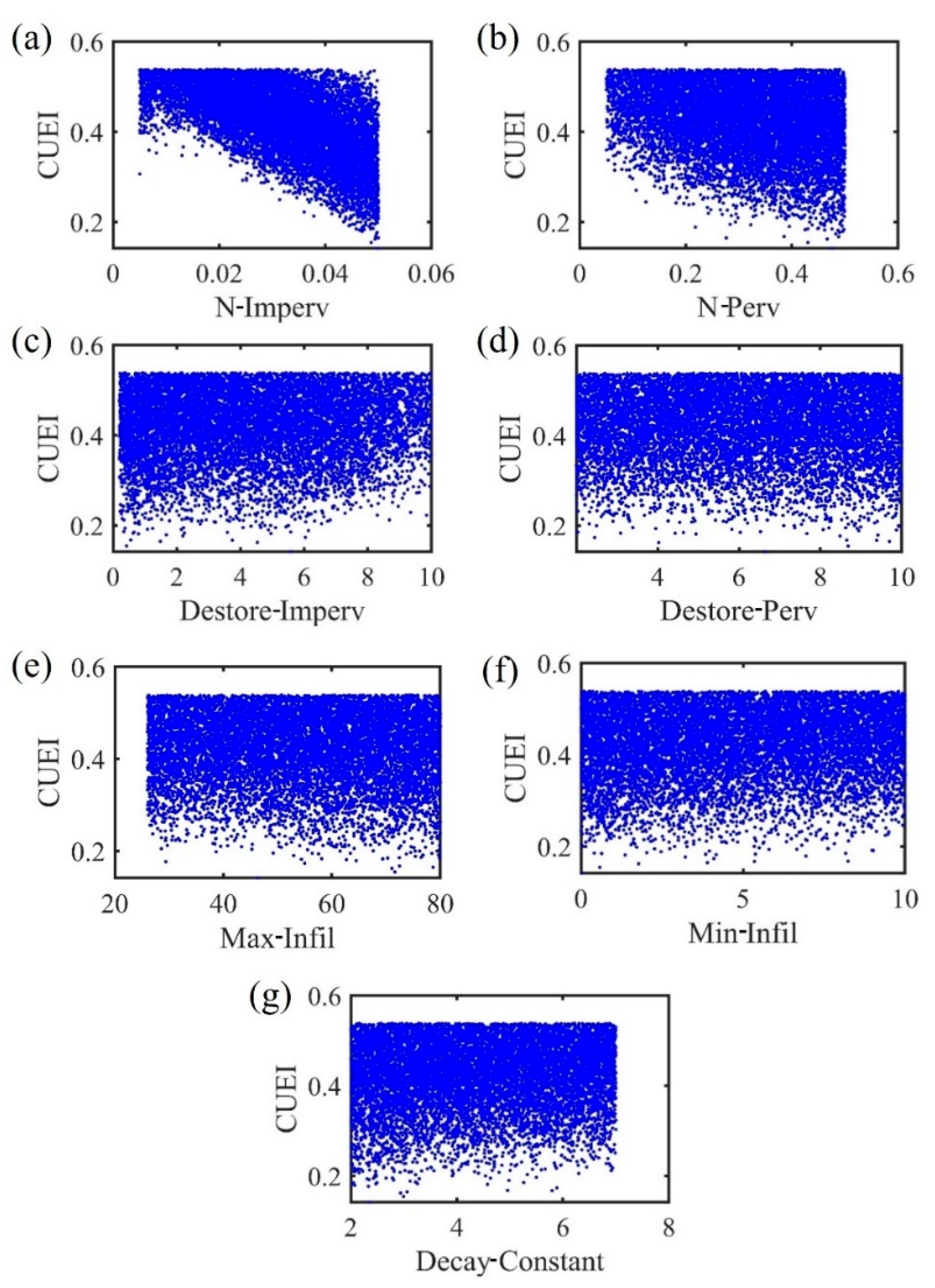
Figure 3 presents the uncertainty-distribution scatter plot for seven SWMM model parameters. The results indicate that the most significant uncertainty changes occur for the parameters N-Imperv, N-Perv, and Destore-Imperv. The likelihood variation in N-Imperv is the most pronounced, with a notable peak in the CUEI values occurring in the range of 0.4 to 0.5. As CUEI increases, the distribution of N-Perv and Destore-Imperv becomes more concentrated, while it becomes more dispersed when CUEI decreases. This suggests that these parameters are relatively sensitive. In contrast, the likelihood variations for the other parameters are minimal, indicating insensitivity to changes.
Table 1 provides the main parameters in SWMM.
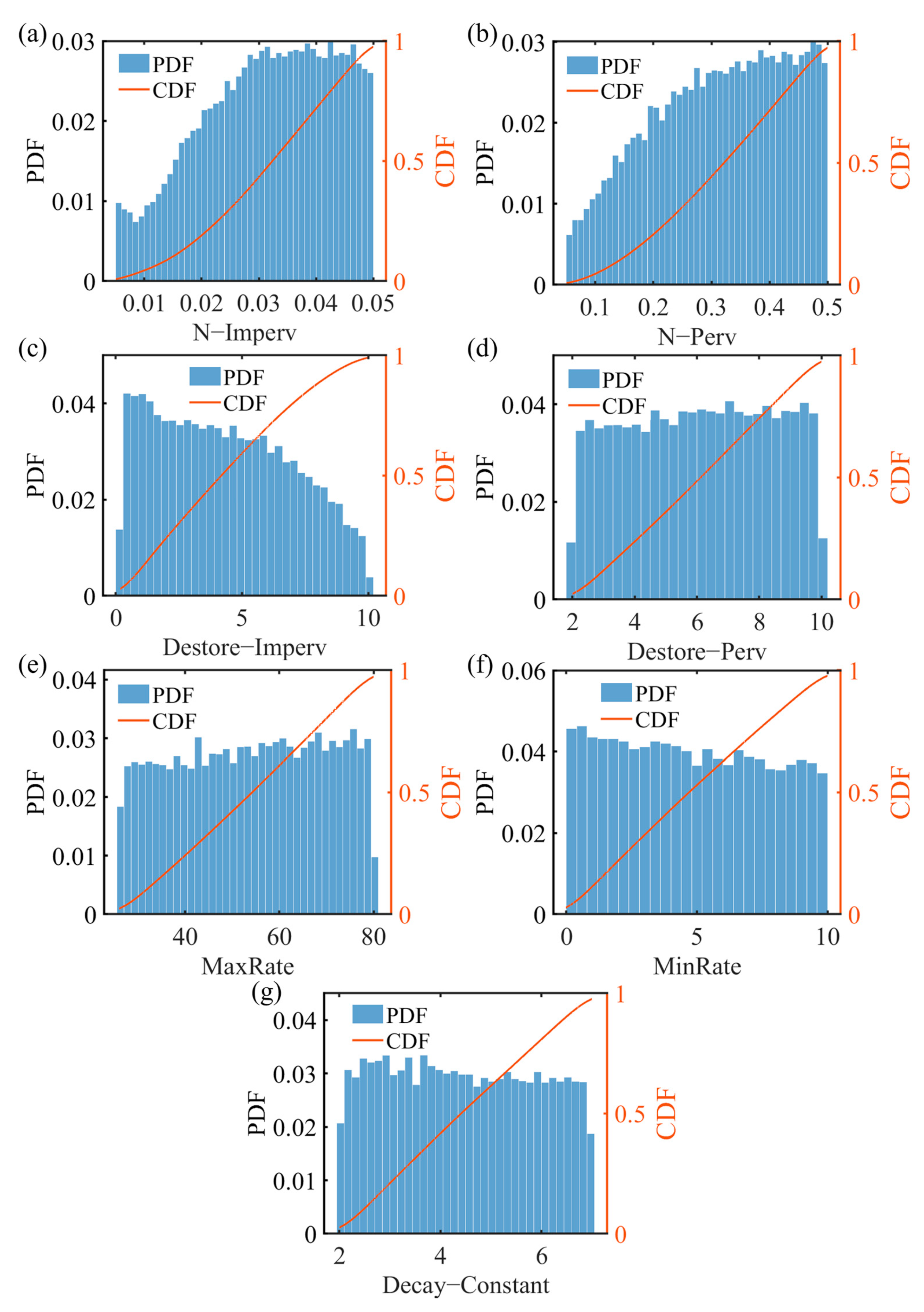
Figure 4 presents the changes in the probability density (PDF) and cumulative probability distribution (CDF) for seven parameters under random storm conditions. The posterior probability densities for the parameters N-Imperv, N-Perv, and Destore-Imperv exhibit non-uniform distributions, indicating their sensitivity, with N-Imperv showing the most significant variation. In contrast, the posterior distributions for the other four parameters remain largely consistent, with negligible changes in uncertainty, indicating their insensitivity. In urban areas with a high proportion of impervious surfaces, the infiltration capacity of hardened surfaces is poor, and parameters related to permeable surfaces and infiltration have a relatively weak effect on stormwater management. Additionally, under heavy rainfall conditions, the rapid surface runoff prevents rainwater from being discharged in time through the drainage system. When the drainage capacity of the network is saturated, overflow occurs, resulting in the minimal impact of parameter changes on model simulation outcomes.
To facilitate the evaluation of CUEI, this study will conduct a comprehensive analysis based on the calculation results and weights of each uncertainty indicator, according to the selection criteria shown in
Table 2.
Based on the GLUE method, multiple parameter combinations with significant correlations were selected to calculate the evaluation indicators of the symmetry of the uncertainty interval (
Table 3).
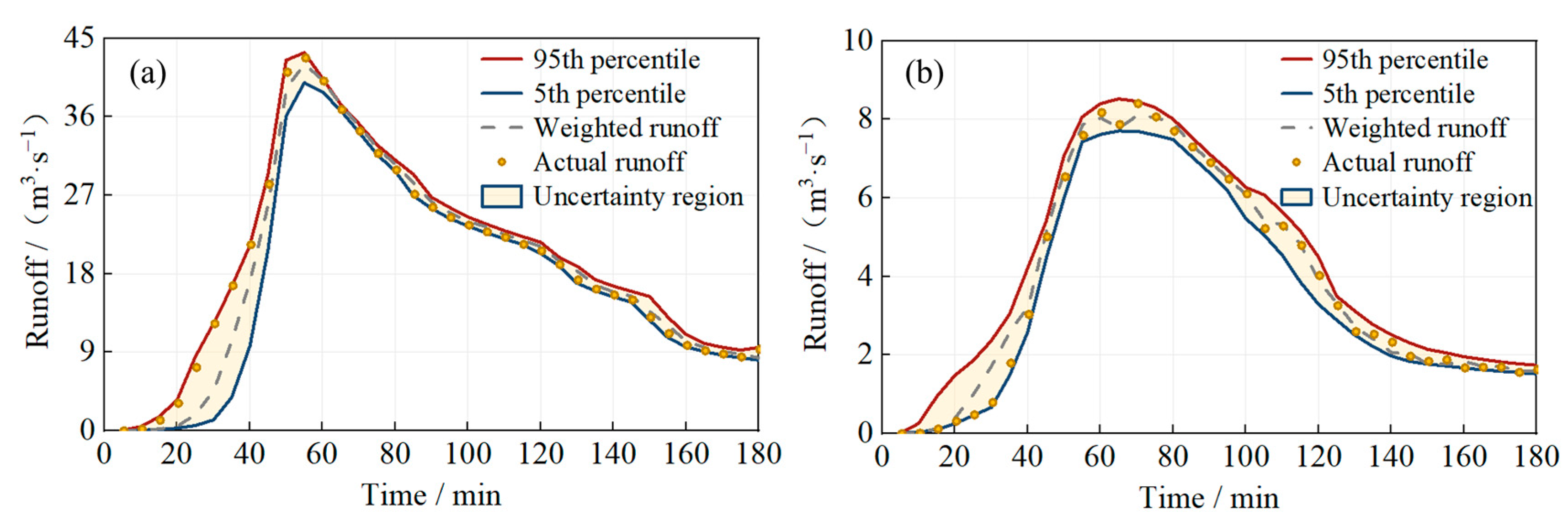
Figure 5 presents the flow variation process for outfalls O1 and O2 under different parameter combinations and shows the outflow range for the drainage outlets within the 95% confidence interval of the parameters. For outlet O1, B
w is 2.35, D is 2.07, CR is 25.00, and S is 0.85. In contrast, for outlet O2, B
w is 0.69, D is 0.51, CR is 80.56, and S is 0.69. It can be observed that the B
w, D, and S values for O1 are higher than those for O2, indicating greater uncertainty in the model for O1. Meanwhile, CR for O2 is significantly higher than that of O1, suggesting that O2 exhibits a broader range of variability, reflecting stronger uncertainty influences. Overall, the parameters for O2 show greater volatility, whereas O1 remains relatively stable.
4.2. Analysis of Control Effect Based on Posterior Distribution (PODM)
4.2.1. Edge Distribution Fitting of Governance Effect Index Based on PODM
Based on the GLUE uncertainty analysis results, the posterior distribution of SWMM parameters is used for marginal fitting to achieve a joint analysis of the control-effect evaluation indicators. The evaluation indicators, including surface-runoff reduction rate (S
R), peak-flow reduction rate at outfall O2 (S
210), and peak-flow reduction rate at outfall O4 (S
45), are jointly analyzed. The frequency values of flood-control effectiveness indicators are calculated using the cumulative distribution function, and empirical and theoretical frequency distributions are plotted (
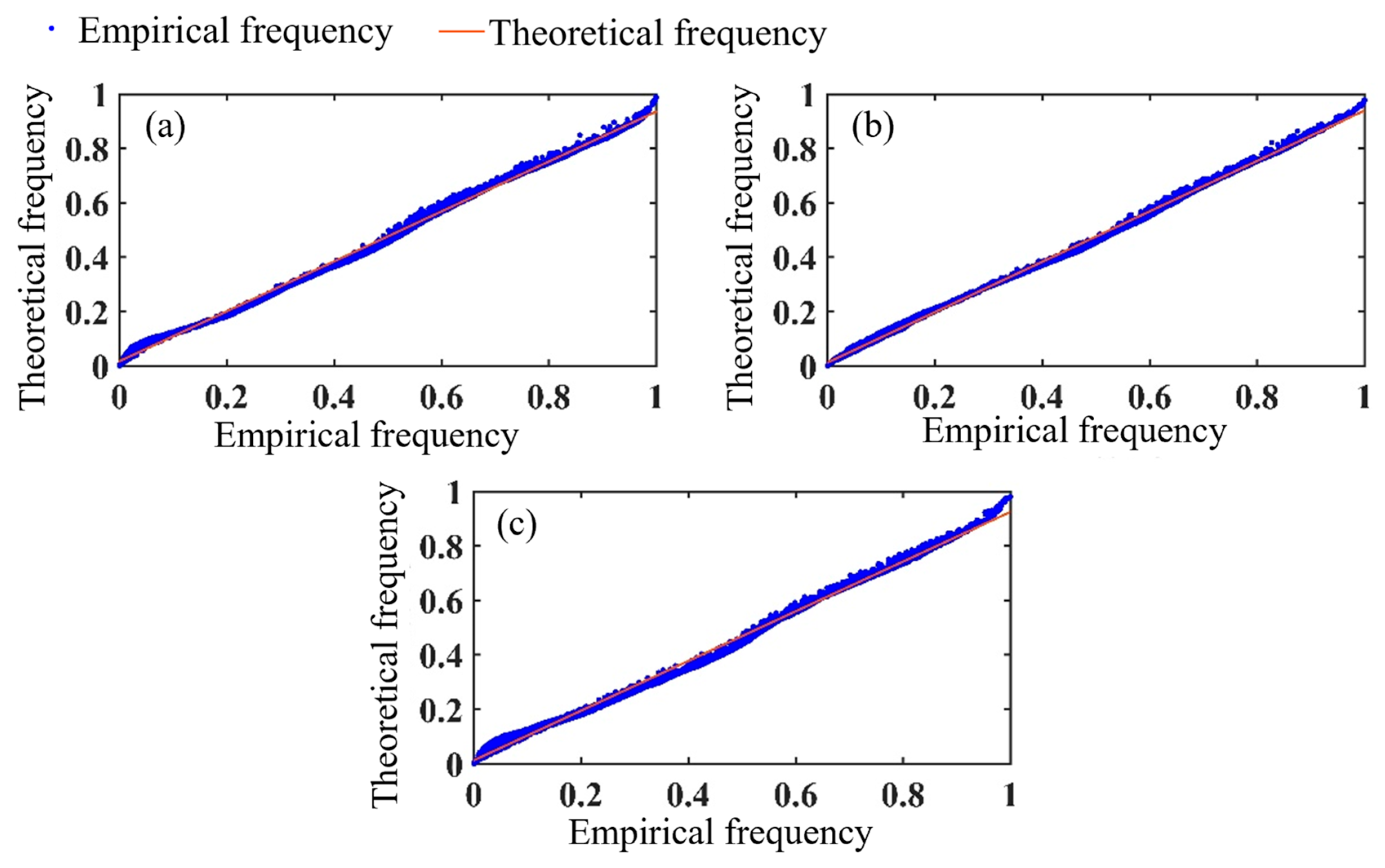
Figure 6). Theoretical and empirical frequencies calculated using the Copula function both distribute closely along the 45° line, indicating that the fitting performance using kernel-density non-parametric test methods is quite good.
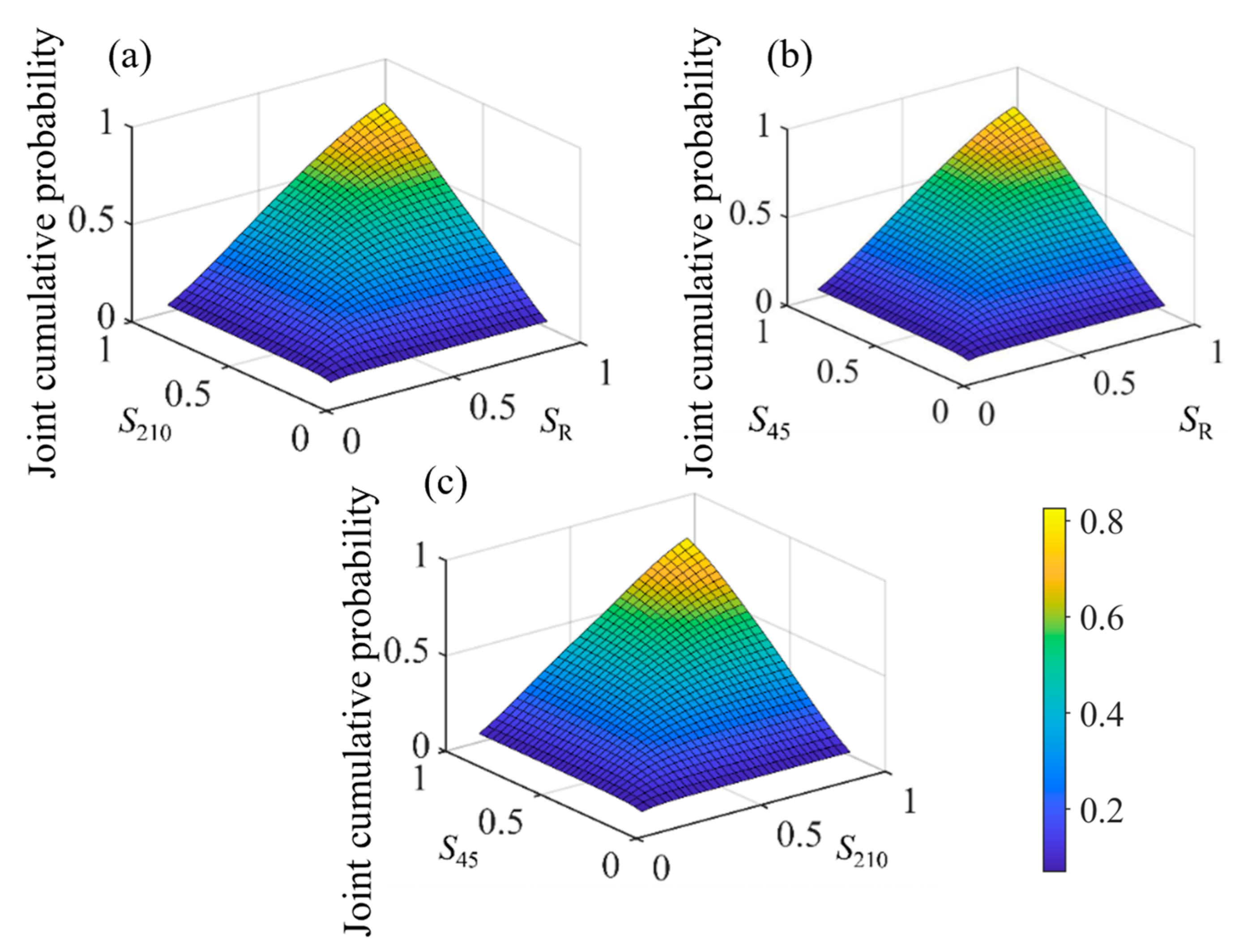
Figure 7 presents the joint probability distributions. As S
R and S
210 increase, the overall control effect continues to improve, showing a trend of increasing initially and then decreasing.
4.2.2. Joint Distribution of Surface-Runoff Reduction Rate and Peak-Flow Reduction Rate Based on PODM
The denser the contour lines, the smaller the fluctuations of this variable; conversely, it indicates greater parameter variability, and the trend line of the joint control-effect distribution will be biased toward the side with denser contour lines.
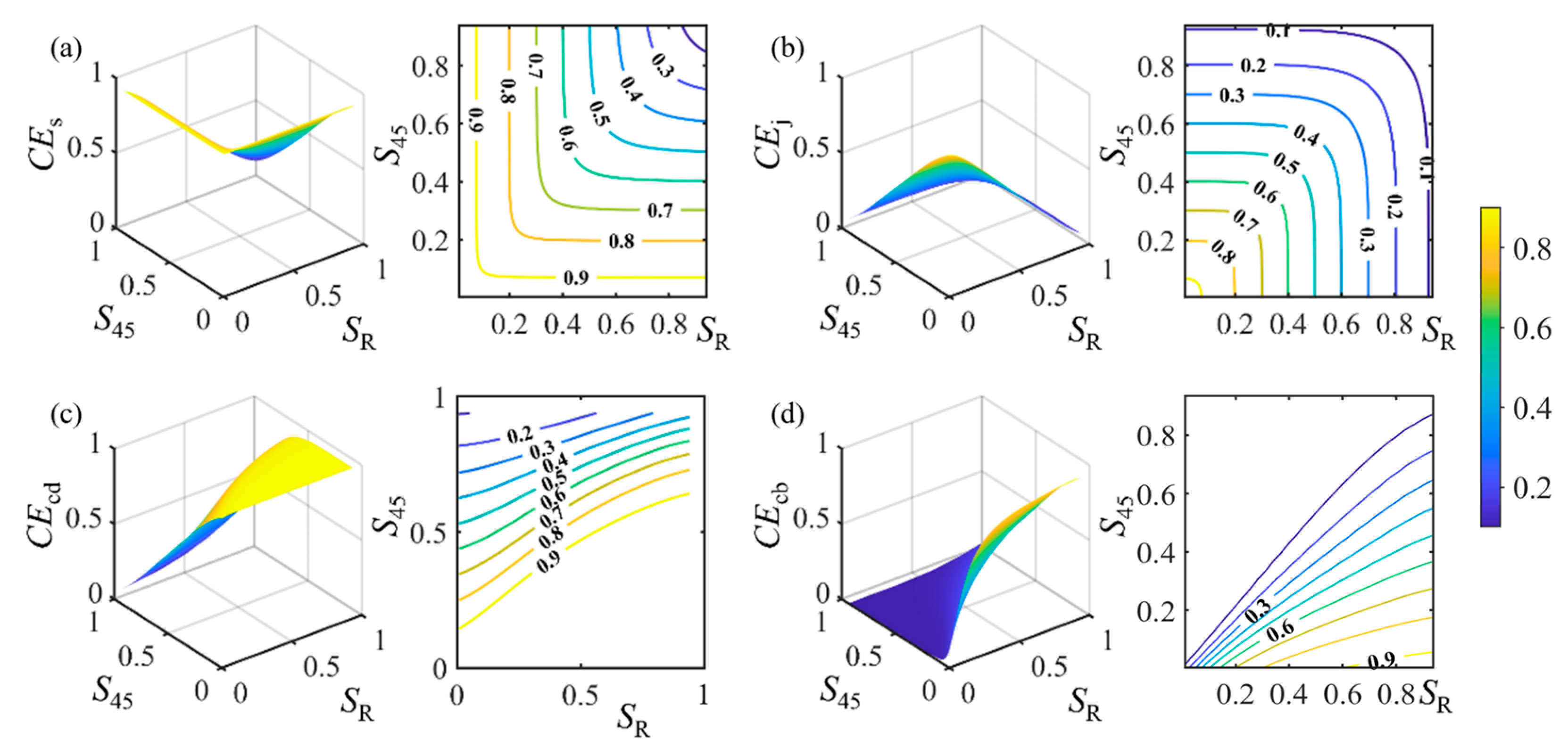
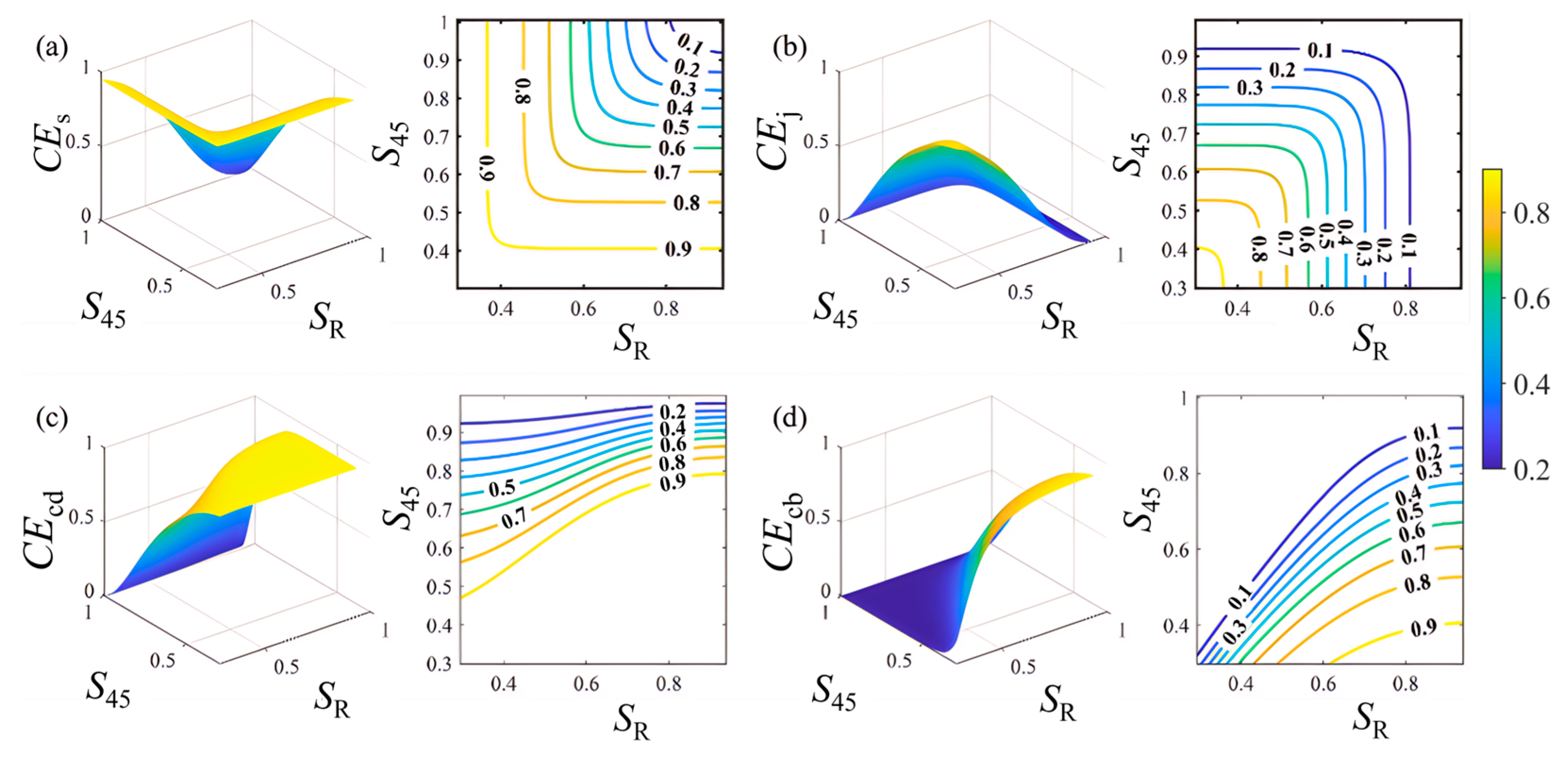
Figure 8 presents the control effects of S
R and S
210.
CEs decreases as S
R and S
210 increase. When S
R and S
210 are 0.84% and 1.37%, respectively,
CEs reaches 94.81%. However, when S
R and S
210 reach 94.15% and 92.73%, the control efficiency drops to 14.76%. When S
R reaches 75% and S
210 is below 7.56%, the joint control effect can exceed 90%. However, when S
210 exceeds 82.73%, the control effect falls below 30%. When S
R and S
210 are 1.00% and 1.47%,
CEj reaches its maximum value of 93.06%, but subsequently,
CEj decreases as S
R and S
210 increase. When S
R reaches 75%, the value of
CEj fluctuates between 0% and 24.99% with changes in S
210. When S
R remains constant,
CEcd decreases as S
210 increases, and the rate of decrease becomes slower as S
R increases. When S
210 is below 30%,
CEcd remains relatively stable with changes in S
R. However, when S
210 exceeds 30%,
CEcd increases significantly with S
R, although the rate of increase slows as S
210 increases. When S
210 is fixed,
CEcb increases gradually as S
R increases. The rate of increase first rises and then decreases with higher values of S
210. When S
210 is 30.12%,
CEcb increases from 13.49% at S
R = 34.33% to 59.32% at S
R = 75.00%. When S
R remains constant,
CEcb gradually decreases as S
210 increases, and the rate of change diminishes as S
R increases. When S
R is 75.01%,
CEcb reaches its maximum value of 91.93% at S
210 = 1.37%, and falls below 10% when S
R exceeds 76.74%.
Figure 9 presents the control effects of S
R and S
45.
CEs decreases as S
R and S
45 increase. When S
R and S
45 are 0.90% and 0.37%, respectively,
CEs reaches its maximum value of 94.79%. However, when S
R and S
45 exceed 92.65% and 71.77%,
CEs drops below 30%. When S
R and S
45 are 0.92% and 0.56%,
CEj reaches its maximum value of 93.08%, but subsequently,
CEj decreases as S
R and S
45 increase. When S
R remains constant,
CEcd decreases as S
45 increases, and the rate of decrease becomes slower as S
R increases. When S
45 is below 30%,
CEcd remains relatively stable with changes in S
R. However, when S
45 exceeds 30%,
CEcd increases significantly with S
R, although the rate of increase slows as S
45 increases. When S
45 is fixed,
CEcb increases gradually as S
R increases. The rate of increase first rises and then decreases with higher values of S
45. When S
45 is 70.06%,
CEcb reaches a maximum value of 24.65% at S
R = 93.97%. When S
R remains constant,
CEcb decreases as S
45 increases. When S
R is relatively small,
CEcb decreases significantly as S
45 increases. When S
R is 75.08%,
CEcb remains above 80% when S
45 exceeds 13.61%, respectively. However, when S
45 exceeds 54.16%,
CEcb drops below 30%.
4.2.3. Joint Distribution of Peak-Flow Reduction Rate Based on PODM
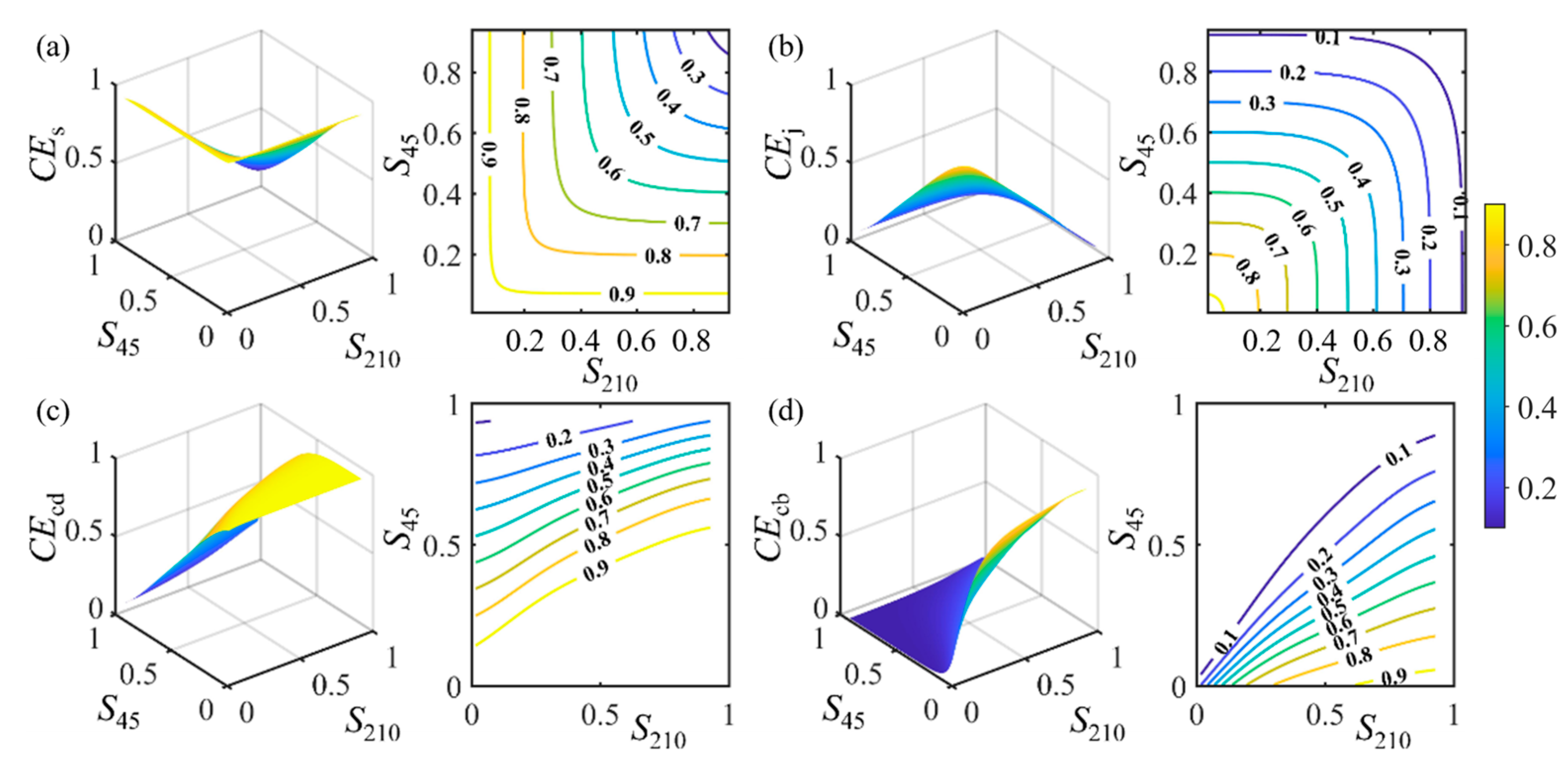
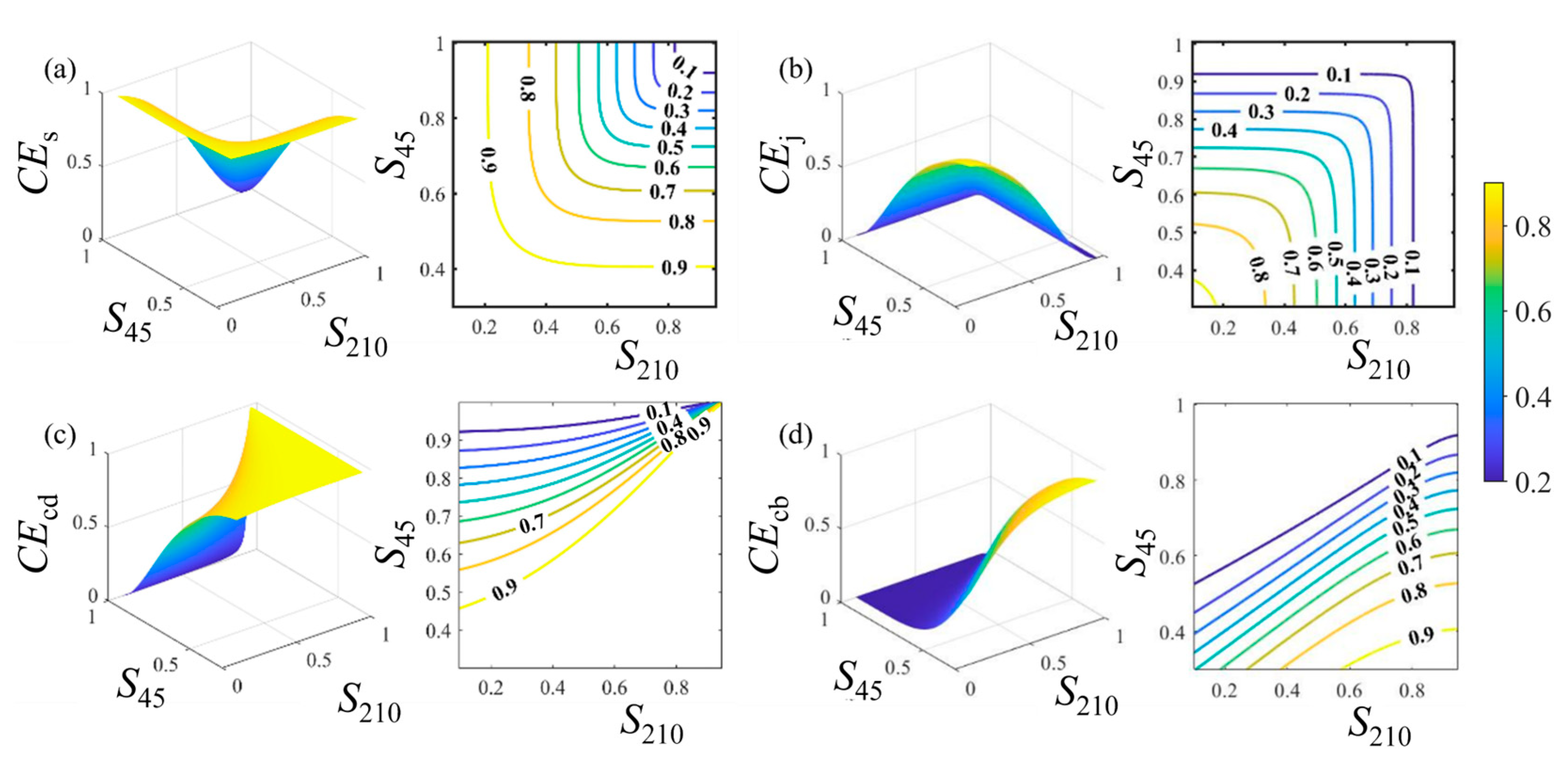
Figure 10 presents the control effects of S
210 and S
45.
CEs decreases as S
210 and S
45 increase.
CEs decreases as S
210 and S
45 increase, reaching a maximum of 95.04% when S
210 is 1.31% and S
45 is 0.86%.
CEs shows larger variation with smaller S
210 as S
45 increases. Similarly,
CEj reaches a maximum of 92.76% when S
210 is 1.50% and S
45 is 0.42%, then decreases as both increase. When S
210 exceeds 70.49%,
CEj remains below 30% regardless of S
45. When S
210 is fixed,
CEcd decreases as S
45 increases, with a more significant decrease at larger S
210 values. When S
45 is small,
CEcd increases slightly with S
210, but the change becomes more significant at larger S
45, especially with high S
210. When S
210 is 60.08%,
CEcd stays above 80% if S
45 is below 55.83%, and below 30.01% if S
45 exceeds 86.87%. When S
210 is fixed,
CEcb decreases as S
45 increases. The change is more significant at smaller S
210 and uniform at larger values. When S
45 is small,
CEcb changes more with smaller S
210, but remains stable at larger S
210. When S
210 is 60.62%,
CEcb stays above 80% if S
45 is below 9.80%, and below 30.20% if S
45 exceeds 45.58%.
4.3. Analysis of Control Effect Based on Prior Distribution (PRDM)
4.3.1. Edge Distribution Fitting of Governance Effect Index Based on PRDM
Using a non-parametric kernel-density analysis method, the frequency values of the flood-control effectiveness indicators are calculated based on the cumulative distribution function, resulting in empirical and theoretical frequency distributions (
Figure 11). The theoretical and empirical frequencies calculated using the Copula function are both distributed near the 45° line, indicating a good fitting performance.
Based on the optimized Gumbel Copula function, the joint probability distribution of the variables is constructed (
Figure 12). As S
R and S
210 increase, the overall control effect continues to improve, exhibiting a trend of increasing initially and then decreasing.
4.3.2. Joint Distribution of Surface-Runoff Reduction Rate and Peak-Flow Reduction Rate Based on PRDM
Figure 13 presents the control effects of S
R and S
210.
CEs decreases as S
R and S
210 increase. When S
R and S
210 are 29.32% and 10.00%, respectively,
CEs reaches its maximum value of 97.41%. When S
R reaches 75%, and S
210 is less than 21.1%, the joint control effect can exceed 90%. However, when S
210 exceeds 69.78%, the joint control effect falls below 30%. When S
R and S
210 are 29.37% and 10.51%, respectively,
CEj reaches its maximum value of 92.28%, after which
CEj gradually decreases as S
R and S
210 increase. When S
R remains constant,
CEcd decreases as S
210 increases. The larger S
R becomes, the more gradual the decrease in
CEcd as S
210 increases. When S
210 is below 30%,
CEcd remains relatively stable with changes in S
R. However, when S
210 exceeds 30%,
CEcd increases significantly with S
R, although the rate of increase slows as S
210 increases. When S
210 is fixed,
CEcb increases gradually as S
R increases. The rate of increase first rises and then decreases with higher values of S
210. When S
210 is 30.12%,
CEcb increases from 20.12% at S
R = 34.48% to 79.66% at S
R = 75.01%. When S
R remains constant,
CEcb decreases as S
210 increases. The rate of decrease becomes slower as S
R increases. When S
R is 75.01%,
CEcb increases from 9.92% at S
210 = 9.92% to a maximum value of 93.56% at S
210 = 44.45%.
Figure 14 presents the control effects of S
R and S
45.
CEs decreases as S
R and S
45 increase. When S
R and S
45 are 29.47% and 30.08%, respectively,
CEs reaches its maximum value of 95.68%. However, when S
R and S
45 exceed 71.20% and 92.61%,
CEs falls below 30%. When S
R and S
45 are 30.01% and 29.79%, respectively,
CEj reaches its maximum value of 93.99%, after which
CEj decreases gradually as S
R and S
45 increase. When S
R exceeds 70.33% and S
45 exceeds 56.88%,
CEj remains below 30%. When S
R remains constant,
CEcd decreases as S
45 increases, and the rate of decrease becomes slower as S
R increases. Conversely, when S
45 is below 70%,
CEcd decreases uniformly with S
R. However, when S
45 exceeds 70%,
CEcd shows a decreasing trend that first slows and then accelerates as S
R increases. When S
R reaches 75%,
CEcd remains below 20.12%, and when S
45 exceeds 88.30%,
CEcd drops below 10%. When S
45 is fixed,
CEcb increases gradually as S
R increases. The rate of increase first rises and then decreases as S
45 increases. When S
45 is 70.03%,
CEcb increases from 74% at S
R = 50.12% to 97.69% at S
R = 80.09%, and reaches its maximum value of 98.29% at S
R = 93.80%. When S
R remains constant,
CEcb decreases as S
45 increases, and the rate of change first decreases and then increases as S
R increases.
4.3.3. Joint Distribution of Peak-Flow Reduction Rate Based on PRDM
Figure 15 presents the control effects of S
210 and S
45.
CEs decreases as S
210 and S
45 increase. When S
210 and S
45 are 9.73% and 29.87%, respectively,
CEs reaches its maximum value of 97.42%. However,
CEs remains above 40% as S
45 continues to increase. Compared to situations with larger values of S
210, when S
210 is smaller,
CEs exhibits a larger variation as S
45 increases, and S
45 follows a similar pattern of change. When S
210 and S
45 are 9.77% and 30.18%, respectively,
CEj reaches its maximum value of 92.41%, after which
CEj decreases gradually as S
210 and S
45 increase. When S
210 exceeds 28.81%,
CEj remains below 30% with changes in S
45. When S
210 remains constant,
CEcd decreases as S
45 increases. The decrease is uniform when S
210 is small, but more significant when S
210 is large. When S
45 is constant,
CEcd increases with S
210, with a more pronounced change at higher S
45 values. When S
210 is constant,
CEcb decreases as S
45 increases. The change is more significant at smaller S
210 and uniform at larger S
210. When S
45 is small,
CEcb changes more significantly with smaller S
210; when S
45 is large,
CEcb stays stable as S
210 increases. When S
210 is 60.04%,
CEcb stays above 80% if S
45 is below 42.13%, and below 30% if S
45 exceeds 67.43%.
4.4. Comparison and Analysis of PODM and PRDM Management Effectiveness
Based on the LID treatment effects obtained through prior and posterior analysis, the trends of change under different conditions are similar. In the evaluation of treatment effects, when indicators E1 and E2 remain unchanged, CEs varies with the increase in E2, showing a smaller variation. However, when both E2 and E1 change, the variation in CEj increases with the increase in E2, and the volatility of the treatment effect becomes larger. Furthermore, when E2 changes over a larger time scale, the treatment effect shows more significant changes, while CEcd decreases with the increase in E2, exhibiting smaller fluctuations in the treatment effect. Lastly, when E2 remains unchanged, CEcb shows a trend of changing with the increase in E1, and the volatility of the treatment effect is larger.
4.5. Limitations and Application Value
This study evaluates the uncertainty of the SWMM model using the GLUE method and deeply analyzes the rainwater and flood-control benefits of LID through the Copula method, providing a comprehensive analysis framework. By performing parameter sampling under both prior and posterior distributions and combining the Copula method to assess LID’s rainwater and flood-control benefits, the study effectively captures the impact of uncertainty on the results. This approach not only considers the uncertainty of model parameters, avoiding the limitations of LID benefit analysis under a single condition, but also simulates LID performance under different scenarios, providing support for understanding the overall rainwater and flood-control benefits of LID under various conditions. Based on this framework, we can more effectively select and adjust LID measures to improve the adaptability and accuracy of urban stormwater management.
This study still has certain limitations. Firstly, LID parameters rely on empirical data and are often difficult to determine precisely, so the results of the uncertainty analysis may be influenced by parameter assignment and model assumptions. Additionally, although sampling from the posterior distribution is more realistic than using a uniform distribution, the heteroscedasticity of parameters may still affect the results, especially in applications across different regions and rainfall patterns. Therefore, urban managers need to carefully adjust LID designs and parameter settings based on local experience and actual conditions to ensure optimized rainwater and flood-control effects. Thus, this research aids in evaluating the effectiveness of various LID implementation strategies, promoting environmental protection, water conservation, and climate adaptation goals in alignment with sustainable development objectives.
5. Conclusions
We have developed an analytical framework for evaluating urban pluvial-flood-control uncertainty, with the following main conclusions:
(1) The GLUE method can identify the sensitive parameters of the model and calculate the uncertainty in regional drainage processes. The highly sensitive parameters of SWMM are the Manning’s coefficient for impervious surfaces, the Manning’s coefficient for pervious surfaces, and the impervious surface-depression storage. The sensitivity differences in the other parameters are relatively small under different rainfall scenarios. The GLUE method can select multiple sets of equivalent simulation-parameter combinations and characterize the parameter interactions and heterogeneous parameter equivalence present in the hydrological model.
(2) Based on the analysis, the model uncertainty for outlet O1 is higher than for O2, as indicated by the higher values of B (2.35), D (2.07), and S (0.85) for O1. This suggests that O1 has more stability in its uncertainty. In contrast, outlet O2 shows lower values of B (0.69), D (0.51), and S (0.69), but a significantly higher CR (80.56), indicating a wider range of uncertainty and greater variability. In summary, O2 is more volatile, while O1 remains more stable.
(3) A comparison of the posterior and prior joint distributions of uncertainty based on the GLUE method reveals that for different governance performance metrics, the joint governance effect, synergistic governance effect, conditional governance effect, and combined governance effect exhibit consistent patterns of variation, with differences in their ranges.
The framework provides valuable assistance in analyzing uncertainty in urban pluvial-flood control and urban sustainable development.