The Role of Marketing Efforts in Enhancing Closed-Loop Supply Chains Under Recycling Competition
Abstract
1. Introduction
- (1)
- When comparing the first three models, which is the preferred option for retailers, manufacturers, and the overall supply chain? How does the intensity of recycling competition influence their preferences?
- (2)
- How do consumer surplus and environmental damage levels vary across different models?
- (3)
- Can a marketing cost-sharing contract be implemented to optimize the profits for manufacturers, retailers, and the overall supply chain?
- (4)
- What impact will government subsidy for remanufacturing have on the supply chain?
2. Literature Review
2.1. Recycling Channel Management in CLSCs
2.2. Channel Competition in CLSCs
2.3. Marketing Efforts in CLSCs
2.4. Consumer Behavior in the Circular Economy
3. Problem Description
- (1)
- We assume the products produced by virgin and recycled materials have the same utility to consumers and that all products are sold at the same price [50,63]. This assumption holds true particularly in specific industries, such as printers and engines, where remanufacturing enables recycled old products to achieve performance levels that are either on par with or even surpass those of new products. For example, KODAK Remanufactured Toner Cartridges are made by recycling empty, used, original HP, Brother, or Samsung toner cartridges. They look and feel just like original cartridges. The print quality also matches or exceeds that of the originals, and most consumers do not know that the new products they buy contain “remanufactured parts” [64]. In another example, Caterpillar demonstrates its commitment to sustainability by assembling recycled components into new parts while strictly adhering to the original equipment manufacturer’s (OEM) performance specifications. These parts undergo rigorous testing to ensure they meet the same high standards as new Caterpillar components. Furthermore, they are backed by the same warranty, offering the same reliability and durability as newly manufactured parts, thus ensuring consistent quality and performance [65].
- (2)
- (3)
- (4)
- We assume to ensure that the cost of the promotion is high enough to ensure the existence of an optimal marketing intensity solution [50].
4. Model Formulation and Solution
4.1. Model B (Without Marketing Efforts)
4.2. Model M (Manufacturer Invests in Marketing Efforts)
4.3. Model R (Retailer Invests in Marketing Efforts)
4.4. Model C (Centralized Supply Chain Exerts Marketing Efforts)
5. Discussion
- (1)
- ;
- (2)
- When , then ; when , then ; when , then ; when , then .
- (1)
- .
- (2)
- .
- (3)
- .
- (4)
- .
- (5)
- .
- (6)
- .
- (7)
- When , then ; when , ; when , then and ; when , then and .
- (8)
- .
- (9)
- .
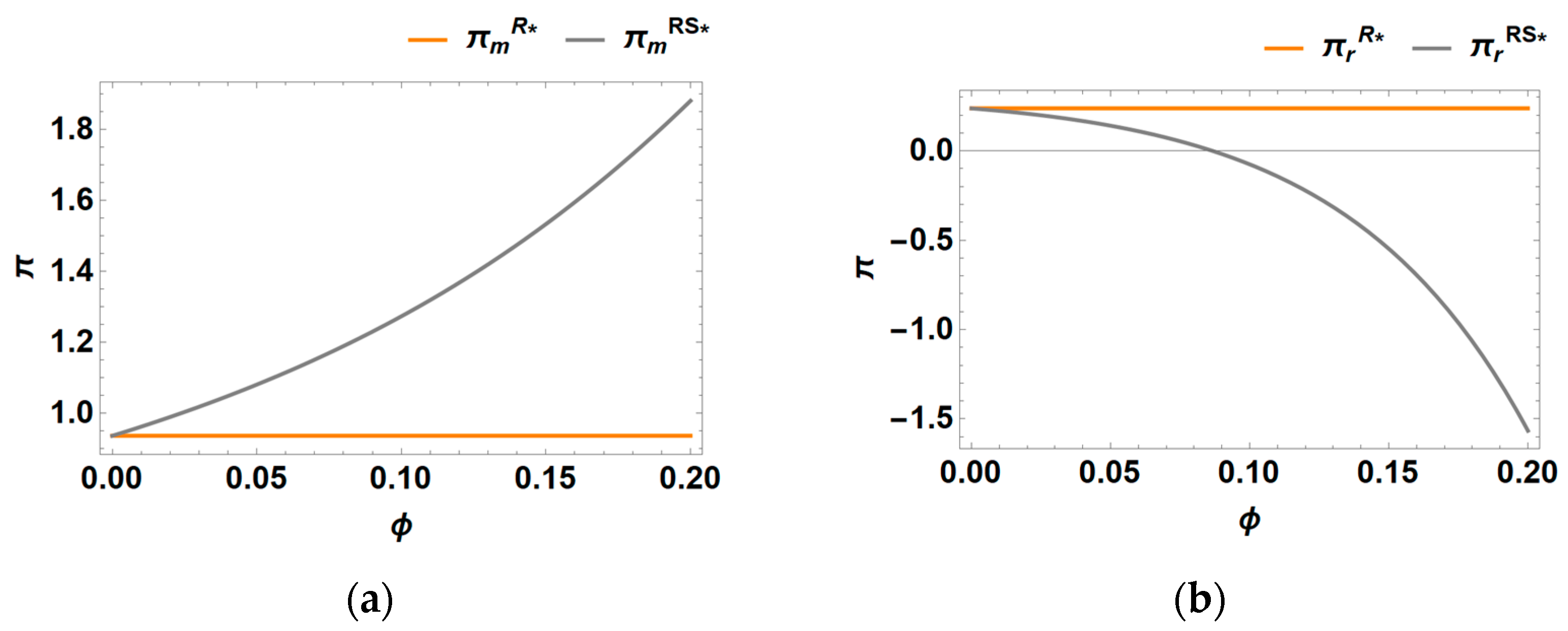
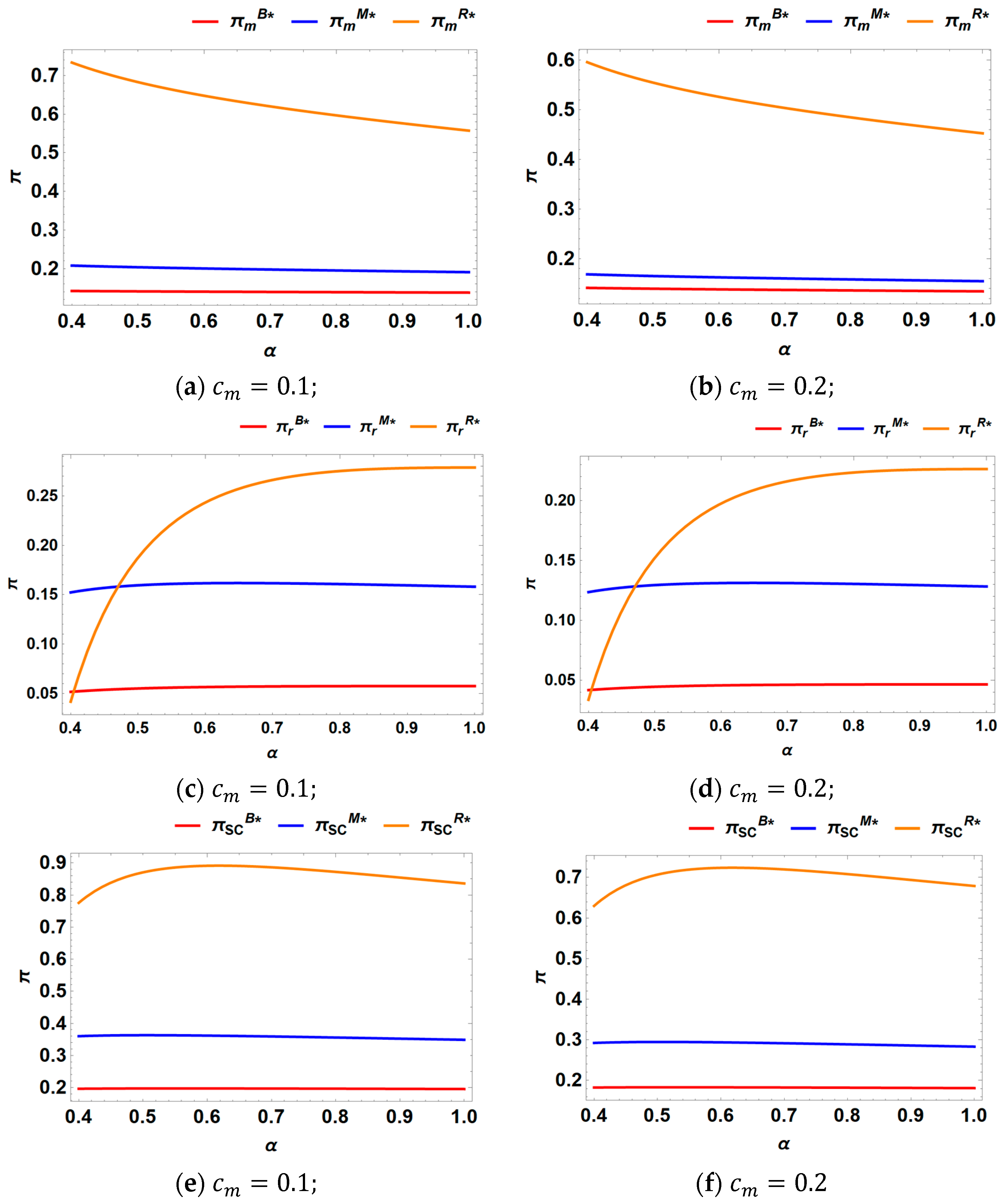
6. Numerical Analysis
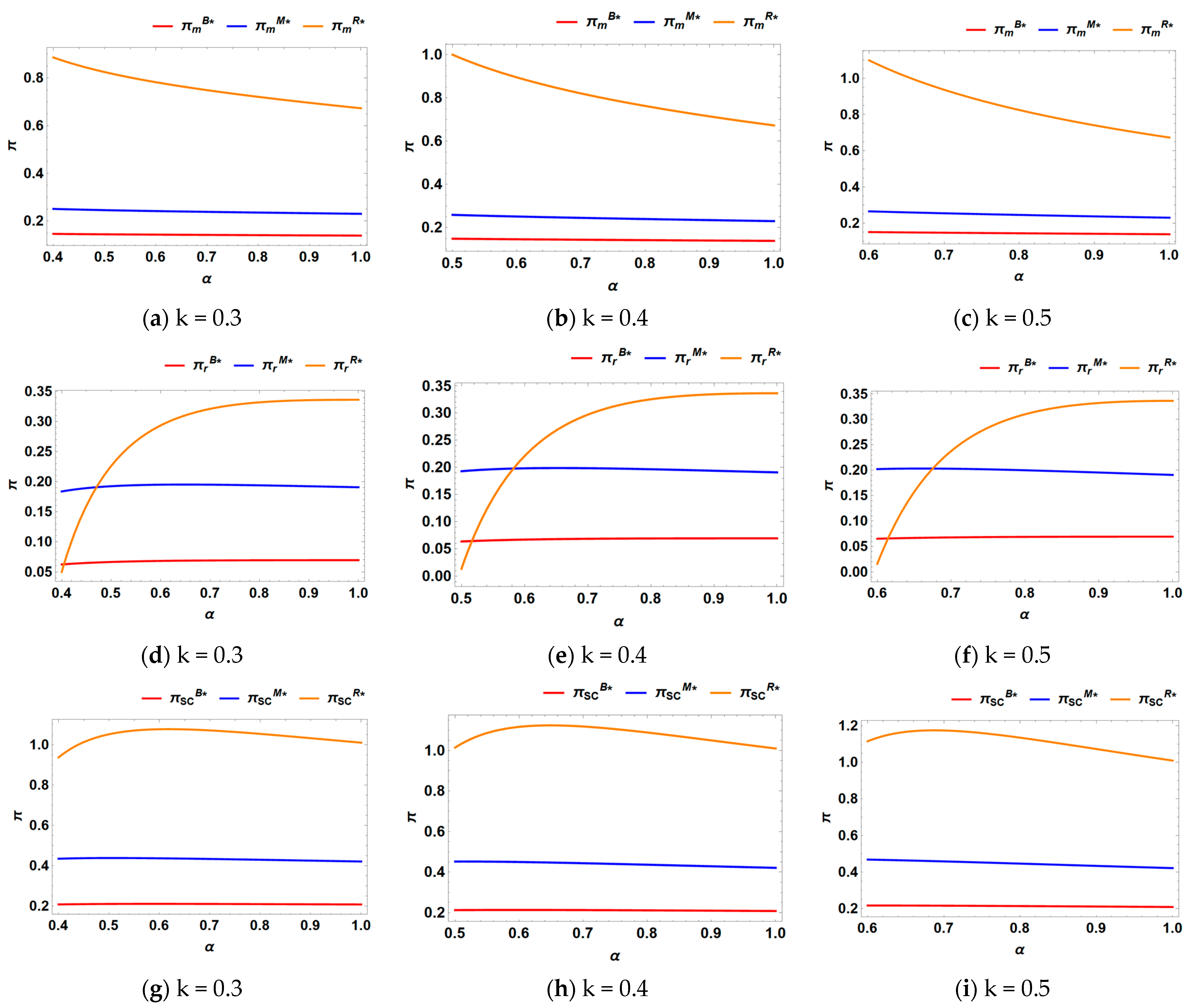
6.1. Profits of Supply Chain and Environmental Damage
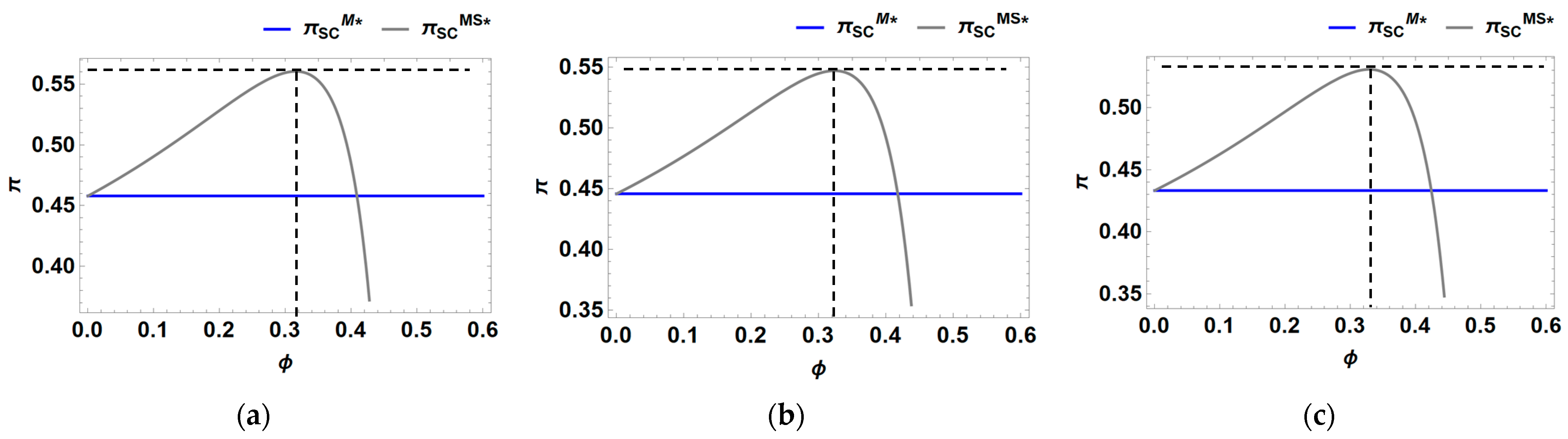
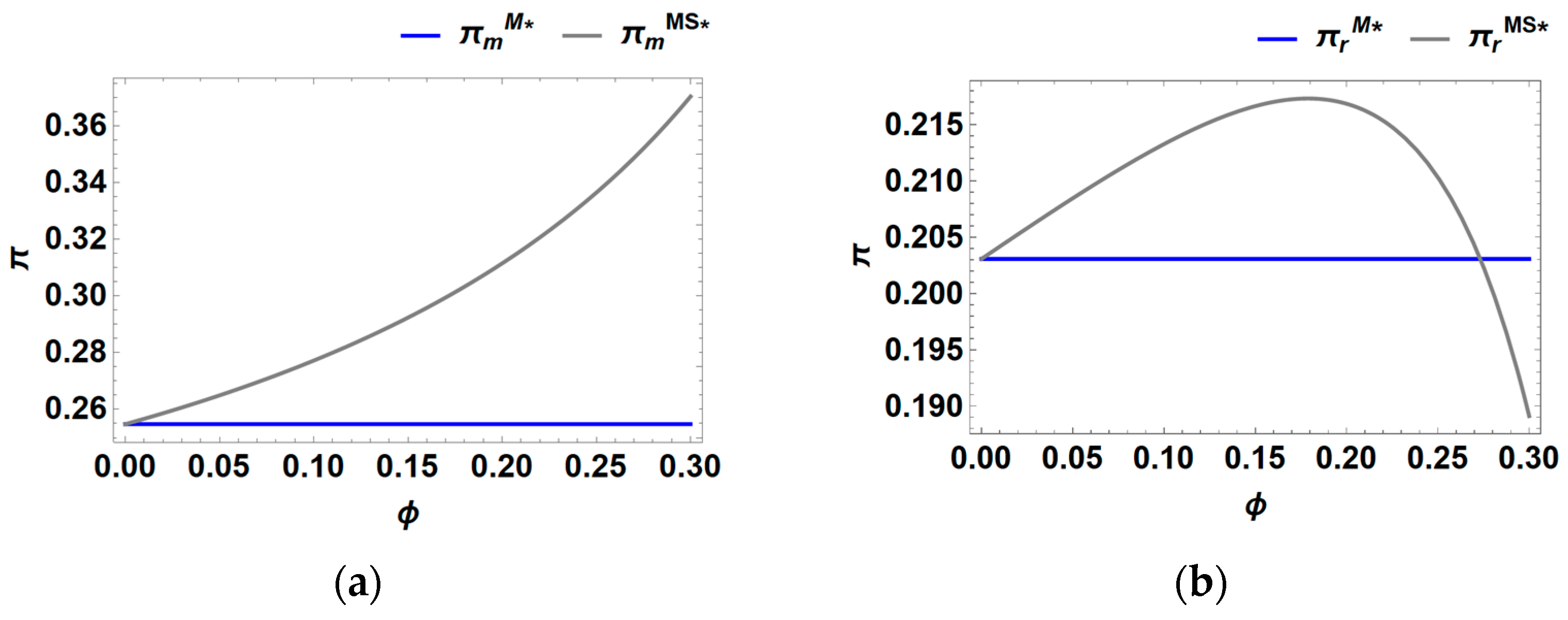
6.2. Marketing Cost Sharing
6.2.1. Under Model M
6.2.2. Under Model R
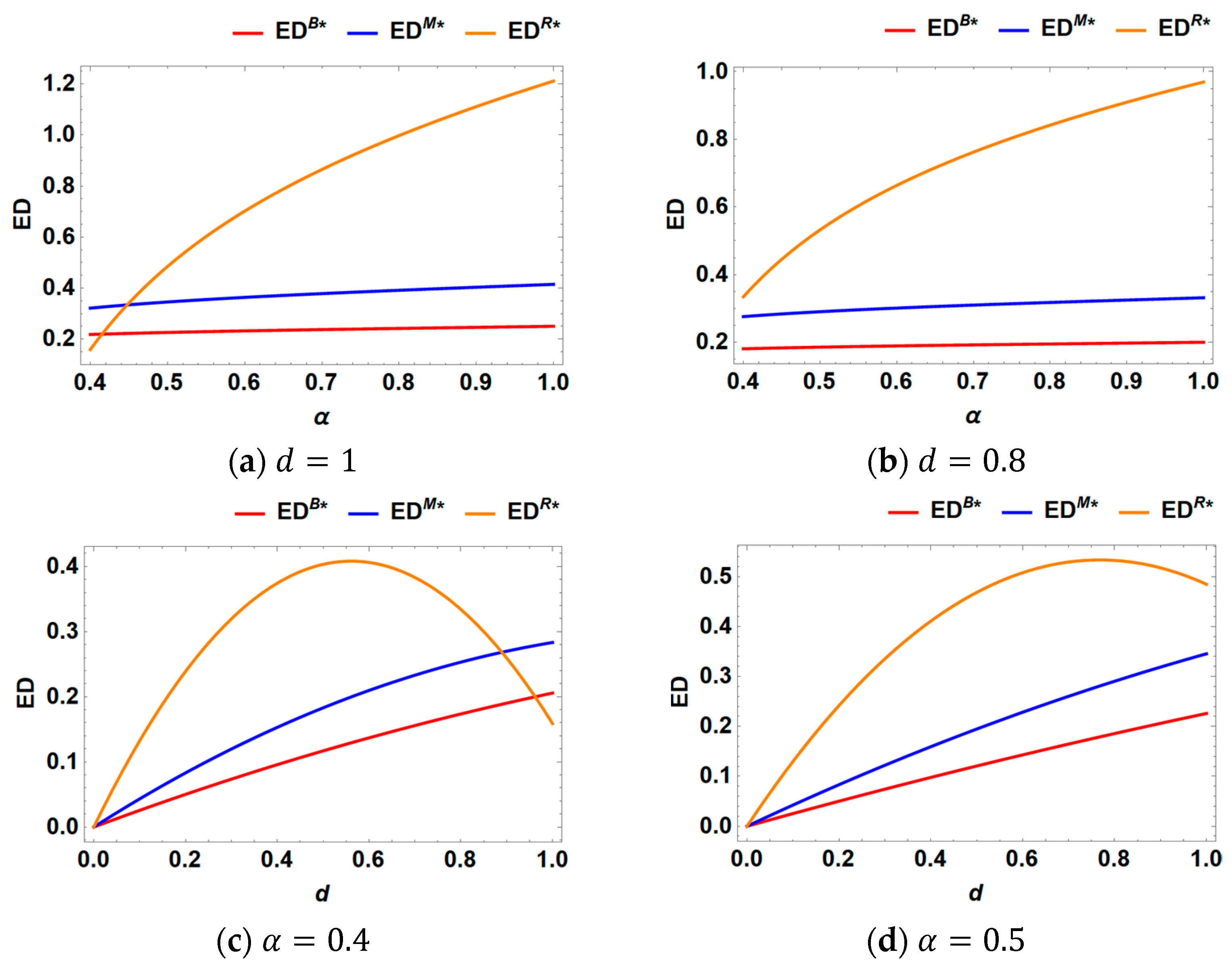
6.3. Consider the Production Cost
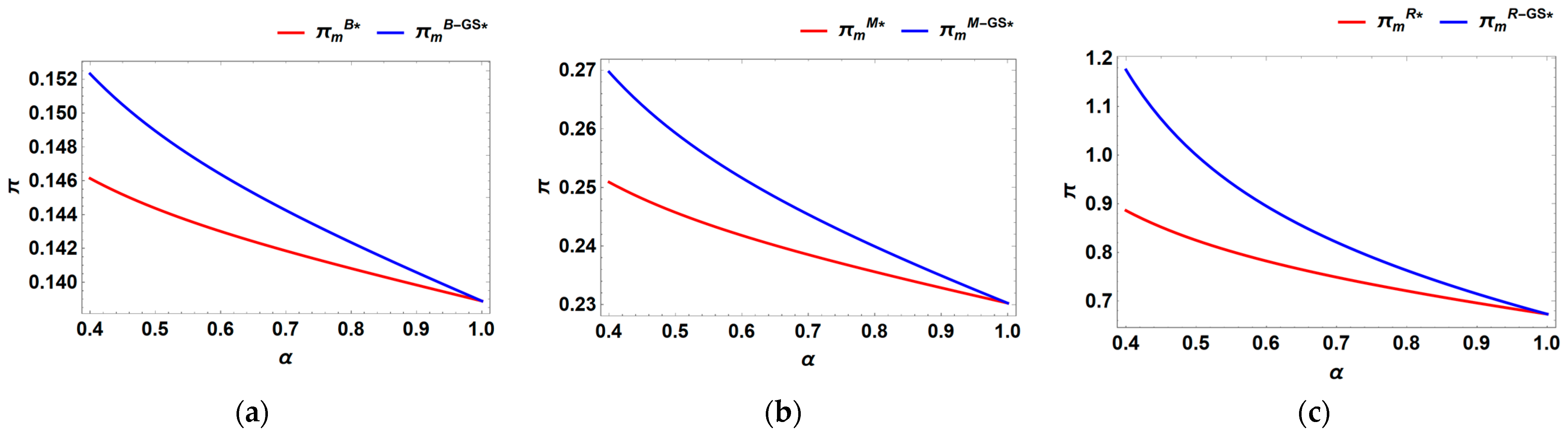
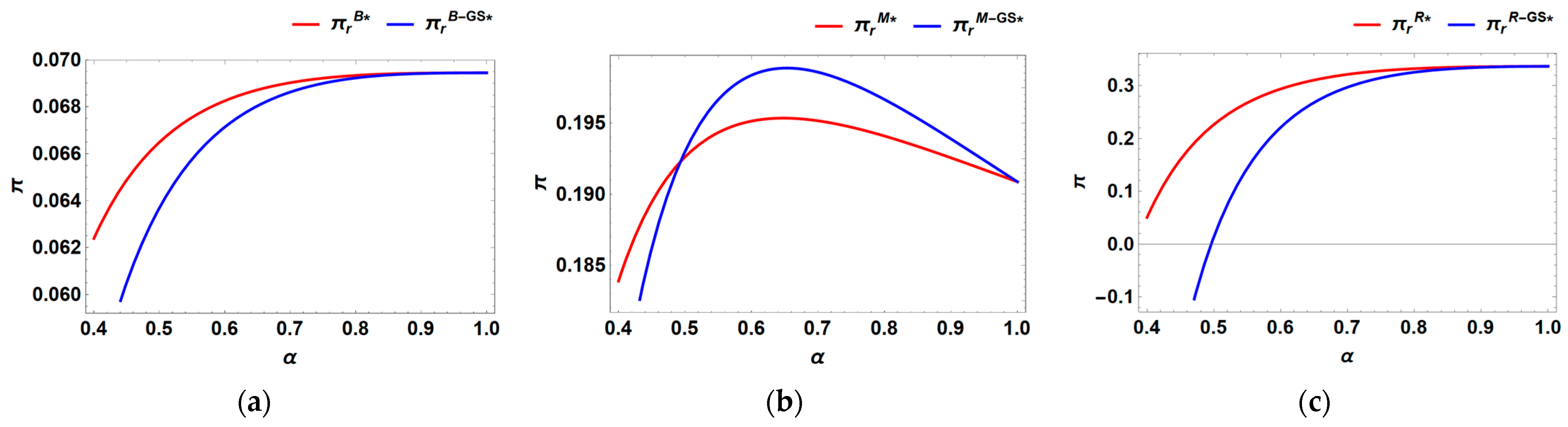
6.4. Consider the Government Subsidy
7. Conclusions
7.1. Theoretical Contributions
7.2. Main Results and Managerial Insights
- (1)
- Implementing marketing measures consistently leads to higher profits for the manufacturer, retailer, and overall supply chain compared to scenarios where no marketing efforts are undertaken. However, the manufacturer consistently prefers the retailer to undertake marketing efforts. In contrast, the retailer’s strategic preference varies based on the intensity of recycling competition. Specifically, the retailer prefers the manufacturer to handle marketing when the competition intensity is low, whereas they opt to undertake their own marketing efforts when the competition intensity is high.
- (2)
- Retailer-led marketing leads to higher prices, greater marketing efforts, increased demand, enhanced recycling efforts, and lower wholesale prices compared to manufacturer-led marketing. However, the buyback prices of recycled materials remain unaffected by which party undertakes the marketing. In addition, the environmental impact of different models is influenced by the underlying demand. As the base demand increases, the order of models with the lowest environmental damage shifts progressively: no marketing, marketing by manufacturers, and marketing by retailers.
- (3)
- Higher competitive intensity in recycling results in reduced recycling efforts, lower buyback prices, decreased wholesale prices, and diminished marketing efforts. However, in the absence of marketing, prices increase as recycling competition intensity rises. Conversely, when marketing is present, prices decrease as recycling competition intensity increases. As the intensity of competition rises, manufacturers’ margins always fall, while retailers’ margins tend to rise, and the margins of the entire supply chain rise and then fall. The impact of recycling competition intensity on environmental damage depends on the base demand: it decreases with higher competition intensity when the base demand is low but increases when the base demand is high.
- (4)
- There is always an optimal marketing cost-sharing ratio that enhances supply chain profits. When the manufacturer undertakes marketing, cost sharing improves the profits of both the retailer and the manufacturer. However, when the retailer handles marketing, cost sharing reduces the retailer’s profits, necessitating a contract for coordination.
- (1)
- An optimal level of recycling competition, rather than an excessively high or low intensity, enhances the profitability of the entire supply chain by strengthening the retailer’s position in recycling and balancing the power dynamics between the manufacturer and retailer. Moreover, at this appropriate level of competition, manufacturers and retailers are more likely to align their marketing strategies, such as delegating marketing responsibilities to retailers. Therefore, supply chain members can intensify recycling promotion efforts to maintain recycling competition within an optimal range, thereby facilitating the coordination of marketing strategies and boosting the profits of supply chain members.
- (2)
- Supply chain members can further optimize profits by sharing marketing costs and establishing contracts. This approach remains effective even in the context of recycling competition.
- (3)
- From an environmental protection standpoint, a larger demand base can lead to increased recycling efforts and reduced environmental harm. Consequently, government and relevant environmental agencies can enhance recycling rates by encouraging the integration of smaller enterprises with larger ones, thereby fostering collective environmental responsibility. This approach helps optimize resources, reduce waste, and protect the environment more effectively.
- (4)
- A government subsidy to the manufacturer invariably enhances its profitability. However, when recycling competition is weak, such a subsidy can significantly harm the retailer’s profitability and consequently disrupt the entire supply chain. The government should implement a subsidy when recycling competition is at a moderate level, as this can lead to greater overall profitability across the supply chain.
7.3. Limitations and Future Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- The European Remanufacturing Network. Available online: https://www.remanufacturing.eu/ (accessed on 22 February 2025).
- Du, S.; Huang, C.; Yan, X.; Tang, W. Voluntary green technology adoption: The effects of regulatory uncertainty and competition. Eur. J. Oper. Res. 2024, 315, 528–540. [Google Scholar] [CrossRef]
- Zhiyuan Consulting. Available online: https://www.chyxx.com/industry/1203122.html (accessed on 22 February 2025).
- Kodak. Kodak Sustainability Report 2023. Available online: https://www.kodak.com/content/pdfs/Kodak-Sustainability-Report-2023-EN.pdf (accessed on 6 January 2025).
- HP. HP Planet Partners. Available online: https://www.hp.com/cn-zh/sustainable-impact/planet-product-recycling.html (accessed on 6 January 2025).
- Atasu, A.; Sarvary, M.; Van Wassenhove, L.N. Remanufacturing as a marketing strategy. Manage. Sci. 2008, 54, 1731–1746. [Google Scholar] [CrossRef]
- Guide, V., Jr.; Daniel, R.; Van Wassenhove, L.N. OR FORUM—The evolution of closed-loop supply chain research. Oper. Res. 2009, 57, 10–18. [Google Scholar] [CrossRef]
- Opinions on Promoting the Development of the Remanufacturing Industry. Available online: https://www.gov.cn/zwgk/2010-05/31/content_1617310.htm (accessed on 6 January 2025).
- Matsui, K. Optimal timing of acquisition price announcement for used products in a dual-recycling channel reverse supply chain. Eur. J. Oper. Res. 2022, 300, 615–632. [Google Scholar] [CrossRef]
- Matsui, K. Dual-recycling channel reverse supply chain design of recycling platforms under acquisition price competition. Int. J. Prod. Econ. 2023, 259, 108769. [Google Scholar] [CrossRef]
- Feng, D.; Mao, Y.; Li, S.; Zhang, Y. Quality and Pricing Decisions in a Dual-Channel Closed-Loop Supply Chain Considering Imperfect Product Recycling. Sustainability 2024, 16, 5606. [Google Scholar] [CrossRef]
- Apple. Trade In. Available online: https://www.apple.com.cn/shop/trade-in (accessed on 6 January 2025).
- Govindan, K.; Jiménez-Parra, B.; Rubio, S.; Vicente-Molina, M.A. Marketing issues for remanufactured products. J. Clean. Prod. 2019, 227, 890–899. [Google Scholar] [CrossRef]
- Chen, C.K.; Akmalul’Ulya, M.; Mancasari, U.A. A study of product quality and marketing efforts in closed-loop supply chains with remanufacturing. IEEE Trans. Syst. Man. Cybern. 2018, 50, 4870–4881. [Google Scholar] [CrossRef]
- Ma, P.; Li, K.W.; Wang, Z.J. Pricing decisions in closed-loop supply chains with marketing effort and fairness concerns. Int. J. Prod. Res. 2017, 55, 6710–6731. [Google Scholar] [CrossRef]
- Huang, C.; Du, S.; Wang, B.; Tang, W. Accelerate or hinder it? Manufacturer transformation under competition and carbon emission trading. Int. J. Prod. Res. 2023, 61, 6230–6250. [Google Scholar] [CrossRef]
- Sabharwal, S.; Garg, S. Determining cost effectiveness index of remanufacturing: A graph theoretic approach. Int. J. Prod. Econ. 2013, 144, 521–532. [Google Scholar] [CrossRef]
- Liao, B.; Li, L.; Yang, Z. Perceived social green preference: The motivation mechanism of inducing green behaviour. Curr. Psychol. 2022, 41, 1–17. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, Y. Pricing strategies for bundled products considering consumers’ green preference. J. Clean. Prod. 2022, 344, 130962. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, Z.; Zhang, H.; Hu, G. Research on the Impact Mechanism of Self-Quantification on Consumers’ Green Behavioral Innovation. Sustainability 2024, 16, 8383. [Google Scholar] [CrossRef]
- Duan, C.; Yao, F.; Xiu, G.; Zhang, Y.; Zhang, X. Multi-period closed-loop supply chain network equilibrium: Perspective of marketing and corporate social responsibility. IEEE Access 2020, 9, 1495–1511. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, W.; Du, S.; Sun, X. How to achieve targeted advertising with the e-commerce platform’s membership system? Omega 2025, 130, 103156. [Google Scholar] [CrossRef]
- Nike. Move to Zero. Available online: https://www.nike.com.cn/sustainability (accessed on 6 January 2025).
- Seuring, S.; Müller, M. From a literature review to a conceptual framework for sustainable supply chain management. J. Clean. Prod. 2008, 16, 1699–1710. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Bhattacharya, S.; Van Wassenhove, L.N. Closed-loop supply chain models with product remanufacturing. Manag. Sci. 2004, 50, 239–252. [Google Scholar] [CrossRef]
- Alegoz, M.; Kaya, O.; Bayindir, Z.P. A comparison of pure manufacturing and hybrid manufacturing–remanufacturing systems under carbon tax policy. Eur. J. Oper. Res. 2021, 294, 161–173. [Google Scholar] [CrossRef]
- Zheng, B.; Chu, J.; Jin, L. Recycling channel selection and coordination in dual sales channel closed-loop supply chains. Appl. Math. Model. 2021, 95, 484–502. [Google Scholar] [CrossRef]
- Giri, B.C.; Chakraborty, A.; Maiti, T. Pricing and return product collection decisions in a closed-loop supply chain with dual-channel in both forward and reverse logistics. J. Manuf. Syst. 2017, 42, 104–123. [Google Scholar] [CrossRef]
- Atasu, A.; Toktay, L.B.; Van Wassenhove, L.N. How collection cost structure drives a manufacturer’s reverse channel choice. Prod. Oper. Manag. 2013, 22, 1089–1102. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wang, C.X.; Zhao, Y. Closed-loop supply chain models for a high-tech product under alternative reverse channel and collection cost structures. Int. J. Product. Econ. 2014, 156, 108–123. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, J. Decision-Making in Remanufacturing Supply Chains: Game Theory Analysis of Recycling Models and Consumer Value Perception. Sustainability 2024, 16, 10476. [Google Scholar] [CrossRef]
- Ziaei, M.; Ameli, M.; Rasti-Barzoki, M.; Shavandi, A. A game-theoretic approach for pricing in a dual-channel socially responsible closed-loop supply chain under reward-penalty mechanism. Environ. Dev. Sustain. 2024, 26, 31201–31223. [Google Scholar] [CrossRef]
- Yu, H.; Mi, J.; Xu, N. Recycling, pricing decisions, and coordination in the dual-channel closed-loop supply chain: A dynamic perspective. J. Clean. Prod. 2024, 456, 142297. [Google Scholar] [CrossRef]
- Li, B.; Liu, K.; Chen, Q.; Lau, Y.Y.; Dulebenets, M.A. A necessity-based optimization approach for closed-loop logistics considering carbon emission penalties and rewards under uncertainty. Mathematics 2023, 11, 4516. [Google Scholar] [CrossRef]
- Confente, I.; Russo, I.; Peinkofer, S.; Frankel, R. The challenge of remanufactured products: The role of returns policy and channel structure to reduce consumers’ perceived risk. Int. J. Phys. Distrib. Logist. Manag. 2021, 51, 350–380. [Google Scholar] [CrossRef]
- Bhatia, M.S.; Kumar, S.; Gangwani, K.K.; Kaur, B. Key capabilities for closed-loop supply chain: Empirical evidence from manufacturing firms. Technol. Forecast. Soc. Chang. 2024, 208, 123717. [Google Scholar] [CrossRef]
- Martin, P.; Guide, V.D.R., Jr.; Craighead, C.W. Supply chain sourcing in remanufacturing operations: An empirical investigation of remake versus buy. Decis. Sci. 2010, 41, 301–324. [Google Scholar] [CrossRef]
- Zheng, B.; Yang, C.; Yang, J.; Zhang, M. Dual-channel closed loop supply chains: Forward channel competition, power structures and coordination. Int. J. Prod. Res. 2017, 55, 3510–3527. [Google Scholar] [CrossRef]
- Jalapathy, P.; Unnissa, M.M. Extended Warranty and Retailing Strategies in CLSC Competition with (Re) manufacturing Manufacturer. IEEE Access 2024, 12, 119697–119732. [Google Scholar] [CrossRef]
- Qiang, Q.P. The closed-loop supply chain network with competition and design for remanufactureability. J. Clean. Prod. 2015, 105, 348–356. [Google Scholar] [CrossRef]
- Zhang, C.T.; Ren, M.L. Closed-loop supply chain coordination strategy for the remanufacture of patented products under competitive demand. Appl. Math. Model. 2016, 40, 6243–6255. [Google Scholar] [CrossRef]
- Hosseini-Motlagh, S.M.; Nouri-Harzvili, M.; Johari, M.; Sarker, B.R. Coordinating economic incentives, customer service and pricing decisions in a competitive closed-loop supply chain. J. Clean. Prod. 2020, 255, 120241. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed-loop supply chain with dual recycling channel. Int. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- He, Q.; Wang, N.; Yang, Z.; Jiang, B. Competitive collection under channel inconvenience in closed-loop supply chain. Eur. J. Oper. Res. 2019, 275, 155–166. [Google Scholar] [CrossRef]
- Wang, N.; He, Q.; Jiang, B. Hybrid closed-loop supply chains with competition in recycling and product markets. Int. J. Prod. Econ. 2019, 217, 246–258. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Wahab, M.I.M.; Goh, M. Channel leadership and performance for a closed-loop supply chain considering competition. Transp. Res. Part E Logist. Transp. Rev. 2023, 175, 103151. [Google Scholar] [CrossRef]
- Feng, D.; Zhang, X.; Zhang, Y. Collection decisions and coordination in a closed-loop supply chain under recovery price and service competition. J. Ind. Manag. 2022, 18, 5. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, H.; Hang, T.; Meng, Q. How to Choose Recycling Mode between Monopoly and Competition by Considering Blockchain Technology? Sustainability 2024, 16, 6296. [Google Scholar] [CrossRef]
- He, Q.; Wang, N.; Jiang, B. Hybrid closed-loop supply chain with different collection competition in reverse channel. Int. J. Prod. Econ. 2024, 276, 109371. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Sane-Zerang, E.; Choi, T.M. The effect of marketing effort on dual-channel closed-loop supply chain systems. IEEE Trans. Syst. Man. Cybern. 2016, 48, 265–276. [Google Scholar] [CrossRef]
- Hong, Z.; Guo, X. Green product supply chain contracts considering environmental responsibilities. Omega 2019, 83, 155–166. [Google Scholar] [CrossRef]
- Li, G.; Wu, H.; Sethi, S.P.; Zhang, X. Contracting green product supply chains considering marketing efforts in the circular economy era. Int. J. Prod. Econ. 2021, 234, 108041. [Google Scholar] [CrossRef]
- Gao, J.; Han, H.; Hou, L.; Wang, H. Pricing and effort decisions in a closed-loop supply chain under different channel power structures. J. Clean. Prod. 2016, 112, 2043–2057. [Google Scholar] [CrossRef]
- Hu, Y.; Meng, L.; Huang, Z. Pricing and Sales Effort Decisions in a Closed-Loop Supply Chain Considering the Network Externality of Remanufactured Product. Sustainability 2023, 15, 5771. [Google Scholar] [CrossRef]
- Asghari, M.; Afshari, H.; Mirzapour Al-e-hashem, S.M.J.; Fathollahi-Fard, A.M.; Dulebenets, M.A. Pricing and advertising decisions in a direct-sales closed-loop supply chain. Comput. Ind. Eng. 2022, 171, 108439. [Google Scholar] [CrossRef]
- Zhai, M.; Wang, X.; Zhao, X. The importance of online customer reviews characteristics on remanufactured product sales: Evidence from the mobile phone market on Amazon. com. J. Retail. Consum. Serv. 2024, 77, 103677. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Jia, X. Refurbished or remanufactured?—An experimental study on consumer choice behavior. Front. Psychol. 2020, 11, 781. [Google Scholar] [CrossRef]
- Lakatos, E.S.; Nan, L.M.; Bacali, L.; Ciobanu, G.; Ciobanu, A.M.; Cioca, L.I. Consumer satisfaction towards green products: Empirical insights from romania. Sustainability 2021, 13, 10982. [Google Scholar] [CrossRef]
- Fu, H.; He, W.; Feng, K.; Guo, X.; Hou, C. Understanding consumers’ willingness to pay for circular products: A multiple model-comparison approach. Sustain. Prod. Consum. 2024, 45, 67–78. [Google Scholar] [CrossRef]
- Zhang, W.; Luo, B. Do environmental concern and perceived risk contribute to consumers’ intention toward buying remanufactured products? An empirical study from China. Clean Technol. Environ. Policy 2021, 23, 463–474. [Google Scholar] [CrossRef]
- Chinen, K.; Matsumoto, M.; Tong, P.; Han, Y.S.; Niu, K.H.J. Electric vehicle owners’ perception of remanufactured batteries: An empirical study in China. Sustainability 2022, 14, 10846. [Google Scholar] [CrossRef]
- Chun, Y.Y.; Matsumoto, M.; Chinen, K.; Endo, H.; Gan, S.S.; Tahara, K. What will lead Asian consumers into circular consumption? An empirical study of purchasing refurbished smartphones in Japan and Indonesia. Sustain. Prod. Consum. 2022, 33, 158–167. [Google Scholar] [CrossRef]
- Choi, T.M.; Li, Y.; Xu, L. Channel leadership, performance and coordination in closed loop supply chains. Int. J. Prod. Econ. 2013, 146, 371–380. [Google Scholar] [CrossRef]
- KODAK Remanufactured Toner Cartridges. Available online: https://www.kodak.com/en/consumer/product/printing-scanning/ink-cartridges/remanufactured-toner/ (accessed on 12 February 2025).
- How the Caterpillar Remanufacturing Process Works. Available online: https://www.cat.com/en_US/products/new/parts/reman/the-remanufacturing-process.html (accessed on 12 February 2025).
- Hu, L.; Zhou, X.; Choi, T.M.; Du, S. Making Delivery Platform Drivers Safer: Platform Responsibility Versus Consumer Empowerment; Working paper; University of Liverpool Management School: Liverpool, UK, 2024. [Google Scholar]
- Panda, S. Coordination of a socially responsible supply chain using revenue sharing contract. Transp. Res. Part E Logist. Transp. Rev. 2014, 67, 92–104. [Google Scholar] [CrossRef]
- Du, S.; Li, Z.; Choi, T.M.; Hu, L. Optimal Bundling Cooperation Strategies for Online Paid Membership Programs. Nav. Res. Logists 2024, 72, 390–408. [Google Scholar] [CrossRef]


| Notations | Definitions |
|---|---|
| Indices | |
| Index of the CLSC members (subscript): (manufacturer), (retailer), and (the entire CLSC) | |
| j | Index of models (superscript): (no marketing efforts), (manufacturer exerting marketing efforts), (retailer exerting marketing efforts), (centralized supply with marketing efforts), (retailer shares the marketing costs of the manufacturer), (manufacturer shares the marketing costs of the retailer) |
| Parameters | |
| Base demand | |
| Cost saving per unit by producing products with recycled materials | |
| Price–demand coefficient | |
| Competition intensity | |
| Recycling cost parameter | |
| Marketing efforts cost parameter | |
| Environmental damage parameter | |
| Decision variables | |
| Sales price of product under model () | |
| Wholesale price of product under model () | |
| Recycling rate by member () under Model () | |
| Recycling investment by member () | |
| Marketing effort under model () | |
| Buyback price under model () | |
| Functions | |
| Demand under model () | |
| ’s recycling investment cost () under model () | |
| ’s profit () under model () | |
| Consumer surplus under model () | |
| Environmental damage under model () |
| Case | Manufacturer’s Profit |
|---|---|
| Model B | |
| Model M | |
| Model R |
| Case | Manufacturer’s Profit |
|---|---|
| Model B | |
| Model M | |
| Model R |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, X.; Wang, L.; Luo, Z. The Role of Marketing Efforts in Enhancing Closed-Loop Supply Chains Under Recycling Competition. Sustainability 2025, 17, 2531. https://doi.org/10.3390/su17062531
Tian X, Wang L, Luo Z. The Role of Marketing Efforts in Enhancing Closed-Loop Supply Chains Under Recycling Competition. Sustainability. 2025; 17(6):2531. https://doi.org/10.3390/su17062531
Chicago/Turabian StyleTian, Xu, Lei Wang, and Zaichen Luo. 2025. "The Role of Marketing Efforts in Enhancing Closed-Loop Supply Chains Under Recycling Competition" Sustainability 17, no. 6: 2531. https://doi.org/10.3390/su17062531
APA StyleTian, X., Wang, L., & Luo, Z. (2025). The Role of Marketing Efforts in Enhancing Closed-Loop Supply Chains Under Recycling Competition. Sustainability, 17(6), 2531. https://doi.org/10.3390/su17062531







