Sustainable Reservoir Management: Simulating Water Flooding to Optimize Oil Recovery in Heterogeneous Reservoirs Through the Evaluation of Relative Permeability Models
Abstract
1. Introduction
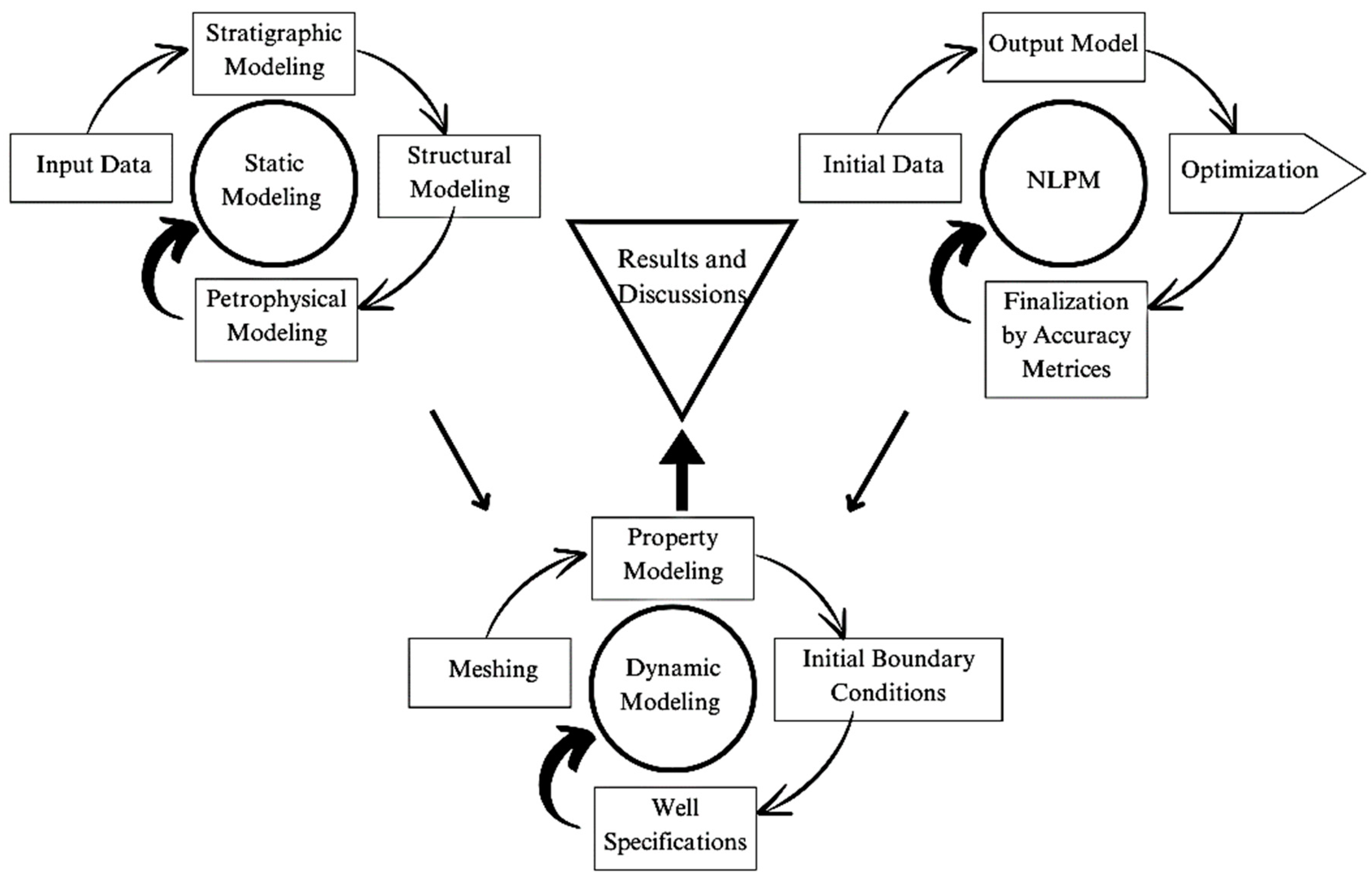
2. Method and Materials
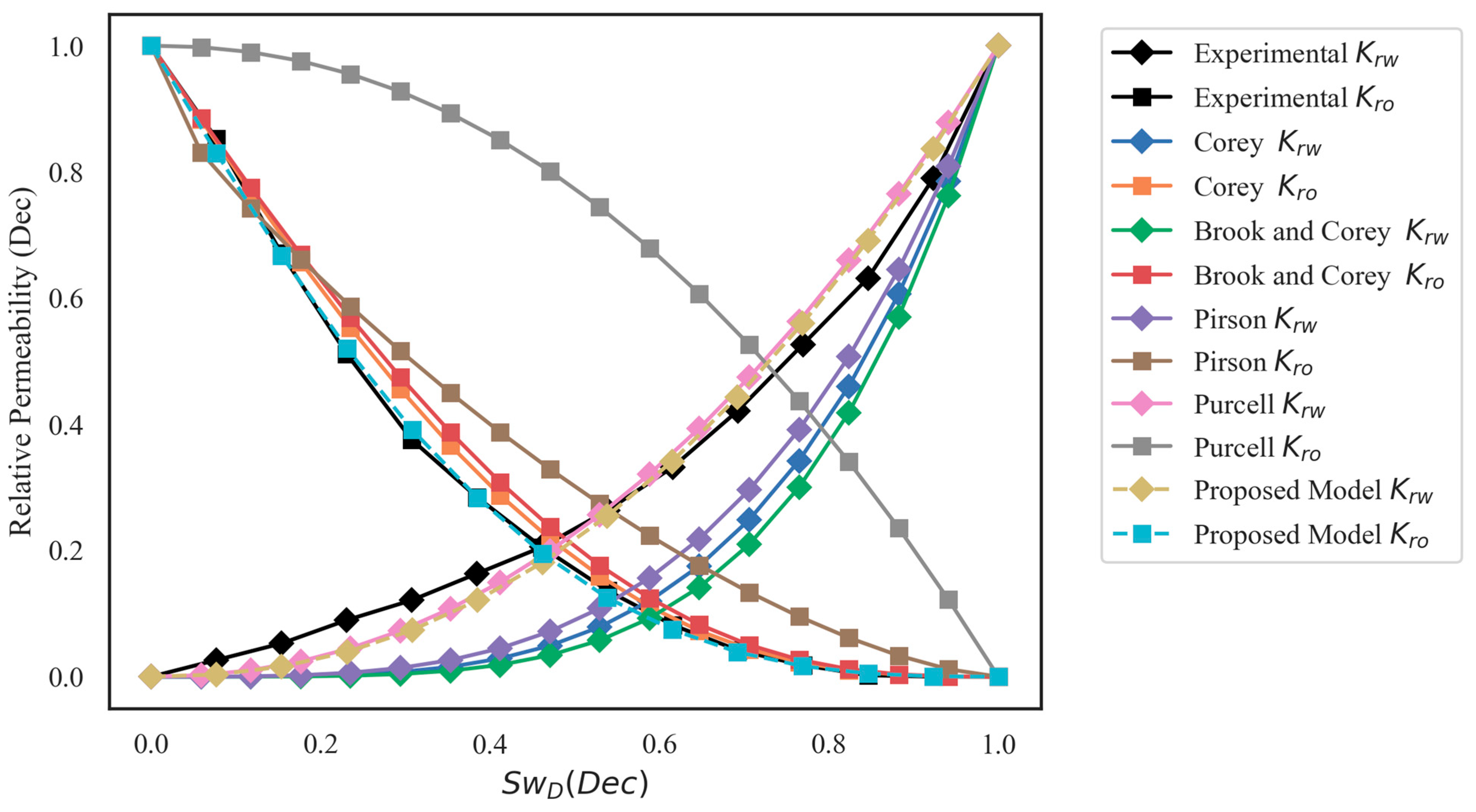
2.1. Relative Permeability Models
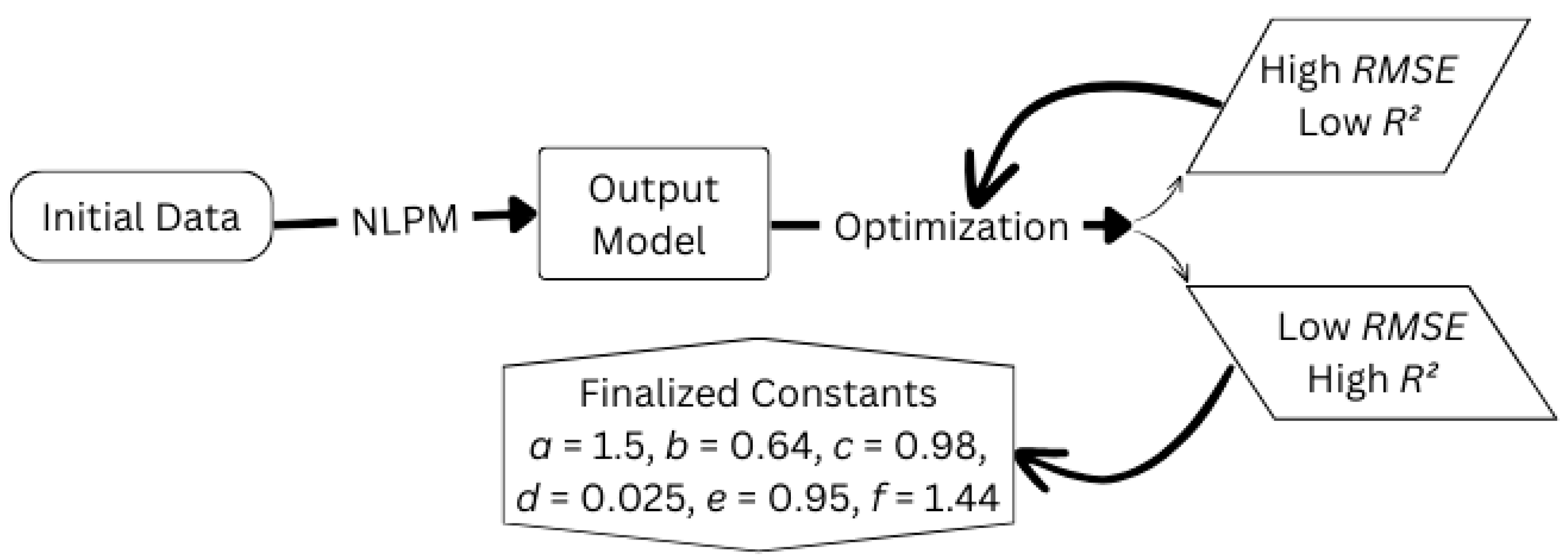
2.2. Non-Linear Predictive Modeling
2.3. Model Prediction Performance Indices
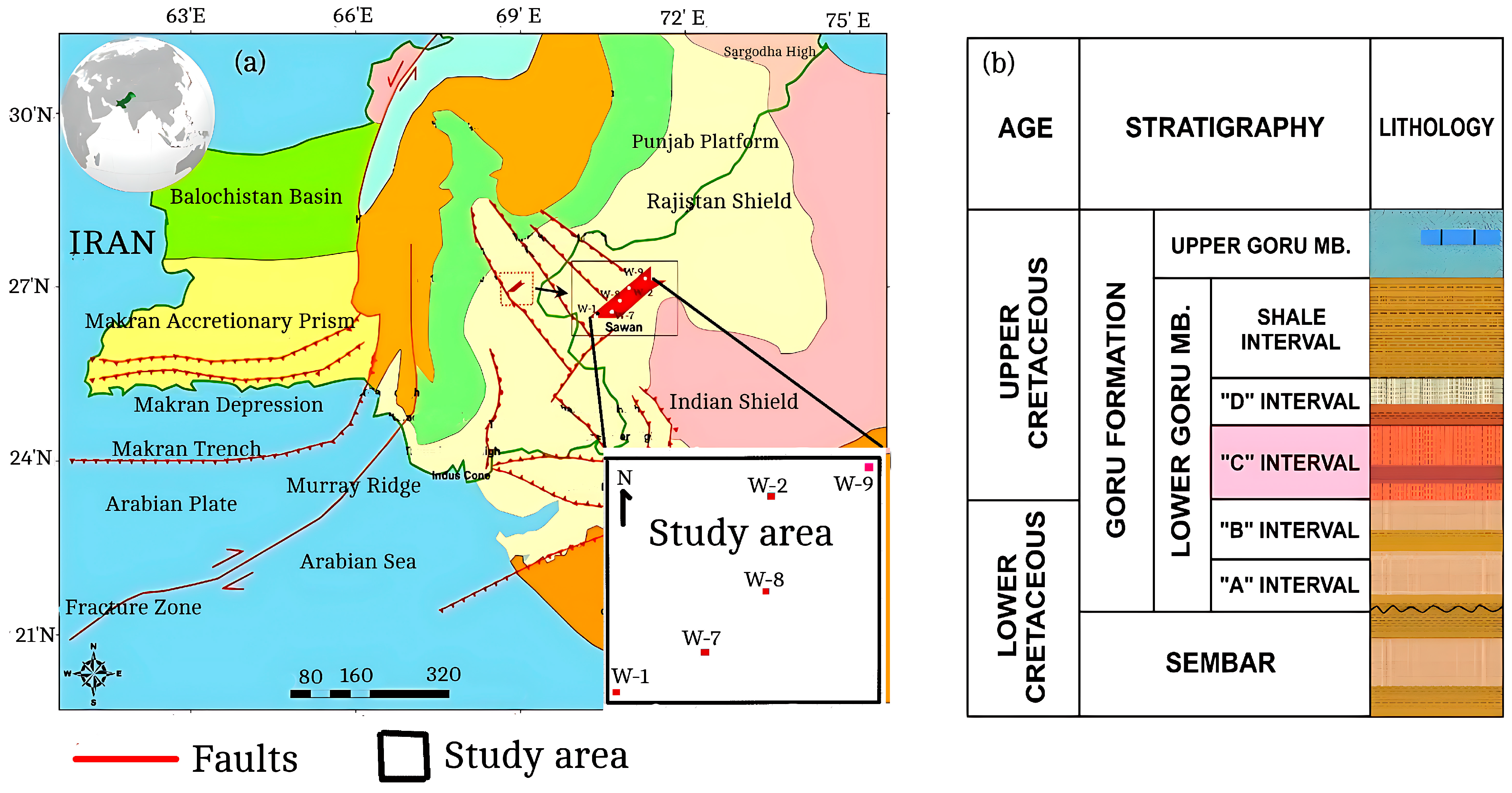
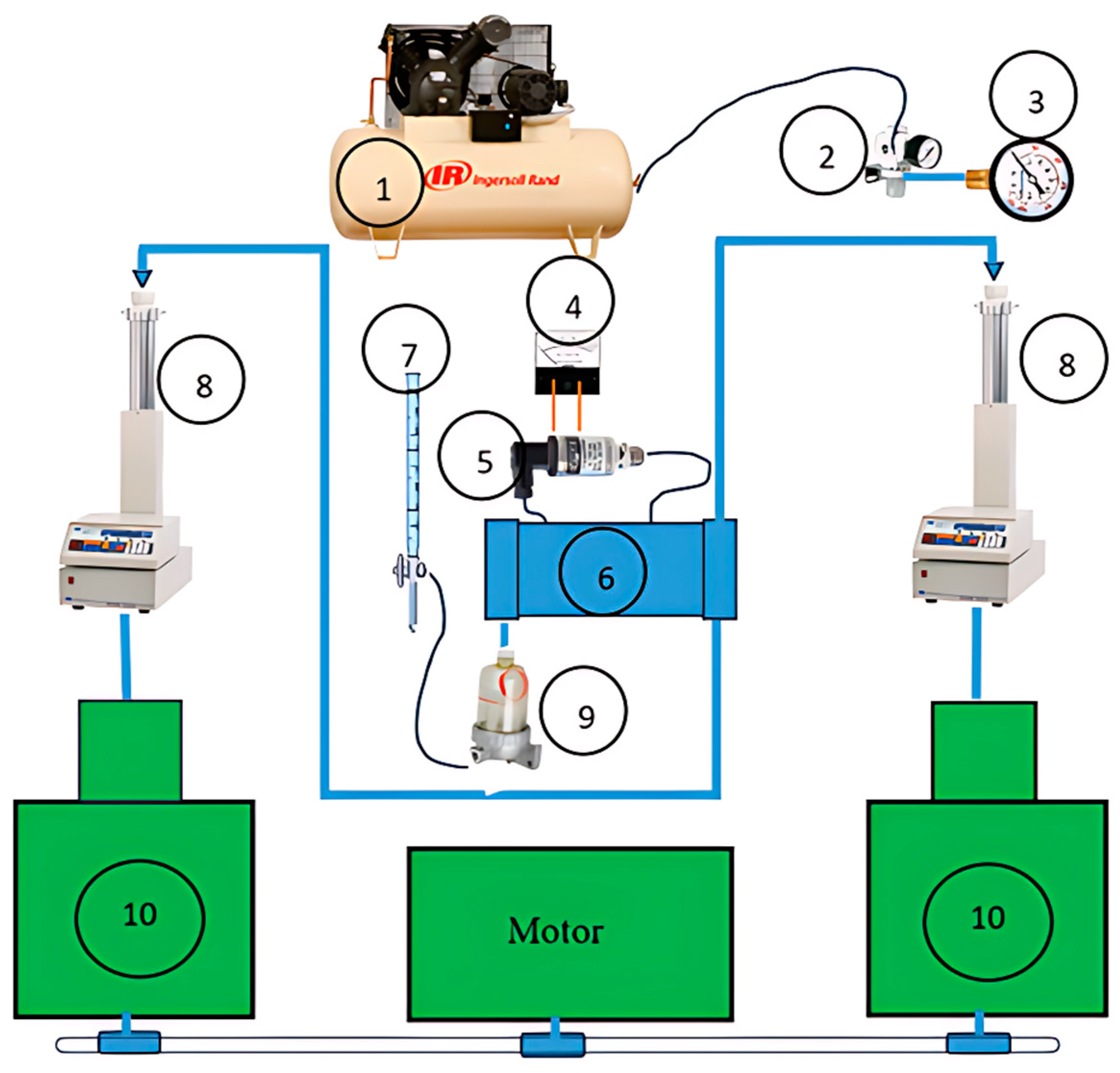
2.4. Description of the Reservoir and Numerical Model
3. Results
4. Discussion
5. Conclusions
- The proposed NLPM predicted relative permeability with the highest accuracy compared to existing relative permeability models with significantly lower RMSE values of 0.028 and 0.010 for krw and kro, respectively. The Purcell model cannot predict kro due to its assumption that krw + kro = 1. However, the Corey kro model and the Purcell krw model can be utilized together to reliably predict relative permeability since they are the models that most closely match experimental data.
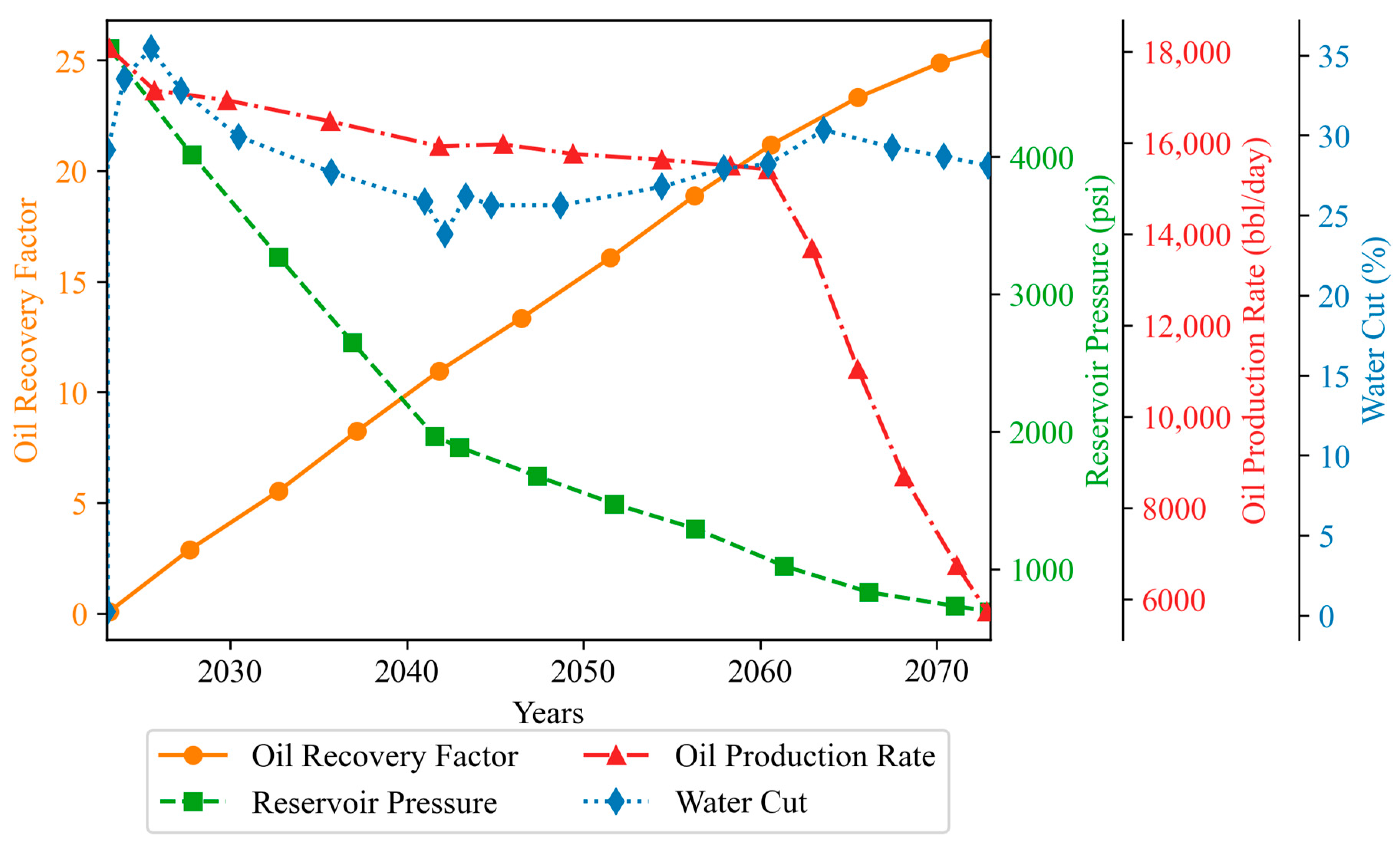
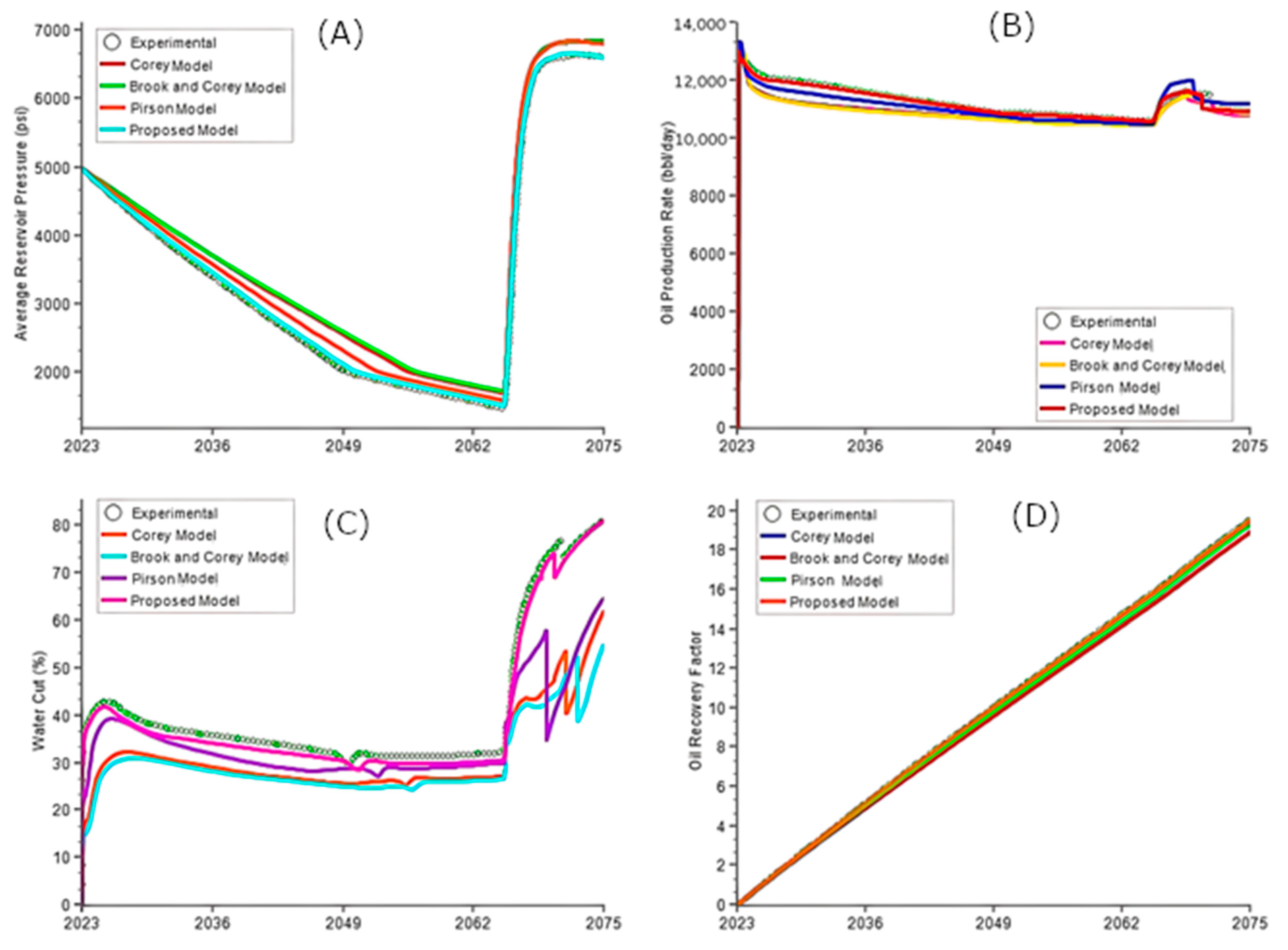
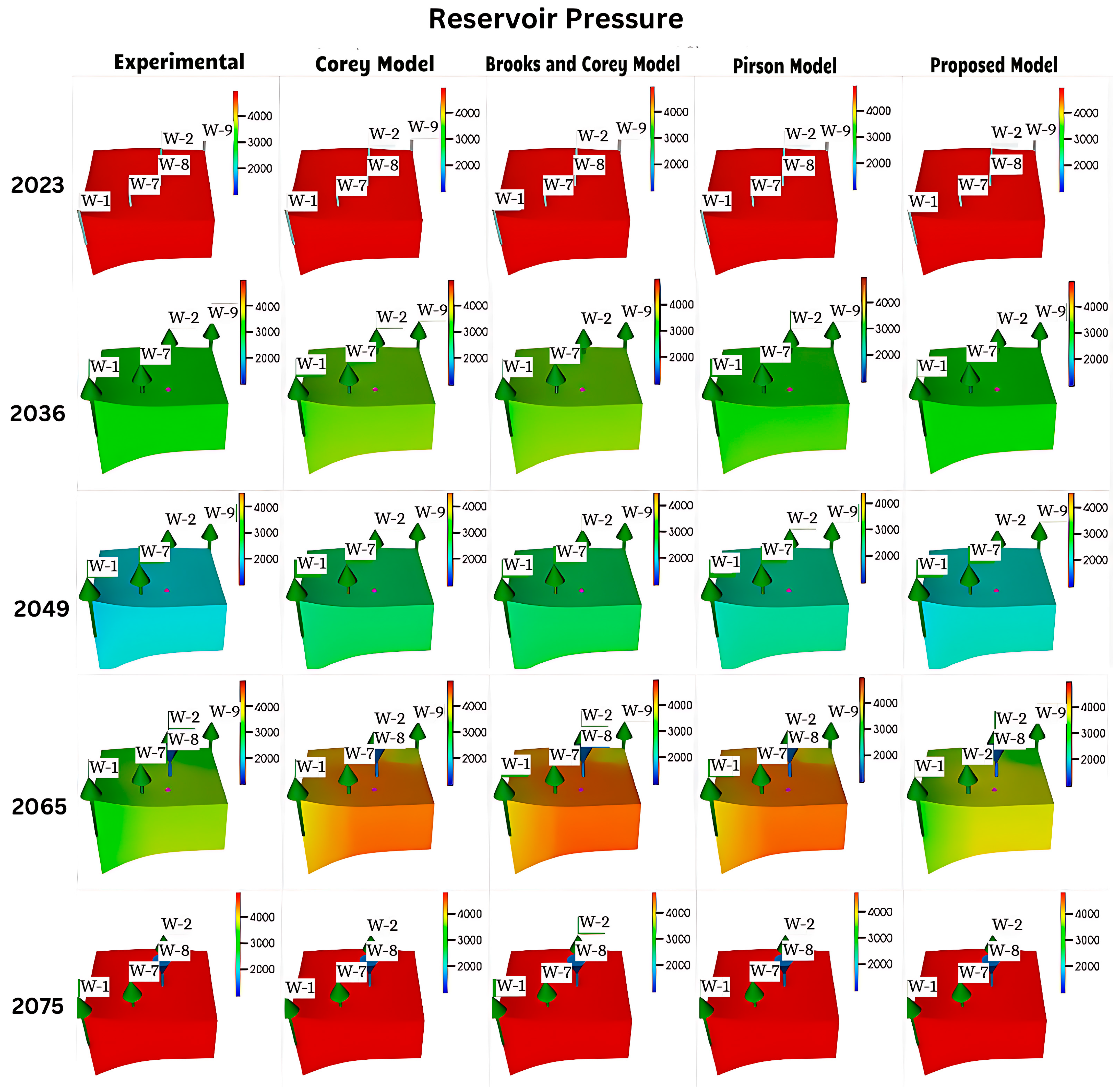
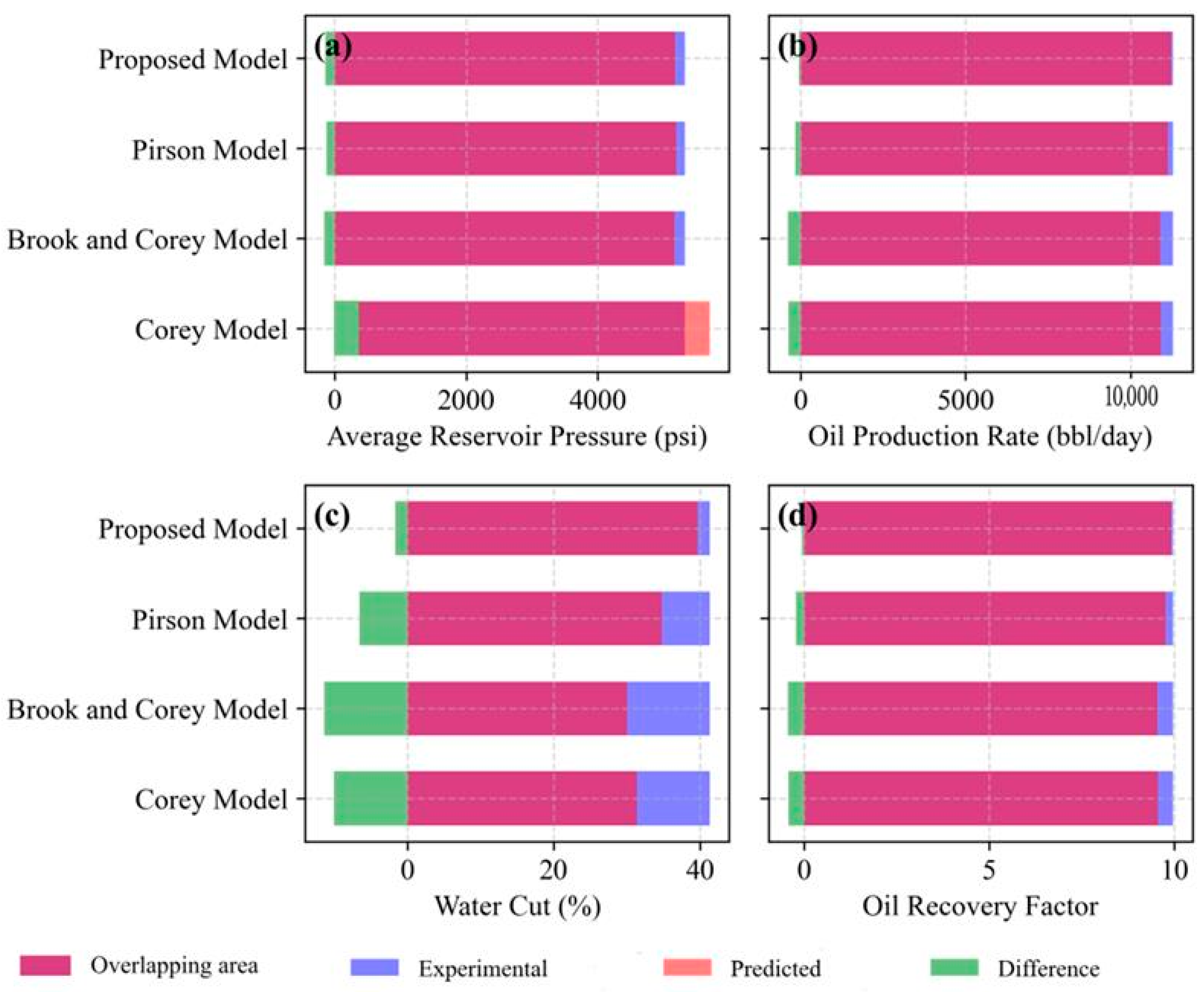
- The pre-injection Corey and Brooks and Corey models overestimated average reservoir pressures, while the Pirson model was comparatively closer to experimental data. Due to water injection, pressures surged from 1500 psi to 6800 psi between the years 2065 and 2068. The proposed NLPM’s results were closest to the experimental data in the reservoir pressure simulation.
- The oil production rate of the proposed NLPM followed almost the same trend as that of experimental data numerical simulation, except for the sudden increase in oil production rate after the water injection commenced, between the years 2065 to 2070. The Corey, and Brooks and Corey models achieved higher accuracy in predicting oil production rate after the water injection.
- Relative permeability models with higher water–oil mobility yield higher water cuts, indicating greater sensitivity to water production in simulations. These models become less effective post-water injection in predicting reservoir pressure and oil production rates. Before water injection, the Corey, and Brooks and Corey models displayed similar water cut trends, while the proposed model closely matched experimental results.
- Relative permeability models initially showed similar oil recovery factors up to the year 2032; divergences increased as the simulation progressed. The proposed model most closely matched the experimental data, followed by the Pirson, Corey, and Brooks and Corey models, in that order.
- The results confirm that it is essential to select the most appropriate relative permeability models based on the specific reservoir characteristics when constructing water-injection simulation models. The prediction accuracy of these models plays a crucial role in optimizing oil production and recovery processes. Hence, applying the proposed NLPM to the studied field would improve field development performance, decision-making and sustainability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Sw | krw | kro | Pc |
|---|---|---|---|
| 0.150 | 0 | 0.88 | 2.750 |
| 0.200 | 0.005 | 0.75 | 0.660 |
| 0.250 | 0.01 | 0.59 | 0.540 |
| 0.300 | 0.017 | 0.45 | 0.480 |
| 0.350 | 0.023 | 0.33 | 0.420 |
| 0.400 | 0.031 | 0.25 | 0.380 |
| 0.450 | 0.039 | 0.18 | 0.340 |
| 0.500 | 0.05 | 0.12 | 0.300 |
| 0.550 | 0.063 | 0.072 | 0.270 |
| 0.600 | 0.08 | 0.037 | 0.240 |
| 0.650 | 0.1 | 0.016 | 0.210 |
| 0.700 | 0.12 | 0.002 | 0.170 |
| 0.750 | 0.15 | 0.0001 | 0.120 |
| 0.800 | 0.19 | 0 | 0.050 |
References
- Krause, M.H.; Benson, S.M. Accurate determination of characteristic relative permeability curves. Adv. Water Resour. 2015, 83, 376–388. [Google Scholar] [CrossRef]
- Xu, J.; Guo, C.; Jiang, R.; Wei, M. Study on relative permeability characteristics affected by displacement pressure gradient: Experimental study and numerical simulation. Fuel 2016, 163, 314–323. [Google Scholar] [CrossRef]
- Zhou, Y.; Yin, D.; Cao, R.; Zhang, C. The mechanism for pore-throat scale emulsion displacing residual oil after water flooding. J. Pet. Sci. Eng. 2018, 163, 519–525. [Google Scholar] [CrossRef]
- Sakhaei, Z.; Azin, R.; Osfouri, S. Assessment of empirical/theoretical relative permeability correlations for gas-oil/condensate systems. In Proceedings of the 1st Biennial Persian Gulf Oil, Gas and Petrochemical Energy and Environment Conference, Bushehr, Iran, 20 April 2016. [Google Scholar]
- Sorop, T.G.; Masalmeh, S.K.; Suijkerbuijk, B.M.; van der Linde, H.A.; Mahani, H.; Brussee, N.J.; Marcelis, F.A.; Coorn, A. Relative permeability measurements to quantify the low salinity flooding effect at field scale. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2015; SPE: Richardson, TX, USA, 2015. [Google Scholar]
- Fan, H. Performance evaluation of waterflood reservoirs in high water cut period based on new relative permeability model. Petrol. Sci. Eng. 2020, 4, 64–69. [Google Scholar] [CrossRef]
- Loahardjo, N.; Xie, X.; Winoto, W.; Buckley, J.; Morrow, N.R. Oil recovery by sequential waterflooding: The effects of aging at residual oil and initial water saturation. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 14–18 April 2012; SPE: Richardson, TX, USA, 2012. [Google Scholar]
- Niu, Q.; Hu, M.; Chang, J.; Wang, W.; Yuan, W.; Wang, Q.; Zheng, Y.; Shang, S. Explosive fracturing mechanism in low-permeability sandstone-type uranium deposits considering different acidification reactions. Energy 2024, 312, 133676. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Yang, Y.; Wang, K.; Yao, J.; Zhang, K.; Sun, H.; Zhang, L.; Song, W.; Lisitsa, V. Effect of particle content on relative permeabilities in water flooding. J. Pet. Sci. Eng. 2021, 205, 108856. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, X.; Jin, Y.; Yan, K.; Li, Z.; Fu, H.; Li, S. Prediction model and real-time diagnostics of hydraulic fracturing pressure for highly deviated wells in deep oil and gas reservoirs. Sci. Rep. 2025, 15, 3559. [Google Scholar] [CrossRef]
- Purcell, W. Capillary pressures-their measurement using mercury and the calculation of permeability therefrom. J. Pet. Technol. 1949, 1, 39–48. [Google Scholar] [CrossRef]
- Burdine, N. Relative permeability calculations from pore size distribution data. J. Pet. Technol. 1953, 5, 71–78. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Properties of porous media affecting fluid flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar] [CrossRef]
- Mukherjee, S.; Johns, R.T. Relative Permeability Modeling for CO2 Storage Using Physically Constrained Artificial Neural Networks. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 22–25 April 2024; SPE: Richardson, TX, USA, 2024. [Google Scholar]
- Pirson, S.J. Oil Reservoir Engineering; McGraw Hill: New York, NY, USA, 1958. [Google Scholar]
- Li, K.; Shapiro, M.; Horne, R.N.; Ma, S.; Hajari, A.; Mudhhi, M. In situ estimation of relative permeability from resistivity measurements. Pet. Geosci. 2014, 20, 143–151. [Google Scholar] [CrossRef]
- Chai, X.; Tian, L.; Wang, J.; Chen, S.; Mo, S.; Zhang, K. A novel prediction model of oil-water relative permeability based on fractal theory in porous media. Fuel 2024, 372, 131840. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, X.; Wang, B.; Ren, X. Two-phase relative permeability of hydrate-bearing sediments: A theoretical model. Energy 2023, 275, 127441. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, X.; Luo, L.; Tian, Y.; Zeng, S. Seepage Characteristics of Broken Carbonaceous Shale under Cyclic Loading and Unloading Conditions. Energy Fuels 2024, 38, 1192–1203. [Google Scholar] [CrossRef]
- Dong, Z.; Tian, S.; Xue, H.; Lu, S.; Liu, B.; Erastova, V.; Wu, M.; Wu, R. Analysis of Pore Types in Lower Cretaceous Qingshankou Shale Influenced by Electric Heating. Energy Fuels 2024, 38, 20577–20590. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, C.; Liu, S. Characteristic analysis and fractal model of the gas-water relative permeability of coal under different confining pressures. J. Pet. Sci. Eng. 2017, 159, 488–496. [Google Scholar] [CrossRef]
- Gan, B.; Li, Z.; Huo, W.; Zhang, Y.; Li, Z.; Fan, R.; Zhang, H.; Xu, Y.; He, Y. Phase transitions of CH4 hydrates in mud-bearing sediments with oceanic laminar distribution: Mechanical response and stabilization-type evolution. Fuel 2025, 380, 133185. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, G.; Qu, B.; Gong, C. Characterization of a fly ash-based hybrid well cement under different temperature curing conditions for natural gas hydrate drilling. Constr. Build. Mater. 2024, 445, 137874. [Google Scholar] [CrossRef]
- Druetta, P.; Tesi, P.; De Persis, C.; Picchioni, F. Methods in oil recovery processes and reservoir simulation. Adv. Chem. Eng. Sci. 2016, 6, 399–435. [Google Scholar] [CrossRef]
- Cao, R.; Jia, Z.; Cheng, L.; Wang, Z.; Ye, T.; Rui, Z. Using high-intensity water flooding relative permeability curve for predicting mature oilfield performance after long-term water flooding in order to realize sustainable development. J. Pet. Sci. Eng. 2022, 215, 110629. [Google Scholar] [CrossRef]
- Zhou, Z.; Jia, H.; Zhang, R.; Ding, B.; Geng, X. Three dimensional time-variation simulator for water flooding reservoir based on “effective water flux”. Phys. Fluids 2024, 36, 103101. [Google Scholar] [CrossRef]
- Al-Fattah, S.M. Empirical equations for water/oil relative permeability in Saudi sandstone reservoirs. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Abuja, Nigeria, 4–6 August 2003; SPE: Richardson, TX, USA, 2003. [Google Scholar]
- Li, K.; Horne, R.N. Numerical simulation without using experimental data of relative permeability. J. Pet. Sci. Eng. 2008, 61, 67–74. [Google Scholar] [CrossRef]
- Corey, A.T. The interrelation between gas and oil relative permeabilities. Prod. Mon. 1954, 19, 38–41. [Google Scholar]
- Al-Mossawy, M.I. A simple approach to identify the proper relative permeability model. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019. [Google Scholar]
- Zahoor, M.K. In-house developed Kr estimator: Implemented to analyze the sensitivity of relative permeability data to variations in wetting phase saturation. Energy Explor. Exploit. 2011, 29, 817–825. [Google Scholar] [CrossRef]
- Waqas, U.; Ahmed, M.F. Prediction modeling for the estimation of dynamic elastic Young’s modulus of thermally treated sedimentary rocks using linear–nonlinear regression analysis, regularization, and ANFIS. Rock Mech. Rock Eng. 2020, 53, 5411–5428. [Google Scholar] [CrossRef]
- Seber, G.; Wild, C. NonLinear Regression; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Cheng, H.; Wang, F.; Yang, G.; Guan, X.; Cheng, Z.; Li, H.; Yu, C.; Feng, G.; Yuan, Y. Prediction of relative permeability from capillary pressure based on the fractal capillary bundle model. Appl. Therm. Eng. 2024, 239, 122093. [Google Scholar] [CrossRef]
- Ismail, A.; Torabi, F.; Azadbakht, S.; Yasin, Q. Identification of natural fractures in shale gas reservoirs using fracture signature function and machine learning models. Unconv. Resour. 2024, 4, 100069. [Google Scholar] [CrossRef]
- Ismail, A.; Azadbakht, S.; Rashid, H.M.A.; Yasin, Q.; Liu, B.; Ijaz, W. Statistical and machine learning hybridization for predicting shear wave velocity in tight sand reservoirs: A case study. Geoenergy Sci. Eng. 2023, 231, 212420. [Google Scholar] [CrossRef]
- Qin, X.; Cai, J.; Wang, G. Pore-scale modeling of pore structure properties and wettability effect on permeability of low-rank coal. Int. J. Min. Sci. Technol. 2023, 33, 573–584. [Google Scholar] [CrossRef]
- Taghavi, B.; Hajizadeh, F.; Moomivand, H. Comparison of artificial intelligence and multivariate regression methods in predicting the uniaxial compressive strength of rock during the specific resistivity monitoring. Bull. Eng. Geol. Environ. 2023, 82, 409. [Google Scholar] [CrossRef]
- Alizadeh, S.M.; Iraji, A.; Tabasi, S.; Ahmed, A.A.A.; Motahari, M.R. Estimation of dynamic properties of sandstones based on index properties using artificial neural network and multivariate linear regression methods. Acta Geophys. 2022, 70, 225–242. [Google Scholar] [CrossRef]
- Du, Q.; Yasin, Q.; Ismail, A.; Sohail, G.M. Combining classification and regression for improving shear wave velocity estimation from well logs data. J. Pet. Sci. Eng. 2019, 182, 106260. [Google Scholar] [CrossRef]
- Ismail, A.; Yasin, Q.; Du, Q.; Bhatti, A.A. A comparative study of empirical, statistical and virtual analysis for the estimation of pore network permeability. J. Nat. Gas Sci. Eng. 2017, 45, 825–839. [Google Scholar] [CrossRef]
- Zhou, Y.; Guan, W.; Sun, Q.; Zou, X.; He, Z. Effect of multi-scale rough surfaces on oil-phase trapping in fractures: Pore-scale modeling accelerated by wavelet decomposition. Comput. Geotech. 2025, 179, 106951. [Google Scholar] [CrossRef]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 2022, 5481–5487. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Bhatti, A.A.; Ismail, A.; Raza, A.; Gholami, R.; Rezaee, R.; Nagarajan, R.; Saffou, E. Permeability prediction using hydraulic flow units and electrofacies analysis. Energy Geosci. 2020, 1, 81–91. [Google Scholar] [CrossRef]
- Ismail, A.; Yasin, Q.; Du, Q. Application of hydraulic flow unit for pore size distribution analysis in highly heterogeneous sandstone reservoir: A case study. J. Jpn. Pet. Inst. 2018, 61, 246–255. [Google Scholar] [CrossRef]
- Dar, Q.U.Z.; Renhai, P.; Ghazi, S.; Ahmed, S.; Ali, R.I.; Mehmood, M. Depositional facies and reservoir characteristics of the Early Cretaceous Lower Goru Formation, Lower Indus Basin Pakistan: Integration of petrographic and gamma-ray log analysis. Petroleum 2023, 9, 331–341. [Google Scholar] [CrossRef]
- Munir, K.; Iqbal, M.A.; Farid, A.; Shabih, S.M. Mapping the productive sands of Lower Goru Formation by using seismic stratigraphy and rock physical studies in Sawan area, southern Pakistan: A case study. J. Pet. Explor. Prod. Technol. 2011, 1, 33–42. [Google Scholar] [CrossRef]
- Yasin, Q.; Du, Q.; Ismail, A.; Shaikh, A. A new integrated workflow for improving permeability estimation in a highly heterogeneous reservoir of Sawan Gas Field from well logs data. Geomech. Geophys. Geo-Energy Geo-Resour. 2019, 5, 121–142. [Google Scholar] [CrossRef]
- Berger, A.; Gier, S.; Krois, P. Porosity-preserving chlorite cements in shallow-marine volcaniclastic sandstones: Evidence from Cretaceous sandstones of the Sawan gas field, Pakistan. AAPG Bull. 2009, 93, 595–615. [Google Scholar] [CrossRef]
- Li, Z.; Huang, X.; Xu, X.; Bai, Y.; Zou, C. Unstable Coalescence Mechanism and Influencing Factors of Heterogeneous Oil Droplets. Molecules 2024, 29, 1582. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Chen, L.; Xu, X.; Tang, G.; Hu, Y.; Guo, B.; Liu, M.; Yuan, C.; Li, G. Coupling model of wellbore heat transfer and cuttings bed height during horizontal well drilling. Phys. Fluids 2024, 36, 097163. [Google Scholar] [CrossRef]
- Niu, Q.; Wang, J.; He, J.; Yuan, W.; Chang, J.; Wang, W.; Yuan, J.; Wang, Q.; Zheng, Y.; Shang, S. Evolution of pore structure, fracture morphology and permeability during CO2+O2 in-situ leaching process of fractured sandstone. Energy 2025, 315, 134348. [Google Scholar] [CrossRef]
- Morris, R.; Biggs, W. Using log-derived values of water saturation and porosity. In Proceedings of the SPWLA Annual Logging Symposium, Denver, CO, USA, 12–14 June 1967; SPWLA: Houston, TX, USA, 1967. [Google Scholar]
- Ismail, A.; Raza, A.; Gholami, R.; Rezaee, R. Reservoir characterization for sweet spot detection using color transformation overlay scheme. J. Pet. Explor. Prod. Technol. 2020, 10, 2313–2334. [Google Scholar] [CrossRef]
- Li, K.; Home, R. Calculation of steam-water relative permeability using capillary pressure data. In Proceedings of the 27th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 28–30 January 2002; Citeseer: University Park, PA, USA, 2025. [Google Scholar]
- Purswani, P.; Johns, R.T.; Karpyn, Z.T.; Blunt, M. Predictive modeling of relative permeability using a generalized equation of state. SPE J. 2021, 26, 191–205. [Google Scholar] [CrossRef]
- Wang, F.; Jiao, L.; Zhao, J.; Cai, J. A more generalized model for relative permeability prediction in unsaturated fractal porous media. J. Nat. Gas Sci. Eng. 2019, 67, 82–92. [Google Scholar] [CrossRef]
- Avdeef, A. Do you know your r2? ADMET DMPK 2021, 9, 69–74. [Google Scholar] [CrossRef]
- Meng, W.; Zhang, Y.; Pei, H.; Yu, J.; Hu, Y.; Gu, Z.; Su, J. Pore-scale investigation on the effect of capillary barrier on two-phase displacement in dual-structure porous media. Phys. Fluids 2024, 36, 012003. [Google Scholar] [CrossRef]
- Ogbeiwi, P.; Aladeitan, Y.; Udebhulu, D. An approach to waterflood optimization: Case study of the reservoir X. J. Pet. Explor. Prod. Technol. 2018, 8, 271–289. [Google Scholar] [CrossRef]
- Deng, R.; Dong, J.; Dang, L. Numerical simulation and evaluation of residual oil saturation in waterflooded reservoirs. Fuel 2025, 384, 134018. [Google Scholar] [CrossRef]
- Moodie, N.; Ampomah, W.; Jia, W.; McPherson, B. Relative permeability: A critical parameter in numerical simulations of multiphase flow in porous media. Energies 2021, 14, 2370. [Google Scholar] [CrossRef]
- Li, Y.; Jia, D.; Wang, S.; Qu, R.; Qiao, M.; Liu, H. Surrogate model for reservoir performance prediction with time-varying well control based on depth generative network. Pet. Explor. Dev. 2024, 51, 1287–1300. [Google Scholar] [CrossRef]
- Alpak, F.O.; Lake, L.W.; Embid, S.M. Validation of a modified Carman-Kozeny equation to model two-phase relative permeabilities. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999; SPE: Richardson, TX, USA, 1999. [Google Scholar]

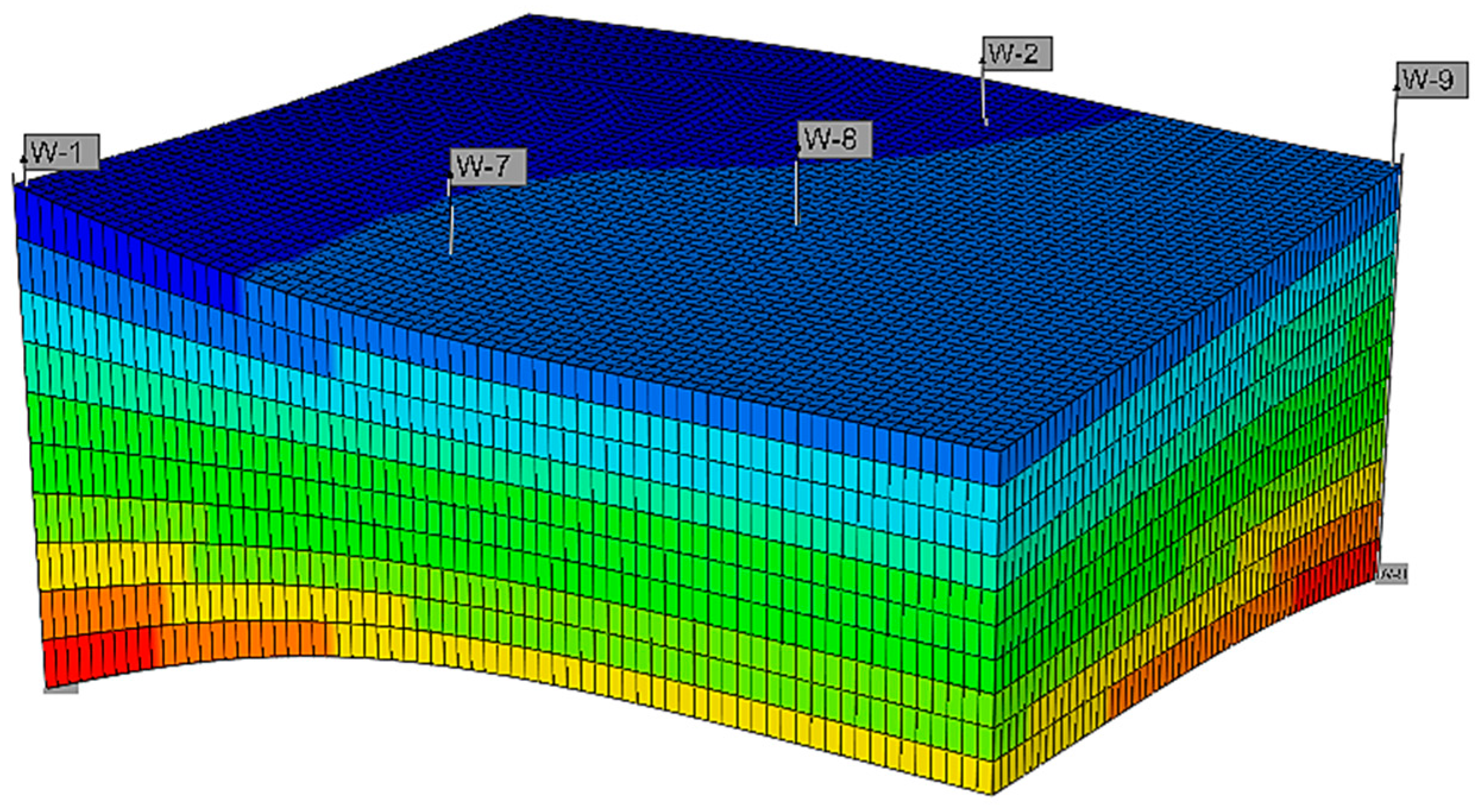



| Base Parameters in All Cases | |
|---|---|
| Porosity | 0.06–0.22 |
| Permeability (i, j = i, k = i × 0.1) | Geostatistical model |
| Thickness of reservoir | 456 ft |
| Grid size | 70 × 60 × 10 = 42,000 |
| No of layers | 10 |
| Grid thickness | 26–46 ft |
| Reservoir pressure | 5000 psi |
| Water oil contact | 10,935 ft |
| Lithology | Sandstone |
| Perforation length | 30–45 ft |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, A.; Torabi, F.; Azadbakht, S.; Ahammad, F.; Yasin, Q.; Wood, D.A.; Mohammadian, E. Sustainable Reservoir Management: Simulating Water Flooding to Optimize Oil Recovery in Heterogeneous Reservoirs Through the Evaluation of Relative Permeability Models. Sustainability 2025, 17, 2526. https://doi.org/10.3390/su17062526
Ismail A, Torabi F, Azadbakht S, Ahammad F, Yasin Q, Wood DA, Mohammadian E. Sustainable Reservoir Management: Simulating Water Flooding to Optimize Oil Recovery in Heterogeneous Reservoirs Through the Evaluation of Relative Permeability Models. Sustainability. 2025; 17(6):2526. https://doi.org/10.3390/su17062526
Chicago/Turabian StyleIsmail, Atif, Farshid Torabi, Saman Azadbakht, Faysal Ahammad, Qamar Yasin, David A. Wood, and Erfan Mohammadian. 2025. "Sustainable Reservoir Management: Simulating Water Flooding to Optimize Oil Recovery in Heterogeneous Reservoirs Through the Evaluation of Relative Permeability Models" Sustainability 17, no. 6: 2526. https://doi.org/10.3390/su17062526
APA StyleIsmail, A., Torabi, F., Azadbakht, S., Ahammad, F., Yasin, Q., Wood, D. A., & Mohammadian, E. (2025). Sustainable Reservoir Management: Simulating Water Flooding to Optimize Oil Recovery in Heterogeneous Reservoirs Through the Evaluation of Relative Permeability Models. Sustainability, 17(6), 2526. https://doi.org/10.3390/su17062526






