An Analysis of Wireless Power Transfer with a Hybrid Energy Storage System and Its Sustainable Optimization
Abstract
1. Introduction
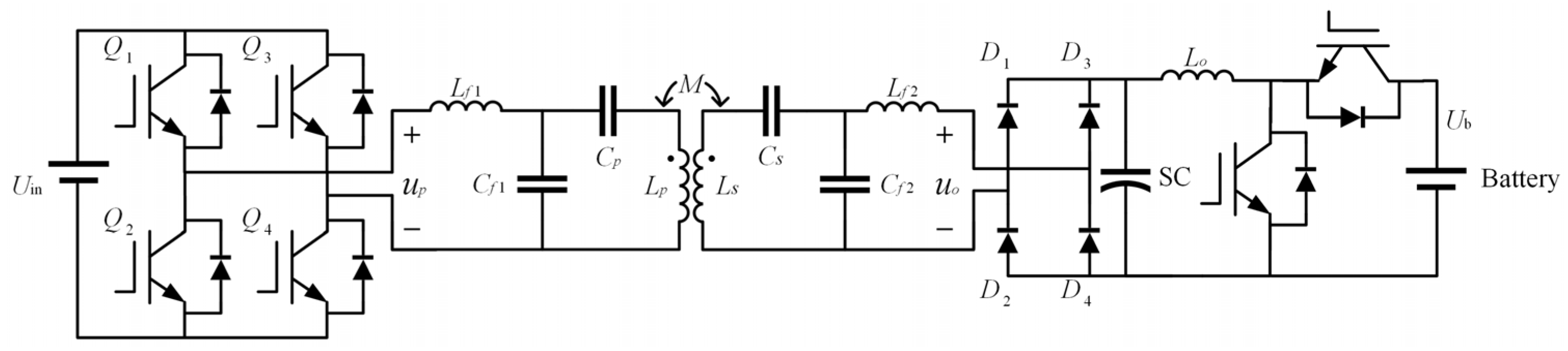
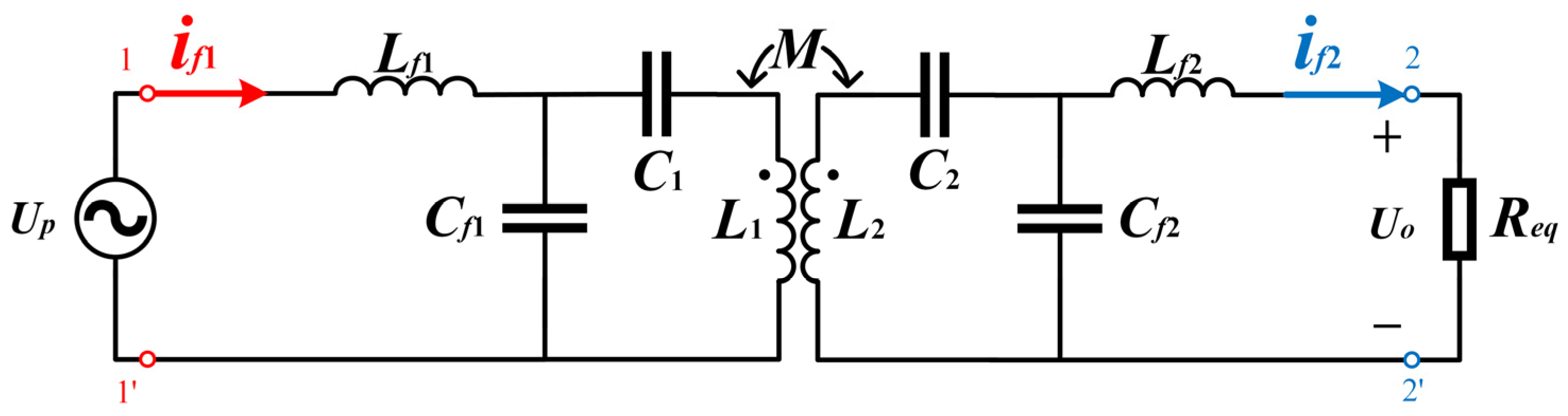
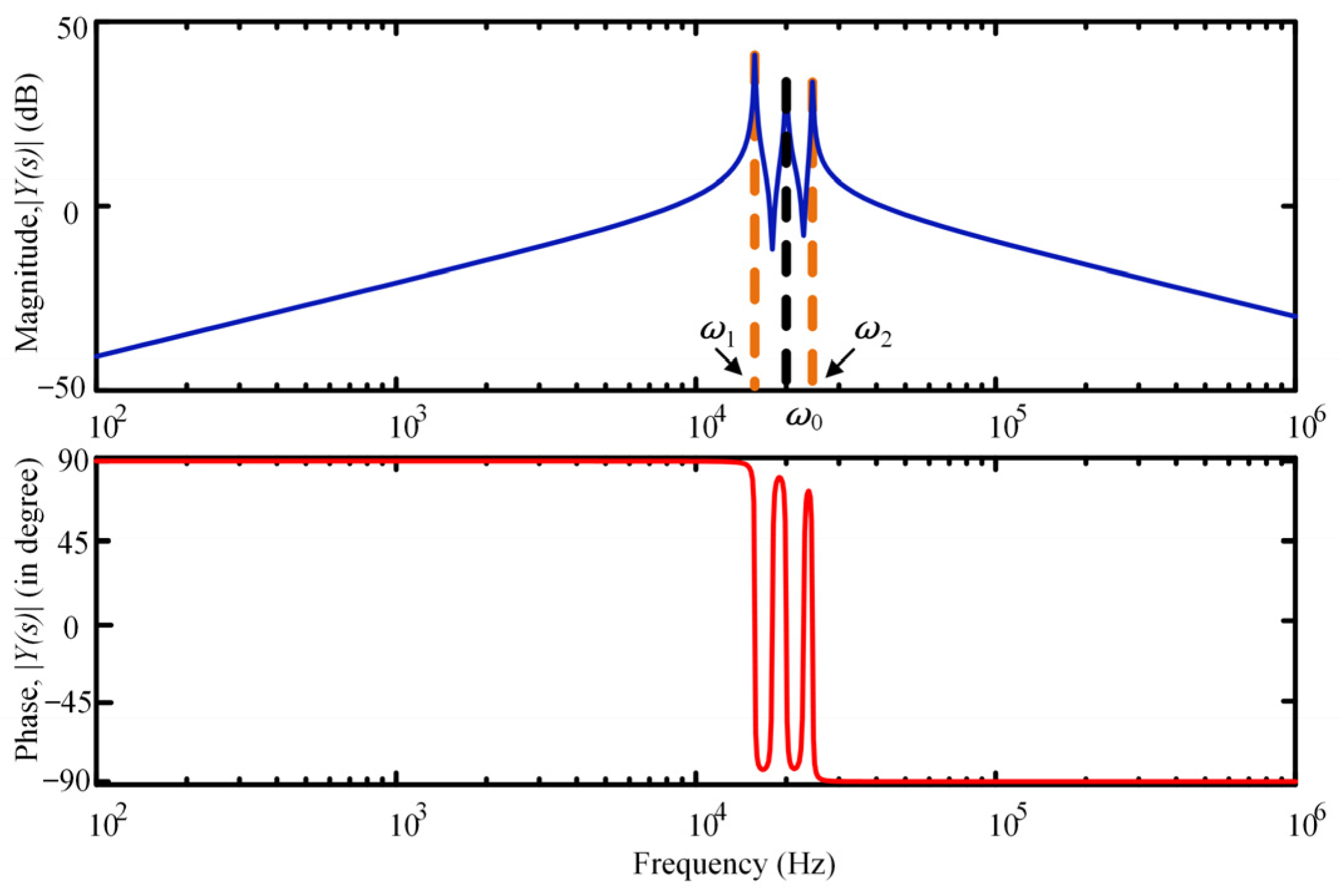
2. Working Principle of the Wireless Power Transfer System
3. Analysis of the DC Converter
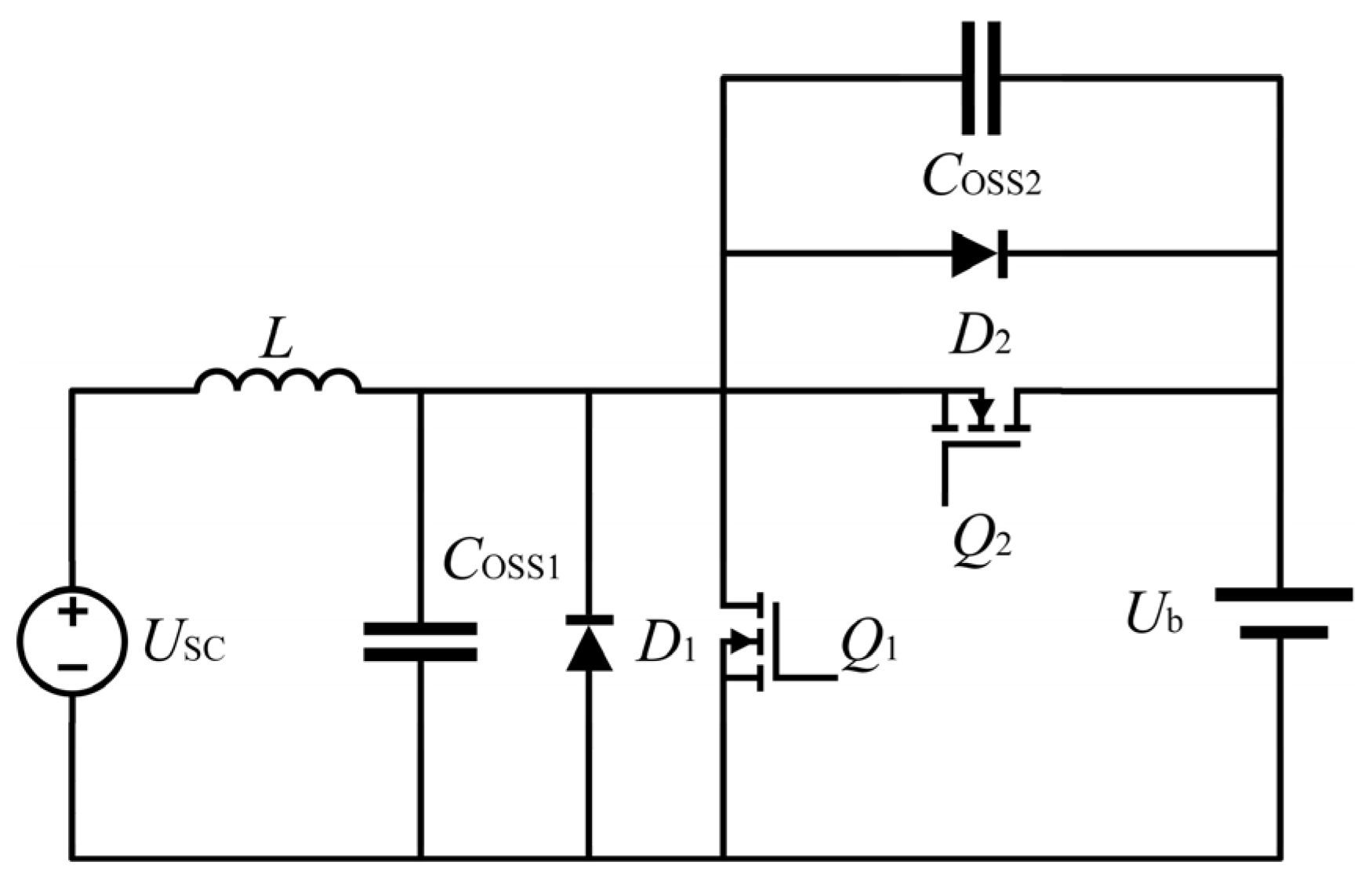
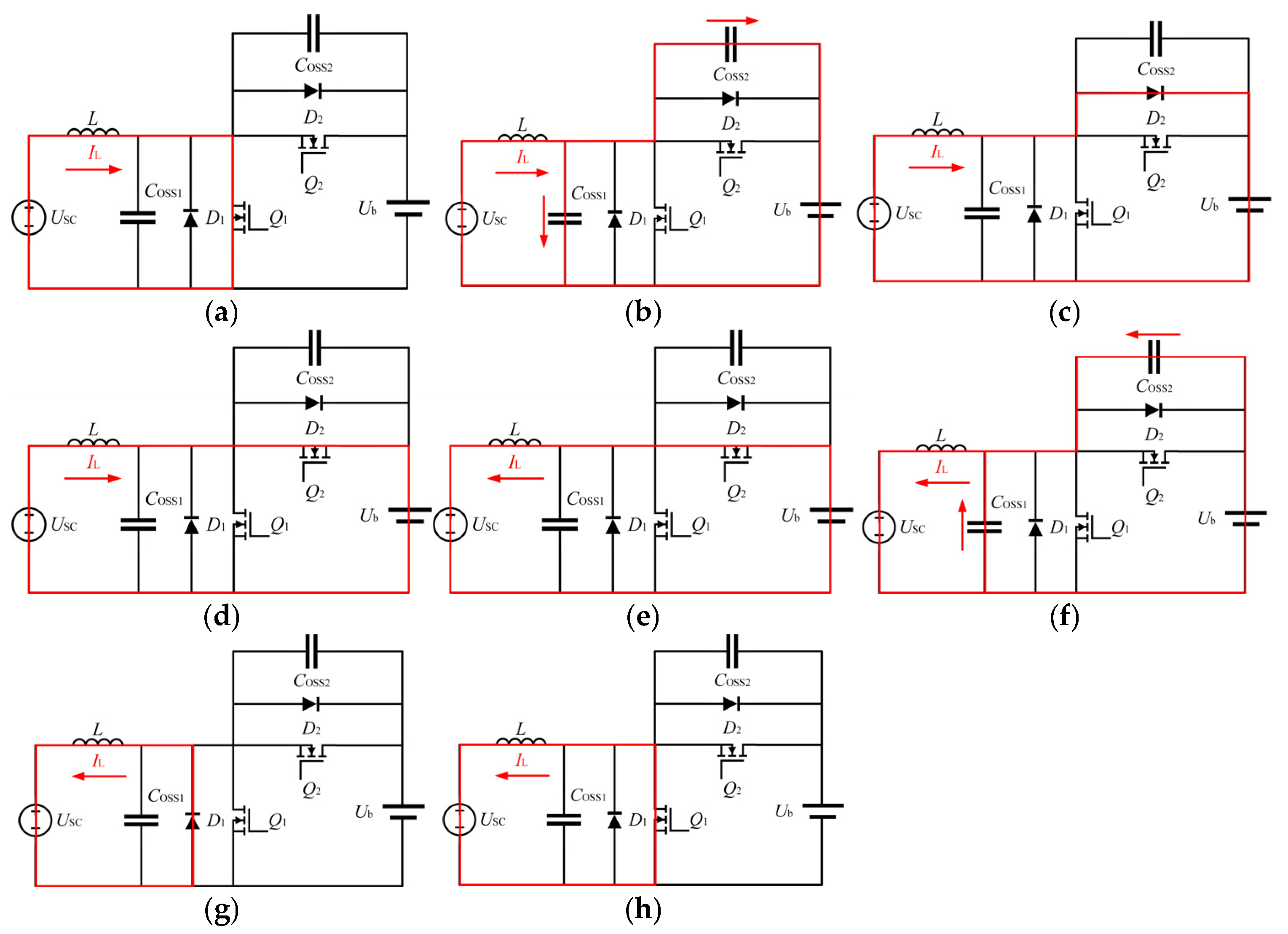
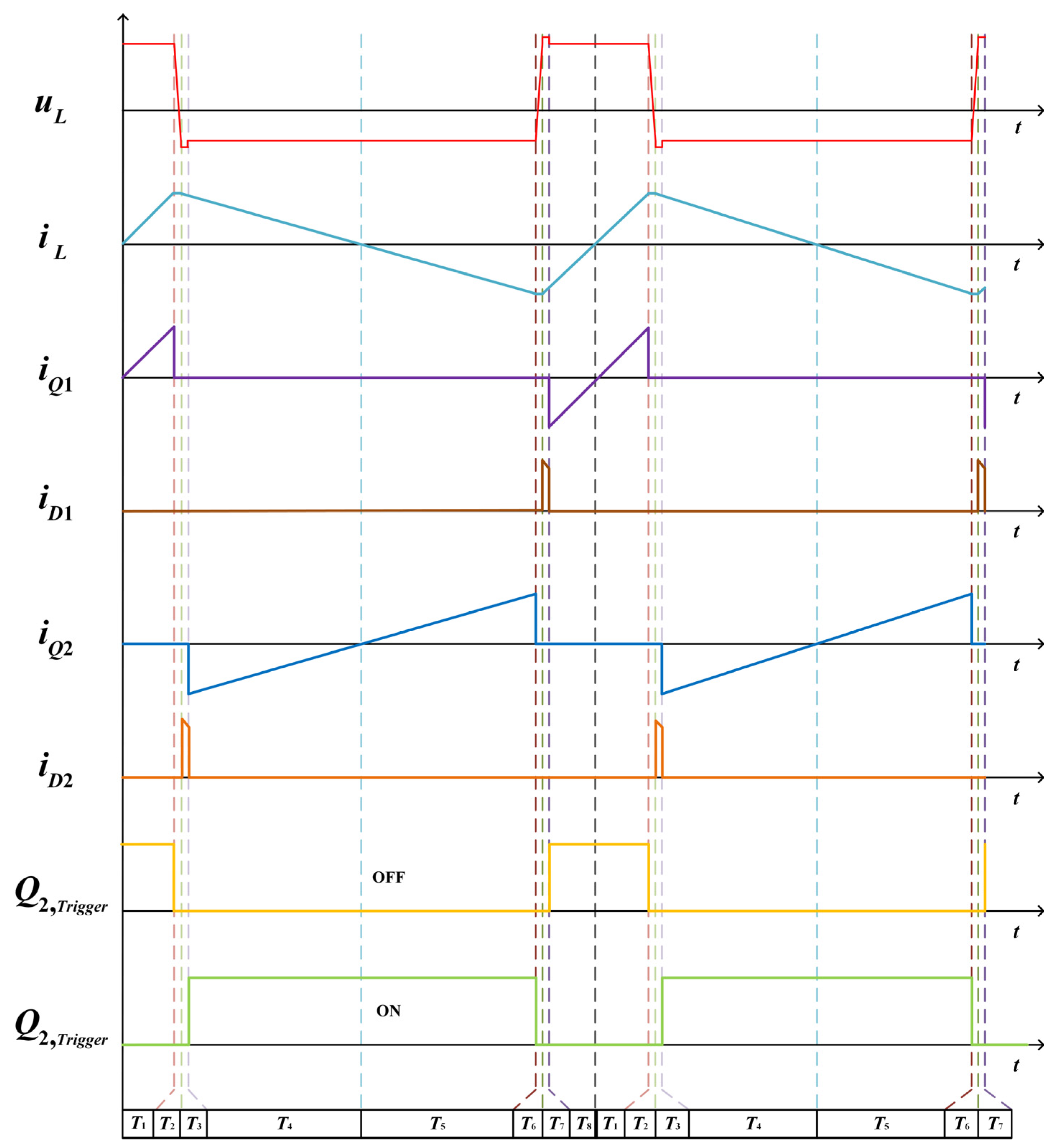
3.1. Operation of the DC Converter
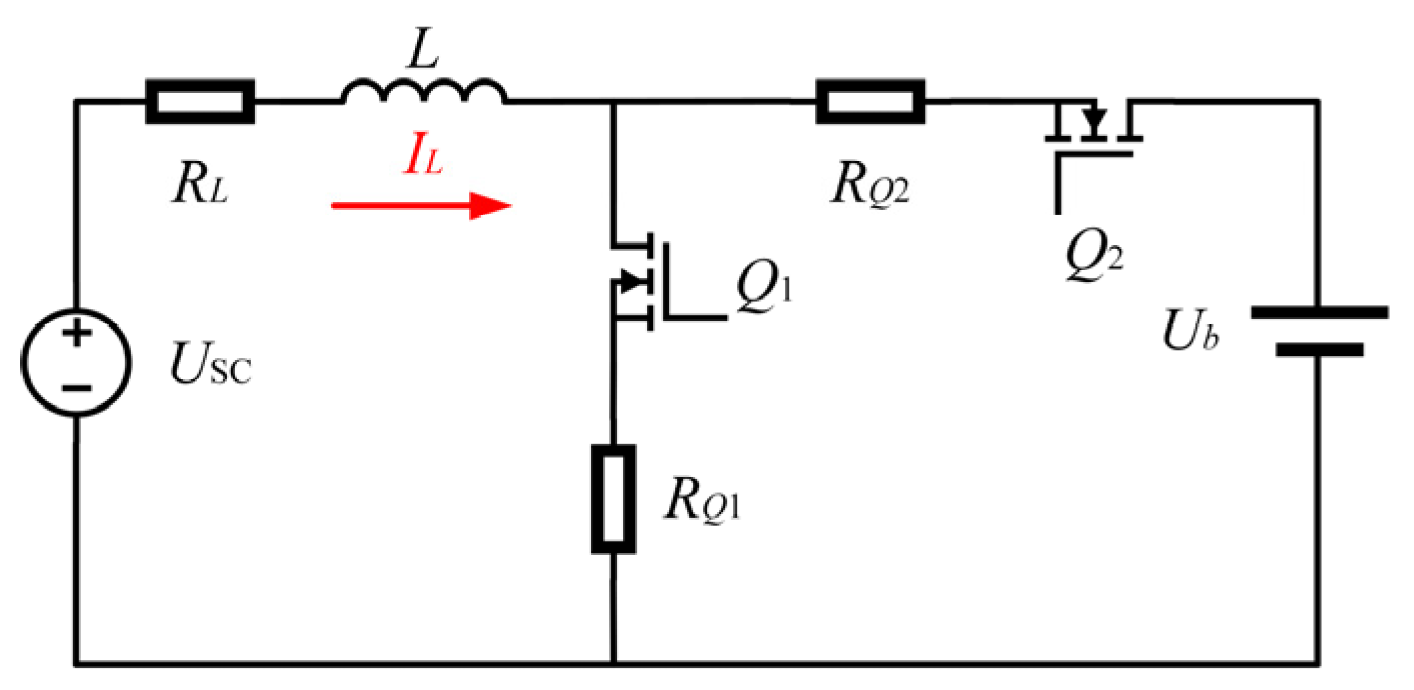
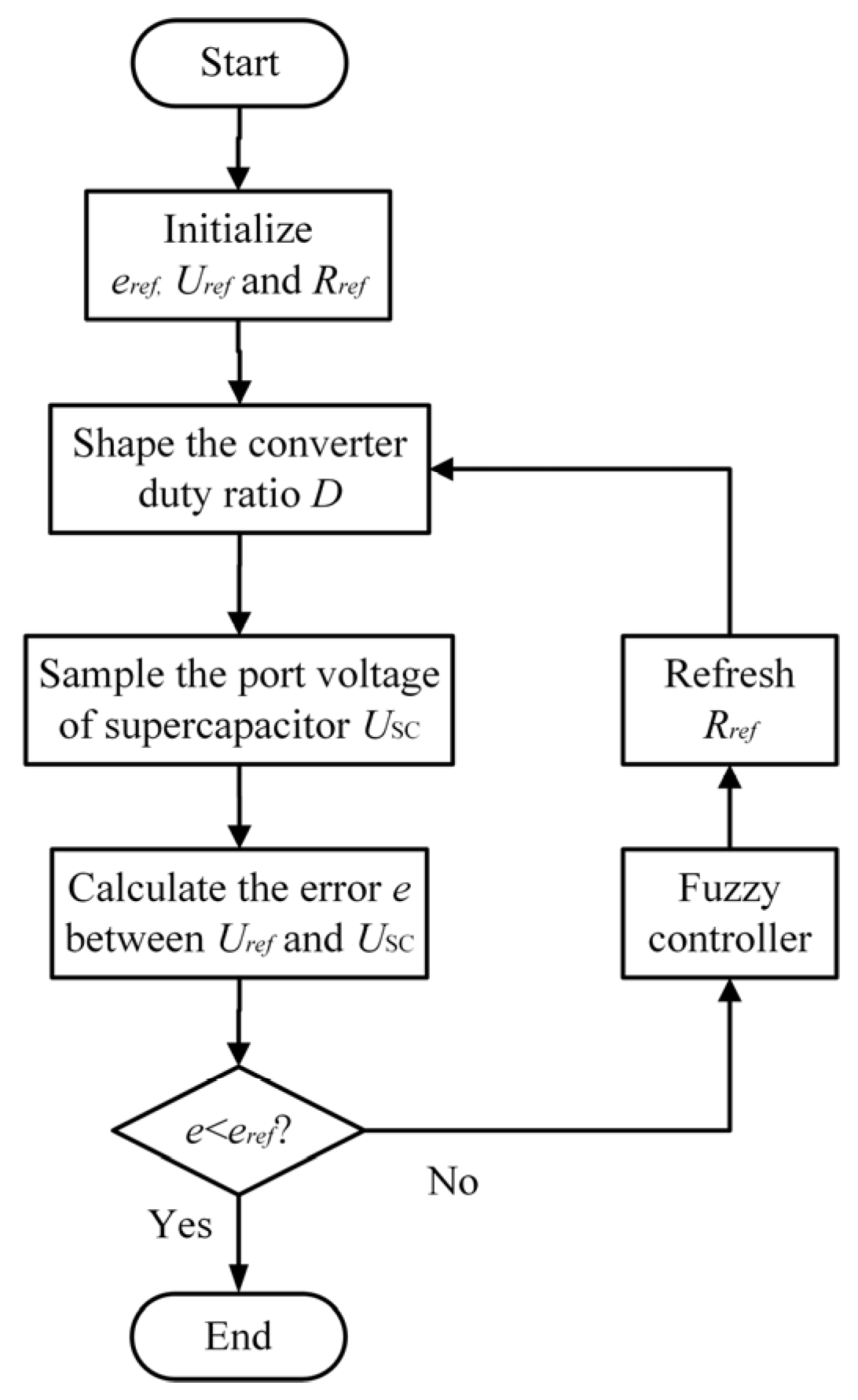
3.2. Circuit Analysis and Controller
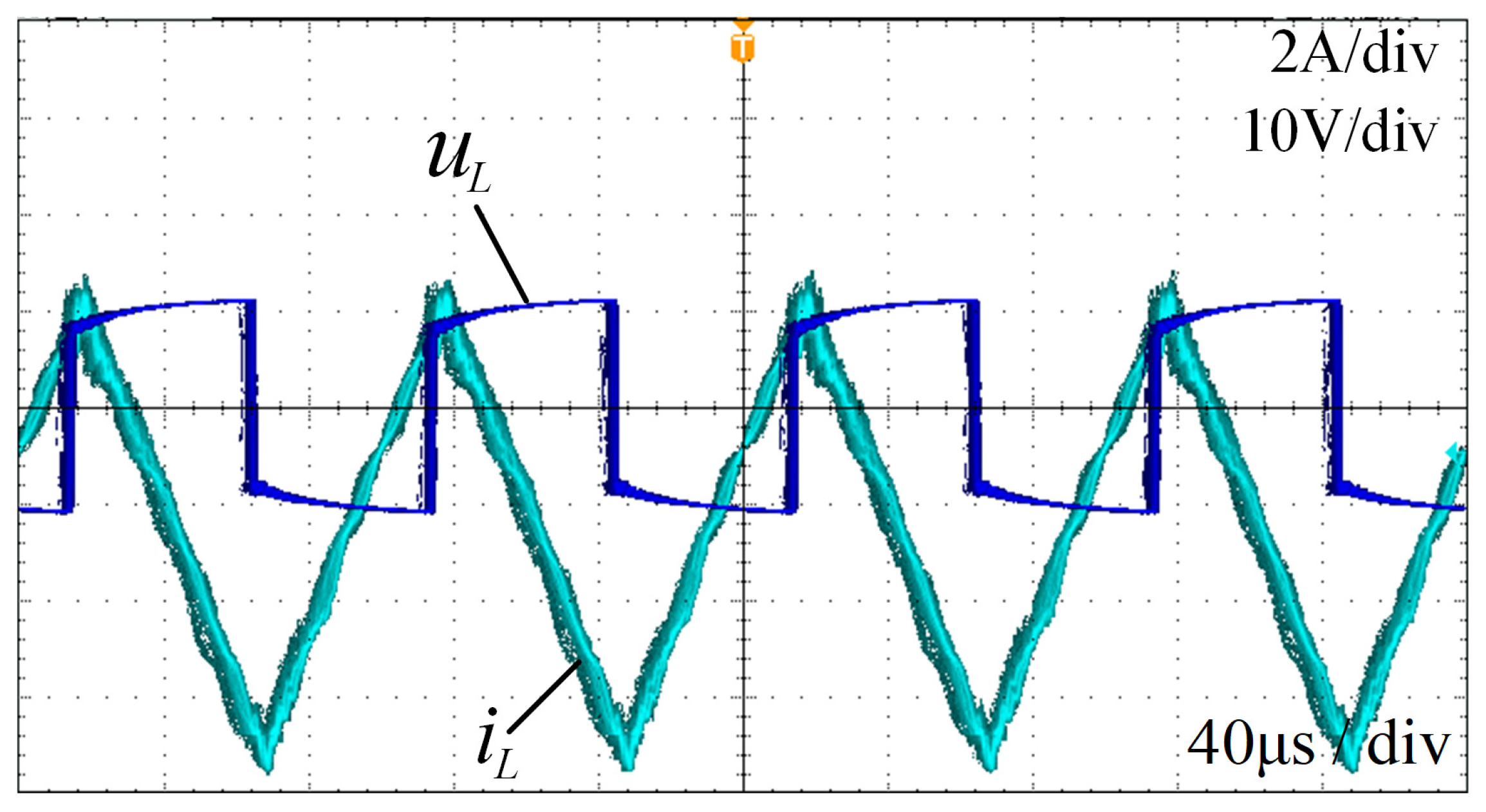
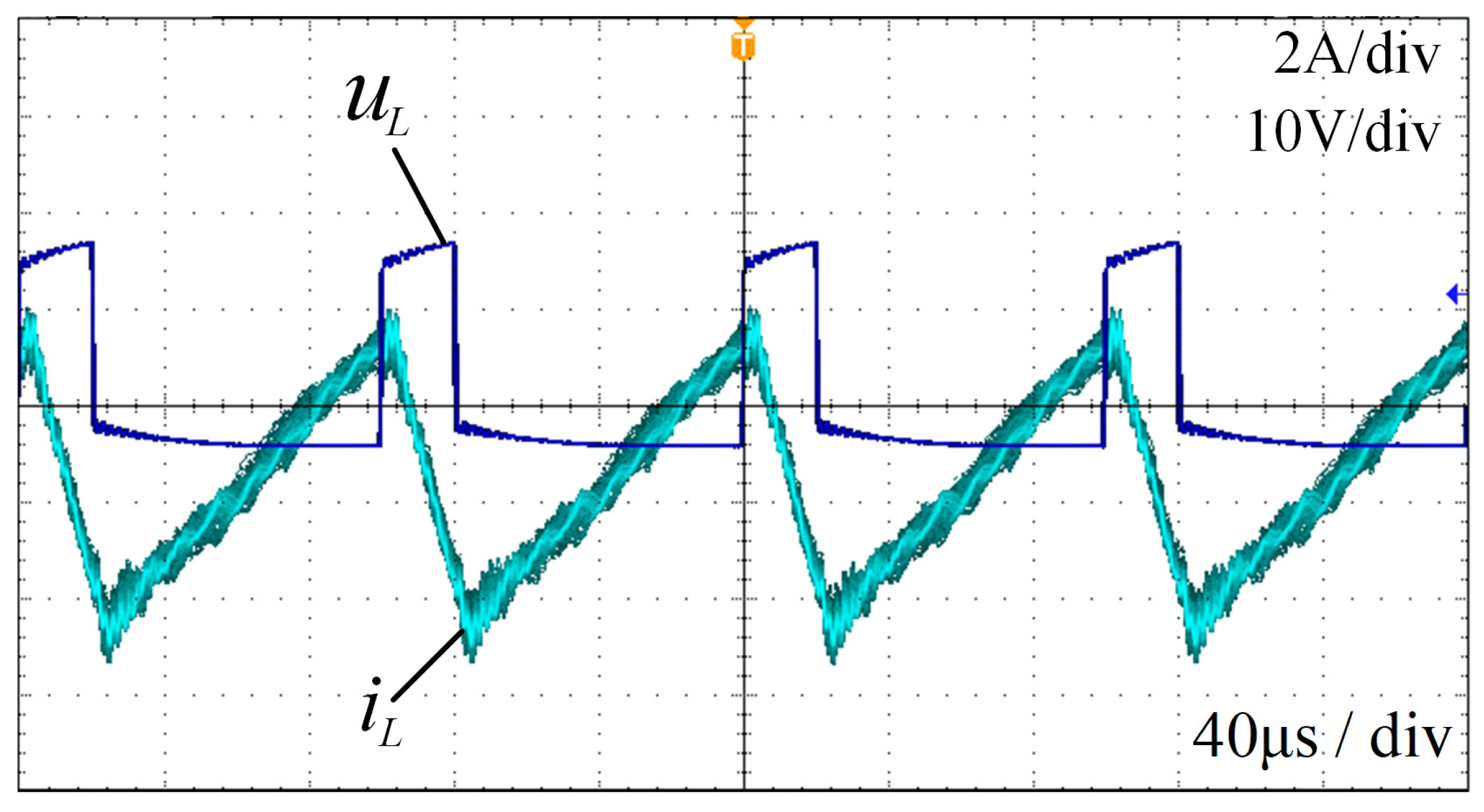
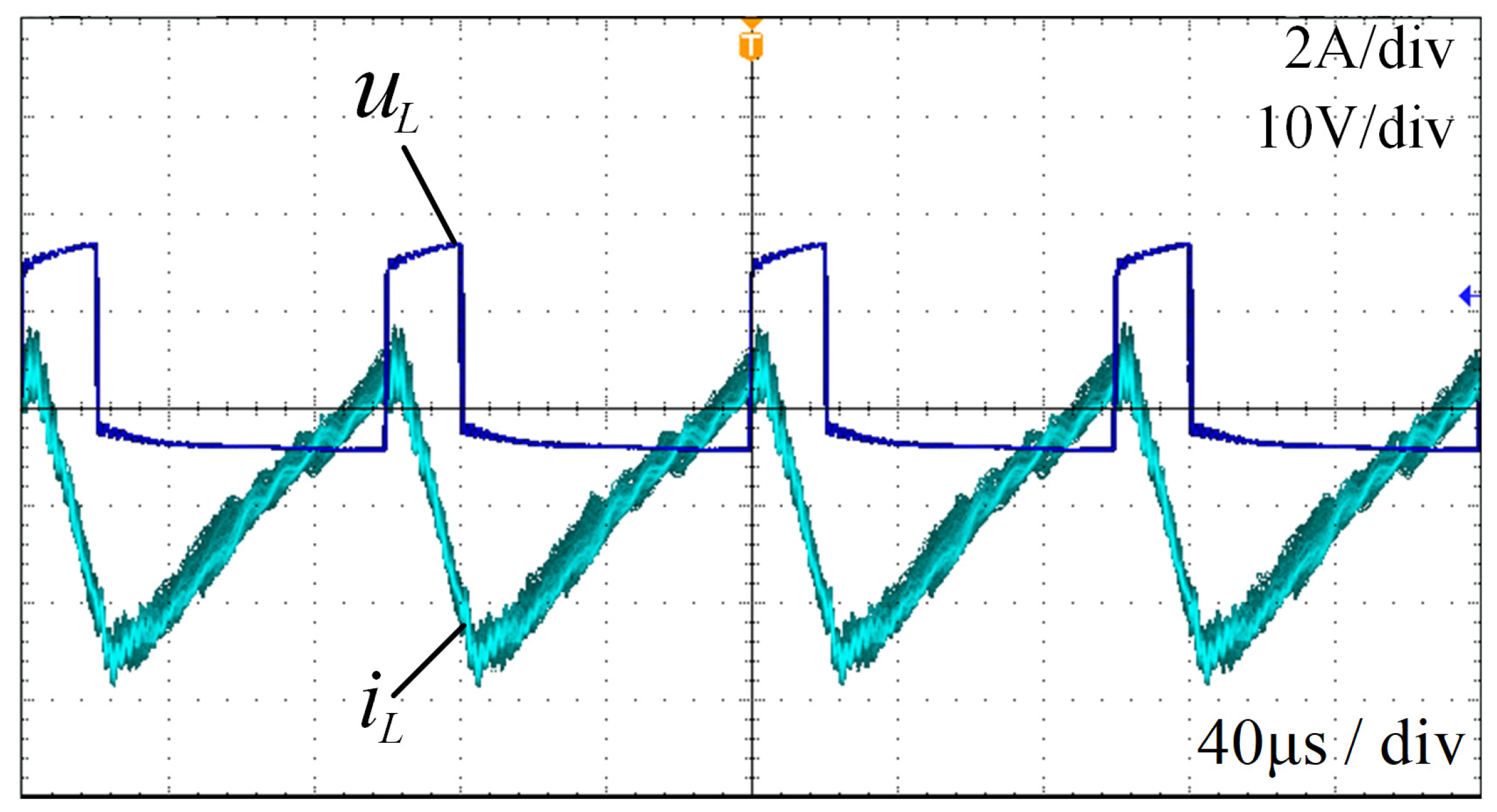
4. Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, L.; Wang, L.; Wu, M.; Zhao, C.; Yu, L. Precise Modeling and Design of Self-Resonant for High-Efficiency Mid-Range Wireless Power Transfer System. IEEE Trans. Power Electr. 2023, 38, 7848–7862. [Google Scholar] [CrossRef]
- Chen, Y.; Niu, W.; Yang, Y.; Amirat, Y. Experimental Results and Analysis of Midrange Underwater Asymmetric Wireless Power Transfer. J. Mar. Sci. Eng. 2024, 12, 567. [Google Scholar] [CrossRef]
- Ma, Y.; Liang, B.; Wang, J.; Cheng, B.; Yan, Z.; Dong, M.; Mao, Z. A Novel Hill Climbing-Golden Section Search Maximum Energy Efficiency Tracking Method for Wireless Power Transfer Systems in Unmanned Underwater Vehicles. J. Mar. Sci. Eng. 2024, 12, 1336. [Google Scholar] [CrossRef]
- Feng, H.; Tavakoli, R.; Onar, O.C.; Pantic, Z. Advances in High-Power Wireless Charging Systems: Overview and Design Considerations. IEEE Trans. Transp. Electr. 2020, 6, 886–919. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, C.; Song, J.; Chau, K.T. An Effective Sandwiched Wireless Power Transfer System for Charging Implantable Cardiac Pacemaker. IEEE Trans. Ind. Electron. 2019, 66, 4108–4117. [Google Scholar] [CrossRef]
- Moore, J.; Castellanos, S.; Xu, S.; Wood, B.; Ren, H.; Tse, Z.T.H. Applications of Wireless Power Transfer in Medicine: State-of-the-Art Reviews. Ann. Biomed. Eng. 2019, 47, 22–38. [Google Scholar] [CrossRef]
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electr. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Li, K.; Liu, Y.; Sun, X.; Tian, X.; Lei, G. Applications of Wireless Power Transfer System in Motors: A Review. IEEE Access 2024, 12, 80590–80606. [Google Scholar] [CrossRef]
- Sun, L.; Ma, D.; Tang, H. A review of recent trends in wireless power transfer technology and its applications in electric vehicle wireless charging. Renew. Sustain. Energy Rev. 2018, 91, 490–503. [Google Scholar] [CrossRef]
- Fan, M.; Shi, L.; Yin, Z.; Jiang, L.; Zhang, F. Improved Pulse Density Modulation for Semi-bridgeless Active Rectifier in Inductive Power Transfer System. IEEE Trans. Power Electr. 2019, 34, 5893–5902. [Google Scholar] [CrossRef]
- Chen, S.; Zeng, J.; Tang, Y. A Super-Resonant Frequency Control for Handshaking of an Inductive Power Transfer System with Adjacent Units. IEEE Trans. Ind. Electron. 2024, 71, 1073–1076. [Google Scholar] [CrossRef]
- Huang, J.; He, X.; Huo, P.; Xu, R. A Hybrid Modulation Strategy for LCC–LCC Compensated Bidirectional Wireless Power Transfer System to Achieve High Efficiency in the Whole Operating Range. IEEE Trans. Ind. Electron. 2024, 71, 327–337. [Google Scholar] [CrossRef]
- Luo, B.; Long, T.; Guo, L.; Dai, R.; Mai, R.; He, Z. Analysis and Design of Inductive and Capacitive Hybrid Wireless Power Transfer System for Railway Application. IEEE Trans. Ind. Appl. 2020, 56, 3034–3042. [Google Scholar] [CrossRef]
- Tan, T.; Chen, K.; Lin, Q.; Jiang, Y.; Yuan, L.; Zhao, Z. Impedance Shaping Control Strategy for Wireless Power Transfer System Based on Dynamic Small-Signal Analysis. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1354–1365. [Google Scholar] [CrossRef]
- Song, K.; Lan, Y.; Zhang, X.; Jiang, J.; Sun, C.; Yang, G.; Yang, F.; Lan, H. A Review on Interoperability of Wireless Charging Systems for Electric Vehicles. Energies 2023, 16, 1653. [Google Scholar] [CrossRef]
- Lan, Y.; Jiang, J.; Yang, F.; Song, K.; Fan, F.; Sun, C.; Yang, G.; Zhang, B.; Lan, H. Research on Impedance Boundary and Tolerance Zone for Improving Wireless Charging Interoperability Evaluation of Electric Vehicles. IEEE Trans. Power Electr. 2024, 39, 12035–12040. [Google Scholar] [CrossRef]
- Chang, X.; Huang, L.; Zhang, X.; Yang, J.; Liu, H. Study on the Dynamic Optimal Control Strategy of an Electric-Hydrogen Hybrid Energy Storage System for a Direct Drive Wave Power Generation System. J. Mar. Sci. Eng. 2023, 11, 1347. [Google Scholar] [CrossRef]
- Saeed, M.; Briz, F.; Guerrero, J.M.; Larrazabal, I.; Ortega, D.; Lopez, V.; Valera, J.J. Onboard Energy Storage Systems for Railway: Present and Trends. IEEE Open J. Ind. Appl. 2023, 4, 238–259. [Google Scholar] [CrossRef]
- Zhao, J.; Li, L.; Wu, H.; Luo, B.; Li, H.; Zhang, Y.; Liu, S.; Zhao, L. An Optimized Multi-Level Control Method for Wireless Power Transfer System Using the Particle Swarm Optimization Algorithm. Electronics 2024, 13, 4341. [Google Scholar] [CrossRef]
- Gao, P.; Li, Y.; Yao, W.; Zheng, X.; Zhang, C. Optimization of Hybrid Energy Storage System Sizing with Considering Energy Management Strategy for High-Power Pulsed Load in Aircraft. IEEE Trans. Veh. Technol. 2023, 72, 4525–4537. [Google Scholar] [CrossRef]
- Shevchenko, V.; Husev, O.; Strzelecki, R.; Pakhaliuk, B.; Poliakov, N.; Strzelecka, N. Compensation Topologies in IPT Systems: Standards, Requirements, Classification, Analysis, Comparison and Application. IEEE Access 2019, 7, 120559–120580. [Google Scholar] [CrossRef]
- Iam, I.; Choi, C.; Lam, C.; Mak, P.; Martins, R.P. A Constant-Power and Optimal-Transfer-Efficiency Wireless Inductive Power Transfer Converter for Battery Charger. IEEE Trans. Ind. Electron. 2024, 71, 450–461. [Google Scholar] [CrossRef]
- Lu, Y.; Ge, D.; Meng, L.; Sun, C.; Tang, Q.; Gao, Y.; Chen, M.; Xia, C. A Novel Optimization Method of Compensation Network Parameters for LCC Topology Wireless Power Transfer System with Anti-Offset Characteristics. IEEE Access 2024, 12, 5960–5972. [Google Scholar] [CrossRef]
- Xiong, M.; Dai, H.; Li, Q.; Jiang, Z.; Luo, Z.; Wei, X. Design of theLCC -SP Topology with a Current Doubler for 11-kW Wireless Charging System of Electric Vehicles. IEEE Trans. Transp. Electr. 2021, 7, 2128–2142. [Google Scholar] [CrossRef]
- Hou, X.; Hu, H.; Su, Y.; Liu, Z.; Deng, Z.; Deng, R. A Multirelay Wireless Power Transfer System with Double-Sided LCC Compensation Network for Online Monitoring Equipment. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 1262–1271. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, W.; Ye, L.; Guo, J.; Liu, K.; Do, H.T. A Design Method to Implement ZVS for Electric Vehicle Wireless Charging System with Double-Side LCC Compensation. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3791–3801. [Google Scholar] [CrossRef]
- Zhong, W.X.; Hui, S.Y.R. Maximum Energy Efficiency Tracking for Wireless Power Transfer Systems. IEEE Trans. Power Electr. 2015, 30, 4025–4034. [Google Scholar] [CrossRef]
- Wu, H.H.; Gilchrist, A.; Sealy, K.D.; Bronson, D. A High Efficiency 5 kW Inductive Charger for EVs Using Dual Side Control. IEEE Trans. Ind. Inf. Inform. 2012, 8, 585–595. [Google Scholar] [CrossRef]
- Wang, L.J.; Gonder, J.; Burton, E.; Brooker, A.; Meintz, A.; Konan, A. IEEE A Cost Effectiveness Analysis of Quasi-Static Wireless Power Transfer for Plug-In Hybrid Electric Transit Buses. In Proceedings of the 2015 12th IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015. [Google Scholar]
- Hata, K.; Huang, X.L.; Hori, Y. IEEE Power Flow Control of Magnetic Resonance Wireless Charing for Hybrid Energy Storage System of Electric Vehicles Application. In Proceedings of the 2015 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, 28–30 July 2015; pp. 1459–1462. [Google Scholar]
- Geng, Y.Y.; Li, B.; Yang, Z.P.; Lin, F.; Sun, H. A High Efficiency Charging Strategy for a Supercapacitor Using a Wireless Power Transfer System Based on Inductor/Capacitor/Capacitor (LCC) Compensation Topology. Energies 2017, 10, 135. [Google Scholar] [CrossRef]
- Nguyen, V.; Vu, V.; Gohil, G.; Fahimi, B. Coil-to-Coil Efficiency Optimization of Double-Sided LCC Topology for Electric Vehicle Inductive Chargers. IEEE Trans. Ind. Electron. 2022, 69, 11242–11252. [Google Scholar] [CrossRef]

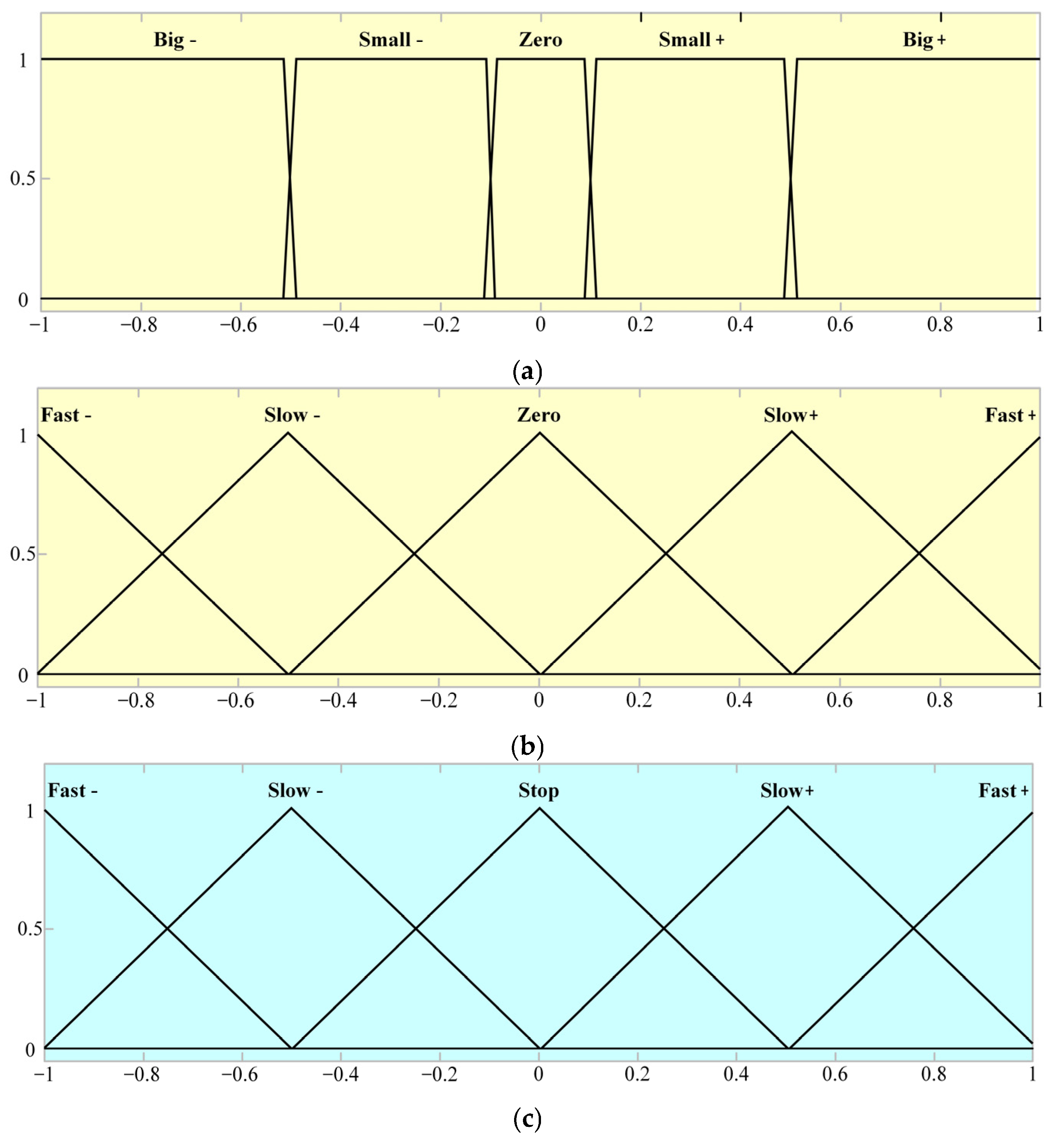

| e | Big− | Small− | Zero | Small+ | Big+ |
| ∆R | Fast+ | Slow+ | Stop | Slow− | Big− |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Uin/V | 15 | Ub/V | 24 |
| Lf1/μH | 35 | CSC/F | 3 |
| Cf1/μF | 7.2 | L/μH | 60 |
| C1/μF | 50.7 | C2/μF | 5.1 |
| L1/μH | 40.07 | Cf2/μF | 16.9 |
| L2/μH | 65.22 | Lf2/μH | 15 |
| Uin/V | 15 | Ub/V | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Zhang, L.; Xiu, S. An Analysis of Wireless Power Transfer with a Hybrid Energy Storage System and Its Sustainable Optimization. Sustainability 2025, 17, 2358. https://doi.org/10.3390/su17062358
Yang C, Zhang L, Xiu S. An Analysis of Wireless Power Transfer with a Hybrid Energy Storage System and Its Sustainable Optimization. Sustainability. 2025; 17(6):2358. https://doi.org/10.3390/su17062358
Chicago/Turabian StyleYang, Changqing, Liwei Zhang, and Sanmu Xiu. 2025. "An Analysis of Wireless Power Transfer with a Hybrid Energy Storage System and Its Sustainable Optimization" Sustainability 17, no. 6: 2358. https://doi.org/10.3390/su17062358
APA StyleYang, C., Zhang, L., & Xiu, S. (2025). An Analysis of Wireless Power Transfer with a Hybrid Energy Storage System and Its Sustainable Optimization. Sustainability, 17(6), 2358. https://doi.org/10.3390/su17062358








