A Stochastic Process-Based Approach for Power System Modeling and Simulation: A Case Study on China’s Long-Term Coal-Fired Power Phaseout
Abstract
1. Introduction
2. Methods and Materials
2.1. Stochastic Process-Based Modeling
2.2. Unit-Level System Model
2.3. Phaseout Path of Coal-Fired Power
2.3.1. Unit Reducing
2.3.2. Decarbonizing
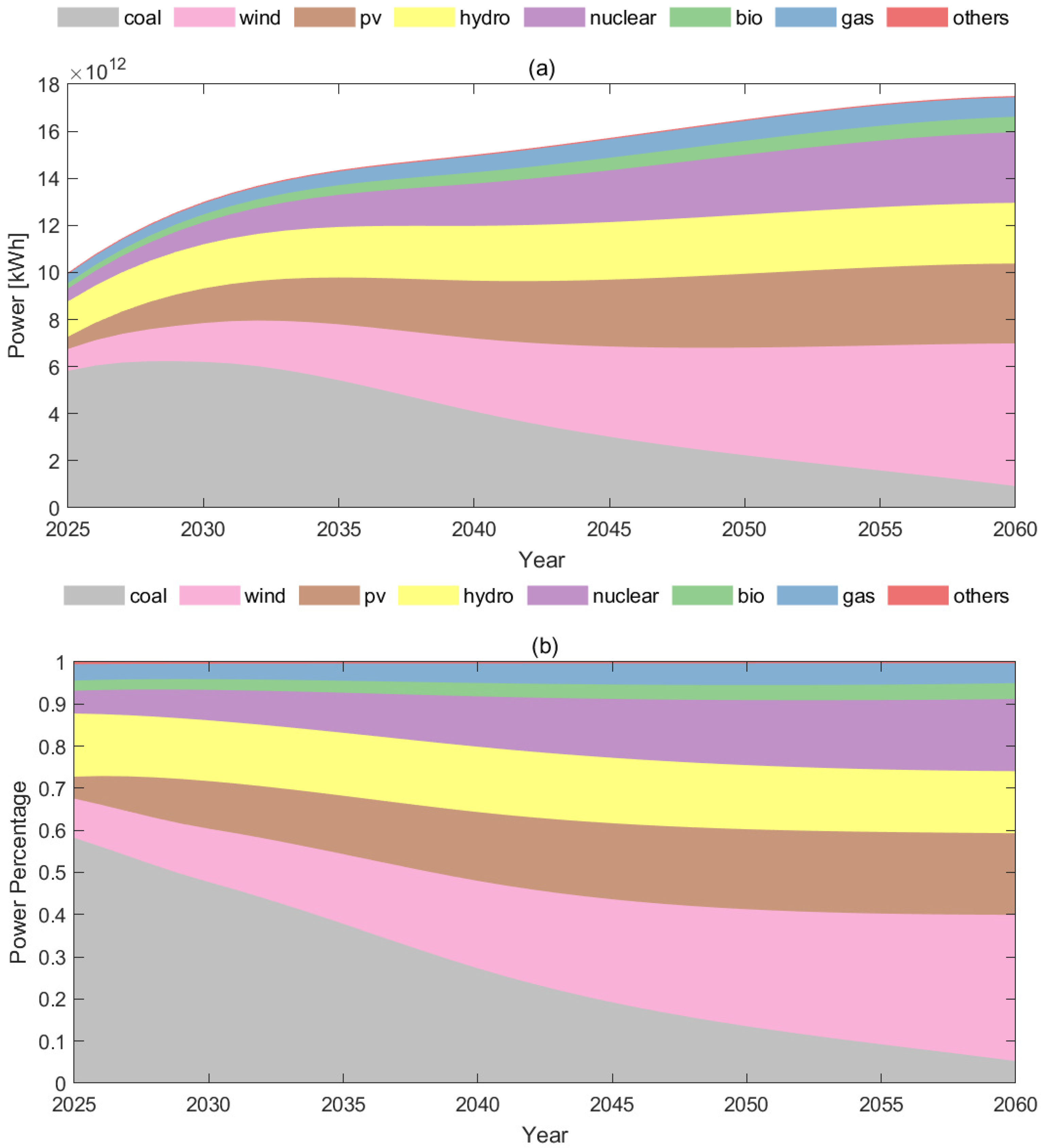
2.4. Long-Term Remaining Demands
2.5. Simulation Settings
3. Results
3.1. Demand-Side Results
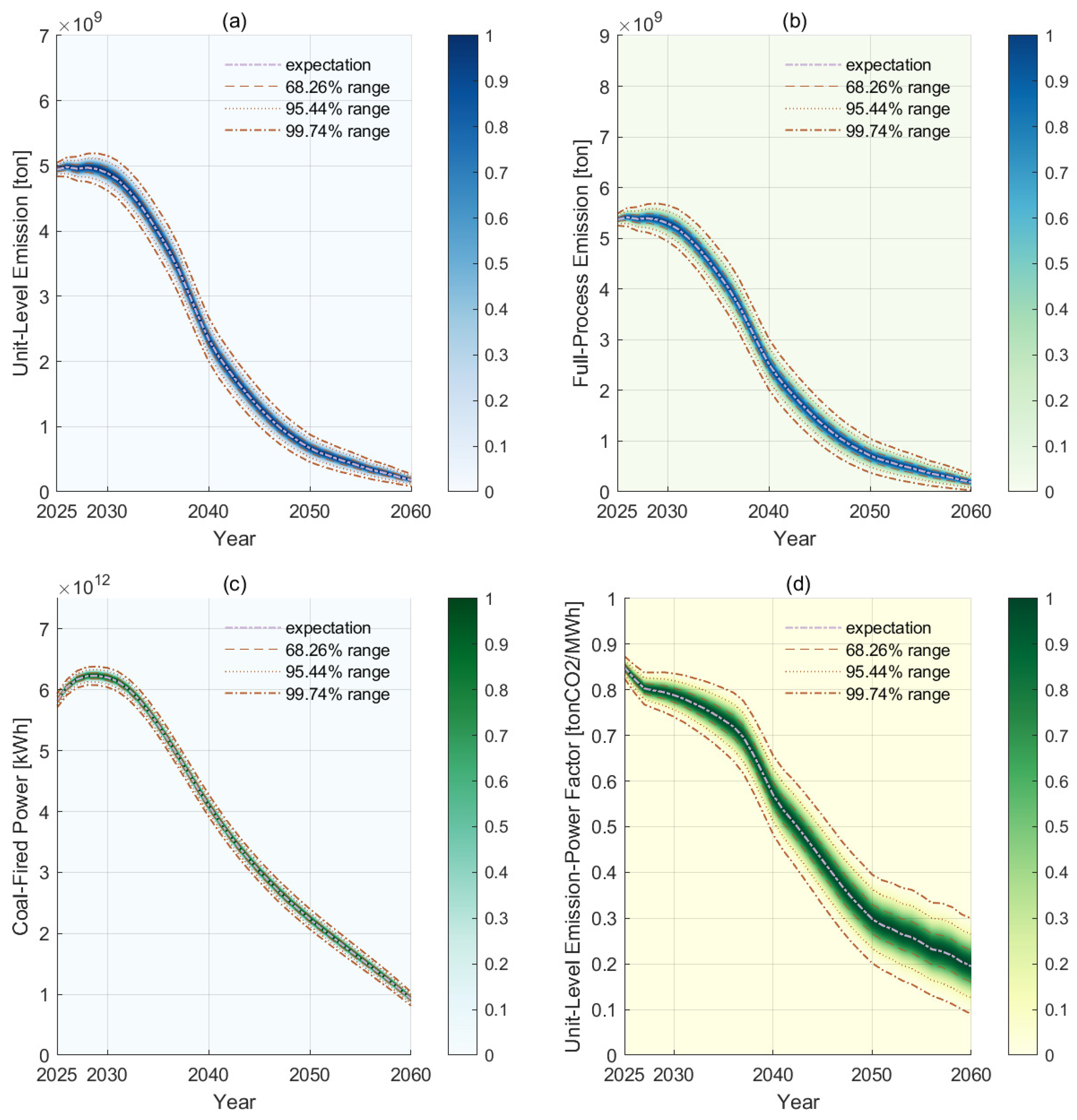
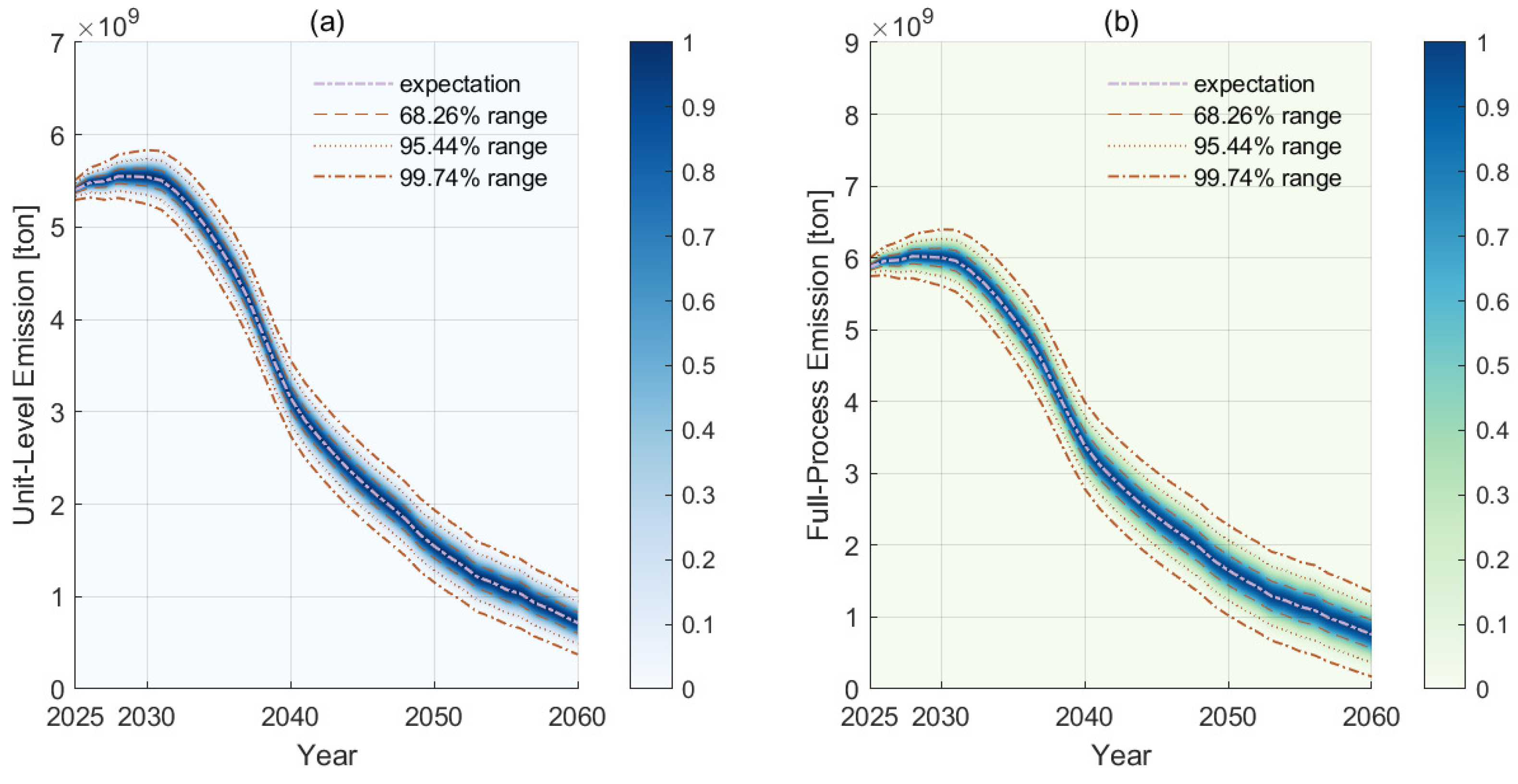
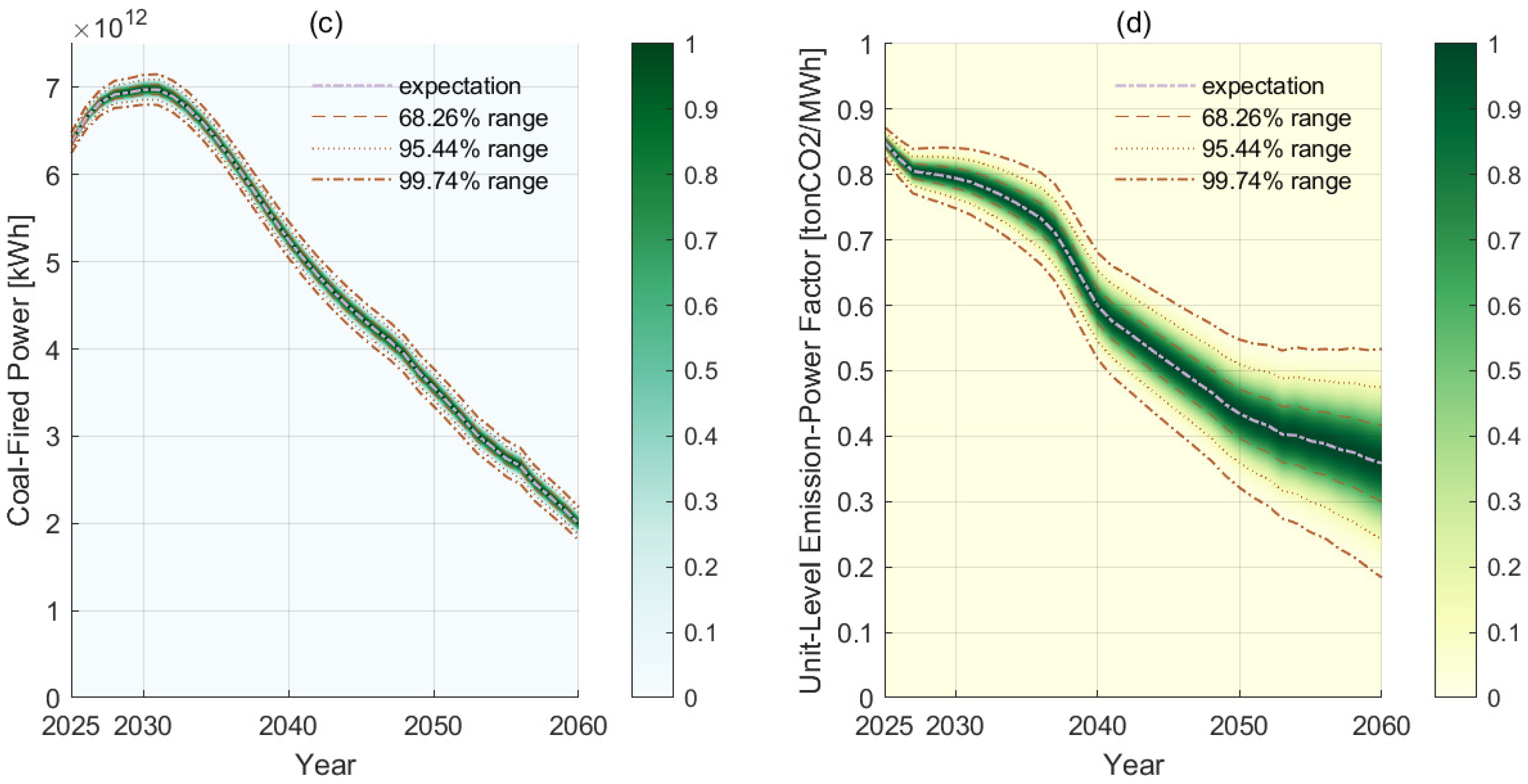
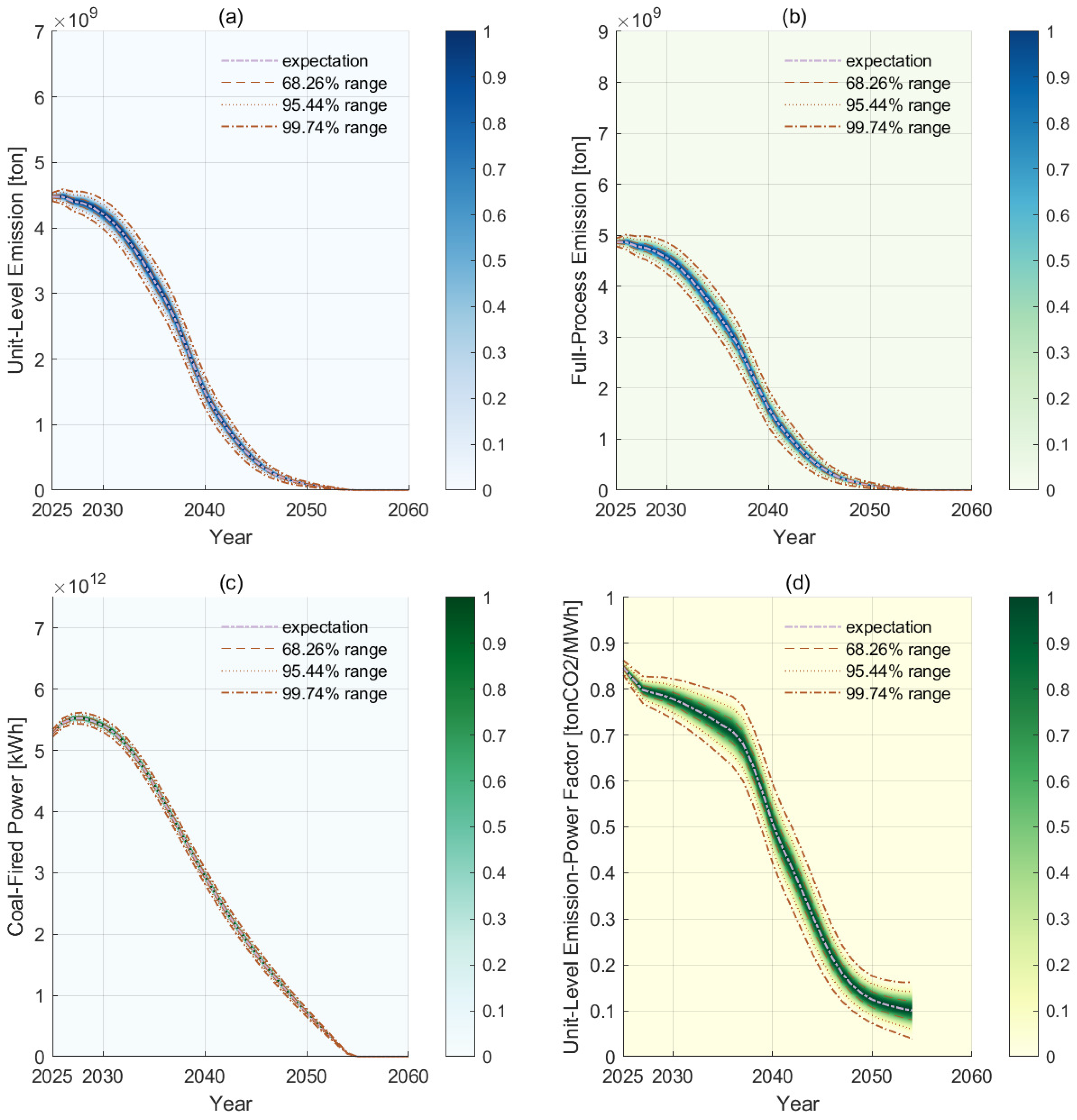
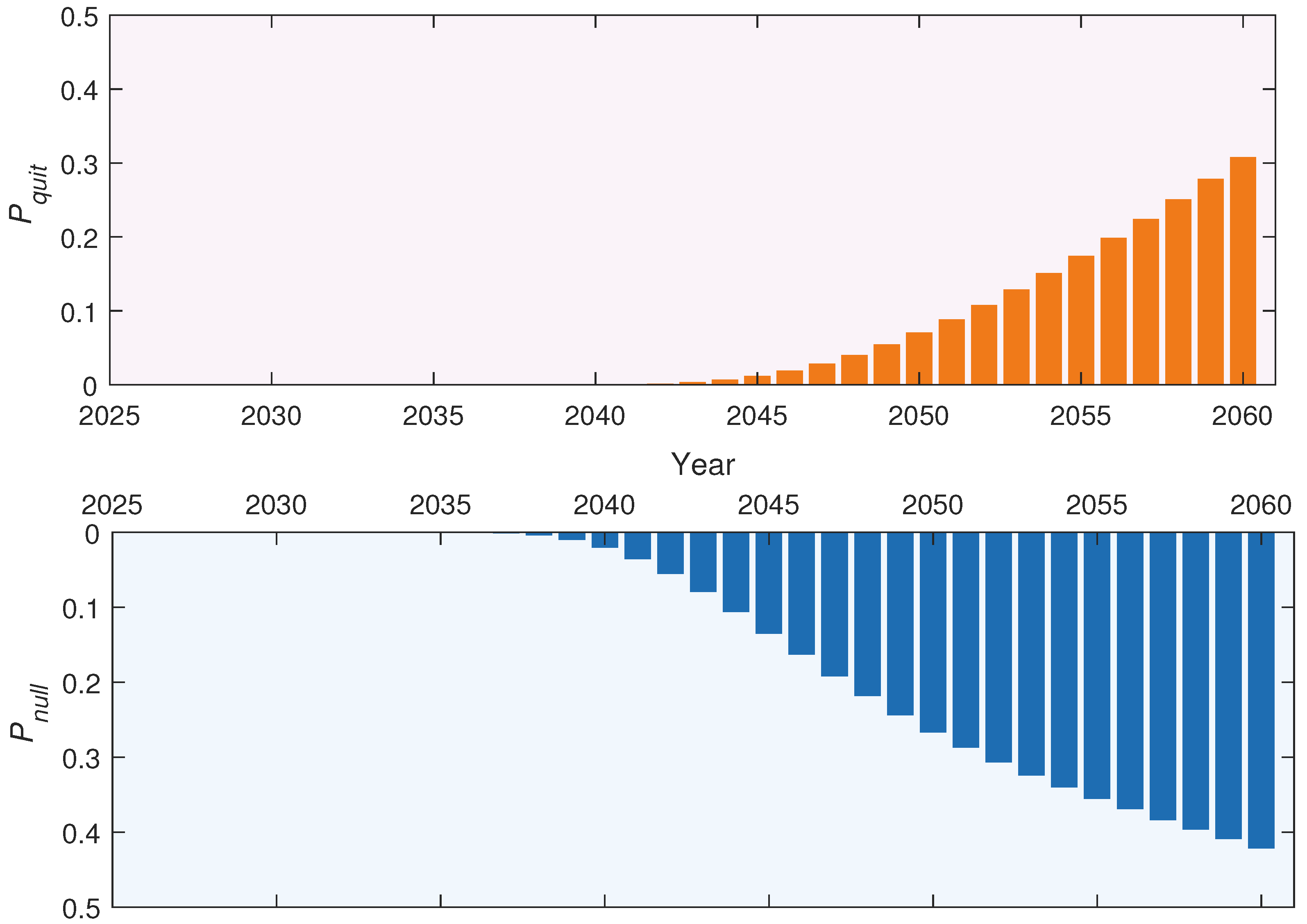
3.2. Phaseout Paths upon Fixed-Value Demands
3.3. Phaseout Paths upon Stochastic Demands
4. Discussions
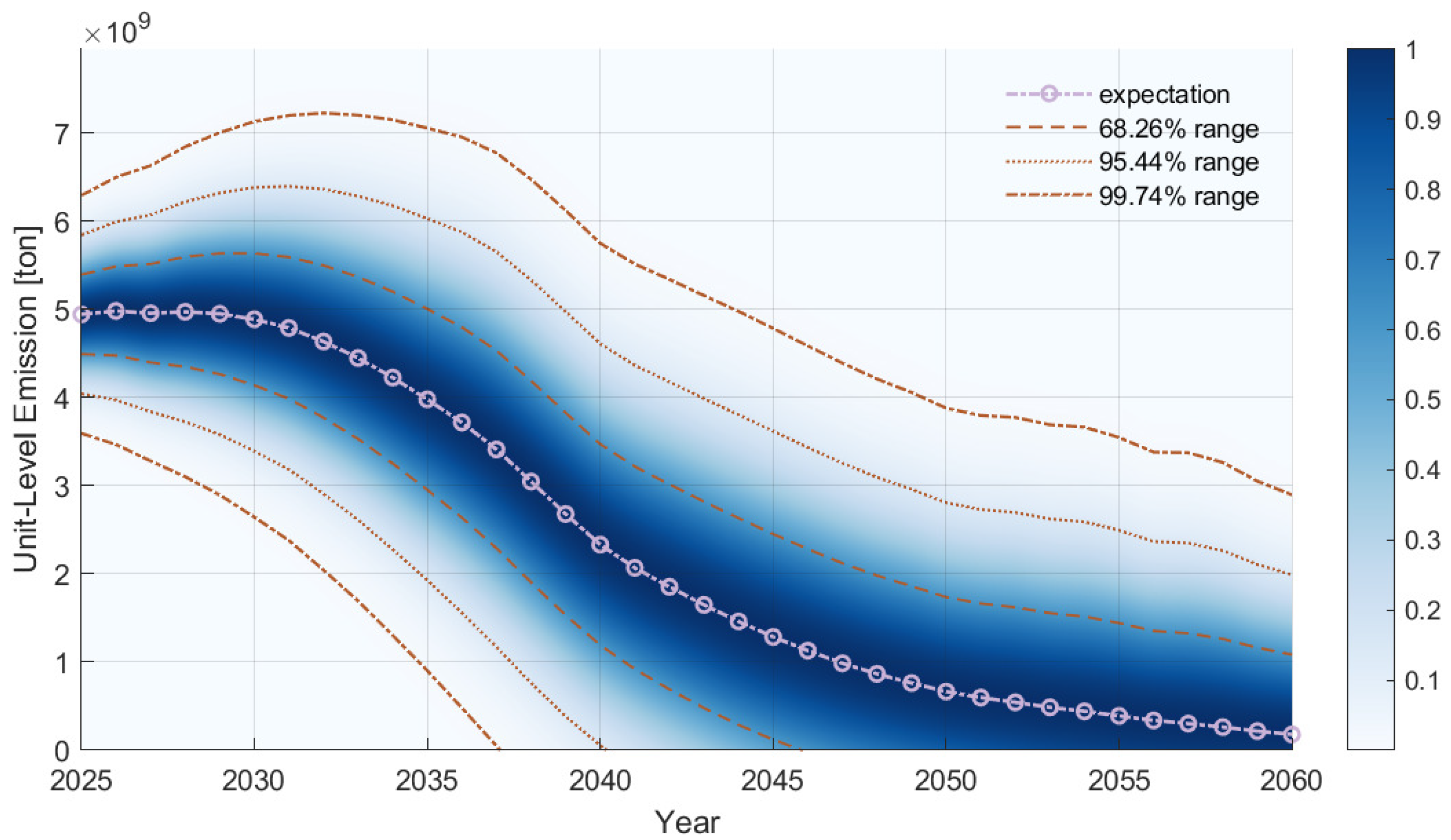
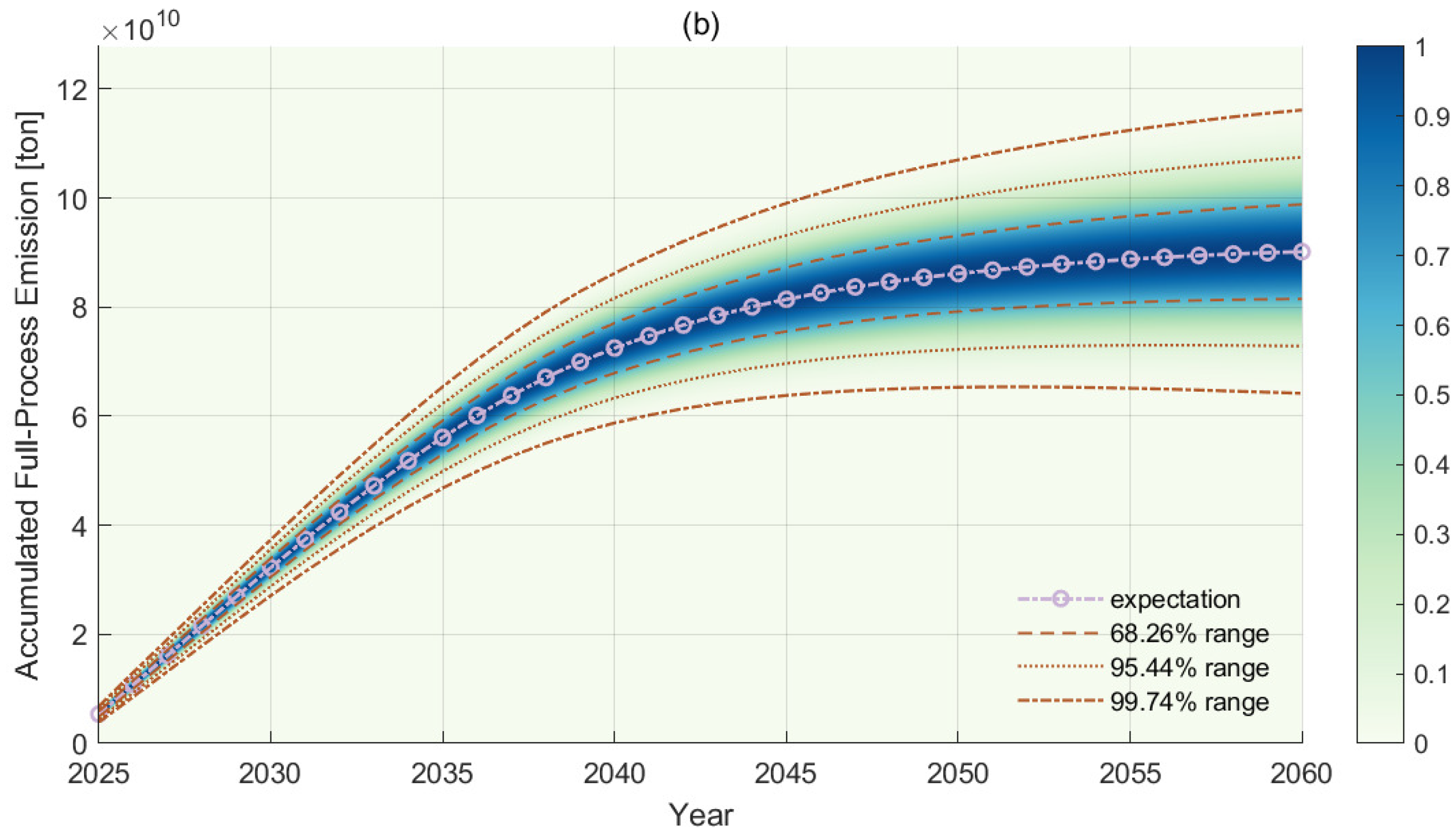
4.1. Probabilistic Information
4.2. Emission-Reduction Potential
4.3. Policy Recommendations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, G.; Lin, J.; Sifuentes, F.; Liu, X.; Abhyankar, N.; Phadke, A. Rapid cost decrease of renewables and storage accelerates the decarbonization of China’s power system. Nat. Commun. 2020, 11, 2486. [Google Scholar] [CrossRef] [PubMed]
- United Nations. The Paris Agreement. 2015. Available online: https://unfccc.int/sites/default/files/resource/parisagreement_publication.pdf (accessed on 27 February 2025).
- Department of State Bulletin. For Man and Nature: Building a Community of Life Together, 2021. Available online: https://www.gov.cn/gongbao/content/2021/content_5605101.htm (accessed on 27 February 2025).
- National Development and Reform Commission, National Energy Administration. Notice on Further Improving the Elimination of Backward Production Capacity in the Coal-Fired Power Industry. 2016. Available online: https://zfxxgk.ndrc.gov.cn/web/iteminfo.jsp?id=19494 (accessed on 27 February 2025).
- National Development and Reform Commission, National Energy Administration. National Implementation Plan for the Transformation and Upgrading of Coal-Fired Power Units. 2021. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/tz/202111/P020211103333054582799.pdf (accessed on 27 February 2025).
- National Development and Reform Commission, National Energy Administration. Action Plan for Low-Carbon Transformation and Construction of Coal-Fired Power (2024–2027). 2024. Available online: https://www.gov.cn/zhengce/zhengceku/202407/content_6963501.htm (accessed on 27 February 2025).
- National Development and Reform Commission, National Energy Administration. 14th Five-Year Plan for Modern Power System. 2022. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/ghwb/202203/P020220322582066837126.pdf (accessed on 27 February 2025).
- European Commission. State of the Energy Union Report 2023. 2023. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2023%3A650%3AFIN&qid=1698237100377 (accessed on 27 February 2025).
- International Energy Agency. Power Systems in Transition. 2020. Available online: https://www.iea.org/reports/power-systems-in-transition (accessed on 27 February 2025).
- International Energy Agency. World Energy Outlook 2023. 2023. Available online: https://origin.iea.org/reports/world-energy-outlook-2023 (accessed on 27 February 2025).
- Brinkerink, M.; Mayfield, E.; Deane, P. The role of spatial resolution in global electricity systems modelling. Energy Strategy Rev. 2024, 53, 101370. [Google Scholar] [CrossRef]
- Brown, P.R.; Williams, T.; Brown, M.L.; Murphy, C. System-cost-minimizing deployment of PV-wind hybrids in low-carbon U.S. power systems. Appl. Energy 2024, 365, 123151. [Google Scholar] [CrossRef]
- Chen, H.; Ding, X.; Zhong, B.; Zhou, X.; Peng, M.; Ning, K. A short-term stochastic production simulation method for new energy power systems considering operation timing characteristics. J. Radiat. Res. Appl. Sci. 2024, 17, 101132. [Google Scholar] [CrossRef]
- He, J.; Li, Z.; Zhang, X.; Wang, H.; Dong, W.; Du, E.; Chang, S.; Ou, X.; Guo, S.; Tian, Z.; et al. Towards carbon neutrality: A study on China’s long-term low-carbon transition pathways and strategies. Environ. Sci. Ecotechnology 2022, 9, 100134. [Google Scholar] [CrossRef]
- Luo, S.; Hu, W.; Liu, W.; Zhang, Z.; Bai, C.; Huang, Q.; Chen, Z. Study on the decarbonization in China’s power sector under the background of carbon neutrality by 2060. Renew. Sustain. Energy Rev. 2022, 166, 112618. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, Q.; Yu, X.; Wang, Q.; Tan, J. Exploring phase-out path of China’s coal power plants with its dynamic impact on electricity balance. Energy Policy 2024, 187, 114021. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Z.; Zhang, L.; Liu, Y.; Shan, Y.; Wang, X.; Liu, Y.; Zhang, L.; Li, X.; Li, X.; et al. Modelling the socio-economic impacts of coal-fired electricity phaseout under carbon neutrality target: A dynamic CGE-based study of China. Resour. Conserv. Recycl. 2024, 205, 107563. [Google Scholar] [CrossRef]
- Duan, H.; Mo, J.; Fan, Y.; Wang, S. Achieving China’s energy and climate policy targets in 2030 under multiple uncertainties. Energy Econ. 2018, 70, 45–60. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Liu, B.; Wang, K.; Wang, Z.; Kang, J. Optimization of coal power phaseout pathways ensuring energy security: Evidence from Shandong, China’s largest coal power province. Energy Policy 2024, 192, 114180. [Google Scholar] [CrossRef]
- Yang, R.; Wang, W. Potential of China’s national policies on reducing carbon emissions from coal-fired power plants in the period of the 14th Five-Year Plan. Heliyon 2023, 9, e19868. [Google Scholar] [CrossRef] [PubMed]
- Xin, L.; Li, S.; Rene, E.R.; Lun, X.; Zhang, P.; Ma, W. Prediction of carbon emissions peak and carbon neutrality based on life cycle CO2 emissions in megacity building sector: Dynamic scenario simulations of Beijing. Environ. Res. 2023, 238, 117160. [Google Scholar] [CrossRef] [PubMed]
- Cui, R.Y.; Hultman, N.; Cui, D.; McJeon, H.; Yu, S.; Edwards, M.R.; Sen, A.; Song, K.; Bowman, C.; Clarke, L.; et al. A plant-by-plant strategy for high-ambition coal power phaseout in China. Nat. Commun. 2021, 12, 1468. [Google Scholar] [CrossRef] [PubMed]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Xu, M.; Li, Q.; Zhao, Z.; Sun, C. Bilinear-DRTFT: Uncertainty prediction in electricity load considering multiple demand responses. Energy 2024, 309, 133067. [Google Scholar] [CrossRef]
- He, Y.; Li, H. Probability density forecasting of wind power using quantile regression neural network and kernel density estimation. Energy Convers. Manag. 2018, 164, 374–384. [Google Scholar] [CrossRef]
- Wang, J.; Cui, Y.; Liu, Z.; Zeng, L.; Yue, C.; Agbodjan, Y.S. Multi-energy complementary integrated energy system optimization with electric vehicle participation considering uncertainties. Energy 2024, 309, 133109. [Google Scholar] [CrossRef]
- Panos, E.; Glynn, J.; Kypreos, S.; Lehtilä, A.; Yue, X.; Ó Gallachóir, B.; Daniels, D.; Dai, H. Deep decarbonisation pathways of the energy system in times of unprecedented uncertainty in the energy sector. Energy Policy 2023, 180, 113642. [Google Scholar] [CrossRef]
- Mavromatidis, G.; Orehounig, K.; Carmeliet, J. Design of distributed energy systems under uncertainty: A two-stage stochastic programming approach. Appl. Energy 2018, 222, 932–950. [Google Scholar] [CrossRef]
- Karlin, S.; Taylor, H.M. A First Course in Stochastic Processes, 2nd ed.; Academic Press: Boston, MA, USA, 1975; Chapter 1; pp. 1–44. [Google Scholar] [CrossRef]
- Dang, H.N.; Nhu, N.N.; George, Y. General nonlinear stochastic systems motivated by chemostat models: Complete characterization of long-time behavior, optimal controls, and applications to wastewater treatment. Stoch. Process. Their Appl. 2020, 130, 4608–4642. [Google Scholar] [CrossRef]
- Kumawat, G.L.; Roy, D.; De Koster, R.; Adan, I. Stochastic modeling of parallel process flows in intra-logistics systems: Applications in container terminals and compact storage systems. Eur. J. Oper. Res. 2021, 290, 159–176. [Google Scholar] [CrossRef]
- Yao, Q.; Bing, H.; Zhu, G.; Xiang, L.; Hu, A. A novel stochastic process diffusion model for wind turbines condition monitoring and fault identification with multi-parameter information fusion. Mech. Syst. Signal Process. 2024, 214, 111397. [Google Scholar] [CrossRef]
- Bittner, M.; Behrendt, M.; Beer, M. Relaxed evolutionary power spectral density functions: A probabilistic approach to model uncertainties of non-stationary stochastic signals. Mech. Syst. Signal Process. 2024, 211, 111210. [Google Scholar] [CrossRef]
- Durbach, I.N.; Calder, J.M. Modelling uncertainty in stochastic multicriteria acceptability analysis. Omega 2016, 64, 13–23. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Z.; Bai, X.; Su, J.; Chang, X. Stochastic real-time dispatch considering AGC and electric-gas dynamic interaction: Fine-grained modeling and noniterative decentralized solutions. Appl. Energy 2024, 375, 123976. [Google Scholar] [CrossRef]
- Song, Y.; Chen, X.; Lin, J.; Liu, F.; Qiu, Y. Stochastic processes in renewable power systems: From frequency domain to time domain. Sci. China Technol. Sci. 2019, 62, 2093–2103. [Google Scholar] [CrossRef]
- Adeen, M.; Milano, F. Modeling of Correlated Stochastic Processes for the Transient Stability Analysis of Power Systems. IEEE Trans. Power Syst. 2021, 36, 4445–4456. [Google Scholar] [CrossRef]
- Alfeus, M.; Collins, J. A novel stochastic modeling framework for coal production and logistics through options pricing analysis. Financ. Innov. 2023, 9, 54. [Google Scholar] [CrossRef]
- Yiting, D. The Coordination Between Carbon Reduction and Energy Security Based on National Conditions. 2022. Available online: https://www.nea.gov.cn/2022-02/18/c_1310478264.htm (accessed on 27 February 2025).
- Global Energy Monitor. Global Coal Plant Tracker. 2024. Available online: https://globalenergymonitor.org/projects/global-coal-plant-tracker/download-data/ (accessed on 27 February 2025).
- Lee, B.J.; Lee, J.I.; Yun, S.Y.; Hwang, B.G.; Lim, C.-S.; Park, Y.-K. Methodology to Calculate the CO2 Emission Reduction at the Coal-Fired Power Plant: CO2 Capture and Utilization Applying Technology of Mineral Carbonation. Sustainability 2020, 12, 7402. [Google Scholar] [CrossRef]
- Song, C.; Li, M.; Zhang, F.; He, Y.; Tao, W. Analysis of Energy Efficiency for Coal-fired Power Units Based on Data Envelopment Analysis Model. Energy Procedia 2014, 61, 904–909. [Google Scholar] [CrossRef]
- de Caprariis, B.; De Filippis, P.; Herce, C.; Verdone, N. Double-Gaussian Distributed Activation Energy Model for Coal Devolatilization. Energy Fuels 2012, 26, 6153–6159. [Google Scholar] [CrossRef]
- Ersoy, A.; Yünsel, T.Y. Assessment of Lignite Quality Variables: A Practical Approach with Sequential Gaussian Simulation. Energy Sources Part Recover. Util. Environ. Eff. 2008, 31, 175–190. [Google Scholar] [CrossRef]
- Zhu, Y.; Tong, Q.L.; Yan, X.X.; Li, Y.X. Development of an uncertain Gaussian diffusion model with its application to production-emission system management in coal-dependent city—A case study of Yulin, China. Energy Procedia 2019, 158, 3253–3258. [Google Scholar] [CrossRef]
- Cui, G.; Yu, X.; Iommelli, S.; Kong, L. Exact Distribution for the Product of Two Correlated Gaussian Random Variables. IEEE Signal Process. Lett. 2016, 23, 1662–1666. [Google Scholar] [CrossRef]
- Samaniego, F.J. Stochastic Modeling and Mathematical Statistics; CRC Press: Boca Raton, FL, USA, 2014; Chapter 5. [Google Scholar]
- China Electricity Council. China Power Statistics Yearbook 2023; China Statistics Press: Beijing, China, 2023. [Google Scholar]
- China Electricity Council. China Power Statistics Yearbook 2022; China Statistics Press: Beijing, China, 2022. [Google Scholar]
- U.S. Energy Information Administration. Capital Cost and Performance Characteristics for Utility-Scale Electric Power Generating Technologies. 2024. Available online: https://www.eia.gov/analysis/studies/powerplants/capitalcost/pdf/capital_cost_AEO2025.pdf (accessed on 27 February 2025).
- Sargent & Lundy. New Coal-Fired Power Plant Performance and Cost Estimates. 2009. Available online: https://www.epa.gov/sites/default/files/2015-08/documents/coalperform.pdf (accessed on 27 February 2025).
- Su, S.; Fang, X.; Zhao, J.; Hu, J. Spatiotemporal characteristics of consumption based CO2 emissions from China’s power sector. Resour. Conserv. Recycl. 2016, 121, 156–163. [Google Scholar] [CrossRef]
- Liu, J.; Xu, X.; Li, S. Lifecycle carbon footprint analysis of China’s power industry. China Popul. Resour. Environ. 2022, 32, 31–41. [Google Scholar] [CrossRef]
- Stefanía, Ó.G.; Lisa, G.; Fredrik, N.; Filip, J. Improving the flexibility of coal-fired power generators: Impact on the composition of a cost-optimal electricity system. Appl. Energy 2018, 209, 277–289. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Q.; Ye, N.; Zhang, N.; Wu, X.; Fan, H. A review on flexible peak shaving development of coal-fired boilers in China under the carbon peak and carbon neutrality goals. Therm. Sci. Eng. Prog. 2024, 55, 103004. [Google Scholar] [CrossRef]
- The State Council Information Office. China’s Energy Transition. 2024. Available online: https://www.gov.cn/zhengce/202408/content_6971115.htm (accessed on 27 February 2025).
- China Energy Media Group Co., Ltd. China Energy Big Data Report (2024). 2024. Available online: https://yb.1qh.cn/reports/2024-06-27/837a32825a42ba07eda081d285d6bef4f038eef2.pdf (accessed on 27 February 2025).
- Zhuo, L.; Lu, Y.; Deng, X. Study on the Contribution Rate of Scientific and Technological Progress to Economic Growth in a Coal Enterprise. In Proceedings of the Ninth International Conference on Management Science and Engineering Management, Karlsruhe, Germany, 21–23 July 2015; Volume 362, pp. 1319–1328. [Google Scholar] [CrossRef]
- Zhang, X. Transition to a Carbon Neutral Energy Economy by 2060. 2021. Available online: https://www.mee.gov.cn/home/ztbd/2020/wfcsjssdgz/wfcsxwbd/ylgd/202104/P020210401595660592840.pdf (accessed on 27 February 2025).
- Chen, W.; Lu, X. Research on the optimization of CCUS cluster deployment of coal-fired power plants in China under the goal of carbon neutrality. Clim. Change Res. 2022, 18, 261–271. [Google Scholar]
- Global Energy Interconnection Development and Cooperation Organization. China’s 2030 Energy and Power Development Plan and 2060 Outlook. 2021. Available online: https://journal.geidco.org.cn/cn/wonderfulReportCn/20211209/1468969880752623616.html (accessed on 27 February 2025).
- China Electricity Council. China Power Industry Annual Development Report 2023. 2023. Available online: http://www.chinapower.com.cn/tynfd/hyyw/20230713/208506.html (accessed on 27 February 2025).
- China Electricity Council. China Power Industry Annual Development Report 2024. 2024. Available online: https://www.cec.org.cn/detail/index.html?3-334911 (accessed on 27 February 2025).
- National Development and Reform Commission. The 14th Five-Year Plan for the Development of Renewable Energy. 2022. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/ghwb/202206/P020220601501054858882.pdf (accessed on 27 February 2025).
- Institute of Carbon Neutrality Tsinghua University. Technology Outlook on Wind and Solar Power Toward China’s Carbon Neutrality Goal. 2024. Available online: https://www.icon.tsinghua.edu.cn/info/1079/1429.html (accessed on 27 February 2025).
- China Nuclear Energy Association. Keynote Speech for International Forum on Sustaintable Nuclear Energy Development. 2024. Available online: https://www.china-nea.cn/site/content/44714.html (accessed on 27 February 2025).
- China Association for the Promotion of Industrial Development. 2030–2060 Blue Book on the Development Potential of Zero-Carbon Biomass Energy. 2021. Available online: https://news.bjx.com.cn/html/20210915/1177029.shtml (accessed on 27 February 2025).
- The Oxford Institute for Energy Studies. Natural Gar in China’s Power Sector: Challenges and The Road Ahead. 2020. Available online: https://www.oxfordenergy.org/publications/natural-gas-in-chinas-power-sector-challenges-and-the-road-ahead/ (accessed on 27 February 2025).
- Shafer, D.S.; Zhang, Z. Introductory Statistics; Saylor Academy: Washington, DC, USA, 2012; Chapter 2. [Google Scholar]
- Zhao, J.; Xie, H.; Ma, J.; Wang, K. Integrated remote sensing and model approach for impact assessment of future climate change on the carbon budget of global forest ecosystems. Glob. Planet. Change 2021, 203, 103542. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Climate Change 2021: The Physical Science Basis. 2021. Available online: https://www.ipcc.ch/report/ar6/wg1/ (accessed on 27 February 2025).
- Chen, H. Study of the Long-Term Low-Carbon Transition in China’s Power Sector: Based on Enterprise Behavior Simulation. 2018. Available online: https://newetds.lib.tsinghua.edu.cn/qh/paper/summary?dbCode=ETDQH&sysId=250700 (accessed on 27 February 2025).
- Wang, S.J.; Mo, H.B.; Fang, C.L. Carbon emissions dynamic simulation and its peak of cities in the Pearl River Delta Urban Agglomeration. China Sci. Bull. 2022, 67, 670–684. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Z.; Yang, Q.; Li, C. Prediction Model of Electric Power Carbon Emissions Based on Extended System Dynamics. Energies 2024, 17, 472. [Google Scholar] [CrossRef]
- Hu, Y.; Chi, Y.; Zhou, W.; Wang, Z.; Yuan, Y.; Li, R. Research on Energy Structure Optimization and Carbon Emission Reduction Path in Beijing under the Dual Carbon Target. Energies 2022, 15, 5954. [Google Scholar] [CrossRef]
- Xiaohe, D. National Energy Administration: Coal Power will Continue to Play an Important Role in Ensuring Power SECURITY for a long Time. 2022. Available online: https://www.gov.cn/xinwen/2022-04/24/content_5686931.htm (accessed on 27 February 2025).
- General Office of Ministry of Ecology and Environment. Notice on the Management of Greenhouse Gas Emission Reports of Enterprises in the Power Generation Industry from 2023 to 2025. 2023. Available online: https://www.mee.gov.cn/xxgk2018/xxgk/xxgk06/202302/t20230207_1015569.html (accessed on 27 February 2025).
- Fan, J.L.; Xu, M.; Wei, S.; Shen, S.; Diao, Y.; Zhang, X. Carbon reduction potential of China’s coal-fired power plants based on a CCUS source-sink matching model. Resour. Conserv. Recycl. 2021, 168, 105320. [Google Scholar] [CrossRef]
- Greig, C.; Uden, S. The value of CCUS in transitions to net-zero emissions. Electr. J. 2021, 34, 107004. [Google Scholar] [CrossRef]
- Macrotrends. Manufacturing Output by Country. 2024. Available online: https://www.macrotrends.net/global-metrics/countries/ranking/manufacturing-output (accessed on 27 February 2025).
- International Council on Archives. List of Developing Countries. 2024. Available online: https://www.ica.org/app/uploads/2024/03/List-of-Developing-Countries-2024_Updated.pdf (accessed on 27 February 2025).
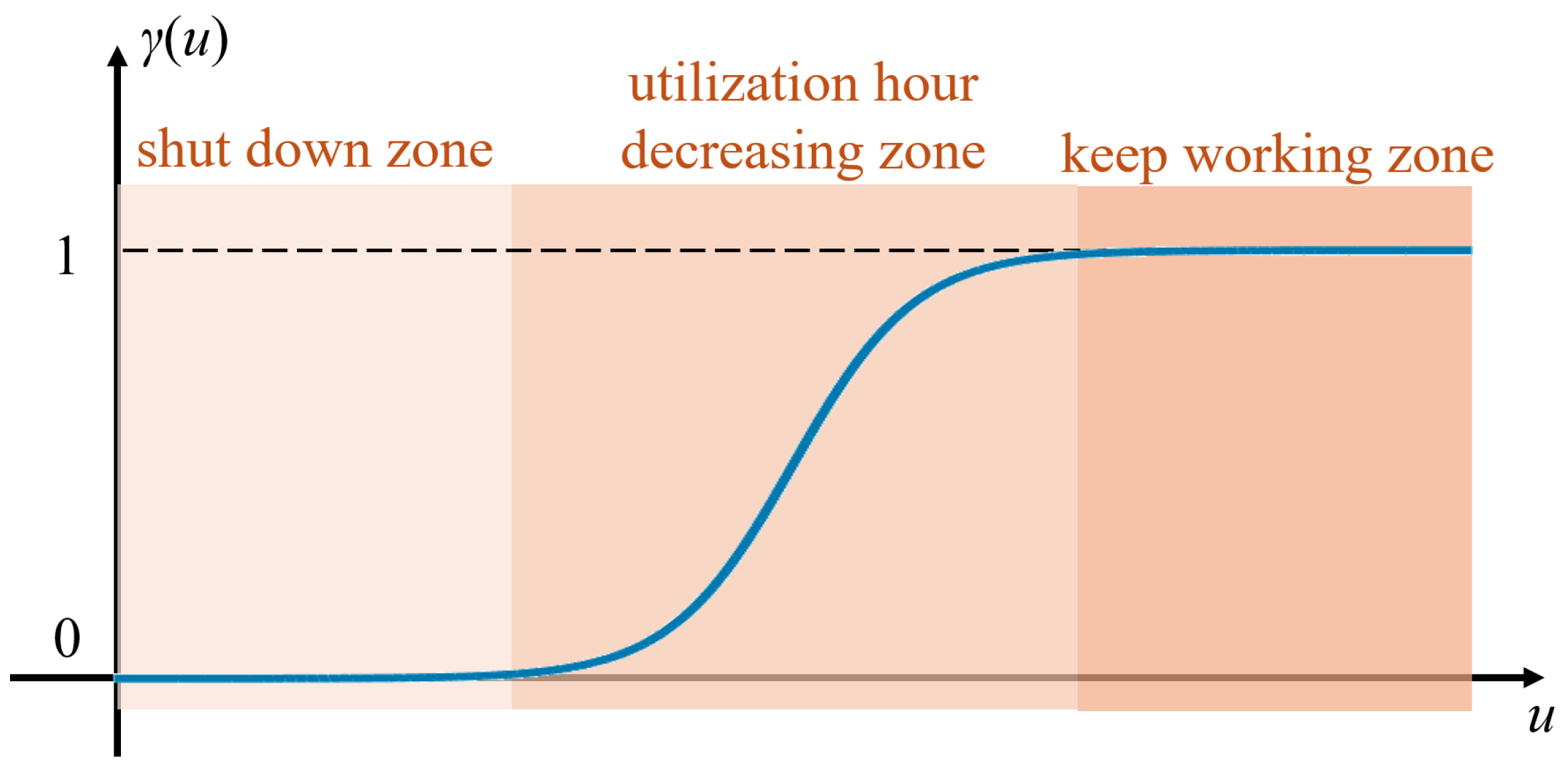
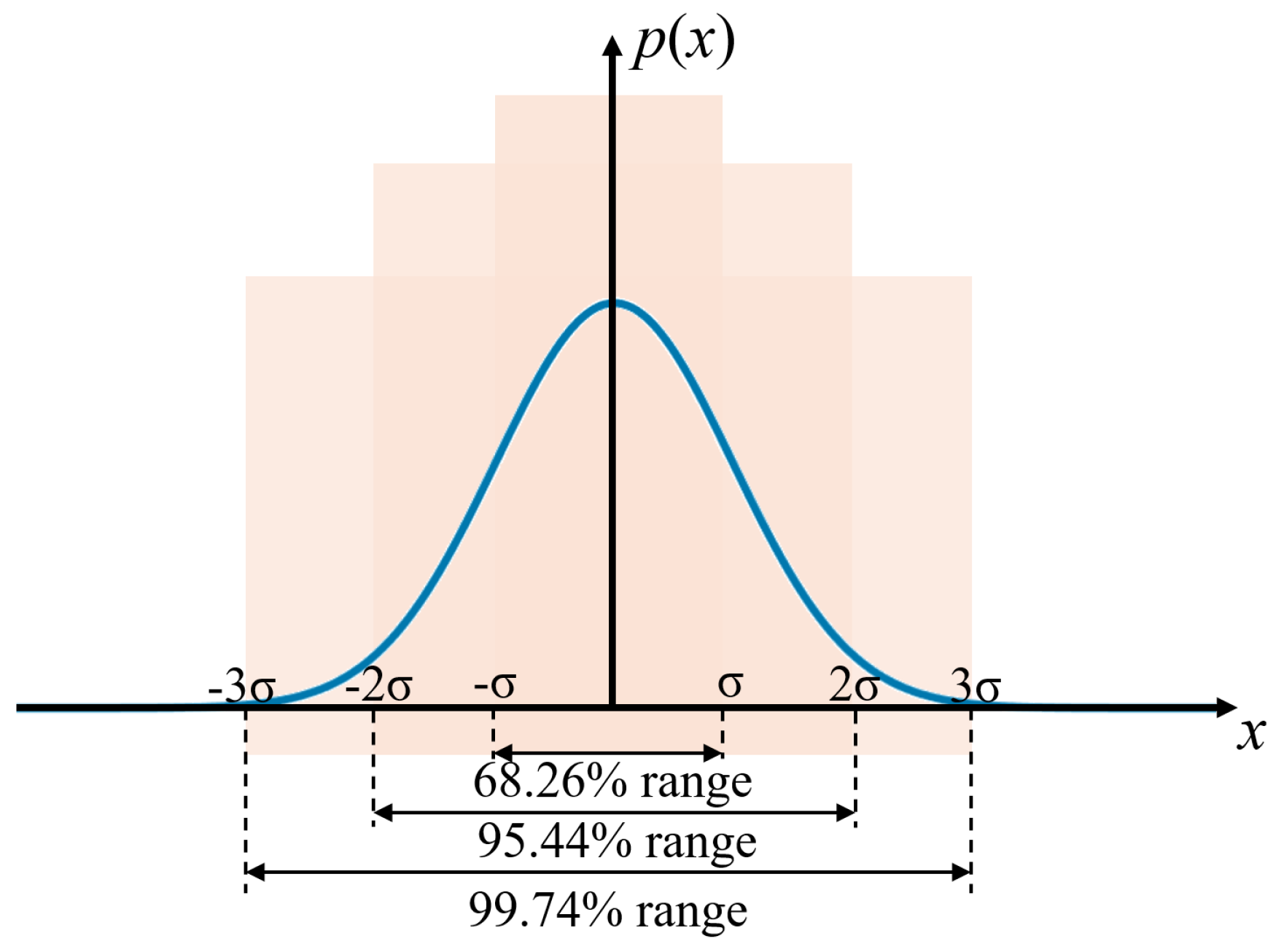
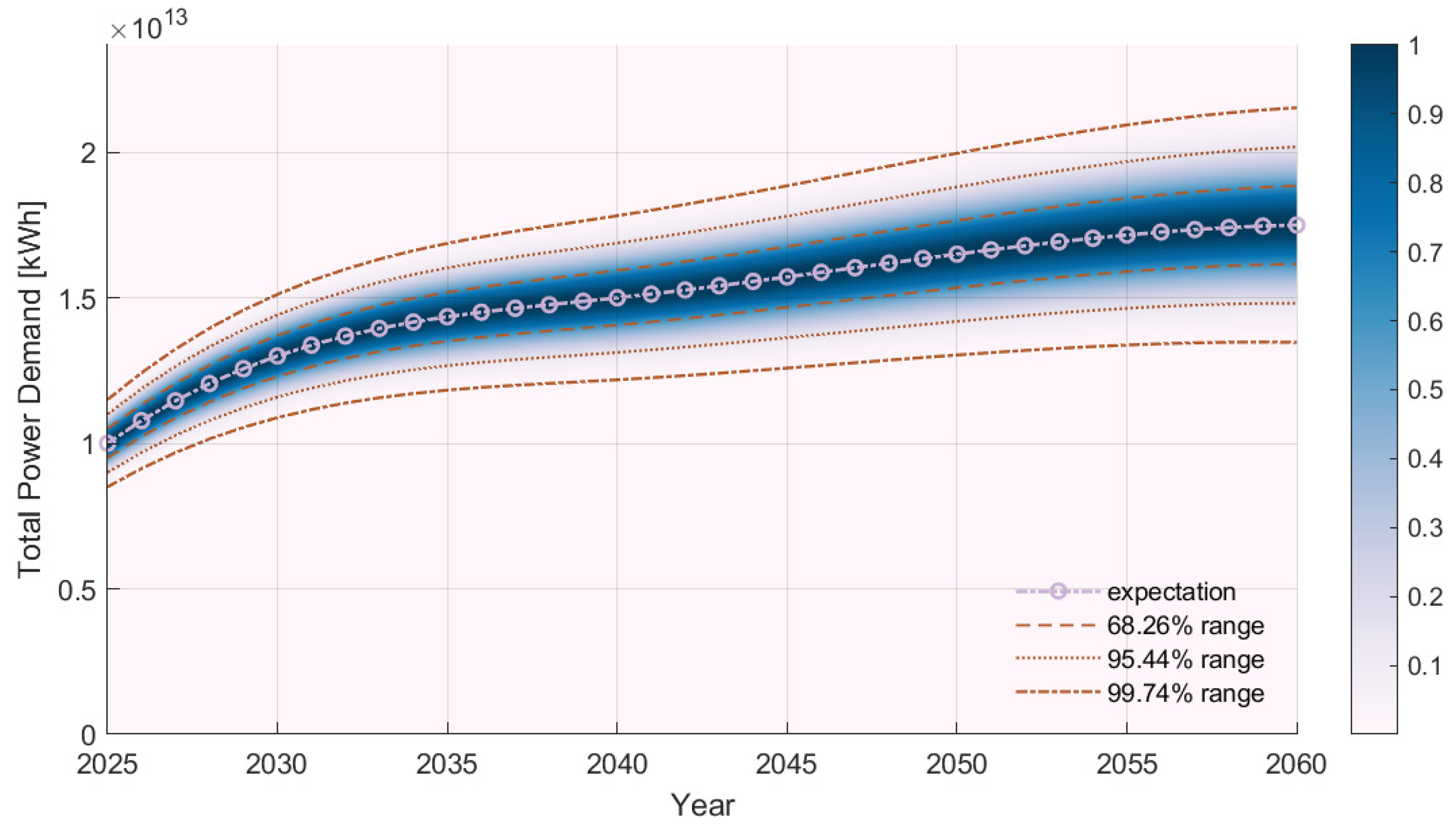
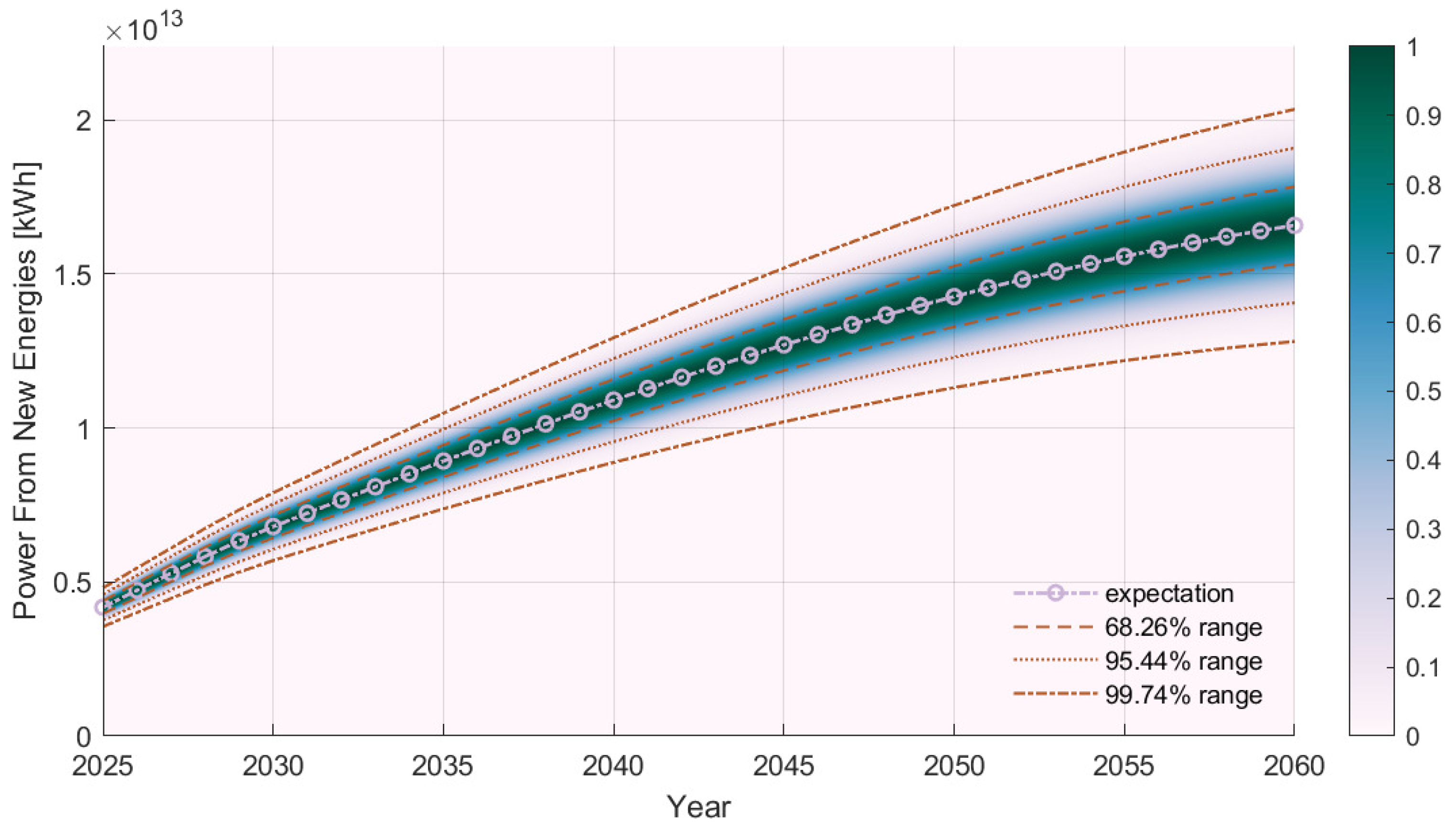


| Attribute | Scoring Type | Scoring for Unit Sorting |
|---|---|---|
| Start year | Quantitative | age < 1985→0; age ∈ [1985, 2025]→[0, 1]; |
| age > 2025→1 | ||
| Installed capacity | Quantitative | |
| CCUS | Categorical | Yes→10; No→0 |
| Combustion Type | Categorical | Ultra-Super→4; Supercritical→3; |
| Subcritical→2; Others→1 |
| Index | 2025 | 2030 | 2040 | 2050 | 2060 | Refs. 3 | |
|---|---|---|---|---|---|---|---|
| National Power demand | / | 10.0 1 | 13.0 | 15.0 | 16.5 | 17.5 | [61,62,63] |
| Wind | 1 | 0.93 | 1.65 | / 2 | / | 6.07 | [64,65] |
| Photovoltaic | 2 | 0.52 | 1.47 | / | / | 3.39 | [64,65] |
| Hydro | 3 | 1.50 | 1.88 | / | 2.51 | 2.58 | [57,61] |
| Nuclear | 4 | 0.54 | 0.94 | / | 2.55 | 3.00 | [66] |
| Biomass | 5 | 0.24 | 0.33 | / | / | 0.66 | [67] |
| Gas | 6 | 0.39 | 0.48 | / | 0.85 | 0.83 | [61,68] |
| Other Energy 4 | 7 | 0.05 | / | / | / | 0.05 | / |
| Parameter | I.U. 1 | A.U. 2 | Parameter | I.U. | A.U. |
|---|---|---|---|---|---|
| 15% | 5% | 15% | 5% | ||
| 30% | 0% | 30% | 20% | ||
| 30% | 20% | 30% | 20% | ||
| 30% | 20% | CCUS | 0% | 20% |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 0.99 | 0.995 | 0.99 | |||
| 1.2 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Wang, W.; Chang, C.; Wang, Z. A Stochastic Process-Based Approach for Power System Modeling and Simulation: A Case Study on China’s Long-Term Coal-Fired Power Phaseout. Sustainability 2025, 17, 2303. https://doi.org/10.3390/su17052303
Yang R, Wang W, Chang C, Wang Z. A Stochastic Process-Based Approach for Power System Modeling and Simulation: A Case Study on China’s Long-Term Coal-Fired Power Phaseout. Sustainability. 2025; 17(5):2303. https://doi.org/10.3390/su17052303
Chicago/Turabian StyleYang, Rui, Wensheng Wang, Chuangye Chang, and Zhuoqi Wang. 2025. "A Stochastic Process-Based Approach for Power System Modeling and Simulation: A Case Study on China’s Long-Term Coal-Fired Power Phaseout" Sustainability 17, no. 5: 2303. https://doi.org/10.3390/su17052303
APA StyleYang, R., Wang, W., Chang, C., & Wang, Z. (2025). A Stochastic Process-Based Approach for Power System Modeling and Simulation: A Case Study on China’s Long-Term Coal-Fired Power Phaseout. Sustainability, 17(5), 2303. https://doi.org/10.3390/su17052303





