Research on Stochastic Evolution Game of Green Technology Innovation Alliance of Government, Industry, University, and Research with Fuzzy Income
Abstract
1. Introduction
2. Literature Review
2.1. Game Model of GIUR
2.2. The Stochastic Evolutionary Game Model
2.3. A Game Model with Fuzzy Numbers
3. Theoretical Analysis and Model Construction
3.1. The Basic Knowledge of Fuzzy Numbers
3.2. Problem Description and Model Construction
3.2.1. Description and Analysis of the Game Problem of the GIUR Alliance with Fuzzy Numbers
3.2.2. The Evolution Game Model of the GIUR Considering Reputation Gains
3.2.3. The Stochastic Evolution Game Model of the GIUR Alliance Considering Reputation Gains
4. Model Stability Analysis
4.1. Analysis of Strategic Nash Equilibrium Solution of the GIUR League Game with Triangular Fuzzy Numbers
4.2. Analysis of Nash Equilibrium Solution of Stochastic Evolutionary Game Model of the GIUR Alliance Game
5. Numerical Simulation
5.1. Stochastic Taylor Expansion of Replicated Dynamic Equations
5.2. Variable Sensitivity Analysis
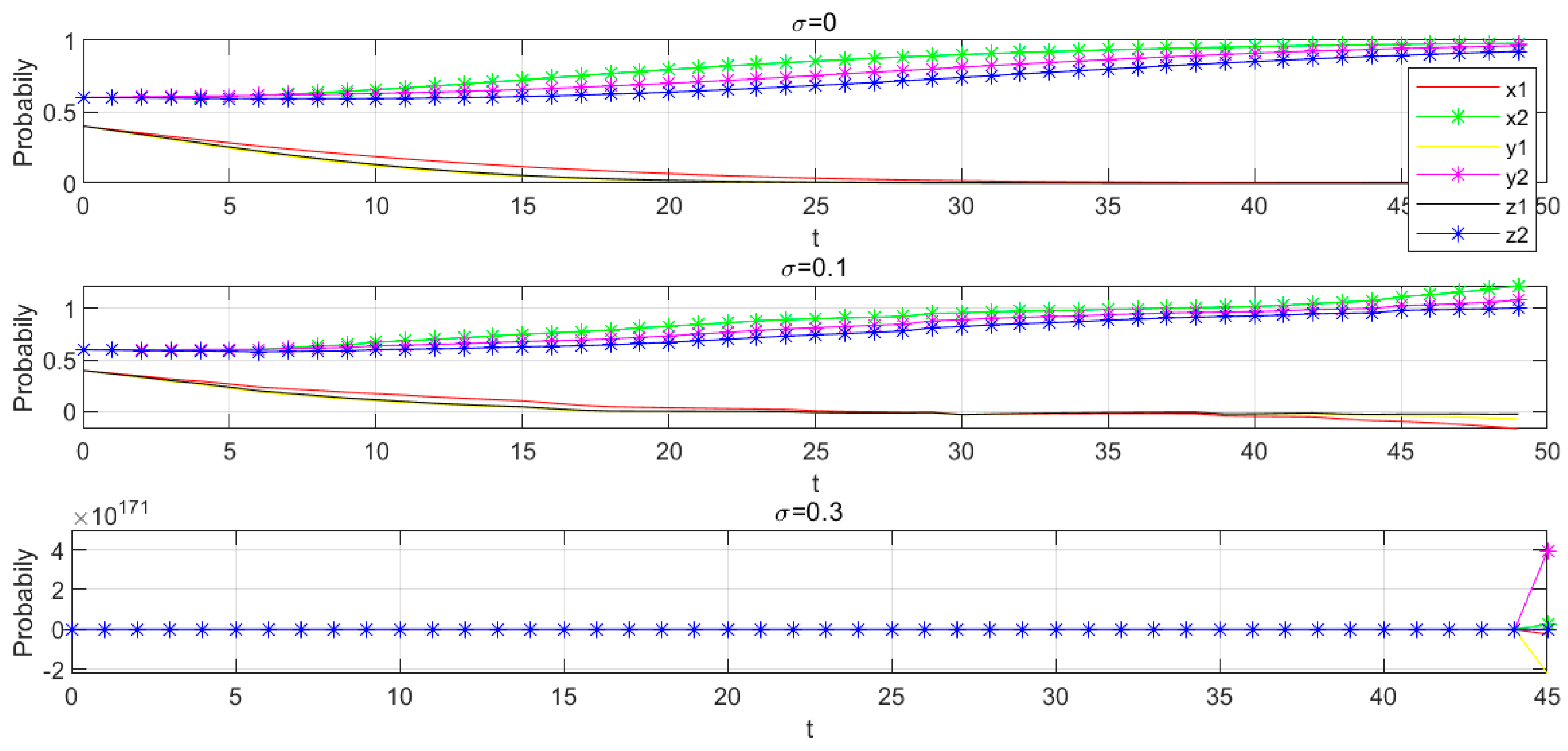
5.2.1. Random Interference Intensity
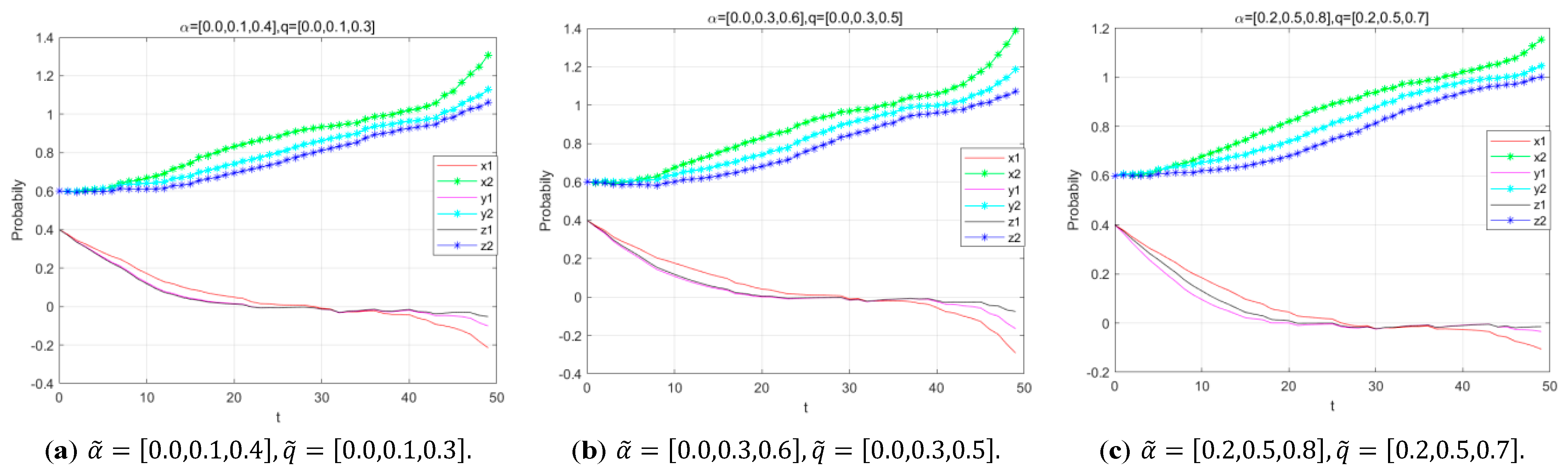
5.2.2. Influence of Reputation Gains on the Evolution Process
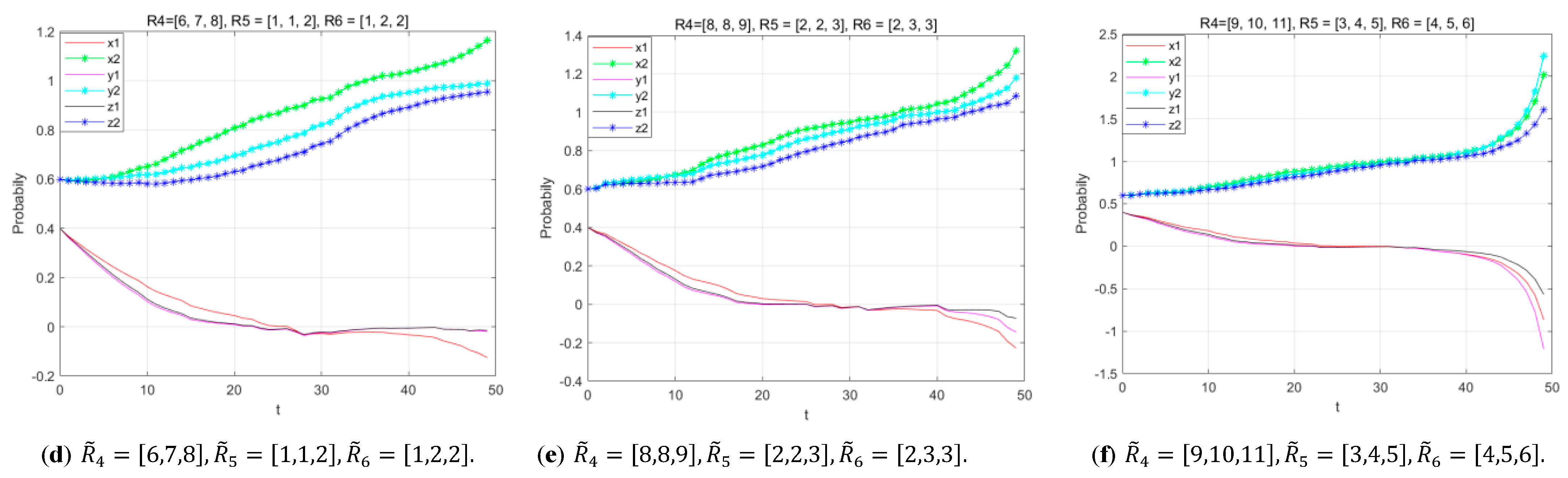
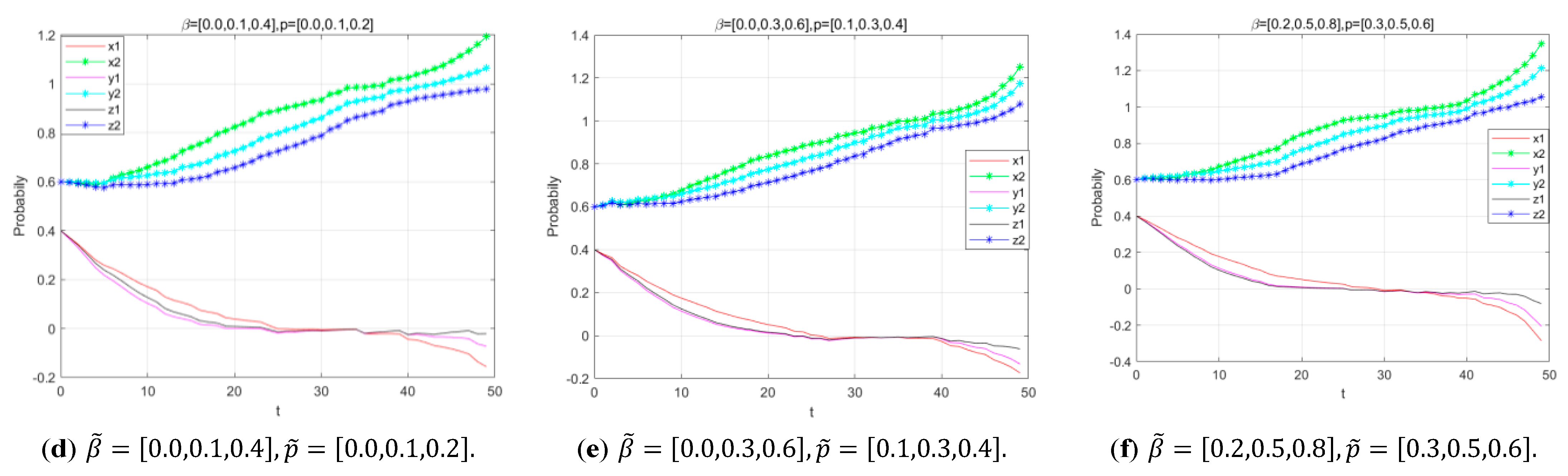
5.2.3. Influence of Product Greenness on Evolution Process
5.2.4. The Influence of the Capabilities of Industry and the UR on the Evolution Process
6. Conclusions and Discussion
6.1. Discussion
6.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Binmore, Ken. Playing for Real: A Text on Game Theory. 2007. Available online: https://api.semanticscholar.org/CorpusID:63932187 (accessed on 10 September 2024).
- Smith, J.M.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Nie, L.; Zhang, L. Evolutionary Game Analysis and Simulation of Government and Pollutant Discharge Enterprises in Green Technology Innovation. Econ. Issues 2019, 10, 79–86. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, L.; Xue, L.; Zhou, Y. How do low-carbon policies promote green diffusion among alliance-based firms in China? An evolutionary-game model of complex networks. J. Clean. Prod. 2019, 210, 518–529. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, M. The Stability of Industry-University-Research Innovation Alliance Based on Evolutionary Game. Oper. Res. Manag. Sci. 2020, 29, 67–73. (In Chinese) [Google Scholar] [CrossRef]
- Etzkowitz, H.; Leydesdorff, L. The dynamics of innovation: From National Systems and “Mode 2” to a Triple Helix of university–industry–government relations. Res. Policy 2000, 29, 109–123. [Google Scholar] [CrossRef]
- Senker, J. Rationale for Partnerships: Building National Innovation System. STI Rev. 1998, 23, 23–38. [Google Scholar]
- Fan, R.; Dong, L.; Yang, W.; Sun, J. Study on the optimal supervision strategy of government low-carbon subsidy and the corresponding efficiency and stability in the small-world network context. J. Clean. Prod. 2017, 168, 536–550. [Google Scholar] [CrossRef]
- Chen, W.; Hu, Z.-H. Using evolutionary game theory to study governments and manufacturers’ behavioral strategies under various carbon taxes and subsidies. J. Clean. Prod. 2018, 201, 123–141. [Google Scholar] [CrossRef]
- Chen, H.; Yang, Z.; Qi, K. Research on the Stability of the Green Technology Innovation Alliance of the Government, Industry, University and Research Institute under the Multi party Game Scenario. Oper. Res. Manag. 2021, 30, 108–114. (In Chinese) [Google Scholar]
- Cabrales, A. Stochastic replicator dynamics. Int. Econ. Rev. 2010, 41, 451–481. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionarily stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Holmes, S.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Xu, Y.; Hu, B.; Qian, R. Analysis on stability of strategic alliances based on stochastic evolutionary game including simulations. Syst. Eng.-Theory Pract. 2011, 31, 920–926. (In Chinese) [Google Scholar]
- Baker, C.T.; Buckwar, E. Exponential stability in p-th mean of solutions, and of convergent euler-type solutions, of stochastic delay differential equations. J. Comput. Appl. Math. 2004, 184, 404–427. [Google Scholar] [CrossRef]
- Fudenberg, D. Game Theory; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Gibbons, R. Game Theory for Applied Economists; Princeton University Press: Princeton, NJ, USA, 1992. [Google Scholar]
- Zhang, Y.; Yang, S.; Guo, J. Theoretical analyses of stochastic evolutionary game systems. EPL (Europhys. Lett.) 2022, 139, 12001. [Google Scholar] [CrossRef]
- Ramachandran, K.M.; Tsokos, C.P. Stochastic Differential Games. Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 2. [Google Scholar]
- Zhang, Q.; Yang, Y.; Liu, B. Research on operation strategy of online trading platform based on stochastic evolutionary game. Int. J. Innov. Comput. Inf. Control. 2022, 2, 18. [Google Scholar] [CrossRef]
- Wallace, C.; Young, H.P.; Li, J.; Ren, H.; Zhang, C.; Li, Q.; Duan, K. Stochastic evolutionary game dynamics. In Handbook of Game Theory with Economic Applications; Springer: Berlin/Heidelberg, Germany, 2015; Volume 4, pp. 327–380. [Google Scholar] [CrossRef]
- Li, J.; Ren, H.; Zhang, C.; Li, Q.; Duan, K. Substantive innovation or strategic innovation? Research on multiplayer stochastic evolutionary game model and simulation. Complexity 2020, 2020, 9640412. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Aubin, P.J. Coeur et valeur des jeux flous à paiments latéraux. C. R. I Acad. Sci. Paris Sér. A 1974, 279, 891–894. [Google Scholar]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems—Theory and Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Campos, L. Fuzzy linear programming models to solve fuzzy matrix games. Fuzzy Sets Syst. 1989, 32, 275–289. [Google Scholar] [CrossRef]
- Sakawa, M.; Nishizaki, I. Max-min solutions for fuzzy multi-objective matrix games. Fuzzy Sets Syst. 1994, 67, 53–69. [Google Scholar] [CrossRef]
- Buckley, J.J.; Jowers, L.J. Fuzzy Two-Person Zero-Sum Games; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Chavoshlou, A.S.; Khamseh, A.A.; Naderi, B. An optimization model of three-player payoff based on fuzzy game theory in green supply chain. Comput. Ind. 2019, 128, 782–794. [Google Scholar] [CrossRef]
- Figueroa-García, J.C.; Mehra, A.; Chandra, S. Optimal solutions for group matrix games involving interval-valued fuzzy numbers. Fuzzy Sets Syst. 2018, 362, 55–70. [Google Scholar] [CrossRef]
- Maeda, T. Characterization of the equilibrium strategy of the bi-matrix game with fuzzy payoff. J. Math. Anal. Appl. 2000, 251, 885–896. [Google Scholar] [CrossRef]
- Maeda, T. On characterization of equilibrium strategy of two-person zero-sum games with fuzzy payoffs. Fuzzy Sets Syst. 2003, 139, 283–296. [Google Scholar] [CrossRef]
- Monroy, L.; Hinojosa, M.; Mármol, A.; Fernández, F. Set-valued cooperative games with fuzzy payoffs. The fuzzy assignment game. Eur. J. Oper. Res. 2013, 225, 85–90. [Google Scholar] [CrossRef]
- Gu, C.; Wang, X.; Zhao, J.; Ding, R.; He, Q. Evolutionary game dynamics of moran process with fuzzy payoffs and its application. Appl. Math. Comput. 2020, 378, 125227. [Google Scholar] [CrossRef]
- Sun, L.; Sun, S.R. Cooperation mechanism research for joint regional air pollution control of Beijing-Tianjin-Hebei based on the fuzzy game behavior. Operat. Res. Manag. Sci. 2017, 26, 48–53. [Google Scholar]
- Wang, S.N.; Hu, Z.H. Modeling green supply chain games considering retailer’s risk preference in fuzzy environment. Control. Decis. 2019, 10, 1–13. [Google Scholar]
- Yang, D.Y.; Liu, J. Game analysis of government and green manufacturer based on fuzzy number. Operat. Res. Manag. Sci. 2016, 25, 85–92. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, Y.; Fan, Z. A practical method for sorting triangular fuzzy number complementary judgment matrix. Syst. Eng. 2002, 20, 89–92. (In Chinese) [Google Scholar]
- Chang, D.-Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Xu, Y.J.; Da, Q.L. Linear objective programming method for ranking interval mixed judgment matrices. Syst. Eng. Electron. 2008, 30, 1079–1085. (In Chinese) [Google Scholar]
- Moore, R.E. Methods and Applications of Interval Analysis; SIAM: Philadelphia, PA, USA, 1979. [Google Scholar]
- Ma, Y.; Wan, Z.; Jin, C. Evolutionary Game Analysis of Green Production Supervision Considering Limited Resources of the Enterprise. Pol. J. Environ. Stud. 2021, 30, 1715–1724. [Google Scholar] [CrossRef]
- Qian, Y.; Yu, X.-A.; Chen, X.; Song, M. Research on stability of major engineering technology innovation consortia based on evolutionary game theory. Comput. Ind. Eng. 2023, 186, 109734. [Google Scholar] [CrossRef]
- Liang, H.; Cui, Y.; Ren, X.; Wang, X. Almost sure exponential stability of two-strategy evolutionary games with multiplicative noise. Inf. Sci. 2021, 579, 888–903. [Google Scholar] [CrossRef]
- Yu, J. Selected Lectures on Game Theory; Science Press: Alexandria, NSW, Australia, 2014. (In Chinese) [Google Scholar]
- Yang, H.; Mo, J. Research on the bidding behavior of generation-side enterprises based on stochastic evolutionary games. IEEE Trans. Power Syst. 2022, 37, 3693–3703. [Google Scholar] [CrossRef]
- Zhu, Q.; Zheng, K.; Wei, Y. Three-party stochastic evolutionary game analysis of reward and punishment mechanism for green credit. Discret. Dyn. Nat. Soc. 2021, 2021, 5596015. [Google Scholar] [CrossRef]
- Feng, T.-J.; Li, C.; Zheng, X.-D.; Lessard, S.; Tao, Y. Stochastic replicator dynamics and evolutionary stability. Phys. Rev. E 2022, 105, 044403. [Google Scholar] [CrossRef]
- Dong, C.; Liu, J.; Mi, J. How to enhance data sharing in digital government construction: A tripartite stochastic evolutionary game approach. Systems 2023, 11, 212. [Google Scholar] [CrossRef]
- Wei, F.; Cai, Y. Existence, uniqueness and stability of the solution to neutral stochastic functional differential equations with infinite delay under non-Lipschitz conditions. Adv. Differ. Equ. 2013, 2013, 151. [Google Scholar] [CrossRef]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Abbas, H.; Zhao, L.; Gong, X.; Jiang, M.; Faiz, T. Environmental and economic influences of postharvest losses across the fish-food products supply chain in the developing regions. Environ. Dev. Sustain. 2023, 26, 28335–28366. [Google Scholar] [CrossRef]
- Abbas, H.; Zhao, L.; Gong, X.; Jiang, M.; Faiz, N. Environmental effects on perishable product quality and trading under OBOR supply chain different route scenarios. Environ. Sci. Pollut. Res. 2022, 29, 68016–68034. [Google Scholar] [CrossRef]
- Geng, Y.; Chen, J.; Liu, T.; Tao, D. Public environmental attention, media coverage, and corporate green innovation: Evidence from heavily polluting industries in China. Environ. Sci. Pollut. Res. 2023, 30, 86911–86926. [Google Scholar] [CrossRef]
- Song, Z.; He, S.; Wang, Y.; An, J. Green pharmaceutical supply chain coordination considering green investment, green logistics, and government intervention. Environ. Sci. Pollut. Res. 2022, 29, 63321–63343. [Google Scholar] [CrossRef]
- Singh, A.; Srivastava, Y. Cutting-edge developments in the field of green innovation and diffusion of green technology. In Patent Law, Green Technology and Innovation; Routledge: Abingdon, UK, 2022. [Google Scholar]
- Hotte, K. How to Accelerate Green Technology Diffusion? Directed Technological Change in the Presence of Coevolving Absorptive Capacity; Sorbonne Pantheon, Bielefeld University: Paris, France, 2019; pp. 61–65. [Google Scholar] [CrossRef]



| Define the Number | Define the Name | Mathematical Expressions | Ilustrate |
|---|---|---|---|
| Definition 1 | Fuzzy sets | is the membership degree of an element to a fuzzy set | |
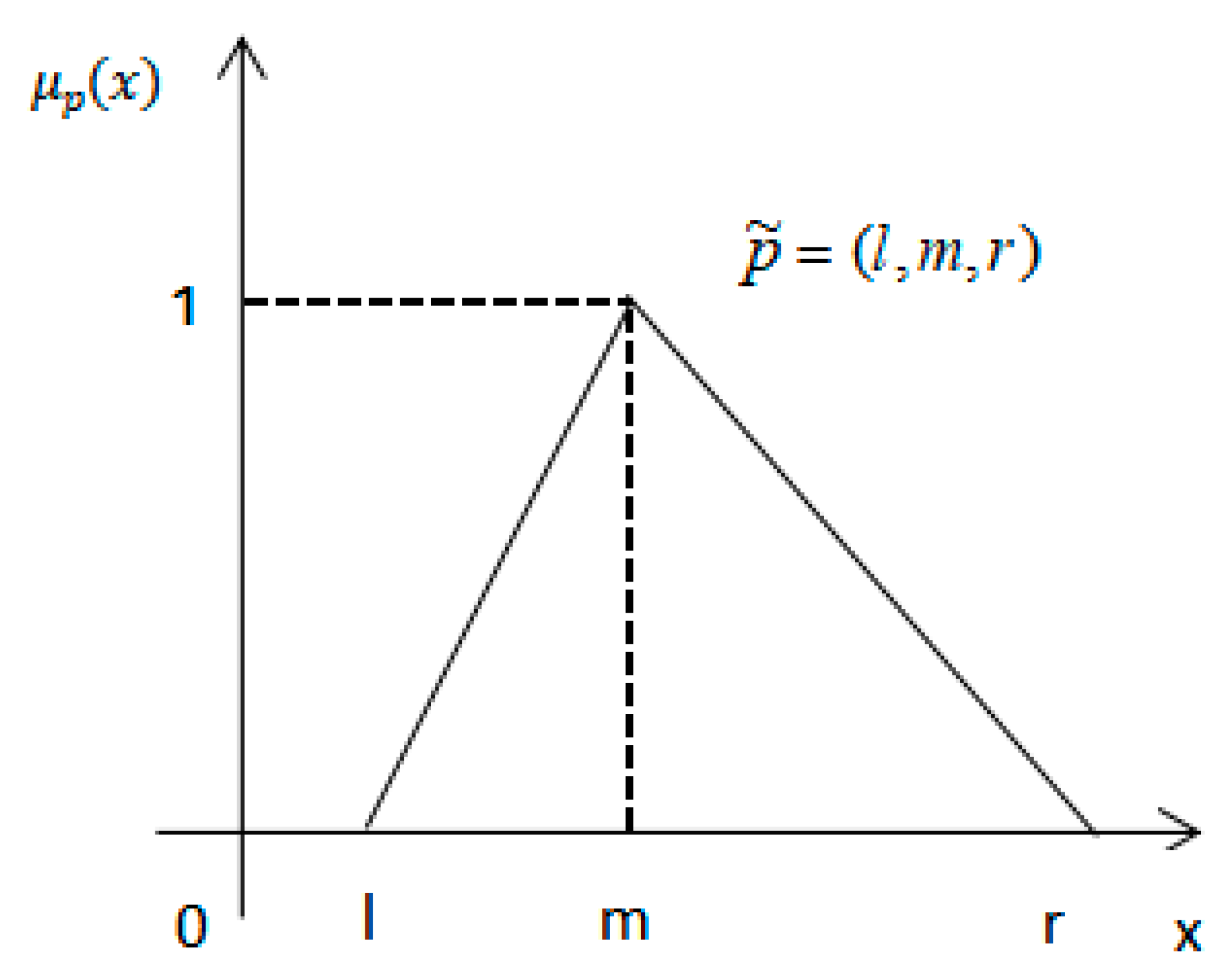
| Definition 2 | Trigonometric fuzzy number | , and are lower bound and upper bound, respectively, where , . In particular, as , degenerated into a real number , making . Then, is called thetriangular fuzzy number. | |
| Definition 3 | Rules for the operation of trigonometric fuzzy numbers | Addition: . Subtraction: . Multiplication: . Number multiplication: . Division: . | Arithmetic rules based on interval endpoints. |
| Definition 4 | Trigonometric fuzzy number comparison rules | The possibility of the of any two numbers. | |
| Definition 5 | Multiple triangular fuzzy numbers are compared to the rule | The possibility of . | |
| Definition 6 | Optimal strategy solution | , and needs to be satisfied . | The optimal pure strategy solution of the probability is sufficient and necessary. |
| Definition 7 | -cut set | is called the -cut set of . | |
| Definition 8 | Rules for the operation of interval number rules | (1) . (2) . (3) . (4) If , then . (5) . (6) If , then . (7) If , then ; if , then . | Including addition, negation, subtraction, reciprocal, multiplication, division, and number multiplication operations of interval numbers. |
| Definition 9 | Interval number comparison rules | , | This definition does not apply to the number of intervals where two intervals overlap. |
| Strategy Selection | Academia and Research Parties | ||||
|---|---|---|---|---|---|
| Actively Research and Develop (z) | Betray in the Middle (1 − z) | ||||
| Government | Supervise () | Companies | Cooperate () |
|
|
| Midway betray () |
|
| |||
| Not supervise () | Companies | Cooperate () | | | |
| Midway betray () | | | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Q.; Cui, H.; Yang, M.; Ling, C. Research on Stochastic Evolution Game of Green Technology Innovation Alliance of Government, Industry, University, and Research with Fuzzy Income. Sustainability 2025, 17, 2294. https://doi.org/10.3390/su17052294
Zhong Q, Cui H, Yang M, Ling C. Research on Stochastic Evolution Game of Green Technology Innovation Alliance of Government, Industry, University, and Research with Fuzzy Income. Sustainability. 2025; 17(5):2294. https://doi.org/10.3390/su17052294
Chicago/Turabian StyleZhong, Qing, Haiyang Cui, Mei Yang, and Cheng Ling. 2025. "Research on Stochastic Evolution Game of Green Technology Innovation Alliance of Government, Industry, University, and Research with Fuzzy Income" Sustainability 17, no. 5: 2294. https://doi.org/10.3390/su17052294
APA StyleZhong, Q., Cui, H., Yang, M., & Ling, C. (2025). Research on Stochastic Evolution Game of Green Technology Innovation Alliance of Government, Industry, University, and Research with Fuzzy Income. Sustainability, 17(5), 2294. https://doi.org/10.3390/su17052294






